2321中心对称[可修改版ppt]
合集下载
最新文档-23.2.1 中心对称-PPT精品文档

S A B C
3.如图所示,在下列四组图形中,右边图形与左边图形成中心对称的是 (1)(2)(3) .
4.如图所示,已知△ABC与△CDA关于AC的中点O成中心对称,添加一个条件
,使
AB=BC
四边形ABCD为菱形.
5.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的
解:如图所示
【方法技巧】 要画一个多边形关于已知点的对称图形,只要画出这个多边形的各 个顶点关于已知点的对称点,再顺次连接各点即可.
类型二:已知两个图形成中心对称,找它们的对称中心 例2 如图所示,△ABC和△DEF是成中心对称的两个三角形,请找出它们的对称中心.
【思路点拨】 分别连接两对对应点,交点就是所求.
23.2 中心对称 23.2.1 中心对称
1.认识中心对称
把一个图形绕着某一点旋转 180° ,如果它能够与另一个图形 重合 ,那么就说这
两个图形关于这个点对称或 中心对称 合的对应点叫做关于对称中心的
对称点 2.中心对称的性质
,这个点叫做 对称中心 ,旋转后能够重 .
中心对称的两个图形,对称点所连线段都经过 .中心对称的两个图形是
坐标是
.
(3,-1)
点击进入 课后训练
解:如图所示.
1.下列说法中正确的有( C ) (A)全等的两个图形成中心对称 (B)成中心对称的两个图形必须重合 (C)成中心对称的两个图形全等 (D)旋转后能够重合的两个图形成中心对称 2.如图所示,△ABC与△A′B′C′是成中心对称的两个图形,则下列说法不正确 的是( ) (A)AB=AD′B′,BC=B′C′ (B)AB∥A′B′,BC∥B′C′ (C)S△ABC= (D)△ABC≌△A′OC′
3.如图所示,在下列四组图形中,右边图形与左边图形成中心对称的是 (1)(2)(3) .
4.如图所示,已知△ABC与△CDA关于AC的中点O成中心对称,添加一个条件
,使
AB=BC
四边形ABCD为菱形.
5.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的
解:如图所示
【方法技巧】 要画一个多边形关于已知点的对称图形,只要画出这个多边形的各 个顶点关于已知点的对称点,再顺次连接各点即可.
类型二:已知两个图形成中心对称,找它们的对称中心 例2 如图所示,△ABC和△DEF是成中心对称的两个三角形,请找出它们的对称中心.
【思路点拨】 分别连接两对对应点,交点就是所求.
23.2 中心对称 23.2.1 中心对称
1.认识中心对称
把一个图形绕着某一点旋转 180° ,如果它能够与另一个图形 重合 ,那么就说这
两个图形关于这个点对称或 中心对称 合的对应点叫做关于对称中心的
对称点 2.中心对称的性质
,这个点叫做 对称中心 ,旋转后能够重 .
中心对称的两个图形,对称点所连线段都经过 .中心对称的两个图形是
坐标是
.
(3,-1)
点击进入 课后训练
解:如图所示.
1.下列说法中正确的有( C ) (A)全等的两个图形成中心对称 (B)成中心对称的两个图形必须重合 (C)成中心对称的两个图形全等 (D)旋转后能够重合的两个图形成中心对称 2.如图所示,△ABC与△A′B′C′是成中心对称的两个图形,则下列说法不正确 的是( ) (A)AB=AD′B′,BC=B′C′ (B)AB∥A′B′,BC∥B′C′ (C)S△ABC= (D)△ABC≌△A′OC′
2321中心对称1课件

可持续发展理念的融入
未来中心对称的应用将更加注重与可 持续发展理念的结合,推动绿色、环 保、节能等方面的发展。
THANKS 感谢观看
且图形关于该轴对称。
02 中心对称在数学领域应用
几何问题中心对称解法
1 2 3
利用中心对称性质简化几何图形
通过找到图形的中心对称点,可以将复杂的几何 图形简化为更易于分析和解决的图形。
解决几何证明问题
利用中心对称的性质,可以证明一些几何定理和 性质,如等腰三角形的性质、平行四边形的性质 等。
求解几何最值问题
生物体的组织结构也常表现出中 心对称性,如人体左右对称的器 官布局。
生物遗传信息传递过程中中心对称作用
DNA双螺旋结构的中心对称
DNA的双螺旋结构具有中心对称性,这种结构保证了遗传信息的 稳定传递和复制。
遗传密码的中心对称
遗传密码中的碱基互补配对原则体现了中心对称性,确保了基因表 达的准确性和稳定性。
三角函数在解三角形中的应用
03
在解三角形时,利用三角函数的中心对称性质可以简化计算过
程,提高解题效率。
03 中心对称在物理学中应用
光学现象中心对称原理
光的反射和折射
当光线遇到平滑表面时,会遵循 反射定律,反射光线与入射光线 关于法线对称;折射现象中,折 射光线与入射光线也呈现一定的
对称性。
干涉和衍射
晶体结构中心对称性描述
晶体结构的对称性分析
通过对晶体结构的观察和计算,判断其是否具有中心对称性。
对称中心的确定
确定晶体结构的对称中心,即找到一个点,使得晶体结构关于该点对称。
对称性的分类
根据对称中心的性质和数量,对晶体结构的对称性进行分类,如点对称、面对称等。同时 ,还可以根据晶体结构中原子排列的周期性,进一步描述其对称性特征。
23.2.1 中心对称(共43张PPT)
15 8
2
OF
15 8
同理OE 15 ,即 OF OE OF 15
8
4
A
D
C′
D′
O 重合
B′
A′
B
C
(4)将平行四边形ABCD绕中心O逆时针旋 转180°,这两个图形有怎样的位置关系?
有的轴对称, 有的重合。
绕中心旋转180°,旋转后的图 形与原图的位置关系有什么不同?
教学目标
【知识与能力】
了解中心对称、对称中心、关于中心的对称 点等概念。 通过具体实例认识两个图形关于某一点成中 心对称的本质:就是一个图形绕一点旋转180° 而成。 作出中心对称的图形。
它是轴对称图形吗? 不是轴对称图形。
这个图形是否能够通过某种图形运动与自 身重合?
探究
下列图形是否能够通过某种图形运动与自
身重合?图旋Biblioteka 形转绕后中与
线段绕中点旋转180°
心原 旋图
旋转后与原图重合
转重
180 合
°
知识要点
把一个图形绕着某一个点旋转180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对称 (central symmetry),这个点叫做对称中 心。这两个图形中的对应点叫做关于中心 的对称点。
经历对日常生活中与中心对称有关的图形进行 观察、分析、欣赏、动手操作、画图等过程,发 展审美能力,增强对图形的欣赏意识。
从图形变化过程中,树立正确的辩证唯物主义 观点。
认识几何图形的对称美,培养学生热爱数学, 热爱生活。
教学重难点
利用中心对称、对称中心、关于中心的 对称点的概念解决一些问题。 从一般旋转中导入中心对称。 中心对称的性质及初步应用。 中心对称与旋转之间的关系。
人教版九级数学上册2321 中心对称新课课件(共24张PPT)[可修改版ppt]
![人教版九级数学上册2321 中心对称新课课件(共24张PPT)[可修改版ppt]](https://img.taocdn.com/s3/m/18fee323172ded630a1cb607.png)
折叠后与另一图形重合 对应点的连线被对称轴垂直平分
你知道旋转的性质吗?
旋转的性质
对应点到旋转中心的距离相等 对应点与旋转中心所连线段的夹角等于旋转角
旋转前、后的图形全等
情景1
• 观察下面的2组图形,看一看各组中2个图形
No 的形状、大小是否相同?怎样将一个图形旋
转得到另一个图形?
Image
情景2
(2)画一个图形关于某点的对称图形的画法是:
先画出图形中的几个特殊点(线段的端点、如多 边形的顶点、圆的圆心等)关于某点的对称点,然后 再顺次连结有关对称点即可。
课堂练习
1、如图,已知等边△ABC和点O,画△ A' B' C‘ 使△A′B′C′和△ABC关于点O成中心对称.
A
C′
B′
O
B
C
A′
2、画一个与已知四边形ABCD中心对称图形。
(村庄)在不改变AB两点之间的距离的情况下,移
动到适当位置。首先在河塘岸边适当的位置取一点C
(如下图),连接AC、BC(使保持AC、BC不经过河 塘),分别将
AC、BC延长到点A’、B’,使A’CAC, B’CBC;这样即是作线段AB
关于点C的中心对
称图形A’B’,根据中心对称的特征有
A’B’AB,所以测出A’、B’两点间的距
人教版九年级数 学上册2321 中 心对称新课课件 (共24张PPT)
学习目标
1.掌握中心对称的定义,理解中心对称 的性质. 2.能够依据中心对称的性质解决相关作 图问题. 学习重点: 中心对称的定义与性质 学习难点: 图以及利用性质解决问题
你知道轴对称吗?
轴对 称
有一条对称轴——直线 图形沿对称轴对折(翻折180°)后重合
你知道旋转的性质吗?
旋转的性质
对应点到旋转中心的距离相等 对应点与旋转中心所连线段的夹角等于旋转角
旋转前、后的图形全等
情景1
• 观察下面的2组图形,看一看各组中2个图形
No 的形状、大小是否相同?怎样将一个图形旋
转得到另一个图形?
Image
情景2
(2)画一个图形关于某点的对称图形的画法是:
先画出图形中的几个特殊点(线段的端点、如多 边形的顶点、圆的圆心等)关于某点的对称点,然后 再顺次连结有关对称点即可。
课堂练习
1、如图,已知等边△ABC和点O,画△ A' B' C‘ 使△A′B′C′和△ABC关于点O成中心对称.
A
C′
B′
O
B
C
A′
2、画一个与已知四边形ABCD中心对称图形。
(村庄)在不改变AB两点之间的距离的情况下,移
动到适当位置。首先在河塘岸边适当的位置取一点C
(如下图),连接AC、BC(使保持AC、BC不经过河 塘),分别将
AC、BC延长到点A’、B’,使A’CAC, B’CBC;这样即是作线段AB
关于点C的中心对
称图形A’B’,根据中心对称的特征有
A’B’AB,所以测出A’、B’两点间的距
人教版九年级数 学上册2321 中 心对称新课课件 (共24张PPT)
学习目标
1.掌握中心对称的定义,理解中心对称 的性质. 2.能够依据中心对称的性质解决相关作 图问题. 学习重点: 中心对称的定义与性质 学习难点: 图以及利用性质解决问题
你知道轴对称吗?
轴对 称
有一条对称轴——直线 图形沿对称轴对折(翻折180°)后重合
人教版九级数学上册2321中心对称共59张PPT[可修改版ppt]
![人教版九级数学上册2321中心对称共59张PPT[可修改版ppt]](https://img.taocdn.com/s3/m/0b0e0d1d360cba1aa911da4d.png)
3 翻转后和另一个图形重合 旋转后和另一个图形重合
探究 旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;
第三步,移开三角板.
画出的△ABC与△A′B′C′ 关于点O对称.分别连接对称点 AA′、BB′、CC′。点O 在线段AA′上吗?如果在, 在什么位置? △ABC与△A′B′C′有 什么关系?
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
有什么发现?
新课讲解
点把A一绕个着图点形O绕旋着转某18个0 点°后与
B`
关的于对点应O点对叫称做,关点于O是中对心称的中对心称。点。
(先看动画)
C
180°
)12600°°
O
B
中心如对图称:与对轴应对点A称和的A`区、B别和:B`、 C`
A
C和C`是关于中心O的对称点。
A
C1
B1
B
轴对称
O
人教版九级上册数学 2321 中心对称教学课件(共35张PPT)[可修改版ppt]
![人教版九级上册数学 2321 中心对称教学课件(共35张PPT)[可修改版ppt]](https://img.taocdn.com/s3/m/7188789cfab069dc51220149.png)
则得A的对称点A'
A O
连结BO,在BO的延长线上截取O B' =OB,
则得B的对称点B'
A'
连结 A' B' ,则线段A' B'是所求的线
B
段
例1 (3).如图.选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
怎么办?可以帮 帮我吗? B′
A′
C′
△A′B′C′即为所求的三角形。
AAʹ
CCʹ
BBʹ
O
B
C
A
合作探究:
旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋
转180°,画出△A′B′C′;
第三步,移开三角板.
很显然画出的△ABC与
△AʹBʹCʹ关于点O对称. 分别连接AAʹ,BBʹ,CCʹ。 Aʹ
点O在线段AA′上吗?
二、创设情境,导入新课
问题1 (1)如图,把其中一个图案绕点 O 旋转 180°,你有什么发现?
两个图案能够完全重合在一起.
O
问题1 (2)如图,线段 AC,BD 相交于点 O,OA =OC,OB=OD.把 △OCD 绕点 O 旋转 180°,你有什 么发现?
两个图案能够完全重合在一起.
A
D
O
B
一、回顾旧知
旋转的定义
在平面内,把一个图形绕一个 定点,沿某个方向转动一个角度, 像这样的图形变换称作旋转 这个定点称为旋转中心 所转动的角称为旋转角
旋转三要素
旋转中心、旋转方向、
旋转角度
旋转的基本性质
1、旋转前后的图形全等 2、对应点到旋转中心的距离相等 3、对应点与旋转中心连线的夹角
2024年度2321中心对称(课件)

2321中心对称(课件 )
THE FIRST LESSON OF THE SCHOOL YEAR
2024/3/23
1
2024/3/23
目录CONTENTS
• 中心对称基本概念 • 中心对称与轴对称关系 • 中心对称在几何变换中应用 • 坐标系中的中心对称问题 • 拓展延伸:复杂图形中的中心对称
问题 • 总结回顾与课堂互动环节
策略一
识别并利用已知的中心对称图形 。在复杂图形中找出明显的中心 对称部分,并以此为出发点进行
解题。
策略二
通过添加辅助线构造中心对称图 形。当复杂图形中没有明显的中 心对称部分时,可以尝试通过添 加辅助线来构造出中心对称图形
,从而简化问题。
策略三
利用中心对称性质进行证明或计 算。在解题过程中,充分利用中 心对称图形的性质,如面积相等 、线段相等或角度相等,来进行
在平面内,将一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个 图形关于这条直线对称。翻折前后图形全等,对应点连线被对称轴垂直平分。
14
利用中心对称性质解题技巧
确定对称中心
根据题目条件,确定图 形的对称中心。
2024/3/23
找出对称点
根据中心对称的性质, 找出图形上关键点的对
称点。
图形2
平行四边形ABCD,其对称中心 为两条对角线AC和BD的交点O, 旋转180度后A与C重合,B与D重 合。
7
中心对称在生活中的应用
建筑设计
标志设计
中心对称在建筑设计中常被用来创造平衡 和和谐的美感,如对称的门窗设计、庭院 布局等。
许多标志和徽章采用中心对称设计,以确 保其在任何方向都保持一致的视觉效果, 如国徽、公司标志等。
THE FIRST LESSON OF THE SCHOOL YEAR
2024/3/23
1
2024/3/23
目录CONTENTS
• 中心对称基本概念 • 中心对称与轴对称关系 • 中心对称在几何变换中应用 • 坐标系中的中心对称问题 • 拓展延伸:复杂图形中的中心对称
问题 • 总结回顾与课堂互动环节
策略一
识别并利用已知的中心对称图形 。在复杂图形中找出明显的中心 对称部分,并以此为出发点进行
解题。
策略二
通过添加辅助线构造中心对称图 形。当复杂图形中没有明显的中 心对称部分时,可以尝试通过添 加辅助线来构造出中心对称图形
,从而简化问题。
策略三
利用中心对称性质进行证明或计 算。在解题过程中,充分利用中 心对称图形的性质,如面积相等 、线段相等或角度相等,来进行
在平面内,将一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个 图形关于这条直线对称。翻折前后图形全等,对应点连线被对称轴垂直平分。
14
利用中心对称性质解题技巧
确定对称中心
根据题目条件,确定图 形的对称中心。
2024/3/23
找出对称点
根据中心对称的性质, 找出图形上关键点的对
称点。
图形2
平行四边形ABCD,其对称中心 为两条对角线AC和BD的交点O, 旋转180度后A与C重合,B与D重 合。
7
中心对称在生活中的应用
建筑设计
标志设计
中心对称在建筑设计中常被用来创造平衡 和和谐的美感,如对称的门窗设计、庭院 布局等。
许多标志和徽章采用中心对称设计,以确 保其在任何方向都保持一致的视觉效果, 如国徽、公司标志等。
23.2.1中心对称PPT教学课件
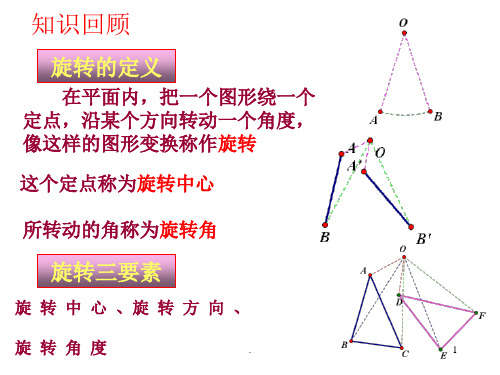
与已知四边形关于点O对称。
D
.
A’ B’
o
C
B
C’
D’
.
. A
画法:1. 连结AO并延长到A’,使OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点B’、C’、D’.
3. 顺次连结A’、B’、C’、D’各点. 四边形A’B’C’D’就是所求的四边形 . .
29
D
. A . B C` . D`
. 25
归纳性质
A C B O A' B' C'
(1)关于中心对称的两个图形是全等形; (2)关于中心对称的两个图形,对称点 所连线段都经过对称中心,而且被对称中 心平分.
. 26
灵活运用,体会内涵 1、点的中心对称点的作法 以点O为对称中心,作出点A的对称点A′;
A O A′
点A′即为所求的点
O
.
. B`
C
若点O是BC的中点呢?
A`
∴四边形 A`B`C`D是 所求的四 边形。
30
. D` . C` . A . B`
`
.
若点O与点A 重合呢?
∴四边形A`B`C`D`就是 所求的四边形。
31
如图,已知△ABC与△A’B’C’中心对称,求出它
们的对称中心O。 C A’ B A B’
C’
. 32
B’
A’ O C’ C B
A
这个点叫作对称中心
2个图形中的对应点叫做对称点
. 23
下图中△A′B′C′与△ABC 关于点O是成中心对称的, 你能从图中找到哪些等量 关系?
(1)OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′ .
D
.
A’ B’
o
C
B
C’
D’
.
. A
画法:1. 连结AO并延长到A’,使OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点B’、C’、D’.
3. 顺次连结A’、B’、C’、D’各点. 四边形A’B’C’D’就是所求的四边形 . .
29
D
. A . B C` . D`
. 25
归纳性质
A C B O A' B' C'
(1)关于中心对称的两个图形是全等形; (2)关于中心对称的两个图形,对称点 所连线段都经过对称中心,而且被对称中 心平分.
. 26
灵活运用,体会内涵 1、点的中心对称点的作法 以点O为对称中心,作出点A的对称点A′;
A O A′
点A′即为所求的点
O
.
. B`
C
若点O是BC的中点呢?
A`
∴四边形 A`B`C`D是 所求的四 边形。
30
. D` . C` . A . B`
`
.
若点O与点A 重合呢?
∴四边形A`B`C`D`就是 所求的四边形。
31
如图,已知△ABC与△A’B’C’中心对称,求出它
们的对称中心O。 C A’ B A B’
C’
. 32
B’
A’ O C’ C B
A
这个点叫作对称中心
2个图形中的对应点叫做对称点
. 23
下图中△A′B′C′与△ABC 关于点O是成中心对称的, 你能从图中找到哪些等量 关系?
(1)OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′ .
23.2.1中心对称_PPT
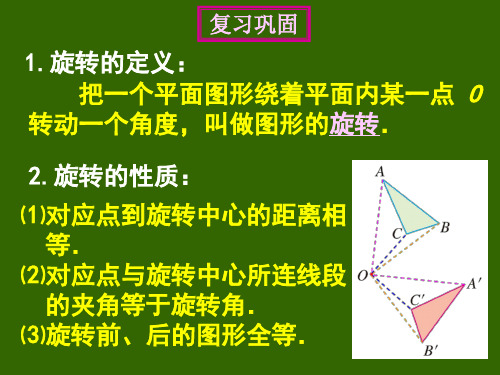
复习巩固
1.旋转的定义:
把一个平面图形绕着平面内某一点 O
转动一个角度,叫做图形的旋转.
2.旋转的性质:
⑴对应点到旋转中心的距离相 等.
⑵对应点与旋转中心所连线段 的夹角等于旋转角.
⑶旋转前、后的图形全等.
第二十三章 Biblioteka 转23.2 中心对称23.2.1中心对称
1.了解中心对称的概念
问题1(1)如图,把其中一个图案绕 点 O 旋转180°,你有什么发现?
(3)两个图形的关系?
(重合)
这个我点们对称称具或有中这心样对特称点.A的两个图形关D于 你能试着O给中心对称B下个定O义吗C?
中心对称的概念:
把一个图形绕着某一点旋转 180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对 称.这个点叫做对称中心.
这两个图形在旋转后能重合的对应点
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
1.了解中心对称的概念
问题3 中心对称与一般旋转的联系和区别?
联系:中心对称和一般的旋转都是绕 着某一点进行旋转;
区别:中心对称的旋转角度都是180°, 一般的旋转的旋转角度不固定,中心对称 是特殊的旋转.
叫做关于对称中心的对称点.A
D
O
B
C
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/62021/9/6Monday, September 06, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/62021/9/62021/9/69/6/2021 8:55:22 PM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/62021/9/62021/9/6Sep-216-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/62021/9/62021/9/6Monday, September 06, 2021
1.旋转的定义:
把一个平面图形绕着平面内某一点 O
转动一个角度,叫做图形的旋转.
2.旋转的性质:
⑴对应点到旋转中心的距离相 等.
⑵对应点与旋转中心所连线段 的夹角等于旋转角.
⑶旋转前、后的图形全等.
第二十三章 Biblioteka 转23.2 中心对称23.2.1中心对称
1.了解中心对称的概念
问题1(1)如图,把其中一个图案绕 点 O 旋转180°,你有什么发现?
(3)两个图形的关系?
(重合)
这个我点们对称称具或有中这心样对特称点.A的两个图形关D于 你能试着O给中心对称B下个定O义吗C?
中心对称的概念:
把一个图形绕着某一点旋转 180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对 称.这个点叫做对称中心.
这两个图形在旋转后能重合的对应点
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
1.了解中心对称的概念
问题3 中心对称与一般旋转的联系和区别?
联系:中心对称和一般的旋转都是绕 着某一点进行旋转;
区别:中心对称的旋转角度都是180°, 一般的旋转的旋转角度不固定,中心对称 是特殊的旋转.
叫做关于对称中心的对称点.A
D
O
B
C
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/62021/9/6Monday, September 06, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/62021/9/62021/9/69/6/2021 8:55:22 PM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/62021/9/62021/9/6Sep-216-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/62021/9/62021/9/6Monday, September 06, 2021
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2321中心对称
23.2.1 中心对称
A 知识要点分类练
知识点 1 中心对称的概念
1.下列说法正确的是( D ) A.全等的两个图形成中心对称 B.能够完全重合的两个图形成中心对称 C.绕某点旋转后能够重合的两个图形成中心对称 D.绕某点旋转 180°后能够重合的两个图形成中心对称
23.2.1 中心对称
对称,则下列结论不成立的是( D )
A.点 A 与点 A′是对称点 B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
图 23-2-2
23.2.1 中心对称
【解析】根据中心对称的性质可知选项 A,B 正确;
因为 OA=OA′,∠AOB=∠A′OB′,OB=OB′, 所以△AOB≌△A′OB′, 所以∠ABO=∠A′B′O,
图 23-2-5
23.2.1 中心对称
【解析】过点 A 作 AE⊥b 于点 E.∵AB⊥a,AE⊥b, ∴四边形 ABOE 是矩形. 由中心对称的性质知 S 阴影=S 矩形 ABOE=AB·OB=3×2=6.
23.2.1 中心对称
7.如图 23-2-6,在△ABC 中,AB=AC,将△ABC 绕点 C 旋转 180° 得到△FEC.
2.如图 23-2-1,已知菱形 ABCD 与菱形 EFGH 关于直线 BD 上的 某个点成中心对称,则点 B 的对称点是( D )
A.点 E B.点 F C.点 G D.点 H
图 23-2-1
23.2.1 中心对称
知识点 2 中心对称的性质
3.如图 23-2-2 所示,△ABC 与△A′B′C′关于点 O 成中心
则 AB∥A′B′,故 C 选项正确;
由中心对称的性质可知∠ACB=∠A′C′B′, 而不能说明∠ACB=∠C′A′B′,
故 D 选项错误.故选 D.
23.2.1 中心对称
知识点 3 利用中心对称的性质作图
4.已知△ABC 及点 E,求作△ABC 关于点 E 成中心对称的图形.
图 23-2-3
23.2.1 中心对称
(2)易证△ADB≌△EDC,则 AB=EC. 又∵EC-AC<AE<EC+AC,
∴2 cm<2AD<10 cm, ∴1 cm<AD<5 cm.
(2)∵AC=FC,∴S△ABC=S△BCF=3 cm2. 又∵BC=EC,∴S△ABC=S△ACE=3 cm2, S△ECF=S△BCF=3 cm2, ∴S△ABC=S△BCF=S△ECF=S△ACE=3 cm2, ∴四边形 ABFE 的面积为 4×3=12(cm2).
23.2.1 中心对称
(3)当∠ACB=60°时,四边形 ABFE 为矩形. 理由:∵AB=AC,∴∠ABC=∠ACB=60°, ∴△ABC 为等边三角形,∴BC=AC=FC=EC. 又∵四边形 ABFE 为平行四边形, ∴四边形 ABFE 为矩形.
解:依次寻找点 A,B,C 关于点 E 的中心对称点,顺次连接,所作图形 如图所示:
23.2.1 中心对称
B 规律方法综合练
5.如图 23-2-4,在平面直角坐标系中,若△ABC 与△A′B′C′ 关于点 E 成中心对称,则点 E 的坐标是( A )
A.(3,-1) B.(0,0) C.(2,-1) D.(-1,3)
23.2.1 中心对称
C新拓知广梳探理究创新练
8.如图 23-2-7,已知 AD 是△ABC 的中线. (1)画出以点 D 为对称中心,与△ABC 成中心对称的三角形; (2)若 AB=6 cm,AC=4 cm,求 AD 的取值范围.
图 23-2-7
23.2.1 中心对称
解:(1)如图,延长 ADB 为所 求作的三角形.
图 23-2-4
23.2.1 中心对称
【解析】连接 AA′,CC′,它们的交点就是对称中心点 E.观察图形知,
点 E 的坐标是(3,-1).故选 A.
23.2.1 中心对称
6.2017·乐山 如图 23-2-5,直线 a,b 垂直相交于点 O,曲 线 C 关于点 O 成中心对称,点 A 的对称点是点 A′,AB⊥a 于点 B,A′ D⊥b 于点 D.若 OB=3,AB=2,则阴影部分的面积之和为___6_____.
(1)试猜想 AE 与 BF 有何关系,并说明理由; (2)若△ABC 的面积为 3 cm2,求四边形 ABFE 的面积; (3)当∠ACB 为多少度时,四边形 ABFE 为矩形?并说明理由.
图 23-2-6
23.2.1 中心对称
解:(1)AE 与 BF 平行且相等.理由: ∵△ABC 绕点 C 旋转 180°得到△FEC, ∴△ABC 与△FEC 关于点 C 成中心对称,AC=FC,BC=EC, ∴四边形 ABFE 是平行四边形,∴AE∥BF 且 AE=BF.
23.2.1 中心对称
A 知识要点分类练
知识点 1 中心对称的概念
1.下列说法正确的是( D ) A.全等的两个图形成中心对称 B.能够完全重合的两个图形成中心对称 C.绕某点旋转后能够重合的两个图形成中心对称 D.绕某点旋转 180°后能够重合的两个图形成中心对称
23.2.1 中心对称
对称,则下列结论不成立的是( D )
A.点 A 与点 A′是对称点 B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
图 23-2-2
23.2.1 中心对称
【解析】根据中心对称的性质可知选项 A,B 正确;
因为 OA=OA′,∠AOB=∠A′OB′,OB=OB′, 所以△AOB≌△A′OB′, 所以∠ABO=∠A′B′O,
图 23-2-5
23.2.1 中心对称
【解析】过点 A 作 AE⊥b 于点 E.∵AB⊥a,AE⊥b, ∴四边形 ABOE 是矩形. 由中心对称的性质知 S 阴影=S 矩形 ABOE=AB·OB=3×2=6.
23.2.1 中心对称
7.如图 23-2-6,在△ABC 中,AB=AC,将△ABC 绕点 C 旋转 180° 得到△FEC.
2.如图 23-2-1,已知菱形 ABCD 与菱形 EFGH 关于直线 BD 上的 某个点成中心对称,则点 B 的对称点是( D )
A.点 E B.点 F C.点 G D.点 H
图 23-2-1
23.2.1 中心对称
知识点 2 中心对称的性质
3.如图 23-2-2 所示,△ABC 与△A′B′C′关于点 O 成中心
则 AB∥A′B′,故 C 选项正确;
由中心对称的性质可知∠ACB=∠A′C′B′, 而不能说明∠ACB=∠C′A′B′,
故 D 选项错误.故选 D.
23.2.1 中心对称
知识点 3 利用中心对称的性质作图
4.已知△ABC 及点 E,求作△ABC 关于点 E 成中心对称的图形.
图 23-2-3
23.2.1 中心对称
(2)易证△ADB≌△EDC,则 AB=EC. 又∵EC-AC<AE<EC+AC,
∴2 cm<2AD<10 cm, ∴1 cm<AD<5 cm.
(2)∵AC=FC,∴S△ABC=S△BCF=3 cm2. 又∵BC=EC,∴S△ABC=S△ACE=3 cm2, S△ECF=S△BCF=3 cm2, ∴S△ABC=S△BCF=S△ECF=S△ACE=3 cm2, ∴四边形 ABFE 的面积为 4×3=12(cm2).
23.2.1 中心对称
(3)当∠ACB=60°时,四边形 ABFE 为矩形. 理由:∵AB=AC,∴∠ABC=∠ACB=60°, ∴△ABC 为等边三角形,∴BC=AC=FC=EC. 又∵四边形 ABFE 为平行四边形, ∴四边形 ABFE 为矩形.
解:依次寻找点 A,B,C 关于点 E 的中心对称点,顺次连接,所作图形 如图所示:
23.2.1 中心对称
B 规律方法综合练
5.如图 23-2-4,在平面直角坐标系中,若△ABC 与△A′B′C′ 关于点 E 成中心对称,则点 E 的坐标是( A )
A.(3,-1) B.(0,0) C.(2,-1) D.(-1,3)
23.2.1 中心对称
C新拓知广梳探理究创新练
8.如图 23-2-7,已知 AD 是△ABC 的中线. (1)画出以点 D 为对称中心,与△ABC 成中心对称的三角形; (2)若 AB=6 cm,AC=4 cm,求 AD 的取值范围.
图 23-2-7
23.2.1 中心对称
解:(1)如图,延长 ADB 为所 求作的三角形.
图 23-2-4
23.2.1 中心对称
【解析】连接 AA′,CC′,它们的交点就是对称中心点 E.观察图形知,
点 E 的坐标是(3,-1).故选 A.
23.2.1 中心对称
6.2017·乐山 如图 23-2-5,直线 a,b 垂直相交于点 O,曲 线 C 关于点 O 成中心对称,点 A 的对称点是点 A′,AB⊥a 于点 B,A′ D⊥b 于点 D.若 OB=3,AB=2,则阴影部分的面积之和为___6_____.
(1)试猜想 AE 与 BF 有何关系,并说明理由; (2)若△ABC 的面积为 3 cm2,求四边形 ABFE 的面积; (3)当∠ACB 为多少度时,四边形 ABFE 为矩形?并说明理由.
图 23-2-6
23.2.1 中心对称
解:(1)AE 与 BF 平行且相等.理由: ∵△ABC 绕点 C 旋转 180°得到△FEC, ∴△ABC 与△FEC 关于点 C 成中心对称,AC=FC,BC=EC, ∴四边形 ABFE 是平行四边形,∴AE∥BF 且 AE=BF.
