高三基础知识天天练3-3. 数学 数学doc人教版
高三基础知识天天练2-7. 数学 数学doc人教版
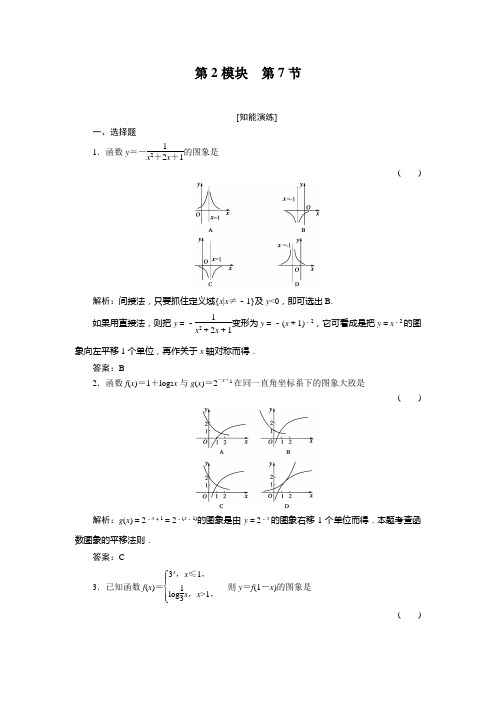
第2模块 第7节[知能演练]一、选择题1.函数y =-1x 2+2x +1的图象是( )解析:间接法,只要抓住定义域{x |x ≠-1}及y <0,即可选出B. 如果用直接法,则把y =-1x 2+2x +1变形为y =-(x +1)-2,它可看成是把y =x -2的图象向左平移1个单位,再作关于x 轴对称而得.答案:B2.函数f (x )=1+log 2x 与g (x )=2-x +1在同一直角坐标系下的图象大致是( )解析:g (x )=2-x +1=2-(x -1)的图象是由y =2-x的图象右移1个单位而得.本题考查函数图象的平移法则.答案:C3.已知函数f (x )=⎩⎪⎨⎪⎧3x,x ≤1,log 13x ,x >1,则y =f (1-x )的图象是( )解析:画出y =f (x )的图象,再作其关于y 轴对称的图象,得到y =f (-x )的图象,再将所得图象向右移动1个单位,得到y =f [-(x -1)]=f (-x +1)的图象,故选C.答案:C4.设函数y =f (x )定义在实数集上,则函数y =f (x -1)与y =f (1-x )的图象关于( )A .直线y =0对称B .直线x =0对称C .直线y =1对称D .直线x =1对称解析:函数y =f (x )与y =f (-x )的图象关于y 轴对称,y =f (1-x )=f [-(x -1)]. 把y =f (x )与y =f (-x )的图象同时都向右平移一个单位,就得到y =f (x -1)与y =f (1-x )的图象,对称轴y 轴向右平移一个单位得直线x =1,故选D.答案:D 二、填空题5.函数y =2-xx -1的图象关于点________对称.解析:y =2-x x -1=-1+1x -1,y =2-x x -1的图象是由y =1x 的图象先右移1个单位,再下移1个单位而得到,故对称点为(1,-1).答案:(1,-1)6.已知0<a <1,则方程a |x |=|log a x |的实根的个数是________.解析:a |x |=|log a x |有意义,则x >0,问题即a x=|log a x |.画出两个函数y =a x ,y =|log a x |的图象,则可以得到交点有2个.答案:2 三、解答题7.已知函数y =f (x )同时满足以下五个条件: (1)f (x +1)的定义域是[-3,1]; (2)f (x )是奇函数; (3)在[-2,0)上,f ′(x )>0; (4)f (-1)=0;(5)f (x )既有最大值又有最小值.请画出函数y =f (x )的一个图象,并写出相应于这个图象的函数解析式. 解:由(1)知,-3≤x ≤1,-2≤x +1≤2, 故f (x )的定义域是[-2,2].由(3)知,f (x )在[-2,0)上是增函数.综合(2)和(4)知,f (x )在(0,2]上也是增函数,且f (-1)=f (1)=0,f (0)=0. 故函数y =f (x )的一个图象如右图所示,与之相应的函数解析式是f (x )= ⎩⎪⎨⎪⎧x +1,-2≤x <0,0,x =0,x -1,0<x ≤2.8.已知函数f (x )=|x -8|-|x -4|.(1)作出函数y =f (x )的图象; (2)解不等式|x -8|-|x -4|>2. 解:(1)f (x )=⎩⎪⎨⎪⎧4,x ≤4,-2x +12,4<x ≤8,-4,x >8.图象如下:(2)不等式|x -8|-|x -4|>2,即f (x )>2, 由-2x +12=2,得x =5.由函数f (x )的图象可知原不等式的解集为(-∞,5).[高考·模拟·预测]1.函数y =f (x )的图象如图所示,则函数y =log 12f (x )的图象大致是( )解析:∵0<12<1,∴y =log 12f (x )的图象在(0,1]上递增,在[1,2)上递减(同增异减).故选C.答案:C2.下列三件事与如下图中吻合最好的顺序为( )①我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学; ②我骑车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一段时间; ③我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速. A .(1)(2)(4) B .(4)(2)(3) C .(4)(1)(3) D .(4)(1)(2)解析:根据其速度的变化判断函数图象的单调性可得①②③对应图象为(4)(1)(2),选D. 答案:D3.如右图所示,一质点P (x ,y )在xOy 平面上沿曲线运动,速度大小不变,其在x 轴上的投影点Q (x,0)的运动速度V =V (t )的图象大致为( )解析:由图可知,当质点P (x ,y )在两个封闭曲线上运动时,投影点Q (x,0)的速度先由正到0,到负,到0,再到正,故A 错误;投影点Q (x,0)在终点的速度是由大到小接近0,故D 错误;质点P (x ,y )在开始时沿直线运动,故投影点Q (x,0)的速度为常数,因此C 是错误的,故选B.答案:B4.把函数f (x )=x 3-3x 的图象C 1向右平移u 个单位长度,再向下平移v 个单位长度后得到图象C 2,若对任意u >0,曲线C 1与C 2至多只有一个交点,则v 的最小值为( )A .2B .4C .6D .8解析:C 2的解析式为y =(x -u )3-3(x -u )-v .由题意对于关于x 的方程(x -u )3-3(x -u )-v =x 3-3x ,即3ux 2-3u 2x -3u +u 3+v =0对于任意u >0至多只有一个实数解,∴Δ=9u 4-12u (u 3-3u +v )≤0,即v ≥-14u 3+3u ,令f (u )=-14u 3+3u ,则f ′(u )=-34u 2+3=-34(u 2-4),∴当u =2时f (u )取得最大值f (2)=4.∴v ≥4.故选B.答案:B5.已知f (x )是以2为周期的偶函数,当x ∈[0,1]时,f (x )=x ,且在[-1,3]内,关于x 的方程f (x )=kx +k +1(k ∈R ,k ≠-1)有四个根,则k 的取值范围是________.解析:由题意作出f (x )在[-1,3]上的示意图如下:记y =k (x +1)+1,∴y =k (x +1)+1的图象过定点A (-1,1).记B (2,0),由图象知,方程有四个根,即函数y =f (x )与y =kx +k +1有四个交点,故k AB <k <0.∴-13<k <0.答案:(-13,0)6.已知函数f (x )=m (x +1x )的图象与h (x )=12(x +1x )+2的图象关于点A (0,1)对称.(1)求m 的值;(2)若g (x )=f (x )+a2x,且g (x )在区间(0,2]上为减函数,求实数a 的取值范围.解:(1)解法一:设P (x ,y )是函数h (x )的图象上任意一点,则点P 关于A 点的对称点(x ′,y ′)在函数f (x )的图象上.∵⎩⎪⎨⎪⎧ x ′+x =0,y ′+y =2,故⎩⎪⎨⎪⎧x ′=-x ,y ′=2-y .于是有2-y =m (-x -1x ),即得y =m (x +1x )+2,∴m =12.解法二:易知h (x )经过点(1,3),故f (x )经过点(-1,-1),代入得m =12.(2)由(1)得f (x )=12(x +1x),故有g (x )=12(x +1x )+a 2x =12(x +a +1x),解法一:g ′(x )=12(1-a +1x 2).当0<x ≤a +1(a ≥-1)时,g ′(x )≤0,∵g (x )在区间(0,2]上为减函数,故有a +1≥2,得a ≥3. 即a 的取值范围为[3,+∞).解法二:任意取x 1,x 2∈(0,2],不妨设x 1<x 2. 则g (x 1)-g (x 2)=12(x 1-x 2)x 1x 2-(a +1)x 1x 2>0恒成立.故x 1x 2-(a +1)<0,对0<x 1<x 2≤2恒成立. ∴1+a ≥4,∴a ≥3.即a 的取值范围为[3,+∞).。
高三数学(文)日日练基础题(含答案)

高三数学(文) 天天练(一)1.如果复数i a a a a z )23(222+-+-+=为纯虚数,那么实数a 的值为( )。
A .-2B .1C .2D .1或 -22. 已知等差数列{a n }中,a 2+a 8=8,则该数列前9项和S 9等于( )。
A .18B .27C .36D .453.棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______.4.若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算,其参考数据如下: f (1) = -2f (1.5) = 0.625 f (1.25) = -0.984 f (1.375) = -0.260 f (1.4375) = 0.162 f (1.40625) = -0.054那么方程32220x x x +--=的一个近似根(精确到0.1)为( )。
A .1.2B .1.3C .1.4D .1.55.若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( )。
A .2- B .2 C .4- D .46.已知定义域为(-1,1)的奇函数y =f (x)又是减函数,且f (a -3)+f (9-a 2)<0,则a 的取值范围是( )。
A .(22,3)B .(3,10)C .(22,4)D .(-2,3) 7.已知简谐运动)3sin(2)(ϕ+π=x x f (2||π<ϕ)的图象经过点(0,1),则该简谐运动的最小正周期T 和初相ϕ分别为A .6=T ,6π=ϕB .6=T ,3π=ϕC .π=6T ,6π=ϕD .π=6T ,3π=ϕ 8.下图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为 .9.函数y=3x 2-2lnx 的单调递减区间为_________. 10.设向量a 与b 的夹角为θ,)3,3(=a ,)1,1(2-=-a b ,则cos θ= .11.已知函数x x x x f cos sin sin 3)(2+-=(I )求函数)(x f 的最小正周期; (II )求函数⎥⎦⎤⎢⎣⎡∈2,0)(πx x f 在的值域. 答案:1.C 2.C 3.108π 4.C 5.D 6.A 7.A 8. 4.6 9.(-√6/6,√6/6) 10.3√10/10 11.(1)π (2)[-√3,1-√3/2]。
高三基础知识天天练2-12. 数学 数学doc人教版

第2模块 第12节[知能演练]一、选择题1.如下图,阴影部分面积为( )A.⎠⎛ac[f (x )-g (x )]d xB.⎠⎛a c [g (x )-f (x )]d x +⎠⎛c b [f (x )-g (x )]d xC.⎠⎛ac [f (x )-g (x )]d x +⎠⎛cb [g (x )-f (x )]d x D.⎠⎛cb [g (x )-f (x )]d x答案:B( )解析:本题应画图求解,更为清晰,故选C.,⎠⎛02f (x )d x =⎠⎛01x 2d x +⎠⎛12(2-x )d x=13x 3| 10+(2x -12x 2)| 21 =13+(4-2-2+12)=56. 答案:C3.设f (x )=⎠⎛0x sin t d t ,则f [f (π2)]等于( )A .-1B .1C .-cos1D .1-cos1解析:由于⎠⎛0x sin t d t =(-cos t )| x0=1-cos x . ∴f (x )=1-cos x .∴f (π2)=1-cos π2=1.∴f [f (π2)]=f (1)=1-cos1.答案:D4.函数F (x )=⎠⎛0x t (t -4)d t 在[-1,5]上( )A .有最大值0,无最小值B .有最大值0和最小值-323C .有最小值-323,无最大值D .既无最大值也无最小值解析:F (x )=⎠⎛0x t (t -4)d t =⎠⎛0x (t 2-4t )d t=(13t 3-2t 2)| x 0=13x 3-2x 2,x ∈[-1,5]. 令F ′(x )=x (x -4)=0,∴x 1=0,x 2=4,∴F (-1)=-73,F (0)=0,F (4)=-323,F (5)=-253.∴最大值为0,最小值为-323.答案:B 二、填空题5.汽车以v =3t +2(单位:m/s)作变速直线运动时,在第1 s 至第2 s 间的1 s 内经过的路程是________.解析:s =⎠⎛12(3t +2)d t =(32t 2+2t )| 21 =32×4+4-(32+2) =10-72=132(m).答案:6.5 m6.若f (x )是一次函数,且⎠⎛01f (x )d x =5,⎠⎛01xf (x )d x =176,那么函数f (x )的解析式是________. 解析:设f (x )=ax +b (a ≠0),则⎠⎛01(ax +b )d x =(12ax 2+bx )| 10=12a +b =5. ⎠⎛01x (ax +b )d x =⎠⎛01(ax 2+bx )d x =(13ax 3+12bx 2)| 10 =13a +12b =176. 由⎩⎨⎧12a +b =513a +12b =176,解得⎩⎪⎨⎪⎧a =4b =3,∴f (x )=4x +3. 答案:f (x )=4x +3 三、解答题7.设函数f (x )=x 3+ax 2+bx 在点x =1处有极值-2.(1)求常数a ,b 的值;(2)求曲线y =f (x )与x 轴所围成的图形的面积. 解:(1)由题意知f ′(x )=3x 2+2ax +b , f (1)=-2且f ′(1)=0, 即⎩⎪⎨⎪⎧1+a +b =-23+2a +b =0,解得a =0,b =-3, 即f (x )=x 3-3x .(2)作出曲线y =x 3-3x 的草图,所求面积为阴影部分的面积,由x 3-3x =0得曲线y =x 3-3x 与x 轴的交点坐标是(-3,0),(0,0)和(3,0),而y =x 3-3x 是R 上的奇函数,函数图象关于原点中心对称.所以(-3,0)的阴影面积与(0,3)的阴影面积相等.所以所求图形的面积为=-2(14x 4-32x 2)| 30=92.8.如图所示,抛物线y =4-x 2与直线y =3x 的两交点为A 、B ,点P 在抛物线上从A 向B 运动.(1)求使△P AB 的面积最大的P 点的坐标(a ,b );(2)证明由抛物线与线段AB 围成的图形,被直线x =a 分为面积相等的两部分.(1)解:解方程组⎩⎪⎨⎪⎧y =4-x 2y =3x ,得x 1=1,x 2=-4.∴抛物线y =4-x 2与直线y =3x 的交点为 A (1,3),B (-4,-12),∴P 点的横坐标a ∈(-4,1).点P (a ,b )到直线y =3x 的距离为d =|3a -b |12+32,由题知b >3a ,∴d =b -3a10∵P 点在抛物线上,∴b =4-a 2,d ′a =110·(4-3a -a 2)′=110(-2a -3)=0,∴a =-32,即当a =-32时,d 最大,这时b =4-94=74,∴P 点的坐标为(-32,74)时,△P AB 的面积最大.(2)证明:设上述抛物线与直线所围成图形的面积为S ,位于x =-32右侧的面积为S 1.S =⎠⎛1-4(4-x 2-3x )d x =1256,S 1=⎠⎛1-32(4-x 2-3x )d x =12512,∴S =2S 1,即直线x =-32平分抛物线与线段AB 围成的图形的面积.[高考·模拟·预测]1.(sin x -a cos x )d x =2,则实数a 等于( )A .-1B .1C .- 3D. 3解析: (sin x -a cos x )dx =(-cos x -a sin x )=-a +1=2,a =-1.答案:A2.若⎠⎛1a (2x +1x )d x =3+ln2且a >1,则实数a 的值是( )A .2B .3C .5D .6解析:⎠⎛1a (2x +1x )d x =(x 2+ln x )| a 1=a 2+ln a -1=3+ln2,所以有a =2. 答案:A3.物体A 以速度v =3t 2+1(m/s)在一直线l 上运动,物体B 在直线l 上,且在物体A 的正前方5 m 处,同时以v =10t (m/s)的速度与A 同向运动,出发后物体A 追上物体B 所用的时间(s)为( )A .3B .4C .5D .6解析:由路程关于时间的函数关系式可知,物体A 的路程s =⎠⎛0t (3t 2+1)d t =t 3+t ,物体B 的路程s =⎠⎛0t 10t d t =5t 2,又因为物体A 、B 均在同一直线l 上运动,故当物体A 追上物体B 时,应有t 3+t =5t 2+5,解之得t =5.答案:C4.由两曲线y =sin x (x ∈[0,2π])和y =cos x (x ∈[0,2π])所围成的封闭图形的面积为________.解析:S = (sin x -cos x )d x =(-cos x -sin x ) =2 2. 答案:2 25.设函数f (x )=ax 2+c (a ≠0),若⎠⎛01f (x )d x =f (x 0),0≤x 0≤1,则x 0的值为________. 解析:⎠⎛01f (x )d x =⎠⎛01(ax 2+c )d x =(ax 33+cx )| 10=a 3+c ,故a 3+c =ax 20+c ,即ax 20=a 3,又a ≠0,所以x 20=13,又0≤x 0≤1,所以x 0=33.答案:336.已知二次函数f (x )=ax 2+bx +c ,直线l 1:y =-t 2+8t ,其中(0≤t ≤2,t 为常数),l 2:x =2.若直线l 1,l 2与函数f (x )的图象以及l 1,y 轴与函数f (x )的图象所围成的封闭图形如下图中的阴影部分所示.(1)求a ,b ,c 的值;(2)求阴影部分的面积S 关于t 的函数S (t )的解析式;(3)若g (x )=6ln x +m ,问是否存在实数m ,使得y =f (x )的图象与y =g (x )的图象有且只有两个不同的交点?若存在,求出m 的值;若不存在,请说明理由.解:(1)由图形知⎩⎪⎨⎪⎧c =0a ×82+b ×8+c =04ac -b 24a =16,解之得⎩⎪⎨⎪⎧a =-1b =8c =0.(2)由⎩⎪⎨⎪⎧y =-t 2+8t y =-x 2+8x得x 2-8x -t (t -8)=0, ∴x 1=t ,x 2=8-t . ∵0≤t ≤2,∴直线l 1与f (x )的图象的左交点坐标为(t ,-t 2+8t ). 由定积分的几何意义知:S (t )=⎠⎛0t [(-t 2+8t )-(-x 2+8x )]d x +⎠⎛t2[(-x 2+8x )-(-t 2+8t )]d x=[(-t 2+8t )x -(-x 33+4x 2)]| t 0+[(-x33+4x 2)-(-t 2+8t )x ]| 2t =-43t 3+10t 2-16t +403.(3)令φ(x )=g (x )-f (x )=x 2-8x +6ln x +m .∵x >0,要使函数f (x )与函数g (x )有且仅有两个不同的交点,则函数φ(x )=x 2-8x +6ln x +m 的图象与x 轴的正半轴有且只有两个不同的交点.φ′(x )=2x -8+6x=2x 2-8x +6x =2(x -1)(x -3)x(x >0).当x ∈(0,1)时,φ′(x )>0,φ(x )是增函数;当x ∈(1,3)时,φ′(x )<0,φ(x )是减函数;当x ∈(3,+∞)时,φ′(x )>0,φ(x )是增函数; 当x =1或x =3时,φ′(x )=0. ∴φ(x )的极大值为φ(1)=m -7; φ(x )的极小值为φ(3)=m +6ln3-15.当x 无限趋近于零时,φ(x )<0,当x 无限大时,φ(x )>0.∴要使φ(x )=0有且仅有两个不同的正根,必须且只需⎩⎪⎨⎪⎧ φ(1)=0φ(3)<0或⎩⎪⎨⎪⎧φ(3)=0φ(1)>0,即⎩⎪⎨⎪⎧ m -7=0m +6ln3-15<0或⎩⎪⎨⎪⎧m +6ln3-15=0m -7>0. ∴m =7或m =15-6ln3.∴当m =7或m =15-6ln3时,函数f (x )与g (x )的图象有且只有两个不同的交点.。
人教版高中数学必修3知识点和练习题(K12教育文档)

人教版高中数学必修3知识点和练习题(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(人教版高中数学必修3知识点和练习题(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为人教版高中数学必修3知识点和练习题(word版可编辑修改)的全部内容。
人教版高中数学必修3知识点和练习题第一章算法初步1.1.1算法的概念1、算法概念:在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成。
2. 算法的特点:(1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的。
(2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可。
(3)顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题。
(4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法.(5)普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决.1.1.2程序框图1、程序框图基本概念:(一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。
一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
(二)构成程序框的图形符号及其作用学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下:1、使用标准的图形符号。
高三基础知识天天练2-3. 数学 数学doc人教版

第2模块第3节[知能演练]一、选择题1.函数y=-x2(x∈R)是() A.左减右增的偶函数B.左增右减的偶函数C.减函数、奇函数D.增函数、奇函数解析:∵y=-x2是开口向下的一条抛物线,∴y=-x2在(-∞,0)上为增函数,(0,+∞)上为减函数,不妨设y=f(x)=-x2,则f(-x)=-(-x)2=-x2=f(x),∴f(x)为偶函数.答案:B2.已知函数f(x)在R上是奇函数,且当x>0时,f(x)=x2-2x,则f(x)在R上的解析式是() A.f(x)=x·(x-2)B.f(x)=|x|(x-2)C.f(x)=|x|(|x|-2)D.f(x)=x(|x|-2)答案:D3.f(x)、g(x)都是定义在R上的奇函数,且F(x)=3f(x)+5g(x)+2,若F(a)=b,则F(-a)等于() A.-b+4 B.-b+2C.b-2 D.b+2解析:依题设F(-x)=3f(-x)+5g(-x)+2=-3f(x)-5g(x)+2,∴F(x)+F(-x)=4,则F(a)+F(-a)=4,F(-a)=4-F(a)=4-b.答案:A4.定义在R上的函数f(x)既是奇函数又是周期函数,T是它的一个正周期.若将方程f(x)=0在闭区间[-T,T]上的根的个数记为n,则n可能为() A.0 B.1C.3 D.5解析:定义在R上的函数f(x)是奇函数,则f(0)=0,又f(x)是周期函数,T是它的一个正周期,∴f (T )=f (-T )=0,f (-T 2)=-f (T 2)=f (-T 2+T )=f (T2).∴f (-T 2)=f (T2)=0,则n 可能为5,选D.答案:D 二、填空题5.设函数f (x )=(x +1)(x +a )x 为奇函数,则a =________.解析:∵f (1)+f (-1)=0⇒2(1+a )+0=0, ∴a =-1. 答案:-16.已知函数f (x )=x 2-cos x ,对于[-π2,π2]上的任意x 1,x 2,有如下条件:①x 1>x 2;②x 21>x 22;③|x 1|>x 2.其中能使f (x 1)>f (x 2)恒成立的条件序号是________.解析:函数f (x )=x 2-cos x 显然是偶函数,其导数y ′=2x +sin x 在0<x <π2时,显然也大于0,是增函数,想象其图象,不难发现,x 的取值离对称轴越远,函数值就越大,②满足这一点.当x 1=π2,x 2=-π2时,①③均不成立.答案:② 三、解答题7.已知f (x )=px 2+23x +q 是奇函数,且f (2)=53.(1)求实数p ,q 的值;(2)判断函数f (x )在(-∞,-1)上的单调性,并加以证明. 解:(1)∵f (x )是奇函数,∴f (-x )=-f (x ),即px 2+2-3x +q =-px 2+23x +q .从而q =0,因此f (x )=px 2+23x .又∵f (2)=53,∴4p +26=53.∴p =2.(2)f (x )=2x 2+23x,任取x 1<x 2<-1,则f (x 1)-f (x 2)=2x 21+23x 1-2x 22+23x 2=2(x 2-x 1)(1-x 1x 2)3x 1x 2.∵x 1<x 2<-1,∴x 2-x 1>0,1-x 1x 2<0,x 1x 2>0. ∴f (x 1)-f (x 2)<0.∴f (x )在(-∞,-1)上是单调增函数.8.已知定义在R 上的奇函数f (x )有最小正周期2,且当x ∈(0,1)时,f (x )=2x4x +1.(1)求f (x )在[-1,1]上的解析式; (2)证明f (x )在(0,1)上是减函数.(1)解:只需求出f (x )在x ∈(-1,0)和x =±1,x =0时的解析式即可,因此,要注意应用奇偶性和周期性,当x ∈(-1,0)时,-x ∈(0,1).∵f (x )是奇函数,∴f (x )=-f (-x )=-2-x4-x +1=-2x4x +1,由f (0)=f (-0)=-f (0),且f (1)=f (-2+1)=f (-1)=-f (1), 得f (0)=f (1)=f (-1)=0. ∴在区间[-1,1]上有f (x )=⎩⎨⎧2x4x +1x ∈(0,1),-2x 4x+1x ∈(-1,0),0 x ∈{-1,0,1}.(2)证明:当x ∈(0,1)时,f (x )=2x4x +1.设0<x 1<x 2<1, f (x 1)-f (x 2)=2x 14x 1+1-2x 24x 2+1=(2x 2-2x 1)(2x 1+x 2-1)(4x 1+1)(4x 2+1).∵0<x 1<x 2<1.∴2x 2-2x 1>0,2x 1+x 2-1>0. ∴f (x 1)-f (x 2)>0, 即f (x 1)>f (x 2),故f (x )在(0,1)上单调递减.[高考·模拟·预测]1.已知函数f (x )是(-∞,+∞)上的偶函数,若对于x ≥0,都有f (x +2)=f (x ),且当x ∈[0,2)时,f (x )=log 2(x +1),则f (-2008)+f (2009)的值为( )A .-2B .-1C .1D .2解析:f (-2008)+f (2009)=f (0)+f (1)=log 21+log 22=1.答案:C2.已知函数f (x )是定义在实数集R 上的不恒为零的偶函数,且对任意实数x 都有xf (x +1)=(1+x )·f (x ),则f (52)的值是( )A .0 B.12 C .1D.52解析:令g (x )=f (x )x ,则g (-x )=f (-x )-x =-f (x )x =-g (x ),∴g (x )为奇函数.又g (x +1)=f (x +1)x +1=f (x )x =g (x ).∴g (52)=f (52)52=g (12)=g (-12)=-g (12),∴g (12)=0,∴f (52)=0.故选A. 答案:A3.已知定义在R 上的奇函数f (x )满足f (x -4)=-f (x ),且在区间[0,2]上是增函数,则( )A .f (-25)<f (11)<f (80)B .f (80)<f (11)<f (-25)C .f (11)<f (80)<f (-25)D .f (-25)<f (80)<f (11)解析:∵f (x -4)=-f (x ),∴f (x +4)=-f (x ),∴f (x +8)=f (x ).∴f (-25)=f (-1)=-f (1),f (11)=f (3)=-f (-1)=f (1),f (80)=f (0)=0.而f (x )在[0,2]上是增函数,∴f (1)≥f (0)=0.∴f (-25)<f (80)<f (11).故选D.答案:D4.函数f (x )的定义域为R ,若f (x +1)与f (x -1)都是奇函数,则( ) A .f (x )是偶函数 B .f (x )是奇函数 C .f (x )=f (x +2) D .f (x +3)是奇函数解析:由题意f (-x +1)=-f (x +1),f (-x -1)=-f (x -1),即f (x )=-f (2-x )且f (x )=-f (-2-x ).∴f (x )=-f (2-x )=f [-2-(2-x )]=f (x -4),∴f (-x +3)=f (-x -1)=-f [2-(-x -1)]=-f (x +3),故选D. 答案:D5.定义在R 上的增函数y =f (x )对任意x ,y ∈R 都有f (x +y )=f (x )+f (y ). (1)求f (0);(2)求证:f (x )为奇函数;(3)若f (k ·3x )+f (3x -9x -2)<0对任意x ∈R 恒成立,求实数k 的取值范围. 解:(1)令x =y =0,得f (0+0)=f (0)+f (0),即f (0)=0. (2)令y =-x ,得f (x -x )=f (x )+f (-x ),又f (0)=0,则有 0=f (x )+f (-x ).即f (-x )=-f (x )对任意x ∈R 成立, 所以f (x )是奇函数.(3)证法一:因为f (x )在R 上是增函数,又由(2)知f (x )是奇函数.f (k ·3x )<-f (3x -9x -2)=f (-3x +9x +2), 所以k ·3x <-3x +9x +2,32x -(1+k )·3x +2>0对任意x ∈R 成立.令t =3x >0,问题等价于t 2-(1+k )t +2>0对任意t >0恒成立. 令f (t )=t 2-(1+k )t +2,其对称轴为x =1+k 2,当1+k2<0即k <-1时,f (0)=2>0,符合题意; 当1+k2≥0即k ≥-1时,对任意t >0,f (t )>0恒成立⇔⎩⎪⎨⎪⎧1+k 2≥0,Δ=(1+k )2-4×2<0,解得-1≤k <-1+2 2. 综上所述,当k <-1+22时,f (k ·3x )+f (3x -9x -2)<0对任意x ∈R 恒成立. 解法二:由k ·3x <-3x +9x +2, 得k <3x +23x -1.u =3x +23x -1≥22-1,即u 的最小值为22-1,要使对x ∈R 不等式k <3x +23x -1恒成立,只要使k <22-1.所以满足题意的k 的取值范围是(-∞,22-1)[备选精题]6.已知函数f (x )=x 2+ax (x ≠0,常数a ∈R ).(1)讨论函数f (x )的奇偶性,并说明理由;(2)若函数f (x )在x ∈[2,+∞)上为增函数,求a 的取值范围. 解:(1)当a =0时,f (x )=x 2,对任意x ∈(-∞,0)∪(0,+∞), f (-x )=(-x )2=x 2=f (x ),∴f (x )为偶函数. 当a ≠0时,f (x )=x 2+ax (a ≠0,x ≠0),取x =±1,得f (-1)+f (1)=2≠0,f (-1)-f (1)= -2a ≠0.∴f (-1)≠-f (1),f (-1)≠f (1).∴函数f (x )既不是奇函数,也不是偶函数.(2)解法一:要使函数f (x )在x ∈[2,+∞)上为增函数, 等价于f ′(x )≥0在x ∈[2,+∞)上恒成立,即f ′(x )=2x -ax 2≥0在x ∈[2,+∞)上恒成立,故a ≤2x 3在x ∈[2,+∞)上恒成立.∴a ≤(2x 3)min =16.∴a 的取值范围是(-∞,16]. 解法二:设2≤x 1<x 2,f(x1)-f(x2)=x21+ax1-x22-ax2=(x1-x2)x1x2[x1x2(x1+x2)-a],要使函数f(x)在x∈[2,+∞)上为增函数,必须f(x1)-f(x2)<0恒成立,∵x1-x2<0,即a<x1x2(x1+x2)恒成立,又∵x1+x2>4,x1x2>4,∴x1x2(x1+x2)>16.∴a的取值范围是(-∞,16].。
高三基础知识天天练4-2. 数学 数学doc人教版

第4模块 第2节[知能演练]一、选择题1.已知向量a =(2,3),b =(-1,2),若m a +n b 与a -2b 共线,则mn等于( )A .-12B .2 C.12D .-2解析:m a +n b =(2m,3m )+(-n,2n ) =(2m -n,3m +2n ),a -2b =(2,3)-(-2,4)=(4,-1). 由m a +n b 与a -2b 共线, 则有2m -n 4=3m +2n-1∴n -2m =12m +8n ,∴m n =-12.答案:A2.已知向量OM →=(3,-2),ON →=(-5,-1),则12MN →等于( )A .(8,1)B .(-8,1)C .(4,-12D .(-4,12)解析:∵OM →=(3,-2),ON →=(-5,-1), ∴12MN →=12(ON →-OM →) =12[(-5,-1)-(3,-2)] =12×(-8,1)=(-4,12). 答案:D3.在四边形ABCD 中,AB →=a +2b ,BC →=-4a -b ,CD →=-5a -3b ,其中a ,b 不共线,则四边形ABCD 是( )A .梯形B .矩形C .菱形D .正方形解析:∵AB →+BC →+CD →=a +2b -4a -b -5a -3b =-8a -2b ,∴AD →=2(-4a -b )=2BC →,∴AD →∥BC →且|AD →|=2|BC →|,故四边形是梯形. 答案:A4.平面直角坐标系中,O 为坐标原点,已知两点A (3,1),B (-1,3),若点C (x ,y )满足OC →=αOA →+βOB →,其中α、β∈R ,且α+β=1,则x ,y 满足的关系式为( )A .3x +2y -11=0B .(x -1)2+(y -1)2=5C .2x -y =0D .x +2y -5=0解析:由OC →=αOA →+βOB →, ∴(x ,y )=(3α-β,α+3β).∴⎩⎪⎨⎪⎧x =3α-β,y =α+3β.∴⎩⎨⎧α=3x +y10,β=-x +3y10.∵α+β=1,∴x +2y -5=0. 答案:D 二、填空题5.设向量a =(1,2),b =(2,3),若向量λa +b 与向量c = (-4,-7)共线,则λ=________. 解析:由题意得λa +b =(2+λ,2λ+3), 又λa +b 与c 共线,因此有(λ+2)×(-7)-(2λ+3)×(-4)=0, ∴λ=2. 答案:26.已知点A (1,-2),若向量AB →与a =(2,3)同向,|AB →|=213,则点B 的坐标为________. 解析:∵向量AB →与a 同向, ∴设AB →=(2t,3t )(t >0).由|AB →|=213,∴4t 2+9t 2=4×13.∴t 2=4. ∵t >0,∴t =2.∴AB →=(4,6). 设B 为(x ,y ), ∴⎩⎪⎨⎪⎧x -1=4,y +2=6.∴⎩⎪⎨⎪⎧x =5,y =4. 答案:(5,4) 三、解答题7.已知A (-2,4),B (3,-1),C (-3,-4). 设AB →=a ,BC →=b ,CA →=c ,且CM →=3c ,CN →=-2b , (1)求:3a +b -3c ;(2)求满足a =m b +n c 的实数m ,n . 解:由已知得a =(5,-5), b =(-6,-3),c =(1,8). (1)3a +b -3c=3(5,-5)+(-6,-3)-3(1,8)=(15-6-3,-15-3-24)=(6,-42). (2)∵m b +n c =(-6m +n ,-3m +8n ),∴⎩⎪⎨⎪⎧ -6m +n =5-3m +8n =-5,解得⎩⎪⎨⎪⎧m =-1n =-1. 8.在▱ABCD 中,A (1,1),AB →=(6,0),点M 是线段AB 的中点,线段CM 与BD 交于点P .(1)若AD →=(3,5),求点C 的坐标; (2)当|AB →|=|AD →|时,求点P 的轨迹. 解:(1)设点C 坐标为(x 0,y 0), 又AC →=AD →+AB →=(3,5)+(6,0)=(9,5), 即(x 0-1,y 0-1)=(9,5), ∴x 0=10,y 0=6,即点C (10,6). (2)由三角形相似,不难得出PC →=2MP →设P (x ,y ),则BP →=AP →-AB →=(x -1,y -1)-(6,0)=(x -7,y -1),AC →=AM →+MC →=12AB →+3MP →=12AB →+3(AP →-12AB →) =3AP →-AB →=(3(x -1),3(y -1))-(6,0) =(3x -9,3y -3),∵|AB →|=|AD →|,∴▱ABCD 为菱形,∴AC ⊥BD . ∴AC →⊥BP →,即(x -7,y -1)·(3x -9,3y -3)=0. (x -7)(3x -9)+(y -1)(3y -3)=0, ∴x 2+y 2-10x -2y +22=0(y ≠1). ∴(x -5)2+(y -1)2=4(y ≠1).故点P 的轨迹是以(5,1)为圆心,2为半径的圆去掉与直线y =1的两个交点.[高考·模拟·预测]1.已知平面向量a =(x,1),b =(-x ,x 2),则向量a +b( )A .平行于x 轴B .平行于第一、三象限的角平分线C .平行于y 轴D .平行于第一、四象限的角平分线解析:a +b =(0,1+x 2),由1+x 2≠0及向量的性质可知,C 正确.故选C. 答案:C2.在平行四边形ABCD 中,AC 为一条对角线,若AB →=(2,4),AC →=(1,3),则BD →等于( )A .(-2,-4)B .(-3,-5)C .(3,5)D .(2,4)解析:在平行四边形ABCD 中,AC →=AB →+AD →,BD →=AD →-AB →, ∴BD →=(AC →-AB →)-AB →=(1,3)-2(2,4)=(1,3)-(4,8)=(-3,-5). 答案:B3.在平行四边形ABCD 中,AC 与BD 交于点O ,E 是线段OD 的中点,AE 的延长线与CD 交于点F .若AC →=a ,BD →=b ,则AF →=( )A.14a +12bB.23a +13C.12a +14bD.13a +23b 解析:由已知得DE =13EB ,则DF =13DC ,∴CF =23CD ,∴CF →=23CD →=23(OD →-OC →)=23(12b -12a )=13b -13a , ∴AF →=AC →+CF →=a +13b -13a=23a +13b . 答案:B4.已知向量a =(3,1),b =(1,3),c =(k,7),若(a -c )∥b ,则k =________. 解析:3-k 1=-63⇒k =5.故填5.答案:55.已知向量a =(1,2),b =(-2,1),k ,t 为正实数,x =a +(t 2+1)b ,y =-1k a +1t b ,问是否存在k 、t ,使x ∥y ,若存在,求出k 的取值范围;若不存在,请说明理由.解:x =a +(t 2+1)b=(1+2)+(t 2+1)(-2,1)=(-2t 2-1,t 2+3) y =-1k a +1t b =-1k (1,2)+1t (-2,1)=(-1k -2t ,-2k +1t,假设存在正实数k ,t ,使x ∥y ,则 (-2t 2-1)(-2k +1t )-(t 2+3)(-1k -2t )=0,化简得t 2+1k +1t=0,即t 3+t +k =0,∵k ,t 是正实数,故满足上式的k ,t 不存在. ∴不存在这样的正实数k ,t ,使x ∥y .[备选精题]6.已知向量a =(sin θ,cos θ-2sin θ),b =(1,2). (1)若a ∥b ,求tan θ的值; (2)若|a |=|b |,0<θ<π,求θ的值.解:(1)因为a ∥b ,所以2sin θ=cos θ-2sin θ,于是4sin θ=cos θ,故tan θ=14.(2)由|a |=|b |知,sin 2θ+(cos θ-2sin θ)2=5,所以1-2sin2θ+4sin 2θ=5.从而-2sin2θ+2(1-cos2θ)=4,即sin2θ+cos2θ=-1,于是sin(2θ+π4)=-22.又由0<θ<π知,π4<2θ+π4<9π4,所以2θ+π4=5π4,或2θ+π4=7π4.因此θ=π2,或θ=3π4.。
基础知识天天练3-2. 数学 数学doc

第3模块 第2节[知能演练]一、选择题1.α是第四象限角,tan α=-512,则sin α等于 ( )A.15B .-15 C.513D .-513 解析:⎩⎪⎨⎪⎧sin αcos α=-512,sin 2α+cos 2α=1,∴⎩⎨⎧ sin α=513,cos α=-1213或⎩⎨⎧ sin α=-513,cos α=1213.∵α是第四象限角,∴sin α<0,cos α>0.∴sin α=-513.选D. 答案:D2.已知cos(π2+φ)=32,且|φ|<π2,则tan φ等于 ( )A .-33B.33 C .- 3 D. 3解析:由cos(π2+φ)=32,得sin φ=-32. 又|φ|<π2,∴cos φ=12.∴tan φ=- 3. 答案:C3.若α是第三象限角,且cos(75°+α)=13,则tan(15°-α)的值为 ( )A .-223B .-24C.223D.24解析:cos(75°+α)=sin(90°-75°-α)=sin(15°-α)=13>0,又∵α为第三象限角, ∴-α为第二象限角.∴-α+15°为第二象限角.∴cos(15°-α)=-1-19=-223. ∴tan(15°-α)=-24. 答案:B4.若△ABC 的内角A 满足sin2A =23,则sin A +cos A 等于 ( )A.153B .-153 C.53 D .-53解析:在△ABC 中,2sin A cos A =23>0, ∴sin A >0,cos A >0. ∴sin A +cos A =(sin A +cos A )2=sin 2A +cos 2A +2sin A cos A =1+23=53=153. 答案:A二、填空题5.如果cos α=15,且α是第四象限角,那么cos(α+π2)=________. 解析:由已知⇒cos(α+π2)=-sin α=-(-1-cos 2α)=265. 答案:2656.化简:sin 2(α+π)·cos(π+α)·cos(-α-2π)tan(π+α)·sin 3(π2+α)·sin(-α-2π)=________.解析:sin 2(α+π)·cos(π+α)·cos(-α-2π)tan(π+α)·sin 3(π2+α)·sin(-α-2π) =(-sin α)2·(-cos α)·cos(-α)tan α·cos 3α·sin(-α)=-sin 2α·cos α·cos αsin αcos α·cos 3α·(-sin α)=sin 2αcos 2αsin 2αcos 2α=1. 答案:1三、解答题7.已知cos(π+α)=-12,且α是第四象限角,计算: (1)sin(2π-α);(2)sin[α+(2n +1)π]+sin[α-(2n +1)π]sin(α+2nπ)·cos(α-2nπ)(n ∈Z). 解:∵cos(π+α)=-12,∴-cos α=-12,cos α=12, 又∵α是第四象限角,∴sin α=-1-cos 2α=-32. (1)sin(2π-α)=sin[2π+(-α)]=sin(-α)=-sin α=32. (2)sin[α+(2n +1)π]+sin[α-(2n +1)π]sin(α+2nπ)·cos(α-2nπ)=sin(2nπ+π+α)+sin(-2nπ-π+α)sin(2nπ+α)·cos(-2nπ+α)=sin(π+α)+sin(-π+α)sin α·cos α=-sin α-sin(π-α)sin α·cos α=-2sin αsin αcos α=-2cos α=-4. 8.已知sin(π-α)-cos(π+α)=23(π2<α<π).求下列各式的值: (1)sin α-cos α;(2)sin 3(π2-α)+cos 3(π2+α). 解:由sin(π-α)-cos(π+α)=23, 得sin α+cos α=23.① 将①式两边平方,得1+2sin α·cos α=29, 故2sin α·cos α=-79, 又π2<α<π,∴sin α>0,cos α<0. ∴sin α-cos α>0.(1)(sin α-cos α)2=1-2sin α·cos α=1-(-79)=169,∴sin α-cos α=43. (2)sin 3(π2-α)+cos 3(π2+α)=cos 3α-sin 3α =(cos α-sin α)(cos 2α+cos α·sin α+sin 2α)=(-43)×(1-718)=-2227.[高考·模拟·预测]1.已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ=( )A .-43B.54 C .-34 D.45解析:由于tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ=sin 2θ+sin θcos θ-2cos 2θsin 2θ+cos 2θ=tan 2θ+tan θ-2tan 2θ+1=22+2-222+1=45,故选D. 答案:D2.已知△ABC 中,1tan A =-125,则cos A = ( )A.1213B.513 C .-513 D .-1213解析:∵1tan A =-125,∴tan A =-512,∴π2<A <π,∴cos A =-11+tan 2A=-1213,选D. 答案:D3.下列关系式中正确的是( )A .sin11°<cos10°<sin168°B .sin168°<sin11°<cos10°C .sin11°<sin168°<cos10°D .sin168°<cos10°<sin11°解析:注意到sin168°=sin(180°-12°)=sin12°,cos10°=sin80°,且0°<11°<12°<80°<90°,因此sin11°<sin12°<sin80°,即sin11°<sin168°<cos10°,选C. 答案:C4.若sin θ=-45,tan θ>0,则cos θ=________. 解析:∵sin θ<0,tan θ>0,θ在第三象限内,cos θ=-1-sin 2θ=-35.答案:-355.已知cos θ=-23,θ∈(π2,π),求2sin2θ-cos θsin θ的值. 解:原式=22sin θcos θ-cos θsin θ=1-cos 2θsin θcos θ=sin θcos θ. 又cos θ=-23,θ∈(π2,π), ∴sin θ=1-29=73,2sin2θ-cos θsin θ=-142. [备选精题] 6.已知函数f (x )=1-2sin(2x -π4)cos x. (1)求f (x )的定义域;(2)设α是第四象限的角,且tan α=-43,求f (α)的值. 解:(1)由cos x ≠0得x ≠kπ+π2(k ∈Z), 故f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠kπ+π2,k ∈Z . (2)因为tan α=-43,且α是第四象限的角, 所以sin α=-45,cos α=35, 故f (α)=1-2sin(2α-π4)cos α =1-2(22sin2α-22cos2α)cos α=1-sin2α+cos2αcos α=2cos 2α-2sin αcos αcos α=2(cos α-sin α)=145.。
高三基础知识天天练 数学检测4.人教版

单元质量检测(四)一、选择题1.若复数(a 2-4a +3)+(a -1)i 是纯虚数,则实数a 的值是( )A .1B .3C .1或3D .-1解析:由题意知⎩⎪⎨⎪⎧a 2-4a +3=0a -1≠0,解得a =3.答案:B2.复数1-2+i +11-2i的虚部是( )A.15i B.15 C .-15iD .-15解析:∵1-2+i +11-2i=-2-i (-2+i )(-2-i )+1+2i(1-2i )(1+2i )=-2-i 5+1+2i 5=-15+15i , ∴虚部为15.答案:B3.平面向量a ,b 共线的充要条件是( )A .a ,b 方向相同B .a ,b 两向量中至少有一个为零向量C .∃λ∈R ,b =λaD .存在不全为零的实数λ1,λ2,λ1a +λ2b =0解析:A 中,a ,b 同向则a ,b 共线;但a ,b 共线则a ,b 不一定同向,因此A 不是充要条件.若a ,b 两向量中至少有一个为零向量,则a ,b 共线;但a ,b 共线时,a ,b 不一定是零向量,如a =(1,2),b =(2,4),从而B 不是充要条件.当b =λa 时,a ,b 一定共线;但a ,b 共线时,若b ≠0,a =0,则b =λa 就不成立,从而C 也不是充要条件.对于D ,假设λ1≠0,则a =-λ2λ1b ,因此a ,b 共线;反之,若a ,b 共线,则a =nm b ,即m a -n b =0.令λ1=m ,λ2=-n ,则λ1a +λ2b =0. 答案:D4.如下图所示,已知梯形ABCD 中,AB ∥CD ,且AB =3CD ,M ,N 分别是AB ,CD 的中点,设AB →=e 1,AD →=e 2,MN →可表示为( )A .e 2+16e 1B .e 2-12e 1C .e 2-13e 1D .e 2+131解析:MN →=12(MD →+MC →)=12(MD →+MD →+DC →)=12[2(MA →+AD →)+DC →]=12[2(-12e 1+e 2)+131]=-12e 1+e 2+16e 1=e 2-13e 1. 答案:C5.向量a ,b 满足|a |=1,|b |=2,(a +b )⊥(2a -b ),则向量a 与b 的夹角为( )A .45°B .60°C .90°D .120°解析:由(a +b )⊥(2a -b )得(a +b )·(2a -b )=0, 即2|a |2+|a |·|b |cos α-|b |2=0,把|a |=1,|b |=2代入得cos α=0,∴α=90°(其中α为两向量的夹角). 答案:C6.设D 、E 、F 分别是△ABC 的三边BC 、CA 、AB 上的点,且DC →=2BD →,CE →=2EA →,AF →=2FB →,则AD →+BE →+CF →与BC →( )A .反向平行B .同向平行C .互相垂直D .既不平行也不垂直解析:∵DC →=2BD →,∴BC →-BD →=2BD →,∴BD →=13→.∵CE →=2EA →,∴BE →-BC →=2BA →-2BE →, ∴BE →=23BA →+13BC →.∵AF →=2FB →,∴BF →-BA →=-2BF →,∴BF →=13BA →.∴AD →+BE →+CF →=BD →-BA →+BE →+BF →-BC → =13BC →-BA →+23BA →+13BC →+13BA →-BC → =-13BC →.∴AD →+BE →+CF →与BC →反向平行. 答案:A7.已知非零向量a ,b ,若a ·b =0,则|a -2b ||a +2b |等于( )A.14 B .2 C.12D .1解析:|a -2b ||a +2b |=(a -2b )2(a +2b )2=a 2+4b 2a 2+4b 2=1.答案:D8.在△ABC 中,若BC →2=AB →·BC →+CB →·CA →+BC →·BA →,则△ABC 是( )A .锐角三角形B .直角三角形C .钝角三角形D .等边三角形解析:因为AB →·BC →+CB →·CA →+BC →·BA → =BC →·(AB →-CA →+BA →)=BC →·AC →,故BC →2-BC →·AC →=BC →·(BC →-AC →)=BC →·BA →=0, 即∠B =π2.答案:B9.一质点受到平面上的三个力F 1,F 2,F 3(单位:牛顿)的作用而处于平衡状态.已知F 1,F 2成60°角,且F 1,F 2的大小分别为2和4,则F 3的大小为( )A .6B .2C .2 5D .27解析:如图,F 3的大小等于F 1、F 2的合力的大小.由平面向量加法的三角形法则知,在△OAB 中OB 的长就是F 1、F 2的合力的大小,且在△OAB 中,∠OAB =120°,OB =F 21+F 22-2F 1·F 2cos120°=28=27,即F 3为27.答案:D10.函数y =tan(π4-π2)的部分图象如下图所示,则(OA →+OB →)·AB →=( )A .-6B .-4C .4D .6解析:函数y =tan(π4x -π2)的图象是由y =tan x 的图象向右平移π2坐标扩大为原来的4π倍得到,所以点A 的坐标为(2,0),令tan(π4x -π2)=1得π4x -π2=π4,故可得B 点坐标为(3,1),所以(OA →+OB →)·AB →=(5,1)·(1,1)=6.答案:D11.设点P 为△ABC 的外心(三条边垂直平分线的交点),若AB =2,AC =4,则AP →·BC →=( )A .8B .6C .4D .2解析:我们可以采用特殊方法解答,设A (-1,0),B (1,0),C (-1,4),则外心P 为(0,2),故AP →=(1,2),BC →=(-2,4),故AP →·BC →=6.答案:B12.已知P 是△ABC 所在平面内的一点,若CB →=λPA →+PB →(其中λ∈R ),则点P 一定在( )A .△ABC 的内部B .AC 边所在的直线上 C .AB 边所在的直线上D .BC 边所在的直线上解析:CB →=PB →-PC →=λPA →+PB →化简即得-PC →=λPA →,由共线向量的充要条件可知,点P ,A ,C 三点共线,所以答案选B.答案:B 二、填空题13.若复数a +3i1+2i (a ∈R ,i 是虚数单位)是纯虚数,则实数a =________.解析:∵a +3i 1+2i =(a +3i )(1-2i )(1+2i )(1-2i )=a +65+3-2a5i , ∴⎩⎨⎧a +6503-2a 5≠0,∴a =-6.答案:-614.向量a =(cos10°,sin10°),b =(cos70°,sin70°),|a -2b |=________. 解析:|a -2b |=a 2+4b 2-4a ·b =1+4-4(cos10°cos70°+sin10°sin70°) =5-4cos60°= 3. 答案: 315.已知AD 是△ABC 的中线,AD →=λAB →+μAC →(λ,μ∈R ),那么λ+μ=________;若∠A =120°,AB →·AC →=-2,则|AD →|的最小值是________.解析:若AD 为△ABC 的中线,则有AD →=12(AB →+AC →),∴λ+μ=1.|AD →|2=14(AB →+AC →)2=14(|AB →|2+|AC →|2+2AB →·AC →)=14(|AB →|2+|AC →|2-4),∵|AB →|2+|AC →|2≥2|AB →|·|AC →|=2AB →·AC →cos120°8,所以|AD →|≥1.答案:1 116.给定两个长度为1的平面向量OA →和OB →,它们的夹角为120°.如图所示,点C 在以O 为圆心的圆弧AB 上变动.若OC →=xOA →+yOB →,其中x ,y ∈R ,则x +y 的最大值是________.解析:以O 为坐标原点,OA 为x 轴建立平面直角坐标系,则可知A (1,0),B (-12,32),设C (cos α,sin α)(α∈[0,2π3]),则有x =cos α+33sin α,y =233sin α,所以x +y =cos α+3sin α=2sin(α+π6),所以当α=π3时,x +y 取得最大值为2.答案:2 三、解答题17.如图,在平行四边形ABCD 中,M ,N 分别为DC ,BC 的中点,已知AM →=c ,AN →=d ,试用c ,d 表示AB →,AD →.解法一:设AB →=a ,AD →=b , 则a =AN →+NB →=d +(-12)①b =AM →+MD →=c +(-12a )②将②代入①得a =d +(-12)[c +(-12a )]⇒a =43d -23,代入②得b =c +(-12)(43d -23c )=43c -23d .解法二:设AB →=a ,AD →=b . 因M ,N 分别为CD ,BC 中点, 所以BN →=12b ,DM →=12a .因而⎩⎨⎧c =b +12a d =a +12b ⇒⎩⎨⎧a =23(2d -c )b =23(2c -d ),即AB →=23(2d -c ),AD →=23(2c -d ).18.设a =(-1,1),b =(4,3),c =(5,-2),(1)求证a 与b 不共线,并求a 与b 的夹角的余弦值; (2)求c 在a 方向上的投影; (3)求λ1和λ2,使c =λ1a +λ2b .解:(1)∵a =(-1,1),b =(4,3),且-1×3≠1×4,∴a 与b 不共线. 又a ·b =-1×4+1×3=-1,|a |=2,|b |=5, ∴cos 〈a ,b 〉=a ·b |a ||b |=-152=-210. (2)∵a ·c =-1×5+1×(-2)=-7, ∴c 在a 方向上的投影为a ·c |a |=-72=-72 2.(3)∵c =λ1a +λ2b ,∴(5,-2)=λ1(-1,1)+λ2(4,3)=(4λ2-λ1,λ1+3λ2),∴⎩⎪⎨⎪⎧4λ2-λ1=5λ1+3λ2=-2,解得⎩⎨⎧λ1=-237λ2=37.19.设△ABC 的外心为O ,则圆O 为△ABC 的外接圆,垂心为H .求证:OH →=OA →+OB →+OC →.证明:延长BO 交圆O 于D 点,连AD 、DC , 则BD 为圆O 的直径,故∠BCD =∠BAD =90°. 又∵AE ⊥BC ,DC ⊥BC , 得AH ∥DC ,同理DA ∥CH . ∴四边形AHCD 为平行四边形, ∴AH →=DC →.又∵DC →=OC →-OD →=OC →+OB →, ∴AH →=OB →+OC →. 又∵OH →=OA →+AH →, ∴OH →=OA →+OB →+OC →.20.(1)如图,设点P ,Q 是线段AB 的三等分点,若OA →=a ,OB →=b ,试用a ,b 表示OP →,OQ →,并判断OP →+OQ →与OA →+OB →的关系;(2)受(1)的启示,如果点A 1,A 2,A 3,…,A n -1是AB 的n (n ≥3)等分点,你能得到什么结论?请证明你的结论.解:(1)OP →=OA →+AP →=OA →+13AB →=OA →+13OB →-OA →)=13OB →+23OA →=23a +13.同理OQ →=13a +23b ,∴OP →+OQ →=a +b =OA →+OB →.(2)OA 1→+OA n -1 =OA 2→+OA n -2 =…=OA →+OB →. 证明如下:由(1)可推出OA 1→=OA →+AA 1→=OA →+1n AB →=OA →+1n OB →-OA →)=n -1n OA →+1n OB →,∴OA 1→=n -1n a +1n b ,同理OA n -1=1n a +n -1nb ,OA 2→=n -2n a +2n b ,OA n -2=2n a +n -2n b ,…因此有OA 1→+OA n -1=OA 2→+OA n -2=…=OA →+OB →.21.已知△ABC 的面积S 满足3≤S ≤3,且AB →·BC →=6,AB →与BC →的夹角为θ. (1)求θ的取值范围;(2)求函数f (θ)=sin 2θ+2sin θ·cos θ+3cos 2θ的最小值. 解:(1)由题意知: AB →·BC →=|AB →|·|BC →|·cos θ=6① S =12|AB →|·|BC →|·sin(π-θ)=12|AB →|·|BC →|·sin θ② ②÷①得S 6=12tan θ,即3tan θ=S .由3≤S ≤3,得3≤3tan θ≤3,即33≤tan θ≤1. ∵θ为AB →与BC →的夹角,∴θ∈(0,π),∴θ∈[π6,π4].(2)f (θ)=sin 2θ+2sin θ·cos θ+3cos 2θ =1+sin2θ+2cos 2θ=2+sin2θ+cos2θ =2+2sin(2θ+π4).∵θ∈[π6,π4],∴2θ+π4∈[7π12,3π4].∴当2θ+π4=3π4,即θ=π4时,f (θ)有最小值为3.22.设向量a =(4cos α,sin α),b =(sin β,4cos β),c =(cos β,-4sin β). (1)若a 与b -2c 垂直,求tan(α+β)的值; (2)求|b +c |的最大值;(3)若tan αtan β=16,求证:a ∥b . 解:(1)因为a 与b -2c 垂直,所以a ·(b -2c )=4cos αsin β-8cos αcos β+4sin αcos β+8sin αsin β=4sin(α+β)-8cos(α+β)=0, 因此tan(α+β)=2.(2)由b +c =(sin β+cos β,4cos β-4sin β),得 |b +c |=(sin β+cos β)2+(4cos β-4sin β)2 =17-15sin2β≤4 2.又当β=-π4时,等号成立,所以|b +c |的最大值为4 2.(3)由tan αtan β=16得4cos αsin β=sin α4cos β,所以a ∥b .。
高三基础知识天天练4-4. 数学 数学doc人教版

第4模块 第4节[知能演练]一、选择题1.复数z =(a 2-2a )+(a 2-a -2)i (a ∈R )对应的点在虚轴上,则( )A .a ≠2或a ≠1B .a ≠2且a ≠1C .a =2或a =0D .a =0解析:由题意知a 2-2a =0,∴a =2或a =0. 答案:C2.设z 的共轭复数是z ,若z +z =4,z ·z =8,则z z 等于( )A .iB .-iC .±1D .±i解析:设z =x +yi (x ,y ∈R ),z =x -yi . 由z +z =4,z ·z =8得⎩⎪⎨⎪⎧x +yi +x -yi =4(x +yi )(x -yi )=8, ∴⎩⎪⎨⎪⎧x =2x 2+y 2=8, 解得⎩⎪⎨⎪⎧ x =2y =2或⎩⎪⎨⎪⎧x =2y =-2,∴zz =x -yi x +yi =x 2-y 2-2xyi x 2+y 2=±i . 答案:D3.如果实数b 与纯虚数z 满足关系式(2-i )z =4-bi (其中i 为虚数单位),那么b 等于( )A .8B .-8C .2D .-2解析:设z =ai (a ≠0),由(2-i )z =4-bi ,得(2-i )×ai =4-bi , 即a +2ai =4-bi ,∴⎩⎪⎨⎪⎧ a =42a =-b ,解得⎩⎪⎨⎪⎧a =4b =-8. 答案:B4.在复平面内,向量AB →对应的复数是2+i ,向量CB →对应的复数是-1-3i ,则向量CA →对应的复数为( )A .1-2iB .-1+2iC .3+4iD .-3-4i解析:向量AB →对应的复数是2+i ,则BA →对应的复数为-2-i ,∵CA →=CB →+BA →. ∴CA →对应的复数为(-1-3i )+(-2-i )=-3-4i . 答案:D 二、填空题5.已知z =(2+2i )2(4+5i )(5-4i )(1-i ),则|z |=________.解析:|z |=|(2+2i )2(4+5i )(5-4i )(1-i )|=|2+2i |2|4+5i ||5-4i ||1-i |=22×4141×2=2 2.答案:2 26.若复数z =(a 2-3)-(a +3)i ,(a ∈R )为纯虚数,则a +i 20073-3i=________.解析:∵z =(a 2-3)-(a +3)i 为纯虚数,∴⎩⎨⎧a 2-3=0a +3≠0,解得a =3, ∴a +i 20073-3i =3-i 3-3i =3-i 3(3-i )=33. 答案:33三、解答题7.若复数z 1与z 2在复平面上所对应的点关于y 轴对称,且z 1(3-i )=z 2(1+3i ),|z 1|=2,求z 1.解:设z 1=a +bi ,则z 2=-a +bi ,∵z 1(3-i )=z 2(1+3i ),且|z 1|=2, ∴⎩⎪⎨⎪⎧(a +bi )(3-i )=(-a +bi )(1+3i )a 2+b 2=2解得⎩⎪⎨⎪⎧ a =1b =-1或⎩⎪⎨⎪⎧a =-1b =1, 则z 1=1-i 或z 1=-1+i .8.已知z 是复数,z +2i 、z 2-i 均为实数(i 为虚数单位),且复数(z +ai )2在复平面上对应的点在第一象限,求实数a 的取值范围.解:设z =x +yi (x 、y ∈R ),∴z +2i =x +(y +2)i ,由题意得y =-2.z 2-i =x -2i 2-i =15(x -2i )(2+i )=15(2x +2)+15(x -4)i . 由题意得x =4,∴z =4-2i .∵(z +ai )2=(12+4a -a 2)+8(a -2)i ,根据条件,已知⎩⎪⎨⎪⎧12+4a -a 2>08(a -2)>0,解得2<a <6,∴实数a 的取值范围是(2,6).[高考·模拟·预测]1. i 是虚数单位,若1+7i2-i=a +bi (a ,b ∈R ),则乘积ab 的值是( )A .-15B .-3C .3D .15解析:1+7i 2-i =(1+7i )(2+i )(2-i )(2+i )=-1+3i ,所以a =-1,b =3,故选B.答案:B2.复数3+2i 2-3i -3-2i2+3i=( )A .0B .2C .-2iD .2i解析:3+2i 2-3i -3-2i 2+3i =(3+2i )(2+3i )-(2-3i )(3-2i )(2+3i )(2-3i )=26i13=2i ,答案为D.答案:D3.已知z1+i=2+i ,则复数z = ( )A .-1+3iB .1-3iC .3+iD .3-i解析:依题意得z =(1+i )(2+i )=1+3i ,故z =1-3i .选B. 答案:B4.设z 是复数,α(z )表示满足z n =1的最小正整数n ,则对虚数单位i ,α(i )=( )A .8B .6C .4D .2解析:∵α(z )表示满足z n =1的最小正整数n ,∴α(i )表示满足i n =1的最小正整数n ,∵i 2=-1,∴i 4=1,∴α(i )=4.答案:C5.已知复数z 1=a +2i ,z 2=a +(a +3)i ,且z 1z 2>0,则实数a 的值为( )A .0B .-5C .0或-5D .0或5解析:由已知条件可得z 1z 2=(a +2i )·[a +(a +3)i ]=a 2-2(a +3)+(a 2+5a )i ,又z 1z 2>0,所以⎩⎪⎨⎪⎧a 2-2(a +3)>0a 2+5a =0,解得a =-5,故选B.答案:B6.若z =sin θ-35+i (cos θ-45)是纯虚数,则tan θ的值为( )A .±34B .±43C .-34D.34解析:由纯虚数定义知,sin θ=35,cos θ≠45,∴cos θ=-45,∴tan θ=-34.答案:C7.若复数z 1=4+29i ,z 2=6+9i ,其中i 是虚数单位,则复数(z 1-z 2)i 的实部为________. 解析:因为(z 1-z 2)i =(-2+20i )i =-20-2i ,所以可知复数(z 1-z 2)i 的实部为-20. 答案:-208.若21-i=a +bi (i 为虚数单位,a ,b ∈R ),则a +b =________. 解析:∵21-i=a +bi ,∴1+i =a +bi ,∴a =b =1,∴a +b =2. 答案:29.若复数m +2i1-i (m ∈R ,i 是虚数单位)为纯虚数,则m =________.解析:因为m +2i 1-i =(m +2i )(1+i )(1-i )(1+i )=m -2+(m +2)i2为纯虚数,所以m =2.答案:2 10.复数1-3i2+i-(1+i )2在复平面内的对应点位于第________象限. 解析:1-3i 2+i -(1+i )2=(1-3i )(2-i )5-2i =-1-7i 5-2i =-1-17i5,所以其对应点位于第三象限.答案:三。
高三基础知识天天练2-9. 数学 数学doc人教版

第2模块 第9节[知能演练]一、选择题1.某种商品进价为每件100元,按进价增加25%出售,后因库存积压降价,按九折出售,每件还获利( )A .25元B .20.5元C .15元D .12.5元解析:每件获利100(1+25%)×0.9-100=100(1.25×0.9-1)=12.5元. 答案:D2.某债券市场常年发行三种债券,A 种面值为1000元,一年到期本息和为1040元;B 种债券面值为1000元,买入价为960元,一年到期本息之和为1000元;C 种面值为1000元,半年到期本息和为1020元.设三种债券的年收益分别为a ,b ,c ,则a ,b ,c 的大小关系是( )A .a =c <bB .a <b <cC .a <c <bD .c <a <b解析:设年初为1000元,则A 种债券收益40元,B 种债券收益1000960×40≈41.67元.C 种债券收益为20+10201000×20=40.4元.∴b >c >a . 答案:C3.在一次数学试验中,运用图形计算器采集到如下一组数据:则x ,y ( )A .y =a +bxB .y =a +b xC .y =ax 2+bD .y =a +bx解析:由表格数据逐个验证,知模拟函数为y =a +b x . 答案:B4.国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800元而不超过4000元的按超过800元部分的14%纳税;超过4000元的按全部稿酬的11%纳税.已知某人出版一本书,共纳税420元,这个人应得稿费(扣税前)为( )A .2800元B .3000元C .3800元D .3818元解析:设扣税前应得稿费为x 元,则应纳税额为分段函数,由题意,得y =⎩⎪⎨⎪⎧0 (x ≤800)(x -800)×14% (800<x ≤4000)11%·x (x >4000). 如果稿费为4000元应纳税为448元,现知某人共纳税420元,所以稿费应在800~4000元之间,∴(x -800)×14%=420,∴x =3800.答案:C 二、填空题5.计算机的价格大约每3年下降23,那么今年花8100元买的一台计算机,9年后的价格大约是________元.解析:设计算机价格平均每年下降p %,由题意可得13=(1-p %)3,∴p %=1-(13)13,∴9年后的价格y =8100[1+(13)13-1]9=8100×(13)3=300(元).答案:3006.如图是一份统计图表,根据此图表得到的以下说法中,正确的是________.①这几年人民生活水平逐年得到提高;②人民生活费收入增长最快的一年是2000年; ③生活价格指数上涨速度最快的一年是2001年;④虽然2002年生活费收入增长缓慢,但由于生活价格指数也略有降低,因而人民生活有较大的改善.解析:由题意,“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故①正确;“生活费收入指数”在2000年~2001年最陡,故②正确;“生活价格指数”在2001年~2002年上涨速度不是最快的,故③不正确;由于“生活价格指数”略呈下降,而“生活费收入指数”曲线呈上升趋势,故④正确.答案:①②④ 三、解答题7.某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如下图).(1)分别写出两种产品的收益与投资的函数关系;(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?解:(1)设投资债券收益与投资额的函数关系为f (x )=k 1x ,投资股票的收益与投资额的函数关系为g (x )=k 2x ,由图象得f (1)=18=k 1,g (1)=k 2=12,f (x )=18x (x ≥0),g (x )=12x (x ≥0).(2)设投资债券类产品x 万元, 则股票类投资为20-x 万元.y =f (x )+g (20-x )=x 8+1220-x (0≤x ≤20).令t =20-x ,则y =20-t 28+12t =-18(t 2-4t -20)=-18(t -2)2+3.所以当t =2,即x =16时,投资债券16万元,股票4万元时,收益最大,y max =3万元. 8.某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每超过1元,租不出的自行车就增加3辆.为了便于结算,每辆自行车的日租金x (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).(1)求函数y =f (x )的解析式及其定义域;(2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多? 解:(1)当x ≤6时,y =50x -115,令50x -115>0, 解得x >2.3.∵x ∈N *,∴x ≥3,∴3≤x ≤6,x ∈N *, 当x >6时,y =[50-3(x -6)]x -115.令[50-3(x -6)]x -115>0,有3x 2-68x +115<0, 上述不等式的整数解为2≤x ≤20(x ∈N *), ∴6<x ≤20(x ∈N *). 故y =⎩⎪⎨⎪⎧50x -115 (3≤x ≤6,x ∈N *)-3x 2+68x -115 (6<x ≤20,x ∈N *), 定义域为{x |3≤x ≤20,x ∈N *}.(2)对于y =50x -115(3≤x ≤6,x ∈N *). 显然当x =6时,y max =185(元), 对于y =-3x 2+68x -115=-3(x -343)2+8113(6<x ≤20,x ∈N *).当x =11时,y max =270(元).∵270>185,∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多.[高考·模拟·预测]1.某种细胞在培养过程中正常情况下,时刻t (单位:分)与细胞数n (单位:个)的部分数据如下:( )A .200B .220C .240D .260解析:由表格中所给数据可以得出n 与t 的函数关系为n =2t 20,令n =1000,得2t20=1000,又210=1024,所以时刻t 最接近200分,故选A.答案:A2.某化工厂打算投入一条新的生产线,但需要经环保部门审批同意方可投入生产.已知该生产线连续生产n 年的累计产量为f (n )=12n (n +1)(2n +1)吨,但如果年产量超过150吨,将会给环境造成危害.为保证环境,环保部门应给该厂这条生产线拟定最长的生产期限是( )A .5年B .6年C .7年D .8年解析:由题知第一年产量为a 1=12×1×2×3=3;以后各年产量分别为a n =f (n )-f (n -1)=12n (n +1)(2n +1)-12n (n -1)(2n -1)=3n 2(n ∈N *),令3n 2≤150,得1≤n ≤52⇒1≤n ≤7,故生产期限最长为7年.答案:C3.某市出租车收费标准如下: 起步价为8元,起步里程为3 km(不超过3 km 按起步价付费);超过3 km 但不超过8 km 时,超过部分按每千米2.15元收费;超过8 km 时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶了________ km.解析:设乘客每次乘坐出租车需付费用为f (x )元,由题意可得: f (x )=4.一位设计师在边长为3的正方形ABCD 中设计图案,他分别以A ,B ,C ,D 为圆心,以b (0<b ≤32)为半径画圆,由正方形内的圆弧与正方形边上线段(圆弧端点在正方形边上的连线)构成了丰富多彩的图形,则这些图形中实线部分总长度的最小值为________.解析:由题意实线部分的总长度为l =4(3-2b )+2πb =(2π-8)b +12,l 关于b 的一次函数的一次项系数2π-8<0,故l 关于b 为单调减函数,因此,当b 取最大值时,l 取得最小值,结合图形知,b 的最大值为32,代入上式得l 最小=(2π-8)×32+12=3π.答案:3π5.如右图,一个铝合金窗分为上、下两栏,圆周框架和中间隔档的材料为铝合金,宽均为6 cm ,上栏与下栏的框内高度(不含铝合金部分)的比为1∶2,此铝合金窗占用的墙面面积为28800 cm 2,设该铝合金窗的宽和高分别为a (cm),b (cm),铝合金窗的透光部分的面积为S (cm 2).(1)试用a ,b 表示S ;(2)若要使S 最大,则铝合金窗的宽和高分别为多少? 解:(1)∵铝合金窗宽为a (cm),高为b (cm),a >0,b >0, ∴ab =28800. ①又设上栏框内高度为h (cm),下栏框内高度为2h (cm),则3h +18=b ,∴h =b -183,∴透光部分的面积S =(a -18)×2(b -18)3+(a -12)×b -183=(a -16)(b -18)=ab -2(9a +8b )+288 =28800-2(9a +8b )+288 =29088-2(9a +8b ). (2)∵9a +8b ≥29a ·8b=29×8×28800=2880,当且仅当9a =8b 时等号成立,此时b =98a ,代入①得a =160,从而b =180,即当a =160,b =180时,S 取得最大值.答:铝合金窗的宽为160 cm ,高为180 cm 时,可使透光部分的面积最大.[备选精题] 6.两县城A 和B 相距20 km ,现计划在两县城外以AB 为直径的半圆弧上选择一点C 建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A 和城B 的总影响度为对城A 与对城B 的影响度之和,记C 点到城A 的距离为x km ,建在C 处的垃圾处理厂对城A 和城B 的总影响度为y .统计调查表明:垃圾处理厂对城A 的影响度与所选地点到城A 的距离的平方成反比,比例系数为4;对城B 的影响度与所选地点到城B 的距离的平方成反比,比例系数为k ,当垃圾处理厂建在弧的中点时,对城A 和城B 的总影响度为0.065.(Ⅰ)将y 表示成x 的函数;(Ⅱ)讨论(Ⅰ)中函数的单调性,并判断弧上是否存在一点,使建在此处的垃圾处理厂对城A 和城B 的总影响度最小?若存在,求出该点到城A 的距离;若不存在,说明理由.解:(Ⅰ)根据题意∠ACB =90°,AC =x km ,BC =400-x 2 km ,且建在C 处的垃圾处理厂对城A 的影响度为4x 2,对城B 的影响度为k400-x 2,因此,总影响度y =4x 2+k400-x 2(0<x <20).又因为垃圾处理厂建在弧的中点时,对城A 和城B 的总影响度为0.065,所以4(102+102)2+k400-(102+102)2=0.065, 解得k =9,所以y =4x 2+9400-x 2(0<x <20).(Ⅱ)因为y ′=-8x 3+18x(400-x 2)2=18x 4-8×(400-x 2)2x 3(400-x 2)2=(x 2+800)(10x 2-1600)x 3(400-x 2)2.由y ′=0解得x =410或x =-410(舍去), 易知410∈(0,20).y ,y ′随xy最小值=y|x=410=116,此时x=410,故在弧AB上存在一点,使得建在此处的垃圾处理厂对城A和城B的总影响度最小,该点与城A的距离x=410 km.。
高三基础知识天天练2-8. 数学 数学doc人教版

第2模块 第8节[知能演练]一、选择题1.函数f (x )=(x -1)ln xx -3的零点有( )A .0个B .1个C .2个D .3个解析:由f (x )=(x -1)ln xx -3=0得:x =1,∴f (x )=(x -1)ln xx -3只有一个零点,故选B.答案:B 2.若函数f (x )在(1,2)内有一个零点,要使零点的近似值满足精确度为0.01,则对区间(1,2)至少二等分( )A .5次B .6次C .7次D .8次解析:设对区间(1,2)至少二等分n 次,此时区间长为1,第1次二等分后区间长为12,第2次二等分后区间长为122,第3次二等分后区间长为123,…,第n 次二等分后区间长为12n ,依题意得12n <0.01,∴n >log 2100由于6<log 2100<7,∴n ≥7,即n =7为所求.答案:C3.f (x )是定义在R 上的以3为周期的偶函数,且f (2)=0.则方程f (x )=0在区间(0,6)内解的个数的最小值是( )A .5B .4C .3D .2解析:∵f (x )是定义在R 上的偶函数,且周期是3,f (2)=0,∴f (2)=f (5)=f (-2)=f (1)=f (4)=0.答案:B4.设函数y =x 3与y =(12)x -2的图象的交点为(x 0,y 0),则x 0所在的区间是( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)解析:令g (x )=x 3-22-x ,可求得:g (0)<0,g (1)<0,g (2)>0,g (3)>0,g (4)>0,易知函数g (x )的零点所在区间为(1,2).答案:B二、填空题5.若函数f (x )=x 2+ax +b 的两个零点是-2和3,则不等式a ·f (-2x )>0的解集是________.解析:由于f (x )=x 2+ax +b 的两个零点是-2和3, 即方程x 2+ax +b =0的两个根是-2和3,因此⎩⎪⎨⎪⎧ -2+3=-a -2·3=b ⇒⎩⎪⎨⎪⎧a =-1b =-6,因此f (x )=x 2-x -6, 所以不等式a ·f (-2x )>0,即-(4x 2+2x -6)>0,即2x 2+x -3<0,解集为{x |-32<x <1}.答案:{x |-32<x <1}6.若一元二次方程ax 2+bx +c =0(a >0)的两根x 1、x 2满足m <x 1<n <x 2<p ,则f (m )·f (n )·f (p )________0(填“>”、“=”或“<”).解析:∵a >0,∴f (x )=ax 2+bx +c 的图象开口向上.∴f (m )>0,f (n )<0,f (p )>0. 答案:< 三、解答题7.已知函数f (x )=x 3-x 2+x 2+14.证明:存在x 0∈(0,12),使f (x 0)=x 0.解:令g (x )=f (x )-x .∵g (0)=14,g (12)=f (12)-12=-18,∴g (0)·g (12)<0.又函数g (x )在[0,12]上连续,所以存在x 0∈(0,12),使g (x 0)=0.即f (x 0)=x 0.8.函数f (x )=x 3-12x 2-2x +5-λ在区间[-1,2]上有三个零点,求λ的值.解:设g (x )=x 3-12x 2-2x +5,则g ′(x )=3x 2-x -2=(3x +2)(x -1), ∴g (x )在(-1,-23)和(1,2)上单调递增,在(-23,1)上单调递减.又g (-1)=112,g (-23)=15727,g (1)=72,g (2)=7,由题意知g (x )=λ有三个根,∴λ∈[112,15727). [高考·模拟·预测]1.为了求函数f (x )=2x -x 2的一个零点,某同学利用计算器,得到自变量x 和函数值f (x )( )A .(0.6,1.0)B .(1.4,1.8)C .(1.8,2.2)D .(2.6,3.0) 解析:∵f (1.8)·f (2.2)=0.24×(-0.24)<0, ∴零点在(1.8,2.2)上.故选C. 答案:C2.已知函数f (x )=(13)x -log 2x ,若实数x 0是方程f (x )=0的解,且0<x 1<x 0.则f (x 1)的值为( )A .恒为正值B .等于0C .恒为负值D .不大于0解析:∵f (x )在定义域(0,+∞)上单调递减,当x →0时,f (x )→+∞, ∵f (x 0)=0,∴f (x )=0只有一个实根. ∴当0<x 1<x 0时,f (x 1)>0恒成立,故选A. 答案:A3.若函数f (x )的零点与g (x )=4x +2x -2的零点之差的绝对值不超过0.25,则f (x )可以是( )A .f (x )=4x -1B .f (x )=(x -1)2C .f (x )=e x -1D .f (x )=ln(x -12)解析:∵g ′(x )=4x ln4+2>0,∴g (x )在(-∞,+∞)上是增函数.又g (0)=1-2=-1<0,g (12)=2+1-2=1>0,∴g (x )只有一个零点x 0,且x 0∈(0,12).对于选项A :f (x )=4x -1,其零点为x =14,∴|14-x 0|<14,故选项A 符合.答案:A4.已知方程|x |-ax -1=0仅有一个实根且小于0,则a 的取值范围为________.解析:利用数形结合判断显然有a ≥1. 答案:a ≥15.已知函数f (x )=e x -k -x ,其中x ∈R . (1)k =0时,求函数f (x )的值域;(2)当k >1时,函数f (x )在[k,2k ]内是否存在零点,并说明理由. 解:(1)k =0时,f (x )=e x -x ,f ′(x )=e x -1, 令f ′(x )=0,得x =0.又x ∈(-∞,0)时,f ′(x )<0, ∴f (x )在(-∞,0)内单调递减. x ∈(0,+∞)时,f ′(x )>0, ∴f (x )在(0,+∞)内单调递增. ∴x =0时,f (x )取到极小值.又∵这个极小值是R 上的唯一的极小值, ∴x =0时,f (x )min =f (0)=1. 即函数f (x )的值域为[1,+∞).(2)f (k )·f (2k )=(e k -k -k )·(e 2k -k -2k ) =(1-k )·(e k -2k ). ∵k >1,∴1-k <0.令g (k )=e k -2k ,g (1)=e 1-2>0, 又g ′(k )=e k -2,当k >1时,g ′(k )>e 1-2>0, ∴k ∈(1,+∞),g (k )为增函数. ∴g (k )>g (1)>0.∴k >1时,e k -2k >0. ∴f (k )·f (2k )<0.∴即函数f (x )当k >1时在[k,2k ]内存在零点.[备选精题]6.已知二次函数y =g (x )的导函数的图象与直线y =2x 平行,且y =g (x )在x =-1处取得极小值m -1(m ≠0).设f (x )=g (x )x. (1)若曲线y =f (x )上的点P 到点Q (0,2)的距离的最小值为2,求m 的值. (2)k (k ∈R )如何取值时,函数y =f (x )-kx 存在零点,并求出零点. 解:设二次函数为g (x )=ax 2+bx +c ,∵y =g ′(x )=2ax +b 的图象与直线y =2x 平行, ∴a =1.又∵y =g (x )在x =-1处取得极小值m -1, ∴-b2a=-1,g (-1)=a (-1)2+b (-1)+c =m -1,∴b =2,c =m , 从而f (x )=g (x )x =mx+x +2.(1)已知m ≠0,设曲线y =f (x )上点P 的坐标为P (x ,y ),则点P 到点Q (0,2)的距离为 |PQ |=(x -0)2+(y -2)2=x 2+(mx+x )2=2x 2+m 2x2+2m≥22x 2·m 2x2+2m =22|m |+2m ,当且仅当2x 2=m 2x 2⇒x =±|m |2时等号成立. ∵|PQ |的最小值为2,∴22|m |+2m =2⇒2|m |+m =1. ①当m >0时,解得m =12+1=2-1. ②当m <0时,解得m =11-2=-2-1. 故m =2-1或m =-2-1.(2)y =f (x )-kx 的零点即方程mx +(1-k )x +2=0的解,∵m ≠0,∴mx +(1-k )x +2=0与(k -1)x 2-2x -m =0有相同的解. ①若k =1,(k -1)x 2-2x -m =0⇒x =-m2≠0,∴函数y =f (x )-kx 有零点x =-m2.②若k ≠1,(k -1)x 2-2x -m =0的判别式Δ=4[1+m (k -1)]. 若Δ=0⇒k =1-1m ,此时函数y =f (x )-kx 有一个零点x =-m .若Δ>0⇒1+m (k -1)>0,∴当m >0,k >1-1m ,或m <0,k <1-1m 时,方程(k -1)x 2-2x -m =0有两个解 x 1=1+1+m (k -1)k -1和x 2=1-1+m (k -1)k -1.此时函数y =f (x )-kx 有两个零点x 1和x 2. ③若Δ<0⇒1+m (k -1)<0,∴当m >0,k <1-1m ,或m <0,k >1-1m时,方程(k-1)x2-2x-m=0无实数解.此时函数y=f(x)-kx没有零点.。
高三基础知识天天练1-1. 数学 数学doc人教版

第1模块 第1节[知能演练]一、选择题1.满足条件M ∪{1}={1,2,3}的集合M 的个数是( )A .1B .2C .3D .4解析:满足条件M ∪{1}={1,2,3}的集合M 为{2,3},{1,2,3},共两个. 答案:B2.已知集合P ={(x ,y )||x |+|y |=1},Q ={(x ,y )|x 2+y 2≤1},则( )A .P ⊆QB .P =QC .P ⊇QD .P ∩Q =Ø 答案:A3.若集合A ={x |2a +1≤x ≤3a -5},B ={x |3≤x ≤22},则能使A ⊆B 成立的所有a 的集合是( )A .{a |1≤a ≤9}B .{a |6≤a ≤9}C .{a |a ≤9}D .Ø解析:若2a +1>3a -5,即a <6时,A =Ø⊆B ; 若2a +1=3a -5,即a =6时,A ={x |x =13}⊆B ; 若2a +1<3a -5,即a >6时,由A ⊆B 得⎩⎪⎨⎪⎧2a +1≥33a -5≤22,解得6<a ≤9.综上可得a ≤9. 答案:C4.已知集合A ={x |x <a },B ={x |1<x <2},且A ∪ (∁R B )=R ,则实数a 的取值范围是( )A .a ≤1B .a <1C .a ≥2D .a >2解析:∁R B =(-∞,1]∪[2,+∞),又A ∪(∁R B )=R ,数轴上画图可得a ≥2,故选C. 答案:C 二、填空题5.若集合{(x ,y )|x +y -2=0且x -2y +4=0} {(x ,y )|y =3x +b },则b =________.解析:由⎩⎪⎨⎪⎧ x +y -2=0,x -2y +4=0.⇒⎩⎪⎨⎪⎧x =0,y =2.点(0,2)在y =3x +b 上,∴b =2.答案:26.对于集合M 、N 定义M -N ={x |x ∈M ,且x ∉N },M ⊕N =(M -N )∪(N -M ),设A ={t |t =x 2-3x ,x ∈R },B ={x |y =lg(-x )},则A ⊕B =________.解析:∵t =x 2-3x =(x -32)2-94≥-94,∴A ={t |t ≥-94}.又由B 可知y =lg(-x ),则-x >0,得x <0, ∴B ={x |x <0},∴A -B ={x |x ≥0},B -A ={x |x <-94},∴A ⊕B =(-∞,-94)∪[0,+∞).答案:(-∞,-94)∪[0,+∞)三、解答题7.已知集合A ={x |x 2-5x +6=0},B ={x |mx +1=0},且B ⊆A ,求实数m 的值组成的集合.解:A ={x |(x -2)(x -3)=0}={2,3}, 若m =0,B =Ø⊆A ;若m ≠0,B ={x |x =-1m},由B ⊆A 得-1m =2,或-1m =3,解得m =-12,m =-13, 因此实数m 的值组成的集合是{0,-12,-13}.8.已知集合E ={x ||x -1|≥m },F ={x |10x +6>1}.(1)若m =3,求E ∩F ;(2)若E ∪F =R ,求实数m 的取值范围; (3)若E ∩F =Ø,求实数m 的取值范围. 解:(1)当m =3时,E ={x ||x -1|≥3}={x |x ≤-2或x ≥4},F ={x |10x +6>1}={x |x -4x +6<0}={x |-6<x <4}.∴E ∩F ={x |x ≤-2或x ≥4}∩{x |-6<x <4} ={x |-6<x ≤-2}. (2)∵E ={x ||x -1|≥m },①m ≤0时,E =R ,E ∪F =R ,满足条件. ②m >0时,E ={x |x ≤1-m 或x ≥1+m }, 由E ∪F =R ,F ={x |-6<x <4},∴⎩⎪⎨⎪⎧ 1-m ≥-6,1+m ≤4,m >0,解得0<m ≤3.∴综上,实数m 的取值范围为(-∞,3]. (3)∵E ={x ||x -1|≥m },①m ≤0时,E =R ,E ∩F =F ≠Ø,不满足条件.②m >0时,E ={x |x ≤1-m 或x ≥1+m },由E ∩F =Ø,F ={x |-6<x <4}, ∴⎩⎪⎨⎪⎧1-m ≤-6,1+m ≥4,m >0,解得m ≥7.∴综上,实数m 的取值范围为[7,+∞).[高考·模拟·预测]1.已知全集U =R ,集合M ={x |-2≤x -1≤2}和N ={x |x =2k -1,k =1,2,…}的关系的韦恩(Venn)图如下图所示,则阴影部分所示的集合的元素共有( )A .3个B .2个C .1个D .无穷多个解析:∵阴影部分M ∩N ={x |-2≤x -1≤2}∩{x |x =2k -1,k =1,2,…}={x |-1≤x ≤3}∩{x |x =2k -1,k =1,2,…}={1,3},∴阴影部分所示的集合的元素共有2个,故选B.答案:B 2.已知全集U =R ,则正确表示集合M ={-1,0,1}和N ={x |x 2+x =0}关系的韦恩(Venn)图是( )解析:N ={x |x 2+x =0}={-1,0},而M ={-1,0,1},故N M ,所以选B. 答案:B3.设全集U =A ∪B ={x ∈N *|lg x <1}.若A ∩(∁U B )={m |m =2n +1,n =0,1,2,3,4},则集合B =______________.解析:由题意得U =A ∪B ={1,2,3,4,5,6,7,8,9},A ∩(∁U B )={1,3,5,7,9},所以B ={2,4,6,8}. 答案:{2,4,6,8}4.设P 是一个数集,且至少含有两个数,若对任意a 、b ∈P ,都有a +b 、a -b 、ab 、ab∈P (除数b ≠0),则称P 是一个数域.例如有理数集Q 是数域;数集F ={a +b 2|a ,b ∈Q }也是数域,有下列命题:①整数集是数域;②若有理数集Q ⊆M ,则数集M 必为数域; ③数域必为无限集; ④存在无穷多个数域.其中正确命题的序号是________.(把你认为正确的命题的序号都填上)解析:对于整数集Z ,a =1,b =2时,a b =12∉Z ,故整数集不是数域,①错;对于满足Q ⊆M 的集合M =Q ∪{2},1+2∉M ,M 不是数域,②错;若P 是数域,则存在a ∈P 且a ≠0,依定义,2a,3a,4a …均是P 中的元素,故P 中有无数个无素,③正确;类似数集F ,{a +b 3|a ,b ∈Q },{a +b 5|a ,b ∈Q }等均是数域,④正确.答案:③④5.已知集合A ={x |(x -2)[x -(3a +1)]<0},B ={x |x -2ax -(a 2+1)<0}.(1)当a =2时,求A ∩B ;(2)求使B ⊆A 的实数a 的取值范围. 解:(1)当a =2时,A ={x |2<x <7},B ={x |4<x <5}. ∴A ∩B ={x |4<x <5}, (2)B ={x |2a <x <a 2+1},①当B =Ø时,2a ≥a 2+1,∴a =1, 此时A ={x |2<x <4},B ⊆A 符合题意.②若B ≠Ø,方程(x -2)[x -(3a +1)]=0的两根为x 1=2,x 2=3a +1. ∵B ≠Ø.∴A ≠Ø∴3a +1≠2,即a ≠13.当3a +1>2,即a >13时,⎩⎪⎨⎪⎧2a ≥2a 2+1≤3a +12a <a 2+1⇒⎩⎪⎨⎪⎧a ≥10≤a ≤3⇒1<a ≤3a ≠1.当3a +1<2,即a <13时,⎩⎪⎨⎪⎧ 2a ≥3a +1a 2+1≤2⇒⎩⎪⎨⎪⎧a ≤-1-1≤a ≤1⇒a =-1. ∴a 的取值范围为[1,3]∪{-1}.[备选精题]6.集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1}. (1)若B ⊆A ,求实数m 的取值范围;(2)当x ∈Z 时,求A 的非空真子集的个数;(3)当x ∈R 时,没有元素x 使x ∈A 与x ∈B 同时成立,求实数m 的取值范围. 解:(1)当m +1>2m -1,即m <2时,B =Ø满足B ⊆A . 当m +1≤2m -1,即m ≥2时,要使B ⊆A 成立, 需⎩⎪⎨⎪⎧m +1≥-22m -1≤5,可得2≤m ≤3, 综上,m 的取值范围是m ≤3.(2)当x ∈Z 时,A ={-2,-1,0,1,2,3,4,5}, 所以A 的非空真子集个数为28-2=254.(3)因为x ∈R ,且A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},又没有元素x 使x ∈A 与x ∈B 同时成立.则①若B =Ø,即m +1>2m -1,得m <2时满足条件. ②若B ≠Ø,则要满足的条件是 ⎩⎪⎨⎪⎧ m +1≤2m -1m +1>5或⎩⎪⎨⎪⎧m +1≤2m -12m -1<-2,解得m >4. 综上,m 的取值范围是m <2或m >4.。
高三基础知识天天练 数学检测3.人教版

答案:等边三角形
15.函数f(x)=sinx+2|sinx|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是________.
如下图所示,则k的取值范围是1<k<3.
答案:1<k<3
16.下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是π;
()
解析:根据题意,可得f(x)=|π-x-x|=|π-2x|,图象即为选项A.
答案:A
9.如下图所示,函数y=2sin(ωx+θ)(|θ|<)的图象,那么
()
A.ω=,θ=B.ω=,θ=-
C.ω=2,θ=D.ω=2,θ=-
解析:由图知周期T=π-(-)=π,
∴ω==2,∴y=2sin(2x+θ),
解析:把y=3sin(x+)的图象向左平移个单位,得到的图象解析式为y=3sin(x++)=3sin(x+),然后再把得到的图象横坐标缩短到原来的倍,纵坐标不变,得到的图象解析式为y=3sin(2x+π).
答案:B
11.已知函数f(x)=2sinωx在区间[-,]上的最小值为-2,则ω的取值范围是
()
②终边在y轴上的角的集合是{α|α=,k∈Z};
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④把函数y=3sin(2x+)的图象向右平移个单位得到y=3sin2x的图象;
⑤函数y=sin(x-)在[0,π]上是减函数.
其中真命题的序号是________.
解析:①y=sin2x-cos2x=-cos2x,故最小正周期为π,①正确.
C.D.
解析:设函数f(x)的最小正周期为T,
三上《53天天练》人教版数学2023

三上《53天天练》人教版数学2023引言在学习数学时,练习是非常重要的一部分。
而三上的《53天天练》人教版数学2023是一本非常受学生欢迎的练习题集。
本文将简要介绍该书的内容,并提供一些学习该书的建议。
1. 书籍概述《53天天练》人教版数学2023是三上出版社出版的一本数学练习题集。
该书主要针对中学生,特别是初中学生。
书中包含了许多与课程内容相符的练习题,涵盖了数学各个方面的知识点。
这本书的目的是帮助学生提高数学解题能力,并加深对数学知识的理解。
2. 内容结构该书分为53个单元,每个单元对应一天的练习内容。
每天的练习包括选择题、填空题和解答题。
书中的题目涵盖了数学的各个分支,包括代数、几何、概率等。
每天的题目数量适中,能够让学生在一定的时间内完成。
3. 学习建议•按照计划学习:将学习时间分配给每天的练习,按照计划进行学习。
这样能够让学习过程更有条理,避免拖延。
•认真分析错题:在做完每天的练习后,认真分析错题并找出解题的错误之处。
通过对错误的反思和复习,能够加深对知识点的理解。
•持续复习:不仅在做完每天的练习后进行错题复习,还需要定期进行全书的复习。
这样能够巩固已学知识,提高解题能力。
•解答题找出解题思路:对于解答题,除了求解答案外,还要重点关注解题的思路和方法。
找出解题的规律和技巧,并灵活运用。
4. 学习效果评估学习《53天天练》人教版数学2023后,学生可以通过以下方式来评估学习效果:•完成每天的练习:能够按时完成每天的练习,并做到准确无误。
•在考试中取得好成绩:通过对书中各个知识点的练习,能够在考试中取得较好的成绩。
•解题能力的提升:通过多次的练习,解题能力得到显著提升,能够迅速找出解题的方法和思路。
结论《53天天练》人教版数学2023是一本非常有益的数学练习题集。
通过坚持每天的练习,能够提高解题能力,加深对数学知识的理解。
希望通过本文的介绍和建议,能够帮助学生正确使用该书,并取得好的学习效果。
高三基础知识天天练3-6. 数学 数学doc人教版

第3模块 第6节[知能演练]一、选择题1.若tan α=3,tan β=43,则tan(α-β)等于( )A .-3B .-13C .3D.13 解析:tan(α-β)=tan α-tan β1+tan αtan β=3-431+3×43=535=13.答案:D2.已知450°<α<540°,则12+1212+12cos2α的值是 ( )A .-sin α2B .cos α2C .sin α2D .-cos α2解析:原式=12+121+cos2α2=12-12cos α=⎪⎪sinα2. ∵450°<α<540°,∴225°<α2<270°.∴原式=-sin α2.答案:A3.等式|sin αcos α|+122α-cos 2α|=12成立的充要条件是( )A .α=kπ(k ∈Z )B .α=kπ2(k ∈Z ) C .α=kπ4(k ∈Z )D .α=kπ8(k ∈Z )解析:由题意知:原式=12|sin2α|+12|cos2α|=12∴|sin2α|+|cos2α|=1,∴1+2|sin2αcos2α|=1. |sin4α|=0,α=kπ4(k ∈Z ). 答案:C4.设M (cos πx 3+cos πx 5sin πx 3+sin πx5)(x ∈R )为坐标平面内一点,O 为坐标原点,记f (x )=|OM |,当x 变化时,函数f (x )的最小正周期是( )A .30πB .15πC .30D .15解析:f (x )=|OM | =2+2(cos π3x cos π5x +sin π3x sin π5x )=2+2cos(π3x -π5x )=2(1+cos 215πx )=2(1+2cos 2π15x -1)=4cos 2π15x=2|cos π15x |.所以其最小正周期T =ππ15=15.答案:D 二、填空题5.求值:cos 4π8+cos 43π8+cos 45π8+cos 47π8=________.解析:原式=2⎝⎛⎭⎫cos 4π8+cos 43π8=2⎝⎛⎭⎫cos 4π8+sin 4π8=2⎝⎛⎭⎫1-2sin 2π8cos 2π8 =2⎝⎛⎭⎫1-12sin 2π4=32. 答案:326.若锐角α、β满足(1+3tan α)(1+3tan β)=4,则α+β=________. 解析:由(1+3tan α)(1+3tan β)=4, 可得tan α+tan β1-tan αtan β=3,即tan(α+β)= 3.又α+β∈(0,π),∴α+β=π3.答案:π3三、解答题7.用tan α表示sin2α,cos2α. 解:sin2α=2sin αcos α=2sin αcos αsin 2α+cos 2α=2tan αtan 2α+1,cos2α=cos 2α-sin 2α=cos 2α-sin 2αsin 2α+cos 2α=1-tan 2α1+tan 2α.8.已知0<α<π4,β为f (x )=cos ⎝⎛⎭⎫2x +π8的最小正周期,a =⎝⎛⎭⎫tan ⎝⎛⎭⎫α+14,-1,b =(cos α,2),且a·b =m ,求2cos 2α+sin2(α+β)cos α-sin α的值.解:因为β为f (x )=cos ⎝⎛⎭⎫2x +π8的最小正周期,故β=π.因a·b =cos αtan ⎝⎛⎭⎫α+14β-2=m , 故cos αtan ⎝⎛⎭⎫α+π4=m +2.由于0<α<π4,所以2cos 2α+sin2(α+β)cos α-sin α=2cos 2α+sin(2α+2π)cos α-sin α=2cos 2α+sin2αcos α-sin α=2cos α(cos α+sin α)cos α-sin α=2cos α·1+tan α1-tan α=2cos αtan ⎝⎛⎭⎫α+π4=4+2m .[高考·模拟·预测]1.函数f (x )=sin x -13-2cos x -2sin x(0≤x ≤2π)的值域为( )A .[-22,0] B .[-1,0] C .[-2,0]D .[-3,0]解析:f (x )=sin x -13-2cos x -2sin x=sin x -13-22sin(x +π4),此函数的最大值必为0,当x =0时,分子为-1,分母为1,此时函数值最小,最小值为-1,故选B.答案:B2.函数f (x )=(sin 2x +12009sin 2x )(cos 2x +12009cos 2x)的最小值是 ( )A.42009 B.22009(2010-1) C.22009D.22009(2009-1) 解析:f (x )=(2009sin 4x +1)(2009cos 4x +1)20092sin 2x cos 2x=20092sin 4x cos 4x +2009(sin 4x +cos 4x )+120092sin 2x cos 2x=20092sin 4x cos 4x +2009[(sin 2x +cos 2x )2-2sin 2x cos 2x ]+120092sin 2x cos 2x=sin 2x cos 2x +201020092sin 2x cos 2x -22009≥22009(2010-1). 答案:B3.若sin θ22cos θ2=0,则tan θ=________.解析:由sin θ2-2cos θ2=0得tan θ2=2,代入二倍角公式可得tan θ=2tanθ21-tan 2θ2=-43.答案:-434.俗话说“一石激起千层浪”,小时候在水上打“水漂”的游戏一定不会忘记吧.现在一个圆形波浪实验水池的中心已有两个振动源,在t 秒内,它们引发的水面波动可分别由函数y 1=sin t 和y 2=sin(t +2π3)来描述,当这两个振动源同时开始工作时,要使原本平静的水面保持平静,则需再增加一个振动源(假设不计其他因素,则水面波动由几个函数的和表达),请你写出这个新增振动源的函数解析式:________________.解析:因为y 1+y 2+y 3=sin t +sin(t +2π3)+y 3=sin t -12t +32cos t +y 3=0,所以y 3=sin(t +4π3)时符合题意.本题也可为y 3=sin(t -2π3)(答案不唯一). 答案:y 3=sin(t +4π3)(答案不唯一). 5.设函数f (x )=cos(2x +π3)+sin 2x .(Ⅰ)求函数f (x )的最大值和最小正周期;(Ⅱ)设A ,B ,C 为△ABC 的三个内角,若cos B =13f (C 2)=-14C 为锐角,求sin A .解:(Ⅰ)f (x )=cos2x cos π3-sin2x sin π3+1-cos2x2=12cos2x -32sin2x +12-12cos2x =12-32sin2x . 所以当2x =-π2+2kπ,即x =-π4+kπ(k ∈Z )时,f (x )取得最大值,[f (x )]最大值=1+32,f (x )的最小正周期T =2π2=π,故函数f (x )的最大值为1+32,最小正周期为π.(Ⅱ)由f (C 2)=-14,即12-32sin C =-14,解得sin C =32,又C 为锐角,所以C =π3由cos B =13求得sin B =223.因此sin A =sin[π-(B +C )]=sin(B +C ) =sin B cos C +cos B sin C =223×12+13×32=22+36. [备选精题]6.已知A ,B 是△ABC 的两个内角,向量a =(2cos A +B 2,sin A -B 2),若|a |=62.(1)证明:tan A tan B 为定值;(2)当tan C 取最大值时,求△ABC 的三个内角的大小.解:(1)由条件可知32=(62)2=|a |2=2cos 2A +B 2+sin 2A -B 2=1+cos(A +B )+1-cos(A -B )2,∴cos(A +B )=12cos(A -B ),∴3sin A sin B =cos A cos B ,∵A ,B 是△ABC 的两个内角,∴tan A tan B =13为定值.(2)tan C =-tan(A +B )=-tan A +tan B1-tan A tan B由(1)知tan A tan B =13,∴tan A >0,tan B >0,从而tan C =-32(tan A +tan B )≤-32·2·tan A tan B =-3, ∴取等号的条件是当且仅当tan A =tan B =33,即A =B =π6时,tan C 取得最大值,此时△ABC 的三个内角分别是π6,π6,2π3.。
高三基础知识天天练3-7. 数学 数学doc人教版

第3模块 第7节[知能演练]一、选择题1.在△ABC 中,a 2-c 2+b 2=ab ,则角C 为( )A .60°B .45°或135°C .120°D .30°解析:∵a 2-c 2+b 2=ab ,∴cos C =a 2+b 2-c 22ab =ab 2ab =12.又∵0°<C <180°,∴C =60°.答案:A2.在△ABC 中,A =120°,AB =5,BC =7,则sin Bsin C的值为 ( )A.85B.58C.53D.35解析:由余弦定理得BC 2=AB 2+AC 2-2AB ·AC ·cos A ,即72=52+AC 2-10AC ·cos120°,∴AC =3.由正弦定理得sin B sin C =AC AB =35.答案:D3.已知△ABC 的三边长分别为a ,b ,c ,且面积S △ABC =14(b 2+c 2-a 2),则A 等于( )A .45°B .30°C .120°D .15°解析:由S △ABC =14(b 2+c 2-a 2)=12bc sin A得sin A =b 2+c 2-a 22bc =cos A ,∴A =45°.答案:A4.在△ABC 中,BC =2,B =π3,若△ABC 的面积为32,则tan C 为( )A. 3 B .1 C.33D.32解析:由S △ABC =12BC ·BA sin B =32得BA =1,由余弦定理得AC 2=AB 2+BC 2-2AB ×BC cos B ,∴AC =3,∴△ABC 为直角三角形,其中A 为直角,∴tan C =AB AC =33.答案:C 二、填空题5.某人向正东方向走了x 千米,他右转150°,然后朝新方向走了3千米,结果他离出发点恰好3千米,那么x 的值是________.解析:如图所示,该问题转化为已知△ABC 中BC =3,AC =3,B =30°,求AB 的长.由正弦定理AC sin B =BC sin A 可求得角A ,进而可求出角C 再由AB sin C =ACsin B可求得AB ,即x . 答案:3或2 36.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =1,b =7,c =3,则B =________.解析:由余弦定理变形得cos B =a 2+c 2-b 22ac =1+3-72×1×3=-32.又∵B ∈(0,π),∴B =5π6.答案:5π6三、解答题7.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,并且a 2=b (b +c ). (1)求证:A =2B ;(2)若a =3b ,判断△ABC 的形状. (1)证明:因为a 2=b (b +c ),即a 2=b 2+bc , 所以在△ABC 中,由余弦定理可得, cos B =a 2+c 2-b 22bc =c 2+bc 2ac=b +c 2a =a 22ab =a 2b =sin A2sin B, 所以sin A =sin2B ,∴A =2B 或A +2B =π,而当A +2B =π时有B =C 即b =c ,代回已知得a =2b ,此时a 2=b 2+c 2,故A =90°,而B =C =45°也即A =2B .故A =2B .(2)解:因为a =3b ,所以ab =3,由a 2=b (b +c )可得c =2b ,cos B =a 2+c 2-b 22ac =3b 2+4b 2-b 243b 2=32所以B =30°,A =2B =60°,C =90°. 所以△ABC 为直角三角形.8.已知a 、b 、c 是△ABC 的三边长,关于x 的方程ax 2-2c 2-b 2x -b =0(a >c >b )的两根之差的平方等于4,△ABC 的面积S =103,c =7. (1)求角C ; (2)求a ,b 的值.解:(1)设x 1、x 2为方程ax 2-2c 2-b 2x -b =0的两根,则x 1+x 2=2c 2-b 2a,x 1·x 2=-b a. ∴(x 1-x 2)2=(x 1+x 2)2-4x 1x 2 =4(c 2-b 2)a 2+4b a =4.∴a 2+b 2-c 2=ab .又cos C =a 2+b 2-c 22ab =ab 2ab =12,又∵C ∈(0°,180°),∴C =60°. (2)由S =12ab sin C =103,∴ab =40.①由余弦定理c 2=a 2+b 2-2ab cos C , 即c 2=(a +b )2-2ab (1+cos60°). ∴72=(a +b )2-2×40×(1+12).∴a +b =13.又∵a >b ② ∴由①②,得a =8,b =5.[高考·模拟·预测]1.△ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边,且cos2B +3cos(A +C )+2=0,b =3,则c ∶sin C 等于( )A .3∶1 B.3∶1 C.2∶1D .2∶1解析:cos2B +3cos(A +C )+2=2cos 2B -3cos B +1=0,∴cos B =12或cos B =1(舍).∴B=π3.∴c sin C =b sin B =332=2.故选D. 答案:D2.△ABC 中,AB =3,AC =1,B =30°,则△ABC 的面积等于( )A.32B.34C.32或 3D.32或34解析:1sin30°=3sin C ,∴sin C =32.∴C =60°或120°. (1)当C =60°时,A =90°,∴BC =2,此时,S △ABC =32; (2)当C =120°时,A =30°,S △ABC =12×3×1×sin30°=34,故选D.答案:D3.在锐角△ABC 中,b =2,B =π3,sin2A +sin(A -C )-sin B =0,则△ABC 的面积为________.解析:sin2A +sin(A -C )-sin B =sin2A +sin(A -C )-sin(A +C )=sin2A -2sin C cos A =2cos A (sin A -sin C )=0,∵△ABC 是锐角三角形, ∴cos A ≠0.∴sin A =sin C ,即A =C . 又B =π3,∴△ABC 为正三角形.∴S =34×22= 3. 答案: 34.已知△ABC 中,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,若a =c =6+2且∠A =75°,则b =( )A .2B .4+2 3C .4-2 3D.6- 2解析:sin A =sin75°=sin(30°+45°)=sin30°cos45°+sin45°cos30°=2+64.由a =c =6+2可知,∠C =75°,所以∠B =30°,sin B =12.由正弦定理得b =asin A ·sin B=2+62+64×12=2,故选A. 答案:A5.在△ABC 中,BC =5,AC =3,sin C =2sin A . (1)求AB 的值; (2)求sin ⎝⎛⎭⎫2A -π4的值. 解:(1)在△ABC 中,根据正弦定理,AB sin C =BCsin A .于是AB =sin Csin A BC =2BC =2 5.(2)在△ABC 中,根据余弦定理得 cos A =AB 2+AC 2-BC 22AB ·AC =255.于是sin A =1-cos 2A =55. 从而sin2A =2sin A cos A =45,cos2A =cos 2A -sin 2A =35.所以sin ⎝⎛⎫2A -π4=sin2A cos π4-cos2A sin π4=210. [备选精题]6.已知函数f (x )=2sin x cos 2φ2+cos x sin φ-sin x (0<φ<π)在x =π处取最小值.(1)求φ的值;(2)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边.已知a =1,b =2,f (A )=32,求角C .解:(1)f (x )=2sin x 1+cos φ2+cos x sin φ-sin x=sin x +sin x cos φ+cos x sin φ-sin x =sin x cos φ+cos x sin φ=sin(x +φ). 因为f (x )在x =π时取最小值. 所以sin(π+φ)=-1,故sin φ=1. 又0<φ<π,所以φ=π2.(2)由(1)知f (x )=sin ⎝⎛⎭⎫x +π2=cos x .因为f (A )=cos A =32,且A 为△ABC 的内角, 所以A =π6.由正弦定理得sin B =b sin A a =22.又b >a ,所以B =π4或B =3π4.当B =π4时,C =π-A -B =π-π6-π4=7π12,当B =3π4时,C =π-A -B =π-π6-3π4=π12.综上所述,C =7π12或C =π12.。
高考数学全程训练计划:天天练3 函数的概念及表示

天天练3 函数的概念及表示小题狂练③一、选择题1.[2019·惠州二调]已知函数f(x)=x +1x -1,f(a)=2,则f(-a)=( )A .2B .-2C .4D .-4 答案:D解析:解法一 由已知得f(a)=a +1a -1=2,即a +1a =3,所以f(-a)=-a -1a -1=-⎝ ⎛⎭⎪⎫a +1a -1=-3-1=-4.解法二 因为f(x)+1=x +1x ,设g(x)=f(x)+1=x +1x ,易判断g(x)=x +1x 为奇函数,故g(x)+g(-x)=x +1x -x -1x =0,即f(x)+1+f(-x)+1=0,故f(x)+f(-x)=-2,所以f(a)+f(-a)=-2,故f(-a)=-4.2.下列所给图象是函数图象的个数为( )A .1B .2C .3D .4 答案:B解析:①中当x>0时,每一个x 的值对应两个不同的y 值,因此不是函数图象;②中当x =x 0时,y 的值有两个,因此不是函数图象,③④中每一个x 的值对应唯一的y 值,因此是函数图象.故选B.3.[2019·河南豫东、豫北十所名校段测]设函数f(x)=⎩⎪⎨⎪⎧log 3x ,0<x≤9,f x -4,x >9,则f(13)+2f ⎝ ⎛⎭⎪⎫13的值为( )A .1B .0C .-2D .2 答案:B解析:因为f(13)=f(13-4)=f(9)=log 39=2,2f ⎝ ⎛⎭⎪⎫13=2log 313=-2,所以f(13)+2f ⎝ ⎛⎭⎪⎫13=2-2=0.故选B.4.[2019·山东潍坊青州段测]函数f(x)=ln(x -1)+12-x的定义域为( )A .(1,2)B .[1,2)C .(1,2]D .[1,2] 答案:A解析:函数f(x)=ln(x -1)+12-x 的定义域为⎩⎪⎨⎪⎧x -1>0,2-x >0的解集,解得1<x <2,所以函数f(x)的定义域为(1,2).故选A.5.[2019·福建省六校联考]下列函数中,满足f(x 2)=[f(x)]2的是( ) A .f(x)=lnx B .f(x)=|x +1| C .f(x)=x 3D .f(x)=e x答案:C解析:解法一 对于函数f(x)=x 3,有f(x 2)=(x 2)3=x 6,[f(x)]2=(x 3)2=x 6,所以f(x 2)=[f(x)]2,故选C.解法二 因为f(x 2)=[f(x)]2,对选项A,f(22)=ln4,[f(2)]2=(ln2)2,排除A ;对选项B,则有f(12)=|12+1|=2,[f(1)]2=|1+1|2=4,排除B ;对选项D,则有f(12)=e,[f(1)]2=e 2,排除D.故选C.6.[2019·重庆二诊]如图所示,对应关系f 是从A 到B 的映射的是( )答案:D解析:A 到B 的映射为对于A 中的每一个元素在B 中都有唯一的元素与之对应,所以不能出现一对多的情况,因此D 表示A 到B 的映射.7.已知函数y =f(x +2)的定义域是[-2,5),则y =f(3x -1)的定义域为( ) A .[-7,14) B .(-7,14] C.⎝ ⎛⎦⎥⎤13,83 D.⎣⎢⎡⎭⎪⎫13,83答案:D解析:因为函数y =f(x +2)的定义域是[-2,5),所以-2≤x<5,所以0≤x+2<7,所以函数f(x)的定义域为[0,7),对于函数y =f(3x -1),0≤3x-1<7,解得13≤x<83,故y =f(3x -1)的定义域是⎣⎢⎡⎭⎪⎫13,83,故选D.8.[2019·山东德州模拟]设函数y =9-x 2的定义域为A,函数y =ln(3-x)的定义域为B,则A∩∁R B =( )A .(-∞,3)B .(-∞,-3)C .{3}D .[-3,3) 答案:C解析:由9-x 2≥0解得-3≤x≤3,可得A =[-3,3],由3-x>0解得x<3,可得B =(-∞,3),因此∁R B =[3,+∞).∴A∩(∁R B)=[-3,3]∩[3,+∞)={3}.故选C.二、非选择题9.[2018·全国卷Ⅰ]已知函数f(x)=log2(x 2+a).若f(3)=1,则a =________. 答案:-7解析:∵ f(x)=log2(x 2+a)且f(3)=1,∴ 1=log2(9+a),∴ 9+a =2,∴ a=-7.10.[2019·南阳模拟]已知函数y =f(x)满足f(x)=2f ⎝ ⎛⎭⎪⎫1x +3x,则f(x)的解析式为________. 答案:f(x)=-x -2x(x≠0)解析:由题意知函数y =f(x)满足f(x)=2f ⎝ ⎛⎭⎪⎫1x +3x,即f(x)-2f ⎝ ⎛⎭⎪⎫1x =3x,用1x 代换上式中的x,可得f ⎝ ⎛⎭⎪⎫1x -2f(x)=3x,联立得,⎩⎪⎨⎪⎧fx -2f ⎝ ⎛⎭⎪⎫1x =3x ,f ⎝ ⎛⎭⎪⎫1x -2f x =3x,解得f(x)=-x -2x(x≠0).11.[2019·河南开封模拟]f(x)=⎩⎪⎨⎪⎧2e x -1,x<2,log 3x 2-1,x≥2,则f(f(2))的值为________.答案:2解析:∵当x≥2时,f(x)=log 3(x 2-1),∴f(2)=log 3(22-1)=1<2,∴f(f(2))=f(1)=2e1-1=2.12.[2019·湖北黄冈浠水县实验高中模拟]已知函数f(x)的定义域为(-1,0),则函数f(2x +1)的定义域为________.答案:⎝⎛⎭⎪⎫-1,-12解析:∵函数f(x)的定义域为(-1,0), ∴由-1<2x +1<0,解得-1<x<-12.∴函数f(2x +1)的定义域为⎝ ⎛⎭⎪⎫-1,-12.课时测评③一、选择题1.下列各组函数中表示同一函数的是( ) A .f(x)=x 2,g(x)=(x)2B .f(x)=1,g(x)=x 2C .f(x)=⎩⎪⎨⎪⎧x ,x≥0,-x ,x<0,g(t)=|t|D .f(x)=x +1,g(x)=x 2-1x -1答案:C解析:选项A 中,f(x)=x 2的定义域是R,g(x)=(x)2的定义域是{x|x≥0},故f(x)与g(x)不表示同一函数,排除A ;选项B 中,f(x)与g(x)定义域相同,但对应关系和值域不同,故f(x)与g(x)不表示同一函数,排除B ;选项D 中,f(x)=x +1的定义域为R,g(x)=x 2-1x -1的定义域为{x|x≠1},故f(x)与g(x)不表示同一函数,排除D ;选项C 中,f(x)=⎩⎪⎨⎪⎧x ,x≥0,-x ,x<0可化为f(x)=|x|,所以其与g(t)=|t|表示同一函数.故选C.2.已知函数f(x)=⎩⎪⎨⎪⎧2x-2,x>0,x ,x≤0,若f(a)+f(3)=5,则实数a =( )A .2B .-1C .-1或0D .0 答案:B解析:解法一 因为f(a)+f(3)=5,又f(3)=23-2=6,所以f(a)=-1,所以⎩⎪⎨⎪⎧2a-2=-1,a>0或⎩⎪⎨⎪⎧a =-1,a≤0,解得a =-1,故选B.解法二 因为f(3)=23-2=6,f(2)=22-2=2,所以f(2)+f(3)=2+6=8≠5,所以a≠2,排除A ;因为f(0)=0,所以f(0)+f(3)=0+6=6≠5,所以a≠0,排除C,D.故选B.3.函数f(x)=(x -2)0+23x +1的定义域是( ) A.⎝ ⎛⎭⎪⎫-13,+∞ B.⎝⎛⎭⎪⎫-∞,-13 C .R D.⎝ ⎛⎭⎪⎫-13,2∪(2,+∞)答案:D解析:要使函数f(x)有意义,只需⎩⎪⎨⎪⎧x≠2,3x +1>0,所以x>-13且x≠2,所以函数f(x)的定义域是⎝ ⎛⎭⎪⎫-13,2∪(2,+∞),故选D.4.[2019·湖南邵阳模拟]设函数f(x)=log 2(x -1)+2-x,则函数f ⎝ ⎛⎭⎪⎫x 2的定义域为( )A .[1,2]B .(2,4]C .[1,2)D .[2,4) 答案:B解析:∵函数f(x)=log 2(x -1)+2-x 有意义,∴⎩⎪⎨⎪⎧x -1>0,2-x≥0,解得1<x≤2,∴函数的f(x)定义域为(1,2],∴1<x 2≤2,解得x∈(2,4],则函数f ⎝ ⎛⎭⎪⎫x 2的定义域为(2,4].故选B.5.[2019·陕西西安长安区质量检测大联考]已知函数f(x)=-x 2+4x,x∈[m,5]的值域是[-5,4],则实数m 的取值范围是( )A .(-∞,-1)B .(-1,2]C .[-1,2]D .[2,5] 答案:C解析:∵f(x)=-x 2+4x =-(x -2)2+4,∴当x =2时,f(2)=4,由f(x)=-x 2+4x =-5,解得x =5或x =-1,∴结合图象可知,要使函数在[m,5]上的值域是[-5,4],则-1≤m≤2.故选C.6.[2019·新疆乌鲁木齐一诊]函数f(x)=⎩⎪⎨⎪⎧e x -1,x<2,-log 3x -1,x≥2,则不等式f(x)>1的解集为( )A .(1,2) B.⎝⎛⎭⎪⎫-∞,43 C.⎝ ⎛⎭⎪⎫1,43 D .[2,+∞)答案:A解析:当x<2时,不等式f(x)>1即e x -1>1,∴x-1>0,∴x>1,则1<x<2;当x≥2时,不等式f(x)>1即-log 3(x -1)>1, ∴0<x-1<13,∴1<x<43,此时不等式无解.综上可得,不等式的解集为(1,2).故选A.7.[2019·定州模拟]设函数f(x)=⎩⎪⎨⎪⎧log 2x 2,x<0,-e x,x≥0,若f(f(t))≤2,则实数t 的取值范围是( )A.⎝⎛⎦⎥⎤-∞,-12∪[0,ln2]B .[ln2,+∞) C.⎝⎛⎦⎥⎤-∞,-12 D .[-2,+∞) 答案:A解析:令m =f(t),则f(m)≤2,则⎩⎪⎨⎪⎧m<0,log 2m 2≤2或⎩⎪⎨⎪⎧m≥0,-e m≤2,即-2≤m<0或m≥0,所以m≥-2,则f(t)≥-2,即⎩⎪⎨⎪⎧t<0,log 2t 2≥-2或⎩⎪⎨⎪⎧t≥0,-e t≥-2,即t≤-12或0≤t≤ln2,所以实数t 的取值范围是⎝ ⎛⎦⎥⎤-∞,-12∪[0,ln2].故选A. 8.[2019·福建福清校际联盟模拟]定义函数f(x),g(x)如下表:则满足f(g(x))>g(f(x))的x A .0或1 B .0或2 C .1或7 D .2或7 答案:D解析:由表格可以看出,当x =0时,g(0)=2,f(g(0))=f(2)=0,同理g(f(0))=g(1)=1,不满足f(g(x))>g(f(x)),排除A,B.当x =1时,f(g(1))=f(1)=2,g(f(1))=g(2)=7,不满足f(g(x))>g(f(x)),排除C.当x =2时,f(2)=0,g(2)=7,f(g(2))=f(7)=7,同理g(f(2))=g(0)=2,满足f(g(x))>g(f(x)). 当x =7时,f(g(7))=f(0)=1,g(f(7))=g(7)=0,满足f(g(x))>g(f(x)).故选D. 二、非选择题9.[2019·唐山五校联考]函数y =110x-2的定义域为________.答案:(lg2,+∞)解析:依题意,10x>2,解得x>lg2,所以函数的定义域为(lg2,+∞). 10.已知函数f(3x +2)=x 2-3x +1,则函数f(x)的解析式为________. 答案:f(x)=19x 2-13x 9+319解析:设t =3x +2,则x =t -23,所以f(t)=⎝ ⎛⎭⎪⎫t -232-3·t -23+1=19t 2-13t 9+319,所以函数f(x)的解析式为f(x)=19x 2-13x 9+319.11.对于每个实数x,设f(x)取y =4x +1,y =x +2,y =-2x +4三个函数中的最小值,用分段函数写出f(x)的解析式,并求f(x)的最大值.解析:由直线y =4x +1与y =x +2求得交点A ⎝ ⎛⎭⎪⎫13,73;由直线y =x +2与y =-2x +4,求出交点B ⎝ ⎛⎭⎪⎫23,83. 由图象可看出:f(x)=⎩⎪⎨⎪⎧-2x +4 ⎝ ⎛⎭⎪⎫x ≥23x +2 ⎝ ⎛⎭⎪⎫13<x<234x +1 ⎝ ⎛⎭⎪⎫x ≤13f(x)的最大值为f ⎝ ⎛⎭⎪⎫23=83.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3模块 第3节[知能演练]一、选择题1.函数y =xsin x,x ∈(-π,0)∪(0,π)的图象可能是下列图象中的()解析:∵y =xsin x 是偶函数,排除A ,当x =2时,y =2sin2>2,排除D. 当x =π6时,y =π6sin π6=π3>1,排除B.答案:C2.函数f (x )=tan ωx (ω>0)图象的相邻的两支截直线y =π4所得线段长为π4,则f (π4)的值是( )A .0B .1C .-1D.π4解析:由题意知T =π4,由πω=π4得ω=4,∴f (x )=tan4x ,∴f (π4)=tan π=0.答案:A3.函数f (x )=sin x -3cos x (x ∈[-π,0])的单调递增区间是( )A .[-π,-5π6]B .[-5π6,-π6]C .[-π3,0]D .[-π6,0]解析:f (x )=sin x -3cos x =2sin(x -π3)∵-π≤x ≤0,∴-4π3≤x -π3≤-π3当-π2≤x -π3≤-π3时,即-π6≤x ≤0时,f (x )递增.答案:D4.对于函数f (x )=sin x +1sin x(0<x <π),下列结论中正确的是( )A .有最大值而无最小值B .有最小值而无最大值C .有最大值且有最小值D .既无最大值又无最小值解析:f (x )=sin x +1sin x =1+1sin x ,∵0<x <π,∴0<sin x ≤1,∴1sin x ≥1,∴1+1sin x≥2.∴f (x )有最小值而无最大值. 答案:B 二、填空题 5.函数y =lgsin x + cos x -12的定义域为____________,函数y =12sin(π4-23x )的单调递增区间为________.解析:(1)要使函数有意义必须有⎩⎪⎨⎪⎧sin x >0cos x -12≥0, 即⎩⎪⎨⎪⎧sin x >0cos x ≥12,解得⎩⎪⎨⎪⎧2kπ<x <π+2kπ-π3+2kπ≤x ≤π3+2kπ(k ∈Z ), ∴2kπ<x ≤π3+2kπ,k ∈Z ,∴函数的定义域为{x |2kπ<x ≤π3+2kπ,k ∈Z }.(2)由y =12sin(π4-23x )得y =-12sin(23x -π4),由π2+2kπ≤23x -π4≤32π+2kπ,得 98π+3kπ≤x ≤21π8+3kπ,k ∈Z ,故函数的单调递增区间为 [98π+3kπ,21π8+3kπ](k ∈Z ). 答案:{x |2kπ<x ≤π3+2kπ,k ∈Z }[98π+3kπ,21π8+3kπ](k ∈Z ) 6.对于函数f (x )=⎩⎪⎨⎪⎧sin x ,sin x ≤cos x cos x ,sin x >cos x ,给出下列四个命题:①该函数是以π为最小正周期的周期函数;②当且仅当x =π+kπ(k ∈Z )时,该函数取得最小值-1; ③该函数的图象关于x =5π4+2kπ(k ∈Z )对称;④当且仅当2kπ<x <π2+2kπ(k ∈Z )时,0<f (x )≤22.其中正确命题的序号是________.(请将所有正确命题的序号都填上) 解析:画出f (x )在一个周期[0,2π]上的图象.由图象知,函数f (x )的最小正周期为2π,在x =π+2kπ(k ∈Z )和x =32π+2kπ(x ∈Z )时,该函数都取得最小值-1,故①②错误,由图象知,函数图象关于直线x =54π+2kπ(k ∈Z )对称,在2kπ<x <π2+2kπ(k ∈Z )时,0<f (x )≤22.故③④正确.答案:③④ 三、解答题7.已知函数y =f (x )=2sin x1+cos 2x -sin 2x.(1)求函数定义域;(2)用定义判断f (x )的奇偶性; (3)在[-π,π]上作出f (x )的图象; (4)写出f (x )的最小正周期及单调区间. 解:(1)∵f (x )=2sin x 2cos 2x=sin x|cos x |, ∴函数的定义域是{x |x ≠kπ+π2,k ∈Z }.(2)由(1)知f (-x )=sin(-x )|cos(-x )|=-sin x|cos x |=-f (x ),∴f (x )是奇函数. (3)f (x )=⎩⎨⎧tan x (-π2<x <π2)-tan x (-π≤x <-π2或π2<x ≤π),y =f (x )(x ∈[-π,π])的图象如图所示.(4)f (x )的最小正周期为2π,单调递增区间是(-π2+2kπ,π2+2kπ)(k ∈Z ),单调递减区间是(π2+2kπ,3π2+2kπ)(k ∈Z ).8.已知a >0,函数f (x )=-2a sin(2x +π6)+2a +b ,当x ∈[0,π2]时,-5≤f (x )≤1.(1)求常数a ,b 的值;(2)设g (x )=f (x +π2)且lg[g (x )]>0,求g (x )的单调区间.解:(1)∵x ∈[0,π2],∴2x +π6∈[π6,7π6],∴sin(2x +π6)∈[-12,1],∴-2a sin(2x +π6)∈[-2a ,a ],∴f (x )∈[b,3a +b ],又-5≤f (x )≤1.∴⎩⎪⎨⎪⎧ b =-53a +b =1,解得⎩⎪⎨⎪⎧a =2b =-5. (2)f (x )=-4sin(2x +π6)-1,g (x )=f (x +π2)=-4sin(2x +7π6)-1=4sin(2x +π6)-1,又由lg[g (x )]>0,得g (x )>1, ∴4sin(2x +π6)-1>1,∴sin(2x +π6)>12,∴π6+2kπ<2x +π6<56π+2kπ,k ∈Z ,由π6+2kπ<2x +π6≤2kπ+π2,得 kπ<x ≤kπ+π6,k ∈Z .由π2+2kπ≤2x +π6<56π+2kπ得 π6+kπ≤x <π3+kπ,k ∈Z . ∴函数g (x )的单调递增区间为(kπ,π6+kπ](k ∈Z ),单调递减区间为[π6+kπ,π3+kπ)(k ∈Z ).[高考·模拟·预测]1.若函数f (x )=(1+3tan x )cos x,0≤x <π2,则f (x )的最大值为( )A .1B .2 C.3+1D.3+2解析:因为f (x )=(1+3tan x )cos x =cos x +3sin x =2cos(x -π3),当x =π3时,函数取得最大值为2.故选B.答案:B2.若将函数y =tan(ωx +π4)(ω>0)的图象向右平移π6个单位长度后,与函数y =tan(ωx +π6)的图象重合,则ω的最小值为( )A.16 B.14 C.13D.12解析:将函数y =tan(ωx +π4)的图象向右平移π6个单位后,得到的函数为y =tan[ω(x -π6)+π4]=tan(ωx -πω6+π4),这个函数的图象与函数y =tan(ωx +π6)的图象重合,根据正切函数的周期是kπ,故其充要条件是-πω6+π4=kπ+π6(k ∈Z ),即ω=-6k +12(k ∈Z ),当k =0时,ω的最小值为12,故选D.答案:D3.已知函数f (x )=sin(x -π2)(x ∈R ),下面结论中错误的是( )A .函数f (x )的最小正周期为2πB .函数f (x )在区间[0,π2]上是增函数C .函数f (x )在图象关于直线x =0对称D .函数f (x )是奇函数解析:∵f (x )=-cos x ,∴f (x )为偶函数,故选D. 答案:D4.已知α∈(0,π4),a =(sin α)cos α,b =(sin α)sin α,c =(cos α)sin α,则a 、b 、c 的大小关系是________.解析:α∈(0,π4),1>cos α>sin α>0,y =(sin α)x 为减函数,∴a <b .而y =x sin α在(0,+∞)上为增函数,∴c >b .故c >b >a .答案:a <b <c5.已知函数f (x )=3(sin 2x -cos 2x )-2sin x cos x . (1)求f (x )的最小正周期;(2)设x ∈[-π3,π3],求f (x )的值域和单调递增区间.解:(1)∵f (x )=-3(cos 2x -sin 2x )-2sin x cos x =-3cos2x -sin2x =-2sin(2x +π3)∴f (x )的最小正周期为π.(2)∵x ∈[-π3,π3],∴-π3≤2x +π3≤π,∴-32≤sin(2x +π3)≤1. ∴f (x )的值域为[-2,3].∵当y =sin(2x +π3)递减时,f (x )递增,令2kπ+π2≤2x +π3≤2kπ+3π2,则kπ+π12≤x ≤kπ+7π12,k ∈Z ,又x ∈[-π3,π3],∴π12≤x ≤π3.故f (x )的递增区间为[π12,π3].[备选精题]6.设函数f (x )=sin(π4x -π6)-2cos 2π8x +1.(1)求f (x )的最小正周期;(2)若函数y =g (x )与y =f (x )的图象关于直线x =1对称,求当x ∈[0,43]时y =g (x )的最大值.解:(1)f (x )=sin π4x cos π6-cos π4x sin π6-cos π4x =32sin π4x -32cos π4x =3sin(π4x -π3),故f (x )的最小正周期为T =2ππ4=8.(2)解法一:在y =g (x )的图象上任取一点(x ,g (x )),它关于x =1的对称点为(2-x ,g (x )).由题设条件,点(2-x ,g (x ))在y =f (x )的图象上,可知g (x )=f (2-x )=3sin[π4(2-x )-π3]=3sin(π2-π4x -π3)=3cos(π4x +π3).当0≤x ≤43时,π3≤π4x +π3≤2π3,因此y =g (x )在区间[0,43]上的最大值为g (x )max =3cos π3=32.解法二:因区间[0,43]关于x =1的对称区间为[23,2],且y =g (x )与y =f (x )的图象关于x=1对称,故y =g (x )在[0,43]上的最大值即为y =f (x )在[23,2]上的最大值.由(1)知f (x )=3sin(π4x -π3),当23≤x ≤2时,-π6≤π4x -π3≤π6. 因此y =g (x )在[0,43]上的最大值为g (x )max =3sin π6=32.。
