经典:8、逻辑函数最小项表达式
卡诺图

11 1 1 1 1 1 1
1 1
1
1
1
L B AD
18
例 用卡诺图化简逻辑函数 Y(A、B、C、D)=∑m(0,1,2,3,4,5,6,7,8,10,11) 解:
19
A
BC B D
Y A BC B D
20
例 化简图示逻辑函数。 解:
1
2 多余 的圈
4
3
Y ACD A B C A C D ABC
ABC D ABCD ABD ABC D ABCD ABD
ABD ABD AD
11
10
AD AD D
相邻项相加时,反复应用 A A 1公式,函数 表达式的项数和每项所含的因子数就会减小.
11
两个最小项合并
12
四个最小项合并
13
CD 00 AB 00 01 11 10 1 1
A BCD A BCD ABCD A BCD A BC D A BC D ABC D A BC D C
(c )
(d )
八个最小项的合并
14
用卡诺图化简逻辑函数的步骤:
画出逻辑函数的卡诺图。 • 合并最小项,即根据前述原则画圈。 • 写出化简后的表达式。每一个圈写一个最简 与项,规则是:取值为l的变量用原变量表示,取 值为0的变量用反变量表示,将这些变量相与,然 后将所有与项进行或运算,即得最简与—或表达 式。
例1 将
L( A, B, C ) AB AC 化成最小项表达式
L( A, B, C ) AB(C C ) A( B B)C
ABC ABC A BC A B C
= m7+m6+m3+m1
逻辑函数的图形化简法

逻辑函数的图形化简法一、最小项1.最小项的特点(以三变量A,B,C为例)每项都只有三个因子(A,B,C);每个变量都是它的一个因子;每一变量或以原变量(A,B,C)形式消失,或以非变量(A非,B非,C非)形式消失;每个乘积项的组合仅消失一次,且取值为1;最小项可以编码。
2.最小项表达式及书写形式:最小项表达式是由若干个最小项相加的与—或表达式。
任何一个规律表达式都可以化成最小项表达式。
2.一个规律函数,假如有n个变量,则有2n个最小项。
最小项的基本性质:a.只有一组取值使之为“1” b.任二最小项乘积与“0” c.所的最小项之和为“1”例:3变量A,B,C,有23=8个最小项,其形式为:二、卡诺图(Karnaugh Map)1.卡诺图画法:三变量卡诺图:说明:三变量卡诺图由8个最小项m0—m7组成,每个最小项占一个方格;AB组合中左数位代表A变量,右数位代表B变量。
沿横向从一个方格进行到下一个方格时,两个数位只变化一个;原变量与非变量各占4格。
四变量卡诺图:说明:四变量卡诺图由16个最小项m0—m15组成,每个最小项占一个方格;纵向方向因有两个变量CD,增加了8个方格,CD变化规律同AB;原变量与非变量各占8格。
2.相邻的概念二小格相邻组合:例如:卡诺图中,有F(A,B,C,D)=∑m(2,3,8,10,12)(m8、m12)、(m2、m3)几何相邻,(m2、m10)规律相邻四小格相邻组合:四小格相邻时,4个最小项可合并成1项,且可消去两个变量。
八方格相邻组合:八方格相邻时,8个最小项可合并成1项,且可消去三个变量。
三、用卡诺图简化规律函数1.用卡诺图化简规律函数基本步骤:2.几个留意点:必需使每个方格(最小项)至少被包含一次;使每个组合包含尽可能多的方格;全部的方格包含在尽可能少的不同组合中。
未用最小项表示的规律函数的简化:规律函数未用(最小项)表示照样可以化简。
(/版权全部)假如F采纳与—或表达式,在填入卡诺图过程中先把函数绽开成标准与--或式,再填入卡诺图中进行化简。
电子技术及应用第七章-第四节-3逻辑函数表达式的最简标准

2、最简与非—与非表达式
最简与非-或非表达式,就是 式中的非号最少、并且每个非号下 面乘积项中的变量也最少的与非与非表达式。
பைடு நூலகம்
Y A B AC A B AC
__________ ____ _____ _____ __ __ __________ __ __________ __ __ __
__
__
A B A C
3、最简或与表达式
最简或与表达式,就是式中的 括号最少、并且每个括号内相加的 变量也最少。
__ __
Y A B AC ( A B)( A C )
__ __
4、最简与或非表达式
最简与或非表达式,就是式中非 号下面相加的乘积项最少、并且每个 乘积项中相乘的变量也最少的与或非 表达式。
Y A B AC ( A B )( A C ) A B AC
__________ ____ __ __ __ __
__
__
所以,对逻辑函数进 从上面所介绍的函数的 各种最简表达式可知, 只要得到了函数的最简 与或表达式,再利用摩 根定律进行适当的变换, 就可以得到其他几种类 型的最简表达式。
逻辑函数的最小项
如果一个函数的某个乘积项包含了函数的全部 变量,其中每个变量都以原变量或反变量的形式出 现,且仅出现一次,则这个乘积项称为该函数的一
个标准积项,标准积项通常称为最小项。
逻辑函数的最小项表达式
任一个逻辑函数均可以表示成一
函数的标准 与或表达式
组最小项的和,这种表达式称为函数
的最小项表达式,也称为函数的标准 与或表达式,或称为函数的标准积之 和表达式。任何一个n变量的函数都 有一个且仅有一个最小项表达式。
第四次课逻函数的表示方法和最大项最小项

F ( A, B, C ) = M 0 ⋅ M 2 ⋅ M 4 ⋅ M 5 ⋅ M 7 = ( A + B + C )( A + B′ + C )( A′ + B + C )( A′ + B + C ′)( A′ + B′ + C ′)
标准或与型特点:1.式子为和项之积的形式; 2.逻辑函数不一定包含所有的最大 项, 但每一项必须为最大项
在输入变量任一取值下,有且仅有一个最大项的 值为0; 全体最大项之积为 0; 任何两个最大项之和为 1; 只有一个变量不同的两个最大项的乘积等于各相 同变量之和。
( A + B + C) • ( A ′ + B + C) = B + C
26
四、 逻辑函数的标准或与式型-最大项 之积标准型
如
Y ( A, B ) = M 1 ⋅ M 3 = ( A + B′)( A′ + B′)
Y = AC + B′C = ( AC + B′ )( AC + C ) = ( A + B′ )( B ′ + C )C = ( A + B′ + CC ′ )( B′ + C + AA′ )(C + AA′ ) = ( A + B′ + C )( A + B′ + C ′ )( B′ + C + A) • ( B′ + C + A′ )(C + A)(C + A′ ) = M 2 M 3 M 6 ( A + C + BB′ )( A′ + C + BB′ ) = M 2 M 3 M 6 ( A + C + B )( A + C + B′ )( A′ + C + B )( A′ + C + B ′ )
逻辑函数的三个规则和标准形式

A B C = m2
0
1
1
A B C = m3
1
0
0
A B C = m4
1
0
1
A B C = m5
1
1
0
A B C = m6
1
1
1
A B C = m7
① n 个变量的所有最小项(2n个)之和为1 ;
② 相同变量的任意两个最小项mi 和mj 之积为0(i≠j); ③ n变量最小项有n 个相邻最小项。
数字电路与逻辑设计
数字电路与逻辑设计
第二章 逻辑函数及其简化
数字电路与逻辑设计
(2) 最大项表达式 全部由最大项相与而构成的或-与表达式称为最大项表达式,又称为标准或-与式, 或标准和之积式。
最大项表达式的书写形式:
对于逻辑函数:F A B C A B C A B C
可以简写成: 或写成:
F A, B, C M0×M1×M4 F A, B,C M 0,1,4
等式仍成立。 解:
原式左边=A[B +(C +D )]=AB +A(C +D ) = AB +AC +AD 原式右边=AB +A(C +D ) = AB +AC +AD
所以等式仍然成立。
第二章 逻辑函数及其简化
数字电路与逻辑设计
2.反演规则
设F 是一个逻辑函数表达式,若将其中所有的与、或互换,“0”、“1”互换,原、 反变量互换,长非号(两个或两个以上变量上的非号)不变,这样可得F 的反函数。
第二章 逻辑函数及其简化
数字电路与逻辑设计
(2) 最小项表达式 全部由最小项相加而构成的与-或表达式称为最小项表达式,又称为标准与-
5.最小项
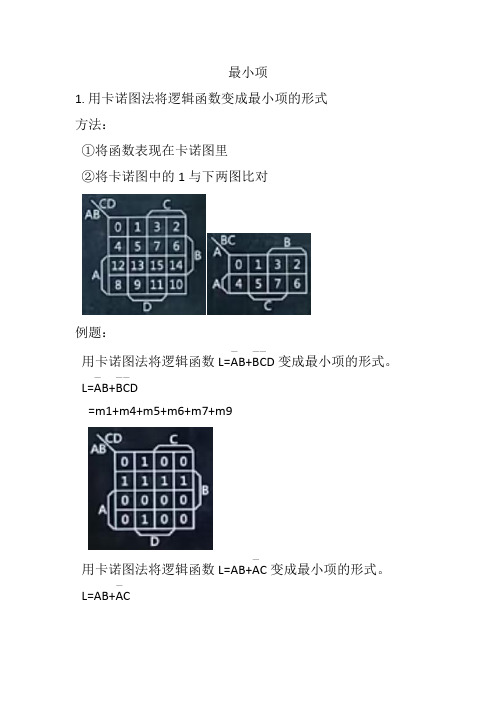
最小项1.用卡诺图法将逻辑函数变成最小项的形式方法:①将函数表现在卡诺图里②将卡诺图中的1与下两图比对例题:用卡诺图法将逻辑函数L=A—B+B—C—D变成最小项的形式。
L=A—B+B—C—D=m1+m4+m5+m6+m7+m9用卡诺图法将逻辑函数L=AB+A—C变成最小项的形式。
L=AB+A—C2. 用公式法将逻辑函数变成最小项的形式方法:①利用A(B —+B)=A ,令每一项都包含全部代号②整理①的结果,令每一项都是A 、B 、C 、D 的顺序③将每一项的A 、B 、C 、D 变成1,将A —、B —、C —、D —变成0 ④将③的结果由二进制数变成十进制数⑤在m 后加上④中的结果例题:用公式法将逻辑函数L=AB+A __C 变成最小项的形式 ① L= AB + A __C=AB(C+C __) + A __C(B+B __)② =ABC+ ABC __+ A __BC+ A __B __C③ 111 110 011 001④ 7 6 3 1⑤ L=m7+m6+m3+ m13. 将最小项的形式化成变量形式方法:①取出m后的数字②将数字变成二进制数(3输入即变成3位,4输入即变成4位)③每个二进制数的第一个数是0则变成A—,是1则变成A第二个数是0则变成B—,是1则变成B第三个数是0则变成C—,是1则变成C第四个数是0则变成D—,是1则变成D④用公式法或者卡诺图法化简逻辑函数例题:将L(A,B,C,D)=m1+m4+m5+m6+m7+m9化成变量形式。
① 1 4 5 6 7 9②0001 0100 0101 0110 0111 1001③A__B__C__D A__BC__D__A__BC__D A__BCD__A__BCD AB__C__DL(A,B,C,D)=m1+m4+m5+m6+m7+m9=A__B__C__D+A__BC__D__+A__BC__D+A__BCD__+A__BCD+AB__C__D④=A__B+B__C__D4.将L=∑m+∑d形式的式子用卡诺图化简方法:①根据下图,在m对应代号处写1,d对应代号处写X,在其他代号处写0②将卡诺图表示成逻辑表达式注意:1、表示的过程中,可以将X当作1来凑8个1、4个1、2个1、1个12、将所有1都表示完即可,不需要表示完所有X例题:将L(A,B,C,D)=∑m(1,4,5,6,7,9)+∑d(10,11,12,13,14,15)用卡诺图法化简。
逻辑函数的表达式

(2) 消项法 利用消项公式 A + AB = A 或多余项公式 AB+AC+BC=AB+AC 例1: F = A B + A B C + A B D
=AB+AB(C+D) =AB 例2: F = A C + C D + A D E + A D G =AC+CD
28
(3) 消去互补因子法 利用 消去互补因子公式 A + AB = A + B 例1:F = A B + A C + B C
作业题 2.1 2.8 (1) 2.10 (1) 2.11 (1)
33
000
0
001
0
010
0
011
0
100
0
101
1
110
0
111
0
A B C A+B+C(M5)
000
1
001
1
010
1
011
1
100
1
101
0
110
1
111
1
17
(2)若F mj ,则F mk
(k为0 ~ (2n 1)中除了j以外的所有正整数)
证明:
因为mj mk 1
当 mj 0时, mk 1 当 mj 1时, mk 0 所以 mj mk
6
(2)最大项表达式(标准或与式) 例:F(A,B,C) = (A + B + C ) ·( A + B + C ) ·( A +
B+C) M0 M2 M4
(M0, M2, M4 ) M (0,2,4)
逻辑函数的最小项及其表达式

二 逻辑函数的最小项表达式
例: Y ( A, B, C ) AB AC
AB(C C ) AC (B B) ABC ABC ABC ABC
m7 m6 m3 m1
二 逻辑函数的最小项表达式
m3,5,6,7
即:3个变量组成 8(23)个最小项 mi
3个逻辑变量所有最小项可记为:m0 ~m7
n变量取值组 合排成二进制所 对应的十进制数
ABC
00m3
原变量形式视为1 反变量形式视为0
一 逻辑函数的最小项
3 变量全部最小项的真值表
A B C m0 m1 m2 m3 m4 m5 m6 m7 000 1 0 0 0 0 0 0 0 001 0 1 0 0 0 0 0 0 010 0 0 1 0 0 0 0 0 011 0 0 0 1 0 0 0 0 100 0 0 0 0 1 0 0 0 101 0 0 0 0 0 1 0 0 110 0 0 0 0 0 0 1 0 111 0 0 0 0 0 0 0 1
逻辑函数的 最小项及其表达式
一 逻辑函数的最小项
在n变量逻辑函数中,若m为包含n个因子的乘积 项,而且这n个变量都以原变量或反变量的形式在m 中出现,且仅出现一次,则这个乘积项m称为该函数 的最小项。
一 逻辑函数的最小项
A、B、C 三个逻辑变量构成的最小项有:
ABC ABC ABC ABC ABC ABC ABC ABC
例:将逻辑函数转换成最小项表达式。
Y AB AB AB C
解: Y AB AB AB C
AB ( A B)( A B)C AB ABC ABC
逻辑函数最小项.

下标i的确定:把最小项中的原变量记为1,反变量记 为0,当变量顺序确定后,可以按顺序排列成一个二进制数, 则与这个二进制数相对应的十进制数,就是这个最小项的 下标i 。
3个变量A、B、C的8个最小项可以分别表示为:
m0 A B C 、m1 A B C、m2 A BC 、m3 A BC m4 AB C 、m5 AB C、m6 ABC 、m7 ABC
逻辑函数最小项
学 校:常州高级技工学校 说课人:朱文彬 时 间:2013.12
组合逻辑电路
5.逻辑函数的最小项及其性质 (1)最小项: 如果一个函数的某个乘积项包含了函数的全部变 量,其中每个变量都以原变量或反变量的形式出现, 且该乘积项仅出现一次,则这个乘积项称为该函数的 一个标准积项,又称为最小项。
组合逻辑电路
5.逻辑函数的最小项及其性质 (1)最小项: 如果一个函数的某个乘积项包含了函数的全部变 量,其中每个变量都以原变量或反变量的形式出现, 且该乘积项仅出现一次,则这个乘积项称为该函数的 一个标准积项,又称为最小项。 3个变量A、B、C可组成8个最小项:
A B C 、A B C、A BC 、A BC、AB C 、AB C、ABC 、ABC
②任意两个不同的最小项的乘积必为0。 ③全部最小项的和必为1。
m6 0 0 0 0 0 0 1 0
m7 0 0 0 0 0 0 0 1
①任意一个最小项,只有一组乘积项取值使其值为1。
m6 0 0 0 0 0 0 1 0
m7 0 0 0 0 0 0 0 1
组合逻辑电路
(3)最小项的性质:
3 变量全部最小项的真值表 A B C m0 m1 m2 m3 m4 m5 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0
逻辑函数的标准表达式

逻辑函数的标准表达式
一个逻辑函数的表达式可以是多种多样的,通过布尔代数的公式可以将函数的表达式从一种形式转换为另一种形式。
例如:标准形式
逻辑函数有“最小项之和”及“最大项之积”两种标准形式。
表示方法
◆布尔代数法
按一定逻辑规律进行运算的代数。
与普通代数不同,布尔代数中的变量是二元值的逻辑变量。
◆真值表法
采用一种表格来表示逻辑函数的运算关系,其中输入部分列出输入逻辑变量的所有可能组合,输出部分给出相应的输出逻辑变量值。
◆逻辑图法
采用规定的图形符号,来构成逻辑函数运算关系的网络图形。
◆卡诺图法
卡诺图是一种几何图形,可以用来表示和简化逻辑函数表达式。
◆波形图法
一种表示输入输出变量动态变化的图形,反映了函数值随时间变
化的规律。
◆点阵图法
是早期可编程逻辑器件中直观描述逻辑函数的一种方法。
◆硬件设计语言法
是采用计算机高级语言来描述逻辑函数并进行逻辑设计的一种方法,它应用于可编程逻辑器件中。
目前采用最广泛的硬件设计语言有ABLE-HDL、VHDL等。
逻辑函数表达式的形式

m6
AB
__
C
__m3
A BC
__m1
AB
C
可以表示为: L(A, B, C) m1 m3 m6 m7
简化为: L(A, B,C) m(1, 3, 6, 7 )
任何一个逻辑函数经过转换,都能表示成唯一的最小项表达式 。
转换的方法有:①.代数转换法, ②.真值表转换法
2.2.2 最小项与最小项表达式
性质3 全部最小项之和为1 。 三变量最小项真值表
ABC
000 001 010 011 100 101 110 111
m0 m1 m2
ABC ABC ABC
1 00 0 10 0 01 0 00 0 00 0 00 0 00 0 00
m3 m4
ABC ABC
00 00 00 10 01 00 00 00
F m2 m4 m5 m6 m2, 4, 5, 6
用真值表法求最小项表达式
结果形如:F ( A, B,C) ABC ABC ABC ABC
例:函数 F=AB + AC
ABC
F
000
0
001 010 011 100 101
1 0 1 1
1
其
F m1 m3 m4 m5
余
m(1,3,4,5)
__
对于三个变量来说,A B , AB C A , A(B C) 不是最小项。
2.2.2 最小项与最小项表达式 为了书写方便,用mi表示最小项。下标i的取值规则是最小项
中原变量用1表示,反变量用0表示,由此得到一个二进制数,与 该二进制数对应的十进制数即下标i的值。
最小项 ABC ABC ABC ABC ABC ABC ABC ABC
第四讲 逻辑函数表示方法转换及最小项最大项

(2)逻辑图到逻辑式 从输入端到输出端 逐级写出每个图形符号对应的逻辑式。
先写出符号对应的逻辑式子
( A B )
B
A'
Y (( A B) ( A B)' ) ( A B)( A B) AB AB (( A B) ( A B)') A B
③ 任意两个最大项之和为1。 最大项,而且只有一个最大项的值为 积等于各相同变量之和。 0。
最小项和最大项的关系:
m0 A' B' C'、m4 AB' C'
M 0 A B C、M 4 A' B C
m0' ( A' B' C ' )' A B C M0
m4' ( AB' C ' )' A' B C M 4
即:
mi ' M i或mi Mi '
三、逻辑函数的两种标准形式
1. 逻辑函数的最小项之和形式——标准与或式
如果在一个与或表达式中,所有与项均为最小项, 则称这种表达式为最小项之和形式,或称为标准与或式、 标准积之和式。 例如: Y ( A, B, C )
数字电子技术基础
河北科技大学信息学院
内容回顾
逻辑代数的基本公式
1 2 3 4 5
0· A=0 A· 1=A
A A A
11 12 13 14 15
A+1=1 A+0=A
A A A
A A' 1
A A' 0
A• B=B • A
A• (B • C)=(A • B) • C
逻辑函数的卡诺图

1.最小项的基本概念由A、B、C三个逻辑变量构成的许多乘积项中有八个被称为A、B、C的最小项的乘积项,它们的特点是1. 每项都只有三个因子2. 每个变量都是它的一个因子3. 每一变量或以原变量(A、B、C)的形式出现,或以反(非)变量(A、B、C)的形式出现,各出现一次一般情况下,对n个变量来说,最小项共有2n个,如n=3时,最小项有23=8个2.最小项的性质为了分析最小项的性质,以下列出3个变量的所有最小项的真值表。
由此可见,最小项具有下列性质:(1)对于任意一个最小项,只有一组变量取值使得它的值为1,而在变量取其他各组值时,这个最小项的值都是0。
(2)不同的最小项,使它的值为1的那一组变量取值也不同。
(3)对于变量的任一组取值,任意两个最小项的乘积为0。
(4)对于变量的任一组取值,全体最小项之和为1。
3.最小项的编号表示,下标i即最小项编号,用十进制数表示。
以ABC为最小项通常用mi例,因为它和011相对应,所以就称ABC是和变量取值011相对应的最小项,而按此原则,3个变量的最小项011相当于十进制中的3,所以把ABC记为m3二、逻辑函数的最小项表达式利用逻辑代数的基本公式,可以把任一个逻辑函数化成一种典型的表达式,这种典型的表达式是一组最小项之和,称为最小项表达式。
下面举例说明把逻辑表达式展开为最小项表达式的方法。
例如,要将化成最小项表达式,这时可利用的基本运算关系,将逻辑函数中的每一项都化成包含所有变量A、B、C的项,然后再用最小项下标编号来代表最小项,即又如,要将化成最小项表达式,可经下列几步:(1)多次利用摩根定律去掉非号,直至最后得到一个只在单个变量上有非号的表达式;(2)利用分配律除去括号,直至得到一个与或表达式;(3)在以上第5个等式中,有一项AB不是最小项(缺少变量C),可用乘此项,正如第6个等式所示。
由此可见,任一个逻辑函数都可化成为唯一的最小项表达式。
三、用卡诺图表示逻辑函数1.卡诺图的引出一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各最小项相应地填入一个特定的方格图内,此方格图称为卡诺图。
逻辑函数f=abc的最小项之和形式为

逻辑函数f=abc的最小项之和形式为
abcf
0000
0010
0101
0111
1001
1011
1102
1112
根据真值表可以确定函数f的其他表示形式,如最小项表达式。
最小项表示形式是指将逻辑函数表示为所有输出结果等于1的输入组
合的逻辑与(AND)的结果。
在上述真值表中,当 f=1 时,对应的输入组合有(0,1,0)和(0,1,1)。
因此最小项表达式为:(a'bc).
最小项之和形式是指将逻辑函数表示为所有输出结果等于1的输入组
合的逻辑或(OR)的结果。
在上述真值表中,当 f=1 时,对应的输入组合有(0,1,0)和(0,1,1)。
因此最小项之和表达式为:(a'bc + a'b'c + a'bc')。
综上所述,逻辑函数 f=a+bc 的最小项之和形式为 (a'bc + a'b'c + a'bc')。
13、逻辑函数的最小项

2020/10/16
8
四、最小项表达式 任何一个逻辑函数都可以表示为最小项之和的 形式——标准与或表达式。而且这种形式是惟一的, 就是说一个逻辑函数只有一种最小项表达式。
例2-8 将Y=AB+BC展开成最小项表达式。
解:Y AB BC AB(C C) ( A A)BC
卡诺图的基本组成单元是最小项,所以先讨论一 下最小项及最小项表达式。
2020/10/16
4
一.最小项及最小项表达式
1、最小项
设A、B、C是三个逻辑变量,若由这三个逻辑变 量按以下规则构成乘积项:
(1)每个乘积项都只含三个因子,且每个变量 都是它的一个因子;
(2)每个变量都以反变量(A、B、C)或以原变量 (A、B、C)的形式出现一次,且仅出现一次。
思考练习
1
2.6 逻辑函数的卡诺图化简法
2.6.1 逻辑函数的最小项
课程引入 教学目标 重点难点 教学内容
教学目标: 1.知道最小项及最小项表达式的定义 2. 掌握最小项的性质 3. 能对最小项进行编号
思考练习
2
2.6 逻辑函数的卡诺图化简法
2.6.1 逻辑函数的最小项
课程引入 教学目标 重点难点
重点难点: 1.最小项的性质 2.最小项的编号
教学内容
思考练习
3
2.6.1 逻辑函数的最小项
公式化简法评价: 优点:变量个数不受限制。 缺点:目前尚无一套完整的方法,结果是否最简 有时不易判断。
利用卡诺图可以直观而方便地化简逻辑函数。它 克服了公式化简法对最终化简结果难以确定等缺点。
卡诺图是按一定规则画出来的方框图,是逻辑函 数的图解化简法,同时它也是表示逻辑函数的一种方 法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
__
__ __ __ __ __
ABC ABC ABC A BC A BC
重叠定律
__ __ __
ABC ABC A BC
m7 m6 m2
4
例4、已知逻辑函数f(A,B,C)的真值表如
下,试写出它的最小项表达式。
A
B
C
f(A,B,C)
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
1
1
补足的方法是:例如项A__B需补足变量C, 只要构建 AB AB(C C)
3
__ __ __
例3将逻辑函数f (A, B,C) AB BC A BC
表示为最小项表达式。
__ __ __
பைடு நூலகம்
解:f (A, B,C) AB BC A BC
__
__ __ __ __
AB(C C) (A A)BC A BC
8
9
10
小结
1、逻辑函数的最小项表达式:任何 一个逻辑函数都可以写成它的最小项 的与或式。 方法:最小项表达式:首先要将逻 辑函数写成与或式,然后将因子不 足的项补足。 2、在真值表中值等于1的最小项的与 或式为逻辑函数的最小项表达式。
11
最小项表达式
盐高职高二数学组:陆军
1
2
定义:任何一个逻辑函数都可以写成
它的最小项的与或式,这叫做该逻辑函数
的最小项表达式。
__ __ __
例3、将逻辑函数f (A, B,C) AB BC A BC
表示为最小项表达式
分析:为了获得最小项表达式:首先要将 逻辑函数写成与或式,然后将因子不足的 项补足。
1
0
0
1
1
1
1
5
解:因为由表得:当ABC分别是000,001,101,111 时,逻辑函数f(A,B,C)的值为1。
即:在真值表中值等于1的最小项的与或式 为逻辑函数的最小项表达式。
__ __ __ __ __
__
f (A, B,C) A BC A BC A BC ABC
m0 m1 m5 m7
6
学生练习:
1、将下列各逻辑函数表达式表示为最小项表达式:
(1)Y__
AC BC __ __ __ __
AB;
(2)
1、Y ABC A B C ABC A B C A BC m7 m5 m6 m2 m3
__
__ __ __ __ __
2、Y ABC A BC A B C A B C m7 m3 m5 m0
Y BC AC ABC;
(3) Y AB BC ABC.
2、已知逻辑函数f(A,B)的真值表如下,试写出它的
最小项表达式。 A
B
f(A,B)
0
0
1
0
1
0
1
0
1
1
1
1
7
__ __ __
3、列出f (A, B,C) A BC AC BC的真值表, 并表示为最小项的表达式。
1 0 1 0 1 0 0 1
