任意角的三角函数第一课时作业

合集下载

任意角的三角函数(第一课时)

�� 4
�� 3
cos
tan
sin �� cos �� tan ��
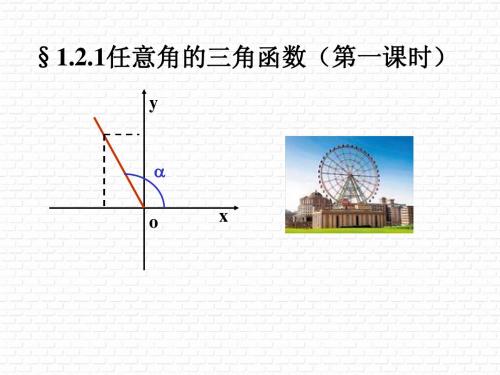
探讨：当角α 不是锐角时，sinα ，cosα ，tanα 的值又如何去求呢？知识探究一：任意角的三角函数问题 1：为了研究方便，我们把锐角 α 放到直角坐标系中，并使角 α 的顶点与原点 O 重合, 始边与 x 轴的非负半轴重合.在角 α 的终边上取一点 P（x，y）,设点 P 与原点的距离为 r，那么，sinα，cosα，tanα 的值分别如何表示？
其中： OM x MP y OP r x 2 y 2
问题 2：如果改变点Ｐ在终边上的位置，这三个比值会改变吗？
sin
MP y OP r OM x cos OP r MP y tan OM x
问题 3：为了使sin ��， cos ��的表示式更简单，你认为点 P 的位置选在何处最好？此时， sin ��， cos ��分别等于什么？
任意角的三角函数(第一课时) 学习目标: 1、掌握任意角的正弦、余弦、正切的定义 2、理解任意角的三角函数不同的定义方法学习重点：任意角的正弦、余弦、正切的定义学习难点：用角的终边上的点的坐标来刻画三角函数学习过程：复习回顾：我们已经学习过锐角的三角函数，如图：
sin
α
�� 6
在直角坐标系中，以原点 O 为圆心，以单位长度为半径的圆称为单位圆. 问题 4：设角��是一个任意角，对于角��的终边上一点 P，要使|OP|=1，点 P 的位置如何确定？
任意
角
的三角函数定义
P( x, y)

1.2.1任意角的三角函数(1)

2 若a 0则r -17a, 于是
8a 8 15a 15 8a 8 sin , cos , tan 17a 17 17a 17 15a 15
3、已知角的终边在直线y 2 x上，求角的sin ,cos , tan 的值.
OP0 (3) 2 (4) 2 5
y
M0
M
Px, y
M 0 P0 4
OM 0 3
OM x MP y
O
x
OMP ∽ OM 0 P0
P0 3,4
于是， sin y y | MP | M 0 P0 4 ; 1 OP OP0 5 OM 0 x OM 3 cos x ; 1 OP OP0 5
P(a, b)
1
cos a
x

o
M
b tan a
同样的，我们可以利用单位圆来定义任意角的三角函数。
任意角的三角函数定义
设是一个任意角，它的终边与单位圆交于点P( x, y )
那么:（1）y 叫做
的正弦，记作 sin ，即 sin y ；（2）x 叫做的余弦，记作 cos ，即 cos x ； y y tan （3）叫做的正切，记作，即 tan ( x 0)
y
MP b sin OP r
OM a cos OP r
﹒Pa, b

MP b tan OM a
o
﹒
M
x
问2：对于确定的角，这三个比值的大小和 P 点在角的终边上的位置是否有关呢？
y
P
P(a,b)
﹒
M

2020-2021学年第一学期高中数学新教材必修第一册苏教版第七章第3课时任意角的三角函数(1)

第3课时任意角的三角函数(1)一、学习目标1.掌握任意角的正弦、余弦、正切的定义.2.掌握正弦、余弦、正切函数的定义域和这三种函数的值在各象限的符号.二、问题导引预习教材P166——170的内容,思考下面的问题.在前面的学习中,我们在初中角的基础上将角的概念进行了推广,得到了任意角的概念,另外,还学习了角的另一种度量方法——弧度制.在初中学习了锐角后,我们研究了锐角的三角函数,现在,学习了任意角,那么我们能研究任意角的三角函数吗?如果能,又该如何研究呢?能通过锐角的三角函数来研究任意角的三角函数吗?三、即时体验1.填表:角正弦余弦正切2.已知角α的终边过点P(-3, 4),则sinα=, cosα=, tanα=.3.角-1328°的正弦值、余弦值、正切值的符号分别是、、.四、导学过程类型1由角的终边上的点求三角函数值【例1】已知角α的终边经过点P(2, -5),求α的正弦值、余弦值、正切值.类型2三角函数值的符号的判定【例2】确定下列三角函数值的符号:(1) cos; (2) sin(-565°); (3) tan.类型3由三角函数值求角的终边上的点的坐标【例3】已知角θ的顶点为坐标原点,始边为x轴的正半轴,若P(4, y)是角θ终边上一点, 且sinθ=-,求y的值.五、课堂练习1. (多选)若sinθcosθ<0,则角θ的终边在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.若<θ<π,则点P(cosθ, sinθ)位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.已知角α的终边经过点P(5, 12),则sinα+cosα=.4. sin1 cos2 tan3值的符号是.5.已知角α的终边经过点P(5t, 12t)(t≠0),求sinα+cosα的值.六、课后作业1. 若－<θ<－π,则点在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.若角α的终边过点P(2sin30°, －2cos30°),则sinα的值等于 ()A. B. － C. － D. －3.若sinαcosα>0, cosαtanα<0,则角α的终边落在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. (多选)已知θ是第二象限角,则下列判断中正确的是()A. sin cos>0B. sin<0C. cos<0D. tan>05.已知角α的终边经过点P,则sinα=, tanα=.6. sin cos tan的值的符号是(填“正”或“负”).7. 已知角α的终边落在射线y=2x(x≥0)上,那么sinα·cosα=.8.设是第一象限角,且|cosα|=－cosα,则α可能是()A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角9. (多选)函数y=++的可能取值为()A. －3B. －1C. 1D. 310.已知角θ的终边过点P(x, 3)(x≠0),且cosθ=x,那么tanθ=.11.若角α的终边过点P(－4m, 3m)(m≠0),求2sinα+cosα的值.12.已知角α的终边在直线y=kx上,若sinα=－,且cosα<0,试求k的值.13.已知角α的终边上一点P到x轴、y轴的距离之比为4∶3,且cosα<0,求cosα－sinα的值.。

任意角的三角函数及弧度制教案及练习(含答案)

第一章：三角函数第一课时教材：角的概念的推广目的：要求学生掌握用“旋转”定义角的概念，并进而理解“正角”“负角”“象限角”“终边相同的角”的含义。

过程：一、提出课题：“三角函数”回忆初中学过的“锐角三角函数”——它是利用直角三角形中两边的比值来定义的。

相对于现在，我们研究的三角函数是“任意角的三角函数”，它对我们今后的学习和研究都起着十分重要的作用，并且在各门学科技术中都有广泛应用。

二、角的概念的推广1.回忆：初中是任何定义角的？（从一个点出发引出的两条射线构成的几何图形）这种概念的优点是形象、直观、容易理解，但它的弊端在于“狭隘”2.讲解：“旋转”形成角突出“旋转”注意：“顶点”“始边”“终边”“始边”往往合于x轴正半轴3.“正角”与“负角”——这是由旋转的方向所决定的。

记法：角α或α∠可以简记成α4.由于用“旋转”定义角之后，角的范围大大地扩大了。

1︒角有正负之分如：α=210︒β=-150︒γ=-660︒2︒角可以任意大实例：体操动作：旋转2周（360︒³2=720︒） 3周（360︒³3=1080︒）3︒还有零角一条射线，没有旋转三、关于“象限角”为了研究方便，我们往往在平面直角坐标系中来讨论角角的顶点合于坐标原点，角的始边合于x轴的正半轴，这样一来，角的终边落在第几象限，我们就说这个角是第几象限的角（角的终边落在坐标轴上，则此角不属于任何一个象限）例如：30︒ 390︒-330︒是第Ⅰ象限角， 300︒-60︒是第Ⅳ象限角585︒ 1180︒是第Ⅲ象限角，-2000︒是第Ⅱ象限角等四、关于终边相同的角1．观察：390︒，-330︒角，它们的终边都与30︒角的终边相同2．终边相同的角都可以表示成一个0︒到360︒的角与)k∈个周角的和(Zk390︒=30︒+360︒)1k(=-330︒=30︒-360︒ )1(-=k 30︒=30︒+0³360︒ )0(=k 1470︒=30︒+4³360︒ )4(=k -1770︒=30︒-5³360︒ )5(-=k3．所有与α终边相同的角连同α在内可以构成一个集合 {}Z k k S ∈⋅+==,360| αββ即：任何一个与角α终边相同的角，都可以表示成角α与整数个周角的和五、小结： 1︒ 角的概念的推广，用“旋转”定义角，角的范围的扩大 2︒“象限角”与“终边相同的角”第二课时教材：弧度制目的：要求学生掌握弧度制的定义，学会弧度制与角度制互化，并进而建立角的集合与实数集R 一一对应关系的概念。

高中数学第一章三角函数1.2.1任意角的三角函数(1)课时提升作业1新人教A版必修4

任意角的三角函数(一）(15分钟30分）一、选择题（每小题4分，共12分)1。

求值sin750°=( ）A。

- B. — C.D。

【解析】选C.sin 750°= sin（2×360°+ 30°)=sin 30°=。

2.(2015·晋江高一检测）如果角θ的终边经过点(，-1），那么cosθ的值是( ）A.—B。

- C. D.【解析】选C。

点（，-1）到原点的距离r==2，所以cosθ=.【延伸探究】将本题中点的坐标改为(—1，），求sinθ-cosθ。

【解析】点（-1,）到原点的距离r==2，所以sinθ=，cosθ=-,所以sinθ-cosθ=—=。

3.(2015·北京高一检测）已知α∈（0,2π)，且sinα<0，cosα〉0,则角α的取值范围是( ）A。

B.C. D.【解析】选D。

因为sinα〈0，cosα〉0，所以角α是第四象限角，又α∈(0，2π），所以α∈.二、填空题（每小题4分，共8分)4。

求值：cosπ+tan=______【解析】cosπ=cos=cos=,tan=tan=tan=，所以cosπ+tan=+.答案：+5.(2015·南通高一检测)若角135°的终边上有一点(—4，a），则a的值是________.【解析】因为角135°的终边与单位圆交点的坐标为，所以tan 135°==-1，又因为点(—4，a)在角135°的终边上，所以tan 135°=,所以=-1,所以a=4.答案：4【补偿训练】如果角α的终边过点P(2sin 30°，—2cos 30°）,则cosα的值等于________。

【解析】2sin 30°=1,—2cos 30°=—，所以r=2，所以cosα=.答案：三、解答题6.（10分)判断下列各式的符号.（1)sinα·cosα（其中α是第二象限角）。

高中数学第五章三角函数5-1任意角和蝗制5-1-1任意角课时作业新人教A版必修第一册

5.1.1 任意角必备知识基础练1．下列命题中正确的是( )A．第一象限角小于第二象限角B．锐角一定是第一象限角C．第二象限角是钝角D．平角大于第二象限角2．440°角的终边落在( )A．第一象限 B．第二象限C．第三象限 D．第四象限3．终边在第四象限的角α的集合是( )A．{α|－90°<α<0°)B．{α|270°＋k·360°<α<k·360°，k∈Z}C．{α|k·360°－90°<α<k·360°，k∈Z}D．{α|k·180°－90°<α<k·180°，k∈Z}4．已知点P在圆O上按顺时针方向每秒转30°，2秒钟后，OP转过的角等于( ) A．－60° B．－30°C．60° D．30°5．下列各角中，与－30°终边相同的角为( )A．210° B．－390°C．390° D．30°6．[2022·广东韶关田家炳中学高一期末](多选)下列四个角为第二象限角的是( ) A．－200°B．100° C．220°D．420°7．第24届冬季奥运会于2022年2月4日至2月20日在北京举行，中国运动员通过顽强拼搏，共获得9枚金牌，列金牌榜第三名，创造了冬奥会上新的辉煌．在冬奥会的比赛中有一位滑雪运动员做了一个空中翻腾五周的高难度动作，那么“空中翻腾五周”等于________度(不考虑符号).8．集合{α|k·180°＋45°≤α≤k·180°＋90°，k∈Z}中，角所表示的取值范围(阴影部分)正确的是________(填序号).关键能力综合练1．已知角α为锐角，则下列各角中为第四象限角的是( )A．α＋90° B．α＋180°C．α－90° D．α－180°2．与－525°角的终边相同的角可表示为( )A．525°－k·360°(k∈Z)B．185°＋k·360°(k∈Z)C．195°＋k·360°(k∈Z)D．－195°＋k·360°(k∈Z)3．[2022·山东枣庄高一期末]与－390°角的终边相同的最小正角是( )A．－30°B．30° C．60° D．330°4．若角α，β的终边相同，则α－β的终边落在( )A．x轴的非负半轴上 B．x轴的非正半轴上C．x轴上 D．y轴的非负半轴上5．若α＝45°＋k·180°(k∈Z)，则α的终边在( )A．第二或第三象限 B．第一或第三象限C．第二或第四象限 D．第三或第四象限6．(多选)下列条件中，能使α和β的终边关于y轴对称的是( )A．α＋β＝540° B．α＋β＝360°C．α＋β＝180° D．α＋β＝90°7．自行车大链轮有36齿，小链轮有24齿，当大链轮转过一周时，小链轮转过的角度是________度．8．若角α＝2 022°，则与角α具有相同终边的最小正角为________，最大负角为________．9．在区间[0°，360°)内找出与下列各角终边相同的角α，并判断它是第几象限角：(1)－165°；(2)1 390°；(3)－567°26′.10．已知角β为以O为顶点，x轴为始边，逆时针旋转60°所成的角．(1)写出角β的集合S；(2)写出S中适合不等式－360°<β<720°的元素．核心素养升级练1．终边为第一象限和第三象限的平分线的角的集合是( )A．{α|α＝45°＋k·360°，k∈Z}B．{α|α＝－135°＋k·180°，k∈Z}C．{α|α＝－135°＋k·360°，k∈Z}D．{α|α＝135°＋k·180°，k∈Z}2．若角α的终边在函数y＝－x的图象上，试写出角α的集合为________．3．如图所示，分别写出适合下列条件的角的集合：(1)终边落在射线OB上；(2)终边落在直线OA上．5．1.1 任意角必备知识基础练1．答案：B解析：390°为第一象限角，120°为第二象限角，故A错误；因为0°<锐角<90°，所以锐角一定是第一象限角，故B正确；因为90°<钝角<180°，平角＝180°，480°为第二象限角，故C、D错误．2．答案：A解析：因为440°＝360°＋80°，所以440°角的终边与80°角的终边相同，所以440°角的终边落在第一象限．3．答案：C解析：终边在第四象限的角α的集合是{α|k·360°－90°<α<k·360°，k∈Z}或{α|k·360°＋270°<α<360°＋k·360°，k∈Z}．4．答案：A解析：∵点P在圆O上按顺时针方向旋转，则OP转过的角为负角，又每秒转30°，∴2秒钟后，OP转过的角等于2×(－30°)＝－60°.5．答案：B解析：与－30°终边相同的角的集合为：{α|α＝－30°＋k·360°，k∈Z}，当k＝－1时，得α＝－390°.6．答案：AB解析：对于A选项，－200°＝160°－360°，故－200°为第二象限角；对于B选项，100°是第二象限角；对于C选项，220°是第三象限角；对于D选项，420°＝60°＋360°，故420°为第一象限角．7．答案：1 800解析：“空中翻腾五周”等于5×360°＝1 800°.8．答案：③解析：当k＝0时，集合{α|45°≤α≤90°}，当k＝1时，集合{α|225°≤α≤270°}，则可得出角所表示的取值范围为③.关键能力综合练1．答案：C解析：因为角α为锐角，所以90°<α＋90°<180°，α＋90°为第二象限角；180°<α＋180°<270°，α＋180°为第三象限角；－90°<α－90°<0°，α－90°为第四象限角；－180°<α－180°<－90°，α－180°为第三象限角．2．答案：C解析：－525°＝195°－2×360°，所以－525°角的终边与195°角的终边相同，所以与－525°角的终边相同的角可表示为195°＋k·360°(k∈Z).3．答案：D解析：与－390°角终边相同角的集合为{α|α＝－390°＋k·360°，k∈Z}，当k＝2时，取得最小正角为330°.4．答案：A解析：因为角α，β的终边相同，故α－β＝k·360°，k∈Z.所以α－β的终边落在x轴的非负半轴上．5．答案：B解析：当k为奇数时，记k＝2n＋1，n∈Z，则α＝225°＋n·360°(n∈Z)，此时α为第三象限角；当k为偶数时，记k＝2n，n∈Z，则α＝45°＋n·360°(n∈Z)，此时α为第一象限角．6．答案：AC解析：假设α，β为0°～180°内的角，如图所示：由α和β的终边关于y 轴对称，所以α＋β＝180°，根据终边相同角的概念，可得α＋β＝k ·360°＋180°＝(2k ＋1)180°，k ∈Z ，所以满足条件的为A 、C.7．答案：540解析：因为大链轮转过一周时，小链轮转36齿．而小链轮有24齿，故小链轮转3624＝32周，一周为360°，故小链轮转过的角度为360°×32＝540°. 8．答案：222° －138°解析：∵2 022°＝5×360°＋222°，∴与角α终边相同的角的集合为{α|α＝222°＋k ·360°，k ∈Z }，∴最小正角是222°，最大负角是－138°.9．解析：(1)与－165°终边相同的角为－165°＋k ·360°，k ∈Z ，当k ＝1时，为195°，∴在[0°，360°)内，与－165°终边相同的角是195°，它是第三象限角；(2)与1 390°终边相同的角可以表示为1 390°＋k ·360°，k ∈Z ，当k ＝－3时，为310°，∴在[0°，360°)内，与1 390°终边相同的角是310°，它是第四象限角；(3)与－567°26′终边相同的角为－567°26′＋k ·360°，k ∈Z ，当k ＝2时，为152°34′，∴在[0°，360°)内，与－567°26′终边相同的角是152°34′，它是第二象限角．10．解析：(1)依题意，角β的集合S ＝{β|β＝60°＋k ·180°，k ∈Z }．(2)在S ＝{β|β＝60°＋k ·180°，k ∈Z }中，取k ＝－2，得β＝－300°，取k ＝－1，得β＝－120°，取k＝0，得β＝60°，取k＝1，得β＝240°，取k＝2，得β＝420°，取k＝3，得β＝600°.所以S中适合不等式－360°<β<720°的元素分别是－300°，－120°，60°，240°，420°，600°.核心素养升级练1．答案：B解析：终边为第一象限的平分线的角的集合是{α|α＝45°＋k·360°，k∈Z} ①，终边为第三象限的平分线的角的集合是{α|α＝－135°＋k·360°，k∈Z} ②，由①②得{α|α＝－135°＋k·180°，k∈Z}．2．答案：{α|α＝k·180°＋135°，k∈Z}解析：函数y＝－x的图象是第二、四象限的平分线，在0°～360°范围内，以第二象限平分线为终边的角为135°，以第四象限平分线为终边的角为315°，∴α的集合为{α|α＝k·360°＋135°或α＝k·360°＋315°，k∈Z}＝{α|α＝k·180°＋135°，k∈Z}．3．解析：(1)终边落在射线OB上的角的集合为S1＝{α|α＝60°＋k·360°，k∈Z}．(2)终边落在直线OA上的角为α＝30°＋k·360°或α＝210°＋k·360°，k∈Z，即α＝30°＋2k·180°或α＝30°＋(2k＋1)·180°，k∈Z，所以终边落在直线OA上的角的集合为S2＝{α|α＝30°＋k·180°，k∈Z}．。

高中数学第七章三角函数7.2任意角的三角函数7.2.3第1课时同角三角函数的基本关系式(1)作业b

综合②得m2 ＝
43，所以
m＝
3 2.
由③得 m≤4＋82
3＝2＋4
3，而
3 2＋ 2< 4
3，
所以
m＝
3 2.
12/13/2021
(2)当 m＝ 23时，原方程变为 2x2－( 3＋1)x＋ 23＝0，解得 x1＝ 23， x2＝12.
sinθ＝所以
23，
cosθ＝12
cosθ＝或
23，
sinθ＝12.
A．锐角三角形 B．钝角三角形 C．直角三角形 D．三种形状都有可能解析：∵sinθ＋cosθ＝m，∴1＋2sinθcosθ＝m2. ∵m∈(0,1)，∴2sinθcosθ＝m2－1<0.∵0<θ<π， ∴sinθ>0，cosθ<0，∴θ 为钝角．∴△ABC 为钝角三角形．
12/13/2021
二、填空题(每小题 5 分，共 15 分)
① ②
把②代入①得 cosα＝nm－＋mn.
12/13/2021
三、解答题(共 25 分) 10．(12 分)已知 cosα＝－187，求 sinα，tanα 的值．解：∵cosα＝－187<0， ∴α 是第二或第三象限角．若 α 是第二象限角，则 sinα>0，tanα<0. ∴sinα＝ 1－cos2α＝1157，tanα＝csoinsαα＝－185. 若 α 是第三象限角，则 sinα<0，tanα>0. ∴sinα＝－ 1－cos2α＝－1157，tanα＝csoinsαα＝185.
12/13/2021
13．(多选)(5 分)已知 0＜θ＜2π，且 sinθ＋cosθ＝a，其中 a∈(0,1)，

2020版高中数学人教A版必修4 导学案《任意角三角函数一》(含答案解析)学生版

思考 1 角α的正弦、余弦、正切分别等于什么？
思考 2 对确定的锐角α，sin α，cos α，tan α的值是否随 P 点在终边上的位置的改变而改变？
思考 3 在思考 1 中，当取|OP|=1 时，sin α，cos α，tan α的值怎样表示？
梳理
(1)单位圆
在直角坐标系中，我们称以原点 O 为圆心，以单位长度为半径的圆为单位圆.
位圆上点的坐标或坐标的比值为函数值的函数，统称为三角函数.
知识点二正弦、余弦、正切函数的定义域思考对于任意角α，sin α，cos α，tan α都有意义吗？梳理三角函数的定义域
知识点三正弦、余弦、正切函数值在各象限的符号思考根据三角函数的定义，你能判断正弦、余弦、正切函数的值在各象限的符号吗？
四、探究与拓展
14.已知角θ的终边上有一点 P(x，-1)(x≠0)，且 tan θ=-x，则 sin θ＋cos θ=
.
1
1
15.已知
=-
，且 lg(cos α)有意义.
|sin α| sin α
(1)试判断角α所在的象限；
3 ，m
(2)若角α的终边与单位圆相交于点 M 5 ，求 m 的值及 sin α的值.
C.第三象限角
D.第四象限角
2π
2π
sin ，cos
4.已知角α的终边上一点的坐标为
3
3 ，则角α的最小正值为( )
5π A.
6
2π B.
3
4π C.
3
11π D.
6
3 5.已知角α的终边经过点 P(3，4t)，且 sin(2kπ＋α)=- (k∈Z)，则 t 等于( )
5
9 A.-

1.2.1任意角的三角函数的定义(第一课时)

第一章三角函数 1.2 任意角的三角函数1.2.1 任意角的三角函数(第一课时)学习目标1.掌握任意角的三角函数的定义;2.已知角α终边上一点,会求角α的各三角函数值;3.记住三角函数的定义域及在各象限的符号.学习过程1.复习:初中锐角的三角函数是如何定义的?Rt △ABC 中,设A 的对边为a ,B 的对边为b ,C 的对边为c ,锐角A 的正弦、余弦、正切依次为sin A=,cos A= ,tan A= .2.探究:1.坐标法求三角函数.锐角α可放在坐标系中,在角α的终边上任取一点P (a ,b ),点P 与原点的距离r=,sin α= ;cos α= ;tan α= . 思考:对确定的锐角α，sin α，cos α，tan α的值是否随P 点在终边上的位置的改变而改变？答案不会．因为三角函数值是比值，其大小与点P (x ，y )在终边上的位置无关，只与角α的终边位置有关，即三角函数值的大小只与角有关．.思考:怎样适当地选取P 点使比值简化?其中,以原点为圆心,以为半径的圆为单位圆. 新知:1.任意角的三角函数.设α为一个任意角,它的终边与单位圆交于点P (x ,y ): 那么:(1)y 叫做α的正弦,记作sin α,即sin α=y ; (2)x 叫作α的余弦,记作cos α,即 ;(3)叫作α的正切,记作 ,即tan α=(x ≠0).三角函数:对于确定的角α,上面三个函数值都是唯一确定的,所以,正弦、余弦、正切都是以角为 ,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数.由于角的集合和实数集之间可以建立一一对应的关系,三角函数可以看成是自变量为实数的函数.3.正弦、余弦、正切函数值在各象限的符号思考根据三角函数的定义，你能判断正弦、余弦、正切函数的值在各象限的符号吗？答案由三角函数定义可知，在平面直角坐标系中，设α是一个任意角，它的终边与单位圆交于点P (x ，y )，则sin α＝y ，cos α＝x ，tan α＝yx (x ≠0)．当α为第一象限角时，y >0, x >0，故sin α>0，cos α>0，tan α>0，同理可得当α在其他象限时三角函数值的符号，如图所示．梳理记忆口诀：“一全正，二正弦，三正切，四余弦”．4.思考当角α分别为30°，390°，－330°时，它们的终边有什么特点？它们的三角函数值呢？答案它们的终边重合．由三角函数的定义知，它们的三角函数值相等．梳理诱导公式一典型例题【例1】求π的正弦、余弦和正切值.解:在直角坐标系中,作∠AOB=,∠AOB 的终边与单位圆的交点坐标为(,-),所以sin=-,cos,tan=-.【例2】已知角α的终边过点P 0(-3,-4),求角α的正弦、余弦和正切值. 解:sin α==-,cos α==-,tan α=.【例3】求证:当下列不等式组成立时,角α为第三象限角,反之也对.证明:如果sin α<0成立,那么角α的终边可能位于第三或第四象限,也可能与y 轴的非负半轴重合;如果tan α>0,则角α的终边位于第一或第三象限.所以,角α的终边只能位于第三象限.【例4】确定下列三角函数值的符号.(1)cos250°; (2)sin(-4π); (3)tan(-672°); (4)tan3π. 解:(1)因为250°是第三象限角,所以 cos250°<0; (2)因为-是第四象限角,所以sin(-)<0;(3)因为tan(-672°)=tan(48°-2×360°)=tan48°,而48°是第一象限角,所以tan(-672°)>0; (4)因为tan3π=tan(π+2π)=tan π,而π的终边在x 轴上,所以tan π=0. 【例5】求下列三角函数值. (1)sin1480°10'; (2)cos; (3)tan(-).解:(1)sin1480°10'=sin(40°10'+4×360°)=sin40°10'≈0.645; (2)cos =cos(+2π)=cos ;(3)tan(-)=tan(-2π)=tan.【例6】已知θ终边上一点P (x,3)(x ≠0)，且cos θ＝1010x ，求sin θ，tan θ. 考点任意角的三角函数题点用定义求三角函数的值解由题意知r ＝|OP |＝x 2＋9，由三角函数定义得cos θ＝x r ＝xx 2＋9.又∵cos θ＝1010x ，∴x x 2＋9＝1010x . ∵x ≠0，∴x ＝±1. 当x ＝1时，P (1,3)，此时sin θ＝312＋32＝31010，tan θ＝31＝3.当x ＝－1时，P (－1,3)，此时sin θ＝3(－1)2＋32＝31010，tan θ＝3－1＝－3.反思与感悟 (1)已知角α终边上任意一点的坐标求三角函数值的方法在α的终边上任选一点P (x ，y )，设P 到原点的距离为r (r >0)，则sin α＝y r ，cos α＝xr .当已知α的终边上一点求α的三角函数值时，用该方法更方便．(2)当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论．跟踪训练1 已知角α的终边过点P (－3a,4a )(a ≠0)，求2sin α＋cos α的值．考点任意角的三角函数题点用定义求三角函数的值解 r ＝(－3a )2＋(4a )2＝5|a |.①若a >0，则r ＝5a ，角α在第二象限， sin α＝y r ＝4a 5a ＝45，cos α＝x r ＝－3a 5a ＝－35，∴2sin α＋cos α＝85－35＝1.②若a <0，则r ＝－5a ，角α在第四象限， sin α＝4a －5a ＝－45，cos α＝－3a －5a ＝35，∴2sin α＋cos α＝－85＋35＝－1.综上所述，2sin α＋cos α＝±1.命题角度2 已知角α终边所在直线求三角函数值【例7】判断下列各式的符号： (1)sin145°cos(－210°)；(2)sin3·cos4·tan5. 考点三角函数值在各象限的符号题点三角函数值在各象限的符号解 (1)∵145°是第二象限角，∴sin145°＞0. ∵－210°＝－360°＋150°，∴－210°是第二象限角， ∴cos (－210°)＜0，∴sin145°cos(－210°)＜0. (2)∵π2＜3＜π＜4＜3π2＜5＜2π，∴sin3＞0，cos4＜0，tan5＜0， ∴sin3·cos4·tan5＞0.反思与感悟角的三角函数值的符号由角的终边所在位置确定，解题的关键是准确确定角的终边所在的象限，同时牢记各三角函数值在各象限的符号，记忆口诀：一全正，二正弦，三正切，四余弦．跟踪训练3 已知点P (tan α，cos α)在第三象限，则α是第________象限角．考点三角函数值在各象限的符号题点三角函数值在各象限的符号答案二解析由题意知tan α<0，cos α<0， ∴α是第二象限角．类型三诱导公式一的应用例4 求下列各式的值：(1)sin(－1395°)cos1110°＋cos(－1020°)sin750°；(2)sin ⎝⎛⎭⎫－11π6＋cos 12π5·tan4π. 考点诱导公式一题点诱导公式一解 (1)原式＝sin(－4×360°＋45°)cos(3×360°＋30°)＋cos(－3×360°＋60°)sin(2×360°＋30°)＝sin45°cos30°＋cos60°sin30°＝22×32＋12×12＝64＋14＝1＋64. (2)原式＝sin ⎝⎛⎭⎫－2π＋π6＋cos ⎝⎛⎭⎫2π＋2π5·tan(4π＋0)＝sin π6＋cos 2π5×0＝12. 反思与感悟利用诱导公式一可把负角的三角函数化为0到2π间的三角函数，也可把大于2π的角的三角函数化为0到2π间的三角函数，即实现了“负化正，大化小”．跟踪训练4 求下列各式的值： (1)cos 25π3＋tan ⎝⎛⎭⎫－15π4； (2)sin810°＋tan765°－cos360°. 考点诱导公式一题点诱导公式一解 (1)原式＝cos ⎝⎛⎭⎫8π＋π3＋tan ⎝⎛⎭⎫－4π＋π4 ＝cos π3＋tan π4＝12＋1＝32.(2)原式＝sin(90°＋2×360°)＋tan(45°＋2×360°)－cos360°＝sin90°＋tan45°－1＝1＋1－1＝1.一、选择题1．(2017·长沙检测)sin(－315°)的值是( ) A ．－22B ．－12C.22D.12答案 C解析 sin(－315°)＝sin(－360°＋45°)＝sin45°＝22. 2．(2017·山西太原外国语学校月考)如果角α的终边过点P (2sin30°，－2cos30°)，则sin α等于( )A.12B ．－12C ．－32D ．－33 答案 C解析由题意得P (1，－3)，它与原点的距离r ＝12＋(－3)2＝2，∴sin α＝－32. 3．已知sin θ<0，且tan θ<0，则θ为( )A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角答案 D4．已知α是第二象限角，P (x ，5)为其终边上一点，且cos α＝24x ，则x 的值为( ) A.3 B ．±3 C ．－ 2 D ．－ 3答案 D解析 ∵cos α＝x r ＝x x 2＋5＝24x ，∴x ＝0或2(x 2＋5)＝16，∴x ＝0或x 2＝3，∴x ＝0(∵α是第二象限角，∴舍去)或x ＝3(舍去)或x ＝－ 3.故选D. 5．(2017·嘉兴模拟)sin2·cos3·tan4的值( ) A ．小于0 B ．大于0 C ．等于0 D ．不存在答案 A解析 ∵sin2>0，cos3<0，tan4>0， ∴sin2·cos3·tan4<0.6．(2017·湖州期末)点P 从点(1,0)出发，沿单位圆顺时针方向运动5π6弧长到达Q 点，则Q 点的坐标是( )A.⎝⎛⎭⎫－12，32B.⎝⎛⎭⎫－12，－32C.⎝⎛⎭⎫－32，－12D.⎝⎛⎭⎫－32，12 答案 C解析根据题意可得：x Q ＝cos ⎝⎛⎭⎫－5π6＝－32， y Q ＝sin ⎝⎛⎭⎫－5π6＝－12. 则Q 点的坐标是⎝⎛⎭⎫－32，－12. 7．如果点P (sin θ＋cos θ，sin θcos θ)位于第二象限，那么角θ的终边在( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限答案 C解析由题意知sin θ＋cos θ＜0，且sin θcos θ＞0，∴⎩⎪⎨⎪⎧sin θ＜0，cos θ＜0，∴θ为第三象限角．二、填空题8．tan405°－sin450°＋cos750°＝________. 答案32解析 tan405°－sin450°＋cos750°＝tan(360°＋45°)－sin(360°＋90°)＋cos(720°＋30°)＝tan45°－sin90°＋cos30°＝1－1＋32＝32. 9．(2017·绍兴柯桥区期末)已知α的顶点在原点，始边在x 轴上，终边与单位圆相交于点M ⎝⎛⎭⎫－32，12，则cos α＝________. 答案－3210．(2017·山东烟台一中期末)已知角α的终边经过点(3a －9，a ＋2)，且sin α>0，cos α≤0，则实数a 的取值范围是________．答案 (－2,3]解析 ∵点(3a －9，a ＋2)在角α的终边上， sin α>0，cos α≤0，∴⎩⎪⎨⎪⎧a ＋2>0，3a －9≤0，解得－2<a ≤3. 11．已知角θ的终边上有一点P (x ，－1)(x ≠0)，且tan θ＝－x ，则sin θ＋cos θ＝________. 答案 0或－ 2解析 ∵θ的终边过点P (x ，－1)(x ≠0)， ∴tan θ＝－1x .又tan θ＝－x ， ∴x 2＝1，即x ＝±1. 当x ＝1时，sin θ＝－22，cos θ＝22，因此sin θ＋cos θ＝0；当x ＝－1时，sin θ＝－22，cos θ＝－22，因此sin θ＋cos θ＝－ 2. 故sin θ＋cos θ的值为0或－ 2.12．已知角α的终边在直线y ＝3x 上，则sin α，cos α，tan α的值分别为________．答案32，12，3或－32，－12， 3 解析因为角α的终边在直线y ＝3x 上，所以可设P (a ，3a )(a ≠0)为角α终边上任意一点，则r ＝a 2＋(3a )2＝2|a |(a ≠0)．若a >0，则α为第一象限角，r ＝2a ，所以sin α＝3a 2a ＝32，cos α＝a 2a ＝12， tan α＝3aa＝ 3. 若a <0，则α为第三象限角，r ＝－2a ，所以sin α＝3a －2a ＝－32，cos α＝－a 2a ＝－12，tan α＝3aa＝ 3. 13．sin 72π＋cos 52π＋cos(－5π)＋tan π4＝________.答案－1解析原式＝sin 32π＋cos π2＋cosπ＋1＝－1＋0－1＋1＝－1.14．函数y ＝|sin x |sin x ＋|cos x |cos x －2|sin x cos x |sin x cos x 的值域是________________．答案 {－4,0,2}解析由sin x ≠0，cos x ≠0知，x 的终边不能落在坐标轴上，当x 为第一象限角时，sin x >0，cos x >0， sin x cos x >0，y ＝0；当x 为第二象限角时，sin x >0，cos x <0， sin x cos x <0，y ＝2；当x 为第三象限角时，sin x <0，cos x <0， sin x cos x >0，y ＝－4；当x 为第四象限角时，sin x <0，cos x >0， sin x cos x <0，y ＝2.故函数y ＝|sin x |sin x ＋|cos x |cos x －2|sin x cos x |sin x cos x 的值域为{－4,0,2}．三、解答题15．已知1|sin α|＝－1sin α，且lg(cos α)有意义．(1)试判断角α所在的象限；(2)若角α的终边与单位圆相交于点M ⎝⎛⎭⎫35，m ，求m 的值及sin α的值．解 (1)∵1|sin α|＝－1sin α， ∴sin α＜0.①∵lg(cos α)有意义， ∴cos α＞0.②由①②得角α的终边在第四象限． (2)∵点M ⎝⎛⎭⎫35，m 在单位圆上， ∴⎝⎛⎭⎫352＋m 2＝1，解得m ＝±45. 又α是第四象限角，∴m ＜0，∴m ＝－45.由三角函数定义知，sin α＝－45.达标检测1.α是第四象限角,则下列数值中一定是正值的是( ) A.sin αB.cos αC.tan αD.2.已知点P (tan α,cos α)在第三象限,则角α在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.已知角α的终边过点P (-1,2),则cos α的值为 .4.已知角α的终边过点(a ,2a )(a ≠0),求α的正弦、余弦和正切值.5.判断sin4·tan(-)的符号.参考答案复习:探究:1.坐标法求三角函数.锐角α可放在坐标系中,在角α的终边上任取一点P (a ,b ), 点P 与原点的距离r=,sin α=,cos α=,tan α=.由三角形相似,确定的α可对应相似的直角三角形,这三个比值对应相等,不会随P 在角的终边的位置改变而改变. 2.单位圆.不难想到,当r=1时形式上比较简单,即sin α=b ,cos α=a ,tan α=,而当r=1时,可构设一个以原点为圆心以单位长为半径的圆,角α的终边与圆的交点选为P 点.此时,点P 与原点的距离r=1.其中,以原点为圆心,以1个单位长度为半径的圆为单位圆. 新知:1.cos α=x ;tan α;自变量2.≠+k反思:在直角坐标系中,设α是一个任意角,α终边上任意一点P(除了原点)的坐标为(x,y),则sinα=,cosα=,tanα=.3.终边相同的角同一三角函数值相等.典型例题【例1】解:在直角坐标系中,作∠AOB=,∠AOB的终边与单位圆的交点坐标为(,-),所以sin=-,cos,tan=-.【例2】解:sinα==-,cosα==-,tanα=.【例3】证明:如果sinα<0成立,那么角α的终边可能位于第三或第四象限,也可能与y轴的非负半轴重合;如果tanα>0,则角α的终边位于第一或第三象限.所以,角α的终边只能位于第三象限.【例4】解:(1)因为250°是第三象限角,所以cos250°<0;(2)因为-是第四象限角,所以sin(-)<0;(3)因为tan(-672°)=tan(48°-2×360°)=tan48°,而48°是第一象限角,所以tan(-672°)>0;(4)因为tan3π=tan(π+2π)=tanπ,而π的终边在x轴上,所以tanπ=0.【例5】解:(1)sin1480°10'=sin(40°10'+4×360°)=sin40°10'≈0.645;(2)cos=cos(+2π)=cos;(3)tan(-)=tan(-2π)=tan.达标检测1.B2.B3.-4.当a>0时,sinα=,cosα=,tanα=2;当a<0时,sinα=-,cosα=-,tanα=2.5.略。

人教版数学必修四：1.2.1任意角的三角函数(1)(作业纸)

课题：§1.2任意角的三角函数（一）作业总第____课时班级_______________姓名_______________一．填空题：1．已知角α的终边过点P （－8,—6）, 则sin α= ；cos α= ； tan α= .2．已知角α的终边过点P （0,—2）, 则sin α= ；cos α= ； tan α= .3．已知角α的终边过点P （4a ,－3a ）（a <0），则2sin α＋cos α的值是 . 4．已知角α的终边经过点P ),,(a a )0(≠a ，则=αsin . 5．已知点P （ααcos ,tan ）在第三象限，则角α在第象限.6．函数xxx x x x y tan tan cos cos sin sin ++=的值域是 . 7．已知角α的终边过点)4,32(a a --，且0sin ,0cos >≤αα，那么实数a 的取值范围是 .8．已知α是第二象限角，P （x , 5 ）为其终边上一点，且cos α=42x ，则sin α= . 9．计算：2sin cos 6tan 31cos 4cos 6sin22ππππππ+---= . 10．确定下列三角函数值的符号：6cos )1( 0 ； (2))8tan(- 0； (3)611tan 54cos 45sinπππ 0 .二、解答题：11．根据下列条件，确定α是第几象限角或那个坐标轴上的角：（1）0cos ,0sin ><αα （2）0cos sin >αα（3）0tan sin >αα（4）ααsin sin =12．已知角α的终边在直线kx y =上，若52sin =α，且0cos <α，求实数k 的值。

13．已知αcos <0, 且αtan >0.（1）求符合题意的角α的集合；（2）求角2α的终边所在的象限；（3）试判断2tan 2cos 2sin ααα⋅⋅的符号。

1.2.1任意角三角函数

1.2.1任意角三角函数（命题人：乔更云审题人：郑伟锋自主预习认真阅读教材P 11－14，回答下列问题： 1．任意角的三角函数(1)单位圆：在直角坐标系中，称以为圆心，以为半径的圆为单位圆．(2)锐角的三角函数：如图所示，在Rt △OAB 中，∠OAB ＝90°，OA ＝a ，AB ＝b ，OB ＝r ，设∠BOA ＝α，则有：示，α是任意角，以α的顶点O 坐标原点，以α的始边为x 轴的非负半轴，建立平面直角坐标系．设P (x ，y )是α的终边与单位圆的交点，则有：(4)定义：当a ＝ (k ∈Z )时，tan α无意义．除此之外，对于每一个确定的α，都分别有确定的正弦值、余弦值、正切值与之对应，所以这三个对应法则都是以角α为，以单位圆上点的坐标或坐标的比值为函数值的函数，分别叫做正弦函数、余弦函数、正切函数，这三个函数统称为，分别记作y ＝sin x ，y ＝cos x ，y ＝tan x .典例讲解[例1] 已知角的终边落在直线y ＝2x 上，求sin α，cos α，tan α的值．变式1 （1）求2π3的正弦、余弦和正切值．（2）已知角α的终边经过点P (3,4)，求sin α，cos α，tan α.（3）已知角α的终边过点P (5，a )，且tan α＝－125，求sin α－cos α的值．[例2]确定下列各式的符号：(1)sin105°·cos230°；(2)sin 7π8·tan7π8；(3)cos6·tan6.变式2. （1）若sinθ>0且tanθ<0，则θ是()A．第一象限角B．第二象限角C．第三象限角D．第四象限角（2）判断下列三角函数值的符号：(1)in(－670°)cos1230°；(2)sin8·cos8.[例3]求下列各式的值．(1)cos 253π＋tan(－154π)；(2)sin810°＋tan765°－cos360°.变式3求下列三角函数值：(1)cos(－1050°)；(2)tan19π3；(3)sin(－31π4)．[例4]已知角α的终边上一点P(4t，－3t)(t≠0)，求α的各三角函数值．例5已知sinα＝12，求出角α的取值集合．变式5.利用单位圆，求使下列不等式成立的x的取值范围：(1)sin x≤12；(2)tan x≤1；(3)cos x≥22.1.2.1任意角三角函数课后作业 1．若sin α<0且tan α>0，则α的终边在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．若角α的终边过点(－3，－2)，则( )A ．sin αtan α>0B ．cos αtan α>0C ．sin αcos α>0D ．sin αcos α<0 3．cos1110°的值为( ) A.12 B.32 C ．－12 D ．－32 4．已知P (2，－3)是角θ终边上一点，则tan(2π＋θ)等于( )A.32B.23 C ．－32 D ．－23 5.cos 2201.2°可化为( ) A ．cos201.2° B ．－cos201.2° C ．sin201.2° D ．tan201.2°6．已知角α的终边经过点P (m ，－3)，且cos α＝－45，则m 等于( )A ．－114 B.114 C ．－4 D ．4P 在第二或三象限，所以m <0，则m ＝－4.7．如果点P (sin θ＋cos θ，sin θcos θ)位于第二象限，那么角θ所在的象限是( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．α是第二象限角，P (x ，5)为其终边上一点，且cos α＝24x ，则sin α的值为( )A.104B.64C.24 D ．－1049．如果α的终边过点P (2sin30°，－2cos30°)，则sin α的值等于( )A.12 B ．－12 C ．－32 D ．－33 10．函数y ＝|sin x |sin x ＋cos x |cos x |＋|tan x |tan x 的值域是( )A ．{－1,1,3}B ．{1,3}C ．{－1,3}D ．R 11.已知11π6的正弦线为MP ，正切线为AT ，则有( )A ．MP 与AT 的方向相同B ．|MP |＝|AT |C ．MP >0，AT <0D ．MP <0，AT >012已知sin α>0，tan α<0，则α的( ) A ．余弦线方向向右，正切线方向向下 B ．余弦线方向向右，正切线方向向上 C ．余弦线方向向左，正切线方向向下 D ．余弦线方向向上，正切线方向向左 13．使得lg(cos θ·tan θ)有意义的角θ是第________象限角．14．已知角α的终边过点(3a －9，a ＋2)且cos α≤0，sin α>0，求实数a 的取值范围．15．求下列各式的值： (1)sin 25π3＋tan(－23π4)；(2)sin 1170°＋cos360°－tan 125°.16．已知1|sin α|＝－1sin α，且lgcos α有意义．(1)试判断角α所在的象限；(2)若角α的终边上一点是M (35，m )，且|OM |＝1(O 为坐标原点)，求m 的值及sin α的值．18．(2011～2012·黑龙江五校联考)已知角θ的终边上有一点P (－3，m )，且sin θ＝24m ，求cos θ与tan θ的值．1.2.1任意角三角函数（第一课时）1.（1）原点，单位长度（2）（3）y, x y/x (4) 唯一，自变量，三角函数例 1 [解析] 当角的终边在第一象限时，在角的终边上取点P (1,2)，由r ＝|OP |＝12＋22＝5，得sin α＝25＝255，cos α＝15＝55，tan α＝21＝2.当角的终边在第三象限时，在角的终边上取点Q (－1，－2)，由r ＝|OQ |＝(－1)2＋(－2)2＝5，得：sin α＝－25＝－255，cos α＝－15＝－55，tan α＝－2－1＝2. 变式1（1）因为角2π3的终边与单位圆的交点为(－12，32)，所以sin 2π3＝32，cos 2π3＝－12，tan 2π3＝－ 3.（2）x ＝3，y ＝4，得由r ＝32＋42＝5.∴sin α＝y r ＝45，cos α＝x r ＝35，tan α＝y x ＝43. （3）由正切函数定义得： a 5＝－125，∴a ＝－12，r ＝52＋(－12)2＝13 ∴sin α＝a 13＝－1213，cos α＝513 ∴sin α－cos α＝－1213－513＝－1713.π2＋k π例2(1)∵105°、230°分别为第二、第三象限角，∴sin105°>0，cos230°<0. 于是sin105°·cos230°<0. (2)∵π2<7π8<π，∴7π8是第二象限角，则sin 7π8>0，tan 7π8<0. ∴sin7π8·tan 7π8<0. (3)∵3π2<6<2π，∴6是第四象限角．变式2（1）B,(2) (1)∵－670°＝－2×360°＋50°，∴－670°是第一象限角，∴sin(－670°)>0.又1230°＝3×360°＋150°， ∴1230°是第二象限角，∴cos1230°<0，∴sin(－670°)cos1230°<0. (2)∵52π<8<3π，即8 rad 的角是第二象限角，∴sin8>0，cos8<0.∴sin8·cos8<0.例3(1)∵－670°＝－2×360°＋50°，∴－670°是第一象限角，∴sin(－670°)>0.又1230°＝3×360°＋150°， ∴1230°是第二象限角，∴cos1230°<0，∴sin(－670°)cos1230°<0. (2)∵52π<8<3π，即8 rad 的角是第二象限角，∴sin8>0，cos8<0.∴sin8·cos8<0.变式3(1)∵－1050°＝－3×360°＋30°， ∴cos(－1050°)＝cos(－3×360°＋30°)＝cos30°＝32. (2)∵19π3＝3×2π＋π3，∴tan 19π3＝tan(3×2π＋π3)＝tan π3＝ 3.(3)∵－31π4＝－4×2π＋π4，∴sin(－31π4)＝sin(－4×2π＋π4)＝sin π4＝22.例4因为点P 的坐标是(4t ，－3t )且t ≠0，所以r ＝|PO |＝(4t )2＋(－3t )2＝5|t |. 当t >0时，α是第四象限角，r ＝|PO |＝5t .sin α＝y r ＝－3t 5t ＝－35，cos α＝x r ＝4t 5t ＝45，tan α＝y x ＝－3t 4t ＝－34；当t <0时，α是第二象限角，r ＝|PO |＝－5t ，sin α＝y r ＝－3t －5t ＝35，cos α＝x r ＝4t －5t ＝－45，tan α＝y x ＝－3t 4t ＝－34. 例5[解析] 已知角α的正弦值，可知MP ＝12，则P 点纵坐标为12.所以在y 轴上取点(0，12)，过这点作x 轴的平行线y ＝12，交单位圆于P 1、P 2两点，则OP 1、OP 2是角α的终边，因而角α的集合为{α|α＝2k π＋π6或α＝2k π＋5π6，k ∈Z }，如图：变式5[解析] (1)如图所示，在0～2π内作出正弦值等于12的角：π6和56π.在图中所示的阴影区域内的每一个角x ，其正弦值都满足sin x ≤12，所以不等式sin x ≤12的解集为：{x |5π6＋2k π≤x ≤136π＋2k π，k ∈Z }．(2)如图所示，在0～2π内作出正切值等于1的角：π4和5π4，则在图中所示的阴影区域内的每个角x (不包括终边在y 轴上的角)均满足tan x ≤1.课后作业答案1. C [解析] 由于sin α<0，则α的终边在第三或四象限，又tan α>0，则α的终边在第一或三象限，所以α的终边在第三象限．2 C [解析] ∵角α的终边过点(－3，－2)，∴sin α<0，cos α<0，tan α>0，∴sin αcos α>0，故选C.3 B [解析] cos1110°＝cos(3×360°＋30°)＝cos30°＝32. 4 C [解析] tan(2π＋θ)＝tan θ＝－32＝－32. 5 B [解析] ∵201.2°是第三象限角，∴cos201.2°<0，6 C [解析] 由题意得cos α＝mm 2＋9＝－45，解得m ＝±4.又cos α＝－45<0，则α的终边在第二或三象限，则点P 在第二或三象限，所以m <0，则m ＝－4.7. C [解析] 由于点P (sin θ＋cos θ，sin θcos θ)位于第二象限，则⎩⎪⎨⎪⎧sin θ＋cos θ<0，sin θcos θ>0，所以有sin θ<0，cos θ<0，所以θ是第三象限角．8 A [解析] ∵|OP |＝x 2＋5，∴cos α＝xx 2＋5＝24x ，又因为α是第二象限角，∴x <0，得x ＝－ 3∴sin α＝5x 2＋5＝104，故选A.9 C [解析] ∵P (1，－3)，∴r ＝12＋(－3)2＝2，∴sin α＝－32.10 C [解析] ∵该函数的定义域是{x |x ∈R 且x ≠k π2，k ∈Z}，∴当x 是第一象限角时，y ＝3；当x 是第二象限角时，y ＝1－1－1＝－1；当x 是第三象限角时，y ＝－1－1＋1＝－1；当x 是第四象限角时，y ＝－1＋1－1＝－1.综上，函数的值域是{－1,3}． 11[答案] A[解析] 三角函数线的方向和三角函数值的符号是一致的．MP ＝sin 11π6<0，AT ＝tan11π6<0.12[答案] C[解析] ∵sin α>0，tan α<0，∴α是第二象限角．∴cos α<0.∴余弦线方向向左，正切线方向向下．13 一或二，12 －33， 13 ±2在角α终边上任取一点P (x ，y )，则y ＝x ，当x >0时，r ＝x 2＋y 2＝2x ，sin α＋cos α＝y r ＋x r ＝22＋22＝2，当x <0时，r ＝x 2＋y 2＝－2x ，sin α＋cos α＝y r ＋x r ＝－22－22＝－ 2.，14 ∵cos α≤0，sin α>0，∴角α的终边在第二象限或y 轴非负半轴上，∵α终边过(3a －9，a ＋2)，∴⎩⎪⎨⎪⎧3a －9≤0a ＋2＞0，∴－2<a ≤3. 15(1)sin25π3＋tan(－23π4)＝sin(8π＋π3)＋tan(－6π＋π4)＝sin π3＋tan π4＝32＋1＝3＋22.(2)sin1170°＋cos360°－tan1125° ＝sin(3×360°＋90°)＋cos(0°＋360°)－tan(3×360°＋45°)＝sin90°＋cos0°－tan45°＝1＋1－1＝1.16(1)由1|sin α|＝－1sin α可知sin α<0，∴α是第三或第四象限角或终边在y 轴的负半轴上的角．由lgcos α有意义可知cos α>0， ∴α是第一或第四象限角或终边在x 轴的正半轴上的角．综上可知角α是第四象限的角． (2)∵|OM |＝1，∴(35)2＋m 2＝1，解得m ＝±45. 又α是第四象限角，故m <0，从而m ＝－45.由正弦函数的定义可知 sin α＝y r ＝m |OM |＝－451＝－45.18 (1)当m ＝0时，cos θ＝－1，tan θ＝0； (2)当m ＝5时，cos θ＝－64，tan θ＝－153； (3)当m ＝－5时，cos θ＝－64，tan θ＝153.。

2021上海沪教新版高一数学下学期同步练习6.1.3任意角的三角函数详解版(01)

6.1.3任意角的三角函数（作业）一、单选题1．（2020·上海静安区·高一期末）设3sin 5α=-，4cos 5α=，那么下列的点在角α的终边上的是（） A ．()3,4-B ．()4,3-C ．()4,3-D ．()3,4-2．（2020·上海高一课时练习）若角α的终边经过点(5,12)P -，则sin tan αα+的值为( )A ．125-B ．513C ．9665-D ．1213-3．（2020·上海高一课时练习）若点(1,)P y 是角α终边上一点，且cos α=y 的值为( )AB ．C ．D ．无法确定4．（2020·上海高一课时练习）若点(5,0)P -为角α终边上一点，则下列三角比不存在的是（） A ．sin αB ．cos αC ．sec αD ．cot α5．（2019·上海市文来中学高一期末）“tan 3x =-”是“56x π=”的（）A ．充分非必要条件.B ．必要非充分条件.C ．充要条件.D ．既非充分也非必要条件.6．（2017·上海市七宝中学高一期中）角α终边上一点()(2sin5,2cos5),0,2P απ-∈，则α=（） A ．52π-B ．35π-C ．5D ．52π+7．（2016·上海虹口区·上外附中高一期中）锐角α终边上一点A 的坐标为()2sin3,2cos3-，则角α的弧度数为（） A ．3π-B ．3π-C ．32π-D ．32二、填空题8．（2020·上海市奉贤区奉城高级中学高一期末）若角α的终边经过点P (3m ，-4m )(m <0)，则sin α+cos α=_____.9．（2017·上海市金山中学高一期中）已知角α的终边经过点(),3P m -，且，则m 等于__________．4cos 5α=-10．（2016·上海普陀区·曹杨二中高一期末）已知角α的终边上一点()P m ，且sin 4m α=，则tan α的值为________. 11．（2020·上海市进才中学高一期中）求值：πarccos sin 3⎛⎫= ⎪⎝⎭__________．三、解答题12．（2020·上海高一课时练习）已知3x π=是方程()2cos 1x α+=的解，其中()0,2απ∈，求α的值.13．（2020·上海高一课时练习）已知角θ终边上一点P （异于原点）与x 轴的距离和与y 轴的距离之比为4∶3，且cos 0θ<，求sin ,tan θθ的值.14．（2020·上海高一课时练习）解方程：()2sin 5150︒-=x (x 为锐角).15．（2020·上海高一课时练习）已知cos 0α>且tan 0α<. （1）求角α的集合；（2）若cos02α<，求角2α终边所在象限；（3）判断tan,sincos222ααα的符号.16．（2020·上海高一课时练习）已知角α的终边与直线3y x =-重合，求角α的正弦、余弦和正切值.17．（2018·上海市北虹高级中学高一期中）已知角α的顶点在原点，始边与x 轴的正半轴重合，终边经过点()3,4,0P t t t ->，求sin cos αα+的值.6.1.3任意角的三角函数（作业）一、单选题1．（2020·上海静安区·高一期末）设3sin 5α=-，4cos 5α=，那么下列的点在角α的终边上的是（） A ．()3,4- B ．()4,3-C ．()4,3-D ．()3,4-【答案】B【分析】利用任意角的三角函数的定义逐个分析判断即可【详解】解：对于A ，若点()3,4-在角α的终边上，则43sin ,cos 55y x r r αα====-，所以A 错误；对于B ，若点()4,3-在角α的终边上，则3sin 5α=-，4cos 5α=，所以B 正确；对于C ，若点()4,3-在角α的终边上，则3sin 5α=，4cos 5α=-，所以C 错误；对于D ，若点()3,4-在角α的终边上，则4sin 5α=-，3cos 5α=，所以D 错误，故选：B【点睛】此题考查任意角的三角函数的定义的应用，属于基础题2．（2020·上海高一课时练习）若角α的终边经过点(5,12)P -，则sin tan αα+的值为( )A ．125-B ．513C ．9665-D ．1213-【答案】C【分析】利用三角函数的定义求出sin α、tan α即可求解. 【详解】由角α的终边经过点(5,12)P -，则12sin 13α==，1212tan 55α==--，所以121296sin tan 13565αα+=-=-.故选：C 【点睛】本题考查了三角函数的定义，掌握三角函数的定义是解题的关键，考查了基本运算能力，属于基础题.3．（2020·上海高一课时练习）若点(1,)P y 是角α终边上一点，且cos α=y 的值为( )A B ．C ．D ．无法确定【答案】B【分析】根据三角函数的定义，建立关于y 的方程，解得y 的值即可．【详解】∵点(1,)P y 是角α终边上一点，且cos α=，∴cos α==，化简得：2112y +=，解之得：y =．故选：B .【点睛】本题考查任意角的三角函数的定义的应用，侧重考查学生对基础知识的理解和掌握，属于基础题.4．（2020·上海高一课时练习）若点(5,0)P -为角α终边上一点，则下列三角比不存在的是（） A ．sin α B ．cos αC ．sec αD ．cot α【答案】D【分析】根据三角比的概念对选项进行逐一判断，即可得到答案. 【详解】由题意点(5,0)P -为角α终边上一点，则5r OP ==.所以0sin 05y r α===，-5cos 15x r α===-，5sec 1-5r x α===- 由cot xyα=，因为0y =，所以cot α不存在.故选：D 【点睛】本题考查三角函数的定义的应用，利用定义求对应的三角比，属于基础题.5．（2019·上海市文来中学高一期末）“tan x =”是“56x π=”的（）A ．充分非必要条件.B ．必要非充分条件.C ．充要条件.D ．既非充分也非必要条件.【答案】B【分析】根据充分条件、必要条件的定义，即可判断.【详解】由56x π=，可推出tan 3x =-，而由tan x =()56x k k Z ππ=+∈，有多个解，即不能推出56x π=，故“tan x =56x π=”的必要非充分条件.故选：B【点睛】本题考查了充分条件、必要条件的定义以及三角函数值与角的关系，属于基础题. 6．（2017·上海市七宝中学高一期中）角α终边上一点()(2sin5,2cos5),0,2P απ-∈，则α=（） A ．52π-B ．35π-C ．5D ．52π+【答案】A【分析】根据任意角三角函数的定义，分别计算sin α与cos α，再根据诱导公式求解角α，即可.【详解】3522ππ<<，sin50∴<，cos50>令2r ====则2cos5sin cos502y r α-===-<，2sin 5cos sin 502x r α===< 所以角α在第三象限，即32ππα<<，由诱导公式可知，52πα=- 故选：A【点睛】本题考查任意角三角函数的定义，以及诱导公式，属于中档题.7．（2016·上海虹口区·上外附中高一期中）锐角α终边上一点A 的坐标为()2sin3,2cos3-，则角α的弧度数为（） A ．3π-B ．3π-C ．32π-D ．32【答案】C【分析】利用终边上的点确定正切值，结合终边所在的象限，从而得到角α的弧度数. 【详解】因为锐角α终边上一点A 的坐标为()2sin3,2cos3-，所以sin(3)2cos32tan(3)tan(3)2sin 322cos t )a 32n (ππαππ---===--=--，因为3(0,)22ππ-∈，所以32πα=-.故选：C【点睛】本题考查三角函数的定义、诱导公式，考查逻辑推理能力和运算求解能力. 二、填空题8．（2020·上海市奉贤区奉城高级中学高一期末）若角α的终边经过点P (3m ，-4m )(m <0)，则sin α+cos α=_____.【答案】15【分析】利用任意角三角函数的定义求解即可．【详解】由题意得：55r OP m m ====-则44sin 55y m r m α-===-，33cos 55x m r m α===-- 故431sin cos 555αα+=-=，故答案为：159．（2017·上海市金山中学高一期中）已知角α的终边经过点(),3P m -，且，则m 等于__________．4cos 5α=-【答案】－4【解析】由题意，4cos 5α==-，解得4m =-，故答案为4-.10．（2016·上海普陀区·曹杨二中高一期末）已知角α的终边上一点()P m ，且sin 4m α=，则tan α的值为________.【答案】3±或0 【分析】利用正弦函数的定义求出m ,利用正切函数的定义求出tan α的值.【详解】角α的终边上一点()P m根据正弦函数的定义得:sin 4m α==解得0m =或m =当0m =时,tan 0α=;当m =, tan 3α=-当m =, tan 3α=则tan α的值为:或0故答案为: 或0. 【点睛】本题考查三角函数的定义,掌握三角函数的定义是解本题关键,考查学生的计算能力,是基础题.11．（2020·上海市进才中学高一期中）求值：πarccos sin 3⎛⎫= ⎪⎝⎭__________．【答案】π6【分析】先求sin 32π=，再结合余弦函数的值，求arccos 2即可得解.【详解】sin 32π=，cos 62π=，πarccos sin 36π⎛⎫∴== ⎪⎝⎭.故答案为：π6 【点睛】本题考查了反余弦函数，重点考查了反余弦函数求值问题，属基础题.三、解答题 12．（2020·上海高一课时练习）已知3x π=是方程()2cos 1x α+=的解，其中()0,2απ∈，求α的值.【答案】43πα= 【分析】由已知条件得出1cos 32πα⎛⎫+= ⎪⎝⎭，求出角3πα+的取值范围，可得出角3πα+的值，进而可求得角α的值. 【详解】由题意可得2cos 13πα⎛⎫+= ⎪⎝⎭，则1cos 32πα⎛⎫+= ⎪⎝⎭， 02απ<<，7333πππα∴<+<，则533ππα+=，解得43πα=. 【点睛】本题考查余弦方程的求解，考查计算能力，属于基础题.13．（2020·上海高一课时练习）已知角θ终边上一点P （异于原点）与x 轴的距离和与y 轴的距离之比为4∶3，且cos 0θ<，求sin ,tan θθ的值. 【答案】当θ在第二象限时，44sin ,tan 53==-θθ；当θ在第三象限时，44sin ,tan 53=-=θθ. 【分析】根据cos 0θ<确定θ在第二象限或第三象限，讨论两种情况，结合距离之比为4∶3解得答案.【详解】cos 0θ<，故θ在第二象限或第三象限，当θ在第二象限时，()3,4P m m -，0m >，故4sin 5θ==，44tan 33m m θ==--；当θ在第三象限时，()3,4P m m --，0m >，故4sin 5θ==-，44tan 33m m θ-==-. 综上所述：当θ在第二象限时，44sin ,tan 53==-θθ；当θ在第三象限时，44sin ,tan 53=-=θθ. 【点睛】本题考查了根据三角函数定义求三角函数值，意在考查学生的计算能力和应用能力，漏解是容易发生的错误.14．（2020·上海高一课时练习）解方程：()2sin 5150︒-=x (x 为锐角). 【答案】{}15,27,87︒︒︒【分析】由题意可得()5151,5435x ︒︒︒-∈-，转化条件为()sin 515x ︒-=，求得515x ︒-的值后，即可得解. 【详解】 x 为锐角，∴(),090x ︒︒∈，()5151,5435x ︒︒︒-∈-，又()2sin 5150︒-=x ，∴()sin 5152x ︒-=， ∴65015x ︒︒=-或120515x ︒︒=-或420515x ︒︒=-，∴15x ︒=或27x ︒=或87x ︒=，∴原方程的解集为{}15,27,87︒︒︒.【点睛】本题考查了特殊角三角函数值的应用，考查了运算求解能力，准确识记特殊角的三角函数值是解题关键，属于基础题.15．（2020·上海高一课时练习）已知cos 0α>且tan 0α<.（1）求角α的集合；（2）若cos 02α<，求角2α终边所在象限；（3）判断tan ,sin cos 222ααα的符号.【答案】（1）22,2k k k Z παπαπ⎧⎫-<<∈⎨⎬⎩⎭；（2）2α终边在第二象限；（3）tan 0,sin cos 0222<⋅<ααα.【分析】（1）由三角函数值的符号可得α角的集合；（2）由（1）由不等式的性质可得2α的范围，可得所在象限；（3）由2α的象限可得三角函数值的符号，可得乘积的符号．【详解】解：（1）cos 0α>，tan 0α<，所以α位于第四象限， α角的集合为22,2k k k Z παπαπ⎧⎫-<<∈⎨⎬⎩⎭；（2）由（1）可得22,2k k k Z παπαπ⎧⎫-<<∈⎨⎬⎩⎭；所以,242k k k Z απαππ⎧⎫-<<∈⎨⎬⎩⎭； ∴2α终边在第二、四象限，又cos 02α<，所以2α终边在第二象限；（3）由（2）知2α终边在第二、四象限，当2α终边在第二象限时tan 02α<，sin 02α>，cos 02α<，所以sin cos 022αα< 当2α终边在第四象限时tan 02α<，sin 02α<，cos 02α>，所以sin cos 022αα<综上可得tan 02α<，sin cos 022αα<【点睛】本题考查三角函数值的符号及象限角，属于基础题．16．（2020·上海高一课时练习）已知角α的终边与直线3y x =-重合，求角α的正弦、余弦和正切值.【答案】当α的终边在第二象限时，sin tan 310==-=-ααα；当α的终边在第四象限时，sin tan 310===-ααα【分析】在角α的终边上取一点(,3)(0)A a a a -≠，则|||r OA a ==，分0a >，0a <两种情况，结合三角函数的定义即可解决.【详解】在角α的终边上取一点(,3)(0)A a a a -≠，则||||r OA a ===，当0a >时，此时角α的终边在第四象限，r =，所以cos10x r α===，sin10y r α-===，tan 3y x α==-；当0a <时，此时角α的终边在第二象限，r =，所以cos10x r α===-，sin 10y r α===，tan 3y x α==-. 【点睛】本题主要考查已知终边的位置求三角函数值，涉及到三角函数的定义，考查学生的数学运算能力，是一道容易题.17．（2018·上海市北虹高级中学高一期中）已知角α的顶点在原点，始边与x 轴的正半轴重合，终边经过点()3,4,0P t t t ->，求sin cos αα+的值. 【答案】15【分析】由()3,4,0P t t t ->，所以5OP t ==，再结合三角函数的定义运算即可得解.【详解】解：因为()3,4,0P t t t ->，所以5OP t ==，由三角函数的定义可得：44sin 55t t α==，33cos 55t t -α==-，即431sin cos ()555αα=+-=+. 【点睛】本题考查了三角函数的定义，重点考查了t 符号问题，属基础题.。

新人教版必修4第1章第1节任意角的三角函数(第二课时)

sin y cos x y tan x 0
x
问题 2:角的概念推广以后，我们应该如何推广到任意角呢？新知：任意角三角函数的定义
设α 是一个任意角，它的终边与单位圆交于点P(x,y), 那么：
（1）y叫做的正弦，记作sinα
（2）x叫做的余弦，记作cosα y （3）叫做的正切，记作tanα x
思考：对于确定的角α ，上述三个比值是否随点P在角α 的终边上的位置的改变而改变呢？为什么？
二、新课导学探究任务一：任意角的三角函数的定义.
问题1 能否通过取适当点而将表达式简化?
新知：在直角坐标系中,我们称以原点O 为圆心,以单位长度为半径的圆叫做单位圆.
y r
O

P (x,y)

M 1x
变式练习
(其中r x y )
2 2
已知角的终边过点 P(12,5), 求角的三角函数值。
如果角的终边落在坐标轴呢？请完成下表。
角Байду номын сангаас 角的弧度数
sin cos tan
0。
90。
π 2
180。 270。

3π 2
360。
2
0 0 1 0
1
0
1
0
不存在
1 0
不存在
0
1 0
0
三、总结提升
§1.2.1任意角的三角函数（第一课时）
y
o
x
一、复习引入锐角的三角函数如何定义？ A
P (x,y)
y r
O
y 对边 MP sin r 斜边 OP

M
B
x
邻边 OM x cos 斜边 OP r 对边 MP y x 0 tan 邻边 OM x

高中数学人教A版必修四课时训练：第一章三角函数1-2任意角的三角函数

11．解 (1)
图1
作直线 y＝ 23交单位圆于 A、B，连结 OA、OB，则 OA 与 OB 围成的区域(图 1 阴影部分)，即为角 α 的终边的范围．故满足条件的角 α 的集合为 {α|2kπ＋π3≤α≤2kπ＋23π，k∈Z}． (2)
∴sin 2cos 3tan 4<0.
10．2
解析 ∵y＝3x，sin α<0，∴点 P(m，n)位于 y＝3x 在第三象限的图象上，且 m<0，n<0，
n＝3m.
∴|OP|＝ m2＋n2＝ 10|m|＝－ 10m＝ 10.
∴m＝－1，n＝－3，∴m－n＝2.
11．解 (1)原式＝cosπ3＋－4×2π＋tanπ4＋2×2π＝cos π3＋tan π4＝12＋1＝32.
3．诱导公式一的实质是说终边相同的角的三角函数值相等．作用是把求任意角的三角函数值转化为求 0～2π(或 0°～360°)角的三角函数值．
答案
知识梳理
y 1.r
x r
y x
3.相等
sinα
cosα
tanα
作业设计
1．A 2.B
3．C [∵sinα<0，∴α 是第三、四象限角．又 tanα>0，
∴α 是第一、三象限角，故 α 是第三象限角．]
4．C [∵1,1.2,1.5 均在0，π2内，正弦线在0，π2内随 α 的增大而逐渐增大，
∴sin1.5>sin1.2>sin1.] 5．D [在同一单位圆中，利用三角函数线可得 D 正确．] 6．A [
如图所示，在单位圆中分别作出 α 的正弦线 MP、余弦线 OM、正切线 AT，很容易地观察出
OM<MP<AT，即 cosα<sinα<tanα.]

5.3诱导公式(第一课时)2024-2025学年高一上学期数学人教A版(2019)必修第一册

公式四
sin( − ) = sin
cos( − ) = −cos
tan( − ) = −tan
试一试
3
tan
4

= tan( − )
4

= − tan
4
= −1
二、新授
公式一
sin （ + 2） = sin
cos（ + 2） = cos ��
tan （ + 2） = tan
它们的三角函数之间有什么关系？
y
P(, )
的终边
x
o
-的终边
2 (x, −y)
cos(−) = x

tan(−) = −

公式三
sin( −) = − sin
cos(−) = cos
tan(−) = −tan
试一试

sin(− )
3

= − sin
3
3
=−
2
二、新授
公式二
sin( + ) = − sin
cos( + ) = − cos
tan( + ) = tan
公式三
sin( −) = − sin
cos(−) = cos
tan(−) = −tan
公式四
sin( − ) = sin
cos( − ) = −cos

公式二
sin( + ) = − sin
cos( + ) = − cos
tan( + ) = tan
试一试

cos +
6

= − cos

任意角的三角函数(第1课时)

第一课时：任意角的三角函数（第1课时）编写人：潘有金审核人：张广泉审批：苏自先学习目标：1.理解并掌握任意角三角函数的定义；2.理解三角函数是以实数为自变量的函数；3.掌握正弦、余弦、正切函数的定义域；4.掌握三角函数的值在各个象限的符号。

5.掌握公式（一），体会三角函数值“周而复始”的变化规律。

预习案一、教材助读认真阅读课本P 11 –P15 ,完成下列问题1.在初中，我们学习了锐角三角函数。

锐角三角函数是如何定义的？3.在直角坐标系中，我们称_________________________的圆为单位圆。

4. 设α是一个任意角，它的终边与单位圆交于点P(x,y)，那么⑴y叫做α的______，记作sinα,即sinα=____.⑵x叫做α的______，记作cosα,即cosα=____.⑶y叫做α的______，记作tanα,即tanα=____.x6..三角函数值在各个象限的符号sin αcos αtan α7.根据三角函数的定义可知：终边相同的角的同一个三角函数的值相等，由此得到公式（一）二、预习自测（牛刀小试）1.已知角α的终边与单位圆的交点为P，12-），则tan α=( )A. B. 12-C. -2.下列三角函数值中，小于0的是（） A. sin156° B. cos450° C. tan178πD.tan （165π-） 3.已知角θ的终边经过点P （－12,5）求角θ的各三角函数值。

三、我的疑惑在下面记下预习中的困惑在课上和同学讨论或向老师请教第一课时：任意角的三角函数（第1课时）导学案一、学始于疑同学们首先认真独立思考如下问题问题1.锐角三角函数是以角为自变量，以比值为函数值的函数。

在直角坐标系中，能不能用终边上点的坐标来表示锐角三角函数呢？问题2. 对于任意角α，能不能用终边上点的坐标来定义角α三角函数呢？二、质疑探究小组内讨论上述问题，准备展示，将组内不能解决的问题用小纸条交给老师探究一锐角三角函数与锐角终边上点的坐标的关系探究二任意角三角函数的定义设α是一个任意角，它的终边上任意一点P的坐标为(x,y)，点P与原点的距离为r（r=），则：sinα=yr ；cosα=xr；tanα=yx.探究三单位圆探究四任意角的三角函数与单位圆的关系设α是一个任意角，它的终边与单位圆交于点P(x,y)，那么⑴y叫做α的正弦，记作sinα,即sinα=y;⑵x叫做α的余弦，记作cosα,即cosα=x；⑶yx 叫做α的正切，记作tanα,即tanα=yx.探究四弧度制下，三角函数的定义域探究五三角函数值在各个象限的符号探究六公式（一）因为终边相同的角的同一个三角函数值相等，由此得到公式（一） sin(α+k ²360°)=sin α cos(α+k ²360°)= cos αtan(α+k ²360°)=tan α 其中k ∈Z三、拓展提升例1.已知角α的终边经过点P （-3，-4），求角α的正弦、余弦和正切值例2.利用定义求53π的正弦、余弦和正切值。

《4.8 已知三角函数值求角》作业设计方案

《已知三角函数值求角》作业设计方案（第一课时）一、作业目标：1. 理解和掌握任意角的概念，知道角的表示方法；2. 通过实践操作，学会运用已知三角函数值求角的方法；3. 提高学生对三角函数的应用能力，增强数学在实际生活中的应用意识。

二、作业内容：1. 完成课本相关练习题，包括直接运用诱导公式、二倍角公式等基础知识，以及综合运用这些知识解决一些简单的实际问题。

2. 观察和记录身边的三角形物体，测量并记录其角度，尝试使用已知三角函数值求出这些角度对应的角。

3. 搜集一些实际生活中的三角形，尝试用已知三角函数值求出这些三角形中未知角度的大小。

三、作业要求：1. 认真完成练习题，确保准确率；2. 观察和记录身边的三角形物体时，注意安全，使用合适的工具进行测量；3. 搜集实际生活中的三角形时，注意选择合适的生活场景，确保数据的真实性和有效性；4. 遇到问题时，积极思考、查阅资料，或与同学讨论解决，不要轻易放弃。

四、作业评价：1. 练习题的完成情况将作为个人成绩的一部分，准确率应达到80% 以上；2. 观察和记录身边的三角形物体以及搜集实际生活中的三角形的情况，将作为小组讨论和交流的重要内容；3. 评价标准将综合考虑准确率、完成质量和实际应用效果。

五、作业反馈：1. 请同学们认真完成作业，并及时提交；2. 作业反馈应包括对作业的自我评价、对其他同学的作业评价以及对本次作业的总结和建议。

本次作业的目的是让学生理解和掌握任意角的概念，学会运用已知三角函数值求角的方法，提高学生对三角函数的应用能力，增强数学在实际生活中的应用意识。

为此，作业内容设计成三个部分：完成课本相关练习题、观察和记录身边的三角形物体、搜集实际生活中的三角形。

同时，作业要求也考虑到学生的实际情况，包括准确率、完成质量和实际应用效果等方面。

通过本次作业，希望学生能够进一步理解和掌握三角函数知识，提高解决实际问题的能力，增强数学在实际生活中的应用意识。

任意角的三角函数第一课时作业