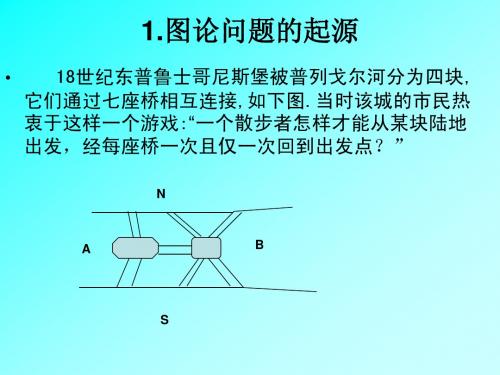
第一章图的基本概念节
合集下载
第一章 图的基本概念(5)——极图理论简介
0.5
00
1 0.8
0.6 0.4 x 0.2
如果 m(G) m(Tl ,n )
则有 m(H ) m(G)
G与H有相同度序列，由定理4：G H
又由 m(G) m(Tl ,n ) ，且由定理3，有：
H Tl ,n 所以有： G Tl ,n
13
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
4部图
4
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
定义2 如果在一个l 部图G中，任意部Vi中的每个顶点， 和G中其它各部中的每个顶点均邻接，称G为完全l 部 图。记作：
G Kn1,n2 , ,nl , (ni Vi ,1 i l)
例如：
显然：
00
1 0.8
0.6 0.4 x 0.2
几个有趣的相关结果：
设m (n, H)表示n阶单图中不含子图H的最多边数，则：
1, m(n,
K3 )
n2
4
2, m(n, Kl 1 )
(l
1)(n 2 2l
r2)
Cr2
其中，n r(modl), 0 r l
3,
m(n, Cn
)
1
(n
1)(n 2
由此可以推出： G= G1V G2 因为 G= G1V G2和H= G2V H1有相同度序列，于是 得到G1和H1有相同度序列，所以：
GH
定理5（Turán）若G是简单图，并且不包含 Kl+1,则：
m(G) m(Tl,n )
仅当 G Tl ,n 时，有 m(G) m(Tl ,n )
00
1 0.8
0.6 0.4 x 0.2
如果 m(G) m(Tl ,n )
则有 m(H ) m(G)
G与H有相同度序列，由定理4：G H
又由 m(G) m(Tl ,n ) ，且由定理3，有：
H Tl ,n 所以有： G Tl ,n
13
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
4部图
4
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
定义2 如果在一个l 部图G中，任意部Vi中的每个顶点， 和G中其它各部中的每个顶点均邻接，称G为完全l 部 图。记作：
G Kn1,n2 , ,nl , (ni Vi ,1 i l)
例如：
显然：
00
1 0.8
0.6 0.4 x 0.2
几个有趣的相关结果：
设m (n, H)表示n阶单图中不含子图H的最多边数，则：
1, m(n,
K3 )
n2
4
2, m(n, Kl 1 )
(l
1)(n 2 2l
r2)
Cr2
其中，n r(modl), 0 r l
3,
m(n, Cn
)
1
(n
1)(n 2
由此可以推出： G= G1V G2 因为 G= G1V G2和H= G2V H1有相同度序列，于是 得到G1和H1有相同度序列，所以：
GH
定理5（Turán）若G是简单图，并且不包含 Kl+1,则：
m(G) m(Tl,n )
仅当 G Tl ,n 时，有 m(G) m(Tl ,n )
第一章(图论的基本概念)
第二节 图的顶点度和图的同构(4)
图序列:简单图的度序列. (d1, d 2 , , d p )(d1 d 2 d p ) 定理4 非负整数序列 是图序列当 p 且仅当 d i 是偶数,并且对一切整数k, 1 k p 1, 有
i 1
第二节 图的顶点度和图的同构(1)
定义1 设G是任意图,x为G的任意结点,与结点x关联的 边数(一条环计算两次)称为x的度数.记作deg(x)或d(x). 定义2 设G为无向图,对于G的每个结点x,若d(x)=K,则 称G为K正则的无向图.设G为有向图,对于G的每个结点 x,若d+(x)=d-(x), 则称G为平衡有向图.在有向图G中, 若 (G) (G) (G) (G) K , 则称G为K正则有向图. 定理1(握手定理，图论基本定理)每个图中,结点度数的 总和等于边数的二倍,即 deg(x) 2 E .
•
A
N
S
B
欧拉的结论 • 欧拉指出:一个线图中存在通过每边一次仅一次 回到出发点的路线的充要条件是: • 1)图是连通的,即任意两点可由图中的一些边连 接起来; • 2)与图中每一顶点相连的边必须是偶数. • 由此得出结论:七桥问题无解. 欧拉由七桥问题所引发的研究论文是图论的开 篇之作,因此称欧拉为图论之父.
xV
定理2 每个图中,度数为奇数的结点必定是偶数个.
第二节 图的顶点度和图的同构(2)
• 定理3 在任何有向图中,所有结点入度之和等于所有结 点出度之和. • 证明 因为每条有向边必对应一个入度和出度,若一个结 点具有一个入度或出度,则必关联一条有向边,因此,有向 图中各结点的入度之和等于边数,各结点出度之和也等 于边数. • 定义 度序列,若V(G)={v1,v2,…,vp},称非负整数序列 (d(v1),d(v2),…,d(vp))为图G的度序列.
(图论)图的基本概念--第一章
证明 设G＝<V，E>为任意一图，令
V1＝{v|v∈V∧d(v)为奇数} V2＝{v|v∈V∧d(v)为偶数} 则V1∪V2＝V，V1∩V2＝ ，由握手定理可知
2m d (v) d (v) d (v)
vV
vV1
vV2
由于2m和 d (v) ，所以 d (v) 为偶数，
举例
NG(v1) ＝ {v2，v5} NG(v1) ＝ {v1，v2，v5} IG(v1) ＝ {e1，e2，e3}
Г+D(d ) ＝ {c} Г-D(d ) ＝ {a，c} ND(d ) ＝ {a，c} ND(d ) ＝ {a，c，d}
简单图与多重图
定义1.3 在无向图中，关联一对顶点的无向边如果多于1条，则 称这些边为平行边，平行边的条数称为重数。 在有向图中，关联一对顶点的有向边如果多于1条，并且这些 边的始点和终点相同(也就是它们的方向相同)，则称这些边 为平行边。 含平行边的图称为多重图。 既不含平行边也不含环的图称为简单图。
无向图和有向图
定义1 一个无向图是一个有序的二元组<V，E>,记作G，其中 （1）V≠称为顶点集，其元素称为顶点或结点。 （2）E称为边集，它是无序积V&V的多重子集，其元素称为无向 边，简称边。
定义2 一个有向图是一个有序的二元组<V，E>，记作D，其中 （1）V≠称为顶点集，其元素称为顶点或结点。 （2）E为边集，它是笛卡儿积V×V的多重子集，其元素称为有向 边，简称边。
vV2
vV1
但因V1中顶点度数为奇数， 所以|V1|必为偶数。
问题研究
问题：在一个部门的25个人中间，由于意见不同，是否可能每 个人恰好与其他5个人意见一致？
图论第一章课后习题解答
bi 个 (i = 1,2,…,s)，则有 列。 定理 7
bi = n。故非整数组(b ,b ,…, b )是 n 的一个划分，称为 G 的频序
1 2 s
s
i 1
一个 n 阶图 G 和它的补图 G 有相同的频序列。
§1.2 子图与图的运算
且 H 中边的重数不超过 G 中对应边的 定义 1 如果 V H V G ，E H E G ， 重数，则称 H 是 G 的子图，记为 H G 。有时又称 G 是 H 的母图。 当 H G ，但 H G 时，则记为 H G ，且称 H 为 G 的真子图。G 的生成子图是 指满足 V(H) = V(G)的子图 H。 假设 V 是 V 的一个非空子集。以 V 为顶点集，以两端点均在 V 中的边的全体为边集 所组成的子图，称为 G 的由 V 导出的子图，记为 G[ V ]；简称为 G 的导出子图，导出子图 G[V\ V ]记为 G V ； 它是 G 中删除 V 中的顶点以及与这些顶点相关联的边所得到的子图。 若 V = {v}, 则把 G-{v}简记为 G–v。 假设 E 是 E 的非空子集。以 E 为边集，以 E 中边的端点全体为顶点集所组成的子图 称为 G 的由 E 导出的子图，记为 G E ；简称为 G 的边导出子图，边集为 E \ E 的 G 的 导出子图简记为 G E 。若 E e ，则用 G–e 来代替 G-{e}。 定理 8 简单图 G 中所有不同的生成子图（包括 G 和空图）的个数是 2m 个。 定义 2 设 G1，G2 是 G 的子图。若 G1 和 G2 无公共顶点，则称它们是不相交的；若 G1 和 G2 无公共边，则称它们是边不重的。G1 和 G2 的并图 G1∪G2 是指 G 的一个子图，其顶点 集为 V(G1)∪V(G2)，其边集为 E(G1)∪E(G2)；如果 G1 和 G2 是不相交的，有时就记其并图为 G1+G2。类似地可定义 G1 和 G2 的交图 G1∩G2，但此时 G1 和 G2 至少要有一个公共顶点。
图论-图的基本概念
若 i, j 中有奇数，比如 i 是奇数，则路 P 上 v0 到 vi 的一段与边 v0vi 构成一个偶圈； 若 i, j 都是偶数，则路 P 上 vi 到 v j 的一段与边 v0vi 及 v0v j 构成一个偶圈。证毕。 例 1.1.4 设 G 是简单图，若δ (G) ≥ 3 ,则 G 中各个圈长的最大公因数是 1 或 2。 证明：由上例知，G 中有长分别为 i + 1, j + 1和 j − i + 2 的圈。若 i + 1, j + 1， j − i + 2 三 数有公因数 m > 2 ，则 m | ( j − i) ，于是 m | 2 ，这是不可能的。因此 i + 1, j + 1， j − i + 2
证明：按每个顶点的度来计数边，每条边恰数了两次。 推论 1.1.1 任何图中，奇度顶点的个数总是偶数（包括 0）。 4. 子图
子图(subgraph)：如果 V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ，则称图 H 是 G 的子图，记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ，则称 H 是 G 的生成子图。
这便定义出一个图。
2. 图的图示
通常，图的顶点可用平面上的一个点来表示，边可用平面上的线段来表示（直的或曲的）。 这样画出的平面图形称为图的图示。
例如，例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注：（1）由于表示顶点的平面点的位置的任意性，同一个图可以画出形状迥异的很多图示。
证明：按每个顶点的度来计数边，每条边恰数了两次。 推论 1.1.1 任何图中，奇度顶点的个数总是偶数（包括 0）。 4. 子图
子图(subgraph)：如果 V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ，则称图 H 是 G 的子图，记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ，则称 H 是 G 的生成子图。
这便定义出一个图。
2. 图的图示
通常，图的顶点可用平面上的一个点来表示，边可用平面上的线段来表示（直的或曲的）。 这样画出的平面图形称为图的图示。
例如，例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注：（1）由于表示顶点的平面点的位置的任意性，同一个图可以画出形状迥异的很多图示。
图论讲义第1章-图的概念
图论与网络流理论（Graph Theory and Network Flow Theory）高随祥中科院研究生院专业基础课学时/学分：60/3本课程适合基础数学、应用数学、计算数学、运筹学与控制论、概率论与数理统计各专业的硕士学位研究生作为专业基础课，也可供物理学、化学、天文学、地学、生物科学、计算机科学与技术、计算机软件、管理科学与工程以及通信、信号等学科专业的硕士研究生选修。
主要讲授图论与网络流理论的基本概念、方法和定理，介绍该领域重要的问题以及典型的算法，展示图论与网络流模型及方法的广泛应用。
为学习者将来从事有关方面的理论研究打下基础，也为进行应用性研究提供一种有力的工具。
内容提要第一章 图的基本概念图的基本概念；二部图及其性质；图的同构；关联矩阵与邻接矩阵。
路、圈与连通图；最短路问题。
树及其基本性质；生成树；最小生成树。
第二章 图的连通性割点、割边和块；边连通与点连通；连通度；Whitney定理；可靠通信网络的设计。
第三章 匹配问题匹配与最大匹配；完美匹配；二部图的最大匹配；指派问题与最大权匹配。
第四章 欧拉图与哈密尔顿图欧拉图；中国邮递员问题；哈密尔顿图；旅行商问题。
第五章 支配集、独立集、覆盖集与团支配集、点独立集、点覆盖集、边覆盖集与团的概念及其求法。
第六章图的着色问题点着色；边着色；平面图；四色猜想；色多项式；色数的应用。
第七章网络流理论有向图；网络与网络流的基本概念；最大流最小割定理；求最大流的标号算法；最小费用流问题；最小费用最大流；网络流理论的应用。
主要参考书[1] J.A. Bondy and U.S. Murty, Graph theory with applications, 1976, 有中译本（吴望名等译）。
[2] B.Bollobas, Modern graph theory (现代图论)，科学出版社，2001。
[3] 蒋长浩，图论与网络流，中国林业出版社，2001。
图论
顶点标以二十个城市的名字，要求 有二十个顶点标以二十个城市的名字， 游戏者找一条从某一城市出发的路线， 游戏者找一条从某一城市出发的路线，它经过每 一个城市恰好一次，并且最后回到出发点。 一个城市恰好一次，并且最后回到出发点。 点：城市 边：城市之间的道路 问题：游戏者怎么走才能恰好每个城市走一次， 问题：游戏者怎么走才能恰好每个城市走一次，而 且不重复？如图： 且不重复？如图：
例：有甲、乙、丙、丁、戊五个球队，各队之间比赛 有甲、 戊五个球队， 情况如表： 情况如表： 甲
乙 胜 × 负
丙 负 胜 × 负
丁 胜
戊 胜
甲 乙 丙 丁 戊
× 负 胜 负 负
胜 × 胜 负 ×
点：球队； 球队； 连线：两个球队之间比赛过，如甲胜乙， 连线：两个球队之间比赛过，如甲胜乙，用 v1 v2表示。 表示。
三 、一些特殊图类
1.平凡图 1.平凡图 2.零图 2.零图 3. 连通图 给定图G=（V，E），任何两点间至少有一条链，则 称G是连通图，否则为不连通图。 若G是不连通的，它的每个连通部分称为G的连通分 图。 节点数n=1,边数m=0的图。
边数m=0的图。
4.树 4.树 无圈连通图。 5. 完备图 无向图的完备图：任何两点之间有一条边； 有向图的完备图：任何两点u与v之间有两条有向 边（u，v）及（v，u）。 基本图：把有向图的每条边除去方向得到的无 向图。 6.二分图 6.二分图 若V(G)=X ∪ Y,X ∩ Y= Ф，X 、Y中的任两顶 点不相邻，则G称为二分图，记为（S,X,Y）。
无向图： 无向图：由点及边构成 ，边[vi，vj]
有向图：由点及弧构成， 有向图：由点及弧构成，弧（ vi，vj）
中点集V的顶点个数 图G中点集 的顶点个数，记为 (G) ，边数记为 中点集 的顶点个数，记为p q(G),简记 ，q。 简记p， 。 简记
例：有甲、乙、丙、丁、戊五个球队，各队之间比赛 有甲、 戊五个球队， 情况如表： 情况如表： 甲
乙 胜 × 负
丙 负 胜 × 负
丁 胜
戊 胜
甲 乙 丙 丁 戊
× 负 胜 负 负
胜 × 胜 负 ×
点：球队； 球队； 连线：两个球队之间比赛过，如甲胜乙， 连线：两个球队之间比赛过，如甲胜乙，用 v1 v2表示。 表示。
三 、一些特殊图类
1.平凡图 1.平凡图 2.零图 2.零图 3. 连通图 给定图G=（V，E），任何两点间至少有一条链，则 称G是连通图，否则为不连通图。 若G是不连通的，它的每个连通部分称为G的连通分 图。 节点数n=1,边数m=0的图。
边数m=0的图。
4.树 4.树 无圈连通图。 5. 完备图 无向图的完备图：任何两点之间有一条边； 有向图的完备图：任何两点u与v之间有两条有向 边（u，v）及（v，u）。 基本图：把有向图的每条边除去方向得到的无 向图。 6.二分图 6.二分图 若V(G)=X ∪ Y,X ∩ Y= Ф，X 、Y中的任两顶 点不相邻，则G称为二分图，记为（S,X,Y）。
无向图： 无向图：由点及边构成 ，边[vi，vj]
有向图：由点及弧构成， 有向图：由点及弧构成，弧（ vi，vj）
中点集V的顶点个数 图G中点集 的顶点个数，记为 (G) ，边数记为 中点集 的顶点个数，记为p q(G),简记 ，q。 简记p， 。 简记
ppt2 完全图、偶图与补图 度序列
证明 ： 设G是k-正则图，若k为奇数，则由推论1知 正则图G的点数必为偶数
例4 Δ与δ是简单图G的最大度与最小度，求证： 2m
n
11
H G 1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
证明：由握手定理有：
n d (v) 2m n vV (G)
1 (d2 1, d3 1, , dd11 1, dd12 , , dn )
是图序列。
15
H G 1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
例5 (6, 5, 4, 3, 2, 2, 2) 是否为图序列？如果是， 作出对应的一个简单图。
解： 1 (4, 3, 2,1,1,1)
定理: 一个满足d2=dn-1的图序列 (d1, d2 ,
, dn )
是唯一图序列的充分必要条件是下列条件之一满足：
(1), d1 dn, dn 1, n 1, n 2
(2), d1 dn 2, n 5 (3), d1 d2 dn 1
(4), d1 d2 dn 2, d1 n 1,n 2
图1
图2
图1与图2均是偶图，图2是K2,3
4
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
偶图是一种常见数学模型。
例1 学校有6位教师将开设6门课程。六位教师的代号是 xi（i=1,2,3,4,5,6)，六门课程代号是yi （i=1,2,3,4,5,6)。已知， 教师x1能够胜任课程y2和y3；教师x2能够胜任课程y4和y5； 教师x3能够胜任课程y2；教师x4能够胜任课程y6和y3； 教师x5能够胜任课程y1和y6；教师x6能够胜任课程y5和y6。 请画出老师和课程之间的状态图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
eC
v1
3 5
v2
4 2
v3 5 3 1 邮局 v0
4 2
1
v4
v5
6
v6
18
• 问题分析： （1）如果道路正好是一个Euler图，则容易求 解，用Fleury算法求出一个Euler回路即可； （2）如果不是Euler图，则加上如干重复边， 使之变成Euler图，然后求Euler回路。
现在问题的关键：如何加重复边！ 中国邮路问题是Euler回路的近似求解。
4
(3) B=A2。
a11 a12 … a21 a22 … …… an1 an2 … a1n a2n ann a11 a12 … a21 a22 … …… an1 an2 … a1n a2n ann
B=A2=
×
＝(bij)n×n bij表示vi两步到达vj的路径数目
5
(4) 有向图中：C=AAT。
11Βιβλιοθήκη • 另一方面，即使两个图具有相同的阶和相同 的变数，也不能确保它们同构。
• 定理：图G和H是同构图，则它们对应的顶点 有相同的度。 • 从以上定理可知，若两图同构，则它们具有相 同的度序列。 • 实际上，即便具有相同的度序列，也只是两个 图同构的必要条件，而非充分条件。
12
举例：判断下面两图是否同构。
C= (cij)=
a11 a12 … a21 a22 … …… an1 an2 …
a1n a2n
ann
×
a11 a21 … a12 a22 … …… a1n a2n …
an1 an2
ann
cij=∑αik αjk cij表示以vi,vj为始点的终点数目。
vi
vj
vk
6
(5) 有向图中：D=ATA。
9
• 判别定理：图G1 ，G2同构的充要条件是：存 在置换矩阵P，使得：A1＝PA2P。 其中A1，A2分别是G1 ，G2的邻接矩阵。 如何判断两图同构是图论中一个困难问题， 下面我们来探讨一些判断同构的一些策略。
10
• 根据同构的定义可知，如果两个图G和H是同 构的，则从G的顶点集到H的顶点集必须存在 一个一一对应，这意味着G的顶点和H的顶点 必能够完全匹配，所以G和H有相同的阶，因 此讨论两个图是否相同，我们先考虑他们的阶 是否相同。 • 同理，根据定义，边也存在一一对应，因此， 若两个图同构，则必有相同的边数。 • 因此，若两个图的阶或边数不同，则它们一定 不同构。
14
2
a e5 e4 3 e7 d k1
b
k2
k3 c k6
k4 k7
k5
e
课堂练习答案
解：同构。 对应关系 顶点对应：1－a；2－b；3－e；4－d；5－c； 边对应： e1－k1；e2－k2；e3－k3；e4－k4； E5－k5；e6－k6；e7－k7；
15
§5 中国邮路问题
16
§5 中国邮路问题
a11 a21 … a12 a22 … …… a1n a2n … an1 an2
ann
D= (cij)=
×
a11 a12 … a21 a22 … …… an1 an2 …
a1n a2n
ann
dij=∑αki αkj dij表示以vi,vj为终点的始点数目。
vi
vk
vj
7
•图的同构
• 定义：若两个图顶点数相同且相对应，对应顶 点之间的边也相对应，则称两个图同构。 G1＝(V1,E1)， G2＝(V2,E2)，G1<－>G2 若u1,v1∈V1， u2,v2∈V2，u1 <－>u2， v1 <－>v2，则(u1,v1) ∈E1<－> (u2,v2) ∈E2。
P＝
A＝
PA ＝
a11 a12 a31 a32 a21 a22
a13 a33 a23
a11 a13 (PA)P ＝ a31 a33 a21 a23
a12 a32 a22
P就是一个置换矩阵
2
• 邻接矩阵中图的性质：
v1 v3 0 1 1 0
无向图的邻接 矩阵是对称的！
1 0 1 1 1 1 0 0 0 1 0 0
§4 图的矩阵表示法
• 定义：对于图G=(V,E)，构造一个矩阵 A = ( aij ) n×n 其中n＝|V|；
aij =
1 0
(vi,vj)∈E； 否则；
称A是图G的邻接矩阵。
1
• 置换矩阵：相当于将单位矩阵中相应的行与 行，或者列与列互换的矩阵。
1 0 0 0 0 1 0 1 0 a11 a12 a21 a22 a31 a32 a13 a23 a33
A＝
v2
v4
(1)A=(αij)n×n中，第i行或第i列中非0元素 的个数等于顶点vi的度。(无向图)
3
v1
v3 A＝ v4 0 0 0 1 1 0 1 0 1 0 0 1 0 1 1 0
v2
竖入横出
(2) A=(αij)n×n中，第i列中非0元素的个数等于 顶点vi的入度，第i行中非0元素的个数等于顶点 vi的出度。(有向图)
v1 v3 v4 va
v2
vb
vc
vd
8
v1
v1<->va
v2<->vb
va
v2
v3
v4
图G1
1 A1＝ 0 1 1 1 2 1 0 1 1 3 1 1 0 1 4 1 1 1 0
v3<->vc
v4<->vd
vb
vc
图G2
vd
a A2＝ 0 1 1 1
b 1 0 1 1
c 1 1 0 1
d 1 1 1 0
e 1 e1
2 e2 3 e3 e6 图1 e4 e5 4 e7 5 b k3 d 图2
6
a k2
k1 k5 k6 k4 c
k7
f
• 以上2个图的度序列均为（4,3,3,2,1,1），事实 上它们并不同构。为什么？
13
课堂练习
1、判断下面两图是否同构，若同构写出对 应关系，若不同构则写出理由。
1
e1 e2 e3 4 e6 5 图1 图2
中国邮路问题(Chinese postman problem)，
是我国数学家管梅谷于1960年首次提出的。 • 问题描述： 设邮递员从邮局出发，遍历他所管辖的每 一条街道，将信件送到后返回邮局，求所走 的路径最短。
17
• 中国邮路问题的图论模型为： 设G=(V,E)是连通图，而且对于所有的 e∈E都赋以权c(e)≥0，求从点v0∈V出发， 通过所有边至少一次最后返回v0的回路C， c ( e) 使得 达到最小。
19
E*是重复边 集合
• 定理：设E* E是使W(E*)= c(e) 达到最小 的重复边集合，当且仅当对于Ga图的任一回 路 C，恒有W( C∩E*)≤W(E( ) -E*) C
eE*
v1 3 v3 4
v1
3 5
v2
4 2
v3 5 3 1 邮局 v0
4 2
1
v4
v5
6
v6
18
• 问题分析： （1）如果道路正好是一个Euler图，则容易求 解，用Fleury算法求出一个Euler回路即可； （2）如果不是Euler图，则加上如干重复边， 使之变成Euler图，然后求Euler回路。
现在问题的关键：如何加重复边！ 中国邮路问题是Euler回路的近似求解。
4
(3) B=A2。
a11 a12 … a21 a22 … …… an1 an2 … a1n a2n ann a11 a12 … a21 a22 … …… an1 an2 … a1n a2n ann
B=A2=
×
＝(bij)n×n bij表示vi两步到达vj的路径数目
5
(4) 有向图中：C=AAT。
11Βιβλιοθήκη • 另一方面，即使两个图具有相同的阶和相同 的变数，也不能确保它们同构。
• 定理：图G和H是同构图，则它们对应的顶点 有相同的度。 • 从以上定理可知，若两图同构，则它们具有相 同的度序列。 • 实际上，即便具有相同的度序列，也只是两个 图同构的必要条件，而非充分条件。
12
举例：判断下面两图是否同构。
C= (cij)=
a11 a12 … a21 a22 … …… an1 an2 …
a1n a2n
ann
×
a11 a21 … a12 a22 … …… a1n a2n …
an1 an2
ann
cij=∑αik αjk cij表示以vi,vj为始点的终点数目。
vi
vj
vk
6
(5) 有向图中：D=ATA。
9
• 判别定理：图G1 ，G2同构的充要条件是：存 在置换矩阵P，使得：A1＝PA2P。 其中A1，A2分别是G1 ，G2的邻接矩阵。 如何判断两图同构是图论中一个困难问题， 下面我们来探讨一些判断同构的一些策略。
10
• 根据同构的定义可知，如果两个图G和H是同 构的，则从G的顶点集到H的顶点集必须存在 一个一一对应，这意味着G的顶点和H的顶点 必能够完全匹配，所以G和H有相同的阶，因 此讨论两个图是否相同，我们先考虑他们的阶 是否相同。 • 同理，根据定义，边也存在一一对应，因此， 若两个图同构，则必有相同的边数。 • 因此，若两个图的阶或边数不同，则它们一定 不同构。
14
2
a e5 e4 3 e7 d k1
b
k2
k3 c k6
k4 k7
k5
e
课堂练习答案
解：同构。 对应关系 顶点对应：1－a；2－b；3－e；4－d；5－c； 边对应： e1－k1；e2－k2；e3－k3；e4－k4； E5－k5；e6－k6；e7－k7；
15
§5 中国邮路问题
16
§5 中国邮路问题
a11 a21 … a12 a22 … …… a1n a2n … an1 an2
ann
D= (cij)=
×
a11 a12 … a21 a22 … …… an1 an2 …
a1n a2n
ann
dij=∑αki αkj dij表示以vi,vj为终点的始点数目。
vi
vk
vj
7
•图的同构
• 定义：若两个图顶点数相同且相对应，对应顶 点之间的边也相对应，则称两个图同构。 G1＝(V1,E1)， G2＝(V2,E2)，G1<－>G2 若u1,v1∈V1， u2,v2∈V2，u1 <－>u2， v1 <－>v2，则(u1,v1) ∈E1<－> (u2,v2) ∈E2。
P＝
A＝
PA ＝
a11 a12 a31 a32 a21 a22
a13 a33 a23
a11 a13 (PA)P ＝ a31 a33 a21 a23
a12 a32 a22
P就是一个置换矩阵
2
• 邻接矩阵中图的性质：
v1 v3 0 1 1 0
无向图的邻接 矩阵是对称的！
1 0 1 1 1 1 0 0 0 1 0 0
§4 图的矩阵表示法
• 定义：对于图G=(V,E)，构造一个矩阵 A = ( aij ) n×n 其中n＝|V|；
aij =
1 0
(vi,vj)∈E； 否则；
称A是图G的邻接矩阵。
1
• 置换矩阵：相当于将单位矩阵中相应的行与 行，或者列与列互换的矩阵。
1 0 0 0 0 1 0 1 0 a11 a12 a21 a22 a31 a32 a13 a23 a33
A＝
v2
v4
(1)A=(αij)n×n中，第i行或第i列中非0元素 的个数等于顶点vi的度。(无向图)
3
v1
v3 A＝ v4 0 0 0 1 1 0 1 0 1 0 0 1 0 1 1 0
v2
竖入横出
(2) A=(αij)n×n中，第i列中非0元素的个数等于 顶点vi的入度，第i行中非0元素的个数等于顶点 vi的出度。(有向图)
v1 v3 v4 va
v2
vb
vc
vd
8
v1
v1<->va
v2<->vb
va
v2
v3
v4
图G1
1 A1＝ 0 1 1 1 2 1 0 1 1 3 1 1 0 1 4 1 1 1 0
v3<->vc
v4<->vd
vb
vc
图G2
vd
a A2＝ 0 1 1 1
b 1 0 1 1
c 1 1 0 1
d 1 1 1 0
e 1 e1
2 e2 3 e3 e6 图1 e4 e5 4 e7 5 b k3 d 图2
6
a k2
k1 k5 k6 k4 c
k7
f
• 以上2个图的度序列均为（4,3,3,2,1,1），事实 上它们并不同构。为什么？
13
课堂练习
1、判断下面两图是否同构，若同构写出对 应关系，若不同构则写出理由。
1
e1 e2 e3 4 e6 5 图1 图2
中国邮路问题(Chinese postman problem)，
是我国数学家管梅谷于1960年首次提出的。 • 问题描述： 设邮递员从邮局出发，遍历他所管辖的每 一条街道，将信件送到后返回邮局，求所走 的路径最短。
17
• 中国邮路问题的图论模型为： 设G=(V,E)是连通图，而且对于所有的 e∈E都赋以权c(e)≥0，求从点v0∈V出发， 通过所有边至少一次最后返回v0的回路C， c ( e) 使得 达到最小。
19
E*是重复边 集合
• 定理：设E* E是使W(E*)= c(e) 达到最小 的重复边集合，当且仅当对于Ga图的任一回 路 C，恒有W( C∩E*)≤W(E( ) -E*) C
eE*
v1 3 v3 4