初一数学单项式和多项式试讲教案
单项式和多项式的教案

单项式和多项式的教案教案标题:探索单项式和多项式教学目标:1. 理解单项式和多项式的概念及其特点。
2. 能够识别和区分单项式和多项式。
3. 能够进行单项式和多项式的基本运算。
4. 能够应用单项式和多项式解决实际问题。
教学准备:1. 教师准备:教学课件、黑板、白板笔、单项式和多项式的示例、练习题、实际问题。
2. 学生准备:课本、笔记本、铅笔、橡皮擦。
教学过程:引入:1. 在黑板上写下单项式和多项式的定义,并解释其特点。
2. 通过示例,引导学生思考并区分单项式和多项式。
探索单项式:1. 让学生回顾单项式的定义,并通过示例解释单项式的各个部分(系数、字母、指数)的含义。
2. 给学生提供一些单项式的例子,并让他们识别和写出每个单项式的系数、字母和指数。
3. 引导学生进行单项式的基本运算,如加法、减法和乘法。
4. 提供一些练习题,让学生巩固单项式的概念和运算技巧。
探索多项式:1. 让学生回顾多项式的定义,并通过示例解释多项式的各个部分(项、项数、次数)的含义。
2. 给学生提供一些多项式的例子,并让他们识别和写出每个多项式的项、项数和次数。
3. 引导学生进行多项式的基本运算,如加法、减法和乘法。
4. 提供一些练习题,让学生巩固多项式的概念和运算技巧。
应用实际问题:1. 给学生提供一些实际问题,让他们能够应用单项式和多项式解决问题。
2. 引导学生分析问题,将问题转化为数学表达式,并通过单项式和多项式进行计算和求解。
3. 鼓励学生在解决实际问题过程中思考和讨论,培养他们的问题解决能力。
总结:1. 回顾单项式和多项式的概念和特点。
2. 强调单项式和多项式的基本运算技巧。
3. 提醒学生在解决实际问题时要灵活运用单项式和多项式。
扩展活动:1. 让学生自主查找更多关于单项式和多项式的例子,并进行分析和讨论。
2. 鼓励学生设计自己的实际问题,并用单项式和多项式解决。
评估方法:1. 教师观察学生在课堂上的参与和表现。
2. 教师布置练习题或小测验,检验学生对单项式和多项式的理解和运用能力。
七年级数学上册 2.1 单项式与多项式教案 (新版)新人教版

2.1单项式与多项式 (2 )教学目标:1、掌握整式、单项式及其系数与次数 ,多项式的项、次数 ,常数项;2、明确以上各概念之间的关系 .重点:单项式、系数、次数的概念 .难点: 次数、单项式的识别、多项式的次数 .过程:一、复习引入二、新课1、单项式:都是由数和字母的乘积组成的 ,这样的代数式叫单项式 .特别地:单独一个数或一个字母也是单项式 .举例判断: (1 )1+x ; (2 )x 1; (3 )2r π; (4 )b a 223- 提问:单项式与代数式有什么关系 ?单项式是一种特殊的代数式 ,它是由数与字母的乘积组成的一类代数式 .2、单项式的系数:单项式中的数字因数 ,叫单项式的系数 .注意系数中的1或 -1中的1可以省略 ,π是数 .如:h r 2-;r π31;22h a -;227y x -;xyz ;327xy 注意:系数一般不写成带分数 .3、单项式的次数:单项式中 ,所有字母的指数的和 ,叫这个单项式的次数 .如:以上各单项式的次数分别是什么 ?4、多项式:几个单项式的和 .多项式的项:组成多项式的各单项式 .无字母的项叫常数项 .多项式的次数:多项式中 ,次数最|高项的次数 .多项式的项数:多项式中项的个数 .如:3232917y x yz x y x ++-+-叫四次五项式 .请指出它的项、次数、项数 .5、整式:单项式和多项式的统称 .如以上各式 . 教学反思1 、要主动学习、虚心请教,不得偷懒. 老老实实做"徒弟〞,认认真真学经验,扎扎实实搞教研.2 、要勤于记录,善于总结、扬长避短. 记录的过程是个学习积累的过程, 总结的过程就是一个自我提高的过程.通过总结, 要经常反思自己的优点与缺点,从而取长补短,不断进步、不断完善.3 、要突破创新、富有个性,倾心投入. 要多听课、多思考、多改良,要正确处理好模仿与开展的关系,对指导教师的工作不能照搬照抄,要学会扬弃,在原有的根底上,根据自身条件创造性实施教育教学,逐步形成自己的教学思路、教学特色和教学风格, 弘扬工匠精神, 努力追求自身教学的高品位.。
沪科版数学七年级上册《单项式和多项式》教学设计

沪科版数学七年级上册《单项式和多项式》教学设计一. 教材分析沪科版数学七年级上册《单项式和多项式》是学生在初入中学阶段首次接触代数领域的重要内容。
这一章节的主要目的是让学生理解并掌握单项式和多项式的概念,以及它们的运算规则。
教材通过例题和练习题的引导,使学生逐步建立起对这些代数概念的认识,为后续的代数学习打下坚实的基础。
二. 学情分析七年级的学生大多具有较强的直观思维能力,但代数知识相对较为抽象,因此在学习本章节内容时可能会感到一定的困难。
因此,在教学过程中,我将以生动的生活实例引入单项式和多项式的概念,并通过大量的练习题让学生逐步理解和掌握。
三. 说教学目标1.知识与技能:学生能够理解单项式和多项式的概念,掌握它们的运算规则。
2.过程与方法:通过实例引入单项式和多项式的概念,培养学生的抽象思维能力。
3.情感态度与价值观:激发学生对代数学习的兴趣,培养学生的逻辑思维能力。
四. 说教学重难点1.重点:单项式和多项式的概念及其运算规则。
2.难点:理解单项式和多项式的概念,并能运用其运算规则解决实际问题。
五. 说教学方法与手段1.采用问题驱动的教学方法,以生活实例引导学生思考,激发学生的学习兴趣。
2.利用多媒体课件,直观展示单项式和多项式的运算过程,帮助学生理解和记忆。
3.运用分组讨论、合作交流的教学手段,培养学生团队协作能力和沟通能力。
六. 说教学过程1.导入新课:以生活实例引入单项式和多项式的概念,激发学生的学习兴趣。
2.知识讲解:讲解单项式和多项式的定义及运算规则,引导学生理解和掌握。
3.例题讲解:分析并讲解典型例题,让学生学会运用所学知识解决实际问题。
4.练习巩固:布置适量练习题,让学生独立完成,检测学习效果。
5.课堂小结:总结本节课的主要内容和知识点,提醒学生注意易错点。
6.课后作业:布置课后作业,巩固所学知识,提高学生的实际应用能力。
七. 说板书设计板书设计要简洁明了,突出单项式和多项式的关键信息。
《单项式与多项式》教案
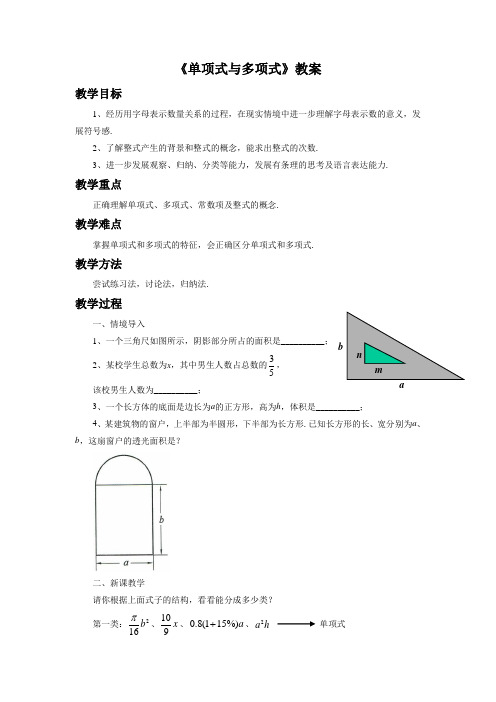
《单项式与多项式》教案教学目标1、经历用字母表示数量关系的过程,在现实情境中进一步理解字母表示数的意义,发展符号感.2、了解整式产生的背景和整式的概念,能求出整式的次数.3、进一步发展观察、归纳、分类等能力,发展有条理的思考及语言表达能力. 教学重点正确理解单项式、多项式、常数项及整式的概念.教学难点掌握单项式和多项式的特征,会正确区分单项式和多项式.教学方法尝试练习法,讨论法,归纳法.教学过程一、情境导入1、一个三角尺如图所示,阴影部分所占的面积是__________;2、某校学生总数为x ,其中男生人数占总数的35, 该校男生人数为__________; 3、一个长方体的底面是边长为a 的正方形,高为h ,体积是__________; 4、某建筑物的窗户,上半部为半圆形,下半部为长方形.已知长方形的长、宽分别为a 、b ,这扇窗户的透光面积是?二、新课教学请你根据上面式子的结构,看看能分成多少类? 第一类:216b π、109x 、0.8(115%)a +、2a h单项式第二类:24ab c -、2a +2b 多项式引出概念:单项式、多项式、整式、系数、次数、常数项……只含有加、减、乘、乘方运算的代数式叫做整式.其中,不含有加、减运算的整式叫做单项式.几个单项式的和叫做多项式.……单项式与多项式的区别:x 53、h a 2、ab 、722y x -、216b π、a 、—b 、1的次数和系数. 2、多项式的项数和次数,练习:216b ab π-、2a +2b 、mn ab 2121-、2532232-+-b a b a 、b a ab -+23的项数和次数. 注:1、单独一个非零数的次数是0.2、当单项式的系数为1或—1时,这个“1”应省略不写.3、确定多项式的次数时,应注意先确定每个单项式每个字母的指数;再计算这个单项式中所有字母的指数的和.4、单独一个数或一个字母也是单项式在讲解完单项式、多项式、整式的概念及整式的次数后,立即让学生把上一环节中的代数式进行归类并求出它们的次数.三、巩固练习:1、在代数式231a ,2243b a -,-ab ,)(1y x a +,)(21b a +,712+x 中, 单项式有________________,它们各自的系数分别为____________,多项式有______________________________.2、单项式的次数:字 母 字母的指数 指数和 次 数3x225ab -bc a 2-3 项数 项 各项次数 最高次数 多项式次数16b ab π-bc a 32-2212+y x 四、拓展思维:师生共同探讨完成书本“挑战自我”.五、小结:(1)这节课,你学到了什么?(2)整式是指什么?(3)单项式、多项式的次数是怎样求的?。
《单项式与多项式》教学设计

《单项式与多项式》教学设计第一篇:《单项式与多项式》教学设计《单项式与多项式》教案横山中学沈习兵2014.10.14 【教学目标】一、知识与技能:1.了解整式的有关概念,会识别单项式、多项式和整式。
2.能说出一个单项式的系数和次数,多项式的项的系数和次数,以及多项式的项数和次数。
二、过程与方法:在参与对单项式、多项式识别的过程中,培养观察、归纳、概括和语言表达的能力。
三、情感、态度与价值观:通过单项式与多项式有关概念的探究,培养学生发现问题、解决问题的科学思想。
【重点与难点】1.能说出单项式的系数、次数2.能说出多项式每一项的系数、次数,及整个多项式是几次几项式。
【教学过程】2.1 代数式(3、你能举出一些单项式的例子吗?三、问题与思考(1)“9”是不是单项式?“a”是不是单项式?注意:单独一个数或一个字母也是单项式。
(2)是不是单项式?“2x+1”和“a–b” 是不是单项式?都不是单项式,单项式只含有一个乘积运算。
注意:单项式的分母中不含字母,且不含加减运算四、单项式系数与次数1、单项式是由数字因数和字母因数组成,如3ab •2、单项式中的数字因数叫作单项式的系数如:3a2的系数是3,-0.6x2y的系数是-0.63、问:a的系数是多少?-a的系数呢?4、一个单项式中,所有字母的指数的和叫作这个单项式的次数如: 3a2的次数是2,-0.6x2y的次数是35、问:8的次数是多少?五、几点说明:1、单项式的系数必须包括前面的符号2、注意:单项式的系数是1时,1可省略。
单项式的系数是-1时,1可省略,但负号不可省略。
•3、单独一个数字的次数为0 •4、圆周率π是常数,不要把它看成字母5、如果一个单项式的次数为n,我们就把它叫作n次单项式。
如x2y3的次数为5,我们就说x2y3是五次单项式六、大家一起练:• 例1 判断下列各代数式是否是单项式。
如果不是,请简要说明理由;如果是,请指出它的系数与次数:(1)x+1(2) r22(3)1 / x(4)-½ab 解答:(1)不是.因为原代数式中出现了加法运算.(2)是.它的系数是∏,次数是2.(3)不是.因为原代数式是1与x的商.(4)是.它的系数是3x+4(3)b-5 + ab3-a22、已知:3xmy2m-x2y-4是一个六次多项式,m的值为。
七年级数学上册《单项式与多项式》教案、教学设计

3.提醒学生注意在解决实际问题时,要灵活运用所学知识,提高解题能力。
4.鼓励学生课后进行自主学习和探究,为下一节课的学习做好准备。
五、作业布置
为了巩固学生对单项式与多项式的理解,提高他们合并同类项的能力,特布置以下作业:
1.基础知识巩固:
-完成课本习题:课后练习题第1、2、3题,要求学生独立完成,巩固单项式与多项式的定义及合并同类项的基本方法。
-自主设计练习:请学生自己设计一道包含多个单项式的数学表达式,并运用合并同类项法则进行简化。
2.实践应用提高:
-生活实例应用:请学生收集家庭购物小票或价目表,将其中的商品价格用单项式表示,并进行同类项的合并,计算总价。
-数学问题解决:解决课后习题中的一些实际问题,如求解包含单项式与多项式的简单方程,让学生体会数学知识在实际问题中的应用。
3.拓展延伸思考:
-研究性问题:讨论并思考如何将合并同类项的法则应用于更复杂的代数表达式中,例如含有多个变量或不同指数的单项式。
-探究性问题:分组讨论,探究合并同类项法则在几何图形面积和体积计算中的应用。
4.阅读理解与反思:
-阅读材料:阅读教材中关于单项式与多项式的相关阅读材料,加深对概念的理解。
-反思日记:要求学生写一篇关于本节课学习的反思日记,内容包括学习收获、困惑和改进措施。
(四)课堂练习
1.设计不同难度层次的练习题,涵盖识别单项式、合并同类项等方面,让学生在练习中巩固所学知识。
2.引导学生运用合并同类项法则解决实际问题,如购物计算、求解方程等。
3.及时反馈:针对学生的解答,给予评价和指导,指出错误原因,提供解题思路。
(五)总结归纳
1.让学生回顾本节课所学内容,总结单项式与多项式的定义、合并同类项的法则等知识点。
单项式与多项式教案

单项式与多项式教案第一章:单项式的概念与性质1.1 引入单项式的概念:引导学生通过具体的例子,理解单项式的定义,即数字与字母的乘积。
1.2 掌握单项式的系数:解释单项式中数字因数叫做单项式的系数,并进行相关练习。
1.3 理解单项式的次数:引导学生了解单项式中,所有字母的指数和叫做这个单项式的次数,并进行相关练习。
1.4 探索单项式的性质:通过练习,让学生掌握单项式的大小比较、相等条件等性质。
第二章:多项式的概念与性质2.1 引入多项式的概念:通过具体的例子,让学生理解多项式的定义,即几个单项式的和。
2.2 理解多项式的项:解释多项式中每个单项式叫做多项式的项,并进行相关练习。
2.3 掌握多项式的次数:引导学生了解多项式中,最高次项的次数叫做这个多项式的次数,并进行相关练习。
2.4 探索多项式的性质:通过练习,让学生掌握多项式的相等条件、大小比较等性质。
第三章:单项式与多项式的运算3.1 单项式乘以单项式:引导学生理解单项式乘以单项式的运算规则,并进行相关练习。
3.2 单项式乘以多项式:解释单项式乘以多项式的运算规则,并进行相关练习。
3.3 多项式乘以多项式:引导学生理解多项式乘以多项式的运算规则,并进行相关练习。
3.4 单项式除以单项式:解释单项式除以单项式的运算规则,并进行相关练习。
3.5 多项式除以单项式:引导学生理解多项式除以单项式的运算规则,并进行相关练习。
第四章:单项式与多项式的应用4.1 求解含单项式的方程:通过具体的例子,让学生学会求解含有单项式的方程。
4.2 求解含多项式的方程:引导学生学会求解含有多项式的方程。
4.3 实际问题中的应用:通过实际问题,让学生运用单项式和多项式的知识解决问题。
第五章:单项式与多项式的进一步探讨5.1 同类项的概念:解释同类项的定义,即字母相同且相同字母的指数也相同的项。
5.2 合并同类项:引导学生掌握合并同类项的方法,并进行相关练习。
5.3 单项式的因式分解:解释单项式的因式分解方法,并进行相关练习。
单项式和多项式教案精选全文

一、教学内容:
1、用含字母的式子填空,看看列出的式子有什么特点。
⑴边长为a的正方形的表面积为,体积为;
⑵铅笔的单价是x元,圆珠笔的单价是铅笔的单价的2.5倍,圆珠笔的单价是元;
⑶一辆汽车的速度是v千米/时,它t小时行驶的路程为千米;
⑷数n的相反数是。
⑸直径为m的圆面积是
2、像6 , ,2.5 ,tv,—n, 他们都是一个数字或字母的积,叫做单项式。单独一个数和字母也叫单项式。
A、 B、 C、 D、
二.填空题
1.当a=-1时, =;
2.单项式: 的系数是,次数是;
3.多项式: 是次项
4. 是次单项式;
5. 的一次项系数是,常数项是;
6.单项式 xy2z是_____次单项式.
7.当x=2,y=-1时,代数式 的值是;
8.多项式x3y2-2xy2- -9是___次___项式,其中最高次项的系数是,二次项是,常数项是.
A.2个B.3个C.4个D5个
2.多项式-23m2-n2是()
A.二次二项式
B.三次二项式
C.四次二项式
D.五次二项式
3.下列说法正确的是()
A.3x2―2x+5的项是3x2,2x,5
B. - 与2x2―2xy-5都是多项式
C.多项式-2x2+4xy的次数是3
D.一个多项式的次数是6,则这个多项式中只有一项的次数是6
例:
多项式4x-5,次数最高的是4x,这个多项式的次数是1,
多项式6 -2x+7,次数最高的是二次项6 ,这个多项式的次数是2
一个多项式含有几项,就叫几项式。如4x-5是二项式,6 -2x+7, +ab+ 都是三项式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(或课堂反思)
课堂小结
作业
对学生或
家长建议
学生或家长签字
教务部门签章
其含义有:①不含有加、减运算符号.②字母不出现在分母里.③单独的一个数或者字母也是单项式.④不含“符号”.
(2)一个单项式中,所有字母的指数的和叫做这个单项式的次数。如 是6次单项式。注意系数与指数的区别与联系:①从位置上看;②从表示的意义上看。
2多项式
(1)几个单项式的和叫做多项式。其中每个单项式叫做这个多项式的项。多项式中不含字母的项叫做常数项。多项式中次数最高的项的次数,叫做这个多项式的次数。
(2).有括号的情况
有括号的先去括号,然后再合并同类项,根据多重括号的去括号法则,可由里向外,也可由外向里逐层推进,在计算过程中要注意符号的变化.
例21-3(2ab+a)十[1-2(2a-3ab)].
(3).先代入后化简
例3已知A=x2+xy+y2,B=-3xy-x2,求2A-3B.
类型五、求代数式的值
姓名
学生姓名
上课时间
辅导科目
数学
年级
初一
课时
2
教材版本
人教版
课题名称
复习-----整式
教学目标
掌握整式的相关概念及整式的加减运算
教学重点
锻炼解题综合运用的能力
教学难点
先化简再求值的代数运算
教学及辅导过程
一相关概念
1单项式
(1)数或字母的积的代数式叫做单项式。注意:单项式是由系数、字母、字母的指数构成的,其中系数不能用带分数表示,如 ,这类型一 概念题
1.(2011广东湛江)多项式 是____次___项式.
2、若3a2bn-1与- am+1b2是同类项,则( )
A.m=3,n=2B.m=2,n=3C.m=3,n=- D.m=1,n=3
类型二 列代数式
1. (2011浙江温州,)汛期来临前,滨海区决定实施“海堤加固”工程,某工程队承包了该项目,计划每天 加固60米.在施工前,得到气象部门的预报,近期有“台风”袭击滨海区,于是工程队改变计划,每天加固的海堤长度是原计划的1.5倍,这样赶在“台风”来临前完成加固任务.设滨海区要加固的海堤长为a米,则完成整个任务的实际时间比原计划时间少用了____天(用含a的代数式表示).
(2)单项式和多项式统称整式。
3同类项
所有字母相同,并且相同字母的指数也分别相同的项叫做同类项。几个常数项也是同类项。
条件:①字母相同;②相同字母的指数相同
合并依据:乘法分配律
4代数式
由数和表示数的字母经有限次加、减、乘、除、乘方等代数运算所得的式子,或含字母的表达式称为代数式、
用数值代替代数式中的字母,按照代数式指明的运算,计算出结果,叫做代数式的值。
1.直接求值法先把整式化简,然后代入求值.
例1先化简,再求值:3-2xy+2yx2+6xy-4x2y,其中x=-1,y=-2.
2.隐含条件求值法先通过隐含条件将字母取值求出,然后化简求值.
例2若单项式-3a2-mb与bn+1a2是同类项,求代数式m2-(-3mn+3n2)+2n2的值.
例3已知 +(b+1)2=0,求5ab2-[2a2b-(4ab2-2a2b)]的值.
A.28 B.56 C.60 D. 124
2.(2011广东肇庆)如图5所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第 ( 是大于0的整数)个图形需要黑色棋子的个数是____
类型四整式的加减运算
1、a,b,c都是有理数,那么a-b+c的相反数是( )
A.b-a-cB.b+a-cC.-b-a+cD.b-a+c
2、下列去括号正确的是( )
A.2y2-(3x-y+3z)=2y2-3x-y+3zB.9x2-[y-(5z+4)]=9x2-y+5z+4
C.4x+[-6y+(5z-1)]=4x-6y-5z+1D.-(9x+2y)+(z+4)=-9x-2y-z-4
3、计算题
(1).不含括号的直接合并同类项
例1合并同类项3x2-4xy+4y2-5x2+2xy-2y2;
注意:(1)求代数式的值,一般是先将代数式化简,然后再将字母的取值代入。
(2)求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入。
5、整式的加减
1).整式加减法法则
几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接,然后去括号,合并同类项.
2).合并同类项法则合并同类项时,把系数相加,字母和字母指数不变.
2. (2011四川乐山)体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元。则代数式500-3a-2b表示的数为____。
类型三 规律题
1. (2011浙江省)如图,下面是按照一定规律画出的“数形图”,经观察可以发现:图A2比图A1多出2个“树枝”, 图A3比图A2多出4个“树枝”, 图A4比图A3多出8个“树枝”,……,照此规律,图A6比图A2多出“树枝”( )
