第五节__条件分布与条件期望

F ( x , y ) y d FY ( y ) dy
亦即 FX |Y
( x | y)
x
p( u, y )du pY ( y )
，或写成 FX |Y ( x | y )
x
p( u, y ) du pY ( y )
类似地可以定义 FX |Y ( y | x )和 FY | X ( y | x )
由条件概率密度定义知, p( x , y ) pY ( y ) p X |Y ( x | y ) p X ( x ) pY | X ( y | x ), 故
pX ( x ) pY ( y ) pX |Y ( x | y )dy.

pY ( y ) pX ( x ) pY | X ( y | x )dx.
2
2,),求
( x 1 )( y 2 )
1 2

( y 2 )2
2
2
]}
由以前的例子知道
pX ( x )
1 e 2 1
x ， y
( x 1 ) 2 2 1 2
所以X=x条件下Y的条件概率密度为
pY | X ( y | x )
Y
Y=0
X
Y=3/2 Y=2
X1= -1 1/12 2/12 3/12
X2=1 0 1/12 1/12
X3=2 3/12 1/12 0
求条件分布律P{X=xi|Y=2}.
解：X与Y的边缘分布如表：
X Y Y=0
Y=3/2 Y=2 pi .
X1=-1 1/12 2/12 3/12 6/12
X2=1 0 1/12 1/12 2/12
例: 设数X在区间(0,1)上随机地取值,当观察到X=x(0<x<1)时, 数Y在区间(x,1)上随机取值.求Y的概率密度pY(y).
解: 按题意X具有概率密度
1 pX ( x ) 0 0 x 1 其它
对于任意的x(0<x<1),在X=x的条件下,Y的条件概率密度
1 pY | X ( y | x ) 1 x 0 0 x y1 其它
y
p( x, v ) dv pX ( x )
3.条件概率密度定义 p X |Y ( x | y ) p( x , y )
pY ( y )
称为在Y=y条件下X的条件概率密度，且满足概率密度的两个性质。
p( x , y ) 同理， pY | X ( y | x ) pX ( x )
称为在X=x条件下X的条件概率密度，且满足概率密度的两个性质。
X3=2 3/12 1/12 0 2/12
p.j 4/12 4/12 4/12 4/12
P{X=-1|Y=2}=p13/p.3=3/4； P{X=1|Y=2}=p /p =1/4； 23 .3 P{X=2|Y=2}=p33/p.3=0；又如：P{X=1|Y=0}=p21/p.1=0等；
二、连续型随机变量条件分布的定义
的概率,由条件概率公式,
P{ X x i | Y y j } P{ X x i , Y y j } P{Y y j } pij p j , i 1,2,.
显然，上述条件概率具有分布律的特性 (1).P{X=xi|Y=yj}≥0；
(2). P{ X xi | Y y j }
i 1 i 1
pij p j

p j p j
1
1．定义设(X,Y)是二维离散型随机变量,对于固定的j，若P{Y=yj}>0，则称
P{ X xi | Y y j } P{ X xi , Y y j } P{Y y j } pij p j , i 1,2 .
于是得关于Y的边缘概率密度为
y 1 dx ln(1 y ) pY ( y ) f ( x, y )dx 0 1 x 0 其它
0 y1

pX ( x ) pY | X ( y | x )dx
三、连续场合的全概率公式和贝叶斯公式

e

( x )2 ( y x )2 2 2 2 1 2 2
按x 配方积分
dx .

1 2 ( 1 2 )
2 2
e

( y )2
2 2 2 ( 1 2 )
.
2 ). 即 Y仍服从正态分布 N ( , 1 2 2
二、条件数学期望
1 定义: X在Y=y的条件下的条件分布的数学期望(若存在)称为X在Y=y的条件下的条件期望.
上式给出了在任意y-ε ＜Y≤y+ε 下X的条件分布函数,现在我们引入以下的定义.
1.条件分布函数的定义：给定y,设对于任意实数x,若极限
0
lim P{ X x | y Y y }
P{ X x , y Y y } lim 0 P{ y Y y }
设(X,Y)是二维连续型随机变量,这时由于对任意x,y有 P{X=x}=0 , P{Y=y}=0 ,因此不能直接用条件概率公式引入条件分布函数P{X≤x|Y＝y}.下面我们用极限的方法来处理. 给定y,设对于任意固定的正数ε ,P{y-ε ＜Y≤y+ε }>0 , 于是对于任意x有
P{ X x , y Y y } P{ X x | y Y y } P{ y Y y }
2.重期望公式
定理: 设(X,Y)为二维随机向量, 且E(X)存在, 则
E ( X ) E ( E ( X | Y )).
证明:略.
特殊的情形
(1) Y离散情形下
E ( X ) Eg(Y ) E ( X | Y y j ) P (Y y j ).
j
给定Y=y时算X的条件期望,然后按 Y=y的可能性大小进行加权平均
1 2 2
e

( y x )2
2 2 2
故
pY ( y ) pX ( x ) pY | X ( y | x )dx.

1 e 2 1
( x )2
2 2 1

1 2 2
e

( y x )2
2 2 2
dx .

1 2 1 2

当 x [20, 30] 时,
1 E (T | x ) 0.03 y dy 0.45 10 10
具体定义式: (1) 当(X,Y)为离散随机向量时,
E ( X | Y y ) xi P ( X xi | Y y ),
i
(2) 当(X,Y)为连续随机向量时,
E ( X | Y y ) xpX |Y ( x | y )dx,

同样地可定义Y在X= x的条件下的条件期望.
为在Y=yj条件下随机变量X的条件分布律。
同理，对于固定的i，若P{X=xi}>0，则称
P{Y y j | X xi } P{ X x i , Y y j } P{ X x i } pij pi , j 1,2,.
为在X=xi条件下随机变量Y的条件分布律。 2. 条件分布函数
p X ( x ) pY | X ( y | x )
全概率公式的密度函数形式
代入条件概率密度定义式,即得
p X |Y ( x | y ) pY | X ( y | x )

. .

p X ( x ) pY | X ( y | x )dx pY ( y ) p X |Y ( x | y ) pY ( y ) p X |Y ( x | y )dy
p( x , y ) pX ( x )
2 2 (y x 2 1 ) 1 1 ] e xp[ 2 2 2 2 2 2 1 2 1

这正是正态分布
N (2
2 x 1 , 2 2 1 2 ) 1
(2) Y连续情形下
E ( X ) Eg(Y )

E ( X | Y y ) pY ( y ).
条件期望的应用例设在一个指定的时间内供给一水电公司的电能ξ是一个随机变量,且 ξ 在[10, 30]上服从均匀分布.该公司对于电能的需要量η也是一个随机变量,且 η 在[10, 20] 上服从均匀分布. 对于所供给的电能,公司取得每千瓦0.03元利润,如果需要量超过所能供给的电能,公司就从另外的来源取得附加的电能加以补充,并取得每千瓦0.01元利润,问在所考虑的指定时间内,公司所获得的利润的期望值是多少? 解:设 T 是公司所获得的利润,则
可以看出,X在Y=y的条件下的条件期望是y的函数,它是一个变量. 这不同于无条件期望E(X).
E( X | Y y) E( X | Y )
Y取确定值y的条件下
Y取值随机的条件下
若记 g( y ) E ( X | Y y ), 则 g(Y ) E ( X | Y ) 作为随机变量Y 的函数, 我们可称之为在给定Y的条件下X的条件期望, 它是随机变量.
FX |Y ( x | y j ) P{ X x | Y y j }

xi x
p
p ij
j

xi x
p
p j
xi x
P{ X x
i
|Y yj}
ij
同理：
FY | X ( y | x i )
yjy
p

合集下载

随机变量的条件分布与条件期望

随机变量的条件分布与条件期望随机变量是概率论中十分重要的概念之一，它描述了在概率模型中可能出现的各种结果。

随机变量可以是离散的，也可以是连续的。

在概率论中，我们经常关注的是随机变量的分布以及其与其他变量之间的关系。

本文将重点讨论条件分布与条件期望。

一、条件分布条件分布是指在给定某些条件下，随机变量满足的分布。

对于离散型随机变量，条件分布的计算可以通过条件概率来进行。

假设X和Y是两个离散型随机变量，我们想要求解在给定X的取值为x的条件下，Y的取值为y的概率。

可以表示为P(Y=y|X=x)。

这个概率可以通过联合概率分布和边缘概率分布来计算。

具体计算方法为：P(Y=y|X=x) = P(X=x,Y=y) / P(X=x)对于连续型随机变量，条件分布的计算可以通过条件密度函数来进行。

假设X和Y是两个连续型随机变量，我们想要求解在给定X的取值为x的条件下，Y的取值在a到b之间的概率。

可以表示为P(a <= Y <= b | X = x)。

这个概率可以通过联合概率密度函数和边缘概率密度函数来计算。

具体计算方法为：P(a <= Y <= b | X = x) = ∫[a, b] f(x, y) dy / f_X(x)二、条件期望条件期望是指在给定某些条件下，随机变量的期望值。

对于离散型随机变量，条件期望的计算可以通过条件概率和随机变量的取值来进行。

假设X和Y是两个离散型随机变量，我们想要求解在给定X的取值为x的条件下，Y的期望值E(Y|X=x)。

可以表示为：E(Y|X=x) = Σy y * P(Y=y|X=x)其中Σ为求和符号，y为随机变量Y的取值。

对于连续型随机变量，条件期望的计算可以通过条件密度函数和随机变量的取值来进行。

假设X和Y是两个连续型随机变量，我们想要求解在给定X的取值为x的条件下，Y的期望值E(Y|X=x)。

可以表示为：E(Y|X=x) = ∫y y * f(y|x) dy其中∫为积分符号，f(y|x)为在给定X=x的条件下，Y的概率密度函数。

条件分布与条件期望

33
XY 3 1 2
P
61
77
43 P
77 4
例2. 设随机变量X ,Y相互独立,X P(1), Y P(2 ) ，
在X Y n的条件下，求X的条件分布.
解：X Y P(1 2 )
P(X k X Y n) P(X k, X Y n) P(X k,Y n k)
P(X Y n)
pY ( y)E( X Y y) dy E( X Y y)看作是y的函数.
E[E( X Y )]
13
例5 一矿工被困在有三个门的矿井里，第一个门通甲坑道，须走3小时到达安全区；第二个门通乙坑道，走5小时回到原处；第三个门通丙坑道，走7小时回到原处。问他平均用多长时间能够到达安全区。分析：到达安全区的时间与第一次选择的门有关，
i
1 (1 (2 EX )
yi )P(Y yi )
(n EX ))
EX
n(n 1) . 2
n
17
作业：
P197 2 4
18
The End！
Thank You！
Department of Mathematics
19
即有
P(X x Y y)
x p( x, y) dx;
pY ( y)
同样可得 P(Y y X x)
y p( x, y) dy .
pX ( x)
8
2、连续随机变量的条件分布
定义3：对y,且pY ( y) 0，在给定Y y条件下
X的条件分布函数和条件密度函数分别是：
F ( x y)
3 E( X Y 2) 5 EX; E( X Y 3) 7 EX .
E( X ) E( X Y y j )P(Y y j )

§3.5---条件分布与条件期望

条件分布与条件期望

为例，
将上式左边乘以 dx , 右边乘以 dx·dy/dy 即得
pX|Y(x|y)dxp(pxY,(yy))d dxydy P {xXxd x,yYyd y}
P {yYyd y}
P { x X x d x | y Y y d y }
pX|Y(x| y)dx P { x X x d x | y Y y d y } 换句话说，对很小的dx和 dy，pX|Y(x| y)dx 表示已知 Y 取值于y和y+dy之间的条件下，X 取值于x和x+dx之间的条件概率.
E [g(X )|y] i g g ((x x i))p P ((x X | y)d x x i|,Yy),
在离散场合在连续场合
定理3.5.1 (重期望公式)条件期望的期望就是(无条件)期望，即 E[E(X|Y)] = E(X) .
证: 在连续场合
E(X)
0x1，p(y| 其它
x)11x, 0,
0xy1 其它
求(X,Y)的联合密度p(x,y)和Y的边际密度pY(y) 及
解P(：Y>0.5).
p(x,y)p(y|x)pX(x) 1 1x, 0xy1
0,
其它
y
pY(y)
x<y
y =x
0
1
x
p(x,y)0的区域
0
1
y
pY(y)的图形
y1
pY(y)
p X |Y ( x | y ) 可知，当X与Y相互独立时，
p(x, y) pY ( y )
pY|X(y|x)pY(y), pX |Y(x|y)pX(x)
也可用此条件判别二维连续型r.v(X,Y)的两个分量X与Y是否相互独立.

概率论与数理统计公式精粹条件期望条件方差与条件分布

概率论与数理统计公式精粹条件期望条件方差与条件分布条件期望、条件方差和条件分布是概率论与数理统计中重要的概念和技巧。

它们能帮助我们更准确地描述和计算随机现象的特征和性质。

本文将对条件期望、条件方差和条件分布进行精炼的介绍和讨论。

一、条件期望条件期望是指在给定某些信息或条件下，对随机变量的期望进行计算的概念。

对于随机变量X和事件A，条件期望E(X|A)表示在事件A发生的条件下，随机变量X的平均取值。

条件期望的计算可以通过基本的期望定义进行推导。

对于离散型随机变量，条件期望的计算公式为：E(X|A) = ∑x P(X=x|A) * x其中，P(X=x|A)表示在事件A发生的条件下，随机变量X取值为x的概率。

对于连续型随机变量，条件期望的计算公式为：E(X|A) = ∫xf(x|A) dx其中，f(x|A)表示在事件A发生的条件下，随机变量X的概率密度函数。

二、条件方差条件方差是在给定某些信息或条件下，对随机变量的方差进行计算的概念。

对于随机变量X和事件A，条件方差Var(X|A)表示在事件A发生的条件下，随机变量X的离散程度。

条件方差的计算可以通过基本的方差定义进行推导。

对于随机变量X和事件A，条件方差的计算公式为：Var(X|A) = E[(X-E(X|A))^2|A]其中，E(X|A)表示在事件A发生的条件下，随机变量X的条件期望。

三、条件分布条件分布是指在给定某些信息或条件下，随机变量的分布情况。

对于随机变量X和事件A，条件分布P(X=x|A)表示在事件A发生的条件下，随机变量X取值为x的概率。

条件分布的计算可以通过基本的概率计算进行推导。

对于随机变量X和事件A，条件分布的计算公式为：P(X=x|A) = P(X=x, A) / P(A)其中，P(X=x, A)表示事件A发生且随机变量X取值为x的概率，P(A)表示事件A的概率。

四、应用与扩展条件期望、条件方差和条件分布在实际问题中有广泛的应用。

条件分布与期望(1)2010122002

−∞
+∞
例3 矿工困在矿井里，他的面前有三扇门，走第一扇门3个小时后到达安全区；第二扇门走5个小时又 ∑ E ( X | Y = y j ) p (Y = 回到原处；第三扇门走7个小时也回到原处。y j ) 离散 j E( X ) = +∞ 假定矿工总是等可能地在三个门中选择一个，试求他 E ( X | Y = y ) pY ( y )dy 连续 ∫−∞ 的平均要用多少时间到达安全区。
−∞
p ( x, y ) = p ( x | y ) pY ( y ) p X ( x) = ∫ p ( x | y ) pY ( y )dy
−∞ +∞
二、条件数学期望
∑ xi P ( X = xi | Y = y ) 离散 i E ( X | Y = y) = +∞ ∫ xp( x | y )dx 连续 −∞
例2 设（X,Y）服从G={(x,y)|x2+y2≤1}上的均匀分布，试求给定Y=y的条件下X的条件密度函数p(x|y) • 解：
1 p ( x, y ) = π 0 x2 + y2 ≤ 1 其他
2 1− y2 pY ( y ) = π • Y的边际密度函数为 0 • 当-1<y<1时，有 1 1 p( x, y) = π = p( x | y) = 2 2 2 1− y2 pY ( y) 1− y
P ( X = 1 | Y = 3) =
X 1 2 Pj
Y 1 0.1 0.2
0.3
2 0.3 0.05
0.35
3 0.2 0.15
0.35
Pi
0.6 0.4
P ( X = 1, Y = 3) 0.2 4 = = 0.35 7 P (Y = 3)

条件概率-条件分布-条件期望

y}.
定义设二维随机变量( X ,Y ) 的概率密度为
f ( x, y),( X ,Y ) 关于 Y 的边缘概率密度为fY ( y).若
对于固定的 y,
fY ( y) 0, 则称
f ( x, y) 为在Y fY ( y)
y
的条件下 X 的条件概率密度,记为
f (x, y)
f (x y)
.
XY
（2）无放回抽样
YX
01
02
2
7
7
12
1
7
7
二、连续型随机变量的条件分布
条件分布函数 FX Y (x y)
条件分布是指在一个随机变量取某个确定值的条件下,另一个随机变量的分布, 即 FX Y ( x y) P{ X x Y y} .
由于P{Y y}可能为零(连续型时一定为零).故直接用条件概率来定义时, 会出现分母为零. 因此,在条件分布中,作为条件的注意点 • E(X| Y=y) 是 y 的函数.
所以记 g(y) = E(X| Y=y). 进一步记 g(Y) = E(X| Y).
f (x, y)d x
1 π
1 y2 d x 2
1 y2
π
1 y2 , 1 y 1,
0,
其他.
于是当 1 y 1时,有
fX
Y
(x
y)
(2
1 π)
π 1
y2
2
1 , 1 y2
1 y2 x
1 y2,
0,
其他.
条件数学期望
定义
E ( X
|Y
y)
i
xi P( X xi | Y y)
二条件分布
一、离散型随机变量的条件

条件概率,条件分布,条件期望

FX Y ( x y )
x
y
f X Y ( x y ) d x [ f ( x , y ) fY ( y )]d x .
y
x
FY X ( y x )
说明

fY X ( y x ) d y [ f ( x , y ) f X ( x )]d y .
定义
设二维随机变量( X ,Y ) 的概率密度为
f ( x , y ), ( X ,Y ) 关于 Y 的边缘概率密度为 fY ( y ).若 f ( x, y) 对于固定的 y , fY ( y ) 0, 则称为在Y y fY ( y ) 的条件下 X 的条件概率密度 , 记为 f ( x, y) f X Y ( x y) . fY ( y )
为在事件A发生的条件下事件B发生的条件概率.
二
条件分布
一、离散型随机变量的条件分布
问题
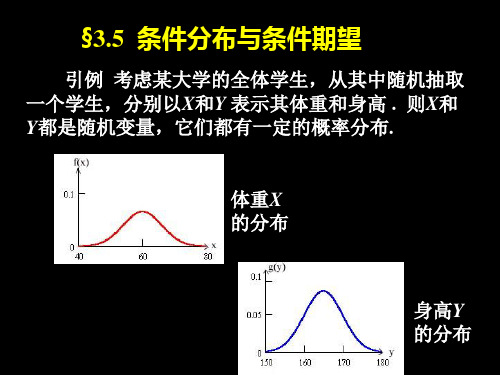
考虑一大群人, 从其中随机挑选一个人 , 分别用 X 和 Y 记此人的体重和身高 , 则X 和 Y 都是随机变量, 他们都有自己的分布 .
现在如果限制Y 取值从1.5 m 到1.6 m , 在这个限制下求X 的分布 .
一条件概率 (Conditional Probability) 条件概率是指在事件A发生的条件下，另一事件B发生的概率，记用 P（B|A）.
引例从所有有两个孩子的家庭随机抽取一个家庭记录男孩女孩的情况。
则试验所有可能的结果为（男孩记为“b”，女孩记为“g”） (b，b) (b，g) (g，b) (g，g) 设A={ 至少一个男孩}， B ={ 至少一个女孩}，考虑在事件A发生的条件下，事件B发生的概率。
定义设 ( X ,Y ) 是二维离散型随机变量 , 对于固定

条件分布与条件期望

这表明，二元正态分布的条件分布仍为正态分布：
1 2 2 N r y ， 1 r 2 1 1 2

．
31
二．条件数学期望
32
1．条件数学期望的概念
33
条件分布的数学期望称为条件数学期望．
34
对于离散型随机变量，当 Y y j 时，随机变量 X 的条件分布律为
1 2 PX Y n
n!
n
e
1 2
．
所以，当 X Y n 时， X 的取值为 0, 1,
2, , n ．
13
PX k X Y n
PX k , X Y n PX k , Y n k PX Y n PX Y n
PX k PY n k k! n k ! PX Y n 1 2 n e 1 2 n!
n! 1 k!n k ! 1 2
k
1k
e 1
2 n k
e 2
2 2 1
17
所以，
PY k PX nP Y k X n
n 0

PX nP Y k X n PX nP Y k X n
n 0 nk
k 1

n 0
k 1
n
n!
e 0
nk

n
n!
e C p 1 p
f X x 0 ．
26
例
设二维随机变量 X , Y 服从平面区域
x, D
y:
x y 1

3.3多维随机变量函数的分布x

k
i0
1i
i!
e 1
ki
e 2
2
(k i)!
k
k
e 1
2
(12 )
k!
i0
i
k! !(k
i)!
1 1 2
i
2 1 2
ki
1 2
k!
k
e(1 2 )
1 1 2
2 1 2
k
1 2
k
e(1 2 ) , k 0,1, 2,L .
y x yz
O
x
z
f (u y, y)d y d u.
由此可得概率密度函数为
fZ (z) f (z y, y)d y.
由于 X 与 Y 对称,
fZ (z) f ( x, z x)d x.
当 X, Y 独立时, fZ (z)也可表示为
fZ (z) fX (z y) fY ( y)d y,
2 12
12 2 12 12 12
(X ,Y )
(1,2)
(1,1) (1,0)
1 2
,2
1 2
,1
(3,2)
(3,0)
1
概率 12
1
32
1 22
12 12 12 12 12 12
( X ,Y ) (1,2)
(1,1) (1,0)
1 2
,2
1 2
,1
(3,2)
(3,0)
X Y 3
证 Z X Y的取值为0，1，2，L 非负整数，而事件Z k
是k 1个互不相容事件X i,Y k i, i 0,1,L , k
的并，则对于任意非负整数k，有
k
P(Z k) P( X i)P(Y k i) i0

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。