载流长直导线的磁场.共21页文档
合集下载
载流长直导线的磁场
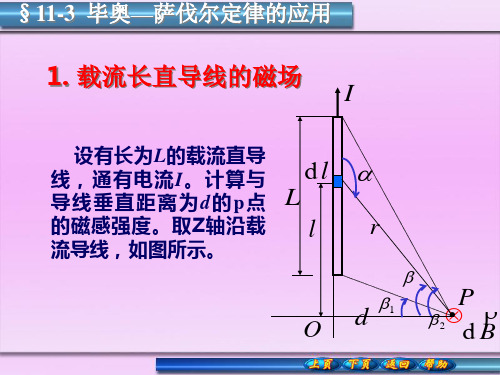
A B = 9.273×1024 A m2
原子中的电子除沿轨道运动外,还有自旋, 原子中的电子除沿轨道运动外,还有自旋,电子的 自旋是一种量子现象,它有自己的磁矩和角动量, 自旋是一种量子现象,它有自己的磁矩和角动量, 电子自旋磁矩的量值等于玻尔磁子。 电子自旋磁矩的量值等于玻尔磁子。
载流圆线圈轴线上的磁场
§11-3 毕奥 萨伐尔定律的应用 毕奥—萨伐尔定律的应用
1. 载流长直导线的磁场
设有长为L的 设有长为 的 载流直 导线, 通有电流I。 导线 , 通有电流 。 计算 与 导 线垂 直 距离 为 d 的 p 点的磁感强度。 点的磁感强度 。 取 Z 轴沿 载流导线,如图所示。 载流导线,如图所示。
O
d
β1
β 2
P
dB
载流长直导线的磁场
0 I dl sin α B = ∫d B = ∫ L L4 π r2
由几何关系有: 由几何关系有:
I
sin α = cos β
l = d tan β
dl = d sec β d β
2
r = d sec β
dl
L
α
r
β
l
P β 0 I dl sin α d β B=∫ O 2 dB L4 π r 0 β I 0I = ∫β d cos β d β = 4πd (sin β2 sin β1) 4π
点位于导线延长线上, = (3)P点位于导线延长线上,B=0 点位于导线延长线上
O
d
β 2
P
dB
2. 载流圆线圈轴线上的磁场
设有圆形线圈L,半径为 ,通以电流I 设有圆形线圈 ,半径为R,通以电流 。
I dl
R
r
载流直导线的磁场

超导体的研究和应用已经取得了一些重要的成果,如超导 电缆、超导变压器等。未来随着超导技术的不断进步和应 用范围的扩大,有望在能源、交通、医疗等领域发挥更大 的作用。
THANKS FOR WATCHING
感谢您的观看
载流直导线的磁场
目录
• 磁场的基本概念 • 载流直导线产生的磁场 • 磁场与电流的关系 • 磁场的应用 • 磁场与现代科技
01
磁场的基本概念
磁场定义
01
磁场:是存在于磁体或电流周围 的一种特殊物质,它对放入其中 的磁体或电流产生力的作用。
02
磁场是由电荷的运动所产生的。 磁场对放入其中的电流或磁体产 生力的作用,这种力称为安培力 或洛伦兹力。
无线通信利用电磁波传 递信息,如手机、电视、
广播等。
利用磁场记录信息,如 硬盘、磁带等存储设备。
利用磁场力使物体悬浮, 如磁悬浮列车和磁悬浮
轴承。
某些磁场可以影响人体 生理功能,如磁疗和电
磁疗法。
05
磁场与现代科技
磁悬浮列车
磁悬浮列车是一种利用磁场力使列车悬浮于轨道之上的高速列车,具有速度快、能耗低、无噪音等优 点。磁悬浮列车的磁场来源通常是通过电流在导轨中产生的强磁场,通过与列车上的磁铁相互作用实 现悬浮和导向。
奥斯特(Oe)
奥斯特是高斯和安培之间 的转换系数,用于表示磁 场与电流之间的关系。
安培力(F)
安培力是描述磁场对电流 作用力的物理量,单位为 牛顿(N)。
02
载流直导线产生的磁场
安培环路定律
总结词
安培环路定律描述了载流直导线产生的磁场分布,是磁场分 析的重要基础。
详细描述
安培环路定律指出,在磁感应线圈中,磁场强度矢量沿闭合 路径的线积分等于穿过该路径所围面积的电流代数和。该定 律是电磁学中的基本定理之一,对于分析载流导线的磁场分 布和磁感应强度计算具有重要意义。
THANKS FOR WATCHING
感谢您的观看
载流直导线的磁场
目录
• 磁场的基本概念 • 载流直导线产生的磁场 • 磁场与电流的关系 • 磁场的应用 • 磁场与现代科技
01
磁场的基本概念
磁场定义
01
磁场:是存在于磁体或电流周围 的一种特殊物质,它对放入其中 的磁体或电流产生力的作用。
02
磁场是由电荷的运动所产生的。 磁场对放入其中的电流或磁体产 生力的作用,这种力称为安培力 或洛伦兹力。
无线通信利用电磁波传 递信息,如手机、电视、
广播等。
利用磁场记录信息,如 硬盘、磁带等存储设备。
利用磁场力使物体悬浮, 如磁悬浮列车和磁悬浮
轴承。
某些磁场可以影响人体 生理功能,如磁疗和电
磁疗法。
05
磁场与现代科技
磁悬浮列车
磁悬浮列车是一种利用磁场力使列车悬浮于轨道之上的高速列车,具有速度快、能耗低、无噪音等优 点。磁悬浮列车的磁场来源通常是通过电流在导轨中产生的强磁场,通过与列车上的磁铁相互作用实 现悬浮和导向。
奥斯特(Oe)
奥斯特是高斯和安培之间 的转换系数,用于表示磁 场与电流之间的关系。
安培力(F)
安培力是描述磁场对电流 作用力的物理量,单位为 牛顿(N)。
02
载流直导线产生的磁场
安培环路定律
总结词
安培环路定律描述了载流直导线产生的磁场分布,是磁场分 析的重要基础。
详细描述
安培环路定律指出,在磁感应线圈中,磁场强度矢量沿闭合 路径的线积分等于穿过该路径所围面积的电流代数和。该定 律是电磁学中的基本定理之一,对于分析载流导线的磁场分 布和磁感应强度计算具有重要意义。
载流长直导线磁场

2(R2 x2 )32
0 2
(R2
IS
x
2
)
3 2
S R2
第6页/共21页
载流圆线圈轴线上的磁场
B
0 IR 2
2(R2
x2
)3 2
0 2
IS
(R2
x2
)3 2
讨论:
(1)在圆心处 x 0 B 0 I
2R
载流线圈 的磁矩
(2)在远离线圈处 x R,x r
B 0 IS 0 IS 0 pm 2 x3 2 r 3 2 r 3
O1
Q1
P
Q2
O2
第16页/共21页
载流圆线圈轴线上的磁场
例题11-2 在玻尔的氢原子模型中,电子绕原子核运 动相当于一个圆电流,具有相应的磁矩,称为轨道磁 矩。试求轨道磁矩μ与轨道角动量L之间的关系,并计 算氢原子在基态时电子的轨道磁矩。
解 为简单起见,设电子绕核作匀速圆周运动,圆的 半径为r,转速为n。电子的运动相当于一个圆电流, 电流的量值为I=ne,圆电流的面积为S=πr2,所以 相应的磁矩为
l dl
B
L
0R2nI d l
2(R2 l 2 )3/
2
0 nI
2
2 1
sin
d
0
2
nI (cos
2
cos
1 )
第10页/共21页
载流圆线圈轴线上的磁场
讨论:
B
0nI
2
(cos
2
cos
1 )
(1)螺线管无限长 1 , 2 0 B 0nI
(2)半无限长螺线管的端点圆心处
B 0nI / 2
电子的轨道角动量是满足量子化条件的,在玻尔
0 2
(R2
IS
x
2
)
3 2
S R2
第6页/共21页
载流圆线圈轴线上的磁场
B
0 IR 2
2(R2
x2
)3 2
0 2
IS
(R2
x2
)3 2
讨论:
(1)在圆心处 x 0 B 0 I
2R
载流线圈 的磁矩
(2)在远离线圈处 x R,x r
B 0 IS 0 IS 0 pm 2 x3 2 r 3 2 r 3
O1
Q1
P
Q2
O2
第16页/共21页
载流圆线圈轴线上的磁场
例题11-2 在玻尔的氢原子模型中,电子绕原子核运 动相当于一个圆电流,具有相应的磁矩,称为轨道磁 矩。试求轨道磁矩μ与轨道角动量L之间的关系,并计 算氢原子在基态时电子的轨道磁矩。
解 为简单起见,设电子绕核作匀速圆周运动,圆的 半径为r,转速为n。电子的运动相当于一个圆电流, 电流的量值为I=ne,圆电流的面积为S=πr2,所以 相应的磁矩为
l dl
B
L
0R2nI d l
2(R2 l 2 )3/
2
0 nI
2
2 1
sin
d
0
2
nI (cos
2
cos
1 )
第10页/共21页
载流圆线圈轴线上的磁场
讨论:
B
0nI
2
(cos
2
cos
1 )
(1)螺线管无限长 1 , 2 0 B 0nI
(2)半无限长螺线管的端点圆心处
B 0nI / 2
电子的轨道角动量是满足量子化条件的,在玻尔
大学物理-磁场 安培环路定律
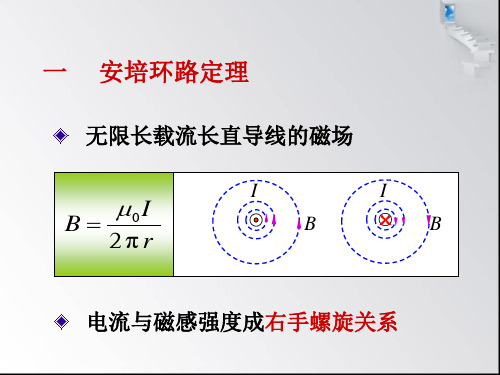
Φ BS cos BS
s
一般情况 Φ s BdS
dS2
B
S 2
dS1
1
B1
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
B2
SB cosdS 0
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的磁通
量必等于零(故磁场是无源的).
B B1 B2 B3
Bdl
l
0(I2 I3)
推广:
➢ 安培环路定理
n
B dl 0 Ii
i 1
n
安培环路定理
B dl 0 Ii
i 1
在真空的恒定磁场中,磁感强度 B沿任
一闭合路径的积分的值,等于 0乘以该闭合
路径所穿过的各电流的代数和.
注意
电流 I 正负的规定: I 与 L 成右螺旋
而与环路外电流无关。
3. B为环路上一点的磁感应强度,它与环路内外电流
都有关。
若
B
dl
0
并不一定说明环路上各点的 B 都为 0。
若 B dl 0 环路内并不一定无电流。
4.环路定理只适用于闭合电流或无限电流,
应用 安培环路定理的应用举例
例1
求载流螺绕环内的磁场
解 (1)对称性分析:环内B 线为同心
B dl B 2r 0 I
B 0 I 1 2r r
I
r LR
r L
分布曲线
B
0 I 2R B r
B 1 r
o
R
r
例4 无限大均匀带电(线密度为i)平面的磁场
解 如图,作安培环路
abcda,应用安培环路 定理
b
l B d l 2a B dl
载流直导线的磁场

如图4-42c所示,经过死点后,线圈中电流反向,即沿DCBA方向流
动,这时它所受的力矩将使它沿原方向继续旋转。由于换向器的作用使线圈 中的电流每转半圈改变一次方向,就可以使线圈不停地朝着一个方向旋转起 来。
24
第24页,本讲稿共33页
单匝线圈所组成的直流电动机虽然能够按一定方 向旋转,但力矩太小,不能承担什么负荷。而且由 于在转动过程中线圈受的力矩时大时小,转速也很 不稳定。因此单匝线圈的电动机实用价值不大。
可见,力矩的计算只与载流线圈的磁矩有关,而与 线圈的形状无关。
由 LPmBsin 可以看出,在均匀磁场和载流平面
线圈给定的情况下,线圈所受的力矩只与θ有关。
19
第19页,本讲稿共33页
[讨论] 当θ=0时, M=0,线圈处于稳定平衡状态, 如果外力稍使线圈偏转,磁场对线圈的力矩将使他回 到平衡位置;当θ=π时,M=0,线圈处于不稳定平衡 状态,如果外力稍使线圈离开平衡位置,磁场对线圈 的力矩将使它继续偏转,直到θ=0的稳定平衡位置; 当θ=π/2时,力矩有最大值 。
9
第9页,本讲稿共33页
二、平行无限长载流直导线间的相互作用力
设有两要根无限长载流直导线之间距离为a ,分别
通有电流I1和I2,且电流的流向相同,则导线1中电流 在导线2处的磁感应强度为:
B1
0 I1 2 a
方向垂直纸面向里。
根据安培定律,导线2中任一电流
元I2dl2所受安培力大小为:
dF12I2dl2B120I1a I2dl2
的大小。经过标准电流计量仪
器标定之后,就可以直接从偏
转角读出待测电流的数值。这
就是磁电式电流计的简要工作
原理。
30
第30页,本讲稿共33页
动,这时它所受的力矩将使它沿原方向继续旋转。由于换向器的作用使线圈 中的电流每转半圈改变一次方向,就可以使线圈不停地朝着一个方向旋转起 来。
24
第24页,本讲稿共33页
单匝线圈所组成的直流电动机虽然能够按一定方 向旋转,但力矩太小,不能承担什么负荷。而且由 于在转动过程中线圈受的力矩时大时小,转速也很 不稳定。因此单匝线圈的电动机实用价值不大。
可见,力矩的计算只与载流线圈的磁矩有关,而与 线圈的形状无关。
由 LPmBsin 可以看出,在均匀磁场和载流平面
线圈给定的情况下,线圈所受的力矩只与θ有关。
19
第19页,本讲稿共33页
[讨论] 当θ=0时, M=0,线圈处于稳定平衡状态, 如果外力稍使线圈偏转,磁场对线圈的力矩将使他回 到平衡位置;当θ=π时,M=0,线圈处于不稳定平衡 状态,如果外力稍使线圈离开平衡位置,磁场对线圈 的力矩将使它继续偏转,直到θ=0的稳定平衡位置; 当θ=π/2时,力矩有最大值 。
9
第9页,本讲稿共33页
二、平行无限长载流直导线间的相互作用力
设有两要根无限长载流直导线之间距离为a ,分别
通有电流I1和I2,且电流的流向相同,则导线1中电流 在导线2处的磁感应强度为:
B1
0 I1 2 a
方向垂直纸面向里。
根据安培定律,导线2中任一电流
元I2dl2所受安培力大小为:
dF12I2dl2B120I1a I2dl2
的大小。经过标准电流计量仪
器标定之后,就可以直接从偏
转角读出待测电流的数值。这
就是磁电式电流计的简要工作
原理。
30
第30页,本讲稿共33页
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
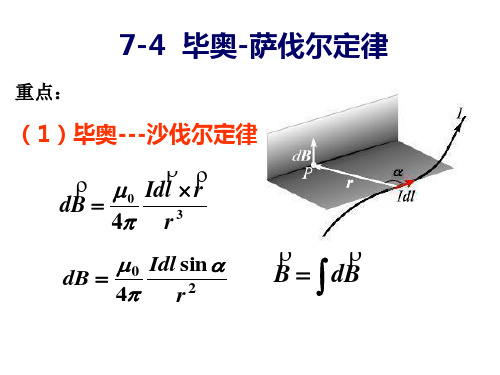
0 Idz sin B dB 4 r2
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
载流长直导线的磁场

THANKS
感谢观看
电磁辐射
长期暴露在电磁场中可能导致头痛、失眠、记忆力减退等健康问 题。
电磁波对人体的影响
高强度的电磁波可能对人体的免疫系统、神经系统和生殖系统产生 负面影响。
电磁辐射的防护
为了减少电磁辐射对人体的影响,应采取适当的防护措施,如远离 高强度电磁场、穿戴防护服等。
04
载流长直导线在科研领域 的应用
磁场对带电粒子的影响
磁场的方向
右手定则
根据右手定则,环绕着通电长直导线的四指指向电流方向, 大拇指所指方向即为磁场方向。
磁场方向与电流方向的关系
磁场方向总是与电流方向垂直,这是由安培定律决定的。
磁感应线的形状
磁感应线是闭合曲线
磁感应线总是围绕着通电长直导线形 成闭合曲线,类似于电流周围的电场 线。
磁感应线的分布
磁感应线的分布与电流大小和导线材 料有关,电流越大,磁感应线越密集 ;导线的导磁率越高,磁感应线越密 集。
磁力线
磁场中磁力方向相同的路径,形成闭 合曲线。
安培环路定律
01
02
03
安培环路定律
描述磁场与电流之间的关 系,即磁场与电流成正比, 沿导线周围环绕。
定律公式
B = μ₀ * I / 2πr,其中B 为磁感应强度,I为电流强 度,r为距离导线的垂直距 离。
应用场景
适用于长直导线或线圈周 围的磁场计算。
感应炉
利用电磁感应产生的高温 来熔炼金属。
感应电机的运行
利用电磁感应原理,实现 电机的启动、调速和制动。
电磁铁的应用
电磁起重机
利用电磁铁产生的强大磁场,实 现对金属材料的吸附和搬运。
扬声器
利用电磁铁推动振膜产生振动,从 而产生声音。
例1求载流长直导线的磁场,已知

讨论:
B
0I 4r0
(cos1
cos 2 )
⑴ 无限长载流长直导线的磁场
1 0 2
I
I
B 0I
2π r
BX
电流与磁感强度成右螺旋关系
⑵ 半无限长载流长直导线的磁场
1
π 2
或 1 0
2 π
2
2
BP
0I
4π r
2
B o 1r0 +p
I
o r *P
例2. 圆电流轴线上的磁场。已知R和Iz
dB
z
2
)
3 2
2. z 0 B 0 I (圆心处)
2R
x
3. z R
B
0 IR 2
2z3
0 IS 2 z 3
4.一段圆弧导线圆心处的磁感强度
z
dBz
dB
p•
z r dB
0 R
y
Idl
B 0 I 0 I 2 0 I 2R 4 R 4 R
θ─圆弧所对圆心角,用弧度表示。
例3. 如图所示导线,已知I、R、θ=/4,求O点的
(R2
x2
3
)2
x Rctg dx R csc2 d R2 x2 R2 csc2
B
2 1
0
2
nI
sin
d
0 nI
2
(c os 2
cos1)
B
0nI
2
cos2
cos1
1
2
R
P
x
讨论:
(1)P点位于管内轴线中点
1
l
π
2
cos 1 cos 2
cos2
毕奥-萨伐尔定律和载流回路的磁场资料

0 IR2
2( R x )
2 3 2 2
载流圆线圈轴线上的磁场
0 IS B 2 ( R 2 x 2 ) 2( R 2 x 2 )
2
3 2
0 IR
3
2
讨论:
(1)在圆心处
x0
B
0I
2R
(2)在远离线圈处
载流线圈 的磁矩
x R, x r
0 B 2 0 B 2
载流长直导线的磁场
考虑三种情况:
0 I sin 2 sin 1 B 4d
1 2 2
2
(1)导线无限长,即
I
0 I B 2d 0 I B 4d
dl
L
r
(2) 导线半无限长,场点与一端 的连线垂直于导线
l
(3)P点位于导线延长线上,B=0
O
d
2 2 3/ 2
dB
0 R nI d l
2
载流圆线圈轴线上的磁场
l R cot
d l R csc d
2 2 2 2 2
1
A1
r
dB
p
2
R
A2
又 R l R csc
B L
0 R nI d l
2
l
dl
2( R l )
2
2 3/ 2
IS 0 IS 3 3 x 2 r pm r3
引入 pm ISen
(3) 载流圆弧
圆心角
0 I 0 I B 2 R 2 4R
B
I
例 如图所示,两根长直导线沿半径方向接到 粗细均匀的铁质圆环上的A和B两点,并与很 远处的电源相接, 试求环中心o点处的磁感应 强度. 解 三段直导线在圆心处 B 产生的磁场为零. 2 1 o 0 Idl r dB 3 A 4 r
物理:载流导线的磁场

若以右手四指環繞方向代表電流方向,則拇指伸直 的方向為中心軸上的磁場方向。
载流圆形线圈所生的磁场(4/4)
若 x=0,則可得到載流圓形線圈在中心點處之磁場量值為 B=µ20aI
(A)載流圓形線圈電流方向與磁力線方向的示意圖。圖中只顯示出一 包含中心軸之平面上的磁力線,實際的磁力線分布是以中心軸為 對稱軸的立體分布。
(B)載流線圈附近的鐵粉排列出磁力線的形狀。
范例 8-3
試ห้องสมุดไป่ตู้必歐-沙伐定律,計算圖中
1 2
圓弧狀載流導線圓心
處的磁場量值,其中 I=5.0 A,a=3. 0 cm。
范例 8-3
概念 策略
必歐-沙伐定律與圓形導線在中心點處之磁場。
1. 如右圖,每一小段 IΔ 在圓心處產生的磁場量值為
ΔB=4µπ0
BP=2B=2×2µπ0aI =µπ0aI ,沿 x 軸方向
兩條導線在 Q 點所生的磁場B' = 2π
µ0I x2+a2
,其 y 分量相互抵消,故
Q 點的磁場量值為
BQ=2B'
cos
θ=2× 2π
µ0I x2+a2
×
a x2+a2
=π(xµ20+Iaa2)
,沿 x 軸方向
载流圆形线圈所生的磁场(1/4)
为 B=µ0nI
–其中 n 为螺线管单位长度内的匝数,亦即线圈
的疏密程度。如果右手握住螺线管,弯曲的手 指所指的方向与电流方向相同,则大拇指伸直 所指的方向,就是管内磁场 N 极的方向。
载流螺线管所生的磁场(3/3)
(A)螺线管缠绕较松,内部磁场较弱;螺线管缠绕较 紧密,内部磁场较强。
(B)螺线管剖面图上排电流产生的磁场,在管内向左 ,上方管外向右,下方管外向左;下排电流产生 的磁场,在管内向左,上方管外向左,下方管外 向右。
载流长直导线在磁场中所受的力讲解

範例6
邊長5 m、4 m、3 m 的直角三 角形電路,通以2 A電流,置於 方向向右且強度3 T的均勻磁場 中。若電路的平面與磁場方向 平行,則整個線圈所受之淨磁 力與淨磁力矩各為何? (A) 磁 力0、磁力矩0 (B) 磁力18 N、 磁力矩0 (C) 磁力18 N、磁力矩 36 N.m (D) 磁力0、磁力矩36 N.m (E) 磁力24 N、磁力矩 72 N.m 。
及磁場的方向,即指離另
一導線的方向。
a兩導線之間的磁力為量值相等、方向相反的斥力。 換言之,兩平行載流直導線若電流方向相反時,則 兩導線互相 排斥 。
F 0i1i2 L 2 d
※安培的定義
上述公式被用來定義SI制單位中的電流的單位 --安培。如兩載相同電流的無限長細直導線, 互相平行排列,在真空中相距 1 公尺,而導 線上每公尺的作用力為 2×10-7 牛 頓,則導 線上電流的值定為 1 安培。
如下圖所示,將四種導線的首尾相接:
(1)甲導線的長度為 4L 所受磁力
L
所 受 的 磁 力 i 4 L B
2L
4iLB
Hale Waihona Puke L4L(2)乙導線的長度為 2L 所受磁力
L
2L
2L 2L
所 受 的 磁 力 i 2 L B
L
L L
LL
2iLB
2L
2L
L
L
LL
2L
2L
(1)甲 導 線 所 受 的 磁 力 4iLB。 (2)乙 導 線 所 受 的 磁 力 2iLB。
( 4 ) F d a 4 2 0 .5 s in 9 0 2 2 ( N ) , 方 向 平 行 於 O c 。
(2 )F b c4 1 0 .5 sin9 0 2 (N ), 方 向 平 行 於 b O (即 x軸 方 向 )。 (3 )F cd42 0 .5 sin4 5 2 (N ), 方 向 平 行 於 zO (即 z軸 方 向 ) 。 (4 )F d a42 0 .5 sin9 0 22 (N ), 方 向 平 行 於 O c 。
载流长直导线产生的磁场

B甲
B合
B乙
流入紙面
流出紙面
B合
B合
B乙
B乙 B甲
B甲
5
甲、乙兩條直導線垂直於紙面,在右圖所示的位置 上,甲電流流出紙面,乙電流流入紙面,且甲、乙 兩條導線的電流相同。
B乙
B甲 B乙
B甲
B甲 B合
B乙
B合
B合
6
三、載流圓形線圈產生的磁場
載流圓形線圈產生的磁場 與一個長形磁鐵產生的磁場相似。 以右手定則決定載流圓形線圈中心 處磁場的方向: 四指順著電流的方向彎曲, 拇指伸直方向是中心磁場的方向。
2
二、載流長直導線產生的磁場
1820年,厄斯特在無意中發現,當導線通有電流 時,導線附近的磁針會發生偏轉。
1820~1826年,安培建立起描述電流與磁場關係 的數學理論。
3
長直導線周圍的磁場
一根通上穩定電流的長直導線(載流長直導線),
周圍產生的磁場,其磁力線是以導線為中心的
同心圓。
以右手定則來描寫磁場的方向: 拇指表示導線的電流方向,而彎 曲四指為磁場的方向。
磁場之大小 與通過的電流成正比, 與導線的距離成反比。
4
有甲、乙兩條平行載流長直導線,垂直貫穿紙面, 已知兩導線上的電流相等,但甲的電流進入紙面,
而乙的電流流出。今紙上有三點 P、Q、R ,其中 Q
點在兩導線中點,則
(1) P、Q、R 三點處的磁場方向為何?
(2) P、Q、R 三點,何者磁場量值最大? Q>P=R
第五章電與磁的統一1第一節電流的磁效應2當q1c??nqe1161019??n6251018個自由電子一電流?金屬導體內有自由電子可以自由的移動當它們受到電壓作用時電荷就移動而形成電流
大学物理学第五版马文蔚高等教育出版社磁场2

L
(7-19)
讨论: (1) 式中各量的含义: B ~环路上各点的磁感应强度。 由环路内、外电流共同产生的。 I ~穿过环路内的电流的代数和。注意 I 的正负的确定方法。 L1 I2 I1 L2 I
I1
L3 L4
I2
① B d l 0 ( 2 I 2 I1 ) L1 ③ B d l 0 ( I1 I 2 )
n1 O
n2
7-4 毕奥-萨伐尔定律(Biot-Savart law) 四.运动电荷的磁场
L
E
r
•P
+++ ++++ + ++++ +++ +++ +++ ++++++++ ++++ ++++ + ++ + ++ + +++ + ++ + +++ + ++ ++ ++ + + + +++ ++ ++ + + ++++ I d l e r +++ + ++++ +++++++++ + +++++ ++++++ +++d B 0 + + + + +++++ +++ +++ ++ ++ + + + + + + + (7-12c) 2 4 r dl S 运动电荷 q 产生的磁场 导体单位体积内电荷数 n dB 0 (qnvS)dl B dl内电荷数: dN= nSdl sin 2 dN 4r (nSdl ) 0 I d l 0 dB sin vq sin 2 2 4 r 4 r 方向与 d B 同向,仍为 I d l r 。 q 的平均速度 v 取dl = v dt 0 qv r (7-15a) 矢量式:B 3 则电流元体积dV = Sdl = Svdt 4 r 0 qv er dN=ndV=nSvdt 此体积内电荷数: B (7-15b) 2 4 r dq qdN q(nSvdt) 说明: B 的方向垂直于 v 和 I qnvS 所确定的平面。 dt dt dt r
(7-19)
讨论: (1) 式中各量的含义: B ~环路上各点的磁感应强度。 由环路内、外电流共同产生的。 I ~穿过环路内的电流的代数和。注意 I 的正负的确定方法。 L1 I2 I1 L2 I
I1
L3 L4
I2
① B d l 0 ( 2 I 2 I1 ) L1 ③ B d l 0 ( I1 I 2 )
n1 O
n2
7-4 毕奥-萨伐尔定律(Biot-Savart law) 四.运动电荷的磁场
L
E
r
•P
+++ ++++ + ++++ +++ +++ +++ ++++++++ ++++ ++++ + ++ + ++ + +++ + ++ + +++ + ++ ++ ++ + + + +++ ++ ++ + + ++++ I d l e r +++ + ++++ +++++++++ + +++++ ++++++ +++d B 0 + + + + +++++ +++ +++ ++ ++ + + + + + + + (7-12c) 2 4 r dl S 运动电荷 q 产生的磁场 导体单位体积内电荷数 n dB 0 (qnvS)dl B dl内电荷数: dN= nSdl sin 2 dN 4r (nSdl ) 0 I d l 0 dB sin vq sin 2 2 4 r 4 r 方向与 d B 同向,仍为 I d l r 。 q 的平均速度 v 取dl = v dt 0 qv r (7-15a) 矢量式:B 3 则电流元体积dV = Sdl = Svdt 4 r 0 qv er dN=ndV=nSvdt 此体积内电荷数: B (7-15b) 2 4 r dq qdN q(nSvdt) 说明: B 的方向垂直于 v 和 I qnvS 所确定的平面。 dt dt dt r
载流直导线的磁场

通过电流为I,
F1 BIl1 sin BIl1 sin
15
作用F2在 一F2条 直BI线l2 上,,F1 互与相F1抵 大消小;相F等2 与,方F2向 大相小反相,等, 方向相反,但不在一条直线上,因此,形成一力偶,
力臂为
,l所1 co以s作用在线圈上的力矩为:
L F2l1 cos BIS cos BIS sin PmB sin
B1
0 I1 2 a
方向垂直纸面向里。
根据安培定律,导线2中任一电流
元I2dl2所受安培力大小为:
dF12
I 2 dl2 B1
0 I1I2 2 a
dl2
方向在平行导线所在的平面内,并且垂直于 I2dl2 指向
导线1。
10
导线2单位长度上所受的安培力大小为:
f12
dF12 dl2
0 I1I2 2 a
考虑三个物理的大小和方向的关系可写成:
L Pm B
16
五、任意平面闭合电流在磁场中的力矩
以上虽是从矩形线圈的特例得到的结果,其实它
适用于任意形状的平面载流线圈。
同理,可以计算出导线2产生的磁场对导线1单位长
度上安培力的大小为:
f21
dF21 dl1
0 I1I2 2 a
f12
方向与 f12 方向相反。可见,平行载流直导线同向 电流时相互吸引。
不难验证平行载流直导线反向电流时相互排斥,而单
位长度上所受安培力大小与上式相同。
11
三、电流单位“安培”的定义
若两导线中通有相同电流强度时,即I1 = I2 = I 时,
数和的
2
注意:
(1)电流I有正负取值。
(2)如果电流I不穿过回路L,则它对上式右端无贡献。
《大学物理》第25章_磁场的来源

解:导线2所受的的重力竖直向下,每米 长度导线所受重力的大小为
F mg (0.12103 kg / m)(1.0m)(9.8m / s2 ) 1.18103 N
导线2受到的安培力的方向必须向上 令上述两个力的大小相等,l = 1.0 m
F 0 I1I2 l 2 d
I2
2 d 0 I1
D
F 0 I1I2 (4 107 T m / A) (1A)(1A) 2 107 N / m
l 2 d
(2 )
(1m)
“安培”的定义:两根相距1米的平行长直载流导线,若每
根导线每米长度受到的力恰好等于2×10-7N,则每根导线
通过的电流为1安培(1A)。
“库仑”的定义:1A电流在1s内输运的电量:1C=1A·s
§25-4 安培环路定理
长直载流导线产生的磁场
B 0 I 2 r
任意形状载流导线产生的磁场
?
验证
B dl 0Iencl
考虑载流长直导线的磁场
在恒定电流的磁场中,磁感应 强度 B 矢量沿任一闭合路径 L的线 积分(即环路积分),等于什么?
在垂直于导线的平面内任
选的回路上取一点p,该点到导
L2
L1
O
P
结果为零!
B d l B d l B d l
L
L1
L2
0 I ( d d ) 0
2 L1
L2
闭合曲线不包围电流,磁感应强度矢量的环流为零。
磁感应强度的环流与闭合曲
线的形状无关,它只和闭合曲
线所包围的电流有关。 安培环路定理 磁场中,沿任一闭合曲线 B矢量的线积分(也
F mg (0.12103 kg / m)(1.0m)(9.8m / s2 ) 1.18103 N
导线2受到的安培力的方向必须向上 令上述两个力的大小相等,l = 1.0 m
F 0 I1I2 l 2 d
I2
2 d 0 I1
D
F 0 I1I2 (4 107 T m / A) (1A)(1A) 2 107 N / m
l 2 d
(2 )
(1m)
“安培”的定义:两根相距1米的平行长直载流导线,若每
根导线每米长度受到的力恰好等于2×10-7N,则每根导线
通过的电流为1安培(1A)。
“库仑”的定义:1A电流在1s内输运的电量:1C=1A·s
§25-4 安培环路定理
长直载流导线产生的磁场
B 0 I 2 r
任意形状载流导线产生的磁场
?
验证
B dl 0Iencl
考虑载流长直导线的磁场
在恒定电流的磁场中,磁感应 强度 B 矢量沿任一闭合路径 L的线 积分(即环路积分),等于什么?
在垂直于导线的平面内任
选的回路上取一点p,该点到导
L2
L1
O
P
结果为零!
B d l B d l B d l
L
L1
L2
0 I ( d d ) 0
2 L1
L2
闭合曲线不包围电流,磁感应强度矢量的环流为零。
磁感应强度的环流与闭合曲
线的形状无关,它只和闭合曲
线所包围的电流有关。 安培环路定理 磁场中,沿任一闭合曲线 B矢量的线积分(也
载流直导线的磁场-精选文档

d F 0I 1I2 1 2 f12 d l2 2 a
同理,可以计算出导线2产生的磁场对导线1单位长 度上安培力的大小为:
II d F 0 12 2 1 f2 f 1 1 2 d l 2 a 1
方向与 f 1 2 方向相反。可见,平行载流直导线同向 电流时相互吸引。 不难验证平行载流直导线反向电流时相互排斥,而单 11 位长度上所受安培力大小与上式相同。
13
例题:如图所示,试求导线所受的安培力。
Id l
dF sin
F
I
1
d R O
dF
·
F
I
F
3
2
解:F1=F2=BIl,方向向下,对半圆形导线,由对称性分析可知, 只有垂直向下的分量互相加强,而水平分量互相抵消,
F dF sin sin d 2 IRB 3 IRB
0 I1 B1 2 a
方向垂直纸面向里。
根据安培定律,导线2中任一电流 元I2dl2所受安培力大小为:
II 0 12 d F Id lB d l 1 2 2 2 1 2 2 a
方向在平行导线所在的平面内,并且垂直于 I2dl2 指向 10 导线1。
导线2单位长度上所受的安培力大小为:
12
据此,电流强度的单位安培定义为:
一恒定电流,若保持在处于真空中相距1米的两 无限长、而圆截面可忽略的平行上导线内,则在此两 导线间产生的力在每米长度上等于2×10 – 7 N , 则流 过两导线的电流强度即为1安培。这是国家标准总局
根据国际计量委员会的正式文件1993年12月27日批
准的,于1994年7月1日实施的安培的定义。
2
F
大学物理之载流导线在磁场中所受的力_图文_图文

例 2 如图一通有电流 的闭合回路放
在磁感应强度为 的均匀磁场中,回路平
面与磁感强度 垂直 .回路由
直导线 AB 和半径为
的圆弧导线 BCA 组成 ,
C
电流为顺时针方向,
求磁场作用于闭合
B
A
导线的力.
o
解 根据对称性分析
C
B
A
o
因
C
由于
B
A
故
o
例3:求一无限长直载流导线的磁场对另一直载流导
线ab的作用力。 已知:I1、I2、d、L
解:
a
b
x
d
L
例 3 半径为 载有电流 的导体圆
环与电流为 的长直导线 放在同一平
面(如图),直导
线与圆心相距为 d ,
d
且 R < d 两者间绝缘 ,
求 作用在圆电流上的
磁场力.
OR
解
.
d
OR
.
d
OR
.
d
OR
二 磁场作用于载流线圈的磁力矩
如图 均匀磁场中有 一矩形载流线圈 MNOP
M
P
大学物理之载流导线在磁场中所受的力_图文_ 图文.ppt
一般情况
导线是曲线 , 磁场为非均匀场。 导线上各长度元 上的速度 不相同
电流源受力
整个导线L上受磁场力
均匀磁场 直线电流
L
例 1 求如图不 规则的平面载流导线 在均匀磁场中所受的 力,已知 和 .
解 取一段电流元
P L
P L
结论 任意平面载流导线在均匀磁场 中所受的力 , 与其始点和终点相同的载流 直导线所受的磁场力相同;任意形状闭合 载流线圈在均匀磁场中受合力为零。
