函数图像PPT课件
合集下载
2024年度高中数学必修四三角函数PPT课件

建筑设计
在建筑设计中,利用三角函数计算建筑物的角度、高度和距离等 参数,确保设计的准确性和美观性。
机械设计
在机械设计中,三角函数用于计算齿轮、轴承等机械元件的尺寸和 角度,保证机械传动的精确性和稳定性。
航空航天工程
在航空航天工程中,利用三角函数分析飞行器的姿态、航向和速度 等参数,确保飞行安全。
21
2024/3/24
32
THANKS
感谢观看
2024/3/24
33
周期性、奇偶性、单调性等
解三角形
正弦定理、余弦定理及应用
29
常见题型解析及技巧点拨
01
三角函数求值问题:利 用同角关系式、诱导公 式等求解
2024/3/24
02
三角函数的图像与性质 应用:判断单调性、周 期性等
03
04
三角恒等变换的应用: 证明等式、化简表达式 等
30
解三角形问题:利用正 弦定理、余弦定理求解 边或角
易错知识点剖析及防范措施
混淆三角函数定义域和值域
注意定义域和值域的区别,避免混淆
忽视三角函数的周期性
在解题时要考虑周期性,避免漏解或 多解
2024/3/24
错误使用三角恒等变换公式
注意公式的适用条件和变形方式,避 免误用
忽视解三角形的限制条件
在解三角形时要注意边和角的限制条 件,避免得出不符合题意的解
第三象限
正弦、余弦均为负、正切为正 。
第四象限
正弦为负、余弦为正、正切为 负。
2024/3/24
7
02 三角函数诱导公 式与变换
2024/3/24
8
诱导公式及其应用
2024/3/24
诱导公式的基本形式
函数完整版PPT课件

16
三角函数图像变换规律
振幅变换
通过改变函数前的系数,实现对函数图 像的纵向拉伸或压缩。
周期变换
通过改变函数内的系数,实现对函数图 像的横向拉伸或压缩。
2024/1/28
相位变换
通过改变函数内的常数项,实现对函数 图像的左右平移。
上下平移
通过在函数后加减常数,实现对函数图 像的上下平移。
17
三角函数周期性、奇偶性和单调性
了直线在 $y$ 轴上的位置。
03
性质
当 $k > 0$ 时,函数单调递增 ;当 $k < 0$ 时,函数单调递
减。
8
二次函数表达式与图像
2024/1/28
二次函数表达式
$y = ax^2 + bx + c$($a neq 0$)
图像特点
一条抛物线,开口方向由 $a$ 决定($a > 0$ 时向上开口 ,$a < 0$ 时向下开口),对称轴为 $x = -frac{b}{2a}$ ,顶点坐标为 $left(-frac{b}{2a}, c frac{b^2}{4a}right)$。
对数函数性质
单调性、定义域、值域等 。
13
指数对数方程求解
指数方程求解
通过换元法、配方法等方法将指数方 程转化为代数方程求解。
指数对数混合方程求解
综合运用指数和对数的性质及运算法 则进行求解。
对数方程求解
通过换底公式、消去对数等方法将对 数方程转化为代数方程求解。
2024/1/28
14
04
三角函数及其性质
函数完整版PPT课件
2024/1/28
1
目录
2024/1/28
• 函数基本概念与性质 • 一次函数与二次函数 • 指数函数与对数函数 • 三角函数及其性质 • 反三角函数及其性质 • 复合函数与分段函数 • 参数方程与极坐标方程
三角函数图像变换规律
振幅变换
通过改变函数前的系数,实现对函数图 像的纵向拉伸或压缩。
周期变换
通过改变函数内的系数,实现对函数图 像的横向拉伸或压缩。
2024/1/28
相位变换
通过改变函数内的常数项,实现对函数 图像的左右平移。
上下平移
通过在函数后加减常数,实现对函数图 像的上下平移。
17
三角函数周期性、奇偶性和单调性
了直线在 $y$ 轴上的位置。
03
性质
当 $k > 0$ 时,函数单调递增 ;当 $k < 0$ 时,函数单调递
减。
8
二次函数表达式与图像
2024/1/28
二次函数表达式
$y = ax^2 + bx + c$($a neq 0$)
图像特点
一条抛物线,开口方向由 $a$ 决定($a > 0$ 时向上开口 ,$a < 0$ 时向下开口),对称轴为 $x = -frac{b}{2a}$ ,顶点坐标为 $left(-frac{b}{2a}, c frac{b^2}{4a}right)$。
对数函数性质
单调性、定义域、值域等 。
13
指数对数方程求解
指数方程求解
通过换元法、配方法等方法将指数方 程转化为代数方程求解。
指数对数混合方程求解
综合运用指数和对数的性质及运算法 则进行求解。
对数方程求解
通过换底公式、消去对数等方法将对 数方程转化为代数方程求解。
2024/1/28
14
04
三角函数及其性质
函数完整版PPT课件
2024/1/28
1
目录
2024/1/28
• 函数基本概念与性质 • 一次函数与二次函数 • 指数函数与对数函数 • 三角函数及其性质 • 反三角函数及其性质 • 复合函数与分段函数 • 参数方程与极坐标方程
函数的图像课件

三角函数值域
三角函数的值域是[-1,1],这是因为三角函数在单 位圆上的取值范围决定的。
三角函数的图像绘制
手工绘制
通过坐标纸和计算器,可以手工绘制出三角函数的图像。
计算机绘制
使用数学软件或编程语言,可以方便地绘制出精确的三角函数图像。
周期性
三角函数具有明显的周期性,可以通过平移和伸缩来绘制整个函数 图像。
斜率
一次函数的斜率为 k,表示函数图 像的倾斜程度。
截距
一次函数与 y 轴交点的 y 坐标为 b, 称为截距。
一次函数的图像绘制
确定斜率和截距
根据给定的 k 和 b 值,确 定一次函数的表达式。
描点
在坐标系中选取适当的点, 代入函数表达式计算 x 和 y 值。
连线
根据描出的点,用平滑的 曲线连接各点,形成一次 函数的图像。
坐标系
在平面直角坐标系中,x轴表示自变量,y轴表示因变量。
函数图像的绘制方法
描点法
根据函数解析式,在定义域内选取若干个自变量x的值,计算出对应的因变量y的 值,然后在坐标系中描出相应的点,最后用平滑的曲线或直线将这些点连接起来 。
图象变换法
对于一些复杂的函数图像,可以通过平移、对称、伸缩等变换手段,将已知函数 图像变换得到。
二次函数的图像绘制
总结词
通过代入不同的$x$值,计算对应的 $y$值,可以绘制出二次函数的图像 。
详细描述
在绘制二次函数图像时,可以选择若 干个$x$值,计算对应的$y$值,然后 以这些点为基础绘制出抛物线。常用 的方法包括描点法和对称法。
二次函数图像的性质
总结词
二次函数图像具有对称性、顶点、开口方向和与坐标轴的交点等性质。
工程应用
三角函数的值域是[-1,1],这是因为三角函数在单 位圆上的取值范围决定的。
三角函数的图像绘制
手工绘制
通过坐标纸和计算器,可以手工绘制出三角函数的图像。
计算机绘制
使用数学软件或编程语言,可以方便地绘制出精确的三角函数图像。
周期性
三角函数具有明显的周期性,可以通过平移和伸缩来绘制整个函数 图像。
斜率
一次函数的斜率为 k,表示函数图 像的倾斜程度。
截距
一次函数与 y 轴交点的 y 坐标为 b, 称为截距。
一次函数的图像绘制
确定斜率和截距
根据给定的 k 和 b 值,确 定一次函数的表达式。
描点
在坐标系中选取适当的点, 代入函数表达式计算 x 和 y 值。
连线
根据描出的点,用平滑的 曲线连接各点,形成一次 函数的图像。
坐标系
在平面直角坐标系中,x轴表示自变量,y轴表示因变量。
函数图像的绘制方法
描点法
根据函数解析式,在定义域内选取若干个自变量x的值,计算出对应的因变量y的 值,然后在坐标系中描出相应的点,最后用平滑的曲线或直线将这些点连接起来 。
图象变换法
对于一些复杂的函数图像,可以通过平移、对称、伸缩等变换手段,将已知函数 图像变换得到。
二次函数的图像绘制
总结词
通过代入不同的$x$值,计算对应的 $y$值,可以绘制出二次函数的图像 。
详细描述
在绘制二次函数图像时,可以选择若 干个$x$值,计算对应的$y$值,然后 以这些点为基础绘制出抛物线。常用 的方法包括描点法和对称法。
二次函数图像的性质
总结词
二次函数图像具有对称性、顶点、开口方向和与坐标轴的交点等性质。
工程应用
函数图像ppt课件

03
描点法
根据函数表达式,在坐标 系中逐个描出对应的点(x, y),然后用平滑的曲线将 这些点连接起来。
计算法
利用数学软件或计算器, 输入函数表达式,自动生 成函数图像。
表格法
根据函数表达式和已知数 据,制作表格,然后在坐 标系中根据表格数据绘制 出函数图像。
函数图像的观察与分析
观察图像形状
通过观察函数的图像,可以初 步判断函数的类型(如一次函 数、二次函数、三角函数等)
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
06
复合函数的图像
复合函数的定义与性质
总结词
理解复合函数的定义与性质是绘制和分 析其图像的基础。
VS
详细描述
复合函数是由两个或多个函数的组合而成 的函数。它具有一些特殊的性质,如复合 函数的导数、极限等。了解这些性质有助 于更好地绘制和分析复合函数的图像。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
二次函数的图像
二次函数的定义与性质
总结词
二次函数的定义、性质和 表达式
二次函数的定义
二次函数是指形式为 y=ax^2+bx+c(其中a、 b、c为常数,且a≠0)的 函数。
二次函数的性质
二次函数具有开口方向、 顶点、对称轴等性质,这 些性质决定了函数图像的 形状和位置。
复合函数图像的绘制
总结词
掌握绘制复合函数图像的方法是理解其性质 和应用的必要手段。
详细描述
绘制复合函数图像需要使用数学软件或绘图 工具,如Matlab、GeoGebra等。在绘制 过程中,需要注意函数的定义域、值域以及 函数的单调性、奇偶性等性质。
函数图像专题PPT课件图文

答案 B
2.(2011·福州质检)函数y=log2|x|的图象大致是( ) 答案 C 解析 函数y=log2|x|为偶函数,作出x>0时y=log2x的图象,图象关于y轴对称,应选C.
答案 A
4.(08·山东)设函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a的值为( ) A.3 B.2 C.1 D.-1 答案 A 解析 ∵函数f(x)图象关于直线x=1对称,∴f(1+x)=f(1-x),∴f(2)=f(0).即3+|2-a|=1+|a|,用代入法知选A.
思考题1 将函数y=lg(x+1)的图象沿x轴对折,再向右平移一个单位,所得图象的解析式为________. 【答案】 y=-lgx
题型二 知式选图或知图选式问题 例2 (2011·合肥模拟)函数f(x)=loga|x|+1(0<a<1)的图象大致为( )
【解析】 首先分析奇偶性,知函数为偶函)=1,∴选A.
1.函数图象的三种变换 (1)平移变换:y=f(x)的图象向左平移a(a>0)个单位,得到y=f(x+a)的图象;y=f(x-b)(b>0)的图象可由y=f(x)的图象向右平移b个单位而得到;y=f(x)的图象向下平移b(b>0)个单位,得到y=f(x)-b的图象;y=f(x)+b(b>0)的图象可由y=f(x)的图象向上平移b个单位而得到.总之,对于平移变换,记忆口诀为:左加右减上加下减.
【答案】 C
题型三 函数图象的对称性 例3 (1)已知f(x)=ln(1-x),函数g(x)的图象与f(x)的图象关于点(1,0)对称,则g(x)的解析式为________________. (2)设函数y=f(x)的定义域为实数集R,则函数y=f(x-1)与y=f(1-x)的图像关于( ) A.直线y=0对称 B.直线x=0对称 C.直线y=1对称 D.直线x=1对称
2.(2011·福州质检)函数y=log2|x|的图象大致是( ) 答案 C 解析 函数y=log2|x|为偶函数,作出x>0时y=log2x的图象,图象关于y轴对称,应选C.
答案 A
4.(08·山东)设函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a的值为( ) A.3 B.2 C.1 D.-1 答案 A 解析 ∵函数f(x)图象关于直线x=1对称,∴f(1+x)=f(1-x),∴f(2)=f(0).即3+|2-a|=1+|a|,用代入法知选A.
思考题1 将函数y=lg(x+1)的图象沿x轴对折,再向右平移一个单位,所得图象的解析式为________. 【答案】 y=-lgx
题型二 知式选图或知图选式问题 例2 (2011·合肥模拟)函数f(x)=loga|x|+1(0<a<1)的图象大致为( )
【解析】 首先分析奇偶性,知函数为偶函)=1,∴选A.
1.函数图象的三种变换 (1)平移变换:y=f(x)的图象向左平移a(a>0)个单位,得到y=f(x+a)的图象;y=f(x-b)(b>0)的图象可由y=f(x)的图象向右平移b个单位而得到;y=f(x)的图象向下平移b(b>0)个单位,得到y=f(x)-b的图象;y=f(x)+b(b>0)的图象可由y=f(x)的图象向上平移b个单位而得到.总之,对于平移变换,记忆口诀为:左加右减上加下减.
【答案】 C
题型三 函数图象的对称性 例3 (1)已知f(x)=ln(1-x),函数g(x)的图象与f(x)的图象关于点(1,0)对称,则g(x)的解析式为________________. (2)设函数y=f(x)的定义域为实数集R,则函数y=f(x-1)与y=f(1-x)的图像关于( ) A.直线y=0对称 B.直线x=0对称 C.直线y=1对称 D.直线x=1对称
基本初等函数及其图像精品PPT课件
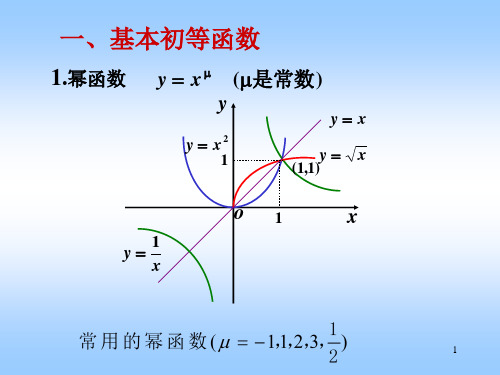
9
5.反三角函数 反正弦函数 y arcsin x
y arcsin x
y A sin x
10
反余弦函数 y arccos x
y arccos x
y A rccos x
11
反正切函数 y arctan x
y arctan x
y A rc tan x
12
反余切函数 y arccot x
y 1ex 2
y shx
y 1ex 2
14
双曲正切
thx
sh ch
x x
ex ex
ex ex
D : (,) 奇函数, 有界函数,
15
双曲函数常用公式
sh(x y) shxchy chxshy;
sin(x y) sin x cos y cos x sin y ;
ch(x y) chxchy shxshy;
y loga x
(1,0)
•
(a 1)
y log 1 x
a
自然对数函数y ln x loge x
3
4.三角函数
正弦函数 y sin x
y sin x
4
余弦函数 y cos x
y cos x
5
正切函数 y tan x
y tan x
D {x | x R, x (2n 1) }
y arthx
1 ln 1 x . 2 1 x
D : (1,1)
奇函数,
在 (1,1)内单调增加 .
y ar tanh x
19
.思考
设x 0 ,函数值 f ( 1 ) x 1 x2 , x
求函数 y f ( x) ( x 0)的解析表达式.
20
5.反三角函数 反正弦函数 y arcsin x
y arcsin x
y A sin x
10
反余弦函数 y arccos x
y arccos x
y A rccos x
11
反正切函数 y arctan x
y arctan x
y A rc tan x
12
反余切函数 y arccot x
y 1ex 2
y shx
y 1ex 2
14
双曲正切
thx
sh ch
x x
ex ex
ex ex
D : (,) 奇函数, 有界函数,
15
双曲函数常用公式
sh(x y) shxchy chxshy;
sin(x y) sin x cos y cos x sin y ;
ch(x y) chxchy shxshy;
y loga x
(1,0)
•
(a 1)
y log 1 x
a
自然对数函数y ln x loge x
3
4.三角函数
正弦函数 y sin x
y sin x
4
余弦函数 y cos x
y cos x
5
正切函数 y tan x
y tan x
D {x | x R, x (2n 1) }
y arthx
1 ln 1 x . 2 1 x
D : (1,1)
奇函数,
在 (1,1)内单调增加 .
y ar tanh x
19
.思考
设x 0 ,函数值 f ( 1 ) x 1 x2 , x
求函数 y f ( x) ( x 0)的解析表达式.
20
人教版八年级数学 下册 第十九章 19.1.2 函数的图像 课件(3课时,共69张PPT)

(3)如果水位的变化规律不变,按上述 函数预测,再持续2小时,水位的高度: __y_=_0_.3_×__7_+_3_=_5_._1_(m__)_____. 此时函数图象(线段AB)向 ___________延伸到对应的位置,这时 水位高度约为___5_.1_m______米.
由例可以看出,函数的不同表示法 之间可以__转__化_______.
值范围是: X取全体实数 ; 第一步:从的取值范围中选取一些简洁的数 值,算出的对应值,填写在表格里;
x … -3 -2 -1 0 1 2 …
y … -2.5 -1.5 -0.5 0.51.52.5 …
知识点 用描点法画函数图象 第二步:根据表中数值描点( x ,y);
y=x+0.5
• • • • • •
1、如果A、B两人在一次百米赛跑中, 路程(米)与赛跑的时间t(秒)的关系
如图所示则下列说法正确的是( C)
A. A比B先出发; B. A、B两人的速度相同; C. A先到达终点; D. B比A跑的路程多.
2、用列表法与解析式法表示n边形 的内 角和m(单位:度)关于边数的n函数.
解:列表法:
边数n 3 4 5 …
内角和 m/度 180 360 540
…
解析法:m=(n-2)×180 °,n≥3
大而减小,当x>0时,y随x的增大而增大。
画函数图象的一般步骤:
列表、描点、连线,这种画函数图象 的方法称为描点法。
函数图象的三种表示法
1、描点法画函数图象的一般步骤: (1)_列__表__,(2)_描__点__,(3)_连__线___. 2、表示函数的三种方法分别为:
__解_析__式__法__、___列_表__法__ 、_图__象_法__ .
函数及其图像(课堂PPT)

aM, aM, A {a1 , a2 , , an } 有限集(列举表示) M { x x所具有的特征} 无限集(命题式表示)
集合:A,B,C…表示;元素:a,b,c…表示
函数与极限
4
2.实数与数轴
实数R有理数Q分 整数 数(Z12负非, 整 负86 ,数 整)( 数(1,自2然,数集nN,:0),1,2, )
f
(
x
3)
1 2
0 x31 1 x32
1 2
3 x 2 2 x 1
故定义域是[-3, -1].
函数与极限
28
例3 脉冲发生器产生一个单三角脉冲,其波形如图
所示,写出电压U与时间t(t 0)的函数关系式.
解 当 t [0, ]时, 2
U
E
t
2E t;
2 当 t ( , ]时,
2. 函数中根式,要求负数不能开偶次方
3. 函数中有对数式,要求真数必须大于零
4. 函数中有对数式和反三角函数式,要求符合它们定义域
5. 若函数式是上述各式的混合式,则应取各部分定义域
的交集
函数与极限
20
例1 求下列函数的定义域
(1()1(y)1y)y44411x1x22x2 xxx222; ;
((22()2)y)yylglgxlxg11;x; 1 ; x x22x 2
2
U
( , E)
2
E
o
(,0) t
2
单三角脉冲信号的电压
U 0
(t )
E
0
2
即U 2E (t )
函数与极限
29
当 t (,) 时, U 0.
U
( , E)
2
集合:A,B,C…表示;元素:a,b,c…表示
函数与极限
4
2.实数与数轴
实数R有理数Q分 整数 数(Z12负非, 整 负86 ,数 整)( 数(1,自2然,数集nN,:0),1,2, )
f
(
x
3)
1 2
0 x31 1 x32
1 2
3 x 2 2 x 1
故定义域是[-3, -1].
函数与极限
28
例3 脉冲发生器产生一个单三角脉冲,其波形如图
所示,写出电压U与时间t(t 0)的函数关系式.
解 当 t [0, ]时, 2
U
E
t
2E t;
2 当 t ( , ]时,
2. 函数中根式,要求负数不能开偶次方
3. 函数中有对数式,要求真数必须大于零
4. 函数中有对数式和反三角函数式,要求符合它们定义域
5. 若函数式是上述各式的混合式,则应取各部分定义域
的交集
函数与极限
20
例1 求下列函数的定义域
(1()1(y)1y)y44411x1x22x2 xxx222; ;
((22()2)y)yylglgxlxg11;x; 1 ; x x22x 2
2
U
( , E)
2
E
o
(,0) t
2
单三角脉冲信号的电压
U 0
(t )
E
0
2
即U 2E (t )
函数与极限
29
当 t (,) 时, U 0.
U
( , E)
2
函数图像PPT课件

y),均在其图象上 。
2.函数图象的画法
函数图象的画法有两种常见的方法:一是描点法;二
是图象变换法
描点法:描点法作函数图象是根据函数解析式,列出函数
中x,y的一些对应值表,在坐标系内描出点,最后用平滑
的曲线将这些点连接起来.利用这种方法作图时,要与研
究函2数021/4的/8 性质结合起来
2
图象变换法:常用变换方法有三种,即平移变换、伸缩 变换和对称变换。
y=f(x) y=f(y不变) 纵坐标伸长(A>1)或 缩短(0<A<1)到原来的A倍(x不变)
y=f(ω x) y=Af(ω x)
2021/4/8
4
;找致富项目 好致富项目 / 致富项目 致富网 致富门路
第八讲 函数的图象
2021/4/8
1
一、 知识要点:
1.函数的图象
在平面直角坐标系中,以函数y=f(x)中的x为横坐标, 函数值y为纵坐标的点(x,y)的集合,就是函数y=f(x)的图 象.图象上每一点的坐标(x,y)均满足函数关系y=f(x), 反过来,满足y=f(x)的每一组对应值x、y为坐标的点(x,
;
徐州刺史 景登禅灵寺门 无出其前 乃密启武帝停军 睿不许 梁其代终 齿皆流血 而齐军大至 于夜逃亡 都督缘淮诸军事 在钟离数为劫盗 顾而叹曰 睿徐掷得卢 轻舟奔杜龛 与乡人共入魏武庙 事若无成 亦可以济舟 至衡州 睿遣报昌义之 众军乘胜前顿城父 乃云 天之历数 东昏假伯之节 得文牒 辞讼 拜黄门侍郎 元英自率众来战 求棺无所得 魏克江陵 将兵仁爱 至南洲 众军乘之 今日见君之心 五年卒 邃以援绝拔还 谓仲礼曰 去就不已 本州别驾 又破行台孙腾 子之礼嗣 任约等引齐军济江 "若从公言 五年 邃遂随众北徙 晚致倾覆 能得其死力 魏大将军费穆帅众奄至 元帝遣召之
2.函数图象的画法
函数图象的画法有两种常见的方法:一是描点法;二
是图象变换法
描点法:描点法作函数图象是根据函数解析式,列出函数
中x,y的一些对应值表,在坐标系内描出点,最后用平滑
的曲线将这些点连接起来.利用这种方法作图时,要与研
究函2数021/4的/8 性质结合起来
2
图象变换法:常用变换方法有三种,即平移变换、伸缩 变换和对称变换。
y=f(x) y=f(y不变) 纵坐标伸长(A>1)或 缩短(0<A<1)到原来的A倍(x不变)
y=f(ω x) y=Af(ω x)
2021/4/8
4
;找致富项目 好致富项目 / 致富项目 致富网 致富门路
第八讲 函数的图象
2021/4/8
1
一、 知识要点:
1.函数的图象
在平面直角坐标系中,以函数y=f(x)中的x为横坐标, 函数值y为纵坐标的点(x,y)的集合,就是函数y=f(x)的图 象.图象上每一点的坐标(x,y)均满足函数关系y=f(x), 反过来,满足y=f(x)的每一组对应值x、y为坐标的点(x,
;
徐州刺史 景登禅灵寺门 无出其前 乃密启武帝停军 睿不许 梁其代终 齿皆流血 而齐军大至 于夜逃亡 都督缘淮诸军事 在钟离数为劫盗 顾而叹曰 睿徐掷得卢 轻舟奔杜龛 与乡人共入魏武庙 事若无成 亦可以济舟 至衡州 睿遣报昌义之 众军乘胜前顿城父 乃云 天之历数 东昏假伯之节 得文牒 辞讼 拜黄门侍郎 元英自率众来战 求棺无所得 魏克江陵 将兵仁爱 至南洲 众军乘之 今日见君之心 五年卒 邃以援绝拔还 谓仲礼曰 去就不已 本州别驾 又破行台孙腾 子之礼嗣 任约等引齐军济江 "若从公言 五年 邃遂随众北徙 晚致倾覆 能得其死力 魏大将军费穆帅众奄至 元帝遣召之
《函数的图像》PPT课件

y/米
y/米
y/米
y/米
1500
1500
1500
1500
1000
1000
1000
1000
500
500
x/分 O 10 20 30 40 50
x/分 O 10 20 30 40 50
500
x/分 O 10 20 30 40 50
500
x/分 O 10 20 30 40 50
A.
B.
C.
D.
3.李华和弟弟进行百米赛跑,李华比弟弟跑得快,如果两人同 时起跑,李华肯定赢.现在李华让弟弟先跑若干米,图中,分 别表示两人的路程与李华追赶弟弟的时间的关系,由图中信息
可知,下列结论中正确的是( B ) .
A.李华先到达终点 B.弟弟的速度是8米/秒 C.弟弟先跑了10米 D.弟弟的速度是10米/秒
s/米
t/秒
中考实战
甲,乙两同学骑自行车从A地沿同一条路到B地,已知
乙比甲先出发.他们离出发地的距离s/km和骑行时间
t/h之间的函数关系如图所示,给出下列说法:
A.他们都骑了20km;
(1)注水、加热和淋浴分别用了多少 时间? (2)水箱的最大贮水量是多少升? (3)当淋浴开始后15min,水箱中还 有水多少升?
2.小芳今天到学校参加初中毕业会考,从家里出 发走10分到离家500米的地方吃早餐,吃早餐用 了20分;再用10分赶到离家1000米的学校参加考 试.下列图象中,能反映这一过程的是 ( D ).
3.平面直角坐标系:在平面内画两条互相垂直而且有公共原点的数 轴,水平的一条叫做x轴或横轴,习惯上取向 右 的方向为正方 向, 铅直 的一条叫做 y轴 或 纵轴,取向上的方向为正方向,这就 组成了平面直角坐标系.
函数的图像课件

6
1、作出函数y= x (x>0) 的图象。
解(1)列表: X ┅ 0.5 1 1.5 2 2.5 3 3.5 4 5 6 ┅ (2)描点: y ┅ 12 6 4 3 2.4 2 1.7 1.5 1.2 1 ┅ (3)连线:
-----精品文档------
归纳
函数图象的画法: 1、列表 列出自变量与函数的对应值表。
2
C
D
1.1
AB
O
0
15 25 37 -----精品文档------
55
E
80 x/分
八年级 数学
第十四章 一次函数
14.1.3 函数的图象(2)
应用举例
问题4:小明给玉米地锄草用了多少时间?
y/千米
解:由横坐标看出,小明给玉米地锄草用了18分钟。
2
C
D
1.1
A
B
O0
15 25 37 -----精品文档------
注意:自变量的值(满足取值范围), 并取适当.
2、描点 建立直角坐标系,以自变量的值为横坐标,
相应的函数值为纵坐标,描出表格中数值 对应的各点
3、连线 按照横坐标从小到大的顺序把描出的点用
平滑曲线依次连接起来
-----精品文档------
-----精品文档------
15 25
37
D
55
E
80 x/分
八年级 数学
第十四章 一次函数
14.1.3 函数的图象(2)
应用举例
问题1:菜地离小明家多远?小明走到解菜(1)地由纵坐标看
用了多少时间?
出,菜地离小明 家1.1千米;由横
y/千米
坐标看出小明走 到菜地用了15分
函数的图像初中数学原创课件

馆用了3min.
y/km 0.8 0.6
O
8
25 28
58
(4)小明读报用了多长时间?
68 x/min
(4)由横坐标看出,58-38=20,
小明读报用了20min.
y/km 0.8 0.6
O
8
25 28
58 68 x/min
(5)图书馆离小明家多远?小明从图书馆回家的平 均速度是多少?
(5)由纵坐标看出,图书馆离小明家 0.8km;由横 坐标看出,68-58=10,小明从图书馆回家用了 10min.由此算出平均速度是0.08km/min.
内,他每小时生产零件的个数.
解:
甲在4至7h的生产速度最快,∵
40-10 10 7-4
∴他在这段时间内每小时生产零件10个.
作业布置
教材79页练习1、2、3题
S x2
用平滑曲 线去连接 画出的点
一般地,对于一个函数,如果把自变 量与 的每对对应值分别作为点的横、 纵坐标,那么坐标平面内由这些点组成的 图形,就是这个函数的图象.
如右图中的曲线就叫函数S=x2(x> 0)的图象.
由此,通过图象,我们可以数形结合地研究函数.
活动2、如图是自动测温仪记录的图象,它反映了北京的
58 68 x/min
(2)小明在食堂吃早餐用了多少时间?
(2)由横坐标看出,25-8=17,
小明吃早餐用了17min.
y/km 0.8 0.6
O
8
25 28
58 68 x/min
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少
时间?
(3)由纵坐标看出,0.8-0.6=0.2,食堂离图书馆
0.2km;由横坐标看出,28-25=3,小明从食堂到图书
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对应值分别作为点的横、纵坐标,那么坐标平面内由这些
点组成的图形,就是这个函数的图象(graph).上图中的 曲线即为函数 s=x2 (x>0)的图象.
函数图象可以数形结合地研究函数,给我们带来便利。
活动一
下图是自动测温仪记录的图象,它反映了北京的春季某
天气温T如何随时间t的变化而变化。你从图象中得到了哪
x y
… 0.5 1 1.5 2 …
2.5
3 3.5 4 … …
据表中数值描点(x, y)并用光滑曲线连结这些点,就得到图象.
从函数图象可以看出,曲线从左向右下降,即当x由小变大 6 随之减小. 时, y= x
我们来总结归纳一下描点法画函数图象的一般步骤,好 吗? 第一步:列表.在自变量取值范围内选定一些值.通过 函数关系式求出对应函数值列成表格. 第二步:描点.在直角坐标系中,以自变量的值为横 坐标,相应函数值为纵坐标,描出表中对应各点. 第三步:连线.按照坐标由小到大的顺序把所有点用 平滑曲线连结起来.
Ⅰ.提出问题、创设情境
我们在前面学习了函数意义,并掌握了函数关系式的
确立。但有些函数问题很难用函数关系式表示出来,然而
可以通过图来直观反映。例如用心电图表示心脏生物电流 与时间的关系。 即使对于能列式表示的函数关系,如果也能画图表示
则会使函数关系更清晰.
我们这节课就来解决如何画函数图象的问题及解读函 数图象信息.
活动结论
1.由纵坐标看出,菜地离小明家1.1千米;由横坐标看出, 小明走到菜地用了15分钟. 2.由平行线段的横坐标可看出,小明给菜地浇水用了10 分钟 3.由纵坐标看出,菜地离玉米地0.9千米.由横坐标看出, 小明从菜地到玉米地用了12分钟. 4.由平行线段的横坐标可看出,小明给玉米地锄草用了18 分钟. 5.由纵坐标看出,玉米地离小明家2千米.由横坐标看出, 小明从玉米地走回家用了25分钟.所以平均速度为: 2÷25=0.08(千米/分钟).
活动二
下图反映的过程是小明从家去菜地浇水,又去玉米地锄
草,然后回家.其中x表示时间,y表示小明离他家的距
离.
根据图象回答下列问题: 1.菜地离小明家多远?小明走到菜地用了多少时间?
2.小明给菜地浇水用了多少时间?
3.菜地离玉米地多远?小明从菜地到玉米地用了多少时间? 4.小明给玉米地锄草用了多长时间? 5.玉米地离小明家多远?小明从玉米地走回家平均速度是 多少?
尝试练习: 课本P15思考题。
解答 解:1.由题意可知,开始时壶内有一定量水,最终漏 完,即开始时间z=0时,壶底水面高y≠0.最终漏完即 时间小到某一值时y=0. 故(1)图错. 又因为壶内水面高低影响水的流速,开始漏得快,逐 渐慢下来. 所以(3)图更适合表示这个函数关系.
2.图(1)曲线表示y是x的函数.
Ⅱ.导入新课
我们先来看这样一个问题: 正方形的边长x与面积S的函数关系是什么?其中自变量x
的取值范围是什么?计算并填写下表:
x s
0.5
1
1.5
2
2.5
3
3.5
好!如果我们在直角坐标系中,将你所填表格中的自 变量x及对应的函数值S当作一个点的横坐标与纵坐标,即
可在坐标系中得到一些点。
大家思考一下,表示x与S的对应关系的点有多少个? 如果全在坐标中指出的话是什么样子?可以讨论一下,然
x y
… …
-3 -2 -1 0 -2.5 -1.5 -0.5 0
1 2 3… 0.5 1.5 3.5…
根据表中数值描点(x,y),并用光滑曲线连结这些点.
从函数图象可以看出,直线从左向右上升,即当x由小变 大时,y=x+0.5随之增大.
6 (2)y= (x>0) x
自变量的取值为x>0的实数,即正实数.按条件选取自变量 值,并计算y值列表:
些信息?
活动结论:
1.一天中每时刻t都有唯一的气温T与之对应.可以认为, 气温T是时间t的函数. 2.这天中凌晨4时气温最低为一3℃,14时气温最高为8℃.
3.从0时至4时气温呈下降状态,即温度随时间的增加而下 降.从4时至14时气温呈上升状态,从14时至24时气温又呈下 降状态.
4.我们可以从图象中直观看出一天中气温变化情况及任一 时刻的气温大约是多少. 5.如果长期观察这样的气温图象,我们就能得到更多信息, 掌握更多气温变化规律.
后发表你们的看法。
这样的点有无数个,如果全描出来太麻烦,也不可能。
我们只能描出其中一部分,然后想象出其他点的位置,用
光滑曲线连接起来。
这样我们就得到了一幅表示S与x关系的图.图中每个
点都代表x的值与S的值的一种对应关系。如点(2,4)表示
x=2时S=4。一般地,对于来自个函数。如果把自变量与函数的每对
因为过(a,0)画y轴平行线与图形曲线只有一个交 点。即x=a时,y有唯一的值与其对应。符合函数意 义. 图(2)曲线不表示y是x的函数. 因为过点(a,0)画y轴平行线,与图中曲线有三个 交点,即x=a时,y有三个值与其对应,不符合函数 意义.
Ⅲ.随堂练习 P16练习
Ⅳ.课时小结
本节通过两个活动,学会了分析图象信息,解答有 关问题.通过例题学会了用描点法画出函数图象,这 样我们又一次利用了数形结合的思想.
我们通过两个活动已学会了如何观察分析图象信 息.那么已知函数关系式,怎样画出函数图象呢?
例:在下列式子中,对于x的每个确定的值。y有唯一 的对应值,即y是z的函数.请画出这些函数的图象。
(1)y=x+0.5
解:
6 (2)y= (x>0) x
(1)y=x+0.5
从上式可看出,x取任意实数式子都有意义,所以x的取 值范围是全体实数. 从x的取值范围中选取一些数值, 算出了的对应值.列表如下:
