2.1晶体结合能的普遍规律
固体物理学课程综述

固体物理学课程综述固体物理学是20世纪物理学发展最快的一门学科,几十年来,以固体物理学的能带理论为基础,科学家在半导体、激光、超导、磁学等现代科学研究方面取得了重大突破,有关研究成果已经迅速转化为生产力,并带动了整个信息科学技术群的高速发展。
第一章、晶体结构1、晶体的宏观特性1、长程有序:晶体内部的原子的排列是按照一定得规则排列的。
这种至少在微米级范围内的规则排列称为长程有序。
长程有序是晶体材料具有的共同特征。
在熔化过程中,晶体长程有序解体时对应一定得熔点。
2、自限性与解理性:晶体具有自发形成封闭多面体的性质称为晶体的自限性。
晶体外形上的这种特性是晶体内部原子有序排列的反应。
一个理想完整的晶体,相应地晶体面具有相同的面积。
晶体具有沿某些确定方位的晶面劈裂的性质称为晶体的解理性,相应地晶面称为解理面。
3、晶面角守恒:由于生长条件的不同,同一种晶体外形会有一定得差异,但相应的两晶面之间的夹角却总是恒定的。
即属于同种晶体的两个对应晶面之间夹角恒定不变的规律称为晶面守恒定律。
4、各向异性:晶体的物理性质在不同方向上存在着差异的现象称为晶体的各向异性。
晶体的晶面往往排列成带状,晶面间的交线互相平行,这些晶面的组合称为晶带,晶棱的共同方向称为该晶带的带轴。
由于各向异性,在不同带轴方向上,晶体的物理性质是不同的。
晶体的各向异性是晶体区别于非晶体的重要特性。
因此对于一个给定的晶体,其弹性常数、压力常数、介电常数、电阻率等一般不再是一个确定的常数。
通常要用张量来表述。
2、固体物理学原胞(原胞)与布拉维原胞(晶胞、结晶学原胞)的区别答:晶格具有三维周期性,因此可取一个以结点为顶点、边长分别为3个不同方向上的平行六面体作为重复单元来反映晶格的周期性,这个体积最小的重复单元称为固体物理学原胞,简称原胞。
在同一晶格中原胞的选取不是唯一的,但他们的体积都是相等的。
为了反映周期性的同时,还要反映每种晶体的对称性,因而所选取的重复单元的体积不一定最小。
晶体的结合能,内能,原子间的相互作用势能

晶体的结合能、内能、原子间的相互作用势能
晶体是由大量排列有序的原子或分子所组成的固体结构,在晶体中,原子或分
子之间存在着结合能和相互作用势能。
晶体的结合能、内能和原子间的相互作用势能密切相关,对于晶体的性质和稳定性起着至关重要的作用。
结合能
晶体的结合能是指晶体内部所有原子或分子之间相互结合所需要的能量。
晶体
的结合能决定了晶体的熔点、硬度、脆性等物理性质。
晶体的结合能可以通过实验方法或计算模拟方法来确定。
通常来说,结合能越大,晶体的稳定性越高,其熔点和硬度也会相应增加。
内能
晶体的内能是指晶体内部原子或分子的总能量。
内能包括晶体的结合能以及原
子或分子在晶体内部的动能和位能。
内能的大小与晶体的温度和压力有关。
晶体的内能是晶体的热力学性质的重要参数,可以通过实验测量或理论计算来确定。
原子间的相互作用势能
晶体中的原子或分子之间存在着相互作用势能,这种相互作用势能决定了晶体
的结构和稳定性。
原子间的相互作用势能可以通过简单的模型来描述,比如晶体中的键能、范德华力等。
不同种类的晶体,其原子间的相互作用势能也有所差异,这种差异导致了不同晶体的性质和行为。
在晶体学研究中,研究晶体的结合能、内能和原子间的相互作用势能是非常重
要的。
通过对这些能量的研究,可以更好地理解晶体的性质和行为,为合成新材料、优化材料性能等提供理论指导和实验依据。
总之,晶体的结合能、内能和原子间的相互作用势能是晶体学研究的核心内容,对于揭示晶体的本质和规律具有重要意义,也为材料科学和工程领域的发展做出了重要贡献。
第二章晶体的结合

金属容易导热,是由于自由电子运动时与金属离子碰撞 把能量从温度高的部分传到温度低的部分,从而使整块金 属达到相同的温度。
(3).金属晶体结构与金属的延展性的关系
金属晶体中由于金属离子与自由电子间的相互作用没有 方向性,各原子层之间发生相对滑动以后,仍可保持这种相 互作用,因而即使在外力作用下,发生形变也不易断裂。
2.411010
7.9
U0
2 N 0 Me 2
8 0 R0
(1
1) n
6.0231023 1.75 (1.61019)
1
4 3.148.851012
2.82 1010
(1
)0实 765KJ/mol
2.3.2 马德隆常数的计算
1.一维结构的马德隆常数的计算
dr r0 r03 r011
由(1)、(2)得
5 4
u(r0 )r02
4.5 1019 eVm 2
5
r08
5.91096eVm10
2)
d 2u(r)
23 1011
dr 2 rm
rm4
rm12
0
1
得临界间距:
rm
55 3
8
0.353nm
4. 晶体的结合能
i, j两原子间距rij ,相互作用势u(rij ),则N个原子构成的晶体总作用势
* 结合力
物理图像:化学键
结合力的不同可以将其分成五个典型的结合类型: 离子晶体, 原子晶体, 金属晶体, 分子晶体, 氢键晶体
本质:原子束缚电子的能力
构成晶体的基本微粒和作用力
• 离子:正负离子间以离子键结合,形成离子晶体。 • 分子:分子间以分子间作用力(又称范德瓦耳斯力)
固体物理期末总结

a2 i j k 2
a3 a i j k 2
平均每个布拉维原 胞包含2个格点。
Ω a1 a2 a3 1 a3 2
典型的晶体结构
结构型 单胞中的 原子在单胞 最近邻 配位数 原子个数 中的位置 距离
fcc
4
(000) (1 1 0)
a
饱和性
(2)金属晶体
方向性
结构:第Ⅰ族、第Ⅱ族及过渡元素晶体都是典型的金属晶体。
结合力:金属键。 多采取配位数为12的密堆积,少数金属为体心立方结构, 配位数为8。
(3)氢键晶体
结构:氢原子同时与两个负电性较大,而原子半径较小
简立方(12),体心立方(13), 面心立方(14)
简单三斜 (1)
简单单斜 (2)
底心单斜 (3)
三角 (4)
简单正交 (5)
底心正交 体心正交
(6)
(7)
面心正交 (8)
简单四角 (9)
体心四角 (10)
六角 (11)
简立方 (12)
体心立方 (13)
面心立方 (14)
倒格
b1 2π a2 a3 Ω
0
(2) K V ( P )
体积弹性模量 V
r0
a (晶格常量)
2U
K V0 ( V 2 )V0
设由N个原子组成的晶体的体积为 V N R3
K
V0
2U V 2
V0
1
9N R0
2U ( R 2 ) R0
(3)
f ( v )vm
2u
Rl S S 0 (为整数) Rl k k0 2π
晶体结合能

q2 n 1 B R0 4π 0 n
设离子最近邻距离为R,由N个离子组成的晶体的体积:
V Nv NR3 ,
2U K V0 V 2
2U K V0 V 2
1 2U 9 N R ( R 2 ) R0 0 V0
N q 2 B U ( n) 2 4π 0 R R
μ q2 K ( n 1) 4 72 β π 0 R0
4 72 β π ε0 R0 n 1 K 2 μq
第 一 节 晶体结合能的普遍规律
本节主要内容: 1 两个原子间的相互作用能
2 晶体总的相互作用能
3 结合能与晶体几个常数的关系
§2.1晶体结合能的普遍规律
晶体的结合能: 晶体的结合能就是将自由的原子(离子或分子)结合成晶
体时所释放的能量。
Eb E N E0
E0是晶体的总能量,EN是组成该晶体的N个原子在自由状 态时的总能量,Eb即为晶体的结合能。
2 ln 2
马德隆常数
2 ln 2
例3:由N个原子(或离子)组成的晶体体积V可以写成
V Nv N R 3
其中
v 为每个原子(离子)平均所占的体积,R为原子(离子)
间的最短距离,是和晶体结构有关的常数。 试求氯化钠型结构的值。
3 R 解: 由题知每个原子(离子)平均所占的体积为:
A B u (r ) m n r r
d 2 u m ( m 1)(n m ) A ( 2) 0 m2 dr ( m 1)r0
可知n >m,排斥作用是短程的。
第二章晶体的结合

两个相互平行的电偶极子的库仑势能可以求 出:
ur
1
40
q2 r
r
q2 l2 l1
q2 r l1
q2 r l2
ur
q2
40r
1 1
1 l2 l1
1 1 l1
1 1 l2
q2l1l2
1 2
N i 1
N j 1
' 4
rij
6
rij
12
N 2
N j 1
'
4
rij
6
rij
12
说明:金属晶体中,价电子不再属于个别 原子,而是为所有原子所共有,在 晶体中做共有化运动,或者说金属中 所有原子都失掉了最外层价电子成为 原子实(离子实),原子实浸没在 共有电子的电子云中,金属晶体的 结合力主要是原子实和共有化电子的 静电库仑力。
4. 范德瓦耳斯键和分子晶体
分子间的相互作用力(范德瓦耳斯力)分为三种:
配位数小,4 特点:
1)饱和性(一个原子只能形成一定数目的共价 键。)
2)方向性:原子只在特定的方向上形成共价键。 3)熔点高、硬度大、导电性差,结合能大 约为800kJ/mol。
饱和性经验公式:当原子的价电子壳层不到半满 时,所有的价电子都未配对,共价键数目与价电 子数相等。N=n(N为价电子数);当原子的价 电子壳层不满但超过半满时,形成的共价键数目n =8-N。
2.1晶体结合能的普遍规律

d 2 u m(m + 1)(n − m ) A ( 2)= >0 m+2 dr (m + 1)r0
可知n 可知 >m,排斥作用是短程的。 ,
df d2u ( ) = −( 2 )rm = 0 dr dr
r = rm , f (rm )
1 2
最大有 效引力 3 i 4
2.1.2 晶体总的相互作用能
U = Nu( v ),V = Nv
dU = − pdV + TdS = − pdV
K ∂ P d 2U ) =V = −V ( dV 2 ∂ V
dU p=− dV
V
平衡时体积弹性模量: 平衡时体积弹性模量:
K =V ( 0 ∂ 2U ∂V ) 0 2 V
3. 抗张强度 晶体的抗张强度等于晶体所能承受的最大张力。 晶体的抗张强度等于晶体所能承受的最大张力。 抗张强度等于晶体所能承受的最大张力
原子数目 原子间距
晶体体积的函数 U(v) ( )
若取E =0,则晶体的结合能: 若取 N=0,则晶体的结合能:
E b = E N − E 0 = − E 0 = −U ( r0 )
2.1.3 结合能与晶体几个常量的关系
1.原胞体积
∂U(r) |r=r0 = 0 ∂r
r0 v0
a
v0
∂U(v) |v=v0 = 0 ∂v
第 一 节 晶体结合能的普遍规律
本节主要内容: 本节主要内容: 2.1.1 两个原子间的相互作用能 2.1.2 晶体总的相互作用能 2.1.3 结合能与晶体几个常数的关系
§2.1晶体结合能的普遍规律
晶体的结合能: 晶体的结合能: 晶体的结合能就是将自由的原子(离子或分子) 晶体的结合能就是将自由的原子(离子或分子)结合成晶 就是将自由的原子 体时所释放的能量。 体时所释放的能量。
固体物理第二章复习

式中
B
1
6
;
A2
A
4B
'N 1
A12
j
a12 j
A6 , A12 是仅与晶体结构有关的常数。
'N 1
A6
j
a6 j
3.原子晶体、金属晶体和氢键晶体
(1)原子晶体
结构:第Ⅳ族、第Ⅴ族、第Ⅵ族、第Ⅶ族元素都可以形成
原子晶体。
结合力: 共价键 (2)金属晶体
饱和性 方向性
层一共有 8 个量子态, 最多能接纳(8- N)个电子, 形成(8- N)个共价键. 这就 是共价结合的 “饱和性”.
共价键的形成只在特定的方向上, 这些方向是配对电子波函数的对称轴方向, 在这个方向上交迭的电子云密度最大. 这就是共价结合的 “方向性”.
10. 为什么许多金属为密积结构? 金属结合中, 受到最小能量原理的约束, 要求原子实与共有电子电子云间的
(2)结合力: 范德瓦尔斯力。
(3)配位数: 通常取密堆积,配位数为12。
(4)互作用势能:
u(r )
4
12
6
r r
U ( R)
2 N
A12
R
12
A6
R
6
雷纳德-琼斯势
r1 rA a, a1 1, r2 rB 2a, a2 2, r3 rC 3a, a3 3,
2( 1 1 1 1 ) ln( 1 x ) x x2 x3 x4
第二章晶体结构结合力和结合能
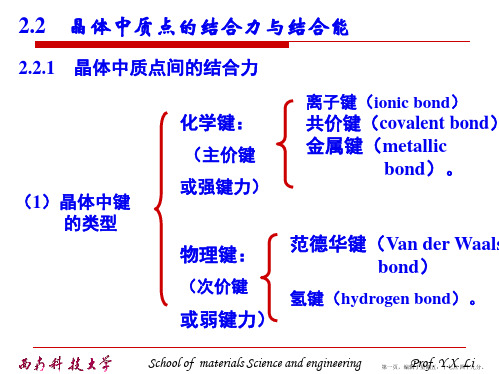
较弱 无方向性键、结构密堆、低 熔点、绝缘
氢键 氢原子核与极性分子 弱 有方向性和饱和性 间的库仑引力School of materials Science and engineering Prof. Y.X. Li 第五页,编辑于星期五:十七点 四十九分。
2.3 晶体中质点的堆积
2.3.1 原子半径和离子半径 原子半径或离子半径
有效半径
离子半径 共价半径 金属半径
一种原子在不同的晶体中,与不同的元素相结合时, 其半径有可能发生变化。晶体极化、共价键的增强和配位 数的降低都可使原子或离子之间距离缩短,而使其半径减 小。
School of materials Science and engineering Prof. Y.X. Li 第十三页,编辑于星期五:十七点 四十九分。
对于1molAX型晶体,原子总数N=2N0,于是晶格
能计算如下:
EL
N0 Az1z2e2 1 1
4 0r0
n
取决于晶体 结构类型
式中:A-马德龙常数见表2.4(P24)
n-Born Index.(与离子的电子层结构有关)。
ε0-真空的介电常数,
取决于电子 ≈8.85×10-12C2.N-1m-2 层结构
School of materials Science and engineering Prof. Y.X. Li 第二十一页,编辑于星期五:十七点 四十九分。
2.3.3 内在因素对晶体结构的影响-化学组成 (1)原子或离子半径
•原子半径或离子半径是定值吗?
•原子半径或离子半径的大小与哪些因 素有关?
氢键:指氢原子同时与两个电负性很大而原子半径较
第二章 晶体结合

方向性------各个共价键之间有确定的取向。 成键时,电子云发生交叠,交叠越多键能越大,系统 能量越低,键越牢固。
例如:金刚石结构的4个键的方向是沿着正四面体的4 个顶角方向,键间的夹角恒为109028‘。
特性:
特性差别较大。典型的原子晶体,具有熔点高、热 膨胀系数小,导电性能差、硬度高等特点。 例如: 从熔点来看,金刚石约为3280k、而Si为1693k,Ge 为1209k。 从导电性来看,金刚石是一种良好的绝缘体,而Si 和Ge在极低温度下才是绝缘体,同时它们的电阻率 随温度升高而急速的下降,是典型的半导体材料。
结合能 强 数ev/键
稳定的正、负离子相 间排列通过库仑静电 力相互吸引。
熔点高:硬度大,膨胀系数 小,易沿解理面劈裂,高温 下有良好的离子导电性。
周期表左右两 边负电性差异 大的原子之间 形成结合。 负电性接近且 较大的原子或 同种原子相互 结合。
共价键:两原子共有 的自旋相反配对的电 子结构。
完整晶体硬度大, 熔点一般较高, 低温下导电性能较差,为绝缘体 或半导体。化学惰性大,由于饱 和性、方向性,决定了原子排列 只能取有限的几种形式。
四、电负性
度量原子吸引电子的能力。一般选定某原子的 电负性为参考值,其他原子的电负性与此参考值作 比较。
穆力肯提出的电负性定义为: 负电性=0.18(电离能+亲和能) 常数的选择以方便为原则,例如一种常用的选择方 法:为使锂(Li)的负电性为1,选上常数为0.18。
泡林提出的电负性计算为:
E(A-B)= [E(A-A)×E(B-B)]1/2+96.5(xA-xB)
xA,xB 原子A和B的电负性;
E(A-B):双原子分子AB的离解能
E(A-A) :双原子分子AA的离解能
晶体结合能的普遍规律 离子晶体-山东大学固体物理

2 34 i
rij
的相互作用势能为:
N
ui ' u(rij )
j 1
则由N个原子组成的晶体的总的相互作用势能为:
u(r )
2 1
i 1
N
ui
2 1
i 1
N
j 1'u( rij
N
)
因为晶体中原子数很多,因此晶体表面原子与晶体内部原 子的差别可以忽略,上式近似为:
r0 a v0
U (v)
v
|vv0 0
v0
2.压缩系数和体积弹性模量(体积压缩模量)
压缩系数: 单位压强引起的体积的相对变化率。
k
1 V
( V P
)T
体积弹性模量是压缩系数的倒数:
K V ( P ) V
由热力学第一定律:
dU pdV TdS pdV
K
构有关的数。
N q2
U
2
4π
0
R
N
)
1 Rn
N
'
j 1
b
a
n j
令
N '
j
1 aj
B
N
j
'b
a
n j
U N ( q2 2 4π0 R
B Rn
)
式中 为马德隆常数,它是仅与晶体几何结构有关的常数。
2.平衡时体积弹性模量K与n的关系及晶体的结合能
§2.2 离子晶体
2.2.1 离子晶体的结构
1.结构
晶体结构结合力和结合能

School of materials Science and engineering
Prof. Y.X. Li
类
作用力来源
型
离子 原子得、失电子后形 键 成负、正离子,正负
离子间的库仑引力
共价 相邻原子价电子各处 键 于相反的自旋状态,
原子核间的库仑引力
金属 自由电子气与正离子 键 实之间的库仑引力
School of materials Science and engineering
Prof. Y.X. Li
2.2.2 晶体的结合力与结合能
(1)结合力的一般性质 两原子的相互作用势能u
(r)的曲线如图2.11所示。
f (r) = - du(r) dr
两原子间的平衡距离 r0用如下公式求得:
du(r ) =0
小的原子(OC、oNva、leFn等t )相结合所形成的键。
Semiconductors
氢键具有饱和性和方向性
Polymers
虽然按结合力的性质分成以上5种晶体类 型M。et但all对ic 大多数晶体来说,结合S力ec的on性da质ry 是 属于Me综ta合ls 性的。复Io合nic材料中更Ce为ra复mi杂cs 。an如d g层lasses 状硅酸盐矿物、石墨等。
K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr
铷37 锶38 钇39 锆40 铌41 钼42 锝43 钌44 铑45 钯46 银47 镉48 铟49 锡50 锑51 碲52 碘53 氙54 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe
分子 原子间瞬时电偶极矩 键 的感应作用
第2章 晶体结合

《固体物理学》 微电子与固体电子学院
15
2.1 晶体结合的普遍特征
结论:同一周期元素自左至右电负性逐渐增大,同一族元素 自上而下电负性逐渐减小,过渡族元素的电负性比较接近。
电负性定性判断晶体类型:
(1)当两个成键原子的电负性差值较大时,晶体结合往往采
取离子键; (2)同种原子之间的成键,主要是共价键或金属键; (3)电负性差值小的原子之间成键主要是共价键。
4
2.1 晶体结合的普遍特征
(3)排斥作用起源于:(a) 同性电荷之间的库仑力;(b) 由于Pauli不相容原理的限制所 引起的排斥作用。
O
U(r)
r0 rm
r
b 排斥势可表示为: u R ( r ) rn
b是晶格参量,n是玻恩指数, 都是实验确定的常数
O
f(r)
r
《固体物理学》 微电子与固体电子学院
12
2.1 晶体结合的普遍特征
3. 体弹性模量
(1)晶体受外力时体积的变化。即∆P与-∆V/V之比。
P U 2U K V V ( ) V V V V V 2
2U T=0时,K V0 2 V V0
弹性模量可由实验测定。
《固体物理学》 微电子与固体电子学院
N 2 2
《固体物理学》 微电子与固体电子学院
20
2.2 离子键与离子晶体
设 rij ij R ,R是最近邻间距:
N U U ( R) 2 2e 2 ' 1 1 ' b ( ) n ( n ) ij R ij 40 R
19
2.2 离子键与离子晶体
第 i 个离子与其它N-1个个离子间的互作用势:
晶体的结合能是

晶体的结合能是
晶体的结合能是描述晶体中原子之间的相互作用力的物理量,它是晶体稳定存在的重要因素。
晶体的结合能受到多种因素的影响,包括原子的电荷、电子云的相互作用、晶体中的空穴和缺陷等。
下面我们将从四个方面进行讨论。
一、晶体的化学组成
晶体的化学组成对结合能有很大的影响。
在同一元素周期表中,原子半径越小,原子的结合能就越大,这是由于原子核吸引外层电子的能力增强所致。
此外,不同元素之间的化学键也会影响结合能。
二、电荷的分布
晶体中原子之间的相互作用力与原子间的电荷分布有关。
原子中的电子云越紧密,结合能就越大。
而当原子之间的电荷相互吸引时,结合能也会增强。
三、晶体中的缺陷
晶体中的缺陷(如空穴和格点缺陷)也会影响结合能。
在晶体中有一个缺陷时,需要消耗一定的能量才能形成缺陷,并且会对原有晶体的结构发生影响。
四、晶体对外界环境的响应
晶体对外界环境的响应也会影响结合能。
例如,温度、压力和化学物质的影响都可以改变晶体的结构和特性,从而影响结合能的大小。
综上所述,晶体的结合能是一项复杂的物理指标,受到多种因素的影响。
我们需要深入了解原子之间的相互作用和晶体中的结构变化,才能更好地理解晶体结合能的本质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
晶体的结合能?物理量
2.1.3 结合能与晶体几个常量的关系
1.原胞体积
U ( r ) r |r r 0
0
r0
v0
a
v0
U ( v ) v
| v v 0
0
2.压缩系数和体积弹性模量(体积压缩模量)
压缩系数: 单位压强引起的体积的相对变化率。
k 1 V ( V P )T
第一节
晶体的结合类型
晶体中原子的有序排列是原子间相互作用的结果; 晶体结合力的形式是决定晶体结构、类型和物理化学性质的重 要因素; 原子间结合力的性质与规律是研究晶体结构与物性的基础。
晶体类型 离子晶体 原子晶体 金属晶体 分子晶体 粒子类型 正、负离子 原子 金属离子和自由电子 分子 结合力形式 离子键 共价键 金属键 范德瓦尔斯力 物理特性 熔点高 硬度大、绝缘、熔点高 硬度大、导电、熔点高 一般只存在于低温
因此,排斥力为短程作用力
可知n >m,排斥作用是短程的。
如何确定 rm 的大小
( df dr ) ( d u dr
2 2
)r
0
m
r rm , f ( rm )
最大有 效引力
2.1.2 晶体总的相互作用能
两个原子之间的互作用能 设晶体中第i个原子与第j个原子之间的
1
2 i
3
4
相互作用势能为u(rij ),
B ro
n2
]
Amro n
nm
A
m 2
n(n 1) ro
A ro
m 2
1
n2
]
[m(m 1)
m(n 1)
]
1 9 Nro ro
A
m 2
m[(m 1) (n 1)]
m(n m) 9 N ro
A
m 3
K
mn
3
A
m
9 N ro ro
子时要克服负电荷之间的排斥力,因此要吸收能量。
例如: O (g) + e - O- (g) O- (g) + e - O2- (g) A1 =-140.0 kJ . mol-1 A2 =844.2 kJ . mol-1
电子亲和能的大小变化的周期性规律如下图:
同一周期:从左到右,Z* 增大,r 减小,最外层电子数依次增 多,趋向于结合电子形成 8 电子结构,A 的负值增大。卤素的 A 呈现最大负值,ⅡA为正值,稀有气体的 A 为最大正值。 同一主族:从上到下,规律不很明显,大部分的 A 负值变小。
Si
1.90 2.44
P
2.19 1.81
S
2.58 2.41
Cl Ar
3.16 3.00 -
K
0.82 0.80
Ca
1.0 -
Pauling Mulliken
负 电 IA Li 1.0 Na 0.9 K 0.8 IIA Be 1.5 Mg 1.2 Ca 1.0 B 2.0 Al 1.5 Ga 1.5
◆晶体的基本结合力是长程的库仑引力和短程的电子云重叠 所产生的斥力(泡利不相容原理,量子效应)。 ◆长程的库仑引力对晶体形成起到主要作用
§2.1晶体结合能的普遍规律
晶体的结合能:
晶体的结合能就是将自由的原子(离子或分子)结合成晶 体时所释放的能量。
Eb E N E0
E0是晶体的总能量,EN是组成该晶体的N个原子在自由状 态时的总能量,Eb即为晶体的结合能。
0.4 电负性
为了统一地衡量不同原子得失电子的难易程度,引入了电
负性的概念,一般选定某原子的电负性为参考值,把其他原子
的电负性与此参考值相比较。 马利肯定义
Li的电负性=1
原子的电负性=0.18(电离能+亲和能) 单位:电子伏特 泡利定义 E(A-B)=[E(A-A)*E(B-B)]1/2+96.5(xA+xB) 单位:kJ/mol
(
nm n
)
mn | U c | 9 N ro
3
3. 抗张强度
晶体的抗张强度等于晶体所能承受的最大张力。
fm (
( f v )v
u v
2
)v
m
r rm , f ( rm )
0 vm
最大有 效引力
m
(
u v
2
)v
m
在三维晶体中,假设晶体的体积为V,包含N个原胞,每个 原胞的体积为v,每个原胞的势能为u (r),U为N个原胞的总的
2
)V
0
T = 0 K时,原子间的平衡间距为 ro。每个原胞的体积为
β ro3。晶体的平衡体积 Vo = Nβ ro3
( r V ) | ro
2
1 ( V r )
2
| ro
1 (3Nro )
2 2
1 9 N ro
2 2 4
1 Vo 9 Nro
K V(
U
2
V
) V( 2
碱金属卤素,Z*增大,r 减小,电离能 增大。
其中碱金属的 I1 最小,稀有气体的 I1 最大
同一主族:
从上到下,最外层电子数相同;Z*增加不多,r 增大为主
要因素,核对外层电子引力依次减弱,电子易失去,I 依
次变小
0.3 电子亲和能
元素的气态原子在基态时获得一个电子成为一价气态负
离子所放出的能量称为电子亲和能。当负一价离子再获得电
的电离能,关系表示为
中性原子——(吸收能量)正离子+(-e)
电离能大小:衡量原子对价电子的束缚强弱,取决
于原子结构(核电荷、原子半径以及电子壳层结构)
从原子中移去第一个电子所需要的能量为第一电离能,从
正1价离子中再移去一个电子所需要的能量为第二电离能。
电离能随原子序数的增加呈现周期性变化
同一周期:
性 VB N 3.0 P 2.1 As 2.0
IIIB
IVB
C 2.5 Si 1.8 Ge 1.8
VIB
O 3.5 S 2.5 Se 2.4
VIIB
F 4.0 Cl 3.0 Br 2.8
✪ 周期表从上到下,元素的电负性逐渐减小;
✪ 一个周期内重元素的电负性差别较小。
通常把元素易于失去电子的倾向称为元素的金属性, 把元素易于获得电子的倾向称为元素的非金属性。因此 电负性小的是金属元素,电负性大的是非金属元素。
2.1.1 两个原子间的相互作用能
1.原子间的相互作用力
吸引力 原子间的相互作用力 排斥力 泡利原理引起 2.原子间的相互作用势能 库仑引力 库仑斥力
u (r )
A r
m
B r
n
2.相互作用势能
u (r ) A r
m
B r
n
r
A r
m
两原子间的距离; 吸引能
A、B、m、n>0,
体积弹性模量是压缩系数的倒数:
K V ( P V )
由热力学第一定律:
dU pdV TdS pd V
K V ( P V ) V
K
V (
P V
)
p
V
dU dV
d U dV 2
2
平衡时体积弹性模量:
K V0 ( 2U V
j
rij
由N个原子组成的晶体总的互作用势能可以视为是原子对间 的互作用势能之和。则晶体内能
则由N个原子组成的晶体的总的相互作用势能为:
ui
u 1
' u ( r ij
j1
N
)
u (r ) 2
ij i j
i≠j,表示不同的原子间的相互作用,系数1/2的出现是为了消除一种相 互作用两个表示形式的问题。
U
2
r
2
)(
r V
)
2
则平衡时晶体的体积弹性模量:
U
2
K V(
r
2
)(
r V
) |ro
2
1 9 N ro
(
U
2
r
2
) |ro
K
1 9 N ro
1 9 Nro
1 9 Nro
[m(m 1) ro
[m(m 1) ro
A ro
m 2
A
m2
n(n 1)
第 一 节 1 两个原子间的相互作用能
2.1.2 晶体总的相互作用能 2.1.3 结合能与晶体几个常数的关系
§0
原子的电负性
0.1 原子的电子分布
原子的电子组态,通常用字母s、p、d来表征角量
子数l=0、1、2、3……,字母的左边的数字是轨道主量 子数,右上标表示该轨道的电子数目。 原子处于基态时,核外电子排布规律必须遵循以下3条 规则:
✪ 包利不相容原理
一个原子轨道最多只能容纳两个电子,且这两个电子的自
旋方向必须相反。
✪ 能量最低原理
在不违背包利不相容原理 的条件下,电子优先占据能量较 低的原子轨道。
✪ 洪特规则
在能量高低相等的轨道上,电子尽可能占据不同的轨道, 且电子自旋平行。
0.2 电离能
使基态原子失去一个价电子所需要的能量称为原子
假定一:晶体中两个最近邻原子间作用为主要部分
