【采矿课件】第4章颗粒在流体中的运动
颗粒在流体中的运动

mdu dt
F
合力为零时,颗粒与流体之间将保持
一个稳定的相对速度。
Fb Fd
FdFg-Fb
Fg
CD2 ut24 d2 p1 6d3 p pg
ut
4 dp p g 3 CD
——重力场中的沉降速度
ut 由颗粒与流体综合特性决定,包括待定的曳力系数CD
10
自由沉降与沉降速度(Free settling and settling velocity)
义的形状系数A。
13
流体通过固定床的流动
固定床(Fixed bed):固定不动的固体颗粒层 例:固定床催化反应器、吸附分离器、离子交换器等。流体 在固定床中的流动状态直接影响到传热、传质与化学反应。
颗粒床层的几何特性
粒度分布 测量颗粒粒度有筛分法、光学法、电学法、流 体力学法等。工业上常见固定床中的混合颗粒,粒度一般大 于70mm,通常采用筛分的方法来分析颗粒群的粒度分布。
主要几何特征。
等体积当量直径 deV
d eV
3
6V
等表面积当量直径 deA
A d eA
等比表面积当量直径 dea
ap Ap 6 Vp dp
d ea
6 a
6 AV
颗粒形状系数
A
ap a
非球形颗粒4个几何参数之间的关系
A
deV deA
2
dea deV
工程上多采用可以测量的等体积当量直径 deV 和具有直观意
——斯托克斯(Stockes)定律
颗粒雷诺数
Rep
d pu
严格说只有在 Rep < 0.1 的爬流条件下才符合上式的求解条件
7
曳力与曳力系数(Drag and drag coefficient)
采矿课件第4章颗粒在流体中的运动

【采矿课件】第4章-颗粒在流体中的运动第4章颗粒在流体中的运动习题1.什么是体积分数、质量分数?两者的关系如何?已知石英与水的密度分别为2650kg/m3和1000kg/m3,将相同质量的石英砂和水配置成悬浮液,求悬浮液的质量分数、体积分数、物理密度和黏度?2.牛顿流体和非牛顿流体的有效黏度和微分黏度有何特点?什么叫屈服切应力?哪些非牛顿流体的流变特性可用幂律模型描述?幂律模型中的参数K和n有何物理意义?3.什么是自由沉降?什么是干涉沉降?4.已知石英与水的密度分别为2650kg/m3和1000kg/m3,水的运动黏度为1.007x10-6 m2/s,求直径为0.2mm的球形石英颗粒在水中的自由沉降速度、雷诺数和阻力系数?5 已知煤与水的密度分别为1350kg/m3和1000kg/m3,水的运动黏度为1.007x10-6 m2/s,测得某个球形煤粒在水中的自由沉降速度为0.02415m/s,求煤粒的直径?6.已知球形石英颗粒的直径为0.2mm,密度为2650kg/m3,某液体的密度为980kg/m3,用落球法测量该液体的粘度时,测得球形石英颗粒的自由沉降速度为0.01 m/s,请运用(4-23)和(4-31)式推导出求粘度的计算公式,并计算该液体的动力粘度和运动粘度。
7.干涉沉降实验测得悬浮体的体积分数为0.4时,上升水流速度为0.0065 m/s,体积分数为0.2时,上升水流速度为0.0205 m/s,求干涉沉降速度公式中V0与n的值。
8.假定某种物料的n值服从(4-52)式,当雷诺数为10时,干涉沉降的n值为3.46;当雷诺数为100时,干涉沉降的n值为2.89;当雷诺数为50时,干涉沉降的n值为多少?(取k=4.53) 9.已知石英与水的密度分别为2650kg/m3和1000kg/m3,水的运动黏度为1.007x10-6 m2/s,用直径为0.0005m的球形石英粒群与水配制成容积浓度为0.4的悬浮液,请估算球形石英粒群的干涉沉降速度(取k=4.53,ψt=0.11,n S=4.65)。
第四章 颗粒与流体之间的相对流动

叶 滤 机
转 鼓 真 空 过 滤 机
流 线 式 过 滤 机 层 滤 器
4-4 非均匀相混合物的分离
过滤基本方程
❖过滤速度
u
dV
Ad
3pc
K 'a2 1 2 L
——由康采尼公式得
对于颗粒床层内的滞流流动K’=5
❖滤饼阻力
设
r
5a2
3
1
2
,则上式变为:
dV pc pc
Ad rL R
r 为滤饼的比阻; R= rL为滤饼阻力。
气力输送
❖气力输送原理
气源
风机
料仓
颗粒进料与加速段
弯管加速区
气-固分离
进料段 颗粒加速段
膨胀段
密相
稀相
Conic bottomed
Flat bottomed
Horiz高on磨t损 al区drying
稳定输送阶段气ch源ambers
气固分离器
4-3 固体流态与气力输送
气力输送
输 送 气 流 速 度 与 流 动 状 态 的 关 系
第四章 颗粒与流体之间的相对运动
本章学习目的与要求
掌握颗粒与流体相对运动的基本理论, 为食品流化加工、沉降分离加工等工艺 设计、设备选型提供原理知识。
要求学生掌握流体绕过颗粒以及颗粒在 流体中沉浮的速度和阻力计算方法。
分析并处理流化加工、气力输送、沉降 和过虑中的工程实际问题。
4-1 流体绕过颗粒及颗粒床层的流动
颗粒床层特性
单颗粒特性 ❖ 球形和非球形 ( dev, des, dea, φs)
✓ 非球形颗粒四个几何参数之间的关系?
床层特性 ❖ 空隙率ε ❖ 各向同性 ❖ 比表面积
【采矿课件】第4章颗粒在流体中的运动

第4章颗粒在流体中的运动习题解答1.什么是体积分数、质量分数?两者的关系如何?石英与水的密度别离为2650kg/m3和1000kg/m3,将不异质量的石英砂和水配置成悬浮液,求悬浮液的质量分数、体积分数、物理密度和黏度?【解】悬浮体的体积分数ΦB〔旧称容积浓度λ〕是指悬浮体中固体颗粒〔或气泡、液滴〕的体积占有率,它是无量纲数,数值上等于单元体积的悬浮体中固体颗粒〔或气泡、液滴〕占有的体积。
悬浮体的质量分数w B〔旧称重量浓度C〕是指悬浮体中固体颗粒的质量占有率,它也是无量纲数。
假设颗粒和流体的密度别离用δ和ρ暗示,体积分数ΦB与质量分数w B有下面的关系:δ=2650kg/m3和ρ=1000kg/m3,设石英砂和水的质量都是W,那么有故质量分数、体积分数、物理密度和黏度别离为0.5000、0.2740、1452kg/m3和2.2902μ。
2.牛顿流体和非牛顿流体的有效黏度和微分黏度有何特点?什么叫屈服切应力?哪些非牛顿流体的流变特性可用幂律模型描述?幂律模型中的参数K和n有何物理意义?【解】有效粘度是流变曲线上指定点到原点的直线斜率;微分粘度是流变曲线上指定点的切线斜率。
牛顿流体的有效黏度等于微分黏度,而且都是常数;宾汉流体,微分粘度为常数,但有效黏度不为常数,而且有效黏度大于微分黏度,当剪切速率趣近于零时有效黏度变为无穷大;假塑性流体的有效黏度大于微分黏度;胀塑性流体的有效黏度小于微分黏度;屈服假塑性流体与宾汉流体有些类似,只是微分黏度不是常数。
宾汉认为,当悬浮液的浓度大到此中的颗粒互相接触之后,就有塑性现象发生,欲使系统开始流动,施加的剪切力必需足以破坏使颗粒形成的网架布局,这个刚好能够破坏颗粒网架布局的切应力就是屈服切应力。
假塑性流体〔包罗胀塑性流体〕的流变特性可用如下幂律模型描述:幂律模型中的参数K也是流体黏性的量度,它不同于黏度,流体越黏,K值越大;指数n是液体非牛顿性的量度,n值与1相差越大,那么非牛顿性越显著;对于假塑性流体的n<1〔对于胀塑性流体n>1〕。
第四章 颗粒与流体之间的相对流动

4.2 基本概念【4-1】阻力系数(曳力系数)是如何定义的?它与哪些因素有关?【4-2】斯托克斯定律区的沉降速度与各物理量的关系如何?应用的前提是什么?颗粒的加速段在什么条件下可忽略不计?【4-3】直径为50μm、密度为2650kg/m3的球形颗粒,在20℃的空气中从静止状态开始作自由沉降,需要多少时间才能完全达到其(终端)沉降速度?需要多少时间便能达到其沉降速度的99%?【4-4】重力降尘室的气体处理量与哪些因素有关?降尘室的高度是否影响气体处理量?【4-5】悬浮液重力沉降分离设备按操作方式,可分为哪几类?有什么异同点?【4-6】强化悬浮液重力沉降的方法?【4-7】评价旋风分离器性能的主要指标有哪两个?【4-8】颗粒在旋风分离器内沿径向沉降的过程中,其沉降速度是否为常数?【4-9】提高流化质量的常用措施有哪些?【4-10】气力输送的主要优点有哪些?【4-11】过滤速率与哪些因素有关?【4-12】过滤常数有哪两个?各与哪些因素有关?什么条件下才为常数?【4-13】以间歇过滤机处理某种悬浮液,若滤布阻力可以忽略,洗水体积与滤液体积之比值为a,试分析洗涤时间与过滤时间的关系。
【4-14】当滤布阻力可以忽略,滤饼不可压缩,试用图定性地表示恒速、恒压、先恒速后恒压三种过滤操作的q-τ、Δp-τ关系,并就先恒速后恒压过滤的q-τ图形讨论当全部非过滤时间(τD+τW)一定时的最佳过滤操作循环周期。
【4-15】当滤布阻力可以忽略时,若要恒压操作的间歇过滤机取得其最大生产能力,在下列两种条件下,分别应如何确定过滤时间τ?1. 已规定每一循环中的辅助操作时间为τD,洗涤时间为τW。
2. 若已规定每一循环中的辅助操作时间为τD,洗水体积与滤液体积之比值为a。
【4-16】转筒真空过滤机的生产能力计算时,过滤面积为什么用A而不用Aφ?该机的滤饼厚度是否与生产能力成正比?【4-17】若分别采用下列各项措施,试分析转筒过滤机的生产能力将如何变化并分析各措施的可行性。
采矿颗粒在流体中的运动

采矿颗粒在流体中的运动引言在矿业领域中,采矿颗粒在流体中的运动是一个重要的研究课题。
这对于矿石的选矿、矿石破碎和研磨、浓缩等都有重要的指导意义。
本文将介绍采矿颗粒在流体中的运动规律、影响因素以及相关的数学模型。
采矿颗粒在流体中的运动规律采矿颗粒在流体中的运动可以在实验室中进行研究,也可以通过数值模拟来模拟。
根据流体力学的基本原理,采矿颗粒在流体中的运动规律可以通过牛顿的第二定律来描述。
根据这个定律,一个物体在流体中受到的合力等于质量乘以加速度,即:$F = m \\cdot a$采矿颗粒在流体中的运动受到以下几个力的作用:1.重力:采矿颗粒受到来自地球引力的作用,即重力。
重力的大小与采矿颗粒的质量成正比,方向向下。
重力可以通过以下公式计算:$F_{gravity} = m \\cdot g$其中,m为采矿颗粒的质量,g为重力加速度。
2.浮力:当采矿颗粒被完全或部分浸入流体中时,会受到浮力的作用。
浮力的大小等于采矿颗粒排开的流体体积乘以流体的密度和重力加速度,方向相反。
浮力可以通过以下公式计算:$F_{buoyancy} = V \\cdot \\rho \\cdot g$其中,V为采矿颗粒排开的流体体积,$\\rho$为流体的密度,g为重力加速度。
3.阻力:采矿颗粒在移动过程中会受到流体的阻力,阻碍其运动。
阻力的大小与采矿颗粒的速度成正比,与流体的粘度和采矿颗粒的表面积成正比,与流体的密度成正比。
阻力可以通过以下公式计算:$F_{drag} = \\frac{1}{2} \\cdot C_d \\cdot A \\cdot \\rho_{fluid} \\cdot v^2$ 其中,C d为阻力系数,A为采矿颗粒的横截面积,$\\rho_{fluid}$为流体的密度,v为采矿颗粒的速度。
根据这些力的作用,采矿颗粒在流体中的运动可以用牛顿的第二定律描述为:$F_{total} = F_{gravity} - F_{buoyancy} - F_{drag} = m \\cdot a$影响因素1.采矿颗粒的质量:质量越大,重力对采矿颗粒的作用越大,影响其运动速度和轨迹。
颗粒在流体中的运动

自由沉降与沉降速度(Free settling and settling velocity) 颗粒-流体体系一定,ut一定,与之对应的Rep 也一定。
根据对应的 Rep,可得到不同Rep范围内 ut 的计算式:
(1) Rep<2,层流区(斯托克斯公式)
ut
2 dp p g
18
0.6 d p p g Re p
自由沉降与沉降速度(Free settling and settling velocity)
ut 是颗粒在流体中受到的曳力、浮力与重力平衡时颗粒与流 体间的相对速度,取决于流固二相的性质,与流体的流动与 否无关。 颗粒在流体中的绝对速度 up 则与流体流动状态直接相关。
当流体以流速 u 向上流动时,三个速度的关系为:
(2) 2<Rep<500,过渡区(阿仑公式) u t 0.27
dp p g
(3) 500<Rep
<2×105,湍流区(牛顿公式)
u t 1.74
因Rep中包含 ut,故需通过试差确定计算公式。 灵活运用上述原理还可以根据颗粒在流体中沉降速度的实验 数据关联出颗粒的粒度 dp 或密度 p。
式中p0为来流压力。
流体对单位面积球体表面的曳力(表面摩擦应力)为
s r
r R
3 u sin 2 R
曳力与曳力系数(Drag and drag coefficient)
r 在 z 轴的分量为
r cos / 2 r sin
z
所以整个球体表面摩擦曳力 在流动方向上的分量 F 为
pb (1 ) 2 150 3 2 u L d ea
颗粒在流体中的运动

自由沉降与沉降速度(Free settling and settling velocity)
ut 是颗粒在流体中受到的曳力、浮力与重力平衡时颗粒与流 体间的相对速度,取决于流固二相的性质,与流体的流动与 否无关。 颗粒在流体中的绝对速度 up 则与流体流动状态直接相关。
当流体以流速 u 向上流动时,三个速度的关系为:
流体通过固定床的压降
工程上为了直观对比的方便而将流体通过颗粒床层的阻力损 失表达为单位床层高度上的压降
2 pb L e 1 u1 L e 1 a u 2 (1 )a u 2 3 L L d eb 2 3 8L
xi p a 1 ai 6 xi d pi
比表面相等
6 d pm a
p
1 xi d pi
对于非球形颗粒, 按同样的原则可得
d pm
1 xi d ea i
1 xi d Ai eVi
m du F dt
Fd Fg Fb
合力为零时,颗粒与流体之间将保持 一个稳定的相对速度。
Fd F g - Fb
CD
u t2 d 2 p
2
1 d3 p g p 4 6
4 dp p g ut 3 C D
——重力场中的沉降速度
ut 由颗粒与流体综合特性决定,包括待定的曳力系数CD
自由沉降与沉降速度(Free settling and settling velocity) 颗粒-流体体系一定,ut一定,与之对应的Rep 也一定。
根据对应的 Rep,可得到不同Rep范围内 ut 的计算式:
第4章流体通过颗粒层的流动
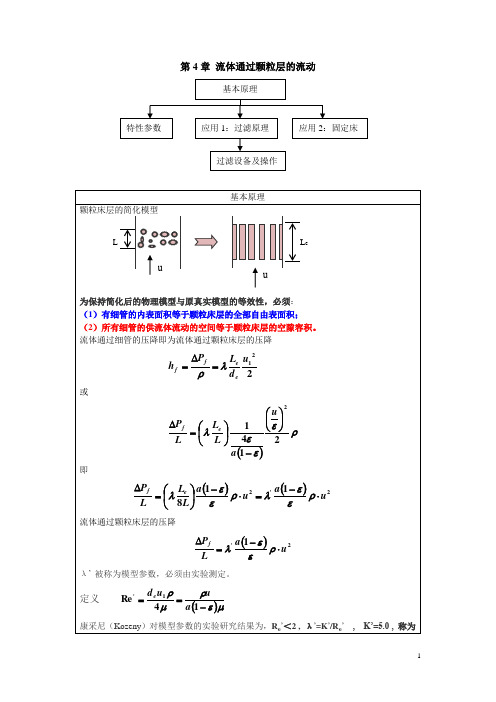
康采尼(Kozeny)对模型参数的实验研究结果为,Re’<2 ,λ’=K’/Re’, K’=5.0 ,称为Kozeny常数。
将模型参数的表达式代入到床层压降的表达式中
欧根(Ergun)在较宽的 范围内, ,获得了关系式
代入到床层压降的表达式中
特性参数
1、颗粒的比表面积
2、颗粒床层的空隙率
3、颗粒床层的比表面积 ,
第4章流体通过颗粒层的流动
基本原理
颗粒床层的简化模型
为保持简化后的物理模型与原真实模型的等效性,必须:
(1)有细管的内表面积等于颗粒床层的全部自由表面积;
(1)
(2)所有细管的供流体流动的空间等于颗粒床层的空隙容积。
流体通过细管的压降即为流体通过颗粒床层的压降
或
即
流体通过颗粒床层的压降
λ’被称为模型参数,必须由实验测定。
单位过滤面积上的滤液体积量
滤饼厚度 、悬浮液中颗粒体积分率 、滤饼空隙率 与单位过滤面积上的滤液体积量 的关系式为
单位过滤面积上过滤速率的表达式则为
定义: , 称为滤饼的比阻。则过滤速率表达式为
或者
考虑过滤介质的阻力后,过滤速率为
令
则
或
定义过滤常数:
自开始即进行恒压过滤,则K为常数,并且 时, ,过滤时间 与累计滤液体积量 (单位面积上累计滤液体积量 )的关系
或
过滤设备及操作
1、板框式压滤机
在保持洗涤水粘度与滤液粘度相同,洗涤操作时的压差与过滤操作时的压差相同时,总面积上的洗涤速率与过滤终了时过滤的速率之间的关系
横穿流洗法, ;置换洗法,
洗涤时间 与过滤时间 的关系
一个生产周期的时间 ,
最佳时间分配:
颗粒在流体中的运动

4.5 颗粒在介质中的干涉沉降
里亚申科公式 • 当上升水流速度Ua很小时,床层保持紧 密,只有当水流速度Ua达到一定值后,粒 群才开始悬浮。 • 当上升水流速度Ua一定时,对于一定量 的粒群悬浮高度H是一定的,增加物料量, 高度H也增加,并存在一定关系。 • 随着上升水流速度Ua增加和减小,H也 发生变化,λ、θ也随之改变。Ua增大, λ 减小,反之亦然,说明干涉沉降速度不是 一个定值,而是λ的函数。 Vb=V0(1- λ)n
阻力公式
斯托克斯阻力公式
FD = 3πµdv
π π FD = ~ d 2 v 2 ρ 20 16
5π 4 Re
当球形颗粒在介质中作 层流运动时,雷诺数小 于1。 当球形颗粒在紊流状态 下时,雷诺数在Re= 103~105时,介质阻力为 压差阻力
牛顿-雷廷格阻力公式
阿连公式
FD =
当介质绕过物体流支 时,在物体背面形成 漩涡,使该处液体内 部压力下降,造成物 体所承受的法向压力 前后不同,而对物体 运动产生阻力。
4.2 颗粒运动时受的阻力
摩擦阻力 又称粘滞阻力,这是 由于运动这的物体牵 动周围的流体也在一 起运动,使得流体自 物体表面向外产生一 定的速度梯度,于是 各流层之间引起了内 摩擦力。所谓摩擦阻 力既是作用在物体表 面所用的切向作用力 在物体引动方向的合 力。
d 2v 2 ρ
当介质Re=25~103
介质阻力公式的通式
FD = ϕd 2 v 2ρ
ψ为阻力系数,与雷诺数 有关的无因此参数。
4.4 颗粒在介质中的自由沉降
颗粒在静止介质中的自由沉降
球形颗粒在介质中沉降时,主要受重力、介质 的浮力和介质的阻力作用,因而其运动方程为: 式中G 0 为颗粒在介质中的有效重力,即重力 与介质浮力之差;m为颗粒质量,dv/dt为颗粒 运动加速度。 在颗粒沉降开始时,G0>FD,颗粒加速沉降 ,随着沉降速度加快,介质阻力F D 不断增大 ,当颗粒沉降达到某一速度时重力G 0 与阻力 F D 达到相等,这时颗粒达到均速沉降,此时 的沉降速度称为沉降末速 沉降末速,以v0表示。由平衡 沉降末速 条件,G0=FD
第四章流体通过颗粒层(含小结).ppt

板框压滤机
XKZ系列全自动快开式压滤机
DY-Q 带式压榨过滤机
45/88
过程:安装 过滤洗涤 拆洗 安装过程:细活(次序、压皱) 助滤剂与絮凝剂的使用 滤液回流(开始) 操作压力:结束信号 流量变化
过滤速度=过滤推动力 过滤阻力
过滤设备可以连续操作吗?
置换洗涤
30/88
过滤的操作方式
过滤:过滤操作中的主要阶段,在过程中滤饼不断增厚、阻 力不断上升,流体的通过能力则不断减小;
洗涤:无论是以滤饼还是滤液为产品,都有必要在卸料之前 用清液置换滤饼中存留的滤液并且洗涤滤饼;
脱湿:以滤饼为产品时洗涤后还可用压缩空气进行脱湿; 卸料:将滤饼从过滤介质上移去; 清洗过滤介质:使被堵塞的网孔“再生”,以便重复使用。
▪ 乱堆的非球形颗粒床层空隙率>球形颗粒,而非均匀空隙率ε <均匀空隙率。
16/88
床层的自由截面积:----------床层横截面上未被颗粒所占据的面积
对于各向同性的床层: 自由截面积 / 床层截面积=空隙率
床层的比表面积: ——单位体积床层具有的颗粒的表面积
忽略由于颗粒之间的相互重叠或接触那部分表面积,则:
1288频率函数曲线设某号筛面上的颗粒占全部试样质量百分率为x些颗粒直径介于相邻两号筛孔直径di1用一矩形面积表示矩形的高度为表示粒径处于di1频率函数的特性1在一定粒度范围内的颗粒占全部颗粒的质量分率等于该粒度范围内频率函数曲线下的面积
第4章 流体通过颗粒层的流动
§1概 述 § 2 颗粒床层的特性 § 3 流体通过固定床的压降 § 4 过滤原理及设备 § 5 过滤过程计算 § 6 加快过滤速率的途径
23/88
数学模型法
对于数学模型法,关键是对复杂过程的合理简化,即 得到简单的数学方程式而又不失真的物理模型,即物 理模型与真实过程是等效的。只有了解过程的内在规 律,深刻理解过程的特殊性,才能对真实的复杂的过 程进行简化。
第4章颗粒与流体优秀课件

解:查得30 ℃、常压下的空气的粘度 和密度分别为: μ,=1.86×10-5 Pa·s,密度ρ,=1.17 kg/m3 实验条件下的雷诺数
RP edP u m ''f' 0.4 5 1 1.8 3 0 6 0 1 .0 5 04 1.1 9 71.3 920
由
umf
dP2(P )g 1650
1.3 流体通过颗粒床层的流动 流体通过固定床的压降由下式给出: 球形颗粒:
L P15(13 0dP)22u1.7(5 13 dP)u2
非球形颗粒用φSdP代替dP即可。 式中u为流体的空床流速,m/s。
当ReP<20时,等式>1000时,右方第一项可略 去,即此时惯性力起主导 作用。
ut
dP2(P )g 18
当RePt>0.4,则应对ut校正,校正 系数ft可由图4-17查出。 ②球形颗粒,且0.4<RePt <500时
1
ut
4(2P25)2g2
3 dP
③对于非球形颗粒的ut,,乘以一 个系数c:
ut,=cut c=0.834×lg(φs/0.065) 注意:在计算umf 时,颗粒直径取 床层中实际颗粒粒度分布的平均 直径,而计算ut时须用具有相当数 量的最小颗粒的粒度。 操作弹性: ut/umf 比值的大小。 对于细颗粒,RePt<0.4,有 ut/umf =91.6
3.1.3 流化床中的传热 传热的特点 : 流化床内部温度分布均匀一致。 (1)床层与床壁或物体表面间的传热 对流传热式为:
Q=αS(Tb-Tw) 式中:Tb为床层内平均温度,K; Tw为器壁表面温度,K。 α为床层与床壁间的对流传热系数, W/m2.K。
α有如下几个计算式: a) 列d文P 斯0.波6(C -沃P尔)顿(dP 关u联)0.3式
颗粒-流体两相运动

第四章颗粒—流体两相流动流体与颗粒的相对运动曳力与曳力系数(Drag and drag coefficient)流体与固体颗粒之间有相对运动时,将发生动量传递。
颗粒表面对流体有阻力,流体则对颗粒表面有曳力。
阻力与曳力是一对作用力与反作用力。
由于颗粒表面几何形状和流体绕颗粒流动的流场这两个方面的复杂性,流体与颗粒表面之间的动量传递规律远比在固体壁面上要复杂得多。
爬流(Creeping flow):来流速度很小,流动很缓慢,颗粒迎流面与背流面的流线对称。
在球坐标系中用连续性方程和N-S 方程可得到颗粒周围流体中剪应力τr θ和静压强p 的分布为式中p 0为来流压力。
流体对单位面积球体表面的曳力(表面摩擦应力)为θμτθsin 234⎪⎭⎫ ⎝⎛=r R R u r θμρcos 2320⎪⎭⎫⎝⎛--=r R R u gz p p 3sin 2s r r Ru Rθμττθ==-=-τr θ在z 轴的分量为()222200d sin sin d 3d sin sin sin d 42r r RF Ru R RuR ππτθππφθτθθμφθθθθπμ==--⎛⎫=⋅= ⎪⎝⎭⎛⎛⎜⎜⎠⎠⎰⎰——表面曳力(Wall drag)所以整个球体表面摩擦曳力在流动方向上的分量F τ为()θτπθτθθsin 2/cos r r =+zθd φd θθθ()2222003d cos sin d 3d cos cos sin cos d 2423nr RF pRu p gR R R R g Ru ππππφθθθμφρθθθθθπρπμ==-⋅⎛⎫=--- ⎪⎝⎭=+⎛⎛⎜⎜⎠⎠⎰⎰0流体静压强对整个球体表面的作用力在流动方向上的分量为浮力F b与流体运动无关流体对颗粒的形体曳力F p正比于流速u——形体曳力(Form drag)流体流动对颗粒表面的总曳力为摩擦曳力与形体曳力之和426d p Ru Ru RuF F F τπμπμπμ=+=+=——斯托克斯(Stockes )定律严格说只有在Re p <0.1的爬流条件下才符合上式的求解条件μρu d Re p p =颗粒雷诺数颗粒表面的总曳力Fd(1)Rep <2,层流区(斯托克斯定律区)22uACFpDdρ=24DpCRe=6.05.18pDReC=0.44DC≈(2)2<Rep<500,过渡区(阿仑定律区)(3)500<Rep<2×105,湍流区(牛顿定律区)(4)Rep>2×105,湍流边界层区边界层内的流动也转变为湍流,流体动能增大使边界层分离点向后移动,尾流收缩、形体曳力骤然下降,实验结果显示此时曳力系数下降且呈现不规则的现象,CD≈0.1。
第四章颗粒与流体之间的相对运动

p
g
与气速无关而始终保持定值,恒定压降是流化床重要优 点,通过测量床层压降以判断床层流化的优劣。
节涌:Δ P有大幅度的起伏波动。
沟流:存在局部死床,比计算值低
临界流化速度
Rep 20
床层由均匀颗粒组成
umf ut
非均匀颗粒组成
umf
de2 ( p )g 1650
流化床最大流化速度,实质上就是颗粒的沉降速度,这是
因为若流体速度大于u
气流带走。
f
ut
粒子就会以很小的速度 u p随
球形颗粒 Rep 0.4 滞流区,斯托克斯公式
Rep 0.4 对ut校正,校正系数查图得
非球形颗粒 乘以C
C 0.834 lg s
0.065
流化操作速度在 umf 与ut 之间,工业上常用操作速度0.2- 1.0m/s.
d pu
dp——颗粒直径(对非球形颗粒而言,则取等体积球 形颗粒的当量直径)
球形颗粒(φ S = 1)在不同雷诺数范围内
滞流区 Re p 1
24
Re p
过渡区 湍流区
1 Re p 500
18.5 Re p0.6
500 Re p 2105 0.44
边界层内为湍流区 Re p 2105 0.1
d
3 p
p
/6
(2)浮力
在数值上等于同体积流体在力场中所受到的场力。流体的密度为ρ
重力场 Fb mg / p
离心力 Fb mrw2 / p m(uT2 / r) p
(3)曳力FD(即固体颗粒在流体中相对运动时所产生的阻力)
FD
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【采矿课件】第4章颗粒在流体中的运动习题解答1.什么是体积分数、质量分数?两者的关系如何?已知石英与水的密度分别为2650kg/m3和1000kg/m3,将相同质量的石英砂和水配置成悬浮液,求悬浮液的质量分数、体积分数、物理密度和黏度?【解】悬浮体的体积分数ΦB(旧称容积浓度λ)是指悬浮体中固体颗粒(或气泡、液滴)的体积占有率,它是无量纲数,数值上等于单位体积的悬浮体中固体颗粒(或气泡、液滴)占有的体积。
悬浮体的质量分数w B(旧称重量浓度C)是指悬浮体中固体颗粒的质量占有率,它也是无量纲数。
若颗粒和流体的密度分别用δ和ρ表示,体积分数ΦB与质量分数w B有下面的关系:已知δ=2650kg/m3和ρ=1000kg/m3,设石英砂和水的质量差不多上W,则有故质量分数、体积分数、物理密度和黏度分别为0.5000、0.2740、1452kg/m3和2.2902μ。
2.牛顿流体和非牛顿流体的有效黏度和微分黏度有何特点?什么叫屈服切应力?哪些非牛顿流体的流变特性可用幂律模型描述?幂律模型中的参数K和n有何物理意义?【解】有效粘度是流变曲线上指定点到原点的直线斜率;微分粘度是流变曲线上指定点的切线斜率。
牛顿流体的有效黏度等于微分黏度,同时差不多上常数;宾汉流体,微分粘度为常数,但有效黏度不为常数,同时有效黏度大于微分黏度,当剪切速率趣近于零时有效黏度变为无穷大;假塑性流体的有效黏度大于微分黏度;胀塑性流体的有效黏度小于微分黏度;屈服假塑性流体与宾汉流体有些类似,只是微分黏度不是常数。
宾汉认为,当悬浮液的浓度大到其中的颗粒互相接触之后,就有塑性现象发生,欲使系统开始流淌,施加的剪切力必须足以破坏使颗粒形成的网架结构,那个刚好能够破坏颗粒网架结构的切应力确实是屈服切应力。
假塑性流体(包括胀塑性流体)的流变特性可用如下幂律模型描述:幂律模型中的参数K也是流体黏性的量度,它不同于黏度,流体越黏,K值越大;指数n是液体非牛顿性的量度,n值与1相差越大,则非牛顿性越显著;关于假塑性流体的n<1(关于胀塑性流体n>1)。
3.什么是自由沉降?什么是干涉沉降?【解】颗粒在流体中沉降时,若不受周围颗粒或容器壁干扰,称为自由沉降。
颗粒在有限空间中的沉降称之为干涉沉降。
矿物加工中粒群在矿浆中的沉降确实是典型的干涉沉降,球体在窄管中的沉降也是干涉沉降。
4.已知石英与水的密度分别为2650kg/m3和1000kg/m3,水的运动黏度为1.007x10-6 m2/s,求直径为0.2mm的球形石英颗粒在水中的自由沉降速度、雷诺数和阻力系数?【解】已知δ=2650kg/m3、ρ=1000kg/m3、ν=1.007x10-6 m2/s和d=0.0002m,则先试用通用公式运算:雷诺数小于5000,符合通用公式的要求,可进一步运算阻力系数:答:直径为0.2mm的球形石英颗粒在水中的自由沉降速度、雷诺数和阻力系数分别为0.02415m/s、4.796和2.904。
5.已知煤与水的密度分别为1350kg/m3和1000kg/m3,水的运动黏度为1.007x10-6 m2/s,测得某个球形煤粒在水中的自由沉降速度为0.02415m/s,求煤粒的直径?【解】已知δ=1350kg/m3、ρ=1000kg/m3、ν=1.007x10-6 m2/s和V0=0.02415m/s,则运算雷诺数:雷诺数小于5000,处于通用公式适用范畴,求出的结果可用。
答:煤粒的直径为0.4805mm。
(比较4、5题可知,沉降速度相等的煤与石英颗粒的直径比为0.4805/0.2=2.4025倍, 那个比值确实是自由沉降的等降比)6.已知球形石英颗粒的直径为0.2mm,密度为2650kg/m3,某液体的密度为980kg/m3,用落球法测量该液体的粘度时,测得球形石英颗粒的自由沉降速度为0.01 m/s,请运用(4-23)和(4-31)式推导出求粘度的运算公式,并运算该液体的动力粘度和运动粘度。
【解】已知δ=2650kg/m3、ρ=980kg/m3、d=0.0002m和V0=0.01m/s,由:可推导出即由(4-31)式可推导出因Re=ρdV0/μ,进一步可推导出即答:该液体的动力黏度和运动黏度分别为3.172X10-3Pa.s和3.237X10-6m2/s。
7.干涉沉降实验测得悬浮体的体积分数为0.4时,上升水流速度为0.0065 m/s,体积分数为0.2时,上升水流速度为0.0205 m/s,求干涉沉降速度公式中V0与n的值。
【解】已知ΦB1=0.4、V h1=0.0065 m/s、ΦB2=0.2和V h2=0.0205m/s,将(4-50)式两边取对数并代入已知条件,得到下面的二元一次联立方程组:两式相减可解出n为再从联立方程组中的任何一个方程可解出V0,即答:干涉沉降速度公式中V0与n的值分别为0.04998m/s与3.993。
8.假定某种物料的n值服从(4-52)式,当雷诺数为10时,干涉沉降的n值为3.46;当雷诺数为100时,干涉沉降的n值为2.89;当雷诺数为50时,干涉沉降的n值为多少?(取k=4.53)【解】已知Re1=10、n1=3.45、Re2=100、n2=2.89和Re3=50,从(4-53)式运算斜率m1、m2和m3,即将(4-52)式改写并代入已知条件,得到下面的二元一次联立方程组:两式相减可解出b为再从联立方程组中的任何一个方程可解出a,即从(4-52)式可求出n3,即答:当雷诺数为50时,干涉沉降的n值为3.051。
9.已知石英与水的密度分别为2650kg/m3和1000kg/m3,水的运动黏度为1.007x10-6 m2/s,用直径为0.0005m的球形石英粒群与水配制成容积浓度为0.4的悬浮液,请估算球形石英粒群的干涉沉降速度(取k=4.53,ψt=0.11,n S=4.65)。
【解】已知δ=2650kg/m3、ρ=1000kg/m3、ν=1.007x10-6 m2/s、d=0.0005m、ΦB=0.4,则先试用(4-37)通用公式运算:雷诺数小于5000,符合通用公式的要求。
用(4-53)式运算瑞利曲线的斜率:用(4-51)式运算n值:则答:球形石英粒群的干涉沉降速度为0.01423m/s。
10.在20℃的水中,空气气泡专门慢地势成,试求在下列条件下,当形成的气泡分离出来时的直径:(1)气泡是在不润湿的孔口的上表面生成的,孔口半径分别为0.1mm、0.5mm、1mm和2mm;(2)气泡在孔口润湿表面的孔中形成,接触角分别为30º、60º、90º、及120º。
【解】水的表面张力取为σ=0.07N/m,水的密度取为ρ=1000kg/m3。
(1)已知孔口直径D1=0.2mm、D2=1mm、D3=2mm和D4=4mm, 由于20℃的水表面张力σ=72.75mN/m,水的密度ρ=kg/m3,气泡的密度δ=2 kg/m3,g=9.8m/s2,则用(4-64)式运算d值:同理算得d2=3.1mm、d3=3.9mm和D4=4.9mm。
(2)已知1=30º,2=60º,3=90º和4=120º,在孔口润湿表面中,结合(1)中已知,用(4-68)式运算d值:同理算得d2=3.4mm、d3=5.1mm和D4=6.8mm。
答:(1)孔口半径分别为0.1mm、0.5mm、1mm和2mm时,形成的气泡分离出来时的直径分别为d1=1.8mm,d2=3.1mm、d3=3.9mm和D4=4.9mm。
(2)接触角分别为30º、60º、90º、及120º时,形成的气泡分离出来时的直径分别为d1=1.7mm,d2=3.4mm、d3=5.1mm和D4=6.8mm。
11.一个盛有0.01m3水的搅拌桶,电机搅拌功率为1kw,求水中平稳气泡的直径。
【解】已知功率P=1000w和水的体积V=0.01 m3,表面张力受水中的药剂与杂质的阻碍专门大,参考12题提供的水的数据,运算取水的表面张力σ=0.07N/m, 水的密度取ρ=1000kg/m3,则用欣兹(HinZe)公式(4-69)估算气泡的尺寸,即答:水中平稳气泡的直径为0.3693mm。
12.已知水的表面张力为0.07N/m,密度为1000kg/m3,动力黏度为0.001 Pa·s,试估算等价半径为2mm、5mm和20mm空气气泡在水中的上升速度。
【解】已知σ=0.07N/m、ρ=1000kg/m3、μ=0.001 Pa·s、R b1=0.002m、R b2=0.005m和R b3=0.020m, 依照(4-79)式、(4-80)式和表4-3中的气泡上升速度公式,有则由(4-81)式得先试用表4-3中Ⅲ区的公式运算R b1=0.002m的气泡上升速度Re b和G2都满足Ⅲ区的条件,结果正确。
再用表4-3中Ⅳ区的公式运算R b2=0.005m的气泡上升速度, 改用更精确的系数1.53代替1.18得Re b和G2都满足Ⅳ区的公式的条件, 结果正确。
要用(4-78)式运算R b2=0.02m的气泡上升速度, 即该结果与图4-12比较是吻合的,证明了哈马赛在Ⅳ区给出的常数值是正确的。
答:等价半径为2mm、5mm和20mm空气气泡在水中的上升速度分别为0.2526m/s、0.2476m/s和0.4427m/s。
13.简述流体中气泡的形成方式,以及颗粒与气泡的碰撞与黏结机理。
【解】流体中气泡的形成方式有两种:一、孔口产动气泡(液滴)。
在静止流体中,将圆形孔口朝上低速吹出气体,近似于球形的气泡附着在孔口上, 当通过孔口的气体流率增加时,由于气泡达到某尺寸后,离开孔口需要有一定的时刻,因此气泡尺寸是增大的。
二、从液体中析出气泡。
气泡也能由围绕液体的蒸发或溶解在液体中的气体(如啤酒、汽水、香滨酒等)的开释而形成。
这些气泡几乎总是在核心的周围形成。
此外,在强迫对流或机械搅拌系统中,气泡的尺寸由剪切应力确定,这些应力既阻碍气泡离开形成点的气泡尺寸,也阻碍在流场中静止的最大的气泡尺寸。
矿粒与气泡的碰撞与粘附可从物理和化学两方面进行机理分析:(1)物理机理物理机理包括感应时刻、动接触角、动量等因素。
a)感应时刻是指矿粒突破气泡的水层而相互接触这段时刻。
克拉辛认为,颗粒愈大,所需感应时刻愈长,感应时刻过长则较难浮。
爱格列斯曾以此评判药剂作用及可浮性。
b)动接触角是指在惯性冲击作用下,气泡弹性变形,矿粒回跳并粘附所形成的角度。
菲力波夫曾求出不同粒度矿粒所需的动接触角:200微米的矿粒为0.7°,而1微米的需1.7°,同时推断细泥难浮的缘故是由于所需动接触角较大。
