3.5 有电介质时的高斯定理
有介质时的高斯定理,写出其物理意义

有介质时的高斯定理,写出其物理意义
高斯定理(也称为高斯通量定理)是电磁学中的一个基本定理,描述了电场或磁场通过一个封闭曲面的总通量与在该曲面内部源的大小之间的关系。
具体表达式为:对一个任意形状的封闭曲面,电场或磁场通过该曲面的总通量等于该曲面内部电荷或磁荷的代数和。
物理意义如下:
1. 电场或磁场通过一个封闭曲面的总通量是该曲面内部电荷或磁荷的性质之一,可以帮助我们了解场的发源和分布。
例如,通过测量通过一个闭合曲面的电场通量,可以推断该闭合曲面内部的电荷分布情况。
2. 高斯定理对于计算电场或磁场的分布以及场源的性质具有重要的应用。
通过选取适当的曲面以及利用高斯定理,可以简化计算复杂电场或磁场的过程,提高计算效率。
3. 高斯定理还有与能量和电荷守恒定律的联系。
当封闭曲面内部不存在电荷时,即电荷守恒定律成立时,通过该曲面的电场通量为零。
这可以用来推导电场能量的守恒。
总的来说,高斯定理在电磁学中具有重要的作用,它可以帮助我们理解场的分布、推断电荷或磁荷的性质,并且简化电场或磁场计算的过程。
有介质时的高斯定理

有电介质时的高斯定理
电位移
2 D dS D 4r q0 q0 D 所以 2 4r q0 写成矢量式为 D r 3 4r 因 D E , 所以离球心r 处P点的场强为 D q0 q0 E E r r 3 3 4r 4 0 r r r
0
r R2
R2 R1
r R1 r R2
由 P n 得束缚电荷的分布 1 2 1
R ln( R / R ) 0 ( r 1)U R2 ln( R2 / R1 ) 0 r ( 1)U
束缚电荷在介质内表面为正,外表面为负。
有电介质时的高斯定理
§9-6 有电介质时的高斯定理 电位移
1.有电介质时的高斯定理
1 E dS
电位移
同时考虑自由电荷和束缚电荷产生的电场自由电荷 总电场
S
0
(q
S内
0
q)
束缚电荷
由电荷守恒定律和面上束缚 电荷,得面内束缚电荷
高斯
有电介质时的高斯定理
电位移
q dS P cosdS SP dS
D3
2 0 r 3
E1d E2 d / 2 E3 d / 2
可解得 r 2 r3 2 1 E1 0 r1 r 2 r1 r 3 2 r 2 r 3 1 r3 4 r1 E2 0 r1 r 2 r1 r 3 2 r 2 r 3 1 4 r2 1 E3 0 r1 r 2 r1 r 3 2 r 2 r 3
0
r R2
有电介质时的高斯定理
电位移
由电位移与电场的关系,知
有介质时的高斯定理
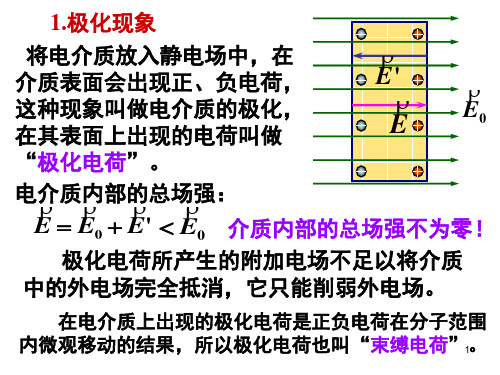
2、电介质的分类 无外场作用条件下,根据分子中正、负电 荷中心位置的不同,可将电介质分成两类:
(polar molecules) (non - polar molecules ) 2
2、电介质的分类 ① 无极分子电介质: 如:氢 H2、氦 He、氮 N2、甲烷 CH4等。 分子的正、负电荷中心重合 在无外场作用下整个分子无电矩。 ② 有极分子电介质: 如:氯化氢 HCl、氨NH3、水蒸汽H2O等。 分子的正、负电荷中心不重合 有极分子等效为一个电偶极子,在无外 场作用下存在固有电偶极矩。
6
二、电极化强度 电介质的极化规律 1、 电极化强度 是描述介质在电场中各点的 极化状态(极化程度和方向)的物理量。
在没有外电场时,电介质未被极化,内部宏观 小体积元中各分子的电偶极矩的矢量和为零; 当有外电场时,电介质被极化,此小体积元 中的电偶极矩的矢量和将不为零。 外电场越强,分子的电偶极矩的矢量和越大。 定义: 电极化强度矢量等于 pe 单位体积中分子电偶 P ΔV 极矩的矢量和,即:
Q0 ε 0 εr 1 ε r 2 S C U εr 1 d 2 εr 2 d 1
16
例题 常用的圆柱形电容器,是由半径为 R1 的长 直圆柱导体和同轴的半径为 R2 的薄导体圆筒组成, 并在直导体与导体圆筒之间充以相对电容率为 r 的 电介质.设直导体和圆筒单位长度上的电荷分别为 和 . 求(1)电介质中的电场强度、电位移; (2)此圆柱形电容器的电容.
8
3
电介质中的电场强度 极化电荷与自由电荷的关系
E E0 E '
r r 1 E'பைடு நூலகம் E0 r
第七节 有电介质时的高斯定理

3
第七节 有电介质时的高斯定理
1. 有极分子和无极分子
电介质
无极分子:(氢、甲烷、石蜡等)
有极分子:(水、有机玻璃等)
有极分子— 极性电介质
特点:分子正负电重心不重合,有固有电偶极矩;
4
第七节 有电介质时的高斯定理
无极分子 — 非极性电介质 例如 H2、O2、CO2、CH4
特点:分子正负电中心重合,无固有电偶极
布求得合场强的分布。
11
第七节 有电介质时的高斯定理
例 7-13 设一带电量为Q 的点电荷周围充满电容率 为 的均匀介质,求场强分布。 解: 根据介质中的高斯定理
2 D ds D 4 r q0
S
r
q0 D 4 r 2
1 q0 E 2 4 r D
8
第七节 有电介质时的高斯定理
(2)有电介质时的高斯定理
1 SE dS ε0 (Q0 Q)
Q0 由 εr Q0 - Q
Q0
Q
Q0 得 E dS S ε0 ε r
S
0 r E dS Q0
9
第七节 有电介质时的高斯定理
S
0 r E dS Q0
S
D 2 π rl l
D
2πr
D E ε0 ε r 2 π ε0 ε r r
( R1 r R2 )
R2
r
R1
14
第七章 静电场
一 电介质的极化
二 有电介质时的高斯定理
1
第七节 有电介质时的高斯定理
一、电介质的极化
电介质指的是导电性极差的物质。在电介质内 几乎不存在自由电子(或正离子)。通常条件下的
有介质时的高斯定理

无极分子在电场中, 正负电荷中心会被
拉开一段距离,产生 感应电偶极矩,这
称为位移极化。
无极分子
l
q q
p ql
感应电偶极矩
(2)分子中的正电荷等效中心 与负电荷等效中心 不重合的称为有极分子(如 HCl、H2O、NH3 )
例如左图的左右表面 上就有极化电荷。
正是这些极化电荷 的电场削弱了电介 质中的电场。
电介质的击穿
当外电场很强时,电介质的正负电中心 有可能进一步被拉开,出现可以自由移动的 电荷,电介质就变为导体了,这称为击穿。
电介质能承受的最大 电场强度称为该电介质 的击穿场强, 或介电强度。
例如. 空气的击穿场强 约 3 kV/mm.
介质中的高斯定理又写为: sD dS q内
… 的高斯定理
即通过任意封闭面的电位移的通量等于 该封闭面所包围的自由电荷的代数和。
说明: 1.它比真空中的E 的高斯定律更普遍,当没有电介质
时, 即r=1, 就过渡到真空中的高斯定律了。
2.如果电场有一定的对称性,我们就可以先从 D 的高
斯定理求出 D 来;然后再求出 来。
实验:插入电介质后,电压变小
U U0
r
Q Q Q Q
r>1……介质的
相对介电常数 (相对电容率)
r 随介质种类和
状
U
为什么插入电介质 会使电场减弱?
1电介质的极化
电介质这类物质中,没有自由电子, 不导电, 但可以极化。 电介质分子可分为有极和无极两类:
有极分子在电场中, 固有电偶极矩会转向 电场的方向,这称为 转向极化。
有电介质时的高斯定理

有电介质时的高斯定理
有电介质时的高斯定理是电学中的一个重要定理,它描述了电场的分布与电荷分布的关系。
此定理的公式表述为:电场穿过一个封闭曲面的通量等于该曲面内部的电荷总量的比例,即ΦE=Q/ε0,其中ΦE为电场的通量,Q为曲面内部的电荷总量,ε0为真空中的电介质常数。
在有电介质时,电场的分布受到电介质的影响。
电介质的存在会使电场强度发生改变,这是因为电介质的分子会被电场极化,从而产生极化电荷。
这些极化电荷会改变电场的分布,使电场在电介质中的强度比在真空中的强度小。
因此,在有电介质时,要考虑电介质对电场的影响,才能准确地计算电荷的分布。
在应用高斯定理时,通常需要选择一个适当的曲面来计算电场的通量。
曲面的选择应当考虑到电荷分布的对称性,以便简化计算。
在有电介质时,曲面的选择也需要考虑到电介质的影响。
如果曲面穿过电介质,那么在计算电荷总量时,需要将电介质中的极化电荷也计算在内。
高斯定理的应用范围很广,包括电场的计算、电容器的设计、电荷分布的测量等。
在电场的计算中,高斯定理可以用来求解各种电场分布,例如电偶极子、均匀带电球面等。
在电容器的设计中,高斯定理可以用来计算电容器的电容量,从而确定电容器的电荷储存能
力。
在电荷分布的测量中,高斯定理可以用来测量电荷的总量,从而确定电荷的分布情况。
有电介质时的高斯定理是电学中的一个重要定理,它描述了电场的分布与电荷分布的关系。
在应用该定理时,需要考虑到电介质的影响,并选择适当的曲面来计算电场的通量。
高斯定理的应用范围很广,包括电场的计算、电容器的设计、电荷分布的测量等。
3.5有电介质时的高斯定理

3.5有电介质时的高斯定理
3.5 有电介质时的高斯定理
3.5.1电介质中的场强
电介质放入外电场中产生极化,电介质中的电场是极化电荷产生的附加电场E ’和外电场E 0的矢量和。
即:E = E 0+ E ’。
电介质中的电场不为零,但显著地被削弱了。
3.5.2电位移,有电介质时的高斯定理
真空中产生电场的电荷是自由电荷。
有介质存在时,电介质的内部或表面上出现极化电荷,极化电荷也要激发电场。
可见,有介质存在时,增加了新的场源电荷即极化电荷。
但是,新的场源只改变原有静电场的大小,不改变静电场的性质。
即对有介质存在时的静电场,高斯定理和环路定理仍然成立。
1、有电介质时的高斯定理
通过前面分析,此时高斯定理应写为:
()001S d q q ε'?=+?? E S
其中q 0和q ’分别为闭合面S 所围区域内的自由点和极化电荷。
而
S
q d '=- P S 00
1S S d q d ε???=- E S P S ()0
0S d q ε+?=?? E P S 引入一个辅助性的矢量(称为电位移)
0ε=+D E P
则上式可改写为
0S d q ?=??
D S 上式叫做有电介质存在时的高斯定理。
对于各向同性电介质有
0εχ=P E
()01εχ=+D E
上式说明电介质中任一点的D 与该点的E 方向同向,大小成正比。
电介质的介电常量:
()01εεχ=+ 电介质的相对介电常量:
01r εεχε==+ 0r εεε==D E E
例1【P103】、例2【P104】。
3-5有介质时的高斯定理

第三章静电场中电介质
r
R2
R1
(3)由(1)可知
U
E dr
R2
E
2π dr
0
r
r
(R1 r R2 ) ln R2
R1 2π 0 r r 2π 0 r R1
C Q 2π U
单位长度电容
0
C l
rl
ln R2 R1
2π 0
r
ln
r C0
R2 R1
真空圆柱形 电容器电容
r 又叫电容率
D2 2R2
3 – 5 有电介质时的高斯定理
第三章静电场中电介质
1 -P1 D1 0E1
2 -P2 D2 0E2
1
-
2R1
1
1
r
2
2R2
1
1
r
思索:可否由其他途 径求极化强度大小?
P 0E 0r 1E
1 P1 0 r 1E1 2 P2 0 r 1E2
3 – 5 有电介质时的高斯定理
-+
-+ -
-+E-1+ E2
-+--+-
-+ +-
0
1' 2'
2'
3 – 5 有电介质时的高斯定理
E1
D
0 r1
0 0 r1
E2
D
0
r2
0 0 r2
U
E dl
l
E1d1 E2d2
Q ( d1 d2 )
0S r1 r2
C Q0 0 r1 r2S U r1d2 r2d1
0
E
P) ds
q0
有电介质时的高斯定理

( r
1)E 1
Vl0 =100(V)
2( r
1
1)
r
0
4 3
0
例:设无限长同轴电缆的芯线半径为R1,外皮 的内半径为R2。芯线与外皮之间充入两层绝缘 的均匀电介质,其相对电容率分别为εr1和εr2。 两层电介质的分界面半径为R,如图。求单位
长度的电容。
R2εr1 R R1
E2
D2
0
2 0
由于导体为等势体: E1d E2d
E1 E2
1 r 2
两极上电量不变: 1S r 2S 2 0S
解得:
1
2 r 1r
0
2
2
1 r
0
板间电压:
V
E2d 2
2
1 r
0 d 0
1
P1n
1r
r
D4r 2
S内
q0
r
当:r R : q0 0 D=0 E=0 P=0
当:r R :
q0 q0
Байду номын сангаас
D
q0
4r 2
E
4
q0
0
r
r
2
P
(r 1)q0 4rr 2
D, E, P 方向沿矢径
R Pn P q 4R 2 R
(1 r )q0
4
(1
rrR)q2 0
r
(2)当:r R :
U r Edr
R
3-5有电介质时的高斯定理3-6有电介质时的场方程
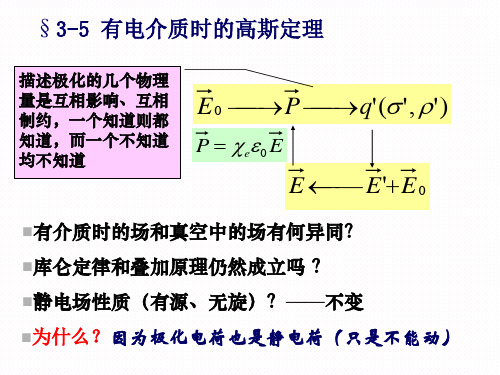
例 一平行板电容器,中间插入厚度比电容器两极板之间距离
略小的均匀电介质平板,介质板与电容器极板平行 ,当电容 器带电后,试粗略地画出电容器内 E f , Ep , E, D, P 等
f f 各矢量的分布以及电荷分布和电势分布情况。
E, P, D
oE P
之间的关系:
2º四个常数之间的关系:
介质介电常数: r o
相对介电常数:
3º解题一般步骤:
DdS
由q0
s
r
q0
1
E
D
D
E
E
P
oE
P
Peˆn
由 由
'
0 1
EdS
1
0
S内
q0
1
0
S内
q'
1
0
S内
q0
S
P d S
S
EdS
S
P
0
dS
1
0
q0
S内
S面内包 围的自 由电荷
D 0 E P
(0 E P) d S q0
S
S内
电位移矢量
电位移矢 量通量
D d S q0
2.环路定理
极化电荷产生的电场与自由电 荷产生的电场性质相同
E dl 0
保守力场
电位移矢量:是一个同时描述电场和电介质极化的复合矢量 电位移线与电场线性质不同
物理 电磁学 第18讲 有电介质时的高斯定理
=
+0 - 0 - - + ++1 S- -+ + - -+ + - S e ˆn - d + ++2 + -
= 0
U E1d E2d
E1 E2
1 2 r
S S 1 2 0S 2 2 2 r 1 0 0 1 r 2 2 0 0 1 r
D 1 1 q P D 0E D 0 1 D 1 2 0 r r r 4 πR
可见,当带电体周围充满电介质时,场强减弱为真空 时的 1 r 倍。
[例] 两平行放置的金属板间原为真空,分别带等量异号电荷 +0、-0,板间电压为 U0,保持板上电荷不变,将板间 一半空间充入介质 (r),求:板间电压。 解:作高斯面
解:利用 D 的高斯定理
q 2 , S D d S q , D 4 πr q , D 2 4 πr q D q ˆ, E ˆ D r r 2 2 0 r 4 π 0 r r 4 πr
q q
D
n R
r
高 斯 面
P n P cos π P, q 4 πR 2 1 r 1q,q q
S
D1 dS D1 dS D1 dS D1 dS
左 右
S
D1 dS q0 int
S
D1 dS D1S 1S
0
侧
D1 1
1 E1 0 r
2 E2 0
* 静电场的边界条件 取矩形回路,由环路定理 E 的切向分量 E 1t E d l E Δl E Δl 0
第18讲 有电介质时的高斯定理

第18讲有电介质时的高斯定理电极化强度 电位移矢量 的高斯定理 DE E E '+= 00E + ++ - - - σ ' 原外电场 σ ' 的电场E ' V p P i i ∆∑= lim ∑=⎰⋅int0d q S D S PE D+=0ε与 的关系 静电场中的各向同性、线性电介质的高斯定理 与 的关系 int 0q D E Pσ'q 'E 与 的关系 与的关系 当自由电荷 q 0int和电介质分布具一定对称性时,应用 高斯定理 便于解决问题。
DEDD P Pσ'σ'q '∑⎰=⋅int 0d q S D S E E D εεε==r 0n ˆeP ⋅=' σ⎰'='S q d σE P )(1r 0-=εε[Q5.18.1] 一无限大各向同性均匀电介质平板,厚度为 d ,相对介电常数为 εr ,内部均匀分布有电荷体密度为 ρ0 的自由电荷。
求:介质板内、外的 、 、 。
drε0ρEPD解: 带电体有面对称,故 、 、 垂直于平板。
dX0S x = 0 = 2DS 0 00022S x DS ρ=xD 0ρ=d S DS 0002ρ=dD 20ρ=r ε0ρ⎰⋅+⎰⋅=⎰⋅两底侧S D S D S D S d d d 2d x ≤, 2d x ≥, , ,∑=⎰⋅int0d q S D SD E P S 0 S ' S 0'r 0εεDE =r00εερx =均匀场 = 0xD 0ρ=dD 20ρ=dX0xr ε0ρEP )(1r 0-=εεερεxP 0r 1)(-=E P )(1r 0-=εεr2d x ≤, 2d x ≥, 0εD E =002ερd =[Q5.18.2]平行板电容器极板面积为S,间距为d,中间有两层厚度各为d1和d2 (d1+d2=d)、相对介电常数分别为εr1和εr2的电介质层。
3-5有介质时的高斯定理

q0和 ′ S所围区域内 q是 所围区域内
的自由电荷及极化电荷
ε0
3 – 5
有电介质时的高斯定理
第三章静电场中电介质
根据第四节的结果 则有
v r q′ = −∫ P⋅ ds
s
s ε0 r r r ∫ (ε 0 E + P ) ⋅ ds = q0 s
r r 1 r r ∫ E ⋅ ds = ( q0 − ∫ P ⋅ ds )
r r r D = ε0εr E = εE
r E
。
3 – 5
有电介质时的高斯定理
第三章静电场中电介质
r D =
q0 r en 2 4π r
r r r D = ε0εr E = εE
r q0 >0, E离开球心向外 , r r e q0 < 0, E 指向球心 r , s e
n
r E=
q0 r en 2 4πε r
1 1 σ ′ = − σ 0 εr εr 1 2
讨论极化电荷正负
ε r −1 σ 1′ = σ0 εr
1 1
两种介质表面极化电荷面密度
εr −1 ′ σ2 = σ0 εr
2 2
3 – 5
有电介质时的高斯定理
第三章静电场中电介质
常用的圆柱形电容器, 例3 常用的圆柱形电容器,是由半径为 R1 的长 的薄导体圆筒组成, 直圆柱导体和同轴的半径为 R2 的薄导体圆筒组成, 并在直导体与导体圆筒之间充以相对电容率为 ε r 的 电介质.设直导体和圆筒单位长度上的电荷分别为 电介质 设直导体和圆筒单位长度上的电荷分别为 + λ )电介质中的电场强度、 和 − λ . 求(1)电介质中的电场强度、电位移和极 化强度; 电介质内、外表面的极化电荷面密度; 化强度;(2)电介质内、外表面的极化电荷面密度; 此圆柱形电容器的电容. (3)此圆柱形电容器的电容.
有介质时的高斯定理公式

有介质时的高斯定理公式有介质时的高斯定理公式是物理学中的基本定理之一,它描述了电场、重力场等物理场在有介质的情况下的分布规律。
本文将介绍有介质时的高斯定理公式及其应用。
高斯定理公式指出,电场的通量与电荷量成正比,与介质极化强度成反比。
在有介质的情况下,电荷会在介质中引起电极化,从而影响电场的分布。
因此,高斯定理公式在描述有介质中电场分布时变得更加复杂。
在有介质时,高斯定理公式可以表示为:$$ \oint_S \mathbf{E} \cdot d\mathbf{S} = \frac{1}{\epsilon_0}\int_V \rho dV - \oint_S \mathbf{P} \cdot d\mathbf{S} $$其中,S是一个封闭曲面,V是该曲面所围成的空间区域,$\mathbf{E}$表示电场强度,$\rho$表示电荷密度,$\mathbf{P}$表示介质的极化强度,$\epsilon_0$为真空介电常数。
公式右边第一项表示电荷在该区域内总共产生的电场通量,第二项表示介质极化所产生的电场通量。
公式左边的积分表示电场穿过曲面S的总通量。
在应用高斯定理公式时,需要注意几个关键点。
首先,曲面S需要是一个封闭曲面,而不是一个任意的曲面。
其次,积分中包含的介质极化强度需要根据具体情况进行计算。
最后,公式只适用于稳态电场的情况,不适用于变化的电场。
高斯定理公式在物理学中有着广泛的应用,特别是在电学、磁学、地球物理学等领域。
在电学中,高斯定理公式可以用于计算电容器的电容量;在磁学中,可以用于计算磁通量;在地球物理学中,可以用于计算地球重力场分布。
有介质时的高斯定理公式是物理学中一个非常基础和重要的定理,描述了物理场在有介质时的分布规律。
在实际应用中,需要注意公式的条件和具体计算方法,才能得到准确的结果。
9-5介质中的高斯定理

一般,
D 与 E 关系为: D = ε 0 E + P
P
电极化强度(矢量)
∑p P=
V
i
单位体积内分子电偶极矩的矢量和
物理意义: 描述了电介质极化强弱,反映了电介质内分子电偶 极矩排列的有序或无序程度。
3. 电位移线
起于正自由电荷,止于负自由电荷。
电场线起止于各种正负电荷
?
σ ′ +σ ′
+σ + + + + + + +
Q 1 1 1 = ε R ε R + R 4π ε0 r 1 r 2 2
UB =
∫
R2
r
E B d r + ∫ E C dr
R2
∞
R1
Q 1 1 1 = + 4π ε0 ε r r ε r R2 R2
R2
C B Q A
εr
UC =
∫
∞
r
E C dr
=
Q 4π ε0 r
R2 Q
εr
Q DB = Dc = 2 4π r EA = 0 D = ε 0ε r E
r
DA = 0
0
Q Q EB = 2 EC = 4π ε 0 ε r r 4π ε0 r 2
U A = ∫ E dr
r
∞
=
∫
R1
r
E A dr + ∫ E B dr + ∫ E C dr
R1 R2
R2
∞
σ ′
+σ 0
E′
+σ ′
E0
-σ 0
当静电场中有电介质时, 则电介质在外电场作用下 产生极化电荷Q ' ,则空间 场强应为Q和Q '共同激发。
介质中的高斯定理

v E
D
介质中的高斯定理
例 自由电荷面密度为0的平行板电容器,其极化电荷面密度
为多少?
解: 由介质中的高斯定理
-+´0
DS 0S D 0
D +´
E
D
0r
0 0 r
- 0
0 0
E0
0 0
E 0
E E0 E
0 r 0 0
1
1
r
0
E
dS S
++++++
-q - - - - - -
移出S面
qi
留在S面内
介质中的高斯定理
v v E dS
S
1
0
qi
1
0
vv P dS
S
S 0E P dS qi
定义电位移矢量: D 0 E P C m2
介质中的高斯定理: 在任何静电场中,通过任意闭合曲面 的电位移通量等于该曲面所包围的自由电荷的代数和.
D S
dS
qi
说明:
D S
dS
qi
介质中的高斯定理
1. 介质中的高斯定理虽说是从平板电容器这一特例推 导出,但它却有普适性.
2. 介质中的高斯定理包含了真空中的高斯定理.
真空中: P 0 所以: D 0E P 0E
v D dS
S
S 0E dS qi
vv E dS
S
1
0
qi
3. 电位移矢量D 是一个辅助量.描写电场的基本物理
介质中的高斯定理
大学物理
静电场中的导体和电介质
第4讲 介质中的高斯定理
介质中的高斯定理
6 有电介质时的高斯定理

于该闭合曲面所包围的自由电荷的代数和.
E dS
S 0r
Q
0i
i
自由电荷 代数和
讨论 电场中充满均匀各向同性电介质的情况下
1、定义:电位移矢量 D 0rE E
: 电容率,决定于电介质种类的常数
说明
(1)是描述电场辅助性矢量
(2) 对应电场线起始于正自由电荷,
(3)
终止于负自由电荷
电位移通量 Ψ D
二、电介质中的静电场环路定理
l E dl 0
D dl 0 l
电位移 有介质时的高斯定理
一、电介质中的高斯定理 电位移矢量 D
加入电介质(εr )
E dS
1
S
0
qi
i
1
0
(
0 )S
'(1 1r Nhomakorabea)
0
EdS Q
S 0r i
E
dS
0S
1
S
0 r 0 r
Q0i
i
0i
自由电荷的代数和
令: D0ErE
电位移矢量
DdS
S
Q0i
i
电介质中通过任一闭合曲面的电位移通量等
D
s
dS
电力线与电位移线的比较
E线
D线
+Q
+Q
r
r
2、电介质中电场 强度
E
、电极化强度
P
和电位移矢量D 之间的 关系
电位移
D 0rE E
电极化强度
P
(r1)0 E
D P 0E
3、电介质中的高斯定理
D dS Q0i
S
i
(自由电荷
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.5 有电介质时的高斯定理
3.5.1电介质中的场强
电介质放入外电场中产生极化,电介质中的电场是极化电荷产生的附加电场E ’和外电场E 0的矢量和。
即:E = E 0+ E ’。
电介质中的电场不为零,但显著地被削弱了。
3.5.2电位移,有电介质时的高斯定理
真空中产生电场的电荷是自由电荷。
有介质存在时,电介质的内部或表面上出现极化电荷,极化电荷也要激发电场。
可见,有介质存在时,增加了新的场源电荷即极化电荷。
但是,新的场源只改变原有静电场的大小,不改变静电场的性质。
即对有介质存在时的静电场,高斯定理和环路定理仍然成立。
1、有电介质时的高斯定理
通过前面分析,此时高斯定理应写为:
()001S d q q ε'⋅=+⎰⎰ E S
其中q 0和q ’分别为闭合面S 所围区域内的自由点和极化电荷。
而
S
q d '=-⋅⎰⎰ P S 00
1S S d q d ε⎡⎤⋅=-⋅⎣⎦⎰⎰⎰⎰ E S P S ()0
0S d q ε+⋅=⎰⎰ E P S 引入一个辅助性的矢量(称为电位移)
0ε=+D E P
则上式可改写为
0S d q ⋅=⎰⎰
D S 上式叫做有电介质存在时的高斯定理。
对于各向同性电介质有
0εχ=P E
()01εχ=+D E
上式说明电介质中任一点的D 与该点的E 方向同向,大小成正比。
电介质的介电常量:
()01εεχ=+ 电介质的相对介电常量:
01r εεχε==+ 0r εεε==D E E
例1【P103】、例2【P104】。
