4.3等效电源定理
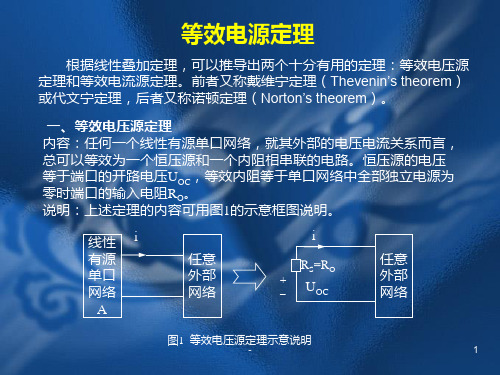
等效电源定理

等效电源定理戴维南定理和诺顿定理分别能把含源二端网络等效成为一个实际电压源支路和实际电流源支路,故统称等效电源定理。
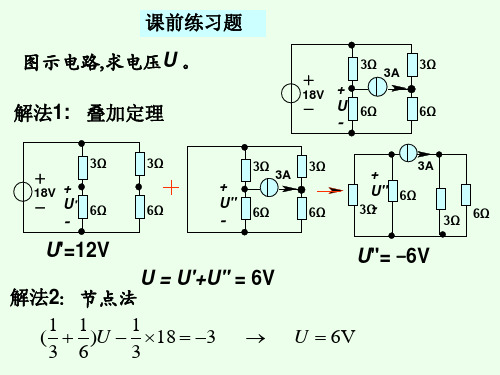
1、戴维南定理任一线性含源二端网络,对外电路讲,可以等效为一个电压源和电阻串联的组合,电压源的电压为该网络的开路电压u oc,串联电阻等于该网络中所有独立源为零时的入端等效电阻R o。
2、诺顿定理任一线性含源二端网络,对外电路讲,可以等效为一个电流源和电阻并联的组合,电流源的电流为该网络的短路电流isc,并联电阻等于该网络中所有独立源为零值时的入端等效电阻R o。
图(a)所示为一接有外电路的含源二端网络,根据替代定律,把R L 支路分别用流过它的电流i和两端电压u作为电压源等效替代,然后运用叠加定理分别得到u=u oc-R o i=i sc-u/R o等效电源电路如图(b)所示。
这两条定律所得到的电压源支路和电流源支路可以互相等效,所以人们多应用戴维南等效电压源定律,然后变化为诺顿等效电流源电路,如图(b)上、下图所示。
戴维南定律对求解电路中某一支路的电压、电流和功率,特别是负载吸收的最大功率最为方便。
求解时含源二端网络必须是线性的,待求支是线性的或非线性、有源或无源均可。
应用这两条定律,一般分三个步骤:(1)断开待求支路或将待求支路短路,分别求得开路电压u oc和短路电流i sc;(2)让全部独立源为零,求入端等效电阻R o。
(3)画出等效电源电路,接上待求支路,求解待求量。
3、用戴维南定律分析含受控源电路根据受控源的性质和等效电源定律的要求,当用戴维南定律和诺顿定律分析受控源电路时,必须掌握:(1)当控制量在端口上时,它要随端口开路或短路变化,必须用变化了的控制量来表示受控源的电压或电流。
(2)当控制量在网络内,则在短路或开路时,必须保证受控源及其控制量同在含源二端网络内。
(3)受控源不能充当激励,具有电阻性。
在求戴维南等效电阻时,独立源为零,受控源和电阻一样要保留,故必须采取:(1)开路短路法:将待求支路开路和短路,分别求得二断网络的开路电压u oc和短路电流i sc,由图所示可知R o=u o/i o。
解释等效电源定理

解释等效电源定理等效电源定理是电路分析中重要的定理之一,它包括戴维南定理和诺顿定理两个主要部分。
这两个定理都是用来将复杂电路简化成简单电路的方法,从而方便我们进行电路的分析和计算。
1.戴维南定理戴维南定理(Thevenin's Theorem)是将一个有源二端网络等效成一个电源模型的方法。
这个电源模型包括一个理想电压源和一个内阻串联,其中电压源等于网络开路电压,内阻等于网络所有元件的电阻之和。
戴维南定理的作用是将复杂的有源二端网络简化成一个简单的电源模型,方便我们进行电路的分析和计算。
应用戴维南定理时,需要注意以下几点:(1)开路电压的求解要正确,不能漏掉任何元件;(2)内阻的计算要将所有元件的电阻相加,不能漏掉任何元件;(3)等效电源模型与原网络在端口处要满足电压电流关系。
2.诺顿定理诺顿定理(Norton's Theorem)是将一个有源二端网络等效成一个电源模型的方法。
这个电源模型包括一个理想电流源和一个内阻并联,其中电流源等于网络短路电流,内阻等于网络所有元件的电阻之和。
诺顿定理的作用是将复杂的有源二端网络简化成一个简单的电源模型,方便我们进行电路的分析和计算。
应用诺顿定理时,需要注意以下几点:(1)短路电流的求解要正确,不能漏掉任何元件;(2)内阻的计算要将所有元件的电阻相加,不能漏掉任何元件;(3)等效电源模型与原网络在端口处要满足电压电流关系。
等效电源定理在电路分析中有着广泛的应用。
例如,我们可以通过应用等效电源定理将复杂电路简化成简单电路,从而方便我们进行电路的分析和计算。
同时,等效电源定理还可以用于电路的匹配和优化,以帮助我们更好地理解和设计电路。
需要注意的是,戴维南定理和诺顿定理虽然都是用来简化电路的方法,但它们在使用上有一定的区别。
一般来说,当电路中存在电压源时,我们通常使用戴维南定理;当电路中存在电流源时,我们通常使用诺顿定理。
此外,在应用等效电源定理时,还需要注意电路的换路定理解题技巧,从而正确地求解出开路电压和短路电流等参数。
4.3等效电源定理

U
s
得
Req
Us I
1
1
0.8
225
300 720
20 中北大学国家级电工电子实验教学示范中心
戴维南定理例题3
③戴维南等效电路如图示,则得电流解
I4
U 225
0.03A
该例题用戴维南定理求解电流,
同时涵盖了含受控源电路之回
路方程的概念和外加电源求解
戴维南定理是有源单口网路的基本属性。
7 中北大学国家级电工电子实验教学示范中心
戴维南定理例题1
[例]图示电路中已知Us2 = 9V , Uab = 9V , Is = 6A , R1 = 1Ω, R2 = 2Ω, R3 = 3Ω,R4 = 4Ω, 试求Us1
解一:用戴维南定理化简ab 端口右边的网路。 ①求ab端的开路电压Uoc,如图 (a)所示,先求Icb再求Uoc最 为捷径,因为
18 中北大学国家级电工电子实验教学示范中心
戴维南定理例题3
可列回路方程解电流 I 3
R1 R2 R3 I3 R2I3 U s
I3
R1
R2
Us
R3
R2
36
420 300 300 0.2 300
0.0375A
Uoc U seq R3I3 300 0.0375 11.25V
(Req RL ) R0 RL
6 中北大学国家级电工电子实验教学示范中心
戴维南定理的证明
结论:前式 i i i uoc useq
(Req RL ) R0 RL
该式正是含内阻电压源的电流表达式。它表明: 从端口上看,有源单口网路对外电路的作用,可 以用一个含内阻的电压源来等效代替。该电压源 的源电压等于有源单口网路的开路电压,其内电 阻R0就是有源单口网路去源后的等效电阻。故戴 维南定理得证。此刻应该认识到:
第4章电路定理th

电流源单独作用时:电压源短路,电路等效如图, 由分流公式(注意方向)得:
南 京 工 业 大 学 信 息 科 学 与 工 程 学 院 通 信 系
I2 4Ω 3Ω
4Ω 4Ω 6A I2 6Ω 3Ω
6A 4Ω 6Ω
I 2 4 A
根据叠加定理,电流为:
I I1 I 2 3 A
第 4-15 页
设I1=1A,则利用OL,KCL, KVL逐次求得
306V 2Ω c 2Ω b 2Ω a 2Ω I7 I6 I5 I4 I3 I2 1Ω US 1Ω 1Ω d I1 1Ω
Ua =(2+1)I1 = 3V I2 = Ua /1 = 3A I3 = I1+ I2 = 1+3 = 4A Ub =2I3+ Ua = 2×4+3 =11V I4 = Ub /1 = 11A I5 = I3+ I4 = 4+11 = 15A
南 京 工 业 大 学 信 息 科 学 与 工 程 学 院 通 信 系
4.1 齐次定理和叠加定理 一、齐次定理 二、叠加定理 4.2 替代定理 一、替代定理 二、替代定理应用举例
4.3 等效电源定理 一、戴维宁定理 二、诺顿定理 三、等效内阻的计算 四、定理的应用举例 4.4 最大功率传输定理 4.5 特勒根定理和互易定理 一、特勒根定理 二、互易定理
4.1 齐次定理和叠加定理
对于一些未知结构(黑盒子)电路,利用性质进行分析,用叠 加定理求解更为方便。
南 京 工 业 大 学 信 息 科 学 与 工 程 学 院 通 信 系
例2 如图电路,N是含有独立源的线性电路,已知 当us = 6V,iS= 0时,开路电压uo= 4V; 当us = 0V,iS= 4A时,uo= 0V; 当us = -3V,iS= -2A时,uo= 2V; 求当us = 3V,iS= 3A时的电压uo
等效电源定理

第 16 页
前一页
下一页
五、应用练习
1、如图所示电路,负载电阻RL可变。求RL =1 Ω时其上电流i;若RL 改变 为6 Ω,再求电流i?
a
6
3
i
-
+
RL
12V
4
4
b
第 17 页
前一页
下一页
五、应用练习
2、如图所示电路,求负载电阻RL上消耗的功率。
4 i1
50
50
2 Ai 1
+
100
40V
-
a
RL
ia
+
N0
u
要关联
a
+
N0 u
i
-
-
b
b
(a) 外加电压源法 (b) 外加电流源法
第9页
前一页
下一页
二、戴维南等效内阻的计算
2、对于含受控源的二端电路N:
(2)开路短路法:
第一步:求出开路电压uOC; 第二步:求出短路电流iSC;
第三步:
R0
u OC iSC
a
+
N
u oc
-
b
(a) 求开路电压
注意uOC和iSC 的方向关系
3A
US R1
R1 4
IS R2 12
1A
aI
电
源
等 RL 效பைடு நூலகம்
R1 R2 3
+
变
6V
换
(
US R1
-
IS
)(
R1
R2)
-
b
I 6 3 RL
RL
a I I 2 3
4等效电源定理4-34
4
2I 2I
ISC
1 8
A
RO
UOC ISC
8
③一步法求解 (直接求端口VAR)
6
I +
I
4V
-
6
I +
4V -
5
a
4
-
ISC
2I ISC
+
b
5
4
2I
+
I a
U
b
例:试求图示电路的戴维南等效电路。
解:法一:UOC
4
4 4
8
24
6V
4
U
'
(4
8)
I1
U ' 4I2 12I '
I1 I2 I ' U' 6I'
54.3
V
RO
2 1.5 2 1.5
0.86
法二:诺顿定理
ISC
60 2
50 1.5
63.3A
RO
2 1.5 2 1.5
0.86
+ 60V
-
2 I1
a
+
I
50V
-
R
1.5
b
I
RO RO
R
ISC
0.86
0.86 2.14
0.86
0.86 4.14
63.3 18.1A 63.3 10.9A
RO
U I
1
a
1
b
a
I1 0
6
+ 4V -
2 - 5I1+ 0
b
aI
+ 6
-
U
电路原理4.3.1戴维宁定理和诺顿定理 - 戴维宁定理
i
a 等效 Req
NS
b i
+ Uoc
-
a
b
返回 上页 下页
电路定理
ia
证明: NS
+ –u
N'
b
a
NS
+ u
–
i = NS
b
ia
Req
+
+
u
Uoc –
–
b a
+u' –
+
N0 Req
b
N'
a + u'' i –
b
根据叠加定理:当电流源 i为零, u'= Uoc (开路电压)
当网络NS中独立源全部置零 , u"= - Req i
和N2分别用戴维宁等效电路代替,到图(b)电路。
单口N1的开路电压Uoc1可从图(c)电路中求得,
列出KVL方程
Uoc1
=
1
gUoc1
+
2
2 +
2
20
=
3Uoc1
+ 10
解得
Uoc1
=
-10 2
V
=
-5V
返回 上页 下页
电路定理
为求Ro1,将20V电压源用短路代替,得到图(d)电路,
再用外加电压源U 计算电流I的方法求得Ro1。列出
U0
–
b
U0 =0.5I0 103 +I0 103 =1500I0
Req = U0 /I0=1500
解毕!
返回 上页 下页
电路定理
例5: 电路如图 (a)所示,其中g=3S。试求Rx为何
等效电源定理

等效电源定理
“等效电源定理”是基本的电子学理论,许多电子电路的模拟计算都需要用到这个定理。
在电子学中,等效电源定理是一个重要的定理,它利用电子学模型的特殊性,将元件的微扰变现为电路的消声效应,从而解决电路的复杂性。
简而言之,等效电源定理就是使用电路模型来描述电子斯压模型,以求得等效电源,其中,等效电源可以用来模拟计算各种电子电路。
等效电源定理的基本原理是,将电子元件的连续电流分解为两个部分,一部分流过元件,另一部分流过电路外部。
根据这个原理,就能够计算出元件的输出电压和输出电流。
可以说,等效电源定理是电子设计中的一个重要基础,它能够有效地利用元件的微扰特性,将其变为电路的消声现象,从而解决电路复杂性和模拟计算难度。
等效电源定理有四个基本步骤,分别是:利用欧拉定律计算电路的电压;对电路中的每个元件利用电子斯压模型,把它们的阻抗分解为两个部分;把这两部分阻抗分别代入电压方程,计算出这两部分的电压;最后再将这两个电压相加,就得到了等效电源的电流。
等效电源定理的应用非常广泛,其应用于电子电路的比较、元件的测量和精确控制等方面,都可以发挥出它的实际作用。
例如,可以利用它来分析电子系统中的瞬态现象,以及元件的线性谐振器特性。
此外,等效电源定理还可以用来计算变压器的工作状态,以便清楚地辨别出其特定的模式。
等效电源定理在许多电子学方面都发挥了重要作用,它能够揭示
电子元件的行为,并为系统设计提供准确的参考。
它的广泛应用反映出,它是目前最有效的电子电路模拟计算方法之一。
必须强调的是,熟悉等效电源定理,可以让我们更好地了解电子电路,使用它们来实现更多的应用。
等效电源定理PPT课件
解: (1)将a,b两端钮向左的
线性有源单口网络用戴维宁 等效电路代替
开路电压为
UOC U R1 1 U R22R2U24V 0
等效内阻为
RORR 11 RR 224 4 2 21.3 3
-
10
(2)端钮c,d向右的无源单口网络等效 内阻Rcd为
R cd
R4 (R5 R6 ) R4 R5 R6
由此也可推知:理想电压源和理想电流源并联的电路可等效为一个 理想电压源。
-
19
习题:
1、如图题1所示单口网络,求其戴维宁等效电路。 2、如图题2所示电路中的i5和U1。
题1图
题2图
-
20
3、如图题3所示含独立电源的单口网络N,其断口ab间外接 一个电阻R。当R=10 Ω时,u=8V;当R=5 Ω时,u=6V,求网 络N的诺顿等效电路。 4、求图题4所示电路等效电压源模型 。
-
3
(3)由此可得线性单口网络的戴维宁等效电路,如图2(b)所示, 加上负载RL后,就可计算电流iL:
iLRO U OR CL
6 2(A) 21
强调: (1)所为等效是对外部的电流i和电压u而言,如果两个电路对外电 路作用的电压和电流相等,则这两个电路是等效的; (2)求单口网络的等效内阻时,要令网络中的所有独立电源为零, 其含义是恒压源短路,恒流源开路。
-
4
证明: 利用线性网络的叠加原理,根据端口电流电压不变的等效概念,可 将外部网络用一个iS=i的理想电流源等效代替,如图3(a)所示。显 然,替代后的电路仍然是线性电路,因此可用叠加原理计算端电压u (如图3(b)):
UUU
其中U’是网络中所有独立电源作用产生的电压分量,U”是由恒流
等效电源定理

等效电源定理等效电源定理又称为费拉里-德米赛特定理,是一种常用的电源控制和电路设计原理,由意大利物理学家费拉里和德米赛特在19世纪末初提出。
它规定了在某一特定信号或场强的作用下,多个电源的特性相似。
等效电源定理认为,在恒定的电路状态下,任何电路内,只要电源数量一定,由它们提供的动力都是相等的,不管它们是有相互抵消和加强作用,还是它们之间发生无相互作用,总之,只要它们有相同的输入和输出,那么它们之间就可以被当成等效的。
现在,市场上的电路板设计一般采用等效电源定理。
它可以极大地提高电路板设计的效率,消除容易引起电路板设计故障的错误,以及大大减少电路板的故障率,因而使电路板设计工作变得更加高效。
首先,等效电源定理使得电路板设计工作变得容易。
一般而言,电路板设计工作往往需要处理大量复杂的电源问题,而等效电源定理表明,一个电路板只需要一种电源,而不需要考虑其他电源有什么影响,这样做可以显著减少电路板设计所需的时间。
其次,等效电源定理消除了导致电路板设计失败的常见错误。
经常发生的一个错误是,在电路板设计中,用于控制不同类型的电源的电子元件可能会出现“浮动”现象,也就是这些电子元件在不同的电源状态下发出的信号不一致,而等效电源定理提出,只要每个电源的输入和输出相同,它们就可以被当成等效的,这使得电路板设计设计人员可以容易地控制和统一不同电源的信号,从而避免了这种错误。
此外,等效电源定理有助于降低电路板的故障率。
如果不采用等效电源定理,由于存在多种电源,可能会造成电路板设计中的“漏洞”,也就是某一种特定的电源所产生的信号有可能溢出到其它不同类型的电源上,从而产生电路板故障。
而等效电源定理则表明,不管电源有多少种,只要它们具有相同的输入和输出,它们就可以被当成等效的,这样就可以大大降低电路板故障率。
综上所述,等效电源定理具有重要的应用价值,对电路板设计中的电源控制具有重要的意义,使得电路板设计工作变得更加高效,提高了电路板的可靠性和性能。
等效电源定理

等效电源定理实验报告一、实验名称等效电源定理二、实验目的1. 验证戴维宁定理和诺顿定理的正确性,加深对该定理的理解。
2. 掌握测量有源二端网络等效参数的一般方法。
三、原理说明1. 任何一个线性含源网络,如果仅研究其中一条支路的电压和电流,则可将电路的其余部分看作是一个有源二端网络(或称为含源一端口网络)。
戴维宁定理指出:任何一个线性有源网络,总可以用一个电压源与一个电阻的串联来等效代替,此电压源的电动势Us等于这个有源二端网络的开路电压Uoc,其等效内阻R0等于该网络中所有独立源均置零(理想电压源视为短接,理想电流源视为开路)时的等效电阻。
诺顿定理指出:任何一个线性有源网络,总可以用一个电流源与一个电阻的并联组合来等效代替,此电流源的电流Is等于这个有源二端网络的短路电流I SC,其等效内阻R0定义同戴维宁定理。
Uoc(Us)和R0或者I SC(I S)和R0称为有源二端网络的等效参数。
2. 有源二端网络等效参数的测量方法(1) 开路电压的测量在有源二端网络输出端开路时,用电压表直接测其输出端的开路电压Uoc。
(2)短路电流的测量在有源二端网络输出端短路,用电流表测其短路电流Isc。
(3)等效内阻R0的测量UocR0=──Isc如果二端网络的内阻很小,若将其输出端口短路,则易损坏其内部元件,因此不宜用此法。
四、实验设备可调直流稳压电源、可调直流恒流源、直流数字毫安表、直流数字电压表、万用表、可调电阻箱;Multisim平台五、实验内容被测有源二端网络如图5-1(a)所示,即HE-12挂箱中“戴维宁定理/诺顿定理”线路(a) (b)图 5-11.用开路电压、短路电流法测定戴维宁等效电路的Uoc、R0。
按图5-1(a)接入稳压电源Us=12V和恒流源Is=10mA,不接入R L。
测出U O c和Isc,并计算出R0(测U OC时,不接入mA表。
),并记录于表1。
U OC(V) I SC(mA)R0(kΩ)8.182 21.429 0.38表1 实验数据表一2. 负载实验按图5-1(a)接入可调电阻箱R L。
等效电源

等效电源(戴维南)定理及应用在分析与解答恒定电流问题时,运用等效代替的思维方法,引人“等效电源”概念,可使解题过程简便、快捷,省时省力,提高解题效率。
这种方法对解决电路的动态分析问题、电源最大输出功率或求可变电阻的最大功率及实验误差分析等方面的问题十分有效。
1.等效电源概念什么是“等效电源”呢?任何一个复杂电路都可以化分成两个组成部分,让其中一部分含有电源,另一部分不含电源.两部分通过两个引出端相联系.像这样从电路中划分出来的有两个引出端的部分叫做“二端网络。
若网络内含有电源,叫做“有源二端网络”。
任何一个“有源二端网络”均可以等效为一个有内阻的电源,即“等效电源”。
2.等效电源定理(戴维南定理)1)等效电源定理(戴维南定理):任何一个线性含源二端网络N ,就其两个端点a 、b 来看,总可以用一个电压源(内阻为零的电源,是理想电源之一)与一电阻(相当于电源内阻)串联支路来代替。
电压源的电压(相当于等效电源电动势 E )等于该网络 (相当于等效电源的内阻)等于该网络中所有独立源为零值时(恒压源短路,恒流源开 路)所得网络等效电阻R ab 最简单的有源二端网络电路分别如图1及图2所示,图 1中有:1、串联等效在电路中,当电源与某一个定值电阻串联时,我们可以将电源与定值电阻看为一个整体,等效为一个新的电源,如图1所示。
令电源电动势为E 0,内阻r 0,定值电阻为R 0,新电源等效电动势为E 1,等效内阻我r 1。
当ab 间外电路断路时,ab 两点间电压等于新电源电动势,则:E 1=E 0电源与定值电阻串联,则:r 1=r 0+R 02、并联等效在电路中,当电源与某一个定值电阻并联时,我们可以将电源与定值电阻看为一个整体,等效为一个新的电源,如图2所示 令电源电动势为E 0,内阻r 0,定值电阻为R 0,新电源等效电动势为E 2,等效内阻我r 2。
当cd 间外电路断路时,cd 两点间电压,即电路中AB 两点间电压,等于新电源电动势,则:E 2=U cd =U ABcd 间外电路断路时,原电源直接对定值电阻R 0供电,则:000000r R R E R I U AB +== 联立以上两式解得:00002r R R E E +=将电源与定值电阻看为一个整体,我们自cd 两端向左看过来,新电源的等效内阻即为电源内阻与定值电阻并联后的总电阻,则: 00002r R r R r += 3、串并混联等效①先串后并联式等效在电路中,当电源与某一个定值电阻串联后再与另一个定值电阻并联时,我们可将电源与这两定值电阻看为一个整体,等效为一个新的电源,如下图3所示。
等效电源定理及最大功率的计算.

结点电导矩阵
G1 G5 G 1 G5
电路
G1 G1 G2 G3 G3
U n1 I s U 0 G3 n2 G3 G4 G5 U n3 0
南京理工大学电光学院
G5
a a NS a
iS=iSC
NS
iSC
b
a
iSC
b
RS=Req
b N0
b
Req
电路
南京理工大学电光学院
2.6 等效电源定理
i
+ N
u
. .
i Rs=Req us=uoc +
+ u _
.
_
_
.
戴维南等效电路
解
2.6 等效电源定理
0.8Ω c 1Ω 1A 1Ω 2Ω 2Ω
a
1、先求左边部分电路 的戴维南等效电路。 a、求开路电压U* 。
oc
* UOC 0.2V
R* eq
*。 b、求等效电阻Req
3 2 Req 0.8 2 32
*
电路 南京理工大学电光学院
2.4 结点电压法
电路中含电压源的结点法
第1类情况:含实际电压源:作一次等效变换
G5
Un1 IS1
G2
Un2
G3 + US _
G4 IS2
Un3
电路
南京理工大学电光学院
2.4 结点电压法
第2类情况:含理想电压源支路 G5 Un1 1 . + Us _
n2 2U .
G1
G2
G3
. 3 Un3
G4
4.
电路 南京理工大学电光学院
等效电源定理

等效电源定理
等效电源定理,也称作替代电源定理,是一个基本的电路定理,该定理可以用来简化复杂的电路。
它的定义是:“任意电路都可以被等同的(即对象、功率、相位和频率相同)源或组合的源来表示”。
等效电源定理的原理很简单,它把一个复杂的电路用一个等效的电源来表示。
这样,复杂的电路可以用更简单的方式来考虑,而不用一个一个元件分析。
等效电源定理的物理意义是,在一个复杂的电路中,电流和电压的变化是由电源的影响所决定的,因此可以用一个等效的电源来表示原电路。
该定理可以用两种方式来实现:一种是将源放进电路中,另一种是将电路的元件放进源中。
首先,将源放进电路,也就是等效电源定理的一般形式,即用一个等效源来代替原电路中的元件。
当将源放进电路中时,可以假设电路中的元件(如电阻、电容、电感)可以被忽略,只保留源。
此时,等效源可以模拟电路中的元件形成新的电路网络,因此可以简化原电路的分析。
然后,将电路的元件放进源中,也就是等效电源定理的特例,即将电路中的元件表示成一个电源的形式,这种
电源称为等效电源。
当将电路的元件放进源中时,可以假设电路中的源(如电压源、电流源)可以被忽略,只保留元件。
此时,等效电源可以模拟电路中的源形成新的电路网络,因此可以简化原电路的分析。
等效电源定理有助于简化电路的分析,使电路的计算更加简单、快速。
它可以用来求解复杂的电路,包括电路中的源和元件,以及电路中的各种参数,如电压、电流、功率等。
总的来说,等效电源定理是一个重要的电路定理,它可以用来简化复杂的电路,减少电路的计算时间,使电路的分析更加简单易行。
等效电源定理

等效电源定理《等效电源定理》是一种有关电学基础理论的定理,它描述了一个电路中各部分之间的能量关系,在电路分析和设计中有很广泛的应用。
据美国科学家大卫沃森于1845年提出,它经过多年的发展和改进,在学术上被公认为是最强有力的电力学定理。
等效电源定理定义了一个电路中各部分之间的能量关系,它表明每一部分都可以用一个等效电源来表示,并用一个等效电流源来表示它们之间的能量转化。
因此,可以将电路中的每一部分抽象为一个等效电源和一个等效电流源,这样就可以更容易地进行电路分析,这对电路设计具有重要意义。
为了消除非等效电源或电流源对电路的影响,需要计算每一部分的电压和电流,然后将计算结果代入等效电源定理,求出等效电源的值。
求解的主要方法有用电路分析法确定等效电源,用拉普拉斯变换确定等效电源,用卡尔曼滤波器确定等效电源等。
等效电源定理在电路设计中有广泛的应用。
它可以用来分析复杂的电路,帮助我们确定元件的电压和电流,以及求解等效电源等。
此外,等效电源定理还可用于有关滤波器、可调电路等电路的分析与设计,它可以更清楚地表示电路的特性,从而为电子工程师们的工作提供了便利,也有利于电子设备的更新和改进。
等效电源定理提供了一种更为简洁的电路分析方法,它能够有效地分析复杂电路中的特性,而不需要考虑电路中每个部分的细节。
此外,它还有助于精确地计算电路中各元件之间的电压、功率、频率等参数,以便于建立起复杂的电路模型,从而实现对电路的更有效的控制。
总之,等效电源定理是一种强大的电力学定理,它为电路分析和设计提供了一种简单的分析方法,具有非常广泛的应用前景。
它将电路中的每一部分抽象为一个等效电源和一个等效电流源,可以用来分析复杂电路,确定元件的电压、电流,求解电路中各元件之间的参数,从而实现对模型电路的更有效的控制。
等效电源定理

注意:并非任何含源线性电阻单口网络都能找到戴维 宁—诺顿等效电路。
例4 求图示单口的戴维宁-诺顿等效电路。
例4 求图示单口的戴维宁-诺顿等效电路。
如图(a)所示单口网络,其端口电压和电流均为零,即 u=i=0,其特性曲线是u-i平面上的坐标原点,如图(b)所示。 该单口不存在戴维宁等效电路和诺顿等效电路。
应用(主要用于电路中某一支路响应的计算):
具体步骤:
1.移去待求支路,使电路成为一个含源的单口网络; 2.求所得到的含源单口网络的开路电压uoc; 3.求所得到的含源单口网络的除源等效输入电阻Ro。 4.画出相应的等效电源电路,接入所移去待求的支路,求支
路响应。
求所得到的含源单口网络的等效输入电阻Ro。
电路分析方法小结
电路分析方法共讲了以下几种: 基尔霍夫定律(KVL,KCL)求解
两种电源等效互换 网孔分析法 节点电位法
总结 每种方法各有 什么特点?适 用于什么情况?
叠加原理 等效电源定理
戴维南定理 诺顿定理
1.关于直流电路分析方法
直流电路的分析方法有多种,如:应用基尔 霍夫定律求解、电源等效变换法、节点电位法、 网孔分析法、应用戴维南及诺顿定理、应用叠 加定理等。
❖ 9-6=6I1-3I2 ④ ❖ 6=3I2+5I ⑤ ❖由①④⑤解得:I1≈0.67A I2≈0.33A
I=1A
2022/1/18
方法二:等效电源法
❖如图
2022/1/18
方法二:等效电源法
❖由分流公式
2022/1/18
方法三: 节点分析法
❖如图1,设B点电位为0,则
2022/1/18
E
UA
分析方法?
如图5,求通过 R4的电流及两端 电压,应该选择 戴维南定理或叠
等效电源定理

等效电源定理等效电源定理包括电压源等效(戴维南定理),和电流源等效(诺顿定理)两个定理。
其中,电压源等效定理在电路故障诊断中应用较多,其内容是:任何一个线性的有源二端网络对外电路而言,可以用一个电压源来等效代替。
如图(1-08)所示,其中:等效电压源的电动势E(或源电压Vo)的数值,等于该有源二端网络的“开路电压”;等效电压源的内阻Ro等于该有源二端网络“除源”后的等效电阻值。
所谓的“开路电压”是指:将负载RL从电路上断开后,a、b间的电压;所谓“除源”是指:假设将有源二端网络中的电源去除(衡压源短路、衡流源开路)。
电压源等效定理是“模块化电路分析方法”和后面将要探讨的“电器故障诊断层次分析法”的理论基础。
根据这个定理,我们可以将任何线性有源二端网络,或者线性四端传输网络的输出端,等效为一个电压源,按照电压源的特性去分析诊断电路故障,从而大大简化了电路分析或故障诊断的难度。
电压源等效定理中的“电动势”既可以是直流的,也可以是交流的,因此,该定理既适合电源环节的电路故障诊断,也适合于信号通道的故障诊断。
在应用于信号通道时,上述“电动势”就是信号源的电压(交流),称为“源电压”;上述等效“内阻”就是信号源得输出电阻。
电流源等效定理类似于电压源等效定理,其内容是:任何一个线性的有源二端网络对外电路而言,可以用一个电流源来等效代替,如图(1-09)所示。
其中,等效电流源的恒流源Is等于该有源二端网络的“短路电流”;等效电流源的内阻Rs等于该有源二端网络“除源”后的等效电阻值。
由此可见,对于同一个有源二端网络,既可以等效为电压源形式,也可以等效为电流源形式,而且,Rs于Ro是相同的,即:Rs=Ro。
例(1-07):有一台实验室使用的直流稳压电源,内部电路不详,希望通过实验的方法求得它的源电压Vo和输出电阻Ro,请设计测量方法。
分析:直流稳压电源的输出端,可以看成是线性有源二端网络,由电压源等效定理可知:等效电压源的电动势E(源电压Vo)的数值,等于该有源二端网络的开路电压。
等效电源定理及应用

电压源的电压等于有源二端网络的开路电压uoc;串联电阻等于有源二端网络全部独立源置零后的等效电阻Ri.
关于无源二端网络的等效电阻的三种计算方法:
I 等效电源定理包括戴维南定理和诺顿定理.
例3、求如图所示电路中3.
18 2A
6 3 (b)中电压源电阻串联电路为戴维南等效电路,电压源电压等于有源二端网络的开路电压,如图(c)所示;
解:(1)求开路电压UOC: 断开所求支路6Ω电阻后得一含源二端网络,如图(b)
所示。由电路图可求二端网络的开路电压为 UOC=2×2=4v
(2)求等效电阻Ri:
将含源泉二端网络中的所有独立源置零,如图(c)所示。 则二端网络的等效电阻为:
Ri=2Ω (3)求支路电流I。
用戴维南等效电路代替含源二端网络,如图(d)所
串联电阻等于有源二端网络除源后得到的无源二端网络的等效电阻,如图(d)所示。
电路如图所示,US1=8V,US2=4V,R1=R2=4Ω,R3=2Ω。
2Ω电阻的电压:用出戴维南等效电路,接上3.
( d ) 图 ( a ) 的 等 效 电 路 下图为戴维南定理示意图:(a)中所示NS为含有独立源、线性电阻或受控源的有源二端网络。
例3、求如图所示电路中3.2Ω电阻两端的电压Uo
解(1)求开路电压UOC 如图(b)所示,则
I1I261401A UOC10I14I2101416V
(2)求等效电阻Ri
电路如图(c)所示: 独立电压源短路后,
外加电源电压U,设 端口电流为I 则有
I
1
6
4
4
I
0.4I
U 10I1 6I1 16I1 6.4I
图(a)的等效电路,如图(d)所示,由图可求得I为: 例1、用戴维南定理求如图所示电路中的电流I
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.3.2 戴维南定理的表述
戴维南定理: ★任何一个线性有源单口网路对外电路的作用, 可用一个含内阻的电压源等效代替。 ★该电压源的us等于有源单口网路两端钮ab间的开 路电压uoc; ★内阻R0等于该单口网路中所有独立电源不作用时 无源单口网路在ab端的等效电阻Req。 ★网路内独立电源不作用是指电流源is置0(开路)、 电压源us置0(短路线取代), ★等效电源的us的极性与开路电压uoc的极性相一致。 请见图解 :
Ucd R3 R4 Icb R2 Is Icb U s2
8 中北大学国家级电工电子实验教学示范中心
戴维南定理例题1
所以 3 4Icb 26 Icb 9
Icb
21 9
7 3
A
U oc
Us2
R3 I c b
9 3
7 3
2V
②求等效电阻如图(b),则
Req
R3 R2 R4
方法再求Us1。感受一下不 同方法的应用。
10 中北大学国家级电工电子实验教学示范中心
例题1另一解
按题意Uab = Us2,db两点等 电位,R3中无电流将其断,此 时得下图(a)电路。再把Us2 与Is的串联组合等效成Is,如图 (b)。最终变成图(c)。
11 中北大学国家级电工电子实验教学示范中心
戴维南定理是有源单口网路的基本属性。
7 中北大学国家级电工电子实验教学示范中心
戴维南定理例题1
[例]图示电路中已知Us2 = 9V , Uab = 9V , Is = 6A , R1 = 1Ω, R2 = 2Ω, R3 = 3Ω,R4 = 4Ω, 试求Us1
解一:用戴维南定理化简ab 端口右边的网路。 ①求ab端的开路电压Uoc,如图 (a)所示,先求Icb再求Uoc最 为捷径,因为
1 中北大学国家级电工电子实验教学示范中心
4.3.1用逻辑推理得到等效电源定理
如图(a)所示的不平衡电桥电路,欲求对角线上 的电流i5或电压u5,我们可把对角线R5拉出来,如图 (b)所示。以ab端口为界,则电路变成两个单口 网路对接的电路。这个概念可以抽象成图(c)的 一般化形式。
2 中北大学国家级电工电子实验教学示范中心
14 中北大学国家级电工电子实验教学示范中心
戴维南定理例题2解答
①断开Ru求ab端的开路电压Uoc如图(a),选d点为 零电位参考点,则
R3 R2 R4
32 4
324
2
由此得戴维南等效电路如下
9 中北大学国家级电工电子实验教学示范中心
戴维南定理例题1
③所得戴维南等效电路如图示,则Us1可求
I1
U ab U oc Req
92 2
3.5 A
U s1 R1I1 U ab 1 3.5 9 12.5 V
另外我们不妨用其它等效
例题1另一解
其中
U seq R2I s 2 6 12 V
Req R2 R4 2 4 6
I1
Uab U seq Req
91 U ab 1 3.5 9 12.5 V
思考:
两种解法不同,但所得到的等效电路结构形式相 同。虽然参数不同,然而得到的解答却相同,其 中蕴涵着什么意义?
4 中北大学国家级电工电子实验教学示范中心
戴维南定理的图解表示
用图解方法表示戴维南定理的全部内容如下:
所以用戴维南定理解题分三步走①求待求端口的 开路电压;②求端口的等效内阻③建立戴维南等 效电路求解。
5 中北大学国家级电工电子实验教学示范中心
戴维南定理的证明
①图(a)为原网路,负载RL上有电流i电压u;②把负载断
12 中北大学国家级电工电子实验教学示范中心
4.3.4 应用戴维南定理应该注意的问题
① 首先应该明白戴维南定理只适用于线性 有源单口网路,网路内部含有非线性元件时 戴维南定理不适用。
② 等效电路的端口和极性一定要与原电路 的端口对应。
③ 含有受控源的有源单口网路应用戴维南 定理时控制量必须在网路的内部。
用逻辑推理得到等效电源定理
把上图例一般化为图(c),左边是一个内部含有独 立源的单口网路N;右边是一个不含独立源的单口 网路N0。从能量观点讲,有源单口网路向无源单 口网路输送能量。那么一个设想会自然产生:在 左边的有源单口网路能否等效成一个电源?回答 是肯定的。这就是下面讲到的两个定理。
3 中北大学国家级电工电子实验教学示范中心
下面请看例题:
13 中北大学国家级电工电子实验教学示范中心
戴维南定理例题2
[例] 图(a)电路中已知Us = 3V,R1 = R2= 1Ω, R3 = R4 = 2Ω, Ru的端口特性为i =67.5u2 A (u ≥ 0)。试 求非线性电阻Ru上的电流、电压和abc各点的电位。
解:经变换可得图(b)的戴维南等效电路
开,有开路电压uoc,i=0;③图(b)与图(c)等效;④
图(d)与图(a)等效。那么依叠加原理:在图(d)的
电路中当us2不作用而其余所有电源作用时,则i' = 0 ,见图
(c);当us2单独作用,其余所有电源不作用时,则
i
us 2
uoc
i i i
uoc
useq
(Req RL ) (Req RL )
(Req RL ) R0 RL
6 中北大学国家级电工电子实验教学示范中心
戴维南定理的证明
结论:前式 i i i uoc useq
(Req RL ) R0 RL
该式正是含内阻电压源的电流表达式。它表明: 从端口上看,有源单口网路对外电路的作用,可 以用一个含内阻的电压源来等效代替。该电压源 的源电压等于有源单口网路的开路电压,其内电 阻R0就是有源单口网路去源后的等效电阻。故戴 维南定理得证。此刻应该认识到:
§4.3 等效电源定理
核心提示: 等效电源定理仍然是电路的等效变换方法,它在 电路分析中占有很重要的地位。学习该定理,可 以很好地锻炼我们的逻辑思维。
等效电源定理包括了现今流行称呼的戴维南定理 和诺顿定理。
1883年由法国的电报工程师戴维(M.L.Thevenin) 提出了现今称谓的戴维南定理。然而事实上与戴 维南定理有相同概念的“等效发电机定理”,早 在1853年就由德国物理学家亥姆霍兹提出来了。
