数字信号处理第三章习题答案
第三章---数字信号处理课后答案刘顺兰版

第三章 部分习题解答(数字信号处理(第二版),刘顺兰,版权归作者所有,未经许可,不得在互联网传播)3.1如果一台通用计算机的速度为平均每次复乘需100μs ,每次复加需20μs ,今用来计算N=1024点的)]([n x DFT ,问用直接运算需要多少时间,用FFT 运算需要多少时间? 解: ∑−=====101010,21024,)()(N n nk N M N Wn x k X直接运算所需的总时间为s N N s N T d μμ20)1(1002×−+×=秒分62126201023102410010242=≈××+×=s s s μμFFT 运算所需总时间为 s NM s M N T F μμ201002×+×=s s s 717.02010102410010102421=××+×××=μμ3.2在基-2FFT 算法中,最后一级或开始一级运算的系数10==N p N W W ,即可以不做乘法运算。
问(1)乘法可节省多少次,所占百分比为多少? 解: 可节省2N 次,所占百分比为 %100log 1%100log 2222×=×N N N N 如 8=N 则为%3.33%10031≈×3.11以20kHz 的采样率对最高频率10kHz 的带限信号()a x t 采样,然后计算)(n x 的1000N =个采样点的DFT ,即210()()N j nk N n X k x n eπ−−==∑,1000N =.(1)试求频谱采样点之间的频率间隔是多少?(2)在()X k 中,200k =对应的模拟频率是多少?(3)在()X k 中,700k =对应的模拟频率是多少?解:(1)频谱采样点之间的频率间隔为:20000201000s f f Hz N Δ=== (2)200k =对应的模拟频率为 20000200400041000s k f f k Hz kHz N ==×== (3)因700k =大于N/2,故其对应的模拟频率为 20000()300600061000s k f f N k Hz kHz N =−=×== 3.12 对一个连续时间信号)(t x α采样1s 得到一个4096个采样点的序列:(1) 若采样后没有发生频谱混叠,)(t x α的最高频率是多少?(2) 若计算采样信号的4096点DFT,DFT 系数之间的频率间隔是多少Hz?(3) 假定我们仅仅对Hz f Hz 300200≤≤频率范围所对应的DFT 采样点感兴趣,若直接用DFT,要计算这些值需要多少次复乘?若用按时间抽取FFT 则需要多少次? 解:(1)由题意可知:4096s f Hz =,故)(t x α的最高频率/22048h s f f Hz == (2)409614096s f f Hz N Δ=== (3)直接用DFT 计算,所需要的复乘次数为(3002001)1014096413696d M N =−+=×=若用按时间抽取FFT 则需要的复乘次数为10log 204812245762F N M N ==×= 3.17若给定两个实序列)(1n x 、)(2n x ,令:)()()(21n jx n x n g +=,)(kG 为其傅里叶变换,可以利用快速傅里叶变换来实现快速运算,试利用傅里叶变换的性质求出用)(k G 表示的)(1n x 、)(2n x 的离散傅里叶变换)(1k X 、)(2k X 。
数字信号处理 Chapter03答案

11
3.2 Properties of the z-Transform
Ex. ( linearity) x(n) = [3(2n) – 4(3n)] u(n) 3 4 – 1 – 2z –1 1 – 3z –1
X(z) =
ROC: |z| > 3
12
3.2 Properties of the z-Transform
z = re
jθ
=
n =−∞
∑ x ( n )r
−n
∞
− n − jθ n
e
X ( z) ≤
n =−∞
∞
∑
−1
x (n) r
+∑
n=0
∞
∞
x ( n) rn
x (n) rn
≤ ∑ x ( −n ) r + ∑
n n =1 n =0
7
3.1 The z-Transform
3.1.1 The Direct z-Transform
3.2 Properties of the z-Transform
X(z) = ∑ x(n) z – n
14
3.2 Properties of the z-Transform
X(z) = ∑ x(n) z – n
15
X(z) = ∑ x(n) z – n
16
3.3 Rational z-Transforms
1 2 −1 1 2 2
X ( z ) = 1+ z + (
X ( z) = 1 1− z
1 2 −1
)
z + .... + (
−2
1 n 2
)
z −n
数字信号处理课后答案+第3章(高西全丁美玉第三版)

k = 0, 1, ⋯, N − 1
(8) 解法一 直接计算:
1 jω 0 n x8 (n) = sin(ω0 n) ⋅ RN (n) = [e − e − jω 0 n ] R N ( n ) 2j
X 8 ( n) =
∑
n =0
N −1 kn x8 (n)WN
1 = [ e jω 0 n − e − jω 0 n ] e 2 j n =0
1− e
j(ω0 −
2π N k) 2π N −1 sin (ω0 − j(ω0 − k )( ) N 2 N 2 =e 2π sin (ω0 − k ) / 2 N
k = 0, 1, ⋯, N − 1
或
X 7 (k ) =
1 − e jω0 N
2π j(ω0 − k ) N 1− e
N −1
N −1
由于 所以
∑
n =0
N −1
n WN ( m + k )
N = 0
m= N −k m ≠ N − k , 0≤ m ≤ N − 1
DFT[X(n)]=Nx(N-k)
N −1 k =0
k=0, 1, …, N-1
5. 如果X(k)=DFT[x(n)], 证明DFT的初值定理
证: 由IDFT定义式
2π mn +θ ) N 2π mn +θ ) N ]
1 = [e 2j
j(
−e
− j(
2π = sin mn + θ N
n=0, 1, …, N-1
3. 已知长度为N=10的两个有限长序列:
1 0 ≤ n ≤ 4 x1 (n) = 0 5 ≤ n ≤ 9
数字信号处理第三版(姚天任、江太辉) 答案 第三章

3.1 图 P3.1 所示的序列 x(n) 是周期为 4 的周期性序列。请确定其傅里叶级数的系数 X (k) 。
∑ ∑ ∑ 解: X (k)
=
N −1
x(n)WNnk
=
N −1
x(−n)WNnk
=
−( N −1)
x(n)WN−nk
=
X (−k)
解:图 P3.5_1 所示的是计算这两个序列的周期卷积 x3 (n) 的过程,可以看出,x3 (n) 是 x1 (n) 延时 1 的结果, 即 x3(n) = x1(n −1) 。
3.6 计算下列序列的N点DFT:
(1) x(n) = δ (n)
(2) x(n) = δ [(n − n0 )]N * RN (n), 0 < n0 < N
总计需要时间: (105 + 21)s = 126s
用 FFT 计算 DFT:
复数乘法:
N 2
log2
N
=
5120次, 5120 ×100μ s
≈
0.512s
复数加法: N log2 N = 10240次,10240× 20μs ≈ 0.2048s
总计需要时间: (0.512 + 0.2048)s = 0.7168s
(2) x2 (n) = x ⎡⎣(2 − n)⎤⎦4 R4 (n)
解: x1(n) 和 x2 (n) 的图形如图 P3.7_1 所示:
3.8 图 P3.8 表示一个 4 点序列 x(n) 。 (1)绘出 x(n) 与 x(n) 的线性卷积结果的图形。 (2)绘出 x(n) 与 x(n) 的 4 点循环卷积结果的图形。 (3)绘出 x(n) 与 x(n) 的 8 点循环卷积结果的图形,并将结果与(1)比较,说明线性卷积与循环卷
数字信号处理第三版(姚天任、江太辉) 答案 第三章

第三章离散傅里叶变换及其快速算法习题答案参考3.1 图P3.1所示的序列(xn 是周期为4的周期性序列。
请确定其傅里叶级数的系数(X k。
解:(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.2 (1设(xn 为实周期序列,证明(x n 的傅里叶级数(X k 是共轭对称的,即*((X k X k =− 。
(2证明当(xn 为实偶函数时,(X k 也是实偶函数。
证明:(1 111**((([(]((N nk N n N N nk nkNNn n Xk x n W Xk x n W xn W X−−=−−−==−=−===∑∑∑ k(2因(xn 为实函数,故由(1知有 *((Xk X k =− 或*((X k X k −= 又因(xn 为偶函数,即((x n x n =− ,所以有(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.3 图P3.3所示的是一个实数周期信号(xn 。
利用DFS 的特性及3.2题的结果,不直接计算其傅里叶级数的系数(Xk ,确定以下式子是否正确。
(1,对于所有的k; ((10Xk X k =+ (2((Xk X k =− ,对于所有的k; (3; (00X=(425(jkX k eπ,对所有的k是实函数。
解:(1正确。
因为(x n 一个周期为N =10的周期序列,故(X k 也是一个周期为N=10的周期序列。
(2不正确。
因为(xn 一个实数周期序列,由例3.2中的(1知,(X k 是共轭对称的,即应有*((Xk X = k −,这里(X k 不一定是实数序列。
(3正确。
因为(xn (0n ==在一个周期内正取样值的个数与负取样值的个数相等,所以有 10(0N n Xx −=∑ (4不正确。
数字信号处理课后第三章习题答案

1 e j 0 N
2 j(0 k ) N 1 e
k 0, 1, , N 1
(8) 解法一
直接计算:
1 j 0 n x8 (n) sin(0 n) RN (n) [e e j 0 n ] R N ( n ) 2j
X 8 (n)
n 0
N 1
kn x8 (n)WN
k 0, 1, , N 1
(4)
X (k ) WNkn
n 0
m1
π j ( m1) k 1 WNkm N e 1 WNk
π sin mk N R (k ) N π sin k N
第3章
离散傅里叶变换(DFT)及其快速算法 (FFT)
所以
DFT[ X (n)] X (n)W
n 0
N 1
N 1
kn N
N 1 mn kn x(m)WN WN n 0 m 0
N 1
n ( m k ) x(m)WN m 0 n 0
N 1
第3章
由于
离散傅里叶变换(DFT)及其快速算法 (FFT)
第3章
离散傅里叶变换(DFT)及其快速算法 (FFT)
(10) 解法一
X (k )
n 0
N 1
kn nWN
k 0, 1, , N 1
上式直接计算较难, 可根据循环移位性质来求解X(k)。 因为x(n)=nRN(n), 所
以
x(n)-x((n-1))NRN(n)+Nδ(n)=RN(n) 等式两边进行DFT, 得到
1 [e j0 n e j0 n ] e 2 j n 0
数字信号处理》课后作业参考答案
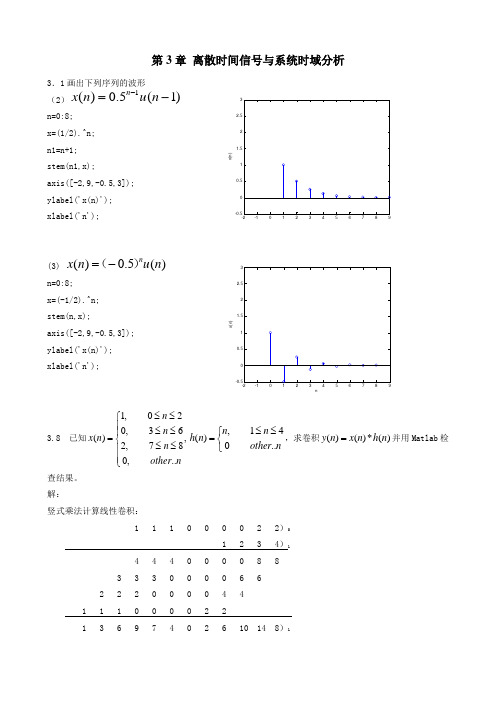
第3章 离散时间信号与系统时域分析3.1画出下列序列的波形(2)1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-()n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩,求卷积()()*()y n x n h n =并用Matlab 检查结果。
解:竖式乘法计算线性卷积: 1 1 1 0 0 0 0 2 2)01 2 3 4)14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8)1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果:x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx (n )=5sin(n) 解:2214337w πππ==,所以N=14 (2) 326n ππ-x (n )=sin()-sin(n)解:22211213322212,2122612T N w T N w N ππππππ=========,所以(6) 3228n π-x (n )=5sin()-cos(n) 解:22161116313822222()T N w T w x n ππππππ=======,为无理数,所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=,()4()nx n u n -=,(1)4y -=,(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应,并画出图形。
数字信号处理第3章答案 史林 赵树杰编著

第三章作业题 答案作业:%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 3.2设()j X e ω是序列()x n 的离散时间傅里叶变换,利用离散时间傅里叶变换的定义及性质,求下列各序列的离散时间傅里叶变换。
(4)()(2)g n x n =解:利用DFT 的定义进行求解。
()22()()(2)()j j nn j nn jmm j G eg n ex n ex m eX eωωωωω+∞-=-∞+∞-=-∞+∞-=-∞====∑∑∑(这是一种错误的解法,正确的如下所示。
)()()()()()()2222222()()2(2)()1()1()21()()211221122j j nn j nj m n m n j nn jn j n n j j j j G eg n em nx n e x m ex n x n e x n e x n e X e X eX eX eωωωωωπωωπωωω+∞-=-∞+∞+∞--=-∞=-∞+∞-=-∞+∞-=-∞+====⎡⎤=+-⎣⎦⎡⎤=+⎣⎦=+=+-∑∑∑∑∑(注意,此处n 为奇数的项为零。
)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 3.3试求以下各序列的离散时间傅里叶变换。
501()()(3)4nm x n n m δ∞==-∑解:利用DTFT 的定义和性质进行求解。
()50030()1()(3)41()(3)41()41114j j nn nj nn m nj nm n j mm j X ex n en m en m eeeωωωωωωδδ+∞-=-∞+∞∞-=-∞=+∞+∞-==-∞+∞-=-==-=-==-∑∑∑∑∑∑%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 3.4设()x n 是一有限长序列,已知0,1,2,3,4,51,2,0,3,2,1;()0,n x n =--⎧=⎨⎩其它它的离散时间傅里叶变换为()j X e ω。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
fl(n)长度为27,f(n)长度为20.前面已推出二者的关系为
f (n) fl (n 20m) R20 (n) m
只有在如上周期延拓序列中无混叠的点上,才满足f(n)=fl(n),所以
f (n) fl (n) x(n) y(n), 7 n 19
图解说明
解 (1) 已知F=50Hz
Tp min
1 F
1 50
0.02s
(2)
1
1
1
Tmax
fs min
2 fmax
2 103
0.5ms
(3)
N min
Tp T
0.02s 0.5 103
40
(4)频带宽度不变就意味着采样间隔T不变,应该使记录时间 扩大一倍为0.04s实现频率分辨率提高1倍(F变为原来的1/2).
2
N
2
N
k) k)
N] 2 ,k 2]
0,1,L
,N
1
1 e j0N
或
X7 (k)
1
e
j (0
2 N
k
)
,k
0,1,L
,N
1
(9) 解法一
x9 (n)
cos(0n)RN
(n)
1 [e 2
j0n
e
] j0n
N 1
X9 (k) x9 (n)WNkn n0
解
(1)
X (k)
N 1
1WNkn
n0
N 1 j 2 kn
eN
n0
j 2 kN
1
e
N j 2
k
1e N
N,
k 0
0,
k 1, 2,L , N 1
N 1
N 1
(3)
X (k)
(n n0 )WNkn
W kn0 N
0,
,0 k N 1 km
(7)
X7 (k)
N 1
e W j0n kn N
n0
e N 1
j
(0
2 N
k
)n
n0
1 e j
(0
2 N
k
)
N
1
e
j
(0
2 N
k
)
ej
(0
2 N
k
)(
N 1) 2
sin[(0 sin[(0
X (k )WNkn , n
k 0
0,1,L
,N
1
可知
x(0)
1
N 1
X (k)
N k0
14. 两个有限长序列x(n)和y(n)的零值区间为
x(n)=0, n<0, 8≤n
y(n)=0, n<0, 20 ≤ n 对每个序列作20点DFT,即
X (k)=DFT [x(n)], k=0,1,…,19
所以
X9 (k) DFT[x9 (n)] X 7e (k)
1 2
[
X7
(k)
X
* 7
(
N
k )]
1 1 e j0N
1 e j0N
2
[ 1
e
j
(0
2 N
k
)
1
e
j
(0
2 N
k
)
]
3. 长度为N=10的两个有限长序列
1, 0 n 4 x1(n) 0, 5 n 9
教材第三章习题解答
1. 计算以下序列的N点DFT,在变换区间0≤n≤N-1内,序列 定义为
(1) x(n) 1
(3) x(n) (n n0 ), 0 n0 N
j 2 mn
(5) x(n) e N , 0 m N
(7) x(n) e j0n RN (n) (9) x(n) cos(0n) RN (n)
1, 0 n 4 x2 (n) 1, 5 n 9 作图表示 x1(n) 、 x2 (n) 和 y(n) x1(n) ,x2 (n)
循环卷积区间长度L=10。
解 x1(n) 、 x2 (n) 和 y(n) x1(n) x2 (n) 分别如题3解图
(a)、(b)、(c)所示。
(n n0 ) WNkn0 ,
n0
n0
k 0,1,L , N 1
(5)
X (k)
N 1 j 2 mn
eN
n0
WNkn
N 1 j 2 (mk )n
eN
n0
j 2 (mk ) N
1 e
N j 2 (mk )
1e N
N, k m
1
N 1
[e j0n
e
]e j0n
j 2 kn N
2 n0
1 1 e j0N
1 e j0N
2
[ 1
e
j
(0
2 N
k
)
1
e
j (0
2 N
k
)
]ห้องสมุดไป่ตู้
解法二 由DFT共轭对称性可得同样的结果。 因为
x9 (n) cos(0n) RN (n) Re[x7 (n)]
1-27 1-7
1-27
21-47
41-67
21-27 8-20
7-19 当从0开始时 候
15.用微处理器对实数序列作谱分析,要求谱分辨率F≤50Hz,
信号最高频率为1kHz,试确定以下各参数;
(1)最小记录时间 Tpmin ; (2)最大取样间隔 Tmax ; (3)最少采样点数 Nmin ; (4)在频带宽度不变的情况下,将频率分辨率提高一倍的N值。
(a)
x1(n)
x2(n)
(b)
y (n)
(c)
(a) x1(n) (b) x2 (n)
(c) y(n) x1(n) x2 (n)
5.如果X(k)=DFT[ x(n)],证明DFT的初值定理
x(0)
1
N 1
X (k)
N k0
证明 由IDFT定义式
x(n)
1 N
N 1
Y(k)=DFT [y(n)], k=0,1,…,19
如果
F(k)=X(k)▪Y(k), k=0,1,…,19
f(n)=IDFT [F(k)], k=0,1,…,19 试问在哪些点上f(n)=x(n)*y(n)?为什么?
解
如前所述,记 fl (n) x(n) y(n) , 而
f (n) IDFT[F(k)] x(n) y(n)
0.04s Nmin 0.5ms 80
