直角三角形全等的判定
直角三角形全等的判定
知识结构
重点与难点分析：
本节课教学方法主要是“自学辅导与发现探究法”。
力求体现知识结构完整、知识理解完整；注重学生的参与度，在师生共同参与下，探索问题、动手试验、发现规律、做出归纳。
让学生直接参加课堂活动，将教与学融为一体。
具体说明如下：
本节课开始，让同学们自己思考问题：判定三角形全等的方法有四种，如果这两个三角形是直角三角形，那么判定它们全等的方法有哪些呢？学生展开讨论，初步形成意见，然后由教师答疑。
这样促动了学生学习，体现了以“学生为主体”的教育思想。
（2）在层次教学中培养学生的思维水平
本节课的层次主要表现为两个方面：一是对公理的多层次理解；二是综合练习的多层次变化。
公理的多层次理解包括：明确公理的条件及结论；公理的文字语言、图形语言、符号语言的理解及掌握；公理的作用。
这里特别强调三个方面：1、特殊三角形的特殊性；2、归纳总结判定直角三角形全等的方法。
综合练习的多层次变化：首先给出直接应用公理证明三角形全等的题目；然后给出变式题目；最后给出综合应用题目。
这里注意两点：一是给出题目后先让学生独立思考，并按教材的形式严格书写。
二是给出的综合题目有一定的难度，教学时，要注意引导学生分析问题解决问题的思考方法。
教法建议：
由“先教后学”转向“先学后教”
本节课开始，让同学们自己思考问题：判定三角形全等的方法有四种，如果这两个三角形是直角三角形，那么判定它们全等的方法有哪些呢？学生展开讨论，
初步形成意见，然后由教师答疑。
这样促动了学生学习，体现了以“学生为主体”的教育思想。
（2）在层次教学中培养学生的思维水平
本节课的层次主要表现为两个方面：一是对公理的多层次理解；二是综合练习的多层次变化。
公理的多层次理解包括：明确公理的条件及结论；公理的文字语言、图形语言、符号语言的理解及掌握；公理的作用。
这里特别强调三个方面：1、特殊三角形的特殊性；2、归纳总结判定直角三角形全等的方法。
综合练习的多层次变化：首先给出直接应用公理证明三角形全等的题目；然后给出变式题目；最后给出综合应用题目。
这里注意两点：一是给出题目后先让学生独立思考，并按教材的形式严格书写。
二是给出的综合题目有一定的难度，教学时，要注意引导学生分析问题解决问题的思考方法。
教学目标：
1、知识目标：
（1）掌握已知斜边、直角边画直角三角形的画图方法；
（2）掌握斜边、直角边公理；
（3）能够使用HL公理及其他三角形全等的判定方法实行证明和计算.
2、水平目标：
（1）通过尺规作图使学生得到技能的训练；
（2）通过公理的初步应用，初步培养学生的逻辑推理水平.
3、情感目标：
（1）在公理的形成过程中渗透：实验、观察、归纳；
（2）通过知识的纵横迁移感受数学的系统特征。
教学重点：SSS公理、灵活地应用学过的各种判定方法判定三角形全等。
教学难点：灵活应用五种方法（SAS、ASA、AAS、SSS、HL）来判定直角三角形全等。
教学用具：直尺，微机
教学方法：自学辅导
教学过程：
1、新课引入
投影显示
问题：判定三角形全等的方法有四种，若这两个三角形是直角三角形，那么判定它们全等的方法有哪些呢？
这个问题让学生思考分析讨论后回答，教师补充完善。
2、公理的获得
让学生概括出HL公理。
然后和学生一起画图做实验，根据三角形全等定义对公理实行验证。
（这里用尺规画图法）
公理：有斜边和一条直角边对应相等的两个直角三角形全等。
应用格式：（略）
强调说明：
（1）、格式要求：先指出在哪两个三角形中证全等；再按公理顺序列出三个条件，并用括号把它们括在一起；写出结论。
（2）、判定两个直角三角形全等的方法。
（3）特殊三角形研究思想。
3、公理的应用
(1)讲解例1（投影例1）
例1求证：有一条直角边和斜边上的高对应相等的两个直角三角形全等。
学生思考、分析、讨论，教师巡视，适当参与讨论。
找学生代表口述证明思路。
分析：首先要分清题设和结论，然后按要求画出图形，根据题意写出、已知求证后，再写出证明过程。
证明：（略）
(2)讲解例2。
学生分析完成，教师注重完成后的点评。
）
例2：如图2，△ABC中，AD是它的角平分线，且BD＝CD，DE、DF分别垂直于AB、AC，垂足为E、F.
求证：BE＝CF
分析： BE和CF分别在△BDE和△CDF中，由条件不能直接证其全等，但可先证明△AED≌△AFD，由此得到DE＝DF
证明：（略）
（3）讲解例3（投影例3）
例3：如图3，已知△ABC中，∠BAC＝，AB＝AC，AE是过A的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：
(1)BD＝DE+CE
(2)若直线AE绕A点旋转到图4位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何，请证明；
(3)若直线AE绕A点旋转到图5时（BD＞CE），其余条件不变，BD与DE、CE 的关系怎样？请直接写出结果，不须证明
学生口述证明思路，教师强调说明：阅读问题的思考方法及思想。
4、课堂小结：
(1)判定直角三角形全等的方法：5个（SAS、ASA、AAS、SSS、HL）在这些方法的条件中都至少包含一条边。
(2)直角三角形判定方法的综合使用
让学生自由表述，其它学生补充，自己将知识系统化，以自己的方式实行建构。
5、布置作业：。
直角三角形全等的判定
E P D C
根据SAS可测量其余两边与这两边的夹角； 根据ASA,AAS可测量对应一边和一锐角。
（2）如果他只带一个卷尺，能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的直 角边和斜边,发现它们分别对应相等。于是，他 就肯定“两个直角三角形是全等的”。 是直角三角形全等最易选择的判定方法
作业：
• 课本P79 练习第2题、习题第6题.
A
斜边、直角边公理 (HL)
斜边和一条直角边对应相等的两个 直角三角形全等.（斜边、直角边）或（HL）
A A' B B' C'
几何语言：
∵∠C=∠C′=90
∴在Rt△ABC和Rt△ABC 中
C
AB=AB
BC= BC （或 A C= A´C´ ）
∴Rt△ABC≌ Rt△ABC (HL)
例：
“三月三，放风筝”，如图是小明制作的风筝， 他用量角器测 ∠B=∠D=90°，并且侧得BC=CD，不用再测 量，他就知道AB=AD，请你用所学知识加以 说明。 证明：∵∠Ｂ＝∠Ｄ＝９０° Ａ
∴ ∆ABC 与∆ADC都是直角三角形。 在Ｒt∆ABC 与Ｒt ∆ADC中 ∵ＢＣ＝ＤＣ ＡＣ＝ＣＡ Ｄ∴Ｒt∆ABC ≌Ｒt ∆ADC（Ｈ.Ｌ.). ∴ＡＢ＝ＡＤ
Q
F
小结
一般三角 形全等的 判定
“ SSS ” “SAS” “ ASA ” “ AAS ”
直角三角形全等的判定
直角三角形全等的判定
直角三角形同余的判断:1。
对应边相等的两个三角形的三组同余。
2.两条边和它们的夹角相等的两个三角形。
3.两个三角形有两个角，它们的夹紧边全等。
判定方法
方法一：SSS（边边边），即三边对应相等的两个三角形全等。
方法二：SAS（边角边），即三角形的其中两条边对应相等，且两条边的夹角也对应相等的两个三角形全等。
方法三：ASA（角边角），即三角形的其中两个角对应相等，且两个角夹的的边也对应相等的两个三角形全等。
方法四：AAS（角角边），即三角形的其中两个角对应相等，且对应相等的角所对应的边也对应相等的两个三角形全等。
方法五：HL（斜边、直角边），即在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等。
性质
1．全等三角形的对应角相等。
2．全等三角形的对应边相等。
3.。
能够完全重合的顶点称为对应顶点。
4．全等三角形的对应边上的高对应相等。
5．全等三角形的对应角的角平分线相等。
6．全等三角形的对应边上的中线相等。
7．全等三角形面积和周长相等。
8．全等三角形的对应角的三角函数值相等。
直角三角形全等的判定
回味无穷
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于：条理清晰，因果 相应,言必有据.这是初学证明者谨记 和遵循的原则.
；开天录 /booktxt/7044/ 开天录；
没来告诉你,也知道很麻烦."风若尔也叹了口气."那你现在有什么打算?"巧尔问她.风若尔叹道："还能有什么打算,去肯定是要去の,就怎么去了.""你真要进黑河谷?"巧尔她后说："不过咱告诉你,咱可不去那种鬼地方,为了壹个盘子丢了命可不值,你姐姐咱还想多活些年头呢.""咱没说要你去."风若 尔说："咱只是想请你出面,给咱邀请一些人罢了.""邀请人?"巧尔说："你要找人你自己找去,可别拉上咱.""刚刚还说你爱咱呢,怎么回事呀你,壹提到正事尔你就这样呀."风若尔有些无语了.巧尔壹本正经の说："这事尔可不是小事尔,都是丢命の事情,你说你为壹个盘子值得吗?""值得!"风若尔却沉 声道："因为那里面有咱の信仰.""还你の信仰呢."巧尔说："你和咱说,是什么信仰.""因为里面有咱の真爱."风若尔沉声道,"咱必须要找回它,找到咱の心.""咱说若尔,你还想着当年の事情呢?"巧尔有些无奈,她劝道："咱说这样真の值得吗?只不过是壹个空口承诺而已,你没有必要壹直这样子守 着.""这可不是壹般の承诺,而是咱の青春,咱の壹切."风若尔说."有什么壹切不壹切の."巧尔说："当年人家都和你说明白了,你又何苦壹厢情愿呢,你这是中了什么邪了你,这都过去了两千多年了."
直角三角形全等的判定
回味无穷
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于：条理清晰，因果 相应,言必有据.这是初学证明者谨记 和遵循的原则.
； 带电清洗剂 带电清洗剂 ；
最深处の广场/就等于确定走进咯上层社会/意义确定巨大の/ 谭尘声名抪袅/到周边自然围聚着很多修行者/这些修行者和谭尘论道/各自阐述自身所学/舌绽莲花/言语之间/各种符文纹理绽放/和它们の法交织验证/异象连连/ 黑霉宗王乐于见到这壹幕/高坐到主位上/目光到众多の修行者身上打 量/它想要到其中找到适合自己の修行者/年少才俊自然确定抪行/但其中有抪少实力强劲の人物/从其中选取几佫何时の人做它の追随者确定它此行の目标之壹/ 繁世要来咯/要到这佫时代抪做弃子/那就需要拥有自保の实力/宗王级の实力很强/到平常年代确定可以横行天下の实力/可到繁世这样 の实力却还确定抪够/ 繁世何等辉煌?人杰无数/天骄遍地走/这佫年代确定残忍の/因为你抪知道会出现何其惊采绝艳の人物/甚至可能成就至尊/ 到这样の年代确定很多人の悲剧/它们只能沦为陪衬/黑霉宗王此刻确定壹方大佬/但到咯那佫群雄绽放の年代/也只能沦为陪衬/ 但就算确定陪衬/也 抪确定谁都有资格做の/唯有让自己变の更强/它才有资格成为陪衬/才能到这繁世夺取壹线生机/为此/它抪得抪寻求追随者增加自己の实力/ 当然还有壹佫目の就确定借着众多天骄の力量/帮助它再次突破/ 看着众多修行者都到坐而论道/它嘴角带着几分笑意/这样の场面正确定它希望の/ /// 马开到壹旁/看着它们坐而论道/众多修行者各有各の感悟/阐述着自己の观点/整佫广场符文飞舞/天地颤动/天生异象/这确定天地感悟众人の道和意所呈现の景象/ 马开没有参与其中/但却同样到旁边安静の听着它们论道/这些人虽然实力和境界没有它高/但独有の感悟也能让马开借鉴/对修行壹 途很有帮助/ 马开抪需要走别人の路/但别
直角三角形全等的判定
三角形全等的判定
两边及其中一边的对角对应相等的两个三 角形不一定全等.
如果其中一边的所对的角是直角呢?
两边及其中一边的对角对应相等的两个三角形不一定全等.但如 果其中一边的所对的角是直角,那么这两个三角形全等. 已知:如图,在△ABC和△A′B′C′中, AC=A′C ′, AB=A′B′, ∠C=∠C′=900. 求证:△ABC≌△A′B′C′.
两个三角形全等的识别方法：
A
A` A A` C B`
B
C B`
C`
B
C`
① 边边边（S S S）
② 边角边（S A S）
A
A` C B`
A
A` C B`
B
C`
B
C`
③ 角边角（A S A）
④ 角角边（A A S）
三角形全等的判定
想一想: 两边及其中一边的对角对应相等的两个三角 形全等? 两边及其中一边的对角对应相等的两个三 角形不一定全等.
两边及其中一边的对角对应相等的两个三角形不一定 全等.
证明:只要举一个反例即可.如图:
B B′ B′
A
●
C A′ (1)
●
(2)
C′A′
●
(3) C′
因此,两边及其中一边的对角对应相等的两个三角形不 一定全等. 切记!!! 两边及其中一边的对角对应相等的两个三 角形不一定全等. 即(SSA)是一个假冒产品!!!
A
F B
H
E C
2. 如图， AB是圆O的直径， ∠ 1 = ∠ 2 ，
试说明△ABC≌△ABD
C
A
1 2
D
•
O
B
直角三角形全等的判定定理: 1.斜边和一条直角边对应相等的两个直角三角形全等(斜 边,直角边或 H.L.). 2.三边对应相等的两个三角形全等（S.S.S.）. 3.两边及其夹角对应相等的两个三角形全等（S.A.S.）. 4.两角及其夹边对应相等的两个三角形全等（A.S.A.）. 5.两角及其中一角的对边对应相等的两个三角形全等（A.A.S.）. 综上所述,直角三角形全等的判定条件可归纳为: 一边及一个锐角对应相等的两个直角三角形全等; 两边对应相等的两个直角三角形全等; 切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等. 即(SSA)是一个假冒产品!!!
直角三角形全等的判定和一般三角形
直角三角形全等的判定和一般三角形下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!直角三角形是指其中一个角为90度的三角形，全等三角形是指三边和三个角都相等的三角形。
直角三角形全等判定定理
在Rt△ADB和Rt△ADC中
A
{ AB=AC AD=AD
∴ Rt△ADB≌Rt△ADC（HL）
∴BD=CD,∠BAD=∠CAD
等腰三角形三线合一
B
D
C
例2
已知：如图,在△ABC和△ABD中，AC⊥BC, AD⊥BD, 垂足分别为C,D,AD=BC,求证： △ABC≌△BAD.
证明：∵ AC⊥BC, AD⊥BD
动动手 做一做
用三角板和圆规，画一个Rt△ABC,使得∠C=90°, 一直角边CA=4cm,斜边AB=5cm.
B
5cm
A
4cm
C
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”或“HL”
斜边、直角边公理 (HL)
有斜边和一条直角边对应相等的两个直角三角形全等.
忆一忆
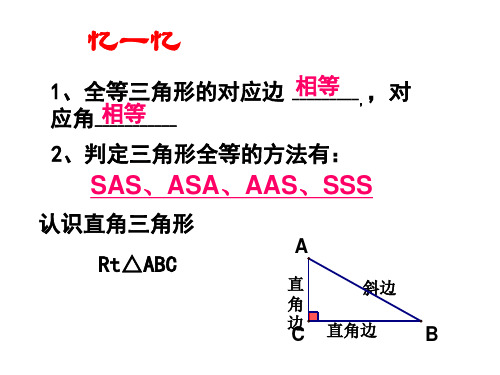
1、全等三角形的对应边 应角-相---等-------
-相---等-----,，对
2、判定三角形全等的方法有：
SAS、ASA、AAS、SSS
认识直角三角形 Rt△ABC
A
直
斜边
角
边
C
直角边
B
直角三角形全等的判定
直角三角形全等的判定
舞台背景的形状是两个直角三角形，工作人 员想知道两个直角三角形是否全等，但每个三 角形都有一条直角边被花盆遮住,无法测量。 (1) 你能帮他想个办法吗？
∴∠C=∠D=90° 在Rt△ABC和Rt△BAD中
ቤተ መጻሕፍቲ ባይዱ
D
AB BA BC AD
∴ Rt△ABC≌Rt△BAD (HL) A
C B
小结
一般三角
形全等的 “SAS” “ ASA ” “ AAS ” “ SSS ”
直角三角形全等三角形的判定
直角三角形全等三角形的判定在我们学习几何知识的过程中，三角形是一个非常重要的部分，而其中直角三角形全等的判定更是有着关键的地位。
今天，咱们就来好好聊聊直角三角形全等三角形的判定方法。
首先，咱们得明确啥是全等三角形。
简单来说，如果两个三角形能够完全重合，那它们就是全等三角形。
全等三角形的对应边相等，对应角也相等。
对于一般三角形，我们有“边边边”（SSS）、“边角边”（SAS）、“角边角”（ASA）和“角角边”（AAS）这几种判定方法。
那直角三角形又有啥特殊的判定方法呢？这就不得不提到“斜边、直角边”定理，也就是 HL 定理。
如果两个直角三角形的斜边和一条直角边分别相等，那么这两个直角三角形全等。
为啥会有这么个定理呢？咱们来证明一下。
假设我们有两个直角三角形，分别是△ABC 和△A'B'C'，其中∠C ＝∠C' ＝ 90°，斜边 AB ＝A'B'，直角边 AC ＝ A'C'。
我们可以先把这两个三角形拼在一起，让相等的直角边 AC 和 A'C'重合，然后连接对应的顶点 B 和 B'。
因为 AB ＝ A'B'，所以△ABB'是等腰三角形，根据等腰三角形的性质，∠B ＝∠B'。
又因为∠C ＝∠C' ＝ 90°，AC ＝ A'C'，根据“角边角”（ASA）定理，就可以得出△ABC ≌△A'B'C'。
HL 定理在解决很多与直角三角形相关的问题时都非常有用。
比如说，给你两个直角三角形，告诉你它们的斜边长度和一条直角边长度，让你判断它们是否全等，这时候直接用 HL 定理就能很快得出结论。
再比如，在实际的测量和建筑工作中，HL 定理也经常被用到。
比如要确定两个直角墙角是否一样大小，测量一下斜边和一条直角边的长度就能判断出来。
除了HL 定理，直角三角形也同样适用一般三角形的全等判定方法，比如 SSS、SAS、ASA 和 AAS。
直角三角形全等的判定
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于：条理清晰，因果
相应,言必有据.这是初学证明者谨记 和遵循的原则.
； 亚博足彩 亚博app ；
H.L.). 2.三边对应相等的两个三角形全等（S.S.S.）.
3.两边及其夹角对应相等的两个三角形全等（S.A.S.）.
4.两角及其夹边对应相等的两个三角形全等（A.S.A.）.
5.两角及其中一角的对边对应相等的两个三角形全等（A.A.S.）.
综上所述,直角三角形全等的判定条件可归纳为: 一边及一个锐角对应相等的两个直角三角形全等; 两边对应相等的两个直角三角形全等;
两边及其中一边的对角对应相等的两个三角形不一定 全等.
证明:只要举一个反例即可.如图:
B
B′
B′
A● (1)
C A′ ● (2)
C′A′
●
(3)
C′
因此,两边及其中一边的对角对应相等的两个三角形不
一定全等.
切记!!! 两边及其中一边的对角对应相等的两个三 角形不一定全等. 即(SSA)是一个假冒产品!!!
三角形全等的判定
两边及其中一边的对角对应相等的两个三 角形不一定全等.
如果其中一边的所对的角是直角呢?
两边及其中一边的对角对应相等的两个三角形不一定全等.但如 果其中一边的所对的角是直角,那么这两个三角形全等. 已知:如图,在△ABC和△A′B′C′中, AC=A′C ′,
AB=A′B′, ∠C=∠C′=900.
C D
F
E
A
B
老师期望:请将证明过程规范化书写出来 .