第八章经典力学的哈密顿理论

合集下载

第八章经典力学的哈密顿理论之四

（2）正则变换
（a）中是否出现循环坐标与我们选取的坐标系有关，例如：在有心力场中极坐标系下：
中不包含所以：
如果通过某种变换能找到新的哈密顿函数，设为，这个新函数使得正则方程不便，这种变换称为正则变换！
设新的广义坐标为：，则拉格朗日方程为：
令：
由哈密顿原理可知，正则方程与哈密顿原理等价，所以，只要使
（a），对于不同的，则不同；
（b）不能完全自由选择，必须满足
（c）
（ii）第二类母函数：
（i）第一类母函数：
所以：
（iii）第三类母函数：
（iv）第四类母函数：
在四类正则变换中：
若不显含时间，则：
由：
得，都是的函数，因此，变换后的已经没有了纯粹空间坐标的意义了。
例如：
这一变换只使动量和坐标的名称相互变换，因此，在哈密顿方程中，广义坐标和广义动量只是名称上不同，并没有物理意义上的差别，因此我们称它们“正则共轭动量”
第二类母函数：
则：
即为拉格朗日坐标变换，坐标和动量之间不发生关系。
则正变换再论：
使有任意变分，，当正则变换满足上式时，因为，，所以：
对原式取时间的微商，
由微商：
对下式取变分：
得：
等式右边：
所以：
所以：
假如经过变换后的新哈密顿函数只是变量和时间的函数，
由
因此，力学体系个积分，而
得到力学体系的问题就解决了，而此时力学体系能否有个积分全靠母函数规定得如何而定，所以，力学体系运动微分方程的积分从正则变换的眼光看，就变成了如何去找适合的母函数问题了，如果母函数规定得当，使变换后能有很多循环坐标出现，问题就可以大大简化了。

经典力学的哈密顿理论(精)

L 1 1 m 2 m ( r ) m( r ) 2 V （1） 2 2
所以
L p m m( r )
（2 ）
p r m
（ 3）
则哈密顿函数
H p L 1 1 [m m( r )] [ m 2 m ( r ) m( r ) 2 V （4） 2 2 1 1 m 2 m( r ) 2 V 2 2
2 p 1 1 2 2 2 2 r ) ( ) (r ( pr 2 ) 2m r 2m r r
于是得正则方程
H pr r pr m r 2 ) 2 m ( r 2 r H p （径向运动方程） p r r mr 3 r 2
（ 3）
p H p mr 2 p mr 2 常数（角动量守恒） p H 0
（ 4）
[例2] 写出粒子在等角速度转动参考系中的H函数和正则方程。解：取图7.3所示的转动参考系。粒子的L函数为（参见5.12式）
故H是p、q、t的函数，表征体系的状态，称为哈密顿函数。若L不显含t，并且约束是稳定的，体系的能量守恒，则
H=E=T+V
（2）哈密顿正则方程哈密顿函数H=H（p，q，t）的全微分为
s H H H dH dp dq dt p q t 1 1 s
7 经典力学的哈密顿理论
内容： · 哈密顿正则方程 · 哈密顿原理 · 正则变换
· 哈密顿—雅可比方程
重点： ·哈密顿正则方程
· 正则变换
难点： · 正则变换

经典力学的哈密顿理论课件

牛顿理论是等价的。哈密顿理论的优点在于便于将力学推广到物理学其他领域。
7.1 哈密顿函数和正则方程
（1）哈密顿函数
拉格朗日函数是 q , q 和t的函数：
L L(q , q，, t它) 的全微分为
dL
s
1
L q
dq
s 1
L q
dq
L dt t
将广义动量和拉格朗日方程：
第2页，共30页。
p
L q
设曲线AB方程为y=y(x)，质点沿曲线运动速度为
2gy ds
(dx)2 (dy)2
1 y'2 dx
dt
dt
dt
质点自A沿曲线y(x)自由滑至B点所需的时间
J
xBdt
xB
1 y'2 dx
xA
xA 2gy
（7.6）
第8页，共30页。
显然J的值与函数y(x)有关，最速落径问题就是求J的极值问题，即y(x)取什么函数时，函数J[y(x)]取极小值。J[y(x)]称为函数y(x)的泛函数。J[y(x)]取极值
（3）哈密顿原理
一个具有s自由度的体系，它的运动由s个广义坐标 q (t ) 来描述。在体系的s维位形空间中，这s个广义坐标的值确定体系的一个位形点，随着时间的变动，位形点在位形）空，间描绘出体系的运动轨道。设在时刻
t1 和 t 2 体系位于位形空间的 P1 点和 P2 点，相应的广义坐标为
q (t1 ) 和 q (t 2 )（或缩写为 q(t1 ) 和 q(t2 ) 由 P1 点通向和 P2 点有多种可能的轨道（路径），但体系运动的真实轨道只能是其中的一条。如何从众多的可能轨道中挑选出体系运动的真实轨道？即在 t1 ~ t2 时间内，为何确定体系的s个广义坐标 q(t )？

哈密顿原理

§7-4 哈密顿原理人们为了追求自然规律的统一、和谐, 按照科学的审美观点, 总是力图用尽可能少的原理(即公理)去概括尽可能多的规律.牛顿提出的三个定律, 是力学的基本原理. 由这些基本原理出发, 经过严格的逻辑推理和数学演绎, 可以获得经典力学的整个理论框架.哈密顿原理是分析力学的基本原理, 它潜藏着经典力学的全部内容并把这门学科的所有命题统一起来. 也就是说, 由它出发, 亦可得到经典力学的整个框架.哈密顿原理是力学中的积分变分原理. 变分原理提供了一个准则, 使我们能从约束许可条件下的一切可能运动中, 将力学系统的真实运动挑选出来. 变分原理的这一思想, 不仅在力学中, 而且在物理学科的其他领域中, 都具有重要意义.一、变分法简介1. 函数的变分.自变量为x 的函数表示为)(x y y =.函数的微分x y y d d ′=是由自变量x 的变化引起的函数的变化.函数的变分也是函数的微变量, 但它不是因为自变量x 的变化, 而是由于函数形式的变化引起的.这种由于函数形式变化造成的函数的变更称为函数的变分, 记作y δ.与函数y 邻近但形式与y 不同的函数有许多, 这些函数可以表示如下:)()0,(),(*x x y x y εηε+= 其中ε是任意小的参数, ()x η是任意给定的可微函数. 因0=ε时()()x y x y =0,, 所以函数形式的变化决定于上式的第二项. 因此, 函数的变分写成()()()x x y x y y εηε=−=0,,δ*在自由度为1的力学系统中讨论变分的概念. 设广义坐标为q , )(t q q =. 建立以t q ,为轴的二维时空坐标系(又称事件空间), 曲线I 是)(t q q =的函数曲线, 代表了系统的真实运动.q t d d →函数的微分.在曲线I 附近, 存在着许多相邻曲线, 这些曲线都满足力学系统的约束条件, 称为可能运动曲线,它们的方程表示为()()()t t q t q εηε+=0,,*在t 不变的情况下, 函数形式的改变也能引起函数的变化, 这种变化纯粹是由函数形式变化引起的, 它就是函数的变分q δ,()()()t t q t q q εηεδ=−=0,,*与q d 不同, q δ与时间变化无关, 称为等时变分. r δ和αq δ都是等时变分.变分的运算法则在形式上与微分运算法则相同. 下面列出几条变分法则.设1y 和2y 是自变量x 的两个函数, 则()2121δδδy y y y +=+()122121δδδy y y y y y +=22211221δδδy y y y y y y −= 现给出第3式的证明:()22222211122122211121*2121δηεηεηεηεηε+−=−++=− =y y y y y y y y y y y y y y22211221δδδy y y y y y y −= 等时变分还有两个重要性质:(1)变分与微分的运算可以交换, 即δ和d 的运算可交换;(2)变分和微商在运算上可以交换, 即δ和t d /d 的运算可交换.首先证明性质(1):设力学系统的1=s ,q . 曲线 I 表示系统的真实运动, 曲线 II 表示与曲线I 邻近的系统的可能运动.Q Q P ′→→, Q ′点的纵坐标为()q q q q d δd +++. Q P P ′→′→, Q ′点的纵坐标成为()q q q q δd δ+++. 于是 ()()q q q q q q q q δd δd δd +++=+++()()q q δd d δ=证明完毕.下面证明性质(2): 因为()()()()2d d δd d δd d d δt t q q t t q −=由于等时变分, ()()0δd d δ==t t . 所以上式可写成()()q t t q t q δd d d d δd d δ==证明完毕.在变分法中, 除等时变分外, 还有全变分. 全变分是由于函数自变量和函数形式的共同变化引起的, 用q ∆表示.()()0,,*x y x x y y −∆+=∆εx xy y y ∆+=∆d d δ 2. 泛函的变分与泛函取极值的条件---欧拉方程.若变量J 由一组函数()x y y i i =, n i ,,2,1 =的选取而确定, 则变量J 称为函数()t y y i i =的泛函, 记作()()()],,,[21x y x y x y J n .泛函J 由n 个函数的形式确定, 是函数形式的函数.泛函与函数的概念不同, 函数中的自变量是数；而对于泛函, 处于自变量地位的是可以变化的函数的形式.举例说明：Oxy 平面中有B A ,两个固定点, 连接两固定点间的曲线的长度L 由下式确定, ()x x y L AB x x d d /d 12∫+= 显然, L 依赖于函数()x y y =的选取, 若函数()x y 的形式发生变化, 则曲线的形状随之变化, 曲线的长度也跟着改变. 长度L 就是函数()x y的泛函.研究形式最简单的泛函及其变分, 该泛函只依赖一个函数()()[]x x x y x y F J x x d ,,10∫′= 或 ()()()()()[]x x x x y x x y F J x x d ,0,,0,10∫′+′+=ηεεηε 其中()()x x y x y d d =′被积函数()()[]x x y x y F ,,′的形式是已知的, 积分的上下限是固定的. 当函数()x y 在形式上发生变化时, 泛函就会发生变化, 这种由于函数形式的变化引起泛函的变化(线性部分)称为泛函的变分,记作J δ.现将被积函数()()()()[]x x x y x x y F F ,0,,0,ηεεη′+′+=在0=ε处展开(只保留线性部分)()()()()[]x x x y x x y F ,0,,0,ηεεη′+′+()()[]()()x y F x y F x x y x y F ηεεηεε′ ′∂∂+ ∂∂+′===00,, 可见函数的变分为()()()()[]()()[]x x y x y F x x x y x x y F F ,,,0,,0,δ′−′+′+=ηεεη()()x y F x y F ηεεηεε′ ′∂∂+ ∂∂===00 y y F y y F ′ ′∂∂+ ∂∂===δδ00εεF 的变分是在0δ=x 的情况下进行的. 在力学中, x 为时间t , 这种变分是等时变分.现将J δ写成()()()()[]()()[]∫∫′−′+′+=1010d ,,d ,0,,0,δx x x x x x x y x y F x x x x y x x y F J ηεεη ()()()()[]()()[]{}∫′−′+′+=10d ,,,0,,0,x x x x x y x y F x x x y x x y F ηεεη∫=10d δx x x F 上式表明当积分变量与变分无关时, 变分算符和积分算符可以交换.在数学中, 变分法的基本问题是通过求泛函的极值(极大值, 或极小值, 或稳定值)去寻找函数)(x y . 泛函中的函数)(x y 的形式需不断改变, 直到J 达到极值. 当J 为极值时, )(x y 就是我们所要寻找的函数.泛函取极值的必要条件是满足欧拉方程. 推出欧拉方程:与函数极值条件类似, 处于极值的泛函, 其变分一定为零, 即()()[]x x x y x y F J x x d ,,δδ10∫′= ()()[]x x x y x y F x x d ,,δ10∫′= 0d δδ10= ′′∂∂+∂∂=∫x y y F y y F x x 考虑到()y x y δd d δ=′, 并对上式中的第二项采用分部积分法()x y y F x y y F x x y x y F x y y F x x x x x x d δd d δd d d δd d d δ101010∫∫∫ ′∂∂− ′∂∂=′∂∂=′′∂∂ 积分上下限是固定的, 即要求各函数曲线有相同的端点, 0δδ10==x x y y , 所以上式第一项 0δd δd d 1010=′∂∂= ′∂∂∫x x x x y y F x y y F x 故0d δ)d d (10=′∂∂−∂∂∫x y y F x y F x xεη=y δ, 由于η是任意函数, 所以y δ也是任意的. 可见, 要使上式成立, 必须0d d =′∂∂−∂∂y F x y F 这就是欧拉方程.可推广到多个函数为变量的泛函中去, 该泛函取极值的欧拉方程为0d d =′∂∂−∂∂ββy F x y F l ,,2,1 =β l 代表函数的个数.3. 变分问题.凡是与求泛函极值有关的问题都称做变分问题. 下面列举3个曾在变分法的发展中起过重要影响的变分问题.(1) 最速落径问题. 通过求泛函极值, 得知竖直平面内不在同一铅垂线上的两个固定点之间的多条曲线中, 能使质点以最短时间从高位置点到低位置点自由滑下的曲线是旋轮线(又称摆线).(2) 短程线问题. 已知曲面方程, 用求泛函极值的方法, 可得出曲面上两固定点之间长度最短的线.(3) 等周问题. 将泛函求极值, 可得知一平面内, 长度一定的封闭曲线, 所围面积最大的曲线是圆.例题6 最速落径问题.(有兴趣者自学)二、哈密顿原理1. 位形空间、真实运动曲线和可能运动曲线.在分析力学中, 由s 个广义坐标s q q q ,,,21 组成的s 维空间称为位形空间.系统某一时刻的位形(即由广义坐标确定的系统的位置)与该空间中的一点相对应. 当位形随时间变化时(时间t 为参数), 位形点就会发生变化而形成一条曲线.用位形空间研究完整系的运动, 不用顾及约束对系统运动的影响. 因为空间由s 个广义坐标轴组成, 每一个广义坐标都可以自由变化. 位形空间中的任何一条曲线, 都表示系统在完整约束下的一种可能的运动过程.设s t q q ,,2,1),( ==ααα代表系统的真实运动, 则由它们决定的曲线称为真实运动曲线.由于函数)(t q q αα=形式发生变化而在真实曲线邻近出现的曲线称为可能运动曲线.2. 完整有势系统的哈密顿原理.哈密顿原理是分析力学中的积分变分原理, 它巧妙地运用泛函求极值的方法, 将真实运动从约束允许的一切可能运动中挑选出来.哈密顿原理是一条力学公理.首先, 定义一个称为作用量的泛函:()∫=10d ,,t t t t q q L S αα 式中的L 称为拉格朗日函数, 定义为V T L −=T 是力学系统相对惯性系的动能),,(t qq T T αα =; 势能),(t q V V α=. 拉格朗日函数是ααqq ,和t 的函数, ),,(t qq L L αα =. 假定位形空间中有两个固定点A 和B , 与A 点相对应的时刻是0t , 与B 点相对应的时刻是1t .两个固定点之间, 存在着由s t q q ,,2,1),( ==ααα决定的真实运动曲线.两固定点B A ,间还存在许多与真实运动曲线邻近的可能运动曲线, 它们是由q q q δ*+=αα s ,,2,1 =α0δδ10====t t t t q q αα s ,,2,1 =α决定的.作用量是依赖于函数)(t q α的泛函. 在位形空间的两个固定点间有许多可能运动轨道, 其中有一条是真实的. 哈密顿原理就是通过变分法中求泛函(在此指作用量)极值的方法, 将真实运动从这许多的可能运动中挑选出来的.哈密顿原理的内容是: 受完整约束的有势系, 在位形空间中, 相同时间内通过两位形点间的一切可能运动曲线中, 真实运动曲线使作用量取极值. (极值为极小值, 故此原理又称为哈密顿最小作用量原理)在哈密顿原理中, 一切可能运动必须具有以下共同的特点:(1) 都是同一系统在相同的约束条件下的可能运动;(2) 都是在时刻0t 和时刻1t 之间相同时间间隔内完成的运动;(3) 在位形空间中有相同的起点和终点, 即 0δδ10====t t t t q q ααs ,,2,1 =α哈密顿原理的数学表述:在位形空间内, 当s q q t t t t ,,2,1,0δδ10 =====ααα时, 对于受完整约束的有势系, 其真实运动使 ()0,,δδ10==∫t t t q q L S αα 综上所述, 当作用量泛函取极值时, 与该作用量所对应的位形空间曲线就是真实运动的曲线, 描绘该曲线的s 个函数)(t q q αα=就是真实运动的运动学方程.拉格朗日函数V T L −=是力学系统的特征函数.如果确定了系统的拉格朗日函数, 则通过哈密顿原理, 就可导出力学系统的动力学方程.由欧拉方程可以得到分析力学中有势系的普遍方程---拉格朗日方程, 我们将在下一章讨论这个问题.[拉格朗日函数不是惟一确定的. 设f 是一个任意广义坐标和时间的函数, 即),(t q f f α=, 设),(d d t q f tL L α+=′, 则∫∫=′1010d d t t t t t L t L δδ. 证明了在原有拉格朗日函数上加上一项广义坐标和时间的任意函数对时间的全微商, 是不会改变系统的运动方程的. 这种不变性称做规范变换不变性, 它对于现代理论物理的研究有重要意义.]例题 7 质量为m 的质点, 在重力场中以与水平线成α角的初速率v 抛射, 根据哈密顿原理, 求质点的运动微分方程.解在抛射体运动的平面内, 以铅垂方向为y 轴, 建立直角坐标系Oxyz , 以y x ,作为质点的广义坐标. 拉格朗日函数为()mgy y x m L −+=2221 作用量为()t mgy y x m t L S t t t t d 21d 101022∫∫ −+== 根据哈密顿原理, 真实运动使()[]0d δδδδ10=−+=∫t y mg y y m x x m S t t ()∫∫∫−==10101010d δδd δd d d δt t t t t t t t t x x m x x m t x tx m t x x m ()∫∫∫−==10101010d δδd δd d d δt t t t t t t t t y y m y y m t y ty m t y y m 由于在10,t t 时刻, 0δδ==y x , 因此 ()[]∫=+−−=100d δδδt t t y mg y m x x m S 又因x δ和y δ是相互独立的, 所以要使上式成立, 必须0=xm 0=+mg ym 3. 一般完整系的哈密顿原理.对一般完整系, 主动力常含有非有势力, 上述哈密顿原理不再适用, 但可以将有势系的哈密顿原理的表达式经修改后推广到一般完整系中:即在位形空间中, 一般完整系的真实运动使0d δδ101= +∫∑=t q Q T t t S ααα 式中T 是系统的动能, αQ 是与广义坐标αq 对应的广义力.[ααq r F Q i ni i ∂∂⋅=∑= 1] 在下一章里, 我们将会根据一般完整系的哈密顿原理, 推导出一般完整系普遍适用的动力学方程, 即一般形式的拉格朗日方程.在物理学的研究中, 对于我们重要的是有势系的哈密顿原理.哈密顿原理具有统一的、简洁完美的形式, 即具有坐标变换的不变性, 从而使哈密顿原理具有很大的普适性.哈密顿原理——有限自由度——无限自由度.哈密顿原理——物理学其他领域.哈密顿原理还可用于创建新的理论, 根据实验结果和假设构造出拉格朗日函数, 便可用哈密顿原理导出运动方程, 其正确性由实践检验.哈密顿原理是作为公理提出的, 并未推证. 它们的正确性由原理演绎出的推论在实践中的检验而得到证实. ——完全不依赖牛顿定律, 它的适用条件也完全不受牛顿定律适用条件的限制, 其普适性比牛顿的运动定律大得多.。

哈密顿力学课件

x
y
F 0 F C
y
y
例4 捷线
T
1
b
1 y2
2g
a
dx y
F 1 y2 F 0 y x
F y F
1
1
y
y 1 y2
2C1
dy 2C1 y
dx
y
y C1 1 cos
dx
2C1 sin2
2
d
C1 1
cos
d
x C1 sin C2
y
C1
1
cos
旋轮线
C1,C2 由边界条件决定
A
F F
sin2 2 sin2
cos0 const.
d sin2 d
tan2 0 cot2
d
d cot
0
tan2 0 cot2
arccos cot0 cot 0 const.
第19页/共57页
cos cos0 sin sin0 cot cot0 0 Rsin sin0 eq. xsin0 cos0 y sin0 sin0 z cos0 0
p,t ,t
p
q,
p,t
力学状态参量变换 q,q q, p
找到新的特征函数，通过对 q, p 的偏导生成力学方程。
第2页/共57页
1．Legendre变换
f f x, y
df f dx f dy x y
udx vdy
d ux xdu vdy
g g u, y
u
f x
u
x,
y
b a
b
a
s 1
F y
d dx
F y
δy dx

简单的论述哈密顿原理

简单的论述哈密顿原理摘要:证明力积分变量与变分无关的情况下积分运算与变分运算次序的可交换性～从不同角度论述了哈密顿原理的含义。

关键词:哈密顿原理～拉格朗日函数～变分～拉格朗日方程1. 引言哈密顿原理是分析力学中几个重要原理之一，但它不是一个独立原理，它可已从其他原理推导出来，因而可以从不同角度说明它的物理含义。

一般理论力学教材都是在拉格朗日方程两边同时乘以虚位移求所有自由度下的虚功之和，然后再求从位形1即( 到位形2，即(之间或时间至之间的作用量得出，最后变换成，并没有说明最后一步为什么要那样做，也没有说明那样做的意义。

本文先证明当积分变量与变分无关的条件下积分运算与变分运算次序的可交换性，然后再从不同角度论述哈密顿原理的意义。

2. 理论2.1变分运算与积分运算次序的可交换性假定变量由一个或一组函数的选取而确定，则变量称为函数的泛函，记作,,。

泛函由n个函数的形式确定，是函数的“函数”。

泛函与函数的概念略有不同，函数中的变量是可以变化的数值，而对于泛函处于自变量地位的是形式可以变化的函数。

下面举例说明，如图1中有，两个固定点，连接两个固定点之间的曲线的长度由下式确定，即显然，依赖于函数的选取，若函数的to East for the neijiang-Kunming highway bridge across the River, maming Creek Bridge, pond bridge, bridge, rongzhou bridge, and South Bridge. There are two bridges across the minjiang River: minjiang River Bridge on neikun highway bridge. Inner-city transportation: Shu Nan road, binjiang road, North Road, the minjiang River, the Yangtze River Road, lingang形式发生变化，则曲线的形状随之变化，曲线的长度也随之变化。

7经典力学的哈密顿理论

H*

H

F3

t
（7.19）
④ 第二类正则变换
( p dq P dQ ) (H * H )dt dF3 (q, Q, t )

p

F3 , q
P
F3 Q
（7.15）
满足正则变换（7.15）式的具体条件（证明见P.256-257）是：
( p dq P dQ ) (H * H )dt dF (q, Q,（t ) 7.16）

式中F为正则变换母函数。
由（7.16）式可得
p

F q
,
P
F Q
,
1,2,, s

p

F2 q
,
P
F2 Q
,
1,2,
H*

H

F2

t
③ 第二类正则变换
( p dq P dQ ) (H * H )dt dF3 (q, Q, t )

p

F3 q
,
P
F3 Q
,
1,2,
p r
m
（3）
（2）
则哈密顿函数
H p L
[m m( r)] [1 m 2 m ( r) 1 m( r)2 V （4）
2
2
1 m 2 1 m( r)2 V
2
2
（3）式代入（4）式，得
q

p
H p
H q
Q
1,2,s
哈密顿正则方程常用来建立体系的运动方程。

哈密顿力学

dH ∂H = dt ∂t
也就是说，哈密顿函数中不显含时间中不显含时间t，也就是说，哈密顿函数H中不显含时间， ∂H =0 ∂t 则有 dH =0 H = h 表示一积分常数 dt 广义能量守恒由拉格朗日动力学可知稳定约束：稳定约束：
H = T + V 体系机械能守恒
不稳定约束：不稳定约束： H = T2 − T0 + V 广义能量守恒
d ∂L ∂L − =0 & dt ∂q ∂q
& qα , pα , t ⇒ L = L[qα , qα (q, p, t ), t ]
s & ∂qβ ∂L & = pα + ∑ pβ ∂qα ∂qα β =1
s & ∂qβ ∂L = ∑ pβ ∂pα β =1 ∂pα
qα , pα , t ⇒ H [qα , pα , t ]
s ∂H ∂H ∂H dH = ∑ dqα + ∑ dpα + dt ∂t α =1 ∂qα α =1 ∂pα s
& H = ∑ pα qα − L
α =1
s
& & dH = ∑ pα dqα + ∑ qα dpα − dL
s s ∂L ∂L ∂L & & & = ∑ pα dqα + ∑ qα dpα − ∑ dqα + ∑ dqα + dt & ∂t α =1 α =1 α =1 ∂qα α =1 ∂qα s s
s & ∂qβ ∂L = ∑ pβ ∂pα β =1 ∂pα
∂ & ∑1 pβ ∂q = ∑1 ∂q ( pβ qβ ) β= β= α α

《哈密顿原理》PPT课件

则 d , H 0
dt t
反之，若 , H 0 则 C
t
是正则方程的一个运动积分，因为有
dt
dq1 H
dq2 H
p1 p2
dqs H
dp1 H
dp2 H
ps
q1
q2
dps H
2q3 s

q
(1)c, 0, c为常数 (2), , 0
n
n
(3)如 j ,则, , j
振动解要求 l 为纯虚数，要做到这一点势能V>0. 令 l il
s
q Aleilt Aleilt , 1, 2, , s
l 1
s
q al coslt bl sinlt , 1, 2, , s
l 1
上式中 l 叫简正频率，共有s个。
6
3.简正坐标
T
1 2
s
a q q
1
V
V0
s 1
V q
q 0
1 s 2V 2 1 q q
1
q q
0
高级项
取 V0 0 对保守系 V 0
q
略去高级项
1 s 2V
1s
V
2
1 1
q
q
q q 0
2 1 c q q
1
2
在稳定约束下，动能只是速度的二次函数
T
1 2
s
a q q
1
1
也展开为泰勒级数
j 1
j 1
(4), ,
(5)
t
,
t
,
,
t
(6) ,, ,, , , 0
1,如
(7) q , p 0,如

哈密顿力学

哈密顿力学哈密尔顿力学是哈密尔顿于1833年建立的经典力学的重新表述。

它由拉格朗日力学演变而来，那是经典力学的另一表述，由拉格朗日于1788年建立。

但它可以使用辛空间不依赖于拉格朗日力学表述。

关于这点请参看其数学表述。

哈密顿力学-简介哈密顿力学是标准的“伽利略加速点运动几何学”的一种力学。

不幸的是，后人将其称作是“新几何力学”，这多多少少显示了后人的数学知识和物理学思想的一种令人遗憾的欠缺。

哈密顿系统可以理解为时间R上的一个纤维丛E,其纤维Et,t∈R是位置空间。

拉格朗日量则是E上的jet丛(射流丛)J上的函数；取拉格朗日量的纤维内的勒让德变换就产生了一个时间上的对偶丛的函数，其在t 的纤维是余切空间T*Et，它有一个自然的辛形式，而这个函数就是哈密顿量。

任何辛流形上的光滑实值函数H可以用来定义一个哈密顿系统。

函数H称为哈密顿量或者能量函数。

该辛流形则称为相空间。

哈密顿量在辛流形上导出一个特殊的向量场，称为辛向量场。

该辛向量场，称为哈密顿向量场，导出一个流形上的哈密顿流。

该向量场的一个积分曲线是一个流形的变换的单参数族；该曲线的参数通常称为时间。

该时间的演变由辛同胚给出。

根据刘维尔定理每个辛同胚保持相空间的体积形式不变。

由哈密顿流到处的辛同胚的族通常称为哈密顿系统的哈密顿力学。

哈密顿向量场也导出一个特殊的操作，泊松括号。

泊松括号作用于辛流形上的函数，给了流形上的函数空间一个李代数的结构。

当余度量是退化的时，它不是可逆的。

在这个情况下，这不是一个黎曼流形，因为它没有一个度量。

但是，哈密顿量依然存在。

这个情况下，在流形Q的每一点q余度量是退化的，因此余度量的阶小于流行Q的维度，因而是一个亚黎曼流形。

这种情况下的哈密顿量称为亚黎曼哈密顿量。

每个这样的哈密顿量唯一的决定余度量，反过来也是一样。

这意味着每个亚黎曼流形由其亚黎曼哈密顿量唯一的决定，而其逆命题也为真：每个亚黎曼流形有唯一的亚黎曼哈密顿量。

亚黎曼测地线的存在性由Chow-Rashevskii定理给出。

理论力学哈密顿理论在物理学中的应用

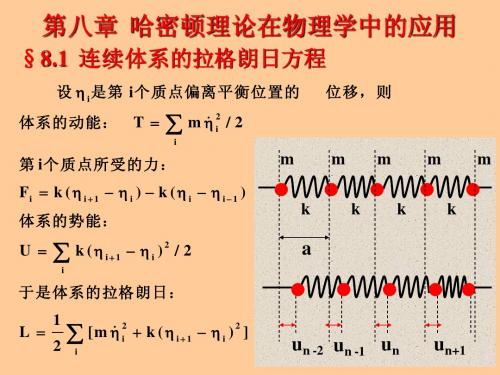
§8.3 薛定谔波动力学方程的建立
采用经典力学的哈密顿理论, 采用经典力学的哈密顿理论,加上电子具有波粒二象性的假设,以氢原子为例, 二象性的假设,以氢原子为例,建立定态波动力学方程.氢原子哈密顿函数为
H = ( p 2 + p 2 + p 2 ) / 2m e 2 / r x y z 哈密顿雅可比方程 : W 2 W 2 W 2 1 e2 = E (1) + y + z 2 2 2 2m x x +y +z 薛定谔对函数作了一个变换 : W = h lg ψ W h ψ W h ψ W h ψ , 代入 (1)式得 : , , = = = x ψ x y ψ y z ψ z
i
m k
m k
m k
m k
m
a
于是体系的拉格朗日: 于是体系的拉格朗日: 1 & L = ∑ [mη i2 + k ( η i + 1 ηi ) 2 ] 2 i
un -2 un -1 un
un+1
1 & 分离体系的拉氏函数: 分离体系的拉氏函数: L = ∑ [m η i2 + k ( η i + 1 η i ) 2 ] 2 i
2
(
)
L = 0,得 η E . λ
2η 2η 波动方程: 波动方程: λ 2 E 2 = 0,波速 v = t x
§8.2 电磁场的拉格朗日方程
麦克斯韦方程给出: 真空中的电磁场规律由麦克斯韦方程给出: r r E = ρ / ε o 广义坐标为矢势 A和标势 r r r × A = 0, × = 0 × E + B / t = 0 r r r E = A / t B = 0 r r r r r × B ε E / t = j B = ×A o o o 拉格朗日密度

经典力学的哈密顿理论.

第八章经典力学的哈密顿理论教学目的和基本要求：理解正则共轭坐标的物理意义并掌握如何用正则坐标表示体系哈密顿函数；能熟练应用正则方程求解简单的力学问题的；了解变分问题的欧拉方程；掌握用变分法表示的哈密顿原理并能正确理解哈密顿原理的物理含义；初步掌握正则变换、泊松括号的物理意义和使用方法。

教学重点：在正确理解正则共轭坐标的物理意义的基础上能熟练应用正则方程求解简单的力学问题。

教学难点：正则共轭坐标的意义和哈密顿原理的物理含义。

§8.1 正则共轭坐标坐标的概念是随着物理学的发展而发展，我们在本节将要讨论一种全新的坐标——正则共轭坐标。

一：坐标的发展历史.1.笛卡儿直角坐标。

为了研究物体在三维空间的位置、速度和加速度而引入的坐标。

其用z y x ,,三个变量来描述物体在空间任一点的位置，坐标轴的方向不随物体的运动而改变，用k j i,,来表示三个坐标轴方向的单位矢量。

2.极坐标、柱坐标和球坐标。

用两个或三个变量来反映物体在平面或空间的位置。

在处理转动问题和中心势场的力学问题时比直角坐标更优越。

其代表坐标轴方向的单位矢量为变矢量，利用这些矢量可以很方便地表达上述力学问题的a v,等物理量。

从直角坐标到极坐标、柱坐标和球坐标等曲线坐标是坐标历史上的第一次飞跃。

另外曲线坐标还包括自然坐标，利用它处理运动规律已知的物体的力学问题更为方便。

3.广义坐标。

反映力学体系在空间位形的独立变量被称为广义坐标。

它是拉格朗日方程建立的基础和优越性所在，也是分析力学的基础。

广义坐标不仅拓宽了坐标的概念，而且由它所列出的动力学方程不含非独立变量，使方程的求解过程得到了简化。

另外我们在研究体系的微振动时引入了简正坐标，使微振动方程的求解过程非常简单，这是坐标概念的第二次飞跃。

下面我们将介绍的正则共轭坐标是坐标概念的第三次飞跃。

二：正则共轭坐标1.拉格朗日函数L 的不确定性如果我们定义满足拉格朗日方程的物理量),,(1t q q L αα 为拉格朗日函数，即1L 满足拉格朗日方程,0)(11=∂∂-∂∂ααq L q L dt d s ,...2,1=α。

第八章经典力学的哈密顿理论

第八章经典力学的哈密顿理论一．正则坐标和哈密顿函数二．三种不同形式的哈密顿动力学方程1．哈密顿正则方程2．哈密顿原理3．哈密顿-雅可比方程一．正则坐标和哈密顿函数为表述空间的位置，引入坐标。

常用坐标：<1）直角坐标；<2）平面极坐标；<3）柱坐标；<4）球坐标等功能：<1）用三个坐标值表示空间的一点的位置<2）确定空间一组相互正交的单位矢量<有了单位矢量，任何一个有方向的力学量都可以统一用这组矢量表示）区别：<1）直角坐标与物体的运动无关，是固定不变的<2）曲线坐标的单位矢量是随着质点所在的位置而改变的， <3）自然坐标由质点的速度方向决定坐标1．广义坐标：设拉格朗日方程为：又设：拉格朗日方程为：令：上式中是变量的任意函数，则：而所以由：可以得到：即：通过拉格朗日方程，对于两个不同的拉格朗日量可以解得同一个广义坐标。

经典力学中，一个力学体系的拉格朗日函数不是唯一的，不同的拉格朗日函数可以相差一项：由于是任意函数，因此，一个力学体系的拉格朗日函数可以有无穷多个。

2．广义动量:若拉格朗日函数是唯一的，则与广义坐标相对应的广义动量也是唯一的，两者一一对应。

但是，由于拉格朗日函数都包含有广义速度因此和将是两个不同的力学量，由于是任意函数的，因此，与广义坐标对应的广义动量也有无穷多个。

用数学语言表述为：广义动量和广义坐标是完全独立的。

b5E2RGbCAP若取，只是时间的函数，则和就一一对应了。

但是，这是一个规范条件，这个规范条件并非理论本身所必需的。

条件：<1）保留广义坐标的概念不变<2）保留广义动量的定义不变，<3）对不做任何限制，问题：若使和保持独立地位：（A）力学理论如何？（B）是否会带来经典力学和拉格朗日理论中没有的优点？回答上述问题的理论即为哈密顿理论！3．两个变量的勒让德变换一组独立变数变为另一组独立变数的变化称为勒让德变换。

第18章_哈密顿原理

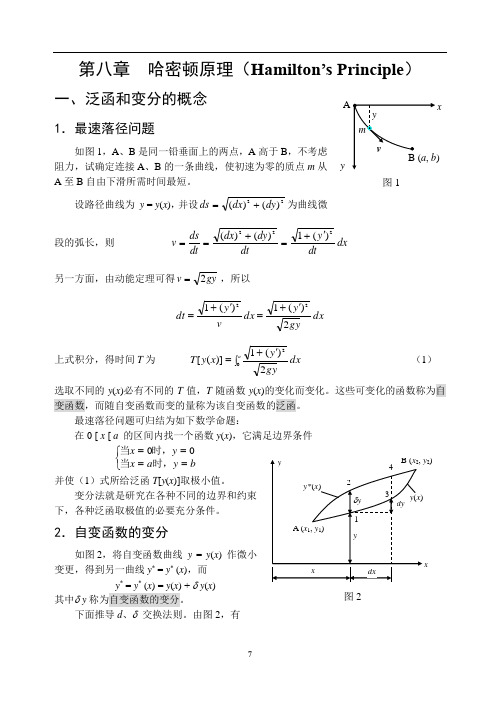
第八章哈密顿原理（Hamilton’s Principle ）一、泛函和变分的概念1．最速落径问题如图1，A 、B 是同一铅垂面上的两点，A 高于B ，不考虑阻力，试确定连接A 、B 的一条曲线，使初速为零的质点m 从A 至B 自由下滑所需时间最短。

设路径曲线为 y = y (x )，并设22)()(dy dx ds +=为曲线微段的弧长，则 dx dty dt dy dx dtds v 222)(1)()('+=+==另一方面，由动能定理可得gy v 2=，所以dx gyy dx v y dt 2)(1)(122'+='+=上式积分，得时间T 为⎰'+=adx gyy x y T 022)(1)]([ （1）选取不同的y (x )必有不同的T 值，T 随函数y (x )的变化而变化。

这些可变化的函数称为自变函数，而随自变函数而变的量称为该自变函数的泛函。

最速落径问题可归结为如下数学命题：在0 [ x [ a 的区间内找一个函数y (x )，它满足边界条件⎩⎨⎧====b y a x y x 时，当时，当00 并使（1）式所给泛函T [y (x )]取极小值。

变分法就是研究在各种不同的边界和约束下，各种泛函取极值的必要充分条件。

2．自变函数的变分如图2，将自变函数曲线 y = y (x ) 作微小变更，得到另一曲线y * = y * (x )，而 y * = y * (x ) = y (x ) + δ y (x )其中δ y 称为自变函数的变分。

下面推导d 、δ 交换法则。

由图2，有dyy y dy y y yy y yy '+=+=+==321δ 若从点3向上算，有)()(334dy y dy y dy y dy y y y y δδδδ+++=+++=+= 若从点2向上算，有)()(224y d dy y y y y d y y dy y y δδδδ+++=+++=+= 比较以上两式，得)()(dy y d δδ= （2）因此，自变函数变分、微分的运算顺序可交换。

第八章经典力学的哈密顿理论之二

2. 哈密顿原理n 个质点的力学体系自由度：3n受k 个约束后，自由度：3n k - 设：1,2,3,s α=广义坐标：()1,2,3,,q q s ααα==运动方程是一个二阶微分方程，故有 2s 个积分常数，即：122,,,s C C C我们可以认为，s 个确定的q α代表着s 维空间的一个点，而描写力学体系运动状态积分：()122,,,,s q q t C C C αα=L Lq q αα∂∂-=∂∂维空间中的一条曲线积分，曲线的两个端点L L q q ααδ⎤∂∂-⎥∂∂⎦()()d q dt L d L L q q q dt q q d Ldt q L q q q ααααααααααδδδδδ⎤⎫⎛⎫⎛⎫∂∂∂=+⎥⎪ ⎪ ⎪∂∂∂⎭⎝⎭⎝⎭⎦⎛⎫⎛⎫∂∂=+ ⎪ ⎪∂∂⎝⎭⎝⎭d()()dq q dtααδ=2211t t t L L Lq q q q q q ααααααδδδ⎛∂∂∂-+ ∂∂∂⎝∑⎰120t t t t q q ααδδ====)12,,,,,,,s s q q q q t20t Ldt δ=⎰)2,,s C 的运动状态积分代表s 维空间的两个点)2,,s C 代入拉格朗日函到2P 对时间)2,,0s C δ+=()21,,t t q q S L dt t αα'''=⎰S S S δ'=-而由：210t t S Ldt δδ==⎰表示：S 具有稳定值！因此，哈密顿原理就是应用变分法中稳定值得办法来挑选真实的轨道，并且由此来确定力学系体的运动定律！哈密顿原理的文字描述：保守的、完整的力学体系，在相同的时间内，由某一个初位形转移到另一个已知的位形的一切可能运动中，真实运动的主函数（作用量）具有稳定值，即对于真实运动来讲，作用量的变分为零。

哈密顿原理和牛顿运动定律是等价的，并且广泛地被人们用来推导其他原理、定律和方程。

我们可以用拉格朗日方程推导哈密顿原理，也可以反过来通过哈密顿原理推导拉格朗日方程。

第八章经典力学的哈密顿理论之5

泊松括号
一．泊松括号：
意义：哈密顿正则方程具有许多优点，因此，它在分析力学中占有非常重要的地位，并发展了一些不同的求解方法。

泊松定理就是其中之一。

设：任何一个物理量：
(),,f f
p q t =
这些物理量有的是随时间变化的，有的是运动积分，不随时间变化，以前我们讨论的中心问题之一是如何寻找循环坐标，即，如何建立运动积分。

现在反过来：对于一个给定的力学体系，如何来判断力学量(),,f f p q t =是否为运动积分。

因为有了哈密顿量H ，我们就可以：
令：
122,,,,x y z
q q q →
则：
123,,,,mx
my mz p p p →
因此：
3222
13132121
x y z j p q q p j p q q p j p q q p ⎧=-⎪
=-⎨⎪
=-⎩
令：
x y j f j g =⎧⎪⎨
=⎪⎩
即：
,x y z j j j ⎡⎤=-⎣⎦
若,x y j j 为运动积分，由泊松定理，z j 也是运动积分。

由例1可知，由泊松定理不一定得到新的运动积分，因为运动积分的总数是有限的，在许多情况下，由两个运动积分所做出的泊松括号是一个恒等式，或者等于一个常数，这就得不出新的运动积分了。

第八章 经典力学的哈密顿理论

第八章 经典力学的哈密顿理论之四

经典力学的哈密顿理论(精)

经典力学的哈密顿理论课件

哈密顿原理

哈密顿力学课件

简单的论述哈密顿原理

7经典力学的哈密顿理论

哈密顿力学

《哈密顿原理》PPT课件

哈密顿力学

理论力学 哈密顿理论在物理学中的应用

经典力学的哈密顿理论.

第八章经典力学的哈密顿理论

第18章_哈密顿原理

第八章 经典力学的哈密顿理论之二

第八章 经典力学的哈密顿理论之5

第八章经典力学的哈密顿理论

第八章经典力学的哈密顿理论之四

理论力学哈密顿理论在物理学中的应用

第八章经典力学的哈密顿理论之二

第八章经典力学的哈密顿理论之5