010-质点、刚体的角动量、角动量守恒定律 (1)
角动量及其守恒定律

m r2 r1 J0
22
因为 1 2, 1 1 2 E k 1 J 1 1 ( J 1 1 ) 1 2 2 相 E k1 E k 2 等 1 1 2 E k 2 J 2 2 ( J 2 2 ) 2 2 2 即系统的机械能不守恒。
23
人双臂收回过程中,内力做功,
J 2
l/2
r dr
2
1 12
l
3
0
1 12
ml
2
如转轴过端点垂直于棒 l 1 2 J r d r ml 2 0 3
例3 一质量为 m 、半径为 R 的均匀圆盘,求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 , 在盘上取半径为 r ,宽为 d r 的圆环
v M (2 gh )
u l 2
1 2
M
h N
B
l 2 1 12
2
2
把M、N和跷板作为 一个系统, 角动量守恒
mvM l 2 J 2 mu
C l
m l 1 2 1 6 m ( 2 gh )
A l/2
ml
2
解得
mvMl 2 m l
2
2
12 ml
2
2 2 2
质量连续分布刚体的转动惯量
J
m
j
j j
r
2
r dm
2
d m :质量元
例2 一质量为 m 、长为 l 的均匀细长棒,求 通过棒中心并与棒垂直的轴的转动惯量 .
O
l 2
O
dr
l 2
r
dr
O´
质点角动量和角动量守恒定律

二、质点角动量: 质点角动量:
r L v
o
r r r r r L = r × P = r × mυ
角动量的大小
P
m r rϕ r
L
L = rP sin ϕ = mυr sin ϕ
角动量的方向 : 右手螺旋
2
当质点作圆周运动时,则有: 当质点作圆周运动时,则有:
L = rmv = mr ω
注意:同一质点相对于不同的点,角动量可以不同。 注意:同一质点相对于不同的点,角动量可以不同。 在说明质点的角动量时, 在说明质点的角动量时,必须指明是对哪个点而言的
a/2 o
由角动量守恒定律, 由角动量守恒定律,得:
V
a/2
(a/2) mv0 =(a/2)2mv+(a/2)mv ( )
ω =2v0/3a
r r r ×F
M = Fr sinα = Fr⊥
(方向用右手螺旋法规定 方向用右手螺旋法规定) 方向用右手螺旋法规定
v M
r M
r r
r┴
r F
α
o
2. 必须指明对那一固定点 必须指明对那一固定点. r r 3. F ≠ 0, M 可能为零
有心力: 有心力: r r 当力F 的作用线与矢径 r 共线时的力
L0 L0+L
α
v
v0
m
如何求角度α 如何求角度α? 由于质点在有心力 作用下运动, 作用下运动,故角 动量守恒。 动量守恒。有:
Q mv 0 L0 = mv sin(π − α ) ⋅ ( L0 + L) ∴sinα = v0 L0 / v( L0 + L)
例5-2、 、
l0
o
l
角动量 角动量守恒定律

h
vN2 2g
1 2g
3mvM m 6m
2
h
3m m 6m
2
19
4-3 角动量 角动量守恒定律
第四章 刚体转动
P104例3 质量很小长度为l 的均匀细杆, 可绕过其中心
O 并与纸面垂直的轴在竖直平面内转动 . 当细杆静止于
水l/4平处位, 置并时背,离有点一O只向小细虫杆以的速端率点vvA0 0垂爬直行落. 设在小距虫点与O细为杆
14
4-3 角动量 角动量守恒定律
比较 动量
F
dP dt
t2
Fdt ΔP
t1
F 0 P 0
F
P
mv
力 动量
t2
Fdt 力的冲量
t1
第四章 刚体转动
角动量
M
dL dt
t2
Mdt ΔL
t1
LMMrrp0F角L力动矩量0或或角动力量矩
其角速度为ω, 求齿轮啮合后两圆盘的角速度.
解: 系统角动量守恒
J11 J22 (J1 J2)
J11 J22
(J1 J2 )
16
4-3 角动量 角动量守恒定律
第四章 刚体转动
P103例2 一杂技演员 M 由距水平跷板高为 h 处自由下
落到跷板的一端 A, 并把跷板另一端的演员 N 弹了起来.
R
x
26
dP
F dt
t2
Fdt ΔP
t1
F 0 P 0
大学物理一复习第四章刚体的转动-文档资料

mg FT2 ma2
FT1 FT2
R
mg FT1 r
m
a1
J
a1 r
a2 R
FT1 r R
FT1'
A
mg
β
FT2
FT2'
B
mg
mg(R r)
J mR2 mr2
a1
r
J
mgr(R r) mR2 mr2
40 半径减小角速度增加。
(2)拉力作功。请考虑合外力矩为0, 为什么拉力还作功呢?
W
0
Md
在定义力矩作功 时,我们认为只 有切向力作功, 而法向力与位移 垂直不作功。
但在例题中,小 球受的拉力与位 移并不垂直,小 球的运动轨迹为 螺旋线,法向力 要作功。
o
F
r d Fn F
解得
a2
R
mgR(R r) J mR2 mr2
FT1 mg ma1
FT2 mg ma2
例2:光滑斜面倾角为 ,顶端固定一半 径为 R ,质量为 M 的定滑轮,质量为 m 的物体用一轻绳缠在定滑轮上沿斜面 下滑,求:下滑的加速度 a 。
解:物体系中先以
物体 m 研究对象,
A
分别根据牛二定律和转动定律列方程:
角量、线量关系式
解得:
a
mB g
mA mB mC 2
T1
mAmB g
mA mB mC
2
T2
(mA mC 2)mBg mA mB mC 2
如令 mC 0,可得:
刚体力学_角动量
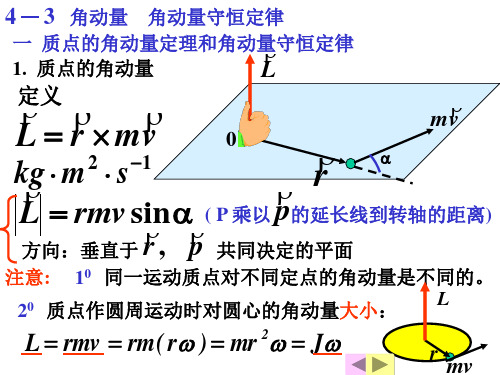
dLi Mi = dt
i内 内
的内力矩之和应为零,所以在遍 的内力矩之和应为零 所以在遍 及刚体内所有质点后,可得 及刚体内所有质点后 可得
d ∑ Mi = ∑ Mi外+ ∑ Mi内= ∑ Mi外= dt ( ∑ Li )
合力矩 合内力矩为零 合外力矩M 合外力矩 刚体角动量L 刚体角动量
dL 刚体作定轴转动时 刚体所受合外力矩等于 刚体作定轴转动时,刚体所受合外力矩等于 即 M= 刚体绕此定轴的角动量随时间的变化率. dt 刚体绕此定轴的角动量随时间的变化率
转动惯量为J的刚体在合外力矩的作用下作定轴转动 在时 转动惯量为 的刚体在合外力矩的作用下作定轴转动,在时 的刚体在合外力矩的作用下作定轴转动 间 t1 到 t2 内,其角速度由 ω 1变为 ω 2 ,则有 其角速度由 则有
∫
t2
t1
Mdt =
∫
L2
L1
dL = L2 − L1 = J ω 2 − J ω 1
m
解:选质点系: 选质点系 两个钢球+泥球 两个钢球 泥球 碰撞过程, 碰撞过程,
a/2 o a/2
m V0 m
质点系对o点的合外力矩为零, 质点系对 点的合外力矩为零, 点的合外力矩为零 系统角动量守恒. 系统角动量守恒
由角动量守恒定律, 由角动量守恒定律,得: (a/2) mv0
m V
=(a/2)2mv+(a/2)mv ( )
v v dL M= dt
v v v M d t = L 2 − L1 ∫t1 t2 v 冲量矩 ∫ M dt
t2
t1
对同一参考点O, 对同一参考点 ,质点所受的冲量矩 等于质点角动量的增量.——质点的角动 等于质点角动量的增量.——质点的角动 量定理
大学物理课件:刚体定轴转动的角动量定理 角动量守恒定律

r
l 2
mv R l mv R l
1
1
2
2
R l
v 2
R
1 v
l 1
2
R
o
l 1
2.刚体的角动量定理及守恒定律
刚体所受合外力矩与角加速度关系为
M J J d
dt
利用角动量表示 M
dJ
dL
dt dt
刚体绕定轴转动时,作用于刚体的合外力矩等于刚 体绕此轴的角动量对时间的变化率。这是刚体角动 量定理的一种形式。
械能守恒。
1 (1 ML2 ma2 ) 2 mga(1 cos60) Mg L (1 cos60)
23
2
3(2ma ML)g 2(3ma2 ML2 )
6(2ma ML)(3ma2 ML2 )
v0
6ma
课后习题 3-9 3-10 3-18
刚体定轴转动的角动量定理 角动量守恒定律
一、冲量矩 角动量
1.冲量矩
定义:力矩与力矩作用时间的乘积称为冲量矩。
数学表达: 2.角动量
t
0 M dt
整个刚体的角动量就是刚体上每一个质元的角动 量——即每个质元的动量对转轴之矩的和。
2.1质点的角动量
v
o
r
m
定义质点 m 相对原点的
角L动 量r定义p为 rmvsin
光滑转轴自由转动。今有一质量为m,速度为v0的子弹, 沿水平方向距水平转轴距离为a射入竖直、静止的杆内。
杆能摆起的最大角度θmax=60°,求v0。 解:把子弹与杆作系统。由于子弹入射杆的瞬间,系统合外力
矩为零故角动量守恒。
设子弹射入后杆起摆的角速度为ω,则有:
m
v0
角动量定理和角动量守恒定律

角动量定理和角动量守恒定律
角动量定理和角动量守恒定律是描述刚体运动时的两个基本定律。
下面进行简单的介绍:
1. 角动量定理
角动量定理是描述角动量变化的定律。
它表示为:物体所受外力矩等于物体角动量对时间的变化率。
即
I*ω= ΔL/Δt
其中,I 为物体的转动惯量,ω为物体的角速度,L 为物体的角动量。
这个定理表明了一个物体的角动量发生变化时,必定受到了外部的力矩作用,即力矩等于角动量的变化率。
2. 角动量守恒定律
角动量守恒定律是描述角动量不变的定律,即如果没有外部力矩作用,系统的总角动量保持不变。
即:
L = L0
其中,L 为系统的总角动量,L0 为系统在某一时刻的总角动量。
这个定律表明,如果没有外部力矩作用,那么系统的总角动量保持不变。
如果一个物体在自由运动时,角动量发生变化,那么它将会改变自身的旋转状态(比如转速、方向等)。
总之,角动量定理和角动量守恒定律是描述刚体运动和角动量变化的基本定理,可以帮助我们更好地理解物体的运动和变化规律。
质点的角动量和角动量守恒

第三章运动的守恒定律§3-6 质点的角动量与角动量守恒定律1.角动量(Angular Momentum)rα定义:质点对点的角动量为Oαr()L r p r mv =⨯=⨯ 角动量大小(面积)αsin rmv L =LvLvm角动量方向O行星在公转轨道上的角动量ppϕϕrrd dpd L =ϕsin pr =(1)质点对点的角动量,不但与质点运动有关,且与参考点位置有关。
讨论(2)方向的确定LLαvrLαvrrαOmαrvL(3)做圆周运动时,由于,质点对圆心的角动量大小为v r⊥rmv L =L质点对圆心O 的角动量为恒量大小不变方向不变方向不变方向不变v角动量2. 角动量守恒定律(Conservation law of angular momentum)F1v 2v 2r 1r om1122r v r v =1122r mv r mv =表明小球对圆心的角动量保持不变实验中发现行星绕太阳的运动常量=pd 常矢量=⨯p r表明行星在运动过程中,对太阳的角动量保持不变。
Oppϕϕrrd dL r p=⨯对t 求导d d ()d d L r p t t =⨯ d d d d r pp r t t=⨯+⨯ 0)(d d ,d d =⨯=⨯=v m v p tr v t rF r tp r t L⨯=⨯=∴d d d d 质点的角动量守恒定律:如果作用在质点上的外力对某给定点O 的力矩为零,则质点对O 点的角动量在运动过程中保持不变。
这就叫做角动量守恒定律。
)(F r⨯角动量守恒定律力矩例题用角动量守恒定律证明开普勒第二定律。
解开普勒第二定律:任一行星和太阳之间的连线,在相等的时间间隔内扫过的面积相等。
O1v 1ϕ2ϕ2r 1r 2v 2d θ1d θ12课本例题3-14与之类似,自学。
11111()2θ=d d s r r 在位置1,d t 时间内,矢径转动的角度为,扫过的面积为1r1θd O1v1ϕ2ϕ2r 1r 2v 2d θ1d θ121111sin θϕ=d d r v t 由于所以11111111(sin )22ϕ==⨯d d d s r v t r v t 12=d L t m11111()2θ=d d s r r 在位置1,d t 时间内,矢径转动的角度为,扫过的面积为1r1θd O1v1ϕ2ϕ2r 1r 2v 2d θ1d θ12所以11111111(sin )22ϕ==⨯d d d s r v t r v t 12=d L t m两边都除以d t ,有O1v 1ϕ2ϕ2r 1r 2v2d θ1d θ12112=d d s L t m 11111()2θ=d d s r r 12=L m在位置1,d t 时间内,矢径转动的角度为,扫过的面积为1r1θd 两边都除以d t ,有在位置2,有O1v 1ϕ2ϕ2r 1r 2v2d θ1d θ12因为行星只受万有引力作用,所以相对于太阳的力矩为0。
第3章 角动量守恒定律

www. ******.com
3.2 质点的角动量守恒定律
力矩等于零,有三种情况:
(1) r 0 , M 0 (2) F 0 , M 0 (3) r 0 , F 0 , M r F 0
这三种情况分别为: (1) 质点处在定点上静止不动; (2) 质点孤立,不受力的作用; (3) 质点受“有心力”作用
规定逆时针转向 为正。
p x
O
刚体定轴转动的运动学方程
= (t) (2) 角位移
为 t时间内刚体所转过的角度。
p x O
www. ******.com
3.3 刚体的运动
(3) 角速度 角速度 lim Δ d Δt0 Δt dt 在定轴转动中,转向只可能有
M Fd
因 Fsin θ F ,即合力切向分量,所以:
M r F
www. ******.com
3.2 质点的角动量守恒定律
M dL dt
由上式:当 M 0 时守恒定律:质点在运动过程中,所 受的合外力矩等于零时,质点对给定点(转轴)的角动 量保持不变。
(1) 刚体上各点都在垂直于固定轴的平面内(转动平面) 做圆周运动.其圆心都在一条固定不动的直线(转轴)上.
(2) 刚体上各点到转轴的垂直线在同样的时间内所转过 的角度都相同。因而用角量描述刚体的运动.
www. ******.com
3.3 刚体的运动
2. 定轴转动的描述
(1) 角坐标 称角位置或角坐标。
LOGO
第3章 角动量守恒定律
第3章 角动量守恒定律
3.1 质点的角动量 力矩 3.2 质点的角动量守恒定律
主要
3.3 刚体的角动量守恒定律
3.3 角动量 角动量守恒定律
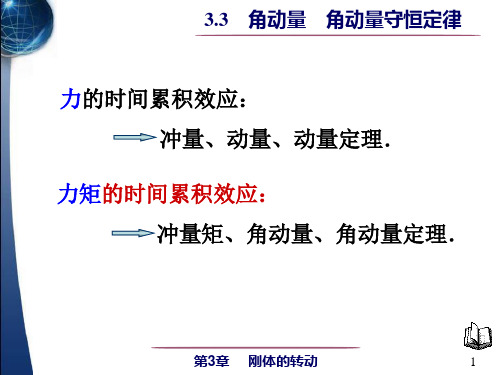
由角动量守恒定律,有
L 1 L 2 L 1 L 2
1 mv l h Ml 3
解得
2013-4-2Leabharlann 2 m l h
2
ω
ω
mv l h 1 3 Ml
2
m l h
2
13
力的空间累积效应: 力的功、动能、动能定理.
力矩的空间累积效应: 力矩的功、转动动能、动能定理.
成的系统在碰撞瞬间角动量守恒。
O
细杆的转动惯量: J 碰前: 细杆对轴O的角动量 子弹对轴O的角动量
2013-4-2
1 3
Ml
2
v P
m
L1 0
h
L 2 rmv mv l h
12
碰后: 细杆对轴O的角动量 子弹对轴O的角动量
L 1 Jω
L 2 rmv l h m ω
3.3
角动量
角动量守恒定律
力的时间累积效应:
冲量、动量、动量定理.
力矩的时间累积效应:
冲量矩、角动量、角动量定理.
第3章
刚体的转动
1
3.3
角动量
角动量守恒定律
一 质点的角动量定理和角动量守恒定律
质点运动描述
2 p m v, E k m v 2
2
刚体定轴转动描述 L J , E k J
冲量矩
t1
t2
M dt
质点的角动量定理:对同一参考点O, 质点所受的冲量矩等于质点角动量的增量. 3 质点的角动量守恒定律 M 0 , L 恒矢量
第3章 刚体的转动
6
3.3
角动量
大学物理学教程马文蔚43角动量-角动量守恒定律1
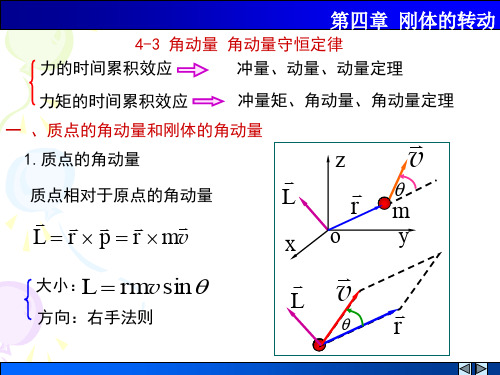
解:(1)对子弹、圆盘系统用角动量守恒定律
m00 R
(1 mR2
m020
m0
R2
)
(
1 2
m
m0
)
R
(2)先求摩擦力矩,在圆盘
上取一同轴圆环,如图,则
mOr R
dr 0
m0
dm ds 2 rdr,
m
R2
摩擦力矩
dM
dmgr
第四章 刚体的转动
M
解:小虫与细杆的碰撞视为完全非弹性碰撞,碰撞前后系统角动 量守恒
mv0
l 4
1 12
ml
2
m(
l 4
)2
12 v0
7l
小虫与细杆系统的外力矩为
M mgr cos
第四章 刚体的转动
角速度恒定,由角动量定理
M dL d(J) dJ J 1 ml 2 mr 2
时0各反自向对滑绳行中,交点错的时角动,各量抓为住L长,为他d们的将绳绳索收一拢端为,然d 后时相,各对自旋的转速,率此
为 20 .
2
L
m0
d 2
2m0
d 2
2m
d/2 2
20
d
例8: 两只同重量的猴子,一只用力往上爬,另一只不爬,若滑轮重 量忽略不计,问哪一只先到达滑轮顶端?
R
R
若 M 0 ,则 L J 恒量
讨论:(1) 守恒条件 M 0
若 J 不变,不变;若J 变, 也变,但 L J 不变.
(2) 内力矩不改变系统的角动量.
第四章 刚体的转动
(3)在冲击等问题中,M in M ex L C
刚体的角动量和角动量守恒定律

如图所示,刚体绕转轴 Oz 以角速度 ω 转动。 由于刚体上的每个质元都绕转轴 Oz 做圆周运动,因此都具有一定的角动量。 设第 i 个质元的质量为 mi ,它到转轴的垂直位矢为 ri ,线速度为 vi ,则该质元对转轴的角动量 Li 大 小为 Li miviri miri2
刚体的角动量和角动量守恒定律
计转轴处的摩擦力和空气阻力)。
【解】 把人和转台看作一个系统,系统不受外力矩作用,
其角动量守恒,即 mR2 1 MR2 0
2
解得 2 m
M 负号表示转台转动的方向与人跑动的方向相反。
大学物理
大学物理
刚体的角动量和角动量守恒定律 1.1 角动量
1.质点的角动量
如图所示,质量为 m 的质点相对于某一参考点 O 运动,在某一时刻,质点相对于参考点 O 的位矢为 r, 质点的速度为 v,质点的动量为 p mv ,则位矢 r 与动量 p 的矢积称为质点相对于 O 点的角动量(动量矩), 用 L 表示,即 L r p r mv
m2 Lv0
Байду номын сангаас
m2 Lv
1 3
m1L2
根据线量与角量的关系 v L ,
可解得子弹和杆一起运动时的角速度 ω 为 3m2v0
(3m2 m1)L
刚体的角动量和角动量守恒定律
, ,
,
,
例题讲解 5
如图所示,质量为 M、半径为 R 的转台,可绕过中心的竖直轴转动。质量为 m 的人站在台的边缘。最
初人和台都静止,后来人在台的边缘开始跑动。设人相对地面的角速度为 ω,求转台转动的角速度 (不
刚体的角动量和角动量守恒定律 1.1 角动量
1.质点的角动量
刚体角动量定理角动量守恒定律
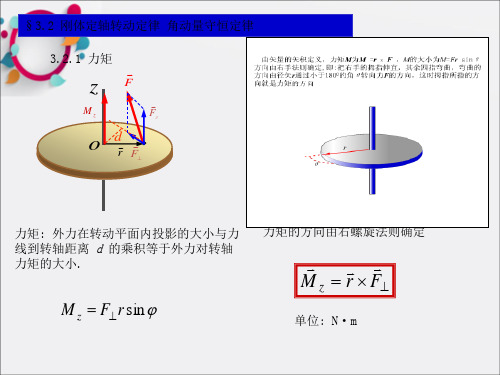
3) 与转轴的位置有关.
4. 刚体定轴转动定律的应用
例3-5. 质量为 M =16kg 的实心滑轮, 半径为 R =0.15m. 一根细绳绕在滑轮上, 细绳一端挂质量为 m=8kg 的物体. 设细 绳不伸长且与滑轮间无相对滑动, 求: (1) 由静止开始 1 秒钟后, 物体下降的距离; (2) 细绳的张力.
§3.2 刚体定轴转动定律 角动量守恒定律
3.2.1 力矩
zF
Mz
F//
o d r F
力矩: 外力在转动平面内投影的大小与力 线到转轴距离 d 的乘积等于外力对转轴 力矩的大小.
M z Fr sin
力矩的方向由右螺旋法则确定
M z r F
单位: N·m
转动定律 M J
刚体定轴转动的角加速度与它所受的合外力矩成正 比, 与刚体的转动惯量成反比 .
解: 将重物, 滑轮隔离分析
由牛顿定律 mg T ma
由转动定律
TR J 1 MR2 2
滑轮与细绳切点
at R
at a
N M
N
m2 > m1
拓展
M
R
T Mg
m
mg
T1 1m
Mg T2 2
m1g
m2g
a m g 810 5 m s2 mM 2 88
h 1 at2 1 512 2.5 m 22
T 1 165 40 N 2
N
m2 > m1 M R
拓展
T1 1m
Mg T2 2
m1g
m2g
m2 g T2 m2a T1 m1g m1a
T2 R T1R J
J 1 MR2 2
a R
N1
m1
刚体的角动量守恒定律

薄圆环 或薄圆筒
m R
J mR2
三、由刚转体动定定轴律转动的M角动dL量定理和转动定理
dt
得
Mdt dL
积分得
t
L
Mdt dL L L0
t0
当转动惯量一定时
t
L0 Mdt
J -J0
当转动惯量变化时
t0
t
Mdt
J
-J
0
0
t0
刚体的角动量定理:当转轴给定时,作用在刚体
四、刚体定轴转动的角动量守恒定律 若刚体所受的合外力矩为零,即M=0
J= 恒 矢 量
角动量守恒定律:当刚体所受的的合外力矩为零,或 者不受合外力的作用,则刚体的角动量保持不变。
讨论:分两种情况: 1) 如果转动惯量不变,刚体作匀速转动; 2) 如果转动惯量发生改变,则刚体的角速度随转动惯 量也发生变化,但二者的乘积不变。当转动惯量变大 时,角速度变小;当转动惯量变小时,角速度变大。
y R x
对于薄板刚体,若建立坐标 系Oxyz,其中z轴与薄板垂直, Oxy平面在薄板内,则薄板刚 体对z 轴的转动惯量等于对x 轴的转动惯量和对y 轴的转动 惯量之和
Jz Jx Jy
几种均匀刚体的转动惯量
细直杆 m
细直杆 m
l
J 1 ml 2 12
圆盘 或圆柱体
J 1 mR2 2
m R
l
J
1 ml2
2l
3
再求角速度
d d d d dt d dt d
d d
3g cosd d
2l
3g cosd
d
0 2l
0
3g sin 1 2
2l
质点角动量定理及角动量守恒定律
角动量的定义为
L=r×mv
将角动量对时间求导,可得
因此上式可变为
所以
上式右方为质点所受合力对参考点的力矩,τ于是就得到
(3.6)
上式表明,在惯性系中,作用在质点上的合力对某参考点的力矩,等于质点对同一参考点角动量对时间的变化率.这个结论叫做质点的角动量定理.
把质点角动量定理在直角坐标系中表达,可得到三个分量方程:
解质点作圆周运动时,其速度v处处与位置矢量r垂直,r和mv
L的方向由右手螺旋法则确定,即将右手的四指由r的正向以小于π的角度转向mv的正向,则拇指所指即为L的方向.这里角动量L的方向垂直于圆平面向外.
设质点的角速度大小为ω,因v=rω,所以上式也可写作
L=mr2ω
(3.3)
如果写作矢量式,则有
L=mr2ω
质点角动量定理及角动量守恒定律
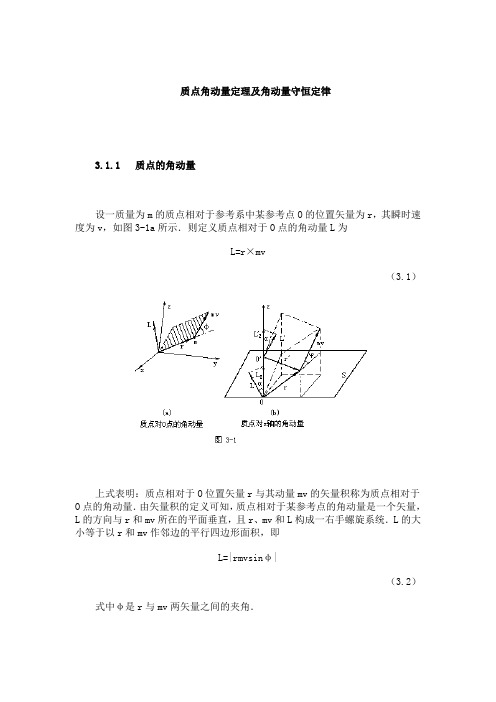
3.1.1质点的角动量
设一质量为m的质点相对于参考系中某参考点O的位置矢量为r,其瞬时速度为v,如图3-1a所示.则定义质点相对于O点的角动量L为
L=r×mv
(3.1)
上式表明:质点相对于O位置矢量r与其动量mv的矢量积称为质点相对于O点的角动量.由矢量积的定义可知,质点相对于某参考点的角动量是一个矢量,L的方向与r和mv所在的平面垂直,且r、mv和L构成一右手螺旋系统.L的大小等于以r和mv作邻边的平行四边形面积,即
例2质量为m的质点在xy平面内以速度v作匀速直线运动,如图3-3所示.求此质点相对于原点O的角动量.
解根据角动量的定义式L=r×mv,设k为沿z轴的单位矢量,则质点的角动量为
L=r×mv=rmvsinφ(k)
即L指向z轴负方向.由图3-3代入上式得
角动量守恒定律是物理学中最基本的定律之一,和动量守恒定律一样,它不仅适用于宏观物体的运动,而且对于牛顿第二定律不能适用的微观粒子的运动,它也适用.
刚体角动量和角动量守恒定律

• 刚体角动量介绍 • 角动量守恒定律 • 刚体角动量的应用 • 刚体角动量与现实世界的关系 • 刚体角动量与未来科技的关系
01
刚体角动量介绍
刚体的定义
刚体
在运动过程中,其内பைடு நூலகம்任意两点 间的距离始终保持不变的物体。
刚体的特性
在刚体的运动过程中,其形状和 大小不会发生变化,只改变其位 置和姿态。
刚体的角动量定义
角动量
一个物体绕固定点旋转时所具有的动 量,其大小等于物体质量、速度和旋 转半径的乘积。
刚体的角动量
当刚体绕固定点旋转时,其角动量等 于刚体质量、旋转轴上的速度和旋转 半径的乘积。
刚体的角动量的计算公式
角动量计算公式:L = mvr
其中,L表示角动量,m表示刚体的质量,v表示刚体上任意一点相对于旋转轴的速度,r表示该点到旋转 轴的距离。
证明方法一
证明方法二
证明方法三
03
刚体角动量的应用
在物理实验中的应用
陀螺仪
刚体角动量在陀螺仪中有着重要 的应用,通过测量旋转轴的角速 度,可以确定物体的方向和姿态。
摆锤实验
通过观察摆锤的摆动,可以验证 刚体角动量守恒定律,了解力矩 对刚体角动量的影响。
磁力矩实验
利用磁力矩对刚体角动量的作用, 可以研究刚体的旋转运动和磁场 的相互作用。
角动量守恒定律在设计和优化机械系 统,如电机、陀螺仪和风力发电机等 方面有广泛应用。
对体育运动的影响
在体育运动中,角动量守恒定律有助于理解旋转运动,如滑冰、花样滑冰和乒乓 球等项目的旋转动作和技巧。
运动员通过合理运用角动量守恒定律,可以调整旋转速度、方向和稳定性,提高 运动表现和竞技水平。
大学物理第5章角动量守恒定律
1 ml2 3
l
m
m 1.73
z2
o
l 2
G
JZ2
1 ml2 3
RGC G 不是质心
转动惯量的计算
例: 求半径为 R,总质量为 m的均匀圆盘绕垂直于盘面
通过中心轴的转动惯量 如下图:
解:
质量面密度
m R 2
J z r 2dm R r 2ds 0
Z ds
R r 2 2rdr 0
R r 2 m 2rdr
a 法向分量
an
v2 r
r 2
O
匀变速直线运动
匀变速定轴转动
v dS dt
a dv dt
v v0 at
S
v0t
1 2
at 2
v2 v02 2aS
d
dt
d
dt
0 t
0t
1t2
2
2 02 2
5.4 定轴转动刚体的角动量定理
1.刚体对转轴的力矩和角动量
z
角动量守恒
质点系的角动量定理
M J
4g
t
3 4
R
1 2
gt
2
LA
r
p
1 2
mpt3gmvg
mgt 0
orRA r源自(2) 对 O 点的角动量m
mv
r r R
LO r p (R r) p R p R mgt
Rg
LO Rmgt
2. 质点的角动量定理
角动量的时间变化率
dL
d
(r
p)
dr
p
r
dp
r 表示从O到速度矢量 v 的垂直距离, 则有
r sin s rs 2
大学物理-角动量守恒定律 PPT

dt 12
dt
考虑到 t
dr g cost 7lg cos(12v0 t)
dt 2
24 v0
7l
37
例6 一杂技演员M由距水平跷板高为h 处 自由下落到跷板的一端A,并把跷板另一端 的演员N弹了起来.问演员N可弹起多高?
M
h
N
C
A
B
l/2
l
38
设跷板是匀质的,长度为l,质量为m',
6mv0
(M 3m)l
v0 m
31
例3 摩擦离合器 飞轮1:J1、 w1 摩擦轮2: J2 静止,两轮沿轴向结合,结合后两轮达到 的共同角速度。 解:两轮对共同转轴的角动量守恒
21
试与下例的齿轮啮合过程比较。
32
例4 两圆盘形齿轮半径r1 、 r2 ,对通过盘心
垂轮直以于0 盘转面动转,轴然的后转两动轮惯正量交为啮J1合、,J2求,啮开合始后1
点o的矢径为 r ,动量为 p ,如下图。在计算其
角动量时,注意有两个特点:
(1) o点到 p 方向的垂直距离 r sin 不变;
(2) L 方向不变;
p2
假如 p 的大小也不变, 显然L 的大小不变。这表
明,自由质点对任意参考 点的角动量保持不变。
p1
1 r1
2
r2
r sin o
5
1.5.2 质点角动量定理
必须指明是对哪个点而言的
注意两点:
(1) 质点的角动量是相对某一参考点而言的,因此
对不同的参考点,角动量 L 不同;
(2) L 的大小在0~ rp 之间变化,如果把动量分解
为径向分量 pcos 和横向分量 psin ,则仅横
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质点、刚体的角动量,角动量守恒定律1、选择题1.人造地球卫星,绕地球作椭圆轨道运动,地球在椭圆的一个焦点上,则卫星的(A)动量不守恒,动能守恒. (C)对地心的角动量守恒,动能不守恒.(B)动量守恒,动能不守恒. (D)对地心的角动量不守恒,动能守恒.[ ]2.人造地球卫星绕地球作椭圆轨道运动,卫星轨道近地点和远地点分别为A 和B .用L 和E K 分别表示卫星对地心的角动量及其动能的瞬时值,则应有(A) L A >L B ,E KA >E kB . (B) L A =L B ,E KA <E KB .(C) L A =L B ,E KA >E KB . (D) L A <L B ,E KA <E KB .[ ]3.一质点作匀速率圆周运动时,(A) 它的动量不变,对圆心的角动量也不变.(B) 它的动量不变,对圆心的角动量不断改变.(C) 它的动量不断改变,对圆心的角动量不变.(D) 它的动量不断改变,对圆心的角动量也不断改变.[ ]4.花样滑冰运动员绕通过自身的竖直轴转动,开始时两臂伸开,转动惯量为J 0,角速度为ω0.然后她将两臂收回,使转动惯量减少为31J 0.这时她转动的角速度变为 (A) 31ω0. (B) ()3/1 ω0. (C) 3 ω0. (D) 3 ω0.[ ]5.如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O 旋转,初始状态为静止悬挂.现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统(A) 只有机械能守恒. (C) 只有对转轴O 的角动量守恒.(B) 只有动量守恒. (D) 机械能、动量和角动量均守恒.[ ]6.刚体角动量守恒的充分而必要的条件是(A) 刚体不受外力矩的作用. (B) 刚体所受合外力矩为零.(C) 刚体所受的合外力和合外力矩均为零.(D) 刚体的转动惯量和角速度均保持不变.[ ]7.一块方板,可以绕通过其一个水平边的光滑固定轴自由转动.最初板自由下垂.今有一小团粘土,垂直板面撞击方板,并粘在板上.对粘土和方板系统,如果忽略空气阻力,在碰撞中守恒的量是(A) 动能. (B) 绕木板转轴的角动量. (C) 机械能. (D) 动量.[ ]8.一个物体正在绕固定光滑轴自由转动,(A) 它受热膨胀或遇冷收缩时,角速度不变.(B) 它受热时角速度变大,遇冷时角速度变小.(C) 它受热或遇冷时,角速度均变大.(D) 它受热时角速度变小,遇冷时角速度变大.[ ]9.将一质量为m 的小球,系于轻绳的一端,绳的另一端穿过光滑水平桌面上的小孔用手拉住.先使小球以角速度ω1在桌面上做半径为r 1的圆周运动,然后缓慢将绳下拉,使半径缩小为r 2,在此过程中小球的(A)速度不变. (B)速度变小. (C)速度变大。
(D)速度怎么变,不能确定.10.如图所示,钢球A 和B 质量相等,正被绳牵着以角速度ω绕竖直轴转动,二球与轴的距离都为r 1.现在把轴上环C 下移,使得两球离轴的距离缩减为r 2.则钢球的角速度(A)变大. (B )变小. (C)不变. (D)角速度怎么变,不能确定.[ ]11.地球绕太阳作椭圆轨道运动,太阳的中心在椭圆的一个焦点上,把地球看作一个质点,则地球的(A) 动能守恒. (C) 对太阳中心的角动量守恒.(B) 动量守恒,. (D) 对太阳中心的角动量守恒,动能守恒.[ ]12.均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示.今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,下述说法哪一种是正确的?(A) 角动量从小到大,角加速度从大到小. (B) 角动量从小到大,角加速度从小到大. (C) 角动量从大到小,角加速度从大到小. (D) 角动量从大到小,角加速度从小到大.[ ]13.有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台中心.随后人沿半径向外跑去,在人跑向转台边缘的过程中,转台的角速度(A) 不变. (B) 变小. (C) 变大. (D)不能确定角速度是否变化.[ ]14.人造地球卫星,绕地球作椭圆轨道运动,地球的中心在椭圆的一个焦点上,设地球的半径为R ,卫星的近地点高度为R ,卫星的远地点高度为2R ,卫星的近地点速度为1v ,则卫星的远地点速度2v 为(A)12v . (B) 121v . (C) 132v . (D) 123v . [ ]15.将一质量为m 的小球,系于轻绳的一端,绳的另一端穿过光滑水平桌面上的小孔用手拉住.先使小球以角速度ω1在桌面上做半径为r 1的圆周运动,然后缓慢将绳放松,使半径扩大为2 r 1 ,此时小球做圆周运动的角速度为(A)1ω. (B) 121ω. (C) 12ω. (D) 141ω. [ ]2.判断题1.如图所示,一水平刚性轻杆,杆长为l ,其上穿有两个小球.初始时,两小球相对杆中心O 对称放置,与O 的距离为d ,二者之间用细线拉紧.现在让细杆绕通过中心O 的竖直固定轴作匀角速的转动,转速为ω 0,再烧断细线让两球向杆的两端滑动.不考虑转轴的和空气的摩擦,在两球都滑至杆端的过程中,杆的角速度变小。
2.一个物体正在绕固定光滑轴自由转动,它受热时角速度变大,遇冷时角速度变小.3.将一质量为m 的小球,系于轻绳的一端,绳的另一端穿过光滑水平桌面上的小孔用手拉住.先使小球以角速度ω1在桌面上做半径为r 1的圆周运动,然后缓慢将绳下拉,使半径缩小为r 2,在此过程中小球速度的大小保持不变.4.长为l 的杆如图悬挂.O 为水平光滑固定转轴,平衡时杆竖直下垂,一子弹水平地射入杆中.则在此过程中,杆和子弹系统的动量守恒.5.一水平的匀质圆盘,可绕通过盘心的竖直光滑固定轴自由转动.圆盘质量为M ,半径为R ,对轴的转动惯量J =21MR 2.当圆盘以角速度ω0转动时,有一质量为m 的子弹沿盘的直径方向射入而嵌在盘的边缘上.子弹射入后,圆盘的角速度不变。
6.均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示.今使棒从水平位置由静止开始自由下落,在棒摆动到竖直位置的过程中,棒的角动量不守恒.7.刚体作定轴转动时,刚体角动量守恒的条件是刚体所受的合外力等于零.8.刚体作定轴转动时,角动量守恒的条件是刚体所受对轴的合外力矩等于零.3.填空题1.质量为0.05 kg 的小块物体,置于一光滑水平桌面上.有一绳一端连接此物,另一端穿过桌面中心的小孔(如图所示).该物体原以3 rad/s的角速度在距孔0.2 m 的圆周上转动.今将绳从小孔缓慢往下拉,使该物体之转动半径减为0.1 m .则物体的角速度ω=_____________________.2.在光滑的水平面上,一根长L =2 m 的绳子,一端固定于O 点,另一端系一质量m =0.5 kg的物体.开始时,物体位于位置A ,OA 间距离d=0.5 m ,绳子处于松弛状态.现在使物体以初速度v A =4 m ·s -1垂直于OA 向右滑动,如图所示.设以后的运动中物体到达位置B ,此时物体速度的方向与绳垂直.则此时刻物体对O点的角动量的大小L B =________ ____.3.在光滑的水平面上,一根长L =2 m 的绳子,一端固定于O 点,另一端系一质量m =0.5 kg 的物体.开始时,物体位于位置A ,OA 间距离d=0.5 m ,绳子处于松弛状态.现在使物体以初速度v A =4 m ·s -1垂直于OA 向右滑动,如图所示.设以后的运动中物体到达位置B ,此时物体速度的方向与绳垂直.则此时刻物体速度的大小v =__________________.4.如图所示,钢球A 和B 质量相等,正被绳牵着以ω0=4 rad/s 的角速度绕竖直轴转动,二球与轴的距离都为r 1=15 cm .现在把轴上环C 下移,使得两球离轴的距离缩减为r 2=5 cm .则钢球的角速度ω =_____ _____.5.哈雷慧星绕太阳的轨道是以太阳为一个焦点的椭圆.它离太阳最近的距离是r 1=8.75×1010 m ,此时它的速率是v 1=5.46×104 m/s .它离太阳最远时的速率是v 2=9.08×102 m/s ,这时它离太阳的距离是r 2=__ ____.6.一质量为m 的质点沿着一条曲线运动,其位置矢量在空间直角座标系中的表达式为j t b i t a r ωωsin cos +=,其中a 、b 、ω 皆为常量,则此质点对原点的角动量L =_ _______.7.如图所示,x 轴沿水平方向,y 轴竖直向下,在t =0时刻将质量为m 的质点由a 处静止释放,让它自由下落,则在任意时刻t ,质点对原点O的角动量L =__________________.8.质量为m 的质点以速度v 沿一直线运动,则它对该直线上任一点的角动量为____. 9.质量为m 的质点以速度v 沿一直线运动,则它对直线外垂直距离为d 的一点的角动量大小是__________.10.一飞轮以角速度ω0绕光滑固定轴旋转,飞轮对轴的转动惯量为J 1;另一静止飞轮突然和上述转动的飞轮啮合,绕同一转轴转动,该飞轮对轴的转动惯量为前者的二倍.啮合后整个系统的角速度ω=__________________.11.有一半径为R 的匀质圆形水平转台,可绕通过盘心O 且垂直于盘面的竖直固定轴OO '转动,转动惯量为J .台上有一人,质量为m .当他站在离转轴r 处时(r <R ),转台和人一起以ω1的角速度转动,如图.若转轴处摩擦可以忽略,问当人走到转台边缘时,转台和人一起转动的角速度ω2=_______________________.12.一个刚体绕轴转动,若刚体所受的合外力矩为零,则刚体的________________守恒.113.长为l 的杆如图悬挂.O 为水平光滑固定转轴,平衡时杆竖直下垂,一子弹水平地射入杆中.则在此过程中,由_____________组成的系统对转轴O的角动量守恒.14.一水平的匀质圆盘,可绕通过盘心的竖直光滑固定轴自由转动.圆盘质量为M ,半径为R ,对轴的转动惯量J =21MR 2.当圆盘以角速度ω0转动时,有一质量为m 的子弹沿盘的直径方向射入而嵌在盘的边缘上.子弹射入后,圆盘的角速度ω=______________.15.一杆长l =50 cm ,可绕通过其上端的水平光滑固定轴O 在竖直平面内转动,相对于O 轴的转动惯量J =5 kg ·m 2.原来杆静止并自然下垂.若在杆的下端水平射入质量m =0.01 kg 、速率为v =400 m/s 的子弹并嵌入杆内,则杆的角速度为ω =__________________.16.一质量均匀分布的圆盘,质量为m ,半径为R ,放在一粗糙水平面上,圆盘可绕通过其中心O 的竖直固定光滑轴转动,圆盘和粗糙水平面之间摩擦力矩的大小为M f .开始时,圆盘的角速度为0ω,经过时间 =∆t 后,圆盘停止转动。
