第01讲 集合
01第一章 集合与计数原理【讲义】

第一讲 集合与计数原理一、基础知识定义1 一般地,一组确定的、互异的、无序的对象的全体构成集合,简称集,用大写字母来表示;集合中的各个对象称为元素,用小写字母来表示,元素x 在集合A 中,称x 属于A ,记为A x ∈,否则称x 不属于A ,记作A x ∉。
例如,通常用N ,Z ,Q ,B ,Q +分别表示自然数集、整数集、有理数集、实数集、正有理数集,不含任何元素的集合称为空集,用∅来表示。
集合分有限集和无限集两种。
集合的表示方法有列举法:将集合中的元素一一列举出来写在大括号内并用逗号隔开表示集合的方法,如{1,2,3};描述法:将集合中的元素的属性写在大括号内表示集合的方法。
例如{有理数},}0{>x x 分别表示有理数集和正实数集。
定义2 子集:对于两个集合A 与B ,如果集合A 中的任何一个元素都是集合B 中的元素,则A 叫做B 的子集,记为B A ⊆,例如Z N ⊆。
规定空集是任何集合的子集,如果A 是B 的子集,B 也是A 的子集,则称A 与B 相等。
如果A 是B 的子集,而且B 中存在元素不属于A ,则A 叫B 的真子集。
定义3 交集,}.{B x A x x B A ∈∈=且 定义4 并集,}.{B x A x x B A ∈∈=或定义5 补集,若},{,1A x I x x A C I A ∉∈=⊆且则称为A 在I 中的补集。
定义6 差集,},{\B x A x x B A ∉∈=且。
定义7 集合},,{b a R x b x a x <∈<<记作开区间),(b a ,集合},,{b a R x b x a x <∈≤≤记作闭区间],[b a ,R 记作).,(+∞-∞定理1 集合的性质:对任意集合A ,B ,C ,有:(1));()()(C A B A C B A = (2))()()(C A B A C B A =; (3));(111B A C B C A C = (4)).(111B A C B C A C =定理2 加法原理:做一件事有n 类办法,第一类办法中有1m 种不同的方法,第二类办法中有2m 种不同的方法,…,第n 类办法中有n m 种不同的方法,那么完成这件事一共有n m m m N +++= 21种不同的方法。
第01讲第一章集合与简易逻辑集合的概念与运算课件新人教A版课件

新疆 源头学子小屋 http://w ww .xj /w xc/ 特级教师 王新敞
w xckt@
6.描述法及两种表述形式:把集合中的元素的公
共属性描述出来,写在大括号内表示集合的方 法. ①数式形式 如由不等式x-3>2的所有解组成的集合,
可表示为 {x│x-3>2};
w xckt@
例6 已知A={x∈R|x2+ax+1=0},B={1,2},且 A B,求实数a的取值范围.
解:由已知,得:A ,或{1},或{2}.
若A , a 2 4 0, 2 a 2.
若A
{1},
12
a
2
a 1 40
10.全集定义:如果集合S含有我们所要研究的各 个集合的全部元素,这个集合就可以看作一个全 集,记作U.
1/2/2020
湖北省随州市第二中学 操厚亮
8
新疆 王新敞
奎屯
二名、称 知识点归纳交集新疆 源头学子小屋 http://w ww .xj /w xc/ 特级教师 王新敞 w xckt@
已知: (1)(CUA)∩(CUB)={4,6,8}; (2)(CUA)∩B={1,9};(3)A∩B={2}.求A、B.
解:∵(CUA)∩(CUB)={4,6,8}
∴ CU(A∪B)= {4,6,8}
∴A∪B={1,2,3,5,7,9}
UB
1,9
2
A
3,5,7
4,6,8
∴B= [(CUA)∩B]∪(A∩B)={1,2,9}
当集合A不包含于集合B,或集合B不包含集合A,则 记作A B(B A)
8.真子集的定义:如果A B,并且 A ≠B,则 集合A是集合B的真子集.
01-第1课时 集合(I)

(3)A={(x,y)|x+y>0,xR,yR},B={(x,y)|x>0,y>0,xR,yR}.
(4)A={y|y= ,x≠0},B={y|y= ,x≠0}.
【选题说明】正确认识周期性的点列及平面区域及函数值域的描述法表示,学习使用描述法正确书写集合.
4.已知集合P={y|y=x2+1,x∈R},Q={y|y=x+1,x∈R},那么P∩Q等于_____
______[1,+∞)_____________.
5.已知全集U={0,1,2,3,4,5},A={x|x2-5x+q=0},且AU,那么q的允许值构成的集合是___{q|q> ,或q=0,或q=4,或q=6}__,所有可能的∁UA分别是____{0,1,2,3,4,5}、{1,2,3,4}、{0,2,3,5}、{0,1,4,5}_______.
6.已知集合P={x|x(x-1)≥0},Q={x| >0},则P∩Q=____{x|x>1}______.
7.设集合A={x||x|<4},B={x|x2-4x+3>0},则集合{x|x∈A且x A∩B}=[1,3].
8.设a,b∈R,集合{1,a+b,a}={0, ,b},则b-a=__2___.
因为a<1,所以a+1>2a,所以B=(2a,a+1).
因为BA,所以2a≥1或a+1≤-1,即a≥ 或a≤-2,而a<1,
所以 ≤a<1或a≤-2,故当BA时,实数a的取值范围是(-∞,-2]∪[ ,1).
第2课时集合的概念和运算(Ⅱ)
教学目标
(1)能正确利用集合表示方程、不等式(组)的解集以及平面上的点集;
解:由A=B得:
(1),或 (2).
2025届高中数学一轮复习课件《 集合》ppt

高考一轮总复习•数学
第15页
解析:(1)方法一(列举法):A=…,-12,12,32,52,72,…, 列举法形象、直观.
B=…,-12,0,12,1,32,2,52,3,72,…. 显然 A B.
方法二(描述法):集合
A = xx=k+12,k∈Z
=
xx=2k+2 1,k∈Z
,B=
xx=2k,k∈Z
高考一轮总复习•数学
第18页
对点练 1(1)已知集合 A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则 A 中元素的个数为( )
A.9
B.8
C.5
D.4
(2)(2024·湖南长沙月考)如果集合 A={x|ax2+4x+1=0}中只有一个元素,则实数 a 的
值是( )
A.0
B.4
C.0 或 4
(2)解:①由 x2-8x+15=0, 得 x=3 或 x=5,∴A={3,5}. 若 a=15,由 ax-1=0,得15x-1=0,即 x=5. ∴B={5}.∴B A. ②∵A={3,5},又 B A, 故若 B=∅,则方程 ax-1=0 无解,有 a=0; 若 B≠∅,则 a≠0,由 ax-1=0,得 x=1a. ∴1a=3 或1a=5,即 a=13或 a=15. 故 C=0,13,15.
高考一轮总复习•数学
第23页
集合间的关系问题的注意点 (1)空集是任何集合的子集,在涉及集合关系问题时,必须考虑是否存在空集的情况, 勤思考,多练习这一特殊情形. 否则易造成漏解. (2)已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系, 集合的包含关系,转化为区间端点的大小关系,这是一个难点,主要是对端点值的取舍, 尤其注意区别开区间和闭区间. 例如:[-1,2)⊆(2a-3,a+2]⇒a2+a-2≥3<2-. 1, 进而转化为参数所满足的关系,常用数轴、Venn 图等来直观解决这类问题.求得参数 后,可以把端点值代入进行验证,以免增解或漏解.
高中数学高考第1讲 集合的概念与运算

第一章 集合与常用逻辑用语
20
(1)已知集合 A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则满足条件
A⊆C⊆B 的集合 C 的个数为
()
A.1
B.2
C.3
D.4
(2)已知集合 A={x|-1<x<3},B={x|-m<x<m},若 B⊆A,则 m 的取值范围为______.
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
24
2.已知集合 A={x|x2-2x-3≤0,x∈N*},则集合 A 的真子集的个数为
()
A.7
B.8
C.15
D.16
解析:选 A.法一:A={x|-1≤x≤3,x∈N*}={1,2,3},其真子集有:∅,{1},{2},
{3},{1,2},{1,3},{2,3}共 7 个.
下一页
第一章 集合与常用逻辑用语
8
2.设集合 A={x|-2≤x≤2},Z 为整数集,则集合 A∩Z 中元素的个数是 ( )
A.3
B.4
C.5
D.6
解析:选 C.A 中包含的整数元素有-2,-1,0,1,2,共 5 个,所以 A∩Z 中的元
素个数为 5.
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
11
2.已知集合 A={x|(x-1)(x-3)<0},B={x|2<x<4},则 A∩B=________,A∪B= ________,(∁RA)∪B=________. 解析:由已知得 A={x|1<x<3},B={x|2<x<4}, 所以 A∩B={x|2<x<3},A∪B={x|1<x<4},(∁RA)∪B={x|x≤1 或 x>2}. 答案:(2,3) (1,4) (-∞,1]∪(2,+∞)
2021年新高考数学一轮专题复习第01讲-集合(解析版)

8.(2020·江苏省泰州中学高三月考)已知集合 A {x | 0 x 2} , B {x | x 1} ,则 A B ______
【答案】{x |1 x 2}
【解析】因为集合 A {x | 0 x 2} , B {x | x 1} , 所以 A B {x |1 x 2}. 故答案为:{x |1 x 2}
2.子集的传递性:A⊆B,B⊆C⇒A⊆C.
3.A⊆B⇔A∩B=A⇔A∪B=B⇔∁UA⊇∁UB. 4.∁U(A∩B)=(∁UA)∪(∁UB),∁U(A∪B)=(∁UA)∩(∁UB).
三、 经典例题
考点一 集合的基本概念
【例 1-1】(2020·全国高三一模(文))已知集合 A x x2 2ax 2a 0 ,若 A 中只有一个元素,则实数 a
④如果 a1 M , a2 M ,那么 a1 a2 M
其中,正确结论的序号是__________. 【答案】①③
【解析】对①:对 b 2n 1, n N ,
总是有 b 2n 1 n 12 n2 , n 1, n z ,故 B M ,则①正确;
对② c 2n, n N ,若 c 2n M ,则存在 x, y Z ,使得
A.30
B.31
C.62
【答案】A
【解析】因为集合 A x | x 6 且 x N* 1, 2,3, 4,5 ,
D.63
所以 A 的非空真子集的个数为 25 2 30 .
故选:A
【例 2-3】(2020·北京牛栏山一中高三月考)已知集合 A={-2,3,1},集合 B={3,m²}.若 B A,则实数 m 的
解不等式 lg x 1 1,得 0 x 1 10 ,解得 1 x 9 .
A x x 1或x 3 , B x 1 x 9 ,则 ðR A x 1 x 3 ,
旧教材适用2023高考数学一轮总复习第一章集合与常用逻辑用语第1讲集合及其运算课件

(2)已知 a,b∈R,若a,ba,1={a2,a+b,0},则 a+b 为(
)
A.1 B.0 C.-1 D.±1
答案 C 解析 由已知得 a≠0,则ba=0,所以 b=0,于是 a2=1,即 a=1 或 a =-1,又根据集合中元素的互异性可知 a=1 应舍去,因此 a=-1,故 a +b=-1.故选 C.
1.若有限集 A 中有 n 个元素,则集合 A 的子集个数为 2n,真子集的个 数为 2n-1,非空真子集的个数为 2n-2.
2.A∪∅=A,A∪A=A,A⊆ (A∪B),B⊆ (A∪B). 3.A∩∅=∅,A∩A=A,A∩B⊆ A,A∩B⊆ B. 4.A∩B=A∪B⇔A=B.
5.A⊆ B⇔A∩B=A⇔A∪B=B⇔(∁UA)⊇ (∁UB)⇔A∩(∁UB)=∅. 6.A∩(∁UA)=∅,A∪(∁UA)=U,∁U(∁UA)=A. 7.(∁UA)∩(∁UB)=∁U(A∪B),(∁UA)∪(∁UB)=∁U(A∩B).
2
PART TWO
核心考向突破
考向一 集合的基本概念 例 1 (1)已知集合 A={0,1,2},则集合 B={x-y|x∈A,y∈A}中元 素的个数是( ) A.1 B.3 C.5 D.9
答案 C
解析 当 x=0 时,若 y=0,则 x-y=0;若 y=1,则 x-y=-1;若 y =2,则 x-y=-2.同理可得,当 x=1 时,x-y=1,0,-1;当 x=2 时,x -y=2,1,0.综上,根据集合中元素的互异性,可知 B 中元素有-2,-1, 0,1,2,共 5 个.
6.(2021·福建泉州质量检测(三))已知集合 A={(x,y)|x+y=8,x,y∈ N*},B={(x,y)|y>x+1},则 A∩B 中元素的个数为( )
高考数学复习考点知识与结论专题讲解1 集合技巧全攻略

高考数学复习考点知识与结论专题讲解第1讲 集合技巧全攻略结论一、集合的互异性对于一个给定的集合,它的任意两个元素是不能相同的.凡是出现含参数的集合,必须首先考虑集合的互异性,即集合中元苏不相等,例如集合{},A a b =,则有a b ≠[例1]设集合{}{1,2,3},4,5,{|,,}A B M x x a b a A b B ====+∈∈,则M 中元素的个数为().A.3B.4C.5D.6[答案]B[解析]因为集合{1,2,3},{4,5},{|,A B M x x a b a A b B ====+∈∈,所以a b +的值可能为:145,156,246,257,347,358+=+=+=+=+=+=.所以M 中元素只有:5,6,7故选B .[变式]已知集合()2{|()10}M x x a x ax a =--+-=各元素之和等于3,则实数a =()[答案] 2或32[解析] 根据集合中元素的互异性,当方程()2()10x a x ax a --+-=重根时,重根只能算一个元素.{()(1)[(1)]0}M x x a x x a =----=∣.当1a =时,{0,1}M =,不合题意;当11a -=,即2a =时,1,2}M =∣,符合题意;当1a ≠,且2a ≠时,1a a ++-13=,则313,,1,222a M ⎧⎫==⎨⎬⎩⎭,符合题意.综上,2a =或32.结论二、集合相等对于两个集合A 与B ,如果A B ⊆,且B A ⊆,那么集合A 与B 相等,记作A B =.[例2]设,R a b ∈,集合{1,,}0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭,则b a -=().A.1B.1-C.2D.2-[答案] C[解析] 由题意知,{}01,,a b a ∈+又0a ≠,故0a b +=,得1ba=-,则集合}{1,0,a {0,1,}b =-,可得1,1a b =-=,则2b a -=.故选C .【变式】设,,{1,},{1,}a b P a Q b ∈==--R ,若P Q =,则a b +=()[解析]因为P Q =,所以11ba =-⎧⎨=-⎩,所以1,1a b =-=-,所以2a b +=-.结论三、集合子集个数真子集有()21n-个,非空真子集有()22n-个.[例3]已知集合{}**(,)|43120,,B x y x y x N y N =+-<∈∈,则B 的子集个数为().A.3B.4C.7D.8[答案] D[解析] 因为集合{}**(,)43120,,B x y x y x y =+-<∈∈N N ∣,所以{(1,1)B =,(1,2),(2,1)},所以B 中含有3个元素,集合B 的子集个数有328=.故选D .【变式】设集合{1,2,3,4A ⊆∣,若A 至少有3个元索,则这样的A 一共有().A.2个B.4个C.5个D.7个[答案] C[解析] 因为集合{1,2,3,4},A A ⊆至少有3个元素,所以满足条件的集合A 有:{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4},所以这样的A 一共有5个.故选C .结论四、子集与交集若A B ⊆,则A B A ⋂=;若A B A ⋂=,则A B ⊆.[例4]已知集合{0,1,2},{1,}A B m ==.若A B B ⋂=,则实数m 的值是().A.0B.2C.0或2D.0或1或2[答案] C[解析] 因为A B B ⋂=,所以B A ⊆,所以0m =或 2.m =故选C .【变式】已知集合2{|320},{|}M x x x N x x a =+->=>,若M N M ⋂=,则实数a 的取值范围是().A.[3,)+∞B. (3,)+∞ C. (,1]-∞ D.(,1)-∞-[答案] C[解析] 由2320x x +->,即2230x x --<,可得13x -<<,故{|13}M x x =-<<.由M N M ⋂=可得M N ⊆,故(,1]a ∈-∞-.故选C .结论五、子集与并集若A B ⊆,则A B B ⋃=;若A B B ⋃=,则A B ⊆.[例5]已知集合{}2|1P x x =≤,{}M a =.若P M P ⋃=,则a 的取值范围是().A.(,1]-∞-B.[1,)+∞C.[1,1]-D.(,1][1,)-∞-⋃+∞ [答案] C[解析] 因为P M P ⋃=,所以M P ⊆,即a P ∈,得21a …,解得11a -剟,所以a 的取值范围是[1,1]-.故选C.【变式】设全集U =R ,若11|,,|,3663k k A x x k B x x k ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭Z Z ,则下列正确的是( ).A.U U C B C A ⊇B.A B A ⋂=C.A B A ⋃=D.U C A B ⊆[答案] B[解析] 由212|,,|,66k k A x x k B x x k ++⎧⎫⎧⎫==∈==∈⎨⎬⎨⎬⎩⎭⎩⎭Z Z 可得A B ⊆,所以A B A ⋂=.故选B.结论六、子集与空集题目中若有条件B A ⊆,则应分B =∅和B ≠∅两种情况进行讨论.[例6]若集合{}2|60M x x x =+-=,{}|10N x ax =-=,且N M ⊆,则实数a =[答案] 0或12或13- [解析] 由260x x +-=可得2x =或3x =-,因此{2,3}.M =- (1)若0a =,得N =∅,此时,N M ⊆; (2)若0a ≠,得1N a ⎧⎫=⎨⎬⎩⎭.若N M ⊆,满足12a =或13a =-,解得12a =或13a =-. 故所求实的值为0或12或13-. 【变式】已知{|25},{|121},A x x B x m x m B A =-=+-⊆剟剟,则m 的取值范围是___________ [答案] 3m …[解析] 应分B =∅和B ≠∅两种情况讨论.当121m m +>-, 即2m <时, B =∅,满足B A ⊆, 即2m <; 当121m m +=-, 即2m =时,{3}B =,满足B A ⊆, 即2m =; 当121m m +<-, 即2m >时,由B A ⊆,得12215m m +-⎧⎨-⎩……即23m <…;综上, 3m …. 故m 的取值范围是3m ….结论七、交集与空集由于A ⋂∅=∅,因此,A B A ⋂=中的A 可以为∅.[例7]已知集合{}2120,{211}A x x x B x m x m =--=-<<+∣∣…,且A B B ⋂=,则实数m 的取值范围为().[).1,2A -[].1,3B -[).2,C +∞[).1,D -+∞[答案] D[解析]由2120x x --…, 得(3)(4)0x x +-…, 得34x -剟, 所以||3A x x =-剟4}.又A B B ⋂=,所以2m …. (1)当B =∅时,有121m m +-…,解得2m …. (2)当B ≠∅时,有321,1 4 ,12211,m m m m m -≤-⎧⎪+≤⇒-≤<⎨⎪-<+⎩综上, [1,)m ∈-+∞. 故选D .【变式】设{}}2|8150,{|10A x x x B x ax =-+==-=, 若A B B ⋂=, 实数a 组成的集合的子集有()个. [答案] 8[解析] 集合A 化简得{3,5}A =,由A B B ⋂=知B A ⊆,故(I )当B =∅时,即方程10ax -=无解,此时0a =符合已知条件.()II 当B ≠∅时, 即方程10ax -=的解为3或5,代人得13a =或1.5综上,满足条件的a 组成的集合为110,,35⎧⎫⎨⎬⎩⎭,故其子集共有328=个.结论八、并集与空集由于A A ⋃∅=,因此,A B B ⋃=中的A 可以为∅.[例8]已知集合}2||230,{10},A x x x B x mx A B A =--==+=⋃=∣,则m 的取值是().A.11,3⎧⎫-⎨⎬⎩⎭B.10,1,3⎧⎫-⎨⎬⎩⎭C.11,3⎧⎫-⎨⎬⎩⎭D.10,1,3⎧⎫-⎨⎬⎩⎭[答案] D[解析]{}2|230{|13}{1,3}A x x x x x x =--===-==-或,{|10}B x mx =+=,当A B A ⋃=时,B A ⊆.若B =∅,则方程10mx +=无实数解,此时0m =;{1}B =-,则方程10mx +=的实数解为1-,此时1m =;若{3}B =,则方程10mx +=的实数解为3,此时13m =-;若{1,3}B =-,则方程10mx +=的实数解为1-和3,此时m 不存在.综上,m 的取值是10,1,3⎧⎫-⎨⎬⎩⎭.故选 D.【变式】已知集合{}{}2|121,|310P x a x a Q x x x =+≤≤+=-≤,若P Q Q ⋃=,实数a 的取值范围为_______ [答案] (,2]-∞[解析] 2{|310}{|25}Q x x x x x =-≤=-≤≤, 因为P Q Q ⋃=,所以P Q ⊆. (1)当P =∅时,即121a a +>+,解得0.a <(2)当P ≠∅时,即121,12, 02215,a a a a a ++⎧⎪+-⇒≤≤⎨⎪+⎩………综上,实数a 的取值范围为(,2]-∞.结论九、反演律(德摩根定律)()()()I I I C A B C A C B ⋂=⋃(交的补等于补的并)()()()I I I C A B C A C B ⋃=⋂(并的补等于补的交)[例9]若U 为全集,下面三个命题中是真命题的有() (1)若A B ⋂=∅,则()()U U C A C B U ⋃=. (2)若A B U ⋃=,则()()U U C A C B ⋂=∅. (3)若A B ⋃=∅,则A B ==∅.A.0个B.1个C.2个D.3个[答案] D[解析] (1)()()()U U U U C A C B C A B C U ⋃=⋂=∅= (2)()()()U U U U C A C B C A B C U ⋂=⋃==∅;(3) 证明:因为()A A B ⊆⋃,即A ⊆∅,而A ∅⊆,所以A =∅; 同理B =∅, 所以A B ==∅ 综上,三个命题均为真命题.故选D.【变式】若全集{1,2,3,4,5,6},{2,3},{1,4}U M N ===,则集合{5,6}等于()..A M N ⋃.B M N ⋂.()()U U C C M C N ⋃.()()U U D C M C N ⋂[答案] D[解析]因为{1,2,3,4}M N ⋃=,所以()()(){5,6}U UU M N M N ⋂=⋃=痧?.故选D.结论十、容斥原理用card()A 表示集合A 中的元素个数(有资料中用A 或其他符号),则通过维恩图可理解其具备的二维运算性质card()card()card()card()A B A B A B ⋃=+-⋂.[例10]高一某班学生参加大舞台和风情秀两个节目情况如下:参加风情秀的人数占该班全体人数的八分之三;参加大舞台的人数比参加风情秀的人数多3人;两个节目都参加的人数比两个节目都不参加的学生人数少7人.则此班的人数为_____[答案] 40人[解析]设{}|U x x =是高一某班学生,{}|A x x =是该班参加大舞台学生,{}|B x x =是该班参加风情秀学生.设该班两个节目都参加的人数为x ,只参加风情秀的人数为y ,由图可知,3(73)8x y x y x y +=+++++,解得15x y +=, 因为315408÷=(人),所以该班总人数为40人. 【变式】设A B ,是有限集,定义(,)card()card()d A B A B A B =⋃-⋂, 其中card()A 表示有限集A 中的元素个数,命题(1):对任意有限集 ,",A B A B ≠"是“(,)0d A B >"的充分必要条件;命题(2):对任意有限集,,,(,)(,)(,)A B C d A C d A B d B C +….下列判断正确的是(). A.命题(1)和命题(2)都成立 B.命题(1)和命题(2)都不成立C.命题(1)成立,命题(2)不成立D.命题(1)不成立,命题(2)成立[答案]A[解析](,)d A B 实际表示的是只在A 中或只在B 中的元素个数.对命题(1),当A B ≠时,至少有1个元素只在A 中或只在中, 所以(,)0;d A B > 对命题(2),如图所示,记图中的各个区域内的元素个数是(1,2,,7)i S i =且0i S …,所以(,)d A C =1245134623,(,),(,)S S S S d A B S S S S d B C S S +++=+++=++56S S +, 所以123456(,)(,)22d A B d B C S S S S S S +=+++++…,1245(,)S S S S d A C +++=,所以命题(2)也成立. 故选A.。
01-第一节 集合的概念高中数学必修一人教A版

【解析】
B.0 ∈
∗
1
C.
3
∈
D. π2 ∈
2是实数,故A错误;由 ∗ 是正整数集,可知0 ∉ ∗ ,故B错
1
误; 是有理数,故C正确;
3
π2 = π 是无理数,是整数集,故D错误.
4.(多选)[2024江苏连云港检测]已知集合 = {| = 3 − 1, ∈ },
故 − ∈ 0 ,故D正确.
6.由实数,− ,
2,
2
2
4
,− 3 组成的集合中最多含有___个元
素.
【解析】 由题可知 ≥ 0,所以− , 2 ,
2
, ,− ,故由实数,− ,
元素.
2,
2
2
2
2 ,− 3 分别可化为− 2 ,
,− 3 组成的集合中最多含有4个
D.{ = −1, = 3}
2 + = 5,
2 + = 5,
= 3,
【解析】 由ቊ
得ቊ
所以方程组ቊ
的解集
= −1,
− − 4 = 0,
−−4=0
是{ 3, −1 }.
9.(多选)集合{1,3,5,7,9}用描述法可表示为(
AB
)
A.{|是不大于9的非负奇数}
D.不等式3 − 10 < 0的所有正整数解
【解析】
A √ 某校2024年入学的全体高一年级新生确定,元素确定,能构成集合.
B × 精确度不一样得到的近似值不一样,元素不确定,不能构成集合.
C × 学习成绩较好是相对的,故这些学生不确定,不能构成集合.
D √
不等式3 − 10 < 0的所有正整数解为1,2,3,元素确定,能构成
【暑假预习】2023年新高一数学 第01讲 集合及其表示法(9种题型)(学生版)

01集合及其表示法(9种题型)【课程细目表】一、知识梳理二、考点剖析1.集合的含义2.元素与集合关系的判断3.集合的确定性、互异性、无序性4.集合相等5.有限集与无限集.6.集合的表示法--描述法7.集合的表示法--列举法8.集合的表示法--区间法9.集合的表示法--综合应用三、过关检测【知识梳理】一、集合的意义1.集合的概念我们把能够确切指定的一些对象组成的整体叫做集合,简称集.集合中的各个对象叫做这个集合的元素.对于一个给定的集合,集合中的元素具有确定性、互异性、无序性.确定性是指一个对象要么是给定集合的元素,要么不是这个集合的元素,二者必居其一.比如“著名的数学家”、“较大的数”、“高一一班成绩好的同学”等都不能构成集合,因为组成集合的元素不确定.互异性是指对于一个给定的集合,集合中的元素是各不相同的,也就是说,一个给定的集合中的任何两个元素都是不同的对象,集合中的元素不重复出现.例如由元素1,2,1组成的集合中含有两个元素:1,2.无序性是指组成集合的元素没有次序,只要构成两个集合的元素是一样的,我们就称这两个集合是相等的.2.集合与元素的字母表示、元素与集合的关系集合常用大写字母A、B、C⋯来表示,集合中的元素用a、b、c⋯表示,如果a是集合A的元素,就记作a∈A,读作“a属于A”;如果a不是集合A的元素,就记作a∉A,读作“a不属于A”3.常用的数集及记法数的集合简称数集,我们把常用的数集用特定的字母表示:全体自然数组成的集合,即自然数集,记作N,不包含零的自然数组成的集合,记作N*全体整数组成的集合,即整数集,记作Z全体有理数组成的集合,即有理数集,记作Q全体实数组成的集合,即实数集,记作R常用的集合的特殊表示法:实数集R(正实数集R+)、有理数集Q(负有理数集Q-)、整数集Z(正整数集Z+)、自然数集N(包含零)、不包含零的自然数集N*;4.集合相等如果两个集合A与B的组成元素完全相同,就称这两个集合相等,记作A=B.5.集合的分类我们把含有有限个元素的集合叫做有限集,含有无限个元素的集合叫做无限集我们引进一个特殊的集合--空集,规定空集不含元素,记作∅,例如,方程x2+1=0的实数解所组成的集合是空集,又如,两个外离的圆,它们的公共点所组成的集合也是空集.6.空集我们把不含任何元素的集合,记作φ。
第01讲 集合(原卷版)备战2023年高考数学一轮复习精讲精练(全国通用版)

第01讲集合(精讲+精练)目录第一部分:思维导图(总览全局)第二部分:知识点精准记忆第三部分:课前自我评估测试第四部分:典型例题剖析高频考点一:集合的基本概念高频考点二:集合的基本关系高频考点三:集合的运算高频考点四:venn图的应用高频考点五:集合新定义问题第五部分:高考真题感悟第六部分:集合(精练)1、元素与集合(1)集合中元素的三个特性:确定性、互异性、无序性.(2)元素与集合的关系:属于 或 不属于,数学符号分别记为:∈和∉.(3)集合的表示方法:列举法、描述法、韦恩图(venn 图).(4)常见数集和数学符号①确定性:给定的集合,它的元素必须是确定的;也就是说,给定一个集合,那么任何一个元素在不在这个集合中就确定了.给定集合{1,2,3,4,5}A =,可知1A ∈,在该集合中,6A ∉,不在该集合中;②互异性:一个给定集合中的元素是互不相同的;也就是说,集合中的元素是不重复出现的.集合{,,}A a b c =应满足a b c ≠≠.③无序性:组成集合的元素间没有顺序之分。
集合{1,2,3,4,5}A =和{1,3,5,2,4}B =是同一个集合. ④列举法把集合的元素一一列举出来,并用花括号“{}”括起来表示集合的方法叫做列举法.⑤描述法用集合所含元素的共同特征表示集合的方法称为描述法.具体方法是:在花括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征.2、集合间的基本关系(1)子集(subset ):一般地,对于两个集合A 、B ,如果集合A 中任意一个元素都是集合B 中的元素,我们就说这两个集合有包含关系,称集合A 为集合B 的子集 ,记作A B ⊆(或B A ⊇),读作“A 包含于B ”(或“B 包含A ”).(2)真子集(proper subset ):如果集合A B ⊆,但存在元素x B ∈,且x A ∉,我们称集合A 是集合B 的真子集,记作A B (或B A ⊃≠).读作“A 真包含于B ”或“B 真包含A ”.(3)相等:如果集合A 是集合B 的子集(A B ⊆,且集合B 是集合A 的子集(B A ⊆),此时,集合A 与集合B 中的元素是一样的,因此,集合A 与集合B 相等,记作A B =.(4)空集的性质: 我们把不含任何元素的集合叫做空集,记作∅;∅是任何集合的子集,是任何非空集合的真子集.3、集合的基本运算(1)交集:一般地,由属于集合A 且属于集合B 的所有元素组成的集合,称为A 与B 的交集,记作A B ,即{|,}A B x x A x B =∈∈且.(2)并集:一般地,由所有属于集合A 或属于集合B 的元素组成的集合,称为A 与B 的并集,记作A B ,即{|,}A B x x A x B =∈∈或.(3)补集:对于一个集合A ,由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,简称为集合A 的补集,记作U C A ,即{|,}U C A x x U x A =∈∉且.4、集合的运算性质(1)AA A =,A ∅=∅,AB B A =. (2)AA A =,A A ∅=,AB B A =. (3)()U AC A =∅,()U A C A U =,()U U C C A A =.5、高频考点结论(1)若有限集A 中有n 个元素,则A 的子集有2n 个,真子集有21n -个,非空子集有21n -个,非空真子集有22n -个.(2)空集是任何集合A 的子集,是任何非空集合B 的真子集.(3)U U A B AB A A B BC B C A ⊆⇔=⇔=⇔⊆. (4)()()()U U U C A B C A C B =,()()()U U U C A B C A C B =.一、判断题1.(2022·江西·贵溪市实验中学高二期末)集合{},,,A a b c d =的子集共有8个 ( )2.(2021·江西·贵溪市实验中学高二阶段练习)集合{}1,2,3,4,5和{}5,4,3,2,1表示同一个集合( ) 3.(2021·江西·贵溪市实验中学高三阶段练习)满足条件{}{}11,2,3M ⋃=的集合M 的个数是2个.( )4.(2021·江西·贵溪市实验中学高三阶段练习)已知集合{}20M x x x =+=∣,则1M -∈.( ) 5.(2021·江西·贵溪市实验中学高二阶段练习)满足条件{}{}11,2,3M ⋃=的集合M 的个数是3 ( )二、单选题1.(2022·广东茂名·高一期末)已知集合{}21A x y x ==+,集合{}21B y y x ==+,则A B =( )A .0B .{}|1x x ≥C .{}|1x x ≤D .R2.(2021·广东·佛山一中高一阶段练习)已知集合{}22,531,=-+A a a ,,{}5,9,1,4=+-B a a ,若{}4A B ⋂=,则实数a 的取值的集合为( )A .{}1,2,2-B .{}1,2C .{}1,2-D .{}13.(2022·河南平顶山·高三阶段练习(文))已知集合{}1A x x =>,{}260B x x x =--<,则()R A B ⋂=( ) A .{}13x x << B .{}12x x << C .{}3x x ≥ D .{}2x x ≥4.(2022·湖南·沅陵县第一中学高二开学考试)如图所示,阴影部分表示的集合是( )A .(UB ⋂)A B .(U A ⋂)BC .() U A B ⋂D .(U A B )高频考点一:集合的基本概念1.(2020·重庆·一模(理))已知集合{}2|280,A x Z x x =∈+-<{}2|B x x A =∈,则B 中元素个数为 A .4 B .5 C .6 D .72.(2021·上海黄浦·一模)已知集合{}2,(R)A x x x =∈,若1A ∈,则x =___________.3.(2012·全国·一模(理))集合中含有的元素个数为 A .4 B .6 C .8 D .124.(2017·河北·武邑宏达学校模拟预测(理))集合{}2*|70,A x x x x N =-<∈,则*6|,B y N y A y ⎧⎫=∈∈⎨⎬⎩⎭中元素的个数为A .1个B .2个C .3个D .4个5.(2020·湖南·邵东市第十中学模拟预测(理))已知集合{}1,0,1A =-,(),|,,x B x y x A y A y ⎧⎫=∈∈∈⎨⎬⎩⎭N ,则集合B 中所含元素的个数为( )A .3B .4C .6D .96.(2021·全国·二模(理))定义集合运算:{},,A B z z xy x A y B *==∈∈,设{1,2}A =,{1,2,3}B =,则集合A B *的所有元素之和为( )A .16B .18C .14D .8高频考点二:集合的基本关系1.(2021·广东肇庆·模拟预测)已知集合{}3P x x =<,{}2Q x Z x =∈<,则( )A .P Q ⊆B .Q P ⊆C .P Q P =D .P Q Q ⋃= 2.(2020·山东·模拟预测)已知集合==2{1,},{}M x N x ,若N M ⊆,则x =__.3.(2020·江苏省如皋中学二模)设{,2}M m =,{2,2}N m m =+,且M N ,则实数m 的值是________. 4.(2021·辽宁·东北育才学校一模)所有满足{}{},,,a M a b c d ⊆的集合M 的个数为________;5.(2022·全国·模拟预测)已知集合{}213M x x =+<,{}N x x a =<,若N M ⊆,则实数a 的取值范围为( )A .[)1,+∞B .[)2,+∞C .(],1-∞D .(),1-∞6.(2020·广西·模拟预测)已知集合{|15}A x x =<≤,{}|04B x x =<<,{}|121C x m x m =+<<-. (1)求A B ,()R A B ⋂:(2)若B C C =,求实数m 的取值范围.7.(2020·广西·模拟预测)已知集合{|121}A x a x a =+≤≤-,{|3B x x =≤或5}x >.(1)若4a =,求A B ; (2)若A B ⊆,求a 的取值范围.高频考点三:集合的运算1.(2022·甘肃陇南·模拟预测(理))已知集合{}|321A x x =->,{}260B x x x =--<,则A B =( ) A .{}13x x <<B .{}12x x <<C .{}21x x -<<D .{}31x x -<<2.(2022·北京丰台·一模)已知集合{|12}A x x =-<≤,{|21}B x x =-<≤,则A B ⋃=( )A .{|11}x x -<<B .{|11}x x -<≤C .{|22}x x -<<D .{|22}x x -<≤3.(2022·河南·模拟预测(理))已知集合{}14A x x =≤≤,(){}214B x x =-≥,则()A B =R ( ) A .[]3,4 B .[]1,4 C .[)1,3 D .[)3,+∞4.(2022·全国·模拟预测(理))设全集U =R ,集合102x A x x ⎧⎫+=≤⎨⎬-⎩⎭,集合{}ln 1B x x =≤,则A B 是( )A .(]0,2B .()2,eC .()0,2D .[)1,e -5.(2022·江西赣州·一模(理))设集合{}1,0,A n =-,{},,B x x a b a A b A ==⋅∈∈.若A B A =,则实数n 的值为( )A .1-B .0C .1D .26.(2021·江西·模拟预测)2021年是中国共产党成立100周年,电影频道推出“经典频传:看电影,学党史”系列短视频,传扬中国共产党的伟大精神,为广大青年群体带来精神感召.现有《青春之歌》《建党伟业》《开国大典》三支短视频,某大学社团有50人,观看了《青春之歌》的有21人,观看了《建党伟业》的有23人,观看了《开国大典》的有26人.其中,只观看了《青春之歌》和《建党伟业》的有4人,只观看了《建党伟业》和《开国大典》的有7人,只观看了《青春之歌》和《开国大典》的有6人,三支短视频全观看了的有3人,则没有观看任何一支短视频的人数为________.7.(2021·上海·模拟预测)已知集合{}2890,U x x x x Z =--≤∈,{}A y y y Z ==∈,则U A__________.高频考点四:venn 图的应用1.(2022·贵州贵阳·一模(理))若全集U 和集合A ,B 的关系如图所示,则图中阴影部分表示的集合为( )A .()U AB ⋂B .()U B AC .()U A BD .()U A B2.(2021·广东·模拟预测)已知全集U =R ,集合{}2,20A x yB x x x ⎧==--<⎨⎩∣∣,它们的关系如图(Venn 图)所示,则阴影部分表示的集合为( )A .{12}x x -≤<∣B .{12}xx -<<∣ C .{12}xx ≤<∣ D .{12}x x <<∣ 3.(2021·黑龙江·哈九中三模(理))如图,U 是全集,,,M P S 是U 的子集,则阴影部分表示的集合是( )A .()M P SB .()M P SC .()U M P S ⋂⋂D .()U M P S ⋂⋃4.(2021·江苏徐州·二模)某班45名学生参加“3·12”植树节活动,每位学生都参加除草、植树两项劳动.依据劳动表现,评定为“优秀”、“合格”2个等级,结果如下表:若在两个项目中都“合格”的学生最多有10人,则在两个项目中都“优秀”的人数最多为( )A .5B .10C .15D .205.(2020·北京市第五中学模拟预测)高二一班共有学生50人,每名学生要从物理、化学、生物、历史、地理、政治这六门课程中选择三门课程进行学习.已知选择物理、化学、生物的学生各有至少20人,这三门课程都不选的有10人,这三门课程都选的有10人,在这三门课程中选择任意两门课程的都至少有13人,物理、化学只选一科的学生都至少6人,那么选择物理和化学这两门课程的学生人数至多( ) A .16 B .17 C .18 D .19高频考点五:集合新定义问题1.定义集合{|A B x x A -=∈ 且}x B ∉.己知集合{}Z 26U x x =∈-<<,{}0,2,4,5A =,{}1,0,3B =-,则()U A B -中元素的个数为( )A .3B .4C .5D .6 2.设A 、B 是非空集合,定义:{|A B x x A B ⨯=∈且}x A B ∉.已知{|A x y =,{|1}B x x =>,则A B ⨯等于( )A .[0,1](2,)+∞B .[0,1)(2,)⋃+∞C .[0,1]D .[0,2]3.已知集合{}1,2,3M =,(){},,,N x y x M y M x y M =∈∈+∈,则集合N 中的元素个数为( ) A .2 B .3 C .8 D .94.已知非空集合A 、B 满足以下两个条件:(1){}1,2,3,4,5A B =,A B =∅;(2)A 的元素个数不是A 中的元素,B 的元素个数不是B 中的元素.则有序集合对(),A B 的个数为( )A .4B .6C .8D .165.(多选)在整数集Z 中,被5除所得余数为k 的所有整数组成一个“类”,记为[k ],即{}[]5k n k n Z =+∈,0,1,2,3,4k =.则下列结论正确的是( )A .2011[1]∈;B .[0][1][2][3][4]Z =⋃⋃⋃⋃;C .3[3]-∈;D .整数a ,b 属于同一“类”的充要条件是“[0]a b -∈”.1.(2021·山东·高考真题)假设集合{}1,2,3A =,{}1,3B =,那么A B 等于( )A .{}1,2,3B .{}1,3C .{}1,2D .{}22.(2021·湖南·高考真题)已知集合{}13,5A =,,{}1,2,3,4B =,且A B =( ) A .{}1,3B .{}1,3,5C .{}1,2,3,4D .{}1,2,3,4,53.(2021·江苏·高考真题)已知集合{}1,3M =,{}1,3N a =-,若{}1,2,3MN =,则a 的值是( ) A .-2 B .-1 C .0 D .14.(2021·天津·高考真题)设集合{}{}{}1,0,11,3,5,0,2,4A B C =-==,,则()A B C ⋂⋃=( ) A .{}0 B .{0,1,3,5} C .{0,1,2,4} D .{0,2,3,4} 5.(2021·全国·高考真题)设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===,则()U A B =( ) A .{3} B .{1,6} C .{5,6} D .{1,3} 6.(2021·浙江·高考真题)设集合{}1A x x =≥,{}12B x x =-<<,则A B =( ) A .{}1x x >- B .{}1x x ≥ C .{}11x x -<< D .{}12x x ≤<7.(2021·全国·高考真题(理))已知集合{}21,S s s n n ==+∈Z ,{}41,T t t n n ==+∈Z ,则S T ( )A .∅B .SC .TD .Z一、单选题1.(2021·北大附中云南实验学校高一阶段练习)下列各对象可以组成集合的是( )A .与1非常接近的全体实数B .北大附中云南实验学校20202021-学年度第二学期全体高一学生C .高一年级视力比较好的同学D .高一年级很有才华的老师2.(2022··模拟预测(理))已知集合A ={}250x x x -≤,B ={}21,x x k k Z =-∈,则A B 中元素的个数为( )A .2B .3C .4D .53.(2022·贵州毕节·模拟预测(理))已知集合(){}10A x x x =-=,{}20,,B m m =,若A B B ⋃=,则m =( )A .1-B .0C .1D .±14.(2022·全国·模拟预测)已知集合{}1,2,3,4,5,6A =,6,1B x x A x ⎧⎫=∈∈⎨⎬-⎩⎭N ,则集合B 的子集的个数是( )A .3B .4C .8D .165.(2022·湖南·长沙一中高三阶段练习)集合1,36n M x x n Z ⎧⎫==+∈⎨⎬⎩⎭,1,63n N x x n Z ⎧⎫==+∈⎨⎬⎩⎭,则M N =( )A .MB .NC .∅D .,6n x x n Z ⎧⎫=∈⎨⎬⎩⎭6.(2022·广东·高二期末)集合{}2230A x x x =--=,{}10B x mx =+=,A B A ⋃=,则m 的取值范围是( )A .11,3⎧⎫-⎨⎬⎩⎭B .{}1,3-C .10,3⎧⎫-⎨⎬⎩⎭D .10,1,3⎧⎫-⎨⎬⎩⎭7.(2022·湖南·长郡中学高二阶段练习)已知集合(){}2ln 4A x y x ==-,{B y x =,则A B =( ) A .()2,3B .()(],22,3-∞-C .()0,3D .(]2,3 8.(2022·河南·温县第一高级中学高三阶段练习(理))已知集合102x A x x ⎧⎫-=≤⎨⎬+⎩⎭,B ={-2,-1,0,1},则A ∩B =( )A .{-2,-1,0,1}B .{-1,0,1}C .{-1,0}D .{-2,-1,0}二、填空题9.(2022·四川·雅安中学高一阶段练习)集合{|13},{|25}A x x B x x =∈<≤=∈<<Z Z ,则A B 的子集的个数为___________.10.(2022·上海金山·高一期末)满足条件:{}a {},,,M a b c d ⊆的集合M 的个数为______.11.(2022·全国·高三专题练习)已知集合{}2{123},280A x a x a B x x x =-<<+=--≤,若()R A B A ⋂=,求实数a 的取值范围是___________.12.(2022·全国·高三专题练习)设集合{}2280A x x x =-->,{B x x a =≤或}5x a ≥+,若()R A B ⋂=∅,则a 的取值范围是___________.三、解答题13.(2022·山西·榆次一中高一开学考试)已知集合{}22150M x x x =--≤,{}N x m x m =-≤≤.(1)当1m =时,求M N ⋂以及()()R R M N ⋃;(2)若M N ,求实数m 的取值范围.14.(2022·江苏省天一中学高一期末)集合1121x A x x +⎧⎫=>⎨⎬-⎩⎭,{}22240B x x ax a =-+-<. (1)若{}23,4,23C a a =+-,()0B C ∈,求实数a 的值;(2)从条件①②③这三个条件中选择一个作为已知条件,求实数a 的取值范围.条件:①A B A =;②()R A B ⋂=∅;③()R B A R ⋃=.(注:答题前先说明选择哪个条件,如果选择多于一条件分别解答,按第一个解答计分).15.(2022·江西·赣州市赣县第三中学高一开学考试)已知集合{}2430A x x x =++=,{}22230B x x ax a a =-+--=. (1)若1a =,求A B ;(2)若A B A ⋃=,求a 的取值集合.16.(2022·江苏·高一)已知集合A 为非空数集,定义:{},,S x x a b a b A ==+∈,{},,T x x a b a b A ==-∈.(1)若集合{}1,3A =,直接写出集合S 、T ;(2)若集合{}1234,,,A x x x x =,且T A =,写出一个满足条件的集合A ,并说明理由;(3)若集合{}02020,A x x x N ⊆≤≤∈,S T ⋂=∅,记A 为集合A 中元素的个数,求A 的最大值.。
第一讲集合——精选推荐

第一讲 集合一、基础知识定义1 有限集A 的元素数目叫做这个集合的阶,记作或.A ()n A 定义2 若M 为由一些给定的集合构成的集合,则称集合M 为集族.设A 为有限集,由A 的若干子集构成的集合称为集合A 的一个子集族.若,则由A 的所有子集构成A n =的子集构成的子集族的阶为.2n 定义3 若,且,则这些子集的I A A A n = 21),,1(j i n j i A A j i ≠≤≤∅= 全集叫I 的一个-划分,n 叫做划分的长度.若A 为有限集,是集合n 12{,,,}n I A A A = A 的一个划分,则有.12n A A A A =+++ 定义4 设是集合A 的非空子集族,如果,那12{,,,}n I A A A = 12n A A A A = 么称I 为集合A 的一个n-覆盖.定理1 集合运算的性质:对任意集合A ,B ,C ,有:(1) (2););()()(C A B A C B A =)()()(C A B A C B A =(3) (4)();U U U C A C B C A B = ().U U U C A C B C A B = 定理2 加法原理:做一件事有类办法,第一类办法中有种不同的方法,第二类办法n 1m 中有种不同的方法,…,第类办法中有种不同的方法,那么完成这件事一共有2m n n m 种不同的方法.n m m m N +++= 21定理3 乘法原理:做一件事分个步骤,第一步有种不同的方法,第二步有种不n 1m 2m 同的方法,…,第步有种不同的方法,那么完成这件事一共有n n m 种不同的方法.n m m m N ⋅⋅⋅= 21定理4 最小数原理:自然数集的任何非空子集必有最小数.定理5 抽屉原理:将个元素放入个抽屉,必有一个抽屉放有不少于1+mn )1(>n n 个元素,也必有一个抽屉放有不多于个元素;将无穷多个元素放入个抽屉必有1+m m n 一个抽屉放有无穷多个元素.定理6 容斥原理:用表示集合A 的元素个数,则:A ,B A B A B A -+=,C B A C B C A B A C B A C B A +---++=此结论可以推广到个集合的情况,即n 111n n i i i j i j k i i j i j k n i AA A A A A A =≠≤<<≤==-+∑∑∑∑ .)1(11 n i i n A =--+-定理7 设是集合A 的一个覆盖,,且I 中每r 个元素的交非12{,,,}k I A A A = A n =空,而每r+1个元素的交集为空集,则且.rk C n ≤1(1,2,,)r i k A n C i k -≤-= 定理8 设集合A ={1,2,…,n},是集合A 的子集族,且F 中任12{,,,}k F A A A = 意两个元素互不包含,则F 中元素个数.,(1)i j A A i j k ≤<≤2[]n n k C ≤二、例题选讲例1 集合A ,B ,C 是I ={1,2,3,4,5,6,7,8,9,0}的子集,(1)若,I B A = 求有序集合对(A ,B )的个数;(2)求I 的非空真子集的个数.【解】(1)集合I 可划分为三个不相交的子集;A \B ,B \A ,中的每个元素恰属于I B A , 其中一个子集,10个元素共有310种可能,每一种可能确定一个满足条件的集合对,所以集合对有310个.(2)I 的子集分三类:空集,非空真子集,集合I 本身,确定一个子集分十步,第一步,1或者属于该子集或者不属于,有两种;第二步,2也有两种,…,第10步,0也有两种,由乘法原理,子集共有个,非空真子集有1022个.1024210=例2 给定集合的个子集:,满足任何两个子集的交集非},,3,2,1{n I =k k A A A ,,,21 空,并且再添加I 的任何一个其它子集后将不再具有该性质,求的值.k 【解】将I 的子集作如下配对:每个子集和它的补集为一对,共得对,每一对不能同12-n 在这个子集中,因此,;其次,每一对中必有一个在这个子集中出现,否则,k 12-≤n k k 若有一对子集未出现,设为C I A 与A ,并设,则,从而可以在个∅=1A A 1I A C A ⊆k 子集中再添加,与已知矛盾,所以.综上,.I C A 12-≥n k 12-=n k 例3 求1,2,3,…,100中不能被2,3,5整除的数的个数.【解】 记,{1,2,3,,100},{1100,22}I A x x x x ==≤≤ 且能被整除(记为),由容斥原理,}5,1001{},3,1001{x x x C x x x B ≤≤=≤≤=+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+---++=31002100C B A A C C B B A C B A C B A ,所以不能被2,3,5整除的数有7430100151001010061005100=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡个.26=-C B A I 例4 S 是集合{1,2,…,2004}的子集,S 中的任意两个数的差不等于4或7,问S 中最多含有多少个元素?【解】将任意连续的11个整数排成一圈如右图所示.由题目条件可知每相邻两个数至多有一个属于S ,将这11个数按连续两个为一组,分成6组,其中一组只有一个数,若S 含有这11个数中至少6个,则必有两个数在同一组,与已知矛盾,所以S 至多含有其中5个数.又因为2004=182×11+2,所以S 一共至多含有182×5+2=912个元素,另一方面,当时,恰有,且S 满足题目条},2004,10,7,4,2,1,11{N k r t t k r r S ∈≤=+==912=S 件,所以最少含有912个元素.例5 集合{1,2,…,3n }可以划分成个互不相交的三元集合,其中,n },,{z y x z y x 3=+求满足条件的最小正整数.n 【解】 设其中第个三元集为则1+2+…+i ,,,2,1},,,{n i z y x i i =∑==n i i zn 1,43所以.当为偶数时,有,所以,当为奇数时,有∑==+n i i z n n 142)13(3n n 388≥n n ,所以,当时,集合{1,11,4},{2,13,5},{3,15,6},138+n 5≥n 5=n {9,12,7},{10,14,8}满足条件,所以的最小值为5.n 例6 设A ={1,2,3,4,5,6},B ={7,8,9,……,n },在A 中取三个数,B 中取两个数组成五个元素的集合,求的最小值.i A .201,2,20,,2,1≤<≤≤=j i A A i j i n 【解】 .16min =n 设B 中每个数在所有中最多重复出现次,则必有.若不然,数出现次(i A k 4≤k m k),则在出现的所有中,至少有一个A 中的数出现3次,不妨设它是4>k .123>k m i A 1,就有集合{1,},其中,121,,,b m a a },,,,1{},,,,,1{365243b m a a b m a a 61,≤≤∈i A a i 为满足题意的集合.必各不相同,但只能是2,3,4,5,6这5个数,这不可能,所以i a .4≤k 20个中,B 中的数有40个,因此至少是10个不同的,所以.当时,如i A 16≥n 16=n 下20个集合满足要求:{1,2,3,7,8}, {1,2,4,12,14}, {1,2,5,15,16}, {1,2,6,9,10},{1,3,4,10,11}, {1,3,5,13,14}, {1,3,6,12,15}, {1,4,5,7,9},{1,4,6,13,16}, {1,5,6,8,11}, {2,3,4,13,15}, {2,3,5,9,11},{2,3,6,14,16}, {2,4,5,8,10}, {2,4,6,7,11}, {2,5,6,12,13},{3,4,5,12,16}, {3,4,6,8,9},{3,5,6,7,10},{4,5,6,14,15}.三、练习题1.{1,2,3,4,5,6,7,8,9},,,{2},()(){1,9},I I I A I B I A B C A C B =⊆⊆== ,则___________.(){4,6,8}I C A B = ()I A C B = 解:{3,5,7},提示用韦恩图。
高中数学必修一专题复习
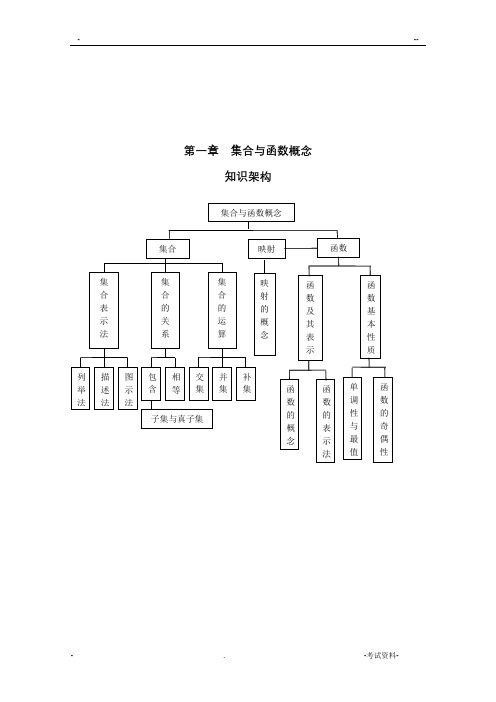
第一章集合与函数概念知识架构第一讲 集合★知识梳理一:集合的含义及其关系1.集合中的元素具有的三个性质:确定性、无序性和互异性;2.集合的3种表示方法:列举法、描述法、韦恩图;3.集合中元素与集合的关系:三:集合的基本运算①两个集合的交集:A B = {}x x A x B ∈∈且; ②两个集合的并集: AB ={}x x A x B ∈∈或;③设全集是U,集合A U ⊆,则U C A ={}x x U x A ∈∉且★重、难点突破重点:集合元素的特征、集合的三种表示方法、集合的交、并、补三种运算。
难点:正确把握集合元素的特征、进行集合的不同表示方法之间的相互转化,准确进行集合的交、并、补三种运算。
重难点: 1.集合的概念掌握集合的概念的关键是把握集合元素的三大特性,要特别注意集合中元素的互异性, 在解题过程中最易被忽视,因此要对结果进行检验; 2.集合的表示法(1)列举法要注意元素的三个特性;(2)描述法要紧紧抓住代表元素以及它所具有的性质,如{})(x f y x =、{})(x f y y =、{})(),(x f y y x =等的差别,如果对集合中代表元素认识不清,将导致求解错误:(3)Venn 图是直观展示集合的很好方法,在解决集合间元素的有关问题和集合的运算时常用Venn 图。
3.集合间的关系的几个重要结论 (1)空集是任何集合的子集,即A ⊆φ (2)任何集合都是它本身的子集,即A A ⊆(3)子集、真子集都有传递性,即若B A ⊆,C B ⊆,则C A ⊆ 4.集合的运算性质(1)交集:①A B B A =;②A A A = ;③φφ= A ;④A B A ⊆ ,B B A ⊆ ⑤B A A B A ⊆⇔= ;(2)并集:①A B B A =;②A A A = ;③A A =φ ;④A B A ⊇ ,B B A ⊇ ⑤A B A B A ⊆⇔= ; (3)交、并、补集的关系 ①φ=A C A U ;U A C A U =②)()()(B C A C B A C U U U =;)()()(B C A C B A C U U U =★热点考点题型探析考点一:集合的定义及其关系题型1:集合元素的基本特征[例1](2008年理)定义集合运算:{}|,,A B z z xy x A y B *==∈∈.设{}{}1,2,0,2A B ==,则集合A B *的所有元素之和为( )A .0;B .2;C .3;D .6[解题思路]根据A B *的定义,让x 在A 中逐一取值,让y 在B 中逐一取值,xy 在值就是A B *的元素[解析]:正确解答本题,必需清楚集合A B *中的元素,显然,根据题中定义的集合运算知A B *={}4,2,0,故应选择D【名师指引】这类将新定义的运算引入集合的问题因为背景公平,所以成为高考的一个热点,这时要充分理解所定义的运算即可,但要特别注意集合元素的互异性。
人教版高一数学必修一第一章-知识点与习题讲解

必修1第一章集合与函数基础知识点整理第1讲 §1.1.1 集合的含义与表示¤知识要点:1. 把一些元素组成的总体叫作集合(set ),其元素具有三个特征,即确定性、互异性、无序性.2. 集合的表示方法有两种:列举法,即把集合的元素一一列举出来,并用花括号“{ }”括起来,基本形式为123{,,,,}n a a a a ⋅⋅⋅,适用于有限集或元素间存在规律的无限集.描述法,即用集合所含元素的共同特征来表示,基本形式为{|()x A P x ∈},既要关注代表元素x ,也要把握其属性()P x ,适用于无限集.3. 通常用大写拉丁字母,,,A B C ⋅⋅⋅表示集合. 要记住一些常见数集的表示,如自然数集N ,正整数集*N 或N +,整数集Z ,有理数集Q ,实数集R .4. 元素与集合之间的关系是属于(belong to )与不属于(not belong to ),分别用符号∈、∉表示,例如3N ∈,2N -∉.¤例题精讲:【例1】试分别用列举法和描述法表示下列集合:(1)由方程2(23)0x x x --=的所有实数根组成的集合;(2)大于2且小于7的整数.解:(1)用描述法表示为:2{|(23)0}x R x x x ∈--=;用列举法表示为{0,1,3}-.(2)用描述法表示为:{|27}x Z x ∈<<;用列举法表示为{3,4,5,6}.【例2】用适当的符号填空:已知{|32,}A x x k k Z ==+∈,{|61,}B x x m m Z ==-∈,则有:17 A ; -5 A ; 17 B .解:由3217k +=,解得5k Z =∈,所以17A ∈;由325k +=-,解得73k Z =∉,所以5A -∉;由6117m -=,解得3m Z =∈,所以17B ∈. 【例3】试选择适当的方法表示下列集合:(教材P 6 练习题2, P 13 A 组题4)(1)一次函数3y x =+与26y x =-+的图象的交点组成的集合; (2)二次函数24y x =-的函数值组成的集合;(3)反比例函数2y x=的自变量的值组成的集合. 解:(1)3{(,)|}{(1,4)}26y x x y y x =+⎧=⎨=-+⎩. (2)2{|4}{|4}y y x y y =-=≥-. (3)2{|}{|0}x y x x x ==≠.点评:以上代表元素,分别是点、函数值、自变量. 在解题中不能把点的坐标混淆为{1,4},也注意对比(2)与(3)中的两个集合,自变量的范围和函数值的范围,有着本质上不同,分析时一定要细心.*【例4】已知集合2{|1}2x a A a x +==-有唯一实数解,试用列举法表示集合A .A B B A A B A B A . B . C . D . 解:化方程212x a x +=-为:2(2)0x x a --+=.应分以下三种情况: ⑴方程有等根且不是2±:由 △=0,得94a =-,此时的解为12x =,合. ⑵方程有一解为2,而另一解不是2-:将2x =代入得2a =-,此时另一解12x =-,合. ⑶方程有一解为2-,而另一解不是2:将2x =-代入得2a =,此时另一解为21x =+,合.综上可知,9{,2,2}4A =--.点评:运用分类讨论思想方法,研究出根的情况,从而列举法表示. 注意分式方程易造成增根的现象.第2讲 §1.1.2 集合间的基本关系¤知识要点:1. 一般地,对于两个集合A 、B ,如果集合A 中的任意一个元素都是集合B 中的元素,则说两个集合有包含关系,其中集合A 是集合B 的子集(subset ),记作A B ⊆(或B A ⊇),读作“A 含于B ”(或“B 包含A ”).2. 如果集合A 是集合B 的子集(A B ⊆),且集合B 是集合A 的子集(B A ⊇),即集合A 与集合B 的元素是一样的,因此集合A 与集合B 相等,记作A B =.3. 如果集合A B ⊆,但存在元素x B ∈,且x A ∉,则称集合A 是集合B 的真子集(proper subset ),记作A ≠⊂B (或B ≠⊃A ).4. 不含任何元素的集合叫作空集(empty set ),记作∅,并规定空集是任何集合的子集.5. 性质:A A ⊆;若A B ⊆,B C ⊆,则A C ⊆;若A B A =,则A B ⊆;若A B A =,则B A ⊆.¤例题精讲:【例1】用适当的符号填空:(1){菱形} {平行四边形}; {等腰三角形} {等边三角形}.(2)∅ 2{|20}x R x ∈+=; 0 {0}; ∅ {0}; N {0}. 解:(1), ;(2)=, ∈, ,.【例2】设集合1,,}22{|,{|n n x n n A x x B x =∈=+∈==Z}Z ,则下列图形能表示A 与B 关系的是( ). 解:简单列举两个集合的一些元素,3113{,1,,0,,1,,}2222A =⋅⋅⋅---⋅⋅⋅,3113{,,,,,}2222B =⋅⋅⋅--⋅⋅⋅, 易知B ≠⊂A ,故答案选A . 另解:由21,}2{|n x n B x +=∈=Z ,易知B ≠⊂A ,故答案选A . 【例3】若集合{}{}2|60,|10M x x x N x ax =+-==-=,且N M ⊆,求实数a 的值. 解:由26023x x x +-=⇒=-或,因此,{}2,3M =-.(i )若0a =时,得N =∅,此时,N M ⊆;(ii )若0a ≠时,得1{}N a =. 若N M ⊆,满足1123a a==-或,解得1123a a ==-或. 故所求实数a 的值为0或12或13-. 点评:在考察“A B ⊆”这一关系时,不要忘记“∅” ,因为A =∅时存在A B ⊆. 从而需要分情况讨论. 题中讨论的主线是依据待定的元素进行.【例4】已知集合A ={a ,a +b ,a +2b },B ={a ,ax ,ax 2}. 若A =B ,求实数x 的值.解:若22a b ax a b ax+=⎧⎨+=⎩⇒a +ax 2-2ax =0, 所以a (x -1)2=0,即a =0或x =1. 当a =0时,集合B 中的元素均为0,故舍去;当x =1时,集合B 中的元素均相同,故舍去.若22a b ax a b ax⎧+=⎨+=⎩⇒2ax 2-ax -a =0. 因为a ≠0,所以2x 2-x -1=0, 即(x -1)(2x +1)=0. 又x ≠1,所以只有12x =-.经检验,此时A =B 成立. 综上所述12x =-.点评:抓住集合相等的定义,分情况进行讨论. 融入方程组思想,结合元素的互异性确定集合.第3讲 §1.1.3 集合的基本运算(一)¤知识要点:集合的基本运算有三种,即交、并、补,学习时先理解概念,并掌握符号等,再B (读作“B (读作“U A (读作“ ¤例题精讲:】设集合,{|15},{|39},,()U U R A x x B x x A B A B ==-≤≤=<<求解:在数轴上表示出集合A 、B ,如右图所示: {|35}A B x x =<≤,(){|1,9}U C A B x x x =<-≥或,【例2】设{|||6}A x Z x =∈≤,{}{}1,2,3,3,4,5,6B C ==,求:(1)()A B C ; (2)()A A B C .解:{}6,5,4,3,2,1,0,1,2,3,4,5,6A =------.(1)又{}3B C =,∴()A B C ={}3;(2)又{}1,2,3,4,5,6B C =,得{}()6,5,4,3,2,1,0A C B C =------. U∴ ()A A C B C {}6,5,4,3,2,1,0=------.【例3】已知集合{|24}A x x =-<<,{|}B x x m =≤,且A B A =,求实数m 的取值范围.解:由A B A =,可得A B ⊆.在数轴上表示集合A 与集合B ,如右图所示:由图形可知,4m ≥. 点评:研究不等式所表示的集合问题,常常由集合之间的关系,得到各端点之间的关系,特别要注意是否含端点的问题.【例4】已知全集*{|10,}U x x x N =<∈且,{2,4,5,8}A =,{1,3,5,8}B =,求()U C A B ,()U C A B ,()()U U C A C B , ()()U U C A C B ,并比较它们的关系.解:由{1,2,3,4,5,8}A B =,则(){6,7,9}U C A B =.由{5,8}A B =,则(){1,2,3,4,6,7,9}U C A B =由{1,3,6,7,9}U C A =,{2,4,6,7,9}U C B =,则()(){6,7,9}U U C A C B =,()(){1,2,3,4,6,7,9}U U C A C B =.由计算结果可以知道,()()()U U U C A C B C A B =,()()()U U U C A C B C A B =.另解:作出Venn 图,如右图所示,由图形可以直接观察出来结果.点评:可用Venn 图研究()()()U U U C A C B C A B =与()()()U U U C A C B C A B = ,在理解的基础记住此结论,有助于今后迅速解决一些集合问题.第4讲 §1.1.3 集合的基本运算(二) ¤知识要点:1. 含两个集合的Venn 图有四个区域,分别对应着这两个集合运算的结果. 我们需通过Venn 图理解和掌握各区域的集合运算表示,解决一类可用列举法表示的集合运算. 通过图形,我们还可以发现一些集合性质:()()()U U U C A B C A C B =,()()()U U U C A B C A C B =.2. 集合元素个数公式:()()()()n A B n A n B n A B =+-.3. 在研究集合问题时,常常用到分类讨论思想、数形结合思想等. 也常由新的定义考查创新思维.¤例题精讲:【例1】设集合{}{}24,21,,9,5,1A a a B a a =--=--,若{}9A B =,求实数a 的值. 解:由于{}{}24,21,,9,5,1A a a B a a =--=--,且{}9A B =,则有:当219 a -=时,解得5a =,此时={4, 9, 25}={9, 0, 4}A B -,-,不合题意,故舍去; 当29a =时,解得33a =或-.3 ={4,5,9} ={9,2,2}a A B =时,-,--,不合题意,故舍去;3={4, 7 9}={9, 8, 4}a A B =-,--,,-,合题意.所以,3a =-.【例2】设集合{|(3)()0,}A x x x a a R =--=∈,{|(4)(1)0}B x x x =--=,求A B , A B .(教材P 14 B 组题2)解:{1,4}B =.当3a =时,{3}A =,则{1,3,4}A B =,A B =∅;当1a =时,{1,3}A =,则{1,3,4}A B =,{1}A B =;当4a =时,{3,4}A =,则{1,3,4}A B =,{4}A B =;-2 4 m x B A当3a ≠且1a ≠且4a ≠时,{3,}A a =,则{1,3,4,}A B a =,A B =∅.点评:集合A 含有参数a ,需要对参数a 进行分情况讨论. 罗列参数a 的各种情况时,需依据集合的性质和影响运算结果的可能而进行分析,不多不少是分类的原则.【例3】设集合A ={x |240x x +=}, B ={x |222(1)10x a x a +++-=,a R ∈},若A B =B ,求实数a 的值.解:先化简集合A ={4,0}-. 由A B =B ,则B ⊆A ,可知集合B 可为∅,或为{0},或{-4},或{4,0}-.(i )若B =∅,则224(1)4(1)0a a ∆=+--<,解得a <1-;(ii )若0∈B ,代入得2a 1-=0⇒a =1或a =1-,当a =1时,B =A ,符合题意;当a =1-时,B ={0}⊆A ,也符合题意.(iii )若-4∈B ,代入得2870a a -+=⇒a =7或a =1,当a =1时,已经讨论,符合题意;当a =7时,B ={-12,-4},不符合题意.综上可得,a =1或a ≤1-.点评:此题考查分类讨论的思想,以及集合间的关系的应用. 通过深刻理解集合表示法的转换,及集合之间的关系,可以把相关问题化归为解方程的问题,这是数学中的化归思想,是重要数学思想方法.解该题时,特别容易出现的错误是遗漏了A =B 和B =∅的情形,从而造成错误.这需要在解题过程中要全方位、多角度审视问题.【例4】对集合A 与B ,若定义{|,}A B x x A x B -=∈∉且,当集合*{|8,}A x x x N =≤∈,集合{|(2)(5)(6)0}B x x x x x =---=时,有A B -= . (由教材P 12 补集定义“集合A 相对于全集U 的补集为{|,}U C A x x x A =∈∉且”而拓展)解:根据题意可知,{1,2,3,4,5,6,7,8}A =,{0,2,5,6}B =由定义{|,}A B x x A x B -=∈∉且,则{1,3,4,7,8}A B -=.点评:运用新定义解题是学习能力的发展,也是一种创新思维的训练,关键是理解定义的实质性内涵,这里新定义的含义是从A 中排除B 的元素. 如果再给定全集U ,则A B -也相当于()U A C B .第5讲 §1.2.1 函数的概念¤知识要点:1. 设A 、B 是非空的数集,如果按某个确定的对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有唯一确定的数y 和它对应,那么就称f :A →B 为从集合A 到集合B 的一个函数(function ),记作y =()f x ,x A ∈.其中,x 叫自变量,x 的取值范围A 叫作定义域(domain ),与x 的值对应的y 值叫函数值,函数值的集合{()|}f x x A ∈叫值域(range ).2. 设a 、b 是两个实数,且a <b ,则:{x |a ≤x ≤b }=[a ,b ] 叫闭区间; {x |a <x <b }=(a ,b ) 叫开区间;{x |a ≤x <b }=[,)a b , {x |a <x ≤b }=(,]a b ,都叫半开半闭区间.符号:“∞”读“无穷大”;“-∞”读“负无穷大”;“+∞”读“正无穷大”. 则{|}(,)x x a a >=+∞,{|}[,)x x a a ≥=+∞,{|}(,)x x b b <=-∞,{|}(,]x x b b ≤=-∞,(,)R =-∞+∞.3. 决定函数的三个要素是定义域、值域和对应法则. 当且仅当函数定义域、对应法则分别相同时,函数才是同一函数.¤例题精讲:【例1】求下列函数的定义域: (1)121y x =+-;(2)y =.解:(1)由210x +-≠,解得1x ≠-且3x ≠-,所以原函数定义域为(,3)(3,1)(1,)-∞----+∞.(2)由3020x -≥⎧⎪≠,解得3x ≥且9x ≠, 所以原函数定义域为[3,9)(9,)+∞.【例2】求下列函数的定义域与值域:(1)3254x y x+=-; (2)22y x x =-++. 解:(1)要使函数有意义,则540x -≠,解得54x ≠. 所以原函数的定义域是5{|}4x x ≠.32112813(45)233233305445445445444x x x y x x x x ++-+==⨯=⨯=-+≠-+=-----,所以值域为3{|}4y y ≠-. (2)22192()24y x x x =-++=--+. 所以原函数的定义域是R ,值域是9(,]4-∞. 【例3】已知函数1()1x f x x-=+. 求:(1)(2)f 的值; (2)()f x 的表达式 解:(1)由121x x -=+,解得13x =-,所以1(2)3f =-. (2)设11x t x -=+,解得11t x t -=+,所以1()1t f t t -=+,即1()1x f x x -=+. 点评:此题解法中突出了换元法的思想. 这类问题的函数式没有直接给出,称为抽象函数的研究,常常需要结合换元法、特值代入、方程思想等. 【例4】已知函数22(),1x f x x R x =∈+. (1)求1()()f x f x+的值;(2)计算:111(1)(2)(3)(4)()()()234f f f f f f f ++++++. 解:(1)由2222222221111()()1111111x x x x f x f x x x x x x ++=+=+==+++++. (2)原式11117(1)((2)())((3)())((4)())323422f f f f f f f =++++++=+= 点评:对规律的发现,能使我们实施巧算. 正确探索出前一问的结论,是解答后一问的关键.第6讲 §1.2.2 函数的表示法¤知识要点:1. 函数有三种表示方法:解析法(用数学表达式表示两个变量之间的对应关系,优点:简明,给自变量可求函数值);图象法(用图象表示两个变量的对应关系,优点:直观形象,反应变化趋势);列表法(列出表格表示两个变量之间的对应关系,优点:不需计算就可看出函数值).2. 分段函数的表示法与意义(一个函数,不同范围的x ,对应法则不同).3. 一般地,设A 、B 是两个非空的集合,如果按某一个确定的对应法则f ,使对于集合A 中的任意一个元素x ,在集合B 中都有唯一确定的元素y 与之对应,那么就称对应:f A B →为从集合A 到集合B 的一个映射(mapping ).记作“:f A B →”. 判别一个对应是否映射的关键:A 中任意,B 中唯一;对应法则f . ¤例题精讲: 【例1】如图,有一块边长为a 的正方形铁皮,将其四个角各截去一个边长为x 的小正方形,然后折成一个无盖的盒子,写出体积V 以x 为自变量的函数式是_____,这个函数的定义域为_______.解:盒子的高为x ,长、宽为2a x -,所以体积为V =2(2)x a x -.又由20a x >-,解得2a x <.所以,体积V 以x 为自变量的函数式是2(2)V x a x =-,定义域为{|0}2a x x <<.【例2】已知f (x )=333322x x x x-⎧++⎪⎨+⎪⎩ (,1)(1,)x x ∈-∞∈+∞,求f [f (0)]的值. 解:∵ 0(,1)∈-∞, ∴ f (0)=32. 又 ∵ 32>1,∴ f (32)=(32)3+(32)-3=2+12=52,即f [f (0)]=52.【例3】画出下列函数的图象:(1)|2|y x =-; (教材P 26 练习题3)(2)|1||24|y x x =-++.解:(1)由绝对值的概念,有2,2|2|2,2x x y x x x -≥⎧=-=⎨-<⎩. 所以,函数|2|y x =-的图象如右图所示. (2)33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩,所以,函数|1||24|y x x =-++的图象如右图所示.点评:含有绝对值的函数式,可以采用分零点讨论去绝对值的方法,将函数式化为分段函数,然后根据定义域的分段情况,选择相应的解析式作出函数图象.【例4】函数()[]f x x =的函数值表示不超过x 的最大整数,例如[3.5]4-=-,[2.1]2=,当( 2.5,3]x ∈-时,写出()f x 的解析式,并作出函数的图象.解:3, 2.522,211,10()0,011,122,233,3x x x f x x x x x --<<-⎧⎪--≤<-⎪--≤<⎪=≤<⎨⎪≤<⎪≤<⎪=⎩. 函数图象如右:点评:解题关键是理解符号[]m 的概念,抓住分段函数的对应函数式.第7讲 §1.3.1 函数的单调性 ¤知识要点: 1. 增函数:设函数y =f (x )的定义域为I ,如果对于定义域I 内的某个区间D 内的任意两个自变量x 1,x 2,当x 1<x 2时,都有f (x 1)<f (x 2),那么就说f (x )在区间D 上是增函数(increasingfunction ). 仿照增函数的定义可定义减函数.2. 如果函数f (x )在某个区间D 上是增函数或减函数,就说f (x )在这一区间上具有(严格的)单调性,区间D 叫f(x )的单调区间. 在单调区间上,增函数的图象是从左向右是上升的(如右图1),减函数的图象从左向右是下降的(如右图2). 由此,可以直观观察函数图象上升与下降的变化趋势,得到函数的单调区间及单调性.3. 判断单调性的步骤:设x 1、x 2∈给定区间,且x 1<x 2;→计算f (x 1)-f (x 2) →判断符号→下结论.¤例题精讲:【例1】试用函数单调性的定义判断函数2()1x f x x =-在区间(0,1)上的单调性. 解:任取12,x x ∈(0,1),且12x x <. 则1221121212222()()()11(1)(1)x x x x f x f x x x x x --=-=----. 由于1201x x <<<,110x -<,210x -<,210x x ->,故12()()0f x f x ->,即12()()f x f x >.所以,函数2()1x f x x =-在(0,1)上是减函数. 【例2】求二次函数2()(0)f x ax bx c a =++<的单调区间及单调性. 解:设任意12,x x R ∈,且12x x <. 则22121122()()()()f x f x ax bx c ax bx c -=++-++221212()()a x x b x x =-+-1212()[()]x x a x x b =-++.若0a <,当122b x x a <≤-时,有120x x -<,12b x x a+<-,即12()0a x x b ++>,从而12()()0f x f x -<,即12()()f x f x <,所以()f x 在(,]2b a-∞-上单调递增. 同理可得()f x 在[,)2b a-+∞上单调递减. 【例3】求下列函数的单调区间:(1)|1||24|y x x =-++;(2)22||3y x x =-++.解:(1)33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩,其图象如右.由图可知,函数在[2,)-+∞上是增函数,在(,2]-∞-上是减函数.(2)22223,02||323,0x x x y x x x x x ⎧-++≥⎪=-++=⎨--+<⎪⎩,其图象如右. 由图可知,函数在(,1]-∞-、[0,1]上是增函数,在[1,0]-、[1,)+∞上是减函数.点评:函数式中含有绝对值,可以采用分零点讨论去绝对值的方法,将函数式化为分段函数. 第2小题也可以由偶函数的对称性,先作y 轴右侧的图象,并把y 轴右侧的图象对折到左侧,得到(||)f x 的图象. 由图象研究单调性,关键在于正确作出函数图象.第8讲 §1.3.1 函数最大(小)值 ¤知识要点: 1. 定义最大值:设函数()y f x =的定义域为I ,如果存在实数M 满足:对于任意的x ∈I ,都有()f x ≤M ;存在x 0∈I ,使得0()f x = M . 那么,称M 是函数()y f x =的最大值(Maximum Value ). 仿照最大值定义,可以给出最小值(Minimum Value )的定义.2. 配方法:研究二次函数2(0)y ax bx c a =++≠的最大(小)值,先配方成224()24b ac b y a x a a -=++后,当0a >时,函数取最小值为244ac b a-;当0a <时,函数取最大值244ac b a-. 3. 单调法:一些函数的单调性,比较容易观察出来,或者可以先证明出函数的单调性,再利用函数的单调性求函数的最大值或最小值.4. 图象法:先作出其函数图象后,然后观察图象得到函数的最大值或最小值. ¤例题精讲:【例1】求函数261y x x =++的最大值. 解:配方为2613()24y x =++,由2133()244x ++≥,得260813()24x <≤++. 所以函数的最大值为8.【例2】某商人如果将进货单价为8元的商品按每件10元售出时,每天可售出100件. 现在他采用提高售出价,减少进货量的办法增加利润,已知这种商品每件提价1元,其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚得的利润最大?并求出最大利润.解:设他将售出价定为x 元,则提高了(10)x -元,减少了10(10)x -件,所赚得的利润为(8)[10010(10)]y x x =---.即2210280160010(14)360y x x x =-+-=--+. 当14x =时,max 360y =.所以,他将售出价定为14元时,才能使每天所赚得的利润最大, 最大利润为360元.【例3】求函数21y x x =+-的最小值.解:此函数的定义域为[)1,+∞,且函数在定义域上是增函数,所以当1x =时,min 2112y =+-=,函数的最小值为2.点评:形如y ax b cx d =+±+的函数最大值或最小值,可以用单调性法研究,也可以用换元法研究.【另解】令1x t -=,则0t ≥,21x t =+,所以22115222()48y t t t =++=++,在0t ≥时是增函数,当0t =时,min 2y =,故函数的最小值为2.【例4】求下列函数的最大值和最小值:(1)25332,[,]22y x x x =--∈-; (2)|1||2|y x x =+--.解:(1)二次函数232y x x =--的对称轴为2b x a =-,即1x =-.画出函数的图象,由图可知,当1x =-时,max 4y =; 当32x =时,min 94y =-. 所以函数25332,[,]22y x x x =--∈-的最大值为4,最小值为94-. (2) 3 (2)|1||2|2 1 (12)3 (1)x y x x x x x ≥⎧⎪=+--=--<<⎨⎪-≤-⎩.作出函数的图象,由图可知,[3,3]y ∈-. 所以函数的最大值为3, 最小值为-3. 点评:二次函数在闭区间上的最大值或最小值,常根据闭区间与对称轴的关系,结合图象进行分析. 含绝对值的函数,常分零点讨论去绝对值,转化为分段函数进行研究. 分段函数的图象注意分段作出.第9讲 §1.3.2 函数的奇偶性¤知识要点:1. 定义:一般地,对于函数()f x 定义域内的任意一个x ,都有()()f x f x -=,那么函数()f x 叫偶函数(even function ). 如果对于函数定义域内的任意一个x ,都有()()f x f x -=-),那么函数()f x 叫奇函数(odd function ).2. 具有奇偶性的函数其定义域关于原点对称,奇函数的图象关于原点中心对称,偶函数图象关于y 轴轴对称.3. 判别方法:先考察定义域是否关于原点对称,再用比较法、计算和差、比商法等判别()f x -与()f x 的关系.¤例题精讲:【例1】判别下列函数的奇偶性:(1)31()f x x x=-; (2)()|1||1|f x x x =-++;(3)23()f x x x =-.解:(1)原函数定义域为{|0}x x ≠,对于定义域的每一个x ,都有3311()()()()f x x x f x x x -=--=--=--, 所以为奇函数. (2)原函数定义域为R ,对于定义域的每一个x ,都有()|1||1||1||1|()f x x x x x f x -=--+-+=-++=,所以为偶函数.(3)由于23()()f x x x f x -=+≠±,所以原函数为非奇非偶函数.【例2】已知()f x 是奇函数,()g x 是偶函数,且1()()1f x g x x -=+,求()f x 、()g x . 解:∵ ()f x 是奇函数,()g x 是偶函数,∴ ()()f x f x -=-,()()g x g x -=.则1()()11()()1f x g x x f x g x x ⎧-=⎪⎪+⎨⎪---=⎪-+⎩,即1()()11()()1f x g x x f x g x x ⎧-=⎪⎪+⎨⎪--=⎪-+⎩. 两式相减,解得2()1x f x x =-;两式相加,解得21()1g x x =-.。
第01讲 集合的概念 2024-2025年新高一暑假自学课(学生版)
第01讲集合的概念1.通过实例了解集合的定义,体会元素与集合间的属于关系;2.能通过自然语言、图形语言、集合语言描述不同的具体问题,感受集合的意义和作用.元素与集合的概念一般地,把一些能够确定的不同的对象看成一个整体,就说这个整体是由这些对象的全体构成的集合(或集),构成集合的每个对象叫做这个集合的元素(或成员).集合的元素特征①确定性:给定一个集合,那么任何一个元素在不在这个集合中就确定了.②互异性:一个集合中的元素是互不相同的,即集合中的元素是不重复出现的.③无序性:集合中的元素无顺序,可以任意排列、调换.元素与集合的关系若是集合的元素,则称属于集合,记作∈;若不是集合的元素,则称不属于集合,记作∉.常用数集自然数集(或非负整数集),记作;正整数集,记作∗或+;整数集,记作;有理数集,记作;实数集,记作.集合的分类有限集,无限集,空集∅.集合的表示方法①列举法把集合中的元素一一列举出来,并用花括号“{}”括起来表示集合的方法叫列举法.②描述法用集合所含元素的共同特征表示集合的方法,称为描述法.方法:在花括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征.一般格式:{∈Uop}.【题型一】集合的概念相关知识点讲解1元素与集合的概念(1)元素:一般地,把研究对象统称为元素,常用小写的拉丁字母s s m表示;(2)s s…表示.比如:四十个学生组成的高一(1)班中,班级就是个集合,每个学生就是其中的元素.2集合的元素特征①确定性:给定一个集合,那么任何一个元素在不在这个集合中就确定了.Eg:街上叫声帅哥,是男的都回个头,帅哥没有明确的标准,故“帅哥”不能组成集合.②互异性:一个集合中的元素是互不相同的,即集合中的元素是不重复出现的.Eg:两个学生名字都是“熊涛”,老师也要给他们起小名"熊大""熊二",以视区别.若集合={1,2,V,就意味≠1且≠2.③无序性:集合中的元素无顺序,可以任意排列、调换.Eg:高一(1)班每月都换座位也改变不了它是(1)班的事实,1,2,3={2,3,1}.【典题1】(多选)下列说法正确的是()A.我校爱好足球的同学组成一个集合B.{1,2,3}是不大于3的正整数组成的集合C.集合{1,2,3,4,5}和{5,4,3,2,1}表示同一集合D.数1,0,5,12,32,64,7个元素变式练习1.下列对象中不能构成一个集合的是()A.某校比较出名的教师B.方程−2=0的根C.不小于3的自然数D.所有锐角三角形2.(23-24高一上·天津南开·期中)下列给出的对象能构成集合的有()①某校2023年入学的全体高一年级新生;②2的所有近似值;③某个班级中学习成绩较好的所有学生;④不等式3−10<0的所有正整数解A.1个B.2个C.3个D.4个3.若a,b,c,d为集合A的四个元素,则以a,b,c,d为边长构成的四边形可能是()A.矩形B.平行四边形C.菱形D.梯形4.(23-24高一上·安徽蚌埠·阶段练习)下列各组对象能构成集合的是()A.充分接近5的所有实数B.所有的正方形C.著名的数学家D.1,2,3,3,4,4,4,4【题型二】元素与集合间的关系相关知识点讲解1常用数集自然数集(或非负整数集),记作;正整数集,记作∗或+;整数集,记作;有理数集,记作;实数集,记作.2元素与集合的关系若是集合的元素,则称属于集合,记作∈;若不是集合的元素,则称不属于集合,记作∉.Eg:菱形∈{平行四边形},0∈,0∉{1,2,3,4}.【典题1】(多选)(23-24高一上·湖北咸宁·阶段练习)已知s s为非零实数,成的集合A,下列判断正确的是()A.−2∈B.0∉C.−4∈D.4∈【典题2】(23-24高一下·安徽安庆·开学考试)已知实数集满足条件:若∈,则1+1−∈,则集合中所有元素的乘积为()A.1B.−1C.±1D.与的取值有关变式练习1.(2022高一上·全国·专题练习)下列关系中,正确的个数为()①5∈R;②13∈Q;③0=∅;④0∉N;⑤π∈Q;⑥−3∈Z.A.6B.5C.4D.32.(2023·河南驻马店·一模)已知集合=+1=0,那么下列结论正确的是()A.0∈B.1∈C.−1∉D.0∉3.已知集合=4,s2,=−2,2,1−,若=,则实数x的取值集合为()A.{−1,0,2}B.{−2,2}C.−1,0,2D.{−2,1,2}4.(多选)(2024·全国·模拟预测)非空集合A具有如下性质:①若s∈,则∈;②若s∈,则+∈下列判断中,正确的有()A.−1∉B.20222023∈C.若s∈,则B∈D.若s∈,则−∈5.设关于的不等式B2−2+≤0的解集为,若0∈且−1∉,则的取值范围是.【题型三】集合互异性的应用相关知识点讲解互异性:一个集合中的元素是互不相同的,即集合中的元素是不重复出现的.Eg:若集合={1,2,V,就意味≠1且≠2.【典题1】(多选)已知集合=−2,22+5,1+2,−3∈,则a的值为().A.−1B.−32C.1D.−2变式练习1.(23-24高三下·山东青岛·开学考试)已知∈1,2,2,则的取值为()A.1B.1或2C.0或2D.0或1或22.(23-24高一上·江西萍乡·期末)已知集合=−1,2−2+1,−4,若4∈,则a的值可能为()A.−1,3B.−1C.−1,3,8D.−1,83.(2024高三·全国·专题练习)已知集合=0,s2−3+2,且2∈,则实数为()A.2B.3C.0或3D.0,2,3【题型四】集合的表示方法角度1列举法相关知识点讲解把集合中的元素一一列举出来,并用花括号“{}”括起来表示集合的方法叫列举法.Eg:11以内偶数的集合为{2,4,6,8,10};一次函数=2与=+1的图象的交点组成的集合为{(1,2)}.【典题1】用列举法表示下列集合:(1)不大于10的非负偶数组成的集合;(2)方程x2=2x的所有实数解组成的集合;(3)直线y=2x+1与y轴的交点所组成的集合;(4)由所有正整数构成的集合.变式练习1.用列举法表示下列集合:(1)一年中有31天的月份的全体;(2)大于−3.5小于12.8的整数的全体;(3)方程2−1+2+1=0的解集;(4)方程−1−2=0的解集;角度2描述法相关知识点讲解用集合所含元素的共同特征表示集合的方法,称为描述法.方法:在花括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征.一般格式:{∈Uop}.用符号描述法表示集合时应注意:(1)弄清元素所具有的形式(即代表元素是什么)是数还是点、还是集合、还是其他形式?(2)元素具有怎么的属性?当题目中用了其他字母来描述元素所具有的属性时,要去伪存真,而不能被表面的字母形式所迷惑.(3)Eg集合元素化简结果{U2−−2=0}方程2−−2=0的解{−1,2}{U2−−2<0}不等式2−−2<0的解集{U−1<<2}{U=2−−2}函数=2−−2中取值范围(定义域){U=2−−2}函数=2−−2中取值范围(值域){U>−94}{(s p|=2−−2}函数=2−−2的图像上的点----看集合先看元素类型.【典题1】(多选)已知集合=∈∈s−9≤≤9,则满足A中有8个元素的m的值可能为() A.6B.−6C.9D.−9【典题2】(多选)已知集合==3−1,∈,==3+1,∈,==3s∈,且∈,∈,∈,则()A.2∈B.2∈C.+∈D.+∈变式练习1.设集合={−1,1,2},集合={U∈且2−∉V,则=()A.{1}B.{2}C.{−1,2}D.{1,2}2.若集合=−2,1,4,8,=−2∣∈s∈,则中元素的最大值为()A.4B.5C.7D.103.(22-23高一下·江苏苏州·开学考试)集合s+≤6,s∈N∗中的元素个数为()A.1B.3C.4D.64.(2024高一上·全国·专题练习)已知集合=UB2−3+2=0,∈,若集合A中至多有一个元素,则实数a应满足()A.=0B.≥98C.=0或≥98D.不确定5.(多选)已知集合==2−1,∈,==2s∈,且1,2∈,3∈,则下列判断正确的是()A.12∈B.23∈C.1+2∈D.1+2+3∈6.(多选)对于集合==2−2,∈s∈.给出如下结论,其中正确的结论是() A.如果1∈,2∈,那么12∈B.如果1∈,2∈,那么1+2∈C.如果==2+1,∈.那么⊆D.若==2s∈.对于∀∈,则有∈【A组---基础题】1.下列说法正确的是()A.0与0的意义相同B.某市文明市民可以组成一个集合C.集合=s+=2,∈N是无限集D.方程2+2+1=0的解集有二个元素2.由2,2−s4组成一个集合,中含有3个元素,则实数的取值不可以是()A.−1B.2C.3D.63.(23-24高一上·上海·期末)数集={U=2−1,∈V,={U=2s∈V,={U=4−1,∈Z},若∈,∈,则+∈()A.B.C.D.A,,都有可能4.集合=63−∈Z∈N*,用列举法可以表示为5.已知集合={0,1,2},={(,p|∈,∈,−∈V,则集合B中有个元素.6.设数集由实数构成,且满足:若∈o≠1且≠0),则11−∈.(1)若2∈,试证明中还有另外两个元素;(2)集合是否为双元素集合,并说明理由;(3)若中元素个数不超过8个,所有元素的和为143,且中有一个元素的平方等于所有元素的积,求集合.7.已知n元有限集=1,2,3,⋯,(≥2,∈Z),若1+2+3+⋯+=1×2×3×⋯×,则称集合A为“n元和谐集”.(1)写出一个“二元和谐集”(无需写计算过程);(2)若正数集=1,2是“二元和谐集”,试证明:元素1,2中至少有一个大于2;(3)是否存在集合中元素均为正整数的“三元和谐集”?如果有,有几个?请说明理由.【B组---提高题】1.若=b=2+s∈s∈,则下列结论中正确结论的个数为()∈;②若1,2∈,则1+2∈;③若1,2∈且2≠0,则12∈;④存在∈且∉,满足−2022∈.A.2B.3C.4D.52.(2024·辽宁丹东·一模)若2−80为完全平方数,则正整数x的取值组成的集合为.3.已知非空集合⊆.用表示集合中元素的个数.设==+s∈s∈且≠,= =−s∈s∈且>.(1)若=1,2,3,直接写出s以及,,的值.(2)若=4,求+的取值范围.4.已知集合A是由元素x组成的,其中=+2,m,∈.(1)设1=2=9−42,3=1−322,试判断1,2,3与A之间的关系;(2)任取1,2∈,试判断1+2,12与A之间的关系.11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《新课标》高三数学(人教版)第一轮复习单元讲座第一讲集合一.课标要求:1.集合的含义与表示(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系;(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用;2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集;(2)在具体情境中,了解全集与空集的含义;3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;(3)能使用V enn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用。
二.命题走向有关集合的高考试题,考查重点是集合与集合之间的关系,近年试题加强了对集合的计算化简的考查,并向无限集发展,考查抽象思维能力,在解决这些问题时,要注意利用几何的直观性,注意运用Venn图解题方法的训练,注意利用特殊值法解题,加强集合表示方法的转换和化简的训练。
考试形式多以一道选择题为主,分值5分。
预测2007年高考将继续体现本章知识的工具作用,多以小题形式出现,也会渗透在解答题的表达之中,相对独立。
具体题型估计为:(1)题型是1个选择题或1个填空题;(2)热点是集合的基本概念、运算和工具作用。
三.要点精讲1.集合:某些指定的对象集在一起成为集合。
a∈;若b不是集合A的元(1)集合中的对象称元素,若a是集合A的元素,记作Ab∉;素,记作A(2)集合中的元素必须满足:确定性、互异性与无序性;确定性:设A是一个给定的集合,x是某一个具体对象,则或者是A的元素,或者不是A的元素,两种情况必有一种且只有一种成立;互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素;无序性:集合中不同的元素之间没有地位差异,集合不同于元素的排列顺序无关;(3)表示一个集合可用列举法、描述法或图示法;列举法:把集合中的元素一一列举出来,写在大括号内;描述法:把集合中的元素的公共属性描述出来,写在大括号{}内。
具体方法:在大括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征。
注意:列举法与描述法各有优点,应该根据具体问题确定采用哪种表示法,要注意,一般集合中元素较多或有无限个元素时,不宜采用列举法。
(4)常用数集及其记法:非负整数集(或自然数集),记作N ;正整数集,记作N *或N +;整数集,记作Z ;有理数集,记作Q ;实数集,记作R 。
2.集合的包含关系:(1)集合A 的任何一个元素都是集合B 的元素,则称A 是B 的子集(或B 包含A ),记作A ⊆B (或B A ⊂);集合相等:构成两个集合的元素完全一样。
若A ⊆B 且B ⊇A ,则称A 等于B ,记作A =B ;若A ⊆B 且A ≠B ,则称A 是B 的真子集,记作A B ;(2)简单性质:1)A ⊆A ;2)Φ⊆A ;3)若A ⊆B ,B ⊆C ,则A ⊆C ;4)若集合A 是n 个元素的集合,则集合A 有2n 个子集(其中2n -1个真子集);3.全集与补集:(1)包含了我们所要研究的各个集合的全部元素的集合称为全集,记作U ;(2)若S 是一个集合,A ⊆S ,则,S C =}|{A x S x x ∉∈且称S 中子集A 的补集;(3)简单性质:1)S C (S C )=A ;2)S C S=Φ,ΦS C =S 。
4.交集与并集:(1)一般地,由属于集合A 且属于集合B 的元素所组成的集合,叫做集合A 与B 的交集。
交集}|{B x A x x B A ∈∈=⋂且。
(2)一般地,由所有属于集合A 或属于集合B 的元素所组成的集合,称为集合A 与B 的并集。
}|{B x A x x B A ∈∈=⋃或并集。
注意:求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn 图或数轴进而用集合语言表达,增强数形结合的思想方法。
5.集合的简单性质:(1);,,A B B A A A A A ⋂=⋂Φ=Φ⋂=⋂(2);,A B B A A A ⋃=⋃=Φ⋃(3));()(B A B A ⋃⊆⋂(4)B B A B A A B A B A =⋃⇔⊆=⋂⇔⊆;;(5)S C (A ∩B )=(S C A )∪(S C B ),S C (A ∪B )=(S C A )∩(S C B )。
四.典例解析题型1:集合的概念例1.设集合},4121|{Z k k x x A ∈+==,若29=x ,则下列关系正确的是( ) A .A x ⊂ B .A x ∈ C .A x ∈}{ D .A x ⊂}{ 解:由于4124121+=+k k 中12+k 只能取到所有的奇数,而41829=中18为偶数。
则A A ⊂∉}29{,29。
选项为D ; 点评:该题考察了元素与集合、集合与集合之间的关系。
首先应该分清楚元素与集合之间是属于与不属于的关系,而集合之间是包含与不包含的关系。
例2.设集合P ={m |-1<m ≤0},Q ={m ∈R |mx 2+4mx -4<0对任意实数x 恒成立},则下列关系中成立的是( )A .P QB .Q PC .P =QD .P ∩Q =Q解:Q ={m ∈R |mx 2+4mx -4<0对任意实数x 恒成立=,对m 分类:①m =0时,-4<0恒成立;②m <0时,需Δ=(4m )2-4×m ×(-4)<0,解得m <0。
综合①②知m ≤0,∴Q ={m ∈R |m ≤0}。
答案为A 。
点评:该题考察了集合间的关系,同时考察了分类讨论的思想。
集合Q 中含有参数m ,需要对参数进行分类讨论,不能忽略m=0的情况。
题型2:集合的性质例3.(2000广东,1)已知集合A ={1,2,3,4},那么A 的真子集的个数是( )A .15B .16C .3D .4解:根据子集的计算应有24-1=15(个)。
选项为A ;点评:该题考察集合子集个数公式。
注意求真子集时千万不要忘记空集∅是任何非空集合的真子集。
同时,A 不是A 的真子集。
变式题:同时满足条件:①};5,4,3,2,1{⊆M ②若M a M a ∈∈-则6,,这样的集合M 有多少个,举出这些集合来。
答案:这样的集合M 有8个。
例4.已知全集32{1,3,2}S x x x =--,A ={1,21x -}如果}0{=A C S ,则这样的实数x 是否存在?若存在,求出x ,若不存在,说明理由。
解:∵}0{=A C S ;∴A S ∉∈00且,即322x x x --=0,解得1230,1,2x x x ==-=当0=x 时,112=-x ,为A 中元素;当1-=x 时,S x ∈=-312当2x =时,213x S -=∈∴这样的实数x 存在,是1x =-或2x =。
另法:∵}0{=A C S∴A S ∉∈00且,3A ∈∴322x x x --=0且213x -=∴1x =-或2x =。
点评:该题考察了集合间的关系以及集合的性质。
分类讨论的过程中“当0=x 时,112=-x ”不能满足集合中元素的互异性。
此题的关键是理解符号}0{=A C S 是两层含义:A S ∉∈00且。
变式题:已知集合2{,,2},{,,}A m m d m d B m mq mq =++=,0m ≠其中,A B =且,求q 的值。
解:由B A =可知,(1)⎩⎨⎧=+=+22mq d m mq d m ,或(2)⎩⎨⎧=+=+mqd m mq d m 22解(1)得1=q ,解(2)得21,1-==q q 或, 又因为当1=q 时,2mq mq m ==与题意不符,所以,21-=q 。
题型3:集合的运算例5.(06全国Ⅱ理,2)已知集合M ={x |x <3},N ={x |log 2x >1},则M ∩N =( )A .∅B .{x |0<x <3}C .{x |1<x <3}D .{x |2<x <3} 解:由对数函数的性质,且2>1,显然由1lo g 2>x 易得),2(+∞=B 。
从而)3,2(=⋂B A 。
故选项为D 。
点评:该题考察了不等式和集合交运算。
例6.(06安徽理,1)设集合{}22,A x x x R =-≤∈,{}2|,12B y y x x ==--≤≤,则()R C A B 等于( )A .RB .{},0x x R x ∈≠C .{}0D .∅ 解:[0,2]A =,[4,0]B =-,所以(){0}R R C A B C = ,故选B 。
点评:该题考察了集合的交、补运算。
题型4:图解法解集合问题例7.(2003上海春,5)已知集合A ={x ||x |≤2,x ∈R },B ={x |x ≥a },且A B ,则实数a 的取值范围是____ _。
解:∵A ={x |-2≤x ≤2},B ={x |x ≥a },又A ⊆B ,利用数轴上覆盖关系:如图所示,因此有a ≤-2。
点评:本题利用数轴解决了集合的概念和集合的关系问题。
例8.(1996全国理,1)已知全集I =N *,集合A ={x |x =2n ,n ∈N *},B ={x |x =4n ,n ∈N },则( )A .I =A ∪BB .I =(IC A )∪B C .I =A ∪(I C B )D .I =(I C A )∪(I C B ) 解:方法一:I C A 中元素是非2的倍数的自然数,I C B 中元素是非4的倍数的自然数,显然,只有C选项正确.方法二:因A ={2,4,6,8…},B ={4,8,12,16,…},所以I C B ={1,2,3,5,6,7,9…},所以I =A ∪I C B,故答案为C.方法三:因B A ,所以(I C )A (I C )B ,(I C )A ∩(I C B )=I C A ,故I =A ∪(I C A )=A ∪(I C B )。
方法四:根据题意,我们画出Venn 图来解,易知B A ,如图:可以清楚看到I =A ∪(I C B )是成立的。
点评:本题考查对集合概念和关系的理解和掌握,注意数形结合的思想方法,用无限集考查,提高了对逻辑思维能力的要求。
题型5:集合的应用例9.向50名学生调查对A 、B 两事件的态度,有如下结果 赞成A 的人数是全体的五分之三,其余的不赞成,赞成B 的比赞成A 的多3人,其余的不赞成;另外,对A 、B 都不赞成的学生数比对A 、B 都赞成的学生数的三分之一多1人。
