2018年秋沪科版九年级上《第23章解直角三角形》测试题含答案
沪科版九年级上册数学第23章 解直角三角形含答案

沪科版九年级上册数学第23章解直角三角形含答案一、单选题(共15题,共计45分)1、在中,,,那么的值等于()A. B. C. D.2、在Rt△ABC中,∠C=90°,AC=4,cosA的值等于,则AB的长度是()A.3B.4C.5D.3、如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的余切值()A.扩大为原来的两倍B.缩小为原来的C.不变D.不能确定4、如图所示,在数轴上点A所表示的数x的范围是()A. sin30°<x<sin60°B.cos30°<x<cos45°C.tan30°<x<tan45 D. cot45°<x<cot30°5、在Rt△ABC中,已知∠ACB=90°,BC=1,AB=2,那么下列结论正确的是()A.sinA=B.tanA=C.cosB=D.cotB=6、如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现在计划在斜坡AB的中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为30°,则平台DE的长约为()(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)A.24.8米B.43.3米C.33.5米D.16.8米7、如图,修建抽水站时,沿着坡度为i=1:的斜坡铺设水管.若测得水管A处铅垂高度为8 m,则所铺设水管AC的长度为()A.8mB.12mC.14mD.16m8、如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则=()A. B. C. D.9、如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2 ,则∠D等于()A. B. C. D.10、在中,,,若,则的长为().A. B. C. D.11、在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为()A. B. C. D.12、如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值()A.不变B.增大C.减小D.先变大再变小13、3tan45°的值等于()A. B.3 C.1 D.314、在△ABC中,∠C=90°,AC= ,AB= ,则cosB的值为( )A. B.C.D.15、在正方形网格中,△ABC的位置如图所示,则cosB的值为()A. B. C. D.二、填空题(共10题,共计30分)16、在中,,AB=3,BC=1,那么的正弦值是________.17、如图,⊙O的半径为6,如果弦AB是⊙O内接正方形的一边,弦AC是⊙O 内接正十二边形的一边,那么弦BC的长为________.18、一条排水管截面圆的半径为2米,∠AOB=120°,则储水部分(阴影部分)的面积是________平方米.19、如图,小杨沿着有一定坡度的坡面前进了5米,这个坡面的坡度为1:2,此时他与水平地面的垂直距离为________米.20、如图所示,在四边形中,,,.连接,,若,则长度是________.21、计算:tan60°﹣cos30°=________ .22、如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是________.23、将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为________.24、在△ABC中,∠C=90°,∠A=30°,BC=4,D为边AB上的一点,若AD=2,则tan∠BDC的值为________。
沪科版九年级上册数学第23章 解直角三角形 含答案

沪科版九年级上册数学第23章解直角三角形含答案一、单选题(共15题,共计45分)1、如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为()A.9:4B.3:2C. :D.3 :22、如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是()A. B. C. D.3、如图,在矩形ABCD中,AD=2,tan∠ABD=2,点E,F在AD,BC上,则菱形AECF的面积为()A.1.25B.5C.D.24、如图,菱形的边长为2,,,则这个菱形的面积是()A.4B.8C.D.5、如果tanα=0.213,那么锐角α的度数大约为()A.8°B.10°C. 12°D.14°6、如图,在梯形ABCD中,AD//BC,AC⊥AB,AD=CD,cos∠DCA=,BC=10,则AB的值是()A.3B.6C.8D.97、在△ABC中,∠A,∠B均为锐角,且有|tanB﹣|+(2cosA﹣1)2=0,则△ABC是()A.直角(不等腰)三角形B.等边三角形C.等腰(不等边)三角形 D.等腰直角三角形8、如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为()A.50mB.25mC.(50﹣)mD.(50﹣25 )m9、如图,坡角为30°的斜坡上两树间的水平距离AC为2m,则两树间的坡面距离AB为( )A.4mB. mC. mD. m10、如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是()A. B. C. D.11、如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为()A. 米B. 米C. 米D. 米12、如图,已知灯塔M方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在A处测得灯塔M在北偏东30°方向,行驶1小时后到达B处,此时刚好进入灯塔M的镭射信号区,测得灯塔M在北偏东45°方向,则轮船通过灯塔M的镭射信号区的时间为()A.(﹣1)小时B.(+1)小时C.2小时D. 小时13、如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于()米.A.asin40°B.acos40°C.atan40°D.14、a,b,c 是△ABC的∠A,∠B,∠C的对边,且a:b:c=1::,则cosB的值为 ( )A. B. C. D.15、正六边形螺帽的边长是,这个扳手的开口的值应是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,AB切⊙O与点A,BE切⊙O于点E,连接AO并延长交⊙O于点C,交BE的延长线于点D,连接EC,若AD=8,tan∠DEC=,则CD=________.17、用“>”或“<”填空:sin50°×cos40°﹣________ 0.(可用计算器计算)18、如图,已知Rt△ABC中,∠ACB=90°,AC=8,BC=6,将△ABC绕点C顺时针旋转得到△MCN,点D、E分别为AB、MN的中点,若点E刚好落在边BC 上,则sin∠DEC=________.19、如图,在平面直角坐标系中,正方形OABC的边长为1,边OA,OC分别在x轴,y轴上,若以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,按此规律做下去,则=________20、如图,点为的AB边上的中点,点E为AD的中点,为正三角形,给出下列结论,①,②,③,④若,点是上一动点,点到、边的距离分别为,,则的最小值是3.其中正确的结论是________(填写正确结论的番号)21、如图,如图,点A(3,m)在第一象限,OA与x轴所夹的锐角为∠1,tan ∠1= ,则m的值是________.22、如图,在菱形ABCD中,DE⊥AB, cos A=,BE=2,则tan∠DBE=________.23、如图所示方格纸中每个小正方形的边长为1,其中有三个格点A、B、C,则sin∠ABC=________.24、如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A 处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是________.25、已知α是锐角,且sinα=,则cosα=________.三、解答题(共5题,共计25分)26、计算:(﹣1)2018﹣+(π﹣3)0+4cos45°.27、如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C 向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:≈1.732)28、如图,某居民楼AB的前面有一围墙CD,在点E处测得楼顶A的仰角为25°,在F处测得楼顶A的仰角为45°,且CE的高度为2米,CF之间的距离为20米(B,F,C在同一条直线上).求居民楼AB的高度.(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,结果保留整数)29、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°.求飞机A与指挥台B的距离(结果取整数).【参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93】30、如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)参考答案一、单选题(共15题,共计45分)1、A2、D3、A4、C5、C6、B7、B8、C9、C10、A11、B12、B13、C14、B15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题,共计25分)26、27、29、。
沪科版九年级上册数学第23章 解直角三角形含答案(综合测试)

沪科版九年级上册数学第23章解直角三角形含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,AC=BC=2,D是BC的中点,过A,C,D三点的⊙O与AB 边相切于点A,则⊙O的半径为( )A. B. C.1 D.2、把三角形三边的长度都扩大为原来的2倍,则锐角A的正弦函数值A.扩大为原来的2倍B.缩小为原来的C.不变D.不能确定3、如图,⊙O的弦AB垂直半径OC于点D,∠CBA=30°,OC=3 cm,则弦AB 的长为()A.9cmB.3 cmC. cmD. cm4、直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是()A. B. C. D.5、中,,,,则的值为()A. B. C. D.6、如图,某地修建高速公路,要从地向地修一条隧道(点在同一水平面上).为了测量两地之间的距离,一架直升飞机从地出发,垂直上升800米到达C处,在C处观察B地的俯角为,则两地之间的距离为()A. 米B. 米C. 米D. 米7、如图,修建抽水站时,沿着坡度为i=1:6的斜坡铺设管道. 下列等式成立的是()A.sinα =B.cosα=C.tanα=D.tanα=28、如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+)海里,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上,则船R到岛P的距离为()A.40海里B.40 海里C.40 海里D.(40+ )海里9、如图,滑雪场有一坡角α为20°的滑雪道,滑雪道AC的长为200米,则滑雪道的坡顶到坡底垂直高度AB的长为()A.200tan20°米B. 米C.200sin20°米D.200cos20°米10、如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为()A. B. C. D.11、在Rt△ABC中,∠C=90°,如果sinA=,则tanB=( )A. B. C. D.12、在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为( )A. B. C. D.13、如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为()A.5米B.6米C.8米D.(3+ )米14、а为锐角,且sinа=0.6,则()A.0°<а<30°B.30°<а<45°C.45°<а<60° D.60°<а<90°15、如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为()A. B.2 C. D.3二、填空题(共10题,共计30分)16、如图,Rt△OAB中,∠OAB=90°,O是坐标原点,点A在x轴的正半轴上,点B在第一象限。
沪科版初中九年级上册数学单元检测 第23章 解直角三角形

解直角三角形测试题与答案一.选择题(共12小题)1.(•义乌市)如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是()A.1B.1.5 C.2D.32.(•巴中)在Rt△ABC中,∠C=90°,sinA=,则tanB的值为()A.B.C.D.3.(•凉山州)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则∠C的度数是()A.45°B.60°C.75°D.105°4.(•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()A.100米B.50米C.米D.50米5.(•凉山州)拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是()A.15m B.20m C.10m D.20m 6.(•百色)从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是()A.(6+6)米B.(6+3)米C.(6+2)米D.12米7.(•苏州)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O 处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为()A.4km B.2km C.2km D.(+1)km8.(•路北区二模)如图,△ABC的项点都在正方形网格的格点上,则cosC 的值为()A.B.C.D.9.(•长宁区一模)如图,在△ABC中,∠ACB=90°,CD⊥AB于D,下边各组边的比不能表示sinB的()A.B.C.D.(•工业园区一模)若tan(α+10°)=1,则锐角α的度数是()10.A.20°B.30°C.40°D.50°11.(•鄂州四月调考)在△ABC中,∠A=120°,AB=4,AC=2,则sinB 的值是()A.B.C.D.12.(•邢台一模)在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于()A.B.C.D.二.填空题(共6小题)13.(•济宁)如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB 的长为_________ .14.(•徐汇区一模)如图,已知梯形ABCD中,AB∥CD,AB⊥BC,且AD⊥BD,若CD=1,BC=3,那么∠A的正切值为_________ .15.(•虹口区一模)计算:cos45°+sin260°=_________ .16.(•武威模拟)某人沿坡度为i=3:4斜坡前进100米,则它上升的高度是_________ 米.17.(•海门市模拟)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB 的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是_________ m.18.(•扬州)在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC= _________ .三.解答题(共6小题)19.(•盘锦)如图,用一根6米长的笔直钢管弯折成如图所示的路灯杆ABC,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,若路灯杆顶端C到地面的距离CD=5.5米,求AB长.20.(•遵义)如图,一楼房AB后有一假山,其坡度为i=1:,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)21.(•哈尔滨)如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.(1)求两建筑物底部之间水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).22.(•邵阳)一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)23.(•射阳县三模)小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡度为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,求树的高度.24.(•崇川区一模)如图,某登山队在山脚A处测得山顶B处的仰角为45°,沿坡角30°的斜坡AD前进1000m后到达D处,又测得山顶B处的仰角为60°.求山的高度BC.参考答案与试题解析一.选择题(共12小题)1.(•义乌市)如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是()A.1B.1.5 C.2D.3考点:锐角三角函数的定义;坐标与图形性质.专题:数形结合.分析:根据正切的定义即可求解.解答:解:∵点A(t,3)在第一象限,∴AB=3,OB=t,又∵tanα==,∴t=2.故选:C.点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.2.(•巴中)在Rt△ABC中,∠C=90°,sinA=,则tanB的值为()A.B.C.D.考点:互余两角三角函数的关系.专题:计算题.分析:根据题意作出直角△ABC,然后根据sinA=,设一条直角边BC为5x,斜边AB为13x,根据勾股定理求出另一条直角边AC的长度,然后根据三角函数的定义可求出tan∠B.解答:解:∵sinA=,∴设BC=5x,AB=13x,则AC==12x,故tan∠B==.故选:D.点评:本题考查了互余两角三角函数的关系,属于基础题,解题的关键是掌握三角函数的定义和勾股定理的运用.3.(•凉山州)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则∠C的度数是()A.45°B.60°C.75°D.105°考点:特殊角的三角函数值;非负数的性质:绝对值;非负数的性质:偶次方;三角形内角和定理.专题:计算题.分析:根据非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,根据三角形的内角和定理可得出∠C的度数.解答:解:由题意,得 cosA=,tanB=1,∴∠A=60°,∠B=45°,∴∠C=180°﹣∠A﹣∠B=180°﹣60°﹣45°=75°.故选:C.点评:此题考查了特殊角的三角形函数值及绝对值、偶次方的非负性,属于基础题,关键是熟记一些特殊角的三角形函数值,也要注意运用三角形的内角和定理.4.(•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()A.100米B.50米C.米D.50米考点:解直角三角形的应用.专题:几何图形问题.分析:过B作BM⊥AD,根据三角形内角与外角的关系可得∠ABC=30°,再根据等角对等边可得BC=AC,然后再计算出∠CBM的度数,进而得到CM长,最后利用勾股定理可得答案.解答:解:过B作BM⊥AD,∵∠BAD=30°,∠BCD=60°,∴∠ABC=30°,∴AC=CB=100米,∵BM⊥AD,∴∠BMC=90°,∴∠CBM=30°,∴CM=BC=50米,∴BM=CM=50米,故选:B.点评:此题主要考查了解直角三角形的应用,关键是证明AC=BC,掌握直角三角形的性质:30°角所对直角边等于斜边的一半.5.(•凉山州)拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是()A.15m B.20m C.10m D.20m考点:解直角三角形的应用-坡度坡角问题.专题:计算题.分析:在Rt△ABC中,已知坡面AB的坡比以及铅直高度BC的值,通过解直角三角形即可求出斜面AB的长.解答:解:Rt△ABC中,BC=10m,tanA=1:;∴AC=BC÷tanA=10m,∴AB==20m.故选:D.点评:此题主要考查学生对坡度坡角的掌握及三角函数的运用能力,熟练运用勾股定理是解答本题的关键.6.(•百色)从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是()A.(6+6)米B.(6+3)米C.(6+2)米D.12米考点:解直角三角形的应用-仰角俯角问题.专题:几何图形问题.分析:在Rt△ABC求出CB,在Rt△ABD中求出BD,继而可求出CD.解答:解:在Rt△ACB中,∠CAB=45°,AB⊥DC,AB=6米,∴BC=6米,在Rt△ABD中,∵tan∠BAD=,∴BD=AB•tan∠BAD=6米,∴DC=CB+BD=6+6(米).故选:A.点评:本题考查仰角俯角的定义,要求学生能借助仰角俯角构造直角三角形并解直角三角形,难度一般.7.(•苏州)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为()A.4km B.2km C.2km D.(+1)km考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:过点A作AD⊥OB于D.先解Rt△AOD,得出AD=OA=2,再由△ABD 是等腰直角三角形,得出BD=AD=2,则AB=AD=2.解答:解:如图,过点A作AD⊥OB于D.在Rt△AOD中,∵∠ADO=90°,∠AOD=30°,OA=4,∴AD=OA=2.在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB﹣∠AOB=75°﹣30°=45°,∴BD=AD=2,∴AB=AD=2.即该船航行的距离(即AB的长)为2km.故选:C.点评:本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.8.(•路北区二模)如图,△ABC的项点都在正方形网格的格点上,则cosC 的值为()A.B.C.D.考点:锐角三角函数的定义;勾股定理.专题:网格型.分析:先构建格点三角形ADC,则AD=2,CD=4,根据勾股定理可计算出AC,然后根据余弦的定义求解.解答:解:在格点三角形ADC中,AD=2,CD=4,∴AC===2,∴cosC===.故选B.点评:本题考查了锐角三角函数的定义:在直角三角形中,一锐角的余弦等于它的邻边与斜边的比值.也考查了勾股定理.9.(•长宁区一模)如图,在△ABC中,∠ACB=90°,CD⊥AB于D,下边各组边的比不能表示sinB的()A.B.C.D.考点:锐角三角函数的定义.分析:利用两角互余关系得出∠B=∠ACD,进而利用锐角三角函数关系得出即可.解答:解:∵在△ABC中,∠ACB=90°,CD⊥AB于D,∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠B=∠ACD,∴sinB===,故不能表示sinB的是.故选:B.点评:此题主要考查了锐角三角函数的定义,正确把握锐角三角函数关系是解题关键.10.(•工业园区一模)若tan(α+10°)=1,则锐角α的度数是()A.20°B.30°C.40°D.50°考点:特殊角的三角函数值.分析:根据tan30°=解答即可.解答:解:∵tan(α+10°)=1,∴tan(α+10°)=.∴α+10°=30°.∴α=20°.故选A.点评:熟记特殊角的三角函数值是解答此题的关键.11.(•鄂州四月调考)在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是()A.B.C.D.考点:解直角三角形.分析:首先延长BA过点C作CD⊥BA延长线于点D,进而得出AD,CD,BC 的长,再利用锐角三角函数关系求出即可.解答:解:延长BA过点C作CD⊥BA延长线于点D,∵∠CAB=120°,∴∠DAC=60°,∴∠ACD=30°,∵AB=4,AC=2,∴AD=1,CD=,BD=5,∴BC==2,∴sinB===.故选:B.点评:此题主要考查了解直角三角形,作出正确辅助线构造直角三角形是解题关键.12.(•邢台一模)在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于()A.B.C.D.考点:解直角三角形.分析:在直角三角形ABC中,由AB与sinA的值,求出BC的长,根据勾股定理求出AC的长,根据面积法求出CD的长,即为斜边上的高.解答:解:根据题意画出图形,如图所示,在Rt△ABC中,AB=4,sinA=,∴BC=ABsinA=2.4,根据勾股定理得:AC==3.2,∵S△ABC=AC•BC=AB•CD,∴CD==.故选C.点评:此题考查了解直角三角形,涉及的知识有:锐角三角函数定义,勾股定理,以及三角形的面积求法,熟练掌握定理及法则是解本题的关键.二.填空题(共6小题)13.(•济宁)如图,在△ABC中,∠A=30°,∠B=45°,AC=,则AB 的长为3+.考点:解直角三角形.专题:几何图形问题.分析:过C作CD⊥AB于D,求出∠BCD=∠B,推出BD=CD,根据含30度角的直角三角形求出CD,根据勾股定理求出AD,相加即可求出答案.解答:解:过C作CD⊥AB于D,∴∠ADC=∠BDC=90°,∵∠B=45°,∴∠BCD=∠B=45°,∴CD=BD,∵∠A=30°,AC=2,∴CD=,∴BD=CD=,由勾股定理得:AD==3,∴AB=AD+BD=3+.故答案为:3+.点评:本题考查了勾股定理,等腰三角形的性质和判定,含30度角的直角三角形性质等知识点的应用,关键是构造直角三角形,题目具有一定的代表性,是一道比较好的题目.14.(•徐汇区一模)如图,已知梯形ABCD中,AB∥CD,AB⊥BC,且AD⊥BD,若CD=1,BC=3,那么∠A 的正切值为.考点:锐角三角函数的定义.分析:求出∠ABC=∠ADB=90°,根据三角形内角和定理求出∠A=∠DBC,解直角三角形求出即可.解答:解:∵AB∥CD,AB⊥BC,∴DC⊥BC,∠ABC=90°,∴∠C=90°,∵AD⊥BD,∴∠ADB=90°,∴∠DBC+∠ABD=∠A+∠ABD=90°,∴∠A=∠DBC,∵CD=1,BC=3,∴∠A的正切值为tanA=tan∠DBC==,故答案为:3.点评:本题考查了锐角三角函数的定义,三角形内角和定理的应用,关键是求出∠A=∠DBC和求出tan∠DBC=.15.(•虹口区一模)计算:cos45°+sin260°=.考点:特殊角的三角函数值.分析:将cos45°=,sin60°=代入求解.解答:解:原式=×+()2=1+=.故答案为:.点评:本题考查了特殊角的三角函数值,解答本题的关键是熟记几个特殊角的三角函数值.16.(•武威模拟)某人沿坡度为i=3:4斜坡前进100米,则它上升的高度是60 米.考点:解直角三角形的应用-坡度坡角问题.分析:根据坡度的定义可以求得AC、BC的比值,根据AC、BC的比值和AB 的长度即可求得AC的值,即可解题.解答:解:由题意得,AB=100米,tanB==3:4,设AC=3x,则BC=4x,则(3x)2+(4x)2=1002,解得:x=20,则AC=3×20=60(米).故答案为:60.点评:本题考查了勾股定理在直角三角形中的运用,坡度的定义及直角三角形中三角函数值的计算,属于基础题.17.(•海门市模拟)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB 的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB 的高度是m.考点:解直角三角形的应用-仰角俯角问题.专题:应用题.分析:设AB=x,在Rt△ABC中表示出BC,在Rt△ABD中表示出BD,再由CD=20米,可得关于x的方程,解出即可得出答案.解答:解:设AB=x,在Rt△ABC中,∠C=30°,则BC==x,在Rt△ABD中,∠ADB=60°,则BD==x,由题意得,x﹣x=20,解得:.故答案为:10.点评:本题考查了解直角三角形的应用,解答本题的关键是熟练掌握三角函数的定义,利用三角函数的知识表示出相关线段的长度.18.(•扬州)在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC= 6 .考点:解直角三角形;等腰三角形的性质.分根据题意做出图形,过点A作AD⊥BC于D,根据AB=AC=5,析:sin∠ABC=0.8,可求出AD的长度,然后根据勾股定理求出BD的长度,继而可求出BC的长度.解答:解:过点A作AD⊥BC于D,∵AB=AC,∴BD=CD,在Rt△ABD中,∵sin∠ABC==0.8,∴AD=5×0.8=4,则BD==3,∴BC=BD+CD=3+3=6.故答案为:6.点评:本题考查了解直角三角形的知识,难度一般,解答本题的关键是构造直角三角形并解直角三角形以及勾股定理的应用.三.解答题(共6小题)19.(•盘锦)如图,用一根6米长的笔直钢管弯折成如图所示的路灯杆ABC,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,若路灯杆顶端C到地面的距离CD=5.5米,求AB长.考点:解直角三角形的应用.专题:几何图形问题.分析:过B作BE⊥DC于E,设AB=x米,则CE=5.5﹣x,BC=6﹣x,根据30°角的正弦值即可求出x,则AB求出.解答:解:过B作BE⊥DC于E,设AB=x米,∴CE=5.5﹣x,BC=6﹣x,∵∠ABC=120°,∴∠CBE=30°,∴sin30°==,解得:x=5,答:AB的长度为5米.点评:考查了解直角三角形,解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.20.(•遵义)如图,一楼房AB后有一假山,其坡度为i=1:,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.专题:应用题.分析:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,根据CE=20米,坡度为i=1:,分别求出EF、CF的长度,在Rt△AEH中求出AH,继而可得楼房AB的高.解答:解:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,在Rt△CEF中,∵i===tan∠ECF,∴∠ECF=30°,∴EF=CE=10米,CF=10米,∴BH=EF=10米,HE=BF=BC+CF=(25+10)米,在Rt△AHE中,∵∠HAE=45°,∴AH=HE=(25+10)米,∴AB=AH+HB=(35+10)米.答:楼房AB的高为(35+10)米.点评:本题考查了解直角三角形的应用,涉及仰角俯角及坡度坡角的知识,构造直角三角形是解题关键.21.(•哈尔滨)如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.(1)求两建筑物底部之间水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).考点:解直角三角形的应用-仰角俯角问题.专题:几何图形问题.分析:(1)根据题意得:BD∥AE,从而得到∠BAD=∠ADB=45°,利用BD=AB=60,求得两建筑物底部之间水平距离BD的长度为60米;(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,根据AF=BD=DF=60,在Rt△AFC中利用∠FAC=30°求得CF,然后即可求得CD的长.解答:解:(1)根据题意得:BD∥AE,∴∠ADB=∠EAD=45°,∵∠ABD=90°,∴∠BAD=∠ADB=45°,∴BD=AB=60,∴两建筑物底部之间水平距离BD的长度为60米;(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,∴AF=BD=DF=60,在Rt△AFC中,∠FAC=30°,∴CF=AF•tan∠FAC=60×=20,又∵FD=60,∴CD=60﹣20,∴建筑物CD的高度为(60﹣20)米.点评:考查解直角三角形的应用;得到以AF为公共边的2个直角三角形是解决本题的突破点.22.(•邵阳)一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CD=AC=40海里,再解Rt△CBD中,得出BC=≈50,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.解答:解:如图,过点C作CD⊥AB交AB延长线于D.在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=AC=40海里.在Rt△CBD中,∵∠CDB=90°,∠CBD=90°﹣37°=53°,∴BC=≈=50(海里),∴海警船到大事故船C处所需的时间大约为:50÷40=(小时).点评:本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.23.(•射阳县三模)小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡度为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,求树的高度.考点:解直角三角形的应用-坡度坡角问题.分析:延长AC交BF延长线于D点,则BD即为AB的影长,然后根据物长和影长的比值计算即可.解答:解:延长AC交BF延长线于D点,则∠CFE=30°,作CE⊥BD于E,在Rt△CFE中,∠CFE=30°,CF=4m,∴CE=2(米),EF=4cos30°=2(米),在Rt△CED中,∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,CE=2(米),CE:DE=1:2,∴DE=4(米),∴BD=BF+EF+ED=12+2(米)在Rt△ABD中,AB=BD=(12+2)=(6+)(米).答:树的高度为:(6+)(米).点评:本题考查了解直角三角形的应用以及相似三角形的性质.解决本题的关键是作出辅助线得到AB的影长.24.(•崇川区一模)如图,某登山队在山脚A处测得山顶B处的仰角为45°,沿坡角30°的斜坡AD前进1000m后到达D处,又测得山顶B处的仰角为60°.求山的高度BC.考点:解直角三角形的应用-仰角俯角问题.分析:过点D作DE⊥AC,△ACB是等腰直角三角形,直角△ADE中满足解直角三角形的条件.在直角△BDF中,根据三角函数可得BF,进一步得到BC,即可求出山高.解答:解:过D分别作DE⊥AC与E,DF⊥BC于F.∵在Rt△ADE中,AD=1000m,∠DAE=30°,∴DE=AD=500m.∵∠BAC=45°,∴∠DAB=45°﹣30°=15°,∠ABC=90°﹣45°=45°.∵在Rt△BDF中,∠BDF=60°,∴∠DBF=90°﹣60°=30°,∴∠DBA=45°﹣30°=15°,∵∠DAB=15°,∴∠DBA=∠DAB,∴BD=AD=1000m,∴在Rt△BDF中,BF=BD=500m,∴山的高度BC为(500+500)m.点评:本题考查了解直角三角形的应用﹣仰角俯角问题的应用,根据已知得出FC,BF的长是解题关键.。
沪科版九年级数学上册试题 第23章《解直角三角形》章节测试卷(含解析)
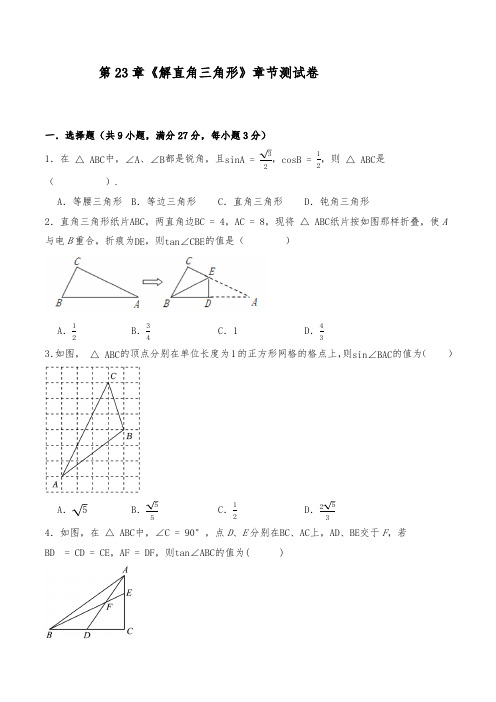
第23章《解直角三角形》章节测试卷一.选择题(共9小题,满分27分,每小题3分)1.在△ABC 中,∠A 、∠B 都是锐角,且sinA =32,cosB =12,则△ABC 是( ).A .等腰三角形B .等边三角形C .直角三角形D .钝角三角形2.直角三角形纸片ABC ,两直角边BC =4,AC =8,现将△ABC 纸片按如图那样折叠,使A 与电B 重合,折痕为DE ,则tan ∠CBE 的值是( )A .12B .34C .1D .433.如图,△ABC 的顶点分别在单位长度为1的正方形网格的格点上,则sin ∠BAC 的值为( )A .5B .55C .12D .2534.如图,在△ABC 中,∠C =90°,点D 、E 分别在BC 、AC 上,AD 、BE 交于F ,若BD=CD =CE ,AF =DF ,则tan ∠ABC 的值为( )A .12B .23C .34D .455.一块直角三角板ABC 按如图放置,顶点A 的坐标为(0,1),直角顶点C 的坐标为(−3,0),∠B =30°,则点B 的坐标为( )A. (−3−33,33)B .(−3+3,3)C .(−3+33,33)D .(−3−3,33)6.在Rt △ABC 中,∠A =90°,有一个锐角为60°,BC =6,若点P 在直线AC 上(不与点A 、C 重合),且∠ABP =30°,则CP 的长为( )A .6或23B .6或43C .23或43D .6或23或437.如图,延长等腰Rt ΔABC 斜边AB 到D ,使BD =2AB ,连接CD ,则tan ∠BCD 的值为( )A .23B .1C .13D .128.如图,在△ABC 中,∠ACB =90∘,分别以AB ,AC ,BC 为边向外作正方形,连结CD ,若sin∠BCD=35,则tan ∠CDB 的值为( )A .23B .34C .710D .9139.如图1是由四个全等的直角三角形组成的“风车”图案,其中∠AOB =90°,延长直角三角形的斜边恰好交于另一直角三角形的斜边中点,得到如图2,若IJ =2,则该“风车”的面积为( )A .2+1B .22C .4−2D .42二.填空题(共6小题,满分18分,每小题3分)10.如图,在Rt △ABC 中,∠C =90°,点D ,E 分别在AC ,BC 边上,且AD =3,BE =4,连接AE ,BD ,交于点F ,BD=10,cos ∠AFD=32,则AE 的长为 .11.如图,在菱形ABCD 中,tan ∠ABC =43,AE ⊥BC 于点E ,AE 的延长线与DC 的延长线交于点F ,则S △ECF :S 四边形ADCE = .(S 表示面积)12.如图,在矩形ABCD中,AB=3,AD=4,E是对角线BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,DE=.13.如图,已知点P是菱形ABCD的对角线AC延长线上一点,过点P分别作AD,DC延长线的垂线,垂足分别为点E,F.若∠ABC=120°,AB=6,则PE−PF的值为.14.如图,在正方形ABCD中,M,N分别是AB,CD的中点,P是线段MN上的一点,BP的延长线交4D 于点E,连接PD,PC,将△DEP绕点P顺时针旋转90°得△GFP,则下列结论:①CP=GP,②tan∠CGF=1;③BC垂直平分FG;④若AB=4,点E在AD边上运动,则D,F两点之间距离的2.其中结论正确的序号有.最小值是3215.如图,△A B1A1,△A1B2A2,△A2B3A3,…是等边三角形,直线y=33x+2经过它们的顶点A,A1,A2,A3,…,点B1,B2,B3,…在x轴上,则线段B2022B2023的长度是.16.如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°,若AH=2,AD=5+3,则四边形EFGH的周长为.三.解答题(共7小题,满分52分)17.(6分)计算:(1)2sin60°−tan45°2−tan30°⋅tan60°−2cos30°+6sin245°. (2)(π−1)0+4sin45°−8+|−3|.18.(6分)如图,在△ABC中,AD⊥BC于点D,若AD=6,BC=12,tan∠ACD=32.求:(1)CD的长;(2)sin∠ABC的值.19.(8分)(2023春·河南南阳·九年级统考期中)如图,已知点A(7,8)、C(0,6),AB⊥x轴,垂足为点B,点D在线段OB上,DE∥AC,交AB于点E,EF∥CD,交AC于点F.(1)求经过A、C两点的直线的表达式;(2)设OD=t,BE=s,求s与t的函数关系式;(3)是否存在点D,使四边形CDEF为矩形?若存在,请直接写出点D的坐标;若不存在,请说明理由.20.(8分)(1)在如图1的正方形网格图中,每个小正方形的边长为1,A,B,C,D均为格点(小正方形的顶点).求证:∠ABC=∠D.(2)在如图2所示的正方形网格图中,每个小正方形的边长为1,A,B,C均为格点,请你仅用无刻度的直尺在线段AC上求作一点P,使得∠PBA=∠C,并简要说明理由.21.(9分)如图,小明为测量宣传牌AB的高度,他站在距离建筑楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°.同时测得建筑楼窗户D处的仰角为30°(A、B、D、E在同一直线上.)然后,小明沿坡度为i=1:2.5的斜坡从C走到F处,此时DF正好与地面CE平行,小明在F处又测得宣传牌顶部A的仰角为45°.(1)填空:∠DAF=__________度,∠BDC=__________度;(2)求F距离地面CE的高度(结果保留根号);(3)求宣传牌AB的高度(结果保留根号).22.(9分)我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边腰=BCAB.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1)sad90°=________.(2)对于0°<A<180°,∠A的正对值sadA的取值范围是________.(3)如图②,已知sinA=35,其中∠A为锐角,试求sadA的值.23.(9分)已知:△ABC 中,AB =AC ,D 为直线BC 上一点.(1)如图1,BH ⊥AD 于点H ,若AD =BD ,求证:BC =2AH .(2)如图2,∠BAC =120°,点D 在CB 延长线上,点E 在BC 上且∠DAE=120°,若AB =6,DB=23,求CE 的值.(3)如图3,D 在CB 延长线上,E 为AB 上一点,且满足:∠BAD=∠BCE ,AE BE=23,若tan ∠ABC =34,BD =5,求BC 的长.答案解析一.选择题1.B【分析】根据特殊角的三角函数值求出∠A=60°,∠B=60°,然后利用三角形内角和定理求出∠C的度数,即可解答.【详解】解:∵sinA=32,cosB=12,∴∠A=60°,∠B=60°,∴∠C=180°−∠A−∠B=60°,∴△ABC是等边三角形,故选:B.2.B【分析】根据折叠的性质得出BE=AE,设CE=x,则BE=AE=8−x,在Rt△BCE中,根据勾股定理得出B C2+C E2=B E2,列出方程求出x的值,最后根据正切的定义,即可解答.【详解】解:∵△ADE沿DE折叠得到△BDE,∴BE=AE,设CE=x,则BE=AE=8−x,在Rt△BCE中,根据勾股定理可得:B C2+C E2=B E2,即42+x2=(8−x)2,解得:x=3,∴tan∠CBE=CEBC =34,故选:B.3.B【分析】过B作BD⊥AC于点D,根据勾股定理得出AB,AC的值,再利用面积公式求出BD的值,由sin∠BAC=BDBA可得角的正弦值.【详解】解:如图,过B作BD⊥AC于点D根据勾股定理得:AB =32+42=5,AC =32+62=35∴S ΔABC =12AC ⋅BD =4×6−12×3×1−12×3×4−12×6×3=152, ∴BD =5∴sin ∠CAB=BD AB =55故选:B .4.C 【分析】如图,过A 作AG ∥BC ,交BE 的延长线于G ,证明△AGF ≌△DBF (AAS ),则AG =BD =12BC ,证明△AEG ∽△CEB ,则AE CE =AG BC =12,解得AE =12CE ,AC =32CE ,根据tan ∠ABC =ACBC,计算求解即可.【详解】解:如图,过A 作AG ∥BC ,交BE 的延长线于G ,∴∠G =∠DBF ,在△AGF 和△DBF 中,∵{∠G =∠DBF∠AFG =∠DFB AF =DF,∴△AGF ≌△DBF (AAS ),∴AG =BD =12BC ,∵∠G =∠CBE ,∠AEG =∠CEB ,∴△AEG ∽△CEB ,∴AE CE =AG BC=12,解得AE =12CE ,∴AC =32CE ,∴tan ∠ABC=AC BC =32CE 2CE =34,故选:C .5.D【分析】过点B 作BE ⊥OC 于点E ,根据ΔABC 为直角三角形可证明ΔBCE ∽ΔCAO ,求出AC =10,求出BC ,再由比例线段可求出BE ,CE 长,则答案可求出.【详解】解:过点B 作BE ⊥OC 于点E ,∵△ABC 为直角三角形,∴∠BCE +∠ACO =90°,∴ΔBCE ∽ΔCAO ,∴ BE OC =BC AC =EC OA ,在Rt △ACO 中,AC =A O 2+C O 2=12+32=10,在Rt △ABC 中,∠CBA=30°,∴ tan ∠CBA=CA BC ,∴ BC =CA tan ∠CBA =10tan30°=30,∴ BE3=3010=EC1,解得BE =33,EC =3,∴ EO =EC +CO =3+3,∴点B 的坐标为(−3−3,33).故选:D .6.D【分析】根据点P在直线AC上的不同位置,∠ABP=30°,利用特殊角的三角函数进行求解.【详解】如图1:当∠C=60°时,∠ABC=30°,与∠ABP=30°矛盾;如图2:当∠C=60°时,∠ABC=30°,∵∠ABP=30°,∴∠CBP=60°,∴△PBC是等边三角形,∴CP=BC=6;如图3:当∠ABC=60°时,∠C=30°,∵∠ABP=30°,∴∠PBC=60°−30°=30°,∴PC=PB,∵BC=6,∴AB=3,∴PC=PB=3cos30°=332=23如图4:当∠ABC=60°时,∠C=30°,∵∠ABP=30°,∴∠PBC=60°+30°=90°,∴PC=BCcos30°=632=43故选:D7.A【分析】过点D作DE垂直于CB的延长线于点E,设AC=BC=a,根据勾股定理得AB=2a,由等腰直角三角形的性质得∠ABC=∠BAC=45°,从而得BD=2AB=22a,在Rt△BDE中,解直角三角形得DE=2a,BE=2a,进而求得CE=BC+BE=3a即可求得tan∠BCD.【详解】解:过点D作DE垂直于CB的延长线于点E,如下图,设AC=BC=a,∵AC⊥BC,AC=BC=a,∴AB=A C2+B C2=2a,∠ABC+∠BAC=90°,∠ABC=∠BAC,∴∠ABC=∠BAC=45°,BD=2AB=22a,∴∠DBE=∠ABC=45°,∵DE⊥CE,∴DE=BD·sin∠DBE=22a·sin45°=2a,BE=BD·cos∠DBE=22a·cos45°=2a,∴CE=BC+BE=3a,∴tan∠BCD=DECE =2a3a=23,故选:A.8.D【分析】过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,可得△ABC,△BED,△BEC,△BCF都是直角三角形,根据sin∠BCE=BEBC =35,设BE=3a,BC=5 a,得CE=B C2−B E2=4 a,过点C作DB延长线于点G,得矩形CFBG,设AC=x,AB=y,然后利用勾股定理和三角形的面积可得y2−9=133,进而利用锐角三角函数即可解决问题.【详解】解:如图,过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,∴△ABC,△BED,△BEC,△BCF都是直角三角形,∵sin∠BCD=35,∴sin∠BCE=BEBC =35,设BE=3a,BC=5a,∴CE=B C2−B E2=4a,过点C作DB延长线于点G,得矩形CFBG,∴BF=CG,设AC=x,AB=y,在Rt△ABC中,根据勾股定理,得AB2﹣AC2=BC2,∴y2﹣x2=25a2,∵S△ABC=12×AB•CF=12×AC•BC,∴y•CF=5ax,∴CF=5axy,在Rt△BCF中,根据勾股定理,得BF=B C2−C F2=25a2−(5axy )2=25ya,∴BF=CG=25ya,在正方形ABDH中,AB=BD=y,在Rt△BDE中,根据勾股定理,得DE=B D2−B E2=y2−9a2,∴CD=CE+ED=4a +y2−9a2,∵S△CBD=12×CD•BE=12×BD•CG,∴CD•BE=BD•CG,∴(4a +y2−9a2)×3=y×25ya,∴y2−9a2=133a,∴tan∠CDB=tan∠EDB=BEDE =3ay2−9a2=913.故选:D.9.B【分析】连接AC,由题意可得Rt△AOB≌Rt△DCO≌Rt△EOF≌Rt△GOH,进而说明△OAC为等腰直角三角形,再说明分CD、GI垂直平分AB,进而说明∠OBH=∠OHB=45°,然后再运用解直角三角形求得AI,然后再求得三角形AOB的面积,最后求风车面积即可.【详解】解:如图:连接AC由题意可得:Rt△AOB≌Rt△DCO≌Rt△EOF≌Rt△GOH∴OA=OC, ∠OAB= ∠OCD∵∠AOC=∠AOB=90°∴△OAC为等腰直角三角形又∵∠OAB= ∠OCD:∴∠AJD=180°-∠ADJ-∠OAB=180°-∠ODC-∠OCD=90°,即AJ⊥CD又∵CJ=DJ∴AJ垂直平分CD同理:GI垂直平分AB∴AC=AD,AJ是等腰三角形顶角∠CAD的角平分线即∠DAJ=12∠CAD=12×45°=22.5°易得IH=BJ,IJ=IB+BJ=IB+IH 又∵IB=IA∴IJ=IB+BJ=IH+IA= 2在Rt△ABO中,∠ABH=∠BAH=22.5°∴∠OBH=OHB=45°设OB=OH=a,即AH=BH=2OB=2a∴tan∠A=BOAO =aa+2a=2−1∴IHIA=tan∠A=2−1设IH=(2−1)x,AI=x ∴IH+IA=2x=2,即x=1∴S△ABH =12×AB×IH=2−1又∵SΔBOHSΔABH =OHAH=12∴S△BOH =1−22∴S△AOB =S△ABH+S△BOH=2−1+1−22=22∴S风车=4S△AOB=4×22=22.故选B.二.填空题10.53【分析】过点A作AG∥BE,BG∥AE交于点G,连接DG,勾股定理求得DG,过点D作DH⊥BG,证明G,H重合,进而勾股定理即可求解.【详解】解:如图所示,过点A作AG∥BE,BG∥AE交于点G,连接DG,则四边形AGBE是平行四边形,∴AG=BE=4,∵∠C=90°,则BC⊥AC∴AG⊥AC∴△ADG是直角三角形,∴DG=5∵cos∠AFD=32∴∠AFD=30°∵AE∥BG∴∠DBG=30°∵DG=5,DB=10过点D作DH⊥BG,∵sin∠DBG=12∴DH=12DB=5,∴G,H重合,∴AE=BG=BH=53故答案为:53.11.4:21【分析】设AE=4k,则BE=3k,根据勾股定理求出AB=5k,然后证明△CEF∽△DAF,最后根据相似三角形的性质求解即可.【详解】解∶∵tan∠ABC=43,AE⊥BC,∴tan∠ABC=43=AEBE,设AE=4k,则BE=3k,∴AB =A E 2+B E 2=5k ,∵四边形ABCD 是菱形,∴CB ∥AD ,AD =BC =AB =5k ,∴CE =BC −BE =2k ,∵CB ∥AD ,∴△CEF ∽△DAF ,∴S △CEF S△DAF =(CE DA )2=(2k 5k )2=425,∴S △CEFS 四边形ADCE =S △CEF S △DAF −S △CEF =425−4=421.故答案为:4:21.12.2或52或75【分析】分AB =AE,BE =BA,EA =EB 三种情况,分别画出图形,即可求解.【详解】解:在矩形ABCD 中,AB =3,AD =4,∴∠BAD=90°,∴BD =A B 2+A D 2=32+42=5,当AB =AE 时,过点A 作AF ⊥AD 于点F ,则AF ⊥BD ,∴cos ∠ABD=AB BD =BF AB ,∴BF =AB 2BD =95∴DE =BD −BE =BD −2BF =5−185=75,当BA =BE 时,DE =BD −BE =5−3=2,当EA =EB 时,过点E 作EG ⊥AB 于点G ,∴EG ∥AD ,AG =GB ,∴BE ED=BG AG =1,∴DE =12BD=52,综上所述DE = 2或52或75,故答案为:2或52或75.13.33【分析】如图,延长BC 交EP 于M ,由菱形的性质可知,CP 为∠BCD ,∠FCM 的平分线,则PF =PM ,PE −PF =PE −PM =EM ,由题意知,EM 为△ABD 底边AD 上的高,由菱形ABCD ,∠ABC=120°,AB =6,可得∠BAD=60°,根据EM=AB ⋅sin ∠BAD ,计算求解,进而可得结果.【详解】解:如图,延长BC 交EP 于M ,由菱形的性质可知,CP为∠BCD,∠FCM的平分线,∵PF⊥CF,PM⊥CM,∴PF=PM,∴PE−PF=PE−PM=EM,由题意知,EM为△ABD底边AD上的高,∵菱形ABCD,∠ABC=120°,AB=6,∴∠BAD=60°,∴EM=AB⋅sin∠BAD=33,∴PE−PF=33,故答案为:33.14.①②③【分析】延长GF交AD于点H,连接FC,FB,FA,由已知可得MN为AB,CD的垂直平分线,由垂直平分线的性质和图形旋转的性质可得①的结论正确;利用三角形的内角和定理和等腰三角形的性质计算可得∠BCG=45°,由四边形内角和定理通过计算可得∠EHF=90°;利用平行线的性质可得BC⊥FG,则∠CGF=45°,可说明②的结论正确;通过证明点A,B,E,F在以点P为圆心,PA为半径的同一个圆上,利用圆周角定理可得∠FAB=45°,得到A,F,C三点共线,得到△CGF为等腰直角三角形,则③的结论正确;由题意点F在对角线AC上运动,当EF⊥AC时,EF的值最小,连接AC,解直角三角形的知识可得④的结论不正确.【详解】解:延长GF交AD于点H,连接FC,FB,FA,如图,∵正方形ABCD中,M,N分别是AB,CD的中点,∴MN是线段BA,CD的垂直平分线.∴PD=PC,PA=PB.∵△FPG是△PED绕点P顺时针旋转90°得到,∴△FPG≌△PED,∴PD=PG.∴PC=PG.∴①的结论正确;∵PD=PC,∴∠PDC=∠PCD=1(180°−∠DPC).2∵PC=PG,∴∠PCG=∠PGC=1(180°−∠CPG).2∴∠PCD+∠PCG=1[360°−(∠DPC+∠CPG)].2∵∠DPC+∠CPG=90°,∴∠PCD+∠PCG=135°.∵∠BCD=90°,∴∠BCG=45°.∵△FPG≌△PED,∴∠DEP=∠GFP.∵∠HFP+∠PFG=180°,∴∠DEP+∠HFP=180°.∵∠DEP+∠HFP+∠EHF+∠EPF=360°,∴∠EHF+∠EPF=180°.∴∠EPF=90°,∴∠EHF=90°.即GH⊥AD.∵AD//BC,∴GF⊥BC.∴∠CGF=45°.∴tan∠CGF=1.∴②的结论正确;∵PA=PB,PM⊥AB,∴∠APM=∠BPM,∵PM//AE,∴∠PEA=∠BPM,∠PAE=APM.∴∠PEA=∠PAE.∴PA=PE.∵PE=PF,∴PA=PB=PE=PF.∴点A,B,E,F在以点P为圆心,PA为半径的同一个圆上.∴∠FAB=12∠FPB=12×90°=45°.∴点F在对角线AC上,∴∠FCB=45°.∵∠BCG=∠CGF=45°,∴△FCG为等腰直角三角形.∵BC平分∠FCG,∴BC垂直平分FG.∴③的结论正确;由以上可知:点F在正方形的对角线AC上运动,∴当EF⊥AC时,EF的值最小.此时点E与点D重合,∴DF=AD⋅sin45°=4×22=22.∴④的结论不正确.综上,结论正确的序号有:①②③,故答案为:①②③.15.220233【分析】设直线y=33x+2与x轴交于点C,求出点A、C的坐标,可得OA=2,OC=23,推出∠C B1A1=90°,∠C B1A=30°,然后求出C B1=2O B1=43=22×3,C B2=2C B1=83=23×3,C B3=2C B2=163=24×3,…,进而可得C B2022=22023×3,C B2023=22024×3,再求出B2022B2023即可.【详解】解:如图所示,设直线y =33x +2与x 轴交于点C ,当x =0时,y =2;当y =0时,x =−23,∴ A (0,2),C (−23,0),∴ OA=2,OC =23,∴ tan ∠ACO =OA OC=223=33,∴ ∠ACO=30°,∵ △A B 1A 1是等边三角形,∴ ∠A A 1B 1=∠A B 1A 1=60°,∴ ∠C B 1A 1=90°,∠C B 1A =30°,∴ AC =A B 1,∵ AO⊥C B 1,∴ O B 1=OC =23,∴ C B 1=2O B 1=43=22×3,同理,C B 2=2C B 1=83=23×3,C B 3=2C B 2=163=24×3,……,∴ C B 2022=22023×3,C B 2023=22024×3,∴ B 2022B 2023=22024×3−22023×3=220233,故答案为:220233.16.8+46【分析】先构造15° 的直角三角形,求得15° 的余弦和正切值;作EK ⊥FH ,可求得EH:EF =2:6;作∠ARH=∠BFT =15°,分别交直线AB 于R 和T ,构造“一线三等角”,先求得FT 的长,进而根据相似三角形求得ER ,进而求得AE ,于是得出∠AEH =30°,进一步求得结果.【详解】解:如图1,Rt △PMN 中,∠P =15°,NQ =PQ ,∠MQN =30°,设MN=1,则PQ =NQ =2,MQ=3,PN =6+2,∴cos15°=6+24,tan15°=2−3,如图2,作EK ⊥FH 于K ,作∠AHR =∠BFT =15°,分别交直线AB 于R 和T ,∵四边形ABCD 是矩形,∴∠A =∠C ,在△AEH 与△CGF 中,{AE =CG ∠A =∠C AH =CF,∴△AEH ≌△CGF(SAS),∴EH =GF ,同理证得△EBF ≌△GDH ,则EF =GH ,∴四边形EFGH 是平行四边形,设HK=a ,则EH=2a ,EK =3a ,∴EF =2EK =6a ,∵∠EAH =∠EBF =90°,∴∠R=∠T =75°,∴∠R=∠T=∠HEF=75°,可得:FT=BFcos15°=3+36+24=26,AR=AH⋅tan15°=4−23,△FTE∽△ERH,∴FTER =EFEH,∴26ER =62,∴ER=4,∴AE=ER−AR=23,∴tan∠AEH=223=33,∴∠AEH=30°,∴HG=2AH=4,∵∠BEF=180°−∠AEH−∠HEF=75°,∴∠BEF=∠T,∴EF=FT=26,∴EH+EF=4+26=2(2+6),∴2(EH+EF)=4(2+6),∴四边形EFGH的周长为:8+46,故答案为:8+46.三.解答题17.(1)原式=2×32−12−33×3−2×32+6×(22)2=3−12−1−3+6×12=3−1−3+3=2.(2)原式=1+4×22−22+3 =1+22−22+3=4.18.(1)解:∵AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△ADC中,tan∠ACD=ADCD =32,AD=6,∴CD=4;(2)解:由(2)得CD=4,∴BD=BC−CD=8,∴AB=A D2+B D2=10,在Rt△ABD中,sin∠ABD=ADAB =35,即sin∠ABC=35.19.解:(1)设直线AC的表达式为y=kx+b 将点A、C的坐标代入,得得:{7k+b=8b=6,解得:{k=27b=6,故直线AC的表达式为:y=27x+6;(2)∵OD=t,BE=s,AB⊥x轴∴则点D(t,0),点E(7,s)∵DE∥AC可设直线DE的解析式为y=27x+c将点D的坐标代入0=27t+c解得:c=﹣27t∴直线的表达式为:y=27x﹣27t,将点E的坐标代入,得s=2﹣27t(根据点D在线段OB上,可得0<t<7);(3)存在,理由:设点D(t,0),由(2)BE=2﹣27t,四边形CDEF为矩形,则∠CDE=90°,∵∠EDB +∠CDO =90°,∠CDO +∠OCD =90°,∴∠OCD =∠BDE ,∴tan ∠OCD =tan ∠BDE ,∴ODOC =BE BD即t 6=2−27t 7−t,解得:t =127或7(因为0<t <7,故舍去7),故点D 的坐标为(127,0).20.(1)如图所示,取格点E ,F ,连接BF,AF ,AE,CE ,∵BF =12+12=2,DF =32+32=32,∴tan ∠D =BF DF=232=13,∵CE =1,BE =3,∴tan ∠ABC=CE BE=13,∴tan ∠D =tan ∠ABC ,∴∠ABC=∠D ;(2)解:如图,取格点D ,E ,同理(1)可得,在Rt△AEC中,tan∠ACE=1,2,在Rt△ABD中,tan∠ABD=12∴tan∠ACE=tan∠ABD,∴∠ACE=∠ABD,直线BD与AC的交点为所求的点P.21.(1)解:由题意,得AD⊥DF,∴∠ADF=90°∴∠DAF=90°−∠AFD=90°−45°=45°,由题意,得FD∥CE,∴∠CDF=∠ECD=30°∴∠BDC=∠ADF+∠CDF=90°+30°=120°.(2)解:如图,过点F作FG⊥EC于G,由题意得,FG∥DE,DF∥GE,∠FGE=90°,∴四边形DEGF是矩形.∴FG=DE.在Rt △CDE 中,DE =CE ⋅tan ∠DCE=6×tan30°=23(米),∴FG =23(米).答:F 距离地面CE 的高度为23米;(3)解:∵斜坡CF 的坡度为i =1:2.5,∴Rt △CFG 中,CG = 2.5FG =23× 2.5=53(米),∴FD =EG =(53+6)(米).∴在Rt △AFD 中,∠AFD=45°,∴AD =FD =(53+6)米.在Rt △BCE 中,BE =CE ⋅tan ∠BCE =6×tan60°=63(米),∴AB =AD +DE −BE =53+6+23−63=(6+3)(米).答:宣传牌AB 的高度约为(6+3)米.22.(1)解:如图,∠BAC=90°,AB =AC ,sad90°=BC AB ,∵cos45°=AB BC=22,∴sad90°=BCAB = 2.(2)解:如图,点A 在BC 的中垂线上,当点A 向BC 靠近时,∠A 增大,逐渐接近180°,腰长AB 接近12BC ,AB >12BC 相应的sadA =BC AB <2;当点A 远离BC 时,∠A 减小,逐渐接近0°,腰长AB 逐渐增大,相应的sadA =BCAB 逐渐接近0,sad A =BCAB >0;∴0<sadA <2(3)解:如图,在AB 上截取AH=AC ,过H 作HD ⊥AC 于D ,sinA =35=DH AH ,设HD =3x,AH =AC =5x ,则,AD =A H 2−H D 2=4x ,∴DC =AC −AD =5x −4x =x .Rt △HDC 中,HC =C D 2+H D 2=10x ,∴sadA =CH AH =10x 5x =105.23.(1)解:证明:如图1,过点A 作AN ⊥BC 于N ,∵AB =AC ,∴BN =12BC ,∵AD =BD ,∴∠ABD =∠BAD ,在△ABN 和△BAH 中,{∠ANB=∠BHA=90°∠ABD=∠DABAB=BA,∴△ABN≌△BAH(AAS),∴BN=AH,∴12BC=AH,∴BC=2AH;(2)如图2,在AC上取一点F,使EF=EC,连接EF,∵∠BAC=∠DAE=120°,∴∠DAB=∠EAC,∵AB=AC,∴∠ABE=∠C=∠CFE=30°,∴∠ABD=∠AFE=150°,∴△ABD∽△AFE,∴ABAF =BDEF,即6AF=23EF,∴AFEF=3,设EF=a,则AF=3a,∵EF=CE=a,∠C=30°,∴CF=2EF·cos30°=3a,∴6−3a=3a,∴a=3,∴CE=EF=3;(3)如图3,过点A作AP⊥BC于P,作AG∥CE交BC的延长线于G,设AE=2m,BE=3m,则AB=AC=5m,∵tan∠ABC=34=AP BP ,∴ BP AB =45,∴BP =CP =4m ,BC =8m ,∵∠BAD =∠BCE =∠G ,∠ABD =∠GCA ,∴△ABD ∽△GCA ,∴ CG AB =AC BD ,即CG 5m =5m 5,∴CG =5m 2,∵AG ∥CE ,∴ BE AE =BC CG ,∴ 3m 2m =8m5m 2,∴m =1615,∴BC =8m =12815.。
2018年秋沪科版九年级上第23章解直角三角形测试题含答案

解直角三角形第23章) 每小题4分,共40分(一、选择题2BAABCC) ,则中,∠sin=90°,若sin 等于=1.在△( 23211 .A. B. C. D222ACAABmABC) ( °,则直角边斜边的长为的长是,∠=Z2.如图23--1,在Rt△35中,mm cos35 B.°A.··sin35°mm C. D.°sin35°cos351 Z-图23-DADBCABC,⊥于点2所示(每个小正方形的边长为1),3.△Z在网格中的位置如图23--) ( 下列选项中,错误的是..ACD2tan∠=α=cosα B.A.sin1=.tanαβ=cosβ DC.sin2--Z 图23AbacCabcBABCA tan,,则=.若54.在△=中,∠,∠3,∠,的对边分别为=,,4)( 的值是4433 C. D. A. B. 5354) .下列式子中不成立的是5(A. 2cos45°=2sin30°12B.sin30°×cos60°=sin45°2C.cos45°-sin45°=0D.sin(30°+30°)=sin30°+sin30°A<90°,则下列各式中成立的是( -3,已知45°<∠) -6.如图23Z AAAA cos.sinsinA.>=cos B AAAA<cossintan.Csin> D.3-图23-Z3ACDADABBCDACBABC等,∠是+的中点,则 tan7.在△∠中,∠=90°,sin tan=5)于(82574 B. C. D. A. 312534OABABx,则点,点∠在=轴上,且sin8.在平面直角坐标系中,点(0的坐标为,3)5B)的坐标为(0)4,(4,0) B.(-A.0),5,0)或(-(4.,0)或(-4,0) D.(5C BBA地100 3 m到23-Z-4所示,小明从地,再从地沿北偏东30°方向走9.如图AC)( 地,此时小明离地向正南方向走200 m到120 m. C.100 m DA.60 m B.80 m4-23-Z图ACCABCACD上一点,若90°,是=62310.如图-Z-5,在等腰直角三角形,中,∠=1ADDBA) ( ∠=,则的长为tan53 C. 2 D.A.12 B.图23-Z-5二、填空题(每小题5分,共20分)15ABCCBCAAB=,则tan=15,________.=90Rt6Z2311.如图--,在△中,∠=°,8图23-Z-6DCDABACBACBCABC,⊥=8,,垂足为Rt23-Z-7,在△=中,∠6=90°,,12.如图BCD________∠.的值是则 tan7-Z-图235BECAEBCEABCD,则这个=于点1, cos-.如图23Z-8,在菱形,已知中,=⊥1313 .菱形的面积是________8--Z图23DCAADCDACABCDADBCAB,错误tan,⊥∠,!914.如图23-Z-,在四边形=中,=∥,ABAC________,则.的长度是=89Z-图23-)分(共40三、解答题ABACABABC的3°,,求10,在△=中,∠°,∠=302 =45-如图.15(8分)23-Z长.图23-Z-10BCAB=,是某小区的一个健身器材的示意图,已知=0.15 mZ)16.(8分如图23--11BODACD的距离.(结果精确到0.1 °,求端点,∠2.70 m=70到底面m.参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)图23-Z-1117.(12分)如图23-Z-12,某小区①号楼与?号楼隔河相望.李明家住在①号楼,他BC点的仰角为60他先在°,点测得然后号楼的高度,很想知道?于是他测量了一些数据.ACCD.号楼的高度30°,请你帮助李明计算到42米高的楼顶?处,测得点的仰角为图23-Z-12OOC方向﹚以45台风中心位于点13Z23)(1218.分如图--,处,并沿北偏东°方向﹙O的千米的区域内会受到台风的影响,在点时的速度匀速移动,40千米/在距离台风中心50A. 2千米的地方有一城市正东方向,距离60A市是否会受到此台风的影响?为什么?(1)OBB市是否会受到,则80在点的北偏东15°方向上,距离千米的地方还有一城市(2)此台风的影响?若受到影响,请求出受到影响的时间;若不受影响,请说明理由.图23-Z-13B 1.ACAC cosBcoscos.35AC] =m·A=,即°35°=,∴2.解析 [mAB22cosCsin,α= [解析] 先构建直角三角形,再根据三角函数的定义,=α3.=2222Csintancos.,故选2=,ββ=)(90°-∠ACD=1DA 4.5.B根据锐角的正弦值随角度的增大而增大,余弦值随角度的增大而减小判] [6.解析断.也可用特殊值检验.3sinA根据直角4k.由勾股定理得AC==3k,AB=7.5k. [解析] 如图,由BCA=,设5tan=∠A,故=∠B,∠ACDADCD==BD,∴∠BCD三角形斜边上的中线等于斜边的一半,得2543tan.=+∠BCD+=∠ACD1234C x轴的正半轴上. [解析] ①如图,点B在8.4sin=∵,∠OAB 5 5x,4x,AB=∴设OB=2224. ==1,∴OB∴由勾股定理,得3+(4x)=(5x),解得x ;(4,0)的坐标是则点B ,40).x 轴的负半轴上时,点B的坐标是(-在②同理,当点B ,0).0)或(-4,则点B的坐标是(4C.9A=AEDE⊥AB,垂足为E.易证△ADE为等腰直角三角形,10.D [解析] 如图,过点作1AEDE tanRt =C中,∠BE=5AE.在等腰直角三角形ABC=在DE.中,△BDEDBA∠==,所以5BEBE6 2,所以AE=2.在等腰直角三角形ADE=,由勾股定理可求出AC90°,=6AB中,利用A.2.AD勾股定理可求出的长为故选15BC1522tan=BC=ACA=,即=,∴AC=8.根据勾股定理,得AB+11.17 [解析] ∵AC8AC2217.=158+3RtRt∴∠°,中,∵∠A+∠B=90°,∠BCD+∠B=12. [解析] 在90△ABC与△BCD 436BC3tantan.A===∠BCD=.A=∠BCD.∴故答案为4AC84539cos,解得15x+12x,则13x=解析13. [] 设BE=5x,由=B,得AB=13x,AE1316391. .所以菱形的面积=BC·AE=13x·12x==x168Rt中求解.C=∠ACB.在△ABC14.6 [解析] 由题意,得∠DCA=∠DA. 作CD⊥AB于点D,则∠ADC=∠BDC=90°15.解:如图,过点C 45°,∵∠B=BD.CD=BCD=∠B=45°,∴∴∠,=AC2 3∵∠A=30°,3.3,∴BD=CD==∴CD22 AC-CD=3,由勾股定理得AD=3.+BD=3+∴AB=ADF. 于点B作BF⊥AEA16.解:如图,过点作AE⊥直线CD于点E,过点,∥OD,∠∵OD⊥CDBOD=70°,∴AE.°=∠BOD=70∴∠A mRtcos+=0.918(AF),∴AE=在,∴△ABF中,∵AB=2.7AF=2.7×0.3470°≈2.7×m=1.068≈1.1().BC≈0.918+0.15m.1.1 的距离约是A到底面CD答:端点E. .解:如图,过点A作AE⊥CD于点17CD tanRt∠CBD在=△BCD中,∵,BD tan3BD. °=60=BD·∴CDCE tanRt,∠在CAE△ACE中,∵=AE3tantan BD. 30=AE·30°=BD·°=∴CE3 AB,-∵CDCE=3 =42,-即3BDBD3∴BD=21 3.).=3BD=63(米∴CD 63米.答:?号楼的高度CD为AE sinRt AOE中,45(1)不会.理由:如图,过点A作AE⊥OC于点E.在°=△.解:18OA2 .千米×)∴AE==60 260(2 50千米,∵60千米> A市不会受到此台风的影响.∴F.BF⊥OC于点(2)会.如图,过点B作Rt°,°=°-1530△BOF中,∵∠BOF=45在BF sin30°=,OB1 .40(BF=80×=千米)∴ 2 千米,∵40千米<50 市会受到台风的影响.∴B Rt40千米,H.在=△BGF中,∵BF,千米为半径作圆交如图,以B为圆心,50OC于点G22=30(千米).∴50GF=-40 30=千米.同理,FH )时,1.5(406060GH∴=千米,÷=小时.∴1.5B市受到台风影响的时间为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23章 解直角三角形一、选择题(每小题4分,共40分) 1.在△ABC 中,∠C =90°,若sin A =22,则sin B 等于( ) A. 12B.22 C. 32D .1 2.如图23-Z -1,在Rt △ABC 中,斜边AB 的长为m ,∠A =35°,则直角边AC 的长是( ) A .m ·sin35° B .m ·cos35°C. m sin35°D. m cos35°图23-Z -13.△ABC 在网格中的位置如图23-Z -2所示(每个小正方形的边长为1),AD ⊥BC 于点D ,下列选项中,错误..的是( ) A .sin α=cos α B .tan ∠ACD =2C .sin β=cos βD .tan α=1图23-Z -24.在△ABC 中,∠A ,∠B ,∠C 的对边分别为a ,b ,c .若a =3,b =4,c =5,则tan A 的值是( )A. 34B. 43C. 35D. 455.下列式子中不成立的是( ) A. 2cos45°=2sin30° B .sin30°×cos60°=12sin 245°C .cos45°-sin45°=0D .sin(30°+30°)=sin30°+sin30°6.如图23-Z -3,已知45°<∠A <90°,则下列各式中成立的是( ) A .sin A =cos A B .sin A >cos A C .sin A >tan A D .sin A <cos A图23-Z -37.在△ABC 中,∠ACB =90°,sin A =35,D 是AB 的中点,则 tan ∠BCD + tan ∠ACD 等于( )A. 2512B. 75C. 43D. 838.在平面直角坐标系中,点A 的坐标为(0,3),点B 在x 轴上,且sin ∠OAB =45,则点B 的坐标为( )A .(4,0)B .(-4,0)C .(4,0)或(-4,0)D .(5,0)或(-5,0)9.如图23-Z -4所示,小明从A 地沿北偏东30°方向走100 3 m 到B 地,再从B 地向正南方向走200 m 到C 地,此时小明离A 地( )A .60 mB .80 mC .100 mD .120 m图23-Z -410.如图23-Z -5,在等腰直角三角形ABC 中,∠C =90°,AC =6,D 是AC 上一点,若tan ∠DBA =15,则AD 的长为( )A .2 B. 3 C. 2 D .1图23-Z -5二、填空题(每小题5分,共20分)11.如图23-Z -6,在Rt △ABC 中,∠C =90°,BC =15,tan A =158,则AB =________.图23-Z -612.如图23-Z-7,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则 tan∠BCD的值是________.图23-Z-713.如图23-Z-8,在菱形ABCD中,AE⊥BC于点E,已知EC=1, cos B=513,则这个菱形的面积是________.图23-Z-814.如图23-Z-9,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,tan∠DCA=错误!,AC=8,则AB的长度是________.图23-Z-9三、解答题(共40分)15.(8分)如图23-Z-10,在△ABC中,∠A=30°,∠B=45°,AC=2 3,求AB的长.图23-Z-1016.(8分)如图23-Z-11是某小区的一个健身器材的示意图,已知BC=0.15 m,AB=2.70 m,∠BOD=70°,求端点A到底面CD的距离.(结果精确到0.1 m.参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)图23-Z-1117.(12分)如图23-Z-12,某小区①号楼与⑪号楼隔河相望.李明家住在①号楼,他很想知道⑪号楼的高度,于是他测量了一些数据.他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算⑪号楼的高度CD.图23-Z-1218.(12分)如图23-Z-13,台风中心位于点O处,并沿北偏东45°方向﹙OC方向﹚以40千米/时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60 2千米的地方有一城市A.(1)A市是否会受到此台风的影响?为什么?(2)在点O的北偏东15°方向上,距离80千米的地方还有一城市B,则B市是否会受到此台风的影响?若受到影响,请求出受到影响的时间;若不受影响,请说明理由.图23-Z-131. B2.B [解析] cos A =AC AB ,即cos 35°=ACm,∴AC =m·cos 35°.3.C [解析] 先构建直角三角形,再根据三角函数的定义,sin α=cos α=22 2=22,tan ∠ACD =21=2,sin β=cos (90°-β),故选C .4.A 5.D6.B [解析] 根据锐角的正弦值随角度的增大而增大,余弦值随角度的增大而减小判断.也可用特殊值检验.7.A [解析] 如图,由sin A =35,设BC =3k ,AB =5k.由勾股定理得AC =4k.根据直角三角形斜边上的中线等于斜边的一半,得CD =AD =BD ,∴∠BCD =∠B,∠ACD =∠A,故tan ∠BCD +tan ∠ACD =43+34=2512.8.C [解析] ①如图,点B 在x 轴的正半轴上. ∵sin ∠OAB =45,∴设OB =4x ,AB =5x ,∴由勾股定理,得32+(4x)2=(5x)2,解得x =1,∴OB =4. 则点B 的坐标是(4,0);②同理,当点B 在x 轴的负半轴上时,点B 的坐标是(-4,0). 则点B 的坐标是(4,0)或(-4,0). 9.C10.A [解析] 如图,过点D 作DE⊥AB,垂足为E.易证△ADE 为等腰直角三角形,AE =DE.在Rt △BDE 中,tan ∠DBA =DE BE =AE BE =15,所以BE =5AE.在等腰直角三角形ABC 中,∠C =90°,AC =6,由勾股定理可求出AB =6 2,所以AE = 2.在等腰直角三角形ADE 中,利用勾股定理可求出AD 的长为2.故选A .11.17 [解析] ∵tan A =BC AC ,即158=15AC ,∴AC =8.根据勾股定理,得AB =AC2+BC2=82+152=17.12.34 [解析] 在Rt △ABC 与Rt △BCD 中,∵∠A +∠B=90°,∠BCD +∠B=90°,∴∠A =∠BCD.∴tan ∠BCD =tan A =BC AC =68=34.故答案为34.13.3916 [解析] 设BE =5x ,由cos B =513,得AB =13x ,AE =12x ,则13x =5x +1,解得x =18.所以菱形的面积=BC·AE=13x·12x=3916. 14.6 [解析] 由题意,得∠DCA=∠DAC=∠ACB.在Rt △ABC 中求解.15.解:如图,过点C 作CD⊥AB 于点D ,则∠ADC=∠BDC=90°. ∵∠B =45°,∴∠BCD =∠B=45°,∴CD =BD.∵∠A =30°,AC =2 3, ∴CD =3,∴BD =CD = 3.由勾股定理得AD =AC2-CD2=3, ∴AB =AD +BD =3+ 3.16.解:如图,过点A 作AE⊥直线CD 于点E ,过点B 作BF⊥AE 于点F. ∵OD ⊥CD ,∠BOD =70°,∴AE ∥OD , ∴∠A =∠BOD=70°.在Rt △ABF 中,∵AB =2.7,∴AF =2.7×cos 70°≈2.7×0.34=0.918(m ),∴AE =AF +BC≈0.918+0.15=1.068≈1.1(m ).答:端点A 到底面CD 的距离约是1.1 m .17.解:如图,过点A 作AE⊥CD 于点E. 在Rt △BCD 中,∵tan ∠CBD =CDBD ,∴CD =BD·tan 60°=3BD. 在Rt △ACE 中,∵tan ∠CAE =CEAE ,∴CE =AE·tan 30°=BD·tan 30°=33BD. ∵CD -CE =AB , 即3BD -33BD =42, ∴BD =21 3.∴CD =3BD =63(米).答:⑪号楼的高度CD 为63米.18.解:(1)不会.理由:如图,过点A 作AE⊥OC 于点E.在Rt △AOE 中,sin 45°=AEOA ,∴AE =60 2×22=60(千米). ∵60千米>50千米,∴A 市不会受到此台风的影响.(2)会.如图,过点B 作BF⊥OC 于点F.在Rt △BOF 中,∵∠BOF =45°-15°=30°,sin 30°=BF OB,∴BF =80×12=40(千米).∵40千米<50千米,∴B 市会受到台风的影响.如图,以B 为圆心,50千米为半径作圆交OC 于点G ,H.在Rt △BGF 中,∵BF =40千米, ∴GF =502-402=30(千米). 同理,FH =30千米.∴GH =60千米,60÷40=1.5(时),∴B 市受到台风影响的时间为1.5小时.。
