2.4公园有多宽
2.4公园有多宽

2.4公园有多宽教学目标:知识与技能目标1.会估算一个无理数的大致范围;2.会比较两个无理数的大小;3.会利用估算解决一些简单的实际问题.过程与方法目标经历实际问题的解决过程和平方根、立方根的估算过程,发展估算意识和数感.情感与态度目标体会数学知识的实用价值,激发学生的学习热情.教学重点:能估计一个无理数的大致范围.教学难点:掌握估算方法,形成估算意识,培养学生用估算法比较大小及解决实际问题.教法和学法:采用教师引导,学生小组合作交流,让学生经历“独立探究—合作交流—总结归纳—反思应用”.教具和学具:教具:多媒体课件学具:计算器教学过程:新课导入师:投影展示:某市开辟了一块长方形的荒地用来建一个以环保为主题的公园.已知这块地的长是宽的两倍,它的面积为400000平方米.此时公园的宽是多少?由此情境情境引出本节课的学习内容――2.4公园有多宽.(板书课题)继续展示::师:公园的宽有1000米吗?生:思考回答(没有)师:那么怎么计算出公园的宽呢?(要求误差小于10米)师:解:设公园的宽为x米,则它的长为2x米,由题意得:生:x·2x=400000,22x=400000,x.=?师:为了能很好的解决这个问题,首先我们一起来研究下边这个例子.设计意图:通过这些问题让学生从现实情境引入,初步建立数感,让学生体会生活中的数学,激发学习的积极性师:投影展示:下列结果正确吗?你是怎样判断的?与同伴交流.20 ; ②0.3;500; ④96.师:让学生说出自己的想法.生:这些结果都不正确.师:怎样估算一个无理数的范围?你能估算它们的大小吗?说出你的方法.误差小于1) ②误差小于1)师:解: ① ∵62<40<72∴∴误差小于16或7仿照老师的解法你能解决第②小题吗?师:仿照老师的解法解决第②小题.师:与同伴间进行交流,归纳出估算的方法. 师生共同总结师:你能解决公园有多宽?这个问题了吗?来尝试一下生:解决上述问题设计意图:同伴间进行交流,教师适时引导.在解决问题的同时引导学生对解决方法进行总结,和学生一起归纳出估算的方法.师:以上我们一起学习了估算,你能用学到的知识解决下边的问题吗?投影展示:例1 你能比较12与12的大小吗?你是怎样想的? 生:思考师:展示:小明是这样想的:12与12>2>1,12>12. 师:你还有其它的办法吗?引导学生回答并板书解题过程:解:∵5>4,2>22,2,>1,即12>12. 师:投影展示:例2画能挂上去吗?生活表明,靠墙摆放梯子时,若梯子底端离墙距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6米的梯子,当梯子稳定摆放时,(1)他的顶端最多能到达多高(使误差小于0.1米)?(2)现在如果请一个同学利用这个梯子在墙高5.9米的地方张贴一副宣传画,他能能挂上去吗?生:解:设梯子稳定摆放时的高度为x 米,此时梯子底端离墙恰好为梯子长度的13,根据勾股定理 :2x +(13×6)2=62, 2x +4=36,2x =32 ,∵25<2x <36,∴5<x <6,∵ 5.62< 2x <5.72,∴ 5.6<x <5.7,∴x 约为5.6米或5.7米.师:他能能挂上去吗?生:思考回答 能师:5.6比5.9小呀,怎么能挂上呢? 613×6 x生:还有人的臂长呢.师:这位同学回答的很好,他很会联系实际,希望大家向他学习!设计意图:让学生从被动学习到主动探究,激发学生的学习热情,培养学生自主学习数学的能力. 在解决实际问题中再次体会估算的方法,从而体验到学习数学的乐趣.小结:师:通过本节课的学习你有什么收获呢?能给大家分享一下你的收获吗?生:学生说出自己的收获,与大家共享设计意图:让学生及时小结,帮助教师反思本节课教学设计的不足,及时做出后面教学的调整.师:那好现在就用我们学到的知识来解决下边几道小题,请大家独立完成 .投影展示1.估算下列数的大小.(10.1) ; (21).2. 通过估算,比较下面各数的大小.(1)12与12; (2 3.85. 3.一个人一生平均要饮用的液体总量大约为40立方米 ,如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高(误差小于1米)?布置作业:习题2.6 1,3,及助学的本节内容板书设计:教学反思:本节课的教学中选取了“修建环保公园”的问题情境引入,与学生平时的生活密切联系,容易把学生的积极性调动起来.注重适时的引导,以免让学生无从下手. 侧重了让学生体会估算的实用价值,从而让学生体会到了数学的学习价值. 作为教师,一定要尊重学生的个体差异,满足多样化的学习需要,鼓励探究方式、表达方式和解题方法的多样化,对学生提出的问题和回答要给于积极的评价.。
八年级数学上册《2.4 公园有多宽》教学设计

公园有多宽一、教学内容与分析:(一)内容:估算一个无理数的大致范围,比较两个无理数的大小,利用估算解决一些简单的实际问题.(二)分析:用估算的方式确信数的平方根和立方根,把被开方数放在相近的两个平方数(立方数)之间,在依照要求估算。
二、教学目标与分析:(一)目标:会估算一个无理数的大致范围,比较两个无理数的大小,会利用估算解决一些简单的实际问题.(二)分析:估算一个无理数,确信误差到哪一名,即估算到哪一名,它与精准到哪一名不同。
三、教学支持条件分析:四、问题诊断分析:本节中学生可能显现的问题是对实际问题数据的处置,关于估算一个无理数关于实际问题要具体分析。
五、教学进程:(一)情境引入由修建环保公园的实际问题情境引出本节课的学习内容――公园有多宽.某市开辟了一块长方形的荒地用来建一个以环保为主题的公园.已知这块地的长是宽的两倍,它的面积为400000平方米.现在公园的宽是多少?长是多少?给出那个问题情境,先让学生凭感觉说出公园的长和宽别离是多少.给出引导问题:公园的宽有1000米吗?(没有)那么怎么计算出公园的长和宽.解:设公园的宽为x米,那么它的长为2x米,由题意得:x·2x=400000,2x2=400000,x200000.200000=?(二)活动探讨1.探讨一个无理数估算结果的合理性.2.学会估算一个无理数的大致范围.例1 以下结果正确吗?你是如何判定的?与同伴交流.①40≈20 ; ②0.9≈0.3;③100000≈500; ④3900≈96.解答:这些结果都不正确.如何估算一个无理数的范围?例2你能估算它们的大小吗?说出你的方式.①40; ②0.9; ③100000; ④3900.(①②误差小于0.1;③误差小于10;④误差小于1.)解答:40≈6.3 ;0.9≈0.9; 100000≈310 ; 3900≈9.(三)深切探讨1.用估算来解决数学和实际问题.例1 你能比较51与12的大小吗?你是如何想的?小明是如此想的:512与12的分母相同,只要比较他们的分子就能够够了,即512>12.例2 解决引入时“公园有多宽?”的问题情境中提出的问题.200000=?(1)若是要求误差小于10米,它的宽大约是?(大约440米或450米)(2)该公园中心有一个圆形花园,它的面积是800平方米,你能估量它的半径吗(误差小于1米)?(15米或16米)例3 给出新的问题情境——画能挂上去吗?生活说明,靠墙摆放梯子时,假设梯子底端离墙距离为梯子长度的三分之一,那么梯子比较稳固.现有一长度为6米的梯子,当梯子稳固摆放时,(1)他的顶端最多能抵达多高(保留到0.1)?(2)此刻若是请一个同窗利用那个梯子在墙高5.9米的地址张贴一副宣传画,他能办到吗?解:设梯子稳固摆放时的高度为x米,现在梯子底端离墙恰好为梯子长度的13,依照勾股定理:2x+(13×6)2=62,2x+4=36,2x=32,x32即∵5〈x<6,25<2x<36,5.6<x<5.7,31.36< 2x<32.49,x≈5.6.1 估算以下数的大小.(113.60.1); (238001).解答:(1)∵3.613.6 3.7,13.6 3.6或3.7(只若是3.6与3.7之间的数都能够).(2)∵9<3800<10,∴3800≈9或10(只若是9与10之间的数都能够).2 通过估算,比较下面各数的大小.(1)312与12; (2)15与3.85.解答:(1)∵3<2, (2)∵3.852=14.8225,∴15>3.85. ∴15>3.85.∴3-1<1,即312<12.3 、给出与生活紧密联系的实际问题情境一个人一生平均要饮用的液体总量大约为40立方米,若是用一圆柱形的容器(底面直径等于高)来装这些液体,那个容器大约有多高(误差小于1米)?六、课时小结:本节课你学到了哪些知识?一、估算:误差小于多少就估算到哪一名,先确信位数,由高位到低位按序进行估算。
公园设计规范【完整版】

第一章总则第1.0.1条为全面地发挥公园的游憩功能和改善环境的作用,确保设计质量,制定本规范。
第1.0.2条本规范适用于全国新建、扩建、改建和修复的各类公园设计。
居住用地、公共设施用地和特殊用地中的附属绿地设计可参照执行。
第1.0.3条公园设计应在批准的城市总体规划和绿地系统规划的基础上进行。
应正确处理公园与城市建设之间,公园的社会效益、环境效益与经济效益之间以及近期建设与远期建设之间的关系。
第1.0.4条公园内各种建筑物、构筑物和市政设施等设计除执行本规范外,尚应符合现行有关标准的规定。
第二章一般规定第一节与城市规划的关系第2.1.1条公园的用地范围和性质,应以批准的城市总体规划和绿地系统规划为依据。
第2.1.2条市、区级公园的范围线应与城市道路红线重合,条件不允许时,必须设通道使主要出入口与城市道路衔接。
第2.1.3条公园沿城市道路部分的地面标高应与该道路路面标高相适应,并采取措施,避免地面迳流冲刷、污染城市道路和公园绿地。
第2.1.4条沿城市主、次干道的市、区级公园主要出入口的位置,必须与城市交通和游人走向、流量相适应,根据规划和交通的需要设置游人集散广场。
第2.1.5条公园沿城市道路、水系部分的景观,应与该地段城市风貌相协调。
第2.1.6条城市高压输配电架空线通道内的用地不应按公园设计。
公园用地与高压输配电架空线通道相邻处,应有明显界限。
第2.1.7条城市高压输配电架空线以外的其他架空线和市政管线不宜通过公园,特殊情况时过境应符合下列规定:一、选线符合公园总体设计要求;二、通过乔、灌木种植区的地下管线与树木的水平距离符合附录二的规定;三、管线从乔、灌木设计位置下部通过,其埋深大于1.5m,从现状大树下部通过,地面不得开槽且埋深大于3m。
根据上部荷载,对管线采取必要的保护措施;四、通过乔木林的架空线,提出保证树木正常生长的措施。
第二节内容和规模第2.2.1条公园设计必须以创造优美的绿色自然环境为基本任务,并根据公园类型确定其特有的内容。
北师大版八年级数学教案-实数-公园有多宽-计算器开方
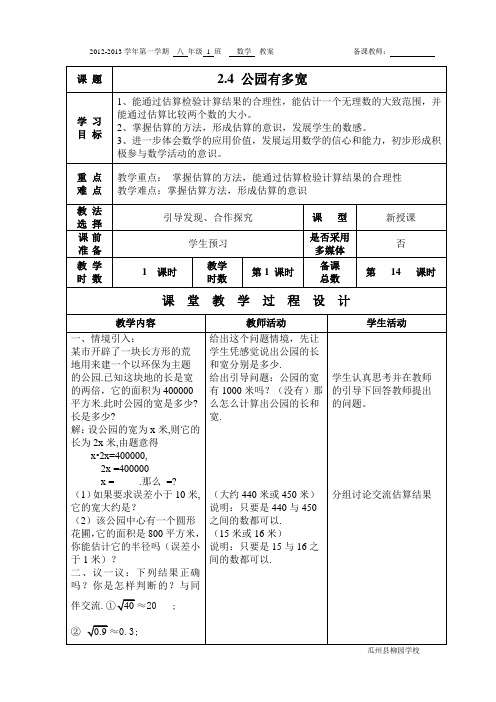
课题 2.4 公园有多宽学习目标1、能通过估算检验计算结果的合理性,能估计一个无理数的大致范围,并能通过估算比较两个数的大小。
2、掌握估算的方法,形成估算的意识,发展学生的数感。
3、进一步体会数学的应用价值,发展运用数学的信心和能力,初步形成积极参与数学活动的意识。
重点难点教学重点:掌握估算的方法,能通过估算检验计算结果的合理性教学难点:掌握估算方法,形成估算的意识教法选择引导发现、合作探究课型新授课课前准备学生预习是否采用多媒体否教学时数1 课时教学时数第1 课时备课总数第14 课时课堂教学过程设计教学内容教师活动学生活动一、情境引入:某市开辟了一块长方形的荒地用来建一个以环保为主题的公园.已知这块地的长是宽的两倍,它的面积为400000平方米.此时公园的宽是多少?长是多少?解:设公园的宽为x米,则它的长为2x米,由题意得x•2x=400000,2x =400000x = .那么=? (1)如果要求误差小于10米,它的宽大约是?(2)该公园中心有一个圆形花圃,它的面积是800平方米,你能估计它的半径吗(误差小于1米)?二、议一议:下列结果正确吗?你是怎样判断的?与同伴交流.①40≈20 ;②0.9≈0.3; 给出这个问题情境,先让学生凭感觉说出公园的长和宽分别是多少.给出引导问题:公园的宽有1000米吗?(没有)那么怎么计算出公园的长和宽.(大约440米或450米)说明:只要是440与450之间的数都可以.(15米或16米)说明:只要是15与16之间的数都可以.学生认真思考并在教师的引导下回答教师提出的问题。
分组讨论交流估算结果③100000≈500;④3900≈96.三、例1:生活表明,靠墙摆放梯子时,若梯子底端离墙距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6米的梯子,当梯子稳定摆放时,他的顶端最多能到达多高(保留到0.1)设梯子稳定摆放时的高度为x 米,此时梯子底端离墙的距离恰为梯子长度的,根据勾股定理有四、你能比较512-与12的大小吗?你是怎样想的?五、随堂练习1.估算下列数的大小:(1)6.13(误差小于0.1)(2)3800(误差小于1)2.估算比较6与2.5的大小.六、小结:你的收获?你得到怎样的启发?教师讲解并板书:x2+(31×6)2=62即x2=32,x=32因为5.62=31.36<32所以32>5.6因此,梯子稳定摆放时,它的顶端能够达到5.6米高的墙教师组织学生讨论交流如何比较大小出示练习,组织学生练习,在运算、交流形成共识后,教师要学生完成。
2_4估算

§2.4估算学习目标:能通过估算检验计算结果的合理性,能估计一个无理数的大致范围,并能通过估算比较两个数的大小;掌握估算的方法,形成估算的意识.学习重点:按要求估算一个无理数的范围,并比较两个无理数的大小.学习难点:估算时精确度的取舍.的长是宽的两倍,它的面积为400000平方米.此时公园的宽是多少?长是多少?请思考:公园的宽有1000米吗?2.阅读课本第33~34页的内容,在书上尝试写出问题的答案.二、课堂研学1.探究活动(一):例1 下列结果准确吗?你是怎样判断的?与同伴交流.≈20 ;②≈0.3;500;④96.想一想:怎样估算一个无理数的范围?2.探究活动(二):例2 你能估算它们的大小吗?说出你的方法.;;0.1).归纳小结:估算无理数的方法是:首先,通过平方或者立方运算,采用“夹逼法”,确定真值所在范围;其次,根据问题中误差允许的范围,在真值所在的范围内取出近似值.3.探究活动(三):例3:你能比较512与12的大小吗?你是怎样想的? 巩固练习:通过估算,比较下列各组数的大小.;与)(5.12161+ (2)1.2263与.解:(1),__________216____,6,4__6,4__6+∴∴∴ 。
即:______216+ (2)归纳:比较无理数与有理数的大小时要先估算出无理数的近似值,再比较无理数与有理数的大小关系.4.学习应用例4:生活经验表明,靠墙摆放梯子时,若梯子底端离墙距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6米的梯子,当梯子稳定摆放时,它的顶端能达到5.6m 高的墙头吗?5.学习小结:--------------------------------------------------------------------四、课堂小测1. 估算下列数的大小.(1)13.6(误差小于0.1) ; (2)3800(误差小于1).2.通过估算,比较下面各数的大小.(1312与12; (2 3.85.3. 写出所有大于-2且小于5的整数:______________________4.=? (1)如果要求误差小于10米,它的宽大约是多少?(2)该公园中心有一个圆形花圃,它的面积是800平方米,你能估计它的半径吗(精确到1米)?五、学习反思--------------------------------------------------------------------六、课后作业1.课本P34: 习题2.62.《导学全程练》P :。
2.4估算

x 3 160 ,
∴X ≈ 4 .
第25页,共39页。
课堂小结
1、估算无理数大小的方法:
(1)利用乘方与开方互为逆运算来确定无理数的
整数部分;
(2)根据所要求的误差确定小数部分。 2.比较两数的大小:
(1)数轴比较
(2)平方比较法 (3)夹逼估算法 (4)作差或作商比较法
第26页,共39页。
比较大小的方法 利用数轴比较
32 12.5的整数部分是3
3.52 12.5 3.62
3.5 12.5 3.6 所以 12.5的估算值是3.5或3.6
注意:误差小于0.1就是指估算出来的值与准确值
之间的差的绝对值小于0.1 第7页,共39页。
1.新知探究
Ⅱ、怎样估算无理数 3 2000(误差小于1)? (3 2000)3 2000
随着开方次数的增加,运算结果越来越接近1。
(2)改用另一个小于1的正数试一试,看看是否仍有类
似的规律。
有
第36页,共39页。
想一想
借助计算器求下列各式的值, 你能发现什么规律?
42 32 9 16 25 5
442 332 1089 1936 3025 55
4442 3332 110889 197136 308025 555
( 0.43)2 0.43 0.0662 0.004356
(3 900)3 900 963 884736
0.43 0.066
3 900 96
(3) 2536 60.4.
( 2536)2 2536 60.42 3648.16
精确计算
2356 60.4
第12页,共39页。
课本p 33页议一议 Ⅳ、下列计算结果正确吗?你是怎样判断的?
北师大版八年级上册数学2.4估算优质教案

2.4 估量第一环节:情境引入内容:由修筑环保公园的实质问题情境引出本节课的学习内容――公园有多宽.某市开拓了一块长方形的荒地用来建一个以环保为主题的公园.已知这块地的长是宽的两倍,它的面积为400000 平方米.此时公园的宽是多少?长是多少 ?给出这个问题情境,先让学生凭感觉说出公园的长和宽分别是多少.给出指引问题:公园的宽有1000 米吗?(没有)那么怎么计算出公园的长和宽.解:设公园的宽为x 米,则它的长为2x 米,由题意得:x·2x =400000,2x 2 =400000,x =200000 .那么200000 =?目的:从现真相境引入,一方面让学生初步成立数感,另一方面让学生领会生活中的数学从而激发学习的踊跃性.成效:学生经过与生活密切联系的问题情境初步感觉到估量的适用价值.第二环节:活动研究内容:1.研究一个无理数估量结果的合理性.2.学会估量一个无理数的大概范围.例 1 以下结果正确吗?你是如何判断的?与伙伴沟通.①40 ≈20 ;② 0.9 ≈ 0.;3③100000≈ 500;④3 900 ≈96.解答:这些结果都不正确.如何估量一个无理数的范围?例 2 你能估量它们的大小吗?说出你的方法.①40;②0.9;③100000 ;④ 3900.(①②偏差小于 0.1;③偏差小于 10;④偏差小于 1.)解答:40 ≈ 6.3;0. 9≈ 0.9;100000≈ 310;3 900 ≈9.说明:偏差小于 10 就是估量出的值与正确值之间的差的绝对值小于10,所以100000的估量值在偏差小于10 的前提下能够是310,也能够是 320,还能够是 310 到 320 之间的任何数.教材使用偏差小于10,而不用精准到哪一位,目的在于降低要求。
目的:伙伴间进行沟通,教师合时指引.在解决问题的同时指引学生对解决方法进行总结,和学生一同概括出估量的方法.让学生从被动学习到主动研究,激发学生的学习热忱,培育学生自主学习数学的能力.成效:经过简单无理数大概范围的预计,初步累积一些解决问题的经验,为接下来的实质应用做好准备.第三环节:深入研究内容:用估量来解决数学的实质问题.例 1你能比较5 - 1与1的大小吗?你是如何想的?22小明是这样想的:5 - 1与1的分母同样,只需比较他们的分子就能够了,22由于 5 >2,因此 5 -1>1,5- 1>1.22解:∵ 5> 4,即(5)2>22,∴ 5 >2,5-1>1,即 5- 1>1.2 2例 2 解决引入时“公园有多宽?”的问题情境中提出的问题.200000 =?( 1)假如要求偏差小于10 米,它的宽大概是?(大概 440 米或 450 米)说明:只假如 440 与 450 之间的数都能够.800 平方米,你能预计它的半径( 2)该公园中心有一个圆形花园,它的面积是吗(偏差小于 1 米)?(15 米或 16 米)说明:只假如 15 与 16 之间的数都能够.例 3给出新的问题情境——画能挂上去吗?生活表示,靠墙摆放梯子时,若梯子底端离墙距离为梯子长度的三分之一,则梯子比较稳固.现有一长度为 6 米的梯子,当梯子稳固摆放时,(1)他的顶端最多能抵达多高(保存到 0.1)?(2)此刻假如请一个同学利用这个梯子在墙高 5.9 米的地方张贴一副宣传画,他能办到吗?解:设梯子稳固摆放时的高度为x 米,此时梯子底端离墙恰巧为梯子长度的 1 ,3依据勾股定理:,212 2x +(3×6) =62x +4=36,2x =32 ,x=32 ,由于 5.6231.3632由于 5.7 232.4932因此画不可以挂上去目的:学生经过独立思虑与小组议论相联合的方式解决新的实质问题,让学生初步领会数学知识的实质应用价值.成效:在解决实质问题中再次领会估量的方法,从而体验到学习数学的乐趣.第四环节:反应练习内容:反应练习 1估量以下数的大小.( 1)13.6 (偏差小于 0.1);(2)3800(偏差小于1).解答:(1)∵3.6< 13.6 <3.7,∴13.6 ≈3.6或 3.7(只假如 3.6 与 3.7 之间的数都能够).(2)∵9<3 800<10,∴3 800 ≈9或 10(只假如 9 与 10 之间的数都能够).反应练习 2 经过估量,比较下边各数的大小.(1)3- 1与1;()与 3.85.22215解答:(1)∵3<2,∴ 3 -1<1,即 3- 1<1.2 2(2)∵ 3.85 2 =14.8225,∴15 > 3.85.反应练习 3给出与生活亲密联系的实质问题情境一个人一世均匀要饮用的液体总量大概为40 立方米,假如用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大概有多高(偏差小于1米)?目的:教课指引学生解决问题,学生经过独立思虑和与伙伴合作沟通的方式解决提出的问题,让学生再次领会估量的方法和估量的实质应用,调换研究的踊跃性.成效:进一步激发学生对利用估量的方法解决问题的兴趣,调换学生学习数学的热情.第五环节:反省概括内容:1.用自己的语言表达学习这节内容的感想(1)经过这节课的学习,你掌握了哪些知识?(2)经过学习这些知识,对你有如何的启迪?(3)关于这节课的学习,你还有哪些疑问?2.阅读给出的知识点概括.目的:指引学生概括本节的基本内容,让学生实时小结,教师展告知识脉络图并反思本节课教课方案的不足,实时做出后边教课的调整.成效:部分学生能勇敢地提出疑问.第六环节:作业稳固内容:习题 2.6 1,2,3,6目的:给出作业内容,学生阅读给出的作业.成效:让学生在练习中实时稳固所学知识.四、教课方案反省(一)突出要点、打破难点的策略“公园有多宽”这节内容是让学生掌握估量的方法,训练他们的估量能力,而学生在生活中接触用估量解决实质问题的状况比较少,因此比较陌生,从而学习起来难度就比较大。
公园设计规范【完整版】

公园设计规范第一章总则第1.0.1条为全面地发挥公园的游憩功能和改善环境的作用,确保设计质量,制定本规范。
第1.0.2条本规范适用于全国新建、扩建、改建和修复的各类公园设计。
居住用地、公共设施用地和特殊用地中的附属绿地设计可参照执行。
第1.0.3条公园设计应在批准的城市总体规划和绿地系统规划的基础上进行。
应正确处理公园与城市建设之间,公园的社会效益、环境效益与经济效益之间以及近期建设与远期建设之间的关系。
第1.0.4条公园内各种建筑物、构筑物和市政设施等设计除执行本规范外,尚应符合现行有关标准的规定。
第二章一般规定第一节与城市规划的关系第2.1.1条公园的用地范围和性质,应以批准的城市总体规划和绿地系统规划为依据。
第2.1.2条市、区级公园的范围线应与城市道路红线重合,条件不允许时,必须设通道使主要出入口与城市道路衔接。
第2.1.3条公园沿城市道路部分的地面标高应与该道路路面标高相适应,并采取措施,避免地面迳流冲刷、污染城市道路和公园绿地。
第2.1.4条沿城市主、次干道的市、区级公园主要出入口的位置,必须与城市交通和游人走向、流量相适应,根据规划和交通的需要设置游人集散广场。
第2.1.5条公园沿城市道路、水系部分的景观,应与该地段城市风貌相协调。
第2.1.6条城市高压输配电架空线通道内的用地不应按公园设计。
公园用地与高压输配电架空线通道相邻处,应有明显界限。
第2.1.7条城市高压输配电架空线以外的其他架空线和市政管线不宜通过公园,特殊情况时过境应符合下列规定:一、选线符合公园总体设计要求;二、通过乔、灌木种植区的地下管线与树木的水平距离符合附录二的规定;三、管线从乔、灌木设计位置下部通过,其埋深大于1.5m,从现状大树下部通过,地面不得开槽且埋深大于3m。
根据上部荷载,对管线采取必要的保护措施;四、通过乔木林的架空线,提出保证树木正常生长的措施。
第二节内容和规模第2.2.1条公园设计必须以创造优美的绿色自然环境为基本任务,并根据公园类型确定其特有的内容。
新疆库车大峡谷地质公园资源调查评价

图 1 库车大峡谷地质公园交通位置图新疆库车大峡谷地质公园资源调查评价刘一玲(四川省地矿局区域地质调查队,四川 双流 610213)摘要:位于古代西域之龟兹国所在地的新疆库车大峡谷地质公园,地貌极具科学价值和视觉震憾力,其中的大小龙池是南天山不可多得的高山湖泊景观;库车河剖面是横跨天山的梦幻之道,是南天山造山带的天然博物馆;著名的西域冶炼中心,是南天山的聚宝盆。
公园蕴含塞上风光、戊边道与商旅、佛教遗址交织的古龟兹文明绚丽夺目,它与公园内的地质遗迹景观紧密联系,相映成辉。
关键词:新疆库车;地质公园;库车大峡谷;库车地貌;龟兹新疆库车大峡谷地质公园拥有以天山神秘大峡谷为代表的库车地貌景观、大小龙池第四纪冰川地貌 景观、火山岩峰丛景观、地质剖面、汉唐冶炼遗址等,地质景观丰富多彩,与古老龟兹文明相映成辉。
优良的自然生态系统、稳定的社会环境,优越的区位条件,其开发潜力巨大。
1 地质背景库车大峡谷地质公园位于古龟兹国之地,行政隶属新疆维吾尔自治区阿克苏地区库车县,沿库车河 谷(国道 217)分布有三个景区——大龙池景区、天山神秘大峡谷景区、屈勒塔格山景区,三者组成的串 珠式公园,总面积 502 km 2。
在地质演化上,早二叠世末的晚海西构造运动是本区最为强烈的一次构造运动,它结束了塔北和南天山广大地区的海侵历史。
随着南天山局限洋盆的关闭,塔里木坂块向南天山发生 A 型俯冲,形成的南天山褶皱增生带不断向南挤压,于海西晚期在造山带边缘发育成为近东西向延伸的前陆盆地。
根据盆地的发展、演化特征及沉积充填序列,大致可划分为五个亚阶段,即晚二叠世~三叠世、侏罗纪、早白垩世、古近纪和新近纪~第四纪。
多期次的构造地质作用,无疑造就了公园举世罕见的地质奇观。
公园地质遗迹景观类型有地质地貌(库车地貌、冰川地貌、火山岩峰丛、雅丹地貌)、地质剖面、古代冶炼遗址、地质灾害遗迹、水 体景观、工程地质等 6 大类 21 中类,其中以库车地貌、地质剖面、冰川地貌、火山岩峰丛与古代冶炼遗 址最具震慑性。
公园设计规范【完整版】

第一章总则第1.0.1条为全面地发挥公园的游憩功能和改善环境的作用,确保设计质量,制定本规范。
第1.0.2条本规范适用于全国新建、扩建、改建和修复的各类公园设计。
居住用地、公共设施用地和特殊用地中的附属绿地设计可参照执行。
第1.0.3条公园设计应在批准的城市总体规划和绿地系统规划的基础上进行。
应正确处理公园与城市建设之间,公园的社会效益、环境效益与经济效益之间以及近期建设与远期建设之间的关系。
第1.0.4条公园内各种建筑物、构筑物和市政设施等设计除执行本规范外,尚应符合现行有关标准的规定。
第二章一般规定第一节与城市规划的关系第2.1.1条公园的用地范围和性质,应以批准的城市总体规划和绿地系统规划为依据。
第2.1.2条市、区级公园的范围线应与城市道路红线重合,条件不允许时,必须设通道使主要出入口与城市道路衔接。
第2.1.3条公园沿城市道路部分的地面标高应与该道路路面标高相适应,并采取措施,避免地面迳流冲刷、污染城市道路和公园绿地。
第2.1.4条沿城市主、次干道的市、区级公园主要出入口的位置,必须与城市交通和游人走向、流量相适应,根据规划和交通的需要设置游人集散广场。
第2.1.5条公园沿城市道路、水系部分的景观,应与该地段城市风貌相协调。
第2.1.6条城市高压输配电架空线通道内的用地不应按公园设计。
公园用地与高压输配电架空线通道相邻处,应有明显界限。
第2.1.7条城市高压输配电架空线以外的其他架空线和市政管线不宜通过公园,特殊情况时过境应符合下列规定:一、选线符合公园总体设计要求;二、通过乔、灌木种植区的地下管线与树木的水平距离符合附录二的规定;三、管线从乔、灌木设计位置下部通过,其埋深大于1.5m,从现状大树下部通过,地面不得开槽且埋深大于3m。
根据上部荷载,对管线采取必要的保护措施;四、通过乔木林的架空线,提出保证树木正常生长的措施。
第二节内容和规模第2.2.1条公园设计必须以创造优美的绿色自然环境为基本任务,并根据公园类型确定其特有的内容。
中华人民共和国行业标准 公园设计规范

中华人民共和国行业标准公园设计规范主编单位:北京市园林局批准部门:中华人民共和国建设部施行日期:1993年1月1日第一章总则第1.0.1条为全面地发挥公园的游憩功能和改善环境的作用,确保设计质量,制定本规范。
第1.0.2条本规范适用于全国新建、扩建、改建和修复的各类公园设计。
居住用地、公共设施用地和特殊用地中的附属绿地设计可参照执行。
第1.0.3条公园设计应在批准的城市总体规划和绿地系统规划的基础上进行。
应正确处理公园与城市建设之间,公园的社会效益、环境效益与经济效益之间以及近期建设与远期建设之间的关系。
第1.0.4条公园内各种建筑物、构筑物和市政设施等设计除执行本规范外,尚应符合现行有关标准的规定。
第二章一般规定第一节与城市规划的关系第2.1.1条公园的用地范围和性质,应以批准的城市总体规划和绿地系统规划为依据。
第2.1.2条市、区级公园的范围线应与城市道路红线重合,条件不允许时,必须设通道使主要出入口与城市道路衔接。
第2.1.3条公园沿城市道路部分的地面标高应与该道路路面标高相适应,并采取措施,避免地面迳流冲刷、污染城市道路和公园绿地。
第2.1.4条沿城市主、次干道的市、区级公园主要出入口的位置,必须与城市交通和游人走向、流量相适应,根据规划和交通的需要设置游人集散广场。
第2.1.5条公园沿城市道路、水系部分的景观,应与该地段城市风貌相协调。
第2.1.6条城市高压输配电架空线通道内的用地不应按公园设计。
公园用地与高压输配电架空线通道相邻处,应有明显界限。
第2.1.7条城市高压输配电架空线以外的其他架空线和市政管线不宜通过公园,特殊情况时过境应符合下列规定:一、选线符合公园总体设计要求;二、通过乔、灌木种植区的地下管线与树木的水平距离符合附录二的规定;三、管线从乔、灌木设计位置下部通过,其埋深大于1.5m,从现状大树下部通过,地面不得开槽且埋深大于3m。
根据上部荷载,对管线采取必要的保护措施;四、通过乔木林的架空线,提出保证树木正常生长的措施。
公园设计规范(设计必备)含图

公园设计规范第一章总则第1.0.1条为全面地发挥公园的游憩功能和改善环境的作用,确保设计质量,制定本规范。
第1.0.2条本规范适用于全国新建、扩建、改建和修复的各类公园设计。
居住用地、公共设施用地和特殊用地中的附属绿地设计可参照执行。
第1.0.3条公园设计应在批准的城市总体规划和绿地系统规划的基础上进行。
应正确处理公园与城市建设之间,公园的社会效益、环境效益与经济效益之间以及近期建设与远期建设之间的关系。
第1.0.4条公园内各种建筑物、构筑物和市政设施等设计除执行本规范外,尚应符合现行有关标准的规定。
第二章一般规定第一节与城市规划的关系第2.1.1条公园的用地范围和性质,应以批准的城市总体规划和绿地系统规划为依据。
第2.1.2条市、区级公园的范围线应与城市道路红线重合,条件不允许时,必须设通道使主要出入口与城市道路衔接。
第2.1.3条公园沿城市道路部分的地面标高应与该道路路面标高相适应,并采取措施,避免地面迳流冲刷、污染城市道路和公园绿地。
第2.1.4条沿城市主、次干道的市、区级公园主要出入口的位置,必须与城市交通和游人走向、流量相适应,根据规划和交通的需要设置游人集散广场。
第2.1.5条公园沿城市道路、水系部分的景观,应与该地段城市风貌相协调。
第2.1.6条城市高压输配电架空线通道内的用地不应按公园设计。
公园用地与高压输配电架空线通道相邻处,应有明显界限。
第2.1.7条城市高压输配电架空线以外的其他架空线和市政管线不宜通过公园,特殊情况时过境应符合下列规定:一、选线符合公园总体设计要求;二、通过乔、灌木种植区的地下管线与树木的水平距离符合附录二的规定;三、管线从乔、灌木设计位置下部通过,其埋深大于1.5m,从现状大树下部通过,地面不得开槽且埋深大于3m。
根据上部荷载,对管线采取必要的保护措施;四、通过乔木林的架空线,提出保证树木正常生长的措施。
第二节内容和规模第2.2.1条公园设计必须以创造优美的绿色自然环境为基本任务,并根据公园类型确定其特有的内容。
CJJ48-92公园设计规范

公园设计规范名称:公园设计规范CJJ48—92主编单位:北京市园林局批准部门:中华人民共和国建设部施行日期:1993年1月1日关于发布行业标准《公园设计规范》的通知建标〔1992〕384号各省、自治区、直辖市建委(建设厅),计划单列市建委,国务院有关部门:根据建设部建标〔1991〕413号文的要求,由北京市园林局主编的《公园设计规范》,业经审查,现批准为行业标准,编号CJJ48—92,自一九九三年一月一日起施行。
本标准由建设部城镇建设标准技术归口单位建设部城市建设研究院归口管理,由北京市园林局负责解释,由建设部标准定额研究所组织出版。
中华人民共和国建设部1992年6月18日第一章总则第1.0.1条为全面地发挥公园的游憩功能和改善环境的作用,确保设计质量,制定本规范。
第1.0.2条本规范适用于全国新建、扩建、改建和修复的各类公园设计。
居住用地、公共设施用地和特殊用地中的附属绿地设计可参照执行。
第 1.0.3条公园设计应在批准的城市总体规划和绿地系统规划的基础上进行。
应正确处理公园与城市建设之间,公园的社会效益、环境效益与经济效益之间以及近期建设与远期建设之间的关系。
第1.0.4条公园内各种建筑物、构筑物和市政设施等设计除执行本规范外,尚应符合现行有关标准的规定。
第二章一般规定第一节与城市规划的关系第2.1.1条公园的用地范围和性质,应以批准的城市总体规划和绿地系统规划为依据。
第2.1.2条市、区级公园的范围线应与城市道路红线重合,条件不允许时,必须设通道使主要出入口与城市道路衔接。
第 2.1.3条公园沿城市道路部分的地面标高应与该道路路面标高相适应,并采取措施,避免地面迳流冲刷、污染城市道路和公园绿地。
第2.1.4条沿城市主、次干道的市、区级公园主要出入口的位置,必须与城市交通和游人走向、流量相适应,根据规划和交通的需要设置游人集散广场。
第2.1.5条公园沿城市道路、水系部分的景观,应与该地段城市风貌相协调。
公园设计规范 GB

公园设计规范 GB本规范旨在全面发挥公园的多种功能,包括游憩、生态、景观、文化传承、科普教育、应急避险等,以及其对经济、社会和环境的效益。
为确保公园设计质量,本规范适用于城乡各类公园的新建、扩建、改建和修复的设计。
同时,公园设计也应符合国家现行的相关标准规定。
2术语2.1公园:向公众开放,以游憩为主要功能,有较完善的设施,兼具生态、美化等作用的绿地。
2.2用地比例:公园内各类用地,包括绿化用地、建筑占地、园路及铺装场地用地等,占公园陆地面积的比例。
2.3绿化用地:公园内用以栽植乔木、灌木、地被植物的用地。
2.4建筑占地:公园内各种建筑基底所占面积。
2.5水体:公园内河、湖、池、塘、水库、湿地等天然水域和人工水景的统称。
2.6公园游憩绿地:公园内可开展游憩活动的绿化用地。
2.7雨水控制利用:对雨水进行强化入渗、收集回用、降低径流污染、调蓄排放处理措施的总称。
2.8竖向控制:对公园内建设场地地形、各种设施、植物等的控制性高程的统筹安排以及与公园外高程的相互协调。
2.9郁闭度:群植乔木树冠垂直投影面积与栽植地表面积之比。
2.10自然安息角:土壤自然堆积形成的一个稳定且坡度一致的土体表面与水平面的夹角,又叫自然倾斜角。
角度的大小与土壤的土质、颗粒大小、含水量等有关系。
3基本规定3.1一般规定3.1.1公园的用地范围和类型应以城乡总体规划、绿地系统规划等上位规划为依据。
3.1.2公园设计应正确处理公园建设与城市建设之间、公园的近期建设与持续发展之间的关系。
2.服务半径应控制在250米以内,即间距不超过500米。
3.公园内的厕位数应根据游人分布密度合理设置,儿童游戏场附近应设置方便儿童使用的厕所。
同时,公园应设有无障碍设施,无障碍厕位或无障碍专用厕所的设计应符合现行国家标准《无障碍设计规范》GB 的相关规定。
3.5.4.休息座椅的设置应符合以下规定:容纳量应按游人容量的20%~30%设置,同时应考虑游人需求合理分布。
城市湿地公园的生态设计

城市湿地公园的生态设计摘要:城市湿地景观,是城市景观的重要主城部分。
本文通过对城市湿地的详细介绍和湿地景观的实例分析,笔者认为景观设计师必须在思想上树立生态观念,并在城市湿地系统景观设计中做到美学与生态兼顾,从而使自然与人类生活环境达到和谐统一。
关键词:城市湿地;景观设计;和谐Abstract: urban wetland landscape, is part of the important main city of the urban landscape. In this paper, a detailed description of the urban wetland and wetland landscape instance, I think the landscape designer must set ecological concepts in terms of ideology, and landscape design in urban wetland system to achieve the aesthetic and ecological balance, so that the natural and human environment achieve harmony and unity.Key words: urban wetlands; landscape design; harmony湿地广泛分布于世界各地,是自然界生物多样性丰富的生态系统,也是人类最重要的环境资本之一。
首先,湿地是许多野生动植物的栖息地;其次,湿地在涵养水源、调节河川径流、补给地下水和维持区域水平衡中,发挥着重要作用,是蓄水防洪的天然屏障;另外,湿地的生物和化学过程还具有降解过滤污染物的功能,使当地河流下游区域受益。
总而言之,各类湿地在保护生物多样性和保护环境方面,都具有极其重要的作用。
1971年2月2日在伊朗的拉姆萨通过的《关于特别是作为水禽栖息地的国际重要湿地公约》(简称《湿地公约》),旨在认证、保护并促进合理使用全球范围内具有重要生态意义的湿地系统。
深圳市社区公园建设标准

深圳市社区公园建设标准(评审修改稿)深圳市公园管理中心华南农业大学热带园林研究中心二〇一五年十月目录标准条文1 总则 (1)2 术语 (1)3 引用标准 (2)4 一般规定 (2)5 总体规划 (3)6 地形水体 (4)7 园路系统 (5)8 公园建筑 (7)9 绿化种植 (8)10 配套服务设施 (9)11 电气、给排水 (11)12 其它建设 (12)条文说明1 总则 (13)2 术语 (13)4 一般规定 (14)5 总体规划 (14)6 地形水体 (15)7 园路系统 (15)8 公园建筑 (16)9 绿化种植 (17)10 配套服务设施 (17)11 电气、给排水 (18)深圳市社区公园建设标准1 总则1.1 为全面发挥社区公园的游憩功能和改善环境作用,促进社区公园的健康发展,确保社区公园的建设水平和质量,特制定本规范。
1.2 本规范适用于深圳市域规划新建和改建的社区公园建设项目。
1.3 社区公园的规划建设应符合适用、经济、安全、环保、美观等基本要求,确保公园建设水平和服务质量。
1.4 社区公园建设应贯彻人与自然和谐共存、生态环境可持续发展、方便居民使用、造价经济合理、景观优美生动等基本原则,创造良好的社区游憩空间和绿化景观效果,促进市民的身心健康。
1.5 本规范中对社区公园建设内容没有作出具体规范的,应符合国家、广东省现行有关技术标准的规定,如《公园设计规范》(CJJ 48-92)、《城市绿地设计规范》(GB 50420-2007)和《广州公园设计规范》(DBJ 440100/T 1-2007)等有关规定。
2 术语2.1 公园向公众开放,以游憩为主要功能,兼具生态、美化、防灾等作用的城市绿地。
2.2 社区城市社区是聚集在一定地域范围内的社会群体和组织,按照一定规范或制度结合而成的社会实体及其生活设施,是一定地域内的城市社会生活的共同体。
2.3 社区公园为城市街区范围内的社区居民提供公共服务,一般面积在1000~50000m2之间,配套有儿童游戏、老人康体等游憩活动内容和设施的城市绿地。
公园设计规范33902

2。
1.1 公园的用地范围和性质,应以批准的城市总体规划和绿地系统规划为依据。
2.1.2 市区级公园的范围线应与城市道路红线重合,条件不允许时,必须设通道使主要出入口与城市道路衔接。
2.1。
3 公园沿城市道路部分的地面标高应与该道路路面标高相适应,并采取措施,避免地面径流冲刷,污染城市道路和公园绿地。
2.1.4 沿城市主次干道的市区级公园主要出入口的位置,必须与城市交通和游人走向,流量相适应,根据规划和交通的需要设置游人集散广场。
2.1。
5 公园沿城市道路,水系部分的景观,应与该地段城市风貌相协调。
2。
1。
6 城市高压输配电架空线通道内的用地不应按公园设计.公园用地与高压输配电架空线通道相邻处,应有明显界限。
2。
1.7 城市高压输配电架空线以外的其他架空线和市政管线不宜通过公园,特殊情况时应符合下列规定:一、选线符合公园总体设计要求;二、通过乔灌木种植区的地下管线与树木的水平距离符合附录二的规定;三、管线从乔灌木设计位置下部通过,其埋深大于1.5m,从现状大树下部通过,地面不得开槽且埋深大于3m。
根据上不荷载,对管线采取必要的保护措施。
四、通过乔木林的架空线,提出保证树木正常生长的措施.内容和规模2。
2。
1公园设计必须以创造优美的绿色自然环境为基本任务,并根据公园类型确定其特有的内容.2。
2.2 综合性公园的内容应包括多种文化娱乐设施、儿童游戏场和安静休憩区。
也可设游戏型体育设施。
在已有动物园的城市,其综合性公园内不宜设大型或猛兽类动物展区。
全园面积不宜小于10hm。
2。
2.3 儿童公园应有儿童科普教育内容和游戏设施,全园面积宜大于2hm。
2。
2。
4 动物园应有适合动物生活的环境;游人参观、休息、科普的设施;安全、卫生隔离的设施和绿带;饲料加工场以及兽医院。
检疫站、隔离场和饲料基地不宜设在园内。
全园面积宜大于20hm。
2.2。
5 植物园应创造适于多种植物生长的立地环境,应有体现本园特点的科普展览区和相应的科研实验区。
初二数学教案:公园有多宽

初二数学教案:公园有多宽以下是查字典数学网为您举荐的公园有多宽,期望本篇文章对您学习有所关心。
公园有多宽●教学目标(一)教学知识点1.能通过估算检验运算结果的合理性,能估量一个无理数的大致范畴,并能通过估算比较两个数的大小.2.把握估算的方法,形成估算的意识,进展学生的数感.(二)能力训练要求1.能估量一个无理数的大致范畴,培养学生估算的意识.2.让学生把握估算的方法,训练他们的估算能力.(三)情感与价值观要求估算也是现实生活中一种常用的解决问题的方法,比如在工厂工人师傅要做一个正方体,使它的体积为900立方米,现有边长为5米,8米,1 0米的三种正方形材料,问用哪一种材料作为正方体的表高比较合适,而工作师傅在领材料之前并不晓得材料的规格,那么在领材料时必须通过估算大致确定用哪一种材料,这确实是估算的用处.如此的例子随处可见,有时问题是突然显现.因此有必要对学生进行这方面的训练,使他们在以后的工作中能处世不惊、沉着应战,用学到的知识去顺利解决实际生活中的难题.●教学重点1.让学生明白得估算的意义,进展学生的数感.2.把握估算的方法,提高学生的估算能力.●教学难点把握估算的方法,并能通过估算比较两个数的大小.●教学方法指导尝试法.●教具预备投影片三张:第一张:公园有多宽(记作2.4 A);第二张:估算的步骤(记作2.4 B);第三张:补充练习(记作2.4 C).●教学过程Ⅰ.导入新课[师]同学们,请大伙儿说出咱们班男生和女生的平均身高.[生]男生大约170厘米,女生大约159厘米.[师]这位同学是如何样得出结果的呢?[生]我猜的.[师]猜字的意思确实是依照自己的判定而估量得出的结果,它并不是准确值,但也不是无中生有,是有一定的理论依照的,本节课我们就来学习有关估算的方法.Ⅱ.讲授新课1.投影片:(2.4 A)某地开创了一块长方形的荒地,新建一个以环保为主题的公园,已知这块荒地的长是宽的2倍,它的面积为400000米2.(1)公园的宽大约是多少?它有1000米吗?(2)假如要求误差小于10米,它的宽大约是多少?(3)该公园中心有一个圆形花圃,它的面积是800米2,你能估量它的半径吗?(误差小于1米)[师]要想明白公园的宽大约是多少,第一应依照已知条件求出已知量与未知量的关系式,那么它们之间有如何样的联系呢?[生]因为已知长方形的长是宽的2倍,且它的面积为40000米2,依照面积公式就能找到它们的关系式.可设公园的宽为x米,则公园的长为2x米,由面积公式得:2x2=400000x2=202100因此公园的宽x确实是面积202100的算术平方根.[师]专门杰出.在估算时我们第一要大致确定数的范畴,因此有必要做一些预备工作.请大伙儿先运算出20以内正整数的平方和10以内正整数的立方.并加以经历,对我们的估算专门有关心.[生]12=1;22=4;32=9;42=16;52=25;62=36;72=49;82=64;92=81;102=100;1 12=121;122=144;132=169;142=196;152=225;162=256;172=289;182=324;192= 381;202=400.13=1;23=8;33=27;43=64;53=125;63=216;73=343;83=512;93=729;103=10 00.[师]下面我们能够进行估算,请同学们分组讨论而后回答.[生]公园的宽没有1000米,因为1000的平方是1000000,而202100小于1000000,因此它没有1000米宽.[师]大伙儿能不能具体确定一下公园的宽是几位数呢?[生]因为100的平方是10000,1000的平方是1000000,而202100大于10000小于1000000,因此公园的宽比100大而比1000小,是三位数.[师]回答问题的这一组同学总结得专门好,大伙儿在估算时就可用如此的方法大致估算一下是几位数,如此使范畴缩小,为下一步的估算作预备.由此看来公园的宽大约是几百米,下面请大伙儿连续讨论做(2)题.[生]因为400的平方等于160000,500的平方为250000,因此公园的宽x应比400大比500小.[师]因此x应为400多,再连续估算,估量十位上的数字是几.[生]因为440的平方为193600,450的平方为202500,因此x应比44 0大比450小,故十位上的数为4.[师]因为题目要求误差小于10米,好应精确到十位,因此我们估算出十位上的数就行了,即公园的宽x应为440米,现在我们能够依照刚才的估算来总结一下步骤.投影片:(2.4 B)1.估量是几位数.2.确定最高位上的数字(如百位).3.确定下一位上的数字.(如十位)4.依次类推,直到确定出个位上的数,或者按要求精确到小数点后的某一位.在以后的估算中我们就可按如此的步骤进行.再看(3)题,先列出关系式.[生]设半径为x米,则有x2=800x2= 255.即x2255因为102=100,1002=10000,因此x应是两位数,又因为152=255,1 62=256,因此x就比15大比16小,应为15点几,因此应为15米.[师]专门好.在题目中要求误差小于1,而不是精确到1,因此15米和1 6米都满足要求,即x应为15米或16米.2.议一议(1)下列运算结果正确吗?你是如何样判定的?与同伴交流.0.066; 60.4(2)你能估算的大小吗?(误差小于1).[师]请大伙儿自己先考虑,小组讨论然后派代表发言.[生甲]因为0.652=0.4225,0.662=0.4356,而0.43大于0.4225小于0.43 56,因此应大于0.65小于0.66,因此估算错误.[生乙]第2个错.因为10的立方是1000,900比1000小,因此900的立方根应比1000的立方根小,即小于10,因此估算错误.[生丙]第3个错.因为60的平方是3600,而2536小于3600,因此应比60小,因此估算错误.[师]第(2)小题请大伙儿按总结的步骤进行.[生](1)先确定位数因为1的立方为1,10的立方为1000,900大于1小于1000,因此应是一位数.(2)确定个位上数字.因为9的立方为729,因此个位上的数字应为9.[师]这位同学差不多把握了估算的步骤,只是有些语言不规范.如在确定位数时,的整数位数应是一位,还有小数部分,由于误差要小于1,因此估算到整数位就行,因此的大小应为9或10.3.例题讲解[例1]生活体会说明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的,则梯子比较稳固,现有一长度为6米的梯子,当梯子稳固摆放时,它的顶端能达到5.6米高的墙头吗?解:如下图中,左图为实际图形,右图为转化成的数学图形.设梯子稳固摆放时的高度为x米,现在梯子底端离墙的距离恰为梯子长度的,依照勾股定理有x2+( 6)2=62即x2=32,x=因为5.62=31.3632因此5.6因此,梯子稳固摆放时,它的顶端能够达到5.6米高的墙头.[例2]通过估算,比较的大小分析:因为这两个数的分母相同,因此只需比较分子即可.解:因为54,即( )222,因此2,因此.即.Ⅲ.课堂练习(一)随堂练习1.估算下列数的大小:(1) (误差小于0.1)(2) (误差小于1)2.通过估算,比较与2.5的大小.解:(1)确定整数位数:因为13.6大于1小于100,因此整数位数应为一位.确定个位数字:因为3的平方是9,4的平方为16,13.6大于9小于16,因此个位上的数为3.确定十分位:因为3.6的平方是12.96,3.7的平方是13.69,误差小于0.1,因此十分位上的数字为6或7.因此应为3.6或3.7.(2)确定整数位数及数字因为9的立方为729,10的立方为1000,因此800的立方根应大于9小于10.又因为误差小于1,因此应为9或10.说明:要求开立方要估算到整数部分,开平方要估算到一位小数.2.解:因为2.52=6.25,因此66.25,因此,即2.5.(二)补充练习投影片:(2.4 C)比较与3.4的大小.解:因为3.4的平方为11.56,因此12大于11.56,即3.4.Ⅳ.课堂小结本节课要紧是让学生把握估算的方法,形成估算的意识,进展学生的数感,并能用估算来比较大小.Ⅴ.课后作业习题2.61.解:设容器的高为x米,得( )2x=40x3=160x3= 51因为3的立方等于27,4的立方等于64,2764,因此x约为3或4米.2.解:9.5,错.因为10的平方为100,而8955大于100,因此应大于10.故错.231错.因为100的立方为1000000,123451000000,因此应小于,即应小于100,而231大于100,故结果错误.3.解:(1)因为6的立方等于216,7的立方等于343,因此于6小于7,又误差小于1,故约等于6或7.(2)因为5.0的平方为25.0,5.1的平方为26.01,25.7大于25.0而小于26.01,因此约等于5.0或5.1.4.通过估算,比较下列各组数的大小.(1) ,;(2) ,3.85解:因为22.5.怕以因此而0.75故.(2)因为3.85的平方等于14.8225,故3.85.Ⅵ.活动与探究一片矩形小树林,长是宽的3倍,而对角线的长为,每棵树占地1平方米,这片树林共有多少棵树?小树林的长大约是多少米(精确到1米)?解:设矩形的宽为x米,则长为3x米,得x2+(3x)2=( )2即10x2=44000x2=4400而矩形的面积为3x2,即为34400=13200平方米,每棵树占地1平方米,故这片树林共有13200棵树.下面估算x2=4400中的x.因为102=100,1002=10000,10010000,因此x的整数位数应是两位.因为602=3600,702=4900,36004900因此x中的十位数字应是6.因为662=4356,672=4489,因此个位上数字应为6.因为66.32=4395.69,66.42=4408.96,因此十分位上的数应为3.因为66.342=4400.9956,因此百分位上的数字小于5应舍去,故x应取66.3.因此3x66.33=198.9199(米)答:这片树林共有13200棵树,小树林的长大约是199米.●板书设计2.4 公园有多宽一、导入二、新课(1)公园有多宽(2)议一议(判定估确实是否正确)三、例题讲解(有关梯子稳固问题)四、练习五、小结唐宋或更早之前,针对“经学”“律学”“算学”和“书学”各科目,其相应传授者称为“博士”,这与当今“博士”含义差不多相去甚远。
2.4 课件 公园有多宽 (北师大版八年级上册)4

A
议一议
(1)通过估算,你能比较 5 1 与 1 的大小吗?
2
2
你是怎样想的?与同伴交流
5 1 (2)小明是这样想的: 2 1
与
它们的分子就可以了。因为
5 >2,所以 5 -1 >1,因此 1 5 1 > 2 2
2
的分母相同,只要比较
———通过估算,比较下面各组数的大小:
( 1) ( 2)
C O
B
A
1 估算无理数的方法是(1)通过平方运算,采 用“接近法”,确定真值所在范围;(2)根据 问题中误差允许的范围,在真值的范围内取出近 似值。
2 “精确到”与“误差小于”意义不同。如精确 到1m是四舍五入到个位,答案惟一;误差小于 1m,答案在真值左右1m都符合题意,答案不惟 一。在本章中误差小于1m就是估算到个位,误差 小于10m就是估算到十位。
1、估算: A、2和3之间
17 1 的值在(
) D、5和6之间
B、3和4之间 C、4和5之间
2、估算下列各数的大小: (1) 15.9 (误差小于0.1)
5 1 2
(2)
3
1111
(误差小于1)
3、求出所有大于 17 且小于 11 的整数。 4、通过估算,比较
5 与 8
的大小。
课本第49页第1、2、3、5题
2 “精确到”与“误差小于”意义不同。如精确 到1m是四舍五入到个位,答案惟一;误差小于 1m,答案在真值左右1m都符合题意,答案不惟 一。在本章中误差小于1m就是估算到个位,误差 小于10m就是估算到十位。
例1 生活经验表明, 靠墙摆放梯子时,若 C 梯子底端离墙的距离 约为梯子长度的1/3, 则梯子比较稳定。现 有一长度为6米的梯子, 当梯子稳定摆放时, B 它的顶端能达到5.6米 高的墙头吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)小明是这样想的: 与 的分母相同,只要比较 它们的分子就可以了。因为 >2,所以 -1 >1,因此 >
你认为小明的想法正确吗?
初中数学资源网
议一议
(1)如何比较
5 1 1 与 的大小 2 2
6 1 3 与 的大小 (2)如何比较 2 4
初中数学资源网
2.4 公园有多宽
பைடு நூலகம்
初中数学资源网
某地开辟了一块长方形的荒地,新建一个 以环保为主题的公园。已知这块荒地的长是宽 的两倍,它的面积为400000米2.
400000米2
(1)公园的宽大约是多少?它有1000米吗? (2)如果要求误差小于10米,它的宽大约 是多少?与同伴交流。
1 下列估算结果正确吗?你是怎样判断 的?与同伴交流。 √0.43≈0.066
3 3
√900≈96
√2536≈60.4
3
2 你能估算√900的大小吗?(误差 小于1)
初中数学资源网
规律小结:
1 估算无理数的方法是:
(1)通过平方运算,采用“夹逼 法”,确定真正值所在范围; (2)根据问题中误差允许的 范围,在真正值的范围内取出 近似值。
3、母亲节前某同学设计制作了 一个精致的礼品盒,其外形是一个 体积为26cm3的圆柱形,其底面直 径与圆柱形的高相等,先想象这个 礼品盒大约有多大?再 计算出这个礼品盒的底 面半径,与你想象的大 小是否相符合? (精确到0.1cm)
初中数学资源网
3、母亲节前某同学设计制作了 一个精致的礼品盒,其外形是一个 体积为26cm3的圆柱形,其底面直 径与圆柱形的高相等,先想象这个 礼品盒大约有多大?再 计算出这个礼品盒的底 面半径,与你想象的大 小是否相符合? (精确到0.1cm)
初中数学资源网
本节课你学习了哪些知识?
作业:作业本(1):2.4公园有多宽 同步练习: 2.4公园有多宽
初中数学资源网
例1生活表明,靠墙摆放梯子时,若梯子
底端离墙的距离约为梯子长度的三分之一, 则梯子比较稳定。现有一长度为6米的梯子, 当梯子稳定摆放时,他的顶端能到达5.6米 高的墙头吗?
初中数学资源网
议一议
(1)如何比较
5 1 1 与 的大小 2 2
初中数学资源网
初中数学资源网
某地开辟了一块长方形的荒地,新建一个 以环保为主题的公园。已知这块荒地的长是宽 的两倍,它的面积为400000米2.
(3)该公园中心有一个圆形花圃,它的面积 是800米2,你能估计它的半径吗? (误差小于1米)
初中数学资源网
一、议一议
初中数学资源网
规律小结:
2 “精确到”与“误差小于”意义不 同。如精确到1m是四舍五入到个位, 答案惟一;误差小于1m,答案在真 正值左右1m都符合题意,答案不惟 一。在本章中误差小于1m就是估算 到个位,误差小于10m就是估算到十 位。
初中数学资源网
