结晶学第十讲—空间群(2)
合集下载
晶体空间群
73种点式空间群中 的对称元素分别换成螺 旋轴、滑移面，并去掉 等价的空间群，便得到 另外157种空间群。合 起来共230种空间群。
等效点系
在晶体构造中，由 一任意点开始，通过空 间群所有对称操作的作 用，重复出来的一系列 规则分布点(等效点)的总 和，称等效位置或等效 点系。
《国际结晶学表》 A卷
The International Union of Crystallography
《International Tables for Crystallography》，是 国际上公认的关于晶体结 构知识的标准手册。该书 最早出版于1952年，以后 五次(1959,1962,1974， 1983，2002）修订再版。
Wyckoff位置是国 际表中最有用的信息， 告知在晶体中何处可 以找到原子。
Site symmetry 原子所在之 处具有的对称点 群。
空间群把 同一个等效 点系中的各 等效点联系 在一起；
167 : D R3c
6 3d
Ca(0, 0, 0)
在晶体构造 中，同一个等 效点系中的等 效点必为等质 点；
73种 点式空间群
三 斜 晶 族
b
a
c
a
b
P
C P1
1 1
c
C P1
1 i
b
a
c
90 90
单 斜 晶 族
a
b
c
90 90
P
2
C
P
2 m 2/m
P2 Pm P2/m
C
2 m 2/m
C2 Cm C2/m
b
a
c
90 90 90
第2部分第3章 空间群(2) 群论讲义PPT
[ 答案: 是 ]
[ 思考题: T 群的不可约表示是几维的? 为什么? ]
[ 答案: 都是一维的, 因为阿贝尔群各元素自成一类, 故不
可约表示数 r 和类数 c 都等于群元数 h ( r = c = h ),
又因为 j nj 2 = h ( j = 1 ---- r ), 则nj 皆为1. ] *
因此有 PT = C ( T )
10
B2 = A-1 B1 A = C4-1 C2 C4 = C2 ( 习题 )
B1 = B2 = C2 D3 ( B1 ) = D4 ( B2 ) = -1 D3 ( B2 ) = D4 ( B1 ) = -1
以上两计算结果表明群C2v 的3 和4 是相对于群C4v 的共轭表示
习题: 用新的点群操作表示法证明下列关系式
则称 1 和 2 为群 H 相对于群 G 的共轭表示 (2) 例1: 群C2v 的 3 和 4 是相对于群C4v 的共轭表示
H: C2v E C2 v’ v” D1 1 1 1 1 1
G: C4v E C2 2v 2d 2C4
D2 2 1 1 -1 -1
D3 3 1 -1 1 -1
D4 4 1 -1 -1 1
Ck = Ck1 Ck2 Ck3 = exp [- 2 i ( P1/N1 + P2/N2 + P3/N3 ) ] = exp [-2 i i (Pi /Ni)] (i = 1, 2, 3) [提问:多少个不可约表示?]
三维平移群 { | R n } 有 N1 N2 N3 个 (群元数) 不可约表示 *
二, 平移群不可约表示的性质
6
(1) 平移群 T = { | R n } 的不可约表示 Ck 为 exp ( i k • R n ),
晶体结构空间群点群
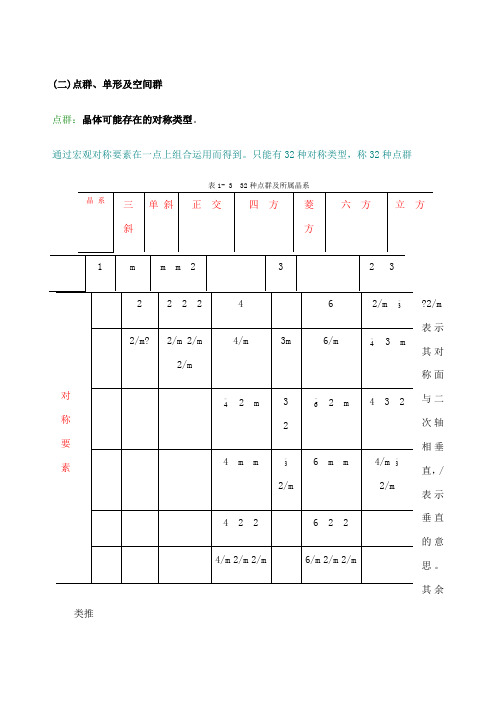
(二)点群、单形及空间群点群：晶体可能存在的对称类型。
通过宏观对称要素在一点上组合运用而得到。
只能有32种对称类型，称32种点群表1- 3 32种点群及所属晶系同一晶系晶体可为不同点群的原因：阵点上原子组合情况不同。
如错误!未找到引用源。
，对称性降低，平行于六面体面的对称面不存在，4次对称轴也不存在。
理想晶体的形态―单形和聚形：单形：由对称要素联系起来的一组同形等大晶面的组合。
32种对称型总共可以导出47种单形，如错误!书签自引用无效。
，错误!书签自引用无效。
，错误!书签自引用无效。
所示聚形：属于同一晶类的两个或两个以上的单形聚合而成的几何多面体。
大量的晶体形态是由属于同一晶类的单形聚合而成的封闭一定空间的几何多面体，如单形四方柱与平行双面形成了四方柱体的真实晶体形态空间群：描述晶体中原子通过宏观和微观对称要素组合的所有可能方式。
属于同一点群的晶体可因其微观对称要素的不同而分属不同的空间群，空间群有230种，见教材中表1- 4国际通用的空间群符号及其所代表的意义为：P：代表原始格子以及六方底心格子（六方底心格子为三方晶系和六方晶系所共有）。
F：代表面心格子。
I：代表体心格子。
C：代表（001）底心格子（即与z轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布）。
A：代表（100）底心格子（即与x轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布）。
R：代表三方原始格子。
其它符号：意义与前述相同表1- 4 晶体的空间群、点群、晶系、晶族一览表续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4/k/174/stu/content/1.1.3.2.htm。
晶体点群、空间群简要归纳
晶体点群、空间群简要归纳本⽂只是很简要的归纳，具体内容还请见李新征⽼师群论书和其在蔻享的群论课。
另外推荐肖瑞春⽼师科学⽹博客的这篇博⽂，介绍了群论及后续的学习：若研究中涉及群论和物理性质相关，其中陈纲的《晶体物理学基础》书特别好，易懂，将主动变换和被动变换等分析得特别清晰，不过此书太厚，注意⽤到什么学什么，⽤minimized的知识来科研，否则被导师批评...1.对称操作、对称元素对称操作：保持系统不变的操作。
对称元素：它是⼀个⼏何实体，对称操作可以依据对称元素施⾏对称操作。
对称元素可以是点、直线、⾯等。
2.点群：1）定义：三维实正交群O(3)群的有限⼦群物理理解：实际上点群是实际的物理系统在三维空间的⼀些对称操作的集合。
这些对称操作会保持⼀个点不动。
2）点群分类第⼀类点群：只包含纯转动元素的点群。
第⼆类点群：点群中，除了纯转动元素，还包含转动反演元素的点群。
因为点群是O(3)群的⼦群，⽽O(3)群中有固有转动和⾮固有转动。
3）点群的性质{()}性质1：点群这个集合可以写成C k(2π/n)、IC k′2π/n′的形式，其中n,→k′,n′取有限个⽅向和值；C k(2π/n)是绕→k轴转2π/n⾓的操作。
性质2：设G是点群，K是G的纯转动部分，由于纯转动部分的乘积以及逆元必属于这个纯转动部分,所以K也是G的纯转动⼦群,即K=G∩SO(3)∘.点群G与其有限⼦群K的关系有以下三种可能的情况：1.G=K, 即点群只包含纯转动操作；称为第⼀类点群。
2.若点群G中除了纯转动操作，还包含纯空间反演操作I, 则可以通过G=K∪IK得到这种情况对应的第⼆类点群。
3.若点群G中除了纯转动操作，且G中不包含纯反演操作I时 , 此第⼆类点群G⼀定与⼀个第⼀类G+同构,其中，G+=K∪K+, ⽽K+定义为:K+={Ig∣g∈G,但g∉K}根据这⾥的第3点，可以知道构造这种情况对应的第⼆类点群的⽅法：根据⼀个已知的第⼀类点群K∪K+，即可以构造⼀个第⼆类点群K∪I K+.还可以证明K必须是K∪K+的不变⼦群，其阶数是K∪K+的⼀半。
空间群
滑移反射
不对称单位先经镜面反射，然后沿平行与镜面的方向平移
滑移反射改变了不对称单位的手性。
滑移面分类
• 轴向滑移面：沿晶轴(a、b， c)方向滑移;
• 对角滑移面：沿晶胞面对角线或体对角线方向滑移，平 移分量为对角线一半;
• 金刚石滑移面：沿晶胞面对角线或体对角线方向滑移， 平移分量对角线1/4的对角滑移面。只有在体心或面心 点阵中出现，这时有关对角线的中点也有一个阵点，所 以平移分量仍然是滑移方向点阵平移点阵周期的一半。
Wyckoff位置 （2）
• 多重性（ multiplicity ）：告诉我们如果安 置一个特定原子在该位置，经过空间群的所 有对称操作，总共会产生多少个原子。 • 记号（ letter ）是从高对称性位置开始按英 文字母顺序指定的位置标记。 • 对称（ symmetry ）告诉我们原子所在之处 具有的对称元素。
空间群的描述
• 俯视图 • 矩阵 • 一般等效位置及对称元素
熊夫利推导230个空间群
• （1） 推导73个点式空间群 • （2） 分析可能的滑移面和螺旋轴 • （3) 把各种可能的布拉菲格子和h个点式 或非点式对称操作结合起来，推导可能的 非点式空间群
三斜晶系
单胞俯视图
新的反演中心是-1和单位平移操作组合而得
Wyckoff位置告诉我们在晶体中何处可以找到原子。
比如：单斜空间群Pm 仅有垂直于b轴的二个镜面。 一个在y = 0， 另一个在y = ½ 位置。 通过镜面操作，在x， y， z的原子 --〉在x， - y， z
第二个原子。如果我们安置原子在其中一个镜面(它的Y座标将必须是0
或½ )，镜面反射操作就不会产生第二个原子。
在非对称基元内任何一点不会再有对称 相关的位置
晶体与空间群概述
个位构成，每个位代表 一个窥视方向。每个晶 系的晶轴选择都有特别 的规定：
极射赤面投影
m3m-Oh点群极射赤平投影图
研究点群的意义
对晶体进一步分类：所有 晶体分属32种晶类，每种晶 类对应一种点群；
点群是空间群的基础； 固体的性质与点群有关。
在32种晶体点群中，有 21种没有对称中心，其中20 种点群的晶体具有压电效应： 10种极性、10种非极性。极 性压电晶体指具有永久偶极 矩，如钛酸钡、铌酸锂晶体 等。
下面一个空间群推导的简单例子，可以帮助我们理解
空间群是如何由对称操作的组合得到的。单斜晶系中 的2/m点群，可能具有2次轴、21螺旋轴、m镜面和c滑
移面这些对称性。为了简明，这里不考虑非标准设置 的单斜晶系空间群及其对称性，即取平行于2次旋转轴 或21螺旋轴方向为b轴，则镜面m和c滑移面垂直于b轴， 则镜面m和c滑移面垂直于b轴。单斜晶体的晶格类型可 能是简单P晶格和底心C晶格。P和C晶格与2次轴、21螺 旋轴、m镜面和c滑移面对称性进行组合，共有8种可能 性：P2/m, P2/c, P21/m, P21/c, C2/m, C2/c, C21/m和 C21/c。 由于21螺旋轴可以由C格子和2次旋转对称操作 组合产生，C21/m与C2/c也是等价的，因此，属于2/m 点群的空间群只有6个：P2/m, P2/c, P21/m, P21/c, C2/m 和C2/c。
分 子 与 晶 体 点 群
n? ？
230种空间群
点群一般用于研究有限图 形的对称性—对称元素有限且 必相交于一点。晶体的内部构 造是由无数个化学质点在三维 空间组合而成的，任何相邻两 质点之间均仅有以nm为单位的 微小距离。
晶体构造可认为是沿三维
空间延伸的无限图形，所有对 称元素(包括对称元素的交点) 在三维空间作平行排列，也不 交于一点。
极射赤面投影
m3m-Oh点群极射赤平投影图
研究点群的意义
对晶体进一步分类：所有 晶体分属32种晶类，每种晶 类对应一种点群；
点群是空间群的基础； 固体的性质与点群有关。
在32种晶体点群中，有 21种没有对称中心，其中20 种点群的晶体具有压电效应： 10种极性、10种非极性。极 性压电晶体指具有永久偶极 矩，如钛酸钡、铌酸锂晶体 等。
下面一个空间群推导的简单例子，可以帮助我们理解
空间群是如何由对称操作的组合得到的。单斜晶系中 的2/m点群，可能具有2次轴、21螺旋轴、m镜面和c滑
移面这些对称性。为了简明，这里不考虑非标准设置 的单斜晶系空间群及其对称性，即取平行于2次旋转轴 或21螺旋轴方向为b轴，则镜面m和c滑移面垂直于b轴， 则镜面m和c滑移面垂直于b轴。单斜晶体的晶格类型可 能是简单P晶格和底心C晶格。P和C晶格与2次轴、21螺 旋轴、m镜面和c滑移面对称性进行组合，共有8种可能 性：P2/m, P2/c, P21/m, P21/c, C2/m, C2/c, C21/m和 C21/c。 由于21螺旋轴可以由C格子和2次旋转对称操作 组合产生，C21/m与C2/c也是等价的，因此，属于2/m 点群的空间群只有6个：P2/m, P2/c, P21/m, P21/c, C2/m 和C2/c。
分 子 与 晶 体 点 群
n? ？
230种空间群
点群一般用于研究有限图 形的对称性—对称元素有限且 必相交于一点。晶体的内部构 造是由无数个化学质点在三维 空间组合而成的，任何相邻两 质点之间均仅有以nm为单位的 微小距离。
晶体构造可认为是沿三维
空间延伸的无限图形，所有对 称元素(包括对称元素的交点) 在三维空间作平行排列，也不 交于一点。
《晶体空间群》课件
正交晶系的晶体空间群具有较低 的对称性，常见于硫磺等材料。
六方晶系
六方晶系的晶体空间群具有特殊 的究
晶体空间群的研究对材料科 学和材料结构设计具有重要 意义。
化学与生物学研究
晶体空间群的研究在化学合 成和蛋白质晶体学研究中发 挥重要作用。
新材料的研发与应用
通过研究晶体空间群和结构， 可以为新材料的研发和应用 提供理论支持。
结论
晶体空间群是研究晶体结构的重要工具，对于材料科学、化学和生物学等领域的发展具有重要意义。
3 推动学科发展
晶体空间群的研究对晶体学、材料科学、化学和生物学等领域的发展具有重要促进作用。
晶体结构与晶体空间群的关系
晶体结构的描述
晶体结构是指晶体中原子、分 子或离子的排列方式和周期性。
三维晶体空间群
三维晶体空间群描述了晶体结 构的点阵和对称性。
二维晶体空间群
二维晶体空间群描述了晶体结 构在平面上的周期性和对称性。
《晶体空间群》PPT课件
这是一个关于晶体空间群的PPT课件，旨在介绍晶体空间群的基本概念、分类、 研究方法，以及其在材料科学、化学和生物学等领域的应用。
晶体空间群的研究意义
1 解析晶体结构
晶体空间群的研究可以帮助我们解析晶体的结构，了解其原子排列和化学组成。
2 探索材料特性
通过研究晶体空间群，我们可以深入了解材料的特性和性能，从而为新材料的研发和应 用提供指导。
晶体空间群的分类与表示法
1
晶体空间群的分类
晶体空间群可以根据其对称特性和点阵
晶体空间群的表示法
2
类型进行分类。
晶体空间群可以使用国际晶体学表符号
进行表示和命名。
3
布拉维格子的表示方法
空间群
包括了这些与平移有关的操作之后，晶体的对称运动可以全部分类成230个对称操作群，称晶体空间群，也 称空间群。
的确定
如果知道了点群和点阵平移以外，还已知非晶格平移矢量，布拉维格子类型，则空间群就完全确定，列举出 所有可能的α和的相容性组合，就可得到所有可能的空间群。空间群共有230种，其中73种为简单空间群，余下 的157种为复杂空间群。
的三要素
非晶格平移矢量决定于与转轴相的坐标原点的选择，因此不是唯一的。 确定空间群必须指出的三个组成部分：
的表达
空间群符号(3张)表示一个空间群时，圣佛利斯符号和国际符号并用。
空间的国际群符号由两部分组成：前一部分是格子类型（布拉维格子）[P，C(A、B)，I，F]；后一部分与点 群的国际符号基本相同，不同的是那三个特定方向上的对称要素取自晶胞中对应方向上对称程度最高的那种对称 要素。
空间群的圣佛利斯符号是在其点群圣佛利斯符号的右上角加上序号即可。
谢谢观看
空间型和对称型（点群）体现了晶体内部结构的对称与晶体外形对称的统一。每个对称型有若干个空间群与 之相适应。即外形上属于同一对称型的晶体，其内部结构可分属于若干空间群。
空间群可以分为两类：一类称为简单空间群或称点空间群；一类称为复杂空间群或称非点空间群。
所谓点空间群，是由一个平移群和一个点群对称操作组合而成的，它的一般对称操作可以写成（R | t (αβγ)），其中R表示点群对称操作，t(αβγ)表示平移操作。具体分析表明，共有73种不同的点空间群。
点阵平移
理想的完整晶体应是无限大的，点阵单元在空间三个方向上的无限平移将给出整个点阵。或者说，无限的点 阵在平移下保持不变。所以平移也是一种对称操作，它的对称要素不是一个轴，一个点，一个面，而是整个点阵。 与平移有关的对称要素有三个：
的确定
如果知道了点群和点阵平移以外，还已知非晶格平移矢量，布拉维格子类型，则空间群就完全确定，列举出 所有可能的α和的相容性组合，就可得到所有可能的空间群。空间群共有230种，其中73种为简单空间群，余下 的157种为复杂空间群。
的三要素
非晶格平移矢量决定于与转轴相的坐标原点的选择，因此不是唯一的。 确定空间群必须指出的三个组成部分：
的表达
空间群符号(3张)表示一个空间群时，圣佛利斯符号和国际符号并用。
空间的国际群符号由两部分组成：前一部分是格子类型（布拉维格子）[P，C(A、B)，I，F]；后一部分与点 群的国际符号基本相同，不同的是那三个特定方向上的对称要素取自晶胞中对应方向上对称程度最高的那种对称 要素。
空间群的圣佛利斯符号是在其点群圣佛利斯符号的右上角加上序号即可。
谢谢观看
空间型和对称型（点群）体现了晶体内部结构的对称与晶体外形对称的统一。每个对称型有若干个空间群与 之相适应。即外形上属于同一对称型的晶体，其内部结构可分属于若干空间群。
空间群可以分为两类：一类称为简单空间群或称点空间群；一类称为复杂空间群或称非点空间群。
所谓点空间群，是由一个平移群和一个点群对称操作组合而成的，它的一般对称操作可以写成（R | t (αβγ)），其中R表示点群对称操作，t(αβγ)表示平移操作。具体分析表明，共有73种不同的点空间群。
点阵平移
理想的完整晶体应是无限大的，点阵单元在空间三个方向上的无限平移将给出整个点阵。或者说，无限的点 阵在平移下保持不变。所以平移也是一种对称操作，它的对称要素不是一个轴，一个点，一个面，而是整个点阵。 与平移有关的对称要素有三个：
点群和空间群ppt课件
如图所示，为4度螺旋轴。晶体绕 A
2
轴转900后，再沿该轴平移a/4，能自身
1
重合。
26
2.滑移反映面
M
经过该面的镜象操作
A2
A2
以后,再沿平行于该面的某
个方向平移T/n的距离(T是
A1
A1
该方向上的周期矢量，n为
2或4)，晶体中的原子和相
A
A
同的原子重合。
M
27
例题1：立方系的对称性简析。
(1) 三 个 相 互 垂 直 的 四 度 轴
❖ 宏观对称要素和微观对称要素在三维空间的组合，称为空 间群。
❖ 经过严格证明可以得出，晶体中可能存在230种空间群，任 何一种晶体的微观结构属于且只属于230种空间群之一。
50
点群与空间群的关系
晶体外形的对称性仅有32个点群，而晶体结构的对称性却有320
种空间群。晶体外形的对称性是晶体结构对称性的反映。 属于同一点群的晶体不一定属于同一空间群。换言之，空间群
结点在单胞中的4种分布方式：
单胞中结点数目：
简单点阵（P）:结点均在角顶上
简单(原始)点阵: 1
底心点阵(C):除角顶外每一对面上各有一个结点 面心点阵： 4
体心点阵(I):除角顶外中央有一个结点
底心点阵： 2
面心点阵(F):除角顶外每个面上均还有一个结点 体心点阵： 2
简单点阵 : 1 ［［000］］
1200
正交晶系 a b c, 900
立方晶系 六方晶系 正交晶系 三斜晶系
单斜晶系 a b c, 900 三斜晶系 a b c, 900
注意： 准确的说划分晶系的依据是特征对称性而不是晶胞参数。55
56
空间群
矩阵乘法
1 0 0 x x 2次旋转矩 0 1 0 y y 阵 0 z z 0 1
倒反中心(Inversion center)
倒反中心：也称为反演中心或对称中心(Center of
0 cos sin 0 0 sin cos 0 1 0 0 1
旋转反映轴--映轴
旋转反映轴，简称映轴(rotoreflection axis)，其对 称操作是先进行绕映轴的旋转操作(n)后立刻再对
垂直于该映轴的反映面进行反映操作m。符号为ñ (Sn)，设对称轴沿[001]方向，其矩阵表示为：
Z Z
无， 2，m X 无， 2，m X
立方 2,m,4, `4
X
3,`3
体对 无， 2，m 面对 角线 角线
点群的Schönflies符号
Cn: 具有一个n次旋转轴的点群。
Cnh: 具有一个n次旋转轴和一个垂直于该轴的镜面的点群。
Cnv: 具有一个n次旋转轴和n个通过该轴的镜面的点群。 Dn: 具有一个n次旋转主轴和n个垂直该轴的二次轴的点群。 Sn:具有一个n次反轴的点群。 T:具有4个3次轴和4个2次轴的正四面体点群。
c)单位元素。 集合G中存在一个单位元素e，对任意元素， f G 有
ef fe f
d)可逆性。 对任意元素 f G ，存在逆元素 f 1 G ，使 f 1 f ff 1 e 则称集合G为一个群。
晶体学点群
晶体中满足群的性质定义的点对称操作的集合称
作晶体学点群。点对称操作的共同特征是进行操
非点式操作，如平移，螺旋转动和滑移反映。
对称操作和对称元素
对称操作：
空间群PPT课件
63
Pmm2
点对称和平移对称操作产生新的非基本操作
2020/1/15
64
P222
2020/1/15
65
PMMM
2020/1/15
66
Cmm2
出现滑移面
2020/1/15
67
2020/1/15
68
2020/1/15
69
2020/1/15
70
2020/1/15
71
各晶系空间群特征概要
• 空间群： 国际符号： 空间群符号的意义： 空间群的熊夫利推导方法：
俯视图
方向
原点
2020/1/15
112
2020/1/15
113
2020/1/15
114
原点位置
• 点式空间群：对称性等于空间群点群的点 上，非点式:取在最高对称性的点上，有反 演中心则取在
不对称单位（ Asymmetric Unit ）
商群与点群一一对应商群不一定是点群商群中不含整数平移操作空间群中的任何操作都可以用h个基本操作与平移群的操作组合而得202011753一般等效位置商群中h个基本操作作用后产生h个一般等效点点阵类型加一般等效点系描述空间群等效位置确定商群的对称性及所属的晶系由点阵类型便知道平移群的对称性确定单胞内的原子数及位置202011754国际表中对称操作的表示202011755对称操作的分类及几何符号202011756由对称操作的矩阵求对应的几何符号1查表确定对应点对称操作2确定对称元素的取向和位置a反映b纯旋转c旋转倒反202011757反映面滑移面滑移分量平行滑移面滑移面的位置分量垂直滑移面滑移面位置
独立原子位置
加心产生新的对称操作：滑移线
33
2020/1/15
晶体空间群
21，31，32，41，42，43，61，62，63，64，
65。
具有螺旋轴对称性晶体
硒的晶体结构：具有31螺旋轴
螺旋轴限制
1，角度（证明略） 2，平移量
• 为了使螺旋轴不与点阵矛盾，除轴次受点阵限制 为1，2，3，4，6次外，还要使螺旋轴的滑移分 量满足这样的条件：
其中，T是平行于螺旋轴的单位平移矢量，n是螺旋轴
第四章 空间群
袁定旺
• 期中考试安排： • 时间：第十一周 周六 12月1号 15:00－－17:00 • 地点：复301（1701-1703） 复302（17041706） • 闭卷，带计算器。 算期末成绩， 不得请假。
从晶系到空间群
7个晶系
（按照晶胞的特征对称元素分类）
旋转，反射，反演
平移
32个点群
3 ，与旋转轴、反映面、对称中心、反轴相应的对称 操作进行时至少有一点不动，我们称其为点操作。这 样的对称元素在有限对称图形如晶体宏观对称性中有， 在无限周期重复对称图形中（如晶体的点阵结构中） 也有。 4，使得对称图形复原的对称动作一共有7种：反映、 倒反（反演）、旋转、旋转倒反（或旋转反映）、平 移、螺旋旋转、滑移反映。其中旋转、平移、螺旋旋 转不能使左右形（手型对称型）重合，只能使相等图 形重合。而反映、倒反（反演）、旋转倒反—反轴（ 或旋转反映—映轴）、滑移反映能使左右形重合 (含 有反映) 。
4 4 4
4
滑移画操作的矩阵表示
ì æ 1 öü m | t í [100] ç 0, ,0÷ ý r è 2 øþ î
ì æ 1 1 öü m | t í [001] ç , ,0÷ ý r è 2 2 øþ î
金刚石滑移只存在于体心、面心点阵结构中
(固体材料结构学)15-空间群2
2 3
1 3
2 3
1 3
1 3
2 3
1 3
2 3
2 3
1 3
1 3
2 3
2 3
1 3
1 号
1 2
1
4
1 2
1 2
1
4
1 2
P212121
1
4
6. 找出点系中的对称素、国际符号
1 2
1 2
1 2
，
，12
Pna21
1 2
7. 找出点系中的对称素、国际符号
第四章：晶体的对称性
§4.6 空间群和国际表
空间群的命名（国际符号）
主轴方向 非主轴方向
布拉菲点阵符号
方向、顺序和 同态点群一致
主轴的垂直方向
非主轴方向的垂直方向
同点群一样，可省略一些派生对称素，得到简略符号。
晶系
对称素及其排列
举例
三斜
P1 P 1
单斜 主轴、垂直于主轴的对称面
P2 Pb C2/m
晶系对称素及其排列举例单斜主轴垂直于主轴的对称面正交三个方向依次排列四方主轴垂直于基面边的对称面或平行于基面边的对称轴垂直于对角线的对称面或平行于对角线的对称轴三角同上六角同上立方坐标轴方向体对角线方向基面对角线方向pba222fm343246空间群和国际表国际表全称
第四章：晶体的对称性
§4.1 对称性的概念 §4.2 空间变换 §4.3 对称群的类型和性质 §4.4 晶体学点群 §4.5 晶系 §4.6 空间群和国际表
1 4
，
1
P 21 21 21 nma
4
，
1 4
，
21 21 21
Pm n b
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4/mmm 6/mmm 3(Li3)
y
432
(3L44L36L2)
(L44L25PC) (L66L27PC)
422
x
622
(L66L2)
3m
(Li33L23P)
m3m
(3L44L36L29PC)
(L44L2)
4 (Li4) 42m
(Li42L22P)
6 (Li6)
62m
(Li63L23P)
x
y
1(C1) 2(C2) 222(D2) 4(C4) 1(Ci) m
全对称点群
1 2/m mmm 4/mmm 3m 6/mmm m3m
菱形
6(C6)或6(S35)
六方
立方
a = b≠c, = = 90o, = 120o
a = b = c, = = = 90o
四个三次轴
1(L1) 2(L2) 222(3L2) 4(L4) 1(C) m(P) mm2
,+ -
,+ -
1/4
单斜 B
滑移面
P222
c a
+ _
_
+
+ _
_
+
b
+ _
_
+
+ _
_
+
y
x
纸面内二次轴
C222
c
a
+ _
_
+
+ _ _ +
+ _
_
+
b
+ _
_
+
+ _
_
+
螺旋轴,21
Pmm2
+
+
,+ ,
+
+
+
,+ ,
+
+
+
,+ ,
+
+
+
,+ ,
+
y
x
反映面
,+ -,+ -
,+ -,+ ,+ -,+ -
(C1h)
6(C6)
6/m
(C6h)
3(C3)
23(T)
mm2
(C2v)
4/m
(C4h)
3m (C3v) m3 (Th)
2/m mmm 4mm
(C2h) (D2h) (C4v)
6mm
(C6v)
32(D3)
43m (Td)
432 (O)
32 种 点 群 符 号
4/mmm 6/mmm 3(S6)
(D4h) (D6h)
空间群点群相同的位置对称性
P1
c b
+
+
+
a
+
P1
_
,
+
_
,
+
_
,
+
_
,
+
+
_
,
+
_
,
P2
c a
b
+
+ +
+ +
+ + &-
P2/m
-
,+ -
,+ ,+ -
-
,+ ,+ -
反映面，镜面
Pm
-
,+
-
,+
,+ -
,+ -
Bm
1/2-
-
,+
-
,+
, 1/2+
1/2-
, 1/2+
二次螺旋轴
平行于纸面
c/2 a/2或b/2 无
4 6
四次反演轴
六次旋转轴
三次旋转轴 三次螺旋轴 三次反演轴
c/3
2c/3 无
61 62 63 六次螺旋轴 64 65
3
6
六次反演轴
对称面符号
符号 对称面
图示符号
垂直于投影面 平行于投影面
滑移特征
没有(如果平面在z=1/4的 高度，就在符号边标注 1/4) 沿[100]滑移a/2，或沿[010] 滑移b/2，或沿<100>滑移
422
(D4)
622
(D6)
3m(D3d)
m3m (Oh)
4 (S4) 42m
(D2d)
6 (C3h)
62 (D3h)
第八讲
14种布拉菲格子
旋转对称性
晶系、参考轴 初基P单胞 (6)
满足点阵条件 + 晶系不变
P点阵中高对称位置加心(体心I, 全面心F, 单面心A, B或C 双面心)
六方格子特殊心 菱形(三方)单胞
P3, P3m1, P312, P3, P31m, P31m, P321, P3m1
三 方 3, 3m, 32,
3, 3m
P
R
R3, R3m, R32, R3, R3m
P6, P6/m, P6mm, P6/mmm, P622, P6, P6m2, P62m
六 方 6, 6/m, 6mm, 622, P
,+ -
-
,+
,+
,+ ,+ -
,+ -
,+ ,+ -
x
第十讲
空间群(II)：非点式操作
点对称操作
1 (E, L1) 2 (C2, L2 )
360o/n (n = 1,2,3,4,6)
1 (i, C) 2 (σ, P), m
+
,
+
_
,
+
3 (C3, L3)
3 (S65, Li3) 4 (S43, Li4)
6, 62m, 6/mmm
立 方 23, m3, 43m,
432, m3m
P I
F
P23, Pm3, P43m, P432, Pm3m I23, Im3, I43m, I432, Im3m F23, Fm3, F43m, F432, Fm3m
第九讲
空间群(I)：点式空间群
晶体的宏观外形可视作一个连续整体的有限图形，而晶体 微观结构是不连续排列的原子在三维空间的无限展开。晶体 宏观对称性是晶体结构(原子排列对称性)即微观对称的反映。 点群中对称要素必须交于一点，只有方向的概念。微观对 称性中对称要素无须交于一点，要引入平移和位置的概念。
m a, b
反映面 (镜面)
轴滑移面
c n d
对角滑移面 (网)
无
沿z轴滑移c/2，或在菱形轴 中沿[111]滑移(a+b+c)/2 (a+b)/2, (b+c)/2, (a+c)/2, 或 (a+b+c)/2(四方和立方) (a±b)/4, (b±c)/4, (a±c)/4, 或(a±b±c)/4(四方和立方)
2 21
二次螺旋轴
平行于纸面
c/2
a/2或b/2
1/2+
+
a/2或b/2
三次螺旋轴 31 32
3 (C3, L3)
+
+
+
3
1/3+
+
2/3+
31 32
3 31 32 3
三次旋转轴
无
c/3 2c/3
2/3+
三次螺旋轴
三次反演轴
无
1/3+
+ +
四次螺旋轴 41 42 43
4 (C4, L4) 4
四次旋转轴 无
点对称条件
1(E)或1(i)
晶系
三 斜 1(C1), 1(Ci)
点群
布拉菲点阵
P
2(C2)或2(m)
单 斜 2(C2), m(C1h), 2/m(C2h)
P, B P, C, I, F
P, I
两个2(C2)或2(m) 正 交 222(D2), mm2(C2v), mmm(D2h)
4(C4)或4(S43) 3(C3)或3(S65) 四 方 4(C4), 4/m(C4h), 4mm(C4v), 4/mmm(D4h), 422 (D4), 4 (S4), 42m (D2d) 三 方 3(C3), 3m (C3v), 32(D3), 3(S6), 3m(D3d) 六 方 6(C6), 6/m(C6h), 6mm(C6v), 6/mmm (D6h), 622 (D6), 6 (C3h), 62 (D3h) 立 方 23(T), m3 (Th), 43m (Td), 432 (O), m3m (Oh)
旋转轴， n
旋转反演轴， n
非点式对称操作
点对称操作：r’ = Rr
r’=x’a + y’b +z’c r=xa + yb +zc
空间群操作：r’ = {R|t}r = Rr + t (赛兹算符) 对非点式操作 t = ，是单胞的分数平移，而对于
点式操作t = = 0
۞ 螺旋轴：11种，21；31、32；41、42、43； 61、62、63、64、65 ۞ 滑移面：a、b、c；n；d
对称轴符号
符 号 对称轴
一次旋转轴 一个反演轴 二次旋转轴
平行于纸面
图示 符号
无
沿轴向的 右手螺旋 平移特征 无 无 无
符 号
对称轴
四次旋转轴