第四章图形的相似练习

合集下载

北师大版九年级上数学《第四章图形的相似》专题练习（含答案）

图形的相似专题练习1．已知△ABC∽△DEF，AB＝1，BC＝3，EF＝5，则△ABC与△DEF的面积比是()A．1∶9 B．1∶25C．9∶25 D．3∶52．如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OB∶OB′＝2∶3，则四边形ABCD与四边形A′B′C′D′的面积比为()图2A．4∶9 B．2∶5C．2∶3 D．2∶ 33．如果3A＝2B(AB≠0)，那么下列比例式中正确的是()A．ab＝32B．ba＝23C．a2＝b3D．a3＝b24．如图，在△ABC中，点D，E分别为边AB，AC上的点，且DE∥B C．若AD＝5，BD＝10，AE＝3，则CE的长为()图4A．3 B．6C．9 D．125．在下面的图形中，相似的一组是(),A) ,B),C) ,D)图56．如图所示，小正方形的边长均为1，则下列选项中阴影部分的三角形与△ABC相似的是(),A) ,B),C) ,D)图67．为测量某河的宽度，小在河对岸选定一个目标点A，再在他所在的这一侧选点B，C，D，使得AB⊥BC，CD⊥BC，然后找出AD与BC的交点E，如图所示．若测得BE＝90 m，EC＝45 m，CD＝60 m，则这条河的宽AB等于()图7A．120 m B．67.5 mC．40 m D．30 m8．如图，在△ABC中，∠A＝70°，AB＝4，AC＝6，将△ABC沿图中的虚线剪开，则剪下的阴影三角形与原三角形不相似的是(),A) ,B),C) ,D)图89．如图，在△ABC 中，D ，E 两点分别在AB ，AC 边上，DE ∥B C ．如果ADDB ＝32，AC ＝10，那么EC ＝________．图910．如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P 处放一水平的平面镜，光线从点A 出发经平面镜反射后刚好到古城墙CD 的顶端C 处．已知AB ⊥BD ，CD ⊥BD ，测得AB ＝2米，BP ＝3米，PD ＝15米，那么该古城墙的高度CD 是_________米．图1011．如图，比例规是一种画图工具，它由长度相等的两脚AD 和BC 交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方(即同时使OA ＝3OD ，OB ＝3OC )，然后张开两脚，使A ，B 两个尖端分别在线段l 的两个端点上，若CD ＝3.2 cm ，则AB 的长为_________ cm.图1112．如图，已知矩形纸片ABCD 中，AB ＝1，剪去正方形ABEF ，得到的矩形ECDF 与矩形ABCD 相似，则AD 的长为__________．图1213．如图，在平面直角坐标系xOy中，以原点为位似中心，线段AB与线段A′B′是位似图形，若A(－1，2)，B(－1，0)，A′(－2，4)，则B′的坐标为___________．图1314．如图，在平面直角坐标系中，△OAB的顶点坐标分别为O(0，0)，A(2，1)，B(1，－2)．(1)以原点O为位似中心，在y轴的右侧画出△OAB的一个位似△OA1B1，使它与△OAB的位似比为2∶1，并分别写出点A，B的对应点A1，B1的坐标；(2)画出将△OAB向左平移2个单位，再向上平移1个单位后得△O2A2B2，并写出点A，B的对应点A2，B2的坐标；(3)△OA1B1和△O2A2B2是位似图形吗？若是，请在图中标出位似中心M，并写出点M的坐标．图1415．如图，在四边形ABCD中，AD∥BC，AB⊥BC，点E在AB上，∠DEC ＝90°.(1)求证：△ADE∽△BEC；(2)若AD＝1，BC＝3，AE＝2，求AB的长．图1516．如图，在正方形ABCD中，点E在边BC上(点E不与点B重合)，连接AE，过点B作BF⊥AE于点F，交CD于点G.(1)求证：△ABF∽△BGC；(2)若AB＝2，G是CD的中点，求AF的长．图1617．如图，BD，CE分别是△ABC的两边上的高，过D作DG⊥BC于G，分别交CE及BA的延长线于F，H，求证：(1)DG2＝BG·CG；(2)BG·CG＝GF·GH.图1718．如图，一圆柱形油桶，高1.5 m，用一根2 m长的木棒从桶盖小口斜插桶内，至另一端的B处，抽出木棒后，量得上面没浸油的部分为1.2 m，求桶内油面高度．图1819．如图，操场上有一根旗杆AH，为测量它的高度，在B和D处各立一根高1.5米的标杆BC，DE，两杆相距30米．测得视线AC与地面的交点为F，视线AE与地面的交点为G，并且H，B，F，D，G都在同一直线上，测得BF为3米，DG为5米，求旗杆AH的高度．图1920．如图1，把两块全等的含45°角的直角三角板ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合．把三角板ABC 固定不动，让三角板DEF绕点D旋转，两边分别与线段AB，BC相交于点P，Q，易说明△APD∽△CDQ.根据以上内容，回答下列问题：(1)如图2，将含30°角的三角板DEF(其中∠EDF＝30°)的锐角顶点D与等腰△ABC(其中∠ABC＝120°)的底边中点O重合，两边DF，DE分别与边AB，BC 相交于点P，Q.写出图中的相似三角形__△APD∽△CDQ__(直接填在横线上)；(2)其他条件不变，将三角板DEF旋转至两边DF，DE分别与边AB的延长线、边BC相交于点P，Q.上述结论还成立吗？请你在图3上补全图形，并说明理由；(3)在(2)的条件下，连接PQ，△APD与△DPQ是否相似？请说明理由；(4)根据(1)(2)的解答过程，你能否将两三角板改为更一般的三角形，使得(1)中的结论仍然成立？若能，请说明两个三角形应满足的条件；若不能，请简要说明理由．,图1),图2),图3)图20参考答案【过关训练】1．C2．A3．C4．B5．C6．A7．A8．D 9．__4__10．__10__11．_9.6__12．_1＋52__13．(－2，0)_14．解：(1)如答图，△OA1B1为所作，点A1，B1的坐标分别为(4，2)，(2，－4)；(2)如答图，△O2A2B2为所作，点A2，B2的坐标分别为(0，2)，(－1，－1)；(3)△OA1B1和△O2A2B2是位似图形，如答图，点M为所，位似中心M的坐标为(－4，2)．15．[解：(1)证明：∵AD∥BC，AB⊥BC，∴AB⊥AD，∠A＝∠B＝90°，∴∠ADE＋∠AED＝90°.∵∠DEC＝90°，∴∠AED＋∠BEC＝90°，∴∠ADE＝∠BEC，∴△ADE∽△BE C．(2)∵△ADE∽△BEC，∴BEAD＝BCAE，即BE1＝32，∴BE＝3 2，∴AB＝AE＋BE＝7 2.16．解：(1)证明：∵四边形ABCD是正方形，∴∠ABE＝∠BCG＝90°.∵BF⊥AE，∴∠BAE＋∠ABF＝90°，∠CBG＋∠ABF＝90°，∴∠BAE＝∠CBG，∴△ABF∽△GB C．(2)∵△ABF∽△BG C．∴ABBG＝AFBC.∵AB＝2，G是CD的中点，四边形ABCD是正方形，∴BC＝2，CG＝1，∴BG＝BC2＋CG2＝5，∴25＝AF2，解得AF＝45 5.17．证明：(1)∵BD⊥AC，DG⊥BC，∴∠BDC＝∠DGC＝90°，∴∠DBC＋∠DCG＝∠GDC＋∠DCG，∴∠GDC＝∠DBC，∴△BDG∽△DCG，∴BG∶DG＝DG∶CG，即DG2＝BG·CG.(2)同(1)中的方法，同理可证△BGH∽△FGC，∴BG∶GF＝GH∶CG，∴BG·CG＝GF·GH.18．解：∵DE∥BC，∴△ADE∽△ABC，∴AEAC＝ADAB，即AE1.5＝1.22，解得AE＝0.9 m，∴EC＝1.5－0.9＝0.6(m)，即油面高0.6 m. 19．解：设AH＝x，BH＝y，由题意知，△AHF∽△CBF，△AHG∽△EDG，∴BFHF＝CBAH，DGHG＝DEAH，∴3x＝1.5×(y＋3)，5x＝1.5×(y＋30＋5)，解得x＝24.则旗杆AH的高度为24 m.20．__△APD∽△CDQ__解：(2)成立，如答图．理由如下：∵AB＝BC，∴∠BAC＝∠BC A．∵∠ABC＝120°，∴∠BAC＝∠BCA＝30°，∴∠ADP＋∠APD＝180°－30°＝150°.∵∠EDF＝30°，∴∠ADP＋∠CDQ＝150°，∴∠APD＝∠CDQ，∴△APD∽△CDQ. (3)△APD∽△DPQ.理由如下：∵△APD∽△CDQ，∴APCD＝DPDQ.∵点D为AC的中点，∴CD＝AD，∴APAD＝DPDQ，即APDP＝ADDQ.又∵∠P AD＝∠PDQ＝30°，∴△APD∽△DPQ.(4)△DEF满足∠EDF＝α，△ABC满足顶角为(180°－2α)的等腰三角形即可．理由：∵∠ABC＝180°－2α，∴∠A＝∠C＝α.∵∠ADP＋∠APD＝180°－α，∠ADP＋∠QDC＝180°－α，∴∠APD＝∠CDQ.又∵∠A＝∠C，∴△APD∽△CDQ.。

第四章图形的相似——证明比例式或等积式的技巧同步练习北师大版数学九年级上册

“十层相似”———相似十大技巧证明比例式或等积式的技巧“三点定型法”是证明线段等积式或比例式以及利用等积式、比例式求线段长时找相似三角形的最常用的方法，即设法找出等积式或比例式（或变化后的式子）中所包含的几个字母，看是否存在可由“三点”确定的两个三角形相似。

通常通过“横看”“竖看”两种方法找相似三角形，横看：即看两比例前项、两比例后项是否分别在两个相似三角形中；竖看：即看比例式等号两边各自的前、后项是否分别在两个相似三角形中。

技巧一：三点定型1．如图，在△ABC 中，点D 、E 分别在AB 、AC 上，∠ADE ＝∠C ，求证：AD •AB ＝AE •AC ．技巧二：等线段代换2．如图，已知在△ABC 中，点D 、E 、F 分别是边AB 、AC 、BC 上的点，且DE ∥BF ，EF ∥BD ，求证：＝FC DE ．技巧三：等比例代换3．如图，在△ABC 中，DE ∥BC ，EF ∥CD ，求证：．技巧四：等积代换4．如图，已知CE是Rt△ABC斜边AB上的高，在EC的延长线上任取一点P，连接AP，BG⊥AP垂足为G，交CE于D，求证：CE2＝PE•DE．5．如图，在△ABC中，D是AB上一点，E是△ABC内一点，DE∥BC，过D作AC的平行线交CE的延长线于F，CF与AB交于P，求证：＝．备注：上述技巧不仅用于证明等积式和比例式的题型，还可以灵活使用在其他题型中。

课堂练习1．如图，已知△ABC是等边三角形，点D、B、C、E在同一条直线上，且∠DAE＝120°，求证：BC2＝CE•DB．2．已知，如图，在Rt△ABC中，CD是斜边上的中线，DE⊥AB交BC于点F，交AC的延长线于点E．求证：（1）△ADE∽△FDB；（2）CD2＝DE•DF．3．已知：如图，在△ABC中，点D，E分别在边AB，BC上，BA•BD＝BC•BE．（1）求证：△BDE∽△BCA；（2）如果AE＝AC，求证：AC2＝AD•AB．4．如图，点D、E分别在△ABC的边AC、AB上，延长DE、CB交于点F，且AE•AB＝AD •AC．（1）求证：∠FEB＝∠C；（2）连接AF，若＝，求证：EF•AB＝AC•FB．5．已知：如图，在△ABC中，点D、E分别在边BC、AC上，点F在DE的延长线上，AD ＝AF，AE•CE＝DE•EF．（1）求证：△ADE∽△ACD；（2）如果AE•BD＝EF•AF，求证：AB＝AC．6．已知：如图，△ADE的顶点E在△ABC的边BC上，DE与AB相交于点F，AE2＝AF•AB，∠DAF＝∠EAC．（1）求证：△ADE∽△ACB；（2）求证：＝．7．如图，M是平行四边形ABCD的对角线上的一点，射线AM与BC交于点F，与DC的延长线交于点H．（1）求证：AM2＝MF•MH．（2）若BC2＝BD•DM，求证：∠AMB＝∠ADC．8．△ABC中，AB＝AC，点D、E、F分别在BC、AB、AC上，∠EDF＝∠B．（1）如图1，求证：DE•CD＝DF•BE；（2）如图2，若D为BC中点，连接EF．求证：ED平分∠BEF．9．如图，已知正方形ABCD，以AB为边在正方形外作等边△ABE，过点E作EF⊥AB与边AB、CD分别交于点F、点G，点O在线段EG上，且DO＝CD．（1）求证：AE∥DO；（2）联结AO、DE，DE分别交AO、AB于点M、Q，求证：．10．如图所示，在等腰三角形ABC中，AB＝AC，点E，F在线段BC上，点Q在线段AB 上，且CF＝BE，AE2＝AQ•AB．求证：（1）∠CAE＝∠BAF；（2）CF•FQ＝AF•BQ．11．已知：如图，在矩形ABCD中，点E在边AD的延长线上，DE＝DC，联结BE，分别交边DC、对角线AC于点F、G，AD＝FD．（1）求证：AC⊥BE；（2）求证：＝．12．已知：如图，在四边形ABCD中，AD∥BC，点E、F分别在边AB、AD上，DE与CF 相交于点G．CD2＝CG•CF，∠AED＝∠CFD．（1）求证：AB＝CD；（2）延长AD至点M，联结CM，当CF＝CM时，求证：EA•AB＝AD•MD．13．如图，已知：△ABC和△ADE都是等边三角形，其中点D在边BC上，点F是AB边上一点，且BF＝CD．（1）求证：DE∥CF；（2）联结DF，设AD、CF的交点为M，如果DF2＝FM•FC，求证：DF∥AC．14．已知：如图，两个△DAB和△EBC中，DA＝DB，EB＝EC，∠ADB＝∠BEC，且点A、B、C在一条直线上，联结AE、ED，AE与BD交于点F．（1）求证：；（2）如果BE2＝BF•BD，求证：DF＝BE．15．已知：如图，四边形ABCD中，∠BAD＝∠BCD＝90°，E为对角线BD的中点，点F 在边AD上，CF交BD于点G，CF∥AE，CF＝BD．（1）求证：四边形AECF为菱形；（2）如果∠DCG＝∠DEC，求证：AE2＝AD•DC．16．如图，AB＝9，AC＝8，P为AB上一点，∠A＝∠CPD＝∠B，连接CD．（1）若AP＝3，求BD的长；（2）若CP平分∠ACD，求证：PD2＝CD•BD．17．如图，在▱ABCD中，对角线AC，BD相交于点O，E为AO上一点，BF⊥BD交DE的延长线于点F，且EF＝DE．（1）求证：四边形ABCD是菱形；（2）DF交AB于点G，若OD2＝OE•OA，求证：DF•AG＝AE•BD．18．如图，将矩形ABCD绕点B旋转，点A落到对角线AC上的点E处，点C、D分别落在点F、G处．（1）联结BG、CG，求证：四边形ABGC是平行四边形；（2）联结GE并延长交边AD于点H，求证：AB2＝AD•AH．19．如图，平行四边形ABCD中，它的两条高DE、BF相交于点H，∠DBC＝45°，BF与AD的延长线相交于点G，连接AH．（1）求证：BH＝AB；（2）求证：AH•BG＝AG•BD．。

第四章相似图形(§4.8)基础练习(含答案)

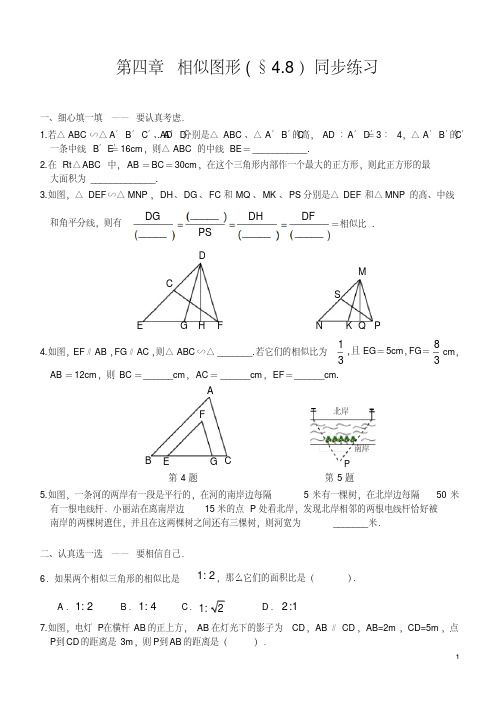
所以（ DE ） 2＝ 1 ，即（
DE
） 2＝
1
,所以
DE ＝2
2
BC
3
26
3
12．由∠ A ＝∠ A , ∠ AED ＝∠ ACB ＝ 90°,故△ ADE ∽△ ABC. 又 AB ＝ 10， BC＝ 6, ∠ C＝ 90°,
1
由勾股定理可得 AC ＝ 8，从而 S△ABC ＝ BC×AC ＝ 24,
）．
A ． 1: 2
B ． 1: 4
C． 1: 2
D ． 2 :1
7.如图，电灯 P在横杆 AB 的正上方， AB 在灯光下的影子为 CD，AB ∥ CD ，AB=2m ，CD=5m ，点
P到 CD 的距离是 3m，则 P到 AB 的距离是（
）．
1
5 A. m
6
6 B. m
7
6 C. m
5
P
10 D. m
.
BC AB 7
（ 1）试说明△ BCD ∽△ BAC ；（ 2）若△ BCD 的周长是 32cm，求△ ABC 的周长 .
A
D
B
C
11．如图，在△ ABC 中， DE ∥ BC，且 S△ADE ： S 四边形 BCED，＝ 1： 2， BC ＝ 2 6 ，求 DE 的长．
2
12．如图，在 △ ABC 中，∠ C＝ 90°，D 是 AC 上一点， DE⊥ AB 于 E，若 AB ＝ 10， BC＝ 6， DE ＝ 2，求四边形 DEBC 的面积．
13.已知：如图，四边形 ABCD 中， AC 平分∠ BAD ，BC ⊥AC ，CD⊥ AD ，且 AB ＝ 18，AC ＝ 12.
（ 1）求 AD 和 CD 的长度；（ 2）若 DE⊥ AC ，CF⊥ AB ，垂足分别为 E， F，求 DE 的值 . CF

第四章相似图形测试(4)(含答案)-

H DF E CB AG第四章相似图形测试(4)一、选择题:1.下列结论正确的是( )A.等腰三角形相似;B.腰长相等的两个等腰三角形相似C.有一个角相等的两个等腰三角形相似D.有一个角对应相等的两个等腰三角形不一定相似2.如图,在□ABCD中,E是AB延长线上一点,H是AD上一点, ED和CH相交于点G,•交BC边于点F,则图中相似的三角形有( )A.3对B.4对C.5对D.6对3.下列四组图形中,必成相似形的是( )A.有一个角是40°的两个等腰三角形;B.有三个角对应相等的两个四边形C.有一个角是105°的两个等腰三角形;D.邻边之比为1:3的两个平行四边形4.已知,a,b,c,d四条线段成比例,其中a=3,c=9,d=15,则线段b的长为( )A.5B.6C. 95D.455.两个相似多边形的面积比是4:9,那么它们的周长比是( )A.4:9B.16:81C.2:3D.9:46.下列命题不正确的是( )A.两个位似图形一定相似;B.位似图形的对应边一定平行C.两个位似图形的位似比就是相似比;D.两个相似图形一定是位似图形二、填空题1.如果23a b cx y z===,那么a b cx y z++++=__________.(其中x+y+z≠0)2.如果长为3cm,5cm,15cm和xcm的线段是成比例线段,那么x=_______.3.△ABC∽△A′B′C′,且AB:A′B′=3:2,且△ABC的周长为18cm,•则这两个三角形的周长和为_____.4.将一个矩形沿两条较长边的中点连线对折,得到的矩形与原矩形相似,则原矩形长与宽的比是_________.5.在Rt△ABC中,∠C=90°,CD⊥AB于D,下面的式子错误的是________.A.AC2=A D·ABB.AB2=A C·BC;C.BC2=B D·ABD.CD2=A D·BD6.某一时刻,一根4米长的旗杆的影长为6•米,•同时附近的一座建筑物的影长为36米,那么这座建筑物高________米.三、计算题1.已知a、b、c、d四条线段成比例,且a=4,d=16,b=c,求线段c的长.2.如图,DE∥BC,AD=5,BD=2,△ADE的面积为20,则梯形DBCE的面积是多少?AD ECB3.如图,D、E分别是△ABC的边AB、AC上的点,∠A=40°,∠C=70°,∠AED=50°,那么AD·AB=AE·AC成立吗?为什么?ADEBC4.如图,小军欲测量学校旗杆AB的高度,他站在旗杆影子上前后移动,•直到他本身影子的顶端与旗杆影子的顶端重叠,此时他距离旗杆2米,已知小军的身高1.6米,•他的影长1米,求旗杆的高度.5.如图,一油桶高1.2米,桶内有油,一根木棒长1.5米,从桶盖小口斜插入桶内,•一端到底,另?一端恰与桶盖小口相齐.抽出木棒,量得棒上未浸油部分长0.5米,•则桶内油的高度是多少6.把如图所示的△ABC放大,且使放大后的△A′B′C′与△ABC相位似,•位似比为2:1,位似中心是BC的中点O.答案:一、1.D 2.B 3.C 4.A 5.C 6.D二、:1 5.B 6.24 三、1.由a 、b 、c 、d 成比例得a cb d= 所以ab=bc,因为b=c,所以c 2=ad=4×16=64,•所以c=8 2.DE ∥BC ⇒∠ADE=∠B,∠AED=∠C ⇒△ADE ∽△ABC⇒22525()()5249ADE ABCS AD SAB ===+ 即202549ABCS=得S △ABC =1965所以S 梯DBCE =S △ABC -S △ADE = 1965-20=9653.成立,理由是∠A=40°,∠C=70°⇒∠B=50° ∠AED=50°△ABC ∽△AED ∠A=∠A⇒AB ACAE AD=⇒AD ·AB=AE ·AC 4.由题意得△ECD ∽△EAB ⇒CD ED AB EB =⇒1.6111AB =+⇒ AB=4.8答:旗杆高4.8米.5.设桶内油的高度是x 米,根据题意得1.20.51.2 1.5x -=解得x=0.8 答:桶内油的高度是0.8米.6.连接OA 、OB 、OC 并延长至A ′、B ′、C ′,使OA ′=2OA,OB ′=2OB,OC ′=2OC,•顺次连接A ′、B ′、C ′,即得△A ′B ′C ′.。

初三数学第四章图形的相似章节练习题及答案

初三数学第四章图形的相似章节练习题及答案刚刚学习过图形的相似这一章节的学生们，大家都掌握了吗下面为大家带来一份初三数学上第四章图形的相似的章节练习题，文末附有答案，有需要的同学可以看一看，更多内容欢迎关注!知识点 1 平行线分线段成比例定理1. 如图，已知直线11 II 12 II 13 , AB=4 BC=6 DE=3 则EF为（）A.2B.4.5C.6D.82. 如图，已知11 II 12 II 13，如果DE： EF=3： 4, BC=8 那么AB 的长是（）A.323B.6C.3D.1633. （乐山中考）如图，1 1 I 12I 13，两条直线与这三条平行线分别交于点A B、C和D E、F.已知ABBC=32则DEDF勺值为（）A.32B.23C.25D.354. 如图，已知11 II 12 II 13 , AB=3 DE=2 EF=4,求AC的长.知识点 2 平行线分线段成比例定理勺推论5. （成都中考）如图，在厶ABC中, DE// BC AD=6 DB=3 AE=4 则EC的长为（）A.1B.2C.3D.46. 如图，在厶ABC中 , D, E分别在AB, AC上,且DE// BC,贝卩下列不成立的比例式是（）A.ADDB=AECEB.ADDB=DEBCC.ADAB=AEACD.ABDB=ACCE7. 已知线段a、b、c,求作线段x使ax二be，下列每个图中的两条虚线都是平行线，则作法正确的是（）8. 如图，已知EG/ BC GF// DC, AE=3 EB=2 AF=6 求AD的值.中档题9. （嘉兴中考）如图，直线11 // 12 // 13 ,直线AC分别交11 ,12 ,13 于点A, B，C;直线DF分别交11，12，13 于点D，E，F，AC与DF相交于点H,且AH=2 HB=1 BC=5则DEEF的值为（）A.12B.2C.25D.3510. （包头中考）如图，在厶ABC中，点D, E，F分别在边AB AC BC上,且DE// BC EF// AB.若AD=2BD 贝卩CFBF的值为（）A.12B.13C.14D.2311. （扬州中考）如图练习本中的横格线都平行且相邻两条横格线间的距离都相等，同一条直线上的三个点A、B、C都在横格线上，若线段AB=4cm 则线段BC= _______ cm.12. 如图已知AD/ BE/ CF 它们依次交直线11 、12 于点A、B、C和点D E、F,如果AB=6 BC=8 DF=21,求DE的长.13. 如图，F是口ABCD勺边CD上一点，连接BF并延长交AD的延长线于点 E. 求证：DEAE=DFDC.14. 如图，在厶ABC中 , DF// AC DE// BC.求证：AE?CB=AC?CF.综合题15. 如图，在矩形ABCD K E是边CB延长线上的点，且EB=ABDE与AB相交于点F, AD=2 CD=1求AE及DF的长.参考答案1.B2.B3.D4. v 11 // 12 // 13，二ABBC=DEEF卩3BC=24「. BC=6.••• AC=AB+BC=3+6=9. 5.B 6.B 7.A 8. v EG/ BCAEEB=AGG又v GF // DC 二AGGC=AFF D.AEEB=AFFD卩32=6FD.「. FD=4.「.AD=AF+FD=10.9.D 10.A 11.12 12. 设DE为x，贝S EF=21-x. v AD// BE// CF, • ABBC 二DEE即68=x21-x.解得x=9.经检验，x=9是原分式方程的解，•DE=9. 13.证明：v 四边形ABCD是平行四边形，• CD// AB AD// BC. •DEAE=EFE同理可得EFEB=DFDC. DEAE=DFDC. 14证明：v DE// BC • ADAB二AEAC.DF// AC • ADAB=CFCB. AEAC=CFCB.AE?CB二AC?CF.5. v 四边形ABCD^矩形，且AD=2CD=1 • BC=AD=2 AB=CD=1 / ABC M C=90°，AB// DC；. EB=AB=1 在Rt△ ABE中, AE 二AB2+BE2二在Rt△ DCE中, DE二DC2+CE2=12+32=T0.AB// DC • EFDF二EBBC=1 设EF二x,贝S DF=2x.v EF+DF=DE • x+2x=10. • x=103.•DF=2x=2310.。

北师大版九年级上册第四章图形的相似各小节练习题(基础)含答案

北师大版九年级上册第四章图形的相似各小节练习题图形的相似及相似图形的性质--巩固练习一．选择题1. 在比例尺为1︰1 000 000的地图上，相距3cm的两地，它们的实际距离为（）A.3kmB.30kmC.300kmD.3 000km2. 下列四条线段中，不能成比例的是（）A.a＝2，b＝4，c＝3，d＝6B.a＝，b＝，c＝1，d＝C.a＝6，b＝4，c＝10，d＝5D.a＝，b＝2，c＝，d＝23. 下列命题正确的是( )A．所有的等腰三角形都相似B．所有的菱形都相似C．所有的矩形都相似D．所有的等腰直角三角形都相似4. 某学习小组在讨论“变化的鱼”时，知道大鱼与小鱼是相似图形，如图所示，则小鱼上的点(a，b)对应大鱼上的点( )A．(-2a，-2b) B．(-a，-2b) C．(-2b，-2a) D．(-2a，-b)5.（2016•兰州模拟）若a：b=2：3，则下列各式中正确的式子是（）A．2a=3b B．3a=2b C．D．6.（2014•闸北区一模）对一个图形进行放缩时，下列说法中正确的是（）A．图形中线段的长度与角的大小都保持不变B．图形中线段的长度与角的大小都会改变C．图形中线段的长度保持不变、角的大小可以改变D．图形中线段的长度可以改变、角的大小保持不变二. 填空题7. （2016•常州）在比例尺为1：40000的地图上，某条道路的长为7cm，则该道路的实际长度是km．8. 若，则________9．已知若-3=,=____;4x y x y y则若5-4=0,x y 则x :y =___. 10.（2015•和平区模拟）有一块三角形的草地，它的一条边长为25m ．在图纸上，这条边的长为5cm ，其他两条边的长都为4cm ，则其他两边的实际长度都是 m ．11. 用一个放大镜看一个四边形ABCD ，若四边形的边长被放大为原来的10倍，下列结论①放大后的∠B 是原来∠B 的10倍；②两个四边形的对应边相等；③两个四边形的对应角相等，则正确的有 . 12. 如图：梯形ADFE 相似于梯形EFCB,若AD=3，BC=4，则______.AEBE=三综合题 13.如果a b c dk b c d a c d a b d a b c====++++++++，一次函数y kx m =+经过点（-1,2），求此一次函数解析式.14.（2014秋•慈溪市期末）一个矩形ABCD 的较短边长为2．（1）如图①，若沿长边对折后得到的矩形与原矩形相似，求它的另一边长；（2）如图②，已知矩形ABCD 的另一边长为4，剪去一个矩形ABEF 后，余下的矩形EFDC 与原矩形相似，求余下矩形EFDC 的面积．15. (2015.新宾县模拟)如图：矩形ABCD的长AB=30，宽BC=20．（1）如图（1）若沿矩形ABCD四周有宽为1的环形区域，图中所形成的两个矩形ABCD与A′B′C′D′相似吗？请说明理由；（2）如图（2），x为多少时，图中的两个矩形ABCD与A′B′C′D′相似？平行线分线段成比例及相似多边形--巩固练习一、选择题1. 下列四组图形中，一定相似的是（） A ．正方形与矩形 B ．正方形与菱形 C ．菱形与菱形 D ．正五边形与正五边形 2相等的是( )AAB EF B CD EF C BO OE D BCBE3．如图，在直角梯形ABCD 中，DC∥AB，∠DAB=90°，AC⊥BC，AC=BC ，∠ABC 的平分线分别交AD、AC 于点E ，F ，则的值是（）4．如图，在平行四边形ABCD 中，AC=4，BD=6，P 是BD 上的任一点，过点P 作EF∥AC，与平行四边形的两条边分别交于点E 、F ，设BP=x ，EF=y ，则能反映y 与x 之间关系的图象是（）A．B ．C ．D ．5．（2015•鄂城区模拟）如图，已知AB∥CD∥EF，AD：AF=3：5，BE=12，那么CE的长等于（）A．2 B．4 C．D．6．如图，直线AB∥CD∥EF，若AC=3，CE=4，则的值是（）A．B．C．D．二、填空题7．（2014秋•江阴市期中）给出下列几何图形：①两个圆；②两个正方形；③两个矩形；④两个正六边形；⑤两个等边三角形；⑥两个直角三角形；⑦两个菱形．其中，一定相似的有（填序号）．8．在一张复印出来的纸上，一个多边形的一条边由原图中的2cm变成了6cm，这次复印的放缩比例是．9．如图，在△ABC中，DE∥BC，AD=2，AB=6，AE=3，则AC的长为．10．如图，在△ABC中，若DE∥BC，=，DE=4cm，则BC的长为．11．如图，直线AD∥BE∥CF，BC=AC，DE=4，那么EF的值是．12．如图，在△ABC中，∠BAC=30°，AB=AC，AD是BC边上的中线，∠ACE=12∠BAC，CE交AB于点E，交AD于点F．若BC=2，则EF的长为．三、解答题13. 如图，直线l1、l2、l3分别交直线l4于点A、B、C，交直线l5于点D、E、F，且l1∥l2∥l3，已知EF：DF=5：8，AC=24．（1）求AB的长；（2）当AD=4，BE=1时，求CF的长．14.（2014秋•慈溪市期末）一个矩形ABCD的较短边长为2．（1）如图①，若沿长边对折后得到的矩形与原矩形相似，求它的另一边长；（2）如图②，已知矩形ABCD的另一边长为4，剪去一个矩形ABEF后，余下的矩形EFDC与原矩形相似，求余下矩形EFDC的面积．15．己知：如图，在菱形ABCD中，点E、F分别在边BC、CD，∠BAF=∠DAE，AE与BD交于点G．（1）求证：BE=DF；（2）当=时，求证：四边形BEFG是平行四边形．探索三角形相似的条件--巩固练习（基础）一、选择题1. 在△ABC和△A1B1C1中，下列四个命题：（1）若AB= A1B1，AC= A1C1，∠A=∠A1，则△ABC≌△A1B1C1；（2）若AB= A1B1，AC= A1C1，∠B=∠B1，则△ABC≌△A1B1C1；（3）若∠A=∠A1，∠C=∠C1，则△ABC∽△A1B1C1；（4）若AC：A1C1=CB：B1C1，∠C=∠C1，则△ABC∽△A1B1C1．其中真命题的个数为（）A． 4个B． 3个C． 2个D． 1个2．（2015•大庆校级模拟）如图，小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△ABC 相似的是（）A．B．C．D．3．）如图，在方格纸中，△ABC和△EPD的顶点均在格点上，要使△ABC∽△EPD，则点P所在的格点为（）A．P1 B． P2 C． P3 D． P44．如图，在△ABC中，如果DE与BC不平行，那么下列条件中，不能判断△ADE∽△ABC的是（）A.4cmB.6cmC.8cmD.10cm二、填空题7.（2015•伊春模拟）如图，在△ABC中，D为AB边上的一点，要使△ABC△△AED成立，还需要添加一个条件为．8．如图，已知四边形ABCD中，∠A=∠B=∠DEC，且点E为AB边中点，则图中有对相似三角形．9．如图，在边长为1的正方形网格中有点P、A、B、C，则图中所形成的三角形中，相似的三角形是．10．在Rt△ABC和Rt△DEF中，∠C=∠F=90°，当AC=3，AB=5，DE=10，EF=8时，Rt△ABC和Rt△DEF 是的．（填“相似”或者“不相似”）11. 如图是一种贝壳的俯视图，点C分线段AB近似于黄金分割．已知AB=10cm，则AC的长约为__________cm（结果精确到0.1cm）.△BDC、△DEC都是黄金三角形，已知AB=4，则DE=__________．三、解答题13. 如图，已知在△ABC与△DEF中，∠C=54°，∠A=47°，∠F=54°，∠E=79°，求证：△ABC∽△DEF．14．如图，△ABC中，∠ABC=60°，AD，CE分别为BC，AB上的高，F为AC的中点，试判断△DEF的形状，并证明你的结论．15.（2014秋•元宝区校级月考）如图，在三角形ABC中，AB=8，AC=16，点P从点B开始沿边BA向点A以2厘米每秒的速度移动，点Q从点A向点C以4厘米每秒的速度移动，如果点P、Q分别从点B、A同时出发，经过多少秒时，以A、P、Q为顶点的三角形与三角形ABC相似？相似三角形判定定理的证明--巩固练习（基础）一、选择题1. 如图，已知∠C=∠E，则不一定能使△ABC∽△ADE的条件是（）A ∠BAD=∠CAEB ∠B=∠DC BC ACDE AE= DAB ACAD AE=2．在Rt△ACB中，∠C=90°，AC=BC，一直角三角板的直角顶角O在AB边的中点上，这块三角板绕O点旋转，两条直角边始终与AC、BC边分别相交于E、F，连接EF，则在运动过程中，△OEF与△ABC的关系是（）A．一定相似B．当E是AC中点时相似 C．不一定相似D．无法判断3．如图，在正方形ABCD中，E是CD的中点，点F在BC上，且FC=BC．图中相似三角形共有（）A． 1对B． 2对C． 3对D． 4对4. （2015•荆州）如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A．∠ABP=∠C B．∠APB=∠ABC C．=D．=5．下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是（）A B C D6．在△ABC与△A′B′C′中，有下列条件：（1）；（2）；（3）∠A=∠A′；（4）∠C=∠C′．如果从中任取两个条件组成一组，那么能判断△ABC∽△A′B′C′的共有多少组（）A． 1 B． 2 C． 3 D． 4二、填空题7.（2015春•工业园区期中）如图，在△ABC中，P为AB上一点，则下列四个条件中（1）∠ACP=∠B；（2）∠APC=∠ACB；（3）AC2=AP•AB；（4）AB•CP=AP•CB，其中能满足△APC和△ACB相似的条件有（填序号）．8．如图，△ABC中，AB＞AC，D，E两点分别在边AC，AB上，且DE与BC不平行．请填上一个你认为合适的条件：，使△ADE∽△ABC．（不再添加其他的字母和线段；只填一个条件，多填不给分！）9．如图，△ABC与△DEF的顶点均在方格纸中的小正方形方格（边长为一个单位长）的顶点处，则△ABC △DEF（在横线上方填写“一定相似”或“不一定相似”或“一定不相似”）．10．如图，AC与BD相交于点O，在△AOB和△DOC中，已知，又因为，可证明△AOB∽△DOC．11．如图，△ABD与△AEC都是等边三角形，AB≠AC，下列结论中：①BE=DC；②∠BOD=60°；③△BOD ∽△COE．正确的序号是．12．如图，D是△ABC的边BC上的一点，∠BAD=∠C，∠ABC的平分线分别与AC、AD相交于点E、F，则图形中共有对相似三角形．（不添加任何辅助线）三、解答题13.（2014秋•射阳县校级月考）如图，在△ABC中，已知∠BAC=90°，AD⊥BC于D，E是AB上一点，AF⊥CE 于F，AD交CE于G点，（1）求证：AC2=CE•CF；（2）若∠B=38°，求∠CFD的度数．14．如图，AB=3AC，BD=3AE，又BD∥AC，点B，A，E在同一条直线上．（1）求证：△ABD∽△CAE；（2）如果AC=BD，AD=2BD，设BD=a，求BC的长．15．已知：正方形ABCD中，E、F分别是边CD、DA上的点，且CE=DF，AE与BF交于点M．（1）求证：△ABF≌△DAE；（2）找出图中与△ABM相似的所有三角形（不添加任何辅助线）．相似三角形的性质及应用--巩固练习一、选择题1．（2015•酒泉）如图，D、E分别是△ABC的边AB、BC上的点，DE△AC，若S△BDE：S△CDE=1：3，则S△DOE：S△AOC的值为（）A．B．C．D．2. （2016•临夏州）如果两个相似三角形的面积比是1：4，那么它们的周长比是（）A．1：16B．1：4C．1：6D．1：23．某校有两块相似的多边形草坪，其面积比为9∶4，其中一块草坪的周长是36米，则另一块草坪的周长是（）．A．24米B．54米C．24米或54米D．36米或54米4. 图为△ABC与△DEC重叠的情形，其中E在BC上，AC交DE于F点，且AB// DE.若△ABC与△DEC的面积相等，且EF=9，AB=12，则DF=( ).A．3 B．7 C．12 D．155．如图是小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12米，那么该古城墙的高度是（）.A．6米 B．8米 C．18米D．24米6.要把一个三角形的面积扩大到原来面积的8倍，而它的形状不变，那么它的边长要增大到原来的（）倍.A.2B.4C.2D.64二、填空题7. 如图所示，为了测量一棵树AB的高度，测量者在D点立一高CD＝2m的标杆，现测量者从E处可以看到杆顶C与树顶A在同一条直线上，如果测得BD＝20m，FD＝4m，EF＝1.8m，则树AB的高度为______m．8. 已知两个相似三角形的相似比为，面积之差为25，则较大三角形的面积为______.9．（2015•吉林）如图，利用标杆BE 测量建筑物的高度，标杆BE 高1.5m ，测得AB=2m ，BC=14cm ，则楼高CD 为m ．10. （2016•徐州）如图，△ABC 中，D 、E 分别为AB 、AC 的中点，则△ADE 与△ABC 的面积比为．11.如图，在平行四边形ABCD 中，点E 为CD 上一点，DE:CE=2:3，连接AE,BE,BD,且AE,BD 交于点F ，则________________.12.把一个三角形改做成和它相似的三角形，如果面积缩小到原来的倍，那么边长应缩小到原来的________倍.三、解答题13. 一位同学想利用树影测量树高，他在某一时刻测得长为1m 的竹竿影长0.9m ，但当他马上测量树影时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子在墙上，如图，他先测得留在墙上的影高1.2m ，又测得地面部分的影长2.7m ，他求得树高是多少？14.（2015•蓬溪县校级模拟）小红用下面的方法来测量学校教学大楼AB 的高度：如图，在水平地面点E 处放一面平面镜，镜子与教学大楼的距离AE=20米．当她与镜子的距离CE=2.5米时，她刚好能从镜::DEF EF BAF S S S △△B △21子中看到教学大楼的顶端B．已知她的眼睛距地面高度DC=1.6米，请你帮助小红测量出大楼AB的高度（注：入射角=反射角）．15. 在正方形中，是上一动点，(与不重合)，使为直角，交正方形一边所在直线于点.(1)找出与相似的三角形.(2)当位于的中点时，与相似的三角形周长为，则的周长为多少？图形的位似--巩固练习一. 选择题1.下面给出了相似的一些命题：（1）菱形都相似；（2）等腰直角三角形都相似；（3）正方形都相似；（4）矩形都相似；（5）正六边形都相似；其中正确的有（）.A．2个 B．3个 C．4个 D．5个2.下列说法错误的是（）.A.位似图形一定是相似图形.B.相似图形不一定是位似图形.C.位似图形上任意一对对应点到位似中心的距离之比等于相似比.D.位似图形中每组对应点所在的直线必相互平行.3.下列说法正确的是（） .A.分别在ABC的边AB、AC的反向延长线上取点D、E，使DE∥BC，则ADE是ABC放大后的图形.B.两位似图形的面积之比等于相似比.C.位似多边形中对应对角线之比等于相似比.D.位似图形的周长之比等于相似比的平方.4．（2016•东营）如图，在平面直角坐标系中，已知点A（﹣3，6），B（﹣9，﹣3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（）A．（﹣1，2）B．（﹣9，18）C．（﹣9，18）或（9，﹣18）D．（﹣1，2）或（1，﹣2）5. 下列命题：①两个正方形是位似图形；②两个等边三角形是位似图形；③两个同心圆是位似图形；④平行于三角形一边的直线截这个三角形的两边，所得的三角形与原三角形是位似图形.其中正确的有( ).A.1个B.2个C.3个D.4个二.填空题8. 如果两个位似图形的对应线段长分别为3cm和5cm，且较小图形周长为30cm，则较大图形周长为__________.9.（2016•三明）如图，在平面直角坐标系中，已知A （1，0），D（3，0），△ABC与△DEF位似，原点O是位似中心．若AB=1.5，则DE=．10．如图，以点O为位似中心，将五边形ABCDE放大后得到五边形，已知OA=10cm，OA′=20cm，则五边形ABCDE的周长与五边形的周长的比值是__________．11. △ABC中，D、E分别在AB、AC上，DE∥BC，△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分，则AD：AB=________.12. 把一矩形纸片对折，如果对折后的矩形与原矩形相似，则原矩形纸片的长与宽之比为____________________.13.（2015•钦州）如图，以O为位似中心，将边长为256的正方形OABC依次作位似变换，经第一次变化后得正方形OA1B1C1，其边长OA1缩小为OA的，经第二次变化后得正方形OA2B2C2，其边长OA2缩小为OA1的，经第，三次变化后得正方形OA3B3C3，其边长OA3缩小为OA2的，…，依次规律，经第n次变化后，所得正方形OA n B n C n的边长为正方形OABC边长的倒数，则n=．A B C D E'''''A B C D E'''''14. 如图，△ABC中，AB=AC=4，∠BAC=36°，∠ABC的平分线与AC边的交点D为边AC的黄金分割点（AD＞DC），则BC=______________.三．综合题15.如图，D、E分别AB、AC上的点.(1)如果DE∥BC，那么△ADE和△ABC是位似图形吗？为什么？(2)如果△ADE和△ABC是位似图形，那么DE∥BC吗？为什么？16.（2014秋•海陵区校级月考）如图，F在BD上，BC、AD相交于点E，且AB△CD△EF，（1）图中有哪几对位似三角形，选其中一对加以证明；（2）若AB=2，CD=3，求EF的长．17. 如图1，矩形ODEF的一边落在矩形ABCO的一边上，并且矩形ODEF∽矩形ABCO，其相似比为1：（1）求矩形ODEF的面积；（2）将图1中的矩形ODEF绕点O逆时针旋转一周，连接EC、EA，△ACE的面积是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，请说明理由．图形的相似及相似图形的性质--巩固练习答案及解析一、选择题1．【答案】B．【解析】图上距离︰实际距离＝比例尺．2．【答案】C．【解析】求出最大与最小的两数的积，以及余下两数的积，看所得积是否相等来鉴别它们是否成比例．3．【答案】 D4．【答案】 A【解析】由图可知，小鱼和大鱼的相似比为1：2，若将小鱼放大1倍，则小鱼和大鱼关于原点对称.5.【答案】B【解析】A、2a=3b⇒a：b=3：2，故选项错误；B、3a=2b⇒a：b=2：3，故选项正确；C、=⇒b：a=2：3，故选项错误；D、=⇒a：b=4：3，故选项错误．故选B．6．【答案】D【解析】根据相似多边形的性质：相似多边形的对应边成比例，对应角相等，∴对一个图形进行收缩时，图形中线段的长度改变，角的大小不变，故选D．二、填空题7.【答案】2.8【解析】设这条道路的实际长度为x，则：，解得x=280000cm=2.8km．∴这条道路的实际长度为2.8km．故答案为：2.88.【答案】【解析】由可得，故填.9.【答案】74;.4510.【答案】20.【解析】设其他两边的实际长度分别为xm 、ym ，由题意得，==，解得x=y=20．即其他两边的实际长度都是20m ．11.【答案】 ③12.【答案】【解析】因为梯形ADFE 相似于梯形EFCB ，所以AD EFEF BC=,即EF=所以AE AD BE EF === 三、解答题13.【解析】∵a b c dk b c d a c d a b d a b c====++++++++∴+1=+1=+1=+1=+1++++++++c a b c dk b c d a c d a b d a b ∴++++++++++++====+1++++++++c a b c d a b c d a b c d a b c dk b c d a c d a b d a b 则分两种情况：（1）+++=0a b c d ，即+1=0k ,=-1k(2)++=++=++=++b c d a c d a b d a b c ,即===,a b c d 1=3k 则所以当=-1k ，过点（-1,2）时，=-+1y x 当1=3k ，过点（-1,2）时，17=+33y x . 14.【解析】解：（1）由已知得MN=AB=2，MD=AD=BC ， △沿长边对折后得到的矩形与原矩形相似， △矩形DMNC 与矩形ABCD 相似，=，△DM •BC=AB •MN ，即BC 2=4， △BC=2，即它的另一边长为2；（2）△矩形EFDC 与原矩形ABCD 相似， △=，△AB=CD=2，BC=4，△DF==1，△矩形EFDC的面积=CD•DF=2×1=2．15.【解析】解：（1）不相似，AB=30，A′B′=28，BC=20，B′C′=18，而≠；（2）矩形ABCD与A′B′C′D′相似，则=，则：=，解得x=1.5，或=，解得x=9．平行线分线段成比例及相似多边形--巩固练习答案及解析一、选择题1．【答案】D；【解析】解：A、正方形与矩形，对应角相等，对应边不一定成比例，故不符合题意；B、正方形与菱形，对应边成比例，对应角不一定相等，不符合相似的定义，故不符合题意；C、菱形与菱形，对应边比值相等，但是对应角不一定相等，故不符合题意；D、正五边形与正五边形，对应角相等，对应边一定成比例，符合相似的定义，故符合题意．故选：D．2.【答案】D.【解析】解：根据AB∥CD∥EF得到：AD BC AF BE．3.【答案】C；【解析】解：作FG⊥AB于点G，∵∠DAB=90°，∴AE∥FG，∴=，∵AC⊥BC，∴∠ACB=90°，又∵BE是∠ABC的平分线，∴FG=FC，在Rt△BGF和Rt△BCF中，∴Rt△BGF≌Rt△BCF（HL），∴CB=GB，∵AC=BC，∴∠CBA=45°，∴AB=BC，∴====+1．故选：C．4.【答案】C；【解析】解：设AC交BD于O，∵四边形ABCD是平行四边形，∴OD=OB=BD=3，当P在OB上时，∵EF∥AC，∴==，∴=，∴y=x，当P在OD上时，同法可得：==，∴=，∴y=﹣x+8，∵两种情况都是一次函数，图象是直线．故选C．5.【答案】C；【解析】∵AB∥CD∥EF，∴=，即=，∴BC=，∴CE=BE﹣BC=12﹣=．故选C．6.【答案】C；【解析】解：∵AB∥CD∥EF∴∵AC=3，CE=4∴=．故选C．二、填空题7．【答案】①②④⑤；8．【答案】1：3；【解析】解：由题意可知，相似多边形的边长之比=相似比=2：6=1：3，故答案为：1：3；9．【答案】9；【解析】解：∵DE∥BC，∴△ADE∽△ABC，∴=，∴=，∴AC=9，故答案为：9．10．【答案】12cm.【解析】解：∵DE∥BC，∴=，又∵=，∴，∴=，∴BC=12cm．故答案为12cm．11．【答案】2.【解析】解：∵BC=AC，∴=，∵AD∥BE∥CF，∴=，∵DE=4，∴=2，∴EF=2．故答案为：2．12．【答案】﹣1.【解析】解：过F点作FG∥BC．∵在△ABC中，AB=AC，AD是BC边上的中线，∴BD=CD=BC=1，∠BAD=∠CAD=∠BAC=15°，AD⊥BC，∵∠ACE=∠BAC，∴∠CAD=∠ACE=15°，∴AF=CF，∵∠ACD=（180°﹣30°）÷2=75°，∴∠DCE=75°﹣15°=60°，∵∠ACE=∠BAC，∴AF=CF.=，在Rt△CDF中， CF=2，DF=221∵FG∥BC，∴GF：BD=AF：AD，即GF：1=2：（2+），解得GF=4﹣2，∴EF：EC=GF：BC，即EF：（EF+2）=（4﹣2）：2，解得EF=﹣1．故答案为：﹣1．三、解答题13.【解析】（1）解：∵l1∥l2∥l3，EF：DF=5：8，AC=24，∴==，∴=，∴BC=15，∴AB=AC﹣BC=24﹣15=9．（2）解：∵l1∥l2∥l3∴==，∴=，∴OB=3，∴OC=BC﹣OB=15﹣3=12，∴==，∴=，∴CF=4．14. 【答案与解析】解：（1）由已知得MN=AB=2，MD=AD=BC，∵沿长边对折后得到的矩形与原矩形相似，∴矩形DMNC与矩形ABCD相似，=，∴DM•BC=AB•MN，即BC2=4，∴BC=2，即它的另一边长为2；（2）∵矩形EFDC与原矩形ABCD相似，∴=，∵AB=CD=2，BC=4，∴DF==1，∴矩形EFDC的面积=CD•DF=2×1=2．15.【解析】证明：（1）∵四边形ABCD是菱形，∴AB=AD，∠ABC=∠ADF，∵∠BAF=∠DAE，∴∠BAF﹣∠EAF=∠DAE﹣∠EAF，即：∠BAE=∠DAF，∴△BAE≌△DAF∴BE=DF；（2）∵四边形ABCD是菱形，∴AD∥BC，∴△ADG∽△EBG∴=又∵BE=DF，=∴==∴GF∥BC （平行线分线段成比例）∴∠DGF=∠DBC∵BC=CD∴∠BDC=∠DBC=∠DGF∴GF=DF=BE∵GF∥BC，GF=BE∴四边形BEFG是平行四边形探索三角形相似的条件--巩固练习答案及解析一、选择题1．【答案】B；【解析】解：（1）若AB=A1B1，AC=A1C1，∠A=∠A1，能用SAS定理判定△ABC≌△A1B1C1，故（1）正确；（2）若AB=A1B1，AC=A1C1，∠B=∠B1，不能用ASS判定△ABC≌△A1B1C1，故（2）错误；（3）若∠A=∠A1，∠C=∠C1，能判定△ABC∽△A1B1C1，故（3）正确；（4）若AC：A1C1=CB：C1B1，∠C=∠C1，能利用两组对应边的比相等且夹角相等的两三角形相似判定△ABC∽△A1B1C1，故（4）正确．正确的个数有3个；故选：B．2.【答案】B.【解析】已知给出的三角形的各边AB、CB、AC分别为、2、、只有选项B的各边为1、、与它的各边对应成比例．故选B．3.【答案】C；【解析】解：∵∠BAC=∠PED，而=，∴=时，△ABC∽△EPD，∵DE=4，∴EP=6，∴点P落在P3处．故选：C．4.【答案】C；【解析】解：A、∠ADE=∠C，∠A=∠A，则可判断△ADE∽△ACB，故本选项错误；B、∠B=∠AED，∠A=∠A，则可判断△ADE∽△ACB，故本选项错误；C、=，此时不等确定∠ADE=∠ACB，故不能确定△ADE∽△ACB，故本选项正确；D、=，∠A=∠A，则可判断△ADE∽△ACB，故本选项错误．故选C．5．【答案】C.【解析】∵点C是线段AB的黄金分割点（AC＞BC），6．【答案】C.【解析】根据已知条件得下半身长是165×0.60=99cm，设需要穿的高跟鞋是ycm，则根据黄金分割的定义得：99+y165+y=0.618，解得：y≈8cm．故选C．二、填空题7.【答案】∠ADE=∠C 或∠AED=∠B或AD AEAC AB.【解析】据判定三角形相似的方法来找条件.8．【答案】；【解析】解：∵∠A=∠B=∠DEC，∴∠1+∠2=∠2+∠4，∴∠1=∠4，又∵∠A=∠B，∴△AED∽△BCE，∴=，∵点E为AB边中点，∴=，∵∠A=∠DEC，∴△AED∽△EDC，∴△AED∽△BCE∽△EDC，故图中有 3对相似三角形．故答案为：3．9．【答案】△APB∽△CPA；【解析】解：△APB∽△CPA，理由如下：由题意可知：AP==，PB=1，PC=5，∴，，∵∠APB=∠CPA，∴△APB∽△CPA，故答案为：△APB∽△CPA．10．【答案】相似;【解析】解：如图所示：∵AC=3，AB=5，DE=10，EF=8，∴BC==4，DF==6，∴==，∵∠C=∠F=90°，∴Rt△ABC∽Rt△DEF．故答案为：相似．11.【答案】6.2或3.8．【解析】由题意知AC：AB=BC：AC，∴AC：AB≈0.618，∴AC=0.618×10cm≈6.2（结果精确到0.1cm）或AC=10-6.2=3.8．故答案为：6.2或3.8．12.【答案】6-25．【解析】根据题意可知，BC=512-AB，∵△ABC顶角是36°的等腰三角形，∴AB=AC，∠ABC=∠C=72°，又∵△BDC也是黄金三角形，∴∠CBD=36°，BC=BD，∴∠ABD=∠ABC-∠CBD=36°=∠A，∴BD=AD，同理可证DE=DC，∴DE=DC=AC-AD=AB-BC=AB-512-AB=6-25．故答案为：6-25．三、解答题13.【解析】解：在△ABC中，∠B=180°﹣∠A﹣∠C=79°，在△ABC和△DEF中，，∴△ABC∽△DEF．14.【解析】解：连接EF，△DEF为等边三角形，由∠ABC=60°，易得：．∴△BDE∽△BAC，∴，∴DE=AC．又∵F为中点，∴在Rt△ADC中，DF=AC，在Rt△ACE中，EF=AC．所以DE=DF=EF．即：△DEF为等边三角形．15.【解析】解：设经过t秒时，以A、P、Q为顶点的三角形与三角形ABC相似，则BP=2t，AP=8﹣2t，AQ=4t，△△PAQ=△BAC，△当=时，△APQ△△ABC，即=，解得t=2（s）；当=时，△APQ△△ACB，即=，解得t=0.8（s）；即经过2秒或0.8秒时，以A、P、Q为顶点的三角形与三角形ABC相似．相似三角形判定定理的证明--巩固练习答案及解析一、选择题1．【答案】D；【解析】由题意得，∠C=∠E，A、若添加∠BAD=∠CAE，则可得∠BAC=∠DAE，利用两角法可判断△ABC∽△ADE，故本选项错误；B、若添加∠B=∠D，利用两角法可判断△ABC∽△ADE，故本选项错误；C、若添加=，利用两边及其夹角法可判断△ABC∽△ADE，故本选项错误；D、若添加=，不能判定△ABC∽△ADE，故本选项正确；故选D．2.【答案】A.【解析】连结OC，∵∠C=90°，AC=BC，∴∠B=45°，∵点O为AB的中点，∴OC=OB，∠ACO=∠BCO=45°，∵∠EOC+∠COF=∠COF+∠BOF=90°，∴∠EOC=∠BOF，在△COE和△BOF中，∴△COE≌△BOF（ASA），∴OE=OF，∴△OEF是等腰直角三角形，∴∠OEF=∠OFE=∠A=∠B=45°，∴△OEF∽△△CAB．故选A．3.【答案】C；【解析】图中相似三角形共有3对．理由如下：∵四边形ABCD是正方形，∴∠D=∠C=90°，AD=DC=CB，∵DE=CE，FC=BC，∴DE：CF=AD：EC=2：1，∴△ADE∽△ECF，∴AE：EF=AD：EC，∠DAE=∠CEF，∴AE：EF=AD：DE，即AD：AE=DE：EF，∵∠DAE+∠AED=90°，∴∠CEF+∠AED=90°，∴∠AEF=90°，∴∠D=∠AEF，∴△ADE∽△AEF，∴△AEF∽△ADE∽△ECF，即△ADE∽△ECF，△ADE∽△AEF，△AEF∽△ECF．故选C．4.【答案】D.【解析】A、当∠ABP=∠C时，又∵∠A=∠A，∴△ABP∽△ACB，故此选项错误；B、当∠APB=∠ABC时，又∵∠A=∠A，∴△ABP∽△ACB，故此选项错误；C、当=时，又∵∠A=∠A，∴△ABP∽△ACB，故此选项错误；D、无法得到△ABP∽△ACB，故此选项正确．故选：D．5.【答案】B；【解析】根据勾股定理，AB==2，BC==，AC==，所以△ABC的三边之比为：2：=1：2：，A、三角形的三边分别为2，=，=3，三边之比为2：：3=：：3，故本选项错误；B、三角形的三边分别为2，4，=2，三边之比为2：4：2=1：2：，故本选项正确；C、三角形的三边分别为2，3，=，三边之比为2：3：，故本选项错误；D、三角形的三边分别为=，=，4，三边之比为：：4，故本选项错误．6.【答案】C；【解析】能判断△ABC∽△A′B′C′的有：（1）（2），（2）（4），（3）（4），∴能判断△ABC∽△A′B′C′的共有3组．故选C．二、填空题7.【答案】（1）、（2）、（3）.【解析】∵∠PAC=∠CAB，∴当∠ACP=∠B时，△ACP∽△APC，所以（1）正确；当∠APC=∠ACB时，△ACP∽△APC，所以（2）正确；当=，即AC2=AP•AB时，△ACP∽△APC，所以（3）正确，（4）错误．故答案为：（1），（2）（3）．8．【答案】∠C=∠2或∠B=∠1或；9．【答案】一定相似；【解析】根据图示知：AB=2，BC=1，AC=；DE=2，EF=，DF=5，∴====，∴△ABC∽△DEF．故答案是：一定相似．10．【答案】∠AOB=∠DOC;【解析】∵=，∠AOB=∠DOC，∴△AOB∽△DOC（两边对应成比例，夹角相等，两三角形相似）．故答案为：∠AOB=∠DOC．11．【答案】①②;【解析】∵△ABD、△AEC都是等边三角形，∴AD=AB，AE=AC，∠DAB=∠CAE=60°，∴∠DAC=∠BAC+60°，∠BAE=∠BAC+60°，∴∠DAC=∠BAE，∴△DAC≌△BAE，∴BE=DC．∴∠ADC=∠ABE，∵∠BOD+∠BDO+∠DBO=180°，∴∠BOD=180°﹣∠BDO﹣∠DBO=180°﹣（60°﹣∠ADC）﹣（60°+∠ABE）=60°，∵△DAC≌△BAE，∴∠ADC=∠ABE，∠AEB=∠ACD，∵∠DBO=∠ABD+∠ABE=60°+∠ABE，∠OCE=∠ACE+∠ACO=60°+∠ACD，∵∠ABE≠∠ACD，∴∠DBO≠∠OCE，∴两个三角形的最大角不相等，∴△BOD不相似于△COE；故答案为：①②．12．【答案】3【解析】在△ABC与△DBA中，∵∠ABD=∠ABD，∠BAD=∠C，∴△ABC∽△DBA，在△ABF与△CBE中，∵BF平分∠ABC，∴∠ABF=∠CBE，又∠BAF=∠BCE，∴△ABF∽△CBE．同理可证得：△ABE∽△DBF，所以图形中共有3对相似三角形．故答案为：3．三、解答题13.【解析】解：（1）∵AD⊥BC，∴∠CFA=90°，∵∠BAC=90°，∴∠CFA=∠BAC，∵∠ACF=∠FCA，∴△CAF∽△CEA，∴=，∴CA2=CE•CF；（2）∵∠CAB=∠CDA，∠ACD=∠BCA，∴△CAD∽△CBA，∴=，∴CA2=CB×CD，同理可得：CA2=CF×CE，∴CD•BC=CF•CE，∴=，∵∠DCF=∠ECB，∴△CDF∽△CEB，∴∠CFD=∠B，∵∠B=38°，∴∠CFD=38°．14.【解析】（1）证明：∵BD∥AC，点B，A，E在同一条直线上，∴∠DBA=∠CAE，又∵==3，∴△ABD∽△CAE；（2）连接BC，∵AB=3AC=3BD，AD=2BD，∴AD2+BD2=8BD2+BD2=9BD2=AB2，∴∠D=90°，由（1）得△ABD∽△CAE∴∠E=∠D=90°，∵AE=BD，EC=AD=BD，AB=3BD，∴在Rt△BCE中，BC2=（AB+AE）2+EC2=（3BD+BD）2+（BD）2=BD2=12a2，∴BC=2a．15.【解析】（1）证明：∵ABCD是正方形，∴AB=AD=CD，∠BAD=∠ADC=90°．∵CE=DF，∴AD﹣DF=CD﹣CE．∴AF=DE．在△ABF与△DAE中，∴△ABF≌△DAE（SAS）．（2）解：与△ABM相似的三角形有：△FAM；△FBA；△EAD，∵△ABF≌△DAE，∴∠FBA=∠EAD．∵∠FBA+∠AFM=90°，∠EAF+∠BAM=90°，∴∠BAM=∠AFM．∴△ABM∽△FAM．同理：△ABM∽△FBA；△ABM∽△EAD．相似三角形的性质及应用--巩固练习答案及解析一．选择题1．【答案】D．【解析】△S△BDE：S△CDE=1：3，△BE：EC=1：3；△BE：BC=1：4；△DE△AC，△△DOE△△AOC，△=，△S△DOE：S△AOC==，故选D．2.【答案】D．【解析】∵两个相似三角形的面积比是1：4，∴两个相似三角形的相似比是1：2，∴两个相似三角形的周长比是1：2.3．【答案】C.4．【答案】B.5．【答案】B.【解析】提示：入射角等于反射角，所以△ABP∽△CDP．6．【答案】C．【解析】提示：面积比等于相似比的平方．二．填空题7．【答案】3.8．【答案】45cm2.9．【答案】12．10.【答案】1：4．【解析】∵D、E分别为AB、AC的中点，∴DE=BC，DE∥BC，∴△ADE∽△ABC，∴=（）2=.11.【答案】4:10:25【解析】∵平行四边形ABCD，∴△DEF∽△BAF,∴∵DE:EC=2:3,∴DE:DC=2:5,即DE:AB=2:5，∴∵△DEF与△BEF是同高的三角形，∴12．.三.综合题2DEFAEBS DES AB⎛⎫= ⎪⎝⎭△△，DEFBAFSS△△DEFBEFSS△△24.510==13．【解析】作CE ∥DA 交AB 于E ，设树高是xm ， ∵ 长为1m 的竹竿影长0.9m ∴即 x ＝4.2m14．【解析】解：如图，△根据反射定律知：△FEB=△FED ， △△BEA=△DEC △△BAE=△DCE=90° △△BAE △△DCE △；△CE=2.5米，DC=1.6米， △；△AB=12.8答：大楼AB 的高为12.8米． 15．【解析】(1)与△BPC 相似的图形可以是图(1)，(2)两种情况： △PDE ∽△BCP ，△PCE ∽△BCP ，△BPE ∽△BCP ．(2)①如图(1)，当点P 位于CD 的中点时，若另一直角边与AD 交于点E ，则∵ △PDE ∽△BCP∴ △PDE 与△BCP 的周长比是1:2 ∴ △BCP 的周长是2a ．②如图(2)，当点P 位于CD 的中点时，若另一直角边与BC 延长线交于点E 时，则， ∵ △PCE ∽△BCP∴ △PCE 与△BCP 的周长比是1:2 ∴ △BCP 的周长是2a ．③如图(2)，当点P 位于CD 的中点时，若另一直角边与BC 延长线交于点E 时， ∴1 1.20.9 2.7x -=12PD BC =12PC BC=BP BC =∵△BPE∽△BCP∴△BPE与△BCP2，∴△BCP．图形的位似--巩固练习答案及解析一、选择题1．【答案】B【解析】（1）菱形的角不一定对应相等，故错误；（2）（3）（5）符合相似的定义，故正确；（4）对应边的比不一定相等．故错误．故正确的是：（2）（3）（5）．故选B ．2．【答案】D.3．【答案】C.4.【答案】D.【解析】∵A （﹣3，6），B （﹣9，﹣3），以原点O 为位似中心，相似比为，把△ABO 缩小，∴点A 的对应点A ′的坐标为（﹣3×，6×）或[﹣3×（﹣），6×（﹣）]，即A ′点的坐标为（﹣1，2）或（1，﹣2）．5．【答案】B【解析】由位似图形的概念可知③和④对，故选B.6．【答案】D.【解析】∵AC ＞BC ，∴AC 是较长的线段，, AB=AC ≈0.618AB ．故选D ．7.【答案】B.【解析】∵AB=1，设AD=x ，则FD=x-1，FE=1，∵四边形EFDC 与矩形ABCD 相似，二、填空题AB 12AC 11x =-8.【答案】50cm.9.【答案】4.5．【解析】∵△ABC 与DEF 是位似图形，它们的位似中心恰好为原点，已知A 点坐标为（1，0），D 点坐标为（3，0），∴AO=2，DO=5，∴==，∵AB=1.5，∴DE=4.5．故答案为：4.5．10.【答案】1：2．【解析】∵五边形ABCDE 与五边形A ′B ′C ′D ′E ′位似，OA=10cm ，OA ′=20cm ，∴五边形ABCDE ∽五边形A ′B ′C ′D ′E ′，且相似比为：OA ：OA ′=10：20=1：2， ∴五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比为：OA ：OA ′=1：2．故答案为：1：2．11.【答案】 .【解析】由BC ∥DE 可得△ADE ∽△ABC ，所以，故.13. 【答案】16.【解析】由图形的变化规律可得×256=，解得n=16．14.【解析】∵AB=AC ，∠A=36°，∴∠ABC=∠C=72°，又BD 平分∠ABC ，∴∠ABD=∠CBD=36°，∴∠BDC=72°，∴BC=BD=AD ，∵D 点是AC 的黄金分割点，三．解答题 15.【答案与解析】(1)△ADE 和 △ABC 是位似图形.理由是：DE ∥BC，所以∠ADE=∠B ， ∠AED=∠C.所以△ADE ∽△ABC ，所以. 又因为点A 是△ADE 和 △ABC 的公共点，点D 和点B 是对应点，点E 和点C是对应点，直线BD 与CE 交于点A ，所以△ADE 和 △ABC 是位似图形.(2)DE ∥BC.理由是：因为△ADE 和△ABC 是位似图形，所以△ADE ∽△ABC所以∠ADE=∠B所以DE ∥BC.16.【答案与解析】解：（1）△DFE 与△DBA ，△BFE 与△BDC ，△AEB 与△DEC 都是位似图形，理由：△AB △CD △EF ，△△DFE △△DBA ，△BFE △△BDC ，△AEB △△DEC ，且对应边都交于一点，△△DFE 与△DBA ，△BFE 与△BDC ，△AEB 与△DEC 都是位似图形；（2）△△BFE △△BDC ，△AEB △△DEC ，AB=2，CD=3，△==， △==，解得：EF=．17.【答案与解析】（1）∵矩形ODEF ∽矩形ABCO ，其相似比为1：4，（2）存在．。

北师大版九年级数学上册第4章《图形的相似》单元练习题(含答案)

北师大版九年级数学上册第4章《图形的相似》单元练习题（含答案）一、单选题1．在如图所示的网格中，以点O 为位似中心，四边形ABCD 的位似图形是（）A ．四边形NPMQB ．四边形NPMRC ．四边形NHMQD ．四边形NHMR2．如图，在正方形网格上有5个三角形（三角形的顶点均在格点上）：①△ABC ，②△ADE ，③△AEF ，④△AFH ，⑤△AHG ，在②至⑤中，与①相似的三角形是（）A ．②④B ．②⑤C ．③④D ．④⑤ 3．生活中到处可见黄金分割的美，如图，在设计人体雕像时，使雕像的腰部以下a 与全身b 的高度比值接近0．618，可以增加视觉美感，若图中b 为2米，则a 约为（）A ．1．24米B ．1．38米C ．1．42米D ．1．62米 4．如图，123l l l ∥∥，若23=AB BC ，15DF =，则EF =（）A ．5B ．6C ．7D ．95．如图，点O 是四边形ABCD 内一点，A '、B '、C '、D 分别是OA 、OB 、OC 、OD 上的点，且::::2:1OA A A OB B B OC CC OD D D '''''''====，若四边形A B C D ''''的面积为12cm 2，则四边形ABCD 的面积为（）A ．18cm 2B ．27cm 2C ．36cm 2D ．54cm 26．已知△ABC 与△A 1B 1C 1是位似图形，位似比是1：3，则△ABC 与△A 1B 1C 1的面积比（）A ．1 ：3B ．1：6C ．1：9D ．3：17．如图，某零件的外径为10cm ，用一个交叉卡钳（两条尺长AC 和BD 相等）可测量零件的内孔直径AB ．如果OA ：OC =OB ：OD =3，且量得CD =3cm ，则零件的厚度x 为（）A ．0.3cmB ．0.5cmC ．0.7cmD ．1cm8．下列图形中，不是相似图形的一组是（）A ．B ．C ．D ．9．如图，在△ABC 中，点D 、E 分别在边AB 、AC 上，下列条件不能满足△ADE ∽△ACB 的条件是（）A ．∠AED =∠BB ．AD AE AC AB = C ．AD ·BC = DE ·ACD ．DE //BC 10．已知23a b =，那么下列等式中成立的是（） A ．23a b = B ．1314a b +=+ C ．53a b b += D ．13a b b -=． 11．如图，在ABC ∆中，AB AC <，将ABC 以点A 为中心逆时针旋转得到ADE ，点D 在BC 边上，DE 交AC 于点F ．下列结论：①AFE DFC △△；②DA 平分BDE ∠；③CDF BAD ∠=∠，其中所有正确结论的序号是（）A ．①②B ．②③C ．①③D ．①②③ 12．如图，ABC 中，点D 是边BC 上一点，下列条件中，不能判定ABC 与ABD △相似的是（）A ．2AB BD BC =⋅B ．BDA BAC ∠=∠ C ．ADC C B ∠=∠+∠D ．AD BC AB AC ⋅=⋅二、填空题13．在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果．如图，利用黄金分割法，所做EF 将矩形窗框ABCD 分为上下两部分，其中E 为边AB 的黄金分割点，即2BE AE AB =⋅．已知AB 为2米，则线段BE 的长为______米．14．为了测量河宽AB ，某同学采用以下方法：如图，取一根标尺，把它横放，使CD ∥AB ，并使点B ，D ，O 和点A ，C ，O 分别在同一条直线上，量得CD ＝10米，OC ＝15米，OA ＝45米，则河宽AB ＝______米．15．如图，△ABC 与△A B C '''是位似图形，点O 是位似中心，若3OA AA '=，9ABC S =，则A B C S '''=________．16．如图，四边形ABCD 中，对角线AC BD 、交于点O ，2AO =，4=AD ，6OC =，8BC =，如果DAO CBO ∠=∠，那么ABCD ∶的值是___________．17．在平面直角坐标系中，点O 为坐标原点，点A 的坐标为（3，4），点B 的坐标为（7，0），D ，E 分别是线段AO ，AB 上的点，以DE 所在直线为对称轴，把△ADE 作轴对称变换得△A′DE ，点A′恰好在x 轴上，若△OA′D 与△OAB 相似，则OA′的长为________.（结果保留2个有效数字）18．如图所示，在ABC 中，90C ∠=︒，4AC =，3BC =．（1）如图1，四边形DEFG 为ABC 的内接正方形，则正方形DEFG 的边长为_________；（2）如图2，若ABC 内有并排的n 个全等的正方形，它们组成的矩形内接于ABC ，则正方形的边长为_________．三、解答题19．如图，DA ⊥AB 于A ，EB ⊥AB 于B ，C 是AB 上的动点，若∠DCE =90°．求证：△ACD ∽△BEC20．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC 于点D，过点D作CA的平行线，交边AB于点E．(1)求线段DE的长；(2)取线段AD的中点M，连接BM，交线段DE于点F，延长线段BM交边AC于点G，求EF DF的值．21．如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上、已知纸板的两条边DF＝0.5m，EF＝0.3m，测得边DF离地面的高度AC＝1.5m，CD＝10m，求树高AB．22．已知a、b、c是△ABC的三边，且满足438324a b c+++==，且a+b+c=12，请你探索△ABC的形状．23．如图，小明家窗外有一堵围墙AB，由于围墙的遮挡，清晨太阳光恰好从窗户的最高点C射进房间的地板F处，中午太阳光恰好能从窗户的最低点D射进房间的地板E处，小明测得窗子距地面的高度OD＝1m，窗高CD＝1.5m，并测得OE＝1m，OF＝5m，求围墙AB的高度．24．如图，在△ABC和△ADE中，AB＝AC，AD＝AE，且∠BAC＝∠DAE．点M，N分别是BD，CE的中点，连接AM，AN，MN．（1）求证：△CAE≌△BAD；（2）求证：△AMN∽△ABC；（3）若AC＝6，AE＝4，∠EAC＝60°，求AN的长．25．如图，小明同学为了测量路灯OP 的高度，先将长2m 的竹竿竖直立在水平地面上的B 处，测得竹竿的影长3m BE =，然后将竹竿向远离路灯的方向移动5m 到D 处，即5m BD =，测得竹竿的影长5m DF =（AB 、CD 为竹竿）．求路灯OP 的高度．26．如图，在ABC 中，90B ，12cm AB =，24cm BC =，动点P 从点A 开始沿着边AB 向点B 以2cm s 的速度移动（不与点B 重合），动点Q 从点B 开始沿着边BC 向点C 以4cm s 的速度移动（不与点C 重合）．若P 、Q 两点同时移动()s t ．(1)当移动几秒时，BPQ 的面积为232cm ．(2)设四边形APQC 的面积为()2cm S ，当移动几秒时，四边形APQC 的面积为2108cm ？(3)当移动几秒时，BPQ与ABC相似？27．如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.5米，到旗杆的水平距离DC＝20米，求旗杆的高度．28．如图，在△ABC中，∠ACB＝90°，CD是高，BE平分∠ABC．BE分别与AC，CD相交于点E，F．（1）求证：△AEB∽△CFB；EF ，BD＝6．求AD的长．（2）若CE＝5，25参考答案1．A2．A3．A4．D5．B6．C7．B8．D9．C10．C11．D12．D 13．(51)##1514．3015．1616．2317．2.0或3.318．6037602512n+19．证明：∵AD⊥AB，BE⊥AB，∴∠DAC=90°=∠EBC，∴∠D+∠ACD=90°，∠E+∠ECB=90°，∵∠DCE=90°，∴∠DCA+∠ECB=90°，∴∠D=∠ECB，∵∠DAC=90°=∠EBC，∴△ACD∽△BEC．20．解：∵AD平分∠BAC，∠BAC＝60°，∴∠DAC＝30°，在Rt△ACD中，∠ACD＝90°，∠DAC＝30°，AC＝6，∴CD＝3在Rt△ACB中，∠ACB＝90°，∠BAC＝60°，AC＝6，∴BC＝3∴BD＝BC－CD＝43∵DE∥CA，∴DECA23 BDBC==，∴DE＝4；（2）解：如图．∵点M 是线段AD 的中点，∴DM ＝AM ，∵DE ∥CA ， ∴DF AG ＝DM AM ． ∴DF ＝AG ．∵DE ∥CA ，∴EF AG ＝BF BG ，BF BG ＝BD BC ． ∴EF AG ＝BD BC ． ∵BD ＝43， BC ＝63， DF ＝AG ， ∴23EF DF =．21．解：∵∠DEF ＝∠BCD ＝90°，∠D ＝∠D ，∴△DEF ∽△DCB ， ∴BC DC EF DE=， ∵DF ＝0.5 m ，EF ＝0.3 m ，AC ＝1.5 m ，CD ＝10 m ，由勾股定理得DE 22DF EF -0.4 m ，∴100.30.4BC =， ∴BC ＝7.5m ，∴AB ＝AC +BC ＝1.5+7.5＝9（m ），答：树高AB 是9m ．22．解：令438324a b c +++===k ， ∴a +4=3k ，b +3=2k ，c +8=4k ，∴a =3k ﹣4，b =2k ﹣3，c =4k ﹣8，又∵a +b +c =12，∴（3k ﹣4）+（2k ﹣3）+（4k ﹣8）=12，∴k =3，∴a =5，b =3，c =4，∵32+42=52，∴△ABC 是直角三角形．23．解：延长OD ，∵DO ⊥BF ，∴∠DOE=90°，∵OD=1m ，OE=1m ，∴∠DEB=45°，∵AB ⊥BF ，∴∠BAE=45°，∴AB=BE ，设AB=EB=x m ，∵AB ⊥BF ，CO ⊥BF ，∴AB ∥CO ，∴△ABF ∽△COF ， ∴ABCOBF OF =，1.51(51)5x x +∴=+-，解得：x=4．经检验：x=4是原方程的解．答：围墙AB 的高度是4m ．24．（1）∵∠BAC=∠AE ，∴∠BAC-∠BAE=∠DAE-∠BAE ，∴∠EAC=∠DAB ，在△CAE 与△BAD 中，AB AC EAC DAB AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△CAE ≌△BAD （SAS ）；（2）由（1）得△CAE ≌△BAD ，∴∠ACE=∠ABD ，CE=BD ，∵M 、N 分别是BD ，CE 的中点，∴CN=BM ，在△CAN 与△BAM 中，AC AB ACE ABD CN BM =⎧⎪∠=∠⎨⎪=⎩，∴△CAN ≌△BAM （SAS ），∴AN=AM ，∠CAN=∠BAM ，∴∠CAN+∠BAN=∠BAM+∠BAN ，即∠CAB=∠NAM ，∵AC=AB ，AN=AM ， ∴AN AM AC AB=， ∴△AMN ∽△ABC ；（3）取AC 的中点F ，连接FN ，过点点N 作NG ⊥AC 于点G ，∵点N 是CE 的中点，∴NF ∥AE ，NF=12AE=2，∴∠GFN=∠EAC=60°，∴∠FNG=30°，∴FG=12FN=1，∴AG=1+3=4，2221-3在Rt △ANG 中，根据勾股定理可知：1925．解：由已知得，2AB CD ==m ，3BE =m ，5BD =m ，5DF =m ， 90POE ABE CDF ∠=∠=∠=︒，AEB PEO ∠=∠，CFD PFO ∠=∠，∴在EAB ∆和EPO ∆中，AEB PEO ABE POE∠=∠⎧⎨∠=∠⎩， ∴EAB ∆∽EPO ∆ ∴AB OP BE OE =，即233OP OB =+， ∴263OB OP +=，在FCD ∆和FPO ∆中CFD PFO CDF POF ∠=∠⎧⎨∠=∠⎩， ∴FCD ∆∽FPO ∆， ∴CD OP DF OF =，即2510OP OB =+， ∴2205OB OP +=，∴263OB OP +=，2205OB OP +=，∴7.5OB =，7OP =，即路灯OP 的高度为7m ．26．（1）求出运动时间为t 秒时PB 、BQ 的长度，根据三角形的面积公式结合△BPQ 的面积为32cm 2，即可得出关于t 的一元二次方程，解之即可得出结论；（2）用△ABC 的面积减去△BPQ 的面积即可得出S ，令其等于108即可得出关于t 的一元二次方程，解之即可得出结论；（3）分两种情况：①当△BPQ ∽△BAC 时，②当△BPQ ∽△BCA 时，分别利用相似三角形的性质列式求解即可．（1）解：运动时间为t 秒时（0≤t ＜6），PB ＝12−2t ，BQ ＝4t ，由题意得：S △BPQ ＝12PB ·BQ ＝12（12−2t ）·4t ＝2244t t -＝32，解得：t 1＝2，t 2＝4，答：当移动2秒或4秒时，△BPQ 的面积为32cm 2；（2）由题意得：()2212444241441082ABC BPQ S S S AB BC t t t t =-=⋅--=-+=△△，解得：t ＝3，答：当移动3秒时，四边形APQC 的面积为108cm 2；（3）分两种情况：①当△BPQ ∽△BAC 时，则BP BQ BA BC=，即12241224t t -=，解得：3t =，②当△BPQ ∽△BCA 时，则BP BQ BC BA=，即12242412t t -=，解得：65t =，综上，当移动3秒或65秒时，BPQ 与ABC 相似． 27．解：由题意可得：△DEF ∽△DCA ，则DE EF DC AC=， ∵DE ＝0.5米，EF ＝0.25米，DG ＝1.5m ，DC ＝20m ， ∴0.50.2520AC=，解得：AC ＝10，故AB ＝AC+BC ＝10+1.5＝11.5（m ）．答：旗杆的高度为11．5m ．28．（1）证明：90ACB ∠=︒，90ACD BCD ∴∠+∠=︒， CD 为AB 边上的高，90A ACD ∴∠+∠=︒，A BCD ∴∠=∠， BE 是ABC ∠的平分线，ABE CBE ∴∠=∠，AEB CFB ∴∆∆∽．（2）解：如图，作CH EF ⊥于H ．∵∠BFD +∠ABE =90°，∠CEB +∠CBE =90°，∠ABE =∠CBE ， ∴∠BFD =∠CEB ，∵∠BFD =∠CFE ，CEF CFE ∴∠=∠，CEF ∴为等腰三角形，CE CF ∴=，CH EF ⊥，∴点H 为EF 的中点，5EH FH ∴==，22225(5)25CH EC EH ∴--=,90BFD CFH CHF BDF ∠=∠∠=∠=︒，BFD CFH ∴∆∆∽， ∴DF BD HF CH =， ∴5253DF ∴=，8CD CF DF =+=，90ADC CDB ∠==︒，,ECH FCH FBD CBF ∠=∠∠=∠，根据BFD CFH ∆∆∽，即FCH FBD ∠=∠，ACD CBD∴∆∆∽，∴AD CD CD BD=，∴8 86 AD=，323 AD∴=．。

北师大版九年级数学上册第四章《图形的相似》单元同步测试题及答案 (1)

图形的相似单元同步练习（典型题汇总）一、选择题1．如图，Rt△ABC中，∠C=90°，D是AC边上一点，AB=5，AC=4，若△ABC∽△BDC，则CD=（）A．2 B．C．D．2．（易错题）已知：如图，∠ADE=∠ACD=∠ABC，图中相似三角形共有（）A．1对B．2对C．3对D．4对3．如图，线段AB两个端点的坐标分别是A（6，4），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C的坐标为（）A．（3，2）B．（4，1）C．（3，1）D．（4，2）4．已知△ABC中，DE∥BC，AD=4，DB=6，AE=3，则AC的值是（）A．4.5 B．5.5 C．6.5 D．7.55．若两个相似三角形的相似比是1：4，则它们的周长比是（）A．1：2 B．1：4 C．1：16 D．1：56．如图，P是Rt△ABC斜边AB上任意一点（A，B两点除外），过P点作一直线，使截得的三角形与Rt△ABC相似，这样的直线可以作（）A．1条B．2条C．3条D．4条7．若△ABC∽△A′B′C′，∠A=40°，∠B=60°，则∠C′等于（）A．20°B．40°C．60°D．80°8．如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O，若AD=1，BC=3，则的值为（）A．B．C．D．9．如图，小明作出了边长为1的第1个正△A1B1C1，算出了正△A1B1C1的面积．然后分别取△A1B1C1三边的中点A2、B2、C2，作出了第2个正△A2B2C2，算出了正△A2B2C2的面积．用同样的方法，作出了第3个正△A3B3C3，算出了正△A3B3C3的面积…，由此可得，第10个正△A10B10C10的面积是（）A． B．C．D．10．关于相似的下列说法正确的是（）A．所有直角三角形相似B．所有等腰三角形相似C．有一角是80°的等腰三角形相似D．所有等腰直角三角形相似11．在小孔成像问题中，根据如图所示，若O到AB的距离是18cm，O到CD的距离是6cm，则像CD的长是物体AB长的（）A．3倍B．C．D．2倍12．如图，P是△ABC的边AC上一点，连接BP，以下条件中不能判定△ABP∽△ACB的是（）A．B．C．∠ABP=∠C D．∠APB=∠ABC 二．填空题13．如图，要得到△ABC∽△ADE，只需要再添加一个条件是______．14．若x：y=2：3，那么x：（x+y）=______．15．如图，AD为△ABC的中线，G为△ABC的重心，若S△BGC =2，则S△ABD=______．16．已知，则=______．17．如图，DE∥BC，AD：DB=3：5，则△ADE与△ABC的面积之比为______．18．为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子放在离树底（B）8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.4米，观察者目高CD=1.6米，则树（AB）的高度为______米．19．如图，在梯形ABCD中，AD∥BC，BE平分∠ABC交CD于E，且BE⊥CD，CE：ED=2：1．如果△BEC的面积为2，那么四边形ABED的面积是______．20．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，则窗口底边离地面的高BC=______m．三．解答题21．（2015秋•滕州市校级期末）如图，Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，一动点P从点A出发沿边AC向点C以1cm/s的速度运动，另一动点Q同时从点C出发沿CB 边向点B以2cm/s的速度运动．问：（1）运动几秒时，△CPQ的面积是8cm2？（2）运动几秒时，△CPQ与△ABC相似？22．（2016•颍泉区一模）如图，在由边长为1的单位正方形组成的网格中，按要求画出坐标系及△A1B1C1及△A2B2C2；（1）若点A、C的坐标分别为（﹣3，0）、（﹣2，3），请画出平面直角坐标系并指出点B的坐标；（2）画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1；（3）以图中的点D为位似中心，将△A1B1C1作位似变换且把边长放大到原来的两倍，得到△A2B2C2．23．（2013•泰安）如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB 的中点，（1）求证：AC2=AB•AD；（2）求证：CE∥AD；（3）若AD=4，AB=6，求的值．24．（2011•武汉）（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：=；（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．①如图2，若AB=AC=1，直接写出MN的长；②如图3，求证：MN2=DM•EN．25．（2006•山西）某中学初三（2）班数学活动小组利用周日开展课外实践活动，他们要在湖面上测量建在地面上某塔AB的高度．如图，在湖面上点C测得塔顶A的仰角为45°，沿直线CD向塔AB方向前进18米到达点D，测得塔顶A的仰角为60度．已知湖面低于地平面1米，请你帮他们计算出塔AB的高度．（结果保留根号）参考答案与试题解析一、选择题1．如图，Rt△ABC中，∠C=90°，D是AC边上一点，AB=5，AC=4，若△ABC∽△BDC，则CD=（）A．2 B．C．D．【考点】相似三角形的性质．【分析】根据△ABC∽△BDC，利用相似三角形对应边成比例解答即可．【解答】解：∵∠C=90°，AB=5，AC=4∴BC=3∵△ABC∽△BDC∴∴∴CD=．故选D．【点评】此题考查了相似三角形的性质，相似三角形的对应角相等，对应边的比相等，还考查了勾股定理．2．（易错题）已知：如图，∠ADE=∠ACD=∠ABC，图中相似三角形共有（）A．1对B．2对C．3对D．4对【考点】相似三角形的判定；平行线的判定．【分析】根据已知先判定线段DE∥BC，再根据相似三角形的判定方法进行分析，从而得到答案．【解答】解：∵∠ADE=∠ACD=∠ABC∴DE∥BC∴△ADE∽△ABC，∵DE∥BC∴∠EDC=∠DCB，∵∠ACD=∠ABC，∴△EDC∽△DCB，同理：∠ACD=∠ABC，∠A=∠A，∴△ABC∽△ACD，∵△ADE∽△ABC，△ABC∽△ACD，∴△ADE∽△ACD∴共4对故选D．【点评】考查了平行线的判定；相似三角形的判定：（1）两角对应相等的两个三角形相似；（2）两边对应成比例且夹角相等的两个三角形相似；（3）三边对应成比例的两个三角形相似；（4）如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．3．如图，线段AB两个端点的坐标分别是A（6，4），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C的坐标为（）A．（3，2） B．（4，1） C．（3，1） D．（4，2）【考点】位似变换；坐标与图形性质．【分析】利用位似图形的性质结合两图形的位似比进而得出C点坐标．【解答】解：∵线段AB的两个端点坐标分别为A（6，4），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，∴端点C的横坐标和纵坐标都变为A点的一半，∴端点C的坐标为：（3，2）．故选：A．【点评】此题主要考查了位似图形的性质，利用两图形的位似比得出对应点横纵坐标关系是解题关键．4．已知△ABC中，DE∥BC，AD=4，DB=6，AE=3，则AC的值是（）A．4.5 B．5.5 C．6.5 D．7.5【考点】平行线分线段成比例．【分析】利用平行线分线段成比例的性质得出=，进而求出EC即可得出答案．【解答】解：∵DE∥BC，∴=，∴=，解得：EC=4.5，故AC=AE+EC=4.5+3=7.5．故选：D．【点评】此题主要考查了平行线分线段成比例定理，得出=是解题关键．5．若两个相似三角形的相似比是1：4，则它们的周长比是（）A．1：2 B．1：4 C．1：16 D．1：5【考点】相似三角形的性质．【分析】根据相似三角形周长的比等于相似比进行解答即可．【解答】解：∵两个相似三角形的相似比为1：4，∴它们对应周长的比为1：4．故选B．【点评】本题考查的是相似三角形的性质，即相似三角形周长的比等于相似比．6．如图，P是Rt△ABC斜边AB上任意一点（A，B两点除外），过P点作一直线，使截得的三角形与Rt△ABC相似，这样的直线可以作（）A．1条B．2条C．3条D．4条【考点】相似三角形的判定．【分析】本题要根据相似三角形的判定方法进行求解．【解答】解：过点P可作PE∥BC或PE∥AC，可得相似三角形；过点P还可作PE⊥AB，可得：∠EPA=∠C=90°，∠A=∠A，∴△APE∽△ACB；所以共有3条．故选：C．【点评】此题考查了相似三角形的判定：①有两个对应角相等的三角形相似；②有两个对应边的比相等，且其夹角相等，则两个三角形相似；③三组对应边的比相等，则两个三角形相似．7．若△ABC∽△A′B′C′，∠A=40°，∠B=60°，则∠C′等于（）A．20°B．40°C．60°D．80°【考点】相似三角形的性质．【分析】根据三角形的内角和定理求出∠C，再根据相似三角形对应角相等可得∠C′=∠C．【解答】解：∵∠A=40°，∠B=60°，∴∠C=180°﹣∠A﹣∠B=180°﹣40°﹣60°=80°，∵△ABC∽△A′B′C′，∴∠C′=∠C=80°．故选D．【点评】本题考查了相似三角形对应角相等的性质，三角形的内角和定理，是基础题，熟记性质是解题的关键．8．如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O，若AD=1，BC=3，则的值为（）A．B．C．D．【考点】相似三角形的判定与性质；梯形．【分析】根据梯形的性质容易证明△AOD∽△COB，然后利用相似三角形的性质即可得到AO：CO的值．【解答】解：∵四边形ABCD是梯形，∴AD∥CB，∴△AOD∽△COB，∴，∵AD=1，BC=3．∴=．故选B．【点评】此题主要考查了梯形的性质，利用梯形的上下底平行得到三角形相似，然后用相似三角形的性质解决问题．9．如图，小明作出了边长为1的第1个正△A1B1C1，算出了正△A1B1C1的面积．然后分别取△A1B1C1三边的中点A2、B2、C2，作出了第2个正△A2B2C2，算出了正△A2B2C2的面积．用同样的方法，作出了第3个正△A3B3C3，算出了正△A3B3C3的面积…，由此可得，第10个正△A10B10C10的面积是（）A． B．C．D．【考点】相似三角形的性质；等边三角形的性质；三角形中位线定理．【分析】根据相似三角形的性质，先求出正△A2B2C2，正△A3B3C3的面积，依此类推△A n B n C n 的面积是（）n﹣1，从而求出第10个正△A10B10C10的面积．【解答】解：正△A1B1C1的面积是，而△A2B2C2与△A1B1C1相似，并且相似比是1：2，则面积的比是，则正△A2B2C2的面积是×；因而正△A3B3C3与正△A2B2C2的面积的比也是，面积是（）2；依此类推△A n B n C n与△A n﹣1B n﹣1C n﹣1的面积的比是，第n个三角形的面积是（）n﹣1．所以第10个正△A10B10C10的面积是，故选A．【点评】本题考查了相似三角形的性质及应用，相似三角形面积的比等于相似比的平方，找出规律是关键．10．关于相似的下列说法正确的是（）A．所有直角三角形相似B．所有等腰三角形相似C．有一角是80°的等腰三角形相似D．所有等腰直角三角形相似【考点】相似三角形的判定．【分析】根据有两组角对应相等的两个三角形相似，可知所有直角三角形不一定相似；所有等腰三角形不一定相似；有一角是80°的等腰三角形也比一定相似；只有所有等腰直角三角形相似．【解答】解：A、所有直角三角形不一定相似；故本选项错误；B、所有等腰三角形不一定相似；故本选项错误；C、∵有一角是80°的等腰三角形可能是：80°、80°、20°或80°、50°、50°，∴不一定相似；故本选项错误；D、所有等腰直角三角形相似；故本选项正确．故选D．【点评】此题考查了相似三角形的判定．注意有两组角对应相等的两个三角形相似．11．在小孔成像问题中，根据如图所示，若O到AB的距离是18cm，O到CD的距离是6cm，则像CD的长是物体AB长的（）A．3倍B．C．D．2倍【考点】相似三角形的应用．【分析】作OE⊥AB于E，OF⊥CD于F，根据题意得到△AOB∽△COD，根据相似三角形的对应高的比等于相似比计算即可．【解答】解：作OE⊥AB于E，OF⊥CD于F，由题意得，AB∥CD，∴△AOB∽△COD，∴==，∴像CD的长是物体AB长的，故选：C．【点评】本题考查的是相似三角形的应用，掌握相似三角形的对应高的比等于相似比是解题的关键．12．如图，P是△ABC的边AC上一点，连接BP，以下条件中不能判定△ABP∽△ACB的是（）A．B．C．∠ABP=∠C D．∠APB=∠ABC【考点】相似三角形的判定．【分析】根据已知及相似三角形的判定方法对各个选项进行分析从而得到最后的答案．【解答】解：A正确，符合两组对应边的比相等且相应的夹角相等的两个三角形相似；B不正确，不符合两组对应边的比相等且相应的夹角相等的两个三角形相似；C正确，符合有两组角对应相等的两个三角形相似；D正确，符合有两组角对应相等的两个三角形相似．故选B．【点评】考查相似三角形的判定定理：（1）两角对应相等的两个三角形相似；（2）两边对应成比例且夹角相等的两个三角形相似；（3）三边对应成比例的两个三角形相似；（4）如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．二．填空题13．如图，要得到△ABC∽△ADE，只需要再添加一个条件是DE∥BC（答案不唯一）．【考点】相似三角形的判定．【分析】由图可得，两三角形已有一组角对应相等，再加一组角对应相等即可．【解答】解：由图可得，∠BAC=∠DAE，根据三角形的判定：两角对应相等，两三角形相似．可添加条件：DE∥BC，则∠ABC=∠ADE，则△ADE∽△ABC，故答案为：DE∥BC（答案不唯一）．【点评】本题考查了相似三角形的判定，此题为开放性试题，首先要找出已经满足的条件，然后再进一步分析需要添加的条件，熟记相似三角形的各种判定方法是解题关键．14．若x：y=2：3，那么x：（x+y）=2：5．【考点】比例的性质．【分析】利用合比性质计算．【解答】解：∵=，∴==．故答案为2：5．【点评】本题考查了比例的性质：常用的性质有：内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质．15．如图，AD为△ABC的中线，G为△ABC的重心，若S△BGC =2，则S△ABD=3．【考点】三角形的重心．【分析】根据重心到顶点的距离是它到对边中点的距离的2倍和已知求出△ABC的面积，根据三角形的中心把三角形分成面积相等的两部分解答即可．【解答】解：∵G为△ABC的重心，∴AD=2GD，=2，∵S△BGC=6，∴S△ABC∵AD为△ABC的中线，=3，∴S△ABD故答案为：3．【点评】本题考查的是三角形的重心的知识，掌握重心到顶点的距离是它到对边中点的距离的2倍是解题的关键．16．已知，则=．【考点】比例的性质．【分析】先由已知条件可得a=b，e=f，再把它们代入，计算即可．【解答】解：∵，∴a=b，e=f，∴===．故答案为．【点评】本题考查了比例的计算及性质，比较简单．本题还可以根据等比性质直接求解．17．如图，DE∥BC，AD：DB=3：5，则△ADE与△ABC的面积之比为9：64．【考点】相似三角形的判定与性质．【分析】先证明△ADE与△ABC相似并求出相似比，再根据相似三角形面积的比等于相似比的平方即可求出．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∵AD：BD=3：5，∴AD：AB=3：8，∴△ADE与△ABC面积之比=9：64，故答案为9：64．【点评】本题主要考查相似三角形面积的比等于相似比的平方的性质，根据平行得到三角形相似是解题的关键．18．为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子放在离树底（B）8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.4米，观察者目高CD=1.6米，则树（AB）的高度为 5.6米．【考点】相似三角形的应用．【分析】根据镜面反射的性质求出△ABE∽△CDE，再根据其相似比解答．【解答】解：根据题意，易得∠CDE=∠ABE=90°，∠CED=∠AEB，则△ABE∽△CDE，则，即，解得：AB=5.6米．故答案为：5.6．【点评】应用反射的基本性质，得出三角形相似，运用相似比即可解答．19．如图，在梯形ABCD 中，AD ∥BC ，BE 平分∠ABC 交CD 于E ，且BE ⊥CD ，CE ：ED =2：1．如果△BEC 的面积为2，那么四边形ABED 的面积是．【考点】相似三角形的判定与性质；等腰三角形的判定与性质；梯形．【分析】首先延长BA ，CD 交于点F ，易证得△BEF ≌△BEC ，则可得DF ：FC =1：4，又由△ADF ∽△BCF ，根据相似三角形的面积比等于相似比的平方，可求得△ADF 的面积，根据S 四边形ABED =S △BEF ﹣S △ADF 继而求得答案．【解答】解：延长BA ，CD 交于点F ，∵BE 平分∠ABC ，∴∠EBF =∠EBC ，∵BE ⊥CD ，∴∠BEF =∠BEC =90°，在△BEF 和△BEC 中，，∴△BEF ≌△BEC （ASA ），∴EC =EF ，S △BEF =S △BEC =2，∴S △BCF =S △BEF +S △BEC =4，∵CE ：ED =2：1∴DF ：FC =1：4，∵AD ∥BC ，∴△ADF ∽△BCF ，∴=（）2=，∴S △ADF =×S △BCF =，∴S 四边形ABED =S △BEF ﹣S △ADF =2﹣=．故答案为：．【点评】此题考查了相似三角形的判定与性质、全等三角形的判定与性质以及梯形的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．20．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，则窗口底边离地面的高BC=4m．【考点】相似三角形的应用．【分析】根据题意易证△BCD∽△ACE，利用相似三角形的性质，对应线段成比例求解即可．【解答】解：∵光线是平行的，即BD∥AE则有∵△BCD∽△ACE∴∴∴BC=4【点评】主要考查了相似的三角形在实际生活中的应用，利用相似对角线的性质，对应线段成比例解题．三．解答题21．（2015秋•滕州市校级期末）如图，Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，一动点P从点A出发沿边AC向点C以1cm/s的速度运动，另一动点Q同时从点C出发沿CB 边向点B以2cm/s的速度运动．问：（1）运动几秒时，△CPQ的面积是8cm2？（2）运动几秒时，△CPQ与△ABC相似？【考点】一元二次方程的应用；相似三角形的判定．【分析】（1）设P、Q同时出发，x秒钟后，AP=xcm，PC=（6﹣x）cm，CQ=2xcm，此时△PCQ的面积为：×2x（6﹣x），令该式=8，由此等量关系列出方程求出符合题意的值；（2）设运动y秒时，△CPQ与△ABC相似，分两种情况讨论：若△CPQ∽△CAB和△CPQ ∽△CBA，根据相似三角形的性质即可得出答案．【解答】解：（1）设x秒后，可使△CPQ的面积为8cm2．由题意得，AP=xcm，PC=（6﹣x）cm，CQ=2xcm，则（6﹣x）•2x=8，整理，得x2﹣6x+8=0，解得x1=2，x2=4．则P、Q同时出发，2秒或4秒后可使△CPQ的面积为8cm2（2）设运动y秒时，△CPQ与△ABC相似．若△CPQ∽△CAB，则=，即=，解得y=2.4秒；若△CPQ∽△CBA，则=，即=，解得y=秒．综上所述，运动2.4秒或秒时，△CPQ与△ABC相似．【点评】本题考查一元二次方程的应用，三角形的面积公式的求法和一元二次方程的解的情况，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．22．（2016•颍泉区一模）如图，在由边长为1的单位正方形组成的网格中，按要求画出坐标系及△A1B1C1及△A2B2C2；（1）若点A、C的坐标分别为（﹣3，0）、（﹣2，3），请画出平面直角坐标系并指出点B的坐标；（2）画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1；（3）以图中的点D为位似中心，将△A1B1C1作位似变换且把边长放大到原来的两倍，得到△A2B2C2．【考点】作图-位似变换；作图-平移变换．【分析】（1）根据A，C点坐标作出直角坐标系，进而求出B点坐标；（2）根据轴对称的性质结合平移的性质得出答案；（3）利用位似图形的性质得出对应点位置进而得出答案．【解答】解：（1）如图所示，B（﹣4，2）；（2）如图所示：△A1B1C1即为所求；（3）如图所示：△A2B2C2即为所求．【点评】此题主要考查了位似变换、轴对称变换和平移变换，根据题意建立正确的坐标系是解题关键．23．（2013•泰安）如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB 的中点，（1）求证：AC2=AB•AD；（2）求证：CE∥AD；（3）若AD=4，AB=6，求的值．【考点】相似三角形的判定与性质；直角三角形斜边上的中线．【分析】（1）由AC平分∠DAB，∠ADC=∠ACB=90°，可证得△ADC∽△ACB，然后由相似三角形的对应边成比例，证得AC2=AB•AD；（2）由E为AB的中点，根据在直角三角形中，斜边上的中线等于斜边的一半，即可证得CE=AB=AE，继而可证得∠DAC=∠ECA，得到CE∥AD；（3）易证得△AFD∽△CFE，然后由相似三角形的对应边成比例，求得的值．【解答】（1）证明：∵AC平分∠DAB，∴∠DAC=∠CAB，∵∠ADC=∠ACB=90°，∴△ADC∽△ACB，∴AD：AC=AC：AB，∴AC2=AB•AD；（2）证明：∵E为AB的中点，∴CE=AB=AE，∴∠EAC=∠ECA，∵∠DAC=∠CAB，∴∠DAC=∠ECA，∴CE∥AD；（3）解：∵CE∥AD，∴△AFD∽△CFE，∴AD：CE=AF：CF，∵CE=AB，∴CE=×6=3，∵AD=4，∴，∴．【点评】此题考查了相似三角形的判定与性质、等腰三角形的性质以及直角三角形的性质．此题难度适中，注意掌握数形结合思想的应用．24．（2011•武汉）（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：=；（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点．①如图2，若AB=AC=1，直接写出MN的长；②如图3，求证：MN2=DM•EN．【考点】相似三角形的判定与性质；正方形的性质．【分析】（1）可证明△ADP∽△ABQ，△ACQ∽△ADP，从而得出=；（2）①根据三角形的面积公式求出BC边上的高，根据△ADE∽△ABC，求出正方形DEFG的边长，根据等于高之比即可求出MN；②可得出△BGD∽△EFC，则DG•EF=CF•BG；又由DG=GF=EF，得GF2=CF•BG，再根据（1）==，从而得出答案．【解答】（1）证明：在△ABQ和△ADP中，∵DP∥BQ，∴△ADP∽△ABQ，∴=，同理在△ACQ和△APE中，=，∴=．（2）①作AQ⊥BC于点Q．∵BC边上的高AQ=，∵DE=DG=GF=EF=BG=CF∴DE：BC=1：3又∵DE∥BC，∴AD：AB=1：3，∴AD=，DE=，∵DE边上的高为，MN：GF=：，∴MN：=：，∴MN=．故答案为：．②证明：∵∠B+∠C=90°∠CEF+∠C=90°，∴∠B=∠CEF，又∵∠BGD=∠EFC，∴△BGD∽△EFC，∴=，∴DG•EF=CF•BG，又∵DG=GF=EF，∴GF2=CF•BG，由（1）得==，∴×=•，∴（）2=•，∵GF2=CF•BG，∴MN2=DM•EN．【点评】本题考查了相似三角形的判定和性质以及正方形的性质，是一道综合题目，难度较大．25．（2006•山西）某中学初三（2）班数学活动小组利用周日开展课外实践活动，他们要在湖面上测量建在地面上某塔AB的高度．如图，在湖面上点C测得塔顶A的仰角为45°，沿直线CD向塔AB方向前进18米到达点D，测得塔顶A的仰角为60度．已知湖面低于地平面1米，请你帮他们计算出塔AB的高度．（结果保留根号）【考点】解直角三角形的应用-仰角俯角问题．【分析】首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形△ACE、△ADE，应利用其公共边AE构造等量关系，借助AB=AE﹣BE构造方程关系式，进而可求出答案．【解答】解：如图，延长CD，交AB的延长线于点E，则∠AEC=90°，∠ACE=45°，∠ADE=60°，CD=18，设线段AE的长为x米，在Rt△ACE中，∵∠ACE=45°，∴CE=x，在Rt△ADE中，∵tan∠ADE=tan60°=，∴DE=x，∵CD=18，且CE﹣DE=CD，∴x﹣x=18，解得：x=27+9，∵BE=1米，∴AB=AE﹣BE=（26+9）（米）．答：塔AB的高度是（26+9）米．【点评】本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．图形的相似单元同步练习（典型题汇总）(时间：100分钟满分：120分)一、选择题(每小题3分，共30分)1．观察下列每组图形，相似图形是()2．(2020·玉林)△ABC与△A′B′C′是位似图形，且△ABC与△A′B′C′的位似比是1∶2，已知△ABC的面积是3，则△A′B′C′的面积是()A．3 B．6 C．9 D．123．下列四组条件中，能判定△ABC与△DEF相似的是()A．∠A＝45°，∠B＝55°；∠D＝45°，∠F＝75°B．AB＝5，BC＝4，∠A＝45°；DE＝5，EF＝4，∠D＝45°C．AB＝6，BC＝5，∠B＝40°；DE＝12，EF＝10，∠E＝40°D．AB＝BC，∠A＝50°；DE＝EF，∠E＝50°4．已知点C是线段AB的黄金分割点，且AC>BC，若AB＝8，则线段AC的长为() A．4(5－1) B．45－1 C．12－4 5 D．8－4 5 5．如图，BE，CD相交于O，且∠1＝∠2，图中的相似三角形有() A．2组B．3组C．5组D．6组第5题图第6题图第7题图第9题图6．小明在一次军事夏令营活动中，进行打靶训练，在用枪瞄准目标点B 时，要使眼睛O ，准星A ，目标B 在同一条直线上．如图所示，在射击时，小明有轻微的抖动，致使准星A 偏离到A ′，若OA ＝0.2米，OB ＝40米，AA ′＝0.0015米，则小明射击到的点B ′偏离目标点B 的长度BB ′为( )A ．3米B ．0.3米C ．0.03米D ．0.2米 7．如图，△ABC 中，∠C ＝90°，四边形DEFC 是内接正方形，AC ＝4 cm ，BC ＝3 cm ，则正方形的面积为( )A.127 cm 2 B ．3 cm 2 C ．4 cm 2 D.14449 cm 2 8．下列四条线段成比例的是( )A ．a ＝4，b ＝6，c ＝5，d ＝10B ．a ＝2，b ＝3，c ＝2，d ＝ 3C ．a ＝2，b ＝5，c ＝15，d ＝2 3D ．a ＝12，b ＝8，c ＝15，d ＝11 9．如图，E (－4，2)，F (－1，－1)，以O 为位似中心，按比例尺1∶2把△EFO 缩小，则点E 的对应点E ′的坐标为( )A ．(2，－1)或(－2，1)B ．(8，－4)或(－8，4)C ．(2，－1)D ．(8，－4)10．将边长分别为2，3，5的三个正方形按如图方式排列，则图中阴影部分的面积为( )A.214B.154C.72D ．3 ,第10题图第13题图第14题图第15题图)二、填空题(每小题3分，共24分)11．如果x 2＝y 3＝z4≠0，那么x ＋2y ＋3z 3x ＋2y －2z的值是____．12．两个相似三角形的面积比为9∶25，其中一个三角形的周长为36，则另一个三角形的周长为_____________________.13．如图，在△ABC 中，点D ，E 分别是边AB ，AC 的中点，则△ADE 与△ABC 的周长之比等于____．14．如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1∶2，点A的坐标为(1，0)，则E点的坐标为__________________．15．如图，▱ABCD中，F是BC上一点，直线DF与AB的延长线相交于E，BP∥DF，且与AD相交于点P，请从图中找出一组相似的三角形：_________________．16．如图，D，E是AB的三等分点，DF∥EG∥BC，则图中三部分面积S1∶S2∶S3＝_______________．第16题图第17题图第18题图17．如图，在边长为3的菱形ABCD中，点E在边CD上，点F为BE延长线与AD延长线的交点，若DE＝1，则DF的长为____．18．如图，正方形ABCD和正方形OEFG中，点A和点F的坐标分别为(3，2)，(－1，－1)，则两个正方形的位似中心的坐标是_____________________________．三、解答题(共66分)19．(6分)一般在室外放映的电影胶片中图片的规格是3.5 cm×3.5 cm，放映的银屏规格为2 m×2 m．若放映机的光源距胶片20 cm，问：银屏拉在距离光源多远的地方时，放映的图象刚好布满整个银屏？20．(7分)如图，在矩形ABCD中，点E，F分别在边AD，DC上，△ABE∽△DEF，AB＝6，AE＝9，DE＝2，求EF的长．21．(8分)图中的两个多边形ABCDEF 和A 1B 1C 1D 1E 1F 1相似(各字母已按对应关系排列)，∠A ＝∠D 1＝135°，∠B ＝∠E 1＝120°，∠C 1＝95°.(1)求∠F 的度数；(2)如果多边形ABCDEF 和A 1B 1C 1D 1E 1F 1的相似比是1∶1.5，且CD ＝15 cm ，求C 1D 1的长度．22．(8分)在平面直角坐标系内有两点A (－2，0)，B (12，0)，CB 所在的直线为y ＝2x ＋b ，连接AC ，求证：△AOC ∽△COB .23．(8分)(2020·汕尾)如图，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F.(1)证明：FD＝AB；(2)当▱ABCD的面积为8时，求△FED的面积．24．(8分)如图，△ABC中，D是BC的中点，且AD＝AC，DE⊥BC与AB相交于点E，EC 与AD相交于点F.(1)△ABC与△FCD相似吗？请说明理由；(2)点F是线段AD的中点吗？为什么？25．(10分)如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连接BD延长交CE于点E.(1)求证：△ABD∽△CED；(2)若AB＝6，AD＝2CD，求BE的长．26．(11分)如图①所示，在等边三角形ABC中，线段AD为其角平分线，过D的直线B1C1⊥AC 于C1，交AB的延长线于B1.(1)请你探究：AC AB ＝CD DB ，AC 1AB 1＝C 1DDB 1是否成立？(2)如图②所示，在Rt △ABC 中，∠ACB ＝90°，AC ＝8，AB ＝403，E 为AB 上一点，且AE ＝5，CE 交△ABC 的角平分线AD 于F ，试求DFFA的值．参考答案一、选择题(每小题3分，共30分) 1．观察下列每组图形，相似图形是( D )2．△ABC 与△A ′B ′C ′是位似图形，且△ABC 与△A ′B ′C ′的位似比是1∶2，已知△ABC 的面积是3，则△A ′B ′C ′的面积是( D )A ．3B ．6C ．9D ．12 3．下列四组条件中，能判定△ABC 与△DEF 相似的是( C )A ．∠A ＝45°，∠B ＝55°；∠D ＝45°，∠F ＝75°B ．AB ＝5，BC ＝4，∠A ＝45°；DE ＝5，EF ＝4，∠D ＝45° C ．AB ＝6，BC ＝5，∠B ＝40°；DE ＝12，EF ＝10，∠E ＝40° D ．AB ＝BC ，∠A ＝50°；DE ＝EF ，∠E ＝50°4．已知点C 是线段AB 的黄金分割点，且AC >BC ，若AB ＝8，则线段AC 的长为( A )A ．4(5－1)B ．45－1C ．12－4 5D ．8－4 5 5．如图，BE ，CD 相交于O ，且∠1＝∠2，图中的相似三角形有( A )A ．2组B ．3组C ．5组D ．6组第5题图第6题图第7题图第9题图6．小明在一次军事夏令营活动中，进行打靶训练，在用枪瞄准目标点B 时，要使眼睛O ，准星A ，目标B 在同一条直线上．如图所示，在射击时，小明有轻微的抖动，致使准星A 偏离到A ′，若OA ＝0.2米，OB ＝40米，AA ′＝0.0015米，则小明射击到的点B ′偏离目标点B 的长度BB ′为( B )A ．3米B ．0.3米C ．0.03米D ．0.2米 7．如图，△ABC 中，∠C ＝90°，四边形DEFC 是内接正方形，AC ＝4 cm ，BC ＝3 cm ，则正方形的面积为( D )A .127 cm 2B ．3 cm 2C ．4 cm 2D .14449 cm 2 8．下列四条线段成比例的是( C )A ．a ＝4，b ＝6，c ＝5，d ＝10B ．a ＝2，b ＝3，c ＝2，d ＝ 3C ．a ＝2，b ＝5，c ＝15，d ＝2 3D ．a ＝12，b ＝8，c ＝15，d ＝11 9．如图，E (－4，2)，F (－1，－1)，以O 为位似中心，按比例尺1∶2把△EFO 缩小，则点E 的对应点E ′的坐标为( A )A ．(2，－1)或(－2，1)B ．(8，－4)或(－8，4)C ．(2，－1)D ．(8，－4)10．将边长分别为2，3，5的三个正方形按如图方式排列，则图中阴影部分的面积为( B )A.214B.154C.72D ．3 ,第10题图第13题图第14题图第15题图)二、填空题(每小题3分，共24分)11．如果x 2＝y 3＝z4≠0，那么x ＋2y ＋3z 3x ＋2y －2z的值是__5__．12．两个相似三角形的面积比为9∶25，其中一个三角形的周长为36，则另一个三角形的周长为__1085或60__.。

4.8 图形的位似(分层练习)(解析版)

第四章图形的相似4.8 图形的位似精选练习一、单选题1．（2022·全国·九年级专题练习）如图，在直角坐标系xOy中，矩形EFGO的两边OE，OG在坐标轴上，以y轴上的某一点P为位似中心，作矩形ABCD，使其与矩形EFGO位似，若点B，F的坐标分别为（4，4），（-2，1），则位似中心P的坐标为（）A．（0，1.5）B．（0，2）C．（0，2.5）D．（0，3）故选：B ．【点睛】此题主要考查了位似中心的概念和位似图形的性质等知识，熟练掌握位似中心的概念和位似图形的性质是解题的关键．2．（2022·江苏·西附初中八年级期末）2020年是紫禁城建成600年暨故宫博物院成立95周年，在此之前有多个国家曾发行过紫禁城元素的邮品．图1所示的摩纳哥发行的小型张中的图案，以敞开的紫禁城大门和大门内的石狮和太和殿作为邮票和小型张的边饰，如果标记出图1中大门的门框并画出相关的几何图形（图2），我们发现设计师巧妙地使用了数学元素（忽略误差），图2中的四边形ABCD 与四边形A B C D ¢¢¢¢是位似图形，点O 是位似中心，点A ¢是线段OA 的中点，那么以下结论正确的是（）A ．四边形ABCD 与四边形ABCD ¢¢¢¢的相似比为1：1B ．四边形ABCD 与四边形A BCD ¢¢¢¢的相似比为1：2C ．四边形ABCD 与四边形A B C D ¢¢¢¢的周长比为3：1D ．四边形ABCD 与四边形A B C D ¢¢¢¢的面积比为4：1【答案】D【分析】根据题意可判断OA ¢：1OA =：2，即得出A B ¢¢：1AB =：2，从而可判断四边形ABCD 与四边形A B C D ¢¢¢¢的相似比为2：1，由相似比即可求出其周长比和面积比，即可选择．【详解】Q 四边形ABCD 与四边形A B C D ¢¢¢¢是位似图形，点O 是位似中心，点A ¢是线段OA 的中点，∴OA ¢：1OA =：2，∴A B ¢¢：1AB =：2，\四边形ABCD 与四边形A B C D ¢¢¢¢的相似比为2：1，周长的比为2：1，面积比为4：1．故选D ．【点睛】本题考查由位似图形求相似比，周长比和面积比．掌握位似图形的定义和性质是解题关键．3．（2022·重庆实验外国语学校八年级阶段练习）如图，在平面点角坐标系中V AOB 与V COD 是位似图形，以原点O 为位似中心，若2AC OA =，B 点坐标为(4，2)，则点D 的坐标为（）A ．( 8，4)B ．(8，6)C ．(12，4)D ．(12，6)4．（2022·全国·九年级专题练习）如图，图形甲与图形乙是位似图形，O 是位似中心，位似比为2：3，点A ，B 的对应点分别为点A ′，B ′．若AB ＝6，则A ′B ′的长为（）A ．8B ．9C ．10D ．156AB =Q ，9A B ¢¢\=，故选：B ．【点睛】本题考查的是位似图形，解题的关键是掌握位似图形的位似比是对应边的比．5．（2022·全国·九年级课时练习）如图，△ABC 与△DEF 是位似图形，且顶点都在格点上，则位似中心的坐标是（）A ．（8，2）B ．（9，1）C ．（9，0）D ．（10，0）【答案】C 【分析】延长EB 、DA 交于点P ，根据位似图形的对应点的连线相交于一点解答即可．【详解】解：延长EB 、DA 交于点P ，则点P 即为位似中心，位似中心的坐标为（9，0），故选：C ．【点睛】本题考查的是位似变换的定义，如果两个图形不仅是相似图形，而且对应点的连线相交于一点，对应边互相平行（或共线），那么这样的两个图形叫做位似图形，这个点叫做位似中心．6．（2022·山东威海·八年级期末）如图，矩形OABC 与矩形ODEF 是位似图形，点P 是位似中心．若点B 的坐标为(2,3)，点E 的横坐标为1-，则点P 的坐标为（）A ．(2,0)-B ．(0,2)-C ．3,02æö-ç÷D ．30,2æö-ç÷二、填空题7．（2022·广东·佛山市三水区三水中学附属初中九年级开学考试）如图，在平面直角坐标系中，以原点O 为位似中心，将ABO V 扩大到原来的2倍，得到A B O ¢¢△，若点A 的坐标是()1,2，则点A ¢的坐标是______．【答案】()2,4--【分析】根据以原点O 为位似中心，将ABO V 扩大到原来的2倍，结合图形，可知将对应点的坐标应乘以2-，即可得出点A ¢的坐标．【详解】解：根据以原点O 为位似中心扩大到原来的2倍，A B O ¢¢△在第三象限，即对应点的坐标应乘以2-，∵点A 的坐标是()1,2，∴点A ¢的坐标是()2,4--，故答案为：()2,4--．【点睛】此题主要考查了关于原点对称的位似图形的性质，得出对应点的坐标乘以k 或k -是解题关键．8．（2022·浙江·九年级单元测试）如图，ABC V 与△A B C ¢¢¢是位似图形，且顶点都在格点上，则位似中心的坐标是________．【答案】（9，0）【分析】根据位似中心的概念解答即可．【详解】解：连接A A ¢和B B ¢并延长相交于点D ，则点D 即为位似中心，作图如下：点D 的坐标为（9，0），即位似中心的坐标为（9，0），故答案为：（9，0）．【点睛】本题考查的是位似变换的概念，解题的关键是掌握各对应点所在直线的交点即为位似中心．9．（2022·甘肃·平凉市第十中学九年级阶段练习）如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形'''A B CD E ，已知10cm OA =，'20cm OA =，则五边形ABCDE 的周长与五边形''''A B CD E 的周长比是______．【答案】1：2【分析】根据已知可得五边形ABCDE 的周长与五边形'''A B CD E 的位似比，然后由相似多边形的性质可证得：五边形ABCDE 的周长与五边形'''A B CD E 的周长比．【详解】Q 以点O 为位似中心，将五边形ABCDE 放大后得到五边形'''''A B C D E ，10OA cm =，'20OA cm =，\五边形ABCDE 的周长与五边形'''''A B C D E 的位似比为：10：201=：2，\五边形ABCDE 的周长与五边形'''''A B C D E 的周长比是：1：2．故答案为1:2．【点睛】此题考查了位似图形的性质，掌握相似多边形的周长比等于相似比是解题关键．10．（2022·吉林省第二实验学校九年级阶段练习）如图，ABC V 与111A B C △位似，位似中心是点O ，则1:1:2OA OA =，ABC V 的面积为3，则111A B C △的面积是___________．三、解答题11．（2022·全国·九年级专题练习）如图所示的平面直角坐标系中，△ABC 的三个顶点坐标分别为A （﹣3，2），B （﹣1，3），C （﹣1，1），请按如下要求画图：(1)以坐标原点O 为旋转中心，将△ABC 顺时针旋转90°，得到111A B C △，请画出111A B C △；(2)以坐标原点O 为位似中心，在x 轴下方，画出△ABC 的位似图形222A B C △，使它与△ABC 的位似比为2：1．【答案】(1)见解析(2)见解析【分析】（1）直接利用旋转的性质得出对应点的位置，画出图形即可；（2）直接利用位似图形的性质得出对应点的位置，画出图形即可．（1）解：如图，111A B C △即为所求．；（2）解：如图，222A B C △即为所求．【点睛】本题考查了位似变换与旋转变换，正确得出对应点的位置是解题的关键．12．（2022·山东烟台·八年级期末）如图，在平面直角坐标系中，△ABC 的顶点坐标分别为A （1，1），B （2，2），C （3，0）．(1)以原点O 为位似中心，在y 轴的右侧画出将△ABC 放大为原来的2倍得到的△A 1B 1C 1，请写出点B 的对应点B 1的坐标；(2)画出将△ABC 向左平移1个单位，再向上平移2个单位后得到的△A 2B 2C 2，写出点C 的对应点C 2的坐标；(3)请在图中标出△A 1B 1C 1与△A 2B 2C 2的位似中心M ，并写出点M 的坐标．【答案】(1)图见解析，（4，4）(2)图见解析，（2，2）(3)图见解析，（﹣2，4）【分析】（1）把A ，B ，C 的横纵坐标都乘以2得到111,,A B C 的坐标，然后描点即可．（2）利用，点平移的坐标特征写出222,,A B C 的坐标，然后描点即可．（3）对应点连线的交点M 即为所求作．（1）如图△A 1B 1C 1即为所求作的三角形，点B 1的坐标（4，4）．（2）如图，△A 2B 2C 2即为所求作的三角形点C 2的坐标（2，2）．（3）如图所示：点M 即为所求作．M （﹣2，4）．【点睛】本题考查了作图一位似变换:在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或k -，也考查了平移变换．一、填空题1．（2022·全国·九年级课时练习）如图，在平面直角坐标系中，以原点O 为位似中心，将△AOB 缩小为原来的12，得到△COD ，若点A 的坐标为（4，2），则AC 的中点E 的坐标是 _____．2．（2022·全国·九年级单元测试）如图所示，在平面直角坐标系中，已知点A （-4，2），B （-2，-2）．以坐标原点O 为位似中心把△AOB 缩小得到△A 1OB 1，△A 1OB 1与△AOB 的位似比为12，则点A 的对应点A 1的坐标为_______．3．（2021·湖北·武汉二中广雅中学九年级阶段练习）在平面直角坐标系中，已知点()2,1A -，()3,2B --，以原点O 为位似中心，相似比为12，把ABO V 缩小，则点A 的对应点A ¢的坐标是______．【答案】11,2æö-ç÷或1(1,2-##1(1,)2-或1(1,2-4．（2022·全国·九年级专题练习）如图，在平面直角坐标系中，等边ABC V 与等边BDE V 是以原点为位似中心的位似图形，且相似比为13，点A 、B 、D 在x 轴上，若等边BDE V 的边长为12，则点C 的坐标为_________．∵等边△ABC 与等边△BDE 是以原点为位似中心的位似图形，∴BC ∥DE ，∴△OBC ∽△ODE ，∴BC OB DE OD=，∵△ABC 与△BDE 的相似比为13，等边△BDE 5．（2022·全国·九年级课时练习）如图，已知ABCD Y 的面积为24，以B 为位似中心，作ABCD Y 的位似图形EBFG Y ，位似图形与原图形的位似比为23，连接AG 、DG ．则ADG V 的面积为________．故答案为：4．【点睛】本题考查了位似图形的性质，平行四边形的性质与判定，掌握这些性质是解题的关键．二、解答题6．（2022·全国·九年级专题练习）如图，△ABO三个顶点的坐标分别为A（﹣2，4），B（﹣4，0），O（0，0），以原点O为位似中心，画出一个三角形，使它与△ABO的位似比为1．2【点睛】本题考查了位似的概念．位似比为对应点到位似中心的距离比．解题关键是根据位似比找到对应7．（2022·山东·聊城江北水城旅游度假区北大培文学校九年级阶段练习）已知：如图，△ABC三个顶点的坐标分别为A（0，-3）、B（3，-2）、C（2，-4），正方形网格中，每个小正方形的边长是1个单位长度．(1)画出△ABC 向上平移6个单位得到的111A B C △；(2)以点C 为位似中心，在网格中画出222A B C △，使222A B C △与△ABC 位似，且222A B C △与△ABC 的位似比为2：1，并直接写出点2C 的坐标．【答案】(1)见解析(2)图见解析，2C 坐标为（2，-4）【分析】（1）直接利用平移的性质得出对应点位置即可得出答案；（2）直接利用位似图形的性质以C 为位似中心，将边长扩大为原来的2倍即可．（1）如图所示：111A B C △即为所求；（2）如图所示：222A B C △即为所求，2C 坐标为：（2，-4）．【点睛】本题考查了平移的性质，位似的性质，能根据性质的特点进行画图是解此题的关键．8．（2021·黑龙江绥化·期末）按要求完成下面各题：(1)三角形AOB 顶点B 的位置用数对表示是．(2)画出三角形AOB 绕点O 逆时针旋转90°后的图形．(3)按2∶1的比画出三角形AOB 放大后的图形．【答案】(1)（2，4）(2)见详解(3)见详解【分析】（1）根据网格即可得三角形AOB 顶点B 的位置；（2）根据旋转的性质即可画出三角形AOB 绕点O 逆时针旋转90°后的图形；（3）根据2：1的比即可画出三角形AOB 放大后的图形．（1）解：三角形AOB 顶点B 的位置用数对表示是（2，4）；故答案为：（2，4）；（2）如图三角形A OB ¢¢即为所求；（3）²²²即为所求．如图，三角形A O B【点睛】本题考查了作图﹣旋转变换，解决本题的关键是掌握旋转的性质．。

北师大版数学九年级上册第四章图形的相似复习练习

初中数学试卷第四章图形的相似一、单选题1．如图，l 1，l 2，l 3，l 4是一组平行线，l 5，l 6与这组平行线依次相交于点A ，B ，C ，D和E ，F ，G ，H ．若AB ∶BC ∶CD=2∶3∶4，EG=10，则EH 的长为（）A ．14B ．16C ．18D ．202．如图是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD 内，点E 是AB 的黄金分割点，BE ＞AE ，若AB ＝2a ，则BE 长为（）A ．（ +1）aB ．（﹣1）a C ．（3﹣）a D ．（﹣2）a3．如图，已知AB ∥CD ，AC 与BD 交于点O ，则下列比例中成立的是( )A ．O C O A O DO B=B ．OC O B OD O D =C ．O C O D A CO B=D ．B D OC A CO D=4．如图，小明为了测量一凉亭的高度AB （顶端A 到水平地面BD 的距离），在凉亭的旁边放置一个与凉亭台阶BC 等高的台阶DE （ 0.5m D E B C == ，A ，C ，B 三点共线），把一面镜子水平放置在平台上的点G 处，测得 15m C G = ，然后沿直线 C G 后退到点E 处，这时在镜子里恰好看到凉亭的顶端A ，测得 3m E G = ．若小明身高1.6m ，则凉亭的高度AB 约为（）A ．8.5mB ．9mC ．9.5mD ．10m5．如图，ABC 与DEF 位似，点O 是位似中心，若OE=3OB ，A B CS =4，则D E FS=（）A ．9B ．12C ．16D ．366．如图，A B C 与D E F 位似，位似中心为点O ，A B C 与D E F 的周长之比为49∶，则A O O D ∶的比为（）A ．2：3B ．2：5C ．4：9D ．4：137．如图，在ΔABC 中,D 、E 分别是AB 、AC 边上的中点，连接DE ，那么ΔADE 与ΔABC 的面积之比是（）A ．1:16B ．1:9C ．1:4D ．1:28．已知：如图，在△ABC 中，B E A C ⊥于点G ，C D A B ⊥于点F ，B A B E =，C A CD =，以下结论：①DE ∠=∠，②DFG E =，③A F A C A GA B=，④D FE G C FB G=，其中正确的是（）A．①②③B．①②④C．①③④D．②③④9．如图，△OAB与△OCD是以点0为位似中心的位似图形，相似比为1：2，∠OCD=90 ︒，CO=CD．若B(2，0)，则点C的坐标为()A．(2，2)B．(1，2)C．（，2 ）D．(2，1)10．如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA'B'C'与矩形OABC关于点O位似，且矩形OA'B'C'的面积等于矩形OABC面积的14，那么点B'的坐标是（）A．（3，2）B．（－2，－3）C．（2，3）或（－2，－3）D．（3，2）或（－3，－2）二、填空题11．已知△ABC∽△A'B'C'，AD和A'D'是它们的对应角平分线，若AD：A'D'=4：3，△ABC的周长为16，则△A'B'C'的周长是．12．如图，////A C E FB D，若:2:3A E E B=，10C D=，则C F=.13．如图，将矩形O A B C置于平面直角坐标系中，4=，点D在B C边O A=，O C m上，且1D C=，将矩形O A B C沿A D折叠，使点B对应点E落在坐标平面内（1）当3m=时，O E的长度为．（2）若点E恰好落在x轴上，则m的值为．14．如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED=1，BD=4，那么AB=.15．已知线段AB＝4，点P是线段AB的黄金分割点，则AP的长为．三、解答题16．如图所示，点D、E分别在AB、AC上，连接DE，△ADE∽△ABC，已知△ADE和△ABC的相似比是1：2，且△ADE的面积是1，求四边形DBCE的面积.17．如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE＝40cm，EF＝20cm，测得边DF离地面的高度AC＝1.5m，CD＝10m，求树高AB．18．如图（图形不全），等边三角形A B C中，3A B=，点D在直线B C上，点E在直线A C上，且B A DC B E∠=∠，当1B D=时，求A E的长．几位同学通过探究得出结论：此题有多种结果．有同学已经得出两个符合题意结论：①当点D在边B C上、点E在边A C上时，2A E=；②当点D在边B C上、点E在A C的延长线上时，92A E=．要求：请针对其它情况，继续求出A E的长，并写出总的正确结论．19．如图，在矩形ABCD中，AB=18，AD=12，点M是边AB的中点，连结DM，DM与AC交于点G。

北师大版九年级数学上册第四章图形的相似综合题练习(含答案)

北师大版九年级数学上册第四章图形的相似综合题练习1、如图，在△ABC 中，D 为BC 中点，过D 的直线交AC 于E ，交AB 的延长线于F.求证：AEEC ＝AF BF.2、如图，在△ABC 中，∠ACB ＝90°，CD ⊥AB 于点D ，E 为AC 的中点，ED ，CB 的延长线交于点F.求证：DFCF＝BC AC.3、如图，点P 是菱形ABCD 的对角线BD 上一点，连接CP 并延长，交AD 于点E ，交BA 的延长线于点F.(1)求证：∠DCP ＝∠DAP ；(2)如果PE ＝3，EF ＝5，求线段PC 的长．4、如图，在△ABC 中，D 在AC 上，且AD ∶DC ＝1∶2，E 为BD 的中点，AE 的延长线交BC 于F.求证：BF ∶FC ＝1∶3.5、已知，如图，AD 是Rt △ABC 斜边上的中线，AE ⊥AD ，AE 交CB 的延长线于点E.(1)求证：△BAE ∽△ACE ；(2)AF ⊥BD ，垂足为F ，且BE ·CE ＝9，求EF ·DE 的值．6、如图，∠ABC ＝∠DBE ＝90°，C 是DE 的中点．(1)求证：△ABD ∽△AEB ；(2)当AB BC ＝43时，求BDBE 的值；7、如图，在△ABC 中，AB ＝AC ，点D ，E 分别是边AC ，AB 的中点，DF ⊥AC ，DF 与CE 相交于点F ，AF 的延长线与BD 相交于点G.(1)求证：AD 2＝DG ·BD ；(2)连接CG ，求证：∠ECB ＝∠DCG.8、如图，在△ABC 中，AB ＝AC ，AD ⊥BC 于点D ，作DE ⊥AC 于点E ，F 是AB 中点，连接EF 交AD 于点G.(1)求证：AD 2＝AB ·AE ；(2)若AB ＝3，AE ＝2，则ADAG的值为_______．9、如图，点P 是线段BD 上一个动点，∠B ＝∠D ＝90°，AB ＝6，CD ＝4，BD ＝a.(1)当∠APC ＝90°，a ＝14时，求BP 的长度；(2)若∠APC ＝90°时，有两个符合要求的点P 1，P 2，且P 1P 2＝2，求a 的值．10、如图，在△ABC 中，AB ＝AC ，点E 在边BC 上移动(点E 不与点B ，C 重合)，满足∠DEF ＝∠B ，且点D ，F 分别在边AB ，AC 上．(1)求证：△BDE ∽△CEF ；(2)当点E 移动到BC 的中点时，求证：FE 平分∠DFC.11、如图，已知四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，DH ⊥AB ，垂足为H ，交AC 于点E ，连接HO 并延长交CD 于点G.求证：(1)∠DHO ＝12∠BCD ；(2)HG ·AE ＝2DE ·CG.12、如图，已知矩形ABCD 的两条对角线相交于点O ，过点A 作AG ⊥BD 分别交BD ，BC 于点G ，E.(1)求证：BE 2＝EG ·EA ；(2)连接CG ，若BE ＝CE ，求证：∠ECG ＝∠EAC.13、已知：如图，在△ABC 中，点D 在BC 上，连接AD ，使得∠CAD ＝∠B ，DC ＝3且S △ACD ∶S △ADB ＝1∶2.(1)求AC 的值；(2)若将△ADC 沿着直线AD 翻折，使点C 落在点E 处，AE 交边BC 于点F ，且AB ∥DE ，求S △EFD S △ADC的值．14、如图，在形状和大小不确定的△ABC 中，BC ＝5，E ，F 分别是AB ，AC 的中点，P 在EF 或EF 的延长线上，BP 交CE 于D ，Q 在CE 上且BQ 平分∠CBP ，设BP ＝y ，PE ＝x.(1)当x ＝14EF 时，求S △DPE ∶S △DBC 的值；(2)当CQ ＝13CE 时，求y 与x 之间的函数关系式．15、如图，在△ABC 中，∠C ＝90°，AC ＝8 cm ，BC ＝6 cm.点P 从点A 出发，沿AB 边以2 cm/s 的速度向点B 匀速移动；点Q 从点B 出发，沿BC 边以1 cm/s 的速度向点C 匀速移动，当一个运动点到达终点时，另一个运动点也随之停止运动，设运动的时间为t s.(1)当PQ ∥AC 时，求t 的值；(2)当t 为何值时，△PBQ 的面积等于245cm 2.答案1、证明：过B作EF的平行线交AC于点G，则AF∶BF＝AE∶EG，BD∶DC＝GE∶EC.∵BD＝DC，∴GE＝EC.∴AE∶EC＝AF∶BF.2、证明：∵∠ACB＝90°，CD⊥AB，∴∠A＋∠ACD＝∠ACD＋∠BCD，∠ACB＝∠BDC＝90°.∴∠A＝∠BCD.∴△ABC∽△CBD.∴BCBD＝ACCD，即BCAC＝BDCD.又∵E为AC中点，∴AE＝CE＝ED.∴∠A＝∠EDA.∵∠EDA＝∠BDF，∴∠FCD＝∠BDF. 又∵∠F为公共角，∴△FDB∽△FCD.∴DFCF＝BDCD.∴DFCF＝BCAC.3、解：(1)证明：∵四边形ABCD是菱形，∴AD＝CD，∠ADB＝∠CDB，CD∥AB.又∵DP＝DP，∴△ADP≌△CDP(SAS)．∴AP＝PC，∠DCP＝∠DAP.(2)∵CD ∥AB ，∴∠DCP ＝∠F. ∵∠DCP ＝∠DAP ，∴∠DAP ＝∠F. 又∵∠APE ＝∠FPA ， ∴△APE ∽△FPA. ∴AP PF ＝PE AP .∴AP 3＋5＝3AP . ∴AP ＝2 6.∴PC ＝2 6. 4、证明：∵AD ∶DC ＝1∶2， ∴AD ∶AC ＝1∶3.作DG ∥AF 交BC 于点G ，则AD AC ＝FG FC ＝13，BE ED ＝BFFG .又∵E 是BD 的中点， ∴BE ＝ED. ∴BF ＝FG.∴BF FC ＝13，即BF ∶FC ＝1∶3.5、解：(1)证明：∵AD 是Rt △ABC 斜边上的中线， ∴AD ＝BD ＝CD. ∴∠C ＝∠DAC.∵AE ⊥AD ，∴∠EAD ＝90°＝∠BAC. ∴∠EAB ＝∠DAC.∴∠EAB ＝∠C. 又∵∠E ＝∠E ， ∴△BAE ∽△ACE.(2)∵△BAE ∽△ACE ，∴AE EC ＝BEAE.∴AE 2＝BE ·CE ＝9.∵∠AFE ＝∠DAE ＝90°，∠E ＝∠E ， ∴△EAF ∽△EDA. ∴AE DE ＝EF AE . ∴EF ·DE ＝AE 2＝9.6、解：(1)证明：∵∠ABC ＝∠DBE ＝90°， ∴∠ABC －∠DBC ＝∠DBE －∠DBC ，即∠ABD ＝∠CBE. ∵∠DBE ＝90°，C 是DE 的中点． ∴BC ＝CD ＝CE.∴∠E ＝∠CBE. ∴∠ABD ＝∠E.又∵∠BAD ＝∠EAB ，∴△ABD ∽△AEB. (2)∵AB BC ＝43，∴设AB ＝4k ，BC ＝3k.∴在Rt △ABC 中，AC ＝AB 2＋BC 2＝5k. ∵BC ＝CD ＝3k ，∴AD ＝AC －CD ＝5k －3k ＝2k. 由(1)可知△ABD ∽△AEB ， ∴BD BE ＝AD AB ＝2k 4k ＝12，即BD BE 的值为12. 7、证明：(1)∵AB ＝AC ，D ，E 分别是AC ，AB 的中点， ∴AD ＝12AC ，AE ＝12AB.∴AD ＝AE.在△BAD 和△CAE 中， ⎩⎪⎨⎪⎧AB ＝AC ，∠BAD ＝∠CAE ，AD ＝AE ，∴△BAD ≌△CAE(SAS)． ∴∠ABD ＝∠ACE.∵DF ⊥AC ，AD ＝CD ，∴AF ＝CF. ∴∠GAD ＝∠ACE.∴∠GAD ＝∠ABD. ∵∠GDA ＝∠ADB ，∴△GDA ∽△ADB. ∴AD BD ＝DG DA.∴AD 2＝DG ·BD. (2)连接CG ，∵AD DB ＝DG AD ，AD ＝CD ，∴CD DB ＝DGCD .∵∠CDG ＝∠BDC ，∴△DCG ∽△DBC. ∴∠DBC ＝∠DCG.∵AB ＝AC ，∴∠ABC ＝∠ACB. 又∵∠ABD ＝∠ACE.∴∠ECB ＝∠DBC.∴∠ECB ＝∠DCG.8、证明：∵AD ⊥BC 于点D ，DE ⊥AC 于点E ， ∴∠ADC ＝∠AED ＝90°. ∠DAE ＝∠DAC ， ∴△DAE ∽△CAD. ∴AD CA ＝AEAD . ∴AD 2＝AC ·AE.∵AC ＝AB ，∴AD 2＝AB ·AE.9、解：(1)∵∠B ＝∠D ＝90°，∠APC ＝90°， ∴∠B ＝∠APC ＝90°，∠A ＋∠B ＝∠APC ＋∠CPD. ∴∠A ＝∠CPD. ∴△ABP ∽△PDC.∴BP CD ＝AB PD ，即BP 4＝614－BP. 解得BP ＝2或12.(2)设BP ＝x ，则PD ＝a －x.∵△ABP ∽△PDC ，∴AB PD ＝BP CD ，即6a －x ＝x 4. ∴x 2－ax ＋24＝0，设方程的两个根为x 1，x 2，则x 1＋x 2＝a ，x 1x 2＝24，∵P 1P 2＝2，∴|x 1－x 2|＝2.∴(x 1－x 2)2＝(x 1＋x 2)2－4x 1x 2＝4，∴a 2－4×24＝4，解得a ＝±10(负值舍去)．∴a ＝10.10、证明：(1)∵AB ＝AC ，∴∠B ＝∠C.∵∠BDE ＝180°－∠B －∠DEB ，∠CEF ＝180°－∠DEF －∠DEB ，且∠DEF ＝∠B ， ∴∠BDE ＝∠CEF.∴△BDE ∽△CEF.(2)∵△BDE ∽△CEF ，∴BE CF ＝DE EF. ∵点E 是BC 的中点，∴BE ＝CE.∴CE CF ＝DE EF .∴CE DE ＝CF EF. ∵∠DEF ＝∠B ＝∠C ，∴△DEF ∽△ECF.∴∠DFE ＝∠CFE ，即FE 平分∠DFC.11、11、证明：(1)∵四边形ABCD 是菱形，∴∠BCD ＝∠BAD ＝2∠BAO ，∠AOB ＝90°，OB ＝OD.∵DH ⊥AB ，∴∠BHD ＝90°.∴OH ＝OD ，∴∠DHO ＝∠BDH.在Rt △BHD 中，∠BDH ＋∠ABO ＝90°，∵∠BAO ＋∠ABO ＝90°，∴∠BDH ＝∠BAO.∴∠DHO ＝∠BAO.∴∠BCD ＝2∠DHO.∴∠DHO ＝12∠BCD. (2)∵AC 是菱形ABCD 的对角线，∴OA ＝OC ，∠DAO ＝∠BAO.∵∠DHO ＝∠BAO ，∴∠DHO ＝∠DAO.∵∠AED ＝∠HEO ，∴∠AOH ＝∠ADE.∵∠AOH ＝∠COG ，∴∠ADH ＝∠COG.∵∠DAE ＝∠OCG ，∴△ADE ∽△COG.∴AE CG ＝DE OG. ∴AE ·OG ＝DE ·CG.在△AOH 和△COG 中，⎩⎪⎨⎪⎧∠AOH ＝∠COG ，AO ＝CO ，∠OAH ＝∠OCG ，∴△AOH ≌△COG(SAS)．∴OH ＝OG ，∴OG ＝12HG. ∴AE ·12HG ＝DE ·CG. ∴HG ·AE ＝2DE ·CG.12、证明：(1)∵四边形ABCD 是矩形，∴∠ABC ＝90°.∵AE⊥BD，∴∠ABC＝∠BGE＝90°. ∵∠AEB＝∠BEG，∴△ABE∽△BGE.∴AEBE＝BEEG.∴BE2＝EG·EA.(2)由(1)得BE2＝EG·EA. ∵BE＝CE，∴CE2＝EG·EA.∴CEEG＝AECE.∵∠CEG＝∠AEC，∴△CEG∽△AEC.∴∠ECG＝∠EAC.13、解：(1)∵S△ACD∶S△ADB＝1∶2，∴BD＝2CD.∵DC＝3，∴BD＝6.∴BC＝BD＋DC＝9. ∵∠B＝∠CAD，∠C＝∠C，∴△ABC∽△DAC.∴ACCD＝BCAC，即AC3＝9AC，解得AC＝3 3.(2)由折叠的性质，得∠E＝∠C，DE＝CD＝3. ∵AB∥DE，∴∠B＝∠EDF.∵∠CAD＝∠B，∴∠EDF＝∠CAD.∴△EFD∽△CDA.∴S△EFDS△ADC＝(DEAC)2＝(333)2＝13.14、解：(1)∵E ，F 分别是AB ，AC 的中点，PE ＝x ＝14EF ， ∴EF ∥BC ，EF ＝12BC.∴△EDP ∽△CDB.∴EP BC ＝18. ∴S △DPE ∶S △DBC ＝1∶64.(2)延长BQ 交EF 的延长线于点H.∵EF ∥BC ，∴△QEH ∽△QCB.∴BC EH ＝CQ QE. ∵CQ ＝13CE ，∴CQ QE ＝12. 又∵BC ＝5，∴EH ＝2BC ＝10.∵△QEH ∽△QCB ，∴∠PHQ ＝∠CBQ.又∵BQ 平分∠CBP ，∴∠CBQ ＝∠PBQ.∴∠PHB ＝∠PBH.∴PB ＝PH.∴EH ＝PE ＋PH ＝PE ＋PB ＝x ＋y ＝2BC ＝10.∴y ＝－x ＋10(0＜x ＜10)．15、解：(1)由题意，得BQ ＝t cm ，AP ＝2t cm. 在Rt △ABC 中，∠C ＝90°，AC ＝8 cm ，BC ＝6 cm ， AB ＝AC 2＋BC 2＝82＋62＝10(cm)．∴BP ＝(10－2t)cm.∵PQ ∥AC ，∴BP BA ＝BQ BC ，即10－2t 10＝t 6. 解得 t ＝3011. (2)过点Q 作QE ⊥AB 于点E ，则∠QEB ＝∠C ＝90°.∵∠B ＝∠B ，∴△BQE ∽△BAC.∴BQ BA ＝QE AC ，即t 10＝QE 8.解得 QE ＝45t. ∴S △PBQ ＝12BP ·QE ＝245. 即12·(10－2t)·45t ＝245. 解得t 1＝2，t 2＝3.∵0＜t ＜5，∴当t 的值为2或3时，△PBQ 的面积等于245cm 2.。

北师大版九年级数学上册第四章图形的相似练习题

北师大版九年级数学上册第四章图形的相似练习题选择题已知2x=3y（y≠0），则下面结论成立的是（）A. B. C. D.【答案】A【解析】试题解析：A、两边都除以2y，得，故A符合题意；B、两边除以不同的整式，故B不符合题意；C、两边都除以2y，得，故C不符合题意；D、两边除以不同的整式，故D不符合题意；故选A．选择题如果两个相似三角形对应边的比为2：3，那么这两个相似三角形面积的比是（）A. 2：3B.C. 4：9D. 8：27【答案】C【解析】试题分析：两个相似三角形面积的比是=4：9．故选C．选择题下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则在网格图中的三角形与△ABC相似的是（）A. B. C. D.【答案】B【解析】试题分析：可利用正方形的边把对应的线段表示出来，利用三边对应成比例两个三角形相似，分别计算各边的长度即可解题．解：根据勾股定理,AB=,BC=，所以,夹直角的两边的比为，计算各选项，只有B选项三角形符合，与所给图形的三角形相似。

故选：B.选择题如图，在△ABC中，DE∥BC，，BC=12，则DE的长是（）A．3 B．4 C．5 D．6【答案】B．【解析】试题分析：∵DE∥BC，∴△ADE∽△ABC，∴=，∵BC=12，∴DE=BC=4．故选B．选择题如图，△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC的面积比是16：25，则OB′：OB为（）A. 2：3B. 3：2C. 4：5D. 4：9【答案】A【解析】根据位似变换的概念得到△A′B′C′∽△ABC，根据相似三角形的性质计算．∵△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，∴△A′B′C′∽△ABC，∵△A′B′C′的面积与△ABC的面积比是16：25，∴△A′B′C′与△ABC的相似比为4：5，即OB′：OB=4：5，故选C．选择题如图，在方格纸中，△ABC和△EPD的顶点均在格点上，要使△ABC∽△EPD，则点P所在的格点为（）A．P1 B．P2 C．P3 D．P4【答案】C．【解析】试题∵∠BAC=∠PED=90°，，∴当=时，△ABC ∽△EPD时．∵DE=4，∴EP=6．∴点P落在P3处．故选C．填空题已知AB∥CD，AD与BC相交于点O．若，AD=10，则AO=_____．【答案】4【解析】∵AB∥CD，解得，AO=4，故答案是：4．填空题如图，在中，，分别为边、AC上的点，，,点为边上一点，添加一个条件:___________，可以使得与相似.（只需写出一个）【答案】∠A=∠BDF答案不唯一【解析】因为，, ，所以,欲使与相似，只需要与相似即可，则可以添加的条件有：∠A=∠BDF，或者∠C=∠BDF,等等，答案不唯一.填空题如图，身高为1.8米的某学生想测量学校旗杆的高度，当他站在B处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AB=2米，BC=18米，则旗杆CD的高度是______米．【答案】18．【解析】试题解析：∵BE⊥AC，CD⊥AC，∴△ABE∽△ACD，解得：故答案为：18.填空题如图，四边形ABCD与四边形EFGH位似，位似中心点是O，，则=_____．【答案】【解析】解：∵四边形ABCD与四边形EFGH位似，∴△OEF∽△OAB，△OFG∽△OBC，∴，∴．故答案为：．解答题如图，已知∠BAC＝∠EAD，AB＝20.4，AC＝48，AE＝17，AD＝40.求证：△ABC∽△AED.【答案】见解析【解析】根据：两组对应边成比例且夹角相等的两个三角形相似.可证明三角形相似.证明：∵AB＝20.4，AC＝48，AE＝17，AD＝40，∴＝＝1.2，＝＝1.2，∴＝.又∵∠BAC＝∠EAD，∴△ABC∽△AED.解答题如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（﹣1，2）、B（2，1）、C（4，5）．（1）画出△ABC关于x对称的△A1B1C1；（2）以原点O为位似中心，在x轴的上方画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2，并求出△A2B2C2的面积．【答案】（1）作图见解析；（2）作图见解析，28．【解析】试题分析：（1）画出A、B、C关于x轴的对称点A1、B1、C1即可解决问题；（2）连接OB延长OB到B2，使得OB=BB2，同法可得A2、C2，△A2B2C2就是所求三角形；试题解析：解：（1）如图所示，△A1B1C1就是所求三角形；（2）如图所示，△A2B2C2就是所求三角形．如图，分别过点A2、C2作y轴的平行线，过点B2作x轴的平行线，交点分别为E、F，∵A（﹣1，2），B（2，1），C（4，5），△A2B2C2与△ABC位似，且位似比为2，∴A2（﹣2，4），B2（4，2），C2（8，10），∴=8×10﹣×6×2﹣×4×8﹣×6×10=28．解答题如图，在▱ABCD中，过点A作AE⊥DC，垂足为E，连接BE，F 为BE上一点，且∠AFE＝∠D.(1)求证：△ABF∽△BEC；(2)若AD＝5，AB＝8，AE∶AD＝4∶5，求AF的长．【答案】（1）见解析；（2）2.【解析】（1）由平行四边形的性质得出AB∥CD，AD∥BC，AD=BC，得出∠D+∠C=180°，∠ABF=∠BEC，证出∠C=∠AFB，即可得出结论；（2）由勾股定理求出BE，由AE∶AD＝4∶5，求出AE，再由相似三角形的性质求出AF的长．(1)证明：∵四边形ABCD是平行四边形，∴AB∥DC，AD∥BC，∴∠D＋∠C＝180°，∠ABF＝∠BEC.∵∠AFB＋∠AFE＝180°，∠AFE＝∠D，∴∠C＝∠AFB，∴△ABF∽△BEC.(2)∵AE⊥DC，AB∥DC，∴∠AED＝∠BAE＝90°.∵AD＝5，AE∶AD＝4∶5，∴AE＝AD×＝5×＝4，在Rt△ABE中，根据勾股定理，得BE＝＝＝4.在▱ABCD中，BC＝AD＝5.由(1)得△ABF∽△BEC，∴＝，即＝，∴AF＝2.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

年级：班级：学生姓名：考号：科目：
总分
（满分100分，时间90分钟）
一、填空题。

（每空2分，共40分）
1、若x 1=1是关于x 的方程x 2
+k x －3=0的一个根，则此方程的另一个根x 2= ， k = . 2、请写出以-2、7为两根且二次项系数为1的一元二次方程是 .
3、布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球．．
的概率是． 4、已知线段AB=5，CD=10，则AB ：CD=
5、若线段a 、b 、c 、d 成比例线段，且a=1，b=2，c=4，则d= ．
6、如果
23a b =，则a =______、 2a =_______、 a b b +=______、 a b b
-=_____ 7、已知570x y -=，则x
y
=_______
8、已知345x y z ==，求x y z
x y z +++-=________
9、已知：
5
3=-b b a ，则b a
=_____ 10、已知578a b c
==，且3a-2b+c=3.则a=___,b=____,c=_____,2a+4b-3c=
11、已知：346z y x ==（x 、y 、z 均不为零），则
=-+z
y y
x 233__________. 12、如图，已知：△ABC 中，DE ∥BC ，AD=3，DB=6，AE=2，则EC= ． 13、若
b a b +＝53，那么b
a
＝ . 二、选择题（每题3分，共18分） 14、已知关于x 的一元二次方程
()2k 1x 2x 10--+=有两个不相等的实数根，则k 的取值范围是
（） A ．k ＜﹣2 B ．k ＜2 C ．k ＞2 D ．k ＜2且k ≠1
15、有一个正方体，6个面上分别标有1~6这6个整数，投掷这个正方体一次，则出现向上一面的数字是偶数的概率为（）
A ．13
B ．16
C ．1
2
D ．
14
17、已知mx ny =，则下列各式中不正确的是（）
A
m x n y
= B
m n y x
= C
y m x n
= D
x y n m
= 18、下列各组线段（单位：cm ）中，成比例线段的是（）
A.1、2、3、4
B.1、2、2、4
C.3、5、9、13
D.1、2、2、3 19、如右图，AB ∥CD ∥EF ，则在图中下列关系式一定成立的是( )
A ．
B ．
C ．
D ．
20、如图，△ABC 中，DE ∥AC 交AB 、BC 于D 、E ，如果AB=7cm ，AC=5cm ，AD=3cm ，则DE=( )
A．B． C．D．
三、计算与简答题（共42分）
21、用适当的方法解下列方程（每题4分，共16分）
(1)t(2t－1)＝3(2t－1) (2)2x2－4x－1=0
（3）y2＋7y＋6＝0 （4）(2x－1)(x－1)＝1
22、（此题6分）在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球，它们除颜色外完全相同，其中
红球有2个，黄球有1个，蓝球有1个. 现有一张电影票，小明和小亮决定通过摸球游戏定输赢（赢的一方得电影票）．游戏规则是：两人各摸1次球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由．
23、（此题6分）已知如图，AD∥CF∥EB，AB=3，AC=5，DF=9，DA=2，CF=8，求DE、EF、BE的长。

24、（此题8分）已知：如图，△ABC中，DE∥BC.
(1)若AD=3，DB=5，AE=2.25，求EC的长；
(2)若AB=5，AD=2，AC=4，求EC的长；
(3)若AE：EC=2：3，DB-AD=3，求AD与DB的长.
F C
E
D
B
A
25、（此题3分）已知：b a ＝d c ＝f
e
＝3(且有b+d+f ＝0)，求证：d b c a ++＝f d e c ++＝3.
26、（此题3分）已知8
75c
b a ==，且20=++
c b a ，求c b a -+2。