自动化车床模型(数学建模)
数学建模 历年试题及论文
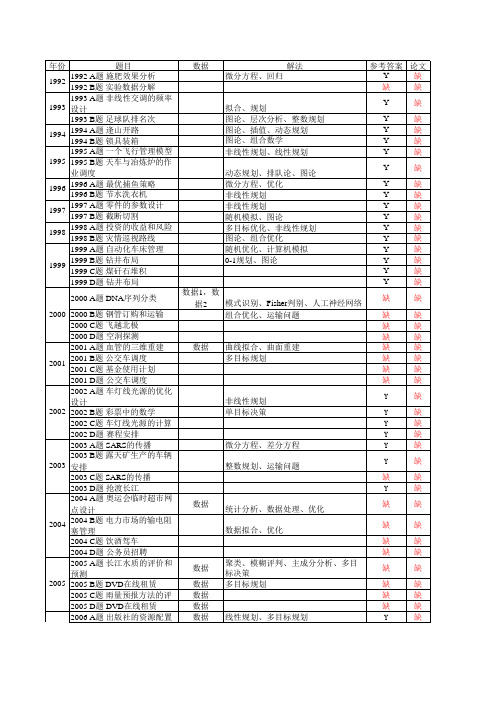
拟合、规划 图论、层次分析、整数队论、图论 微分方程、优化 非线性规划 非线性规划 随机模拟、图论 多目标优化、非线性规划 图论、组合优化 随机优化、计算机模拟 0-1规划、图论
2000 2000 B题 钢管订购和运输 缺 2000 C题 飞越北极 缺 2000 D题 空洞探测 缺 2001 A题 血管的三维重建 数据 曲线拟合、曲面重建 缺 多目标规划 2001 B题 公交车调度 缺 2001 2001 C题 基金使用计划 缺 2001 D题 公交车调度 缺 2002 A题 车灯线光源的优化设计 非线性规划 Y 2002 B题 彩票中的数学 单目标决策 Y 2002 2002 C题 车灯线光源的计算 Y 2002 D题 赛程安排 Y 2003 A题 SARS的传播 微分方程、差分方程 Y 2003 B题 露天矿生产的车辆安排 整数规划、运输问题 Y 2003 2003 C题 SARS的传播 缺 2003 D题 抢渡长江 Y 2004 A题 奥运会临时超市网点设计 数据 统计分析、数据处理、优化 缺 2004 B题 电力市场的输电阻塞管理 数据拟合、优化 缺 2004 2004 C题 饮酒驾车 缺 2004 D题 公务员招聘 缺 2005 A题 长江水质的评价和预测 数据 聚类、模糊评判、主成分分析、多目标决策 缺 2005 B题 DVD在线租赁 数据 多目标规划 缺 2005 2005 C题 雨量预报方法的评价 数据 缺 2005 D题 DVD在线租赁 数据 缺 2006 A题 出版社的资源配置 数据 线性规划、多目标规划 Y 2006 B题 艾滋病疗法的评价及疗效的预测 回归、线性规划 数据 Y 2006 2006 C题 易拉罐形状和尺寸的最优设计 缺 2006 D题 煤矿瓦斯和煤尘的监测与控制 数据 缺 2007 A题 中国人口增长预测 数据 微分、差分方程 Y 2007 B题 乘公交,看奥运 数据 图论、0-1 规划、动态规划 Y 2007 2007 C题 手机“套餐”优惠几何 数据 Y
关于自动化机床管理的数学模型分析

1 问题提出
一道工序用自动化车床连续加工某种零件 , 由于刀具损坏等原因该工序会出现故障 . 其中刀 具损坏故障占 95 % ,其他故障仅占 5 %. 工作人员 通过检查零件来确定工序是否出现故障 . 现计划 在刀具加工一定件数后定期更换新刀具 . 己知生 产工序的费用参数如下 : 出现故障时产出的零件损失费用 f = 200 元 / 件; 进行检查的费用 t = 10 元 / 次 ; 发现故障进行调节使恢复正常的平均费用
d = 3 000 元 / 次 ( 包括刀具费) ;
1 000元/ 次 .
2 模型假设
● 工序出现故障是完全随机的
, 假定在生产任
一零件时出现故障的机会均相同 . ● 设备刀具故障的发生服从参数为 μ 及σ的 正态分布 , 以近似代替泊松分布 . ●设 n 为定期进行检查间隔 , 即每生产 n 个零 件进行依次检查 , 若发现故障立即进行调节 , 使车 床恢复正常 , 假设此时车床和刀具均恢复到原来 状态 . ● 刀具在生产了 m 个零件后因使用时间过长 而必须被更新 , 从而设备又回到原来状态 . ● 假定其他故障的发生服从平均分布 ,并且因 为刀具损坏故障占 95 % ,其他故障仅占 5 %. 可以 假设其他故障发生的概率很小 ; 其概率为刀具故 障的 5/ 95 ,即 1/ 19.
摘 要 : 为解决自动化车床连续加工出现的故障及更换刀具的问题 ,运用数理统计与概率论 ,根据不同的实 际情况和要求 ,建立了两种数学模型 ,设计出合理可行的算法 ,进行编程计算 ,得出最优解 ,并提出了改进后 的检查方式 . 这一数学模型为自动化车床的管理提供了可靠的依据 . 关键词 : 正态分布 ; 数学期望 ; 概率 ; 概率密度 ; 均值 中图分类号 : O213 :TB114 文献标识码 : A
数学建模 自动化车床管理

数学建模自动化车床管理数学建模:自动化车床管理一、引言自动化车床管理是现代制造业中的重要环节,通过合理的管理和优化,可以提高生产效率和产品质量。
为了实现自动化车床管理的科学化、规范化和高效化,需要进行数学建模分析,以便找到最优的管理策略和决策方案。
二、问题描述在自动化车床管理中,存在以下几个关键问题需要解决:1. 生产计划优化问题:如何合理安排车床的生产计划,以最大程度地提高生产效率和资源利用率?2. 设备故障预测问题:如何通过数学建模分析,提前预测车床的故障情况,以便及时进行维修和更换?3. 零部件供应链优化问题:如何通过数学建模分析,优化零部件的供应链管理,以确保及时供应和减少库存成本?三、数学建模方法针对上述问题,可以采用以下数学建模方法进行分析和求解:1. 线性规划模型:通过建立生产计划优化的线性规划模型,考虑生产能力、设备利用率、订单需求等因素,以最大化产量和利润为目标,确定最优的生产计划。
2. 时间序列分析模型:通过对历史数据进行时间序列分析,建立车床故障预测的模型,包括趋势分析、季节性分析、残差分析等,以便提前预测故障情况,采取相应的维修和更换措施。
3. 随机优化模型:通过建立供应链的随机优化模型,考虑供应商的可靠性、交货时间、库存成本等因素,以最小化总成本为目标,确定最优的零部件供应链管理策略。
四、数据收集和处理为了进行数学建模分析,需要收集和处理以下数据:1. 生产数据:包括车床的生产能力、设备利用率、订单需求等数据。
2. 故障数据:包括车床的故障记录、维修时间和维修费用等数据。
3. 供应链数据:包括供应商的可靠性、交货时间、库存成本等数据。
通过对以上数据进行整理和处理,可以得到适用于数学建模的数据集。
五、模型求解和结果分析根据收集和处理的数据,运用上述数学建模方法,可以进行模型求解和结果分析。
具体步骤如下:1. 建立数学模型:根据问题描述,建立相应的数学模型,包括目标函数、约束条件等。
全国大学生数学建模竞赛赛题综合评析
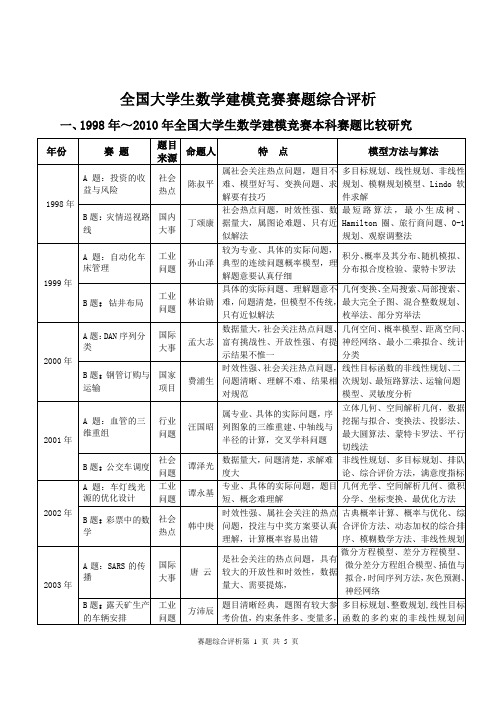
社会热点
叶其孝、周义仓
开放性强、社会关注性强,突出数据来源的可靠性、结论解释的合理性
数据收集与处理、问题的分析与假设,初等数学方法、一般统计方法、多目标规划、回归分析、综合评价方法、灰色预测
2009年
A题:制动器试验台的控制方法分析
工业问题
方沛辰、刘笑羽
问题具体、专业性强,要花时间读懂、理解清楚问题
出版社的资源配置
孟大志
艾滋病疗法的评价及疗效的预测
边馥萍
易拉罐形状和尺寸的最优设计(C题)
叶其孝
煤矿瓦斯和煤尘的监测与控制(D题)
韩中庚
2007年
中国人口增长预测
唐云
乘公交,看奥运
方沛辰、吴孟达
手机“套餐”优惠几何(C题)
韩中庚
体能测试时间安排(D题)
刘雨林
2008年
数码相机定位
谭永基
高等教育学费标准探讨
叶其孝、周义仓
地面搜索(C题)
肖华勇
NBA赛程的分析与评价(D题)
姜启源
2009年
制动器试验台的控制方法分析
方沛辰、刘笑羽
眼科病床的合理安排
吴孟达、毛紫阳
卫星和飞船的跟踪测控(C题)
周义仓
会议筹备(D题)
王宏健
2010年
储油罐的变位识别与罐容表标定
韩中庚
2010年上海世博会影响力的定量评估
杨力平
输油管的布置(C题)
1
6
8
付鹂
重庆大学
1
6
9
姜启源
清华大学
4
3
10
陈叔平
浙江大学、贵州大学
2
5
11
自动化车床管理的数学模型

零件检查的数学模型1问题重述1.1需要解决的问题一道工序用自动化车床连续加工某种零件,由于刀具损坏等原因该工序会出现故障,其中刀具损坏故障占95%, 其它故障仅占5%。
工序出现故障是完全随机的, 假定在生产任一零件时出现故障的机会均相同。
工作人员通过检查零件来确定工序是否出现故障。
现积累有100次刀具故障记录,故障出现时该刀具完成的零件数如附录表一。
现计划在刀具加工一定件数后定期更换新刀具。
问题:假定工序故障时产出的零件均为不合格品,正常时产出的零件均为合格品, 试对该工序设计效益最好的检查间隔(生产多少零件检查一次)和刀具更换策略。
2模型的假设及符号说明2.1模型的假设假设1:假设在生产任一零件时出现故障的机会均相等。
假设3:假设生产任一零件时所需的时间相同。
假设4:假设提供的刀具故障记录数据是独立同分布的.假设5:假设提供的刀具故障记录数据是独立同分布的。
2.2符号说明符号说明μ刀具平均寿命σ样本方差Tc检查零件的单位时间间隔T定期换刀的单位时间间隔TT(c)以检测时间间隔为时,系统工序合格零件的单位期望损失cf(x)系统的失效概率密度F(x)累积失效概率密度,即寿命分布函数3问题分析在自动化车床生产流程中,由于刀具损坏等原因会使工序出现故障,工序故障的出现是完全随机的。
工作人员通过检验零件来确定是否出现故障,并且决定在刀具加工一定的零件后更换刀具。
当发生故障时要及时维修,如果检修周期太长,故障不能及时发现,会给生产带来损失;检查周期太短又会增加费用。
在理论上我们首先将问题转化为概率模型。
通过分析题目所给的100次刀具故障记录,我们通过绘图分析假设刀具的寿命服从正态分布。
再通过假设检验,我们决定接受这一假设。
问题中我们建立离散型随机事件模型I 。
我们选择一个周期T 。
目标函数要求目标函数取最小值的情况下求解检查间T 系统工序的期望总损失总=C 系统工序产生的合格零件数U隔和道具更换策略。
U 总分为两种情况:故障发生在换刀之前与故障发生在换刀之后。
自动化车床管理的数学模型

(m ) (m )
其中 E ( F ) 为各种费用之和的期望值, E (N ) 为零件合格品数目的期望值 .
E (F ) = E (N ) =
m∈ M
m∈ M
∑F ∑N
P P
, .
(m )
(m )
其中, M 为事件的各种可能情况组成的集合. 下面, 我们遍历刀具故障出现与第一次检查出不合格品这两个事件发生的所有情况来 计算 E ( F ) 与 E (N ). 设刀具故障发生在第 i - 1 次检查与第 i 次检查之间 ( 1≤ i ≤n + 2) , ( i = n + 1 表示刀具 故障出在第 n 次检查之后, 生产 u 个零件之前; i = n + 2 表示刀具出现在生产 u 个零件之
( 0. 98 ( j ( s - 1) + j - 1) )
+ 0. 98n ( n t + k + f ( u -
3 模型求解及结果
我们对 s 从 1 至 100, u 从 100 至 600 用穷举法进行搜索, 比较 F ( s, u ) 的值, 求得最优解 为: s= 54, u = 304, 此时目标函数值为 9137681, 若限定 u 为 s 的整数倍, 则最优解为: s = 51, u = 306, 此时目标函数值为 9140044.
( ( 0. 98 j ( s - 1) + j - 1)
+ 0. 98n ( 0. 98 ( h - n ) + 0. 4 ( u - h ) + n ) ] +
∫u n+ ∞ng (x ) d x [
∑0.
j= 1
98
机床任务分配问题数学建模

机床任务分配问题数学建模任务分配到机床摘要本⽂解决的是机床⽣产调度的问题,⽬的是使产品加⼯路径的组合优化。
对于本⽂所研究的机床任务的合理调度问题,由于⽣产⽅式的不确定,我们根据A,B,C,D这4道⼯序是否有序进⾏了分类研究,并分情况得到了最优解或近似最优解,制定出了不同情况下的合理调度⽅案。
对于问题⼀:在⼯序⽆序的情况下,问题转化为⼀个指派问题,以完成任务耗时最长的那台机床的运⾏时间作为指标,以该指标最⼩作为⽬标函数,建⽴了⼀个0-1整数规划模型,⽤Lingo求解得最短加⼯时间为233h各机床加⼯时间的均衡度为3.8%。
在⼯序有序的情况下,问题⼀转化为⼀个柔性作业车间调度问题,此时⽣产调度的任务就是:确定产品的加⼯路径和每⼀⼯序的加⼯开始时间,并使产品通过系统的时间(Makespan)最⼩。
运⽤遗传算法建⽴模型,绘制出最佳调度的⽢特图,并得到加⼯时间的近似最优解为250h,各机床加⼯时间均衡度为1.6%,均衡度很⾼;与⽆序情况所得最优解相⽐,其近似度为92.7%,具有较好的有效性。
对于问题⼆:在⼯序⽆序的情况下,该问题仍为⼀个指派问题,在加⼊调度费⽤与运⾏费⽤的条件下,我们利⽤理想点法将这两个指标的双⽬标问题转化为单⽬标规划模型来进⾏求解,建⽴了⼀个0-1整数规划模型,⽤Lingo求解得加⼯时间为510h,总费⽤为1784600元。
在⼯序有序的情况下,我们运⽤蚁群算法建⽴模型,经过选⼯序,计算加⼯⼯序k的机床的空闲时间段和加⼯序列,计算可选⼯序的EAPT和信息素的积累等过程,得到加⼯时间为441h,总费⽤为1799000元。
为了进⼀步分析该算法的有效性,我们还进⾏了实例规模较⼤的计算机仿真试验。
我们在模型的改进和推⼴⾥对模型四提出了⼀种评价⽅法,⼒求使⼀群算法的精度进⼀步提⾼,以实现更⼤规模的应⽤。
关键词:指派问题柔性调度理想点法遗传算法蚁群算法1.问题重述1.1问题背景车间⽣产调度是制造系统的基础,⽣产调度的优化⽅法是先进制造技术的核⼼技术。
1999年全国大学生数学建模A题车床管理优化模型

11 顺序统计的 n 个零件, 次品率低于 2% , 认为工序正常, 继续生产; 21 顺序统计的 n 个零件, 次品率高于 2% 低于 60% , 但所有已检查零件的次品率低于 2% , 认为工序正常, 继续生产; 31 顺序统计的 n 个零件, 次品率高于 60% , 但所有已检查零件的次品率低于 2% , 认为 工序正常, 继续生产; 41 顺序统计的 n 个零件次品率高于 60% , 并且所有检查零件的次品率高于 2% , 认为 工序故障, 系统自动发出信号并进行调节. (算法框图略)
32
数 学 的 实 践 与 认 识
30 卷
因 n 个零件检查一次, 所以每个零件所分推到的检查费用为 t n, 即:
I= t n 由于检查到故障时才进行调节, 而平均每 θu 个零件出一次故障, 困此, 每个零件所分推 到的调节费是, 即:
= d θu 至于 , 由于检查时生产并不停止, 而检查又需一定时间. 假设检查一个零件的同时,
已又有 l 个零件生产出来. 因此, 每一次故障由于检查滞后造成损失为 l·f , 于是每个零件 所分推到的检查滞后损失为 l·f θu, 即:
= l·f θu 最后来分析 , 注意每 n 个零件才检查一次, 在某检查点一但发现零件为不合格品, 一 般说来, 不合格品就不只这一个, 详细情况见下图:
+
lf
θu 定
+
n+ 2
l
f
θu 定
(5)
令L ′定= 0 得最宜检查间隔为:
n=
2 θu 定 t
广东商学院学生参加国家和省“数模建模”竞赛获奖情况一览表
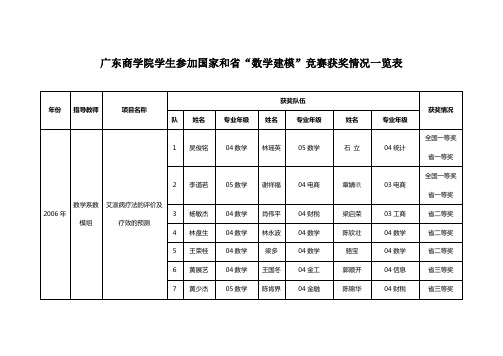
杨敏杰
04数学
肖伟平
04财税
梁启荣
0数学
林永波
04数学
陈钦壮
04数学
省二等奖
5
王荣桂
04数学
梁多
04数学
骆宝
04数学
省二等奖
6
黄展艺
04数学
王国冬
04金工
郭顺开
04信息
省三等奖
7
黄少杰
05数学
陈肯界
04金融
陈锦华
04财税
省三等奖
2005年
数学系数模组
长江水质评价模型
1
郑广珠
02旅游
王宇雯
02金工
谢张一
02统计
全国一等奖
省一等奖
2
谢祥福
04电商
刘真凤
04电商
周立成
04电商
全国二等奖省一等奖
3
刘鹏
02统计
曾翠芬
03统计
谢智聪
03统计
省一等奖
DVD在线租赁模型
4
肖洁
02信息
梁振捷
02旅游
刘幸丹
03统计
省二等奖
2004年
数学系数模组
电力市场输电阻塞管理模型
1
李彬联
陈云
胡秀梨
省参赛成功奖
省参赛成功奖
2000年
数学部数模组
DNA序列分类
钢管定购与运输
1
李家华李绪伟李悦乔
国际三等奖
2
李靖李英日陈文泰
省三等奖
3
何新全姚宇凡詹国梁
4
管志成姚俊生李文达
省参赛成功奖
5
李悦乔蔡麟余壮雄
1999年
数控机床的数学模型与仿真技术

数控机床的数学模型与仿真技术数控机床是机械加工行业中非常重要的设备之一,它能够通过程序控制来完成精密加工,使得生产效率和产品质量都得到了非常大的提升。
而这种精密性能的实现,离不开数学模型和仿真技术的支持。
一、数学模型在数控机床中的应用数学模型在数控机床中的应用是非常广泛的,它们可以描述不同的物理过程,如机床结构的运动、切削过程的力学和热学、刀具的损耗和磨损等等。
这些模型一般是基于物理定律和经验公式建立的,通过计算机程序来求解。
下面我们具体介绍一下数学模型在数控机床中的几个应用。
1. 机床结构运动机床结构运动是数控机床中最基本的数学模型之一,它描述了机床各部分的位置、速度、加速度随时间的变化。
这个模型是机床控制系统的基础,控制系统通过控制各驱动装置的运动来实现加工程序的执行。
机床结构运动模型的求解需要考虑多种因素,如机床的结构、驱动装置的特性、工件的形状等等,通常使用有限元分析或者正逆动力学模型来求解。
2. 切削过程力学模型切削过程力学模型是研究刀具与工件之间力学相互作用的数学模型,它可以描述刀具的进给、切削和退出过程中的切削力和其他作用力。
这个模型可以帮助设计和选择刀具,优化切削参数,以及预测刀具寿命和工件表面形貌等,它是数控加工中非常重要的数学模型之一。
普遍用的刀具力模型包括切削力系数法、影响系数法、弹性回复切削力模型等。
3. 切削过程热学模型切削过程热学模型是描述切削过程中的热处理过程的数学模型,它可以预测切削面温度和刀具温度等。
这个模型可以帮助优化切削参数,提高切削速率、降低刀具磨损、减少工件变形和提高表面质量等。
切削过程热学模型主要包括经验模型和物理模型。
经验模型通常基于实验数据,通过适当的修正,可以很好地预测切削温度和刀具温度。
物理模型则基于热传导、热应力等物理理论,需要更大的计算开销,但是可以准确地反映热传导和热应力的特性。
二、数控机床仿真技术数控机床仿真技术是基于数学模型的的数字仿真技术,它可以模拟机床的运动、加工过程和性能。
全国大学生数学建模竞赛历年试题
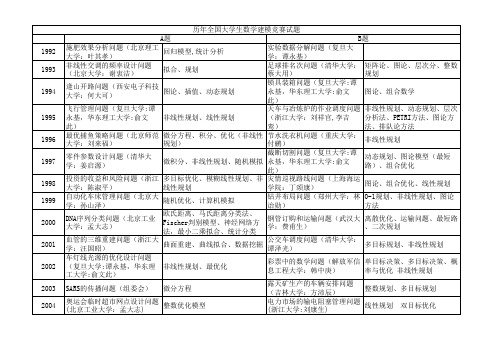
(浙江大学:刘祥官,李吉 分析法、PETRIБайду номын сангаас法、图论方
此)
鸾)
法、排队论方法
最优捕鱼策略问题(北京师范 大学:刘来福)
微分方程、积分、优化(非线性 规划)
节水洗衣机问题(重庆大学: 付鹂)
非线性规划
零件参数设计问题(清华大 学:姜启源)
截断切割问题(复旦大学:谭 微积分、非线性规划、随机模拟 永基,华东理工大学:俞文
微分方程
数码相机定位
非线性方程模型
制动器试验台的控制方法分析
DVD在线租赁问题(清华大学: 谢金星等)
GM
0-1规划 多目标规划
艾滋病疗法的评价及疗效的预
测(天大:边馥萍)
乘公交,看奥运(吉大:方沛
辰,国防科大:吴孟达)
高等教育学费标准探讨
(开放性题目)
眼科病床的合理安排
1999 2000 2001
拟合、规划
足球排名次问题(清华大学: 矩阵论、图论、层次分、整数
蔡大用)
规划
逢山开路问题(西安电子科技 大学:何大可)
图论、插值、动态规划
锁具装箱问题(复旦大学:谭 永基,华东理工大学:俞文 图论、组合数学 此)
飞行管理问题(复旦大学:谭
天车与冶炼炉的作业调度问题 非线性规划、动态规划、层次
永基,华东理工大学:俞文 非线性规划、线性规划
酒后开车问题(清华大学:姜 启源)
微分方程
雨量预报方法的评价问题(复 旦大学:谭永基)
模糊评价 插值
易拉罐形状和尺寸的最优设计
(北理工:叶其孝)
手机“套餐”优惠几何(信息
工程大学:韩中庚)
地面搜索
一笔画问题、数学规划模型
自动化车床模型(数学建模)

自动化车床管理模型摘要本文研究的是自动化车床管理中定期检查和预防性保全刀具问题。
在现代技术下,被动地等待故障发生,然后投入较高资金处理出现的问题,这种传统的处理方法已经不符合工业生产和现代社会的发展要求。
为解决此问题,我们共建立两个模型,使自动化车床管理方略更科学、更合理。
对于问题一:我们通过一定的数学方法,巧妙地建立了生产每一个零件的平均损失费用L (包括预防保全费用1L , 检查费用2L , 和故障造成的不合格品损失和修复费用3L,即123L L L L =++)关于刀具定期更换间隔a 的单变量函数关系,并利用MATLAB等数学计算工具和多种方法,对a 进行逐个赋值,最终得到:当342a =件时,L 取得最小值min5.297L =元,再根据a与固定检查间隔n 之间的函数关系得到:16n =件。
对于问题二:此问中效益函数计算的费用与第一问相比,增加了错误判断带来的损失费用,我们将因误判带来的费用考虑到生产每一个零件的平均损失费用L 中,用与第一问类似的模型求解,得到当299a =件时,L 取得最小值min 7.381L =元,对应固定检查间隔18n =件。
对于问题三:保持问题二的情况,我们建立新的模型,并采取连续检查多个零件(最多3次)的方法,降低误判率,从而达到减少每个零件的平均管理费用,使模型更优化。
最终得到在工序发生故障时误判率为0.208,比检查一次的误判率0.4减少0.192,误判率减小了50%;在工序正常时误判率为0.000792,比检查一次的误判率0.02减少0.019208,误判率降低了96.04%,从而使模型得到优化。
关键词:自动化车床管理 效益函数 正态分布 误判率1.问题重述一道工序用自动化车床连续加工某种零件,由于刀具损坏等原因该工序会出现故障,其中刀具损坏故障占95%, 其它故障仅占5%。
工序出现故障是完全随机的, 假定在生产任一零件时出现故障的机会均相同。
工作人员通过检查零件来确定工序是否出现故障。
自动化车床数学建模

自动化车床数学建模自动化车床数学建模是指利用数学方法和技巧对自动化车床进行建模和分析的过程。
自动化车床是一种能够自动完成加工任务的机械设备,通过数学建模可以对其进行性能评估、优化设计以及控制算法的研究与实施。
在自动化车床数学建模中,常用的数学方法包括几何建模、运动学建模、动力学建模以及控制建模等。
几何建模是描述自动化车床结构和形状的数学模型,通过几何建模可以确定车床的尺寸、形状和位置等参数。
运动学建模是描述自动化车床运动状态和轨迹的数学模型,通过运动学建模可以确定车床的运动范围、速度和加速度等参数。
动力学建模是描述自动化车床运动过程中力学特性的数学模型,通过动力学建模可以确定车床的力学性能、刚度和阻尼等参数。
控制建模是描述自动化车床控制系统的数学模型,通过控制建模可以确定车床的控制算法、控制器参数和控制策略等。
在自动化车床数学建模中,需要运用到的数学工具包括线性代数、微积分、概率论和控制理论等。
线性代数用于描述车床的几何结构和运动关系,微积分用于描述车床的运动学和动力学特性,概率论用于描述车床运动的随机性和不确定性,控制理论用于描述车床的控制过程和控制策略。
自动化车床数学建模的应用范围广泛。
在制造业中,数学建模可以用于优化车床的结构和性能,提高加工效率和质量。
在工程设计中,数学建模可以用于评估车床的性能和可靠性,指导设计和改进。
在控制系统中,数学建模可以用于设计和优化车床的控制算法和控制器。
自动化车床数学建模是一项复杂而重要的工作。
在进行数学建模时,需要全面理解车床的结构和工作原理,合理选择数学方法和工具,准确提取和处理数据,以及合理假设和简化模型。
此外,还需要进行模型验证和仿真实验,以确保建模结果的准确性和可靠性。
自动化车床数学建模是一项关键的技术和方法,对于提高车床的性能、效率和可靠性具有重要意义。
通过数学建模,可以深入理解车床的运动特性和控制过程,为车床的设计、优化和控制提供科学依据和方法。
历年全国数学建模试题及解法

一、历年全国数学建模试题及解法赛题解法93A 非线性交调的频率设计拟合、规划93B 足球队排名图论、层次分析、整数规划94A 逢山开路图论、插值、动态规划94B 锁具装箱问题图论、组合数学95A 飞行管理问题非线性规划、线性规划95B 天车与冶炼炉的作业调度动态规划、排队论、图论96A 最优捕鱼策略微分方程、优化96B 节水洗衣机非线性规划97A 零件的参数设计非线性规划97B 截断切割的最优排列随机模拟、图论98A 一类投资组合问题多目标优化、非线性规划98B 灾情巡视的最灾情巡视的最佳佳路线图论、组合优化99A 自动化车动化车床床管理随机优化、计随机优化、计算算机模拟99B 钻井布局0-1规划、图论00A DNA 序列分类模式识别式识别、、Fisher 判别判别、、人工神经网络00B 钢管订购和运输组合优化、组合优化、运输运输运输问题问题01A 血管三维重建曲线拟合、线拟合、曲面重建曲面重建01B 工交车调度问题多目标规划02A 车灯线光源光源的优化的优化非线性规划02B 彩票彩票问题问题问题 单目标目标决决策 03A SARS 的传播传播 微分方程、微分方程、差差分方程分方程03B 露天矿生产矿生产的车的车的车辆安辆安辆安排排 整数规划、整数规划、运输运输运输问题问题问题 04A 奥运会临时超市网点奥运会临时超市网点设计设计设计 统计分析、数计分析、数据处据处据处理、优化理、优化理、优化 04B 电力市场电力市场的的输电阻塞输电阻塞管理管理管理 数据拟合、优化拟合、优化 05A 长江长江水水质的评价和预测评价和预测 预测评价预测评价、数、数、数据处据处据处理理 05B DVD 在线租赁租赁 随机规划、整数规划随机规划、整数规划二、赛题发展的特点1.对选手对选手的计的计的计算算机能力提出了更高能力提出了更高的的要求:要求:赛题的解赛题的解赛题的解决依赖决依赖决依赖计计算机,题目的数题目的数据较据较据较多多,手工,手工计计算不能完成,如03B ,某些,某些问题问题问题需要需要需要使用使用使用计计算机软件,01A 。
数控机床的数学模型与运动控制理论

数控机床的数学模型与运动控制理论数控机床是一种通过计算机控制的自动化机械设备,它能够根据预先编程的指令,精确地完成各种复杂的加工任务。
数控机床的核心是其数学模型和运动控制理论,它们的优化和应用对于提高机床的加工精度和效率具有重要意义。
一、数学模型数控机床的数学模型是描述机床运动规律和加工过程的数学方程组。
它包括几何模型、运动模型和力学模型。
几何模型是描述机床工作空间和工件形状的数学模型。
通过建立几何模型,可以确定机床坐标系和工件坐标系之间的转换关系,实现机床的坐标控制。
运动模型是描述机床轴向运动规律的数学模型。
它包括直线运动和旋转运动两种形式。
直线运动模型可以通过直线插补算法实现,而旋转运动模型则可以通过圆弧插补算法实现。
力学模型是描述机床切削力和刚度特性的数学模型。
它可以通过力学分析和有限元分析等方法建立。
力学模型可以用于优化机床结构和刀具轨迹,提高机床的加工质量和切削效率。
二、运动控制理论运动控制理论是指控制机床运动的理论和方法。
它包括运动规划、运动插补和运动控制三个方面。
运动规划是指根据加工要求,确定机床的轨迹和速度规划。
通过运动规划,可以实现机床的高速、高精度加工。
运动插补是指根据机床的数学模型和运动规划,计算机实时生成机床的轨迹和速度指令。
运动插补算法可以根据加工要求进行优化,提高机床的加工效率和质量。
运动控制是指根据机床的数学模型和运动指令,控制机床的运动和加工过程。
运动控制可以通过闭环控制和开环控制两种方式实现。
闭环控制可以根据机床的反馈信息进行实时调整,提高机床的运动精度和稳定性。
三、数控机床的应用数控机床的数学模型和运动控制理论在实际应用中具有广泛的应用价值。
首先,数学模型和运动控制理论可以用于优化机床结构和刀具轨迹,提高机床的加工精度和效率。
通过优化机床结构和刀具轨迹,可以减小机床的动态误差和静态误差,提高机床的加工质量和稳定性。
其次,数学模型和运动控制理论可以用于开发新的数控机床和加工工艺。
历年全国大学生数学建模竞赛题目

武汉理工大学队员比赛论文mcm2003_A_王蝉娟_唐兵_隗勇mcm2003_A_万丽军_唐涛_陈正旭mcm2003_A王鹏_邓科_刘文慧mcm2003_B_王雨春_钟原_李霜icm2003_C_刘旺_董显_吴辉icm2003_C_夏立_成浩_易科mcm2004_b 厉化金_谷雨_曾祥智mcm2004_b_夏立_赵明杰_高婷全国比赛优秀论文1993年A题非线性交调的频率设计1993年B题球队排名问题1994年A题逢山开路1994年B题锁具装箱1995年A题一个飞行管理模型1995年B题天车与冶炼炉的作业调度1996年A题最优捕鱼策略1996年B题节水洗衣机1997年A题零件的参数设计1997年B题截断切割1998年A题投资的收益和风险1998年B题灾情巡视路线1999年A题自动化车床管理1999年B题钻井布局2000年A题 DNA序列分类2000年B题钢管定购和运输2001年A题血管的三维重建2001年B题公交车调度中国科大老师对美国赛题目的讲解(题目可从往届试题处下载) MCM 1985 A题(王树禾教授)MCM 1985 B题(侯定丕教授)MCM 1986 A题(常庚哲教授,丁友东老师)MCM 1986 B题(李尚志教授)MCM 1988 A题(苏淳教授)MCM 1988 B题(侯定丕教授)MCM 1989 A题(赵林城老师)MCM 1989 B题(侯定丕教授)MCM 1990 A题(王树禾教授)MCM 1990 B题(王树禾教授)MCM 1991 A题(常庚哲教授,丁友东老师)MCM 1992 B题(侯定丕教授)MCM 1993 A题(苏淳教授)MCM 1993 B题(万战勇老师)MCM 1994 B题(程继新老师)美国赛优秀论文MCM 2001 UMAP MCM 2002 UMAPMCM 2003 UMAP MCM 2004 (Quick Pass)。
自动化车床数学建模

自动化车床数学建模自动化车床是一种通过计算机控制的机械设备,能够自动完成各种加工操作。
数学建模在自动化车床的设计和操作中起着重要的作用。
本文将介绍自动化车床数学建模的相关内容。
一、自动化车床数学建模的意义自动化车床数学建模是通过数学方法对自动化车床的工作过程进行描述和分析,以实现优化设计和操作。
数学建模可以帮助工程师了解车床的运动规律、优化刀具路径、提高加工效率和质量。
同时,数学建模也可以用于车床的控制系统设计,实现自动化程度更高的加工过程。
二、自动化车床数学建模的关键要素1. 运动学建模运动学建模是自动化车床数学建模的基础。
它描述了车床各个部件的运动规律,包括主轴、刀架、进给系统等。
通过建立运动学模型,可以计算出刀具的位置、速度和加速度等参数,为后续的刀具路径规划和控制提供依据。
2. 刀具路径规划刀具路径规划是自动化车床数学建模中的重要环节。
它通过数学方法确定刀具的运动轨迹,使刀具能够高效地完成加工任务。
刀具路径规划需要考虑加工件的几何形状、加工要求和刀具的几何特性等因素,以确保加工过程的精度和效率。
3. 加工力学建模加工力学建模是自动化车床数学建模中的关键环节。
它研究了刀具与工件之间的力学相互作用,以及加工过程中产生的切削力、刀具磨损等现象。
通过建立加工力学模型,可以分析加工过程中的切削力分布、刀具寿命等问题,为工艺参数的选择和刀具的优化设计提供依据。
三、自动化车床数学建模的应用案例1. 刀具路径规划在自动化车床的数学建模中,刀具路径规划是一个重要的应用领域。
通过数学方法确定刀具的运动轨迹,可以实现高效、精确的加工过程。
例如,在螺纹加工中,可以通过数学建模确定刀具的旋转轴心和进给轴心,从而实现螺纹的加工。
2. 加工力学建模在自动化车床的数学建模中,加工力学建模也是一个重要的应用领域。
通过建立加工力学模型,可以分析加工过程中的切削力分布、刀具磨损等问题,为工艺参数的选择和刀具的优化设计提供依据。
数学建模30种经典模型matlab

一、概述数学建模是数学与实际问题相结合的产物,通过建立数学模型来解决现实生活中的复杂问题。
Matlab作为一个强大的数学计算工具,在数学建模中具有重要的应用价值。
本文将介绍30种经典的数学建模模型,以及如何利用Matlab对这些模型进行建模和求解。
二、线性规划模型1. 线性规划是数学建模中常用的一种模型,用于寻找最优化的解决方案。
在Matlab中,可以使用linprog函数对线性规划模型进行建模和求解。
2. 举例:假设有一家工厂生产两种产品,分别为A和B,要求最大化利润。
产品A的利润为$5,产品B的利润为$8,而生产每单位产品A 和B分别需要8个单位的原料X和10个单位的原料Y。
此时,可以建立线性规划模型,使用Matlab求解最大化利润。
三、非线性规划模型3. 非线性规划是一类更加复杂的规划问题,其中目标函数或约束条件存在非线性关系。
在Matlab中,可以使用fmincon函数对非线性规划模型进行建模和求解。
4. 举例:考虑一个有约束条件的目标函数,可以使用fmincon函数在Matlab中进行建模和求解。
四、整数规划模型5. 整数规划是一种特殊的线性规划问题,其中决策变量被限制为整数。
在Matlab中,可以使用intlinprog函数对整数规划模型进行建模和求解。
6. 举例:假设有一家工厂需要决定购物哪种机器设备,以最大化利润。
设备的成本、维护费用和每台设备能生产的产品数量均为已知条件。
可以使用Matlab的intlinprog函数对该整数规划模型进行建模和求解。
五、动态规划模型7. 动态规划是一种数学优化方法,常用于多阶段决策问题。
在Matlab 中,可以使用dynamic programming toolbox对动态规划模型进行建模和求解。
8. 举例:考虑一个多阶段生产问题,在每个阶段都需要做出决策以最大化总利润。
可以使用Matlab的dynamic programming toolbox对该动态规划模型进行建模和求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动化车床管理模型摘要本文研究的是自动化车床管理中定期检查和预防性保全刀具问题。
在现代技术下,被动地等待故障发生,然后投入较高资金处理出现的问题,这种传统的处理方法已经不符合工业生产和现代社会的发展要求。
为解决此问题,我们共建立两个模型,使自动化车床管理方略更科学、更合理。
对于问题一:我们通过一定的数学方法,巧妙地建立了生产每一个零件的平均损失费用L (包括预防保全费用1L , 检查费用2L , 和故障造成的不合格品损失和修复费用3L ,即123LLLL =++)关于刀具定期更换间隔a 的单变量函数关系,并利用MATLAB 等数学计算工具和多种方法,对a 进行逐个赋值,最终得到:当342a =件时,L 取得最小值min 5.297L =元,再根据a 与固定检查间隔n 之间的函数关系得到:16n =件。
对于问题二:此问中效益函数计算的费用与第一问相比,增加了错误判断带来的损失费用,我们将因误判带来的费用考虑到生产每一个零件的平均损失费用L 中,用与第一问类似的模型求解,得到当299a =件时,L 取得最小值min 7.381L =元,对应固定检查间隔18n =件。
对于问题三:保持问题二的情况,我们建立新的模型,并采取连续检查多个零件(最多3次)的方法,降低误判率,从而达到减少每个零件的平均管理费用,使模型更优化。
最终得到在工序发生故障时误判率为0.208,比检查一次的误判率0.4减少0.192,误判率减小了50%;在工序正常时误判率为0.000792,比检查一次的误判率0.02减少0.019208,误判率降低了96.04%,从而使模型得到优化。
关键词:自动化车床管理 效益函数 正态分布 误判率1.问题重述一道工序用自动化车床连续加工某种零件,由于刀具损坏等原因该工序会出现故障,其中刀具损坏故障占95%, 其它故障仅占5%。
工序出现故障是完全随机的, 假定在生产任一零件时出现故障的机会均相同。
工作人员通过检查零件来确定工序是否出现故障。
现积累有100次刀具故障记录,故障出现时该刀具完成的零件数如附表。
现计划在刀具加工一定件数后定期更换新刀具。
已知生产工序的费用参数如下:故障时产出的零件损失费用 f=200元/件;进行检查的费用 t=10元/次;发现故障进行调节使恢复正常的平均费用 d=3000元/次(包括刀具费);未发现故障时更换一把新刀具的费用 k=1000元/次。
要求解的问题:1)假定工序故障时产出的零件均为不合格品,正常时产出的零件均为合格品, 试对该工序设计效益最好的检查间隔(生产多少零件检查一次)和刀具更换策略。
2)如果该工序正常时产出的零件不全是合格品,有2%为不合格品;而工序故障时产出的零件有40%为合格品,60%为不合格品。
工序正常而误认有故障停机产生的损失费用为1500元/次。
对该工序设计效益最好的检查间隔和刀具更换策略。
3)在2)的情况, 可否改进检查方式获得更高的效益。
附:100次刀具故障记录(完成的零件数) (见附录1)2.模型假设和符号说明2.1模型的假设1.换刀间隔和检查间隔很短,这段时间内产生的零件数可以忽略;2.检查时一旦发现不合格品生产立即停止;3.假设该工序只需用一个刀具;4.工序出现故障是随机的,且加工每个零件时出现故障的概率相同。
2.2符号说明3. 问题分析本题研究的是自动化车床管理中定期检查和预防性保全刀具问题。
由于发现故障进行调节使恢复正常的平均费用和故障时产出的零件损失费用较高,而检查费用和更换刀具费用较低,因此,在未进行定期检查和预防性更换刀具时损失费用明显要高,更新管理后,要确定最优的管理方案,得到合适的检查间隔和刀具更换策略,即刀具定期更换间隔和检查间隔,使损失费用最少。
我们选择建立一个效益函数L (生产每个零件的平均损失费用),通过求L 最小值来确定刀具定期更换间隔a 和生产检查间隔n 。
针对问题一:因为效益函数L 包括预防保全费用1L , 检查费用2L , 和故障造成的不合格品损失和修复费用3L (即123L LLL =++),我们按每个零件分摊,分别列式子算出1L 、2L 、3L 求和。
在求解1L 、2L 、3L 过程中,根据样本数据确定刀具寿命的经验分布或拟合分布F (x ),并且得到相关参数,确定无预防性更换刀具时刀具故障的平均间隔和采取有预防性更换策略时刀具故障间隔的表达式,同时利用n 与a 之间的函数关系进行转换,最后得到L 关于刀具定期更换间隔a 的单变量函数,可通过取不同的步长a 逐个求出L 的值,找到L 的最小值和对应的a 值,并通过所得a 求出对应的生产检查间隔n 。
针对问题二:第二问中条件变为该工序正常时产出的零件不全是合格品,有2%为不合格品;而工序故障时产出的零件有40%为合格品,60%为不合格品且工序正常而误认有故障停机产生的损失费用为1500元/次。
所以第二问中计算效益函数L 时要考虑两种误判情况带来的损失,一是工序正常时检查到不合格品,误判停机将使检查的费用增加;二是工序故障时检查到合格品,将继续生产直到下一次检查,使不合格数量增多造成的损失。
效益函数L 的表达式因此有所改变,但建模方法基本与第一问相似。
针对问题三:在第二问情况下只定期检查一个零件造成了许多误判的情况,从而使每个零件的平均管理费用较高。
针对这种情况,我们采取适当连续检查多个零件降低误判率的方法达到减少每个零件的平均管理费用,是模型更优化。
4.数据分析刀具故障时加工的零件服从正态分布根据所给的100个样本数据用Excel 统计可得以下结果:表4.1 样本统计结果图4.1 样本分布直方图再利用6SQ统计软件进行卡方拟合优度检验得到如下结果:表5.问题一解答5.1 模型一的建立首先,在预防保全措施下,定义平均每一个零件的损失费用(效益函数)为L ,表达式为:123f c d k t LLLLanb⋅+=++=++(1)其中,1L 为预防保全费用, 2L 检查费用, 3L 为故障造成的不合格品损失和修 复费用。
b 为工序平均故障间隔,c 为相邻两次检查的后一次检查发现故障时,n 件零件中不合格品的平均数。
令在相邻两次检查的后一次发现故障的条件下,出现i 件不合格品的概率为:1(1)1(1)n i npppp--⋅=--则得 : 111(1)1(1)n ni i n i i i npppc p==--⋅=⋅=⋅--∑∑ (2)上式中1,2,3i n =⋅⋅⋅,上式经运算可得:21112()2122n n n pp co +-+=++≈ 由此得到c 与n 的函数关系,代入(1) 得:(1)2n fkt d Lanb+⋅=+++(3)然后给出的100 个数据分析算出无预防性更换时, 刀具故障平均间隔为μ=600 件,再根据题设刀具故障占95% , 非刀具故障占5% , 故非刀具平均故障间隔为95%5%mμ==11400件,其次由100 个数据确定刀具寿命的经验分布或拟合分布得密度函数:22()2(),0,xf x x x Zeμσ--=<<∞∈22()2001()()xx xF x f t dt dteμσ--⇒==⎰⎰为分布函数。
其中,600μ=,196.629σ=所以当进行预防保全定期n更换刀具时, 刀故障的平均间隔为:[]111()(1)[1()]()aaii F i F i a F aF aμ-=⎧⎫=⋅--+⋅-⎨⎬⎩⎭∑工序的平均故障间隔b由aμ和m决定, 满足111ab mμ=+即:111abmμ=+由此得到b和a之间的函数关系。
5.2模型一的求解对目标函数(3) 的参数进行如下优化:1.给定a,计算出b,代入(3)可得知L是n的函数,易得当n=时目标函数L达到极小;2. 按一定的步长取a的值, 采取逐渐缩小范围并逐个求出L的极小值及相应的n值, 其中使L最小者所对应的a和n即为所求。
本步骤我们在MATLAB软件中计算(对应程序段见附录2)得到的结果如下:min 5.297L=元,此时对应的342a=件,16n=件图5.1 a取值与L的变化关系图5.3结果分析:通过逐步求解,我们得到当定期换刀间隔为342件,定期检查间隔为16件时,使得生产每个零件的平均管理成本(平均损失费用)L达到极小值5.297元。
由a取值与L的变化关系图我们发现,当步长a的取值小于或大于342件时均会使平均损失费用L增大。
6.问题二的解答6.1确立新目标函数关系,令a sn第二问的效益函数要考虑两种误判。
一是工序正常时检查到不合格品误判停机, 将使损失的费用增加;二是工序故障时检查到合格品, 将继续生产直到下一次检查, 使不合格品数量增加,此时两次故障间由此产生的不合格品平均数为:[211(1)(1)(1)1(1)]1(1)12112js j i j njn i i an ppqqqun pqn nq==⎧⎫----⎪⎪⎪⎪-=+⋅⋅-⎨⎬--⎪⎪⎪⎪⎩⎭≈++∑∑+-上式中40%q= 为工序故障时的合格品率,p 为工序在生产一零件时的平均故障率,故在第该问的条件下, 效益函数L 应为:2(1)1n fk d pp t eLa nb bμ⎡⎤=++-⋅+⋅+⎢⎥⎣⎦' (4) 上式中2%p ='是工序正常时零件的不合格品率,1500e =元为第一种误判产生停机的损失费。
6.2问题二的求解计算再应用与问题一相同的模型代入式(4)并用MATLAB 软件求解(对应程序段件附录3)可得以下结果:min 7.381L =元,此时对应的 299a =件,18n =件图6.1 a取值与L的变化关系图6.3结果分析:在第二问的条件下运用和第一问相同的模型逐步求解,我们得到当定期换刀间隔为299件,定期检查间隔为18件时,使得生产每个零件的平均管理成本(平均损失费用)L达到极小值7.381元。
再由a取值与L的变化关系图我们发现,当步长a的取值小于或大于299件时均会使平均损失费用L增大。
7.问题三的解答7.1模型二的建立由于在第二问情况下生产出的零件不完全是合格品或是不合格品,只定期检查一个零件时,不免会出现许多误判,造成不必要的损失.。
今改进检查方式,采取适当连续检查多个零件降低误判率,尽量避免这样的损失,将获得更高的效益。
具体方法如下:①假设工序发生了故障:(表中“1”表示检测到合格品,“0”表示检查到不合格品)7.2结论及分析在进行检查时,不能由一次检查结果妄下结论,这可能因误判造成大的损失。
由以上模型可以得出:在工序发生故障时误判率为0.208,比检查一次的误判率0.4减少0.192;在工序正常时误判率为0.000792,比检查一次的误判率0.02减少0.019208。
因为在工序故障时误判引起的损失为200元/件,工序正常时因误判停机造成的损失为1500/次,这远远大于检查费用10元/次。
