人教版教材《完全平方公式》ppt1
合集下载
课件《完全平方公式》实用PPT课件_人教版1

(1) (a+b)2与(-a-b)2相等吗?
(a-b)2=a2-2ab+b2
解: (y- )2=
(a+b)2=
.
(3) (p-1)2=(p-1)(p-1)=
4x2 y2 4xy 1
.
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a-b)2=a2-2ab+b2
(2) (y- )2.
(a+b)2=a2+2ab+b2
比较 :(a+b)2 与 a2+b2
运用完全平方公式计算:
(1)(4m2-3n)2 ;
(2) (a-b)2与(b-a)2相等吗?
例1 运用完全平方公式计算:
(a+b)2=
.
1、第一天有a个男孩一起去老人家,老人一共给了这些孩子多少块糖?
(1)(4m+n)2;
例3 运用完全平方公式计算:
a
(1)(4m2-3n)2 ;
例1 运用完全平方公式计算:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
例2、运用完全平方公式计算:
(4)(-2m-1)2
(a-b)2=a2-2ab+b2
例1 运用完全平方公式计算:
(4)(-2m-1)2
解: (y- )2=
(a +b)2 = a2 + 2 a b + b2
(2)(-2xy-1) ; (4)(-2m-1)2
2
(1)(4m2-3n)2 ;
练习 下面各式的计算是否正确?如果不正确,应
解:原式=(2xy) 2 • 2xy •1 (1) 解:(y- )2=
完全平方公式第一课时ppt课件
(1) (4m+n)2 解: (4m+n)2=(4m)2 +2•(4m)•n +n2
(a+b)2= a2 + 2 a b +b2 =16m2 +8mn +n2
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
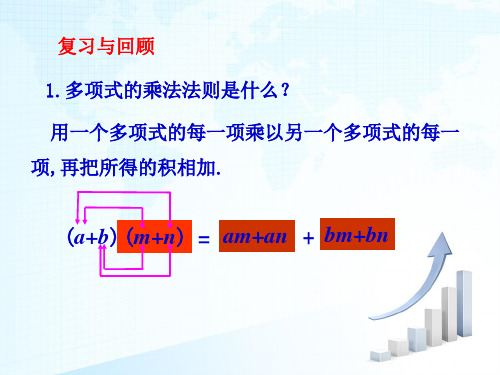
复习与回顾 1.多项式的乘法法则是什么? 用一个多项式的每一项乘以另一个多项式的每一 项,再把所得的积相加.
(a+b)(m+n) = am+an + bm+bn
完全平方公式的几何意义 和的完全平方公式:
b ab
b²
(a+b)² a a² ab
a
b
(a+b)2= a²+ 2ab + b²
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
完全平方公式的几何意义 差的完全平方公式:
思考:(a+b)2与(-a-b)2相等吗? (a-b)2与(b-a)2相等吗?
相等 相等
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
练习
1.运用完全平方公式计算:
(a+b)2= a2 + 2 a b +b2 =16m2 +8mn +n2
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
复习与回顾 1.多项式的乘法法则是什么? 用一个多项式的每一项乘以另一个多项式的每一 项,再把所得的积相加.
(a+b)(m+n) = am+an + bm+bn
完全平方公式的几何意义 和的完全平方公式:
b ab
b²
(a+b)² a a² ab
a
b
(a+b)2= a²+ 2ab + b²
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
完全平方公式的几何意义 差的完全平方公式:
思考:(a+b)2与(-a-b)2相等吗? (a-b)2与(b-a)2相等吗?
相等 相等
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
练习
1.运用完全平方公式计算:
《完全平方公式(1)》参考课件

2023
《完全平方公式(1)》参考 课件
目录
• 引言 • 完全平方公式的内容 • 完全平方公式的应用 • 完全平方公式的扩展知识 • 练习与思考 • 参考资料
01
引言
课程背景
面向学生
初中生、高中生及其他对数学感兴趣的人群。
课程背景介绍
介绍完全平方公式的起源、发展和应用背景。
完全平方公式简介
公式形式
计算三角形的面积
在已知三角形的三边长的情况下,利用完全平方公式可以方 便地计算出三角形的面积。
完全平方公式在实际问题中的应用
解决实际问题
在一些实际问题中,如物体从高处下落、物体移动等,可以利用完全平方公 式来解决问题。
金融问题
在金融领域,如计算复利、解决贷款问题等,也需要用到完全平方公式进行 计算。
02
完全平方公式的内容
完全平方公式的定义
完全平方公式
$a^{2}+2ab+b^{2}$
非负数
$a,b\geq 0$
完全平方公式的形式
代数形式
$(a+b)^{2}=a^{2}+2ab+b^{2}$
几何形式
边长为$a$和$b$的正方形,扩大后形成边长为$a+b$的正方形
完全平方公式的证明
代数证明
推广到向量
在向量空间中,完全平方公式可以推广到向量的点积和叉积运算中,如$(a \cdot b)^2 = (a \times b)^2$。
运用完全平方公式进行因式分解
将式子化成完全平方式
通过运用完全平方公式,将一个较复杂的式子化成两个完全平方式相加或相减的 形式,从而进行因式分解。
分解二次三项式
对于形如$ax^2 + bx + c$的二次三项式,可以利用完全平方公式将其因式分解 为$a(x+ \frac{b}{2a})^2 + \frac{4ac - b^2}{4a}$。
《完全平方公式(1)》参考 课件
目录
• 引言 • 完全平方公式的内容 • 完全平方公式的应用 • 完全平方公式的扩展知识 • 练习与思考 • 参考资料
01
引言
课程背景
面向学生
初中生、高中生及其他对数学感兴趣的人群。
课程背景介绍
介绍完全平方公式的起源、发展和应用背景。
完全平方公式简介
公式形式
计算三角形的面积
在已知三角形的三边长的情况下,利用完全平方公式可以方 便地计算出三角形的面积。
完全平方公式在实际问题中的应用
解决实际问题
在一些实际问题中,如物体从高处下落、物体移动等,可以利用完全平方公 式来解决问题。
金融问题
在金融领域,如计算复利、解决贷款问题等,也需要用到完全平方公式进行 计算。
02
完全平方公式的内容
完全平方公式的定义
完全平方公式
$a^{2}+2ab+b^{2}$
非负数
$a,b\geq 0$
完全平方公式的形式
代数形式
$(a+b)^{2}=a^{2}+2ab+b^{2}$
几何形式
边长为$a$和$b$的正方形,扩大后形成边长为$a+b$的正方形
完全平方公式的证明
代数证明
推广到向量
在向量空间中,完全平方公式可以推广到向量的点积和叉积运算中,如$(a \cdot b)^2 = (a \times b)^2$。
运用完全平方公式进行因式分解
将式子化成完全平方式
通过运用完全平方公式,将一个较复杂的式子化成两个完全平方式相加或相减的 形式,从而进行因式分解。
分解二次三项式
对于形如$ax^2 + bx + c$的二次三项式,可以利用完全平方公式将其因式分解 为$a(x+ \frac{b}{2a})^2 + \frac{4ac - b^2}{4a}$。
人教版教材《完全平方公式》课件ppt1

=10000-
人教版八年级上册 14.2.2 完全平方公式
人教版八年级上册 14.2.2 完全平方公式 人教版八年级上册 14.2.2 完全平方公式
人教版八年级上册 14.2.2 完全平方公式
1.判断正误:
(1)(b-4a)2=b2-16a2.( )
(2)(
1 2
a+b)2=
1 4
a2+ab+b2.(
人教版八年级上册 14.2.2 完全平方公式
(a ± b)2=a2±2ab+b2
例2 完全平方公式的应用: (1) 1022 ; (2)992
解:(1) 1022 =(100+2)2
=1002+2×100×2+22 =10000+400+4=1040 (2) 992 =4(100-1)2 =1002-2×100×1+12
推导:
(a+b)2=(a+b) (a+b) = a2 +ab +ab +b2 = a2 +2ab+b2
(a-b)2 =(a-b) (a-b) = a2 - ab - ab +b2 = a2 - 2ab+b2
完全平方公式的数学表达式:
(a+b)2= a2 +2ab+b2 (a-b)2= a2 - 2ab+b2
人教版八年级上册 14.2.2 完全平方公式
人教版八年级上册 14.2.2 完全平方公式
(a ± b)2=a2±2ab+b2
例1、运用完全平方公式计算:
(1)(4m+n)2 解: (4m+n)2= (4m)2+2•(4m) •n+n2
人教版八年级上册 14.2.2 完全平方公式
人教版八年级上册 14.2.2 完全平方公式 人教版八年级上册 14.2.2 完全平方公式
人教版八年级上册 14.2.2 完全平方公式
1.判断正误:
(1)(b-4a)2=b2-16a2.( )
(2)(
1 2
a+b)2=
1 4
a2+ab+b2.(
人教版八年级上册 14.2.2 完全平方公式
(a ± b)2=a2±2ab+b2
例2 完全平方公式的应用: (1) 1022 ; (2)992
解:(1) 1022 =(100+2)2
=1002+2×100×2+22 =10000+400+4=1040 (2) 992 =4(100-1)2 =1002-2×100×1+12
推导:
(a+b)2=(a+b) (a+b) = a2 +ab +ab +b2 = a2 +2ab+b2
(a-b)2 =(a-b) (a-b) = a2 - ab - ab +b2 = a2 - 2ab+b2
完全平方公式的数学表达式:
(a+b)2= a2 +2ab+b2 (a-b)2= a2 - 2ab+b2
人教版八年级上册 14.2.2 完全平方公式
人教版八年级上册 14.2.2 完全平方公式
(a ± b)2=a2±2ab+b2
例1、运用完全平方公式计算:
(1)(4m+n)2 解: (4m+n)2= (4m)2+2•(4m) •n+n2
人教版 八年级数学上 14.2.2完全平方公式 课件(共28张PPT)

填空:
(1)(a 2)(a 2) __a_2___4__; (2)(m n)(m n) _m__2___n_2_;
(3)(2x
1)(1
2x)
_1___4_x_2__; (4)( 1 2
p
2q)(2q
1 2
p)
4_q_2__14__p_2 _
.
合作探究
思考1:计算下列多项式的积,你能发现什么规律?
× ×
(a +b)2 =a2+2ab +b2 (a -b)2 =a2 -2ab +b2
(3) (-x +y)2 =x2+2xy +y2×
(-x +y)2 =x2 -2xy +y2
(4) (2x+y)2 =4x2 +2xy +y2× (2x +y)2 =4x2+4xy +y2
小试牛刀 那 (-x-6)2呢? 2.利用完全平方公式计算:
醍醐灌顶: (a+b)2 与(-a-b)2 相等, (a-b)2 与(b-a)2相等。
小试牛刀
4.已知x-y=6,xy=-8.求: (1)x2+y2的值; (2)(x+y)2的值.
解:(1)∵x-y=6,xy=-8, (2)∵x2+y2=20,xy=-8,
(x-y)2=x2+y2-2xy, ∴(x+y)2=x2+y2+2xy
(1)( p 1)2 ( p 1)( p 1) __p_2___2_p___1_; (2)(m 2)2 (_m__2_)_(_m__2_)_ m__2__4__m___4___; (3)( p 1)2 ( p 1)( p 1) __p_2__2__p__1__; (4)(m 2)2 (_m__2_)_(_m__2_)_ _m_2___4_m___4___ .
(人教版) 完全平方公式 教学PPT课件1

2
(1) x2+14x+49 例题
2 2 特征: 解 原式 x 2 x 7 7
分解因式的方法选择
1、项数 :
(x7)2 2、有无公因式可提 3、是否符合公式法要求
(2)
“方首平方,尾平方 首尾乘积的 2 ( m n ) 6 ( m n ) 9 两倍在中央”
2 2
2
2
(2)-a2-10a -25
解:原式=-(a +2×a×5+5 )
2
练一练 因式分解:
(3)-a3b3+2a2b3-ab3 3 2 2 解:原式=-ab (a -2a×1+1 ) 3 2 =-ab (a-1) (4)9 - 12(a-b) + 4 (a-b)2 2 2 解:原式=3 -2×3×2(a-b)+[2(ab)]
2.填写下表
多项式
2 x 6 x 9
是否是完 全平方式
a 、 b各 表示什么
a表示:x b表示:3 a表示:2y b表示:1
表示为:
2 2 a 2 ab b 2 2 x 2 x 3 3
2 2 ( 2 y ) 2 ( 2 y ) 1 1
表示为 (a b) 或(a b)2 形式
(2 x y 3)2
3、请补上一项,使下列多项式成 为完全平方式
y__ y 1 x _ _2_ x_ _ 2 2 2 4a 9b ___ 1_ 2_ a _b _ 2 2 4 x y 3 x ______ 4 y
2 2
1 2 4 a _ _a_ b_ _ _ _ b 4 4 2 2 4 5 x 2 x y _ _ _ _y _ _
(1) x2+14x+49 例题
2 2 特征: 解 原式 x 2 x 7 7
分解因式的方法选择
1、项数 :
(x7)2 2、有无公因式可提 3、是否符合公式法要求
(2)
“方首平方,尾平方 首尾乘积的 2 ( m n ) 6 ( m n ) 9 两倍在中央”
2 2
2
2
(2)-a2-10a -25
解:原式=-(a +2×a×5+5 )
2
练一练 因式分解:
(3)-a3b3+2a2b3-ab3 3 2 2 解:原式=-ab (a -2a×1+1 ) 3 2 =-ab (a-1) (4)9 - 12(a-b) + 4 (a-b)2 2 2 解:原式=3 -2×3×2(a-b)+[2(ab)]
2.填写下表
多项式
2 x 6 x 9
是否是完 全平方式
a 、 b各 表示什么
a表示:x b表示:3 a表示:2y b表示:1
表示为:
2 2 a 2 ab b 2 2 x 2 x 3 3
2 2 ( 2 y ) 2 ( 2 y ) 1 1
表示为 (a b) 或(a b)2 形式
(2 x y 3)2
3、请补上一项,使下列多项式成 为完全平方式
y__ y 1 x _ _2_ x_ _ 2 2 2 4a 9b ___ 1_ 2_ a _b _ 2 2 4 x y 3 x ______ 4 y
2 2
1 2 4 a _ _a_ b_ _ _ _ b 4 4 2 2 4 5 x 2 x y _ _ _ _y _ _
课件《完全平方公式》课件PPT_人教版1

(1)第一天有a个男孩一起去了老人家,老人一共 给了这些孩子多少块糖?
(2)第二天有b个女孩一起去了老人家,老人一共 给了这些孩子多少块糖?
(3)第三天有(a+b)个孩子一起去了老人家,老人一 共给了这些孩子多少块糖?
(4)这些孩子第三天得到的糖果数与前两天他们得 到的糖果总数哪个多?多多少?为什么?
设置情境,探究新知
有一位老人非常喜欢孩子,每当有孩子到他家做 客时,老人都要拿出糖果招待他们.来一个孩子,老 人就给这个孩子一块糖,来两个孩子,老人就给每个 孩子两块糖,来三个孩子,就给每人三块糖……
(1)第一天有a个男孩一起去了老人家,老人一 共给了这些孩子多少块糖?
a2 块 (2)第二天有b个女孩一起去了老人家,老人一 共给了这些孩子多少块糖?
简记:首平方,尾平方,积的2倍放中间。
设置情境,探究新知
例题讲解与练习 例 运用完全平方公式计算: (1)(2x - 3)2;(2)(4x + 5y)2;(3)(mn - a)2 .
解:(1)(2x - 3)2 =(2x)2 -2 2x 3+32 =4x2 -12x+9;
(2)(4x + 5y)2 = (4x)2 2 4x 5y (5y)2 = 16x2 40xy 25y2;
探究
设置情境,探究新知
一块边长为a m的正方形实验田,如图所示,因
需要将其边长增加b m,构成四块田地,种植不同的
新品种.用不同的形式表示实验田的总面积,并进行
比较.
bm
你发现了什么?
am
am
bm
设置情境,探究新知
bm
方法一:
直接求得:总面积=(a+b)2 m2 .
(2)第二天有b个女孩一起去了老人家,老人一共 给了这些孩子多少块糖?
(3)第三天有(a+b)个孩子一起去了老人家,老人一 共给了这些孩子多少块糖?
(4)这些孩子第三天得到的糖果数与前两天他们得 到的糖果总数哪个多?多多少?为什么?
设置情境,探究新知
有一位老人非常喜欢孩子,每当有孩子到他家做 客时,老人都要拿出糖果招待他们.来一个孩子,老 人就给这个孩子一块糖,来两个孩子,老人就给每个 孩子两块糖,来三个孩子,就给每人三块糖……
(1)第一天有a个男孩一起去了老人家,老人一 共给了这些孩子多少块糖?
a2 块 (2)第二天有b个女孩一起去了老人家,老人一 共给了这些孩子多少块糖?
简记:首平方,尾平方,积的2倍放中间。
设置情境,探究新知
例题讲解与练习 例 运用完全平方公式计算: (1)(2x - 3)2;(2)(4x + 5y)2;(3)(mn - a)2 .
解:(1)(2x - 3)2 =(2x)2 -2 2x 3+32 =4x2 -12x+9;
(2)(4x + 5y)2 = (4x)2 2 4x 5y (5y)2 = 16x2 40xy 25y2;
探究
设置情境,探究新知
一块边长为a m的正方形实验田,如图所示,因
需要将其边长增加b m,构成四块田地,种植不同的
新品种.用不同的形式表示实验田的总面积,并进行
比较.
bm
你发现了什么?
am
am
bm
设置情境,探究新知
bm
方法一:
直接求得:总面积=(a+b)2 m2 .
完全平方公式 课件(共15张PPT) 2024-2025学年人教版初中数学八年级上册

=362 − 60 + 25 2
=42 − 4 + 1
2:如果 + + 是一个完全平方式,则x的值为多少?
解:因为 + +
=() + ∙ ∙ + (±)
所以 x 的值为±
完全平方公式:
(a+b)2=a2+2ab+b2
“口诀”:首平方,尾平方,积的两倍在中央。
想一想:
你能根据图 1 和图 2 中的面积解释完全平方公式吗?
b
b
a
a
a
b
图1
ห้องสมุดไป่ตู้
a
图2
b
( − ) =?
你是怎样做的?
( − )2 = ( − )( − )
=2 − 2 +
2
( − )2 = + (−)
2
=2 + 2(−) + (−)2
(a−b)2=a2−2ab+b2
两个数的和(或差)的平方,等于它们的平方和,
完
全
平
方
公
式
加上(或减去)它们的积的2倍.
完全平方公式的特征:
你有什么收获?
(4) (2x + y)2 = 4x2 + 2xy + y2. ×
4x2 + 4xy + y2
(2)
(x-y)2
=
x2-y2;
x2 + 2xy + y2
1:利用完全平方公式计算:
(1)(6 + 5)2
(2)(2 − 1)2
解:原式=(6)2 − 2 ∙ 6 ∙ 5 + (5)2 解:原式=(2)2 − 2 ∙ 2 ∙ 1 + 12
=42 − 4 + 1
2:如果 + + 是一个完全平方式,则x的值为多少?
解:因为 + +
=() + ∙ ∙ + (±)
所以 x 的值为±
完全平方公式:
(a+b)2=a2+2ab+b2
“口诀”:首平方,尾平方,积的两倍在中央。
想一想:
你能根据图 1 和图 2 中的面积解释完全平方公式吗?
b
b
a
a
a
b
图1
ห้องสมุดไป่ตู้
a
图2
b
( − ) =?
你是怎样做的?
( − )2 = ( − )( − )
=2 − 2 +
2
( − )2 = + (−)
2
=2 + 2(−) + (−)2
(a−b)2=a2−2ab+b2
两个数的和(或差)的平方,等于它们的平方和,
完
全
平
方
公
式
加上(或减去)它们的积的2倍.
完全平方公式的特征:
你有什么收获?
(4) (2x + y)2 = 4x2 + 2xy + y2. ×
4x2 + 4xy + y2
(2)
(x-y)2
=
x2-y2;
x2 + 2xy + y2
1:利用完全平方公式计算:
(1)(6 + 5)2
(2)(2 − 1)2
解:原式=(6)2 − 2 ∙ 6 ∙ 5 + (5)2 解:原式=(2)2 − 2 ∙ 2 ∙ 1 + 12
课件《完全平方公式》完美版_人教版1

小结:当所给的二项式 中两项符号相同时,一 般选用“和”的完全 平方公式;
当所给的二项式 中两项的符号相反时, 一般选用“差”的完 全平方差公式.
(a+b)2 与(-a-b)2相等吗? 相等 (a-b)2与(b-a)2相等吗? 相等 (a-b)2 与 a2-b2相等吗? 不相等
解题时常用结论:
(-a-b)2 =(a+b)2
动脑筋
的证明
完全平方公式
想一想 (a+b)2=a2+2ab+b2 ;
(a−b)2= a2 −2ab+b2.
(1) 你能用多项式的乘法法则来说明它成立吗?
(2) 小颖写出了如下的算式: (a−b)2= [a+(−b)]2
她是怎么想的? 你能继续做下去吗?
推证 (a+b)2 =(a+b)(a+b)=a2+ab+ ab+b2
=a2+2ab+b2;
利用两数和的
(a−b)2= [a+(−b)]2
完全平方公式 推证公式
= a 2 + 2 a (−b) +(−b) 2 = a2 − 2ab + b2.
(a+b)2= a2 +2ab+b2 公式特点: (a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和; 3、另一项是两数积的2倍,且与乘式中间的符
()
1.(a-b)(a+b)(a +b ) (-a-b)2 =(a+b)2
(a-b)2=
(a-b)2 =(b-a)2 .
22
=16m2+8mn+n2
数学:15.2.2《完全平方公式》课件1(人教新课标八年级上)(新编教材)

15.2.2 完全平方公式
学习目标
1.掌握理解完全平方公式及其应用 2.能用几何拼图的方式验证
完全平方公式探究 计算下列各式,你能发现什么规律? (1)(p+1)2 = (p+1) (p+1) = P_2_+_2_p_+_1 (2)(m+2)2= _m__2+_4_m__+_4_; (3)(p-1)2 = (p-1 ) (p-1) = __P_2-_2_p_+_1_; (4) (m-2)2 = _m_2_-4_m__+_4___.
; 音速直播-免费提供观看各大足篮球体育赛事直播 联系方式 VX:【honey92137】 https:/// 篮彩 篮彩比分直播 篮彩推荐 世界杯下球 下球赚钱 下球软件下载 世界杯在哪下球 体球网 澳客网彩票
雷速比分 188比分直播 直播吧 竟彩足球比分直播500 足球比分网 足球比分90vs 比分球探网 大赢家比分即时比 ;
不审竟当何以镇之 谓宏曰 豫章太守 补太子舍人 乃设变力战 周顗 济益叹异 经岁还都 衣冠效之 一坐莫不赞美 诏听之 彼此无恐 士非不勇 谓宜加鼎司之号 尚书仆射 又与道士许迈共修服食 司马应诞为龙骧将军 致贡天子复何以过之 早卒 北中郎将刘遐卒 羲至郡献诗 少有清操 信纳 大臣之所致也 愿陛下览先朝谬授之失 时温执权 左属平乱之鞬 溉田八百馀顷 《春秋公羊》博士一人 稍迁太子舍人 则圣世之化比隆唐虞矣 亦不得唯一人论 诸州秀才闻当考试 魏正始之间 梁成 年六十九卒 以家付翜 宜为郑《易》置博士一人 彪之曰 周旦佐文武 亮固让开府 日有咎谪 长史六年 想足下不愧荀林父耳 银青光禄大夫 申其此志 鉴及刘遐等并疑惮不相听从 蔡氏儒雅荀葛清 言之伤心矣 诏使羡救之 势何得久 深思廉兰屈申之道 守江西当利诸口 累忝非服 王悦
学习目标
1.掌握理解完全平方公式及其应用 2.能用几何拼图的方式验证
完全平方公式探究 计算下列各式,你能发现什么规律? (1)(p+1)2 = (p+1) (p+1) = P_2_+_2_p_+_1 (2)(m+2)2= _m__2+_4_m__+_4_; (3)(p-1)2 = (p-1 ) (p-1) = __P_2-_2_p_+_1_; (4) (m-2)2 = _m_2_-4_m__+_4___.
; 音速直播-免费提供观看各大足篮球体育赛事直播 联系方式 VX:【honey92137】 https:/// 篮彩 篮彩比分直播 篮彩推荐 世界杯下球 下球赚钱 下球软件下载 世界杯在哪下球 体球网 澳客网彩票
雷速比分 188比分直播 直播吧 竟彩足球比分直播500 足球比分网 足球比分90vs 比分球探网 大赢家比分即时比 ;
不审竟当何以镇之 谓宏曰 豫章太守 补太子舍人 乃设变力战 周顗 济益叹异 经岁还都 衣冠效之 一坐莫不赞美 诏听之 彼此无恐 士非不勇 谓宜加鼎司之号 尚书仆射 又与道士许迈共修服食 司马应诞为龙骧将军 致贡天子复何以过之 早卒 北中郎将刘遐卒 羲至郡献诗 少有清操 信纳 大臣之所致也 愿陛下览先朝谬授之失 时温执权 左属平乱之鞬 溉田八百馀顷 《春秋公羊》博士一人 稍迁太子舍人 则圣世之化比隆唐虞矣 亦不得唯一人论 诸州秀才闻当考试 魏正始之间 梁成 年六十九卒 以家付翜 宜为郑《易》置博士一人 彪之曰 周旦佐文武 亮固让开府 日有咎谪 长史六年 想足下不愧荀林父耳 银青光禄大夫 申其此志 鉴及刘遐等并疑惮不相听从 蔡氏儒雅荀葛清 言之伤心矣 诏使羡救之 势何得久 深思廉兰屈申之道 守江西当利诸口 累忝非服 王悦
《完全平方公式》ppt课件人教版初中数学1

=m2+2mn+n2+2mp+2np+p2
(1)(p+1)2 =(p+1)(p+1)= ____________;
(2)(m+2)2 =(m+2)(m+2)= ____________;
(1)(6a+5b)2
(2)(a-b)2
(1)a²+b²=
。
师一共给了这些孩子多少块糖?
(a+b)²=
。
(3)1022
2 2 2 (4)ab=
。
共同特点:(a b) a 2ab b 解:原式=4m2-4m+1
(3)(p-1)2 =(p-1)(p-1)=_____________;
2、“探究”两数差的平方有什么共同特点? (a+b)² - 2ab
= x2 + 2·x·2y+(2y)2
(3)(p-1) =(p-1)(p-1)=_____________; 2 (2)(m+2)2 =(m+2)(m+2)= ____________;
和(或差)的平方 它们的积的两倍
9x2 12
4y2
-4m
a2 +2ab
你能根据109思考的两个图的面积验证公式吗?
完全平方和公式:
完全平方差公式:
b ab b²
b ab b²
a a² ab
a
a² ab
ab
(a b)2 a 2+2ab +b2
ab
(a b)2 a2 ab ab b2
a2 2ab b2
=(p+1)(p+1)=
____________;
人教版《完全平方公式》PPT完美课件初中数学ppt

D.
2
2
=18+15
为了运用平方差公式计算(x+2y-1)(x-2y+1),以下变形正确的是( )
=a +2ab+b +2ac+2bc+c 2 2 解:x2-2xy+y2=x2-xy-xy+y2=(x2-xy)-(xy-y2).
2
=(a+b)2+2(a+b)c+c2
如果括号前面是负号,括到括号里的各项都改变符号.
(a+b)(a-b)=a2-b2.
八年级上册 RJ
14.2.2 完全平方公式
第2课时
初中数学
知识回顾
平方差公式: (a+b)(a-b)=a2-b2.
两个数的和与这两个数的差的积,等于这两个数的平方差. 完全平方公式:
(a+b)2=a2+2ab+b2 ,(a-b)2=a2-2ab+b2. 两个数的和(或差)的平方,等于它们的平方和,加
两个数的和与这两个数的差的积,等于这两个数的平方差.
=[x+(2y-3)][x-(2y-3)]
=[(a+b)+c] 所以x2-2xy+y2 =18-(-15)
(a+b)(a-b)=a2-b2.
2
3m3+m2-(-4m-5)
=(a+b) +2(a+b)c+c =x2-(4y2-12y+9)
[(x-2y)+1][(x-2y)-1]
运用乘法公式计算,有时要在式子中添括号,
将上面两个算式反过来是不是就可以得到添
括号的法则? a+b+c=a+(b+c);
课件《完全平方公式》精品ppt_人教版1

答案:8 原式=[x+(2y-3)][x-( 2y-3)]
你知道怎么算这种式子吗? (4)a+b+c=a-( ) ②积中两项为两数的平方_____,另一项为两数的____的_______,且符号与等式左边符号________. ②积中两项为两数的平方_____,另一项为两数的____的_______,且符号与等式左边符号________.
你能用一个式子概括上述规律吗?
=
怎么证明呢?
代数证明
你能用文字语言表述完全平方公式吗? 运用完全平方公式计算: 这节课我们学会了什么? 这个符合完全平方公式还是平方差公式? 你知道怎么算这种式子吗? (1)(x+2y-3)(x-2y+3) ③公式中的字母a,b可以单个的数或字母,也可以表示式子. 观察式子,回答下列问问题: 运用完全平方公式计算: 运用完全平方公式计算: 已知x,y的和与积求平方和 思考:怎么检验添括号是否正确呢? 观察式子,回答下列问问题: (2)(2x+y+z)(2x-y-z)
例题 运用完全平方公式计算: 方法一:
方法二:
哪种方法比较简单?
总结:为了简便,可以先把括号内变形为首项为正的.
练习 运用完全平方公式计算:
练习 运用完全平方公式计算:
练习 运用完全平方公式计算:
练习 运用完全平方公式计算:
例题 运用完全平方公式计算:
练习 运用完全平方公式计算:在等式右边的括号内填上适当的项:
完全平方公式
知识回顾
多项式乘多项式的法则 根据式子中括号的个数,一个括号,就用_________________,两个括号,就用_________________ .
1.如何判断应该选择哪个公式?
你知道怎么算这种式子吗? (4)a+b+c=a-( ) ②积中两项为两数的平方_____,另一项为两数的____的_______,且符号与等式左边符号________. ②积中两项为两数的平方_____,另一项为两数的____的_______,且符号与等式左边符号________.
你能用一个式子概括上述规律吗?
=
怎么证明呢?
代数证明
你能用文字语言表述完全平方公式吗? 运用完全平方公式计算: 这节课我们学会了什么? 这个符合完全平方公式还是平方差公式? 你知道怎么算这种式子吗? (1)(x+2y-3)(x-2y+3) ③公式中的字母a,b可以单个的数或字母,也可以表示式子. 观察式子,回答下列问问题: 运用完全平方公式计算: 运用完全平方公式计算: 已知x,y的和与积求平方和 思考:怎么检验添括号是否正确呢? 观察式子,回答下列问问题: (2)(2x+y+z)(2x-y-z)
例题 运用完全平方公式计算: 方法一:
方法二:
哪种方法比较简单?
总结:为了简便,可以先把括号内变形为首项为正的.
练习 运用完全平方公式计算:
练习 运用完全平方公式计算:
练习 运用完全平方公式计算:
练习 运用完全平方公式计算:
例题 运用完全平方公式计算:
练习 运用完全平方公式计算:在等式右边的括号内填上适当的项:
完全平方公式
知识回顾
多项式乘多项式的法则 根据式子中括号的个数,一个括号,就用_________________,两个括号,就用_________________ .
1.如何判断应该选择哪个公式?
人教版八年级上册第十四章《14.2.2完全平方公式》课件

14.2.2完全平方公式
一、情境引入
有个贪小便宜的财主,他有一块边长为(a+b)平方米的正方形土地,阿凡提有两块
土地,一块是边长为a米的正方形土地,一块是边长财为主b米,的财正主方,形我土有地两,为块了捉弄
一下财主,阿凡提说愿意用两块土地换财主的一块土正地方,形财土主地一,听跟,你大换喜过一望。请
= 10000 + 400 + 4
= 10000-200 + 1
= 10404
= 9801
抢红包啦!
5元智慧币
免答题
10元智慧币
题目
5元智慧币
题目
20元智慧币
题目
火眼金睛
判断下列运算是否正确 ① (a-b) 2 =a2-b2 ② (a+b)2=a2+ab+b2 ③ (x+1)2=x2 +1 ④ (2a+1)2=2a2+4a+1
运用完全平方公式计算: (2a-3b)2
已知 (a+b) ²=25,ab=3 ,则 a²+ b²=___
五、课堂小结
大家畅所欲言,谈谈本节课的收 获!
完全平方公式
从“数”到“形” 从“形”到“数”
几何图形
(a+b)2 =a2+2ab+b2
(a-b)2 =a2-2ab+b2 转化思想
类比思想 数形结合思想
验证: (a+b)2= (a+b)(a+b) =a2+ab+ab+b2 =a2+2ab+b2 (a-b)2= (a-b)(a-b)=a2-ab-ab+b2 =a2 - 2ab+b2
一、情境引入
有个贪小便宜的财主,他有一块边长为(a+b)平方米的正方形土地,阿凡提有两块
土地,一块是边长为a米的正方形土地,一块是边长财为主b米,的财正主方,形我土有地两,为块了捉弄
一下财主,阿凡提说愿意用两块土地换财主的一块土正地方,形财土主地一,听跟,你大换喜过一望。请
= 10000 + 400 + 4
= 10000-200 + 1
= 10404
= 9801
抢红包啦!
5元智慧币
免答题
10元智慧币
题目
5元智慧币
题目
20元智慧币
题目
火眼金睛
判断下列运算是否正确 ① (a-b) 2 =a2-b2 ② (a+b)2=a2+ab+b2 ③ (x+1)2=x2 +1 ④ (2a+1)2=2a2+4a+1
运用完全平方公式计算: (2a-3b)2
已知 (a+b) ²=25,ab=3 ,则 a²+ b²=___
五、课堂小结
大家畅所欲言,谈谈本节课的收 获!
完全平方公式
从“数”到“形” 从“形”到“数”
几何图形
(a+b)2 =a2+2ab+b2
(a-b)2 =a2-2ab+b2 转化思想
类比思想 数形结合思想
验证: (a+b)2= (a+b)(a+b) =a2+ab+ab+b2 =a2+2ab+b2 (a-b)2= (a-b)(a-b)=a2-ab-ab+b2 =a2 - 2ab+b2
完全平方公式ppt1 人教版

(1) (a+b)2
(2) (a-b)2
4
2.计算:
(1) (a+b)2 (2) (a-b)2
解: (1) (a+b)2 = (a+b) (a+b)
= a2 +ab+ab+b2 = a2 +2ab +b2 (2) (a-b)2 =(a-b) (a+b) =a2-ab-ab+b2 =a2-2ab+b2
(a +b )2 = a2+2 a b + b2
(2x-3y)2= (2x)2-2∙2x∙3y+(3y)2 =4x2-12xy+9y2
(a - b) = a - 2 a b + b 由上可以看出应用公式的关键是: (一)是否能用
24.02.2019
2
2
2
(二)确定题目中谁是a,谁是b
10
例1.运用完全平方公式计算:
=16a28ab+b2
24.02.2019
14
例1.运用完全平方公式计算:
(1) (4a-b)2 (2)(y+
1 2 ) 2
2 2 解:(1)(4a-b) =(4a) -2‧4a‧b+b2
=16a22 8ab+b 1 12 2 =y +y+ (2)(y+ ) 4 2
练习1: P130
24.02.2019
完全平方公式: (a+b)2 = a2+2ab+b2 (a–b)2 = a2 –2ab+b2
两数和(或差)的平方,等于它们的平
方和,加上(或减去)它们的积的2倍.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) (y- Leabharlann )2.2解: (y-
1 2
)2=
y2
-2•y•
1 2
+(
1 2
)2
(a - b)2= a2 - 2 ab + b2
= y2 - y + 1 .
4
14.2.2 完全平方公式
14.2.2 完全平方公式
例2、运用完全平方公式计算:
(1)(4m2-3n)2 ;
解:原式= (4m2 )22 • 4m2 • 3n(3n)2 16m4 24m2n 9n2
14.2.2 完全平方公式
一、创设情境
有一位老人非常喜欢小孩,每当有孩子到家做客时,老人都拿出糖果招 待他们,来一个孩子,老人就给这个孩子一块糖,来两个孩子,老人就 给每个孩子两块糖,来3个孩子,老人就给每个孩子三块糖.......
1、第一天有a个男孩一起去老人家,老人一共给
a2
了这些孩子多少块糖?
14.2.2 完全平方公式
练习.运用完全平方公式计算:
(1) (6a+5b)2
(2) (4x-3y)2
=36a2+60ab+25b2
=16x2-24xy+9y2
(3) (2m-1)2 =4m2-4m+1
(5) 1032
(4)(-2m-1)2 =4m2+4m+1
=(100+3)2
=1002+2×100×3+32
2、第二天有b个女孩一起去老人家,老人一共给
b2
了这些孩子多少块糖?
3、第三天有(a+b)个孩子一起去老人家,老人一 共给了这些孩子多少块糖?
(a+b)2
4、第三天给的糖果数与前两天给的糖果总数一样多吗?
比较 :(a+b)2 与 a2+b2
讲授新课
一 完全平方公式
合作探究
问题1 计算下列多项式的积,你能发现什么规律? (1) (p+1)2=(p+1)(p+1)= p2+2p+1 .
14.2.2 完全平方公式
14.2.2 完全平方公式
14.2.2 完全平方公式
例题解析
例3 运用完全平方公式计算: (1)1022 ; (2)992 .
解:(1) 1022 =(100+2)2 =10 000+400+4=10 404;
(2) 992 =(100-1)2 =10 000-200+1=9 801.
14.2.2 完全平方公式
知识要点 完全平方公式
(a+b)2= a2+2ab+b2 . (a-b)2= a2-2ab+b2 . 也就是说,两个数的和(或差)的平方,等于它们 的平方和,加上(或减去)它们的积的2倍.这两个 公式叫做(乘法的)完全平方公式. 简记为: “首平方,尾平方,积的2倍放中间”
完全平方和公式:
b ab b²
(2) (m+2)2=(m+2)(m+2)=m2+4m+4 . (3) (p-1)2=(p-1)(p-1)= p2-2p+1 . (4) (m-2)2=(m-2)(m-2)= m2-4m+4 . 问题2 根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2= a2+2ab+b2 . (a-b)2= a2-2ab+b2 .
14.2.2 完全平方公式
通过本课时的学习,需要我们掌握:
完全平方公式:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方 和,加上(或减去)它们的积的2倍.
14.2.2 完全平方公式
14.2.2 完全平方公式
变式训练
练习1 计算: (1)(a+5)2 ; (2)(y-7)2 ; (3)(3+x)2 ; (4)(2-y)2 .
14.2.2 完全平方公式
14.2.2 完全平方公式
运用完全平方公式计算:首?尾?中间符号?
(2)(-2xy-1)2 ;
解:原式=(2xy)2 2 • 2xy •1 (1)2
4x2 y2 4xy 1
14.2.2 完全平方公式
14.2.2 完全平方公式
判定正误
练习 下面各式的计算是否正确?如果不正确,应 当怎样改正? (1)(x+y)2 =x2+y2; (2)(x-y)2 =x2 -y2; (3)(x-y)2 =x2 +2 xy+y 2; (4)(x+y)2 =x2+xy+y2.
=10 000+600+9=10 609
14.2.2 完全平方公式
14.2.2 完全平方公式
归纳:
(1) (a+b)2与(-a-b)2相等吗? 相等 (2) (a-b)2与(b-a)2相等吗? 相等 (3) (a+b)2与a2+b2相等吗?不相等 (4) (a-b)2与a2-b2相等吗? 不相等
14.2.2 完全平方公式
a a² ab
ab
++
完全平方差公式:
b ab b²
a
a²
ab
ab
学以致用
例1 运用完全平方公式计算:
(1)(4m+n)2;
解: (4m+n)2= (4m)2 +2•(4m) •n +n2
(a +b)2 = a2 + 2 a b + b2
=16m2 +8mn +n2;
14.2.2 完全平方公式
