数据的整理与初步处理A卷(通用).pdf
数据的整理与初步处理(教师)

数据的整理与初步处理(一)平均数、中位数、众数:1.(2012济南)在一次体育课上,体育老师对九年级一班的40名同学进行了立定跳远项目的测试,测试所得分数及相应的人数如图所示,则这次测试的平均分为( B )A .53分 B .354分 C .403分 D .8分2.(2012丹东)五名同学在“爱心捐助”活动中,捐款数额为8,10,10,4,6(单位:元),这组数据的中位数是( C )A .10B .9C .8D . 63.(2012红河)四次测试小丽每分钟做仰卧起坐的次数分别为:50、45、48、47,这组数据的中位数为___47.5____.4.(2012年河南中考模拟题2)国家实行一系列“三农”优惠政策后,农民收入大幅度增加,某乡所辖村庄去年年人均收入(单位:元)情况如下表,该乡去年年人均收入的中位数是 3800元 .年人均收入(元) 3500 3700 3800 3900 4500 村庄个数213315.(2012包头)在综合实践课上,六名同学做的作品的数量(单位:件)分别是:5,7,3,x ,6,4;若这组数据的平均数是5,则这组数据的中位数是 件.56.(2012宿迁)有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( B ) A .众数 B .中位数 C .平均数 D .极差7.(2012常德)已知一组数据为:8,9,7,7,8,7,则这组数据的众数为____.7 8.(2012年铁岭市加速度辅导学校)某鞋店试销一种新款女鞋,销售情况如下表所示: 型号 22 22.5 23 23.5 24 24.5 25 数量(双)351015832鞋店经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( B )A .平均数B .众数C .中位数D .方差9.(2012江苏常州)某一公司共有51名员工(包括经理),经理的工资高于其他员工的工资。
第20章《数据的整理与初步处理》单元综合检测试卷(含答案)

第20章数据的整理与初步处理一、选择题1.制鞋厂准备生产一批男皮鞋,经抽样120名中年男子,得知所需鞋号和人数如下:鞋号/cm 20222324252627人数 8 15 20 25 3020 2并求出鞋号的中位数是24,众数是25,平均数是24,下列说法正确的是( )A. 所需27cm鞋的人数太少,27cm鞋可以不生产B. 因为平均数24,所以这批男鞋可以一律按24cm的鞋生产C. 因为中位数是24,故24cm的鞋的生产量应占首位D. 因为众数是25,故25cm的鞋的生产量要占首位2.体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生立定跳远成绩的( )A. 平均数B. 众数C. 中位数D. 方差3.已知n个数据的和为108,平均数为12,则n为()A. 7B. 8C. 9D. 104.要反映2015年末嘉兴市各个县(区)常住人口占嘉兴市总人口的比例,宜采用( )A. 条形统计图B. 折线统计图C. 扇形统计图D. 频数直方图5.某校是海安三门球特色学校,现准备从该校九年级四个班中选出一个班的7名学生组建三门球队,根据各班选出的学生,测量其身高,计算得到的数据如下表所示,表:九年级(1~4班)学生平均身高统计表学生平均身高(单位:m)标准差九(1)班1.570.3九(2)班1.570.7九(3)班1.60.3九(4)班1.60.7要求各班选出的学生身高较为整齐,且平均身高约为1.6m.学校应选择( )A. 九(1)班B. 九(2)班C. 九(3)班D. 九(4)班6.甲、乙、丙三名射击运动员在某场测试中各射击20次,3人的测试成绩如下表,则甲、乙、丙3名运动员测试成绩最稳定的是()A. 甲B. 乙C. 丙D. 3人成绩稳定情况相同7.要了解全区八年级学生身高在某一范围内的学生所占比例的大小,需知道相应的样本的( )A. 平均数B. 频率C. 众数D. 方差8.天籁音乐行出售三种音乐CD,即古典音乐,流行音乐,民族音乐,为了表示这三种唱片的销售量占总销售的百分比,应该用( )A. 扇形统计图B. 折线统计图C. 条形统计图D. 以上都可以9.某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验,得到两个品种每公顷产量的两组数据,其方差分别为s甲2=0.002、s乙2=0.03,则( )A. 甲比乙的产量稳定B. 乙比甲的产量稳定C. 甲、乙的产量一样稳定D. 无法确定哪一品种的产量更稳定10.为纪念雷锋逝世52周年暨毛主席号召“向雷锋同志学习”49周年,育才中学举行了“学雷锋”演讲比赛.下面是8位评委为其中一名参赛者的打分:9.4,9.6,9.8,9.9,9.7,9.9,9.8,9.5.若去掉一个最高分,一个最低分,这名参赛者的最后得分是()A. 9.70B. 9.72C. 9.74D. 9.6811.甲、乙两学生在军训打靶训练中,打靶的总次数相同,且所中环数的平均数也相同,但甲的成绩比乙的成绩稳定,那么两者的方差的大小关系是( )A. s2甲>s2乙B. s2甲=s2乙C. s2甲<s2乙D. 不能确定12.若一组数据x1、x2、x3、x4、x5的平均数是a,则另一组数据x1、x2+1、x3+2、x4+3、x5+4的平均数是( )A. aB. a+2C. a+D. a+10二、填空题13.某招聘考试分笔试和面试两种.其中笔试按60%、面试按40%计算加权平均数作为总成绩.小明笔试成绩为90分.面试成绩为85分,那么小明的总成绩为________ 分.14.某校体育期末考核“立定跳远”、“800米”、“仰卧起坐”三项,并按3:5:2的比重算出期末成绩.已知小林这三项的考试成绩分别为80分、90分、100分,则小林的体育期末成绩为________分.15.某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,根据四人各自的平均成绩,公司将录取________.候选人甲乙丙丁面试86929083测试成绩(百分制)笔试9083839216.我们进入中学以来,已经学习过不少有关数据的统计量,例如________ 等,它们分别从不同的侧面描述了一组数据的特征.17.有一组数据:3,a,4,6,7.它们的平均数是5,那么这组数据的方差是________18.利用计算器求标准差和方差时,首先要进入________计算状态,再依次输入每一个数据,最后按求方差的功能键________,即可得出结果.19.在一次青年歌手大赛上,七位评委为某歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0,去掉一个最高分和一个最低分后,所剩数据的平均数为________ .20.在一次函数y=﹣2x+3中,一组自变量x1、x2、…x n的平均数为a,则这组自变量对应的函数值y1、y2、…y n的平均数为________.21.已知一组数据x1,x2,x3,平均数和方差分别是2,,那么另一组数据2x1﹣1,2x2﹣1,2x3﹣1的平均数和方差分别是,________.三、解答题22.计算数据5,9,8,10,3的平均数.23.为了考察甲、乙两种小麦的长势,分别从中抽取5株麦苗,测得苗高(单位:cm)如下:甲:6、8、9、9、8;乙:10、7、7、7、9.(Ⅰ)分别计算两种小麦的平均苗高;(Ⅱ)哪种小麦的长势比较整齐?为什么?24.在一次期中考试中,(1)一个班级有甲、乙、丙三名学生,分别得到70分、80分、90分.这三名同学的平均得分是多少?(2)一个班级共有40名学生,其中5人得到70分,20人得到80分,15人得到90分.求班级的平均得分.(3)一个班级中,20%的学生得到70分,50%的学生得到80分,30%的学生得到90分.求班级的平均得分.(4)中考的各学科的分值依次为:数学150分,语文150分,物理100分,政治50分,历史50分,合计总分为500分.在这次期中考试中,各门学科的总分都设置为100分,现已知甲、乙两名学生的得分如下表:学科数学语文物理政治历史甲8090808070乙8080708095你认为哪名同学的成绩更理想,写出你的理由.25.某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)每人加工零件数544530242112人数112632(1)写出这15人该月加工零件数的平均数、中位数和众数;(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.参考答案一、选择题D D C C C A B A A B C B二、填空题13.8814.8915.乙16.平均数、众数、中位数、极差、方差、标准差 17.218.MODE;19.9.520.﹣2a+321.3;6三、解答题22.解:数据5,9,8,10,3的平均数是:(5+9+8+10+3)÷5=7.23.解:(Ⅰ)= (6+8+9+9+8)=8,= (10+7+7+7+9)=8;(Ⅱ)S2甲= [(6﹣8)2+(8﹣8)2+(9﹣8)2+(9﹣8)2+(8﹣8)2]=1.2,S2乙= [(,10﹣8)2+(7﹣8)2+(7﹣8)2+(7﹣8)2+(9﹣8)2]=1.6,∵S2甲<S2乙,∴甲种小麦的长势比较整齐.24.解:(1)这三名同学的平均得分是(70+80+90)÷3=80(分);(2)班级的平均得分是(5×70+20×80+15×90)=82.5(分);(3)班级的平均得分是70×20%+80×50%+90×30%=81(分);(4)考虑各学科在中考中所占“权”.甲的均分为80×30%+90×30%+80×20%+80×10%+70×10%=82(分),乙的均分为80×30%+80×30%+70×20%+80×10%+95×10%=79.5(分),因为甲的均分比乙的均分高,所以甲的成绩更为理想.25.(1)解:平均数= = =26(件),将表中的数据按照从大到小的顺序排列,可得出第8名工人的加工零件数为24件,且零件加工数为24的工人最多,故中位数为:24件,众数为:24件.答:这15人该月加工零件数的平均数为26件,中位数为24件,众数为24件.(2)解:24件较为合理,24既是众数,也是中位数,且24小于人均零件加工数,是大多数人能达到的定额.。
初中数学数据的整理与初步处理检测考试卷及答案(新版)华东师大版.docx

xx 学校xx 学年xx 学期xx 试卷姓名:_____________ 年级:____________ 学号:______________一、xx 题(每空xx 分,共xx 分)试题1:某校组织了“讲文明、守秩序、迎南博”知识竞赛活动,从中抽取了7名同学的参赛成绩如下(单位:分):80,90,70,100,60,80,80.则这组数据的中位数和众数分别是( )A .90,80B .70,80C .80,80D .100,80 试题2:制鞋厂准备生产一批男皮鞋,经抽样(120名中年男子),得知所需鞋号和人数如下:并求出鞋号的中位数是24 cm ,众数是25 cm ,平均数约是24 cm ,下列说法正确的是( ) A .因为所需鞋号为27 cm 的人数太少,所以鞋号为27 cm 的鞋可以不生产 B .因为平均数约是24 cm ,所以这批男皮鞋可以一律按24 cm 的鞋生产 C .因为中位数是24 cm ,所以24 cm 的鞋的生产量应占首位 D .因为众数是25 cm ,所以25 cm 的鞋的生产量应占首位 试题3:某市统计部门公布的2016年6~10月份本市居民消费价格指数(CPI)的同比增长率分别为2.3%,2.3%,2%,1.6%,1.6%,业内人士评论说:“这五个月的本市居民消费价格指数同比增长率之间相当平稳”,从统计角度看,“增长率之间相当平稳”反映的统计量是( )A .方差B .平均数C .众数D .中位数 试题4:期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”.上面两位同学的话能反映出的统计量分别是( )A.众数和平均数B.平均数和中位数C.众数和方差D.众数和中位数试题5:10名工人某天生产同一种零件,个数分别是45,50,50,75,20,30,50,80,20,30,设这些零件数的平均数为a,众数为b,中位数为c,那么( )A.a<b<c B.b<c<a C.a<c<b D.b<a<c试题6:济南某中学足球队的18名队员的年龄如下表所示:这18名队员年龄的众数和中位数分别是( )A.13岁,14岁B.14岁,14岁C.14岁,13岁D.14岁,15岁试题7:在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的( )A.平均数B.众数C.中位数 D.方差试题8:某校要从四名学生中选拔一名参加市“风华小主播”大赛,将多轮选拔赛的成绩的数据进行分析得到每名学生的平均成绩x及其方差s2如下表所示,如果要选择一名成绩高且发挥稳定的学生参赛,那么应选择的学生是( )A.甲B.乙C.丙D.丁试题9:已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中有一位同学的年龄登记错误,将14岁写成15岁.经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )A.a<13,b=13 B.a<13,b<13 C.a>13,b<13 D.a>13,b=13试题10:五名学生投篮球,规定每人投20次,统计他们每人投中的次数,得到五个数据.若这五个数据的中位数是6,唯一众数是7,则他们投中次数的总和可能是( )A.20 B.28 C.30 D.31试题11:在演唱比赛中,8位评委给一名歌手的演唱打分如下:9.3,9.5,9.9,9.4,9.3,8.9,9.2,9.6,若去掉一个最高分和一个最低分后的平均分为最后得分,则这名歌手的最后得分约为________.(结果保留一位小数)试题12:小明有五位好友,他们的年龄(单位:岁)分别是15,15,16,17,17,其方差是0.8,则三年后这五位好友年龄的方差是________.试题13:某公司欲招聘工人,对候选人进行三项测试:语言、创新、综合知识,并将测试得分按1∶4∶3的比确定测试总分.已知某位候选人的三项得分分别为88,72,50,则这位候选人的测试总分为________.试题14:已知一组数据10,8,9,x,5的众数是8,那么这组数据的方差是________.试题15:某中学初三(1)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男、女生的人数之比为________.试题16:为响应“书香成都”建设的号召,在全校形成良好的人文阅读风尚,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数是________小时.(第16题)试题17:两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为________.试题18:2014年8月26日,第二届青奥会在南京举行,甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备.在某天“110米跨栏”训练中,每人各跑5次,据统计,他们的平均成绩都是13.2秒,甲、乙、丙、丁的成绩的方差分别是0.11,0.03,0.05,0.02.则当天这四位运动员“110米跨栏”的训练成绩最稳定的是________.试题19:为了了解贯彻执行国家提倡的“阳光体育运动”的情况,将某班50名同学一周的体育锻炼情况绘制成了如图所示的条形统计图,根据统计图提供的数据,该班50名同学一周参加体育锻炼时间的中位数与众数之和为________.(第19题图)试题20:如果一组数据从小到大依次排列为x1,x2,x3,x4,x5,且x1,x2,x3的平均数为25,x3,x4,x5的平均数为35,x1,x2,x3,x4,x5的平均数是30,那么这组数据的中位数为________.试题21:“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款.某市某中学九年级(1)班的全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示.(1)求该班的总人数;(2)将条形统计图补充完整,并写出捐款金额的众数;(3)该班平均每人捐款多少元?试题22:某市为了了解高峰时段16路公交车从总站乘该路车出行的人数情况,随机抽查了10个班次乘该路车的人数,结果如下:14,23,16,25,23,28,26,27,23,25.(1)这组数据的众数为________,中位数为________;(2)计算这10个班次乘该路车人数的平均数;(3)如果16路公交车在高峰时段从总站共出车60个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少人?试题23:某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):利用表中数据,解答下列问题:(1)计算甲、乙测验成绩的平均数.(2)写出甲、乙测验成绩的中位数.(3)计算甲、乙测验成绩的方差.(结果保留小数点后两位)(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.试题24:某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图、趣题巧解、数学应用、魔方复原,每个项目的得分都按一定百分比折算后计入总分.下表为甲、乙、丙三位同学的得分情况(单位:分):(1)比赛后,甲猜测七巧板拼图、趣题巧解、数学应用、魔方复原这四项的得分分别按10%、40%、20%、30%折算计入总分,根据猜测,求出甲的总分.(2)本次大赛组委会最后决定,总分在80分以上(包括80分)的学生获一等奖.现获悉乙、丙的总分分别是70分、80分,甲的七巧板拼图、魔方复原两项的得分折算后的分数和是20分,甲能否获得这次比赛的一等奖?试题25:中华文明,源远流长;中华汉字,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校3 000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:成绩x/分频数频率50≤x<60 10 0.0560≤x<70 20 0.1070≤x<80 30 b80≤x<90 a 0.3090≤x≤100 80 0.40(第25题图)请根据所给信息,解答下列问题:(1)a=________,b=________;(2)请补全频数分布直方图;(3)这次比赛成绩的中位数会落在________分数段;(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3 000名学生中成绩为“优”等的大约有多少人?试题1答案:C 分析:这组数据中80出现了3次,出现的次数最多,所以这组数据的众数是80.把这组数据按照从小到大的顺序排列为60,70,80,80,80,90,100,排在中间的数据是80,所以这组数据的中位数是80.故选C.试题2答案:D 分析:A.所需27 cm的鞋的人数太少,27 cm的鞋可以少生产,不是不生产,所以错误.B.因为平均数约是24 cm,所以这批男皮鞋可以一律按24 cm的鞋生产,不符合实际情况,所以错误.C.哪个号的鞋的生产量占首位,要看需要的人数是否占首位,与中位数无关,所以错误.D.因为众数是25 cm,所以25 cm的鞋的生产量应占首位,哪个号的鞋的生产量占首位,要看需要的人数是否占首位,所以取决于众数,所以正确.故选D.试题3答案:A试题4答案:D 分析:根据众数与中位数的定义可知,众数是一组数据中出现次数最多的数,中位数是将一组数据从小到大(或从大到小)重新排列后,排在最中间的那个数(或排在最中间的两个数的平均数).小明和小英的话能反映出的统计量分别是众数、中位数.故选D.试题5答案:C试题6答案:B试题7答案:C试题8答案:B试题9答案:A 分析:本题考查中位数和平均数,难度中等.由于计算时,将14岁写成了15岁,故重新计算的平均数应小于原来计算的平均数,而中位数不变.故选A.试题10答案:B 分析:由“五个数据的中位数是6,唯一众数是7”,可知其中三个数据分别是6,7,7,这三个数据的和是20.两个较小的数据一定是不大于5的非负数,且不相等,故这五个数据的总和一定大于或等于21且小于或等于29.故选B.试题11答案:9.4 12.试题12答案:0.8试题13答案:65.75试题14答案:2.8试题15答案:3:2试题16答案:1试题17答案:6 分析:根据平均数的概念可得方程组解得故这两组数据分别为3,8,8,5与8,6,4,合并成一组数据并从小到大排列可得3,4,5,6,8,8,8,最中间的数是6,故这组数据的中位数是6.试题18答案:丁分析:方差是用来衡量一组数据波动程度大小的量,方差越大,表明这组数据越分散,即波动越大,数据越不稳定;反之,方差越小,表明这组数据越集中,即波动越小,数据越稳定.因为0.02<0.03<0.05<0.11,所以丁的训练成绩最稳定.试题19答案:17小时试题20答案:30试题21答案:解:(1)14÷28%=50(人).答:该班的总人数为50人.(2)捐款10元的人数为50-9-14-7-4=16,补全条形统计图如图所示;捐款金额的众数是10元.(3) ×(5×9+10×16+15×14+20×7+25×4)=×655=13.1(元),因此,该班平均每人捐款13.1元.试题22答案:解:(1)23;24.(2)×(14+16+23+23+23+25+25+26+27+28)=23(人).故这10个班次乘该路车人数的平均数是23.(3)60×23=1 380(人).所以估计在高峰时段从总站乘该路车出行的乘客共有1 380人.试题23答案:解:(2)甲、乙测验成绩的中位数都是80分.(3)s甲2=[(79-80)2+(78-80)2+(84-80)2+(81-80)2+(83-80)2+(75-80)2]≈9.33,s乙2=[(83-80)2+(77-80)2+(80-80)2+(85-80)2+(80-80)2+(75-80)2]≈11.33. (4)结合以上信息,应该派甲去,因为在平均数和中位数都相同的情况下,甲的测验成绩更稳定.试题24答案:解:(1)甲的总分:66×10%+89×40%+86×20%+68×30%=79.8(分).(2)设趣题巧解所占的百分比为x,数学应用所占的百分比为y,由题意,得解得甲的总分为20+89×30%+86×40%=81.1(分).因为81.1>80,所以甲能获得这次比赛的一等奖.试题25答案:解:(1)60;0.15 (2)略.(3)80≤x<90.(4)3 000×0.4=1 200(人),即该校参加这次比赛的3 000名学生中成绩为“优”等的大约有1 200人.。
数据的整理与初步处理A卷
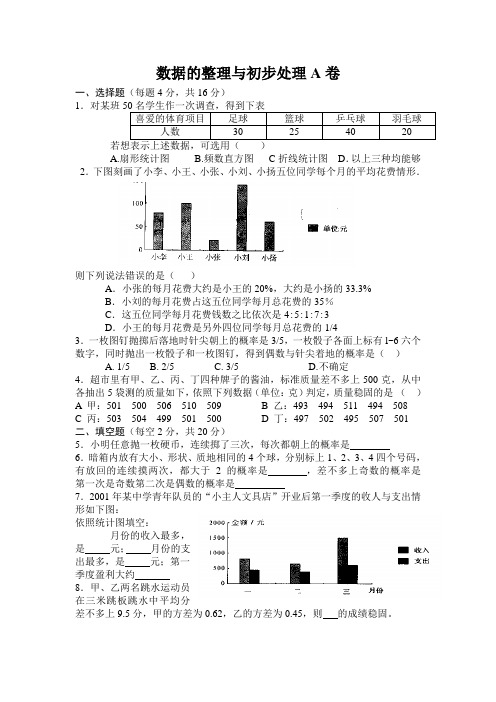
数据的整理与初步处理A卷一、选择题(每题4分,共16分)1.对某班喜爱的体育项目足球篮球乒乓球羽毛球人数30 25 40 20A.扇形统计图B.频数直方图C折线统计图D.以上三种均能够2.下图刻画了小李、小王、小张、小刘、小扬五位同学每个月的平均花费情形.则下列说法错误的是()A.小张的每月花费大约是小王的20%,大约是小扬的33.3%B.小刘的每月花费占这五位同学每月总花费的35%C.这五位同学每月花费钱数之比依次是4:5:1:7:3D.小王的每月花费是另外四位同学每月总花费的1/43.一枚图钉抛掷后落地时针尖朝上的概率是3/5,一枚骰子各面上标有l~6六个数字,同时抛出一枚骰子和一枚图钉,得到偶数与针尖着地的概率是()A. 1/5B. 2/5C. 3/5D.不确定4.超市里有甲、乙、丙、丁四种牌子的酱油,标准质量差不多上500克,从中各抽出5袋测的质量如下,依照下列数据(单位:克)判定,质量稳固的是()A 甲:501 500 506 510 509 B 乙:493 494 511 494 508C 丙:503 504 499 501 500D 丁:497 502 495 507 501二、填空题(每空2分,共20分)5.小明任意抛一枚硬币,连续掷了三次,每次都朝上的概率是6.暗箱内放有大小、形状、质地相同的4个球,分别标上1、2、3、4四个号码,有放回的连续摸两次,都大于2的概率是,差不多上奇数的概率是第一次是奇数第二次是偶数的概率是7.2001年某中学青年队员的“小主人文具店”开业后第一季度的收人与支出情形如下图:依照统计图填空:月份的收入最多,是元;月份的支出最多,是元;第一季度盈利大约8.甲、乙两名跳水运动员在三米跳板跳水中平均分差不多上9.5分,甲的方差为0.62,乙的方差为0.45,则的成绩稳固。
三、简答题(第9题4分,其余每题8分,共36分)9.到医院看病注射青霉素药水,大夫都要给你做皮试,极少数人对青霉素药水过敏,大约也确实是一千个人里有一个,即发生过敏的概率大约是0.1%,大夫什么缘故一定要这么做呢?10.下面的频数直方图表示的是一所菜园农场种植的几种作物的面积.你能依照这幅图,绘制扇形统计图吗?假如能请画出扇形统计图;假如不能,请说明理由.11.下表列出了中国、美国、印度、澳大利亚1996年的国土面积和国家级爱护区中国美国印度澳大利亚国土面积/万平方千米960.0 936.4 328.8 774.1国家级爱护区/千平方千米598.1 1226.7 142.9 563.912.小刚和小华做投掷硬币的游戏,任意投掷一枚平均的硬币三次,假如至少有两次正面朝上,那么小刚获胜;假如至少有两次反面朝上,那么小华获胜.请问,那个游戏公平吗?什么缘故?13.在分别写着数字。
数据的整理与初步处理

数据的整理与初步处理华师版数学八年级下第三个解答题通常是统计图表,“三数”(平均数、中位数、众数)和“一差”(方差)(1)根据图示填写下表:【实践发现】同学们随机收集芒果树、荔枝树的树叶各(单位:cm芒果树叶的长宽比荔枝树叶的长宽比(1)将甲学校的成绩统计图补充完整;(2)补全下面的表格,并根据表格回答问题.学校平均分中位数众数甲学校87.6乙学校87.680①从平均数和中位数角度来比较甲、乙两所学校的成绩;②从平均数和众数角度来比较甲、乙两所学校的成绩.(2)甲学校的中位数就是由低到高排序后第90分,则甲学校的中位数就是90乙学校A等级占44%,人数最多,因此乙学校的众数是补全表格如下:学校平均分中位数众数甲学校87.69090平均数中位数众数方差甲队178178b0.6乙队178a178c(1)在频数分布直方图中,自左向右第四组的频数为________.(2)学生评委计分的中位数是________分;(3)计分办法规定:老师、学生评委的计分各去掉一个最高分、一个最低分,分别计算平均分,并且按老师,学生各占60%、40%的方法计算各班最后得分.已知甲班最后得分为94.4分,求统计表中请你根据以上提供的信息解答下列问题:(1)此次竞赛中,一班成绩在C级以上(包括C级)的人数为______(2)将表格补充完整.班级成绩平均数(分)中位数(分)众数(分)一班______90______二班87______80(3)请根据你在(2)中所求的统计量,你认为选哪个班级参加市知识竞赛?请简述理由.(1)表中a的值为_________;b的值为_________.(3)推荐甲同学,理由如下:(1)前10株西红柿秧上小西红柿个数的平均数是(2)若对这20个数按组距8进行分组,请补全频数分布表及频数分布直方图:(3)通过频数分布直方图试分析此大棚中西红柿的长势.【答案】(1)47,49.5,60;(2)5,7,西红柿个数最集中的株数在第三组,共故答案为:5,7,4;(3)此大棚的西红柿长势普遍较好,最少都有西红柿个数最集中的株数在第三组,共西红柿的个数分布合理,中间多,两端少.14.“华罗庚数学奖”是中国三大顶尖数学奖项之一,为激励中国数学家在发展中国数学事业中做出突出贡献而设立,小华对截止到2023年第十六届b.“华罗庚数学奖”得主获奖时的年龄在6070£<这一组的是:x(3)∵中位数等于69<6869故答案为:小;他的获奖年龄比中位数(4)获奖年龄在6070£<范围内的人数最多,在x15.为弘扬中华传统文化,某校组织七、八年级全体学生参加了诗词大赛(百分制)为优秀,80~89分为良好,60~79分为及格,学生的成绩进行了整理与分析,下面给出了部分信息.c.抽取八年级20名学生成绩的扇形统计图,如图2:d.七年级、八年级各抽取的20名学生成绩的平均数、中位数、优秀率、方差如下表:年级平均数中位数优秀率方差七年级81m25%169.1八年级8282n154.6请根据以上信息,回答下列问题:(2)解:由数据可知,在6070x £<这组的人数为4人.则补全七年级20名学生成绩的频数分布直方图如下:(3)解:()300145%20%30%15´---=(人),故答案为:15.(4)解:学生测试成绩较好的是八年级,理由是从平均数方面看,八年级的平均成绩比七年级更高;从优秀率方面看,八年级的优秀率比七年级更高;从方差方面看,八年级的方差较小,成绩相对更稳定.故答案为:八;从平均数方面看,八年级的平均成绩比七年级更高;从优秀率方面看,八年级的优秀率比七年级更高;从方差方面看,八年级的方差较小,成绩相对更稳定.。
第20章 数据的整理与初步处理自我评估(一)及答案

第20章数据的整理与初步处理测试题(一)(本试卷满分100分)一、选择题(本大题共10小题,每小题3分,共30分)1.某市连续7天的最高气温为:28℃,27℃,30℃,33℃,30℃,30℃,32℃.这组数据的平均数是( )A.28℃B.29℃C.30℃D.32℃2.在学校的体育训练中,小杰投掷实心球的7次成绩如统计图1所示,则这7次成绩的中位数是( )A.9.7mB.9.75 mC.9.8m D.9.65 m图13.(2019年台州)方差是刻画数据波动程度的量.对于一组数据x1,x2,x3,…,x n,可用如下算式计算方差:S2=[(x1-5)2+(x2-5)2+(x3-5)2+…+(x n-5)2],其中“5”是这组数据的( )A.最小值B.平均数C.中位数D.众数4. 某班要进行班干部民主选举,班主任在选举时最值得关注的统计量是( )A.中位数B.众数C.平均数D.方差5. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩平均数都是8.8环,方差分别为s甲2=0.63环2,s乙2=0.42环2,s丙2=0.48环2,s丁2=0.51环2,则四人中成绩最稳定的是( )A.甲B.乙C.丙D.丁6.4月8日,习近平参加首都义务植树活动,他号召全国动员,全民动手,全社会共同参与“爱树、植树、护树”.近日,荔城区某单位也组织职工开展植树活动,植树量与人数之间的关系如图2所示,下列说法不正确的是( )A. 参加本次植树活动的共有30人B.每人植树量的众数是4棵C.每人植树量的中位数是5棵D.每人植树量的平均数是5棵图27. 小勇投标训练4次的成绩(单位:环)分别是:10,10,x,9.已知这组数据的众数和平均数相等,则这组数据中x是( )A.9B.10C.11D.128. 在“我的中国梦”演讲比赛中,有5名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩的( )A.中位数B.众数C.平均数D.方差A.-5 B.-2.5 C.2.5 D.510.(2019年烟台)某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是()A.平均分不变,方差变大B.平均分不变,方差变小C.平均分和方差都不变D.平均分和方差都改变二、填空题(本大题共6小题,每小题3分,共18分)11.一组数据15,13,14,13,16,13的众数是.12. 某中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次为95,90,85.则小桐这学期的体育成绩是.13. 某课外小组的同学们实践活动中调查了20户家庭某月用电量,如下表所示:用电量(度)120140160180220户数23582则这户家庭用电量的中位数是 .14. 一组数据:2,0,1,x,3的平均数为2,则这组数据的方差是 .15.甲、乙两个班级各20名男生测试“引体向上”,成绩如图3所示:图3设甲、乙两个班级男生“引体向上”个数的方差分别为s2甲和s2乙,则s2甲s2乙.(填“>”“<”或“=”)16. 已知一组数据,x1,x2,x3的平均数是5,方差是2,那么另一组数据2x1﹣4,2x2﹣4,2x3﹣4的平均数是 ,方差是 .三、解答题(本大题共7小题,共52分)17.(6分)某甲鱼养殖专业户共养甲鱼200只,为了与客户签订购销合同,对自己所养殖甲鱼的总重量进行评估,随意捞了5只,称得重量分别为1.5,1.4,1.6,2,1.8(单位:千克).(1)根据样本平均数估计甲鱼的总重量约是多少千克?(2)如果甲鱼的市场价为每千克150元,那么该养殖专业户卖出全部甲鱼的收入约为多少元?18.(6分)为了让同学们了解自己的体育水平,八年级(1)班的体育老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,(1)班的体育委员根据这次测试成绩,制作了统计图如图4所示:图4根据以上信息,解答下列问题:(1)这个班共有男生人;(2)八年级(1)班女生体育成绩的众数是多少?男生体育成绩的中位数是多少?20.(7分)某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下表;经过计算,甲进球的平均数为8,方差为3.2.(1)求乙进球的平均数和方差;(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?21. (8分)为准备参加某市2019年度中小学生机器人竞赛,学校对甲、乙两支机器人制作小队所创作的机器人分别从创意、设计、编程与制作三方面进行量化,各项量化满分100分,根据量化结果择优推荐.它们三项量化得分如下表:量化得分量化项目甲队乙队创意8572设计7066编程与制作6484(1)如果根据三项量化的平均分择优推荐,哪队将被推荐参赛?(2)根据本次中小学生机器人竞赛的主题要求,如果学校根据创意、设计、编程与制作三项量化得分按5:3:2的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议.甲1061068乙7978922. (8分)在6.26国际禁毒日到来之际,某市教委为了普及禁毒知识,提高禁毒意识,举办了“关爱生命、拒绝毒品”的知识竞赛,某校七、八年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:68881001007994898510088七年级100909897779496100926769979169981009910090100八年级998997100999479999879(1)根据上述数据,将下列表格补充完成:【整理、描述数据】分数段60≤x≤6970≤x≤7980≤x≤8990≤x≤100七年级人数2 12八年级人数22 15【分析数据】样本数据的平均数、中位数如下表:年级平均数中位数七年级90.193八年级92.3【得出结论】(2)你认为哪个年级掌握禁毒知识的总体水平较好?从两个方面说明你的理由.23. (10分)甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图5所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.图5(1)请填写下表:(2)请回答下列问题:①从平均数和中位数来分析,甲、乙两城市的空气质量;②从平均数和方差来分析,甲、乙两城市的空气质量情况;③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.附加题(20分,不计入总分)24.为了迎接体育中考,九年级(7)班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如图6所示.图6(山西陈岩)第20章数据的整理与初步处理自我评估(一)参考答案一、1. C 2. A 3. B 4. B 5. B 6.D 7.C 8. A 9. C 10.B二、11.13 12.88.5分13. 170度14. 2 15. < 16.6 8三、17.解:(1)根据样本平均数估计甲鱼的总重量约是(1.5+1.4+1.6+2+1.8)÷5×200=332(千克).(2)该养殖专业户卖出全部甲鱼的收入约为332×150=49800(元).18. 解:(1)20 提示:男生人数为1+2+6+3+5+3=20(人).(2)从扇形统计图中可以看出,8分的占比最多,为28%,因此女生的众数为8分;男生20人的成绩从小到大排列后处于第10,11位的两个数都是8分,因此男生的中位数是8分.19. 解:(1)平均数=(3×1+4×3+5×2+6×1+7×1+8×1+20×1)=6.6(万元);出现次数最多的是4万元,所以众数是4万元;按大小顺序排列后第5,6个数均是5万元,所以中位数是5万元.(2)今年每个销售人员统一的销售标准应定为5万元比较合理.理由如下:若规定平均数6.6万元为标准,则多数人无法或不可能超额完成,会挫伤员工的积极性;若规定众数4万元为标准,则大多数人不必努力就可以超额完成,不利于提高年销售额;若规定中位数5万元为标准,则大多数人能完成或超额完成,少数人经过努力也能完成.因此把5万元定为标准比较合理.20. 解:(1)乙进球的平均数为(7+9+7+8+9)=8;乙进球的方差为[(7-8)2+(9-8)2+(7-8)2+(8-8)2+(9-8)2]=0.8.(2)因为甲、乙二人的平均数相同,而s2=3.2,s乙2=0.8,s甲2>s乙2.甲所以乙的成绩更稳定.所以应选乙去参加定点投篮比赛.21.解:(1)因为甲队的平均成绩是(85+70+64)=73(分);乙队的平均成绩是(72+66+84)=74(分),所以乙队将被推荐参赛.(2)因为甲队的平均数是85×+70×+64×=76.3(分);乙队的平均数是72×+66×+84×=72.6(分).所以甲队将被推荐参赛.建议:加强机器人创意方面的开发(答案不唯一).22.(1)表格1从左至右,从上至下依次填2,4,1;表格2中填97.5.(2)八年级较好.理由:从平均数看,八年级的平均数比七年级的高;从中位数看,八年级的也比七年级的高,因此八年级平均水平较高.23. 解:(1)根据折线图,甲的数据依次为:110,90,100,80,90,60,90,50,70,60,有1次空气质量为优;甲的方差为[(110-80)2+(90-80)2+...+(60-80)2]=340;甲的中位数为(80+90)=85;乙的数据依次为:120,120,110,110,90,70,60,50,40,30,有3次空气质量为优;乙的平均数为(120+120+110+110+90+70+60+50+40+30)=80.所以表格从左至右,从上至下依次填340,85, 1, 80, 3.(2)由(1)表中的数据,可知①从平均数和中位数来分析:平均数相同,甲的中位数大于乙的中位数,故乙城市的空气质量好些;②从平均数和方差来分析:平均数相同,s2<s乙2,根据方差的意义,可得空气污染指甲数比较稳定的城市是甲;③根据折线图上两城市的空气污染指数的走势来分析,乙城市的空气污染指数下降得很快,7月以后连续3个月为优,甲只有1个月为优,故治理环境污染效果较好的城市是乙.24. 解:(1)由条形统计图可知,男生的人数为2+6+8+4+4=24(人),其中位数是7分;女生成绩的平均分为(5×4+6×2+7×10+8×6+9×2)=7(分),中位数是=7(分);表格从左至右,从上至下依次填7,7,7.(2)从平均数看,女生平均分高于男生;从方差看,女生的方差低于男生,波动性小;(3)设男生新增优秀人数为x人,则2+4+x+2x=48×50%,解得x=6.6×2=12(人).答:男生新增优秀人数为6人,女生新增优秀人数为12人.。
第20章 数据的整理与初步处理(真题训练卷)(原卷版)

华东师大版八年级下册第20章《数据的整理与初步处理》真题训练卷一、选择题(本大题共12个小题,每小题4分,共48分.以下每小题都给出了A、B、C、D 四个选项,其中只有一个是符合题目要求的。
)1、在一次田径运动会上,参加男子跳高的15名运动员的成绩如表所示:这些运动员跳高成绩的中位数是()A、1.65B、1.70C、4D、32、在抗击新型冠状病毒肺炎疫情中,某社区志愿者小分队10名队员年龄统计如下表:则这10名队员年龄的中位数、众数分别是()A、20岁,35岁B、26岁,22岁C、22岁,26岁D、30岁,30岁3、某校举行了以“致敬抗美援朝,争做时代新人”为主题的演讲比赛、在比赛中,7位评委分别对某位选手的演讲进行评分、评分规则是:从7个原始评分中去掉一个最高分和个最低分,得到5个有效评分取平均分即为选手的最终得分。
5个有效评分与7个原始评分相比,这两组数据一定不变的是()A、方差B、众数C、平均数D、中位数4、甲,乙两个班参加了学校组织的“故事力大赛”国学知识竞赛选拔赛,他们成绩的平均数、中位数、方差如下表所示,规定成绩大于等于95分为优异,则下列说法正确的是()A、甲、乙两班的平均水平相同B、甲、乙两班竞赛成绩的众数相同C、甲班的成绩比乙班的成绩稳定D、甲班成绩优异的人数比乙班多5、下表是某地援鄂医疗人员的年龄分布对于不同的m,下列关于年龄的统计量不会发生改变的是()A、众数、中位数B、众数、方差C、平均数、方差D、平均数、中位数6、某校有25名同学参加比赛,预赛成绩各不相同,要取前12名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需再知道这25名同学成绩的()A、中位数B、众数C、平均数D、方差7、为了调查某校同学的体质健康状况,随机抽查了若干名同学的每天锻炼时间如表:则关于这些同学的每天锻炼时间,下列说法错误的是( )A 、平均数是21B 、众数是60C 、抽查了10个同学D 、中位数是508、在一次献爱心的捐款活动中,八(2)班50名同学捐款金额如图所示,则在这次捐款活动中,该班同学捐款金额的众数和中位数分别是( )A 、20,10B 、10,20C 、10,10D 、10,159、如图为我市5月某一周每天的最高气温统计,则这组数据(最高气温)的众数与中位数分别是( )A 、29,29B 、29,30C 、30,30D 、30,29.510、某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:关于该班学生一周读书时间的数据有下列说法:①一周读书时间数据的中位数是9小时;②一周读书时间数据的众数是8小时;③一周读书时间数据的平均数是9小时;④一周读书时间不少于9小时的人数占抽查学生的50%。
八年级数学下册《数据的整理与初步处理》练习题与答案(华师大版)

八年级数学下册《数据的整理与初步处理》练习题与答案(华师大版)一、选择题1.在﹣2,1,2,1,4,6中正确的是()A.平均数3B.众数是﹣2C.中位数是1D.极差为82.一次数学测试后,随机抽取九年级某班5名学生的成绩如下:91,78,98,85,98.关于这组数据说法错误的是( )A.平均数是91B.极差是20C.中位数是91D.众数是983.将一组数据中的每一个数减去40后,所得新的一组数据的平均数是2,则原来那组数据的平均数是( )A.40B.42C.38D.24.某住宅小区6月1日~6月5日每天的用水量变化情况如图所示,则这5天平均每天的用水量是( ),(第3题))A.30 m3B.31 m3C.32 m3D.33 m35.小明在九年级第一学期的数学成绩分别为:测验一得88分,测验二得92分,测验三得84分,期中考试得90分,期末考试得87分.如果按照平时、期中、期末的权重分别为10%,30%与60%,那么小明该学期的总评成绩为( )A.86B.87C.88D.896.已知一组数据5,15,75,45,25,75,45,35,45,35,那么40是这一组数据的( )A.平均数但不是中位数B.中位数但不是平均数C.众数D.平均数也是中位数7.已知100名学生进行20秒钟跳绳测试,测试成绩统计如下表:跳绳次数x 20<x≤30 30<x≤40 40<x≤50 50<x≤60 60<x≤70 x>70人数 5 2 13 31 23 26A.40<m≤50B.50<m≤60C.60<m≤70D.m>708.已知一组数据﹣2,﹣2,3,﹣2,﹣x,﹣1的平均数是﹣0.5,那么这组数据的众数与中位数分别是( )A.﹣2和3B.﹣2和0.5C.﹣2和﹣1D.﹣2和﹣1.59.若干名工人某天生产同一种零件,将生产的零件数整理成条形统计图,如图所示.设他们生产的零件数的平均数为a个,中位数为b个,众数为c个,则( )A.b>c>aB.c>a>bC.a>b>cD.b>a>c10.为了解班级学生参加体育锻炼的情况,现将九年级(1)班同学一周的体育锻炼情况绘制如图所示的统计图,那么,关于该班同学一周参加体育锻炼时间的说法错误的是( )A.中位数是8小时B.众数是8小时C.平均数是8.5小时D.锻炼时间超过8小时的有20人11.为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据,如下表:甲 2 6 7 7 8乙 2 3 4 8 8( )A.甲、乙的众数相同B.甲、乙的中位数相同C.甲的平均数小于乙的平均数D.甲的方差小于乙的方差12.对于数据3,3,2,3,6,3,10,3,6,3,2.①这组数据的众数是3;②这组数据的众数与中位数的数值不等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等.其中正确的结论有( )A.1个B.2个C.3个D.4个二、填空题13.一组数据﹣3,﹣1,0,3,10的极差是.14.一组数据2,4,a,7,7的平均数x=5,则方差s2=.15.某人开车旅行100km,在前60km内,时速为90km,在后40km内,时速为120km,则此人的平均速度为_________.16.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:测试项目创新能力综合知识语言表达测试成绩(分数) 70 80 90将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是________分.17.已知某次测验的最高分、最低分、平均分、中位数、众数,同学甲要知道自己的成绩,属于班级中较高的一半还是较低的一半,应该利用上述数值中的.18.小明等五名同学四月份参加某次数学测验的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值为________.三、解答题19.在“心系灾区”自愿捐款活动中,某班30名同学的捐款情况如下表:(1)这个班级捐款总数是多少元?(2)求这30名同学捐款的平均数.20.某中学为了了解学生的体育锻炼情况,随机抽查了部分学生一周参加体育锻炼的时间,得到如图的条形统计图,根据图形解答下列问题:(1)这次共抽查了名学生;(2)所抽查的学生一周平均参加体育锻炼多少小时?(3)已知该校有1 200名学生,估计该校有多少名学生一周参加体育锻炼的时间超过6小时?21.某公司招聘人才,对应聘者分别进行阅读、思维和表达能力三项测试,其中甲、乙两人的成绩(单位:分)如下表:项目人员阅读思维表达能力甲93 86 73乙95 81 793∶5∶2的比例确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?22.为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.汉字听写大赛成绩分数段统计表汉字听写大赛成绩分数段条形统计图分数段频数50≤x<60 260≤x<70 670≤x<80 980≤x<90 1890≤x≤100 15(1)补全条形统计图.(2)这次抽取的学生成绩的中位数在的分数段中;这次抽取的学生成绩在60≤x<70的分数段的人数占抽取人数的百分比是.(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?23.某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)请根据图中提供的信息,回答下列问题:(1)α= ,并写出该扇形所对圆心角的度数为 ,请补全条形图.(2)在这次抽样调查中,众数和中位数分别是多少?(3)如果该地共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?24.甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):运动员 \ 环数 \ 次数1 2 3 4 5 甲10 8 9 10 8 乙10 9 9 a b某同学计算出了甲的成绩平均数是9,方差是s 2甲=15[(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,请作答: (1)在图中用折线统计图将甲运动员的成绩表示出来;(2)若甲、乙射击成绩平均数都一样,则a +b = ;(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a,b 的所有可能取值,并说明理由.25.在推进嘉兴市城乡生活垃圾分类的行动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A 、B 两小区分别有500名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:【信息一】A 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值):【信息二】上图中,从左往右第四组的成绩如下:【信息三】A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):根据以上信息,回答下列问题:(1)求A小区50名居民成绩的中位数.(2)请估计A小区500名居民成绩能超过平均数的人数.(3)请尽量从多个角度,选择合适的统计量分析A,B两小区参加测试的居民掌握垃圾分类知识的情况.参考答案1.D2.A.3.B.4.C5.C6.D7.B.8.D9.D.10.C.11.D12.A13.答案为:13.14.答案为:3.6.15.答案为:100km/h16.答案为:7717.答案为:中位数18.答案为:60或11019.解:(1)这个班级捐款总数为5×11+10×9+15×6+20×2+25×1+30×1=330(元).(2)这个班级捐款总数是330元,这30名同学捐款的平均数为11元.20.解:(1)60 (2)4×15+5×10+7×15+8×2060=6.25(时); (3)1 200×15+2060=700(名). 21.解:∵x 甲=93×3+86×5+73×23+5+2=85.5(分) x 乙=95×3+81×5+79×23+5+2=84.8(分) ∴x 乙<x 甲∴甲将被录用.22.解:(1)补全条形图如下:(2)∵被调查的总人数为2+6+9+18+15=50人,而第25、26个数据均落在80≤x <90 ∴这次抽取的学生成绩的中位数在80≤x <90的分数段中这次抽取的学生成绩在60≤x <70的分数段的人数占抽取人数的百分比是×100%=12% 故答案为:80≤x <90,12%;(3)105.答:该年级参加这次比赛的学生中成绩“优”等的约有105人.23.解:(1)a =1﹣(40%+20%+25%+5%)=1﹣90%=10%圆心角的度数为360°×10%=36°;(2)众数是5天,中位数是6天;(3)2000×(25%+10%+5%)=800(人).答:估计“活动时间不少于7天”的学生人数大约有800人.24.解:(1)如图所示;(2)[由题意,知15(10+9+9+a +b)=9,∴a +b =17.] (3)在(2)的条件下,a,b 的值有四种可能:第①种和第②种方差相等:s 2乙=15(1+0+0+4+1)=1.2>s 2甲 ∴甲比乙的成绩较稳定.第③种和第④种方差相等:s 2乙=15(1+0+0+0+1)=0.4<s 2甲 ∴乙比甲的成绩稳定.因此,a=7,b=10或a=10,b=7时,甲比乙的成绩较稳定.25.解:(1)因为有50名居民,所以中位数落在第四组,中位数为75,故答案为75;(2)500×=240(人),答:A 小区500名居民成绩能超过平均数的人数240人;(3)从平均数看,两个小区居民对垃圾分类知识掌握情况的平均水平相同; 从方差看,B 小区居民对垃圾分类知识掌握的情况比A 小区稳定;从中位数看,B 小区至少有一半的居民成绩高于平均数.。
2022年最新华东师大版八年级数学下册第二十章数据的整理与初步处理专题测试试题(含答案解析)

八年级数学下册第二十章数据的整理与初步处理专题测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、要调查多数同学们喜欢看的电视节目,应关注的是()A.平均数B.中位数C.众数2、鞋厂生产不同号码的鞋,其中,生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的()A.平均数B.众数C.中位数D.众数或中位数3、下列说法中正确的是()A.样本7,7,6,5,4的众数是2B.样本2,2,3,4,5,6的中位数是4C.样本39,41,45,45不存在众数D.5,4,5,7,5的众数和中位数相等4、若一组数据3,x,4,5,7的平均数为5,则这组数据中x的值和方差为()A.3和2 B.4和3 C.5和2 D.6 和25、为庆祝中国共产党建党一百周年,某班50名同学进行了党史知识竞赛,测试成绩统计如表,其中有两个数据被遮盖.下列关于成的统计量中、与被遮盖的数据无关的是()A.平均数B.中位数C.中位数、众数D.平均数、众数6、数据1,2,3,4,5的方差是()A B.2 C.3 D.57、在一次射击训练中,甲、乙两人各射击10次,两人10次射击成绩的平均数均是9.1环,方差分别是2S甲=1.2,2S乙=1.1,则关于甲、乙两人在这次射击训练中成绩稳定的描述正确的是()A.乙比甲稳定B.甲比乙稳定C.甲和乙一样稳定D.甲、乙稳定性没法对比8、甲、乙、丙、丁四名学生近4次数学测验成绩的平均数都是110分,方差分别是S甲2=6,S乙2=24,S丙2=25.5,S丁2=36,则这四名学生的数学成绩最稳定的是()A.甲B.乙C.丙D.丁9、5个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个实数,并把自己想好的数如实地告诉他相邻的两个人,然后每个人将他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报4的人心里想的数是()A.7 B.8 C.9 D.1010、一组数据分别为:79、81、77、82、75、82,则这组数据的中位数是()A.82B.77C.79.5D.80第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题4分,共计40分)1、某单位拟招聘一个管理员,其中某位考生笔试、试讲、面试三轮测试得分分别为92分,85分,90分,若依次按40%,40%,20%的比例确定综合成绩,则该名考生的综合成绩为______分.2、一组数据中出现次数_______的数据称为这组数据的众数.注意:(1)一组数据的众数一定出现在这组数据中.(2)一组数据的众数可能不止一个,如1,1,2,3,3,5中众数是_______.(3)众数是一组数据中出现次数最多的数据而不是数据出现的次数,如1,1,1,2,2,5中众数是1而不是3(4)众数的单位与原数据的单位_______.3、将一组数据按照由小到大(或由大到小)的顺序排列:如果数据的个数是______,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的__________为这组数据的中位数.4、一组数据3,-4,1,x的极差为8,则x的值是______.5、八年级某班的教室里,三位同学正在为谁的数学成绩好而争论,他们的五次数学成绩分别是:小华:62;94;95;98;98小明:62;62;98;99;100小丽:40;62;85;99;99他们都认为自己的数学成绩比其他两位同学好,他们的依据是什么?分析:小华成绩的众数是_____,中位数是_____,平均数是_____;小明成绩的众数是_____,中位数是_____,平均数是_____;小丽成绩的众数是_____,中位数是_____,平均数是_____.解:因为他们之中,小华的_____最大,小明的_____最大,小丽的_____最大,所以都认为自己的成绩比其他两位同学好.6、甘肃省白银市广播电视台欲招聘播音员一名,对甲、乙两名候选人进行了两项素质测试,两人的两项测试成绩如下表所示:根据需要广播电视台将面试成绩、综合知识测试成绩按3∶2的比例确定两人的最终成绩,那么_______将被录取.7、已知一组数据:3、4、5、6、8、8、8、10,这组数据的中位数是_________.8a 的方差是_____ 9、从甲、乙两块试验田各随机抽取100株麦苗测量高度(单位:cm ),计算它们的平均数和方差,结果为:13x =甲,13x =乙,2=3.6S 甲,215.8S =乙.则麦苗长势比较整齐的试验田是________(填“甲”或“乙”).10、某校九年级进行了3次体育中考项目—1000米跑的模拟测试,甲、乙、丙三位同学3次模拟测试的平均成绩都是3分55秒,三位同学成绩的方差分别是2S 甲=0.01,2S 乙=0.009,2S 丙=0.0093.则甲、乙、丙三位同学中成绩最稳定的是________.三、解答题(5小题,每小题6分,共计30分)1、某校春季运动会计划从七年级三个班中评选一个精神文明队,评比内容包括:“开幕式得分”,“纪律卫生”和“投稿及播稿情况”三项(得分均为整数分),三个班的各项得分(不完整)如图所示.(1)“开幕式”三个班得分的中位数是;“纪律卫生”三个班得分的众数是;(2)根据大会组委会的规定:“开幕式”,“纪律卫生”,“投稿及播稿情况”三项按4:4:2的比例确定总成绩,总成绩高的当选精神文明队,已知七年级一班的总成绩为79分.①请计算七年级二班的总成绩;②若七年级三班当选精神文明队,请求出七年级三班在“投稿及播稿情况”方面的最少得分?2、某中学九年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛成绩(单位:个)经统计发现两班5名学生踢毽子的总个数相等,此时有学生建议,可以通过考查数据中的其他信息为参考,请你回答下列问题:(1)甲班比赛数据的中位数为,乙班比赛数据的平均数为;(2)计算两班比赛数据的方差;(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.3、某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩计算了甲成绩的平均数和方差(见小宇的作业).(1)求a和乙的方差S乙;(2)请你从平均数和方差的角度分析,谁将被选中.4、为了纪念中国人民志愿军抗美援朝71周年,近两年涌现了很多相关题材的电影作品,《长津湖》和《金刚川》正是其中优秀的代表.为了解学生对这两部作品的评价,某调查小组从该校观看过这两部电影的学生中各随机抽取了20名学生对这两部作品分别进行评分(满分10分),并通过整理和分析,给出了部分信息.《长津湖》得分情况:7,8,7,10,7,6,9,9,10,10,8,9,8,6,6,10,9,7,9,9抽取的学生对两部作品分别打分的平均数,众数和中位数根据以上信息,解答下列问题:(1)直接写出上述图表中的a,b,c的值;(2)根据上述数据,你认为该校观看过这两部作品的学生对哪部作品评价更高?请说明理由(写出一条理由即可);(3)若该校有2000名学生观看过这两部影片,若他们都对这两部作品进行评分,你认为这两部作品一共可得到多少个满分?5、12月,我校初2022届学生进行了一次体育机器模拟测试(包含跳绳、立定跳远、实心球三项,共计满分50分).测试完成后,为了解初2022届学生的体育训练情况,在初2022届的学生中随机抽取了20名男生,20名女生的本次体育机考的测试成绩,对数据进行整理分析,并给出了下列信息:20名女生的测试成绩统计如下:44,47,48,45,50,49,45,60,48,49,50,50,44,50,43,50,44,50,49,45.抽取的20名男生的测试成绩扇形统计图如下:其中,抽取的20名男生的测试成绩中,D组的成绩如下:47,48,48,47,48,48.抽取男生与女生的学生的测试成绩的平均数、中位数、众数如下表所示:a______,b=______,c=______;(1)根据以上信息可以求出:=(2)结合以上的数据分析,针对本次的体育测试成绩中,你认为此次的体育测试成绩男生与女生谁更好?请说明理由(理由写出一条即可);(3)若初2022届学生中男生有700人,女生有900人,(规定49分及以上为优秀)请估计该校初2022届参加此次体育测试的学生中成绩为优秀的学生人数.-参考答案-一、单选题1、C【解析】略2、B【解析】【分析】由鞋厂关心的数据,即大众买的最多的鞋号,也就是出现次数最多的数据,从而可得所构成的数据是众数.【详解】解:生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的众数,故选B【点睛】本题考查的是众数的含义及众数表示的意义,理解众数的含义及在生活中的应用是解本题的关键.3、D【解析】【分析】根据众数定义和中位数定义对各选项进行一一分析判定即可.【详解】A. 样本7,7,6,5,4的重复次数最多的数是7,所以众数是7,故选项A不正确;B. 样本2,2,3,4,5,6的处于中间位置的两个数是3和4,所以中位数是343.52+=,故选项B不正确;C. 样本39,41,45,45重复次数最多的数字是45,故选项C不正确;D. 5,4,5,7,5,将数据重新排序为4,5,5,5,7,重复次数最多的众数是5和中位数为5,所以众数和中位数相等,故选项D正确.故选D.【点睛】本题考查众数与中位数,掌握众数与中位数定义,一组数据中重复次数最多的数据是众数,将一组数据从小到大排序后,处于中间位置,或中间位置上两个数据的平均数是中位数是解题关键.4、D【解析】【分析】先根据平均数定义求出x,再根据方差公式计算即可求解.【详解】解:由题意得345755x++++=,解得x=6,∴这组数据的方差是()()()()()22222 356545557525-+-+-+-+-=.故选:D【点睛】本题考查了平均数的定义和求一组数据的方差,熟知平均数的定义和方差公式是解题关键.5、C【解析】【分析】通过计算成绩为91、92分的人数,进行判断,不影响成绩出现次数最多的结果,因此不影响众数,同时不影响找第25、26位数据,因此不影响中位数的计算,进而进行选择.【详解】解:由表格数据可知,成绩为91分、92分的人数为50-(12+10+8+6+5+3+2+1)=3(人),成绩为100分的,出现次数最多,因此成绩的众数是100,成绩从小到大排列后处在第25、26位的两个数都是98分,因此中位数是98,因此中位数和众数与被遮盖的数据无关,故选:C.【点睛】本题主要考查中位数、众数、方差、平均数的意义和计算方法,理解各个统计量的实际意义,以及每个统计量所反应数据的特征,是正确判断的前提.6、B【解析】【分析】 先计算平均数x =3,代入()()2221515S x x x x ⎡⎤=-+⋯+-⎣⎦计算即可. 【详解】∵1,2,3,4,5, ∴123455x ++++==3, ∴()()()()()222222113233343535S ⎡⎤=-+-+-+-+-⎣⎦ =2,故选B .【点睛】本题考查了方差,熟练掌握方差的计算公式是解题的关键.7、A【解析】【分析】根据方差的性质解答.【详解】解:∵甲乙两人的方差分别是2S 甲=1.2,2S 乙=1.1,∴乙比甲稳定,故选:A .【点睛】此题考查了方差的性质:方差越小越稳定.8、A【解析】【分析】根据方差的意义求解即可.【详解】解:∵S甲2=6,S乙2=24,S丙2=25.5,S丁2=36,∴S甲2<S乙2<S丙2<S丁2,∴这四名学生的数学成绩最稳定的是甲,故选:A.【点睛】本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.掌握方差的意义是解题的关键.9、C【解析】【分析】设报4的人心想的数是x,则可以分别表示报1,3,5,2的人心想的数,最后通过平均数列出方程,解方程即可.【详解】解:设报4的人心想的数是x,报1的人心想的数是10﹣x,报3的人心想的数是x﹣6,报5的人心想的数是14﹣x,报2的人心想的数是x﹣12,所以有x﹣12+x=2×3,解得x=9.故选:C.此题考查了平均数和一元一次方程的应用,解题的关键是正确分析题目中的等量关系列方程求解.10、D【解析】【分析】将数据排序,进而根据中位数的定义,可得答案.【详解】解:数据79、81、77、82、75、82从小到大排列后可得:75、77、79、81、82、82,排在中间的两个数是79,81,所以,其中位数为79+81=802,故选:D.【点睛】本题主要考查中位数,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.二、填空题1、88.8【解析】【分析】根据加权平均数的求解方法求解即可.【详解】解:根据题意,该名考生的综合成绩为92×40%+85×40%+90×20%=88,8(分),故答案为:88.8.本题考查加权平均数,熟知加权平均数的求解方法是解答的关键.2、最多 1和3 一致【解析】略3、奇数平均数【解析】略4、4或-5##-5或4【解析】【分析】根据极差的定义分两种情况讨论,当x最大时和x最小时,分别列出算式进行计算即可.【详解】解:∵数据3,-4,1,x的极差是8,∴当x最大时:x-(-4)=8,解得:x=4;当x最小时,3-x=8,x=-5,故答案为:4或-5.【点睛】此题主要考查了极差的定义,极差反映了一组数据变化范围的大小,求极差的方法是用一组数据中的最大值减去最小值,分两种情况讨论是解决本题的关键.5、 98 95 89.4 62 98 84.2 99 85 77 平均数中位数众数【解析】略6、乙【解析】【分析】分别求出两人的成绩的加权平均数,即可求解.【详解】解:甲候选人的最终成绩为:329085883232⨯+⨯=++,乙候选人的最终成绩为:329580893232⨯+⨯=++,∵8889<,∴乙将被录取.故答案为:乙【点睛】本题主要考查了求加权平均数,熟练掌握加权平均数的求法是解题的关键.7、7【解析】【分析】将一组数据按照从小到大的顺序进行排列,排在中间位置上的数叫作这组数据的中位数,若这组数据的个数为偶数个,那么中间两位数的平均数就是这组数据的中位数,据此解答即可得到答案.【详解】解:按照从小到大的顺序排列为:3、4、4、5、6、8,8,10中位数:(6+8)÷2=7故答案为:7.【点睛】本题主要考查中位数的求解,根据中位数的定义,将数据从小到大进行排列是解决本题的关键. 8、3512##11212【解析】【分析】a 的值,再求出其方差即可. 【详解】 0,∴3030a a +⎧⎨->⎩, 解得33a -<.故a 的所有整数值为3-,2-,1-,0,1,2. 该组数的平均数为:11[3(2)(1)012]62-+-+-+++=-. 方差为:)2222222111111135[(3)(2)(1)(0)(1)(2]622222212S =-++-++-+++++++=. 故填3512.【点睛】此题将分式的意义、二次根式成立的条件和方差相结合,考查了同学们的综合运用数学知识能力.9、甲【解析】【分析】根据题意可得:22S S <甲乙,即可求解.【详解】 解:∵13x =甲,13x =乙,2=3.6S 甲,215.8S =乙. ∴22S S <甲乙,∴甲试验田麦苗长势比较整齐.故答案为:甲【点睛】本题主要考查了利用方差判断稳定性,熟练掌握一组数据方差越小越稳定是解题的关键.10、乙【解析】【分析】根据方差的定义,方差越小数据越稳定.【详解】解:∵s 甲2=0.01,s 乙2=0.009,s 丙2=0.0093,∴s 乙2<s 丙2<s 甲2,∴甲、乙、丙三位同学中成绩最稳定的是乙.故答案为:乙.【点睛】本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.三、解答题1、(1)85;85;(2)①七年级二班的总成绩为80;②七年级三班在“投稿及播稿情况”方面的最少得分是51分.【解析】【分析】(1)将三个班“开幕式”和“纪律卫生”列出来,从中找出中位数和众数即可;(2)①利用加权平均数计算出七年级三班的得分即可;②设七年级三班“投稿及播稿情况”的得分为x,因为三班的成绩要比二班的高,根据加权平均数计算与二班的成绩列出不等式求解即可.【详解】(1)“开幕式”三个班得分分别为:85,75,90,故中位数为85;“纪律卫生”三个班得分分别为:70,85,85,故众数为85;(2)①7548548028008044210⨯+⨯+⨯==++(分),故七年级二班的总成绩为:80分;②设七年级三班在“投稿及播稿情况”方面的得分为x分,若七年级三班当选精神文明对,则七年级三班的总成绩应比七年级二班精神文明成绩要高,则904854280442x⨯+⨯+⨯>++,解得50x>,∵x为整数,∴x 最低为51,∴七年级三班在“投稿及播稿情况”方面的最少得分为51分.【点睛】本题考查了中位数、众数和加权平均数的计算,解题的关键是对定义的理解.2、 (1)100,100(2)246.8S =甲,256S =乙(3)应该把团体第一名的奖状给甲班,因为甲班和乙班的平均数相同,甲班的方差比乙班低,甲班比较稳定,综合评定甲班比较好【解析】(1)解:甲班的成绩重新排列为:89,98,100,103,110,故中位数为100, 乙班成绩的平均数为5001005 , 故答案为:100,100;(2)甲的平均数为:500÷5=100(个),S 甲2=[(100﹣100)2+(98﹣100)2+(110﹣100)2+(89﹣100)2+(103﹣100)2]÷5=46.8; 乙的平均数为:500÷5=100(个),S 乙2=[(90﹣100)2+(97﹣100)2+(101﹣100)2+(113﹣100)2+(99﹣100)2]÷5=56;(3)应该把团体第一名的奖状给甲班,理由如下:因为甲班和乙班的平均数相同,甲班的方差比乙班低,甲班比较稳定,综合评定甲班比较好.【点睛】此题考查了统计计算,正确掌握中位数的定义,平均数的计算公式,方差的计算公式,利用方差做决策是解题的关键.3、 (1)4,=1.6a s =乙(2)因为两人成绩的平均水平(平均数)相同,根据方差得出乙的成绩比甲稳定,所以乙将被选中【解析】【分析】()1根据总成绩相同可以求得a 的值,然后求得平均数,利用方差的公式进行计算即可; ()2因平均数相同,故谁的方差小谁就更稳定,谁就会被选中.(1) 解:∵()1757765x a =++++=乙,4a ∴=, ∴()()()()(222221[7656764676) 1.65S ⎤=-+-+-+-+-=⎦乙; (2)因为两人成绩的平均水平(平均数)相同,根据方差得出乙的成绩比甲稳定,所以乙将被选中.【点睛】本题考查了方差及算术平均数的知识,解决本题的关键是熟记方差的计算公式及意义.4、 (1)a =15,b =8.5,c =8;(2)《长津湖》,理由见解析;(3)385.【解析】【分析】(1)根据《金刚川》调查得分为“10分”所占的百分比,确定a的值,根据中位数、众数的意义可求出b、c的值,(2)通过平均数、中位数、众数的比较得出答案;(3)求出两部作品满分人数所占的百分比即可求.(1)解:《金刚川》调查得分为“10分”所占的百分比为:1﹣10%﹣20%﹣20%﹣126360=15%,即a=15,《长津湖》调查得分从小到大排列,6,6,6,7,7,7,7,8,8,8,9,9,9,9,9,9,10,10,10,10,处在中间位置的两个数的平均数为892+=8.5,因此中位数是8.5分,即b=8.5,《金刚川》调查得分出现次数最多的是8分,共出现126207360⨯=(次),因此众数是8分,即c=8,答:a=15,b=8.5,c=8;(2)《长津湖》,理由为:《长津湖》调查得分的平均数、中位数、众数均比《金刚川》高;(3)《长津湖》满分有4个,《金刚川》满分占15%,所以,两部作品一共可得到满分为:1100×(420+15%)=385(个),答:这两部作品一共可得到385个满分.【点睛】本题考查条形统计图,频数分布表,中位数、众数、平均数,理解中位数、众数、平均数的意义是解决问题的前提,掌握中位数、众数、平均数的计算方法是正确解答的关键.5、(1)15,48,50;(2)女生的成绩较好,理由见解析;(3)755人.【解析】【分析】(1)由扇形统计图,可求出a 的值,根据中位数的意义,将男生成绩排序,找出处于中间位置的两个数的平均值即为中位数,从女生成绩中找出出现次数最多的数即为众数;(2)通过比较平均数、中位数、众数的大小即可解答;(3)抽查女生20人中优秀的有10人,男生20人中优秀的9人,求出两个优秀占抽查总人数的比例,求出该校初2022届参加此次测试的学生中优秀的学生人数即可.【详解】解:(1)1-5%-5%-45%-30%=15%,15a ∴=由扇形统计图中,可知,男生成绩的中位数位于D 组,男生成绩第10,11个数成绩高于46,但不超过48分的成绩的较大的两个48,48,4848482b +∴== 女生成绩出现次数最多的是50,因此众数是50,50c ∴=故答案为:15,48,50;(2)女生的成绩较好,理由:男女生的平均数相等,女生的中位数、众数都比男生大,因此女生的成绩较好.(3)2045%=9⨯(人)1097009003504057552020⨯+⨯=+=(人) 答:估计该校初2022届参加此次体育测试的学生中成绩为优秀的学生人数为755人.【点睛】本题考查平均数、中位数、众数、统计表、理解平均数、中位数、众数的意义是解题关键,样本估计总体是统计中常用的方法.。
第20章 数据的整理与初步处理 A卷-2020-2021学年华东师大版八年级数学下册单元测试题AB卷

第20章 数据的整理与初步处理A 卷考试时间:90分钟;总分:120分一、单选题(将唯一正确答案的代号填在题后括号内,每题3分,共30分) 1.某公司要招聘职员,竟聘者需通过计算机、语言表达和写作能力测试,李美丽的三项成绩百分制依次是70分,90分,80分,其中计算机成绩占50%,语言表达成绩占30%,写作能力成绩占20%,则李美丽最终的成绩是( ) A .76分B .78分C .80分D .82分2.某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( ) A .最高分B .中位数C .方差D .平均数3.对于两组数据A 、B ,如果2A S >2B S ,A x =B x ,则( )A .这两组数据的波动相同.B .数据B 的波动小一些.C .它们的平均水平不一样D .数据A 的波动小一些.4.已知样本数据1、2、2、3、7,下列说法不正确的是( ) A .平均数是3B .中位数是2C .方差是2D .众数是25.某班在一次数学测试后,成绩统计如下表:该班这次数学测试的平均成绩是( ) A .82B .75C .65D .626.某班30名学生的身高情况如下表:则这30名学生身高的众数和中位数分别是( ) A .7,1.71m mB .1.72,1.70m mC .1.72,1.71m mD .1.72,1.72m m7.某校把学生的纸笔测试,实践能力,成长纪录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲,乙,丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是()A.甲B.乙、丙C.甲、乙D.甲、丙8.一鞋店销售一种新鞋,试销期间卖出情况如下表,对于鞋店经理来说最关心哪种尺码的鞋畅销,那么下列统计量对该经理来说最有意义的是()A.平均数B.中位数C.众数D.方差9.某校随机抽查了10名参加2017年我市初中学业水平考试学生的体育成绩,得到的结果如下表:下列说法中,正确的是()A.这10名学生体育成绩的中位数为58B.这10名学生体育成绩的平均数为58C.这10名学生体育成绩的众数为60D.这10名学生体育成绩的方差为6010.甲、乙、丙、丁四位同学五次数学测验的成绩的平均数相同,五次测验的方差如下表.如果从四位同学中选出一位状态稳定的同学参加全国数学联赛,那么应选择()A.甲B.乙C.丙D.丁二、填空题(将正确答案填在题中横线上,每题3分,共24分)11.五个连续偶数中最大数是248,那么这五个数的平均数是__________.12.一组数据3,5,5,4,5,6的众数是_____.13.某校运动会前夕,要选择256名身高基本相同的女同学组成表演方阵,在这个问题中,最值得关注的是该校所有女生身高的________(填“平均数”、“中位数”或“众数”).14.某大学招生考试只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,已知小明数学得分为95分,物理得分为90分,那么小明的综合得分是____分.15.已知一组数据5,8,10,x,9的众数是8,那么这组数据的方差是.16.如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:2S甲_____2S乙(填“>“或“<”).17.某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学习的平均时间是_______小时.18.给出下列五个命题:①32、42、52是一组勾股数;②y=3x是正比例函数,但不是一次函数;③对角线互相垂直且相等的四边形是正方形;④无论x为何值,一定都是二次根式;⑤一组数据的中位数有且只有一个,但众数可能不止一个;其中正确的是____(写出所有正确命题的序号)三、解答题(本题共有8小题,共66分)19.(本题6分)为了解居民的环保意识,社区工作人员在某小区随机抽取了若干名居民开展有奖问卷调查活动,并用得到的数据绘制了如下条形统计图.请根据图中信息,解答下列问题.(1)求本次调查获取的样本数据的平均数;(2)如果对该小区的800名居民全面开展这项有奖问卷活动,得10分者设为一等奖,请你根据调查结果,估计需准备多少份一等奖奖品?19题图20.(本题8分)为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩.数据如下:收集数据:90,91,89,96,90,98,90,97,91,98,99,97,91,88,90,97,95,90,95,88;整理、描述数据:成绩/分88 89 90 91 95 96 97 98 99学生人数 2 1 a 3 2 1 b 2 1数据分析:样本数据的平均数、众数和中位数如下表平均数众数中位数93 c d应用数据(1)由上表填空:a=________,b=________,c=________,d=________,(2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分.(3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号. 请估计评选该荣誉称号的最低分数,并说明理由.21.(本题8分)为了从甲、乙两名选手中选拔一名参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下甲、乙两人射击成绩的折线图:(1)求甲、乙两人射击成绩的中位数;(2)如果规定成绩较稳定者胜出,你认为谁应胜出?请通过计算方差说明理由.22.(本题8分)为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛,初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:年级决赛成绩(单位:分)七年级80 86 88 80 88 99 80 74 91 89八年级85 85 87 97 85 76 88 77 87 88九年级82 80 78 78 81 96 97 88 89 86(1)请你填写下表:年级平均数众数中位数七年级85.5 87八年级85.5 85九年级84(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:①从平均数和众数相结合看(分析哪个年级成绩好些);②从平均数和中位数相结合看(分析哪个年级成绩好些)③如果在每个年级分别选出3人参加决赛,你认为哪个年级的实力更强一些?并说明理由.23.(本题8分)甲、乙两名同学进入八年级后某科6次考试成绩如图所示:平均数方差中位数众数甲75 75乙33.3 70(1)请根据图填写上表;(2)从平均数和方差结合看,你认为谁的成绩稳定性更好些?24.(本题8分)有一道满分12分的解答题,按评分标准,所有考生的得分只有四种:0分,4分,8分,12分.老师为了了解学生的得分情况与题目的难易情况,从所有考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.请根据以上信息解答下列问题:(1)填空:a=______,b=______,并把条形统计图补全;(2)已知难度系数的计算公式为XLW,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0≤L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L≤1时,此题为容易题.试问此题对于这些考生来说属于哪一类?请说明理由.25.(本题10分)甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在某次测试中,从两校各随机抽取了30名学生的测试成绩进行调查分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.(1)请根据乙校的数据补全条形统计图:(2)两组样本数据的平均数. 中位数众数如下表所示,写出m、n的值:(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好些,请为他们各写出条可以使用的理由;甲校:____.乙校:________.(4)综合来看,可以推断出________校学生的数学学业水平更好些,理由为________.26.(本题10分)七年级一班和二班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.(1)填表;(2)如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?第20章 数据的整理与初步处理A 卷参考答案1.B. 解析:由题意可得:70×50%+90×30%+80×20%=78(分).故选B . 2.B. 解析:共有25名学生参加预赛,取前13名,所以小颖需要知道自己的成绩是否进入前13,我们把所有同学的成绩按大小顺序排列,第13名的成绩是这组数据的中位数,所以小颖知道这组数据的中位数,才能知道自己是否进入决赛. 故选B .3.B. 解析:∵22A B s s >,A x =B x ,∴数据B 的波动小一些.故答案为:B .4.C. 解析:因为数据1、2、2、3、7,的众数是2,中位数是3,平均数=,方差,所以选项A 、B 、D 正确,C 错误,故选C .5.A. 解析:这次数学测试的平均成绩是10079014801770860250271417822⨯+⨯+⨯+⨯+⨯+⨯+++++=82.故答案为A .6.D. 解析:由表可得出这组数据中1.72m 出现的次数最多,因此,这30名学生身高的众数是1.72m ;把这一组数据按从小到大的顺序排列,中间的两个数字是1.72m 、1.72m ,因此,这30名学生身高的中位数是1.72m . 故选:D .7.C. 解析:根据题意得:甲的总评成绩是:90×50%+83×20%+95×30%=90.1, 乙的总评成绩是:98×50%+90×20%+92×30%=94.6, 丙的总评成绩是:90×50%+88×20%+90×30%=89.6, 则学期总评成绩优秀的有甲、乙二人, 故选:C .8.C. 解析:A.平均数反映的是一组数据的平均水平,故不合题意; B. 中位数反映的是一组数据的中等水平,故不合题意;C.由于众数是数据中出现最多的数,鞋店的经理最关心的是各种鞋号的鞋的销售量,特别是销售量最多的鞋号,符合题意.D.方差反映的是一组数据的波动程度,故不合题意;故选:C .9.C. 解析:A. ∵这10名学生体育成绩的中位数为59,故不正确; B. 这10名学生体育成绩的平均数为565725859260458.610+⨯++⨯+⨯= ,故不正确;C. 这10名学生体育成绩的众数为60,故正确;D. 这10名学生体育成绩的方差为()()()()()222225658.65758.625858.65958.626058.641.64810-+-⨯+-+-⨯+-⨯= ,故不正确; 故选C.10.B. 解析:∵2222551942S S S S =>=>=>=丁甲乙丙,∴乙较稳定, ∵甲、乙、丙、丁四位同学五次数学测验的成绩的平均数相同,∴应选择乙; 故选:B .11.244. 解析:248-2=246,246-2=244,244-2=242,242-2=240, 平均数是:(248+246+244+242+240)÷5, =1220÷5, =244, 故答案是:244.12.5.解析:这组数据中出现次数最多的数据为:5.故众数为5.故答案为5. 13.众数. 解析:根据题意:在这个问题中我们最值的关注的是队伍的整齐,身高必须差不多;故应该关注该校所有女生身高的众数. 故答案为:众数.14.93. 解析:根据题意得,95×60%+90×40%=93. 故答案为93. 15.2.8. 解析:∵一组数据5,8,10,x ,9的众数是8,∴x=8, ∴这组数据为5,8,10,8,9,该组数据的平均数为:()158108985++++=. ∴这组数据的方差()()()()()222222114S 58881088898 2.855⎡⎤=-+-+-+-+-==⎣⎦16.<. 解析:由图可得,甲10次跳远成绩离散程度小,而乙10次跳远成绩离散程度大,∴2S 甲<2S 乙,故答案为:<.17.3. 解析:根据题意得:这10名学生周末学习的平均时间=(1×1+2×2+4×3+2×4+1×5)÷10=3(小时), 故答案为:3.18.⑤. 解析:3,4,5是一组勾股数,但32、42、52不是一组勾股数,所以①错误;因为y=3x 是正比例函数,也是一次函数,所以②错误;因为对角线互相垂直平分且相等的四边形是正方形,所以③错误; 因为当x≥0时,是二次根式,所以④错误;因为一组数据的中位数有且只有一个,但众数可能不止一个,所以⑤正确. 故答案为⑤. 19.解:(1)6471081591110108.26410151110x ⨯+⨯+⨯+⨯+⨯==++++分,答:本次调查获取的样本数据的平均数为8.26分;(2)800×1050=160份,答:估计需准备160份一等奖奖品.20.解:(1)由题意得:90分的有5个;97分的有3个; 出现次数最多的是90分,∴众数是90分, 第10,第11个数都是91, ∴中位数是:(91+91)÷2=91, 故答案为5a =,3b =,c =90,d =91; (2)20×50%=10, 如果该校想确定七年级前50%的学生为“良好”等次,则“良好”等次的测评成绩至少定为91分; 故答案为91;(3)估计评选该荣誉称号的最低分数为97分;理由如下: ∵20×30%=6, 97分以上含97分的共有:1+2+3=6(人), ∴估计评选该荣誉称号的最低分数为97分.21.(1)由图可知,甲10次射击成绩按从小到大排序为2,6,6,7,7,7,8,9,9,9,故中位数为7; 乙10次射击成绩按从小到大排序为2,4,6,7,7,8,9,9,0,故中位数为787.52+=. (2)甲胜出.理由:甲、乙两人射击成绩的平均数分别是2667778999710x +++++++++==甲24677889910710x +++++++++==乙方差分别是2222(27)(67)(97)410s -+-++-==甲2222(27)(47)(107) 5.410s -+-++-==乙由22s s<甲乙可知,甲的射击成绩更稳定,即甲胜出.22.解:(1)(2)①∵平均数都相同,八年级的众数最高,∴八年级的成绩好一些.②∵平均数都相同,七年级的中位数最高,∴七年级的成绩好一些. ③∵七,八,九各年级前三名学生决赛成绩的平均分分别是93分,91分,94分,∴从各年级参加决赛的选手中分别选出3人参加总决赛,九年级的实力更强一些. 23.解:(1)平均数方差中位数众数甲75 125 75 75乙75 33.3 72.5 70(2)甲、乙两名同学成绩的平均数均为75分,但是甲的方差为125,乙的方差仅为33.3,所以乙的成绩相对比甲稳定些.24.解:(1)∵被调查的总人数为24÷10%=240(人),∴b%=48240×100%=20%,则a%=1-(10%+20%+45%)=25%,∴4分的人数为240×25%=60(人),补全图形如下:故答案为:25、20;(2)∵X=02446081081248240⨯+⨯+⨯+⨯=7分,∴L=712≈0.5833,则此题对于这些考生来说属于中等难度试题.25.解:(1)由表格可得,乙校,70-79的有5人,60-69的有2人,补全条形统计图,如下图各分数段条形统计图(2)乙校数据按照从小到大排列是:57、61、63、71、72、73、76、79、80、83、84、84、84、85、85、87、87、88、89、89、90、90、91、92、92、92、92、92、94、94,∴这组数据的中位数是:8587=862m+=,92n=;(3)甲校:我们学校的平均分高于乙校,所以我们学校的成绩好;乙校:我们学校的众数高于甲校,所以我们学校的成绩好;故答案为我们学校的平均分高于乙校,所以我们学校的成绩好;我们学校的众数高于甲校,所以我们学校的成绩好;(4)综合来看,甲校学生的数学学业水平更好一些,理由:甲校的平均分高于乙校,说明总成绩甲校好于乙校,中位数甲校高于乙校,说明甲校一半以上的学生成绩较好26.解:(1)一班进球平均数:110(10×1+9×1+8×1+7×4+6×0+5×3)=7(个),一班中位数:第五第六名同学进7个球,故中位数为7(个);一班投中7个球的有4人,人数最多,故众数为7(个);二班方差:S22=110[0×(10-7)2+(9-7)2+2×(8-7)2+5×(7-7)2+0×(6-7)2+2×(5-7)2]=1.4.(2)二班选手水平发挥更稳定,争取夺得总进球数团体第一名,应该选择二班;一班前三名选手的成绩突出,分别进10个、9个、8个球,如果要争取个人进球数进入学校前三名,应该选择一班.。
第20章 数据的整理与初步处理单元测试卷

20章《数据的整理与初步处理》单元测试卷一、单选题(每题3分,共27分)1.为响应“节约用水”的号召,小李随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是()A.8,8B.8.4,8C.8.4,8.4D.8,8.42.某居民区的月底统计用电情况,其中3户用电45度,5户用电50度,6户用电42度,则平均用电为()A.41度B.42度C.45.5度D.46度3.七年级学生完成课题学习“从数据谈节水”后,积极践行“节约用水,从我做起”,下表是从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况:0.2 0.25 0.3 0.4 0.5节水量(m3)1 2 2 4 1家庭数(个)那么这组数据的众数和平均数分别是A.0.4和0.34 B.0.4和0.3 C.0.25和0.34 D.0.25和0.34.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的()A.众数B.中位数C.平均数D.方差5.已知一组数据2,1,x,7,3,5,3,2的众数是2,则这组数据的中位数是()A.2B.2.5C.3D.56.某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频数分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.下列说法:(1)学生的成绩≥27分的共有15人;(2)学生成绩的众数在第四小组(22.5~26.5)内;(3)学生成绩的中位数在第四小组(22.5~26.5)范围内.其中正确的说法有()A.0个B.1个C.2个D.3个7.在计算某一样本:12,16,-6, (11)(单位:℃)的方差时,小明按以下算式进行计算:22221s(1220)(1620) (1120)15,则计算式中数字15和20分别表示样本中的()A.众数;中位数B.方差;标准差C.样本中数据的个数;平均数D.样本中数据的个数;中位数8.从某校九年级中随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,5 分.将测量的结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是A.1B.2C.3D.49. 一组数据按从大到小排列为2,4,8,x,10,14.若这组数据的中位数为9,则这组数据的众数()A.6B.8C.9D.10二、填空题(每题3分,共6题18分)10. 要了解某地农户用电情况,抽查了部分农户在某地一个月中用电情况:用电15度的有3户,用电20度的有5户,用电30度的有2户,那么平均每户用电11. 若一组数据15,,11,,7的平均数为6,则的值是12. 某超市招聘收银员一名,对三名应聘者进行了三项素质测试.下面是三名应聘者的素质测试成绩:素质测试测试成绩小李小张小赵计算机709065商品知识507555语言803580公司根据实际需要,对计算机、商品知识、语言三项测试成绩分别赋予权重4、3、2,则这三人中将被录用13.某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析,结果如下:甲=1.69m。
数据的整理与初步处理

- 1 -数据的整理与初步处理(满分:150分;考试时间:120分钟)一、选择题(每小题3分,共21分):1、已知数据是1,5,6,5,5,6,6,6,则下面结论正确的是 ( )A 、平均数是5B 、中位数是5C 、众数是5D 、方差是52、甲、乙两人各射靶8次,命中环数如下:甲:7,8,6,8,6,7,8,8乙:9,5,6,7,8,10,4,10,则射击技术较为稳定的是 ( ) A 、甲 B 、乙 C 、一样 D 、不能确定 3、能反应一组数据离散程度的是( )A 、平均数B 、中位数C 、众数D 、方差4、在一幅扑克牌中任意抽取1张牌,下列事件发生的机会最大的是( )A 、红色B 、黑桃C 、红桃D 不是K5、将三张大小一样而画面不同的卡片从中间剪开,变成六张小卡片,把它们放在一个盒子中,摇匀后,取出两张恰好能拼成原来的一幅画的机会是( ) A 、61 B 、31C 、51D 、526、已知样本甲的平均数60=甲x ,方差2甲s =0.05,样本乙的平均数60=乙x ,方差1.02=乙s ,那么两个样本波动的情况为( )A 、甲、乙两样本波动一样大B 、甲样本的波动比乙样本大C 、乙样本的波动比甲样本大D 、无法比较两样本波动的大小7、甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数,经统计某同学根据上表分析得出如下结论: ①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输出汉字数≥150个优秀); ③甲班的成绩的波动比乙班的成绩的波动大。
上述结论正确的是( )A 、①②③B 、①②C 、①③D 、②③- 2 -二、填空题(每小题4分,共40分):8、要调查你所在的班级同学有无同月同日生的,你应采取的调查方式是 9、从装有3个黄球和2个红球的袋中摸出一个球,恰好为红球的机会是 10、有一个样本的方差是:[]22022212)6(....)6()6(201-++-+-=x x xs ,这个样本是 个数据,平均数为11、一组数据1x ,2x ,3x .....n x 的方差为9,则数据51-x ,52-x ,53-x ,......,5-n x 的方差为 ,标准差为 。
八年级数学下册数据的整理与初步处理A卷华东师大版

数据的整理与初步处理(A卷)一、填空题(每小题6分,本题满分30分)1.我们进入中学以来,已经学习过不少有关数据的统计量,例如等,它们分别从不同的侧面描述了一组数据的特征.2.甲、乙两人进行投篮比赛,共进行了五次,每次每人投10个球.比赛结果投进个数分别为3.右图是某班学生在体检中测得每分钟心率频数的直方图,据此可知道该班参加体检学生的人数是,心率在范围的学生最多,占统计人数的比例是 .4.已知一组数据的一个样本x1,x2,x3,…x n的平均数是0.24,方差是1.02,那么估计这组数据的总体平均数是,方差是 .5.以6为分母,从0到22这23个自然数中任意取一个为分子写出分数,则所得分数不可约的机会是,得到整数的机会是 .二、选择题(每小题5分,本题满分25分)6.下列语句中错误的是( ).(A)一组数据的极差一定是正数(B)同一组数据的标准差不一定小于方差(C)如果一组数据的极差不是正数,那么这组数据的极差、方差、标准差都相等(D)气象预报:“受这次冷空气影响,我省南部地区将普遍降温10°C左右”中的10°C既是平均数,也可以看作某组数据的极差7.在学校开展的小制作评比活动中,二年级六个班都参加了比赛,根据他们上交作品的件数,绘制直方图如右.已知从左至右各长方形高的比为2∶3∶4∶2∶3∶1,小制作件数最多的三班上交了16件.经评选各班获奖件数如下表:在这次评选中,获奖率最高的两个班级依次是( ).(A)5班、3班 (B)3班、4班 (C)5班、6班 (D)6班、5班8.数据21,22,23,24,25,…,40的标准差是S1,数据302,303,304,304,305,…,321的标准差是S2,则( ).(A)S1<S2 (B)S1=S2 (C)S1>S2 (D)不能确定S1、S2的大小9.两组数据如下图,设图(1)中数据的平均数为、方差为,图(2)中数据的平均数为、方差为,则下列关系成立的是( ).10.甲乙两人一起玩游戏,甲先抛掷一枚硬币,如果正面向上,则甲胜;如果反面向上,则由乙抛掷,如果反面向上,则乙胜,否则甲胜.那么在这个游戏中( ).(A)甲乙两人获胜的机会是相等的(B)甲获胜的机会大(C)乙获胜的机会大(D)不能确定两人获胜机会的大小三、解答题(每小题9分,本题满分45分)11.据劳动和社会保障部在5省10市的抽样调查统计:下岗职工按技术素质分,初级技工及没有技术等级的人员占52.6%,中级技工占38.9%,高级技工及技师只占8.5%.根据上述数据绘制扇形统计图表示下岗职工的技术素质.12.下表给出了我国运动员在第23届至第27届奥运会上获得奖牌情况,请据此解答下列问题:(1) 制作一个新的统计表,表示出我国运动员在这五届奥运会上获得的奖牌总数;(2) 请你用恰当的统计图表示你所作出的新的统计表内容;(3) 从制作的统计图中你能得到哪些信息?(4) 分别从金牌数和奖牌总数两个方面比较我国运动员在五届奥运会上的成绩.13.从分别写有1,2,3,4,5五个数字的五张卡片中随意抽出两张,将下列事件按发生的机会从小到大的顺序排列,并写出简要的根据:(1)和是偶数;(2)积是偶数;(3)和是奇数;(4)积是奇数.14.要在甲乙两名学生中选拔一人参加国家数学冬令营集训.经统计,两人近期的8次测试成绩分别制作成统计图、表如下.如果让你选拔,打算让谁参加?两种统计表示中,哪一种较能直观地反映出两者的差异?15.现在发行的体育彩票,购买时号码允许重复,开奖时通过摇号得出特等奖号码.若与该号码相同的奖券只有一张,则独得特等奖奖金总额;若与该号码相同的奖券有几张,则每张券平分特等奖奖金总额.小李和老王各买了两张奖券,小李的两张号码完全相同,老王的两张则号码不同,试问:(1)谁中特等奖的可能性大一些,为什么?(2)若小李或老王中了特等奖,在奖金总额相同的情况下,谁得的奖金多一些?能说明理由吗?数据的整理与初步处理(A卷) 答案1.平均数、众数、中位数、极差、方差、标准差.2.3,1.04,1.0198; 6,4,2.3.43;67.5-75;41.9%.;1.02.6.A.7.D.8.B.9.B. 10.B.11.图略.12.(1)略;(2)采用直方图或折线图较适当,图略;(3)略;(4) 略.13.机会从小到大依次是(4)、(1)、(3)、(2)(提示:各自出现的可能种数分别为3,4,6,7).14.由发展趋势一般宜选拔乙参加,折线图反映两者差异比较明显.15.(1) 老王;(2)当只有一人中特等奖时,两人中奖后所得奖金数额相同;当不止一人中特等奖时,小李得到的奖金多一些.。
达标测试华东师大版八年级数学下册第二十章数据的整理与初步处理专项测评练习题(无超纲)

八年级数学下册第二十章数据的整理与初步处理专项测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、甲、乙、丙、丁四名同学进行立定跳远测试,每人10次立定跳远成绩的平均数都是2.25米,方差分别是20.72S =甲,20.75S =乙,20.68S =丙,20.61S =丁,则这四名同学立定跳远成绩最稳定的是( ).A .甲 B .乙 C .丙 D .丁2、在爱心一日捐活动中,我校初三部50名教师参与献爱心,以下是捐款统计表,则该校初三教师捐款金额的中位数,众数分别是( )A .100,100B .100,150C .150,100D .150,1503、若一组数据3,x ,4,5,7的平均数为5,则这组数据中x 的值和方差为( )A .3和2B .4和3C .5和2D .6 和24、在今年中小学全面落实“双减”政策后小丽同学某周每天的睡眠时间为(单位:小时):8,9,7,9,7,8,8,则小丽该周每天的平均睡眠时间是( )A .7小时B .7.5小时C .8小时D .9小时5、为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm )的平均数与方差为:x x =甲丙=13,x x =乙丁=15:2S 甲=2S 丁=3.6,2S 乙=2S 丙=6.3.则麦苗又高又整齐的是( )A .甲B .乙C .丙D .丁 6、在对一组样本数据进行分析时,小华列出了方差的计算公式S 2=22222(5)(4)(4)(3)(3)5x x x x x -+-+-+-+-,下列说法错误的是( ) A .样本容量是5B .样本的中位数是4C .样本的平均数是3.8D .样本的众数是47、九年级(1)班学生在引体向上测试中,第一小组6名同学的测试成绩如下(单位:个):4,5,6,7,7,8,这组数据的中位数与众数分别是( )A .7,7B .6,7C .6.5,7D .5,68、某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95,90,88,则小彤这学期的体育成绩为( )A .89B .90C .91D .929、新冠疫情防控形势下,学校要求学生每日测量体温.某同学连续一周的体温情况如表所示,则该同学这一周的体温数据的众数和中位数分别是( )A .36.3和36.2B .36.2和36.3C .36.3和36.3D .36.2和36.110、为了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间条形统计图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )A .7h ,7hB .8h ,7.5hC .7h ,7.5hD .8h ,8h第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题4分,共计40分)1、某学校决定招聘数学教师一名,一位应聘者测试的成绩如表:将笔试成绩,面试成绩按6:4的比例计入总成绩,则该应聘者的总成绩是______分.2、为了考察某种小麦的长势,从中抽取了10株麦苗,测得苗高(单位:cm )为:16,9,14,11,12,10,16,8,17,19,则这组数据的极差是____.3、某次测试中,小颖语文,数学两科分数共计176分,如果再加上英语分数,三科的平均分就比语文和数学的两科平均分多3分,则小颖的英语成绩是______分.4、在统计学中,样本的方差可以近似地反映总体的______.(在①“集中趋势”,②“波动大小”,③“平均值”,④“最大值”中选择合适的序号填写在横线上)5、一组数据8,2,6,10,5的极差是_________.6、为充分弘扬“人道、博爱、奉献”的红十字精神,某校开展了“博爱在京城”募捐活动,每位学生积极参与募捐活动,用自己力量帮助那些需要帮助的人.其中7个班的捐款的金额分别是(单位:元):100,60,100,110,155,60,120.则这组数据的众数是______,中位数是______.7、若一组数据1x ,2x ,…n x 的平均数是2,方差是1.则132x +,232x +,…32n x +的平均数是_______,方差是_______.8、样本5、6、7、8、9的方差是_______________.9、我区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为95分,面试成绩为85分,那么吴老师的总成绩为__________分.10、已知一组按大小排列的整数数据1,2,2,x,3,4,5,7的众数是2,则这组数据的平均数是_______.三、解答题(5小题,每小题6分,共计30分)1、某校开展了以“不忘初心,奋斗新时代”为主题的读书活动,校德育处对本校八年级学生九月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了抽样调查,随机抽取八年级部分学生,对他们的“读书量”(单位:本)进行了统计,并将统计结果绘制成了如下统计图:(1)本次所抽取学生九月份“读书量”的众数为______本,中位数为______本;(2)求本次所抽取学生九月份“读书量”的平均数.2、某小区有500户居民,从中随机抽取了100户,调查了他们11月的用水量(单位:吨).整理抽取的这100户的月用水量,其中小于等于15吨的户数有60户.按月用水量(单位:吨)0~5,5~10,10~15,15~20,20~25,25~30,30~35进行分组,绘制了频数分布直方图.(1)直接写出直方图中x,y的值,以及这100户居民月用水量的中位数所在的组别;(2)把图中每组用水量的值用该组的中间值(如0~5的中间值为2.5)来代替,估计该小区11月的用水总量.说明:0~5是指大于等于0且小于等于5,5~10是指大于5且小于等于10,以此类推,30~35是指大于30且小于等于35)3、射击比赛中,某队员的10次射击成绩如图所示,试估计他的平均成绩.4、5,16,16,28,32,51,51的众数是什么?5、甲、乙两名射击选手各自射击十组,按射击的时间顺序把每组射中靶的环数值记录如下表:(1)根据上表数据,完成下列分析表:(2)如果要从甲、乙两名选手中选择一个参加比赛,应选哪一个?为什么?-参考答案-一、单选题1、D【解析】【分析】平均数相同,方差值越小越稳定,比较四名同学方差值的大小即可.【详解】解:∵2222S S S S >>>乙甲丁丙∴丁同学的成绩最稳定故选D .【点睛】本题考查了方差.解题的关键在于理解方差值越小的数据越稳定.2、C【解析】【分析】根据中位数和众数的定义:一组数据中,出现次数最多的数就叫这组数据的众数。
第20章 数据的整理与初步处理 章节复习(重点练)原卷版

第20章数据的整理与初步处理(章节复习)(重点练)一.选择题(共10小题)1.(2021春•木兰县期末)某专卖店专营某品牌的皮鞋,店主统计了一周不同尺码的皮鞋销售量如表:尺码39404142平均内天销售量/双10122012如果每双皮鞋的利润相同,你认为该店主最关注的销售数据是下列统计量中的()A.平均数B.方差C.众数D.中位数2.(2021秋•成都期末)金沙遗址陈列馆有5个展厅,分别是第一展厅:远古家园;第二展厅:王都剪影;第三展厅:天地不绝;第四展厅:千载遗珍:第五展厅:解读金沙.某班同学分小组到以上五个展厅进行研学活动,人数分别为:9,11,8,11,10(单位:人),这组数据的众数和中位数分别是()A.11人,10人B.11人,8人C.11人,9人D.9人,8人3.(2021•开化县模拟)衢州市2021届初中毕业生体育与健康考试中运动技能素质新增一分钟跳绳选测项目,据统计,某校九(3)班学生在一次跳绳模拟考试中,一组7人一分钟跳的次数依次是:186,178,185,182,186,176,188.这组数据的中位数和众数分别是()A.182和186B.182和178C.185和186D.185和188 4.(2021秋•沙坪坝区校级期中)某手机公司新推出了W10、X10、Y10、Z10四款新型手机,公司为了了解各款手机的性能,随机抽取了每款手机各50台进行测试,以下是四款手机的性能得分(满分100分,分数越高,性能越好)的平均分和方差,则这四款新型手机中性能好且稳定的是()W10X10Y10Z10平均成绩(分)95989698方差3322 A.W10B.X10C.Y10D.Z10 5.(2021•安徽模拟)某校创新班和实验班各选出六名学生参加IMO(国际数学奥林匹克竞赛,满分42分)选拔赛,如表是这两班6名学生参加这次比赛的成绩(单位:分),下列说法正确的是()123456选手班级创新班362630292936实验班253333362732A.创新班6名学生成绩的平均数大于实验班6名学生成绩的平均数B.创新班6名学生成绩的中位数大于实验班6名学生成绩的中位数C.创新班6名学生成绩的众数一定大于实验班6名学生成绩的众数D.创新班6名学生成绩比实验班6名学生成绩更稳定6.(2021春•昆明期末)水稻科研人员为了比较甲乙两种水稻秧苗谁出苗更整齐,每种秧苗各随机抽取60株,分别量出每株高度,发现两组秧苗的平均高度和中位数均相同,甲、乙的方差分别是3.6,6.3,则下列说法正确的是()A.甲秧苗出苗更整齐B.乙秧苗出苗更整齐C.甲、乙出苗一样整齐D.无法确定甲、乙出苗谁更整齐7.(2021春•雨花区期末)为深入开展“健好身,读好书,写好字”活动,测试某班15名男同学引体向上次数,每人只测一次,测试结果统计如表:引体向上数/个012345678人数112133211这15名男同学引体向上个数的中位数是()A.2B.3C.4D.58.(2021秋•宣化区期末)数据4,3,5,3,6,3,4的众数和中位数是()A.3,4B.3,5C.4,3D.4,5 9.(2021•宁波模拟)随机调查某市100名普通职工的个人年收入(单位:元)情况,得到这100人年收入的数据,记这100个数据的平均数为a,中位数为b,方差为c.若将其中一名职工的个人年收入数据换成世界首富的年收入数据,则a一定增大,那么对b与c的判断正确的是()A.b一定增大,c可能增大B.b可能增大,c可能不变C.b一定不变,c一定增大D.b可能不变,c一定增大10.(2021•中宁县模拟)在我校“英语课本剧”表演比赛中,初二年级的10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中正确的是()A.众数是90B.平均数是88C.中位数是85D.方差是6二.填空题(共8小题)11.(2021•连云港)一组数据2,1,3,1,2,4的中位数是.12.(2021秋•普陀区期末)十个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个整数,并把自己想好的数如实告诉他两旁的两个人,然后每人将他两旁的人告诉他的数计算出平均数并报出来.已知每个人报的结果如图所示,那么报“3”的人自己心里想的数是.13.(2021秋•武功县期末)某班举行辩论比赛,除参赛选手外,其他同学作为观众评委,分别给正方、反方两队的表现进行打分,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为5分,4分,3分,2分,小雯将反方队的成绩整理并绘制成如图统计图,由图可知,反方的平均得分为分.14.(2021秋•莱芜区期末)“阳光小区”开展“节约用水,从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较,统计出节水情况如表:节水量(m3)0.30.40.50.60.7家庭数(个)32311那么这10个家庭的节水量(m3)的平均数是.15.(2021秋•长沙期末)从2022年起长沙市学校体育中考增加素质类选测项目:立定跳远和1分钟跳绳.小熙选择了1分钟跳绳项目,她10次跳绳训练的成绩为140,155,142,155,166,167,166,170,180,176,这组数据的中位数是.16.(2021•咸宁模拟)某班五个兴趣小组的人数分别为4,5,4,x,6,已知这组数据的平均数是5,则这组数据的中位数是.17.(2021•高唐县一模)已知一组数据:92,94,98,91,95的中位数为a,方差为b,则a+b =.18.(2021•中宁县模拟)学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如表,请你根据表中的数据选一人参加比赛,最适合的人选是.(填甲、乙中的一个)选手甲乙平均数(环)9.59.5方差0.0350.015三.解答题(共10小题)19.(2021秋•沙坡头区校级期末)某校初二学生开展毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每踢100个(含100)为优秀.下表是成绩最好的甲班和乙班各5名学生的比赛数据(单位:个).经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:1号2号3号4号5号总分甲班1009811089103500乙班891009511997500(1)计算两班比赛数据的中位数;(2)通过计算方差比较哪一个班级学生的比赛成绩相互之间更接近,为什么?(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?说明理由!20.(2021秋•云龙区校级月考)徐州市今年参加初中学业水平测试的人数(以下简称“中考人数”)的情况如图所示.根据图中信息,解决下列问题:(1)这11年间,徐州市中考人数的中位数是万人;(2)与上年相比,徐州市中考人数增加最多的年份是年;(3)下列选项中,与徐州市2022年中考人数最有可能接近的是;A.12.8万B.14.0万C.15.0万.(4)2019年上半年,徐州市七、八、九三个年级的学生总数约为;A.23.1万B.28.1万C.34.4万.(5)据统计,徐州市2021年某校九年级共1500人,共825人最终被中专院校录取,其余人被普通高中录取,若2022年保持升学率不变,根据前提的结论,该市2022年共有多少人能步入高中殿堂.21.(2021秋•郎溪县期末)为落实国家“双减”政策,七(1)班老师逐步减少学生作业量,学生完成作业时间逐步减少.作业有书面作业和非书面作业两种,据统计,该班级2021年10月平均每天完成作业总时间比9月份减少了25%,其中书面作业减少了30%,非书面作业减少了10%.(1)若9月份平均每天完成作业总时间为2小时40分钟,求10月份平均每天完成作业总时间是多少分钟.(2)设9月份平均每天完成作业总时间为a分钟,书面作业为b分钟.①请用含a或b的代数式表示10月份平均每天完成作业总时间为分钟,10月份平均每天完成书面作业时间为分钟;②求10月份平均每天完成书面作业时间占平均每天完成作业总时间的百分比.22.(2021秋•莱芜区期末)2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:抽取七年级教师的竞赛成绩(单位:分)6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10.七、八年级教师竞赛成绩统计表年级七年级八年级平均数8.58.5中位数8a众数89优秀率b55%根据以上信息,解答下列问题:(1)填空:a=,b=;(2)估计该校七年级80名教师中竞赛成绩达到8分及以上的人数;(3)根据以上数据分析,评价两个年级教师学习党史的竞赛成绩谁更优异.23.(2021秋•鼓楼区期末)近日,“复旦学霸图书馆”新闻引发网友热议,其中,“风雨无阻爱学习”的潘同学一年时间图书馆打卡301次,更是成为众多学子膜拜的对象.某大学图书馆为了更好服务学子,对某周来馆人数进行统计,统计数据如下(单位:人):时间周一周二周三周四周五周六周日人数65055071042065023203100(1)该周到馆人数的平均数为人、众数为人、中位数为人;(2)周一至周五到馆人数相差不多,用这五天的数据估算该周的平均数合适吗?为什么?(3)选择合适的数据,估算该校一个月的到馆人数(一个月按30天计).24.(2021秋•渝北区期末)为普及新冠防疫知识,某校开展了“新冠防疫知识竞赛”,现随机抽取该校八年级九年级各二十名同学的成锁进行调查.满分为10分,6分以下为不及格.八年级二十个同学的得分为:6,10,7,5,5,9,9,10,8,9,10,5,5,9,7,8,9,8,8,10.八、九年级抽取同学成绩统计表年级八年级九年级平均数7.857.5中位数a8众数9b及格率80%85%(1)填空:a=,b=,n=.(2)根据以上数据分析,该校“新冠防疫知识竞赛”中八年级和九年级的新冠防疫知识哪个年级掌握的情况更好?并说明理由.(3)八年级有800人,九年级有600人,请估计该校八、九年级参加“新冠防疫知识竞赛”及格的学生约有多少人?25.(2021秋•玄武区期末)某公司20名销售人员某月销售某种商品的数量如下表(单位:件):月销售量2000700600400300200人数235721(1)月销售量的中位数为件,众数为件;(2)求该公司销售人员月销售量的平均数;(3)假设你是销售部负责人,你认为应怎样制定每位销售人员的月销售量指标?说明理由.26.(2021秋•寻乌县期末)某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中的最小的数,例如,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:(1)①M{(﹣1)2,22,﹣22}=,②min{(﹣1)2,22,﹣22}=.(2)若M{3﹣2x,1+3x,﹣5}=min{2,﹣5,﹣3},求x的值;27.(2021•灌南县校级模拟)为宣传普及新冠肺炎防控知识,引导学生做好防控,某校举行了主题为“防控新冠,从我做起“的线上知识竞赛活动,测试内容为20道判断题,每道题5分,满分100分.为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级各抽取了20名参赛学生的成绩,已知抽取得到的八年级的数据如下(单位:分):80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.为了便于分析数据,统计员对八年级数据进行了整理,得到下表:成绩等级分数(单位:分)学生数D等60<x≤705C等70<x≤80aB等80<x≤90bA等90<x≤1002八、九年级成绩的平均数、中位数、优秀率如下:(分数80分以上、不含80分为优秀)年级平均数中位数优秀率八年级78分c分m%九年级76分82.5分50%(1)根据题目信息填空:a=,c=,m=;(2)八年级王宇和九年级程义的分数都为80分,请判断王宇、程义在各自年级的排名哪位更靠前?请简述你的理由.28.(2021秋•盐都区月考)甲、乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)数与代数空间与图形统计与概率综合与实践学生甲93938990学生乙94929486(1)甲成绩的众数是分,乙成绩的中位数是分;(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按4:3:1:2计算,那么甲、乙的数学综合素质成绩分别为多少分?。
华师大版初中数学八年级下册《第20章 数据的整理与初步处理》单元测试卷(含答案解析

华师大新版八年级下学期《第20章数据的整理与初步处理》单元测试卷一.选择题(共15小题)1.小明测得一周的体温并登记在下表(单位:℃)其中星期四的体温被墨迹污染.根据表中数据,可得此日的体温是()A.36.6℃B.36.7℃C.36.8℃D.37.0℃2.在黑板上从1开始,写出一组相继的正整数,然后擦去一个数,其余数的平均值为35,擦去的数是()A.5B.6C.7D.83.某单位有1名经理、2名主任、2名助理和11名普通职员,他们的月工资各不相同.若该单位员工的月平均工资是1500元,则下列说法中正确的是()A.所有员工的月工资都是1500元B.一定有一名员工的月工资是1500元C.至少有一名员工的月工资高于1500元D.一定有一半员工的月工资高于1500元4.某汽车从甲地以速度v1匀速行驶至乙地后,又从乙地以速度v2匀速返回甲地,则汽车在整个行驶过程中的平均速度为()A.B.C.D.5.已知数据:x1+3,x2+3,x3+3,x4+3的平均数是9,则数据x1,x2,x3,x4的平均数是()A.5B.6C.7D.86.某同学使用计算器计算30个数据的平均数时,错将其中一个数据15输入为150,那么由此求出的平均数与实际相差()A.5B.4.5C.﹣5D.﹣4.57.数学课上,全班同学每人各报一个数.如果男生所报的数之和与女生所报的数之和相等,且男生所报数的平均值是,女生所报数的平均值是,那么全班同学所报数的平均值是()A.B.C.D.8.综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品()A.12件B.8.625件C.8.5件D.9件9.有甲、乙两个箱子,其中甲箱内有98颗球,分别标记号码1~98,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出49颗球放入乙箱后,乙箱内球的号码的中位数为40.若此时甲箱内有a颗球的号码小于40,有b 颗球的号码大于40,则关于a、b之值,下列何者正确?()A.a=16B.a=24C.b=24D.b=3410.某班随机抽取6名同学的一次地生测试成绩如下:82,95,82,76,76,82.数据中的众数和中位数分别是()A.82,76B.76,82C.82,79D.82,8211.漳州中闽百汇某服装专柜在进行市场占有情况的调查时,他们应该最关注已售出服装型号的()A.中位数B.众数C.平均数D.方差12.鞋厂生产不同号码的鞋,其中,生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的()A.平均数B.众数C.中位数D.众数或中位数13.在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是()A.①③B.①④C.②③D.②④14.已知样本x1,x2,x3,…,x n的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2x n+3的方差是()A.1B.2C.3D.415.数据8,10,12,9,11的平均数和方差分别是()A.10和B.10和2C.50和D.50和2二.填空题(共12小题)16.某工厂生产同一型号的电池.现随机抽取了6节电池,测试其连续使用时间(小时)分别为:47,49,50,51,50,53.这6节电池连续使用时间的平均数为小时.17.如果一组数据:2,4,6,x,y的平均数为4.8,那么x,y的平均数为.18.在一次捐款活动中,某班50名同学人人拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的.如图统计图反映了不同捐款数的人数比例,那么该班同学平均每人捐款元.19.已知一组数据1,2,3,…,n(从左往右数,第1个数是1,第2个数是2,第3个数是3,依此类推,第n个数是n).设这组数据的各数之和是s,中位数是k,则s=(用只含有k的代数式表示).20.已知一组数据:0,2,x,4,5的众数是4,那么这组数据的平均数是.21.某校举办“汉字听写大赛”,7名学生进入决赛,他们所得分数互不相同,比赛共设3个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是(填“平均数”、“众数”或“中位数”).22.一组数据:1、﹣1、0、4的方差是.23.学校篮球队五名队员的年龄分别为17,15,17,16,15,其方差为0.8,则三年后这五名队员年龄的方差为.24.用科学记算器求得271,315,263,289,300,277,286,293,297,280的平均数为,标准差为.(精确到0.1)25.五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,则这五个正整数的和为.26.小明同学5次数学单元测试成绩(分数取整数)的平均分是90分,且每次测试都没有低于80分得成绩,中位数是93分,唯一众数是96分,则最低的一次成绩可能是分.27.在一次中学生田径运动会上,参加男子跳高的14名运动员的成绩如下表:这些运动员跳高成绩的中位数是,众数是.三.解答题(共7小题)28.某开发公司现有员工50名,所有员工的月工资情况如下表:请你根据上述内容,解答下列问题:(1)该公司“高级技工”有人;(2)该公司的工资极差是元;(3)小张到这家公司应聘普通工作人员,咨询过程中得到两个答案,你认为用哪个数据向小张介绍员工的月工资实际水平更合理些?(4)去掉最高工资的前五名,再去掉最低工资的后五名,然后算一算余下的40人的平均工资,说说你的看法.29.荆州古城是闻名遐迩的历史文化名城,下表图是荆州古城某历史景点一周的抽样统计参观人数和门票价格.(1)把上表中一周的参观人数作为一个样本,直接指出这个样本的中位数,众数和平均数,分析表中数据还可得到一些信息,如双休日参观人数远远高于平时等,请你尝试再写出两条相关信息;(2)若“五•一”黄金周有甲,乙两个旅行团到该景点参观,两团人数之和恰为上述样本数据的中位数,乙团不超过50人,设两团分别购票共付W元,甲团人数x人,①求W与x的函数关系式;②若甲团人数不超过100人,请说明两团合起来购票比分开购票最多可节约多少元?30.某私立中学准备招聘教职员工60名,所有员工的月工资情况如下:请根据上表提供的信息,回答下列问题:(1)如果学校准备招聘“高级教师”和“中级教师”共40名(其他员工人数不变),其中高级教师至少要招聘13人,而且学校对高级、中级教师的月支付工资不超过83000元,按学校要求,对高级、中级教师有几种招聘方案?(2)(1)中的哪种方案对学校所支付的月工资最少?并说明理由;(3)在学校所支付的月工资最少时,将上表补充完整,并求所有员工月工资的中位数和众数.31.一个公司的所有员工的月收入情况如下:(1)该公司所有员工月收入的平均数是元,中位数是元,众数是元.(2)你觉得用以上三个数据中的哪一个来描述该公司员工的月收入水平更为恰当?说明理由.(3)某天,一个员工辞职了,若其他员工的月收入不变,但平均收入下降了,你认为辞职的可能是哪个岗位上的员工?说明理由.32.小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”,可奶奶经营不善,经常有品种的牛奶滞销(没卖完)或脱销(量不够),造成了浪费或亏损,细心的小红结合所学的统计知识帮奶奶统计了一个星期牛奶的销售情况,并绘制了下表:(1)计算各品种牛奶的日平均销售量:金键学生奶,金键酸牛奶,金键原味奶;根据计算结果分析,你认为哪种牛奶销量最高;(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定.金键学生奶,金键酸牛奶,金键原味奶;(3)根据计算结果分析,你认为哪种牛奶销量最稳定.33.我市今年体育中考于5月18日开始,考试前,九(2)班的王茜和夏洁两位同学进行了8次50m短跑训练测试,她们的成绩分别如下:(单位:秒)(1)王茜和夏洁这8次训练的平均成绩分别是多少?(2)按规定,女同学50m短跑达到8.3秒就可得到该项目满分15分,如果按她们目前的水平参加考试,你认为王茜和夏洁在该项目上谁得15分的可能性更大些?请说明理由.34.某校七年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分多少排列名次,在规定的时间内每人踢100个以上(含100)为优秀.下表是甲班和乙班成绩最好的5名学生的比赛数据(单位:个)统计发现两班总分相等,S,此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:(1)计算两班的优秀率;(2)求两班比赛数据的中位数;(3)根椐以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.华师大新版八年级下学期《第20章数据的整理与初步处理》单元测试卷参考答案与试题解析一.选择题(共15小题)1.小明测得一周的体温并登记在下表(单位:℃)其中星期四的体温被墨迹污染.根据表中数据,可得此日的体温是()A.36.6℃B.36.7℃C.36.8℃D.37.0℃【分析】设星期四的体温是x℃,根据平均数的概念列出方程求解.【解答】解:设星期四的体温是x℃,依题意可得:(36.6+36.7+37.0+37.3+x+36.9+37.1)÷7=36.9,解得,x=36.7(℃).故选:B.【点评】本题考查了平均数的概念和一元一次方程的解法.熟记公式:是解决本题的关键.2.在黑板上从1开始,写出一组相继的正整数,然后擦去一个数,其余数的平均值为35,擦去的数是()A.5B.6C.7D.8【分析】设n个数,因为其余数的平均值为35,所以n﹣1是17的倍数,确定n个数的取值范围,计算求解.【解答】解:设一共有n个数,∵擦去一个其余数的平均值为35,∴n﹣1是17的倍数,即17个,34个,51个,68个,85个等,显然只有68个时所得平均数与35相差无几,∴n=69,则1+2+…+69==2415,那么n﹣1=68,则其他数的和是68×35=2408,∵2415﹣2408=7,∴擦去的数是7.故选:C.【点评】本题考查了平均数的综合运用,正确运用分类讨论的思想是解答本题的关键.3.某单位有1名经理、2名主任、2名助理和11名普通职员,他们的月工资各不相同.若该单位员工的月平均工资是1500元,则下列说法中正确的是()A.所有员工的月工资都是1500元B.一定有一名员工的月工资是1500元C.至少有一名员工的月工资高于1500元D.一定有一半员工的月工资高于1500元【分析】算术平均数:对于n个数x1,x2,…,x n,则x¯=(x1+x2+…+x n)就叫做这n个数的算术平均数,依此即可作出选择.【解答】解:∵某单位有1名经理、2名主任、2名助理和11名普通职员,普通职员的人数占多数,该单位员工的月平均工资是1500元,∴至少有一名员工的月工资高于1500元是正确的.故选:C.【点评】考查了算术平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.4.某汽车从甲地以速度v1匀速行驶至乙地后,又从乙地以速度v2匀速返回甲地,则汽车在整个行驶过程中的平均速度为()A.B.C.D.【分析】由题意知,设两地距离为S,从甲地行驶至乙地的时间为T1,从乙地返回甲地的时间为T2,则关键时间的计算公式求得T1及T2,再关键平均速度的计算公式即可求得平均速度.【解答】解:设两地距离为S,从甲地行驶至乙地的时间为T1,从乙地返回甲地的时间为T2,则有T1=,T2=;∴平均速度===;故选:D.【点评】本题考查了平均数实际中的运用.平均速度=总路程÷总时间.5.已知数据:x1+3,x2+3,x3+3,x4+3的平均数是9,则数据x1,x2,x3,x4的平均数是()A.5B.6C.7D.8【分析】根据平均数的计算公式即可求解.先求出数据x1+3,x2+3,x3+3,x4+3的和,然后利用平均数的计算公式表示数据x1,x2,x3,x4的平均数,经过代数式的变形可得答案.【解答】解:∵x1+3,x2+3,x3+3,x4+3的平均数是9.∴x1+3,x2+3,x3+3,x4+3的和是4×9=36.∴x1,x2,x3,x4的平均数是:(x1+x2+x3+x4)=[(x1+3)+(x2+3)+(x3+3)+(x4+3)﹣3×4]=(36﹣12)=×24=6.故选:B.【点评】本题主要考查了平均数的计算.正确理解公式是解题的关键,在计算中正确使用整体代入的思想.6.某同学使用计算器计算30个数据的平均数时,错将其中一个数据15输入为150,那么由此求出的平均数与实际相差()A.5B.4.5C.﹣5D.﹣4.5【分析】因为错将其中一个数据15输入为150,可求出多加了的数,进而即可求出答案.【解答】解:由题意知,错将其中一个数据15输入为150,则多加了150﹣15=9135,所以平均数多了135÷30=4.5.故选:B.【点评】本题考查了平均数的概念.平均数是指在一组数据中所有数据之和再除以数据的个数.平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标.7.数学课上,全班同学每人各报一个数.如果男生所报的数之和与女生所报的数之和相等,且男生所报数的平均值是,女生所报数的平均值是,那么全班同学所报数的平均值是()A.B.C.D.【分析】可设男生人数为x人,根据平均数公式即可求出男生所报的数之和为x;由于男生所报的数之和与女生所报的数之和相等,则女生人数可求,再根据平均数公式即可求出全班同学所报数的平均值.【解答】解:设男生人数为x人,则女生人数为:x÷()=x.全班同学所报数的平均值为:x×2÷(x+x)=.故选:C.【点评】本题考查了平均数的求法.解题关键是先设男生人数为x人,再用x表示女生人数,从而得出全班同学的人数.8.综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品()A.12件B.8.625件C.8.5件D.9件【分析】根据加权平均数的计算方法,用作品的总件数除以总人数,计算即可得解.【解答】解:==8.625(件).故选:B.【点评】本题考查了加权平均数的计算,要注意作品件数相应的权重.9.有甲、乙两个箱子,其中甲箱内有98颗球,分别标记号码1~98,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出49颗球放入乙箱后,乙箱内球的号码的中位数为40.若此时甲箱内有a颗球的号码小于40,有b 颗球的号码大于40,则关于a、b之值,下列何者正确?()A.a=16B.a=24C.b=24D.b=34【分析】先求出甲箱的球数,再根据乙箱中位数40,得出乙箱中小于、大于40的球数,从而得出甲箱中小于40的球数和大于40的球数,即可求出答案.【解答】解:甲箱98﹣49=49(颗),∵乙箱中位数40,∴小于、大于40各有(49﹣1)÷2=24(颗),∴甲箱中小于40的球有39﹣24=15(颗),大于40的有49﹣15=34(颗),即a=15,b=34.故选:D.【点评】此题考查了中位数,掌握中位数的定义是本题的关键,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.10.某班随机抽取6名同学的一次地生测试成绩如下:82,95,82,76,76,82.数据中的众数和中位数分别是()A.82,76B.76,82C.82,79D.82,82【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.【解答】解:在这一组数据中82是出现次数最多的,故众数是82;而将这组数据从小到大的顺序排列(76,76,82,82,82,95),处于中间位置的两个数的平均数是,那么由中位数的定义可知,这组数据的中位数是82.故选:D.【点评】此题考查了中位数、众数的意义,解题的关键是正确理解各概念的含义.11.漳州中闽百汇某服装专柜在进行市场占有情况的调查时,他们应该最关注已售出服装型号的()A.中位数B.众数C.平均数D.方差【分析】们应该最关注的是哪种服装售出的最多,因而最关心的是众数.【解答】解:漳州中闽百汇某服装专柜在进行市场占有情况的调查时,他们应该最关注的是哪种服装售出的最多,因而最关心的是众数.故选:B.【点评】此题主要考查统计的有关知识,主要包括平均数、中位数、众数的意义.反映数据集中程度的统计量有平均数、中位数、众数等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.12.鞋厂生产不同号码的鞋,其中,生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的()A.平均数B.众数C.中位数D.众数或中位数【分析】根据众数也是数据的一种代表数,反映了一组数据的集中程度,众数可作为描述一组数据集中趋势的量进行解答即可.【解答】解:生产数量最多的鞋号是调查不同年龄的人的鞋号所构成的数据的众数.故选:B.【点评】本题考查统计量的选择,关键是根据众数就是出现次数最多的数,反映了一组数据的集中程度.13.在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是()A.①③B.①④C.②③D.②④【分析】从折线图中得出甲乙的射击成绩,再利用方差的公式计算,即可得出答案.【解答】解:由图中知,甲的成绩为7,7,8,9,8,9,10,9,9,9,乙的成绩为8,9,7,8,10,7,9,10,7,10,甲=(7+7+8+9+8+9+10+9+9+9)÷10=8.5,乙=(8+9+7+8+10+7+9+10+7+10)÷10=8.5,甲的方差S甲2=[2×(7﹣8.5)2+2×(8﹣8.5)2+(10﹣8.5)2+5×(9﹣8.5)2]÷10=0.85,乙的方差S乙2=[3×(7﹣8.5)2+2×(8﹣8.5)2+2×(9﹣8.5)2+3×(10﹣8.5)2]÷10=1.45∴S2甲<S2乙,∴甲的射击成绩比乙稳定;故选:C.【点评】本题考查方差的定义与意义:一般地设n个数据,x1,x2,…x n的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(x n﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.14.已知样本x1,x2,x3,…,x n的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2x n+3的方差是()A.1B.2C.3D.4【分析】根据方差的意义分析,数据都加3,方差不变,原数据都乘2,则方差是原来的4倍.【解答】解:设样本x1,x2,x3,…,x n的平均数为m,则其方差为S12=[(x1﹣m)2+(x2﹣m)2+…+(x n﹣m)2]=1,则样本2x1+3,2x2+3,2x3+3,…,2x n+3的平均数为2m+3,其方差为S22=4S12=4.故选:D.【点评】本题考查方差的计算公式及其运用:一般地设有n个数据,x1,x2,…x n,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.15.数据8,10,12,9,11的平均数和方差分别是()A.10和B.10和2C.50和D.50和2【分析】应用平均数计算公式和方差的计算公式求平均数和方差.【解答】解:平均数=(8+10+12+9+11)=10,方差是S2=[(8﹣10)2+(10﹣10)2+(12﹣10)2+(9﹣10)2+(11﹣10)2]=×10=2.故选:B.【点评】正确理解平均数和方差的概念.掌握求平均数和方差的公式,是解决本题的关键.二.填空题(共12小题)16.某工厂生产同一型号的电池.现随机抽取了6节电池,测试其连续使用时间(小时)分别为:47,49,50,51,50,53.这6节电池连续使用时间的平均数为50小时.【分析】只要运用求平均数公式:即可求出,为简单题.【解答】解:本组数据分别为:47,49,50,51,50,53,故平均数==50(小时).故答案为50.【点评】本题考查的是样本平均数的求法.熟记公式是解决本题的关键.17.如果一组数据:2,4,6,x,y的平均数为4.8,那么x,y的平均数为6.【分析】首先运用求平均数公式:得出x与y的和,再运用此公式求出x,y的平均数.【解答】解:由题意知,(2+4+6+x+y)=4.8,∴x+y=24﹣2﹣4﹣6=12,∴x,y的平均数=×12=6.故答案为6.【点评】本题考查的是样本平均数的求法.熟记公式是解决本题的关键.18.在一次捐款活动中,某班50名同学人人拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的.如图统计图反映了不同捐款数的人数比例,那么该班同学平均每人捐款31.2元.【分析】根据扇形统计图的定义,各部分占总体的百分比之和为1,用捐的具体钱数乘以所占的百分比,再相加,即可得该班同学平均每人捐款数.【解答】解:该班同学平均每人捐款:100×12%+50×16%+20×44%+10×20%+5×8%=31.2元.故答案为:31.2.【点评】本题主要考查扇形统计图的定义.统计的思想就是用样本的信息来估计总体的信息,本题体现了统计思想,考查了用样本估计总体.19.已知一组数据1,2,3,…,n(从左往右数,第1个数是1,第2个数是2,第3个数是3,依此类推,第n个数是n).设这组数据的各数之和是s,中位数是k,则s=2k2﹣k(用只含有k的代数式表示).【分析】由于已知一组数据1,2,3,…,n(从左往右数,第1个数是1,第2个数是2,第3个数是3,依此类推,第n个数是n),所以这组数据的中位数与平均数相等,即可求出这组数据的各数之和s的值.【解答】解:∵一组数据1,2,3,…,n(从左往右数,第1个数是1,第2个数是2,第3个数是3,依此类推,第n个数是n),∴这组数据的中位数与平均数相等,∵这组数据的各数之和是s,中位数是k,∴s=nk.∵=k,∴n=2k﹣1,∴s=nk=(2k﹣1)k=2k2﹣k,故答案为:2k2﹣k.【点评】本题考查了中位数与平均数的定义,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是所有数据的和除以数据的个数.20.已知一组数据:0,2,x,4,5的众数是4,那么这组数据的平均数是3.【分析】先根据众数的定义求出x的值,再根据平均数的计算公式列式计算即可.【解答】解:∵0,2,x,4,5的众数是4,∴x=4,∴这组数据的平均数是(0+2+4+4+5)÷5=3;故答案为:3;【点评】此题考查了众数和平均数,根据众数的定义求出x的值是本题的关键,众数是一组数据中出现次数最多的数.21.某校举办“汉字听写大赛”,7名学生进入决赛,他们所得分数互不相同,比赛共设3个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数(填“平均数”、“众数”或“中位数”).【分析】由于比赛设置了3个获奖名额,共有7名选手参加,故应根据中位数的意义分析.【解答】解:因为3位获奖者的分数肯定是7名参赛选手中最高的,而且7个不同的分数按从小到大排序后,中位数及中位数之后的共有3个数,故只要知道自己的分数和中位数就可以知道是否获奖了.故答案为:中位数.【点评】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数、方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.22.一组数据:1、﹣1、0、4的方差是.【分析】先求出该组数据的平均数,再根据方差公式求出其方差.【解答】解:∵=(1﹣1+0+4)=1,∴S2=[(1﹣1)2+(1+1)2+(0﹣1)2+(4﹣1)2]=(4+1+9)=,故答案为.【点评】本题考查方差的定义与意义:一般地设n个数据,x1,x2,…x n的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(x n﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.23.学校篮球队五名队员的年龄分别为17,15,17,16,15,其方差为0.8,则三年后这五名队员年龄的方差为0.8.【分析】方差是用来衡量一组数据波动大小的量,每个数都加了3所以波动不会变,方差不变.【解答】解:由题意知,原来的平均年龄为,每位同学的年龄三年后都变大了3岁,则平均年龄变为+3,则每个人的年龄相当于加了3岁,原来的方差s12=[(x1﹣)2+(x2﹣)2+…+(x n﹣)2]=0.8,现在的方差s22=[(x1+3﹣﹣3)2+(x2+3﹣﹣3)2+…+(x n+3﹣﹣3)2]=[(x1﹣)2+(x2﹣)2+…+(x n﹣)2]=0.8,方差不变.故填0.8.【点评】本题说明了当数据都加上一个数(或减去一个数)时,方差不变,即数据的波动情况不变.24.用科学记算器求得271,315,263,289,300,277,286,293,297,280的平均数为287.1,标准差为14.4.(精确到0.1)【分析】根据平均数、标准差的概念计算.方差S2=[(x1﹣)2+(x2﹣)2+…+(x n﹣)2],标准差是方差的算术平方根.【解答】解:由题意知,数据的平均数=(271+315+263+289+300+277+286+293+297+280)=287.1方差S2=[(271﹣287.1)2+(315﹣287.1)2+(263﹣287.1)2+(289﹣287.1)2+(300﹣287.1)2+(277﹣287.1)2+(286﹣287.1)2+(293﹣287.1)2+(297﹣287.1)2+(280﹣287.1)2]=207.4标准差为≈14.4.故填287.1,14.4.【点评】本题考查了平均数,方差和标准差的概念.标准差是方差的算术平方根.25.五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,则这五个正整数的和为17或18或19.【分析】将五个正整数从小到大重新排列后,有5个数,中位数一定也是数组中的数,根据中位数与众数就可以确定数组中的后三个数.而另外两个不相等且是正整数,就可以确定这两个数,进而得到这五个数.【解答】解:将五个正整数从小到大重新排列后,最中间的那个数是这组数据的中位数,即4;唯一的众数是5,最多出现两次,即第四、五两个数都是5.第一二两个数不能相等,可以为1与2或1与3或2与3;则这五个正整数的和为17或18或19.【点评】本题考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数。
华师大版数学数据的整理与初步处理单元测试题及试卷答案下载

华师大版数学《数据的整理与初步处理》单元测试题及试卷答案免费下载一、选择题1、频率分布反映了()A、样本数据的多少B、样本数据的平均水平C、样本数据的离散程度D、样本数据在各个小范围所占比例的大小2、袋中有5个绿球,有个白球,从中任意取一个球,恰为白球的机会为2/3,则为()A、16B、10C、20D、183、在统计中,样本的方差可以近似反映总体的()A、平均状态B、波动大小C、分布规律D、最大值、最小值4、口袋中有1个黄球,2个黑球,搅匀后从中摸出一个球,你认为下列说法中不正确的是()A、摸出的不是黄球就是黑球B、摸出黄球和黑球的机会均等C、摸出黄球的机会比摸出黑球的机会小D、若给小球编号,就可以说摸出黄球,摸出黑1球,黑2球,这三个事件是等可能的5、从总体中抽取一个样本,计算出样本方差为2,可以估计总体方差()A、一定大于2B、约等于2C、一定小于2D、与样本方差无关6、甲、乙两同学在一次考试中学科平均分相等,但他们的方差不相等,正确评价他们的学习情况的是()一、选择题1、频率分布反映了()A、样本数据的多少B、样本数据的平均水平C、样本数据的离散程度D、样本数据在各个小范围所占比例的大小2、袋中有5个绿球,有个白球,从中任意取一个球,恰为白球的机会为2/3,则为()A、16B、10C、20D、183、在统计中,样本的方差可以近似反映总体的()A、平均状态B、波动大小C、分布规律D、最大值、最小值4、口袋中有1个黄球,2个黑球,搅匀后从中摸出一个球,你认为下列说法中不正确的是()A、摸出的不是黄球就是黑球B、摸出黄球和黑球的机会均等C、摸出黄球的机会比摸出黑球的机会小D、若给小球编号,就可以说摸出黄球,摸出黑1球,黑2球,这三个事件是等可能的5、从总体中抽取一个样本,计算出样本方差为2,可以估计总体方差()A、一定大于2B、约等于2C、一定小于2D、与样本方差无关6、甲、乙两同学在一次考试中学科平均分相等,但他们的方差不相等,正确评价他们的学习情况的是()一、选择题1、频率分布反映了()A、样本数据的多少B、样本数据的平均水平C、样本数据的离散程度D、样本数据在各个小范围所占比例的大小2、袋中有5个绿球,有个白球,从中任意取一个球,恰为白球的机会为2/3,则为()A、16B、10C、20D、183、在统计中,样本的方差可以近似反映总体的()A、平均状态B、波动大小C、分布规律D、最大值、最小值4、口袋中有1个黄球,2个黑球,搅匀后从中摸出一个球,你认为下列说法中不正确的是()A、摸出的不是黄球就是黑球B、摸出黄球和黑球的机会均等C、摸出黄球的机会比摸出黑球的机会小D、若给小球编号,就可以说摸出黄球,摸出黑1球,黑2球,这三个事件是等可能的5、从总体中抽取一个样本,计算出样本方差为2,可以估计总体方差()A、一定大于2B、约等于2C、一定小于2D、与样本方差无关6、甲、乙两同学在一次考试中学科平均分相等,但他们的方差不相等,正确评价他们的学习情况的是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华东师大版八年级下《数据的整理与初步处
理》A卷
一、选择题(每题4分,共16分)
1.对某班50名学生作一次调查,得到下表
喜欢的体育项目足球篮球乒乓球羽毛球
人数30 25 40 20 若想表示上述数据,可选用()
A.扇形统计图
B.频数直方图 C折线统计图 D.以上三种均可以
2.下图刻画了小李、小王、小张、小刘、小扬五位同学每个月的平均花费情况.
则下列说法错误的是()
A.小张的每月花费大约是小王的20%,大约是小扬的33.3%
B.小刘的每月花费占这五位同学每月总花费的35%
C.这五位同学每月花费钱数之比依次是4:5:1:7:3
D.小王的每月花费是另外四位同学每月总花费的1/4
3.一枚图钉抛掷后落地时针尖朝上的概率是3/5,一枚骰子各面上标有l~6六个数字,同时抛出一枚骰子和一枚图钉,得到偶数与针尖着地的概率是()
A. 1/5
B. 2/5
C. 3/5
D.不确定
4.超市里有甲、乙、丙、丁四种牌子的酱油,标准质量都是500克,从中各抽出5袋测的质量如下,根据下列数据(单位:克)判断,质量稳定的是() A 甲:501 500 506 510 509 B 乙:493 494 511 494 508
C 丙:503 504 499 501 500
D 丁:497 502 495 507 501
二、填空题(每空2分,共20分)
5.小明任意抛一枚硬币,连续掷了三次,每次都朝上的概率是
6.暗箱内放有大小、形状、质地相同的4个球,分别标上1、2、3、4四个号码,有放回的连续摸两次,都大于2的概率是,都是奇数的概率是第一次是奇数第二次是偶数的概率是
7.2001年某中学少年队员的“小主人文具店”开业后第一季度的收人与支出情况
如下图:
根据统计图填空:
月份的收入最多,
是元;月份的支出最多,是元;第一
季度盈利大约
8.甲、乙两名跳水运动员在三米跳板跳水中平均分都是9.5分,甲的方差为0.62,乙的方差为0.45,则的成绩稳定。
三、简答题(第9题4分,其余每题8分,共36分)
9.到医院看病注射青霉素药水,医生都要给你做皮试,极少数人对青霉素药水过敏,大约也就是一千个人里有一个,即发生过敏的概率大约是0.1%,医生为什么一定要这么做呢?
10.下面的频数直方图表示的是一所菜园农场种植的几种作物的面积.你能根据这
幅图,绘制扇形统计图吗?如果能
请画出扇形统计图;如果不能,请
说明理由.
11.下表列出了中国、美国、印度、澳大利亚1996年的国土面积和国家级保护区的
面积情况:
中国美国印度澳大利亚
国土面积/万平方千米960.0 936.4 328.8 774.1
国家级保护区/千平方千米598.1 1226.7 142.9 563.9
根据以上数据绘制统计图,并说说你从图中得到了哪些信息?。
