第4章 随机变量的数字特征4.2 方差
合集下载
概率论方差
第四章数字特征4.1 数学期望4.2 方差4.3 协方差与相关系数4.4 矩与协方差矩阵()()22()Var X E XE X =−⎡⎤⎣⎦证明:()Var X =()()222E X XE X EX ⎡⎤=−+⎣⎦()()222[()][]E XE EX X E EX =−+()()()()()222c E X E X E X E X E X ==−+⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦代回()()E X E X c==为常数设)()(222c E cX E EX +−()()(),E cX cE X E c c ==⎡⎤⎣⎦()()222E XcE X c =−+()()22.E X E X =−⎡⎤⎣⎦()()()2222E X E X E X =−+⎡⎤⎡⎤⎣⎦⎣⎦()0Var X ≥()()22.E XE X ∴≥⎡⎤⎣⎦注：由知：()2E X EX ⎡⎤−⎣⎦()()22().Var X E XE X ∴=−⎡⎤⎣⎦（方差的简算公式）x y=1x= 0594.()()().E XY E X E Y =⋅随机变量X 与Y 相互独立，则(与数学期望对比来学习)n X X Y X ,,,,1⋯设为随机变量，c 为常数。
().0=c Var 性质1性质2 性质3,()()()2cov(,)X Y Var X Y Var X Var Y X Y ±=+±对于任意、有如果记:()()()EY Y EX X E Y X −−=),cov(的协方差与为称Y X Y X ),cov(().c c E =性质1 ()().E kX c kE X c +=+性质2(),,X Y E X Y EX EY∀+=+有性质3性质4()).()(Y Var X Var Y X Var +=+性质44.2.2 方差的性质随机变量X 与Y 相互独立,则()2+().Var kX c k Var X =().0=c Var 性质1()2+().Var kX c k Var X =性质2 证明:()Var c =0Ec c==()2E c Ec −()Var kX c +=证明:[]2()kX k E c c X E E +−−[]{}22()E k X E X =−2().k Var X =[]2()E c k kX X E c =+−−()2kX c kX E c E −=⎡⎤⎣⎦++[]2()E k X E k X =−证明:=+)(,Y X Var Y X 有和对于任意()(){}{}2E X EY X E Y =+⎡⎤⎡⎣−⎤⎦⎣⎦−()()()(){}222E X E X Y E Y X E X Y E Y =−+−+−−⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦()()()()222E X E X E Y E Y E X E X X E X =−+−+−−⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦),cov(2)()(Y X Y Var X Var ++=(同理可得到减法的公式)记:()()()()cov(,)X Y E X E X Y E Y ⎡⎤=−−⎣⎦，的协方差与为称Y X Y X ),cov(性质3),cov(2)()()(,Y X Y Var X Var Y X Var Y X ±+=±有和对于任意{}2([()])E E Y X X Y −++。
概率论与数理统计复习4-5章
+∞
∑ g ( x ) p 绝对收敛,则Y的期望为 ∞
k =1 k k
∑ g(x
k =1
k
) pk
(2) 设X是连续型随机变量,概率密度为 f ( x) , 如果积分 ∫−∞ g ( x) f ( x)dx 绝对收敛,则Y的期望为
E (Y ) = E[ g ( X )] = ∫ g ( x ) f ( x )dx
例 设X的概率分布律为
X −1
0 12
1
2
p 1 3 1 6 1 6 1 12 1 4
试求Y=－X+1及 Z = X 2 的期望和方差。 X －1 0 1/2 解 由于 P 1/3 1/6 1/6 Y =－X+1 2 1 1/2 Z = X2 1 0 1/4
1 1 1 1 1 1 2 E (Y ) = ( −1) ⋅ + 0 ⋅ + ⋅ + 1⋅ + 2 ⋅ = 4 12 2 6 6 3 3
2 2
D( Z ) = E ( Z 2 ) + [ E ( Z )]2 = 2.23264
1 + x − 1 < x < 0 例 设随机变量X的概率密度为 f ( x ) = 1 − x 0 ≤ x < 1 1)求D(X）, 2)求 D ( X 2 )
解 (1) E ( X ) = ∫ x(1 + x)dx + ∫ x(1 − x)dx
第四章 随机变量的数字特征
离散型随机变量的数学期望 连续型随机变量的数学期望 数学期望的性质及随机变量函数的期望 方差及其性质
4.1数学期望 数学期望
数学期望——描述随机变量取值的平均特征 数学期望——描述随机变量取值的平均特征 一、离散型随机变量的数学期望 定义 设离散型随机变量X的概率分布为
∑ g ( x ) p 绝对收敛,则Y的期望为 ∞
k =1 k k
∑ g(x
k =1
k
) pk
(2) 设X是连续型随机变量,概率密度为 f ( x) , 如果积分 ∫−∞ g ( x) f ( x)dx 绝对收敛,则Y的期望为
E (Y ) = E[ g ( X )] = ∫ g ( x ) f ( x )dx
例 设X的概率分布律为
X −1
0 12
1
2
p 1 3 1 6 1 6 1 12 1 4
试求Y=－X+1及 Z = X 2 的期望和方差。 X －1 0 1/2 解 由于 P 1/3 1/6 1/6 Y =－X+1 2 1 1/2 Z = X2 1 0 1/4
1 1 1 1 1 1 2 E (Y ) = ( −1) ⋅ + 0 ⋅ + ⋅ + 1⋅ + 2 ⋅ = 4 12 2 6 6 3 3
2 2
D( Z ) = E ( Z 2 ) + [ E ( Z )]2 = 2.23264
1 + x − 1 < x < 0 例 设随机变量X的概率密度为 f ( x ) = 1 − x 0 ≤ x < 1 1)求D(X）, 2)求 D ( X 2 )
解 (1) E ( X ) = ∫ x(1 + x)dx + ∫ x(1 − x)dx
第四章 随机变量的数字特征
离散型随机变量的数学期望 连续型随机变量的数学期望 数学期望的性质及随机变量函数的期望 方差及其性质
4.1数学期望 数学期望
数学期望——描述随机变量取值的平均特征 数学期望——描述随机变量取值的平均特征 一、离散型随机变量的数学期望 定义 设离散型随机变量X的概率分布为
概率论与数理统计第四章
)
(
)
(
)
,
(
Y
D
X
Dபைடு நூலகம்
Y
X
Cov
xy
=
r
=4[E(WV)]2-4E(W2)×E(V2)≤0
01
得到[E(WV)]2≤E(W2)×E(V2). →(8)式得到证明.
02
设W=X-E(X),V=Y-E(Y),那么
03
其判别式
由(9)式知, |ρ xy|=1 等价于 [E(WV)]2=E(W2)E(V2). 即 g(t)= E[tW-V)2] =t2E(W2)-2tE(WV)+E(V2) =0 (10) 由于 E[X-E(X)]=E(x)-E(X) =0, E[Y-E(Y)]=E(Y)-E(Y) =0.故 E(tW-V)=tE(W)-E(V)=tE[X-E(X)]-E[Y-E(Y)]=0 所以 D(tW-V)=E{[tW-V-E(tW-V)]2}=E[(tW-V)2]=0 (11) 由于数学期望为0,方差也为0,即(11)式成立的充分必要条件是 P{tW-V=0}=1
随机变量X的数学期望是随机变量的平均数.它是将随机变量 x及它所取的数和相应频率的乘积和.
=
(1)
)
2
3
(
)
(
-
=
ò
µ
µ
-
dx
x
x
E
j
x
可见均匀分布的数学期望为区间的中值.
例2 计算在区间[a,b]上服从均匀分布的随机变量 的数学期望
泊松分布的数学期望和方差都等于参数λ.
其他
02
f(x)=
01
（4-6）
03
（4）指数分布
概率论与数理统计第4章 随机变量的数字特征与极限定理
4.2.1 随机变量方差的概念 数学期望是随机变量重要的数字特征．但是，在 刻画随机变量的性质时，仅有数学期望是不够的．例如， 有两批钢筋，每批各10根，它们的抗拉强度指数如下：
25
定义4.3 设X是随机变量，若E［X－E（X）］2存 在，则称它为X的方差，记为D（X），即
由定义4.2，随机变量X的方差反映了X的可能取值 与其数学期望的平均偏离程度．若D（X）较小，则X的 取值比较集中，否则，X的取值比较分散．因此，方差 D（X）是刻画X取值离散程度的一个量．
3
定义4.1 设离散型随机变量X的分布律为
4
5
6
7
8
9
4.1.2 几个常用分布的数学期望 1.0—1分布 设随机变量X服从以p为参数的（0—1）分布，则X 的数学期望为
２.二项分布 设随机变量X～B（n,p），则X的数学期望为
10
3.泊松分布 设随机变量X～P（λ）分布，则X的数学期望为
41
Hale Waihona Puke 424.３ 协方差、相关系数及矩
4.3.1 协方差 对于二维随机变量（X，Y），除了分量X，Y的数 字特征外，还需要找出能体现各分量之间的联系的数字 特征．
43
44
4.3.2 相关系数 定义4.5 设（X,Y）为二维随机变量，cov （X,Y）,D（X）,D（X）均存在，且D（X）>0,D（X） >0，称
15
16
17
定理4.2 设（X,Y）是二维随机变量，z=g（x,y） 是一个连续函数． （1）如果（X,Y）为离散型随机变量，其联合分布 律为
18
19
20
4.1.4 数学期望的性质 数学期望有如下常用性质（以下的讨论中，假设所 遇到的数学期望均存在）：
25
定义4.3 设X是随机变量，若E［X－E（X）］2存 在，则称它为X的方差，记为D（X），即
由定义4.2，随机变量X的方差反映了X的可能取值 与其数学期望的平均偏离程度．若D（X）较小，则X的 取值比较集中，否则，X的取值比较分散．因此，方差 D（X）是刻画X取值离散程度的一个量．
3
定义4.1 设离散型随机变量X的分布律为
4
5
6
7
8
9
4.1.2 几个常用分布的数学期望 1.0—1分布 设随机变量X服从以p为参数的（0—1）分布，则X 的数学期望为
２.二项分布 设随机变量X～B（n,p），则X的数学期望为
10
3.泊松分布 设随机变量X～P（λ）分布，则X的数学期望为
41
Hale Waihona Puke 424.３ 协方差、相关系数及矩
4.3.1 协方差 对于二维随机变量（X，Y），除了分量X，Y的数 字特征外，还需要找出能体现各分量之间的联系的数字 特征．
43
44
4.3.2 相关系数 定义4.5 设（X,Y）为二维随机变量，cov （X,Y）,D（X）,D（X）均存在，且D（X）>0,D（X） >0，称
15
16
17
定理4.2 设（X,Y）是二维随机变量，z=g（x,y） 是一个连续函数． （1）如果（X,Y）为离散型随机变量，其联合分布 律为
18
19
20
4.1.4 数学期望的性质 数学期望有如下常用性质（以下的讨论中，假设所 遇到的数学期望均存在）：
应用概率统计
0
3
E( X EX )2 E( X )2
(x
)2
f
( x)dx
2
2
(x )2 1 dx 2
0
2
12
返回
例8 设国际市场每年对我国某种商品的需求量
为随机变量X(单位:吨),它服从[2000,4000]上的均匀分布,已 知该商品每售出1吨获利3万美元,若销售不出去,每吨将损 失各种费用1万美元,问如何组织货源可使收益最大?
(1)若X为离散型,P(X=xn)=pn,n=1,2,...,则 E(g(X )) g(xn ) pn
n
(2)若X为连续型随机变量,X~f(x),则E(
g(
X
))
g(
x
)
f
(
x
)dx
例如 则
X -1 0 1 2
P 0.2 0.1 0.4 0.3
EX 2 xn2 pn
n
(1)2 0.2 02 0.1 12 0.4 22 0.3 1.8
ex
f (x)
0
x0 x0
所以,
EX=
xf ( x )dx
xexdx xd( ex )
0
0
xex
0
exdx
0
lim
x
x ex
1
exdx
0
lim
x
1
ex
1
exdx
0
1
类似计算可得: 若X~N(μ,σ2), 则EX= μ.
返回
计算可得
X~U[a,b] X~E(λ)
解 设Y表示产值,Y取值为0,10,30,40,
P(Y=0)= P(X<500)
概率论与数理统计 第4章 随机变量的数字特征
解：
1 (5 0.5x)( 3 x2 x)dx
0
2
4.65(元)
2021/7/22
21
4.1.2 随机变量函数的数学期望
将定理4.1推广到二维随机变量的情形．
定理4.2 设Z是随机变量X，Y的函数Z = g(X，Y)， g是连续函数．
(1) 若(X，Y)是二维离散型随机变量，其分布律
为P{X xi ,Y yj } pij, i, j 1,2,, 则有
解：由于 P{ X k} k e ，k = 0，1，2，…，
k!
因而
E( X ) kP{ X k} k k e
k0
k0 k!
k e
k1 (k 1)!
e
k 1
k1 (k 1)!
e k ee k0 k!
2021/7/22
12
4.1.1 数学期望的概念
2. 连续型随机变量的数学期望
2021/7/22
18
4.1.2 随机变量函数的数学期望
定理4.1 设Y为随机变量X的函数:Y = g(X) (g是连续
函数).
(1) 设X是离散型随机变量，其分布律为
P{X xk } pk , k 1,2,
若级数 g( xk ) pk绝对收敛,则 E(Y ) E[g( X )] g( xk ) pk
f ( x) 25( x 4.2)， 4 x 4.2，
0，
其 它.
求pH值X的数学期望E(X).
解：
E( X ) xf ( x)dx
4
4.2
x 25( x 3.8)dx x (25)(x 4.2)dx
3.8
4
4
2021/7/22
15
10第四章随机变量的数字特征4.2
例4-18 设随机变量X的期望E(X)=2，方差D(X)=4， 求E(X2)。
解： 由于D( X ) E( X 2 ) E2( X )
所以E( X 2 ) E2 ( X ) D( X )
故E( X 2 ) 22 4 8
例4-19 设随机变量X的概率密度如下，求D(X)。
x, 0 x 1
则有
0 p 1.
n
E( X ) k P{X k} np.
k0
E( X 2 ) E[X ( X 1) X ]
E[X ( X 1)] E( X )
n
k(k
1)C
k n
pk
(1
p)nk
np
k0
n k(k 1)n!pk (1 p)nk np k0 k!(n k)!
n
n(n 1) p2
D(X ) 1 求 X 的概率密度函数。 3
解 由 E(X) a b 3 2
(b a)2 1
D(X )
.
12 3
得 a 2, b 4.
从而
X的概率密度为
f
(
x)
1 2
,
2
x
4
0, 其他
5. 指数分布
设随机变量 X 服从指数分布, 其概率密度为
ex , x 0,
f (x)
其中 0.
3
2
12
12 6
[E(X
3 )]2
(2)3
1 3
03
1 2
13
1 12
33
1 12
2
1, 9
故 D(2X 3 5) 4[E( X 6 ) (E( X 3 ))2] 2954. 9
练习 设随机变量 X 具有概率密度
方差__随机变量的数字特征.
>0, 不等式P{| X | } 2 / 2成立，
或
P{| X | } 1 2 / 2
证明：（只证 X 是连续型）
P{| X
|
}
f
|x|
( x)dx
|x|
|
x
2
|2
f (x)dx
1
2
(x
)2
f
(x)dx
DX
2
2
2
。
返回主目录
第四章 随机变量的数字特征 §2 方差
这个不等式给出了随机变量 X 的分布未知情 况下，事件{| X | } 的概率的一种估计方法。
§2 方差
引言
随机变量的数学期望体现了随机变量所有可能取值的加权
平均．
离散型： 若级数
k 1
xk
pk
绝对收敛，则
E(X )
k 1
xk
pk
连续型： 若积分 xf ( x)dx 绝对收敛，则
E( X ) xf ( x)dx
§2 方差
设有一批灯泡寿命为：一半约950小时，另一半约1050小时→平均寿命为1000小时； 另一批灯泡寿命为： 一半约1300小时，另一半约700小时→平均寿命为1000小时；
方差D(X ) 2
0，记X *
X
证明：E( X *) 0，D( X *) 1，称X *为X的标准化变量
例2：设随机变量X具有0-1分布，其分布律为：
P( X 0) 1 p，P( X 1) p，求D( X )。
解：
E(X ) 0 (1 p) 1 p p E( X 2 ) 02 (1 p) 12 p p
返回主目录
例 已知正常男性成人血液中，每一毫升白细胞数平均
第4随机变量的数字特征知识课件
n
n p
(n 1 )!
pq k 1(n 1 ) (k 1 )
k 1 (k 1 )[! n ( 1 ) (k 1 )]!
= 令rk1
mn1
m
npCmr r 0
prqmr
np
(2). Poisson分布
X的概率分布为：P{Xk}k k0,1,2，
k!
k
E(X)k
k0 k!
k1
k1(k 1)!
第4章：随机变量的数字特征 §1.数学期望 §2.方差 §3.几种重要随机变量的数学期望与方差 §4.协方差及相关系数 §5.矩、协方差矩阵
例1 某车间对工人的生产情况进行考察. 车工
小张每天生产的废品数X是一个随机变量. 如
何定义X的平均值呢？
32天没有出废品;
统计100天,可得这100天 每天的平均废品数为
一般来说,若统计n天,
ni表示每天出i件废品
(假定小张每天至多出三件废品)
i=0,1,2,3.
得n天中每天的平均废品数为
以频率为权
0n01n12n23n3
的加权平均
nn n n
当统计天数趋于时，才是小张每天的平均废品数
由频率和概率的关系，用概率代替频率：
0 p 0 1 p 1 2 p 2 3 p 3
(3).E(X+Y)=E(X)+E(Y) (4).当X与Y相互独立时： E(XY)=E(X)E(Y) (其中X，Y为随机变量；a为常数。)
例5.某机器有3个部件,各部件需要调整的概率分 别为0.1, 0.2, 0.3记X为需要调整的部件数.求E(X).
解法1：先求X的概率分布： 设：Ai为第i个部件不需要调整 P{X=0}=P(A1A2A3)=0.9×0.8×0.7=0.504 P{X=1}=P(A1A2A3)+P(A1A2A3)+P(A1A2A3)
(第4章) 随机变量的数字特征
x fX (x)dx yfY ( y)dy E(X) E(Y)
例 一民航机场的送客车，载有20名乘客自机场开出， 旅客有10个车站可以下车，如到达一站没旅客下车 就不停车．设每位旅客在各站下车是等可能的，且 旅客之间在哪一站下车相互独立．以X表示停车次数， 求E(X)．
二. 方差的性质
性质1 D(X )≥0 若C是常数，则 D(C )=0
性质2 设k是常数，则 D(kX )=k2D(X ) 若 a,b是常数，则 D(aX+b)=a2D(X )
证明：
D(kX)=E(k2X2)E2(kX)
=k2E(X2)k2E2(X)
=k2[E(X2)E2(X)] =k2D(X)
方差实质上就是随机变量X 的函数 g(X )=[X-E(X )]2 的数学期望
若 X 为离散型随机变量，其概率分布律为
则X 的方差为 若 X 为连续型随机变量，其概率密度为f (x)
则X 的方差为
二维离散型随机变量(X,Y)的方差 ④二维连续型随机变量(X,Y)的方差
方差计算公式
证明： D(X)=E{[X-E(X)]2 } 展开
D(XY)=D(X)+D(Y)
推广 若随机变量X1,X2,…,Xn相互独立，则有
性质4 D(X)=E[(X-a)2]-[E(X)-a]2 (a为任意常数) 推论 对于任意常数a, 均有D(X )E[(X –a )2]
当且仅当a=E(X )时等号成立
k!
令i=k1
= e e =
常见离散型随机变量的数学期望
分布
概率 分布
数学 期望
参数为p 的 0-1分布
p
二项分布
np
B(n,p)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n
np[ p (1 p)]n1
np.
E ( X 2 ) E[ X ( X 1) X ]
E[ X ( X 1)] E ( X )
k k k ( k 1) p (1 p)n k np n k 0
n
k ( k 1)n! k p (1 p)n k np k 0 k !( n k )!
2{ E ( XY ) E ( X ) E (Y ) E (Y ) E ( X )
E ( X ) E (Y )}
2{ E ( XY ) E ( X ) E (Y )}.
若 X ,Y 相互独立,由数学期望的性质 4 知道上
于是 式右端为0，
D( X Y ) D( X ) D(Y ).
2. 二项分布
设随机变量 X 服从参数为 n, p 二项分布, 其 分布律为
n k p (1 p)n k , ( k 0,1,2,, n), P{ X k } k 0 p 1. 则有
E ( X ) k P{ X k }
k 0 n
n k n k k p (1 p) k 0 k
0 0
0
1 x θ x e dx θ
xe
x θ
e x θ d x θ .
E ( X ) x 2 f ( x ) d x
2
0
1 x θ x e dx θ
2
x e
2 x θ 0
2 xe x θ d x
0
θ2.
D( X ) E ( X 2 ) [ E ( X )]2
(n2 n) p2 np (np)2
np (1 p) ).
3. 泊松分布
设 X ~ π( ), 且分布律为
k k 0,1,2,, P{ X k } e , 0.
k!
则有
E( X ) k
D( X ) E ( X 2 ) [ E ( X )]2 2θ 2 θ 2 θ 2 .
指数分布的期望和方差 分别为 θ 和 θ 2 .
6. 正态分布
设 X ~ N ( μ, σ 2 ), 其概率密度为
1 f ( x) e 2πσ
( x μ )2 2σ 2
, σ 0, x .
例1
设随机变量 X 具有数学期望 E ( X ) ,
2
0. 记 X X , 方差D( X ) 1 1 [ E ( X ) ] 0; 则 E( X ) E ( X )
D( X ) E ( X 2 ) [ E ( X )]2
x x
O
2. 方差的定义
定义 设 X 是一个随机变量, 若{[ X E ( X )]2 }
存在, 记为 D( X ) 或 Var( X ) , 即
D( X ) Var( X ) E{[ X E ( X )]2 }.
记为 σ ( X ), 称为标 在应用上还引入量 D( X )，
准差或均方差 .
i 1 i 1 n n
例如, 若 X ~ N (1,3) , Y ~ N ( 2,4) 且 X ,Y 相互
独立 , 则Z 2 X 3Y 也服从正态分布, 而
E (Z ) 2 1 3 2 4, D(Z ) D( 2 X 3Y ) 4 D( X ) 9 D(Y ) 48.
x μ 先求标准正态变量 Z 的数学期望和方差. σ
1 t 2 2 e , Z的概率密度为 ( t ) 2π
于是 E (Z )
1 t 2 2 1 t 2 2 te d t 2π e 0， 2π
D(Z ) E ( Z 2 )
1 2 t 2 2 t e d t 2π
其中 f ( x ) 为X的概率密度.
(2) 利用公式计算
D( X ) E ( X 2 ) [ E ( X )]2 .
证
D( X ) E{[ X E ( X )]2 }
E{ X 2 2 XE( X ) [ E ( X )]2 }
2 2 E ( X ) 2 E ( X ) E ( X ) [ E ( X )]
1 t 2 2 1 t 2 2 te e d t 2π 2π 1，
因 即得
X Z ,
E ( X ) E ( Z ) μ . D( X ) D( Z ) D(Z ) 2 D( Z ) σ 2 .
正态分布的期望和方差分别为两个参数 μ 和 σ 2 .
k 0
k
k!
e
e
k 1
k 1
( k 1)!
e e .
E ( X ) E[ X ( X 1) X ]
2
E[ X ( X 1)] E ( X ) k ( k 1)
k 0
k
k!
e
第二节
方
差
一、随机变量方差的概念及性质
二、重要概率分布的方差
三、例题讲解 四、小结
一、随机变量方差的概念及性质
1. 概念的引入
方差是一个常用来体现随机变量取值分散程度 的量. 实例 有两批灯泡,其平均寿命都是 E(X)=1000小时.
O
1000 1000
若X i ~ N ( i , i2 ), i 1,2,, n, 且它们相互独
C 立， 则它们的线性组合： 1 X 1 C2 X 2 Cn X n
(C1 , C2 ,, Cn是不全为0的常数)仍然服从正态分布 ,
于是由数学期望和方差的性质知道
C1 X 1 C 2 X 2 C n X n ~ N ( C i i , C i2 i2 )
证 D(CX ) E{[CX E (CX )]2 } C 2 E{[ X E ( X )]2 }
C 2 D( X ).
D( X C ) E{[ X C E ( X C )]2 }
E{[ X E ( X )]2 } D( X ).
3 设 X ,Y 是两个随机变量， 则有
D( X Y )
D( X ) D(Y ) 2 E {( X E ( X ))( X E (Y ))}.
若 X ,Y 相互独立, 则有
D( X Y ) D( X ) D(Y ).
证
D( X Y )
E{[( X Y ) E ( X Y )]2 } E{ )]}2 E[ X E ( X )]2 E[Y E (Y )]2
f ( x)
1 , ba
a x b,
0,
其他.
b
1 xd x 则有E ( X ) xf ( x ) d x aba 1 (a b ). 2
结论
均匀分布的数学期望位于区间的中点.
D( X ) E ( X 2 ) [ E ( X )]2
X 2 1 2 2 E 2 E[( X ) ] 2 1.
X
X
,
则
E( X )
1
1 E ( X ) [ E ( X ) ] 0;
2e
k 2
2e e 2 . ( k 2)!
k 2
所以 D( X ) E ( X 2 ) [ E ( X )]2 2 2 .
泊松分布的期望和方差 都等于参数 .
4. 均匀分布
设 X ~ U (a , b) , 其概率密度为
2 E {[ X E ( X )][Y E (Y )]}
D( X ) D(Y ) 2 E {( X E ( X ))( X E (Y ))}.
上式右端第三项:
2 E {( X E ( X ))( X E (Y ))}
2 E{ XY XE (Y ) YE ( X ) E ( X ) E (Y )}
即
P { X C } 1.
二、重要概率分布的方差
1. 两点分布
已知随机变量 X 的分布律为
X
1
0
p
则有
p
1 p
E ( X ) 1 p 0 q p,
D( X ) E ( X 2 ) [ E ( X )]2
12 p 02 (1 p) p2 pq.
这一性质可以推广到任意有限多个相互独立的随
机变量之和的情况.
推广 若 X1 , X 2 ,, X n 相互独立, 则有
D( X 1 X 2 X n ) D( X 1 ) D( X 2 ) D( X n ).
(4) D( X ) 0 的充要条件是 X 以概率 1 取常数 C ,
E ( X 2 ) [ E ( X )]2
5. 方差的性质
则 1 设C 是常数， D(C ) 0.
证 D(C ) E{[C E (C )]2 } 0.
2 设 X 是一个随机变量， C是常数， 则有
D(CX ) C 2 D( X )， D( X C ) D( X ).
n
kn! p k (1 p)n k k 0 k !( n k )! np( n 1)! p k 1 (1 p)( n1)( k 1) k 1 ( k 1)![( n 1) ( k 1)]!
np[ p (1 p)]n1
np.
E ( X 2 ) E[ X ( X 1) X ]
E[ X ( X 1)] E ( X )
k k k ( k 1) p (1 p)n k np n k 0
n
k ( k 1)n! k p (1 p)n k np k 0 k !( n k )!
2{ E ( XY ) E ( X ) E (Y ) E (Y ) E ( X )
E ( X ) E (Y )}
2{ E ( XY ) E ( X ) E (Y )}.
若 X ,Y 相互独立,由数学期望的性质 4 知道上
于是 式右端为0，
D( X Y ) D( X ) D(Y ).
2. 二项分布
设随机变量 X 服从参数为 n, p 二项分布, 其 分布律为
n k p (1 p)n k , ( k 0,1,2,, n), P{ X k } k 0 p 1. 则有
E ( X ) k P{ X k }
k 0 n
n k n k k p (1 p) k 0 k
0 0
0
1 x θ x e dx θ
xe
x θ
e x θ d x θ .
E ( X ) x 2 f ( x ) d x
2
0
1 x θ x e dx θ
2
x e
2 x θ 0
2 xe x θ d x
0
θ2.
D( X ) E ( X 2 ) [ E ( X )]2
(n2 n) p2 np (np)2
np (1 p) ).
3. 泊松分布
设 X ~ π( ), 且分布律为
k k 0,1,2,, P{ X k } e , 0.
k!
则有
E( X ) k
D( X ) E ( X 2 ) [ E ( X )]2 2θ 2 θ 2 θ 2 .
指数分布的期望和方差 分别为 θ 和 θ 2 .
6. 正态分布
设 X ~ N ( μ, σ 2 ), 其概率密度为
1 f ( x) e 2πσ
( x μ )2 2σ 2
, σ 0, x .
例1
设随机变量 X 具有数学期望 E ( X ) ,
2
0. 记 X X , 方差D( X ) 1 1 [ E ( X ) ] 0; 则 E( X ) E ( X )
D( X ) E ( X 2 ) [ E ( X )]2
x x
O
2. 方差的定义
定义 设 X 是一个随机变量, 若{[ X E ( X )]2 }
存在, 记为 D( X ) 或 Var( X ) , 即
D( X ) Var( X ) E{[ X E ( X )]2 }.
记为 σ ( X ), 称为标 在应用上还引入量 D( X )，
准差或均方差 .
i 1 i 1 n n
例如, 若 X ~ N (1,3) , Y ~ N ( 2,4) 且 X ,Y 相互
独立 , 则Z 2 X 3Y 也服从正态分布, 而
E (Z ) 2 1 3 2 4, D(Z ) D( 2 X 3Y ) 4 D( X ) 9 D(Y ) 48.
x μ 先求标准正态变量 Z 的数学期望和方差. σ
1 t 2 2 e , Z的概率密度为 ( t ) 2π
于是 E (Z )
1 t 2 2 1 t 2 2 te d t 2π e 0， 2π
D(Z ) E ( Z 2 )
1 2 t 2 2 t e d t 2π
其中 f ( x ) 为X的概率密度.
(2) 利用公式计算
D( X ) E ( X 2 ) [ E ( X )]2 .
证
D( X ) E{[ X E ( X )]2 }
E{ X 2 2 XE( X ) [ E ( X )]2 }
2 2 E ( X ) 2 E ( X ) E ( X ) [ E ( X )]
1 t 2 2 1 t 2 2 te e d t 2π 2π 1，
因 即得
X Z ,
E ( X ) E ( Z ) μ . D( X ) D( Z ) D(Z ) 2 D( Z ) σ 2 .
正态分布的期望和方差分别为两个参数 μ 和 σ 2 .
k 0
k
k!
e
e
k 1
k 1
( k 1)!
e e .
E ( X ) E[ X ( X 1) X ]
2
E[ X ( X 1)] E ( X ) k ( k 1)
k 0
k
k!
e
第二节
方
差
一、随机变量方差的概念及性质
二、重要概率分布的方差
三、例题讲解 四、小结
一、随机变量方差的概念及性质
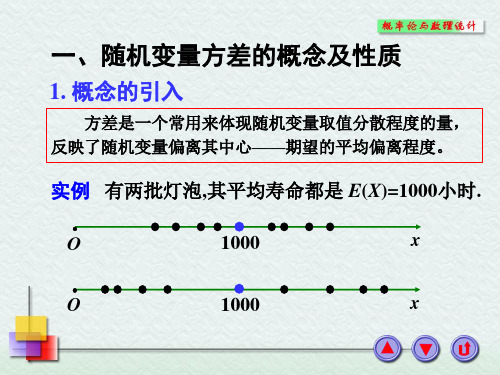
1. 概念的引入
方差是一个常用来体现随机变量取值分散程度 的量. 实例 有两批灯泡,其平均寿命都是 E(X)=1000小时.
O
1000 1000
若X i ~ N ( i , i2 ), i 1,2,, n, 且它们相互独
C 立， 则它们的线性组合： 1 X 1 C2 X 2 Cn X n
(C1 , C2 ,, Cn是不全为0的常数)仍然服从正态分布 ,
于是由数学期望和方差的性质知道
C1 X 1 C 2 X 2 C n X n ~ N ( C i i , C i2 i2 )
证 D(CX ) E{[CX E (CX )]2 } C 2 E{[ X E ( X )]2 }
C 2 D( X ).
D( X C ) E{[ X C E ( X C )]2 }
E{[ X E ( X )]2 } D( X ).
3 设 X ,Y 是两个随机变量， 则有
D( X Y )
D( X ) D(Y ) 2 E {( X E ( X ))( X E (Y ))}.
若 X ,Y 相互独立, 则有
D( X Y ) D( X ) D(Y ).
证
D( X Y )
E{[( X Y ) E ( X Y )]2 } E{ )]}2 E[ X E ( X )]2 E[Y E (Y )]2
f ( x)
1 , ba
a x b,
0,
其他.
b
1 xd x 则有E ( X ) xf ( x ) d x aba 1 (a b ). 2
结论
均匀分布的数学期望位于区间的中点.
D( X ) E ( X 2 ) [ E ( X )]2
X 2 1 2 2 E 2 E[( X ) ] 2 1.
X
X
,
则
E( X )
1
1 E ( X ) [ E ( X ) ] 0;
2e
k 2
2e e 2 . ( k 2)!
k 2
所以 D( X ) E ( X 2 ) [ E ( X )]2 2 2 .
泊松分布的期望和方差 都等于参数 .
4. 均匀分布
设 X ~ U (a , b) , 其概率密度为
2 E {[ X E ( X )][Y E (Y )]}
D( X ) D(Y ) 2 E {( X E ( X ))( X E (Y ))}.
上式右端第三项:
2 E {( X E ( X ))( X E (Y ))}
2 E{ XY XE (Y ) YE ( X ) E ( X ) E (Y )}
即
P { X C } 1.
二、重要概率分布的方差
1. 两点分布
已知随机变量 X 的分布律为
X
1
0
p
则有
p
1 p
E ( X ) 1 p 0 q p,
D( X ) E ( X 2 ) [ E ( X )]2
12 p 02 (1 p) p2 pq.
这一性质可以推广到任意有限多个相互独立的随
机变量之和的情况.
推广 若 X1 , X 2 ,, X n 相互独立, 则有
D( X 1 X 2 X n ) D( X 1 ) D( X 2 ) D( X n ).
(4) D( X ) 0 的充要条件是 X 以概率 1 取常数 C ,
E ( X 2 ) [ E ( X )]2
5. 方差的性质
则 1 设C 是常数， D(C ) 0.
证 D(C ) E{[C E (C )]2 } 0.
2 设 X 是一个随机变量， C是常数， 则有
D(CX ) C 2 D( X )， D( X C ) D( X ).
n
kn! p k (1 p)n k k 0 k !( n k )! np( n 1)! p k 1 (1 p)( n1)( k 1) k 1 ( k 1)![( n 1) ( k 1)]!