函数图像课件1
合集下载
《函数》第09讲 函数的图像(1)
像如图:
则函数y=f(x)· g(x)的图像可能是( A )
1.（2012· 四川）函数y=ax-a（a＞0,且a≠1） 的图像可能是( B )
2.（2013· 十校联考）函数f(x)=lg(|x|-1)的 大致图像是 (B )
辨识函数的图像可以从以下方面入手：
2 x 2x 1, x 0， (3)∵y x 2 2x 1, x＜0, 且函数为偶函数，先用
描点法作出［0，+∞）上的图像，再根据 对称性作出（-∞，0）上的图像，得图像 如图.
【练习】分别画出下列函数的图像：
（1） y=2x-1. （2）y=|x-2|(x+1).
（3）翻折变换
①y＝f(x)
保留 x 轴上方图像
把 x 轴下方图像沿 x 轴翻折上去 y＝ |f(x)| ②y＝f(x) .
保留 y 轴右侧的图像 把 y 轴右侧的图像沿 y 轴对称过去
y＝ f(|x|) ．
【例1】画出下列函数的图像：
（1）y=|log2(x+1)|.
2x 1 （2）y x 1
1. 定义域 [ 左右位置
2. 值 域 [ 上下位置 3. 单调性 [ 升降趋势 4. 奇偶性 [ 图象对称 5. 周期性 [ 循环往复 6. 特殊点 [ 必经之路
]
] ] ] ] ]
函数的图像(1)
1
2 3
会作图 会识图
会用图
1．描点法作图 (1)确定函数的定义域； (2)化简函数的解析式； (3)讨论函数的性质即奇偶性、周期性、 单调性、最值(甚至变化趋势)； (4)描点连线，画出函数的图像．
2.图像的变换
（1）平移变换 f(x)+k
f(x+h)
则函数y=f(x)· g(x)的图像可能是( A )
1.（2012· 四川）函数y=ax-a（a＞0,且a≠1） 的图像可能是( B )
2.（2013· 十校联考）函数f(x)=lg(|x|-1)的 大致图像是 (B )
辨识函数的图像可以从以下方面入手：
2 x 2x 1, x 0， (3)∵y x 2 2x 1, x＜0, 且函数为偶函数，先用
描点法作出［0，+∞）上的图像，再根据 对称性作出（-∞，0）上的图像，得图像 如图.
【练习】分别画出下列函数的图像：
（1） y=2x-1. （2）y=|x-2|(x+1).
（3）翻折变换
①y＝f(x)
保留 x 轴上方图像
把 x 轴下方图像沿 x 轴翻折上去 y＝ |f(x)| ②y＝f(x) .
保留 y 轴右侧的图像 把 y 轴右侧的图像沿 y 轴对称过去
y＝ f(|x|) ．
【例1】画出下列函数的图像：
（1）y=|log2(x+1)|.
2x 1 （2）y x 1
1. 定义域 [ 左右位置
2. 值 域 [ 上下位置 3. 单调性 [ 升降趋势 4. 奇偶性 [ 图象对称 5. 周期性 [ 循环往复 6. 特殊点 [ 必经之路
]
] ] ] ] ]
函数的图像(1)
1
2 3
会作图 会识图
会用图
1．描点法作图 (1)确定函数的定义域； (2)化简函数的解析式； (3)讨论函数的性质即奇偶性、周期性、 单调性、最值(甚至变化趋势)； (4)描点连线，画出函数的图像．
2.图像的变换
（1）平移变换 f(x)+k
f(x+h)
正弦函数图像课件
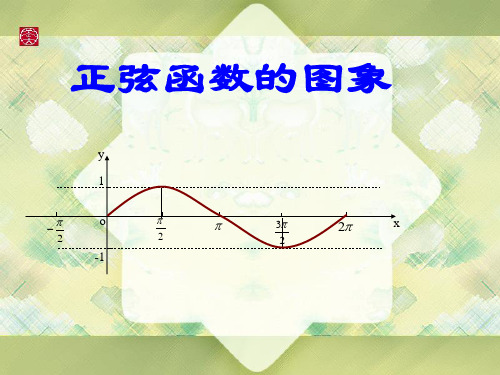
y=sinx
终边相同角的同一三角函数值相等
即： sin(x+2k)=sinx, kZ
x[0,2]
y=sinx
f (x 2k ) f (x) 利用图象平移
xR
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
函数y=sinx, xR的图象
2
3
4
正弦曲线
5 6 x
3)作正弦函数的简图（在精确度要求不太高时）
y 1
(0,0)o
2
-1
( 2 ,1)
2
五点画图法
( ,0)
3 2
3
( 2 ,-1)
( 2 ,0)
2
x
五点法
x
3
0
2
2
2
0
1
0
-1
0
y=sinx
4）函数的图象变换
y x2
向右平移 一个单位
y
(x
1)2
向下平移 一个单位
y (x 1)2 1
y
o1
x
-1
四. 解题示范
例1：用五点法作函数y=1+sinx, [0,2]的图象
x
0
2
y=sinx 0
1
3
2
2
0
-1
0
1
2
1
y=1+sin
0
1
x
. 2
y=1+sinx, x[0,2]
1.
.
.
.
o
/2
3/2
作函数 y sin x , x [0,2 ] 的图象
《函数》数学PPT课件
经济领域中常见问题建模为函数关系
供需关系
在经济学中，供给和需求是两个重要的概念，它们之间的 关系可以用函数来表示。供给函数和需求函数的交点即为 市场均衡点。
生产成本与产量的关系
在制造业中，生产成本通常与产量有关。随着产量的增加 ，单位产品的成本可能会降低，这可以通过一个递减的函 数来表示。
投资回报与风险的关系
生活中常见问题建模为函数关系
路程、速度和时间的关系
s = vt，其中s是路程，v是速度，t是 时间。这是一个典型的线性函数关系 。
温度随时间的变化
在一天中，气温随时间变化而变化， 可以建立一个以时间为自变量、气温 为因变量的函数关系。
购物总价与数量的关系
总价 = 单价 × 数量。这也是一个线 性函数关系，可以通过函数图像来表 示。
三角函数定义
正弦、余弦、正切等函数 的定义域、值域及基本性 质。
三角函数图像
正弦、余弦、正切函数的 图像及其特点，如周期性 、振幅、相位等。
三角函数关系
同角三角函数关系式，如 平方关系、倒数关系、商 数关系等。
三角函数诱导公式和周期性质
诱导公式
通过角度的加减、倍角、半角等 变换，得到三角函数的诱导公式
当a>0时，二次函数有最小值，无最大值；当a<0时， 二次函数有最大值，无最小值
在实际问题中，可以通过二次函数的最值来解决最优化 问题
03
指数函数与对数函数
指数函数图像与性质
指数函数定义
形如y=a^x（a>0且a≠1）的函 数称为指数函数。
指数函数图像
当a>1时，图像在x轴上方，且随 着x的增大而增大；当0<a<1时， 图像在x轴上方，但随着x的增大而 减小。
函数图像ppt课件
03
描点法
根据函数表达式，在坐标 系中逐个描出对应的点(x, y)，然后用平滑的曲线将 这些点连接起来。
计算法
利用数学软件或计算器， 输入函数表达式，自动生 成函数图像。
表格法
根据函数表达式和已知数 据，制作表格，然后在坐 标系中根据表格数据绘制 出函数图像。
函数图像的观察与分析
观察图像形状
通过观察函数的图像，可以初 步判断函数的类型（如一次函 数、二次函数、三角函数等）
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
06
复合函数的图像
复合函数的定义与性质
总结词
理解复合函数的定义与性质是绘制和分 析其图像的基础。
VS
详细描述
复合函数是由两个或多个函数的组合而成 的函数。它具有一些特殊的性质，如复合 函数的导数、极限等。了解这些性质有助 于更好地绘制和分析复合函数的图像。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
二次函数的图像
二次函数的定义与性质
总结词
二次函数的定义、性质和 表达式
二次函数的定义
二次函数是指形式为 y=ax^2+bx+c（其中a、 b、c为常数，且a≠0）的 函数。
二次函数的性质
二次函数具有开口方向、 顶点、对称轴等性质，这 些性质决定了函数图像的 形状和位置。
复合函数图像的绘制
总结词
掌握绘制复合函数图像的方法是理解其性质 和应用的必要手段。
详细描述
绘制复合函数图像需要使用数学软件或绘图 工具，如Matlab、GeoGebra等。在绘制 过程中，需要注意函数的定义域、值域以及 函数的单调性、奇偶性等性质。
函数图像专题PPT课件图文
答案 B
2．(2011·福州质检)函数y＝log2|x|的图象大致是( ) 答案 C 解析 函数y＝log2|x|为偶函数，作出x>0时y＝log2x的图象，图象关于y轴对称，应选C.
答案 A
4．(08·山东)设函数f(x)＝|x＋1|＋|x－a|的图象关于直线x＝1对称，则a的值为( ) A．3 B．2 C．1 D．－1 答案 A 解析 ∵函数f(x)图象关于直线x＝1对称，∴f(1＋x)＝f(1－x)，∴f(2)＝f(0)．即3＋|2－a|＝1＋|a|，用代入法知选A.
思考题1 将函数y＝lg(x＋1)的图象沿x轴对折，再向右平移一个单位，所得图象的解析式为________． 【答案】 y＝－lgx
题型二 知式选图或知图选式问题 例2 (2011·合肥模拟)函数f(x)＝loga|x|＋1(0<a<1)的图象大致为( )
【解析】 首先分析奇偶性，知函数为偶函)＝1，∴选A.
1.函数图象的三种变换 (1)平移变换：y＝f(x)的图象向左平移a(a>0)个单位，得到y＝f(x＋a)的图象；y＝f(x－b)(b>0)的图象可由y＝f(x)的图象向右平移b个单位而得到；y＝f(x)的图象向下平移b(b>0)个单位，得到y＝f(x)－b的图象；y＝f(x)＋b(b>0)的图象可由y＝f(x)的图象向上平移b个单位而得到．总之，对于平移变换，记忆口诀为：左加右减上加下减．
【答案】 C
题型三 函数图象的对称性 例3 (1)已知f(x)＝ln(1－x)，函数g(x)的图象与f(x)的图象关于点(1,0)对称，则g(x)的解析式为________________． (2)设函数y＝f(x)的定义域为实数集R，则函数y＝f(x－1)与y＝f(1－x)的图像关于( ) A．直线y＝0对称 B．直线x＝0对称 C．直线y＝1对称 D．直线x＝1对称
2．(2011·福州质检)函数y＝log2|x|的图象大致是( ) 答案 C 解析 函数y＝log2|x|为偶函数，作出x>0时y＝log2x的图象，图象关于y轴对称，应选C.
答案 A
4．(08·山东)设函数f(x)＝|x＋1|＋|x－a|的图象关于直线x＝1对称，则a的值为( ) A．3 B．2 C．1 D．－1 答案 A 解析 ∵函数f(x)图象关于直线x＝1对称，∴f(1＋x)＝f(1－x)，∴f(2)＝f(0)．即3＋|2－a|＝1＋|a|，用代入法知选A.
思考题1 将函数y＝lg(x＋1)的图象沿x轴对折，再向右平移一个单位，所得图象的解析式为________． 【答案】 y＝－lgx
题型二 知式选图或知图选式问题 例2 (2011·合肥模拟)函数f(x)＝loga|x|＋1(0<a<1)的图象大致为( )
【解析】 首先分析奇偶性，知函数为偶函)＝1，∴选A.
1.函数图象的三种变换 (1)平移变换：y＝f(x)的图象向左平移a(a>0)个单位，得到y＝f(x＋a)的图象；y＝f(x－b)(b>0)的图象可由y＝f(x)的图象向右平移b个单位而得到；y＝f(x)的图象向下平移b(b>0)个单位，得到y＝f(x)－b的图象；y＝f(x)＋b(b>0)的图象可由y＝f(x)的图象向上平移b个单位而得到．总之，对于平移变换，记忆口诀为：左加右减上加下减．
【答案】 C
题型三 函数图象的对称性 例3 (1)已知f(x)＝ln(1－x)，函数g(x)的图象与f(x)的图象关于点(1,0)对称，则g(x)的解析式为________________． (2)设函数y＝f(x)的定义域为实数集R，则函数y＝f(x－1)与y＝f(1－x)的图像关于( ) A．直线y＝0对称 B．直线x＝0对称 C．直线y＝1对称 D．直线x＝1对称
一次函数的图像(第1课时)同步课件
列表法： 把自变量的值和对应的函数值列成表格来表示函数关系的方法叫做列表法.
函数表达式法: 表示两个变量之间函数关系的式子称为函数表达式.
图像法: 在平面直角坐标系中，以函数的自变量的值为横坐标、对应的函数值为纵
坐标的点所组成的图形叫做这个函数的图像.
2.什么是一次函数？
一般地，形如y=kx+b(k、b 是常数，且k≠0)的函数，叫做一次函数，其中x是自变量，
y
y＝－2x+3 5
解：
＝＋，
(2)
＝－＋ ，
∴
=
=
，
.
∴交点
坐标为( ， )
y＝x＋2
4
3
2
1
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5
-1
-2
-3
-4
-5
x
新知巩固
2.已知一次函数y＝x＋2与y＝－2x＋3 ，
(3)求这两条直线与坐标轴所围成的图形面积．
在平面直角坐标系中描出相应的点；
③连线：顺次连接描出的各点.
5
4
3
2
1
-2 -1 O 1 2 3 4 5
-1
-2
-3
x
尝试与交流
仿照上述方法，在下图中画出y＝－x＋2的图像.
判断点(0，2)、(2，0)、(3，1)、(－1，3)是否在此函数图像上.
y
①列表：
x
··· -2
-1
0
1
2
···
y
···
3
3
3
平行
6. 直线y＝2x＋3与直线y＝2x－1的位置关系是________．
函数表达式法: 表示两个变量之间函数关系的式子称为函数表达式.
图像法: 在平面直角坐标系中，以函数的自变量的值为横坐标、对应的函数值为纵
坐标的点所组成的图形叫做这个函数的图像.
2.什么是一次函数？
一般地，形如y=kx+b(k、b 是常数，且k≠0)的函数，叫做一次函数，其中x是自变量，
y
y＝－2x+3 5
解：
＝＋，
(2)
＝－＋ ，
∴
=
=
，
.
∴交点
坐标为( ， )
y＝x＋2
4
3
2
1
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5
-1
-2
-3
-4
-5
x
新知巩固
2.已知一次函数y＝x＋2与y＝－2x＋3 ，
(3)求这两条直线与坐标轴所围成的图形面积．
在平面直角坐标系中描出相应的点；
③连线：顺次连接描出的各点.
5
4
3
2
1
-2 -1 O 1 2 3 4 5
-1
-2
-3
x
尝试与交流
仿照上述方法，在下图中画出y＝－x＋2的图像.
判断点(0，2)、(2，0)、(3，1)、(－1，3)是否在此函数图像上.
y
①列表：
x
··· -2
-1
0
1
2
···
y
···
3
3
3
平行
6. 直线y＝2x＋3与直线y＝2x－1的位置关系是________．
5.4一次函数的图象(1)课件
一次函数的图象
——第一课时
浙教版 八年级上
情感态度和价值观目标
学习 目标 能力目标
知识目标
1．经历作图过程,归纳总结作函数 图象的一般步骤,发展学生的总结 概括能力．
2.已知函数的代数表达式作函数 的图象，培养学生数形结合的意 识和能力．
1.经历函数图象的作图过程，初 步了解作函数图象的一般步骤．
-1
3.连线
-2
-3
新教课学讲目解
标
4、观察y=2x与y=-3x的图象，它们有什么异同？你能得出一次
函数的图象特点吗？
相同点： 两图象都经过原点
不同点： 函数y=2x的图象经过第一、三象限，从左向右呈上 升状态，函数y=-3x的图象经过第二、四象限，从左 向右呈下降状态。
一次函数的图象特点：
y=2x （-2，-4） （-1，-2）...
y=2x+1 （-2，-3） （0，1）...
新教课学讲目解 3、画一个直角坐标系，并在直角坐标系中画
标
出这组点。
y
y y=2X+1
5
y=2x
7 6
4
5
3
2
4
1
3
-5 -4 -3 -2 -1 0 1 2 3 4 5 -1 -2 -3 -4 -5
x
2
1
-4 -3 -2 -1 0 1 2 3 4 5 x
s=25，这样把自变量t作为点的 50
横坐标，把函数s作为点的纵坐 25
标就得到点（3，25）
0
3 6 6.2
5
甲乙 12 12.5 t（s）
当t=6时，s=50，就得到点（6，50）……，所有这些点就组成 了这个函数的图象。
——第一课时
浙教版 八年级上
情感态度和价值观目标
学习 目标 能力目标
知识目标
1．经历作图过程,归纳总结作函数 图象的一般步骤,发展学生的总结 概括能力．
2.已知函数的代数表达式作函数 的图象，培养学生数形结合的意 识和能力．
1.经历函数图象的作图过程，初 步了解作函数图象的一般步骤．
-1
3.连线
-2
-3
新教课学讲目解
标
4、观察y=2x与y=-3x的图象，它们有什么异同？你能得出一次
函数的图象特点吗？
相同点： 两图象都经过原点
不同点： 函数y=2x的图象经过第一、三象限，从左向右呈上 升状态，函数y=-3x的图象经过第二、四象限，从左 向右呈下降状态。
一次函数的图象特点：
y=2x （-2，-4） （-1，-2）...
y=2x+1 （-2，-3） （0，1）...
新教课学讲目解 3、画一个直角坐标系，并在直角坐标系中画
标
出这组点。
y
y y=2X+1
5
y=2x
7 6
4
5
3
2
4
1
3
-5 -4 -3 -2 -1 0 1 2 3 4 5 -1 -2 -3 -4 -5
x
2
1
-4 -3 -2 -1 0 1 2 3 4 5 x
s=25，这样把自变量t作为点的 50
横坐标，把函数s作为点的纵坐 25
标就得到点（3，25）
0
3 6 6.2
5
甲乙 12 12.5 t（s）
当t=6时，s=50，就得到点（6，50）……，所有这些点就组成 了这个函数的图象。
高中数学函数的图像ppt课件
34
真题透析 例 (2010 年高考湖南卷)函数 y＝ax2＋bx 与 y ＝ logb x(ab≠0，|a|≠|b|)在同一直角坐标系中的图
a
像可能是( )
35
【解析】 从对数的底数入手进行讨论，再 结合各个选项的图像从抛物线对称轴的取值 范围进行判断，故选D. 【答案】 D 【名师点评】 (1)本题易出现以下错误：① 忽视 y＝ logb x 中底数的绝对值，误认为 a，b
(2)图像的左右平移，只体现出x的变化，与x 的系数无关；图像的上下平移，只与y的变化 有关．
19
识图 对于给定函数的图像，可从图像上下左右分布范 围，变化趋势，特殊点的坐标等方面进行判断， 必要时可借助解方程、解(证)不等式等手段进行 判断，未必非要写出函数的解析式进行判断．
20
例2
(2010年高考山东卷)函数y＝2x－x2的图像
过点 P 且与 AB 垂直的截面面积记为 y，则 y＝
12f(x)的大致图像是(
)
38
解析：选A.先从起始点排除B，D，再用验证 法，当点P为OA的中点时，截面面积大于大圆 面积的一半，即可判定A正确．
39
x＋1，x∈[－1，0 2．已知 f(x)＝x2＋1，x∈[0，1] ，则下 列函数的图像错误的是( )
11
5．已知下列曲线： 以下编号为①②③④的四个方程 ① x－ y＝0；②|x|－|y|＝0；③x－|y|＝0； ④|x|－y＝0. 请按曲线 A、B、C、D 的顺序，依次写出与 之对应的方程的编号________．
答案：④②①③
12
考点探究•挑战高考
考点突破
作图 1．熟悉基本初等函数的图像． 2．会通过函数的性质确定图像的形状：如奇偶 性→对称性；函数值的正负→x轴上方下方；渐 近线→变化趋势；过哪些特殊点、定点；极值、 最值等．
真题透析 例 (2010 年高考湖南卷)函数 y＝ax2＋bx 与 y ＝ logb x(ab≠0，|a|≠|b|)在同一直角坐标系中的图
a
像可能是( )
35
【解析】 从对数的底数入手进行讨论，再 结合各个选项的图像从抛物线对称轴的取值 范围进行判断，故选D. 【答案】 D 【名师点评】 (1)本题易出现以下错误：① 忽视 y＝ logb x 中底数的绝对值，误认为 a，b
(2)图像的左右平移，只体现出x的变化，与x 的系数无关；图像的上下平移，只与y的变化 有关．
19
识图 对于给定函数的图像，可从图像上下左右分布范 围，变化趋势，特殊点的坐标等方面进行判断， 必要时可借助解方程、解(证)不等式等手段进行 判断，未必非要写出函数的解析式进行判断．
20
例2
(2010年高考山东卷)函数y＝2x－x2的图像
过点 P 且与 AB 垂直的截面面积记为 y，则 y＝
12f(x)的大致图像是(
)
38
解析：选A.先从起始点排除B，D，再用验证 法，当点P为OA的中点时，截面面积大于大圆 面积的一半，即可判定A正确．
39
x＋1，x∈[－1，0 2．已知 f(x)＝x2＋1，x∈[0，1] ，则下 列函数的图像错误的是( )
11
5．已知下列曲线： 以下编号为①②③④的四个方程 ① x－ y＝0；②|x|－|y|＝0；③x－|y|＝0； ④|x|－y＝0. 请按曲线 A、B、C、D 的顺序，依次写出与 之对应的方程的编号________．
答案：④②①③
12
考点探究•挑战高考
考点突破
作图 1．熟悉基本初等函数的图像． 2．会通过函数的性质确定图像的形状：如奇偶 性→对称性；函数值的正负→x轴上方下方；渐 近线→变化趋势；过哪些特殊点、定点；极值、 最值等．
一次函数的图像(1) 课件
1 (A) m 3
1 (B) m 3
(C) m > 1
(D)m < 1
4、若函数 y 2 x
m 2
为正比例函数，则m=(
-1
),
5、在正比例函数y=4x中， y随x的增大而（ 增大 ）。在 正比例函数
1 y x 3
中， y随的增大而（ 减小 ）。
6、任意写一个图象经过二、四象限的正比例函数的解 析式为 （ y=-6x ）。
例函数的解析式为 y = 2x 。
达标测试 1.函数y=kx的图象经过点P(3，-1)，则k的值为 (D) A ．3 B．-3
1 C． 3 1 D．3
2.下列函数中，图象经过原点的为( C ) A．y=5x+1
x C．y=- 5
B．y=-5x-1
x 1 D．y= 5
3．如果函数y=(3m-1)x是正比例函数，且y随x的增 大而增大，那么m的取值范围是（ A ）
x y=-3x 0 0 -1 3 (-1.5,4.5) 满足
•
5 4
•
(-0.5,1.5)
3
•
• 0
2 1
-3
-2
-1
-1 1
2
3
x
议一议 ( 1 ) 满足关系式y=-3x的x,y所对应的点(x,y)是 否都在它的图象上? 在
( 2 ) 正比例函数y=-3x的图象上的点(x,y)都满足 它的关系式吗? 满足
y=3x增加的更快，因为 |k|值更大 1
2 • （2）正比例函数y=-0.5x和y=-4x中，随着x值的增
大y的值都减小了，其中哪一个减小得更快？你是
如何判断的？ y=-4x减小的更快，因为|k|值更大
1 (B) m 3
(C) m > 1
(D)m < 1
4、若函数 y 2 x
m 2
为正比例函数，则m=(
-1
),
5、在正比例函数y=4x中， y随x的增大而（ 增大 ）。在 正比例函数
1 y x 3
中， y随的增大而（ 减小 ）。
6、任意写一个图象经过二、四象限的正比例函数的解 析式为 （ y=-6x ）。
例函数的解析式为 y = 2x 。
达标测试 1.函数y=kx的图象经过点P(3，-1)，则k的值为 (D) A ．3 B．-3
1 C． 3 1 D．3
2.下列函数中，图象经过原点的为( C ) A．y=5x+1
x C．y=- 5
B．y=-5x-1
x 1 D．y= 5
3．如果函数y=(3m-1)x是正比例函数，且y随x的增 大而增大，那么m的取值范围是（ A ）
x y=-3x 0 0 -1 3 (-1.5,4.5) 满足
•
5 4
•
(-0.5,1.5)
3
•
• 0
2 1
-3
-2
-1
-1 1
2
3
x
议一议 ( 1 ) 满足关系式y=-3x的x,y所对应的点(x,y)是 否都在它的图象上? 在
( 2 ) 正比例函数y=-3x的图象上的点(x,y)都满足 它的关系式吗? 满足
y=3x增加的更快，因为 |k|值更大 1
2 • （2）正比例函数y=-0.5x和y=-4x中，随着x值的增
大y的值都减小了，其中哪一个减小得更快？你是
如何判断的？ y=-4x减小的更快，因为|k|值更大
1.4.1-正弦函数、余弦函数的图像课件
课后作业
X
1.课本习题1.4A组第1题、B组第一题
2.预习三角函数的性质
提高题：当x∈[0，2π]时，求不等式
cos x 1 的解集.
y2
1 y1 2
O
π
5 2π x
-பைடு நூலகம் 3 2
23
0
，
3
U
5
3
，2
变式 当x∈[0，2π]时，求不等式
sin x 1 的解集.
y2
1
3pπ
π
2
2π
回顾（一）
分别指出 sin a , cos a , tan a 的三角函
数线? y PT
正弦线MP
A(1,0) 余弦线OM
-1
OM
xx
正切线AT
回顾：（二）
• 作函数图象的基本步骤？
作正弦函数 y=sinx (x∈R) 的图象
（一）先作出函数 y sin x, x 0,2 的图象
1、描点法
1)
三.用五点法作y=sinx , x∈[ π ,π ]的简
图 x
-π
π 2
0
π
2π
sin x 0 -1 0 1 0
y1
.
-π
π
2.
.
O -1
.
.
π πx
2
y
三、正弦函数y=sinx, x∈R的图象
1-
6
4
2
o
2
4
6
x
-1-
正弦曲线
-
-
因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，
2
2
-
1
3
精美获奖课件54《一次函数的图像》课件(1)
精美获奖课件54《一次函数的图像》课件一、教学内容本节课的内容为《一次函数的图像》，选自人教版八年级数学下册第十一章第一节。
详细内容包括：一次函数的定义、图像及其性质；一次函数图像的绘制方法；一次函数图像在实际问题中的应用。
二、教学目标1. 让学生掌握一次函数的定义、图像及其性质，能熟练绘制一次函数的图像。
2. 培养学生运用一次函数图像解决实际问题的能力，提高学生的数学思维。
3. 培养学生合作交流、动手实践的能力。
三、教学难点与重点教学难点：一次函数图像的绘制方法，一次函数图像在实际问题中的应用。
教学重点：一次函数的定义、图像及其性质。
四、教具与学具准备教具：多媒体课件、黑板、粉笔。
学具：直尺、圆规、量角器。
五、教学过程1. 导入：通过展示一次函数在实际生活中的应用实例，激发学生兴趣，引出本节课的主题。
2. 新课导入：（1）讲解一次函数的定义，引导学生理解并掌握。
（2）通过例题讲解，让学生学会一次函数图像的绘制方法。
3. 随堂练习：（1）让学生独立绘制一次函数的图像。
4. 应用拓展：（1）展示一次函数在实际问题中的应用，引导学生学会运用。
（2）分组讨论，让学生互相交流，提高解决问题的能力。
（1）让学生回顾本节课所学内容，加深对一次函数的认识。
六、板书设计1. 定义：一次函数的定义。
2. 图像：一次函数的图像及其性质。
3. 绘制方法：一次函数图像的绘制方法。
4. 应用：一次函数在实际问题中的应用。
七、作业设计1. 作业题目：情境一：小明骑自行车去学校，速度为4km/h，行驶1小时后，距离学校还有6km。
情境二：小华买了一个玩具车，原价100元，每过一年，价值降低10元。
2. 答案：（1）略。
（2）情境一：y = 4x + 10；情境二：y = 10x + 100。
八、课后反思及拓展延伸1. 反思：本节课学生对一次函数的定义和图像绘制方法掌握较好，但在实际问题中的应用还需加强。
2. 拓展延伸：（1）引导学生探究一次函数图像的平移、伸缩变换。
高中阶段常见函数图像(高清)(1)
函数表达式
图像
函数表达式
y ln x x
y ln x x
函数极值点
1, 1
y x ln x
函数极值点
1 e
,
1 e
y ln x x
函数极值点
e,
1 e
y x ln x
函数极值点
e, e
y ex x
过定点
0,1
y ex x
函数极值点
0,1
y ex x
函数极值点
1, e
y ln x x 1
函数极值点
e, e
ln x x 1
y ln x 1 ex
函数极值点
0,1 ln x 1 ex
函数表达式
y sin x
y ex x 1
函数极值点
e,
1 e
ex x 1
y ex x 1
过定点
0,1
ex 1 x
y ln 1 1 1 xx
函数极值点
函数表达式
y x2 ex
图像
y
x2 ex
y
ex x2
y ex sin x y ex sin x
4 / 41
y ex sin x y ex sin x
y
sin ex
x
y ex cos x
函数表达式
图像
函数表达式
图像
y ex cos x
y ex cos x
y
cos ex
x
y x2 sin x
y xex
函数极值点
1,
1 e
y
x ex
函数极值点
1,
1 e
图像
1 / 41
函数表达式
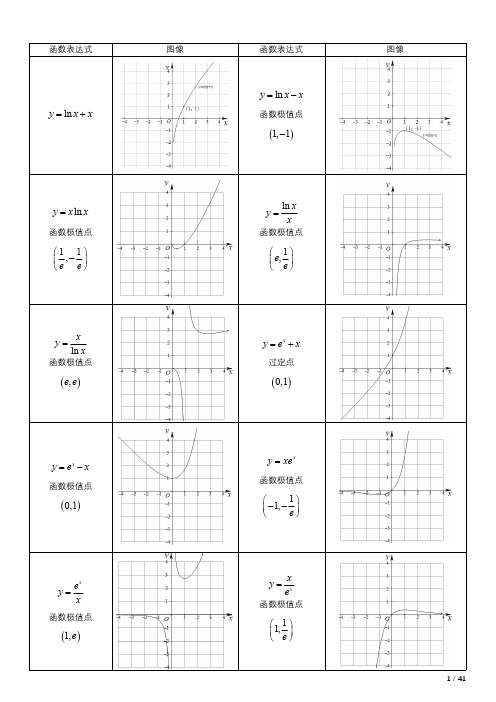
图像
函数表达式
y ln x x
y ln x x
函数极值点
1, 1
y x ln x
函数极值点
1 e
,
1 e
y ln x x
函数极值点
e,
1 e
y x ln x
函数极值点
e, e
y ex x
过定点
0,1
y ex x
函数极值点
0,1
y ex x
函数极值点
1, e
y ln x x 1
函数极值点
e, e
ln x x 1
y ln x 1 ex
函数极值点
0,1 ln x 1 ex
函数表达式
y sin x
y ex x 1
函数极值点
e,
1 e
ex x 1
y ex x 1
过定点
0,1
ex 1 x
y ln 1 1 1 xx
函数极值点
函数表达式
y x2 ex
图像
y
x2 ex
y
ex x2
y ex sin x y ex sin x
4 / 41
y ex sin x y ex sin x
y
sin ex
x
y ex cos x
函数表达式
图像
函数表达式
图像
y ex cos x
y ex cos x
y
cos ex
x
y x2 sin x
y xex
函数极值点
1,
1 e
y
x ex
函数极值点
1,
1 e
图像
1 / 41
函数表达式
函数图像课件 (1)
A.④①②③ C.③④②①
B.①④③② D.①④②③
解析答案
考向三 借助动点变化探究函数图象 例 5：(2015· 全国卷Ⅱ)如图，长方形 ABCD 的边 AB＝2，BC＝1，O 是 AB 的 中点， 点 P 沿着边 BC， CD 与 DA 运动， 记∠BOP＝x，将动点 P 到 A，B 两点距 离之和表示为 x 的函数 f(x)，则 y＝f(x)的图象大致为( )
函数图像及应用
知识梳理 1.掌握基本初等函数的图象特征，能熟练运用基本初 等函数的图象解决问题． 2．掌握图象的作法：描点法和图象变换． 3．会运用函数的图象理解和研究函数的性质．
利用描点法作函数图象
其基本步骤是列表、描点、连线，首先：①确定函数的 定 义 域 ； ② 化 简 函 数 ________ ； ③ 讨 论 函 数 的 性 质 (___________)；其次：列表(尤其注意特殊点、零点、最大 值点、最小值点、与坐标轴的交点)；最后：描点，连线．
x R ，满足f (4) f (1) 0， 题3：偶函数 f ( x ) ， 且在区间[0，3]和 (3, ) 上分别递减和递增， (, 4) (1, 0) (1,． 4) 则不等式xf ( x) 0 的解集为
变题：“偶函数”变为“奇函数”，改 0,3 为 0,3 ，则不等式 xf ( x) 0 的解集 为 ．
识图
函数图象的识别是高考的一个热点内容， 主要考查以下 几个问题：(1)知式选图；(2)知图选式；(3)借助动点变化探 究函数图象． 考向 1 知式选图
【例 3】 (2015· 浙江卷)函数 ≤π 且 x≠0)的图象可能为( )
1 f(x)＝x－x cosx(－π
≤x
【解析】
《函数的图像》PPT课件
y/米
y/米
y/米
y/米
1500
1500
1500
1500
1000
1000
1000
1000
500
500
x/分 O 10 20 30 40 50
x/分 O 10 20 30 40 50
500
x/分 O 10 20 30 40 50
500
x/分 O 10 20 30 40 50
A．
B．
C．
D．
3.李华和弟弟进行百米赛跑，李华比弟弟跑得快，如果两人同 时起跑，李华肯定赢．现在李华让弟弟先跑若干米，图中，分 别表示两人的路程与李华追赶弟弟的时间的关系，由图中信息
可知，下列结论中正确的是（ B ） ．
Ａ．李华先到达终点 Ｂ．弟弟的速度是8米／秒 Ｃ．弟弟先跑了10米 Ｄ．弟弟的速度是10米／秒
s/米
t/秒
中考实战
甲，乙两同学骑自行车从Ａ地沿同一条路到Ｂ地，已知
乙比甲先出发．他们离出发地的距离s／km和骑行时间
t/h之间的函数关系如图所示，给出下列说法：
Ａ.他们都骑了２０km；
（1）注水、加热和淋浴分别用了多少 时间？ （2）水箱的最大贮水量是多少升？ （3）当淋浴开始后15min，水箱中还 有水多少升？
2．小芳今天到学校参加初中毕业会考，从家里出 发走10分到离家500米的地方吃早餐，吃早餐用 了20分；再用10分赶到离家1000米的学校参加考 试．下列图象中，能反映这一过程的是 （ D ）．
3.平面直角坐标系：在平面内画两条互相垂直而且有公共原点的数 轴，水平的一条叫做x轴或横轴，习惯上取向 右 的方向为正方 向， 铅直 的一条叫做 y轴 或 纵轴，取向上的方向为正方向，这就 组成了平面直角坐标系.
八下数学：函数的图像PPT课件
2 2.5 4 6.25
3… 9…
用平滑曲线去连接画 出的点
2 3 4 5x
这样我们就得到了一幅表示S与x关系的图． 图中每个点都代表x的值与S的值的一种对应关系。
如点(2，4)表示x=2时S=4。
归纳
函数的图象的意义：
一般地，对于一个函数，如果把自变量 与函数的每对对应值分别作为点的横坐标和 纵坐标，那么坐标平面内由这些点组 成的图形就是这个函数的图象。
函数图象可以数形结合地研究函数，给我们带来便利。
归纳
函数图象的画法：
1、列表
列出自变量与函数的对应值表。 注意：自变量的值（满足取值范围），并取适当.
2、描点 3、连线
建立直角坐标系，以自变量的值为横坐标， 相应的函数值为纵坐标，描出表格中数值 对应的各点 按照横坐标从小到大的顺序把描出的点用 平滑曲线依次连接起来
你能解释x＞0这个范围是怎样确定的吗？
从式子s = x2来看,边长x越大,面积 s 也越大。能不能 用图象直观的反映出来呢？
1、列表： 2、描点：
3、连线：
S = x2(x>0)
x0
0.5
1 1.5
s 0 0.25
1 2.25
s
5
4
3
用空心圈表示不在曲
线的点
2
1
-5 -4 -3 -2 -1 0
1
-1
巩固
1、画出函数 y = x + 0.5 的图象 解： 1、列表
x … -3 -2
-1
0 1 2 3…
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
2、描点 3、连线
请画出函数y= x+0.5的图象
人教版数学八年级下册函数的图像(第1课时)教学课件
停留了5 min；③甲、乙两组同时到达景点；④相遇后，乙组的速度
小于甲组的速度．根据图象信息，以上说法正确的
有 ①②
．
s/km
55
乙 甲
t/min O 10 20 30 40 50 60 70
第二十九页，共三十三页。
课堂检测 拓广探索题
某车间的甲、乙两名工人分别同时生产同种零件，他们一天生产零件y(个)
由小到的大顺序，把所描出的各
第十二页，共三十三页。
巩固练习
(1)在所给的平面直角坐标系中画出函数 y 1 x的图象.
2
（先填写下表，再描点、连线）
x … -3 -2 -1 0 1 2 3 …
y
…
3 2
-1 1
2
பைடு நூலகம்
0
1 2
1
3
2…
(2)点P(5，2)
不在 该函数的图象
y 3
(tú xiànɡ)上(填“在”或“不在”). 2
第四页，共三十三页。
探究新知
知识点 1 函数(hánshù)的图象
写出正方形的面积S与边长x的函数解析式，并确定 (quèdìng)自变量x的取值范围.
S=x2 （x＞0）
x 0 0.5 1 1.5 2 2.5 3 3.5 4
S 0 0.25 1 2.25 4 6.25 9 12.25 16
第五页，共三十三页。
第二十二页，共三十三页。
连接(liánjiē)中考
甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后
，乙车才沿相同路线行驶．乙车先到达(dàodá)B地并停留1h后，再以原
速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.某人早上进行登山活动，从山脚到山顶休息一会儿又 沿原路返回，若用横轴表示时间t，纵轴表示与山脚距离 D h，那么下列四个图中反映全程h与t的关系图是（ ）
3．小芳今天到学校参加初中毕业会考，从 家里出发走10分到离家500米的地方吃早餐，吃 早餐用了20分；再用10分赶到离家1000米的学 校参加考试．下列图象中，能反映这一过程的 是（ D ） ．
y/米 y/米 y/米 y/米 1500 1500 1500 1500
1000
1000
10001000来自500500500
500
x/分 O 10 20 30 40 50 O 10 20 30 40 50
x/分 O 10 20 30 40 50
x/分 O 10 20 30 40 50
x/分
A
B
C
D
4．某装水的水池按一定的速度放掉水池的一 半后，停止放水并立即按一定的速度注水，水 池注满后，停止注水，又立即按一定的速度放 完水池的水。若水池的存水量为v（立方米）， 放水或注水的时间为t（分钟），则v与t的关 系的大致图象只能是（ ） A
5．一枝蜡烛长20厘米，点燃后每小时燃烧掉5厘 米，则下列3幅图象中能大致刻画出这枝蜡烛点燃 后剩下的长度h（厘米）与点燃时间t之间的函数关 系的是（ C ）.
巩固 1、画出函数 y = x + 0.5 的图象
解： 1、列表
x … -3 -2 -1 0 1 2 3
… …
y … -2.5 -1.5
因为过(a，0)画y轴平行线与图形曲线只有一个交 点。即x=a时，y有唯一的值与其对应。符合函数意 义． 图(2)曲线不表示y是x的函数． 因为过点(a，0)画y轴平行线，与图中曲线有三个 交点，即x=a时，y有三个值与其对应，不符合函数 意义．
Ⅲ．随堂练习 P104练习
Ⅳ．课时小结
本节通过两个活动，学会了分析图象信息，解答有 关问题．通过例题学会了用描点法画出函数图象，这 样我们又一次利用了数形结合的思想．
x y
… …
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
… …
根据表中数值描点(x，y)，并用光滑曲线连结这些点．
从函数图象可以看出，直线从左向右上升，即当x由小变 大时，y=x+0.5随之增大．
6 (2)y= (x>0) x
自变量的取值范围x>0 列表:
x y
… 0.5 1 1.5 2 2.5 3 2.4 … 12 6 4
2.25 4 6.25 9
如果我们在直角坐标系中，将你所填表格中的自变量x 及对应的函数值S当作一个点的横坐标与纵坐标，即可在 坐标系中得到一些点。
x S=x2 (x>0)
但 同 实 时 际 表根 … 0 0.25 1 2.25 4 6.25 9 上 示据 我 描 与 们 S 出 9 描 的 2 的 S=x (x>0) 出 对点 的 应想 6.25 点 关象 只 出 用空心圈表 系 4 能 的其 示不在曲线 是 2.25 他 点 上的点 有 有点 1 限 0.25 的 无 0 11325 3 数位 x多 2 2 2 个 个置
3、图象法：直观地反映了函数随 自变量的变化而变化的规律。
• 例 一个水库的水位在最近5h内持续上涨。下表记录 了这5h内6个时间点的水位高度，其中t表示时间，y 表示水位高度。 （1）在平面直角坐标系中描出表中数据对应的点，这 些点是否在一条直线上？由此你能发现水位变化有什 么规律吗？ （2）水位高度y是否为时间t的函数？如果是，试写出 一个符合表中数据的函数解析式，并画出这个函数的 图象。这个函数能表示水位的变化规律吗？ （3）据估计这种上涨规律还会持续2h,预测再过2h水位 高度将为多少米？
二、自主探究
我们先来思考这样一个问题：
正方形的边长x与面积S的函数关系式为 其中自变量x的取值范围是
sx,
2
x>0
。
你能解释x＞0这个范围是怎样确定的吗？ 因为x表示的实际含义是正方形的边 长，边长只能为正。
计算并填写下表： x 0 0.5 1 1.5 2 2.5 3 S=x2(x>0) 0 0.25 1
t/h y/m
0 3
1 3.3
2 3.6
3 3.9
4 4.2
5 4.5
（二）.小明从家里出发，外出散步，到一个公共阅 报栏前看了一会报后，继续散步了一段时间，然后 回家.下面的图描述了小明在散步过程中离家的距 离s（米）与散步所用时间t（分）之间的函数关系. 请你由图具体说明小明散步的情况.
解：
小明先走了约3分钟， 到达离家250米处 的一个阅报栏前看 了5分钟报，又向前 走了2分钟，到达离 家450米处返回， 走了6分钟到家。
3 4 … 2 1.5 …
据表中数值描点(x, y)并用光滑曲线连结这些点，就得到图象．
从函数图象可以看出，曲线从左向右下降，即当x由小变大 6 随之减小． 时， y= x
我们来总结归纳一下描点法画函数图象的一般步骤
第一步：列表．在自变量取值范围内选定一些值．通过 函数关系式求出对应函数值列成表格． 第二步：描点．在直角坐标系中，以自变量的值为横 坐标，相应函数值为纵坐标，描出表中对应各点． 第三步：连线．按照坐标由小到大的顺序把所有点用 平滑曲线连结起来．
八年级 数学
第十一章 函数
14.1.3 函数的图象1
课堂练习
┅ ┅
6 1、作出函数y= x (x>0) 的图象。
解(1)列表: (2)描点: (3)连线:
X y
┅ ┅
0.5 12
1 6
1.5 4
2 3
2.5 2.4
3 2
3.5 1.7
4 1.5
5 1.2
6 1
归纳 表示函数关系的方法：
1、解析法：准确地反映了函数与 自变量之间的数量关系。 2、列表法：具体地反映了自变量 与函数的数值对应关系。
0 0.5 1 1.5 2 2.5 3
…
x s
这样我们就得到了一幅表示S与x关系的图． 图中每个点都代表x的值与S的值的一种对应关系。 如点(2，4)表示x=2时 S=4。
八年级 数学
第十一章 函数的图象 第十四章 函数
函数的图象 一般的，对于一个函数，如果 把 自变量 与函数的每对对应值分别 作为点的横、纵坐标，那么坐标平 面内由这些 点组成的图形，就是这 个函数的图象。
上图中的曲线即为函数
sx
2
(x＞0)的图象．
函数图象可以数形结合地研究函数，给我们带来便利。
活动一
下图是自动测温仪记录的图象，它反映了北京的春季某
天气温T如何随时间t的变化而变化。你从图象中得到了哪
些信息?
T/℃ 8
-3
0
4
14 时间
24
t/时
横坐标表示 时间 ，纵坐标表示 温度 温度T 随 时间t 的变化而变化?
尝试练习： 课本P103思考题。
解答 解：1．由题意可知，开始时壶内有一定量水，最终漏 完，即开始时间z=0时，壶底水面高y≠0．最终漏完即 时间小到某一值时y=0． 故(1)图错． 又因为壶内水面高低影响水的流速，开始漏得快，逐 渐慢下来． 所以(3)图更适合表示这个函数关系．
2．图(1)曲线表示y是x的函数．
北京的春季某天气温 T 随时间 如图所示：
t 变化而变化的规律
1.哪个时间温度最高？是多少度？ 2.哪个时间温度最低？是多少度？ 3.什么时间段温度在下降？什么时间段温度 在上升？ 5. x轴的交点表示什么？ 4.曲线与 温度在零度以下的时间长呢？还是在零度以 上的时间长？
T/℃
8
O
4
14
3
24
从家到菜地 从玉米地回家 从菜地到玉米地
y/千 米
2
1.1
o
15 25
37
55
80
从玉米地回家
从家到菜地 从菜地到玉米地 给玉米 地锄草
在菜地浇水
y/千 米
2
1.1
o
15
25
37
55
80
x/分
你能回答下列问题了吗?
1.从家到菜地用了多少时间?
千 米
2
菜地离小明家有多远?
2.小明给菜地浇水用了多少 时间?
列表 2、画函数图象的步骤： 描点 连线
七、作业
• 必做：课本P107第7题。
• 思考：课本P103“思考1”。
例：在下列式子中，对于x的每个确定的值。y有唯一 的对应值，即y是x的函数．请画出这些函数的图象。
(1)y=x+0.5
解：
6 (2)y= (x>0) x
(1)y=x+0.5
x取值范围是全体实数值， 列表如下：
1.1
o
15 25
37
55
80
x/分
菜地离玉米地有多远?
3.从菜地到玉米地用了多少时间?
4.小明给玉米地锄草用了多少时间? 5.玉米地离家有多远? 小明从玉米地回家的平均速度是多少?
（一）、选择题： 1.如果A、B两人在一次百米赛跑中，路程s（米） 与赛跑的时间t（秒）的关系如图所示，则下列说 法正确的是（ C ） （A） A比B先出发 （B） A、B两人的速度相同 （C） A先到达终点 （D） B比A跑的路程多
s/km
20
乙 甲 A.1个 B.２个
O
0.5
1
2
2.5
t/h
C.３个
D.４个
龟兔赛跑
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉, 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已 经来不及了,乌龟先到达了终点………现在用 S 1和 S 2 分别表示乌龟、兔子所走的路程，t为时间，则下列 图象中，能够表示S 和t之间的函数关系式的是（C ）