现代控制理论第一章答案

合集下载

现代控制理论第版课后习题答案

习题答案Document number : WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1试求图1-27系统的模拟结构图，并建立其状态空间表达式。

解：系统的模拟结构图如下：系统的状态方程如下：令0(s) = y,则，=册所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。

以电压"⑴为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻R?上的电压作为输出量的输出方程。

解：由图,令ii =x}J2 =x2,u c =x3l输出量y = R2X2• & 1 1Rg + L, Xj + x y = u有电路原理可知:L2XI+R2X2=X3= x2 +C x3写成矢量矩阵形式为：14两输入也，两输出比，比的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。

解：系统的状态空间表达式如下所示：1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。

解：令x, = y,吃=，，兀3 =，，则有相应的模拟结构图如下:并画岀相应的模拟结构图10 £初・ 117/ \ 6(5 + 1) -4 V 3 a解:VV (5)= ------ ---------- = --------- +— + ------------+ 丄s(s + 2)(s + 3y (s + 3y 5 + 3 s + 2 s1- 7给定下列状态空间表达式y = [0 0 1 x 2_V 3_(1) 画出其模拟结构图 (2) 求系统的传递函数解：-1 0(2) W(s) = (s/ — A)= 25 + 31 — 1 5 + 31-8求下列矩阵的特征矢量_0 1 0 _ (3)32-12 -7 -6-1 0解：A 的特征方程 |刀—A|= —3 2-2 =23+6/l 2 + lU + 6 = 0 1272 + 6解之得：入=—1,/?2 = —2,/?3 = —31-6 (2)已知系统传递函数W(s)=6(5 + 1)5(5 +2)(5+ 3)2，试求岀系统的约旦标准型的实现,■ 010 '/AiP113 0 2 P11 =— P21 -12 -7 -6_ ■皿■叽当人=一1时,令內=1Ai-1 （或令Pll =一1,得片=P21 =1 )1■ 0 1 0 ■P\2Pn 3 02 Pll =-2 P22-12 -7 _6. L/^2.解得：”22=一2卩2丿32 =>12'P22 =P\2(或令从2 T,得4 = "22“320 1当人=一3时， 3 0 -12 -71 -2£ 2解得：〃23=-3/心〃33=3门3令戸3 = 1得1・9将下列状态空间表达式化成约旦标准型（并联分解）~4 1 -2■3 fX 2 = 1 0 2X 2 + 2 7⑵-.1-1 d_5 3_得解得：P 2] =^31 =-P\\当人=一2时,令门2 = 2 得P 2 = 2 -41'4 1 -2'当人=3时， 1 02=3 "211 -13 .解之得 Pl2 = P12 + 1，P22 = “32 令 Pl2 =1并联联结(第3版教材)已知如图1・22所示的系统，其中子系统1、2的传递函数阵分别求系统的闭环传递函数_4 1 -2 P11PwT 1 0 2 "21 =3 P21 + 11 -1 3 -■叽丄当An =3时,解：A 的特征方程2-4 -1 |27 - A| = -12 -1 1 2-2 =(2-1)(2-3)2 =02- 3解之得 P2! =Pj] =P11令/“iPw■fP21 = 1■叽丄当人=1时, 解之得 P13 = °，“23 = 2^33 令 “33 = 1约旦标准型1- 10已知两系统的传递函数分别为W|(s)和W 2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果解： (D 串联联结MlR = 得10 -1得1-H （第2版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：M2已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数I】的系数b（即控制列阵）为⑴b=；解法1 :解法2 ：求T,使得厂，；得宀鳥所以T=所以，状态空间表达式为第二章习题答案2-4用三种方法计算以下矩阵指数函数屛‘。

现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Prepared on 22 November 2020《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

解：系统的模拟结构图如下：系统的状态方程如下：令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

解：系统的状态空间表达式如下所示： 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。

解：令..3.21y x y x y x ===，，，则有相应的模拟结构图如下： 1-6 （2）已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘（1）画出其模拟结构图（2）求系统的传递函数解：（2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量（3）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解：A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得：3,2,1321-=-=-=λλλ当11-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得： 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P（或令111-=p ，得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ）当21-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得： 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P（或令112=p ，得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P ）当31-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得： 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型（并联分解）（2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解：A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果解：（1）串联联结（2）并联联结1-11 （第3版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-11（第2版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-12 已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数u 的系数b(即控制列阵)为（1）⎥⎦⎤⎢⎣⎡=11b解法1：解法2：求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以，状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。

现代控制理论课后习题答案

现代控制理论课后习题答案第⼀章习题1.2求下列多项式矩阵()s D 和()s N 的两个不同的gcrd:()2223(),()1232s s s s s s s s s ??++== ? ?+-??D N 解：()()22232321s s s s s s s++ =++ ? ?D S N S ； ()3r 2,1,2E -：223381s s s s s s ??++ ?-- ? ???；()3r 2,3,3E ：223051s s s s s ??++ ?- ? ???；()3r 1,3,2E s --：01051s s ?? ?- ? ；()3r 2,1,5E s -：01001s ?? ?；()3r 3,1,1E -：01000s ?? ? ? ???；()1r 2,3E ：01000s ?? ? ? ???；()1r 1,2E ：00100s ?? ?；所以⼀个gcrd 为001s ??；取任⼀单模矩阵预制相乘即可得另⼀个gcrd 。

1.9 求转移矩阵t A e (1)已知1141??=A ，根据拉⽒反变换求解转移矩阵tA e 。

(2) 已知412102113-?? ?= ? ?-??A ，根据C-H 有限项展开法求解转移矩阵t A e 。

解：(1)11()41s s s --??-= ?--??I A1110.50.50.250.2511(3)(1)(3)(1)13131()4141110.50.5(3)(1)(3)(1)(3)(1)3131s s s s s s s s s s s s s s s s s s s s s s s --+---+-+??-+-+ ? ?-=== ? ?---+ ?-+ ? ?-+-+-+-+?I A 3311330.5e 0.5e 0.25e 0.25e e ()e e 0.5e 0.5e t t t t t t tt t s ------??+-??=-= ??? ?-+?A L I A (2)由2412()12(1)(3)0113λλλλλλ--?? ?=--=--= ? ?--??A I -，得1,233,1λλ== 对1,23λ=，可以计算1,2()2rank λ=A I -，所以该特征值的⼏何重数为1。

《现代控制理论》第三版_.习题答案

或者
1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ； 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1－5. 根据微分方程，写状态方程，画模拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法： 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1

《现代控制理论》第3版课后习题答案

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：u K x K x K x X K x K x x x x J K x J x J K x J K x x J K x x x p n pb1611166131534615141313322211+--=+-==++--===••••••——所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：——[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

《现代控制理论》第三版第一章.习题答案

第一章作业参考答案1－1. 求模拟结构图，并建立其状态空间表达式。

解：状态方程：()()()1223235634134561111435163131161611116111()bp pp n p p p p p K xx x x J xx K x x x J K K x x x x J J J J 16xK x xK x x K x K x K K x u x x K K K K K x x u K K K ===+--=--++==-=-+⎡⎤=--⎢⎥⎢⎥⎣⎦=--+输出方程：1x θ=矩阵形式： =xAx +B u y =Cx 其中：211111110100000000011000000000000000b 1p p n p p K J K K J J J J K K K K K K K ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥--⎢⎥⎣⎦A = 100000Tp K B K ⎡⎤=⎢⎥⎢⎥⎣⎦[]100000C =；1－3. 图1－29机械系统。

1M 2M 受外力作用1f 2f 作用，求1M 2M 运动速度输出的状态空间表达式。

解：微分方程111112112()()M yf K c c B y y =---- 22222221121()12()M yf K c B y K c c B =--+-+ y y - 设状态变量[]1212Tc c y y x =[]12Ty y y =，[]12Tf f =u令11x c =，22x c =，31x y =，42x y = 13xx = 24xx = 1111312341111111K K B B x x x x x M M M M M =-+-++ f1121214124322221K K K B B B x x x x x M M M M M ++=--++22f所以 =xAx +B u y =Cx 其中：11111111112112220100001K K B B M M M M K K K B B B M M M M ⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥++⎢⎥--⎢⎥⎣⎦A =22 1200001010B M M ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦C 00100001⎡⎤=⎢⎥⎦ ⎣1－5. 根据微分方程，写状态方程，画模拟结构图。

现代控制理论试题与答案

现代控制理论试题与答案《现代控制理论参考答案》第一章答案1-1试求图1-27系统的模拟结构图，并建立其状态空间表达式。

解：系统的模拟结构图如下：系统的状态方程如下：令，则所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。

以电压为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻上的电压作为输出量的输出方程。

解：由图，令，输出量有电路原理可知：既得写成矢量矩阵形式为：1-4两输入，，两输出，的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。

解：系统的状态空间表达式如下所示：1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。

解：令，则有相应的模拟结构图如下：1-6（2）已知系统传递函数,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：1-7给定下列状态空间表达式‘画出其模拟结构图求系统的传递函数解：（2）1-8求下列矩阵的特征矢量（3）解：A 的特征方程解之得：当时，解得：令得（或令，得）当时，解得：令得（或令，得）当时，解得：令得1-9将下列状态空间表达式化成约旦标准型（并联分解）（2）解：A的特征方程当时，解之得令得当时，解之得令得当时，解之得令得约旦标准型1-10已知两系统的传递函数分别为W1(s)和W2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果解：（1）串联联结（2）并联联结1-11（第3版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-11（第2版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-12已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数u的系数b(即控制列阵)为（1）解法1：解法2：求T,使得得所以所以，状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数。

现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Document number：WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

解：系统的模拟结构图如下：系统的状态方程如下：令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

解：系统的状态空间表达式如下所示： 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。

现代控制理论基础第一章习题答案

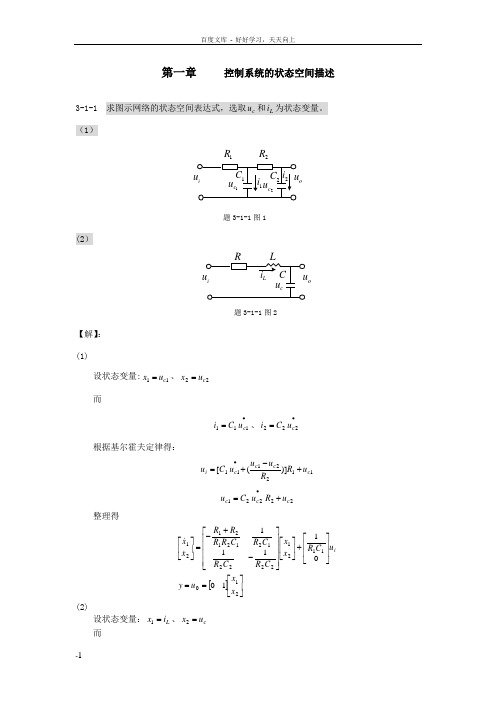
第一章控制系统的状态空间描述3-1-1 求图示网络的状态空间表达式，选取c u 和L i 为状态变量。

（1）1R 2Ro题3-1-1图1(2）o题3-1-1图2【解】： (1)设状态变量:11c u x =、22c u x = 而•=111c u C i 、•=222c u C i根据基尔霍夫定律得：1122111)]([c c c c i u R R u u u C u +-+=•22221c c c u R u C u +=•整理得[]⎥⎦⎤⎢⎣⎡==⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-=⎥⎦⎤⎢⎣⎡210112122221212121211001111x x u y u C R x x C R C R C R C R R R R x x i(2)设状态变量：L i x =1、c u x =2 而•=c L u C i根据基尔霍夫定律得：c L L i u i L i R u ++⋅=•整理得[]⎥⎦⎤⎢⎣⎡==⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡21021211001011x x u y u L x x CL L R x x i3-1-2 如图所示电枢电压控制的它励直流电动机，输入为电枢电压a u 输出为电动机角速度ω，电动机轴上阻尼系数为f ，转动惯量J ，试列写状态方程和输出方程。

L题3-1-2图【解】：设状态变量为：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡ωa i x x 21 其中a i 为流过电感上的电流，ω电动机轴上的角速度。

电动机电枢回路的电压方程为：b a a a a a e i R i L u +⋅+=•b e 为电动机反电势。

电动机力矩平衡方程为L D M f J M ++=•ωω由电磁力矩和反电势的关系，有ωe b c e =，a M D i c M =式中e c 为电动机反电势系数，M c 为电动机的转矩系数。

J 为电动机轴上粘性摩擦系数，f 电动机轴上等效转动惯量。

《现代控制理论》第3版(刘豹_唐万生)课后习题答案

，试求出系统的约旦标准型的实现，并画出相应的模拟结构图
（本题思路：使用教材 P41 方法，专门用来把传递函数转化为约旦标准型）
6
7
10(−1)
解：(1)由 () = (+1)(+3)可得到系统表达式为
6(+1)
−4
−
10
3
3
(2)() = (+2)(+3)2 = (+3)2 + +3 + +2 +
2
则状态空间表达式为：
.
1
0
1
0 1
0
.
[2 ] = [ 0
0
1 ] [2 ] + [0]
.
−3 −7 −5 3
1
3
1

= [2 3 1] [ 2 ]
3
相应的模拟结构图如下：
1
3
+
u
-
-

2
+
+
y
5
x3
x2
x1
7
3
1-6
(−)
(+)
已知系统传递函数(1)() = (+)(+) (2)() = (+)(+)
11
0
1
0 11
当1 = −1时，[ 3
0
2 ] [21 ] = − [21 ]
31
−12 −7 −6 31
10
解得： 21 = 31 = −11
（或令11
令11 = 1
11
1
1 = [21 ] = [−1]
31

王金城现代控制理论第一章_习题答案

王金城化工出版社第1章习题参考答案：1-1（a ）选123123,,,,,y y y v v v 为状态变量，根据牛顿定律，对1M ，有()11112121dv M g K y K y y M dt---= 对2M ，有()()222123232dv M g K y y K y y M dt+---= 对3M ，有()33323433dv M g K y y K y M dt+--= 令312112233415263,,,,,dy dy dyx y x y x y x v x v x v dt dt dt=========，整理得 ()()()122214253641112334233251262322233,,,,,K K K x x x x x x x x xg M M K K K K K x K K xx x g x x x g M M M M M +====-++++=-++=-+()()()1221123222223433300010000001000000010000001100010000K K K M M x x g K K K K M M M K K K M M ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥-⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥+-⎢⎥⎢⎥⎣⎦100000010000001000y x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦（b ）选12,12,,y y v v 为状态变量，根据牛顿定律，对1M ，有()11121111dv M g B v v K y M dt+--= 对2M ，有()22221212dv f M g B v B v v M dt+---= 令1211223142,,,dy dyx y x y x v x v dt dt ======，整理得 11113243134111,,K B Bxx x x x x x x g M M M ===--++ ，112434222B B B f x x x g M M M +=-++所以状态空间描述为1111111122220010000001000011100K B B xx g f M M M B B B M M M ⎡⎤⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎢⎥-⎢⎥⎣⎦⎣⎦10000100y x ⎡⎤=⎢⎥⎣⎦1-2（a ）取电感电流i 和电容电压u 为状态变量，列回路方程122c rc c c u u R (i )u u R di L u u dt u du C dt R ⎧=+++⎪⎪⎪=+⎨⎪⎪=⎪⎩令12c x i,x u,y u ===()1212121212112121211r R R R R L(R R )L(R R )L(R R )xx u R C R RC(R R )C(R R )-⎡⎤⎡⎤⎢⎥⎢⎥+++⎢⎥⎢⎥=+⎢⎥⎢⎥--⎢⎥⎢⎥+++⎣⎦⎣⎦1222121212r R RR R y x u R R R R R R ⎡⎤=--+⎢⎥+++⎣⎦ （b ）选择回路电流a i 和电枢角速度ω为状态变量，有aa a a ae di u R i L K dt ω=++ 力矩平衡方程：a a d J B K i ,dtωω+= 其中a K 为转矩常数 1a a e a a a a adi R K i u dt L L L ω=--+a a K d B i dt J J ωω=-- 令12a x i ,x ,ω==有10a e a aa a R K L L L xx u K B JJ -⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦ ， []01y x ω==1-3 （1）传递函数为3221375Y(s )U(s )s s s =+++将传递函数中的公因子提出，于是有3123211375Y(s )s U(s )s s s----=+++ 按梅逊公式构建系统的状态变量图能控标准形：0100001057131x x ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦u []200y x =能观标准形：0052107001130x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]001y =x(2)传递函数为：2332132223123Y(s )s s s U(s )s s s s----++==++++ 按梅逊公式构建系统的状态变量图能控标准形：010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦[]210y x =能观标准形：003210010120x x u -⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]001y x =（3）传递函数为：3212332123324515471547Y(s )s s s s s s U(s )s s s s s s------+++---==+++++++ 按梅逊公式构建系统的状态变量图状态空间描述为：010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦[]514y x u =---+（4）①12121221212121b s b b s b s Y(s )U(s )s a s a a s a s ----++==++++ 状态空间描述为：1322140101xx u x a a x ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦ ，[]21y b b x =②22121201200111s c Z(s )c c Y(s )c s c s c s s c c ---==++++ 状态空间描述为：332144000101x x y c c x x c c ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦ ，301z x c = 两系统串联，得112122332121440001000001000100x x a a x x u x x c c b b x x c c ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦（5）由G(z)有，y(k+3)+4y(k+2)+5y(k+1)+2y(k)=u(k)令12312x (k )y(k )x (k )y(k )x (k )y(k )=⎧⎪=+⎨⎪=+⎩ 1230100100102541x (k )x(k )x (k )u(k )x (k )⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦[]123100x (k )y(k )x (k )x (k )⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦（6）由G(z)有，y(k+3)+6y(k+2)+11y(k+1)+6y(k)=2u(k+2)+u(k+1)+2u(k)01001001061161x(k )x(k )u(k )⎡⎤⎡⎤⎢⎥⎢⎥+=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦[]123212x (k )y(k )x (k )x (k )⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1-4 （a ）化简系统结构图得系统状态空间描述：1234010000010024220025025x x x u x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ []0100y x =(b) 化简系统结构图得系统状态空间描述：1112221323255223735353xx u ///x x u ////--⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ []110y x = []201y x =1-5 (1) 传递函数为21233212332322461246s s s s s G(s )s s s s s s ------++++==++++++ 能控标准形：010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦[]231y x =能观标准形：006210430121x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]001y x =（2）传递函数为24422431332132s s s G(s )s s s s -----+-+==++++ 能控标准形：01000001000001020301xx u ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦[]1300y x =-能观标准形：00021100030103000100x x u -⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=+⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦[]0010y x = 1-6（1） 24512122123123(s )(s )G(s )(s )(s )(s )s s s ++-==++++++++状态空间描述：100102010031x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦，[]12122y x =- （2）223533313313(s )G(s )(s )(s )s s (s )+--==+++++++ 状态空间描述：310003010011x x u -⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦，[]333y x =-- 1-7（1）∵31I A ()()λλλ-=++ 1213,λλ=-=-∴1003A -⎡⎤=⎢⎥-⎣⎦11111111,p Ap ,p λλ⎡⎤=-==⎢⎥⎣⎦，22222131,p Ap ,p λλ⎡⎤=-==⎢⎥-⎣⎦∴1111P ⎡⎤=⎢⎥-⎣⎦1111112P ---⎡⎤=-⎢⎥-⎣⎦ 11112B P B -⎡⎤==⎢⎥-⎣⎦∴11020312x x u ⎡⎤⎢⎥-⎡⎤=+⎢⎥⎢⎥-⎣⎦⎢⎥-⎢⎥⎣⎦（2）1230123I A ,,,λλλλ-==-=-=-∴100020003A -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦111111111,p Ap ,p λλ⎡⎤⎢⎥=-==-⎢⎥⎢⎥-⎣⎦，2222212212,p Ap ,p λλ⎡⎤⎢⎥⎢⎥=-==-⎢⎥⎢⎥⎢⎥⎣⎦333331333,p Ap ,p λλ⎡⎤⎢⎥=-==-⎢⎥⎢⎥⎣⎦∴1111231132P ⎡⎤⎢⎥⎢⎥=---⎢⎥⎢⎥-⎢⎥⎣⎦137272304027162B P B -⎡⎤⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎣⎦∴37271002020304000327162x x u ⎡⎤⎢⎥-⎡⎤⎢⎥⎢⎥=-+--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥⎣⎦（3）519400433030114003433114j x j x j j ⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥-+⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦+⎢⎥⎢⎥⎣⎦1-8 （1）∵A 为友矩阵123012I A ,,λλλλ-====∴ 110010002A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 101112124P ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 1111B P B --⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦ ∴100101010021x x u -⎡⎤⎡⎤⎢⎥⎢⎥=+-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦（2）212331031I A ()(),,λλλλλλ-=--====310030001A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 120112111P ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 11335234B P B --⎡⎤⎢⎥==-⎢⎥⎢⎥-⎣⎦ ∴3101330305200134x x u -⎡⎤⎡⎤⎢⎥⎢⎥=+-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦1-9（1）110061031002P -⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦111000062300100111000152020233302100313000222AP AP -⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦1106203502BP B -⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦203640C CP ⎡⎤==⎢⎥⎣⎦ 11000621102203333502022xx u ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦203640y x ⎡⎤=⎢⎥⎣⎦ （2）①1111I A I P AP P P P AP P (I A)P λλλλ-----=-=-=-11I A P I A P P P I A I A λλλλ---=-=-=-∴特征值不变②1111G(s )C(sI A)B CP(sI P AP )P B ----=-=- 111C P(sI P AP )P B ---⎡⎤=-⎣⎦11111C P(sI )P PP APP B C(sI A )B -----⎡⎤=-=-⎣⎦∴传递函数不变1-10证明：11G (s )c(sI A)b -=- 12G (s )c(sI A)b -=- ∵T T TA A ,b c ,c b ===∴12T T T T T T TG (s )b (sI A )c b (sI )A c -⎡⎤=-=-⎣⎦ [11T T T T T Tb (sI A )c b (sI A)c --⎤⎡⎤=-=-⎦⎣⎦11TTc(sI A )b G (s )-⎡⎤=-=⎣⎦ ∵系统为单输入单输出，11T G (s )G (S )= ∴两者传递函数相同。

《现代控制理论》第3版课后习题答案

《现代控制理论参考答案》第一章答案1-1 试求图1—27系统的模拟结构图，并建立其状态空间表达式。

解：系统的模拟结构图如下：系统的状态方程如下：令y s =)(θ，则1x y =所以,系统的状态空间表达式及输出方程表达式为1—2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得 22213322222131111111111x R y x Cx C x x L x L R x u L x L x L R x =+-=+-=+--=••• 写成矢量矩阵形式为：1—4 两输入1u ,2u ，两输出1y ，2y 的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵. 解：系统的状态空间表达式如下所示：1—5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。

解：令..3.21y x y x y x ===，，，则有相应的模拟结构图如下：1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ，试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：s s s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘ （1）画出其模拟结构图（2）求系统的传递函数解:(2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1—8 求下列矩阵的特征矢量（3）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解：A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得： 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ）当21-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得： 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=14222122p p p P（或令112=p ，得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P ）当31-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得： 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P 1-9将下列状态空间表达式化成约旦标准型（并联分解）(2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x 解：A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--23132313311201214p p p p p p解之得 3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P 约旦标准型1—10 已知两系统的传递函数分别为W 1（s)和W 2（s)试求两子系统串联联结和并联连接时，系统的传递函数阵,并讨论所得结果解:（1）串联联结(2）并联联结1-11 （第3版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1—11(第2版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1—12 已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数u 的系数b(即控制列阵)为（1)⎥⎦⎤⎢⎣⎡=11b解法1：解法2：求T ，使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以，状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。

《现代控制理论》课后习题全部答案(最完整打印版)

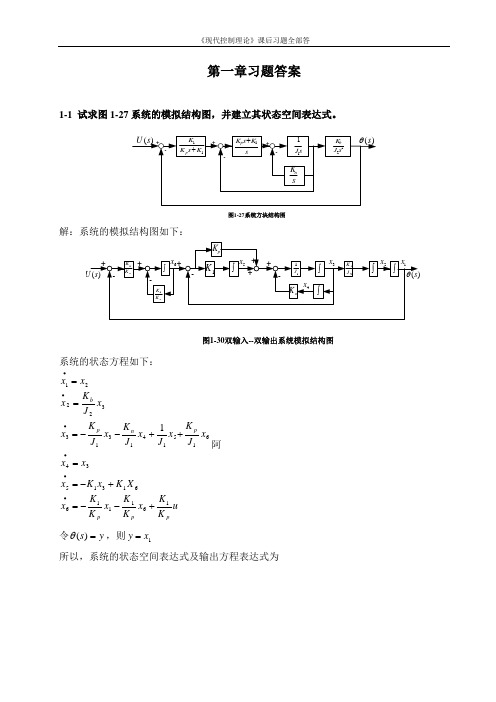
第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。

《现代控制理论》刘豹著(第3版)课后习题答案

第一章习题答案1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc ---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x C C L L R L L R x x x 。

1-5系统的动态特性由下列微分方程描述u u u y y y y 23375)2(......++=+++列写其相应的状态空间表达式，并画出相应的模拟结构图。

解：令..3.21y x y x y x ===，，，则有[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡321321321132100573100010x x x y u x x x x x x 。

相应的模拟结构图如下：573⎰⎰⎰uy+++---31x 2x 3x 211-6 （2）已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡432143214321313310411100000020*********x x x x y u x x x x x x x x1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘（1）画出其模拟结构图（2）求系统的传递函数解：（2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W )1)(2)(3()3(2)3(2+++=+++=-s s s s s s A sI()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++---++-+++++=--)2)(1(150)3()3(2033)1)(2)(3(1)(21s s s s s s s s s s s s A sI ()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++---++-+++++=-=-)3)(12()3()3()1)(2)(3(1210)2)(1(150)3()3(2033)1)(2)(3(1)()(21s s s s s s s s s s s s s s s s s s s s B A sI s W ux[])1)(2()12()1)(2)(3(1)3)(12()3()3(100)()(1+++=+++⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++=-=-s s s s s s s s s s s B A sI C s W uy 1-9将下列状态空间表达式化成约旦标准型（并联分解）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x （2）解：A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 1,332,1==λλ当31=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得 3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101201011T ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-1102112101T⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=-4325183572131102112101B T⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=302413101201011110021CT约旦标准型x ~y ux ~x ~⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=302413432518100030013 1-12 已知差分方程为)(3)1(2)(2)1(3)2(k u k u k y k y k y ++=++++试将其用离散状态空间表达式表示，并使驱动函数u 的系数b(即控制列阵)为（1）⎥⎦⎤⎢⎣⎡=11b解法1：21112332)(2+++=+++=z z z z z z W)(11)(2001)1(k u k x k x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=+ [])(11)(k x k y =解法2：)(2)(3)()(3)(2)1()()1(2121221k x k x k y u k x k x k x k x k x +=+--=+=+ [])(23)()(10)(3210)1(k x k y k u k x k x =⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=+ 求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡=-15041011321010111AT T [][]13101123-=⎥⎦⎤⎢⎣⎡-=CT 所以，状态空间表达式为[])(13)()(11)(1504)1(k z k y k u k z k z -=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡---=+第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。

现代控制理论第一章答案

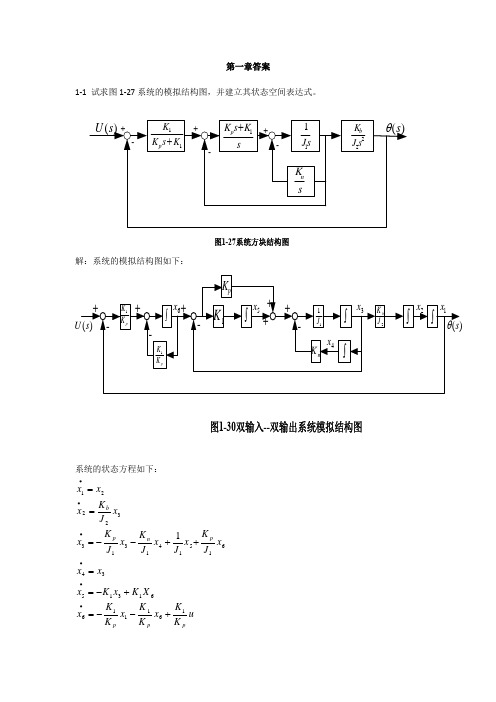
第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：uKK x KK x KK x X K x K x x x x J Kx J x J K x J Kx x J K x x x ppppn pb 1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙65432116543211111111265432100000100000000000000010010000000000010x x x x x x y uK K x x x xx x K K KK K K J K J J K J KJ K x x x x x xp p p p n pb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

L1L2U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x Cx Cx x L x L R x uL x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000010111010x x x R y u L x x x CCL L R L L R x x x 。

《现代控制理论》习题解答 2016-5-18

2s 7 ( s 3)( s 4) 1-13 G ( s ) 1 s3
1 0 0 x 1 0 x 1-14 2 x 3 a2 0 4 a4 0 x y( z) 2( z 1) 2 1-15 u ( z ) ( z 3z 1)
10 s 26 ( s 2)( s 3)( s 4) 。 2s 10 ( s 2)( s 3)
0 x1 0 u1 y1 1 0 0 0 x2 ；。 0 u2 y2 0 1 0 0 x3 b2 x4
x1 x2 x3 。 u ； (0 0 0 0 0 1) x4 x 5 x 6
1-04 设状态变量为 x1 i1 ， x2 i2 ， x3 uC ，状态方程，： x1 i1 , x2 i2 , x3 uC ，状态方程
2( s 2) ( s 1)( s 3) 并联 G ( s ) W1 ( s ) W2 ( s ) 1 s 1
2( s 3) ( s 2)( s 4) 。 s 1 s2
第二章习题解答
1 0 0 A 2-01 (1) 注意 A 0 1 0 1 0 1 2 1 0 A1t 1 1 t ，其中 A1 1 ， A2 ，而 e L [( sI A1 ) ] e ， 1 2 A2
1 ( s 1)( s 3) 1-18 串联 G ( s ) W2 ( s )W1 ( s ) 1 ( s 1)2 s 2 5s 7 ( s 2)( s 3)( s 4) ； 1 ( s 1)( s 2)

《现代控制理论》刘豹著(第3版)课后习题答案

《现代控制理论》刘豹著（第3版）课后习题答案《现代控制理论》刘豹著(第3版)课后习题答案第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

解：系统的模拟结构图如下：系统的状态方程如下：令，那么所以，系统的状态空间表达式及输出方程表达式为 1-2有电路如图1-28所示。

以电压为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻上的电压作为输出量的输出方程。

解：由图，令，输出量有电路原理可知：既得写成矢量矩阵形式为： 1-3 参考例子1-3（P19）. 1-4 两输入，，两输出，的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。

解：系统的状态空间表达式如下所示： 1-5系统的动态特性由以下微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。

解：令，那么有相应的模拟结构图如下： 1-6 （2）系统传递函数,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：1-7 给定以下状态空间表达式‘ （1）画出其模拟结构图（2）求系统的传递函数解：（2） 1-8 求以下矩阵的特征矢量（3）解：A的特征方程解之得：当时，解得：令得（或令，得）当时，解得：令得（或令，得）当时，解得：令得 1-9将以下状态空间表达式化成约旦标准型（并联分解）（2）解：A的特征方程当时，解之得令得当时，解之得令得当时，解之得令得约旦标准型 1-10 两系统的传递函数分别为W1(s)和W2(s) 试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果解：（1）串联联结（2）并联联结 1-11 （第3版教材）如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解： 1-11（第2版教材）如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-12 差分方程为试将其用离散状态空间表达式表示，并使驱动函数u的系数b(即控制列阵)为（1）解法1：解法2：求T,使得得所以所以，状态空间表达式为第二章习题答案 2-4 用三种方法计算以下矩阵指数函数。