工学控制系统的时间响应分析举例
控制系统时间响应分析

控制系统时间响应分析控制系统的时间响应分析是控制系统工程中至关重要的一个环节。
控制系统时间响应分析的目的是对系统的动态性能进行分析和评价,以便设计和改进控制系统以满足系统的性能指标和要求。
时间响应分析是分析系统动态特性最常用的方法之一,由于其简单易行、直观、实用而被广泛采用。
控制系统的时间响应是指系统在输入信号发生突变时,输出信号发生的变化情况,它是衡量控制系统动态响应能力的重要参数之一。
在时间响应分析中,我们通常关注的是控制系统的过渡过程、超调量以及调节时间。
其中,过渡过程是指系统从稳态到达目标状态所需的时间,超调量是指系统在调节过程中输出信号超过目标值的最大值的百分比,调节时间是指系统达到目标状态所需要的时间。
基于这些性能指标的分析,可以确定系统的性能表现和稳定性,进而设计和优化控制系统。
时间响应分析的基本方法是利用系统的数学模型,通过激励系统并观测其输出信号随时间的变化,进而分析系统的响应特性。
此外,还可以通过脉冲响应、阶跃响应、正弦响应等不同的激励信号来分析系统的响应特性。
在针对实际系统时,时间响应分析需要考虑系统的复杂性和非线性因素等影响因素,以便获得更加准确且实用的分析结果。
对于控制系统时间响应分析而言,评价系统的性能指标是非常重要的。
标准的性能指标包括调节时间、超调量、稳态误差和振荡等。
以调节时间为例,当系统从失稳状态开始到达稳态状态的时间越短,则表示系统的响应性能越好。
超调量表示系统在达到目标状态后,输出信号超过设定值的最大值。
稳态误差则反映了系统达到稳定状态后,系统输出值与目标值之间的偏差。
工程控制基础 第3章 系统的时间响应分析

总结 当ζ一定时ωn增大ts就减小; 当ωn一定时ζ增大,ts也减小
华中科技大学 易朋兴
2019/12/30
机械工程控制基础
30
3.4 二阶系统性能指标
➢ 总结
➢ 要使二阶系统具有合适动态特性,应合理选择ζ和ωn。一般的做法是先根据 最大超调量Mp 、振荡次数N等要求选择系统的阻尼比ζ ,然后再根据上升 时间tr、峰值时间tp、调整时间ts等要求,确定系统无阻尼固有频率ωn
➢ 单位脉冲响应
➢ 单位阶跃响应
华中科技大学 易朋兴
2019/12/30
机械工程控制基础
3.2 一阶系统时间响应
➢ 一阶系统:微分方程
传递函数:
➢ 单位斜坡响应
12
T:时间常数
华中科技大学 易朋兴
2019/12/30
机械工程控制基础
3.2 一阶系统时间响应
➢ 一阶系统:微分方程
传递函数:
➢ 不同输入函数不同时间常数下输出响应比较
当ζ一定时ωn增大ts就减小; 当ωn一定时ζ增大,ts也减小
2019/12/30
机械工程控制基础
29
3.4 二阶系统性能指标
➢ 二阶欠阻尼系统瞬态性能指标:
上升时间 tr 、峰值时间 t p 、最大超调量 M p 、调整时间 ts 、振荡次数 N
二阶欠阻尼单位阶跃响应
➢ 振荡次数N :在过渡过程时间内, xo(t)穿越其稳态值的次数的一半
2 n
s2
2n s
2 n
ωn、ζ
:特征参数
➢ 单位脉冲响应
• 当 ,0系统为零阻尼系统时
华中科技大学 易朋兴
2019/12/30
机械工程控制基础
机械工程控制基础-时间响应分析

工程控制基础
第三章 时间响应分析
二、二阶系统对典型输入信号的响应
1、二阶系统的单位脉冲响应
工程控制基础
第三章 时间响应分析
(t≥0)
d n 1 (2 有阻尼固有频率)
工程控制基础 0<ζ<1
第三章 时间响应分析
不同阻尼比时的单位脉冲响应情况
工程控制基础
第三章 时间响应分析
(t≥0)
工程控制基础
(3)
第三章 时间响应分析
(c)特征根的实部≤0
工程控制基础
第三章 时间响应分析
2)
Im[si]绝对值越大,则自由响应项振荡频率越高, 它影响着【系统响应的准确性】。
工程控制基础
第三章 时间响应分析
3.2 典型输入信号
在控制工程中,常用的输入信号有两大类:
•其一是系统正常工作时的输入信号;
•其二是外加的测试信号。
1)一阶系统的单位脉冲响应
➢ω(t)=
ω(tc()t)
1 T
初初始始斜斜率率==T1-T12
(t )
1 T
t
e T (t≥0)
0.368 1
T
0.135
1 T
1 0.018 T
0 T 2T 3T 4T
t
图3-2 一阶系统的 单位脉冲响应曲线
工程控制基础
第三章 时间响应分析
➢一阶系统的调整时间为4T
an
y(n)
(t)
a y(n1) n1
(t)
...
a1 y(t)
a0
y(t)
x(t)
工程控制基础
第三章 时间响应分析
输入引起的
n
n
y(t) A1iesit A2iesit B(t)
控制系统的时间响应

控制系统的时间响应时间响应是描述控制系统对输入信号的处理速度和稳定性的重要指标。
它可以用来评估控制系统在输入信号变化时的动态性能和响应速度。
在控制系统中,时间响应通常被描述为系统的输出随时间变化的情况。
它可以通过观察系统的单位跃跃响应来获得,这是由一个单位输入信号(例如单位阶跃信号)引起的输出响应。
时间响应通常包括以下几个重要的参数:1. 延迟时间(T_d): 时间响应中的延迟时间是系统响应达到稳定状态所需要的时间。
它是输出响应与输入信号出现变化之间的时间差。
2. 实现时间(T_r): 实现时间是从控制系统开始响应到输出达到一定百分比(通常是90%)的时间,即系统从稳定状态到达一定百分比的时间。
3. 峰值时间(T_p): 峰值时间是输出响应达到峰值的时间。
它表示了系统的响应速度。
4. 上升时间(T_rise): 上升时间是指从输出响应开始上升到达峰值之间的时间。
5. 超调量(M_p): 超调量是指输出响应超过稳定状态的最大值与稳定状态值的差值。
它用于评估系统的稳定性和控制精度。
通过这些参数,可以评估控制系统的时间响应特性和性能。
在控制系统设计中,通常希望系统的时间响应具有快速的响应速度、稳定的稳态性能和较小的超调量。
因此,在设计控制系统时,需要选择合适的控制算法、参数调节方法和控制器结构,以达到所需的时间响应要求。
总而言之,时间响应是控制系统的重要性能指标,它描述了系统对输入信号的处理速度和稳定性。
通过评估时间响应的各个参数,可以优化控制系统的设计和性能,以实现对输入信号的快速、准确的响应。
控制系统的时间响应在许多实际应用中至关重要。
例如,在工业自动化领域中,时间响应的快速性和稳定性直接影响到控制系统对于输入信号变化的迅速响应和稳态精度。
另外,在飞行器、机器人、交通管理等领域,时间响应的优化也是关键技术,因为它能够提供准确的控制和快速的决策。
时间响应的性能可以通过线性或非线性控制系统的数学建模和分析得到。
自动控制原理(时间响应分析)课件

高阶系统的数学模型
总结词
高阶系统的数学模型通常采用状态空间表示 法,包括状态方程和输出方程。
详细描述
高阶系统的数学模型是描述系统动态行为的 重要工具。通常采用状态空间表示法,包括 状态方程和输出方程。状态方程描述了系统 内部状态变量随时间的变化规律,而输出方 程则描述了系统输出与内部状态变量之间的 关系。通过建立高阶系统的数学模型,可以
03
数学模型
04
高阶系统的数学模型通常表示为 (G(s) = frac{a_n s^n + a_{n-1} s^{n-1} + ldots + a_1 s + a_0}{s^n + b_{n-1} s^{n-1} + ldots + b_1 s + b_0})。
实例
高阶系统的实例包括多级控制系 统、复杂机械系统等。
详细描述
性能指标用于评估二阶系统的动态行为和响应特性。常见的性能指标包括超调量、调节时间和稳态误差等。这些 指标可以通过系统的传递函数或状态空间方程进行计算和分析。
二阶系统的稳定性分析
总结词
二阶系统的稳定性可以通过析系统的 极点和零点来判断。
VS
详细描述
稳定性是评估系统能否正常工作的关键因 素。通过分析二阶系统的极点和零点,可 以判断系统的稳定性。如果所有的极点都 位于复平面的左半部分,则系统是稳定的 。否则,系统是不稳定的。
对系统进行各种分析和设计。
高阶系统的性能指标
总结词
高阶系统的性能指标主要包括稳定性、快速性和准确性 。
详细描述
高阶系统的性能指标是评估系统性能的重要依据。稳定 性是指系统在受到扰动后能够回到原始平衡状态的能力 。快速性是指系统对输入信号的响应速度,即系统达到 稳态值所需的时间。准确性则是指系统输出与理想输出 之间的误差,即系统的跟踪精度。这些性能指标在高阶 系统的分析和设计中具有重要意义。
控制工程基础-第三章时间响应分析第一二节

2020年11月4日星期三2时17分22秒
9
机械工程控制基础
昆明理工大学机电学院
➢ 3.1 时间响应及其组成
第三章 时间响应分析
上面分析的是一个特殊的简单的例子,主要目的是 为下面的一般情况的分析作引子。
对于一般情况(线性常微分方程的输入函数没有导 数项,只有一次项),设系统的动力学方程为:
an
y (n)
如图所示,质量为m与弹簧刚度为k的单自由度系统
在外力(即输入)Fcosωt的作用下,系统的动力学方程用
常微分方程表示为:
my(t) ky(t) F cost
由高等数学知识可知这一 非齐次常微分方程的完全解 由两部分组成:
y(t) y1(t) y2 (t)
式中:yl(t)是齐次微分方程的通解; y2(t)是其一个特解。
的关系和0型、I型、Ⅱ型系统的稳态偏差。 6、单位脉冲函数及单位脉冲响应函数的重要意义。
2020年11月4日星期三2时17分22秒
2
机械工程控制基础
昆明理工大学机电学院
➢ 3.1 时间响应及其组成
第三章 时间响应分析
时间响应及其组成的含义: 时间响应:是指系统的响应(输出)在时域里的表现形
式,或系统的动力学方程在一定初始条件下的解
将系数A、B代入整理得方程的最终解为:
自由响应 强迫响应
y(t) y(0n ) sinnt y(0) cosnt Fk 112 cosntFk 112cost
零输入响应
零状态响应
2020年11月4日星期三2时17分22秒
7
机械工程控制基础
昆明理工大学机电学院
➢ 3.1 时间响应及其组成
第三章 时间响应分析
控制工程基础第四章系统的时间响应分析1

出量随时间的变化规律,并由此来确定系统的性
能。
page 2
机电工程学院
第四章 系统的时间响应分析
第一节 时域响系应统概受到述外加作用激励
一、时域响应的概念
后,从初始状态到最终
时域响应(Time Response)状:态控的制响应系过统程在。外加
作用(输入)激励下,其输出量随时间变化的函数
控 制
关系 。
第四章 系统的时间响应分析
当t>t1时,系统趋于稳定。
当t→∞时,若c(t)趋于
稳态值,则系统是稳定。
t t1
当t→∞时,若c(t)呈
等幅振荡或发散,则系 统是不稳定。
t
图4-1-1 单位阶跃信号作用下的时域响应
0到t1时间内的响应过程称为瞬态响应,反映了系统动态性能。
稳态响应偏离系统期望值的程度可用来衡量系统的精确程度。
Ts 1
(a) 单位反馈的一阶系统
(b) 一阶系统
控
制 工
图4-3-2 一阶系统方框图
程 基
Φ(s) C(s) 1
础
R(s) Ts 1
时间常数
下面就不同的典型输入信号,分析该系统的时间响应。
page 18
机电工程学院
第四章 系统的时间响应分析
二、一阶系统的单位阶跃响应
当输入信号r(t)=u(t)时,系统的响应称为单位阶跃响应。
(一)欠阻尼二阶系统(0 1)
s1,2 n jn 1 2 n jd
j
系统的有阻 尼固有频率
d n 1 2控 制Fra biblioteks1
工
程 基 础
0
欠阻尼二阶系统特征根在
控制系统的时域分析_一二阶时间响应讲述

控制系统的时域分析_一二阶时间响应讲述时域分析是控制系统理论中的重要内容,主要用于分析系统的时间响应。
在时域分析中,我们会关注系统的输入和输出之间的关系,并研究系统在时间上的性能指标和特征。
本文将重点讲述一阶和二阶系统的时间响应。
一、一阶系统的时间响应一阶系统是指系统的传递函数中只有一个一阶多项式的系统,其传递函数形式为:G(s)=K/(Ts+1)其中,K是系统的增益,T是系统的时间常数。
一阶系统的单位阶跃响应是常用的时间响应之一,通过对系统施加一个单位阶跃输入,可以得到系统的响应曲线。
单位阶跃输入可以表示为:u(t)=1由于一阶系统的传递函数是一个一阶多项式,因此它的拉普拉斯变换可以通过部分分式展开得到:G(s)=K/(Ts+1)=A/(s+1/T)通过进行拉普拉斯逆变换,可以得到系统的单位阶跃响应函数y(t):y(t) = K(1 - exp(-t/T))其中,exp(-t/T)为底数为e的指数函数,表示系统的响应曲线在t时刻的衰减程度。
从单位阶跃响应函数可以看出,一阶系统的时间常数T决定了系统的响应速度和衰减程度。
时间常数越小,系统的响应越快速,衰减程度也越快。
二、二阶系统的时间响应二阶系统是指系统的传递函数中有一个二阶多项式的系统,通常可以表示为:G(s) = K / (s^2 + 2ξω_ns+ω_n^2)其中,K是系统的增益,ξ是系统的阻尼比,ω_n是系统的自然频率。
二阶系统的时间常数和质量阻尼比是描述系统性能的重要参数。
时间常数决定了系统响应的速度,质量阻尼比则影响了系统的稳定性和衰减程度。
对于二阶系统的单位阶跃响应,可以通过拉普拉斯逆变换得到响应函数y(t):y(t) = K*(1 - (1-ξ^2)^0.5 * exp(-ξω_nt) * cos((1-ξ^2)^0.5 * ω_nt + φ))其中,φ为相位角,由初始条件和变量确定。
从单位阶跃响应函数可以看出,二阶系统的阻尼比ξ决定了系统的过阻尼、临界阻尼和欠阻尼的响应形式。
控制系统的时域分析_一二阶时间响应
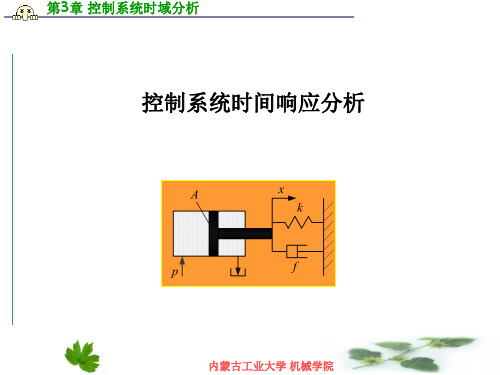
2 At 拉氏变换为: R( s )=L 2 s3
图3-2c 加速度信号
该实验信号相当于控制系统中加入一按恒加速度变化 的信号,加速度为A。当A=1时,称为单位加速度函数。
内蒙古工业大学 机械学院
第3章 控制系统时域分析
4.脉冲信号
脉冲函数如右图所示,定义为
1 , r (t ) h 0, 0 t h t 0, t h
•其中: T — 时间常数;ωn—自然频率; —阻尼比;
1 n T
内蒙古工业大学 机械学院
第3章 控制系统时域分析
方块图
R(s)
G(S )
C(s)
-
G(S)=
(S )
2 n 1 s ( s 2n )
s ( s 2n )
2 n
?
G( S ) S (S 2n )
传递函数:
U c ( s) 1 ( s) U r (s) LCs 2 RCs 1
内蒙古工业大学 机械学院
第3章 控制系统时域分析
2、标准形式
微分方程
2 d c(t ) dc(t ) 2 T 2 T c(t ) r (t ) 2 dt dt
传递函数
2 C ( s) 1 n 2 ( s) 2 2 2 R( s) T s 2 Ts 1 s 2n s n
dc( t ) c( t ) r ( t ) dt
E(s) G(S)
i(t) R
ur (t )
C
uc (t )
T
C ( s) 1 R( s ) Ts 1
C(s)
R(s)
-
G(S)= ?
第三章 控制系统的时间响应分析 举例

例3.1 设二阶系统如图3.16所示,其中ζ=0.5 ,n ω=4弧度/秒。
当输入信号为单位阶跃函数时,试求系统的瞬态性能指标。
图3.16 典型二阶系统方块图 解 由给定的ζ和n ω值,可得46.015122=-=-=ζωωn d (弧度/秒)93.06.06.01arctan 1arctan 22=-=-=ζζϕ(弧度)上升时间r t 为:)(55.0493.014.3秒=-=-=d r t ωϕπ峰值时间pt 为:)(785.0414.3秒===d p t ωπ最大超调量δ%为%48.9%100%100%226.016.014.31=⨯=⨯=-⨯---eeζζπδ调节时间s t为33.156.044=⨯==ns t ζω(秒) (取Δ=2)156.033=⨯==ns t ζω(秒) (取Δ=5)振荡次数N 为85.06.014.36.0121222=⨯-=-=πζζN (取Δ=2)64.06.014.36.015.115.122=⨯-=-=πζζN (取Δ=5)注意,振荡次数N <1,说明动态过程只存在一次超调现象。
这是因为动态过程在一个阻尼振荡周期内就已经结束,即d d s T t ωπ2=<例3.2 考虑如图3.15所示随动系统,K =16,T =0.25秒。
试求:(1)计算瞬态性能指标δ%和t s ;(2)若要求δ%=16%,当T 0不变时K 应取何值?(3)若要求系统的单位阶跃响应无超调,且调节时间10≤s t 秒,开环增益K 应取多大?此时s t为多少?图3.15 随动系统方块图解:(1)容易得到实际参数K 、T 和特征参数ζ、n ω的关系,有(弧度/秒)825.01625.025.0162121====⨯==TK KTn ωζ得%43.44%100%100%2225.0125.014.31=⨯=⨯=-⨯---ee ζζπδ得2825.044=⨯==ns t ζω(秒) (取Δ=2)5.1825.033=⨯==ns t ζω(秒) (取Δ=5)(2)为使%,16%=δ,有δζζπln 12=--将16.0=δ代入,可得5.0=ζ,即应使ζ由0.25增大至0.5。
自动控制原理第五章控制系统时间响应分析
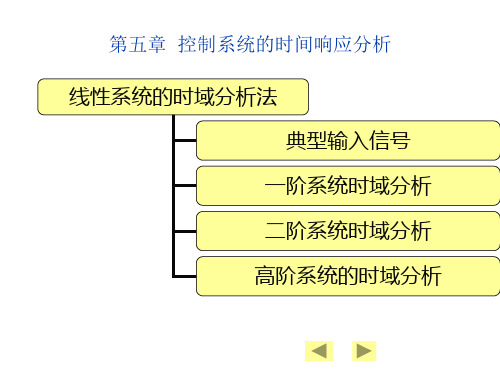
tt
1 e T 0.1
t2
1 e T 0.9
t1 t2
e T 9
tr t2 t1 15 ln 9 33s
5.3 二阶系统的时间响应 Time Response Analysis of Second-order Systems
二阶系统:凡以二阶系统微分方程作为运动方程的控制系统。
一.二阶系统的数学模型
5.2.1 一阶系统单位阶跃响应
Unit-Step Response of First-order System
因为单位阶跃函数的拉氏变换为 R(s) 1
S
,则系统的输出由下式可知为
(s) C(s) 1
C(s) (s)R(s) 1 1 1 T
R(s) TS 1
TS 1 S S TS 1
对上式求拉氏反变换,得:
1t
1t
c(t) t T (1 e T ) t T Te T
因为
1 t
e(t) r(t) c(t) T (1 e T )
r(t) c(t)
所以一阶系统跟踪单位斜坡信号的稳态误差为
ess
lim e(t) T t
上式表明:①一阶系统能跟踪斜坡输入信
r(t) c(t)
% 评价系统的阻尼程度。
5.2 一阶系统时间响应
用一阶微分方程描述的控制系统 称为一阶系统。所示的RC电路, 其微分方程为
R
+
+
r(t)
i(t) C
c(t)
c(t)
1 C
i(t)dt
i(t)
C
dc(t) dt
RC dc(t) c(t) r(t) dt
•
T c(t) c(t) r(t)
控制系统时间响应分析”实验报告

控制系统时间响应分析”实验报告实验⼀、“控制系统时间响应分析”实验报告⼀、实验类型验证性实验⼆、实验⽬的1、求系统在时间常数 T 不同取值时的单位脉冲、单位阶跃响应和任意输⼊响应,熟悉系统时间响应的定义和图形曲线2、求系统的上升时间、峰值时间、最⼤超调量和调整时间等性能指标,熟悉系统瞬态性能指标的定义。
三、实验仪器与设备(或⼯具软件)计算机,MATLAB 软件四、实验内容、实验⽅法与步骤已知系统传递函数50 2 0.05s (1 )s 501、求系统在时间常数 T 不同取值时的单位脉冲、单位阶跃响应和任意输⼊响应。
应⽤impulse 函数,可以得到 T =0, T =0.0125、T 0.025时系统单位脉冲响应;应⽤函数,同样可以得到 T 0, T 0.0125、T 0.025时系统单位阶跃响应。
2、求系统的瞬态性能指标五、实验结果1、系统在时间常数 T 不同取值时的单位脉冲、单位阶跃响应和任意输⼊响 t=[0:0.01:0.8];%仿真时间区段n G=[50];tao=0; dG=[0.05 1+50*tao 50]; G 仁tf(nG ,dG);tao=0.0125; dG=[0.05 1+50*tao 50]; G2=tf( nG ,dG);tao=0.025; dG=[0.05 1+50*tao 50]; G3=tf(nG,dG);% 三种⼯值下,系统的传递函数模型[y1,T]=impulse(G1,t);[y1a,T]=step(G1,t);[y2,T]=impulse(G2,t);[y2a,T]=step(G2,t);[y3,T]=impulse(G3,t);[y3a,T]=step(G3,t);% 系统响应subplot(131),plot(T,y1,'--',T,y2,'-.',T,y3,'-')lege nd('tao=0','tao=0.0125','tao=0.025')xlabel('t(sec)'),ylabel('x(t)');grid on;G(s) stepsubplot(132),plot(T,y1a,'--',T,y2a,'-.',T,y3a,'-')legend('tao=0','tao=0 ?0125','tao=0.025')grid on;xlabel('t(sec)'),ylabel('x(t)');% 产⽣图形t=[0:0.01:1];u=si n(2*pi*t);% 仿真时间区段和输⼊Tao=0.025;nG=[50]; dG=[0.05 1+50*tao 50]; G=tf(nG ,dG);% 系统传递函数模型y=lsim(G,u,t); %求系统响应plot(t,u,'--',t,y,'-',t,u'-y,'-.','l in ewidth',1)lege nd('u(t)','xo(t)','e(t)')grid; xlabel('t(sec)'),ylabel('x(t)');% 产⽣图形t=[0:0.01:1];u=si n(2*pi*t);tao=0.025;n G=[50];dG=[0.05 1+50*tao 50];G=tf( nG ,dG);y=lsim(G,u,t); subplot(133),plot(t,u,'--',t,y,'-',t,u-y','-.','li newidth',1) lege nd('u(t)','xo(t)','e(t)')grid on ;xlabel('t(sec)'),ylabel('x(t)');系统在时间常数T 不同取值时的单位脉冲、单位阶跃响应和任意输⼊响应I (WE) XlfCl2、系统的瞬态性能指标t=0:0.001:1; %设定仿真时间区段和误差限yss=1;dta=0.02;tao=0; dG=[0.05 1+50*tao 50]; G仁tf(nG ,dG);tao=0.0125; dG=[0.05 1+50*tao 50]; G2=tf( nG ,dG);tao=0.025; dG=[0.05 1+50*tao 50]; G3=tf(nG ,dG); %三种T值下,系统的传递函数模型y1=step(G1,t); y2=step(G2,t);y3=step(G3,t); %三种T直下,系统的单位阶跃响应r=1;while y1(r)tr1=(r-1)*0.001; %T =0时的上升时间[ymax,tp]=max(y1);tp 仁(tp-1)*0.001;% 峰值时间mp1=(ymax-yss)/yss;% 最⼤超调量s=1001;while y1(s)>1-dta &y1(s)<1+dta;s=s-1;e ndts1=(s-1)*0.001;% 调整时间r=1;while y2(r)tr2=(r-1)*0.001;[ymax,tp]=max(y2);tp2=(tp-1)*0.001;mp2=(ymax-yss)/yss;s=1001;while y2(s)>1-dta &y2(s)<1+dta;s=s-1;e ndts2=(s-1)*0.001;% T =0.012啲性能指标r=1;while y3(r)tr3=(r-1)*0.001;[ymax,tp]=max(y3);tp3=(tp-1)*0.001;mp3=(ymax-yss)/yss;s=1001;while y3(s)>1-dta &y3(s)<1+dta;s=s-1;e ndts3=(s-1)*0.001;% T =0.025勺性能指标[tri tp1 mp1 ts1;tr2 tp2 mp2 ts2;tr3 tp3 mp3 ts3]% 显⽰ans =0.0640 0.1050 0.3509 0.35300.0780 0.1160 0.1523 0.25000.1070 0.1410 0.0415 0.1880实验⼆“控制系统频率特性分析”实验报告⼀、实验类型验证性实验⼆、实验⽬的1 利⽤MATLAB 绘制Nyquist图2、利⽤MATLAB 绘制Bode图3、利⽤MATLAB求系统的频域特征量三、实验仪器与设备(或⼯具软件)计算机,MATLAB软件四、实验内容、实验⽅法与步骤已知系统传递函数、24(0.25s 0.5)G(s)(2.5s 1)(0.025s 1)1、利⽤MATLAB 绘制Nyquist图2、利⽤MATLAB绘制Bode图3、利⽤MATLAB求系统的频域特征量五、实验结果(1)k=24, numG 仁k*[0.25 0.5];denG仁conv([5 2],[0.05 2]); %系统的传递函数%[re,im]=nyquist(numG1,denG1); % 求时频特性和虚频特性% plot(re,im);grid %⽣成Nyquist 图利⽤MATLAB 绘制Nyquist图:(2)k=24,numG1= k*[0.25 0.5];denG 仁conv([5 2],[0.05 2]); %系统的传递函数 %w=logspace(-2,3,100); % 产⽣介于 10-2(0.01)和 103(1000)之间的 100 个频率点 % bode(numG1,denG1,w);grid % 绘制 Bode 图利⽤MATLAB 绘制Bode 图%:Fr 舒朋riGf (3)⽲9⽤MATLAB 求系统的频域特征量k =24Mr =9.5398Wr =0.0100M0 =9.5398Wb =3.3516 me IJpnII&io'2 1C -1 10°10 1O 2 10i -ir r r?i r -------------- R — t - - lr r mT T —i —■— r T ■上4⼀。
机械工程控制基础时间响应分析3

1
B
0.632 A
63.2% 86.5% 95% 98.2% 99.3% 99.8%
0 1 23 4 56
t
T TT T TT
第三章 时间响应分析
一阶系统单位阶跃响应的特点 响应分为两部分
瞬态响应: et T
表示系统输出量从初态到终态的变化过程
(动态/过渡过程)
稳态响应:1
表示t时,系统的输出状态
第三章 时间响应分析
三、一阶系统的时间响应
1、 一阶系统(惯性环节)
微分方程:T
dxo (t) dt
xo (t)
xi (t),T
:时间常数
G(s) 1 Ts 1
极点(特征根):-1/T
x2o1、(/tT一) 阶系统的单位脉冲响应
Xi (s) 1
0.36T81
斜率
1 T2
xo(t)
X o (s)
第三章 时间响应分析
时间响应的概念
描述系统的微分方程的解就是该系统时间响应的数学 表达式。任一系统的时间响应都是由瞬态响应 和稳态响应组成。
瞬态响应 系统在某一输入信号的作用下,系统的输出 量从初始状态到稳定状态的响应过程称为瞬态(或称暂态) 响应,也称过渡过程。
稳态响应 在某一输入信号的作用后,时间趋于无 穷大时系统的输出状态称为稳态响应。
xo(t)=t-T+Te-t/T
0
t
第三章 时间响应分析
一阶系统单位速度响应的特点
瞬态响应:T e – t /T ;稳态响应:t – T; 经过足够长的时间(稳态时,如t 4T),输
出增长速率近似与输入相同,此时输出为:
t – T,即输出相对于输入滞后时间T;
控制系统的时间响应分析

实验一控制系统的时间响应分析一、实验目的1.学习一、二阶系统阶跃响应曲线的实验测试方法。
2.研究二阶系统的两个重要参数ζ、ωn对阶跃瞬态响应指标的影响。
二、实验仪器1.XK—KL1型自动控制系统实验箱2.计算机三、实验原理1. 模拟实验的原理控制系统模拟实验采用复合网络法来模拟各种典型环节,即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节,然后可按给定的系统电路图将其连接,以获得相应的模拟系统;再将输入信号加到模拟系统的输入端,利用计算机测量系统的输出,便可获得系统的响应曲线及性能指标,若改变系统参数,可进一步分析研究参数对系统性能的影响。
2.控制系统的阶跃响应①时域响应系统的输入(或称受到外加作用)所引起的输出随时间的变化历程,称其为“时域响应”或“时间历程” ;②阶跃输入在分析和设计控制系统时,为了安全和方便,常选择一些典型的输入形式,其中最常用的是阶跃输入,其形式如下图:四.实验内容1)典型环节的阶跃响应①构建典型环节的模拟电路,连接测量系统;比例环节惯性环节G(S)= -R2/R1 G(S)= - (K/(TS+1) )K=R2/R1,T=R2C 积分环节微分环节G(S)=1/TS T=RC G(S)= - RCS②输入阶跃信号,测量阶跃响应,记录波形及其相关数据;2)二阶系统的阶跃响应①构建二阶系统的模拟电路,连接测量系统;典型二阶系统的闭环传递函数为:222 ()2nn nss sωϕξωω=++;系统的闭环传递函数为:2221/()2()/1()(/)Ts U s U sS K T S Tϕ==++;式中, T = RC ,K = R2/R1;其中ζ和ωn对系统的动态品质有决定的影响。
二阶系统模拟电路如下图,经计算得电路的结构图为比较以上两式:nω=1/T=1/RC, ξ= K/2=R2/2R1)由上式可知:改变比值R2 / R1 ,可以改变二阶系统的阻尼比;ω。
改变R C 值可以改变无阻尼自然频率n可取:R 1 = 200 K ;R 2 = 100 K ,200 K ;R = 100 K ;C = 1 µ f ; 0.1μf 。
第五章控制系统的时间响应-18页文档资料

mm
2 mk m m
2 n
k m
c 2 mk
b) 求根据终值定理求 k
xo(∞)
lt im xo(t) lsi m0 sXo(s) ls i0m sm2s1csk8s.9
8 .9 k
=0.03
k=297(N/m)
c) 求 ξ、ωn
Mp
e
12
10% 0 0.00.0032910% 0 =9.6%
=
G(s)Xi(s)
1 Ts
1
10 s2
ess ls im 0s[1s20T1s11s20]lsi m0 s21(T0Tss21) 10T
例2 已知一控制系统如图所示,其中K=40,τ=0.1,当xi(t) 为单位阶跃函数时,求该系统的自由频率ωn、阻尼
比ξ和时间响应性能指标 tr、tp、ts、Mp、N。
Xi(s) + -
K s (s 1)
Xo(s)
K
Gb(s)
1
s ( s
1) K
s ( s 1)
s2
K s
K
s2
K /
1s
K
/
s2
400 10s 400
s2
n2 2ns
n2
ωn=20,ξ=0.25
s2
n2 2ns
n2
12
t r
arctg
n 1 2
=0.094
tp
n
=0.16
二阶系统一般都设计成欠阻尼系统,有关响应性能指标是在 欠阻尼系统单位阶跃响应情况下导出的。
1. 性能指标及其要求 时间响应性能指标应能充分反映系统时间响应的稳定性、 快速性和准确性。根据这一要求,共有五个指标。
控制系统时间响应分析

实验报告课程名称控制工程基础题目实验一控制系统时间响应分析工具 _______matlab系别 _仪器科学与光电工程学院__ 专业测控技术与仪器姓名 ____班级/学号成绩指导教师实验一 控制系统时间响应分析1. 实验目的(1)学习并掌握Matlab 控制系统时间响应分析的简单使用方法; (2)掌握控制系统时间相应的分析方法; (3)掌握控制系统时间响应的性能指标。
2. 实验仪器系统安装有matlab 软件的计算机实验系统。
3. 实验内容一阶系统和二阶系统在单位脉冲、单位阶跃作用下的响应分析。
1)一阶系统形式410As + A=2n+1;n=0,1,2, (9)2)二阶系统形式291120As s ++ A=2n+1;n=0,1,2, (9)4. 实验步骤(1) 打开matlab (2) 建立***.m 文件 (3) 编制程序(主要指令:tf 、step 、impulse ; 注释用“%”开头)(4) 运行所编制程序(5) 运行结果记录(存储) (6)存储所编制程序5. 实验结果分析和实验报告(即分析系统响应快速性、振荡性与系统参数的关系)1101104104+⨯=+s A As 得10A T = (1)一阶系统单位脉冲输入A 1 3 5 7 9 T 0.1 0.3 0.5 0.7 0.9 t s (2%)0.43 1.38 2 3 3.6 t s (5%)0.31 0.95 1.5 2.35 3 程序:num=[0,4];den=[1,10]; %A=2n+1 n=0,1,2,...9 impulse(num,den) gridA=1图形如下:00.10.20.30.40.50.60.511.522.533.54Im pulse ResponseTim e (sec)A m p l i t u d e实验结果分析:随着时间常数的增加,系统达到稳定时所用的时间也不断的增加,放大倍数减小。
(2)一阶系统单位阶跃输入A 1 3 5 7 9 T 0.1 0.3 0.5 0.7 0.9 t s (2%)0.4 1.2 2 2.7 3.55t s (5%)0.3 0.88 1.5 2.1 2.7程序: A=1num=[0,4];den=[1,10]; %A=2n+1 n=0,1,2,...9 step(num,den) gridA=1图形如下:00.10.20.30.40.50.60.050.10.150.20.250.30.350.4Step ResponseTim e (sec)A m p l i t u d e实验结果分析:随着时间常数的增加,系统达到稳定时所用的时间也不断的增加,放大倍数也增大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3.1 设二阶系统如图3.16所示,其中=0.5 ,=4弧度/秒。
当输入信号为
单位阶跃函数时,试求系统的瞬态性能指标。
图3.16 典型二阶系统方块图 解 由给定的和值,可得
4
6.015122=-=-=ζωωn d (弧度/秒)
93
.06.06.01arctan 1arctan
2
2
=-=-=ζ
ζϕ(弧度)
上升时间为:
)(55.0493
.014.3秒=-=-=
d r t ωϕπ
峰值时间为:
)(785.0414.3秒===
d p t ωπ
最大超调量δ%为
%48.9%100%100%2
2
6.016.014.31=⨯=⨯=-⨯-
--
e
e
ζ
ζπ
δ
调节时间为
33.156.04
4=⨯=
=
n
s t ζω(秒) (取Δ=2)
156.03
3
=⨯=
=
n
s t ζω(秒) (取Δ=5)
振荡次数N 为
85.06.014.36.012122
2
=⨯-=-=
πζ
ζN (取Δ=2)
64.06.014.36.015.115.122
=⨯-=-=
πζ
ζN (取Δ=5)
注意,振荡次数N <1,说明动态过程只存在一次超调现象。
这是因为动态过程
在一个阻尼振荡周期内就已经结束,即
d d s T t ωπ
2=
<
例3.2 考虑如图3.15所示随动系统,K =16,T =0.25秒。
试求:(1)计算瞬
态性能指标δ%和t s ;(2)若要求δ%=16%,当T 0不变时K 应取何值?
(3)若要求系统的单位阶跃响应无超调,且调节时间10≤s t 秒,开环增 益K 应取多大?此时为多少?
图3.15 随动系统方块图
解:(1)容易得到实际参数K 、T 和特征参数、的关系,有
(弧度/秒)825.016
25
.025
.0162121===
=⨯=
=
T
K
KT
n ωζ
得
%43.44%100%100%2
2
25.0125.014.31=⨯=⨯=-⨯-
--
e
e ζ
ζπ
δ
得
2
825.04
4
=⨯=
=
n
s t ζω(秒) (取Δ=2)
5
.1825.03
3
=⨯=
=
n
s t ζω(秒) (取Δ=5)
(2)为使%,16%=δ,有
δ
ζ
ζπ
ln 12
=--
将16.0=δ代入,可得5.0=ζ,即应使由0.25增大至0.5。
当T 不变时。
K 应为
4)5.0(25.041412
2=⨯⨯==
ζT K
即K 应缩小4倍。
(3)根据题意,应取1≥ζ。
而1=ζ时系统的响应速度最快,所以取1=ζ。
由调节时间t s 为 )/(75.42s t s -= 将闭环系统特征方程
012=++
T K s T s
与典型二阶系统特征方程
0222=++n n s s ωζω 对比,并将T =0.25,=1代入,有 24==K n ω
从而解出要求的开环增益K =1,即系统闭环特征方程为
0442
=++s s
特征根
221-==s s 所以调节时间
375.2)/(75.42=-=s t s (秒) 满足指标要求。
从上例可以看出,瞬态性能指标和实际系统参数K 、T 之间的关系。
当阻尼系数10<<ζ时:
1、 当K 增大时,值下降,δ%上升,N 增加,即K 越大,系统振荡越 严重。
2、当T 增大时,值下降,δ%和N 都增大,同时又引起减小,从而会引起t s 增大,所以T 增大将使t s 上升。
由此可见,T 增大对系统的瞬态性能指标是不利的。
若>1,K 增大将引起下降,上升,使t s 减小。
T 增大使和均下降,总的效果仍然使t s 上升。
为了改善系统性能,可以在不改变K 的情况下,采用附加速度反馈(即微分反馈)使阻尼系统数提高。
例3.3:图为一个机械振动系统。
当有F=3N 的力(阶跃输入)作用于系统时,系统中质量m 作如图所示的运动,根据这个响应曲线,确定原质量m 、粘性阻尼系数f 和弹簧刚度系数k 的值。
解:
1.数学模型: ()
t F ky dt dy f dt y d m 122⋅=++
2222
21
1)()()(n n n s s k k fs ms s F s Y s G ωςωω++=++==
式中:
m k n =ϖ称无阻尼固有频率,mk f 1
2=
ς称阻尼比 2.由响应曲线的稳态值为1cm 可求出k :
F(s)=3/s
()()()s k fs ms s F s G s Y 3
12++=
=
由拉氏变换的终值定理可得:
()()1
3
lim 0===∞→→k s sY t t y s k=3 (N/cm)=300 (N/m)
3.由最大超调量M p =0.095(cm)和超调时间t p =2(s)求ζ、ωn
()()
()()
%
100095.02
1⨯==∞=
∞∞-=
--
π
ςςσe y M c c t c p p p
得:ζ=0.6。
2
12=-==
ς
ωπωπn d p t
得:ωn =1.96 (rad/s)
4.通过二阶系统的标准形式由ζ、ωn 求得m 和f 。
)(09.7896.130096.12
2kg k m m k
n
n =====
ωω
)/(67.18309.783006.0226.01
2m s N m k f m k
f ⋅=⨯⨯⨯====
ςς。
