人教版高中数学必修五2.3.1 等比数列 (共17张PPT)
人教高中数学等比数列优秀PPT

人教高中数学等比数列优秀PPT
1.中美贸易摩擦已升级为舆论战,坚 持正确 舆论导 向、弘 扬爱国 主义精 神尤为 重要。 2.爱国主义精神具有深厚的历史性, 极强的 传承力 、感染 力,以 及坚韧 性,顽 强性和 理性。
3.爱国主义精神,是在中国共产党近 百年之 奋斗史 中不断 形成, 积聚与 升华而 成的。 4.面对史上规模最大的贸易战,中国 政府和 人民最 重要的 是“集中 力量做 好自己 的事” 5.美方发起贸易战,进行恫吓威胁, 不会给 中国发 展带来 困难和 影响, 只会更 加激发 中国人 民的勇 气、士 气与硬 气。 6.不能把质朴、理性的爱国主义视为 民粹主 义、狭 隘民族 主义, 同时应 防止各 种形式 的民粹 主义和 极端民 族主义 行为。 7. 众多短视频平台成为人们的消遣神 器,但 如果缺 乏内容 创新和 内涵续 航,短 视频的 发展将 不容乐 观。 8. 在这个浅表性阅读时代,越是具有 艺术美 感、内 容穿透 力和人 文内涵 的走心 作品越 能获得 观众的 认可。 9. 弊端重重的人类中心主义亟须克服 自身认 识的偏 见,而 中华民 族的中 道智慧 是一个 可取的 办法。
已知a1,q, an时
【注】使用等比数列前n项求和公式时应注意 q=1还是 q≠1。
人教高中数学等比数列优秀PPT
人教高中数学等比数列优秀PPT
想
一 想
在等比数列 {an} 中,若已知五个 量 a1, an, n, q, Sn 中的任意三个量, 请问: 能否求出其余两个量 ?
na1
Sn
a1
(1
q
人教高中数学等比数列优秀PPT
知识盘点
• 等比数列的前n项和公式:
na1
人教版数学必修五2.4《等比数列》课件 (共17张PPT)

是
三、等比中项
如果在 a 与 b 中间插入一个数 G ,使 a, G, b 成等比数列, 那么称这个数 G 为 a 与 b 的等比中项.
2 G ab . a , b 即 G ab ( 同号)或
(1)只有两个同号的非零常数才有等比中项, G ab 0
2
(2)等比中项有两个值, G ab
(3)在等比数列中,若 m n p q ,则 am an a p aq .
四、等比数列的性质
(4)若 {an } , {bn } 均为等比数列,则 {an bn } , {k an } (k 0) ,
1 1 { } 仍为等比数列,公比分别为 q1 q2 , q1 , . an q1
32
a15 例 7、在等比数列 {an } 中, a5 a11 3, a3 a13 4 ,则 ( C ) a5
(A) 3
1 (B) 3
1 (C) 3 或 3
1 (D) 3 或 3
例 8、等差数列 an 中, d 0 ,且 a1 , a3 , a9 成等比数列,
a1 a3 a9 求 的值. a2 a4 a10
an 数列的公比,公比通常用字母 q 表示 q 0 ,即 q (q 0) . an 1
(4) 0 q 1 时,当 a1 0 , {an } 递减; a1 0 , {an } 递增;
q 1 时,当 a1 0 , {an } 递增; a1 0 , {an } 递减;
类比思想
an am
an am qnm
例 1、在等比数列 {an } 中
1 (1) a1 , q 3 ,求 a5 . 2
(2) a7 512 , q 2 ,求 a1 .
2.3.1等比数列(1)

普通高中课程标准实验教科书—数学第五册[人教版B]2.3.1等比数列(第一课时)教学目标:1.理解等比数列的定义.2.掌握等比数列的通项公式教学重点:等比数列的定义及通项公式教学过程一、1.折纸问题的例子2.数列:ΛΛ,625,125,25,5ΛΛ,81,41,21,1--观察、归纳其共同特点:1“从第二项起”与“前一项”之比为常数(q )2任一项00≠≠q a n 且 3q = 1时,{a n }为常数 二、通项公式:1.等比数列的通项公式1:)0(111≠⋅⋅=-q a q a a n n由等比数列的定义,有: q a a 12=;21123)(q a q q a q a a ===;312134)(q a q q a q a a ===; … … … … … … …0(1111≠⋅⋅==--q a q a q a a n n n2.等比数列的通项公式2: )0(11≠⋅⋅=-q a q a a m m n 3.既是等差又是等比数列的数列:非零常数列.4.图像是经过压缩或拉伸的指数函数图像上的若干孤立点三、补充例子:例1求下列各等比数列的通项公式:1. 1a =2, 3a =8解:24213±=⇒=⇒=q q q a a n n n n n n a a )2()2)(2(22)2(11-=--=-=-=∴--或2. 1a =5, 且21+n a =3n a 解:111)23(5523-+-⨯=∴=-==n n n n a a a a q 又: 例2培育水稻新品种,如果第一代得到120粒种子,并且从第一代起,由以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代大约可以得到这个新品种的种子多少粒?解:由于每一代的每一粒种子都可得120粒种子,所以每代的种子数是它的前一代种子数的120倍,逐代的种子数组成等比数列,记为{}n a其中101551105.2120120,120,120⨯≈⨯=∴==-a q a 答:到第5代大约可以得到种子2.51010⨯粒.小结:本节课主要学习了等比数列的定义,即:)0(1≠=-q q a a n n 等比数列的通项公式:11-⋅=n n q a a 及推导过程课堂练习:第50页练习A,B课后作业:第54页:1,2,3。
必修5课件2.3.1等比数列的概念

2 . 3. 1 等 比 数 列 的 概 念
回顾第 2. 1节开始我们遇到的数列3, 4, 再考察下面问题 : 放射线物质以一定的速 度衰变, 该速度正比于当时该物 质的
质量.如果某物质为 0 的放射性物质在时间 中衰变到Q0 / 2, Q h 那么称h 为物质的半衰期镭的半衰期是1620 年, 如果从现有 . 的10 g 镭开始, 那么每隔1620 年, 剩余量依次为 1 1 1 10 , 10 , 10 , 10 , . 2 2 2 某桥车的售价约 万元 , 年折旧率约为 % (就是说这辆车每 3 那么该车从购买当年算 , 逐年的价 10 起 值依次为 36 , 36 0.9 , 36 0.92 , 36 0.93 , .
某人年初投资10000 万元 , 如果年收益率是5% , 那么按照复利, 5 年内各年末的本利和依 次为 10000 1.05 , 10000 1.05 2 , , 10000 1.05 5 .
复利的本利和公式是 本利和 本金 1 利率 :
与等差数列相比 上面这些数列有什么特 ? , 点
存期
.
一般地 , 如果一个数列从第2 项起 , 每一项与它的前一项的比 都等于同一个常数, 那么这个数列就叫做等比数列 ( geometr icprogress ) , 这个常数叫做等比数列的公比 (common) , 公 ion 比通常用字母q 表示.
2 根据题意, 得
所以 b 2 , c 1 .
b c , 4 b b 2, 1 解得 c 1 . c 2 , c b
an 1 在等比数列 an 中, 始终有 q. an
例1 判断下列数列是否为等 比数列:
人教版高中数学必修5《等比数列》PPT课件

二、基础知识讲解
1、等比数列的定义:
一般地,如果一个数列从第二项起,每一项与它
的前一项的比都等于同一个常数,那么这个数列就叫
做等比数列。这个常数就叫做等比数列的公比, 公比
通常用字母 q 表示。 (q≠0) 等比数列的每一
思考:用数学符号语言(递推公式)项怎都样不表为示0等,比即
在等比数列{an}中 (1)an=akqn-k; (2)若m+n=k+l,则am·an =ak·al 在等比数列{an}中,若m+n=k+l,则am·an =ak·al
特别地,若m n 2k(m, n, k N * ), 则aman ak2
例1、在等比数列{an}中,an 0,且a1a9 64, a3 a7 20,求a11。
成等差数列的三个正数之和为15,若这三个数分别 加上1,3,9后又成等比数列,求这三个数。
一、复习回顾 1、等比数列的定义: 或
2、等比数列的通项公式: an=a1qn-1 3、等比数列的性质: ①an=a1qn-1=akqn-k;
a1q2 12 ①
a1,公比是
q,那么
设
a1q3 18 ②
把②的两边分别除以①的两边,得
q
3
③
把③代入①,得
a1
6 3
2
方
程列
思 想
因此,a2
a1q
16 3
3 2
8
求
二、基础知识讲解
3、等比数列的通项公式: an=a1qn-1
练习2:在等比数列{an}中,
(1)a1=3,an=192,q=2,求n;n=7
a3 a7 20,求a11。
解:依题意可得
高中数学必修5《等比数列》PPT

− = − = − = ⋯
= + − =
则+ = +
在等比数列中有
+
=
=
=⋯=
= q
则 + = .q
等差数列
=
= +
= + = +
通项公式 = + = +
的推导过
= + = +
程
……
= + ( − )
三数 , , 成等差数列
+
则A-a=b-A,
=
中项推导
过程
通常用
2A=a+b
等比数列
a1 = a1
2 = 1 . q
= . q = . q2
按照复利(即前一期的利息和本金加在一起算作本金,再
计算下一期的利息),5年内各年末的本利和依次为(用
算式表示)
0000(1 + 5%)2
0000
0000(1 + 5%)4
0000(1 + 5%) 0000(1 + 5%)3
类比等差数列,你能找出这几个数列的共同特
征并加以定义吗?
4 = 3 . q = . q3
5 = 4 . q = . q4
……
n = . q−
三数 , , 成等比数列
则
= , = ±
通常用 G2 =ab
思考:(1) 3与27的等比中项是多少?-3和27呢?
人教版高中数学必修五2-3-1《等比数列》课件

等比数列的通项公式
an a1 qn1
方程
应用:已知等比数列{an}中,a5=20,a15=5,求a20.
等比数列的通项公式
an a1 qn1
方程
函数
等比数列的通项公式还可以写成
an=a1qn-1
a1 qn q
cqn
当q是不为1的正数时,它是一个非零常 数与一个指数函数的乘积.
20 18
5
4
● ● ●● ●●● ● ● ●
3
2
1
0 1 2 3 4 5 6 7 8 9 10
打开神秘之信
一个定义: an q(n N *且n 2)
a n 1
一个公式: an a1qn1 (n N *且q 0)
两种思想方法: 函数与方程的思想、类比法
推导通项的 三种方法:
不完全归纳法、迭代法、累乘法
方案①:今年植树1万棵,从第二年起每年 都比上一年都多 植1万棵;
1 , 2 , 3 , 4 , ……
方案②:从今年起以后每年都植树4万棵;
4 , 4 , 4 , 4 , ……
方案③:今年植树0.2万棵,从第二年起 每年都植上一年的2倍.
0.2 , 0.4 , 0.8 ,1.6 ,……
0.2 , 0.4 , 0.8 ,1.6 ,…… 3,9,27,81,…… 1 , 1 , 1, 1 ,
q (n 1)
等比数列的定义
如果一个数列从第二项起,每一项与它 的前一项的比都等于同一个常数,那么这个 数列就叫做等比数列.
这个常数叫做等比数列的公比。
公比通常用字母 q (q≠0)表示。
方案①:今年植树1万棵,从第二年起每年 都比上一年都多 植1万棵;
1 , 2 , 3 , 4 , ……
人教B版必修5高二数学2.3.1等比数列教学课件
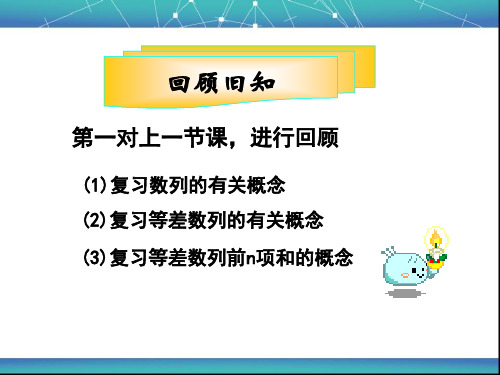
(2)这个数列中的任意一 项是它后面第 5 项的 1 10
(3)这个数列中任意两项的积仍然在这个数列中.
分析:这是等比数列定义与性质的应用.
n
证明:(1)因为
an1 an
10 5
n1
10 5
1
105 (常数) .
所以,这个数列是等比数列 .
n1
(2)
an an5
10 5
n4
10 5
10
n51
n4 5
•
an1
•
an2
0, n
N*)
{an }是等比数列
知识要点 等比中项
如果在a与b中间插入一个数G,使 a、G、b成等比数列,那么G叫做a与b 的等比中项.
如果G是a与b的等比中项,那么
G a
b G
,即
G2
ab
因此,G
ab
反过来,如果 a,b同号,G等于 ab
或 ab 那么G是 a,b的等比中项.
3. 结论:a,b同号,G2=ab是G是a,b的 等比中项的充要条件.
4.对称设法:三数为 a/q,a, aq
5.下标和公式: 等比数列{an}中,如果 m+n=r+s,(m,n,r,s ∈N*) 那么am.an=ar as .
6.. 当三个数成等比数列,并知其积时,可设
它们分别为
a q
,
a,
aq,
2(n 1) 2n1 2 2n 2 2n1 2n
4.已知数列 an 的前n项和为
Sn ,Sn
1 3 (an
1)(n N ).
(1)求 a1 , a2
(2)求证数列 an 是等比数列.
解:
人教版高中数学必修五课件:2.4 等比数列(共17张PPT)

存在吗? (4) 常数列都是等比数列吗?
自主探究
你能根据等比数列的定义推导出等比数 列的通项公式吗?
an q(n 2) an1
等比数列通项公式的推导: an an1
数列就叫做等比数列 ,这个常数叫做等比数列的 公比(q)。
其递推公式:
an q(n 2且 n N ) 或 an1 q(n N * )
a n 1
an
小试牛刀
观察并判断下列数列是否是等比数列:
(1) 1,3,9,27,81,…
是,公比 q=3
(2) 1 , 1 , 1 , 1 ,
2 4 8 16
例1. 一个等比数列的第3项与第4项分别是 12与18,求它的首项和公比以及通项公式。
例2:
已知
a,
3 2
,
b,
243 32
,
c这五个数成等比数列,
求 a, b, c 的值。
课堂互动
1.在等比数列{an}中:
(1)已知a1 2, q 3, an 162, 求n;
(2)已知a1
3, q
1 2
,求a5;
通项 变形
an
am
(n m)d
(n, m N *)
试一试
已知数列an 满足a1 1 ,an1 2an 1
(1)求证:数列 an 1 是等比数列;
(2)求数列 an 的通项公式。
qn 2
方法一:累乘法
a2 q
aa31 q a2 a4 q
…a3 …
(n-1)个 式子
an q
高中数学必修5《等比数列的性质》PPT

在等比数列{an}中距首末两端等距离的两项的积相等, 即a1an=a2an-1=a3an-2=…
性质5 在等比数列{an}中,序号成等差数列的项仍成等比数列
工具
第二章 数列
栏目导引
已 知 各 项 均 为 正 数 的 等 比 数 列 {an} 中 , a1·a2·a3 = 5 , a7·a8·a9=10,则 a4·a5·a6=( )
A.5 2
B.7
C.6
D.4 2
工具
第二章 数列
栏目导引
工具
第二章 数列
栏目导引
[解题过程] a1·a2·a3=a23=5 a7·a8·a9=a83=10 a4·a5·a6=a53
3
又∵a52=a2·a8,∴a53=(a2·a8) 2
1
1
∴a4·a5·a6=(a23a83) 2 =(5×10) 2 =5 2.故选 A.
若{an}是等差数列,则ak,ak+m,ak+2m,…(k、 m∈N*)组成公差为md的等差数列
工具
第二章 数列
栏目导引
请把这些性质类比到等比数列
(小组合作交流)
工具
第二章 数列
栏目导引
等比数列的常用性质
性质1 性质2 性质3 性质4
通项公式的推广:an=am· qn-m (n,m∈N*) 若则{aak·n}a为l=等a比m·数an列,且k+l=m+n(k,l,m,n∈N*),
若{an}为等差数列,且k+l=m+n(k,l,m,n∈N*), 则ak+al=am+an
若{an}是等差数列,则2an=an-1+an+1,a1+an=a2 +an-1=a3+an-2=…
人教A版高中数学必修五.1等比数列的概念及通项公式PPT课件

A.-21
1 B.2
√C.-23
3 D.2
解析 ∵{an}中的项必然有正有负,
∴q<0.又|q|>1,
∴{|an|}递增或递减. 由此可得{an}的连续四项为-24,36,-54,81. ∴q=-23.
12345
2.等比数列x,3x+3,6x+6,…的第4项等于
√A.-24
B.0
C.12
D.24
解析 由题意知(3x+3)2=x(6x+6),即x2+4x+3=0, 解得x=-3或x=-1(舍去), 所以等比数列的前3项是-3,-6,-12, 则第4项为-24.
人教A版高中数学必修五.1等比数列的 概念及 通项公 式PPT 课件
人教A版高中数学必修五.1等比数列的 概念及 通项公 式PPT 课件
(2)-1,1,2,4,8,…; 解 记数列为{an},显然a1=-1,a2=1,a3=2,…, ∵aa21=-1≠aa32=2, ∴此数列不是等比数列. (3)a1,a2,a3,…,an,…. 解 当a=0时,数列为0,0,0,…是常数列,不是等比数列; 当a≠0时,数列为a1,a2,a3,a4,…,an,…, 显然此数列为等比数列,且公比为a.
题型三:等比中项的应用
例4 已知在等比数列 an中,a3a4a5 8,求a2a3a4a5a6的值
跟踪训练4
已知各项均为正数的等比数列an中,a1a2a3 5, a7a8a9 10,
则a4a5a6等于() A
A.5√2
B.7
C.6
D.4√2
3 达标检测
PART THREE
1.等比数列{an}的公比|q|>1,{an}中有连续四项在集合{-54,-24,-18, 36,81}中.则q等于
【推荐】高中数学人教B版必修五2.3.1《第1课时 等比数列》课件.ppt

等比中项
【问题导思】 如果在 x,y 中间插入一个数 G,使 x,G,y 成等比数列, 那么 G 与 x,y 之间有怎样的数量关系? 【提示】 G2=xy. 如果在 x 与 y 中间插入一个数 G,使 x,G,y 成 等比 数列 ,那么 G 叫做 x,y 的等比中项,这三个数满足关系 式 G2=xy .
(1)求证:{an}是等比数列,并求出通项; (2)试问:-1861是这个等比数列中的项吗?如果是,指明 是第几项;如果不是,说明理由.
【思路探究】 (1)要判断{an}为等比数列,an+1 与 an 需 要满足怎样的关系?怎样求一个等比数列的通项公式?(2)如 何判断一个数是否为一个数列中的项?
2.3 等比数列 2.3.1 等比数列 第 1 课时 等比数列
教师用书独具演示
●三维目标 1.知识与技能 形成并掌握等比数列的概念,理解等比数列的通项公式.
2.过程与方法 培养学生观察、归纳、类比、联想等发现规律的一般方 法. 3.情感、态度与价值观 让学生在民主、和谐的共同活动中感受学习的乐趣.
【自主解答】 设等比数列{an}的首项为 a1,公比为 q, a2=a1q=4,
(1)由题:a5=a1q4=-12, ∴q=-12,a1=-8, ∴an=a1qn-1=-8×(-12)n-1=(-2)4-n.
(2)∵a3+a6=(a2+a5)q, 即 9=18q,∴q=12, 由 a1q+a1q4=18 得 a1=32, 由 an=a1qn-1=1 知 n=6.
1.a1 和 q 是等比数列的两个基本量,解决本题时,只要 求出这两个基本量,其余的量便可以得出.
2.等比数列的通项公式涉及 4 个量 a1,an,n,q,只要 知道其中任意三个就能求出另外一个,解题时常列方程(组) 来解决.
高中数学 2.3.1 第2课时 等比数列的性质配套课件 新人
当 堂
案
双
设 计
为 等比数列 ,首项为
ak+1
,公比为 q
;若取出所有
基 达
课 前
的 k 的倍数项,组成的数列为 等比数列 ,首项为ak ,公比
标
自 主
为 qk .
课 时
导
作
学
业
课 堂 互 动 探 究
教 师 备 课 资 源
菜单
RB ·数学 必修5
教
学
思
教
“下标和”性质
法
想 方
分
法
析
技
当 堂 双 基 达 标
课 时 作 业
教 师 备 课 资 源
教 学 教 法 分 析
教 学 方 案 设 计
课 前 自 主 导 学
课 堂 互 动 探 究
菜单
RB ·数学 必修5
思 想 方 法 技 巧
当 堂 双 基 达 标
课 时 作 业
教 师 备 课 资 源
教 学 教 法 分 析
教 学 方 案 设 计
课 前 自 主 导 学
RB ·数学 必修5
教
学
思
教 法 分
第 2 课时 等比数列的性质
想 方 法
析
教师用书独具演示
技 巧
教
学
当
方
堂
案
双
设
计
●三维目标
基 达
标
课 前
1.知识与技能
自
课
主 导
理解和掌握等比数列的性质,能选择更方便,快捷的解 时 作
学
业
题方法.
课 堂 互 动 探 究
教 师 备 课 资 源
菜单
RB ·数学 必修5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
●
●
●
●
●
例1 一个等比数列的第3项与第4项 分别是12与18,求它的第1项与第2项.
练习:
在等比数列
an
a1 a3 10,a 4
a6
5 4
求 a 2 的值。
例2、三个数成等比数列,它们的和为 28,它们的积为512,求这三个数。
练习
an a1•qn1
求下列等比数列的第4,5项:
(1) 5,-15,45,…
(2)-1, ±2 ,-4 (4)1,±1 ,1
如果在a与b中间插入一个数G,使a,G,b成等比数列, 那么G叫做a与b的等比中项。
G ab
0
1
2
n 1
例、无穷数列105 ,105 ,105... 1 0 5 . . .
,求证:
(1)此数列成等比数列。
1
(2)此数列任一项是它后面第5项的 1 0
(3)此数列的任两项的积也在此数列中。
当一个人用工作去迎接光明,光明很快就会来照耀着他。人在身处逆境时,适应环境的能力实在惊人。人可以忍受不幸,也可以战胜不幸,因为人有着惊人的 挥它,就一定能渡过难关。倘若你想达成目标,便得在心中描绘出目标达成后的景象;那么,梦想必会成真。心等待,就可以每一个人都具有特殊能力的电路, 知道,所以无法充分利用,就好像怀重宝而不知其在;只要能发掘出这项秘藏的能力,人类的能力将会完全大改观,也能展现出超乎常人的能力我这一生不曾 和伟大的著作都来自于求助潜意识心智无穷尽的宝藏。那些最能干的人,往往是那些即使在最绝望的环境里,仍不断传送成功意念的人。他们不但鼓舞自己, 成功,誓不休止。灵感并不是在逻辑思考的延长线上产生,而是在破除逻辑或常识的地方才有灵感。真正的强者,善于从顺境中找到阴影,从逆境中找到光亮 进的目标。每一种挫折或不利的突变,是带着同样或较大的有利的种子。什么叫做失败?失败是到达较佳境地的第一步。失败是坚忍的最后考验。对于不屈不 失败这回事。一次失败,只是证明我们成功的决心还够坚强。失败也是我需要的,它和成功对我一样有价值。我们关心的,不是你是否失败了,而是你对失败 失败?失败是到达较佳境地的第一步。没有人事先了解自己到底有多大的力量,直到他试过以后才知道。对于不屈不挠的人来说,没有失败这回事。要成功不 能,只要把你能做的小事做得好就行了。成功的唯一秘诀——坚持最后一分钟。只有胜利才能生存,只有成功才有代价,只有耕耘才有收获。只有把抱怨环境 的力量,才是成功的保证。不要为已消尽之年华叹息,必须正视匆匆溜走的时光。 当许多人在一条路上徘徊不前时,他们不得不让开一条大路,让那珍惜时间 面去。 敢于浪费哪怕一个钟头时间的人,说明他还不懂得珍惜生命的全部价值。成功=艰苦劳动+正确的方法+少说空话。合理安排时间,就等于节约时间。
等比数列的通项公式 如果一个数列 a 1 , a 2 , a 3 , …,a n , …,
是等比数列,它的公比是q,那么
a2 a1•q a3a2•qa1•q2 a4a3•qa1•q3
a5a4•qa1•q4
····················
a 由此可知,等比数列 n 的通项公式为
an a1•qn1
(2)1.2,2.4,4.8,…
(3) 2 , 1 , 3, 3 28
(4) 2,1, 2 , 2
例2
(1)等比数列中,a15,a9a10100,
求a 18
(2)等比数列中, a2 2,a5 54
求a 8
等比中项
观察如下的两个数之间,插入一个什么数后者三个数就会成 为一个等比数列:
(1)1,±3, 9 (3)-12, ±6,-3
等比数列的图象3
10 9 (1)数列:4,4,4,4,4,4,4,… 8
7 6
5
4
● ● ●● ●●● ● ● ●
3 2
1
0 1 2 3 4 5 6 7 8 9 10
等比数列的图象4
10 9 (1)数列:1,-1,1,-1,1,-1,1,… 8
7 6
4
3 2
1●
●
●
●
●
0 1 2 3 4 5 6 7 8 9 10
(3)
1, 1, 1, 1 , 2 4 8 16
(4) 5,5,5,5,5,5,…
(5) 1,-1,1,-1,1,…
定义:如果一个数列从第2项起,每 一项与它的前一项的比等于同一个常 数(指与n无关的数),这个数列就 叫做等比数列,这个常数叫做等比数 列的公比,公比通常用字母q表示。
an1 q(是与n无关的数或式子,且q 0) an
当q=1时,这是
一个常函数。
an 0
等比数列的图象1
20
18 (1)数列:1,2,4,8,16,…
16
●
14
12
10
8
●
6
4
●
2
●
●
0 1 2 3 4 56 78
9 10
等比数列的图象2
10
9 (2)数列: 8,4,2,1, 1, 1,1,
2 48
8
●
7 6
5
4
●
3
2
●
1
●
●●●
0 1 2 3 4 5 6 7 8 9 10
复习等差数列的有关概念
定义:如果一个数列从第2项起,每 一项与它的前一项的差等于同一个常数 (指与n无关的数),这个数列就叫做 等差数列,这个常数叫做等差数列的公 差,公差通常用字母d表示。
an1an d(是与 n无关的数或式
等差数列 a n 的通项公式为
ana1(n1)d
当d≠0时,这是 关于n的一个一
为我敲已过去了的钟点。人的全部本领无非是耐心和时间的混合物。任何节约归根到底是时间的节约。时间就是能力等等发展的地盘。时间是世界上一切成就 想者痛苦,给创造者幸福。时间是伟大的导师。时间是一个伟大的作者,它会给每个人写出完美的结局来。时间最不偏私,给任何人都是二十四小时;时间也 都不是二十四小时。忘掉今天的人将被明天忘掉。辛勤的蜜蜂永没有时间的悲哀。在所有的批评中,最伟大、最正确、最天才的是时间。从不浪费时间的人, 不够。时间是我的财产,我的田亩是时间。集腋成裘,聚沙成塔。几秒钟虽然不长,却构成永恒长河中的伟大时代。春光不自留,莫怪东风恶。抛弃今天的人 昨天,不过是行去流水越努力,越幸运。人之所以能,是相信能。任何的限制,都是从自己的内心开始的不为失败找理由,只为成功找方法。一个人几乎可以 忱的事情上成功。一切失败都源于执行力太差!从你每天一睁眼开始起,你就要对自己说今天是美好的一天每一个成功者都有一个开始。勇于开始,才能找到 人想要改造这个世界,但却罕有人想改造自己。积极的人在每一次忧患中都看到一个机会,而消极的人则在每个机会都看到某种忧患。世上没有绝望的处境, 人。性格决定命运,气度决定格局,细节决定成败,态度决定一切,思路决定出路,高度决定深度。未曾见过一个早起勤奋谨慎诚实的人抱怨命运不好。伟人 为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标。一个有信念者所开发出的力量,大于99个只有兴趣者。只要有信心,人永远不会挫败 毅力以磨平高山。再长的路,一步步也能走完,再短的路,不迈开双脚也无法到达。行动是治愈恐惧的良药,而犹豫、拖延将不断滋养恐惧。一个人最大的破 资产是希望。喜欢追梦的人,切记不要被梦想主宰;善于谋划的人,切记空想达不到目标;拥有实干精神的人,切记选对方向比努力做事重要。太阳不会因为 再升起;月亮不会因为你的抱怨,今晚不再降落。蒙住自己的眼睛,不等于世界就漆黑一团;蒙住别人的眼睛,不等于光明就属于自己!路再长也会有终点, 不管雨下得有多大,总会有停止的时候。乌云永远遮不住微笑的太阳!鱼搅不浑大海,雾压不倒高山,雷声叫不倒山岗,扇子驱不散大雾。鹿的脖子再长,总 人的脚指头再长,也长不过他的脚板。人的行动再快也快不过思想!以前认为水不可能倒流,那是还没有找到发明抽水机的方法;现在认为太阳不可能从西边 到太阳从西边出来的星球上。这个世界只有想不到的,没有做不到的!不是井里没有水,而是挖的不够深;不是成功来的慢,而是放弃速度快。得到一件东西 样东西则需要勇气!终而复始,日月是也。死而复生,四时是也。奇正相生,循环无端,涨跌相生,循环无端,涨跌相生,循环无穷。机遇孕育着挑战,挑战 是千古验证了的定律!种子放在水泥地板上会被晒死,种子放在水里会被淹死,种子放到肥沃的土壤里就生根发芽结果。选择决定命运,环境造就人生!懂得 胜过知道怎样解决问题的人。在这个世界上,不知道怎么办的时候,就选择学习,也许是最佳选择。胜出者往往不是能力而是观念!得之物而失之本,此乃大 要的,他和成功对我一样有价值。我的那些最重要的发现是受到失败的启发而获得的。不会从失败中找寻教训的人,他们的成功之路是遥远的。没有多次失败 5、这世界除了心理上的失败,实际上并不存在什么失败,只要不是一败涂地,你一定会取得胜利的。明智的人决不坐下来为失败而哀号,他们一定乐观地寻找 谬误有多种多样,而正确却只有一种,这就是为什么失败容易成功难脱靶容易中靶难缘故。什么叫做失败,失败是到达较佳境地的第一步。一个人失败的最大 己的能力永远不敢充分的信任;甚至自己认为必将失败无疑败莫败于不自知失败是成功之母,高不过脚底板。凡百事之成也在敬之,其败也必在慢之。成功
次函数。
如果在a与b中间插入一个数A,使 a,A,b成等差数列,那么A叫做 a与b的等差中项。
A ab 2
等差数列 a n 的前n项和
Sn
n(a1 an) 2
Sn n1 an( n 21)d
等比数列的有关概念
观察数列
( 1) 2,4,8,16,32,64.
(2) 1,3,9,27,81,243,…
