专题1.5 一次函数、反比例函数的图象和性质(测)-备战2016年中考数学二轮复习讲练测(原卷版)

合集下载

中考数学考点系统复习第三章函数第四节反比例函数的图象和性质

命题点 2：反比例函数解析式的确定(近 5 年考查 3 次) 4．(2016·省卷第 11 题 4 分)位于第一象限的点 E 在反比例函数 y＝kx的
图象上，点 F 在 x 轴的正半轴上，O 是坐标原点，若 EO＝EF，△EOF 的面
积等于 2，则 k 的值为
(B)
A．4
B．2Leabharlann C．1D．－25．(2021·省卷第 10 题 3 分)若反比例函数的图象经过点(1，－2)，则 2
该反比例函数的解析式(解析式也称表达式)为__yy＝－＝x －__.
重难点：反比例函数的图象和性质已知反比例函数 y＝m－x 1(m≠1)．
(1)若反比例函数 y＝m－x 1(m≠1)的图象在每一个象限内， y 都随 x 的增大而增大，则 m 的取值范围是 mm<<11； (2)若该函数的图象在第一、三象限，则 m 的取值范围 mm＞＞11； (3)若点(1，－3)在该函数图象上，则 m 的值为－－22； (4)若 A(2，3)，B(－2，n)为该函数图象上两点，则 n 的值为－－33；
1)x－(m－1)的图象可能是
( B)
(8)当 m＝－5 且－3≤x≤－1 时，y 的最大值为 66 ；若点 P 是该反比例函数图象上一点，过点 P 作 PE⊥x 轴于点 E，作 PF⊥y 轴于点 F，则△PEF 的面积为 3 3 ； (9)若点 P 是该反比例函数图象上一点，过 P 点作 PE⊥x 轴于点 E，作 PF ⊥y 轴于点 F，四边形 OEPF 的面积为 6，则 m 的值为－－5 5或或77.
第四节反比例函数的图象和性质
【考情分析】云南近 5 年主要以选择和填空的形式考查：①反比例函数图象上点的坐标特征；②由反比例函数图象上一个点的坐标确定反比例函数的解析式，难度小，分值一般 3－4 分．

中考一次函数、反比例函数的图象和性质专题复习题及答案

热点5 一次函数、反比例函数的图象和性质（时间：100分钟分数：100分）一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个符合题目要求的）1．在反比例函数y=2x的图象上的一个点的坐标是（）A．（2，1） B．（-2，1） C．（2，12） D．（12，2）2．函数y=（a-1）x a是反比例函数，则此函数图象位于（）A．第一、三象限； B．第二、四象限； C．第一、四象限； D．第二、三象限3．已知正比例函数y=（3k-1）x，y随着x的增大而增大，则k的取值范围是（）A．k<0 B．k>0 C．k<13D．k>134．直线y=x-1与坐标轴交于A、B两点，点C在坐标轴上，△ABC为等腰三角形，则满足条件的点C最多有（）个 A．4 B．5 C．7 D．85．在函数y=kx（k>0）的图象上有三点A1（x1，y1），A2（x2，y2），A3（x3，y3），已知x1<x2<0<x3，则下列各式中，正确的是（）A．y1<y2<y3B．y3<y2<y1C．y2<y1<y3D．y3<y1<y26．下列说法不正确的是（）A．一次函数不一定是正比例函数 B．不是一次函数就一定不是正比例函数C．正比例函数是特殊的一次函数 D．不是正比例函数就一定不是一次函数7．在同一平面直角坐标系中，对于函数①y=-x-1，②y=x+1，③y=-x+1，④y=-2（x+1）的图象，下列说法正确的是（）A．通过点（-1，0）的是①③ B．交点在y轴上的是②④C．相互平行的是①③ D．关于x轴对称的是②④8．在直线y=12x+12上，到x轴或y轴的距离为1的点有（）个A．1 B．2 C．3 D．49．无论m、n为何实数，直线y=-3x+1与y=mx+n的交点不可能在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限10．一次函数y=kx+（k-3）的函数图象不可能是（）二、填空题（本大题共8小题，每小题3分，共24分）11．一次函数y=kx+b中，y随x的增大而减小，且kb>0，则这个函数的图象一定不经过第______象限．12．如图6-2，点A在反比例函数y=kx的图象上，AB垂直于x轴，若S△AOB=4，•那么这个反比例函数的解析式为________．13．如图6-3，弹簧总长y（cm）与所挂质量x（kg）之间是一次函数关系，则该弹簧不挂物体时的长度为________．14．已知函数y=（k+1）x+k2-1，当k_______时，它是一次函数；当k______时，它是正比例函数．15．一次函数图象与y=6-x交于点A（5，k），且与直线y=2x-3无交点，则这个一次函数的解析式为y=________．16．已知函数y=3x+m与函数y=-3x+n交于点（a，16），则m+n=________．17．已知直线L：y=-3x+2，现有命题：①点P（-1，1）在直线L上；②若直线L与x轴、• y轴分别交于A、B两点，则2103M（13，1），N（a，b）都在直线L上，且a>13，则b>1；•④若点Q到两坐标轴的距离相等，且Q在L上，则点Q在第一或第四象限．•其中正确的命题是_________．18．老师给出一个函数，甲、乙、丙各正确指出了这个函数的一个性质．甲：函数的图象经过了第一象限；乙：函数的图象也经过了第三象限；丙：在每个象限内，y随x的增大而减小。

中考专题--反比例函数和一次函数图像题

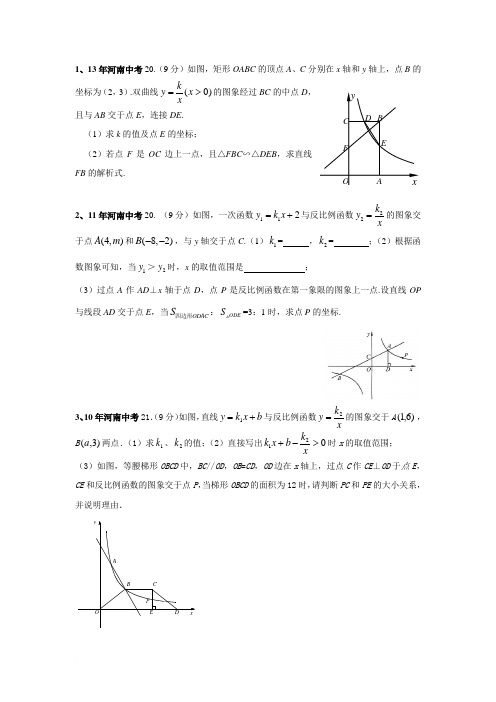
1、13年河南中考20.（9分）如图，矩形OABC 的顶点A 、C 分别在x 轴和y 轴上，点B 的坐标为（2，3）.双曲线)0(>=x xky 的图象经过BC 的中点D ，且与AB 交于点E ，连接DE . （1）求k 的值及点E 的坐标；（2）若点F 是OC 边上一点，且△FBC ∽△DEB ，求直线FB 的解析式.2、11年河南中考20. （9分）如图，一次函数112y k x =+与反比例函数22k y x=的图象交于点(4,)A m 和(8,2)B --，与y 轴交于点C .（1）1k = ，2k = ；（2）根据函数图象可知，当1y ＞2y 时，x 的取值范围是；（3）过点A 作AD ⊥x 轴于点D ，点P 是反比例函数在第一象限的图象上一点.设直线OP 与线段AD 交于点E ，当ODAC S 四边形：ODES=3：1时，求点P 的坐标.3、10年河南中考21．（9分）如图，直线b x k y +=1与反比例函数xk y 2=的图象交于A )6,1(，B )3,(a 两点．（1）求1k 、2k 的值；（2）直接写出021>-+xk b x k 时x 的取值范围；（3）如图，等腰梯形OBCD 中，BC //OD ，OB =CD ，OD 边在x 轴上，过点C 作CE ⊥OD 于点E ，CE 和反比例函数的图象交于点P ，当梯形OBCD 的面积为12时，请判断PC 和PE 的大小关系，并说明理由．OPE DCBAyxEO FC D BAxy4、13年郑州原创模拟（一）23．(本小题满分8分)如图9．一次函数y x b =+的图象经过点B(1-，0)，且与反比例函数ky x= (k 为不等于0的常数)的图象在第一象限交于点A(1，n)．求：(1) 一次函数和反比例函数的解析式； (2)当16x ≤≤时，反比例函数y 的取值范围．5、13年郑州原创模拟（二）19.（9分）如图，四边形ABCD 是正方形，其中A (1，1)，B (3，1)，D (1，3)．反比例函数my x=（x >0）的图象经过对角线BD 的中点M ，与BC ，CD 的边分别交于点P ，Q ．（1）直接写出点M ，C 的坐标；（2）求直线BD 的解析式；（3）线段PQ 与BD 是否平行？并说明理由．PQ M DC BA Oxy6、13年郑州原创模拟（三）23、如图，在方格纸中建立直角坐标系，已知一次函数y 1=-x+b 的图象与反比例函数 xky =的图象相交于点A （5，1）和A 1．（1）求这两个函数的关系式；（2）由反比例函数xky =的图象特征可知：点A 和A 1关于直线y=x 对称．请你根据图象，填写点A 1的坐标及y 1＜y 2时x 的取值范围．3ABCOyx7、13年郑州原创模拟（四）19.（9分）如图，一次函数1y k x b =+与反比例函数2k y x=的图象交于A (2，m )，B (n ，-2)两点．过点B 作BC ⊥x 轴，垂足为C ，且S ABC =5．（1）求一次函数与反比例函数的解析式．（2）若P (p ，y 1)，Q (-2，y 2)是函数2k y x=图象上的两点，且y 1≥y 2，求实数p 的取值范围．（3）若点M 是y 轴上满足MA MB -取最大值的点，求点M 的坐标．CyxOBA8、13年郑州原创模拟（七）19.（9分）已知：如图，在平面直角坐标系中，一次函数y =ax +b（a ≠0）的图象与反比例函数ky x=（k ≠0）的图象交于一、三象限内的A ，B 两点，与x 轴交于C 点，点A 的坐标为(2，m )，点B 的坐标为(n ，-2)，tan ∠BOC 25=．（1）求该反比例函数和一次函数的解析式；（2）在x 轴上有一点E （O 点除外），使得△BCE 与△BCO 的面积相等，求出点E 的坐标；（3）若点C 关于y 轴的对称点为点D ，求△ABD 的面积．9、13年郑州中考原创冲刺卷(9分)如图，一次函数，y=kx+2的图象与反比例函数y=m x 的图象交于点P ，点P 在第一象限.PA ⊥x 轴于点A ，PB ⊥y 轴于点B.一次函数的图象分别交x 轴、y 轴于点C 、D ，且S△PBD=4，OC OA =12．(1)求点D 的坐标；(2)求一次函数与反比例函数的解析式；(3)根据图象写出当x>0时，一次函数的值大于反比例函数的值的x 的取值范围.10、11年新乡市第一次调研22．我们容易发现：反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题．如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x 轴所在的直线绕着原点O 逆时针旋转角α（α＜90°）后的图形.若它与反比例函数3y x=的图象分别交于第一、三象限内的点B 、D ，已知点A(-m ，0)、C(m ，0) ．（1）直接判断并填空：不论α取何值，四边形ABCD 的形状一定是______________；（2）①当点B 为(p ，1)，且四边形ABCD 为矩形时，试求p ，α和m 值；②观察猜想：对于①的m 值，能使四边形ABCD 为矩形的点B 共有哪几个？对应的角α分别是多少度？（不必说理）（3）四边形ABCD 能不能是菱形？为什么？11、11年新乡市二十一中数学一模试卷17．(8分)如图，已知一次函数1（m 为常数）的图象与反比例函数 2ky x =（k 为常数，0k ≠）的图象相交于点 A （1，3）．（1）求这两个函数的解析式及其图象的另一交点B 的坐标；（2）观察图象，写出使函数值12y y ≥的自变量x 的取值范围．12、河南省中招第一次模拟考试18.（9分）如图，已知反比例函数ky x=与一次函数y x b=+的图象在第一象限相交于点(1,4)A k -+．（1）试确定这两个函数的表达式；（2）求出这两个函数图象的另一个交点B 的坐标，并根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．a xyCDO BAyB 1-1- 1 2 33 12A （1，3）13、11年河南省驻马店市确山县新安店中学中考数学模拟27．如图，一条直线与反比例函数xky 的图象交于A（1，4）、B（4，n）两点，与x 轴交于D点，AC⊥x轴，垂足为C．（1）如图甲，①求反比例函数的解析式；②求n的值及D点坐标；（2）如图乙，若点E在线段AD上运动，连接CE，作∠CEF=45°，EF交AC于F点．①试说明△CDE∽△EAF；②当△ECF为等腰三角形时，直接写出F点坐标．14、11年河南省濮阳市一中中考数学模拟19、如图，已知直线y1=x+m与x轴、y轴分别交于点A、B，与双曲线y2＝xk（x＜0）分别交于点C、D，且C点的坐标为（-1，2）．（1）分别求出直线AB及双曲线的解析式；（2）求出点D的坐标；（3）利用图象直接写出：当x在什么范围内取值时，y1＞y2？15、11年河南省八校联考17、如图，在平面直角坐标系中，已知四边形ABCD为菱形，且A（0，3）、B（-4，0）．（1）求经过点C的反比例函数的解析式；（2）设P是（1）中所求函数图象上一点，以P、O、A顶点的三角形的面积与△COD的面积相等．求点P的坐标．516、12年河南省重点中学中考数学模拟17、如图，一次函数y=x 与反比例函数y=xk（x ＞0）的图象交于点A ，点B （3，0）是x 轴正半轴上一点，S △OAB =3．（1）求A 点的坐标和k 的值；（2）点C 是双曲线y ＝xk（x ＞0）图象上一动点，过点C 做x 轴的平行线，与y=x 的图象交于点D ，是否存在以点O 、B 、C 、D 为顶点的四边形为平行四边形？若存在，请求出点C 的坐标；（3）点P 是x 轴上一点，若能得到以点O 、P 、C 、D 为顶点的四边形为等腰梯形，请直接写出点P 横坐标的范围．17、10年河南省漯河市龙城一中19．已知：如图，在直角坐标系xOy 中，Rt△OCD 的一边OC 在x 轴上．∠C=90°，点D 在第一象限，OC=3，DC=4，反比例函数的图象经过OD 的中点A ．（1）求该反比例函数的解析式；（2）若该反比例函数的图象与Rt△OCD 的另一边DC 交于点B ，求过A 、B 两点的直线的解析式．18、12年濮阳17、已知反比例函数13k y x=的图象与一次函数2y k x m =+的图象交于A ()1,a -、B 1,33⎛⎫- ⎪⎝⎭两点，连结AO 。

专题11反比例函数(共51题)-备战2023年中考数学必刷真题考点分类专练(全国通用)【原卷版】

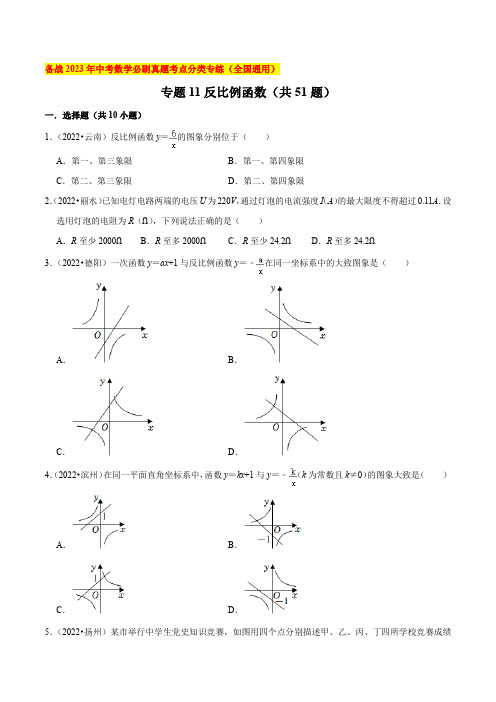
备战2023年中考数学必刷真题考点分类专练（全国通用）专题11反比例函数（共51题）一．选择题（共10小题）1．（2022•云南）反比例函数y＝的图象分别位于（）A．第一、第三象限B．第一、第四象限C．第二、第三象限D．第二、第四象限2．（2022•丽水）已知电灯电路两端的电压U为220V，通过灯泡的电流强度I（A）的最大限度不得超过0.11A．设选用灯泡的电阻为R（Ω），下列说法正确的是（）A．R至少2000ΩB．R至多2000ΩC．R至少24.2ΩD．R至多24.2Ω3．（2022•德阳）一次函数y＝ax+1与反比例函数y＝﹣在同一坐标系中的大致图象是（）A．B．C．D．4．（2022•滨州）在同一平面直角坐标系中，函数y＝kx+1与y＝﹣（k为常数且k≠0）的图象大致是（）A．B．C．D．5．（2022•扬州）某市举行中学生党史知识竞赛，如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率（该校优秀人数与该校参加竞赛人数的比值）y与该校参加竞赛人数x的情况，其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上，则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是（）A．甲B．乙C．丙D．丁6．（2022•邵阳）如图是反比例函数y＝的图象，点A（x，y）是反比例函数图象上任意一点，过点A作AB⊥x轴于点B，连接OA，则△AOB的面积是（）A．1B．C．2D．7．（2022•天津）若点A（x1，2），B（x2，﹣1），C（x3，4）都在反比例函数y＝的图象上，则x1，x2，x3的大小关系是（）A．x1＜x2＜x3B．x2＜x3＜x1C．x1＜x3＜x2D．x2＜x1＜x38．（2022•武汉）已知点A（x1，y1），B（x2，y2）在反比例函数y＝的图象上，且x1＜0＜x2，则下列结论一定正确的是（）A．y1+y2＜0B．y1+y2＞0C．y1＜y2D．y1＞y29．（2022•娄底）在平面直角坐标系中，O为坐标原点，已知点P（m，1）、Q（1，m）（m＞0且m≠1），过点P、Q的直线与两坐标轴相交于A、B两点，连接OP、OQ，则下列结论中成立的有（）①点P、Q在反比例函数y＝的图象上；②△AOB为等腰直角三角形；③0°＜∠POQ＜90°；④∠POQ的值随m的增大而增大．A．②③④B．①③④C．①②④D．①②③10．（2022•怀化）如图，直线AB交x轴于点C，交反比例函数y＝（a＞1）的图象于A、B两点，过点B作BD⊥y轴，垂足为点D，若S△BCD＝5，则a的值为（）A．8B．9C．10D．11二．填空题（共13小题）11．（2022•新疆）若点（1，2）在反比例函数y＝的图象上，则k＝．12．（2022•陕西）已知点A（﹣2，m）在一个反比例函数的图象上，点A'与点A关于y轴对称．若点A'在正比例函数y＝x的图象上，则这个反比例函数的表达式为．13．（2022•江西）已知点A在反比例函数y＝（x＞0）的图象上，点B在x轴正半轴上，若△OAB为等腰三角形，且腰长为5，则AB的长为．14．（2022•滨州）若点A（1，y1）、B（﹣2，y2）、C（﹣3，y3）都在反比例函数y＝的图象上，则y1、y2、y3的大小关系为．15．（2022•广元）如图，已知在平面直角坐标系中，点A在x轴负半轴上，点B在第二象限内，反比例函数y＝的图象经过△OAB的顶点B和边AB的中点C，如果△OAB的面积为6，那么k的值是．16．（2022•随州）如图，在平面直角坐标系中，直线y＝x+1与x轴，y轴分别交于点A，B，与反比例函数y＝的图象在第一象限交于点C，若AB＝BC，则k的值为．17．（2022•乐山）如图，平行四边形ABCD的顶点A在x轴上，点D在y＝（k＞0）上，且AD⊥x轴，CA的延长线交y轴于点E．若S△ABE＝，则k＝．18．（2022•株洲）如图所示，矩形ABCD顶点A、D在y轴上，顶点C在第一象限，x轴为该矩形的一条对称轴，且矩形ABCD的面积为6．若反比例函数y＝的图象经过点C，则k的值为．19．（2022•湖州）如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，tan∠ABO＝3，以AB为边向上作正方形ABCD．若图象经过点C的反比例函数的解析式是y＝，则图象经过点D的反比例函数的解析式是．20．（2022•宁波）如图，四边形OABC为矩形，点A在第二象限，点A关于OB的对称点为点D，点B，D 都在函数y＝（x＞0）的图象上，BE⊥x轴于点E．若DC的延长线交x轴于点F，当矩形OABC 的面积为9时，的值为，点F的坐标为．21．（2022•绍兴）如图，在平面直角坐标系xOy中，点A（0，4），B（3，4），将△ABO向右平移到△CDE 位置，A的对应点是C，O的对应点是E，函数y＝（k≠0）的图象经过点C和DE的中点F，则k的值是．22．（2022•凉山州）如图，点A在反比例函数y＝（x＞0）的图象上，过点A作AB⊥x轴于点B，若△OAB的面积为3，则k＝．23．（2022•成都）在平面直角坐标系xOy中，若反比例函数y＝的图象位于第二、四象限，则k的取值范围是．三．解答题（共28小题）24．（2022•孝感）如图，已知一次函数y1＝kx+b的图象与函数y2＝（x＞0）的图象交于A（6，﹣），B （，n）两点，与y轴交于点C．将直线AB沿y轴向上平移t个单位长度得到直线DE，DE与y轴交于点F．（1）求y1与y2的解析式；（2）观察图象，直接写出y1＜y2时x的取值范围；（3）连接AD，CD，若△ACD的面积为6，则t的值为．25．（2022•广元）如图，在平面直角坐标系xOy中，函数y＝x+b的图象与函数y＝（x＞0）的图象相交于点B（1，6），并与x轴交于点A．点C是线段AB上一点，△OAC与△OAB的面积比为2：3．（1）求k和b的值；（2）若将△OAC绕点O顺时针旋转，使点C的对应点C′落在x轴正半轴上，得到△OA′C′，判断点A′是否在函数y＝（x＞0）的图象上，并说明理由．26．（2022•常德）如图，已知正比例函数y1＝x与反比例函数y2的图象交于A（2，2），B两点．（1）求y2的解析式并直接写出y1＜y2时x的取值范围；（2）以AB为一条对角线作菱形，它的周长为4，在此菱形的四条边中任选一条，求其所在直线的解析式．27．（2022•湘潭）已知A（3，0）、B（0，4）是平面直角坐标系中两点，连接AB．（1）如图①，点P在线段AB上，以点P为圆心的圆与两条坐标轴都相切，求过点P的反比例函数表达；（2）如图②，点N是线段OB上一点，连接AN，将△AON沿AN翻折，使得点O与线段AB上的点M 重合，求经过A、N两点的一次函数表达式．28．（2022•台州）如图，根据小孔成像的科学原理，当像距（小孔到像的距离）和物高（蜡烛火焰高度）不变时，火焰的像高y（单位：cm）是物距（小孔到蜡烛的距离）x（单位：cm）的反比例函数，当x＝6时，y＝2．（1）求y关于x的函数解析式．（2）若火焰的像高为3cm，求小孔到蜡烛的距离．29．（2022•苏州）如图，一次函数y＝kx+2（k≠0）的图象与反比例函数y＝（m≠0，x＞0）的图象交于点A（2，n），与y轴交于点B，与x轴交于点C（﹣4，0）．（1）求k与m的值；（2）P（a，0）为x轴上的一动点，当△APB的面积为时，求a的值．30．（2022•眉山）已知直线y＝x与反比例函数y＝的图象在第一象限交于点M（2，a）．（1）求反比例函数的解析式；（2）如图，将直线y＝x向上平移b个单位后与y＝的图象交于点A（1，m）和点B（n，﹣1），求b 的值；（3）在（2）的条件下，设直线AB与x轴、y轴分别交于点C，D，求证：△AOD≌△BOC．31．（2022•乐山）如图，已知直线l：y＝x+4与反比例函数y＝（x＜0）的图象交于点A（﹣1，n），直线l′经过点A，且与l关于直线x＝﹣1对称．（1）求反比例函数的解析式；（2）求图中阴影部分的面积．32．（2022•衡阳）如图，反比例函数y＝的图象与一次函数y＝kx+b的图象相交于A（3，1），B（﹣1，n）两点．（1）求反比例函数和一次函数的关系式；（2）设直线AB交y轴于点C，点M，N分别在反比例函数和一次函数图象上，若四边形OCNM是平行四边形，求点M的坐标．33．（2022•株洲）如图所示，在平面直角坐标系xOy中，点A、B分别在函数y1＝（x＜0）、y2＝（x＞0，k＞0）的图象上，点C在第二象限内，AC⊥x轴于点P，BC⊥y轴于点Q，连接AB、PQ，已知点A 的纵坐标为﹣2．（1）求点A的横坐标；（2）记四边形APQB的面积为S，若点B的横坐标为2，试用含k的代数式表示S．34．（2022•宁波）如图，正比例函数y＝﹣x的图象与反比例函数y＝（k≠0）的图象都经过点A（a，2）．（1）求点A的坐标和反比例函数表达式．（2）若点P（m，n）在该反比例函数图象上，且它到y轴距离小于3，请根据图象直接写出n的取值范围．35．（2022•杭州）设函数y1＝，函数y2＝k2x+b（k1，k2，b是常数，k1≠0，k2≠0）．（1）若函数y1和函数y2的图象交于点A（1，m），点B（3，1），①求函数y1，y2的表达式；②当2＜x＜3时，比较y1与y2的大小（直接写出结果）．（2）若点C（2，n）在函数y1的图象上，点C先向下平移2个单位，再向左平移4个单位，得点D，点D恰好落在函数y1的图象上，求n的值．36．（2022•泰安）如图，点A在第一象限，AC⊥x轴，垂足为C，OA＝2，tan A＝，反比例函数y＝的图象经过OA的中点B，与AC交于点D．（1）求k值；（2）求△OBD的面积．37．（2022•温州）已知反比例函数y＝（k≠0）的图象的一支如图所示，它经过点（3，﹣2）．（1）求这个反比例函数的表达式，并补画该函数图象的另一支．（2）求当y≤5，且y≠0时自变量x的取值范围．38．（2022•武威）如图，B，C是反比例函数y＝（k≠0）在第一象限图象上的点，过点B的直线y＝x﹣1与x轴交于点A，CD⊥x轴，垂足为D，CD与AB交于点E，OA＝AD，CD＝3．（1）求此反比例函数的表达式；（2）求△BCE的面积．39．（2022•江西）如图，点A（m，4）在反比例函数y＝（x＞0）的图象上，点B在y轴上，OB＝2，将线段AB向右下方平移，得到线段CD，此时点C落在反比例函数的图象上，点D落在x轴正半轴上，且OD＝1．（1）点B的坐标为，点D的坐标为，点C的坐标为（用含m的式子表示）；（2）求k的值和直线AC的表达式．40．（2022•金华）如图，点A在第一象限内，AB⊥x轴于点B，反比例函数y＝（k≠0，x＞0）的图象分别交AO，AB于点C，D．已知点C的坐标为（2，2），BD＝1．（1）求k的值及点D的坐标．（2）已知点P在该反比例函数图象上，且在△ABO的内部（包括边界），直接写出点P的横坐标x的取值范围．41．（2022•连云港）如图，在平面直角坐标系xOy中，一次函数y＝ax+b（a≠0）的图象与反比例函数y＝（k≠0）的图象交于P、Q两点．点P（﹣4，3），点Q的纵坐标为﹣2．（1）求反比例函数与一次函数的表达式；（2）求△POQ的面积．42．（2022•达州）如图，一次函数y＝x+1与反比例函数y＝的图象相交于A（m，2），B两点，分别连接OA，OB．（1）求这个反比例函数的表达式；（2）求△AOB的面积；（3）在平面内是否存在一点P，使以点O，B，A，P为顶点的四边形为平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．43．（2022•重庆）反比例函数y＝的图象如图所示，一次函数y＝kx+b（k≠0）的图象与y＝的图象交于A（m，4），B（﹣2，n）两点．（1）求一次函数的表达式，并在所给的平面直角坐标系中画出该函数的图象；（2）观察图象，直接写出不等式kx+b＜的解集；（3）一次函数y＝kx+b的图象与x轴交于点C，连接OA，求△OAC的面积．44．（2022•南充）如图，直线AB与双曲线交于A（1，6），B（m，﹣2）两点，直线BO与双曲线在第一象限交于点C，连接AC．（1）求直线AB与双曲线的解析式．（2）求△ABC的面积．45．（2022•重庆）已知一次函数y＝kx+b（k≠0）的图象与反比例函数y＝的图象相交于点A（1，m），B （n，﹣2）．（1）求一次函数的表达式，并在图中画出这个一次函数的图象；（2）根据函数图象，直接写出不等式kx+b＞的解集；（3）若点C是点B关于y轴的对称点，连接AC，BC，求△ABC的面积．46．（2022•德阳）如图，一次函数y＝﹣x+1与反比例函数y＝的图象在第二象限交于点A，且点A的横坐标为﹣2．（1）求反比例函数的解析式；（2）点B的坐标是（﹣3，0），若点P在y轴上，且△AOP的面积与△AOB的面积相等，求点P的坐标．47．（2022•泸州）如图，直线y＝﹣x+b与反比例函数y＝的图象相交于点A，B，已知点A的纵坐标为6．（1）求b的值；（2）若点C是x轴上一点，且△ABC的面积为3，求点C的坐标．48．（2022•成都）如图，在平面直角坐标系xOy中，一次函数y＝﹣2x+6的图象与反比例函数y＝的图象相交于A（a，4），B两点．（1）求反比例函数的表达式及点B的坐标；（2）过点A作直线AC，交反比例函数图象于另一点C，连接BC，当线段AC被y轴分成长度比为1：2的两部分时，求BC的长；（3）我们把有两个内角是直角，且一条对角线垂直平分另一条对角线的四边形称为“完美筝形”．设P 是第三象限内的反比例函数图象上一点，Q是平面内一点，当四边形ABPQ是完美筝形时，求P，Q两点的坐标．49．（2022•遂宁）在平面直角坐标系中，如果一个点的横坐标与纵坐标互为相反数，则称该点为“黎点”．例如（﹣1，1），（2022，﹣2022）都是“黎点”．（1）求双曲线y＝上的“黎点”；（2）若抛物线y＝ax2﹣7x+c（a、c为常数）上有且只有一个“黎点”，当a＞1时，求c的取值范围．50．（2022•遂宁）已知一次函数y1＝ax﹣1（a为常数）与x轴交于点A，与反比例函数y2＝交于B、C两点，B点的横坐标为﹣2．（1）求出一次函数的解析式并在图中画出它的图象；（2）求出点C的坐标，并根据图象写出当y1＜y2时对应自变量x的取值范围；（3）若点B与点D关于原点成中心对称，求出△ACD的面积．51．（2022•自贡）如图，在平面直角坐标系中，一次函数y＝kx+b的图象与反比例函数y＝的图象相交于A（﹣1，2），B（m，﹣1）两点．（1）求反比例函数和一次函数的解析式；（2）过点B作直线l∥y轴，过点A作AD⊥l于点D，点C是直线l上一动点，若DC＝2DA，求点C 的坐标．。

一次函数和反比例函数综合问题(3易错7题型)—2024年中考数学(全国通用)(解析版)

一次函数和反比例函数综合问题目录【中考预测】预测考向，总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题，讲解通关策略（含新考法、新情境等）一次函数和反比例函数是全国中考的热点内容，更是全国中考的必考内容.每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分.1．从考点频率看，一次函数和反比例函数的图象和性质是考查的基础，也是高频考点、必考点，所以对一次函数和反比例函数的图象和性质必须熟记.2．从题型角度看，以解答题的第三题或第四题为主，分值8分左右，着实不少！易错点一一次函数与反比例函数中由面积求点坐标【例1】（2024·广东珠海·模拟预测）如图，在平面直角坐标系xOy 中，一次函数图象5y x =−+与y 轴交于点A ，与反比例函数ky x=的图象的一个交点为(),4B a ，过点B 作AB 的垂线l ．(1)求点A 的坐标及反比例函数的表达式；(2)若点C 在直线l 上，且ABC 的面积为5，求点C 的坐标；S=ABCABCS=【例2】（2024·甘肃陇南·一模）如图，在平面直角坐标系xOy 中，一次函数4y x =−与反比例函数ky x=的图象交于A ，B 两点，与x 轴相交于点C ，已知点A ，B 的坐标分别为()5,n n 和(),5m −．(1)求反比例函数的解析式； (2)点P 为反比例函数ky x=图象上任意一点，若2POC AOC S S =△△，求点P 的坐标．【例3】（2024·山东济宁·一模）如图，点()3,6A ，()6,B a 是反比例函数y x=的图象上的两点，连接OA 、OB ．(1)求a 的值； (2)求AOB 的面积；(3)若点C 的坐标为()9,0，点P 是反比例函数图象上的点，若POC △的面积等于AOB 面积的3倍，求点P的坐标． )AOB 的面积为AODBOES S=，由BOEAODAOEB S SS S=−四边形，可得AOBS=1273322POCAOBSOC PE S =⨯⨯==⨯，即可求解，【详解】（1）解：∵点()3,6A ，()6,B a 是反比例函数y x=的图象上的两点， ∴63m=，解得：18m =， ∴反比例函数解析式为：18y x=， ∴186a =，解得：3a =，故答案为：3a =，（2）解：过点A ，B ，作AC x ⊥轴，BD x ⊥轴，垂足分别为D ，E ，由（1）可知，点()3,6A ，()6,3B 是反比例函数18y x=的图象上的两点， ∴6AC =，3OD =，3BD =,6OE =，AODBOES S=，∵BOEAODAOEB AOEB S SS S−=−四边形四边形，∴()()()()()1112763632222AOBADEB SS AD BE DE AD BE OE OD ==+⋅=+⋅−=+−=梯形，故答案为：AOB 的面积为272，（3）解：设点P 坐标为18,p p ⎛⎫⎪⎝⎭，过点P ，作PE x ⊥轴，垂足为E ，∴18180PE p p=−=，9OC =， ∴1273322POCAOBSOC PE S =⨯⨯==⨯，即：118279322p ⨯⨯=⨯，解得：2p =或2p =−， ∴()2,9P 或()2,9P −−，故答案为：点P 的坐标为()2,9或()2,9−−．一次函数中平移问题【例1】（2024·河北邯郸·二模）如图，直线1:4l y x =+与y 轴，x 轴交于点A ，点B ，直线2l 与y 轴，x 轴交于点A ，点,2C OC OA =．(1)求点A 的坐标及直线2l 的解析式；(2)点13,22D m m ⎛⎫+ ⎪⎝⎭在直线3l 上．①直接写出直线3l 的解析式；②若点D 在ABC 内部（含边界），求m 的取值范围；③横纵坐标都为整数的点为整点，将直线3l 向上平移n 个单位长度（n 为整数），直线3l 在第二象限恰有4个整点，直接写出n的值．=OC OA2①点在ABC 内部（含边界）【例2】（2024·河北石家庄·一模）如图，平面直角坐标系中，线段AB 的端点为(2,2)A ，(4,1)B ．直线:2l y x =+与x 轴，y 轴分别交于C ，D 两点，动点P 从点D 出发，沿y 轴以每秒1个单位长度的速度向下移动，设移动时间为t 秒．某同学设计了一个动画：线段AB 为蓝色光带，当有动点或动直线经过线段AB 时，蓝色光带会变成红色．(1)求直线AB 的解析式；(2)①若直线l 随点P 向下平移，当2t =时，蓝色光带是否变红？②点M 是直线l 上的一点，若点M 向下平移4个单位长度的过程中，能使蓝色光带变红，求点M 的横坐标M x 的取值范围；Q m n三点共线时，直接写出m与t的函数关系式．(3)当点C，点P与蓝色光带上的点(,)直线过直线又直线②点A）()20C −，易错点三一次函数与反比例函数中求线段和的最小值问题【例1】（2024·甘肃兰州·模拟预测）如图，一次函数8y x =+的图象与反比例函数()0ky x x=<的图象交于(),6A a ，B 两点．(1)求此反比例函数的表达式及点B 的坐标；(2)在y 轴上存在点P ，使得AP BP +的值最小，求AP BP +的最小值．则AP BP +的最小值A =【例2】（2023·辽宁盘锦·二模）如图，一次函数4y x =+的图象与反比例函数ky x=（k 为常数且0k ≠）的图象交于()1,A a −，B 两点．(1)求此反比例函数的表达式及点B 的坐标；(2)当反比例函数值大于一次函数值时，直接写出x 的取值范围；(3)在y 轴上存在点P ，使得APB △的周长最小，求点P 的坐标并直接写出APB △的周长．）解：点点点A题型一一次函数的图象和性质【例1】（2024·浙江·模拟预测）已知点()11,A m n ，()22,B m n ()12m m <在一次函数y kx b =+的图像上． (1)用含有1m ，1n ，2m ，2n 的代数式表示k 的值．(2)若123m m b +=，124n n kb +=+，2b >．试比较1n 和2n 的大小，并说明理由．【例2】（2024·浙江杭州·一模）设一次函数31y ax a =++（a 是常数，0a ≠）． (1)无论a 取何值，该一次函数图象始终过一个定点，直接写出这个定点坐标： (2)若24x ≤≤时，该一次函数的最大值是6，求a 的值．【详解】（1）解：一次函数1，当3x =−时，11y =，∴无论a 取何值，该一次函数图象始终过定点(3,1)−；（2）解：当0a >时，当4x =时，一次函数14316y a a =++=，1．（2024·北京·一模）在平面直角坐标系xOy 中，一次函数y kx b =+（0k ≠）的图象经过点()0,1，()2,2−，与x 轴交于点A ．(1)求该一次函数的表达式及点A 的坐标；(2)当2x >时，对于x 的每一个值，函数2y x m =+的值大于一次函数y kx b =+（0k ≠）的值，直接写出m 的取值范围．解：一次函数2．（2024·浙江宁波·模拟预测）已知一次函数10y mx n mn =+≠．(1)已知关于x 的一元二次方程20x mx n +−=必有两个不相等的实数根，试说明一次函数1y mx n =+的图象过第一和第二象限．(2)在（1）的条件下，已知另一函数2y nx m =+的图象与y 1图象的交点在第四象限，求不等式12y y >的解．【答案】(1)见解析解：∵关于x 的一元二次方程20x mx n +−=的解，可看作抛物线2y x =与直线y mx n =−+的交点，根据题意得，抛物线2y x =与直线y mx n =−+必有两个不同的交点， ∴0n >，∴一次函数1y mx n =+的图象过第一和第二象限；（2）解：∵2y nx m =+，0n >，∴直线2y nx m =+一定经过第一、三象限， ∵直线2y nx m =+与y 1图象的交点在第四象限，∴直线2y nx m =+一定经过第一、三、四象限， ∴0m <， ∴0m n −<， ∵12y y >， ∴mx n nx m +>+，整理得()m n x m n −>−， ∴1x <，即不等式12y y >的解集为1x <．题型二反比例函数的图象和性质【例1】（2024·陕西西安·一模）已知反比例函数3my x−=． (1)若该反比例函数图象在每一个象限内，y 都随着x 的增大而减小，求m 的取值范围； (2)若点()2,3A 在此反比例函数图象上，求反比例函数的解析式．1．（2024·福建南平·一模）反比例函数ky x=图象经过点(1,6)A ，(,3)B a ． (1)求a 的值；(2)若点(,)C m n 在反比例函数ky x=图象上，其中3n <，求m 的取值范围．题型三一次函数和反比例函数与不等式综合问题【例1】（2024·贵州毕节·一模）如图，一次函数()0y ax b a =+≠与反比例函数()0ky k x=≠的图象在第一象限交于()2,3A 和()3,B m 两点，与x 轴交于点C ．(1)求反比例函数和一次函数的表达式； (2)直接写出关于x 的不等式(0)kax b x x+>>的解集．）解：点又B【例2】（2024·陕西宝鸡·一模）如图所示，一次函数1y x m =−+图象与反比例函数2ky x=图象相交于点(,3)A n 和点(3,1)B −．(1)求反比例函数解析式； (2)当12y y >时，求x 的取值范围．1．（2024·山西朔州·一模）如图，反比例函数()1110,0k y k x x=>>与一次函数()2220y k x b k =+≠的图象交于()2,3A ，3,2B m ⎛⎫⎪⎝⎭两点．(1)求m 的值及一次函数的表达式． (2)直接写出当12y y >时，x 的取值范围．）解：反比例函数与一次函数的图象交于当24x <<时，12y y <，所以，当12y y >时， x 的取值范围为02x <<或4x >．2．（2024·江西九江·一模）如图一次函数y kx b =+的图象与反比例函数4y x=−的图象相交于点()1,A m −，(),1B n −．(1)求一次函数的解析式；(2)结合图象，直接写出不等式4kx b x+>−的解集．3．（2024·河南安阳·模拟预测）如图，一次函数12y x =−的图象与反比例函数(0)y k x=≠的图象交于()(),12,A a B b −，两点，与x 轴相交于点C ．(1)求反比例函数的表达式；(2)观察图象，直接写出不等式112kx x−<的解集；(3)若(),0P m 为x 轴上的一动点，连接AP ，当APC △的面积为52时，求点P 的坐标．）解：函数）函数在112y x =−中，当y =解得：2x =，()2,0C ∴， ()0,P m ，APC S =△题型四一次函数和反比例函数中求三角形面积问题【例1】（2024·山西大同·一模）如图，一次函数y ax b =+的图象与反比例函数()0ky k x=>的图象相交于点()6,32A n −−，点(),3B n −，与y 轴交于点C ．(1)求一次函数和反比例函数的解析式；(2)点D 是点C 关于x 轴的对称点，连接AD BD 、，求ABD △的面积．S=ABD【例2】（2024·吉林白山·一模）如图，在平面直角坐标系中，一次函数5y x =−+的图象与反比例函数(0)ky k x=>的图象相交于()1,A m 、()4,B n 两点，与x 轴相交于点C ，连接OA 、OB ．(1)求反比例函数的解析式； (2)求AOB 的面积． AOBS=1．（2024·湖南长沙·三模）如图，在平面直角坐标系中，一次函数32y x b =−+与反比例函数()0ky k x=≠交于()(),6,4,3A m B −两点，与y 轴交于点C ，连接,OA OB ．(1)求反比例函数和一次函数的表达式； (2)求AOB 的面积．解：点解：点AOBAOCBOCS SS=+与反比例函数(0)ky x x=>的图象交于点()1,C a ，D 是反比例函数图象上的一个动点，过点D 向y 轴作垂线与一次函数图象交于点E ，其中点A 的坐标为(3,0)−．(1)求反比例函数的表达式；(2)连接,DB DC ，当DCE △的面积等于DBC △面积的2倍时，求点E 的坐标；(3)若P 是x 轴上的一个动点，连接,EP DP ，当DPE 与AOB 相似时，求点D 的纵坐标．坐标，根据DPE 与AOB 相似计算即可，注意分情况讨论．()033b =⨯−+∵过点D向y轴作垂线与一次函数图象交于点∴设12D mm⎛⎫⎪⎝⎭，，则点E纵坐标为∴1239y xm=+=，解得x412⎛⎫当AOB PED∽时，当时，AOB PED ∽，此时时，P AOB DE ∽，此时∴12PD m =，DE m ⎛=− ⎝∴1243PD m DE m m m ==⎛⎫−− ⎪⎝⎭时，E AOB PD ∽，此时时，P AOB ED ∽，此时，则N EPM PD ∽∴EM MP PEPN DN PD== 此时12EM DN m==，DE 当D AOB EP ∽时，PE PD 同理当AOB DPE ∽时，PD综上所述，当DPE 与AOB 相似时，求点题型五一次函数和反比例函数中求证问题【例1】（新考法，拓视野）（2024·河南周口·一模）如图，反比例函数ky x=与正比例函数y ax =交于点()3,2A 和点C ，与正比例函数6y x =交于点B 和点D ．(1)求k 与a 的值，并求点B ，C ，D 的坐标； (2)求证：CBD ADB ∠=∠．1．（2024·湖南怀化·一模）在平面直角坐标系中，点O 为坐标原点．如图，一次函数y ax b =+（a 为常数，0a ≠）与反比例函数ky x=（k 为常数，0k ≠）的图象相交于点()25A ，和点()4B m −，．(1)求反比例函数与一次函数的解析式；(2)过点A 作y 轴的垂线，过点B 作x 轴的垂线，相交于点C ；过点A 作x 轴的垂线，过点B 作y 轴的垂线，相交于点D ．求证：C ，O ，D 三点在同一条直线上．2．（2024·河南平顶山·一模）如图，一次函数y ax b =+的图象与反比例函数y x=的图象交于第一象限(1,4)C ，D(4,m)两点，与坐标轴交于A 、B 两点，连接OC ，OD （O 是坐标原点）.(1)求一次函数与反比例函数的解析式；(2)当kax bx+<时，直接写出x的取值范围；(3)将直线AB向下平移多少个单位长度，直线与反比例函数图象只有一个交点？题型六一次函数和反比例函数中求线段长问题【例1】（2024·广东珠海·一模）如图1．直线21y x =+与y 轴交于点B ，与反比例函数()0ky x x=>的图象交于点()1,A a ．图2将线段AB 向右平移m 个单位长度()0m >，得到对应线段CD ，连接AC ，BD ．当点D 恰好落在反比例函数图象上时，过点C 作CF x ⊥轴于点F ，交反比函数图象于点E ．(1)求反比例函数表达式； (2)求EF 的长度．1．（2024·河南·模拟预测）如图所示，在平面直角坐标系中，一次函数1y ()0kx b k =+≠的图象与反比例函数2y ()0mm x=≠的图象相交于第二、四象限内的()1,3A −，(),1B a −两点，与y 轴交于点C ．(1)求该反比例函数和一次函数的解析式；(2)在x 轴上找一点P ，使PA PC −最大，求PA PC −的最大值及点P 的坐标．一次函数的解析式为Rt ADC中，由勾股定理可得题型七利用反比例函数的图象和性质探究平移问题【例1】（新考法，拓视野）（2024·广东深圳·模拟预测）小明在学习了反比例函数的图象与性质后，进一步研究了函数1yx=−的图象与性质．其探究过程如下：(1)绘制函数图象，如图，列表：下表是x与y的几组对应值，其中m=；描点：根据表中各组对应值,x y，在平面直角坐标系中描出各点；连线：用平滑的曲线顺次连接各点，画出了部分图象，请你把图象补充完整；(2)通过观察函数图象，写出该函数的一条性质：．(3)利用函数图象，解不等式1230xx−+＜．观察图形得出函数的性质：图象关于y轴对称；故答案为：图象关于y轴对称；（3）【例2】（2024·陕西西安·一模）乐乐同学在学习了反比例函数的基础上，进一步探究函数21y x =-的性质．以下是他的研究过程，请补充完整．(1)如表是y 与x 的几组对应值．(2)在平面直角坐标系xOy 中，描出了以表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；(3)观察图象，发现这个函数图象为中心对称图形，则它的对称中心为______；(4)若直线2y x =与函数21y x =-的图象交于第一象限内一点(),P x y ，则下面关于x 的取值范围描述正确的是（）A ．1 1.25x <<B ．1.25 1.5x <<C ．1.5 1.75x <<D ．1.752x <<【详解】（1）解：①4x =时，413y ==−， 23m ∴=，故答案为：23；（2）解：如图：（3）解：观察图象，发现这个函数图象为中心对称图形，则它的对称中心为(1,0)；故答案为：(1,0)；（4）解：作出直线2y x =如图：把3y =代入2y x =求得 1.5x =，把3y =代入21y x =-，求得53x =，观察图象，若直线2y x =与函数21y x =-的图象交于第一象限内一点(,)P x y ，则x 的取值范围是51.53x <<， ∴关于x 的取值范围描述正确的是C ，故答案为：C ．1．（2024·山西大同·一模）中考新考法：注重过程性学习，某数学小组在研究函数221x y −+=+时，对函数的图象进行了探究，探究过程如下：(1)①x 与y 的几组对应值如下表，请补全表格；②在上图平面直角坐标系中，描出上表中各组对应值为坐标的点，并根据描出的点画出该函数的图象；(2)我们知道，函数()()20,0,0y a x h k a h k =−+≠>>的图象是由二次函数2y ax =的图象向右平移h 个单位，再向上平移k 个单位得到的．类似地，请直接写出将2y x =−的图象经过怎样的平移可以得到221x y −+=+的图象；(3)若一次函数123y x =−+的图象与函数221x y −+=+的图象交于A B 、两点，连接OA OB 、，求AOB 的面积．【答案】(1)见解析，(2)向左平移1个单位，向上平移2个单位(3)5（2）2y x=−的图象向左平移1（3）一次函数123y x =−+的图象，如图，可知∴AOB 的面积为()12232⨯⨯+=。

一次函数与反比例涵数的专题复习

一次函数与反比例函数专题复习第一部分知识梳理考点一、平面直角坐标系（3分） 1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴，就组成了平面直角坐标系。

其中，水平的数轴叫做x 轴或横轴，取向右为正方向；铅直的数轴叫做y 轴或纵轴，取向上为正方向；两轴的交点O （即公共的原点）叫做直角坐标系的原点；建立了直角坐标系的平面，叫做坐标平面。

为了便于描述坐标平面内点的位置，把坐标平面被x 轴和y 轴分割而成的四个部分，分别叫做第一象限、第二象限、第三象限、第四象限。

注意：x 轴和y 轴上的点，不属于任何象限。

2、点的坐标的概念点的坐标用（a ，b ）表示，其顺序是横坐标在前，纵坐标在后，中间有“，”分开，横、纵坐标的位置不能颠倒。

平面内点的坐标是有序实数对，当b a ≠时，（a ，b ）和（b ，a ）是两个不同点的坐标。

考点二、不同位置的点的坐标的特征（3分） 1、各象限内点的坐标的特征（1）点P(x,y)在第一象限0,0>>⇔y x（2）点P(x,y)在第二象限0,0><⇔y x （3）点P(x,y)在第三象限0,0<<⇔y x （4）点P(x,y)在第四象限0,0<>⇔y x 2、坐标轴上的点的特征（1）点P(x,y)在x 轴上0=⇔y ，x 为任意实数（2）点P(x,y)在y 轴上0=⇔x ，y 为任意实数（3）点P(x,y)既在x 轴上，又在y 轴上⇔x ，y 同时为零，即点P 坐标为（0，0） 3、两条坐标轴夹角平分线上点的坐标的特征（1）点P(x,y)在第一、三象限夹角平分线上⇔x 与y 相等（2）点P(x,y)在第二、四象限夹角平分线上⇔x 与y 互为相反数 4、和坐标轴平行的直线上点的坐标的特征（1）位于平行于x 轴的直线上的各点的纵坐标相同。

（2）位于平行于y 轴的直线上的各点的横坐标相同。

5、关于x 轴、y 轴或远点对称的点的坐标的特征（1）点P 与点p ’关于x 轴对称⇔横坐标相等，纵坐标互为相反数（2）点P 与点p ’关于y 轴对称⇔纵坐标相等，横坐标互为相反数（3）点P 与点p ’关于原点对称⇔横、纵坐标均互为相反数 6、点到坐标轴及原点的距离（1）点P(x,y)到x 轴的距离等于y （2）点P(x,y)到y 轴的距离等于x （3）点P(x,y)到原点的距离等于22y x +考点三、函数及其相关概念（3~8分） 1、变量与常量在某一变化过程中，可以取不同数值的量叫做变量，数值保持不变的量叫做常量。

备战中考数学一轮专项复习——一次函数的图象和性质课件(287张)

【点拨】确定函数解析式常用待定系数法：确定正比例函数解析式，只需一对 x，y 的值；确定一次函数解析式，需要两对 x，y 的值．
03 福建4年中考聚焦
1
2
3
4
5
1．【2020·三明质检·4 分】在平面直角坐标系中，若一个正比例
函数的图象经过 A(m，6)，B(5，n)两点，则 m，n 一定满足
(1)求这个一次函数的解析式；
解：∵一次函数的图象平行于直线 y＝12x， ∴设这个一次函数的解析式为 y＝12x＋b. ∵函数图象经过点 A(2，3)，∴12×2＋b＝3，解得 b＝2. ∴一次函数的解析式为 y＝12x＋2.
(2)设点C在y轴上，当AC＝BC时，求点C的坐标．解：∵一次函数 y＝12x＋2 的图象与 x 轴交于点 B，∴B(－4，0)．设点 C 的坐标为(0，y)， ∵AC＝BC，∴22＋(3－y)2＝42＋y2，解得 y＝－12. ∴点 C 的坐标为0，－12.
的关系式为( D )
A．m－n＝1
B．m＋n＝11
C．mn ＝65
D．mn＝30
2．【2020·泉州质检·4 分】一次函数 y＝－2x＋1 的图象不经过
(C )
A．第一象限
B．第二象限
C．第三象限
D．第四象限
3．【2019·莆田质检·4 分】下列直线与过(－2，0)，(0，3)的直线
的交点在第一象限的是( B )
A．x＝－3
B．x＝3
C．y＝－3
D．y＝3
4．【2020·南平质检·4 分】请写出一个 y 随着 x 增大而减小且图象过点(0，2)的一次函数解析式：__y_＝__－__x_＋__2______． (答案不唯一)

中考复习——平面直角坐标系、一次函数、反比例函数及其图象知识点汇总及典例分析

中考复习——平面直角坐标系、一次函数、反比例函数【知识梳理】一、平面直角坐标系1. 坐标平面上的点与有序实数对构成一一对应；2. 各象限点的坐标的符号；3. 坐标轴上的点的坐标特征．4. 点P （a ，b ）关于x 轴对称的点的坐标为；关于y 轴对称的点的坐标为；关于原点对称的点的坐标为5.两点之间的距离二、函数的概念1.概念：在一个变化过程中有两个变量x 与y ，如果对于x 的每一个值，y 都有的值与它对应，那么就说x 是自变量，y 是x 的函数.2.自变量的取值范围：（1）使解析式（2）实际问题具有意义3.函数的表示方法；（1）（2）（3）三、一次函数的概念、图象、性质1．正比例函数的一般形式是（），一次函数的一般形式是 (k≠0). 2. 一次函数y kx b =+的图象是经过（，）和（，）两点的一条直线.4.若两个一次函数解析式中，k 相等，表示两直线；若两直线垂直，则。

5.的大小决定直线的倾斜程度，越大，直线越；四、反比例函数的概念、图象、性质1．反比例函数：一般地，如果两个变量x 、y 之间的关系可以表示成y ＝或或（k 为常数，k≠0）的形式，那么称y 是x 的反比例函数． 2. 反比例函数的图象和性质k ＞0，b ＞0k ＞0，b ＜0k ＜0，b ＞0k ＜0，21212211P P )0()0()2(y y y P y P -＝，　，，，21212211P P )0()0()1(x x x P x P -＝，　，　，，　3．k 的几何含义：反比例函数y ＝k x(k≠0)中比例系数k 的几何意义，即过双曲线y ＝k x(k≠0)上任意一点P 作x 轴、y 轴垂线，设垂足分别为A 、B ，则所得矩形OAPB 的面积为。

【例题精讲】例1.函数22y x =-中自变量x 的取值范围是 ;函数y =x 的取值范围是．例2.已知点(13)A m -，与点(21)B n +，关于x 轴对称，则m = ，n = ．例3.如图，在平面直角坐标系中，点A 的坐标是（10，0），点B 的坐标为（8，0）,点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形，点C 的坐标为例4．一次函数y=(3a+2)x －(4－b),求满足下列条件的a 、b 的取值范围。

反比例函数的图像及性质

反比例函数的图像及性质人教版数学九年级下册《反比例函数的图象和性质》教学设计一.内容和内容解析1.内容反比例函数的图象和性质2.内容解析本节课是人教版数学九年级下册第二十六章第一节反比例函数的内容，本节分为三课时，这是第二课时的新授课.是在学生已经经历了一次函数、二次函数的研究过程的基础上，在得到反比例函数的概念之后，进一步研究反比例函数的图象，并通过图象的研究和分析，来确定反比例函数的性质.教学过程中首先引导学生用“描点法”画出反比例函数的图象，使反比例函数的解析式表示的函数关系直观化；然后分类观察图象，体现“分类”的思想，首先研究k>0的情况，从特殊k=4,k=6,k=8,k=12的图象观察，进而推广到一般，得出k>0时的反比例函数的图象的特征及反比例函数的特性，体现“从特殊到一般”的思想，然后教师再引导学生从解析式的角度分析图象特征，在整个教学过程中始终贯穿由“数”到“形”再由“形”到“数”的相互转化，让学生体会“数形结合”的数学思想和反比例函数的本质属性所在，对于k<0的研究，完全类比k>0的研究过程，体现“类比”的思想.反比例函数是初中阶段要求学习的三种函数中的最后一种，是继一次函数学习之后，知识的一次扩展，图象由“一条”到“两支”，形态由“直”到“曲”，由“连续”到“间断”，由与坐标轴“相交”到“渐近”，是学习函数的一般方法和规律的再次强化，也是后续构建反比例函数模型的基础，起着承上启下的作用.本节课学生的学习重点是：用描点法画反比例函数的图象，并根据图象理解反比例函数的性质．学习难点是：对x≠0的理解及图象特征的分析．二．目标和目标解析1.目标（1）能画出反比例函数的图象，探索并理解图象的变化情况.（2）在画出反比例函数的图象，并探究其性质的过程中，体会“类比”、“分类讨论”、“从特殊到一般”以及“数形结合”的数学思想.（3）通过观察反比例函数的图象、探究反比例函数的性质，发展探究、归纳及概括的能力.2.目标解析（1）首先运用描点法画出反比例函数的图象，然后根据图象，通过观察、分析、归纳得出反比例函数的性质，因此正确画出反比例函数图象是前提条件，虽然学生之前用描点法经历过画一次函数、二次函数图象的经验，但是由于反比例函数图象结构复杂，具有自身的特殊性，因此，能用“描点法”画出反比例函数图象并根据图象探究其性质仍是本节课的目标.（2）类比正比例函数的研究方法，通过分类讨论的方式首先研究k>0的情况，在研究过程中从图象和解析式两个角度分析，体现了数形结合的思想，通过类比研究k<0的情况，同样体现从特殊到一般的数学思想.（3）在探究反比例函数的性质的过程中，教师利用几何画板给出一系列函数图象，通过对图象的观察、分析，利用数形结合的数学思想，归纳概括反比例函数的图像和性质，所以整个性质的探索过程发展了分析概括的能力.三．教学问题诊断分析学生已经学习了一次函数、二次函数的图象和性质，反比例函数的解析式，已具有描点法画函数图象的初步经验，但是由于反比例函数的图象结构复杂，具有自身的特殊性，因此在画反比函数的图象这个环节，可能遇到的问题有：1.在列表时没注意到自变量的取值范围是x≠0,或者对自变量x的取值只取正或只取负.2.由于列表时只取了有限的几个点，因此在连线时学生容易只把这几点连线，只画出图象的一部分，有明显端点，没有画出双曲线的延伸趋势.3.学生在画双曲线的延伸趋势时可能出现错误，这是因为学生仅仅是通过描点得出图象，并没有深入从解析式的角度分析问题，教师可以引导学生尝试分析理解.在学习一次函数、二次函数的时候，学生已经历过观察、分析图象的特征，概括函数性质的过程，对研究函数性质所用的探究方法也有一定的了解，因此，通过类比，结合反比例函数的图象和表达式探索性质，从使用的方法上不会存在障碍，但是双曲线的特殊性使学生在探究反比例函数增减性时可能会出现问题，教学中教师应该强调从“数”、“形”两方面统一分析.四．教学支持条件分析根据本节课教材内容的特点，为了更直观、形象地突出重点，突破难点，利用几何画板，快速、准确的绘制反比例函数图象，另外通过动态的演示，观察相关数值的变化，研究图象的变化趋势，进而探索反比例函数的性质.五．教学过程分析（一）创设情境多媒体课件展示华罗庚先生的关于“数形结合”的一首词.设计意图：采用名人名言欣赏的方式进行情景引入，不仅调动了学生的积极性，同时又紧扣主题，为本节课的学习进行了方法上的准备.（二）知识链接1.已经学习了哪些函数？2.正比例函数y=kx(k≠0)的图象和性质是什么？3.反比例函数的定义是什么？4.描点法画图象的步骤是什么？师：了解了反比例函数的解析式，也就是从“数”的角度了解了反比例函数，那么对应的反比例函数的“形”的方面，也就是图象是什么呢？函数性质又是怎样的呢？设计意图：通过复习正比例函数的知识，为学习画反比例函数的图象奠定基础，同时提出问题，明确本节课的学习任务.（三）探究图象分以下5个环节完成.1.试一试：学生独立画出6y=的图象.x2.议一议：小组讨论所画作品，选出他们认为画的最好的作品．3.看一看：展示学生选出的作品，进行问题分析.然后教师示范正确画图过程.4.说一说：同桌互说一遍画图像时的注意事项，并修订已画图象.5.练一练：画出反比例函数6y=-的图象.x设计意图：首先让学生独立画图，充分暴露学生存在问题，关注画图的基本步骤及每个细节的处理，培养学生画图象的能力，通过再次画图，使学生及时巩固已获得的作图经验，并且为后面归纳性质增加感性认识.（四）探究性质探究1. 探究反比例函数6y x =和6y x=-的图象有什么共同特征以及不同点？学生活动：主要由学生观察发现，教师适时引导．共同特征：（1 ）它们都由两条曲线组成．反比例函数的图象属于双曲线.（2）随着x 的不断增大（或减小），曲线越来越接近坐标轴．不同特点：（1）位置不同（2）增减性不同教师追问：这些不同特点是由什么因素决定的？生：k 的正负.设计意图：培养学生的观察能力，让学生体会分类的必要性.探究2．利用几何画板再准确作出k =4, k =8, k =12时的三个反比例函数图象．观察这一系列函数图象，思考下列问题：（1）图象形状是什么？（2）图象位于哪几个象限？（3）在每个象限内，y 随x 的变化如何变化?学生活动：先由学生独立思考，然后小组讨论交流，小组代表发言，其他同学补充或质疑.教师板书：形状：双曲线位置：一三象限增减性：在每个象限内，y随x的增大而减小教师追问(1)：哪位同学能从解析式的角度解释第二个和第三个问题?教师设问(2)：第三个问题，如果去掉在每个象限内这个条件，y 随x的变化情况还一致吗？为什么？学生活动：学生尝试解释，教师及时点拨，并利用几何画板直观演示．师：把刚才所研究的问题推广到一般，就得到了k >0时的函数图象和性质．设计意图：使学生经历由特殊到一般的过程，体验知识的产生形成过程；教师的追问引导学生从“数”、“形”两方面解决问题，让学生体会数形结合的思想.探究3.观察下列函数图象特征，归纳k=（k<0）性质.yx学生活动：学生发言，教师板书.形状：双曲线位置：二四象限增减性：在每个象限内，y随x的增大而增大设计意图：让学生自己去观察、类比、发现的方式获得知识，培养学生积极参与的意识和自主探索的能力.归纳: 反比例函数y =k x（k 为常数，k ≠0）的图象和性质．（1）反比例函数y=k x （k 为常数，k ≠0）的图象是双曲线．（2）当k >0时，双曲线的两支分别位于第一、三象限，在每个象限内，y ?值随x 值的增大而减小．（3）当k <0时，双曲线的两支分别位于第二、四象限，在每个象限内，y ?值随x 值的增大而增大．设计意图：培养学生的分类讨论意识和归纳概括能力.探究4.在同一坐标系中反比例函数6y x =与6y x =-的图象之间在位置上有什么对称关系？学生活动：学生观察发现，教师动画演示.师：同学们能再从解析式上分析一下它的对称关系吗？结论：当k 互为相反数时，对应的反比例函数图象既关于x 轴对称，也关于y 轴对称.设计意图：培养学生的观察能力及让学生感知反比例函数图象的对称性和数学美.（五）目标检测1.下列图象中，可以是反比例函数的图象的（）．2.若反比例函数的图象经过（-3,4）则此函数的图象应在（）．A ．第一、三象限B .第一、二象限C .第二、四象限D .第三、四象限3.已知点A (-2，a ）、B (-1,b ) 、C (3，c ）都在反比例函数y =1x图象上，试比较a 、b 、c 的大小.解：把点A (-2，a ）、B (-1，b ）、C (3，c ）分别带入1y x =中得：1a=-2,b ＝-1,13c = 所以b另解：因为k =1>0所以在每个象限内，y 随x 的增大而减小由图知，因为-2<-1<0,所以b 0所以b学生活动：前两题由学生讲解、第三题由学生板书展示.设计意图：通过三个题目巩固反比例函数图像和性质，渗透数形结合的思想方法.（六）课堂小结这节课你有什么收获？有什么疑惑？学生活动：学生发言交流自己的收获，其他同学补充．师：回顾反比例函数的学习过程，我们首先学习了反比例函数的解析式，以解析式为基础，运用数形结合的思想，画出了函数图象，进而研究函数的性质，体现了分类讨论的方法，这其实就是我们研究函数的一般方法.师：同学们，有关反比例函数的知识，经过我们的整理，形成了一颗知识树，像这样让知识体系化，是我们学习数学的一种很好的方法，如果对已每一个知识点，同学们都能进行这样的梳理，那么你就会收获一片知识的森林.设计意图：通过本环节，培养学生分类讨论的思想及归纳概括的能力，通过美丽的知识树，对学生进行了学习方法上的指导，给学生留下深刻印象. （七）分层作业A、习题26.1 第3题B、习题26.1 第8题课外延伸：探究反比例函数k=（k≠0）的图象关于直线y=x与y=-x的对yx称性．设计意图：根据分层教学和因材施教的原则，将作业分成A,B两类，让不同能力的学生在数学上都得到发展.课外延伸让学生带着问题走进课堂，再带着新的问题走出课堂.六、板书设计。

用几何画板探究反比例函数与一次函数的图像性质

用几何画板探究反比例函数与一次函数的图像性质
一、反比例函数
1.定义坐标系。

2.在X轴上绘一个点A，度量其横坐标（变量Xa）。

3.绘函数图像。

4.输入。

5..移动A点，观察函数图象的变化。

附：动画
在X轴上绘一个点B,选中A、B。

出现按钮，点击观察函数图象的自动变化。

二、一次函数
同反比例函数，在X轴上做A、B两个点，分别度量其横坐标（变量Xa,Xb）绘制一次函数：
.移动A、B点，观察函数图象的变化。

作出函数与Y轴交点D，度量D的坐标。

移动B点，观察D的坐标的变化。

附：动画
在X轴上绘一个点C,分别选中AC、BC。

出现按钮。

再设置一个“同时动”按钮：。

点击或者观察函数图象的自动变化及D的坐标的变化。

此方法较方便，不需要再新建参数。

附：“新建参数”法：
定义坐标系
新建参数，定为K
在X轴上取一点A，度量其横坐标。

选中K和Xa:
“数据——计算”
输入
点击和Xa，绘制点B。

选中A、B，构造——轨迹。

增加或减小K的值，观察函数图象的变化。

b
=同上。

kx
y+
总结：
一次函数：k控制斜率，b控制截距。

K大于0，函数呈上升趋势，k 小于0，函数成下降趋势。

函数y=k x向上/下平移k后得
=。

y+
b
kx
反比例函数：K大于零，函数在一、三象限，K越大函数离原点越“远”。

中考数学复习----反比例函数之定义、图像与性质知识点总结与练习题(含答案解析)

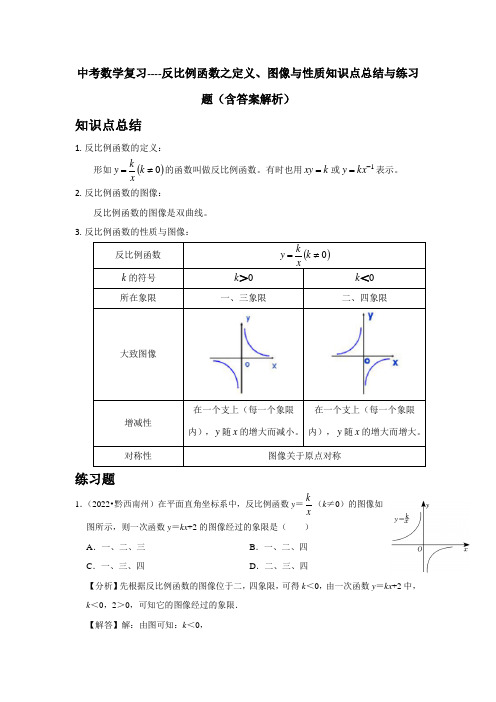
中考数学复习----反比例函数之定义、图像与性质知识点总结与练习题（含答案解析）知识点总结1. 反比例函数的定义：形如()0≠=k xky 的函数叫做反比例函数。

有时也用k xy =或1−=kx y 表示。

2. 反比例函数的图像：反比例函数的图像是双曲线。

3. 反比例函数的性质与图像：反比例函数()0≠=k xky k 的符号0＞k0＜k所在象限一、三象限二、四象限大致图像增减性在一个支上（每一个象限内），y 随x 的增大而减小。

在一个支上（每一个象限内），y 随x 的增大而增大。

对称性图像关于原点对称练习题1．（2022•黔西南州）在平面直角坐标系中，反比例函数y ＝xk（k ≠0）的图像如图所示，则一次函数y ＝kx +2的图像经过的象限是（） A ．一、二、三 B ．一、二、四C ．一、三、四D ．二、三、四【分析】先根据反比例函数的图像位于二，四象限，可得k ＜0，由一次函数y ＝kx +2中，k ＜0，2＞0，可知它的图像经过的象限．【解答】解：由图可知：k ＜0，∴一次函数y ＝kx +2的图像经过的象限是一、二、四．故选：B ．2．（2022•上海）已知反比例函数y ＝xk（k ≠0），且在各自象限内，y 随x 的增大而增大，则下列点可能在这个函数图像上的为（） A ．（2，3）B ．（﹣2，3）C ．（3，0）D ．（﹣3，0）【分析】根据反比例函数的性质判断即可．【解答】解：因为反比例函数y ＝（k ≠0），且在各自象限内，y 随x 的增大而增大，所以k ＜0，A ．2×3＝6＞0，故本选项不符合题意；B ．﹣2×3＝﹣6＜0，故本选项符合题意；C ．3×0＝0，故本选项不符合题意；D ．﹣3×0＝0，故本选项不符合题意；故选：B ．3．（2022•广东）点（1，y 1），（2，y 2），（3，y 3），（4，y 4）在反比例函数y ＝x4图像上，则y 1，y 2，y 3，y 4中最小的是（） A ．y 1B ．y 2C ．y 3D ．y 4【分析】根据k ＞0可知增减性：在每一象限内，y 随x 的增大而减小，根据横坐标的大小关系可作判断．【解答】解：∵k ＝4＞0，∴在第一象限内，y 随x 的增大而减小，∵（1，y 1），（2，y 2），（3，y 3），（4，y 4）在反比例函数y ＝图像上，且1＜2＜3＜4， ∴y 4最小．故选：D ．4．（2022•云南）反比例函数y ＝x6的图像分别位于（） A ．第一、第三象限 B ．第一、第四象限 C ．第二、第三象限D ．第二、第四象限【分析】根据反比例函数的性质，可以得到该函数图像位于哪几个象限，本题得以解决．【解答】解：反比例函数y ＝，k ＝6＞0， ∴该反比例函数图像位于第一、三象限，故选：A ．5．（2022•镇江）反比例函数y ＝xk（k ≠0）的图像经过A （x 1，y 1）、B （x 2，y 2）两点，当x 1＜0＜x 2时，y 1＞y 2，写出符合条件的k 的值（答案不唯一，写出一个即可）．【分析】先根据已知条件判断出函数图像所在的象限，再根据系数k 与函数图像的关系解答即可．【解答】解：∵反比例函数y ＝（k ≠0）的图像经过A （x 1，y 1）、B （x 2，y 2）两点，当x 1＜0＜x 2时，y 1＞y 2，∴此反比例函数的图像在二、四象限， ∴k ＜0，∴k 可为小于0的任意实数，例如，k ＝﹣1等．故答案为：﹣1．6．（2022•福建）已知反比例函数y ＝xk的图像分别位于第二、第四象限，则实数k 的值可以是．（只需写出一个符合条件的实数）【分析】根据图像位于第二、四象限，易知k ＜0，写一个负数即可．【解答】解：∵该反比例图像位于第二、四象限， ∴k ＜0，∴k 取值不唯一，可取﹣3，故答案为：﹣3（答案不唯一）．7．（2022•成都）在平面直角坐标系xOy 中，若反比例函数y ＝xk 2−的图像位于第二、四象限，则k 的取值范围是．【分析】根据反比例函数的性质列不等式即可解得答案．【解答】解：∵反比例函数y ＝的图像位于第二、四象限，∴k ﹣2＜0，解得k ＜2，故答案为：k ＜2．8．（2022•襄阳）二次函数y ＝ax 2+bx +c 的图像如图所示，则一次函数y ＝bx +c 和反比例函数y ＝xa在同一平面直角坐标系中的图像可能是（） A ． B ．C ．D ．【分析】根据二次函数图像开口向下得到a ＜0，再根据对称轴确定出b ，根据与y 轴的交点确定出c ＜0，然后确定出一次函数图像与反比例函数图像的情况，即可得解．【解答】解：∵二次函数图像开口方向向下， ∴a ＜0，∵对称轴为直线x ＝﹣＞0，∴b ＞0，∵与y 轴的负半轴相交， ∴c ＜0，∴y ＝bx +c 的图像经过第一、三、四象限，反比例函数y ＝图像在第二四象限，只有D 选项图像符合．故选：D ．9．（2022•菏泽）根据如图所示的二次函数y ＝ax 2+bx +c 的图像，判断反比例函数y ＝xa与一次函数y ＝bx +c 的图像大致是（）A ．B ．C ．D ．【分析】先根据二次函数的图像，确定a 、b 、c 的符号，再根据a 、b 、c 的符号判断反比例函数y ＝与一次函数y ＝bx +c 的图像经过的象限即可．【解答】解：由二次函数图像可知a ＞0，c ＜0，由对称轴x ＝﹣＞0，可知b ＜0，所以反比例函数y ＝的图像在一、三象限，一次函数y ＝bx +c 图像经过二、三、四象限．故选：A ．10．（2022•安顺）二次函数y ＝ax 2+bx +c （a ≠0）的图像如图所示，则一次函数y ＝ax +b 和反比例函数y ＝xc（c ≠0）在同一直角坐标系中的图像可能是（） A ． B ．C ．D ．【分析】直接利用二次函数图像经过的象限得出a ，b ，c 的取值范围，进而利用一次函数与反比例函数的性质得出答案．【解答】解：∵二次函数y ＝ax 2+bx +c 的图像开口向上， ∴a ＞0，∵该抛物线对称轴位于y 轴的右侧， ∴a 、b 异号，即b ＜0． ∵抛物线交y 轴的负半轴，∴c ＜0，∴一次函数y ＝ax +b 的图像经过第一、三、四象限，反比例函数y ＝（c ≠0）在二、四象限．故选：A ．11．（2022•西藏）在同一平面直角坐标系中，函数y ＝ax +b 与y ＝axb（其中a ，b 是常数，ab ≠0）的大致图像是（）A ．B ．C ．D ．【分析】根据a 、b 的取值，分别判断出两个函数图像所过的象限，要注意分类讨论．【解答】解：若a ＞0，b ＞0，则y ＝ax +b 经过一、二、三象限，反比例函数y ＝（ab ≠0）位于一、三象限，若a ＞0，b ＜0，则y ＝ax +b 经过一、三、四象限，反比例函数数y ＝（ab ≠0）位于二、四象限，若a ＜0，b ＞0，则y ＝ax +b 经过一、二、四象限，反比例函数y ＝（ab ≠0）位于二、四象限，若a ＜0，b ＜0，则y ＝ax +b 经过二、三、四象限，反比例函数y ＝（ab ≠0）位于一、三象限，故选：A ．12．（2022•张家界）在同一平面直角坐标系中，函数y ＝kx +1（k ≠0）和y ＝xk（k ≠0）的图像大致是（）A．B．C．D．【分析】分k＞0或k＜0，根据一次函数与反比例函数的性质即可得出答案．【解答】解：当k＞0时，一次函数y＝kx+1经过第一、二、三象限，反比例函数y＝位于第一、三象限；当k＜0时，一次函数y＝kx+1经过第一、二、四象限，反比例函数y＝位于第二、四象限；故选：D．13．（2022•绥化）已知二次函数y＝ax2+bx+c的部分函数图像如图所示，则一次函数y＝ax+b2﹣4ac与反比例函数y＝xc ba++24在同一平面直角坐标系中的图像大致是（）A．B．C．D．【分析】由二次函数y＝ax2+bx+c的部分函数图像判断a，b2﹣4ac及4a+2b+c的符号，即可得到答案．【解答】解：∵二次函数y＝ax2+bx+c的部分函数图像开口向上，∴a＞0，∵二次函数y ＝ax 2+bx +c 的部分函数图像顶点在x 轴下方，开口向上， ∴二次函数y ＝ax 2+bx +c 的图像与x 轴有两个交点，b 2﹣4ac ＞0， ∴一次函数y ＝ax +b 2﹣4ac 的图像位于第一，二，三象限，由二次函数y ＝ax 2+bx +c 的部分函数图像可知，点（2，4a +2b +c ）在x 轴上方， ∴4a +2b +c ＞0， ∴y ＝的图像位于第一，三象限，据此可知，符合题意的是B ，故选：B ．14．（2022•贺州）已知一次函数y ＝kx +b 的图像如图所示，则y ＝﹣kx +b 与y ＝xb的图像为（）A ．B ．C ．D ．【分析】本题形数结合，根据一次函数y ＝kx +b 的图像位置，可判断k 、b 的符号；再由一次函数y ＝﹣kx +b ，反比例函数y ＝中的系数符号，判断图像的位置．经历：图像位置﹣系数符号﹣图像位置．【解答】解：根据一次函数y ＝kx +b 的图像位置，可判断k ＞0、b ＞0．所以﹣k ＜0．再根据一次函数和反比例函数的图像和性质，故选：A ．15．（2022•广西）已知反比例函数y ＝xb（b ≠0）的图像如图所示，则一次函数y ＝cx ﹣a （c ≠0）和二次函数y ＝ax 2+bx +c （a ≠0）在同一平面直角坐标系中的图像可能是（）A ．B ．C ．D ．【分析】本题形数结合，根据反比例函数y ＝（b ≠0）的图像位置，可判断b ＞0；再由二次函数y ＝ax 2+bx +c （a ≠0）的图像性质，排除A ，B ，再根据一次函数y ＝cx ﹣a （c ≠0）的图像和性质，排除C ．【解答】解：∵反比例函数y ＝（b ≠0）的图像位于一、三象限， ∴b ＞0；∵A 、B 的抛物线都是开口向下，∴a ＜0，根据同左异右，对称轴应该在y 轴的右侧，故A 、B 都是错误的．∵C 、D 的抛物线都是开口向上，∴a ＞0，根据同左异右，对称轴应该在y 轴的左侧， ∵抛物线与y 轴交于负半轴， ∴c ＜0由a ＞0，c ＜0，排除C ．故选：D ．16．（2022•滨州）在同一平面直角坐标系中，函数y ＝kx +1与y ＝﹣xk（k 为常数且k ≠0）的图像大致是（）A ．B ．C ．D ．【分析】根据一次函数和反比例函数的性质即可判断．【解答】解：当k ＞0时，则﹣k ＜0，一次函数y ＝kx +1图像经过第一、二、三象限，反比例函数图像在第二、四象限，所以A 选项正确，C 选项错误；当k ＜0时，一次函数y ＝kx +1图像经过第一、二，四象限，所以B 、D 选项错误．故选：A ．17．（2022•德阳）一次函数y ＝ax +1与反比例函数y ＝﹣xa在同一坐标系中的大致图像是（）A ．B ．C ．D ．【分析】根据一次函数与反比例函数图像的特点，可以从a ＞0，和a ＜0，两方面分类讨论得出答案．【解答】解：分两种情况：（1）当a ＞0，时，一次函数y ＝ax +1的图像过第一、二、三象限，反比例函数y ＝﹣图像在第二、四象限，无选项符合；（2）当a ＜0，时，一次函数y ＝ax +1的图像过第一、二、四象限，反比例函数y ＝﹣图像在第一、三象限，故B 选项正确．故选：B ．18．（2022•阜新）已知反比例函数y ＝x k （k ≠0）的图像经过点（﹣2，4），那么该反比例函数图像也一定经过点（）A ．（4，2）B ．（1，8）C ．（﹣1，8）D ．（﹣1，﹣8）【分析】先把点（﹣2，4）代入反比例函数的解析式求出k 的值，再对各选项进行逐一判断即可．【解答】解：∵反比例函数y ＝（k ≠0）的图像经过点（﹣2，4），∴k ＝﹣2×4＝﹣8，A 、∵4×2＝8≠﹣8，∴此点不在反比例函数的图像上，故本选项错误；B 、∵1×8＝8≠﹣8，∴此点不在反比例函数的图像上，故本选项错误；C 、﹣1×8＝﹣8，∴此点在反比例函数的图像上，故本选项正确；D 、（﹣1）×（﹣8）＝8≠﹣8，∴此点不在反比例函数的图像上，故本选项错误．故选：C ．19．（2022•襄阳）若点A （﹣2，y 1），B （﹣1，y 2）都在反比例函数y ＝x2的图像上，则y 1，y 2的大小关系是（）A ．y 1＜y 2B ．y 1＝y 2C ．y 1＞y 2D ．不能确定【分析】根据反比例函数图像上点的坐标特征即可求解．【解答】解：∵点A （﹣2，y 1），B （﹣1，y 2）都在反比例函数y ＝的图像上，k ＝2＞0，∴在每个象限内y 随x 的增大而减小，∵﹣2＜﹣1，∴y 1＞y 2，故选：C ．20．（2022•海南）若反比例函数y ＝xk （k ≠0）的图像经过点（2，﹣3），则它的图像也一定经过的点是（）A ．（﹣2，﹣3）B ．（﹣3，﹣2）C ．（1，﹣6）D ．（6，1）【分析】将（2，﹣3）代入y ＝（k ≠0）即可求出k 的值，再根据k ＝xy 解答即可．【解答】解：∵反比例函数y ＝（k ≠0）的图像经过点（2，﹣3），∴k ＝2×（﹣3）＝﹣6，A 、﹣2×（﹣3）＝6≠﹣6，故A 不正确，不符合题意；B 、（﹣3）×（﹣2）＝6≠﹣6，故B 不正确，不符合题意；C 、1×（﹣6）＝﹣6，故C 正确，符合题意，D 、6×1＝6≠﹣6，故D 不正确，不符合题意．故选：C ．21．（2022•武汉）已知点A （x 1，y 1），B （x 2，y 2）在反比例函数y ＝x6的图像上，且x 1＜0＜x 2，则下列结论一定正确的是（）A ．y 1+y 2＜0B ．y 1+y 2＞0C ．y 1＜y 2D ．y 1＞y 2 【分析】先根据反比例函数y ＝判断此函数图像所在的象限，再根据x 1＜0＜x 2判断出A （x 1，y 1）、B （x 2，y 2）所在的象限即可得到答案．【解答】解：∵反比例函数y ＝中的6＞0，∴该双曲线位于第一、三象限，且在每一象限内y 随x 的增大而减小，∵点A （x 1，y 1），B （x 2，y 2）在反比例函数y ＝的图像上，且x 1＜0＜x 2，∴点A 位于第三象限，点B 位于第一象限，∴y 1＜y 2．故选：C ．22．（2022•天津）若点A （x 1，2），B （x 2，﹣1），C （x 3，4）都在反比例函数y ＝x8的图像上，则x 1，x 2，x 3的大小关系是（）A ．x 1＜x 2＜x 3B ．x 2＜x 3＜x 1C ．x 1＜x 3＜x 2D ．x 2＜x 1＜x 3 【分析】根据函数解析式算出三个点的横坐标，再比较大小．【解答】解：点A （x 1，2），B （x 2，﹣1），C （x 3，4）都在反比例函数y ＝的图像上， ∴x 1＝＝4，x 2＝＝﹣8，x 3＝＝2． ∴x 2＜x 3＜x 1，故选：B ．23．（2022•淮安）在平面直角坐标系中，将点A （2，3）向下平移5个单位长度得到点B ，若点B 恰好在反比例函数y ＝xk 的图像上，则k 的值是．【分析】点A （2，3）向下平移5个单位长度得到点B （2，﹣2），代入y ＝利用待定系数法即可求得k 的值．【解答】解：将点A （2，3）向下平移5个单位长度得到点B ，则B （2，﹣2）， ∵点B 恰好在反比例函数y ＝的图像上，∴k ＝2×（﹣2）＝﹣4，故答案为：﹣4．24．（2022•北京）在平面直角坐标系xOy 中，若点A （2，y 1），B （5，y 2）在反比例函数y ＝xk （k ＞0）的图像上，则y 1 y 2（填“＞”“＝”或“＜”）．【分析】先根据函数解析式中的比例系数k 确定函数图像所在的象限，再根据各象限内点的坐标特征及函数的增减性解答．【解答】解：∵k ＞0，∴反比例函数y ＝（k ＞0）的图像在一、三象限，∵5＞2＞0，∴点A （2，y 1），B （5，y 2）在第一象限，y 随x 的增大而减小，∴y 1＞y 2，故答案为：＞．。

中考数学专题训练第8讲平面直角坐标系一次函数反比例函数(知识点梳理)

⑵分母中含有自变量：分母不为．
⑶实际问题：符合实际意义．
8.函数图象：函数的图象是由平面直角中的一系列点组成的．描点法画函数图象的步骤：
⑴列表.
⑵描点.
⑶连线．
9.函数解析式与函数图象的关系：
⑴满足函数解析式的有序实数对为坐标的点一定在函数图象上.
⑵函数图象上点的坐标满足函数解析式．
考点03一次函数
（3）函数关系式在书写时有顺序性．例如：是表示是的函数，若写成就表示是的函数．
（4）求与的函数关系时，必须是只用变量的代数式表示，得到的等式右边只含的代数式．
自变量的取值范围：
7.自变量取值范围：在初中阶段，自变量的取值范围考虑下面几个方面：
⑴根式：当根指数为偶数时，被开方数为非负数．
10.用坐标表示地理位置：根据已知条件，建立适当的平面直角坐标系，是确定点的位置的必经过程，一般地只有建立了适当的直角坐标系，点的位置才能得以确定，才能使数与形有机地结合在一起。利用平面直角坐标系绘制区域内一些地点分布情况，也就是绘制平面图的过程：
（1）建立坐标系，选择一个适当的参照点为原点，确定x轴，y轴的正方向.
3.一次函数的图象及其画法：
（1）一次函数（，，为常数）的图象是一条直线．
（2）由于两点确定一条直线，所以在平面直角坐标系内画一次函数的图象时，只要先描出两个点，再连成直线即可．如果这个函数是正比例函数，通常取，两点.如果这个函数是一般的一次函数（），通常取，，即直线与两坐标轴的交点．
（3）反比例函数与一次函数的联系．
③解方程（组），得到待定系数的值.
④将求出的待定系数代回所求的函数解析式中，得到所求的函数解析式．
8.一次函数与一元一次方程的关系：

中考总复习专题3 一次函数、反比例函数的图像、性质与应用(师用)

中考专题总复习3---一次函数、反比例函数的图像、性质与应用★重点★正、反比例函数，一次函数的图象和性质。

一、平面直角坐标系1．各象限内点的坐标的特点2．坐标轴上点的坐标的特点3．关于坐标轴、原点对称的点的坐标的特点4．坐标平面内点与有序实数对的对应关系二、函数1 函数中的三个概念：常量，自变量，因变量。

2．表示方法：⑴解析法;⑵列表法;⑶图象法。

3．确定自变量取值范围的原则：⑴使代数式有意义;⑵使实际问题有意义。

4．画函数图象：⑴列表;⑵描点;⑶连线。

三、几种特殊函数（定义→图象→性质） 1．正比例函数⑴定义：y=kx(k ≠0) 或y/x=k 。

⑵图象：直线（过原点） ⑶性质：①k>0，…②k<0，… 2．一次函数⑴定义：y=kx+b(k ≠0)⑵图象：直线过点（0,b ）—与y 轴的交点和（-b/k,0）—与x 轴的交点。

⑶性质：①k>0,…②k<0,… ⑷图象的四种情况： 4.反比例函数⑴定义：三种形式：1-==kx xky 或xy=k(k ≠0)。

⑵图象：双曲线（两支）—用描点法画出。

⑶性质：①k>0时，图象位于…，y 随x …;②k<0时，图象位于…，y 随x …;③两支曲线无限接近于坐标轴但永远不能到达坐标轴。

四、重要解题方法1．用待定系数法求解析式（列方程[组]求解）2．利用图象一次（正比例）函数、反比例函数、一．填空题 1．（2010年上海）一辆汽车在行驶过程中，路程 y （千米）与时间 x （小时）之间的函数关系如图3所示当时 0≤x ≤1，y 关于x 的函数解析式为 y = 60 x ，那么当 1≤x ≤2时，y 关于x 的函数解析式为_____________.【答案】y=100x －40图32．（2010安徽蚌埠二中）已知点（1，3）在函数)0(>=x xky 的图像上。

正方形ABCD 的边BC 在x 轴上，点E 是对角线BD 的中点，函数)0(>=x xky 的图像又经过A 、E 两点，则点E 的横坐标为__________。

2024年中考数学压轴题型-专题05 与反比例函数有关问题的压轴题之三大题型(解析版)

专题05与反比例函数有关问题的压轴题之三大题型目录【题型一反比例函数与一次函数综合问题】 (1)【题型二实际问题与反比例函数综合问题】 (10)【题型三反比例函数与几何综合问题】 (18)【题型一反比例函数与一次函数综合问题】(1)求k 的值，并在图中画出函数k y x =的图象；(2)直接写出不等式24k x x+>的解集．【答案】(1)6k =，画图见解析；(2)30x -<<或1x >．（2）解：由()1,6A ，()3,B n -，根据函数图象可得：不等式24k x x+>的解集为：30x -<<【变式训练】1．（2023·浙江杭州·模拟预测）如图，一次函数图象交于1A a -（，），B 两点，与x 轴交于点由图可知：当12y y >时，3x >或1x -<<（2）解：点()3,C k 在函数1y kx b =+的图像上，得3k b k +=,2b k =-,12(2)y kx k k x =-=-,当2x =时，10y =，即过定点(2,0)．【点睛】本题是反比例函数与一次函数的交点问题，主要考查了待定系数法求函数解析式，反比例函数图像上点的坐标特征，函数与不等式的关系，数形结合是解题的关键．(【点睛】本题主要考查了一次函数与反比例函数综合，待定系数法求函数解析式，熟练掌握待定系数法求函数解析式是解题的关键．4．（2023·浙江杭州·统考二模）设函数(1)若函数1y和函数2y的图像交于点①求b，n的值．210y y <<∴x 的取值范围是203x <<或1443x <<．【点睛】本题考查了待定系数法求反比例函数解析式、反比例函数与一次函数交点问题，掌握反比例函数和一次函数图像与性质是解题关键．【题型二实际问题与反比例函数综合问题】例题：（2023·浙江衢州·统考中考真题）视力表中蕴含着很多数学知识，如：每个“E ”形图都是正方形结构，同一行的“E ”是全等图形且对应着同一个视力值，不同的检测距离需要不同的视力表．素材1国际通用的视力表以5米为检测距离，任选视力表中7个视力值n ，测得对应行的“E ”形图边长b （mm ），在平面直角坐标系中描点如图1．探究1检测距离为5米时，归纳n 与b 的关系式，并求视力值1.2所对应行的“E ”形图边长．素材2图2为视网膜成像示意图，在检测视力时，眼睛能看清最小“E ”形图所成的角叫做分辨视角θ，视力【变式训练】(1)求EF的长．(2)求y关于x的函数解析式，在图2中画出图像，并写出至少一条该函数性质．(3)若要求CD不小于3dm，求OE的取值范围．【答案】(1)80dm(2)240.3yx=+，图象及性质见解析性质：当0x >时，y 随x 的增大而减小；（3）由3y ≥，240.33x+≥，则0.3243x x +≥，解得809x ≤，()2m S 之间的函数表达式；(2)现将另一长、宽、高分别为0.2m ，0.3m ，0.2m 与长方体A 相同重量的长方体于该水平玻璃桌面上．若桌面所受压强()Pa P 与受力面积()2m S 之间的关系满足（(2)当气体体积为32m时，气球内气体的压强是多少？(3)当气球内气体的压强大于180kpa时，气球就会爆炸．【答案】(1)画图见解析；90 pV =；(2)气球内气体的压强是45kPa；(3)00.5V<<【分析】（1）根据描点，连线即可画出函数图象；设函数解析式为把()1,90代入k p V=，∴90k pV ==；∴函数关系式为：90p V=；（2）当气体体积为2m 3时，气球内气体的压强是（3）当气球内气体的压强大于180kpa 时，气球就会爆炸．即∴90>180V，【题型三反比例函数与几何综合问题】【变式训练】【答案】10【分析】设4,A xx⎛⎫⎪⎝⎭，根据平行四边形对边平行得到点象为4yx=-及中点性质得到【答案】223/223【分析】设CD 的中点为E ，连接OE 股定理求出22112OE =+=，然后【详解】如图所示，设CD 的中点为∵四边形ABCD 是正方形，OA OB =∴根据对称性可得，OE 是AOB ∠∴AOF BOF ∠=∠，∵点E 在反比例函数1(0)y x x =>的图象上，∴()1,1E ，∴22112OE =+=，【答案】24【分析】设4OA a =，则AB 轴，点P 在CD 上，可得P 由于点Q 在反比例函数y =【答案】3【分析】过点B '作B C x '⊥轴于点C 的坐标，即可求解．【详解】解：如图所示，过点B '作∵A 的坐标为()4,0-，则4OA =，将∴4AO A O '==，∴OB '=2OB =，在Rt AOB △中，cos BO BOA AB ∠==【答案】8323【分析】根据题意得出AE 值；先根据反比例函数解析式求出点310y x =-，求出103OF =【详解】解：∵顶点A 的坐标是∴6AE =，又ABCD Y 的面积是24，∴4AD BC ==，则()4,2D ，∴428k =⨯=，y【答案】1322(1)求双曲线k y x=的解析式，并直接写出点。

专题反比例函数大题中考数学

专题02 反比例函数大题（二大题型）通用的解题思路：题型一．反比例函数与一次函数的交点问题反比例函数与一次函数的交点问题（1）求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．（2）判断正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中的交点个数可总结为：①当k 1与k 2同号时，正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中有2个交点；②当k 1与k 2异号时，正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中有0个交点．题型二．反比例函数综合题（1）应用类综合题能够从实际的问题中抽象出反比例函数这一数学模型，是解决实际问题的关键一步，培养了学生的建模能力和从实际问题向数学问题转化的能力．在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识．（2）数形结合类综合题利用图象解决问题，从图上获取有用的信息，是解题的关键所在．已知点在图象上，那么点一定满足这个函数解析式，反过来如果这点满足函数的解析式，那么这个点也一定在函数图象上．还能利用图象直接比较函数值或是自变量的大小．将数形结合在一起，是分析解决问题的一种好方法．题型一．反比例函数与一次函数的交点问题（共25小题）1．（2024•新北区校级模拟）如图，双曲线1ky x=与直线232y x =交于A ，B 两点．点(2,)A a 和点(,3)B b -在双曲线上，点C 为x 轴正半轴上的一点．（1）求双曲线1ky x=的表达式和a ，b 的值；（2）请直接写出使得12y y >的x 的取值范围；（3）若ABC ∆的面积为12，求此时C 点的坐标．2．（2023•苏州）如图，一次函数2y x =的图象与反比例函数(0)ky x x=>的图象交于点(4,)A n ．将点A 沿x 轴正方向平移m 个单位长度得到点B ，D 为x 轴正半轴上的点，点B 的横坐标大于点D 的横坐标，连接BD ，BD 的中点C 在反比例函数(0)ky x x=>的图象上．（1）求n ，k 的值；（2）当m 为何值时，AB OD ⋅的值最大？最大值是多少？3．（2024•常州模拟）如图，反比例函数1k y x=的图象与一次函数2y k x b =+的图象交于点(1,2)A -，1(4,2B -．（1）求函数1k y x=和2y k x b =+的表达式；（2）若在x 轴上有一动点C ，当2ABC AOB S S ∆∆=时，求点C 的坐标．4．（2024•常州模拟）如图，一次函数1(0)y kx b k =+≠与函数为2(0)my x x=>的图象交于1(4,1),(,)2A B a 两点．（1）求这两个函数的解析式；（2）根据图象，直接写出满足120y y ->时x 的取值范围；（3）点P 在线段AB 上，过点P 作x 轴的垂线，垂足为M ，交函数2y 的图象于点Q ，若POQ ∆的面积为3，求点P 的坐标．5．（2024•沭阳县模拟）如图，反比例函数ky x=的图象与一次函数y mx n =+的图象相交于(,1)A a -，(1,3)B -两点．（1）求反比例函数和一次函数的解析式；（2）设直线AB 交y 轴于点C ，点(,0)N t 是x 轴正半轴上的一个动点，过点N 作NM x ⊥轴交反比例函数ky x=的图象于点M ，连接CN ，OM ．若3COMN S >四边形，求t 的取值范围．6．（2024•宿迁二模）已知函数1y x=的图象与函数(0)y kx k =≠的图象交于点(,)P m n （1）若2m n =，求k 的值和点P 的坐标．（2）当||||m n …时，结合函数图象，直接写出实数k 的取值范围．7．（2024•泉山区校级模拟）如图，在平面直角坐标系xOy中，一次函数152y x=+和2y x=-的图象相交于点A，反比例函数kyx=的图象经过点A．（1）求反比例函数的表达式；（2）设一次函数152y x=+的图象与反比例函数kyx=的图象的另一个交点为B，连接OB，求ABO∆的面积．8．（2023•常州）在平面直角坐标系中，一次函数y kx b=+的图象与反比例函数myx=的图象相交于点(2,4)A、(4,)B n．C是y轴上的一点，连接CA、CB．（1）求一次函数、反比例函数的表达式；（2）若ABC∆的面积是6，求点C的坐标．9．（2024•姜堰区一模）如图，一次函数12y x a =-+的图象与反比例函数2(0)ky k x=>的图象在第一象限相交于点(,)A m n ，(2,3)B m n -．（1）求a 、k 的值；（2）当120y y >>时，直接写出x 的取值范围．10．（2024•昆山市模拟）如图，一次函数11(0)y k x b k =+≠的图象与反比例函数22(0)k y k x=≠的图象相交于A ，B 两点，其中点A 的坐标为(2,1)-，点B 的坐标为(1,)n ．（1）求这两个函数的表达式；（2）根据图象，直接写出满足21k k x b x+>的取值范围；（3）求ABO ∆的面积．11．（2024•兴化市一模）已知函数1(k y k x =是常数，0)k ≠，函数2392y x =-+．（1）若函数1y 和函数2y 的图象交于点(2,6)A ，点(4,2)B n -．①求k ，n 的值．②当12y y >时，直接写出x 的取值范围．（2）若点(8,)C m 在函数1y 的图象上，点C 先向下平移1个单位，再向左平移3个单位，得点D ，点D 恰好落在函数1y 的图象上，求m 的值．12．（2024•南通模拟）如图，直线AB 交双曲线ky x=于A 、B 两点，交x 轴于点C ，且B 恰为线段AC 的中点，连接OA ．若6OAC S ∆=．求k 的值．13．（2024•亭湖区模拟）如图，等腰三角形OAB 中，AO AB =，点B 坐标为(4,0)顶点A 在反比例函数k y x=的图象上，且OAB ∆的面积为12．（1）k = ．（2）过B 点直线对应的解析式为y x b =+与双曲线ky x=在第一，三象限交点分别为点M ，N ．①求点M ，N 的坐标．②直接写出不等式0kx b x--…的解集．14．（2024•常熟市模拟）如图，一次函数112y x =-的图象与y 轴相交于B 点，与反比例函数(0,0)ky k x x=≠>图象相交于点(,2)A m ．（1）求反比例函数的表达式；（2）点C 在点A 的左侧，过点C 作y 轴平行线，交反比例函数的图象于点D ，连接BD ．设点C 的横坐标为a ，求当a 为何值时，BCD ∆的面积最大，这个最大值是多少？15．（2024•东海县一模）一次函数5y x=-+与反比例函数kyx=的图象在第一象限交于A，B两点，其中(1,)A a．（1）求反比例函数表达式；（2）结合图象，直接写出5kxx-+…时，x的取值范围；（3）若把一次函数5y x=-+的图象向下平移b个单位，使之与反比例函数kyx=的图象只有一个交点，请直接写出b的值．16．（2024•钟楼区校级模拟）如图，已知反比例函数kyx=的图象与一次函数y ax b=+的图象相交于点(2,3)A和点(,2)B n-．（1）求反比例函数与一次函数的解析式；（2）直接写出不等式kax bx>+的解集；（3）若点P是x轴上一点，且满足PAB∆的面积是10，请求出点P的坐标．17．（2024•姑苏区校级模拟）如图，以x 轴上长为1的线段AB 为宽作矩形ABCD ，矩形长AD 、BC 交直线3y x =-+于点F 、E ，反比例函数(0)ky x x=>的图象正好经过点F 、E ．（1）线段EF 长为；（2）求k 值．18．（2024•昆山市一模）如图，在平面直角坐标系xOy 中，一次函数11(y k x b k =+，b 为常数，且10)k ≠与反比例函数22(k y k x=为常数，且20)k ≠的图象交于点(,6)A m ，(4,3)B -．（1）求反比例函数和一次函数的表达式；（2）当210k k x b x>+>时，直接写出自变量x 的取值范围；（3）已知一次函数1y k x b =+的图象与x 轴交于点C ，点P 在x 轴上，若PAC ∆的面积为9；求点P 的坐标．19．（2024•盐城模拟）如图，已知一次函数11y k x b =+的图象与反比例函数22k y x=，分别交于点A 和点B ，且A 、B 两点的坐标分别是(1,2)A --和(2B ．)m ，连接OA 、OB ．（1）求一次函数11y k x b =+与反比例函数22k y x=的函数表达式；（2）求AOB ∆的面积．20．（2024•天宁区校级模拟）如图，在平面直角坐标系xOy 中，一次函数2y x b =+的图象与x 轴交于点(1,0)A -，与y 轴交于点B ，与反比例函数(0)ky x x=>的图象交于点C ，且AB BC =．点D 是x 轴正半轴上一点，连接CD ，45ODC ∠=︒．（1）求b 和k 的值；（2）求ACD ∆的面积．21．（2024•姑苏区校级一模）如图，一次函数1y kx b =+的图象与反比例函数2(0)my x x=>的图象交于点(4,1)A 和点(2,)B n ．（1）求一次函数和反比例函数解析式；（2）过点B 作BC y ⊥轴于点C ，连接OA ，求四边形OABC 的面积；（3）根据图象直接写出使mkx b x+<成立的x 的取值范围．22．（2024•新北区一模）如图，反比例函数(0)ky x x=>与一次函数2y x m =+的图象交于点(1,4)A ，BC y ⊥轴于点D ，分别交反比例函数与一次函数的图象于点B 、C ．（1）求反比例函数和一次函数的表达式；（2）连接AB ，若1OD =，求ABC ∆的面积．23．（2024•武进区校级模拟）如图，直线3y x =-+与y 轴交于点A ，与x 轴交于点D ，与反比例函数(0)ky k x=≠的图象交于点C ，过点C 作CB x ⊥轴于点B ，3AD AC =．（1）求点A 的坐标及反比例函数的解析式；（2）若点E 是直线3y x =-+与反比例函数(0)ky k x=≠图象的另一个交点，求COE ∆的面积．24．（2024•东海县一模）如图1，在平面直角坐标系中，一次函数y x b =+的图象经过点(2,0)A -，与反比例函数ky x=的图象交于(,4)B a ，C 两点．（1）求一次函数和反比例函数的表达式；（2）点M 是反比例函数图象在第一象限上的点，且4MAB S ∆=，请求出点M 的坐标；（3）反比例函数具有对称性，适当平移就可发现许多神奇的现象．将该双曲线在第一象限的一支沿射线BC 方向平移，使其经过点C ，再将双曲线在第三象限的一支沿射线CB 方向平移，使其经过点B ，平移后的两条曲线相交于P ，Q 两点，如图2，此时平移后的两条曲线围成了一只美丽的“眸”， PQ 为这只“眸”的“眸径”，请求出“眸径” PQ 的长．x 的图象的两个交点．（1）求反比例函数和一次函数的解析式；（2）求直线AB与x轴的交点C的坐标及AOB∆的面积；（3）直接写出一次函数的值小于反比例函数值的x的取值范围．题型二．反比例函数综合题（共8小题）26．（2024•泰兴市一模）如图1，在平面直角坐标系xOy中，O为坐标原点，点A、C在反比例函数2 yx =的图象上，点B、D在反比例函数4yx=-的图象上，顺次连接这四个点得到四边形ABCD．（1）若对角线AC、BD交于点O，直线AC的表达式为8y x=，直线BD的表达式为y x=-．①求证：四边形ABCD为平行四边形；②求ABCD的面积；（2）如图2，四边形ABCD为平行四边形，AB平行于x轴，求AC、BD的交点坐标；（3）如图3，四边形ABCD为平行四边形，求证：AC、BD相交于点O．x图象的两个交点．（1）求反比例函数的解析式；（2）求AOB ∆的面积；（3）在坐标轴上是否存在一点P ，使AOP ∆是等腰三角形？直接写出点P 的坐标．28．（2023•泰州）在平面直角坐标系xOy 中，点(,0)A m 、(B m a -，0)(0)a m >>的位置和函数1(0)my x x=>、2(0)m a y x x -=<的图象如图所示．以AB 为边在x 轴上方作正方形ABCD ，AD 边与函数1y 的图象相交于点E ，CD 边与函数1y 、2y 的图象分别相交于点G 、H ，一次函数3y 的图象经过点E 、G ，与y 轴相交于点P ，连接PH ．（1）若2m =，4a =，求函数3y 的表达式及PGH ∆的面积；（2）当a 、m 在满足0a m >>的条件下任意变化时，PGH ∆的面积是否变化？请说明理由；（3）试判断直线PH 与BC 边的交点是否在函数2y 的图象上？并说明理由．29．（2024•盐城模拟）【发现问题】小明在学习过程中发现：周长为定值的矩形中面积最大的是正方形．那么，面积为定值的矩形中，其周长的取值范围如何呢？【解决问题】小明尝试从函数图象的角度进行探究：（1）建立函数模型设一矩形的面积为4，周长为m ，相邻的两边长为x 、y ，则4xy =，2()x y m +=，即4y x =，2m y x =-+，那么满足要求的(,)x y 应该是函数4y x =与2my x =-+的图象在第象限内的公共点坐标．（2）画出函数图象①画函数4(0)y x x=>的图象；②在同一直角坐标系中直接画出y x =-的图象，则2my x =-+的图象可以看成是由y x =-的图象向上平移个单位长度得到．（3）研究函数图象平移直线y x =-，观察两函数的图象；①当直线平移到与函数4(0)y x x=>的图象有唯一公共点的位置时，公共点的坐标为，周长m 的值为；②在直线平移的过程中，两函数图象公共点的个数还有什么情况？请直接写出公共点的个数及对应周长m 的取值范围．【结论运用】（4）面积为10的矩形的周长m 的取值范围为．30．（2023•镇江）如图，正比例函数3y x =-与反比例函数(0)ky k x=≠的图象交于A 、(1,)B m 两点，C 点在x 轴负半轴上，45ACO ∠=︒．（1）m = ，k = ，点C 的坐标为；（2）点P 在x 轴上，若以B 、O 、P 为顶点的三角形与AOC ∆相似，求点P 的坐标．31．（2023•连云港）【问题情境建构函数】⊥，垂足为E．设BC x=，AB=，M是CD的中点，AE BM（1）如图1，在矩形ABCD中，4=，AE y试用含x的代数式表示y．【由数想形新知初探】（2）在上述表达式中，y与x成函数关系，其图象如图2所示．若x取任意实数，此时的函数图象是否具有对称性？若有，请说明理由，并在图2上补全函数图象．【数形结合深度探究】（3）在“x取任意实数”的条件下，对上述函数继续探究，得出以下结论：①函数值y随x的增大而增大；-<<；③存在一条直线与该函数图象有四个交点；④在图象上存在四②函数值y的取值范围是y点A、B、C、D，使得四边形ABCD是平行四边形．其中正确的是．（写出所有正确结论的序号）【抽象回归拓展总结】AB=”改成“2（4）若将（1）中的“4AB kk≠，=”，此时y关于x的函数表达式是；一般地，当0x取任意实数时，类比一次函数、反比例函数、二次函数的研究过程，探究此类函数的相关性质（直接写出3条即可）．32．（2024•武进区校级模拟）如图，在Rt ABC ∆中，8AC =，4BC =，AC x ⊥轴，垂足为C ，AB 边与y 轴交于点D ，反比例函数(0)ky x x=>，的图象经过点A ．（1）若14BD AB =，求直线AB 和反比例函数的表达式；（2）若8k =，将AB 边沿AC 边所在直线翻折，交反比例函数的图象于点E ，交x 轴于点F ，求点E 的坐标．33．（2024•苏州一模）如图，反比例函数my x=的图象与一次函数y kx b =+的图象相交于(3,1)A ，(1,)B n -两点．（1）求反比例函数和一次函数的关系式；（2）设直线AB 交y 轴于点C ，点M ，N 分别在反比例函数和一次函数图象上，若四边形OCNM 是平行四边形，求点M 的坐标．专题02 反比例函数大题（二大题型）通用的解题思路：题型一．反比例函数与一次函数的交点问题反比例函数与一次函数的交点问题（1）求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．（2）判断正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中的交点个数可总结为：①当k 1与k 2同号时，正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中有2个交点；②当k 1与k 2异号时，正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中有0个交点．题型二．反比例函数综合题（1）应用类综合题能够从实际的问题中抽象出反比例函数这一数学模型，是解决实际问题的关键一步，培养了学生的建模能力和从实际问题向数学问题转化的能力．在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识．（2）数形结合类综合题利用图象解决问题，从图上获取有用的信息，是解题的关键所在．已知点在图象上，那么点一定满足这个函数解析式，反过来如果这点满足函数的解析式，那么这个点也一定在函数图象上．还能利用图象直接比较函数值或是自变量的大小．将数形结合在一起，是分析解决问题的一种好方法．题型一．反比例函数与一次函数的交点问题（共25小题）1．（2024•新北区校级模拟）如图，双曲线1ky x=与直线232y x =交于A ，B 两点．点(2,)A a 和点(,3)B b -在双曲线上，点C 为x 轴正半轴上的一点．（1）求双曲线1ky x=的表达式和a ，b 的值；（2）请直接写出使得12y y >的x 的取值范围；（3）若ABC ∆的面积为12，求此时C 点的坐标．【分析】（1）把点(2,)A a 和点(,3)B b -代入232y x =，求出a 与b 的值，再将A 点坐标代入1k y x=，即可求出反比例函数解析式；（2）根据A 与B 横坐标，利用图象求出反比例函数值大于一次函数值时x 的范围即可；（3）根据12ABC AOC BOC S S S ∆∆∆=+=，求出OC 的长，进而得到此时C 点的坐标．【解答】解：（1）直线232y x =过点(2,)A a 和点(,3)B b -，3232a ∴=⨯=，332b =-，2b ∴=-．双曲线1k y x=过点(2,3)A ，236k ∴=⨯=，∴双曲线1k y x=的表达式为16y x =；（2）观察图象，可得当2x <-或02x <<时，反比例函数值大于一次函数值，即使得12y y >的x 的取值范围是2x <-或02x <<；（3）(2,3)A ，(2,3)B --，12ABC AOC BOC S S S ∆∆∆=+=，∴11331222OC OC ⨯+⨯=，4OC ∴=，∴此时C 点的坐标为(4,0)．【点评】此题考查了待定系数法求反比例函数解析式，一次函数与反比例函数的交点问题，函数图象上点的坐标特征，三角形的面积，利用了数形结合的思想，正确求出反比例函数解析式是解本题的关键．2．（2023•苏州）如图，一次函数2y x =的图象与反比例函数(0)k y x x=>的图象交于点(4,)A n ．将点A 沿x 轴正方向平移m 个单位长度得到点B ，D 为x 轴正半轴上的点，点B 的横坐标大于点D 的横坐标，连接BD ，BD 的中点C 在反比例函数(0)k y x x=>的图象上．（1）求n ，k 的值；（2）当m 为何值时，AB OD ⋅的值最大？最大值是多少？【分析】（1）首先将点(4,)A n 代入2y x =可求出n ，再将点A 的坐标代入/y k x =即可求出k ；（2）过点C 作直线EF x ⊥轴于F ，交AB 于E ，先证ECB ∆和FCD ∆全等，得BE DF =，4CE CF ==，进而可求出点(8,4)C ，根据平移的性质得点(4,8)B m +，则4BE DF m ==-，12OD m =-，据此可得出(12)AB DD m m ⋅=-，最后求出这个二次函数的最大值即可．【解答】解：（1）将点(4,)A n 代入2y x =，得：8n =，∴点A 的坐标为(4,8)，将点(4,8)A 代入k y x=，得：32k =．（2）点B 的横坐标大于点D 的横坐标，∴点B 在点D 的右侧．过点C 作直线EF x ⊥轴于F ，交AB 于E ，由平移的性质得：//AB x 轴，AB m =，B CDF ∴∠=∠，点C 为BD 的中点，BC DC ∴=，在ECB ∆和FCD ∆中，B CDF BC DCBCE DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ECB FCD ASA ∴∆≅∆，BE DF ∴=，CE CF =．//AB x 轴，点A 的坐标为(4,8)，8EF ∴=，4CE CF ∴==，∴点C 的纵坐标为4，由（1）知：反比例函数的解析式为：32y x=，∴当4y =时，8x =，∴点C 的坐标为(8,4)，∴点E 的坐标为(8,8)，点F 的坐标为(8,0)，点(4,8)A ，AB m =，//AB x 轴，∴点B 的坐标为(4,8)m +，484BE m m ∴=+-=-，4DF BE m ∴==-，8(4)12OD m m∴=--=-2(12)(6)36AB OD m m m ⋅=-=--+∴当6m =时，AB OD ⋅取得最大值，最大值为36．【点评】此题主要考查了反比例函数的图象、二次函数的图象和性质，点的坐标平移等，解答此题的关键是熟练掌握待定系数法求函数的解析式，理解点的坐标的平移，难点是在解答（2）时，构造二次函数求最值．3．（2024•常州模拟）如图，反比例函数1k y x=的图象与一次函数2y k x b =+的图象交于点(1,2)A -，1(4,2B -．（1）求函数1k y x=和2y k x b =+的表达式；（2）若在x 轴上有一动点C ，当2ABC AOB S S ∆∆=时，求点C 的坐标．【分析】（1）将点(1,2)A -，1(4,)2B -分别代入反比例函数1k y x=和一次函数2y k x b =+的解析式，求解即可；（2）设AB 与y 轴交于点D ，过点C 作//CE y 轴交AB 于点E ，利用三角形的面积公式，列出方程，求解即可．【解答】解：（1）将点(1,2)A -，1(4,2B -分别代入反比例函数1k y x=和一次函数2y k x b =+的解析式，1122k ∴=-⨯=-，222142k b k b -+=⎧⎪⎨+=-⎪⎩，12k ∴=，21232k b ⎧=-⎪⎪⎨⎪=⎪⎩．∴反比例函数的解析式为：2y x =，一次函数的解析式为：1322y x =-+．（2）如图，设AB 与y 轴交于点D ，过点C 作//CE y 轴交AB 于点E，设(,0)C m ，13(,22E m m ∴-+．13||22CE m ∴=-+．令0x =，则32y =，3(0,2D ∴，32OD ∴=，11315()[4(1)]2224AOB B A S OD x x ∆∴=⋅-=⨯⨯--=．1522ABC AOB S S ∆∆∴==．∴115()22B A CE x x ⋅-=，即11315||52222m ⋅-+⋅=．解得3m =-或9m =，∴点C 的坐标为(3,0)-或(9,0)．【点评】本题考查了反比例函数与一次函数的交点问题，求三角形的面积，求函数的解析式，正确掌握反比例函数的性质是解题的关键．4．（2024•常州模拟）如图，一次函数1(0)y kx b k =+≠与函数为2(0)m y x x=>的图象交于1(4,1),(,)2A B a 两点．（1）求这两个函数的解析式；（2）根据图象，直接写出满足120y y ->时x 的取值范围；（3）点P 在线段AB 上，过点P 作x 轴的垂线，垂足为M ，交函数2y 的图象于点Q ，若POQ ∆的面积为3，求点P 的坐标．【分析】（1）将A 点坐标代入即可得出反比例函数2(0)m y x x=>，求得函数的解析式，进而求得B 的坐标，再将A 、B 两点坐标分别代入1y kx b =+，可用待定系数法确定一次函数的解析式；（2）由题意即求12y y >的x 的取值范围，由函数的图象即可得出反比例函数的值小于一次函数值的x 的取值范围；（3）由题意，设(,29)P p p -+且142p ……，则4(,Q p p ，求得429PQ p p =-+-，根据三角形面积公式得到14(2932POQ S p p p∆=-+-⋅=，解得即可．【解答】解：（1）反比例函数2(0)m y x x=>的图象经过点(4,1)A ，14m ∴=．4m ∴=．∴反比例函数解析式为24(0)y x x=>．把1(2B ，)a 代入24(0)y x x =>，得8a =．∴点B 坐标为1(2，8)，一次函数解析式1y kx b =+图象经过(4,1)A ，1(2B ，8)，∴41182k b k b +=⎧⎪⎨+=⎪⎩．∴29k b =-⎧⎨=⎩．故一次函数解析式为：129y x =-+．（2）由120y y ->，12y y ∴>，即反比例函数值小于一次函数值．由图象可得，142x <<．（3）由题意，设(,29)P p p -+且142p ……，4(,)Q p p∴．429PQ p p∴=-+-．14(29)32POQ S p p p∆∴=-+-⋅=．解得152p =，22p =．5(2P ∴，4)或(2,5)．【点评】本题主要考查一次函数与反比例函数交点问题，熟练掌握待定系数法求函数解析式是解题的关键．5．（2024•沭阳县模拟）如图，反比例函数k y x=的图象与一次函数y mx n =+的图象相交于(,1)A a -，(1,3)B -两点．（1）求反比例函数和一次函数的解析式；（2）设直线AB 交y 轴于点C ，点(,0)N t 是x 轴正半轴上的一个动点，过点N 作NM x ⊥轴交反比例函数k y x=的图象于点M ，连接CN ，OM ．若3COMN S >四边形，求t 的取值范围．【分析】（1）将点B ，点A 坐标代入反比例函数的解析式，可求a 和k 的值，利用待定系数法可求一次函数解析式；（2）先求出点C 坐标，由面积关系可求解．【解答】解：（1）反比例函数k y x =的图象与一次函数y mx n =+的图象相交于(,1)A a -，(1,3)B -两点，13(1)k a ∴=-⨯=⨯-，3k ∴=-，3a =，∴点(3,1)A -，反比例函数的解析式为3y x-=，由题意可得：313m n m n =-+⎧⎨-=+⎩，解得：12m n =-⎧⎨=⎩，∴一次函数解析式为2y x =-+；（2）直线AB 交y 轴于点C ，∴点(0,2)C ，31222OMN OCN COMN S S S t ∆∆∴=+=+⨯⨯四边形，3COMN S > 四边形，∴312322t +⨯⨯>，32t ∴>．【点评】本题考查了反比例函数与一次函数的交点问题，考查了利用待定系数法求解析式，反比例函数的性质等知识，求出两个解析式是解题的关键．6．（2024•宿迁二模）已知函数1y x=的图象与函数(0)y kx k =≠的图象交于点(,)P m n （1）若2m n =，求k 的值和点P 的坐标．（2）当||||m n …时，结合函数图象，直接写出实数k 的取值范围．【分析】（1）由(0)y kx k =≠得n k m=，然后由2m n =可得到k 的值，设(2,)P n n ，将点P 的坐标代入反比例函数解析式可求得n 的值；（2）由(0)y kx k =≠得n k m =，然后结合条件||||m n …可得k 的取值范围．【解答】解：（1）(0)y kx k =≠ ，122y n n k x m n ∴====．2m n = ，(2,)P n n ∴，21n n ∴= ，解得：n =．m ∴=．P ∴或(，．（2）y kx=，y nkx m∴==，||||m n…，1k∴…．【点评】本题主要考查的是反比例函数和一次函数的交点问题，掌握待定系数法求函数解析式的方法是解题的关键．7．（2024•泉山区校级模拟）如图，在平面直角坐标系xOy中，一次函数152y x=+和2y x=-的图象相交于点A，反比例函数kyx=的图象经过点A．（1）求反比例函数的表达式；（2）设一次函数152y x=+的图象与反比例函数kyx=的图象的另一个交点为B，连接OB，求ABO∆的面积．【分析】（1）联立方程求得A的坐标，然后根据待定系数法即可求得；（2）联立方程求得交点B的坐标，进而求得直线与x轴的交点，然后利用三角形面积公式求得即可．【解答】解：（1）由1522y xy x⎧=+⎪⎨⎪=-⎩得24xy=-⎧⎨=⎩，(2,4)A∴-，反比例函数kyx=的图象经过点A，248k∴=-⨯=-，∴反比例函数的表达式是8 yx =-；（2）解8152y x y x ⎧=-⎪⎪⎨⎪=+⎪⎩得24x y =-⎧⎨=⎩或81x y =-⎧⎨=⎩，(8,1)B ∴-，由直线AB 的解析式为152y x =+得到直线与x 轴的交点为(10,0)-，111041011522AOB S ∆∴=⨯⨯-⨯⨯=．【点评】本题考查了一次函数和反比例函数的交点问题，通过方程组求得交点坐标是解题的关键．8．（2023•常州）在平面直角坐标系中，一次函数y kx b =+的图象与反比例函数m y x=的图象相交于点(2,4)A 、(4,)B n ．C 是y 轴上的一点，连接CA 、CB ．（1）求一次函数、反比例函数的表达式；（2）若ABC ∆的面积是6，求点C 的坐标．【分析】（1）利用待定系数法求得即可；（2）先求得(0,6)D ，再根据ABC BCD ACD S S S ∆∆∆=-得1(42)62CD ⨯⋅-=，进而得出6CD =，据此可得点C 的坐标．【解答】解：（1）点(2,4)A 在反比例函数m y x =的图象上，248m ∴=⨯=，∴反比例函数解析式为8y x=；又点(4,)B n 在8y x=上，2n ∴=，∴点B 的坐标为(4,2)，把(2,4)A 和(4,2)B 两点的坐标代入一次函数y kx b =+得2442k b k b +=⎧⎨+=⎩，解得16k b =-⎧⎨=⎩，∴一次函数的解析为6y x =-+．（2）对于一次函数6y x =-+，令0x =，则6y =，即(0,6)D ，根据题意得：1(42)62ABC BCD ACD S S S CD ∆∆∆=-=⨯⋅-=，解得：6CD =，0OC ∴=或12，(0,0)C ∴或(0,12)．【点评】本题主要考查了一次函数与反比例函数交点问题，解题时注意：一次函数与反比例函数交点坐标同时满足一次函数与反比例函数解析式．9．（2024•姜堰区一模）如图，一次函数12y x a =-+的图象与反比例函数2(0)k y k x=>的图象在第一象限相交于点(,)A m n ，(2,3)B m n -．（1）求a 、k 的值；（2）当120y y >>时，直接写出x 的取值范围．【分析】（1）根据反比例函数图象上点的坐标特征，得到3m =，代入A 、B 点的坐标再代入一次函数解析式组成方程组求出n 和a ，最后求出k 值即可；（2）根据函数图象直接写出当120y y >>时自变量取值范围即可．【解答】解：（1）点(,)A m n ，(2,3)B m n -都在反比例函数图象上，3(2)mn n m ∴=⨯-，整理得：2(3)0n m -=，0m ≠ ，0n ≠，30m ∴-=，解得3m =．(3,)A n ，(1,3)B n 在直线12y x a =-+的图象上，∴623a n a n -+=⎧⎨-+=⎩，解得28n a =⎧⎨=⎩，(3,2)A ∴，(3,2)A 在反比例函数图象上，6k ∴=．8a ∴=，6k =．（2）由（1）可知：(3,2)A ，(1,6)B ，根据函数图象可知，120y y >>时，x 的取值范围为：13x <<．【点评】本题考查了一次函数与反比例函数的交点问题，交点坐标满足两个函数解析式是关键．10．（2024•昆山市模拟）如图，一次函数11(0)y k x b k =+≠的图象与反比例函数22(0)k y k x=≠的图象相交于A ，B 两点，其中点A 的坐标为(2,1)-，点B 的坐标为(1,)n ．（1）求这两个函数的表达式；（2）根据图象，直接写出满足21k k x b x+>的取值范围；（3）求ABO ∆的面积．【分析】（1）待定系数法求出两个函数解析式即可；（2）根据图像直接写出不等式的解集即可；（3）根据AOB AOC BOC S S S ∆∆∆=+代入数据计算即可．【解答】解：（1）(2,1)A - ，(1,)B n 在反比例函数图象上，221k n ∴=-⨯=，22k n ∴==-，∴反比例函数解析式为：2y x=-，(2,1)A - ，(1,2)B -在一次函数图象上，∴11212k b k b +-=⎧⎨+=-⎩，解得111k b =-⎧⎨=-⎩，∴一次函数解析式为：1y x =--．（2）根据两个函数图象及交点坐标，不等式21k k x b x+>的解集为：2x <-或01x <<．（3）设直线AB 与y 轴的交点为C ，则(0,1)C -即1OC =，1131211222AOB AOC BOC S S S ∆∆∆∴=+=⨯⨯+⨯⨯=．【点评】本题考查了一次函数与反比例函数的交点问题，交点坐标满足两个函数解析式．11．（2024•兴化市一模）已知函数1(k y k x =是常数，0)k ≠，函数2392y x =-+．（1）若函数1y 和函数2y 的图象交于点(2,6)A ，点(4,2)B n -．①求k ，n 的值．②当12y y >时，直接写出x 的取值范围．（2）若点(8,)C m 在函数1y 的图象上，点C 先向下平移1个单位，再向左平移3个单位，得点D ，点D 恰好落在函数1y 的图象上，求m 的值．【分析】（1）①根据反比例函数图象上点的坐标特征进行解答即可；②根据图形分布和解答横坐标直接写出不等式解集即可；（2）先根据平移条件得到(5,1)D m -，再根据反比例函数图象上点的坐标特征求出m 值即可．【解答】解：（1）① 函数1y 和函数2y 的图象交于点(2,6)A ，点(4,2)B n -，264(2)k n ∴=⨯=⨯-，解得：12k =，5n =．②由①可知，反比例函数解析式为12y x=，图象分布在第一、三象限，(2,6)A ，(4,3)B12y y ∴>时，x 的取值范围为：02x <<或4x >．（2）点(8,)C m 在函数1y 的图象上，点C 先向下平移1个单位，再向左平移3个单位，得点D ，(5,1)D m ∴-，D 恰好落在函数1k y x=图象上，5(1)8m m ∴-=，解得53m =-．【点评】本题考查了反比例函数与一次函数的交点问题，交点坐标满足两个函数解析式是关键．12．（2024•南通模拟）如图，直线AB 交双曲线k y x=于A 、B 两点，交x 轴于点C ，且B 恰为线段AC 的中点，连接OA ．若6OAC S ∆=．求k 的值．【分析】设出点B 的坐标，进而可以表示出点A 和点C 的坐标，再根据OAC ∆的面积即可解决问题．【解答】解：设点B 坐标为(,k a a，点B 为线段AC 的中点，∴22A B k y y a==，则点A 的坐标为2(,)2a k a，∴2A C x x a +=，∴32C x a =，则点C 坐标为3(,0)2a ．又AOC ∆ 的面积为6，∴132622k a a⋅⋅=，解得4k =，故k 的值为4．。

考点08 一次函数的图象与性质-备战2023届中考数学一轮复习考点梳理(解析版)

考点08 一次函数的图象和性质一次函数的图象与性质是中考数学中比较重要的一个考点，也是知识点牵涉比较多的考点。

各地对一次函数的图象与性质的考察也主要集中在一次函数表达式与平移、图象的性质、图象与方程不等式的关系以及一次函数图象与几何图形面积等五个方面。

也因为一次函数是一个结合型比较强的知识点，所以其图象和性质也是后续函数问题学习的一个基础。

故考生在复习这块知识点时，需要特别熟记对应考点的方法规律。

一、一次函数的图象与平移二、一次函数的性质三、待定系数法求解一次函数的表达式四、一次函数与方程、不等式的关系五、一次函数与三角形面积考向一：一次函数的图象与平移一．一次函数的图象二．一次函数图象的画法1．下列函数：①y ＝4x ；②y ＝﹣；③y ＝；④y ＝﹣4x +1，其中一次函数的个数是（）A ．1B ．2C ．3D ．4【分析】根据一次函数的定义条件进行逐一分析即可．【解答】解：y ＝﹣4x ，y ＝﹣，y ＝﹣4x +1都符合一次函数的定义，属于一次函数；y ＝是反比例函数，综上所述，其中y 是x 的一次函数的个数有3个．故选：C．一次函数的图象是经过点和点的一条直线2．如图，在平面直角坐标系中，函数y＝k（x﹣1）（k＞0）的图象大致是（）A．B．C．D．【分析】根据一次函数图象的特点对四个选项进行逐一分析即可．【解答】解：∵y＝k（x﹣1）（k＞0），∴一次函数图象过点（1，0），y随x的增大而增大，故选项B符合题意．故选：B．3．如图，同一直角坐标系中，能表示一次函数y＝x+kb和y＝kx+b（k、b为常数，且k≠0）的图象是（）A．B．C．D．【分析】根据一次函数的系数与图象的关系逐项分析即可．【解答】解：A、一次函数y＝kx+b的图象经过第二、三、四象限，则k＞0，b＜0，则kb＜0；而一次函数y＝x+kb的图象与y轴交于正半轴，则kb＞0，kb＞0与kb＜0相矛盾，不符合题意；B、一次函数y＝kx+b的图象经过第一、三、四象限，则k＞0，b＜0，则kb＜0；而一次函数y＝x+kb的一次项系数为正，与题干图形相矛盾，不符合题意；C、一次函数y＝kx+b的图象经过第一、二、四象限，则k＜0，b＞0，则kb＜0；而一次函数y＝x+kb的图象与y轴交于负半轴，则kb＜0．kb＜0与kb＜0相一致，符合题意；D、一次函数y＝kx+b的图象经过第二、三、四象限，则k＜0，b＜0，则kb＞0；而一次函数y＝x+kb的图象与y轴交于负半轴，则kb＜0．kb＞0与kb＜0相矛盾，不符合题意；故选：C．4．在平面直角坐标系中，直线是函数y＝6x﹣2的图象，将直线l平移后得到直线y＝6x+2，则下列平移方式正确的是（）A．将1向右平移4个单位长度B．将1向左平移4个单位长度C．将1向上平移4个单位长度D．将1向下平移4个单位长度【分析】利用一次函数图象的平移规律，右加左减，上加下减，即可得出答案．【解答】解：设将直线y＝6x﹣2向左平移a个单位后得到直线y＝6x+2（a＞0），∴6（x+a）﹣2＝6x+2，解得：a＝，故将直线y＝6x﹣2向左平移个单位后得到直线y＝6x+2，同理可得，将直线y＝6x﹣2向上平移4个单位后得到直线y＝6x+2，观察选项，只有选项C符合题意．故选：C．5．直线y＝2x﹣4向上平移2个单位后所得的直线与x轴交点的坐标是　（1，0）　．【分析】利用一次函数平移规律，上加下减进而得出平移后函数解析式，再求出图象与坐标轴交点即可．【解答】解：直线y＝2x﹣4沿y轴向上平移2个单位，则平移后直线解析式为：y＝2x﹣4+2＝2x﹣2，当y＝0时，则x＝1，故平移后直线与x轴的交点坐标为：（1，0）．故答案为：（1，0）．6．如图，在同一平面直角坐标系中，一次函数y1＝k1x+b1与y2＝k2x+b2的图象分别为直线l1和直线l2，下列结论正确的是（）A．k1k2＜0B．k1+k2＜0C．b1﹣b2＞0D．b1b2＞0【分析】根据一次函数y＝k1x+b1与y＝k2x+b2的图象位置，可得k1＜0，b1＜0，k2＜0，b2＞0，然后逐一判断即可解答．【解答】解：∵一次函数y＝k1x+b1的图象过四、二、三象限，∴k1＜0，b1＜0，∵一次函数y＝k2x+b2的图象过一、二、四象限，∴k2＜0，b2＞0，∴A、k1•k2＞0，故A不符合题意；B、k1+k2＜0，故B符合题意；C、b1﹣b2＜0，故C不符合题意；D、b1•b2＜0，故D不符合题意；故选：B．考向二：一次函数的性质对于任意一次函数y=kx+b（k≠0），点A (x1,y1）B（x2,y2）在其图象上1．一次函数y＝﹣3x+1的图象经过（）A．第一、二、四象限B．第一、三、四象限C．第一、二、三象限D．第二、三、四象限【分析】利用一次函数的性质即可确定直线经过的象限．【解答】解：∵y＝﹣3x+1，∴k＜0，b＞0，故直线经过第一、二、四象限．故选：A．2．已知点A（﹣3，y1），B（﹣1，y2）都在直线y＝（m2+1）x+m上，则y1，y2的大小关系是（）A．y1＞y2B．y1＜y2C．y1＝y2D．大小不确定【分析】利用偶次方的非负性，可得出m2≥0，进而可得出k＝m2+1＞0，利用一次函数的性质，可得出y随x的增大而增大，结合﹣3＜﹣1，可得出y1＜y2．【解答】解：∵m2≥0，∴k＝m2+1＞0，∴y随x的增大而增大．又∵点A（﹣3，y1），B（﹣1，y2）都在直线y＝（m2+1）x+m上，且﹣3＜﹣1，∴y1＜y2．故选：B．3．已知A（x1，y1），B（x2，y2）是关于x的函数y＝（m﹣1）x图象上的两点，当x1＜x2时，y1＜y2，则m 的取值范围是（）A．m＞0B．m＜0C．m＞1D．m＜1【分析】由“当x1＜x2时，y1＜y2”，可得出y随x的增大而增大，结合一次函数的性质，可得出m﹣1＞0，解之即可得出m的取值范围．【解答】解：∵当x1＜x2时，y1＜y2，∴y随x的增大而增大，∴m﹣1＞0，解得：m＞1，∴m的取值范围是m＞1．故选：C．4．对于一次函数y＝﹣2x+1的相关性质，下列描述错误的是（）A ．函数图象经过第一、二、四象限B ．图象与y 轴的交点坐标为（1，0）C ．y 随x 的增大而减小D ．图象与坐标轴调成三角形的面积为【分析】根据一次函数的性质分别判断后即可确定正确的选项．【解答】解：A ．∵k ＝﹣2＜0，b ＝1＞0，∴函数图象经过第一、二、四象限，正确，不符合题意；B ．当x ＝0时，y ＝1，∴函数图象与y 轴的交点坐标为（0，1），错误，符合题意；C ．∵k ＝﹣2＜0，∴y 的值随着x 增大而减小，正确，不符合题意；D ．令y ＝0可得y ＝1，∴函数图象与坐标轴围成的三角形面积为：×1×＝，故D 正确，不符合题意．故选：B ．5．已知点（﹣2，y 1），（2，y 2）都在直线y ＝2x ﹣3上，则y 1　＜　y 2．（填“＜”或“＞”或“＝”）【分析】由k ＝2＞0，利用一次函数的性质可得出y 随x 的增大而增大，再结合﹣2＜2即可得出y 1＜y 2．【解答】解：∵k ＝2＞0，∴y 随x 的增大而增大，又∵﹣2＜2，∴y 1＜y 2．故答案为：＜．考向三：待定系数法求一次函数的解析式1．一个正比例函数的图象过点（﹣2，3），它的表达式为（）A．B．C．D．【分析】利用待定系数法即可求解．【解答】解：设函数的解析式是y＝kx．根据题意得：﹣2k＝3．解得：k＝﹣．故函数的解析式是：y＝﹣x．故选：A．2．已知一次函数y＝mx﹣4m，当1≤x≤3时，2≤y≤6，则m的值为（）A．2B．﹣2C．2或﹣2D．m的值不存在【分析】结合一次函数的性质，对m分类讨论，当m＞0时，一次函数y随x增大而增大，此时x＝1，y ＝2且x＝3，y＝6；当m＜0时，一次函数y随x增大而减小，此时x＝1，y＝6且x＝3，y＝2；最后利用待定系数法求解即可．【解答】解：当m＞0时，一次函数y随x增大而增大，∴当x＝1时，y＝2且当x＝3时，y＝6，令x＝1，y＝2，解得m＝，不符题意，令x＝3，y＝6，解得m＝﹣6，不符题意，当m＜0时，一次函数y随x增大而减小，∴当x＝1时，y＝6且当x＝3时，y＝2，令x＝1，y＝6，解得m＝﹣2，令x＝3，y＝2，解得m＝﹣2，符合题意，故选：B．3．已知y与x成正比例，且当x＝2时，y＝﹣3．则当x＝﹣时，y＝．【分析】设y＝kx，把x＝2，y＝﹣3代入，求出k得到函数解析式，把x＝﹣代入函数解析式，求出即可．【解答】解：根据题意，设y＝kx，把x＝2，y＝﹣3代入得：﹣3＝2k，解得：k＝﹣，∴y与x的函数关系式为y＝﹣x，把x＝﹣代入y＝﹣x，得y＝﹣×（﹣）＝，故答案为：．4．已知一次函数的图象经过A（2，0），B（0，4）两点．（1）求此一次函数表达式；（2）试判断点（﹣1，6）是否在此一次函数的图象上．【分析】（1）设一次函数的解析式为y＝kx+b（k≠0），再把A（2，0），B（0，4）代入求出k的值即可；（2）把x＝﹣1代入（1）中函数解析式进行检验即可．【解答】解：（1）设一次函数的解析式为y＝kx+b（k≠0），∵A（2，0），B（0，4）在函数图象上，∴，解得，∴一次函数的解析式为：y＝﹣x+4；（2）由（1）知，函数解析式为：y＝﹣x+4，∴当x＝﹣1时，y＝5≠6，∴点（﹣1，6）不一次函数的图象上．5．如图，在平面直角坐标系xOy中，直线y＝﹣2x+a与y轴交于点C（0，6），与x轴交于点B．（1）求这条直线的解析式；（2）直线AD与（1）中所求的直线相交于点D（﹣1，n），点A的坐标为（﹣3，0）．求n的值及直线AD 的解析式．【分析】（1）把C （0，6）代入函数解析式，可得答案．（2）先求D 的坐标，再利用待定系数法求解AD 的解析式．【解答】解：（1）直线y ＝﹣2x +a 与y 轴交于点C （0，6），∴﹣2×0+a ＝6，∴a ＝6，∴直线的解析式为y ＝﹣2x +6；（2）点D （﹣1，n ）在y ＝﹣2x +6上，∴n ＝﹣2×（﹣1）+6＝8，∴D （﹣1，8），设直线AD 的解析式为y ＝kx +b ，把点A （﹣3，0）和D （﹣1，8）代入得，解得，∴直线AD 的解析式为y ＝4x +12．考向四：一次函数与方程不等式间的关系的交点坐标由函数图象直接写出不等式解集的方法归纳：1．已知方程2x ﹣1＝﹣3x +4的解是x ＝1，则直线y ＝2x ﹣1和y ＝﹣3x +4的交点坐标为（）A ．（1，0）B ．（1，1）C ．（﹣1，﹣3）D ．（﹣1，1）【分析】把x ＝1代入直线解析式y ＝2x ﹣1求出y 的值即可得到交点坐标．【解答】解：∵x ＝1是方程2x ﹣1＝﹣3x +4的解，∴把x ＝1代入y ＝2x ﹣1，得y ＝2×1﹣1＝1．∴交点坐标为（1，1）．故选：B ．2．如图，直线y ＝ax +b （a ≠0）过点A （0，1），B （2，0），则关于x 的方程ax +b ＝0的解为 x ＝2　．【分析】所求方程的解，即为函数y ＝ax +b 图象与x 轴交点横坐标，确定出解即可．【解答】解：方程ax +b ＝0的解，即为函数y ＝ax +b 图象与x 轴交点的横坐标，∵直线y ＝ax +b 过B （2，0），∴方程ax +b ＝0的解是x ＝2，故答案为：x ＝2．3．如图，一次函数y ＝2x +1的图象与y ＝kx +b 的图象相交于点A ，则方程组的解是（）A．B．C．D．【分析】先求点A的横坐标，然后根据两条直线的交点坐标即可写出方程组的解．【解答】解：y＝3代入y＝2x+1得2x+1＝3，解得x＝1，所以A点坐标为（1，3），所以方程组的解是．故选：B．4．如图，已知直线y＝ax+b和直线y＝kx交于点P，若二元一次方程组的解为x、y，则x+y＝　3　．【分析】根据由图象可知，直线y＝ax+b和直线y＝kx交于点P（1，2），即可确定二元一次方程组的解，进一步求值即可．【解答】解：由图象可知，直线y＝ax+b和直线y＝kx交于点P（1，2），∴二元一次方程组的解为，∴x+y＝1+2＝3，故答案为：3．5．若定义一种新运算：，例如：2@4＝2+4﹣3＝3，2@1＝2﹣1+3＝4，下列说法：①（﹣1）@（﹣2）＝4；②若x@（x+2）＝5，则x＝3；③x@2x＝3的解为x＝2；④函数y＝（x2+1）@1与x轴交于（﹣1，0）和（1，0）．其中正确的个数是（）A．4B．3C．2D．1【分析】根据新定义，逐项判断即可．【解答】解：（﹣1）@（﹣2）＝﹣1﹣（﹣2）+3＝4，故①正确；∵x@（x+2）＝x+（x+2）﹣3＝2x﹣1，∴x@（x+2）＝5即是2x﹣1＝5，解得x＝3，故②正确；当x＜2x，即x＞0时，∵x@2x＝3，∴x+2x﹣3＝3，解得x＝2；当x≥2x，即x≤0时，∵x@2x＝3，∴x﹣2x+3＝3，解得x＝0，∴x@2x＝3的解是x＝2或x＝0，故③错误；∵x2+1≥1，∴y＝（x2+1）@1＝x2+1﹣1+3＝x2+3，令y＝0得x2+3＝0，方程无实数解，∴函数y＝（x2+1）@1与x轴无交点，故④错误；∴正确的有①②，共2个，故选：C．6．如图，已知一次函数y1＝kx﹣b与y2＝nx函数图象相交于点M，当kx﹣b＝nx时，x的值是　1　，当y1＞y2时，x的取值范围是　x＜1　，当y1＜y2时，x的取值范围是　x＞1　．【分析】根据两条直线的交点、结合图象解答即可．【解答】解：由图象可知，当kx﹣b＝nx时，x的值是1，当y1＞y2时，x的取值范围是x＜1，当y1＜y2时，x的取值范围是x＞1．故答案为：1，x＜1，x＞1．7．小时在学习了一次函数知识后，结合探究一次函数图象与性质的方法，对新函数y＝2﹣|x﹣1|及其图象进行如下探究．（1）自变量x的取值范围是全体实数，x与y的几组对应值如表：x…﹣3﹣2﹣1012345…y…﹣2﹣1m1210n﹣2…其中m＝　0　，n＝　﹣1　．（2）请在给出的平面直角坐标系中画出该函数的图象，并结合图象写出该函数的一条性质：　当x＞1时，y随x的增大而减小；当x＜1时，y随x的增大而增大　．（3）当时，x的取值范围为　x≤﹣1或x≥2　．【分析】（1）把x＝﹣1和x＝4分别代入解析式即可得到m、n的值；（2）利用描点法画出图象，观察图象可得出函数的性质；（3）利用图象即可解决问题．【解答】解：（1）把x＝﹣1代入y＝2﹣|x﹣1|得，y＝2﹣|﹣1﹣1|＝0，∴m＝0；把x＝4代入y＝2﹣|x﹣1|得，y＝2﹣|4﹣1|＝﹣1，∴n＝﹣1；故答案为：0，﹣1；（2）画出函数的图象如图：观察图象可知：当x＞1时，y随x的增大而减小；当x＜1时，y随x的增大而增大；故答案为：当x＞1时，y随x的增大而减小；当x＜1时，y随x的增大而增大；（3）画出一次函数y＝x+的图象，观察图象可知：当时，x的取值范围为x≤﹣1或x≥2，故答案为：x≤﹣1或x≥2．考向五：一次函数与三角形面积一．一次函数与坐标轴围成三角形面积的规律方法归纳1.一次函数y=kx+b（k≠0）与坐标轴交点规律与x轴交点坐标（，0）故：当k、b同号时，直线交于x轴负半轴；当k、b异号时，直线交于x轴正半轴对于直线y=kx+b（k≠0）与y轴交点坐标（0，b）故：当b＞0时，直线交于y轴正半轴；当b＜0时，直线交于y轴负半轴2.求两直线交点坐标方法：联立两直线解析式，得二元一次方程组，解方程组得交点坐标；3.求三角形面积时，三角形有边在水平或者竖直边上，常以这条边为底，再由底所对顶点的坐标确定高；二．一次函数图象与几何图形动点面积1.此类问题需要将动点所在几何图形与一次函数图象同时分析，对照一次函数图象得出动点所在几何图形的边长信息2.对函数图象的分析重点抓住以下两点：①分清坐标系的x轴、y轴的具体意义②特别分析图象的拐点——拐点一般表示动点运动到几何图形的一个顶点3.动点所在几何图形如果是特殊图形，如等腰三角形、等腰直角三角形、含30°的直角三角形，注意对应图形性质与辅助线的应用。

专题05一次函数的图象和性质(练)-2019年中考数学二轮复习

备战2019年中考二轮讲练测（精选重点典型题）专题5 一次函数的图象和性质（练案）一练基础——基础掌握1.定义：点A（x，y）为平面直角坐标系内的点，若满足x=y，则把点A叫做“平衡点”．例如：M（1，1），N（﹣2，﹣2）都是“平衡点”．当﹣1≤x≤3时，直线y=2x+m上有“平衡点”，则m的取值范围是（）A．0≤m≤1B．﹣3≤m≤1C．﹣3≤m≤3D．﹣1≤m≤0【答案】B．【分析】根据x=y，﹣1≤x≤3可得出关于m的不等式，求出m的取值范围即可．【解析】∵x=y，∴x=2x+m，即x=﹣m．∵﹣1≤x≤3，∴﹣1≤﹣m≤3，∴﹣3≤m≤1．故选B．考点：一次函数图象上点的坐标特征；新定义．2.已知直线l1：y=﹣3x+b与直线l2：y=﹣kx+1在同一坐标系中的图象交于点（1，﹣2），那么方程组31 x y b kx y+=⎧⎨+=⎩的解是（）A．12xy=⎧⎨=-⎩B．12xy=⎧⎨=⎩C．12xy=-⎧⎨=-⎩D．12xy=-⎧⎨=⎩【答案】A．考点：一次函数与二元一次方程（组）．学科@网3．一次函数y=kx+b与y=bx+k在同一坐标系中的图象大致是（）【答案】C【解析】考点：一次函数图像与系数的关系学科@网 4．如图，直线323y x =-+与x 轴、y 轴分别交于A 、B 两点，把△AOB 绕点A 顺时针旋转60°后得到△AO ′B ′，则点B ′的坐标是（）A ．（4，23）B ．（23，4）C ．（3，3）D ．（232+，23）【答案】B ．【解析】考点：一次函数综合题；压轴题． 5．已知函数2)2(1+-=-m x m y 是关于x 的一次函数，则m= 。

【答案】0 【解析】试题分析：根据一次函数的自变量指数为1，可得|m1|=1，m=2或m=0，系数不为0可m2≠0，m≠2，所以得m=0．考点：一次函数的定义. 学科@网6．如图，已知函数b x y +=2与函数3-=kx y 的图象交于点P ，则不等式b x kx +>-23的解是 .【答案】x ＜4．【解析】考点：一次函数与一元一次不等式．7．如图，在平面直角坐标系xOy 中，直线l 的表达式是33y x =，点A 1坐标为（0，1），过点A 1作y 轴的垂线交直线l 于点B 1，以原点O 为圆心，OB 1长为半径画弧交y 轴于点A 2；再过点A 2作y 轴的垂线交直线l 于点B 2，以原点O 为圆心，OB 2长为半径画弧交y 轴于点A 3，…，按此作法进行下去，点B 4的坐标为，OA 2015= ．【答案】（83，8），20142．【解析】直线33y x =，点A 1坐标为（0，1），过点A 1作y 轴的垂线交直线l 于点B 1，可知B 1点的坐标为（3，1），以原点O 为圆心，OB 1长为半径画弧交y 一轴于点A 2，OA 2=OB 1=2OA 1=2，点A 2的坐标为（0，2），这种方法可求得B 2的坐标为（23，2），故点A 3的坐标为（0，4），B 3的坐标为（434），3-=kx y xybx y +=24 6O P点A 4的坐标为（0，8），B 4的坐标为（83，8），此类推便可求出点A n 的坐标为（0，12n -）．所以点A 2015的坐标为（0，20142）．所以OA 2015=20142．故答案为：（83，8），20142．考点：一次函数图象上点的坐标特征；规律型．学科@网 8. 已知二元一次方程组522x y x y -=-⎧⎨+=-⎩的解为41x y =-⎧⎨=⎩，则在同一平面直角坐标系中，直线l 1：y =x +5与直线l 2：112y x =--的交点坐标为．【答案】（﹣4，1）．【分析】根据一次函数与二元一次方程组的关系进行解答即可．【解析】∵二元一次方程组522x y x y -=-⎧⎨+=-⎩的解为41x y =-⎧⎨=⎩，∴直线l 1：y =x +5与直线l 2：112y x =--的交点坐标为（﹣4，1），故答案为：（﹣4，1）．考点：一次函数与二元一次方程（组）．9. 我们规定：若m =（a ，b ），n =（c ，d ），则m n ⋅=ac +bd ．如m =（1，2），n =（3，5），则m n ⋅=1×3+2×5=13．（1）已知m =（2，4），n =（2，﹣3），求m n ⋅；（2）已知m =（x ﹣a ，1），n =（x ﹣a ，x +1），求y =m n ⋅，问y =m n ⋅的函数图象与一次函数y =x ﹣1的图象是否相交，请说明理由．【答案】（1）﹣8；（2）不相交．【分析】（1）直接利用m =（a ，b ），n =（c ，d ），则m n ⋅=ac +bd ，进而得出答案；（2）利用已知的出y 与x 之间的函数关系式，再联立方程，结合根的判别式求出答案．【解析】（1）∵m =（2，4），n =（2，﹣3），∴m n ⋅=2×2+4×（﹣3）=﹣8；（2）∵m =（x ﹣a ，1），n =（x ﹣a ，x +1），∴y =m n ⋅=2()(1)x a x -++=22(21)1x a x a --++，∴22(21)1y x a x a =--++，联立方程：22(21)11x a x a x --++=-，化简得：22220x ax a -++=，∵△=24b ac -=﹣8＜0，∴方程无实数根，两函数图象无交点．考点：二次函数的性质；根的判别式；一次函数的性质；新定义．10. 已知点P （0x ，0y ）和直线y =kx +b ，则点P 到直线y =kx +b 的距离证明可用公式d 0021kx y b k-++计算．例如：求点P （﹣1，2）到直线y =3x +7的距离．解：因为直线y =3x +7，其中k =3，b =7．所以点P （﹣1，2）到直线y =3x +7的距离为：d =0021kx y b k -++=23(1)271k ⨯--++=210=105．根据以上材料，解答下列问题：（1）求点P （1，﹣1）到直线y =x ﹣1的距离；（2）已知⊙Q 的圆心Q 坐标为（0，5），半径r 为2，判断⊙Q 与直线39y x =+的位置关系并说明理由；（3）已知直线y =﹣2x +4与y =﹣2x ﹣6平行，求这两条直线之间的距离．【答案】（1）22；（2）相切；（3）25．【分析】（1）根据点P 到直线y =kx +b 的距离公式直接计算即可；（2）先利用点到直线的距离公式计算出圆心Q 到直线39y x =+，然后根据切线的判定方法可判断⊙Q 与直线39y x =+相切；（3）利用两平行线间的距离定义，在直线y =﹣2x +4上任意取一点，然后计算这个点到直线y =﹣2x ﹣6的距离即可．考点：一次函数综合题；综合题；阅读型．学科@网二练能力——综合运用1．P 1（x 1，y 1），P 2（x 2，y 2）是正比例函数12y x =-图象上的两点，下列判断中，正确的是（）A ．y 1＞y 2,B ．y 1＜y 2C ．当x 1＜x 2时，y 1＜y 2D ．当x 1＜x 2时，y 1＞y 2 【答案】D.考点：一次函数图象上点的坐标特征．2.如图，函数y=2x 和y=ax+4的图象相交于点A （m ，3），则不等式2x < ax + 4的解集为（）A ．23<x B ．3<x C ．23>x D ．3>x 【答案】A 【解析】试题分析：由图象可知不等式2x < ax + 4的解集为x ＜m ，因为函数y=2x 和y=ax+4的图象相交于点A （m ，3），所以把点A （m ，3）代入y=2x 得m=23，所以x<23，故选A.考点：1.函数图象的交点；2.函数图像与不等式的关系.3. 已知k 、b 是一元二次方程(21)(31)0x x +-=的两个根，且k ＞b ，则函数y kx b =+的图象不经过（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【答案】B ．考点：1．一次函数图象与系数的关系；2．解一元二次方程因式分解法．4.如图，点A 1（2，2）在直线y =x 上，过点A 1作A 1B 1∥y 轴交直线12y x =于点B 1，以点A 1为直角顶点，A 1B 1为直角边在A 1B 1的右侧作等腰直角△A 1B 1C 1，再过点C 1作A 2B 2∥y 轴，分别交直线y =x 和12y x =于A 2，B 2两点，以点A 2为直角顶点，A 2B 2为直角边在A 2B 2的右侧作等腰直角△A 2B 2C 2…，按此规律进行下去，则等腰直角△A n B n C n 的面积为．（用含正整数n 的代数式表示）【答案】222132n n --．【分析】先根据点A 1的坐标以及A 1B 1∥y 轴，求得B 1的坐标，进而得到A 1B 1的长以及△A 1B 1C 1面积，再根据A 2的坐标以及A 2B 2∥y 轴，求得B 2的坐标，进而得到A 2B 2的长以及△A 2B 2C 2面积，最后根据根据变换规律，求得A n B n 的长，进而得出△A n B n C n 的面积即可．【解析】∵点A 1（2，2），A 1B 1∥y 轴交直线12y x =于点B 1，∴B 1（2，1） ∴A 1B 1=2﹣1=1，即△A 1B 1C 1面积=2112⨯=12； ∵A 1C 1=A 1B 1=1，∴A 2（3，3），又∵A 2B 2∥y 轴，交直线12y x =于点B 2，∴B 2（3，32），∴A 2B 2=3﹣32=32，即△A 2B 2C 2面积=213()22⨯=98；以此类推，A 3B 3=94，即△A 3B 3C 3面积=219()24⨯=8132；A 4B 4=278，即△A 4B 4C 4面积=2127()28⨯=729128；…∴A n B n =13()2n -，即△A n B n C n 的面积=1213[()]22n -⨯=222132n n --．故答案为：222132n n --．考点：一次函数图象上点的坐标特征；等腰直角三角形；规律型；综合题．5. 在直角坐标系中，直线1y x =+与y 轴交于点A ，按如图方式作正方形A 1B 1C 1O 、A 2B 2C 2C 1、A 3B 3C 1C 2…，A 1、A 2、A 3…在直线1y x =+上，点C 1、C 2、C 3…在x 轴上，图中阴影部分三角形的面积从左到游依次记为1S 、2S 、3S 、…n S ，则n S 的值为（用含n 的代数式表示，n 为正整数）．【答案】232n -．6. 如图所示，在平面直角坐标系中，过点A （3-0）的两条直线分别交y 轴于B 、C 两点，且B 、C 两点的纵坐标分别是一元二次方程2230x x --=的两个根．（1）求线段BC 的长度；（2）试问：直线AC 与直线AB 是否垂直？请说明理由；（3）若点D 在直线AC 上，且DB =DC ，求点D 的坐标；（4）在（3）的条件下，直线BD 上是否存在点P ，使以A 、B 、P 三点为顶点的三角形是等腰三角形？若存在，请直接写出P 点的坐标；若不存在，请说明理由．【答案】（1）4；（2）垂直；（3）D （23-，1）；（4）P （33-，0），（3-，2），（﹣3，33-），（3，33+）．【分析】（1）解出方程后，即可求出B 、C 两点的坐标，即可求出BC 的长度；（2）由A 、B 、C 三点坐标可知2OA =OC •OB ，所以可证明△AOC ∽△BOA ，利用对应角相等即可求出∠CAB =90°；（3）容易求得直线AC 的解析式，由DB =DC 可知，点D 在BC 的垂直平分线上，所以D 的纵坐标为1，将其代入直线AC 的解析式即可求出D 的坐标；（4）A 、B 、P 三点为顶点的三角形是等腰三角形，可分为以下三种情况：①AB =AP ；②A B =BP ；③AP =BP ；然后分别求出P 的坐标即可．【解析】（1）∵2230x x --=，∴x =3或x =﹣1，∴B （0，3），C （0，﹣1），∴BC =4；（2）∵A （3-0），B （0，3），C （0，﹣1），∴OA 3OB =3，OC =1，∴2OA =OB •OC ，∵∠AOC =∠BOA =90°，∴△AOC ∽△BOA ，∴∠CAO =∠ABO ，∴∠CAO +∠BAO =∠ABO +∠BAO =90°，∴∠BAC =90°，∴AC ⊥AB ；（3）设直线AC 的解析式为y =kx +b ，把A （3-0）和C （0，﹣1）代入y =kx +b ，∴103b k b-=⎧⎪⎨=+⎪⎩，解得：31k b ⎧=⎪⎨⎪=-⎩，∴直线AC 的解析式为：313y x =--，∵DB =DC ，∴点D 在线段BC 的垂直平分线上，∴D 的纵坐标为1，∴把y =1代入313y x =--，∴x =23-，∴D 的坐标为（23-，1）；（4）设直线BD 的解析式为：y =mx +n ，直线BD 与x 轴交于点E ，把B （0，3）和D （23-，1）代入y =mx +n ，∴3123n m n =⎧⎪⎨=-+⎪⎩，解得：333m n ⎧=⎪⎨⎪=⎩，∴直线BD 的解析式为：333y x =+，令y =0代入333y x =+，∴x =33-，∴E （33-，0），∴OE =33，∴tan ∠BEC =OB OE =33，∴∠BEO =30°，同理可求得：∠ABO =30°，∴∠ABE =30°．当P A =AB 时，如图1，此时，∠BEA =∠ABE =30°，∴EA =AB ，∴P 与E 重合，∴P 的坐标为（33-，0）；当P A =PB 时，如图2，此时，∠P AB =∠PBA =30°，∵∠ABE =∠ABO =30°，∴∠P AB =∠ABO ，∴P A ∥BC ，∴∠P AO =90°，∴点P 的横坐标为3-，令x =3-代入333y x =+，∴y =2，∴P （3-，2）；当PB =AB 时，如图3，∴由勾股定理可求得：A B =23，EB =6，若点P 在y 轴左侧时，记此时点P 为P 1，过点P 1作P 1F ⊥x 轴于点F ，∴P 1B =AB =23，∴EP 1=6﹣23，∴sin ∠BEO =11FP EP ，∴FP 1=33-，令y =33-代入333y x =+，∴x =﹣3，∴P 1（﹣3，33-）；若点P 在y 轴的右侧时，记此时点P 为P 2，过点P 2作P 2G ⊥x 轴于点G ，∴P 2B =A B =23，∴EP 2=6+23，∴sin ∠BEO =22GP EP ，∴GP 2=33+，令y =33+代入333y x =+，∴x =3，∴P 2（3，33+）．综上所述，当A 、B 、P 三点为顶点的三角形是等腰三角形时，点P 的坐标为（33-，0），（3-，2），（﹣3，33-），（3，33+）．考点：一次函数综合题；存在型；分类讨论；压轴题．学科@网7. 为加强公民的节水意识，合理利用水资源．某市对居民用水实行阶梯水价，居民家庭每月用水量划分为三个阶梯，一、二、三级阶梯用水的单价之比等于1：1.5：2．如图折线表示实行阶梯水价后每月水费y （元）与用水量xm3之间的函数关系．其中线段AB表示第二级阶梯时y与x之间的函数关系．（1）写出点B的实际意义；（2）求线段AB所在直线的表达式；（3）某户5月份按照阶梯水价应缴水费102元，其相应用水量为多少立方米？【答案】（1）图中B点的实际意义表示当用水25m3时，所交水费为90元；（2）94522y x=-；（3）27．考点：1．一次函数的应用；2．分段函数；3．综合题．。

专题1.5 一次函数、反比例函数的图象和性质(讲)-备战2016年中考数学二轮复习讲练测(解析版)

备战2016年中考二轮讲练测第一篇专题整合篇专题05一次函数、反比例函数的图象和性质（讲案）一讲考点——考点梳理（一）概念1、一次函数：一般地，如果b kx y +=（k ，b 是常数，k ≠0），那么y 叫做x 的一次函数.正比例函数：特别地，当一次函数b kx y +=中的b 为0时，kx y =（k 为常数，k ≠0）.这时，y 叫做x 的正比例函数.2.反比例函数：一般地，形如y=xk（k 为常数，k ≠0）的函数，叫做反比例函数，其中x 是自变量，y 是函数.自变量x 的取值范围是不等于0的一切实数. 反比例函数也可表示成： y = kx －1(k 为常数，k ≠0)或xy = k(k 为常数，k ≠0)（二）函数的图象1.一次函数的图象：所有一次函数的图象都是一条直线2.反比例函数的图象：双曲线（三）函数图象的主要特征1.一次函数b kx y +=的图象是经过点（0，b ）的直线；正比例函数kx y =的图象是经过原点（0，0）的直线；|k|越大，直线越陡，|k|越小直线越缓.2.反比例函数y=xk的图象与坐标轴没有交点；|k|越大，图象的弯曲度越小，曲线越平直．|k|越小，图象的弯曲度越大．（四）函数的性质 1.正比例函数的性质一般地，正比例函数kx y =有下列性质：（1）当k ＞0时，图象经过第一、三象限，y 随x 的增大而增大；（2）当k ＜0时，图象经过第二、四象限，y 随x 的增大而减小. 2.一次函数的性质一般地，一次函数b kx y +=有下列性质：（1）当k ＞0时，y 随x 的增大而增大（2）当k ＜0时，y 随x 的增大而减小 3.反比例函数的性质一般地，反比例函数y=xk有下列性质：（1）当k ＞0时，图象的两支分别位于一、三象限；在每个象限内，y 随x 的增大而减小；（2）当k ＞0时，图象的两支分别位于二、四象限；在每个象限内，y 随x 的增大而增大．（五）函数解析式的确定待定系数法：先设出函数解析式，再根据条件确定解析式中未知的系数，从而得出函数解析式的方法，叫做待定系数法. （六）反比例函数y=xk（k 为常数，k ≠0）中k 的几何意义如图1，设点P （a ，b ）是双曲线ky x=上任意一点，作PA ⊥x 轴于A 点，PB ⊥y 轴于B 点，则矩形PBOA 的面积是|k|（三角形PAO 和三角形PBO 的面积都是12|k|）．如图2，由双曲线的对称性可知，P 关于原点的对称点Q 也在双曲线上，作QC ⊥PA 的延长线于C ，则有三角形PQC 的面积为2|k|．二讲题型——题型解析（一）对一次函数图象与系数的关系的考查. 例1、（2015·湖南常德）一次函数112y x =-+的图像不经过的象限是：（） A 、第一象限 B 、第二象限C 、第三象限D 、第四象限【答案】C 【解析】考点：一次函数（正比例）图象与系数的关系. （二）对一次函数图象与几何变换的考查.例2、（2015陕西省）在平面直角坐标系中，将直线22:1--=x y l 平移后，得到直线42:2+-=x y l ，则下列平移作法正确的是（）A ．将1l 向右平移3个单位长度B ．将1l 向右平移6个单位长度C ．将1l 向上平移2个单位长度D ．将1l 向上平移4个单位长度【答案】A ．【解析】∵将直线22:1--=x y l 平移后，得到直线42:2+-=x y l ，∴﹣2（x +a ）﹣2=﹣2x +4，解得：a =﹣3，故将1l 向右平移3个单位长度．故选A ．考点：一次函数图象与几何变换；函数的平移．（三）对两条直线相交或平行的考查例3、.(2015·辽宁抚顺）直线y x b =+（0b >）与直线y kx =（0k <）的交点位于（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【答案】B ．【解析】试题分析：直线y x b =+（0b >）与直线y kx =（0k <）的大致图象如图所示：．所以交点A 位于第二象限．故选B ．考点：两条直线相交或平行问题．（四）对反比例函数图象和性质的考查例4、（2015·黑龙江绥化）如图，反比例函数y=xk(x ＜0)的图象经过点P ，则k 的值为（） A. －6 B. －5 C. 6 D. 5【答案】A 【解析】考点：反比例函数的性质. （五）对函数增减性的考查例5、(2015·黑龙江哈尔滨）点A （－1，1y ），B （－2，2y ）在反比例函数2y x的图象上，则1y ，2y 的大小关系是（）（A ）1y ＞2y （B ）1y =2y （C ）1y ＜2y （D ）不能确定【答案】C【解析】试题分析：对于反比例函数y=kx，当k ＞0时，在每一个象限内，y 随x 的增大而减小，,根据题意可得：－1＞－2，则12y y .考点：反比例函数的性质. （六）对待定系数法的考查例6、(2015·温州)如图，点A 的坐标是（2，0），△ABO 是等边三角形，点B 在第一象限。