力学的守恒定律作业

合集下载

练习册第2章《质点力学的运动定律守恒定律》答案（1）

练习册第2章《质点⼒学的运动定律守恒定律》答案（1）第2章质点⼒学的运动定律守恒定律⼀、选择题1(C)，2(E)，3(D)，4(C)，5(C)，6(B)，7(C)，8(C)，9(B)，10(C)，11(D)，12(A)，13(D)⼆、填空题(1). ω2=12rad/s ，A=0.027J (2). 290J (3). 3J (4). 18 N ·s(5). j t i t 2323+ (SI) (6). 16 N ·s ， 176 J (7). 16 N ·s ，176 J (8). M k l /0，Mknm M Ml +0(9). j i5- (10).2m v ，指向正西南或南偏西45°三、计算题1. 已知⼀质量为m 的质点在x 轴上运动，质点只受到指向原点的引⼒的作⽤，引⼒⼤⼩与质点离原点的距离x 的平⽅成反⽐，即2/x k f -=，k 是⽐例常数．设质点在 x =A 时的速度为零，求质点在x =A /4处的速度的⼤⼩．解：根据⽜顿第⼆定律x m t x x m t m xk f d d d d d d d d 2vv v v =?==-= ∴ ??-=-=4/202d d ,d d A Ax mx kmx x k v v v v vk mAA A m k 3)14(212=-=v ∴ )/(6mA k =v2. 质量为m 的⼦弹以速度v 0⽔平射⼊沙⼟中，设⼦弹所受阻⼒与速度反向，⼤⼩与速度成正⽐，⽐例系数为Ｋ，忽略⼦弹的重⼒，求：(1) ⼦弹射⼊沙⼟后，速度随时间变化的函数式； (2) ⼦弹进⼊沙⼟的最⼤深度．解：(1) ⼦弹进⼊沙⼟后受⼒为－Ｋv ，由⽜顿定律tmK d d vv =- ∴ ??=-=-v v v v vv 0d d ,d d 0t t m K t m K∴ mKt /0e -=v v(2) 求最⼤深度解法⼀： t xd d =vt x mKt d ed /0-=vt x m Kt txd e d /000-?=v∴ )e 1()/(/0mKt K m x --=vK m x /0m ax v =解法⼆： x m t x x m t m K d d )d d )(d d (d d vvv v v ===- ∴ v d K mdx -=v v d d 000m a x ??-=K mx x∴ K m x /0m ax v =3. ⼀物体按规律x ＝ct 3在流体媒质中作直线运动，式中c 为常量，t 为时间．设媒质对物体的阻⼒正⽐于速度的平⽅，阻⼒系数为k ，试求物体由x ＝0运动到x ＝l 时，阻⼒所作的功．解：由x ＝ct 3可求物体的速度： 23d d ct tx==v 物体受到的阻⼒⼤⼩为： 343242299x kc t kc k f ===v ⼒对物体所作的功为：=W W d =-lx x kc 03432d 9 =7273732l kc -4. ⼀质量为2 kg 的质点，在xy 平⾯上运动，受到外⼒j t i F 2244-= (SI)的作⽤，t = 0时，它的初速度为j i430+=v (SI)，求t = 1 s 时质点的速度及受到的法向⼒n F .解： j t i m F a 2122/-==t a d /d v = ∴ t j t i d )122(d 2-=v=?vv vd ?-t t j t i 02d )122(∴ j t i t 3042-=-v vj t i t j t i t )44()23(42330-++=-+=v v当t = 1 s 时， i51=v 沿x 轴故这时， j a a y n12-==j a m F n n24-== (SI)5.⼀辆⽔平运动的装煤车，以速率v 0从煤⽃下⾯通过，每单位时间内有质量为m 0的煤卸⼊煤车．如果煤车的速率保持不变，煤车与钢轨间摩擦忽略不计，试求：(1) 牵引煤车的⼒的⼤⼩；(2) 牵引煤车所需功率的⼤⼩；(3) 牵引煤车所提供的能量中有多少转化为煤的动能？其余部分⽤于何处？解：(1) 以煤车和?t 时间内卸⼊车内的煤为研究对象，⽔平⽅向煤车受牵引⼒F 的作⽤，由动量定理： 000)(v v M t m M t F -+=?? 求出： 00v m F = (2) 2000v v m F P ==(3) 单位时间内煤获得的动能： 2021v m E K =单位时间内牵引煤车提供的能量为 P E ===21/E E K 50％即有50％的能量转变为煤的动能，其余部分⽤于在拖动煤时不可避免的滑动摩擦损耗．6.⼀链条总长为l ，质量为m ，放在桌⾯上，并使其部分下垂，下垂⼀段的长度为a ．设链条与桌⾯之间的滑动摩擦系数为µ．令链条由静⽌开始运动，则(1)到链条刚离开桌⾯的过程中，摩擦⼒对链条作了多少功？(2)链条刚离开桌⾯时的速率是多少？解：(1)建⽴如图坐标.某⼀时刻桌⾯上全链条长为y ,则摩擦⼒⼤⼩为 g lym f µ=摩擦⼒的功 ??--==0d d al al f y gy lmy f W µ=22al y lmg-µ =2)(2a l lmg--µ(2)以链条为对象，应⽤质点的动能定理 ∑W ＝222121v v m m - 其中 ∑W = W P ＋W f ，v 0 = 0 W P =?la x P d =la l mg x x l mg la 2)(d 22-=? 由上问知 la l mg W f 2)(2--=µal -a-a1)(22)(v m a l l mg l a l mg =---µ得 []21222)()(a l a l lg ---=µv7. 如图所⽰，在中间有⼀⼩孔O 的⽔平光滑桌⾯上放置⼀个⽤绳⼦连结的、质量m = 4 kg 的⼩块物体．绳的另⼀端穿过⼩孔下垂且⽤⼿拉住．开始时物体以半径R 0 = 0.5 m 在桌⾯上转动，其线速度是4 m/s ．现将绳缓慢地匀速下拉以缩短物体的转动半径．⽽绳最多只能承受 600 N 的拉⼒．求绳刚被拉断时，物体的转动半径R 等于多少？解：物体因受合外⼒矩为零，故⾓动量守恒．设开始时和绳被拉断时物体的切向速度、转动惯量、⾓速度分别为v 0、J 0、ω0和v 、J 、ω．则ωωJ J =00 ①因绳是缓慢地下拉，物体运动可始终视为圆周运动．①式可写成R mR R mR //20020v v =整理后得： v v /00R R =②物体作圆周运动的向⼼⼒由绳的张⼒提供 R m F /2v = 1分再由②式可得： 3/12020)/(F mR R v =当F = 600 N 时，绳刚好被拉断，此时物体的转动半径为R = 0.3 m8.设两个粒⼦之间相互作⽤⼒是排斥⼒，其⼤⼩与粒⼦间距离r 的函数关系为3r k f =，k 为正值常量，试求这两个粒⼦相距为r 时的势能．（设相互作⽤⼒为零的地⽅势能为零．）解：两个粒⼦的相互作⽤⼒ 3r k f =已知f ＝0即r ＝∞处为势能零点, 则势能∞∞∞=?==r r P P r r kW E d d 3r f)2(2r k =1. 汽车发动机内⽓体对活塞的推⼒以及各种传动部件之间的作⽤⼒能使汽车前进吗？使汽车前进的⼒是什么⼒？参考解答：汽车发动机内⽓体对活塞的推⼒以及各种传动部件之间的作⽤⼒都是汽车系统的内⼒，内⼒只会改变内部各质点的运动状态，不会改变系统的总动量，所以不能使汽车前进。

2020年高考回归复习—力学实验之验证动量守恒定律含答案

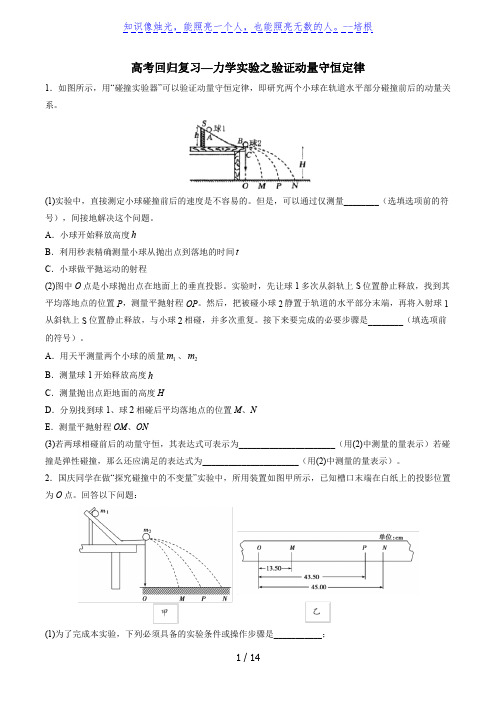
高考回归复习—力学实验之验证动量守恒定律1．如图所示，用“碰撞实验器”可以验证动量守恒定律，即研究两个小球在轨道水平部分碰撞前后的动量关系。

(1)实验中，直接测定小球碰撞前后的速度是不容易的。

但是，可以通过仅测量________（选填选项前的符号），间接地解决这个问题。

A．小球开始释放高度hB．利用秒表精确测量小球从抛出点到落地的时间tC．小球做平抛运动的射程(2)图中O点是小球抛出点在地面上的垂直投影。

实验时，先让球1多次从斜轨上S位置静止释放，找到其平均落地点的位置P，测量平抛射程OP。

然后，把被碰小球2静置于轨道的水平部分末端，再将入射球1从斜轨上S位置静止释放，与小球2相碰，并多次重复。

接下来要完成的必要步骤是________（填选项前的符号）。

A．用天平测量两个小球的质量1m、2mB．测量球1开始释放高度hC．测量抛出点距地面的高度HD．分别找到球1、球2相碰后平均落地点的位置M、NE．测量平抛射程OM、ON(3)若两球相碰前后的动量守恒，其表达式可表示为______________________（用(2)中测量的量表示）若碰撞是弹性碰撞，那么还应满足的表达式为______________________（用(2)中测量的量表示）。

2．国庆同学在做“探究碰撞中的不变量”实验中，所用装置如图甲所示，已知槽口末端在白纸上的投影位置为O点。

回答以下问题：(1)为了完成本实验，下列必须具备的实验条件或操作步骤是___________；A ．斜槽轨道末端的切线必须水平B ．入射球和被碰球半径必须相同C ．入射球和被碰球的质量必须相等D ．必须测出桌面离地的高度HE.斜槽轨道必须光滑(2)国庆同学在实验中正确操作，认真测量，得出的落点情况如图乙所示，则入射小球质量和被碰小球质量之比为____________；(3)为了完成本实验，测得入射小球质量m 1，被碰小球质量m 2，O 点到M 、P 、N 三点的距离分别为y 1、y 2、y 3，若两球间的碰撞是弹性碰撞，应该有等式_______成立。

大学物理第二章习题质点力学的基本规律守恒定律

第2章质点力学的基本规律守恒定律
基本要求
掌握经典力学的基本原理及会应用其分析和处理质点动力学问题，理解力学量的单位和量纲。掌握动量、冲量、动量定理，动量守恒定律。并能分析和计算二维平面简单力学问题。理解惯性系概念及经典力学的基本原理的适用范围。掌握功与功率、动能、势能（重力势能、弹性势能、引力势能）概念，动能定理、功能原理、机械能守恒定律。
教学基本内容、基本公式
1.牛顿定律
解牛顿定律的问题可分为两类：第一类是已知质点的运动，求作用于质点的力；第二类是已知作用于质点的力，求质点的运动.
2.基本定理动量定理
动能定理

I
t2 t1
F (t )dt

mv

mv0
A12

2
F
(r)

dr

1
1 2
mv
2 2

1 2
解：根据牛顿第二定律
f

k x2
m dv dt
m dv d x dx dt
mv
dv dx

k x2
mv
dv dx
v
dv

k
dx mx2

v
v
0
dv

A/4

A
k mx2
d
x
1v2 k (4 1) 3 k 2 m A A mA
另解：根据动能定理
v 6k /(mA)
(2)写出初末态系统的动量
t 时刻水平方向动量
dm m
t+dt时刻水平方向动量
O
x
(3)求出系统水平方向动量的增量

第三章动量定理动量守恒定律(习题)

第三章动量定理及动量守恒定律（习题）3.5.1质量为2kg 的质点的运动学方程为 j ˆ)1t 3t 3(i ˆ)1t 6(r 22+++-=(t 为时间，单位为s ；长度单位为m).求证质点受恒力而运动，并求力的方向大小。

解，j ˆ)3t 6(i ˆt 12v ++= j ˆ6i ˆ12a +=jˆ12i ˆ24a m F +==（恒量）12257.262412tg )N (83.261224F ==θ=+=-3.5.2质量为m 的质点在oxy 平面内运动，质点的运动学方程为ωω+ω=b,a, ,j ˆt sin b i ˆt cos a r为正常数，证明作用于质点的合力总指向原点。

解， ,j ˆt cos b i ˆt sin a v ωω+ωω-= r,j ˆt sin b i ˆt cos a a 22 ω-=ωω-ωω-= r m a m F ω-==3.5.3在脱粒机中往往装有振动鱼鳞筛，一方面由筛孔漏出谷粒，一方面逐出秸杆，筛面微微倾斜，是为了从较底的一边将秸杆逐出，因角度很小，可近似看作水平，筛面与谷粒发生相对运动才可能将谷粒筛出，若谷粒与筛面静摩擦系数为0.4，问筛沿水平方向的加速度至少多大才能使谷物和筛面发生相对运动。

解答，以谷筛为参照系，发生相对运动的条件是,g a ,mg f a m 000μ≥'μ=≥'a ' 最小值为)s /m (92.38.94.0g a 20=⨯=μ='以地面为参照系：解答，静摩擦力使谷粒产生最大加速度为,mg ma 0max μ= ,g a 0max μ=发生相对运动的条件是筛的加速度g a a0max μ=≥'，a '最小值为)s /m (92.38.94.0g a20=⨯=μ='3.5.4桌面上叠放着两块木板，质量各为,m ,m 21如图所示。

2m 和桌面间的摩擦系数为2μ，1m 和2m 间的静摩擦系数为1μ。

牛顿力学中的能量守恒练习题及

牛顿力学中的能量守恒练习题及解答在牛顿力学中，能量守恒是一个重要的概念。

本文将为您介绍一些与能量守恒相关的练习题，并给出详细的解答过程。

练习题一：一个小车以40 km/h的速度行驶，在行驶过程中突然失去动力。

小车在经过30米之后停了下来，求小车受到的摩擦力大小。

解答：根据能量守恒定律，小车失去动力后，其机械能将保持不变。

在失去动力前的机械能主要来自其动能，即1/2mv^2，其中m为小车质量，v为速度。

在停下后，小车的机械能主要来自其势能，即mgh，其中h为停下的高度，即0。

因此可以得到以下方程：1/2mv^2 = mgh根据题目给出的数据，速度v为40 km/h，转化为m/s得：v = 40 km/h = 40 * 1000 / 3600 m/s ≈ 11.11 m/s代入方程中，可以解得：1/2 * m * (11.11)^2 = m * g * 30化简后得：g ≈ (11.11)^2 / (2 * 30)计算得：g ≈ 20.79 m/s^2因此，小车受到的摩擦力大小为20.79 N。

练习题二：一个小球从高处自由落体，其下落的高度为20米。

小球在落地之后弹起，最高弹起的高度为原高度的一半。

求小球在弹起过程中失去的机械能。

解答：在自由落体过程中，小球的机械能主要来自其势能，即mgh，其中m为小球质量，g为重力加速度，h为下落的高度。

在弹起过程中，小球的机械能主要来自其动能，即1/2mv^2，其中v为弹起的速度，根据题目给出的信息，最高弹起的高度为原高度的一半，即10米。

因此，可以得到以下方程：mgh = 1/2mv^2根据题目给出的数据，下落高度h为20米，最高弹起高度为10米。

代入方程中，可以解得：m * 9.8 * 20 = 1/2 * m * v^2化简后得：v ≈ √(2 * 9.8 * 20)计算得：v ≈ √(392) ≈ 19.8 m/s因此，在弹起过程中，小球失去的机械能为：1/2 * m * (19.8)^2 - 1/2 * m * (0)^2 = 1/2 * m * (19.8)^2计算得：1/2 * m * (19.8)^2 ≈ 195.02 J因此，小球在弹起过程中失去的机械能约为195.02焦耳。

高中力学中的机械能守恒定律有哪些典型例题

高中力学中的机械能守恒定律有哪些典型例题在高中力学的学习中，机械能守恒定律是一个非常重要的知识点。

它不仅在解决物理问题时经常用到，也是理解能量转化和守恒的关键。

下面，我们就来一起探讨一些机械能守恒定律的典型例题。

例题一：自由落体运动一个质量为 m 的物体从高度为 h 的地方自由下落，忽略空气阻力，求物体下落至地面时的速度 v。

解析：在自由落体运动中，物体只受到重力的作用，重力势能逐渐转化为动能。

初始时刻，物体的机械能为重力势能 mgh，下落至地面时，物体的机械能为动能 1/2mv²。

因为机械能守恒，所以有 mgh ＝1/2mv²，解得 v ＝√2gh 。

这个例题是机械能守恒定律的最基本应用之一，它清晰地展示了重力势能如何转化为动能。

例题二：竖直上抛运动一个质量为 m 的物体以初速度 v₀竖直上抛，忽略空气阻力，求物体上升的最大高度 h。

解析：物体竖直上抛时，动能逐渐转化为重力势能。

在初始时刻，物体的机械能为动能 1/2mv₀²，当物体上升到最大高度时，速度为 0，机械能为重力势能 mgh。

由于机械能守恒，所以 1/2mv₀²＝ mgh，解得 h ＝ v₀²／ 2g 。

这个例题与自由落体运动相反，是动能转化为重力势能的过程。

例题三：光滑斜面运动一个质量为 m 的物体从光滑斜面的顶端由静止开始下滑，斜面的高度为 h，斜面的长度为 L，求物体滑到底端时的速度 v。

解析：物体在斜面上运动时，重力势能转化为动能。

初始时刻，物体的机械能为重力势能 mgh，滑到底端时，物体的机械能为动能1/2mv²。

因为斜面光滑，没有摩擦力做功，机械能守恒。

根据几何关系，物体下落的高度 h 与斜面长度 L 和斜面倾角θ 有关，h ＝Lsinθ。

所以mgh ＝ 1/2mv²，解得 v ＝√2gh ＝√2gLsinθ 。

这个例题展示了在斜面这种常见的情境中机械能守恒定律的应用。

力学应用动量守恒定律解题

力学应用动量守恒定律解题力学是物理学的一个重要分支，研究物体在运动过程中所受的力及其变化规律。

动量守恒定律是力学中的一条基本定律，表明在一个封闭系统中，当没有外力作用时，系统的总动量保持不变。

应用动量守恒定律可以解决许多实际问题，下面我将以几个例子来说明。

例题一：弹性碰撞假设有两个质量相同的小球，在光滑的水平面上碰撞。

初始时，小球A以速度va向右运动，小球B以速度vb向左运动。

碰撞后，小球A以速度va'向左运动，小球B以速度vb'向右运动。

我们可以利用动量守恒定律来求解碰撞后的速度。

根据动量守恒定律，碰撞前的总动量等于碰撞后的总动量。

设小球A和小球B的质量都为m，速度va为正值，速度vb为负值，则可以写出以下方程：mva + mvb = mva' + mvb'根据题意，可以得到小球A碰撞前的速度va和小球B碰撞前的速度vb都已知，碰撞后的速度va'和vb'是未知的，通过解方程可以求解出碰撞后的速度。

例题二：炮弹问题假设有一个炮弹以速度v0发射出去，形成一个抛物线轨迹。

我们可以利用动量守恒定律来解决炮弹问题。

在潜射前和潜射后，系统的总动量保持不变。

当炮弹发射前，炮弹和大炮的总动量为零；当炮弹发射后，炮弹和大炮的总动量仍为零，只是动量的方向相反。

利用动量守恒定律，我们可以得到以下方程：m0v0 = (m+m0) v其中，m0是炮弹的质量，v0是炮弹的初速度，m是大炮的质量，v是大炮的速度。

通过解方程，我们可以求解出炮弹的速度v和射程等相关参数。

这样，我们就可以用动量守恒定律解答炮弹问题。

例题三：汽车追尾问题假设有两辆质量分别为m1和m2的汽车，汽车1以速度v1追尾汽车2，两车发生完全弹性碰撞。

求解碰撞后两车的速度。

根据动量守恒定律，我们可以得到以下方程：m1v1 + m2v2 = m1v1' + m2v2'其中，v1和v2是碰撞前两车的速度，v1'和v2'是碰撞后两车的速度。

高中物理力学中角动量守恒问题的解题技巧

高中物理力学中角动量守恒问题的解题技巧在高中物理力学学习中，角动量守恒是一个非常重要的概念。

它在解决一些与旋转运动有关的问题时起着至关重要的作用。

本文将通过具体题目的举例，来说明角动量守恒问题的解题技巧，并且尝试给出一些一般性的指导。

例题1：一质点质量为m，在水平光滑桌面上以速度v做匀速圆周运动，半径为r。

一个质量为M的物体以速度V撞击该质点，并与其发生完全弹性碰撞。

碰撞后，质点的圆周运动半径变为R。

求M与m的质量比。

解析：这道题目涉及到了角动量守恒和动量守恒两个重要的物理定律。

我们可以首先分析碰撞前后的角动量和动量是否守恒。

碰撞前，质点的角动量为L1 = mvr，物体的角动量为L2 = MRV。

由于碰撞是完全弹性碰撞，所以碰撞后质点和物体的速度方向不变，仅仅改变了大小。

因此，碰撞后质点的角动量为L3 = mVR，物体的角动量为L4 = MRv。

根据角动量守恒定律，碰撞前后的总角动量应该相等，即L1 + L2 = L3 + L4。

代入数值，得到mvr + MRV = mVR + MRv。

同样地，根据动量守恒定律，碰撞前后的总动量也应该相等，即mv + MV = mV + Mv。

通过以上两个方程，我们可以解得M与m的质量比。

这道题目的解题关键在于正确运用角动量守恒和动量守恒的定律，并将它们转化为数学方程进行求解。

在解题过程中，需要注意将碰撞前后的角动量和动量分别表示出来，并且注意角动量的正负方向。

例题2：一个物体以速度v绕一个半径为r的固定点做匀速圆周运动。

现在将该物体的速度加倍，求此时物体的角动量相对于原来增加了多少倍。

解析：这道题目考察的是角动量与动量的关系。

根据角动量的定义，L = mvr，其中m为物体的质量，v为物体的速度，r为物体到固定点的距离。

当物体的速度加倍时，新的角动量为L' = 2mv(r/2) = 2L。

可以看出，物体的角动量相对于原来增加了2倍。

这道题目的解题关键在于理解角动量与动量的关系，即角动量正比于动量。

2月22日物理作业动量守恒定律

2月22日物理作业《优化》大本9----13页动量守恒定律一、系统内力和外力1．系统：的两个(或多个)物体组成一个整体．2．内力：系统物体间的相互作用力．3．外力：系统的物体对系统的物体的作用力．二、动量守恒定律1．内容：如果一个系统，或者所受外力的矢量和为，这个系统的总动量，这就是动量守恒定律．2．表达式：(系统相互作用前后总动量p、p′相等)．3．成立条件(1)系统不受；(2)系统所受外力之和为零．4．适用范围(1)相互作用的物体无论是还是运动；无论是还是，动量守恒定律都适用．(2)动量守恒定律是一个独立的实验定律，它适用于目前为止物理学研究的一切领域．判一判(1)一个系统初、末状态动量大小相等，即动量守恒．()(2)两个做匀速直线运动的物体发生碰撞，两个物体组成的系统动量守恒．()(3)系统动量守恒也就是系统的动量变化量为零．()(4)只有重力做功或弹力做功的系统内动量守恒．()(5)若系统动量守恒，则系统机械能也守恒．()(6)靠摩擦力相互作用的两个物体，系统动量守恒，但机械能不守恒．()做一做如图所示，小车与木箱紧挨着静止放在光滑的水平冰面上，现有一男孩站在小车上用力向右迅速推木箱．关于上述过程，下列说法中正确的是()A．男孩与木箱组成的系统动量定恒B．小车与木箱组成的系统动量守恒C．男孩、小车与木箱三者组成的系统动量守恒D．木箱的动量增量与男孩、小车的总动量增量相同如图所示，公路上三辆汽车发生了追尾事故．如果将前面两辆汽车看做一个系统，最后面一辆汽车对中间汽车的作用力是内力还是外力？如果将后面两辆汽车看做一个系统呢？对动量守恒定律的理解1．研究对象：相互作用的物体组成的力学系统．2．动量守恒定律的成立条件(1)系统不受外力或所受合外力为零．(2)系统受外力作用，但内力远远大于合外力．此时动量近似守恒．(3)系统所受到的合外力不为零，但在某一方向上合外力为零(或某一方向上内力远远大于外力)，则系统在该方向上动量守恒．3．动量守恒定律的性质关于系统动量守恒的条件，下列说法正确的是()A．只要系统内存在摩擦力，系统动量就不可能守恒B．只要系统中有一个物体具有加速度，系统动量就不守恒C．只要系统所受的合外力为零，系统动量就守恒D．系统中所有物体的加速度为零时，系统的总动量不一定守恒系统动量守恒的判定方法(1)分析动量守恒时研究对象是系统，分清外力与内力．(2)研究系统受到的外力矢量和．(3)外力矢量和为零，则系统动量守恒；若外力在某一方向上合力为零，则在该方向上系统动量守恒．(4)系统动量严格守恒的情况很少，在分析具体问题时要注意把实际过程理想化．(多选)在光滑水平面上，A、B两小车中间有一弹簧，如图所示．用手抓住小车并将弹簧压缩后使小车处于静止状态，将两小车及弹簧看做一个系统，下列说法中正确的是()A．两手同时放开后，系统总动量始终为零B．先放开左手，再放开右手后，动量不守恒C．先放开左手，再放开右手后，总动量向左D．无论何时放手，两手放开后，在弹簧恢复原长的过程中，系统总动量都保持不变，但系统的总动量不一定为零动量守恒定律的应用1．动量守恒定律的常用表达式(1)p＝p′或m1v1＋m2v2＝m1v1′＋m2v2′(系统相互作用前的总动量p等于相互作用后的总动量p′，大小相等，方向相同)．(2)Δp1＝－Δp2或m1Δv1＝－m2Δv2(系统内一个物体的动量变化量与另一物体的动量变化量等大反向)．(3)Δp＝p′－p＝0(系统总动量的变化量为零)．2．解题步骤命题视角1运用动量守恒定律分析求解问题(2019·吉林松原高二期中)在橄榄球比赛中，一个95 kg的橄榄球前锋以5 m/s的速度跑动，想穿越防守队员到底线触地得分．就在他刚要到底线时，迎面撞上了对方两名均为75 kg的队员，一个速度为2 m/s，另一个为4 m/s，然后他们就扭在了一起．(1)他们碰撞后的共同速率是____________；(2)在方框中标出碰撞后他们动量的方向，并说明这名前锋能否得分：____________(选填“能”或“不能”)．命题视角2某一方向上的动量守恒光滑水平面上放着一质量为M的槽，槽与水平面相切且光滑，如图所示，一质量为m的小球以速度v0向槽运动，若开始时槽固定不动，求小球上升的高度(槽足够高)；若槽不固定，则小球又上升多高？命题视角3动量近似守恒的问题如图所示，游乐场上，两位同学各驾着一辆碰碰车迎面相撞，此后，两车以共同的速度运动．设甲同学和他的车的总质量为150 kg，碰撞前向右运动，速度的大小为4.5 m/s；乙同学和他的车的总质量为200 kg，碰撞前向左运动，速度的大小为3.7 m/s.求碰撞后两车共同的运动速度．碰碰车的碰撞示意图应用动量守恒定律注意的事项在应用动量守恒定律时，一定要注意守恒的条件，不要盲目使用，注意选好研究对象及其作用的方向，也许整个系统动量不守恒，但在某一个方向上动量是守恒的．【通关练习】1．如图所示，两辆质量相同的小车置于光滑的水平面上，有一人静止站在A车上，两车静止，若这个人自A车跳到B车上，接着又跳回A车，静止于A车上，则A车的速率()A ．等于零B ．小于B 车的速率C ．大于B 车的速率D ．等于B 车的速率2．光滑水平桌面上有P 、Q 两个物块，Q 的质量是P 的n 倍．将一轻弹簧置于P 、Q 之间，用外力缓慢压P 、Q .撤去外力后，P 、Q 开始运动，P 和Q 的动量大小的比值为( )A ．n 2B ．n C.1nD ．13．(2019·河北衡水高二月考)如图所示，质量为m 的人立于平板车上，人与车的总质量为M ，人与车以速度v 1在光滑水平面上向东运动．当此人相对于车以速度v 2竖直跳起时，车向东的速度大小为( )A.Mv 1－Mv 2M －mB.Mv 1M －mC.Mv 1＋Mv 2M －mD ．v 14．质量m 1＝10 g 的小球在光滑的水平桌面上以v 1＝30 cm/s 的速率向右运动，恰遇上质量为m 2＝50 g 的小球以v 2＝10 cm/s 的速率向左运动，碰撞后，小球m 2恰好停止，则碰后小球m 1的速度大小和方向如何？多物体系统中的动量守恒一个系统如果满足动量守恒条件，并且由两个以上的物体构成，在对问题进行分析时，既要注意系统总动量守恒，又要注意系统内部分物体动量守恒．注重系统内部分物体动量守恒分析，又可以使求解突破关键的未知量，增加方程个数，为问题的最终解答铺平道路．解决问题时应注意：(1)正确分析作用过程中各物体状态的变化情况，建立运动模型． (2)分清作用过程中各个阶段和联系阶段的状态量．(3)合理地选取研究对象，既要符合动量守恒的条件，又要方便解题．命题视角1 多物体多过程问题的求解如图所示，水平光滑地面上依次放置着质量m＝0.08 kg的10块完全相同的长直木板．一质量M＝1.0 kg、大小可忽略的小铜块以初速度v0＝6.0 m/s从长木板左侧滑上木板，当铜块滑离第一块木板时，速度大小为v1＝4.0 m/s.铜块最终停在第二块木板上．(取g＝10 m/s2，结果保留两位有效数字)求：(1)第一块木板的最终速度；(2)铜块的最终速度．命题视角2动量守恒中的临界极值问题如图所示，甲、乙两船的总质量(包括船、人和货物)分别为10m、12m，两船沿同一直线同一方向运动，速度分别为2v0、v0.为避免两船相撞，乙船上的人将一质量为m的货物沿水平方向抛向甲船，甲船上的人将货物接住，求抛出货物的最小速度．(不计水的阻力)动量守恒定律应用中的常见临界情形【通关练习】1．(2019·西藏山南高二期末)如图所示，质量为M的盒子放在光滑的水平面上，盒子内表面不光滑，盒内放有一块质量为m的物体，某时刻给物体一个水平向右的初速度v0，那么在物体与盒子前后壁多次往复碰撞后()A．两者的速度均为零B．两者的速度总不会相等C ．盒子的最终速度为mv 0M ，方向水平向右D ．盒子的最终速度为mv 0M ＋m，方向水平向右2．(2019·宁夏六盘山高二期末)一个人在地面上立定跳远最好成绩是s .假设他站在静止于地面的小车的A 端(车与地面的摩擦不计)，如图所示，他欲从A 端跳上L 远处的站台上，则( )A ．只要L ＜s ，他一定能跳上站台B ．只要L ＜s ，他有可能跳上站台C ．只要L ＝s ，他一定能跳上站台D ．只要L ＝s ，他有可能跳上站台3．如图所示，在光滑的水平面上有两个并排放置的木块A 和B ，已知木块A 、B 的质量分别为m A ＝500 g 、m B ＝300 g ．有一个质量为80 g 的小铁块C 以25 m/s 的水平初速度开始在A表面滑动．由于C与A、B之间有摩擦，铁块最后停在B上，B和C一起以2.5 m/s的速度共同前进．求：(1)木块A的最后速度大小v A′；(2)C在离开A时的速度大小v C′.[随堂检测] [学生用书P13]1．(2019·辽宁营口高二月考)一人静止于完全光滑的冰面上，现欲远离冰面，下列可行的方法是()A．向后踢腿B．手臂向上摆C．在冰面上滚动D．脱下外衣水平抛出2.如图所示，甲、乙两人各站在静止小车的左、右两端，当他俩同时相向行走时，发现小车向右运动．下列说法不正确的是(车与地面之间无摩擦)()A．乙的速度必定大于甲的速度B．乙对小车的冲量必定大于甲对小车的冲量C．乙的动量必定大于甲的动量D．甲、乙动量总和必定不为零3．(多选)如图所示，木块A静置于光滑的水平面上，其曲面部分MN光滑，水平部分NP粗糙．现有一物体B自M点由静止下滑，设NP足够长，则以下叙述正确的是() A．A、B最终以同一不为零的速度运动B．A、B最终速度均为零C．A物体先做加速运动，后做减速运动第 21 页共 21 页 D ．A 物体先做加速运动，后做匀速运动4．(2019·湖北武汉高二期中)下面是一个物理演示实验，它显示：图中自由下落的物体A 和B 经反弹后，B 能上升到比初始位置高得多的地方．A 是某种材料做成的实心球，质量m 1＝0.28 kg ，在其顶部的凹坑中插着质量m 2＝0.10 kg 的木棍B .B 只是松松地插在凹坑中，其下端与坑底之间有小空隙．将此装置从A 下端离地板的高度H ＝1.25 m 处由静止释放．实验中，A 触地后在极短时间内反弹，且其速度大小不变；接着木棍B 脱离球A 开始上升，而球A 恰好停留在地板上．求木棍B 上升的高度，重力加速度g ＝10 m/s 2.5．结冰的湖面上有甲、乙两个小孩分别乘冰车在一条直线上相向滑行，速度大小均为v 1＝2 m/s ，甲与车、乙与车的质量和均为M ＝50 kg.为了使两车不会相碰，甲将冰面上一质量为5 kg 的静止冰块以v 2＝6 m/s(相对于冰面)的速率传给乙，乙接到冰块后又立即以同样的速率将冰块传给甲，如此反复，在甲、乙之间至少传递几次，才能保证两车不相碰？(设开始时两车间距足够远)。

大学物理A 练习题第2章《质点力学的运动定律守恒定律》

《第2章质点力学的运动定律守恒定律》一选择题1. 水平地面上放一物体A ，它与地面间的滑动摩擦系数为μ．现加一恒力F 如图所示．欲使物体A 有最大加速度，则恒力F 与水平方向夹角θ 应满足(A) sin θ ＝μ． (B) cos θ ＝μ． (C) tg θ ＝μ． (D) ctg θ ＝μ．[ ]2. 一质点在力F = 5m (5 - 2t ) (SI)的作用下，t =0时从静止开始作直线运动，式中m 为质点的质量，t 为时间，则当t = 5 s 时，质点的速率为(A) 50 m ·s -1． (B) 25 m ·s -1．(C) 0． (D) -50 m ·s -1．[ ]3. 体重、身高相同的甲乙两人，分别用双手握住跨过无摩擦轻滑轮的绳子各一端．他们从同一高度由初速为零向上爬，经过一定时间，甲相对绳子的速率是乙相对绳子速率的两倍，则到达顶点的情况是(A) 甲先到达． (B) 乙先到达．(C) 同时到达． (D) 谁先到达不能确定．[ ]4．一质点在如图所示的坐标平面内作圆周运动，有一力)(0j y i x F F+=作用在质点上．在该质点从坐标原点运动到(0，2R ）位置过程中，力F 对它所作的功为(A) 20R F ． (B) 202R F ． (C) 203R F ． (D) 204R F ．[ ]5. 对质点组有以下几种说法：(1) 质点组总动量的改变与内力无关． (2) 质点组总动能的改变与内力无关． (3) 质点组机械能的改变与保守内力无关．在上述说法中： (A) 只有(1)是正确的． (B) (1)、(3)是正确的．(C) (1)、(2)是正确的． (D) (2)、(3)是正确的．[ ] 6. 一火箭初质量为M 0，每秒喷出的质量(-d M /d t )恒定，喷气相对火箭的速率恒定为u．设火箭竖直向上发射，不计空气阻力，重力加速度g 恒定，则t = 0时火箭加速度a在竖直方向（向上为正）的投影式为 (A) g t M M u a --=)d d (0． (B) g tM M u a +=)d d (0．(C) d d (0t M M u a -=． (D) g tM M u a -=d d (0 [ ]7. 一竖直向上发射之火箭，原来静止时的初质量为m 0经时间t 燃料耗尽时的末质量为m ，喷气相对火箭的速率恒定为u ，不计空气阻力，重力加速度g 恒定．则燃料耗尽时火箭速率为(A) 2/ln0gt m m u -=v ． (B) gt m m u -=0ln v ． (C) gt m m u +=0ln v ． (D) gt mmu -=0ln v ．[ ]二填空题 1. 某质点在力F ＝(4＋5x )i(SI)的作用下沿x 轴作直线运动，在从x ＝0移动到x ＝10 m的过程中，力F所做的功为__________．2．质量为m ＝0.5kg 的质点，在Oxy 坐标平面内运动，其运动方程为x ＝5t ，y =0.5t 2（SI），从t =2s 到t =4s 这段时间内，外力对质点作的功为_____________.3. 设作用在质量为1 kg 的物体上的力F ＝6t ＋3（SI ）．如果物体在这一力的作用下，由静止开始沿直线运动，在0到2.0 s 的时间间隔内，这个力作用在物体上的冲量大小Ｉ＝__________．4. 质量m ＝1 kg 的物体，在坐标原点处从静止出发在水平面内沿x 轴运动，其所受合力方向与运动方向相同，合力大小为F ＝3＋2x (SI)，那么，物体在开始运动的3 m 内，合力所作的功W ＝_________；且x ＝3 m 时，其速率v ＝_________．5. 质量为0.05 kg 的小块物体，置于一光滑水平桌面上．有一绳一端连接此物，另一端穿过桌面中心的小孔（如图所示）．该物体原以3 rad/s 的角速度在距孔0.2 m 的圆周上转动．今将绳从小孔缓慢往下拉，使该物体之转动半径减为0.1 m ．则拉力所做的功为____________________．6. 粒子B 的质量是粒子A 的质量的4倍，开始时粒子A 的速度j i43+=0A v ,粒子B 的速度j i72-=0B v ；在无外力作用的情况下两者发生碰撞，碰后粒子A 的速度变为j i 47-=A v ，则此时粒子B 的速度B v＝____________________．7. 一维保守力的势能曲线如图所示，有一粒子自右向左运动，通过此保守力场区域时，在 _________________ 区间粒子所受的力F x > 0；在 _________________ 区间粒子所受的力F x < 0；在x = _______________ 时粒子所受的力F x = 0．三计算题1. 一质点沿x 轴运动，其加速度a 与位置坐标x 的关系为a ＝2＋6 x 2 (SI)，如果质点在原点处的速度为零，试求其在任意位置处的速度．2. 质点沿曲线 j t i t r22+= (SI) 运动，其所受摩擦力为 v 2-=f (SI)．求摩擦力在t = 1 s 到t = 2 s 时间内对质点所做的功．3. 一辆水平运动的装煤车，以速率v 0从煤斗下面通过，每单位时间内有质量为m 0的煤卸入煤车．如果煤车的速率保持不变，煤车与钢轨间摩擦忽略不计，试求： (1) 牵引煤车的力的大小； (2) 牵引煤车所需功率的大小；(3) 牵引煤车所提供的能量中有多少转化为煤的动能？其余部分用于何处？4. 一链条总长为l ，质量为m ，放在桌面上，并使其部分下垂，下垂一段的长度为a ．设链条与桌面之间的滑动摩擦系数为．令链条由静止开始运动，则(1)到链条刚离开桌面的过程中，(2)链条刚离开桌面时的速率是多少？a5. 如图所示，在中间有一小孔O 的水平光滑桌面上放置一个用绳子连结的、质量m = 4 kg 的小块物体．绳的另一端穿过小孔下垂且用手拉住．开始时物体以半径R 0 = 0.5 m 在桌面上转动，其线速度是4 m/s ．现将绳缓慢地匀速下拉以缩短物体的转动半径．而绳最多只能承受 600 N 的拉力．求绳刚被拉断时，物体的转动半径R 等于多少？6. 小球A ，自地球的北极点以速度0v 在质量为M 、半径为R 的地球表面水平切向向右飞出，如图所示，地心参考系中轴OO ＇与0v 平行，小球A 的运动轨道与轴OO ＇相交于距O 为3R 的C 点．不考虑空气阻力，求小球A 在C点的速度v 与0v 之间的夹角θ．7. 一个具有单位质量的质点在随时间 t 变化的力j t i t t F)612()43(2-+-= (SI) 作用下运动．设该质点在t = 0时位于原点，且速度为零．求t = 2秒时，该质点受到对原点的力矩和该质点对原点的角动量．四研讨题1. 汽车发动机内气体对活塞的推力以及各种传动部件之间的作用力能使汽车前进吗？使汽车前进的力是什么力？2. 在经典力学范围内，若某物体系对某一惯性系满足机械能守恒条件，则在相对于上述惯性系作匀速直线运动的其它参照系中，该物体系是否一定也满足机械能守恒条件？请举例说明．3. 在车窗都关好的行驶的汽车内，漂浮着一个氢气球，当汽车向左转弯时，氢气球在车内将向左运动还是向右运动？4. 为了避免门与墙壁的撞击，常常在门和墙上安装制动器，目前不少制动器安装在靠近地面的位置上（如图），在开关门的过程中，门与制动器发生碰撞，从而门受到撞击力的作用。

(完整版)高中物理力学学实验验证动量守恒定律(实验+练习)

实验：验证动量守恒定律一．实验原理在一维碰撞中，测出物体的质量m 和碰撞前后物体的速率v 、v ′，找出碰撞前的动量p ＝m 1v 1＋m 2v 2及碰撞后的动量p ′＝m 1v ′1＋m 2v ′2，看碰撞前后动量是否守恒．二．实验方案方案一：利用气垫导轨完成一维碰撞实验(1)测质量：用天平测出滑块质量．(2)安装：正确安装好气垫导轨．(3)实验：接通电源，利用配套的光电计时装置测出两滑块各种情况下碰撞前后的速度(①改变滑块的质量．②改变滑块的初速度大小和方向)．(4)验证：一维碰撞中的动量守恒．方案二：利用等长悬线悬挂等大小球完成一维碰撞实验(1)测质量：用天平测出两小球的质量m 1、m 2.(2)安装：把两个等大小球用等长悬线悬挂起来．(3)实验：一个小球静止，拉起另一个小球，放下时它们相碰．(4)测速度：可以测量小球被拉起的角度，从而算出碰撞前对应小球的速度，测量碰撞后小球摆起的角度，算出碰撞后对应小球的速度．(5)改变条件：改变碰撞条件，重复实验．(6)验证：一维碰撞中的动量守恒．方案三：在光滑桌面上两车碰撞完成一维碰撞实验(1)测质量：用天平测出两小车的质量.(2)安装：将打点计时器固定在光滑长木板的一端，把纸带穿过打点计时器，连在小车的后面，在两小车的碰撞端分别装上撞针和橡皮泥．(3)实验：接通电源，让小车A 运动，小车B 静止，两车碰撞时撞针插入橡皮泥中，把两小车连接成一体运动．(4)测速度：通过纸带上两计数点间的距离及时间由v ＝Δx Δt算出速度． (5)改变条件：改变碰撞条件，重复实验．(6)验证：一维碰撞中的动量守恒．方案四：利用斜槽上滚下的小球验证动量守恒定律(1)用天平测出两小球的质量，并选定质量大的小球为入射小球．(2)按照如图所示安装实验装置，调整固定斜槽使斜槽底端水平．(3)白纸在下，复写纸在上，在适当位置铺放好．记下重垂线所指的位置O .(4)不放被撞小球，让入射小球从斜槽上某固定高度处自由滚下，重复10次．用圆规画尽量小的圆把所有的小球落点圈在里面，圆心P 就是小球落点的平均位置．(5)把被撞小球放在斜槽末端，让入射小球从斜槽同一高度自由滚下，使它们发生碰撞，重复实验10次．用步骤(4)的方法，标出碰后入射小球落点的平均位置M 和被碰小球落点的平均位置N .如图所示．(6)连接ON ，测量线段OP 、OM 、ON 的长度．将测量数据填入表中．最后代入m 1OP ＝m 1OM ＋m 2ON ，看在误差允许的范围内是否成立．(7)整理好实验器材放回原处．(8)实验结论：在实验误差范围内，碰撞系统的动量守恒．三、练习巩固1.用半径相同的小球1和小球2的碰撞验证动量守恒定律，实验装置如图所示，斜槽与水平槽圆滑连接。

力学实验验证动量守恒定律

力学实验验证动量守恒定律动量守恒定律是力学领域中的重要定律之一，它描述了一个封闭系统中的总动量是恒定不变的。

我们可以通过一系列的力学实验来验证这个定律。

实验一：弹球撞击在这个实验中，我们可以选择一个平滑的水平面和两个大小相同的弹性球。

首先，我们以一定速度将一个弹性球A沿水平面运动，并保持另一个球B静止。

当球A撞击到球B时，我们可以观察到球A会停下来，并且球B会开始以相同的速度进行运动。

根据动量守恒定律，如果我们将弹性球A和弹性球B视为一个封闭系统，那么撞击前后总动量应该保持恒定。

在这个实验中，球A的动量在撞击前是$m_av_a$，撞击后是$m_av_a$，而球B的动量在撞击前是0，在撞击后是$m_bv_b$。

因此，根据动量守恒定律的数学表达式，我们有$m_av_a + 0 = m_av_a + m_bv_b$。

由于球A和球B的质量和速度在实验中是一定的，根据实验结果，我们可以验证动量守恒定律的成立。

实验二：火箭发射在这个实验中，我们可以使用一个小型的水箭模型。

首先，我们在水箭上装满压缩空气。

当我们打开气阀时，空气会从箭头处射出，并且由反冲作用产生推动力。

我们可以观察到，当箭头喷出气体的速度越快，箭身向相反方向运动的速度越大。

根据动量守恒定律，当气体从箭头射出时，箭头和箭身构成了一个封闭系统。

在这个实验中，箭身的质量和速度在反冲作用前是0，在反冲作用后是$m_cv_c$；而箭头射出气体的质量在反冲作用前是$m_d$，在反冲作用后是0。

根据动量守恒定律的数学表达式，我们有$0 +m_dv_d = 0 + m_cv_c$。

通过观察箭身和箭头运动的速度，并知道箭身质量与箭头射出气体质量的比例，我们可以验证动量守恒定律的有效性。

实验三：碰撞车碰撞车实验是一种经典的力学实验，可以直观地演示动量守恒定律。

在这个实验中，我们可以使用两个金属车轮，每个车轮上都有一个金属球。

当一个金属球以一定的速度撞向另一个金属球时，我们可以观察到两个金属球会反弹，并且各自以相同的速度向相反方向运动。

中考物理之力学机械能守恒定律经典习题答案

机械能守恒定律1.在只有重力做功的情况下,_________________________,这个结论叫作机械能守恒定律. 答案:物体的动能和势能发生转化,但机械能的总量保持不变2.下列情况中,运动物体机械能一定守恒的是( ).(A)物体所受的合外力为零 (B)物体不受摩擦力(C)物体受到重力和摩擦力 (D)物体只受重力答案:D3.关于机械能是否守恒,下列叙述中正确的是( ).(A)作匀速直线运动的物体的机械能一定守恒 (B)作匀变速运动的物体机械能可能守恒(C)外力对物体做功为零时,机械能一定守恒 (D)只有重力对物体做功,物体机械能一定守恒答案:BD4.下列说法中正确的是( ).(A)一个物体所受的合外力为零,它的机械能一定守恒(B)一个物体所受的合外力恒定不变,它的机械能可能守恒(C)一个物体作匀速直线运动,它的机械能一定守恒(D)一个物体作匀加速直线运动,它的机械能可能守恒答案:BD5.a 、b 、c 三球自同一高度以相同速率抛出,a 球竖直上抛,b 球水平抛出,c 球竖直下抛.设三球落地的迷率分别为v a 、v b ,v c 则( ).(A)v a >v b >v c (B)v a =v b >v c (C)v a >v b =v c (D)v a =v b =v c 答案:D6.质量为m 的物体,以初速度v 0由固定的光滑斜面的底端沿斜面向上滑动,在滑动过程中,当高度为h 时,该物体具有的机械能为( ). (A)20mv 21 (B)mgh mv 2120 (C)mgh (D)mgh -mv 2120 答案:A 7.如图所示,质量相同的两个小球,分别用长l 和2l 的细绳悬挂在天花板上,分别拉起小球使线伸直呈水平状态,然后轻轻释放.当小球到达最低位置时( ).(A)两球运动的线速度相等 (B)两球运动的角速度相等(C)两球的向心加速度相等 (D)细绳对两球的拉力相等答案:CD8.当重力对物体做正功时,物体的( ).(A)重力势能一定增加,动能一定减少 (B)重力势能一定减少,动能一定增加(C)重力势能一定减少,动能不一定增加 (D)重力势能不一定减少,动能一定增加答案:C9.以下运动中机械能守恒的是( ).(A)物体沿斜面匀速下滑(B)物体从高处以g/3的加速度竖直下落(C)不计阻力,细绳一端拴一小球,使小球在竖直平面内作圆周运动(D)物体沿光滑的曲面滑下答案:CD10.图中的四个选项,木块均在固定的斜面上运动,其中图(A)(B)(C)中的斜面是光滑的,图(A)(B)中的F 为木块所受的外力,方向如图中箭头所示,图(A)(B)(D)中的木块向下运动,图(C)中的木块向上运动.在这四个图所示的运动过程中,机械能守恒的是图( ).答案:C11.跳伞运动员在刚跳离飞机、其降落伞尚未打开的一段时间内,下列说法中正确的是( ).(A)空气阻力做正功 (B)重力势能增加 (C)动能增加 (D)空气阻力做负功答案:CD12.如图所示,一艘快艇发动机的冷却水箱离水面的高度为0.8m,现用导管与船底连通到水中,要使水能流进水箱(不考虑导管对水的阻力),快艇的航行速度至少应达到( ).(A)2.0m/s (B)4.0m/s (C)6.0m/s (D)8.0m/s答案:B13.枪竖直向上以初速度v 0发射子弹,忽略空气阻力,当子弹离枪口距离为____时,子弹的动能是其重力势能的一半.答案:3gv 20 14.在验证机械能守恒定律的实验中,要验证的是重锤重力势能的减少等于它动能的增加,以下步骤中仅是实验中的一部分,在这些步骤中多余的或错误的有______(填代号).(A)用天平称出重锤的质量.(B)把打点计时器固定在铁架台上,并用导线把它和低压交流电源连接起来.(C)把纸带的一端固定在重锤上,另一端穿过打点计时器的限位孔,把重锤提升到一定的高度.(D)接通电源,释放纸带.(E)用秒表测出重锤下落的时间.答案:AE15.在”验证机械能守恒定律”的实验中,已知打点计时器所用电源的频率为50Hz,查得当地的重力加速度g=9.80m/s 2,测得所用的重物的质量为1.00㎏.实验中得到一条点迹清晰的纸带如图所示,把第一个点记作0,另选连续的4个点A 、B 、C 、D 作为测量的点.经测量知道A 、B 、C 、D 各点到O 点的距离分别为62.99cm 、70.18cm 、77.76cm 、85.73cm.根据以上数据,可知重物由O 点运动到C 点,重力势能的减少量等于_____J,动能的增加量等于__________J(取三位有效数字).答案:7.62,7.5616.如图所示,一根长l 的细线,一端固定在顶板上,另一端拴一个质量为m 的小球.现使细线偏离竖直方向α=60Δ°角后,从A 点处无初速地释放小球.试问:(1)小球摆到最低点O 时的速度多大?(2)小球摆到左方最高点的高度(相对最低点)多高?(3)若在悬点正下方处有一钉子,O′P=l/3,不计悬线与钉碰撞时的能量损失,则小球碰钉后向左摆动过程中能达到的最大高度有何变化?答案:(1)gl(2)l/2(3)仍与A点等高17.如图所示,一小球从倾角为30°的固定斜面上的A点水平抛出,初动能为6J,问球落到斜面上的B点时动能有多大?答案:14J18.如图所示,通过定滑轮悬拌两个质量为m1、m2的物体(m1>m2),不计绳子质量、绳子与滑轮问的摩擦,在m1向下运动一段距离的过程中,下列说法中正确的是( ).(A)m1势能的减少量等于m2动能的增加量(B)m1势能的减少量等于m2势能的增加量(C)m1机械能的减少量等于m2机械能的增加量(D)m1机械能的减少量大于m2机械能的增加量答案:C19.一物体静止在升降机的地板上,在升降机加速上升的过程中,地板对物体的支持力所做的功等于( ).(1999年全国高考试题)(A)物体势能的增加量(B)物体动能的增加量(C)物体动能的增加量加上物体势能的增加量(D)物体动能的增加量加上克服重力所做的功答案:CD20.如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置,当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)从高于a位置的c位置沿弹簧中轴线自由下落,弹簧被重球压缩到最低位置d.以下关于重球运动过程的正确说法应是( ).(A)重球下落压缩弹簧由a至d的过程中,重球作减速运动(B)重球下落至b处获得最大速度(C)由a至d过程中重球克服弹簧弹力做的功等于小球由c下落至d处时重力势能减少量(D)重球在b位置处具有的动能等于小球由c下落到b处减少的重力势能答案:BC21_如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球,B处固定质量为m的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的同定轴转动.开始时OB与地面相垂直,放手后支架开始运动,在不计任何阻力的情况下,下列说法中正确的是( ).(A)A 球到达最低点时速度为零(B)A 球机械能减少量等于B 球机械能增加量(C)B 球向左摆动所能达到的最高位置应高于A 球开始运动时的高度(D)当支架从左向右返回摆动时,A 球一定能回到起始高度答案:BCD22.如图所示,一个粗细均匀的U 形管内装有同种液体,在管口右端盖板A 密闭,两液面的高度差为h,U 形管内液柱的总长度为4h.现拿去盖板,液体开始运动,当两液面高度相等时,右侧液面下降的速度为( ). (A)gh 21 (B)gh 41 (C)gh 61 (D)gh 81 答案:D23.如图所示,粗细均匀、全长为h 的铁链,对称地挂在轻小光滑的定滑轮上.受到微小扰动后,铁链从静止开始运动,当铁链脱离滑轮的瞬间,其速度大小为( ). (A)gh (B)gh 21 (C)2gh 21 (D)2gh答案:C24.长l 的线的一端系住质量为,的小球,另一端固定,使小球在竖直平面内以绳的固定点为圆心恰能作完整的圆周运动,卜列说法中正确的是( ).(A)小球、地球组成的系统机械能守恒(B)小球作匀速圆周运动(C)小球对绳拉力的最大值与最小值相差6mg(D)以最低点为参考平面,小球机械能的最小值为2mgl答案:AC25.质量m=5㎏的小球系于弹簧的一端,套在光滑竖直圆环上,弹簧的另一端固定在环上的A 点,环半径R=0.5m,弹簧原长l 0=R=0.5m.当球从图中位置C滑至最低点B 时,测得v A =3m/s,则在B 点时弹簧的弹性势能E P =____J.答案:1526.如图所示,小球质量为m,用长为l 的细绳悬挂在一枚细钉上,用一大小为F 的水平恒力拉球,至细绳偏转角度为θ(θ＜90°)时撤去F,如在运动中绳子始终处于伸直状态.求:(1)小球能上升的最大高度.(2)小球又回到最低点时,细绳上张力的大小.答案:(1)当θsin mg F ≤时,mg Flsin h θ=;当θ2sin 5mg F ≥时,h=2l(2)mg+2Fsinθ。

大学物理参考答案(白少民)第2章力学中的守恒定律

f = mg ( 4 + 0) = 4mg 与（1）中结果相同。， 2 （3）因为只有当 H 有足够的值，才能保证在圈顶时，物体具有一定的速度（动能），使得所需向心力大于物体的重力，而不致使物体掉下来。 2.15 如图 2.22 所示，一质量为 m = 0.10kg 的小球，系在绳的一端，放在倾角 α = 30o 的光滑斜面上，绳的另一端固定在斜面上的 O 点，绳长 0.2m，当小球在最低点 A 处，若在垂直于
向心力
F心 = m
2 υc = mg sin α(3 + 2 cos θ) l
它由重力分力和绳子的张力共同提供 F心 = −mg sin αcos θ + Tc
∴T
c
= F心 + mg sin αcos θ = 3mg sin α + 2mg sin αcos θ + mg sin αcos θ
(1 + cos θ) =1.47(1 + cos θ)N = 3mg sin α
第二章力学中的守恒定律 2.1 在下面两种情况中，合外力对物体作的功是否相同 ?(1)使物体匀速铅直地升高 h 。(2) 使物体匀速地在水平面上移动 h。如果物体是在人的作用下运动的，问在两种情况中对物体作的功是否相同? 答：合外力对物体做功不同。 2.2 A 和 B 是两个质量相同的小球，以相同的初速度分别沿着摩擦系数不同的平面滚动。其中 A 球先停止下来，B 球再过了一些时间才停止下来，并且走过的路程也较长，问摩擦力对这两个球所作的功是否相同? 答：摩檫力对两球做功相同。 2.3 有两个大小形状相同的弹簧：一个是铁做成的，另一个是铜做成的，已知铁制弹簧的倔强系数比铜大。 (1) 把它们拉长同样的距离，拉哪一个做功较大？ (2) 用同样的力来拉，拉哪一个做功较大？答：（1）拉铁的所做功较大；（2）拉铜的做功较大。 2.4 当你用双手去接住对方猛掷过来的球时，你用什么方法缓和球的冲力。答：手往回收，延长接球时间。 2.5 要把钉子钉在木板上，用手挥动铁锤对钉打击，钉就容易打进去。如果用铁锤紧压着钉，钉就很难被压进去，这现象如何解释? 答：前者动量变化大，从而冲量大，平均冲力也大。 2.6 "有两个球相向运动，碰撞后两球变为静止，在碰撞前两球各以一定的速度运动，即各具有一定的动量。由此可知，由这两个球组成的系统，在碰撞前的总动量不为零，但在碰撞后，两球的动量都为零，整个系统的总动量也为零。这样的结果不是和动量守恒相矛盾吗?" 指出上述讨论中的错误。答：上述说法是错误的，动能守恒是成立的。虽然碰前各自以一定的速度不为零，相应的动量也不为零，但动量是矢量，系统的总动量在碰前为 0，满足动量守恒定律。 2.7 试问：(1) 一个质点的动量等于零，其角动量是否一定等于零 ?一个质点的角动量等于零，其动量是否一定等于零? (2) 一个系统对某惯性系来说动量守恒，这是否意味着其角动量也守恒? 答：（1）一个质点的动量等于零，其角动量也一定为零；一个质点的角动量等于零，其动量不一定为零。（2）一个系统对某惯性系来说动量守恒，这并不意味其角动量也守恒。 * * * * * * 2 2.8 一蓄水池，面积为 S = 50m ，所蓄的水面比地面低 5.0m，水深 d=1.5m。用抽水机把这池里的水全部抽到地面上，问至少要作多少功？解：池中水的重力为 F = mg = ρsdg =1.0 ×10 3 ×50 ×1.5 ×10 = 7.5 ×10 5

专题9 动量守恒定律的应用(力学部分)(原卷版)

专题9 动量守恒定律的应用一、单选题1．如图所示，质量为m 的小车左端紧靠竖直墙壁但不固定，其左侧AB 部分为14光滑圆弧轨道，半径为R ，轨道最低点B 与水平粗糙轨道BC 相切，2BC R ，将质量也为m 的物块(可视为质点)从A 点无初速释放，只考虑物块与BC 间的摩擦，其动摩擦因数为23，其余一切摩擦不计，则物块相对BC 运动的位移大小为（）A ．34RB ．RC ．43RD ．2R2．如图所示 “牛顿摆”装置，5个完全相同的小钢球用轻绳悬挂在水平支架上，5根轻绳互相平行，5个钢球彼此紧密排列，球心等高．用1、2、3、4、5分别标记5个小钢球．当把小球1向左拉起一定高度，如图甲所示，然后由静止释放，在极短时间内经过小球间的相互碰撞，可观察到球5向右摆起，且达到的最大高度与球1的释放高度相同，如图乙所示．关于此实验，下列说法中正确的是（）A ．上述实验过程中，5个小球组成的系统机械能守恒，动量守恒B ．上述实验过程中，5个小球组成的系统机械能不守恒，动量不守恒C ．如果同时向左拉起小球1、2、3到相同高度（如图丙所示），同时由静止释放，经碰撞后，小球4、5一起向右摆起，且上升的最大高度高于小球1、2、3的释放高度D ．如果同时向左拉起小球1、2、3到相同高度（如图丙所示），同时由静止释放，经碰撞后，小球3、4、5一起向右摆起，且上升的最大高度与小球1、2、3的释放高度相同3．在光滑水平桌面上有两个相同的弹性小球A 、B 质量都为m ，现B 球静止，A 球向B 球运动，发生正碰．已知碰撞过程中总机械能守恒，两球压缩最紧时的弹性势能为E P ，则碰前A 球的速度等于A P E mB 2pE m C ．2P E mD ．22PE m4．如图所示，光滑的水平桌面上有一个内壁光滑的直线槽子，质量相等的A 、B 两球之间由一根长为L 且不可伸长的轻绳相连，A 球始终在槽内，其直径略小于槽的直径，B 球放在水平桌面上．开始时刻A 、B 两球的位置连线垂直于槽，相距2L ，某给B 球一个平行于槽的速度v 0，关于两球以后的运动，下列说法正确的是A ．绳子拉直前后，A 、B 两球组成的系统在平行于槽的方向动量守恒B ．绳子拉直后，A 、B 两球将以相同的速度平行于相的方向运动C ．绳子拉直的瞬间，B 球的机械能的减少量等于A 球机被能的增加量D ．绳子拉直的瞬间，B 球的机械能的减少量小于A 球机械能的增加量 5．质量为m 的箱子静止在光滑水平面上，箱子内侧的两壁间距为l ，另一质量也为m 且可视为质点的物体从箱子中央以v 0=2gl 的速度开始运动（g 为当地重力加速度），如图所示。

动量守恒定律作业

动量作业21. 如图所示，将质量为M1，半径为R 且内壁光滑的半圆槽置于光滑水平面上，左侧靠墙角，右侧靠一质量为M 2的物块．今让一质量为m 的小球自左侧槽口A 的正上方h高处从静止开始落下，与圆弧槽相切自A 点进入槽内，则以下结论中正确的是( )A ．小球在槽内运动的全过程中，小球与半圆槽在水平方向动量守恒B ．小球在槽内运动的全过程中，小球、半圆槽和物块组成的系统动量守恒C ．小球离开C 点以后，将做竖直上抛运动D ．槽将与墙不会再次接触【解析】解析①：小球从AB 的过程中，半圆槽对球的支持力沿半径方向指向圆心，而小球对半圆槽的压力方向相反指向左下方，因为有竖直墙挡住，所以半圆槽不会向左运动，可见，该过程中，小球与半圆槽在水平方向受到外力作用，动量并不守恒，而由小球、半圆槽和物块组成的系统动量也不守恒；从B →C 的过程中，小球对半圆槽的压力方向向右下方，所以半圆槽要向右推动物块一起运动，因而小球参与了两个运动：一个是沿半圆槽的圆周运动，另一个是与半圆槽一起向右运动，小球所受支持力方向与速度方向并不垂直，此过程中，因为有物块挡住，小球与半圆槽在水平方向动量并不守恒，在小球运动的全过程，水平方向动量也不守恒，选项A 、B 错误；当小球运动到C 点时，它的两个分运动的合速度方向并不是竖直向上，所以此后小球做斜上抛运动，即选项C 错误；因为全过程中，整个系统在水平方向上获得了水平向右的冲量，最终槽将与墙不会再次接触，选项D 正确．解析②：据题意，动力守恒的条件是系统不受外力或者所受外力之和为0，A 选项中，小球从A 到B 的过程有墙壁的作用，所以动量不守恒，A 、B 选项错误；小球从B 到C 过程，圆弧槽向右运动，小球离开时斜向上运动，所以C 选项错误；从小球第一次经过B 之后，圆弧槽将一直向右做变速运动，所以D 选项正确．【答案】D2. 如图所示，一根足够长的水平滑杆SS ′上套有一质量为m 的光滑金属圆环，在滑杆的正下方与其平行地放置一足够长的光滑水平的木制轨道PP ′，PP ′穿过金属环的圆心．现使质量为M 的条形磁铁以水平速度v 0沿木制轨道向右运动，则( )A ．磁铁穿过金属环后，两者将先、后停下来B ．磁铁将不会穿越滑环运动C ．磁铁与圆环的最终速度Mv 0M ＋mD ．整个过程最多能产生热量Mm 2(M ＋m )v 02 【解析】由于电磁感应现象，m 所受安培力阻碍磁铁对其的相对运动，安培力水平向右，m 做加速运动，而该安培力的反作用力作用于磁铁，磁铁做减速运动，最终两者达到共同速度．整个过程类似于碰撞，可以将力学中的子弹打击木块的模型迁移过来．根据动量守恒：Mv 0=(M +m )v 共，即v 共=Mv 0M ＋m；在此过程中损失的机械能全部转化为热能，Q =ΔE =－12(M +m )v 共2+12Mv 02=－12·M 2v 02M ＋m +12Mv 02=12·Mm M ＋m v 02．所以正确选项为B 、C 、D ．【答案】CD3. 如图所示，水平轻弹簧与物体A 和B 相连，放在光滑水平面上，处于静止状态，物体A 的质量为m ，物体B 的质量为M ，且M ＞m ．现用大小相等的水平恒力F 1、F 2拉A 和B ，从它们开始运动到弹簧第一次最长的过程中( )A ．因M ＞m ，所以B 的动量大于A 的动量 B ．A 的动能最大时，B 的动能也最大C ．F 1和F 2做的总功为零D ．弹簧第一次最长时A 和B 总动能最大【解析】由于系统受的外力和为零，系统的动量守恒，有mv 1－Mv 2=0，所以A 、B 动量大小相等．当A 的速度达到最大时，B 的速度也最大，所以A 的动能最大时，B 的动能也最大，故A 错误，B 正确．弹簧第一次最长时，A 、B 的速度都为零，D 错误．此过程中F 1和F 2均做正功，二者做的总功等于弹簧的弹性势能，C 错误．【答案】B4. 在光滑水平直线轨道上，有质量分别为2m 和m ，带电量分别为+q 、+2q 的A 、B 两小球，相距很远，相向运动. 某时刻v A =v ，v B =1.5v ，由于静电斥力作用，它们不会相碰. 下列判断正确的是( )A ．A 小球一直沿原方向运动，B 小球要反向运动 B ．A 、B 两小球都要反向运动，但B 小球先反向C ．两小球相距最近时，速度大小相等，方向相反D ．A 小球和B 小球的作用力始终做负功【解析】解析①：水平方向系统动量守恒，由完全非弹性碰撞的知识可知，当两球速度大小相等、方向相同时，系统损失机械能最大，两球相距最小，故C 错误；由题意可知，A 球动量大于B 球动量，因此系统动量水平向右，故B 球运动过程中将反向运动而A 球将一直沿原方向运动（或者根据牛顿第二定律分析，此时A 、B 速度大小一样，而B 的减速的加速度大，故B 先减为零，然后反向加速运动），因此静电斥力对B 球先做负功后做正功，故B 、D 错误，A 正确．故选A ．解析②：由于地面光滑，系统所受合外力为零，满足动量守恒条件，当两球速度相等，系统损失机械能最大，两球相距最近．水平方向系统动量守恒，由完全非弹性碰撞的知识可知，当两球速度相等时，两球相距最小，速度向右；由题意可知，A 球动量大于B 球动量，因此系统动量水平向右，故B 球运动过程中将反向运动而A 球将一直沿原方向运动，（或者根据牛顿第二定律分析，此时A 、B 速度大小一样，而B 的减速的加速度大，故B 先减为零，然后反向加速运动），因此静电斥力对B 球先做负功后做正功．【答案】A 5.在光滑水平面上有一平板车，车上站着一个人，人与车一起做匀速直线运动. 此时人手中拿着一个球，用如下两种方法将球水平抛出：一次沿车前进方向抛出，对球做功为W 1，所施冲量大小为I 1；另一次沿与车运动相反的方向抛出，对球做功为W 2，所施冲量大小为I 2. 若两次球离手时对地的速率相同，则比较两次抛球过程有( ) A ．W 1＝W 2，I 1＝I 2 B ．W 1＜W 2，I 1＞I 2 C ．W 1＝W 2，I 1＜I 2 D ．W 1＜W 2，I 1＜I 2 【答案】C 6.如图所示，质量M =1.99 kg 的木质小车静止在光滑水平面上，其左端板上固定一轻弹簧，弹簧右端靠放着一质量m =2 kg 的小物块，小物块左侧的小车表面光滑，而右侧的小车表面与小物块间动摩擦因数μ=0.2，现有质量m 0=0.01 kg 的子弹以v 0=400 m/s 的水平速度射入小车，取g =10 m/s 2，求： (1)小车在运动过程中，弹簧的弹性势能最大值； (2)为使小物体不从小车上掉下来，车表面粗糙部分至少为多长？【解答】(1)子弹刚停留在车内，木块还没有来得及动的时候，有 m 0v 0=(M +m 0)V 最终三者共速，有 m 0v 0=(m 0+M +m )v 根据机械能守恒，得 12(M +m 0)V 2=E p +12(M +m+m 0)v 2 解得E p =2 J (2)设木块在摩擦表面上的位移为s ，最终三者共速，有 μmgs =12(M +m 0)V 2－12(M +m+m 0)v 2=E p 解得s =E p μmg =0.5 m 7.如图所示，光滑水平面上有一小车B ，右端固定一个砂箱，砂箱左侧连着一水平轻弹簧，小车和砂箱的总质量为M ，车上放有一物块A ，质量也是M ，物块A 随小车以速度v 0向右匀速运动．物块A 与左侧的车面的动摩擦因数为μ，与右侧车面摩擦不计．车匀速运动时，距砂面H 高处有一质量为m 的泥球自由下落，恰好落在砂箱中，求： (1)小车在前进中，弹簧弹性势能的最大值； (2)为使物体A 不从小车上滑下，车面粗糙部分应多长？【解答】(1)泥球C 落入砂箱时，小车B 与泥球C 在水平方向动量守恒，设共同速度为v 1，根据动量守恒定律有： Mv 0＝(M ＋m )v 1 当A 、B 、C 三者取得共同速度时，弹性势能最大，设三者的共同速度为v 2，根据动量守恒定律有： Mv 0＋(M ＋m )v 1＝(2M ＋m )v 2 由泥球落入砂箱后至弹性势能最大中间过程的能量守恒有： E p m ＝12Mv 02＋12(M ＋m )v 12－12(2M ＋m )v 22 解得E p m ＝Mm 2v 022(M ＋m )(2M ＋m )． (2)弹簧再将物块与小车弹开后，A 与小车相对运动，为使A 不从小车上滑落，临界状态为A 滑到小车左端时取得共同速度，且共同速度与v 2相同。

力学的基本概念(四)角动量守恒定律习题及答案

第三章角动量守恒定律序号学号姓名专业、班级一选择题[ C ]1．关于刚体对轴的转动惯量，下列说法中正确的是 (A) 只取决于刚体的质量，与质量的空间分布和轴的位置无关。

(B) 取决于刚体的质量和质量的空间分布，与轴的位置无关。

[ B ]２．均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示。

今使棒从水平位置由静止开始自由下落，在棒摆动到竖直位置的过程中，下述说法哪一种是正确的?(A) 角速度从小到大，角加速度从大到小 ; (B) 角速度从小到大，角加速度从小到大 ; (C) 角速度从大到小，角加速度从大到小 ; (D) 角速度从大到小，角加速度从小到大。

[ B ]３．两个均质圆盘A 和B 密度分别为A ρ和B ρ，若A ρ>B ρ，但两圆盘质量与厚度相同，如两盘对通过盘心垂直于盘面轴的转动惯量各为A J 和B J ，则 (A) A J >B J (B) B J >A J(C) A J ＝B J(D) A J 、B J 哪个大，不能确定[ A ]４．有两个力作用在一个有固定转轴的刚体上：(1) 这两个力都平行于轴作用时，它们对轴的合力矩一定是零； (2) 这两个力都垂直于轴作用时，它们对轴的合力矩一定是零； (3) 当这两个力的合力为零时，它们对轴的合力矩也一定是零； (4) 当这两个力对轴的合力矩为零时，它们的合力也一定是零。

在上述说法中：(A) 只有(1)是正确的。

(B) (1)、(2)正确，(3)、(4)错误。

(D) (1)、(2)、(3)、(4)都正确。

[ A ]5．关于力矩有以下几种说法：(1) 对某个定轴而言，刚体的角动量的改变与内力矩有关。

(2) 作用力和反作用力对同一轴的力矩之和必为零。

力学练习题弹性碰撞与动量守恒的应用

力学练习题弹性碰撞与动量守恒的应用力学练习题：弹性碰撞与动量守恒的应用在力学领域中，弹性碰撞与动量守恒是两个重要的概念。

本文将通过一系列练习题来探讨这些概念的应用。

请注意，为了方便阅读，本文将分为三个部分：弹性碰撞问题、动量守恒问题和综合应用问题。

一、弹性碰撞问题1. 两个质量相同的小球A和B以相等的速度相向运动，并发生完全弹性碰撞，速度不变。

求碰撞前后小球的速度变化。

解析：根据动量守恒定律，碰撞前后系统的总动量保持不变。

由于小球A和B的质量相同，碰撞后它们的速度也应该相同。

2. 在水平桌面上，质量为m1的小球A以速度v1与质量为m2的小球B以速度v2相向运动，发生完全弹性碰撞。

求碰撞后两个小球的速度。

解析：根据动量守恒定律，碰撞前后系统的总动量保持不变。

设碰撞后小球A的速度为v'1，小球B的速度为v'2。

根据动量守恒定律可得：m1 * v1 + m2 * v2 = m1 * v'1 + m2 * v'2由于是完全弹性碰撞，动能守恒定律也成立。

根据动能守恒定律可得：(1/2) * m1 * v1^2 + (1/2) * m2 * v2^2 = (1/2) * m1 * v'1^2 + (1/2) * m2 * v'2^2解上述方程组即可得到碰撞后两个小球的速度。

二、动量守恒问题1. 一辆质量为M的火车以速度v1匀速行驶，在车厢内有一物体以速度v2相对于车厢静止。

物体受到一个作用力F，求物体离开火车后的速度。

解析：在火车内，火车和物体构成一个封闭系统，且没有外力做功。

根据动量守恒定律，系统的总动量保持不变。

设物体离开火车后的速度为v'，根据动量守恒定律可得：M * v1 + 0 = (M + m) * v'其中m为物体的质量。

解上述方程即可求得物体离开火车后的速度。

2. 一枪弹射出子弹，枪和子弹构成一个封闭系统，没有外力做功。

子弹的质量为m1，枪的质量为m2，子弹的初速度为v1，枪的初速度为v2，求子弹和枪的共同速度。

动量守恒定律的应用

动量守恒定律的应用动量守恒定律是力学中的一条基本定律，它表明在一个封闭系统中，当没有外力作用时，系统的总动量将保持不变。

这一定律在很多现实生活中都有广泛应用，例如运动中的碰撞、火箭发射等。

本文将围绕动量守恒定律的应用展开讨论。

首先，我们可以从日常生活中的交通事故中看到动量守恒定律的应用。

当两辆汽车碰撞时，根据动量守恒定律，碰撞前两车的总动量等于碰撞后两车的总动量。

在这个过程中，如果两车的质量和速度都已知，我们可以通过这个定律计算出碰撞后车辆的速度。

这充分体现了动量守恒定律在交通事故研究和车辆安全方面的重要作用。

除了交通事故，动量守恒定律在运动项目中也有广泛应用。

例如，击球运动中的棒球或高尔夫球击球过程。

当球棒或球杆撞击球体时，球体会产生一定的反作用力，而这个反作用力将导致球体的速度发生改变。

根据动量守恒定律，我们可以根据棒球或高尔夫球的质量和速度，计算出撞击球体后球体的速度和方向。

这种应用不仅仅是在运动技巧的强化上，对于杆头和球头的设计也有重要的指导意义。

动量守恒定律的应用还可以从宇宙航天工程中找到例证。

例如，在火箭发射过程中，除了引力外没有其他外力对火箭产生作用。

根据动量守恒定律，火箭燃料的喷射速度越快，火箭的速度也越快。

我们可以通过这一定律计算出火箭在不同阶段的速度和质量变化，从而精确控制火箭的发射轨道和目标飞行轨道。

在运动碰撞中，动量守恒定律也应用于弹道学的研究中。

例如，当子弹或炮弹射出时，根据动量守恒定律，我们可以通过子弹或炮弹的质量和速度，计算其射击目标后的速度和穿透力。

这在战争和安全领域具有重要意义，能够提供有效的伤害评估和防御策略。

动量守恒定律还可以应用于流体力学中的研究。

例如船舶的推进。

船舶在水中航行时，会通过喷水或螺旋桨的方式产生反作用力，从而推动船体前进。

根据动量守恒定律，我们可以计算出船舶的速度和推力大小，进而优化船体设计和推进系统，提高航行的效率。

总之，动量守恒定律在日常生活、运动项目、航天工程、爆炸研究、流体力学等领域的应用都是不可忽视的。