金钥匙学校2011年秋季初一数学期末大串讲
初一数学期末串讲讲义

初一数学期末串讲讲义1.(2007北京卷)3-的倒数是( ).A .13-B .13C .3-D .32.(2008北京卷)6-的绝对值等于 ( )A .6B .16C .16- D .6- 3.(2009北京卷)7的相反数是A.17B.7C.17- D.7- 4.有理数a 、b 、c 在数轴上的位置如图所示,下列结论正确的是 ( ) A. b a c >>B. b a c >->C. a c b >>D. ||b a c >->-b a 0 c5.根据数轴上给出的a 、b 、c 的条件化简b a c c b a c b a --++---+=6.计算:()232331112674⎡⎤⎛⎫--+-÷⨯- ⎪⎢⎥⎣⎦⎝⎭7.(2007北京卷)国家游泳中心——“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260 000平方米,将260 000用科学记数法表示应为( ) A .60.2610⨯ B .42610⨯C .62.610⨯D .52.610⨯8.(2008北京卷)截止到2008年5月19日,已有21 600名中外记者成为北京奥运会的注册记者,创历届奥运会之最.将21 600用科学记数法表示应为( ) A .50.21610⨯ B .321.610⨯ C .32.1610⨯ D .42.1610⨯9.(2009北京卷) 改革开放以来,我国国内生产总值由1978年的3645亿元增长到2008年的300670亿元。
将300670用科学记数法表示应为( ) A.60.3006710⨯ B.53.006710⨯ C.43.006710⨯ D.430.06710⨯ 10.下列说法正确 ( )A.近似数6百和近似数600的精确度是相同的B.近似数有两个有效数字C.数保留两个有效数字得近似数是0.07D.数精确到千分位得近似数是11.(2009太原)已知一个多项式与239x x +的和等于2341x x +-,则这个多项式是( )A .51x --B .51x +C .131x --D .131x + 12.(2009年衡阳)已知33-=-y x ,则y x 35+-的值是( ) A .0 B .2 C .5 D .813.(2007北京卷)若22(1)0m n ++-=,则2m n +的值为( ) A .4- B .1- C .0D .414.(2009年山西省)如图(1),把一个长为m 、宽为n 的长方形(m n >)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( ) A .2m n - B .m n - C .2mD .2n15.(2008西城二模)当矩形一角的平分线分矩形一边为1cm 和3cm 两部分时,则这个矩形的面积为42cm 或122cm .当矩形一角的平分线分矩形一边为1cm 和4cm 两部分时,则这个矩形的面积为52cm 或202cm . 根据以上情况,完成下面填空.(1)矩形一角的平分线分矩形一边为1cm 和5cm 两部分,这个矩形的面积为2cm 或 2cm .(2) 矩形一角的平分线分矩形一边为1cm 和ncm 两部分,则这个矩形的面积为2cm 或 2cm .(n 为正整数)16.(1)平面上有n 个点,其中任意三点都不共线,若过其中两点画一条直线,共可以画多少条?(2)若直线l 上有n 个点,则能形成多少条射线?多少条线段?(3)若在AOB ∠的内部作n 条射线1OC 、2OC 、…n OC ,则能形成多少个角?17.平面内两两相交的6条直线,其交点个数最少为m 个,最多为n 个,则n m +等于( )A 、12B 、16C 、20D 、以上都不对 18.解下列方程:(1) 5x +3=-7x +9 (2)37(1)7173x x +=-(3)334515x x -+=- (4)3221211245x x x +-+-=-m nnn (2)(1)19.(2008北京卷)列方程或方程组解应用题:京津城际铁路将于2008年8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米?20.(2009北京卷)北京市实施交通管理新措施以来,全市公共交通客运量显著增加.据统计,2008年10月11日到2009年2月28日期间,地面公交日均客运量与轨道交通日均客运量总和为1696万人次,地面公交日均客运量比轨道交通日均客运量的4倍少69万人次.在此期间,地面公交和轨道交通日均客运量各为多少万人次?21.(2008西城二模)用“&”定义新运算: 对于任意有理数a ,b 都有b a b a -=2&,如果()23&1&=x ,那么x 等于( ). A.1 B. 32 C. 1222.方程b ax =(a 、b 为常数)中(1)0≠a 时,它为一元一次方程,这时有唯一一解ab x =; (2)0=a 时,它不是一元一次方程,它的解分两种情况:①0=a ,0=b 时,00=x ,这时方程有无数多个解; ②0=a ,0≠b 时,b x =0,这时方程无解.运用以上知识解决下面问题:已知关于x 的方程()6612||3--=+x x a a x ,问当a 取何值时:(1)方程无解 (2)方程有无数多个解23.棱长为a的小正方体,摆放成如左下图所示的形状固定在地面上(1)摆放这个立体图形共需要个小正方体.(2)若对此图形的所有暴露面喷油漆,则油漆面的总面积是.(3)如果这是一个工厂加工的用于拼装的零件,则需要喷油漆的面积是.24.一个画家有14个边长为1m的正方体,他在地面上把它们摆成如右上图所示的形状,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积是_______25.(2008海淀一模)图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形,此时第七个图形中小正方体木块总数应是()(A)25 (B)66(C)91(D)120(1)(2)(3)26.把正方体的表面沿某些棱展开后成一个平面图形,请判断这个平面图形可以围成的正方体是()27.折成正方体后,与右图相同的是( )A 、B 、C 、D 、28.(2007西城一模)一个正方体的展开图如图所示,每一个面上都写有一个自然数并且相对两个面所写的两个数之和相等,那么=-+c b a 2( ) A. 40 B. 38 C. 36 D. 3429.(2008海淀二模)图1是一个正方体,把它按图2中所示方法切割,可以得到一个正六边形的截面,则下列各展开图中正确画出所有的切割线的是( ).30.(2009陕太原市)在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退.开始时骰子如图(1)那样摆放,朝上的点数是2;最后翻动到如图(2)所示的位置,此时骰子朝上的点数不可能...是下列数中的( ) A .5 B .4 C .3 D .1A BCACBB CAABCA BC图(1)图(2)31.(2007北京卷)右图所示是一个三棱柱纸盒,在下面四个图中,只有一个是这个纸盒的展开图,那么这个展开图是()A.B.C.D.32.(2009海淀一模)如图是画有一条对角线的平行四边形纸片ABCD,用此纸片可以围成一个无上下底面的三棱柱纸筒, 则所围成的三棱柱纸筒可能是()33.(2008北京卷)已知O为圆锥的顶点,M为圆锥底面圆上一点,点P在OM 上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如右图所示.若沿OM将圆锥侧面剪开并展平,所得侧面展开图是()34.请阅读下列语句:①射线AB与射线BA是两条相同的射线;②如果C点在线段EF上,那么EC<EF;⑥ 钝角大于直角,锐角小于直角; 其中正确的序号为 .35如果A 、B 、C 三点在同一直线上,A 到B 的距离是8厘米,B 到C 的距离是3厘米,那么A 、C 两点的距离是( )(A )11厘米 (B )5厘米 (C )5或11厘米(D )无法确定36.线段AB 的中点也是线段AC 的三等分点,如果AB =1cm ,那么BC = __________cm37.如图线段AB 和CD 的公共部分为BD ,且BD =31AB =51CD ,线段AB 、CD 的中点E 、F 的距离为6cm ,求AB 、CD 的长.38.计算(1)49°38′+66°22′ (2)180°-79°19′ (3)22°16′×5 (4)182°36′÷439.(1)6°18′36″=____________° (2)33.33°= ° ′ ″40.如果∠α=39°31′,∠α的余角∠β= ,∠α的补角∠γ= ,∠γ-∠β= 41.(1)从2点30分到2点45分,时针和分针各走了多少度? (2)8点30分时针分针成____度角(3)在两点到三点之间,什么时刻时针和分针重合?42.如果点O 在点A 的北偏西 40,在点B 的西南方向,则∠AOB =______43.如图,BD 平分∠ABC ,BE 分∠ABC 为2:5两部分,∠DBE = 21,求∠ABC 的度数.D CAE B44.已知AOC BOC ∠=∠21, 15=∠BOC ,求AOB ∠的度数 45.(2007北京卷)如图,90ACB ∠=°,DE 过点C 且平行于AB ,若35BCE ∠=°,则A ∠的度数为( ) A .35° B .45° C .55° D .65°46.(2007西城一模)如图,已知AB //CD ,直线MN 分别交AB 、CD 于点E 、F ,EG 平分∠BEF ,交CD 于点G ,若∠EFG =40°,则∠EGF 的度数是( )A. 90°B. 80°C. 70°D. 60°47.如左下图,把矩形ABCD 沿EF 对折后使两部分重合,若150∠=°,则AEF ∠=( )A .110°B .115°C .120°D .130°48.(2009年黄石)如右上图,1502110AB CD ∠=∠=∥,°,°,则3∠= . AB D C1 23 A BDC E49.如图,已知AB ∥CD ,36=∠A ,120=∠C ,则E F ∠-∠=________50.已知:如图,AB ∥CD ,求证:∠B+∠D+∠F=∠E+∠G51.如图,已知AB ∥CD ,ABE ∠和CDE ∠的平分线相交于F , 160=∠E ,求BFD ∠的度数52.(2009贺州)在直线AB 上任取一点O ,过点O 作射线OC 、OD ,使OC ⊥OD ,当∠AOC =30o 时,∠BOD 的度数是( ).A .60oB .120oC .60o 或 90oD .60o 或120o FEDC BA ABCDEF GWORD完整版----可编辑----教育资料分享----完整版学习资料分享----。
初一秋季第06讲(找规律的技巧)

,,它们是按一定规律排列的。
(0
,
ab≠
,,那么第
99a a +++
依次在射线上写出数字1,2,3,4,5
填整数之和都相等。
x=,第2015个格子中的数为_______;(1)可求得_______
()()()3323
112______
2222n n n n ++++===33+20______+=319++等于多少吗?并写出你是怎样得到的?²;3×5+1=16=4²;4×2) 1111⎛
⨯+ ⨯⎝
2.用水平线和竖直线将平面分成若干个边长为1,的小正方形格子,小正方形的顶点,叫做标点.以标点为顶点我们可以做三角形、四边形、五边形等多种多边形,它们都叫做格点多边形.设格点多边形的面积为S,它各边上格点的个数和为X,
(1)图中的格点多边形,其内部都只有一个格点,请你填写下表:
根据以上信息,当各边上格点的个数和为x时,则多边形的面积S=
(2)请你在下列方格中在画中一些格点多边形(至少画三个不同形式的),使这样的多边形内部都有而且只有2个格点.
(3)请你继续探索,当格点多边形内部有且只有n个格点时,猜想S与x有怎么样的关系。
观察下面的点阵和相应的等式,探究其中的规律:
)在④和⑤后面的横线上分别写出相应的等式:
1+3+5++19=
++-
(21)
n
++++。
101103199
(+n n n +=
)我们自上往下,在每个圆圈中按图左边这个圆圈中的数是 )求图4中所有圆圈中各数的绝对值之和.
个叠放图形中小正方体木块总数是个,第3个叠放图形中小正方体的木个.
中的几何体如下图所示那样组合在一起,请计算其表面积.。
著名机构七年级数学秋季班讲义第20讲:期末复习(二)
本学期一共学习了三章内容,分别是整式、分式、图形的运动.通过本讲内 容,对本学期所学内容进行全面复习.d 吃玉吉平专]知识结构江法]一戛节暨:辰年转又再至田]T=,L "北用座弓用的短三H 整幸法}工三二五方丽:公W 式法 斯三] {分M&J 二厘可以化成V-次右运h g 式方程分赤:找㈱]5F|旺市达至胃1 3m n y 1一,,,a 7 x y aA. 1个【解析】分式指分子分母均为整式,且分母中必须含有字母. 【总结】本题考查了分式的基本概念.【练习2】小马虎在下面的计算中只做对了一道题,他做对的题目是()2 2 .2 A .(a b ) ab c325C . aa2a-43B . 2 101 1023、26D . ( 2a ) 4a【难度】★ 【答案】D【解析】A 是完全平方公式, 【总结】本题考查了整式的基本运算.【练习3】分式工,彩,° 的最简公分母是()2x 3y 4xy选择题J ^-1七■一 年 接季【练习1】代数式:2,a b 2 a 2 2ab b 2 ; B 答案为1 ; C 不能运算.5【练习4】在下图右侧的四个三角形中,由4ABC既不能经过旋转也不能经过平移得到的三角形是(【难度】★【答案】B【解析】由图可以知道A、C、D都可由ABC经过旋转和平移得到,而B选项必须经过翻折才能和其重合. 【总结】本题主要考查了图形旋转和平移的特征.【练习5】下列图形中,是中心对称图形的是(【解析】如果把一个图形绕某一点旋转180后能与自身重合,这个图形就是中心对称图形.常见的中心对称图形有:线段、矩形、菱形、正方形、平行四边形、圆、边数为偶数的正多边形等.【总结】本题主要考查了中心对称图形的定义.【练习6】从甲到乙的图形变换,判断全正确的是()A. (1)翻折,(2)旋转,(3)平移B. (1)翻折,(2)平移,(3)旋转C.(1)平移,(2)翻折,(3)旋转D.(1)平移,(2)旋转,(3)翻折【难度】★【答案】A【解析】由图可知:(1)把甲翻折即可得到乙;(2)绕甲的直角顶点顺时针旋转90即可得到乙;(3)把甲先向右平移,再向上平移即可得到乙.【总结】本题考查了图形变换的三种方式.【练习71已知2x 5y 3,那么4x 32y的值为()A. 8 B . 9 C.8 D . 9 【难度】★★【答案】C【解析】已知:2x 5y 3,则4x 32y22x 25y22x 5y23 8.【总结】本题考查了同底数骞的运算的综合运用.【练习8】x y 0 ,则下列不等式错误的是()11 _ 1 1 一22 _ 2A.--B.xyC.xyD.xy【难度】★★【答案】A【解析】由x y 。
已知实数 满足 ,求 的
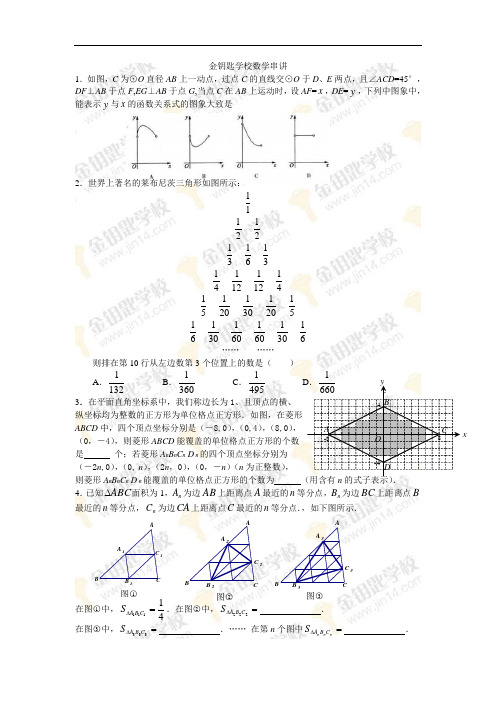
金钥匙学校数学串讲1.如图,C 为⊙O 直径AB 上一动点,过点C 的直线交⊙O 于D 、E 两点,且∠ACD =45°,DF ⊥AB 于点F ,EG ⊥AB 于点G ,当点C 在AB 上运动时,设AF =x ,DE =y ,下列中图象中,能表示y 与x 的函数关系式的图象大致是2.世界上著名的莱布尼茨三角形如图所示:111212131613141121121415120130120151613016016013016…… ……则排在第10行从左边数第3个位置上的数是( ) A .1132B .1360C .149513.在平面直角坐标系中,我们称边长为1、且顶点的横、 纵坐标均为整数的正方形为单位格点正方形.如图,在菱形ABCD 中,四个顶点坐标分别是(-8,0),(0,4),(8,0),(0,-4),则菱形ABCD 能覆盖的单位格点正方形的个数是 个;若菱形A n B n C n D n 的四个顶点坐标分别为(-2n ,0),(0, n ),(2n ,0),(0,-n )(n 为正整数), 则菱形A n B n C n D n 能覆盖的单位格点正方形的个数为 (用含有4.已知ABC ∆面积为1,n A 为边AB 上距离点A 最近的n 等分点,n B 为边BC 上距离点B 最近的n 等分点,n C 为边CA 上距离点C 最近的n 等分点.,如下图所示.在图○1中,41111=∆C B A S .在图○2中,=∆222C B A S .在图○3中,=∆333C B A S .…… 在第n 个图中=∆n n n C B A S .C 1B 1A 1C B A 图○1 C 2B 2A 2A C B 图○2 图○3 C 3B 3A 3A CB x5.已知实数x 满足233322-=+-+xx x x ,求x x 32+的值.6.阅读下列材料:小明遇到一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后,将三角形纸片①绕AB 的中点O 旋转至三角形纸片②处,依此方法继续操作,即可拼接成一个新的正方形DEFG . 请你参考小明的做法解决下列问题:(1)现有5个形状、大小相同的矩形纸片,排列形式如图3所示.请将其分割后拼接成一个平行四边形.要求:在图3中画出并 指明拼接成的平行四边形(画出一个符合条件的平行四边形即可);(2)如图4,在面积为2的平行四边形ABCD 中,点E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点,分别连结AF 、BG 、CH 、DE 得到一个新的平行四边形MNPQ 请在图4中探究平行四边形MNPQ 面积的大小(画图并直接写出结果).7.在△ABC 中, BC =a ,BC 边上的高h =a 2,沿图中线段DE 、CF 将△ABC 剪开,分成的三块图形恰能拼成正方形CFHG ,如图1所示.请你解决如下问题:已知:如图2,在△A ′B ′C ′中, B ′C ′=a ,B ′C ′边上的高h =a 21.请你设计两种不同的分割方法,将△A ′B ′C ′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.A ′B ′C ′图3A ′B ′C ′图4AGHED F C① ②③8.如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值;(3)点G 抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理由(请直接写出点的坐标,不要求写过程).9.问题:如图1,在等边三角形ABC 内有一点P ,且PA=2, PB=3, PC=1.求∠BPC 度数的大小和等边三角形ABC 的边长.李明同学的思路是:将△BPC 绕点B 顺时针旋转60°,画出旋转后的图形(如图2).连接PP′,可得△P′PC 是等边三角形,而△PP′A 又是直角三角形(由勾股定理的逆定理可证).所以∠AP′C=150°,而∠BPC=∠AP′C =150°.进而求出等边△ABC 的边长为7.问题得到解决.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD 内有一点P ,且PA=5,BP=2,PC=1.求∠BPC 度数的大小和正方形ABCD 的边长.10.若P 为A B C △所在平面上一点,且120APB BPC C PA ∠=∠=∠=°,则点P 叫做图3图 1图2A B C △的费马点.(1)若点P 为锐角A B C △的费马点,且60ABC PA PC ∠===°,3,4,则P B 的值为________;(2)如图,在锐角A B C △外侧作等边A C B △′连结B B ′. 求证:B B ′过A B C △的费马点P ,且B B ′=P A P B P C ++.11.已知:ABC ∆是等边三角形,延长BA 至点D ,延长BC 至点E ,使BE AD =. 求证:DE DC =.12.已知:A O B △中,2A B O B ==,C O D △中,3C D O C ==,ABO D C O =∠∠. 连接A D 、B C ,点M 、N 、P 分别为O A 、O D 、B C 的中点.PNMDABOPNM DCBAO图1 图2(1) 如图1,若A 、O 、C 三点在同一直线上,且60ABO =∠,则P M N △的形状是________________,此时A DB C=________;(2) 如图2,若A 、O 、C 三点在同一直线上,且2A B O α=∠,证明P M N B A O △∽△,并计算A DB C的值(用含α的式子表示);(3) 在图2中,固定A O B △,将C O D △绕点O 旋转,直接写出PM 的最大值.13.如图,正方形ABCD 的对角线AC 与BD 相交于点M ,正方形MNPQ 与正方形ABCDA CB B ' 第(25)题E D CBAED C BAD CBAD C BA全等,射线MN 与MQ 不过A 、B 、C 、D 四点且分别交ABCD 的边于E 、F 两点. (1)求证:ME=MF ;(2)若将原题中的正方形改为矩形,且24B C A B ==,其他条件不变,探索线段ME 与线段MF 的数量关系.14.已知点A 、B 分别是x 轴、y 轴上的动点,点C 、D 是某个函数图像上的点,当四边形ABCD (A 、B 、C 、D 各点依次排列)为正方形时,称这个正方形为此函数图像的伴侣正方形.例如:如图,正方形ABCD 是一次函数1y x =+图像的其中一个伴侣正方形. (1)若某函数是一次函数1y x =+,求它的图像的所有伴侣正方形的边长; (2)若某函数是反比例函数(0)k y k x=>,他的图像的伴侣正方形为ABCD ,点D (2,m )(m <2)在反比例函数图像上,求m 的值及反比例函数解析式;(3)若某函数是二次函数2(0)y ax c a =+≠,它的图像的伴侣正方形为ABCD ,C 、D 中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标 # .,写出符合题意的其中一条抛物线解析式 # .,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数? # ..(本小题只需直接写出答案)15.如图,已知点A 的坐标是(-1,0),点B 的坐标是(9,0),以AB 为直径作⊙O′,F EQPNMDCB AABCDM交y 轴的负半轴于点C ,连接AC 、BC ,过A 、B 、C 三点作抛物线.(1)求抛物线的解析式;(2)点E 是AC 延长线上一点,∠BCE 的平分线CD 交⊙O′于点D ,连结BD ,求直线BD 的解析式;(3)在(2)的条件下,抛物线上是否存在点P ,使得∠PDB =∠CBD?如果存在,请求出点P 的坐标;如果不存在,请说明理由.16.把两块全等的直角三角形ABC 和D E F 叠放在一起,使三角板D E F 的锐角顶点D 与三角板ABC 的斜边中点O 重合,其中90ABC DEF ∠=∠= ,45C F ∠=∠= ,4AB D E ==,把三角板ABC 固定不动,让三角板D E F 绕点O 旋转,设射线D E 与射线A B 相交于点P ,射线D F 与线段B C 相交于点Q .(1)如图1,当射线D F 经过点B ,即点Q 与点B 重合时,易证APD CDQ △∽△.此时,AP CQ =· .(2)将三角板D E F 由图1所示的位置绕点O 沿逆时针方向旋转,设旋转角为α.其中090α<<,问AP CQ ·的值是否改变?说明你的理由.(3)在(2)的条件下,设CQ x =,两块三角板重叠面积为y ,求y 与x 的函数关系式.(图2,图3供解题用)BED(O)CQFMBE P AQD(O)D(O)B (Q )CFEAP图1图2图3。
七年级秋季班-第19讲:期末复习(一)-教师版
本学期一共学习了三章内容,分别是整式、分式、图形的运动.通过本讲内容,对本学期所学内容进行全面复习.期末复习(一)内容分析知识结构【练习1】下列各式中,与32x y -是同类项的是().A .33xyB .312yxC .3a b -D .32x yz【难度】★ 【答案】B【解析】同类项是指(1)所含字母相同;(2)相同字母的指数相同. 【总结】本题考查了同类项的定义.【练习2】如果分式212x x +-有意义,那么x 应满足的条件是( ).A .12x ≠-B .2x ≠C .122x x ≠-≠且D .122x x >≠且【难度】★ 【答案】B 【解析】分式BA有意义指的是分母0≠B ,即202x x -≠≠,. 【总结】本题考查了分式有意义的条件.【练习3】若()222(2)a b a b x -=+-,则x 等于(). A .2abB .4abC .8abD .8ab -【难度】★ 【答案】C【解析】()()ab b a b a x 82222=--+=.【总结】本题考查了完全平方公式的公式变形.选择题【练习4】下列图形中是旋转对称图形但不是中心对称图形的是().ABCD【难度】★ 【答案】A【解析】中心对称图形是指把一个图形绕一点旋转180度后能与自身重合;旋转对称图形是 指把一个图形绕一定点旋转一定角度(小于周角)后能与自身重合. 【总结】本题考查了旋转对称图形和中心对称图形的概念.【练习5】下列等式中,从左到右的变形是因式分解的是().A .253(5)3x x x x -+=-+B .()()225310x x x x -+=+-C .()22234129x x x +=++D .243(1)(3)x x x x -+=--【难度】★ 【答案】D【解析】因式分解是指把一个多项式化为几个整式的乘积的形式. 【总结】本题考查了因式分解的概念.【练习6】()()3243a a -÷的计算结果是()A .2aB .6aC .6a -D .2a -【难度】★★ 【答案】C【解析】()()32431266a a a a a -÷=-÷=-,同底数幂相除,底数不变,指数相减.【总结】本题考查了幂的乘方及同底数幂相除运算.【练习7】下列格式中,等式成立的是().A.x y y xy x x y--=--B.22x y y xy x y x--=--C.x y x yy x y x---=-++D.x y x yy x y x--+=--【难度】★★【答案】A【解析】A中()()yxxyyxxyxyyx--=----=--正确.【总结】本题考查了分式的基本性质的运用.【练习8】如果将分式22x yx y-+中的x和y都扩大到原来的3倍,那么分式的值().A.扩大到原来的3倍B.扩大到原来的9倍C.缩小到原来的13D.不变【难度】★★【答案】A【解析】x和y都扩大到原来的3倍,即为x3和y3;则()()()()yxyxyxyxyxyxyxyx+-=+-=+-=+-2222222233933993333,所以原分式的值扩大到原来的3倍.【总结】本题考查了分式的基本性质的运用.【练习9】小敏和小明练习打字,小敏比小明每分钟多打25个字,完成1000字文稿小敏比小明少用2分钟,设小明每分钟打x个字,则可列方程().A.10001000225x x-=+B.10001000225x x-=+C.10001000225x x-=-D.10001000225x x-=-【难度】★★【答案】A【解析】解:设小明每分钟打x个字,则小敏每分钟打()25+x个字,由题意得:10001000225x x-=+,故选A.【总结】本题考查了列分式方程解应用题.【练习10】二次三项式25166m m -+分解因式的结果如下:①1()(1)6m m --;②11()()23m m --;③11(21)()23m m --;④1(21)(31)6m m --.其中正确的个数为( )A .1个B .2个C .3个D .4个【难度】★★ 【答案】C【解析】①错;②③④正确.【总结】本题考查了因式分解的十字相乘法.【练习11】如果41()m x y --能被25()m x y +-整除,则m 可取( )A .1、2、3B .任何整数C .不小于3的整数D .大于3的整数【难度】★★★ 【答案】C 【解析】解:()()()625214-+--=-÷-m m m y x y x y x ;则062≥-m ,3≥m .【总结】本题考查了数的整除及同底数幂的除法.【练习12】若x y 、为实数,则使分式2221x x y -+有意义的是().A .x y =B .x y 、不同时为零C .x y ≠D .x y =但x y 、均不为0【难度】★★★ 【答案】B【解析】使分式有意义,则分母022≠+y x ,即就是x y 、不同时为零. 【总结】本题考查了分式有意义的条件.C【练习13】如图,一长为4cm ,宽为3cm 的长方形木板(其中5BA cm =),在桌面上作无滑动的顺时针方向的翻滚,木板上的点A 位置变化为12A A A →→,其中第二次翻滚时被 桌面上一小木块挡住,使木板和桌面成30︒角,则点A 翻滚到2A 位置时共走过路径长 为().A .10cmB .4cmC .72cm πD .52cm π【难度】★★★ 【答案】C【解析】解:点A 以点B 为旋转中心,以1ABA ∠为旋转角,顺时针旋转得到1A ;同理2A 是 由1A 以点C 为旋转中心,以21CA A ∠为旋转角,顺时针旋转得到. 1121906053ABA ACA AB cm CA cm ∠=∠===,,,∴点A 翻滚到2A 位置时共走过路径长为:()cm l 27180360180590πππ=⋅⋅+⋅⋅=. 【总结】本题考查了旋转的性质及弧长公式的运用.【练习14】将232322x x y xy y -+-按字母x 降幂排列_______________. 【难度】★【答案】322322x y x xy y -++-.【解析】①看清那一个字母;②看清升降幂. 【总结】本题考查了按某以字母的降幂排列.A 2A 1BA填空题【练习15】实验证明:钢轨温度每变化1C ︒,每一米钢轨就伸缩0.0000118米,如果一个月中气温上下相差10C ︒,那么对于100米长的铁路, 最长可伸长_______________米.(用 科学记数法表示) 【难度】★【答案】2-1018.1⨯.【解析】解:2-1018.10118.00000118.010100⨯==⨯⨯(米);绝对值小于1的正数也可以利用科学计数法表示,一般形式为()10110n a a -⨯≤<. 【总结】本题考查了科学计数法负整数指数幂的表示.【练习16】在线段、角、正三角形、长方形、正方形、等腰梯形和圆中,共有 个为旋转对称图形. 【难度】★ 【答案】5【解析】其中线段、正三角形、长方形、正方形、圆是旋转对称图形. 【总结】本题考查了常见的旋转对称图形.【练习17】当x =___________时,方程22969x x x --+的值为零.【难度】★★ 【答案】-3.【解析】当分子092=-x ,即3±=x 时;当3=x 代入分母0962=+-x x ,分式无意义; 当3-=x 代入分母0962≠+-x x ,分式值为0.所以3-=x 时,原分式方程值为零. 【总结】本题考查了分式值为零的条件.【练习18】计算:222222223242a ab b a b a ab b a b ab -+-÷=-+-_______________.【难度】★★【答案】ba ab2+.【解析】()()()()()()b a b a b a ab b a b a b a ab b a b a b ab a b ab a 2224223222222222-+-⋅---=--÷+-+-b a ab2+=. 【总结】本题考查了分式的乘除运算及分式的化简.【练习19】当m =________时,方程111x mx x +=--会产生增根. 【难度】★★ 【答案】1【解析】由题意得方程的增根是01=-x ,即1=x ;方程111-=+-x mx x 两边同时乘以()1-x ,得m x x =-+1,即12-=x m . 将1=x 代入,得1=m ,所以,当1=m 时,原方程有增根.【总结】本题考查了分式方程产生增根的条件及对方程的增根的理解.【练习20】因式分解:(1)244m n mn m +--=_______________;(2)214733x x --=________________;(3)222222()4a b c b c ---=________________. 【难度】★ 【答案】见解析.【解析】(1)()()()()()()44444422--=---=-+-=--+m n m n m n m m m n mn m m mn n m ; (2)()()()3731214317343122+-=--=--x x x x x x ;(3)()()()bc c b a bc c b ac b c b a 224222222222222---+--=---()[]()[]2222c b a c b a +---=()()()()c b a c b a c b a c b a --+++--+=.【总结】本题考查了因式分解的方法与技巧.FEDC BAP ‘PCBA【练习21】如图,4个大小一样的正三角形拼在一起,将DEF ∆绕着点F 旋转与ABF ∆重合, 那么最小旋转角度为_________. 【难度】★★ 【答案】 180.【解析】DEF ∆与ABF ∆重合,即点D 落在点A 上, 点E 落在点B 上,即至少旋转了 180. 【总结】本题考查了旋转的性质及旋转角的大小判定.【练习22】如图,P 是正三角形ABC 内的一点,将三角形ABP 绕点B 顺时针方向旋转能与 三角形'CBP 重合,则'_______PBP ∠=. 【难度】★★ 【答案】60.【解析】由旋转角都相等可知, 60=∠='∠ABC P PB . 【总结】本题考查了旋转的性质和运用.【练习23】若14a b b c -=+=-,,则代数式2ac bc ab a --+的值是________. 【难度】★★ 【答案】-3.【解析】()()()()a c b a b a a b a c a ab bc ac ++=-+-=+--2;又由1=-b a ,所以原式c a +=;341-=-=++-=+c b b a c a ,故原式的值为-3. 【总结】本题考查了因式分解的技巧及整体代入求值的思想.【练习24】小杰从镜子中看到电子钟的示数是 ,那么此时实际时间是____________. 【难度】★★ 【答案】21:05.【解析】镜子中看到的数字与实际数字是关于镜面垂直的线对称. 【总结】本题考查了镜面对称问题.【练习25】若关于m 的方程121m x -=-的解为正数,则m 的取值范围是_________. 【难度】★★【答案】11≠->m m 且【解析】解:原方程整理得:221-=-x m ,则21+=m x ; 原方程有解,01≠-∴x ,即121≠+m ,故1≠m , 又 方程的解为正数,021>+∴m ,故1->m ; 所以11≠->m m 且.【总结】本题考查了分式方程的解及分式方程有意义的综合运用.【练习26】如果关于x 的多项式214x k ++是完全平方式,那么_______k =. 【难度】★★★ 【答案】444x x ±;.【解析】分三种情况:①当1和24x 都为平方项时,x k 4±=;②当24x 为中间项时,44x k =; ③当1为中间项时,2161x k =,此时代数式不是多项式,故不满足. 【总结】本题考查了完全平方公式的应用.【练习27】若6556x y ==,,则用x y 、的代数式来表示3030=________. 【难度】★★★ 【答案】65y x .【解析】()()()6565563030303065656530y x =⨯=⨯=⨯=.【总结】本题考查了幂的乘方及积的乘方的运用.【练习28】已知117131521⨯=,则3211713152013_______⨯-⨯=. 【难度】★★★ 【答案】169.【解析】322211713152013152113152013169⨯-⨯=⨯-⨯=. 【总结】本题考查了同底数幂运算及乘法分配率的综合运用.【练习29】下图是某同学在沙滩上涌石子摆成的“小房子”观察图形的变化规律,写出第n 个小房子用了__________块石子.【难度】★★★ 【答案】()n n 42+.【解析】解:该小房子用的石子数可以分两部分找规律:屋顶:第一个是1,第二个是3,第三个是5,...以此类推,第n 个是12-n ; 下边:第一个是4,第二个是9,第三个是16,...以此类推,第n 个是()21+n .所以共有()n n n n 412122+=-++.【总结】本题考查了用字母表示数观察规律题.【练习30】化简:()()23225x x y -⋅.【难度】★【答案】72200x y -.【解析】()()2323427225825200x x y x x y x y -⋅=-⋅=-.【总结】本题考查了积的乘方及同底数幂的运算.【练习31】因式分解:229446x y y x ---. 【难度】★【答案】()()22323--+y x y x .【解析】()()()x y y x y x x y y x 3222323644922+--+=---()()22323--+=y x y x . 【总结】本题考查了因式分解中分组分解法.【练习32】小明今年12岁,小明的妈妈今年36岁.几年后小明的年龄是他妈妈年龄的23? 【难度】★ 【答案】36.【解析】解:设x 年后小明年龄是他妈妈年龄的32, 由题意得:()x x +=+363212 解得:36=x所以36年后小明年龄是他妈妈年龄的32. 【总结】本题考查了利用列方程解决实际问题.解答题【练习33】先化简,后求值:2112111x x x x x ⎛⎫⎛⎫+-÷- ⎪ ⎪-+-⎝⎭⎝⎭,其中12x =. 【难度】★【答案】47-.【解析】()()()()()()()()()⎥⎦⎤⎢⎣⎡-+--÷⎥⎦⎤⎢⎣⎡+---+++-=⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛+--+11111111121-1111222x x x x x x x x x x x x x x x x ()()()()()21111222--+⋅+-=x x x x x x x 222-=x x . 当21=x 时,原式212427122⨯==-⎛⎫- ⎪⎝⎭. 【总结】本题考查了分式的化简求值问题,注意要先化简后求值.【练习34】计算:211x x x ---.【难度】★【答案】11-x .【解析】()()111111122-=-----=---x x x x x x x x x . 【总结】本题考查了分式的加减运算,要注意先通分再计算.【练习35】解方程: (1)2215124x x x --=+-;(2)22122563x x xx x x x --=--+-. 【难度】★【答案】(1)47-=x ;(2)1=x .【解析】解:(1)分式两边同乘24x -,得()415222-=--x x ,化简得:47x -=,解得:47-=x .经检验:47-=x 是原分式方程的解,所以47-=x 是原分式方程的解;(2)方程两边同乘(2)(3)x x --,得:()()()22132-=---x x x x x 解得:1=x ,经检验:1=x 是原分式方程的解, 所以原分式方程的解是1=x .【总结】本题考查了分式方程的解法步骤,注意要检验根.【练习36】已知31x y xy +==-,,(1)求22x y +的值;(2)求2()x y -的值. 【难度】★★【答案】(1)11;(2)13.【解析】(1)()()1112322222=-⨯-=-+=+xy y x y x ; (2)()()()131434222=-⨯-=-+=-xy y x y x .【总结】本题考查了完全平方公式的变形及计算.【练习37】计算:()()1112a a b a b b a ----+-. 【难度】★★【答案】aba +【解析】()()()()ab a b a a b a a b a b b a a a b b a b a a +=--=-+-=-+----2221211. 【总结】本题考查了负指数幂及分式的加减运算.【练习38】已知n 为自然数,且23nx =,求()4233143n n x x ⎛⎫⎡⎤-÷ ⎪⎢⎥⎣⎦⎝⎭的值. 【难度】★★【答案】121.【解析】 32=nx, ∴()()42333126231111144338132432412n n n n n x x x x x ⎛⎫⎡⎤-÷=÷==⨯= ⎪⎢⎥⎣⎦⎝⎭. 【总结】本题考查了幂的乘方及积的乘方法则的综合运用.【练习39】已知3m a =,2n a =,m 、n 是正整数且m n >. 求下列各式的值:①m n a +;②32m n a -. 【难度】★★ 【答案】①a 3;②274. 【解析】解:①2326m n m a a a +=⋅=⨯=;②()()32323227324m n m n a a a -=÷=÷=. 【总结】本题考查了同底数幂运算法则的运用.【练习40】比较554433345---,,的大小. 【难度】★★【答案】335544-534--<<.【解析】解:()11115115-55-24313133⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛==;()11114114-44-25614144⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==; ()11113113-33-12515155⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==;111111125124312561⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛ ; 335544-534--<<∴.【总结】本题考查了负整数指数幂的大小比较.【练习41】已知:()13200a a -+=≠,把11222a a a --÷-化简后求值. 【难度】★★ 【答案】23-.【解析】解:()aa a a a a a a a a 1222212122121=--=-⋅--=-÷--, 由已知得:123a -=-,即321-=a ;则原式321-==a .【总结】本题考查了分式的运算及代数求值.【练习42】已知两个分式:A =244x -,B =1122x x++-,其中2x ≠且2x ≠-.下面有三个 结论:①A =B ;②A 、B 互为倒数;③A 、B 互为相反数.请问哪个结论正确? 为什么? 【难度】★★ 【答案】③. 【解析】解:()()224442-+=-=x x x A ,()()22421212121-+-=--+=-++=x x x x x x B ; 0=+∴B A ,即A 、B 互为相反数. 【总结】本题考查了分式的化简及运算.【练习43】已知412x y xy +=-=-,,求1111y x x y +++++的值. 【难度】★★【答案】1534-【解析】解:原式()()()()()1212111112222++++++++=+++++=y x xy y y x x x y y x()()()12222++++++-+=y x xy y x xy y x ,当412x y xy +=-=-,时,原式24248234124115+-+==---+.【总结】本题考查了分式的混合运算及整体代入求值的思想运用.【练习44】已知115x y +=,求2322x xy yx xy y-+++的值. 【难度】★★ 【答案】1. 【解析】解:原式()()xyy x xy y x 232++-+=,511=+y x ,5=+∴xyyx ,即xy y x 5=+, ∴原式1777310==-=xyxyxy xy xy .【总结】本题考查了分式化简运算及代入求值的思想运用.【练习45】某班部分同学同学准备新年期间去博物馆参观,按原预定人数估计,共需费用300元,后因人数增加到原来的2倍,可享受优惠,只需480元,而参加的每位同学所分摊的费用比原来估计所需费用少4元,原来预定人数是多少? 【难度】★★ 【答案】15人.【解析】解:设原来预定人数为x 人,则48043002=⎪⎭⎫⎝⎛-x x ,解得:15=x .经检验:15=x 为原分式方程的解. 所以原来预定人数为15人.【总结】本题考查了列分式方程解应用题,注意要进行检验.【练习46】已知230x y z -+=,3260x y z --=,0xyz ≠,求2222222x y z x y z+++-的值. 【难度】★★【答案】2013.【解析】将z 看作已知数,求出x 和y ,代入原式计算, 由23032600x y z x y z xyz -+=--=≠,,得到, ⎩⎨⎧=--=-z y x z y x 62332,解得:⎩⎨⎧==z y z x 34,则原式2013932916222222=-+++=zz z z z z . 【总结】本题考查了分式方程的化简求值.【练习47】(1)如图所示的两个图形成中心对称,你能找到对称中心吗?(2)先将方格纸中的图形向右平移3格,然后再向下平移2格.【难度】★★ 【答案】 【解析】(1)所以点O 为所求.(2)【总结】本题考查了中心对称及图形的平移.【练习48】画出三角形ABC 关于直线MN 的轴对称的三角形. 【难度】★★ 【答案】见解析 【解析】如图111C B A 为所求.【总结】本题考查了成轴对称图形的画法.【练习49】图B C D 、、是用两个如图A 所示的直角三角形拼得的新图形,其中是中心对称 图形的是______________;是轴对称的图形是______________.(A ) (B ) (C ) (D ) 【难度】★★ 【答案】D ;C .【解析】中心对称图形是指把一个图形绕一点旋转180度后能与自身重合;轴对称图形是 在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形. 【总结】本题考查了中心对称图形及轴对称图形的概念.【练习50】分解因式:()()()11224x x x x -++-. 【难度】★★★【答案】()()()3242+-++x x x x【解析】()()()()()()2421124211-+-+=-++-x x x x x x x x ()()24222--++=x x x x ()()242222-+-+=x x x x ()()2246x x x x =+++- ()()()2423x x x x =++-+【总结】本题考查了因式分解的整体换元思想,注意分解要彻底.【练习51】已知多项式22642050x x y y -+-+,求此多项式取最小值时x y 、的值,并求出 此最小值. 【难度】★★★ 【答案】532x y ==,;此时最小值为16. 【解析】 1625204965020462222++-++-=+-+-y y x x y y x x()()1652322+-+-=y x ,且 ()()2230250x y -≥-≥,,∴()()161652322≥+-+-y x ,原多项式的最小值为16,此时532x y ==,. 【总结】本题考查了完全平方公式的运用,注意配方思想的运用.【练习52】解方程:232133648x x -+-+-=. 【难度】★★★【答案】23-=x .【解析】解:648331232-=-+-+x x ,即()648133212-=-+x ,所以412-3813==+x , 所以214x -+= ,解得:23-=x .【总结】本题考查了同底数幂的运用.【练习53】已知1998a b c +=+=+,求代数式222()()()b a c b c a -+-+-的值. 【难度】★★★ 【答案】222.【解析】解:由8919+=+=+c b a ,得:10111b a c b c a -=-=-=,,, 所以原式22211110222=++=.【总结】本题考查了等式的变形及整体代入求值的运用.【练习54】试判断22221111(1)(1)(1)(1)234n ----的值与12的大小关系,并证明你的结论. 【难度】★★★【答案】见解析.【解析】解:222211111111.......12342n ⎛⎫⎛⎫⎛⎫⎛⎫----- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 111111111111111.....112233442n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+- ⎪⎪⎪⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 2111 (45)4334322321-+⨯-⨯⨯⨯⨯⨯⨯⨯=n n n n2121-+=n n021212121>=-+=n n ;所以222211111111.......12342n ⎛⎫⎛⎫⎛⎫⎛⎫----> ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.【总结】本题考查了作差法比较大小及平方差公式的运用.【练习55】阅读下列材料:(1)用作差可以比较两数的大小,即:若0A B ->,则A B >;(2)平方式具有非负性,即()20a b ±≥.请根据材料信息,比较2231A a b a =+++,225912B a b a =+-+的大小.【难度】★★★【答案】B A <.【解析】解: ()()1295132222+-+-+++=-a b a a b a B A111242-+-=a a ()2322---=a ;∵()0322≥-a , ()0322≤--∴a ,即()223220a ---≤-<;0<-∴B A ,即B A <.【总结】本题考查了利用作差法比较两数的大小以及配完全平方的运用.【练习56】如图,将六个正方形无缝拼接在一起构成一个长方形,其中最小的一个正方形边 长为1,求拼成的长方形面积.【难度】★★★【答案】143.【解析】解:设右下角两个相等的小正方形边长为x .由题意得:3212+++=++x x x x解得:4=x即长方形长为13,宽为11,所以面积为1431113=⨯.【总结】 本题考查了字母表示数的应用.【练习57】用四块如图1所示正方形瓷砖拼成一个新的正方形,请你在图2、图3、图4中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.【难度】★★【答案】见解析【解析】【总结】本题考查了中心对称图形及轴对称图形的性质.图4 图3 图2 图1BAa【练习58】如图,在a 上找到M 、N 两点,且10MN =,M 在N 的左边,使四边形ABMN的周长最短.【难度】★★★ 【答案】见解析 【解析】过点A 作关于直线a 的对称点A ',过点B 作 a BD 直线//,使得10=BD ,连接D A '交直线a 于N 在直线a 上截取10=NM ,则四边形ABMN 的周长最短.【总结】本题考查了点的对称及两点之间线段最短的应用.。
初一数学期末总复习

初一数学期末总复习 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN精锐教育学科教师辅导讲义讲义编号_AB CEF ABC DF EO图 8图 9 4. 如图9,AB=CD ,AD=BC ,O 为BD 中点,过O 点作直线与DA 、BC 延长线交于E 、F ,若9. 如图AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则()A. ∠1=∠EFDB. BE=ECC. BF=DF=CDD. FD∥BC10.下列说法正确是()A . 三边对应平行的两个三角形是全等三角形B . 有一边相等,其余两边对应平行的两个三角形是全等三角形C . 有一边重合,其余两边对应平行的两个三角形是全等三角形D. 有三个角对应相等的两个三角形是全等三角形11.已知:如图,O为AB中点,BD⊥CD,AC⊥CD,OE⊥CD,则下列结论不一定成立的是()A. CE=EDB. OC=ODC. ∠ACO=∠ODBD. OE=1/2CD12.如图,已知在△ABC中,AB=AC,D为BC上一点,BF=CD,CE=BD,那么∠EDF等于( )A..90°-∠AB. 90°-21∠A C. 180°-∠A D. 45°-21∠A1.在中,,CD是的平分线,求证:BC=AD+ACB CAD2.已知,如图,在中,D是BC边的中点,E是AD上一点,BE=AC,BE的延长线交AC于点F.求证:.EB CADF3.如图,等腰中,,的平分线交AC于D,过C作BD的垂线交BD的延长线于E。
求证:BD =2CE.DBCA E4.如图,在中,D 是BC 边的中点,交的平分线于E ,交AB 于点F ,交AC 的延长线于点G 。
求证:BF =CG 。
BC AED GF5.如图,已知∆ABC 为等边三角形,延长BC 到D ,延长BA 到E ,并且使AE =BD ,连结CE 、DE 。
求证:EC =EDEBDA C三.回顾总结 四.课后作业 一.填空题⒈ 一个三角形的三个内角的度数的比为1:2:3,则这个三角形是______三角形. ⒉ 一个等腰三角形的两边长分别是3 cm 和6 cm ,则它的周长是_____cm. ⒊ 在∆ABC 中,∠A =30︒,∠B =2∠C ,则∠C =______度,∠B =______度. ⒋ 已知如图18,AB ∥CD ,则∠α=______度.⒌如果一个等腰三角形的顶角是底角的4倍,那么顶角的度数是_____度.二、选择题⒈一个三角形的三边长分别是3,4,x,则x的取值范围是()A.x>3B.x>4C.3<x<4D.1<x<7⒉已知:∆ABC中,∠C=80︒,∠A-∠B=40︒,则∠B的度数是()A.20︒B.30︒C.40︒D.60︒⒊在等腰∆ABC中,AB=AC,BD平分∠ABC交AC于D,∠CDB=150︒,则∠A=()A.130︒B.140︒C.150︒D.160︒⒋下面四个结论中,正确的是()A. 三角形的三个内角中最多有一个锐角B. 等腰三角形的底角一定大于顶角C. 钝角三角形最多有一个锐角D. 三角形的三条内角平分线都在三角形内1∠B,∠C=50︒,则∠BAC的度数是()5.如图,∆ABC中,D是BC上一点,且BA=BD,∠DAC=2A.60︒B.90︒C.120︒D.80︒。
111111 2011年七年级(下)数学期末试卷(含答案)

B ′C ′D ′O ′A ′ODC BA(第5题图)2010—2011学年度下学期七年级期末考试数学试卷题 号 一二三总 分累 分 人得 分卷首语:没有比人更高的山,没有比脚更长的路,亲爱的同学请相信自己,沉着应答,你一定能愉快地完成这次测试之旅,祝你成功! 注意:本试卷共3页,25个小题,总分为120分,考试时间为120分钟.答题时用书写蓝色、黑色字迹的钢笔或圆珠笔. 一、选择题(本大题共8小题,每小题3分,共24分) 1.由四舍五入得到近似数3.00万是 ( )A .精确到万位,有l 个有效数字B .精确到个位,有l 个有效数字C .精确到百分位,有3个有效数字D .精确到百位,有3个有效数字2. 长度分别为3cm ,5cm ,7cm ,9cm 的四根木棒,能搭成(首尾连结)三角形的个数为( )A.1B.2C. 3D.43.室内墙壁上挂一平面镜,小明站在平面镜前看到他背后墙上时钟的示数在镜中如图所示,则这时的实际时间应是 ( )A .3:40B .8:20C .3:2D .4:204.用四舍五入法保留两个有效数字,得到近似数3.0×104的是( ) A .29400 B .29500 C .30725 D .30820 5.已知M 是一个关于未知数x 的五次多项式,N 是一个关于未知数x 的三次多项式,则M -N 是一个五次多项式的概率为( ) A .14 B .12 C .34D .16.如左图,小亮在操场上玩,一段时间内沿M→A→B→M 的路径匀速散步,•能近似刻画小亮离出发点M 的距离y 与时间x 之间关系的图象是右图中的( )7.请仔细观察用直尺和圆规.....作一个角∠A ′O ′B ′等于已知角∠AOB 的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A ′O ′B ′=∠AOB 的依据是( ) A .SAS B .ASA C .AAS D .SSS 8.如图,ABCDE是封闭折线,则∠A +∠B +∠C +∠D +∠E 为( )A.180°B.270°C.360°D.540°二、填空题(本大题共8小题,每小题3分,共24分)学校 菏泽开发区 姓名 班级 考号…………………………………………………装………………订………………线………………………………………………………(1)ABCE D9.根①②③这一天中2时至14④这一天中只有14时至2410.(2﹡3)(2◎3)=(22+32)(2×2×3)=156,则[2﹡(11应为三角形.12不会做,于是随意选了一个答案(是.13.若229a ka++14.如图,两直线a、b被第三条直线∠2=130°,则直线a、b15实际时间应该是_____.16.方格除颜色外完全相同),302112(20053)()33--++--()()()()1x5x13x13x12x2-+-+--,再选取一个你喜欢的数代替x,并求原代数式的值.(8分)在正方形网格内,小格的顶点叫做格点。
著名机构七年级数学秋季拓展班讲义-分式专题-教师版
教师姓名 冯娜娜 学生姓名 年 级 初一 上课时间 单击此处输入日期。
学 科 数学 课题名称 分式专题1、分式定义:形如A B (A 、B 都是整式,且B 中含有字母,B≠0)的式子叫做分式,整式和分式统称有理式.2、分式有意义的条件:分母0≠时,分式有意义.分母= 0时,分式无意义.3、分式的值为0的条件:00=≠,分子分母.4、分式基本性质:分式的分子、分母都乘以或除以一个不为零的整式,分式的值不变.这一性质用式子表示为: B A =M B M A ⨯⨯,B A =MB M A ÷÷(M ≠0). 分式专题【习题1】 下列分式运算,结果正确的是( )A 、 n m mn n m =⋅3454 B 、 bc ad d c b a =⋅ C 、 22224)2(b a a b a a -=- D 、 33343)43(y x y x =【答案】A【习题2】 要使分式22222)(y x ay ax y a x a y x ++⋅--的值等于5,则a 的值是( ) A 、5 B 、5- C 、51 D 、51- 【答案】C【习题3】 分式325x y xy-中的字母x ,y 都扩大为原来的4倍,则分式的值( ) A 、不变 B 、扩大为原来的4倍C 、扩大为原来的8倍D 、缩小为原来的14 【答案】D【习题4】若分式x -51与x322-的值互为相反数,则x =( ) A 、-2.4 B 、125 C 、-8 D 、2.4 【答案】D【习题5】 下列各式从左到右的变形正确的是( )A 、122122x y x y x y x y --=++ B 、0.220.22a b a b a b a b ++=++。
著名机构七年级数学秋季班讲义第一学期期末试卷1(教师)

第14题七年级数学第一学期期末试卷(1)(时间90分钟 满分100分)一、填空题(本大题共16题,每题2分,满分32分) 1. 计算:=32)(b a 36b a . 2. 计算:2246y x y x ÷=24y x .3. “5·12汶川大地震”发生后,中央电视台于2008年5月18日举办了《爱的奉献》晚会,共募集善款约1 514 000 000元,这个数用科学记数法表示是910514.1⨯元. 4. 计算:)3()1215(22334a b a b a -÷-=23245ab b a +-.5. 分解因式:652--a a =()()16+-a a .6.222)221()4(241y x y xy x -=+-7. 由公式am t t Q =-21,求得amQt t -=12. 8. 当x ≠ 2 时,分式2-x x有意义. 9. 计算:2222ab bb a a -+-=b a +1. 10. 如果分式522-+x x 的值为1,那么=x 7 . 11. 将代数式12372--c b a 表示成只含有正整数指数幂的形式为c a b 3272.12. 已知:如图,在正方形ABCD 中,点E 在边BC 上,将△DCE 绕点D 按顺时针方向旋转,与△DAF 重合,那么旋转角等于 90 度. 13. 在所学过的图形中,请你写出一个是旋转对称而不是中心对称的图形.这个图形的名称是: 等边三角形 (答案不唯一) .14. 如图,一块含有60°角(∠BCA =60°)的直角三角板ABC ,在水 平的桌面上绕C 点按顺时针方向旋转到A’B’C 的位置,那么旋转角 是 120 度.ABC DEF (第12题图)15. 如图,把图中的某两个..小方格涂上阴影,使整个图形是以虚线为 对称轴的轴对称图形.16. 下面是用棋子摆成的“上”字:第一个“上”字需用6枚棋子,第二个“上”字需用10枚棋子,第三个“上”字需用14枚棋子,如果按照这样的规律继续摆下去,那么第n 个“上”字需用()22+n 枚棋子. 二、选择题(本大题4题,每题2分,满分8分)17. 下列等式中,从左到右的变形是因式分解的是( D ) A 、253(5)3x x x x -+=-+; B 、2(2)(5)310x x x x -+=+-; C 、22(23)4129x x x +=++;D 、243(1)(3)x x x x -+=--.18. 化简ab b a b a b a --++----1111的结果是( B )A 、0B 、224b a a -C 、224b a b -D 、222ba a-19. 下列说法中正确的是( D ) ① 中心对称图形肯定是旋转对称图形② 关于某一直线对称的两个图形叫做轴对称图形 ③ 圆有无数条对称轴,它的每一条直径都是它的对称轴④ 平行四边形是中心对称图形,它只有一个对称中心,就是两条对角线的交点 ⑤ 等边三角形既是中心对称,又是轴对称A 、①②④B 、③④C 、①③⑤D 、①④20. 在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失( C ) A 、顺时针旋转90°,向下平移; B 、逆时针旋转90°,向下平移; C 、顺时针旋转90°,向右平移; D 、逆时针旋转90°,向右平移.三、计算题(本大题共4分,每题5分,满分20分) 21.xy y x y x y x ----+-+2122解:原式=022.)()(22ba a a ab b b a --÷--+ 解:原式=ba -23.()()1111----+÷-y x y x 解:原式=12+x24. 2111224x x x -⎛⎫+÷⎪--⎝⎭ 解:原式=yx xy +-四、在有理数范围内分解因式(本大题共2题,每题6分,满分12分) 25.361324-+-a a 解:原式()()()()3322-+-+-=a a a a26.xy y x 844122+--解:原式()()y x y x 221221+--+=五、画图题(本题满分6分)27.如图是某设计师设计的图案的一部分,请你帮他完成余下的工作: (1)画出四边形OACB 关于直线l 的轴对称图形OA 1C 1B 1;(2)将四边形OACB 绕点O 顺时针...旋转ο120,画出旋转后的图形OA 2C 2B 2.六、解答题(本大题共3分,28题7分,29题7分,30题8分,满分22分)28.如图,已知R t △ABC 中,∠C=90°,BC=4,AC=4,现将△ABC 沿CB 方向平移到'''C B A ∆的位置,若平移距离为3.(1)求△ABC 与'''C B A ∆的重叠部分的面积;(2)若平移距离为x (0≤x ≤4),求△ABC 与△A’B’C’的重叠部分的面积y ,则y 与x 有怎样关系式.解:(1)211121=⨯⨯=S(2)()842142122+-=-=x x x y29.如图,已知等腰直角∆ACB 的边AC=BC=a ,等腰直角∆BED 的边BE=DE=b ,且b a <,点C 、B 、E 在一条直线上,联结AD . (1)求ABD ∆的面积;(2)如果点P 是线段CE 的中点,联结AP 、DP 得到APD ∆,求APD ∆的面积. (以上结果先用含a 、b 代数式表示,后化简)解:(1)ab b a b a S ABD =--+=∆2222121)(21 (2)221221)(212ba b b a a b a S APD +⋅-+⋅-+=∆ =22111424a ab b ++30.如图,在长方形ABCD 中,AB=8cm ,BC =10cm ,现将长方形ABCD 向右平移x cm ,再向下平移)1(+x cm 后到长方形A'B'C'D' 的位置,(1)用x 的代数式表示长方形ABCD 与长方形A'B'C'D' 的重叠部分的面积,这时x 应满足怎样的条件?(2)用x 的代数式表示六边形ABB'C'D'D (阴影部分)的面积.解:(1)()707017)18(-102≤≤+-=--=x x x x x S )(重 (2)9018)1()18)(10(+=+-+++=x x x x x S 阴。
著名机构七年级数学秋季班讲义期末复习资料

七年级数学上期末复习资料第九章 整式1. 整式⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧数次数:次数最高项的次项数:多项式和次数:所有字母的指数系数:字母因数单项式 2. 同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项,几个常数项也是同类项.3.整式的加减:先去括号,再合并同类项.4.整式的乘法:(1)幂的运算:n m n m a a a +=⋅;mn n m a a =)(;n n n b a ab =)((2)乘法公式:单项式乘以单项式;单项式乘以多项式;多项式乘以多项式 平方差公式: 22))((b a b a b a -=-+完全平方公式:222()2a b a ab b +=++(1)222()2a b a b ab →+=+-222()2a b a ab b -=-+(2)22222a b a ab b →+=-+(3)常用公式变形:xy y x y x 4)()(22+-=+ 211222-⎪⎭⎫ ⎝⎛+=+x x x x 5.因式分解:把一个多项式化为几个整式的积的形式叫做因式分解;(1)提公因式法(2)公式法:22()()a b a b a b -=+-222)(2b a b ab a ±=+±))((2233b ab a b a b a +-+=+))((2233b ab a b a b a ++-=-(3)十字相乘法:))(()(2q x p x pq x q p x ++=+++(4)分组分解法:适合四项及以上的多项式6.整式的除法:(1)幂的运算:m n m n÷=a a a-(2)01(0)=≠a a(3)单项式除以单项式,多项式除以单项式。
著名机构七年级数学秋季拓展班讲义期末复习(二)-教师版
教师姓名冯娜娜学生姓名年级初一上课时间单击此处输入日期。
学科数学课题名称期末复习(二)期末复习(二)C '‘BAC 'B '‘A 'C【例1】 代数式:1a ,37m n +,y x y -,12a+,224a b ab+-中分式有( )A .1个B .2个C .3个D .4个【答案】C【例2】 一小包柠檬茶冲剂,用235克水可冲泡成浓度为6%的饮料,求这包柠檬茶冲剂多 少克?若设这包柠檬茶冲剂有x 克,则得到的方程( )A .235x =6%B .235xx =+6%C .235x +=(16%)+D .235x x+=16%+ 【答案】B【例3】 小明出门前从镜子中看到墙上的时钟正好如图所示,他出门不到一小时后回到家发现该时钟的分钟正好转了180°,那么他出门后到家的时间是 ( ) A 、3:00B 、3:30C 、9:30D 、10:00【答案】D【例4】 在WLZXCYNLJ 这几个字母中,中心对称图形有___________个. 【答案】3【例5】 如图,将腰长为1的等腰直角ABC ∆沿直线翻转,则直角顶点C 走过的路径长为______________.【答案】π23.【例6】 当x =________时,代数式2x xx-的值等于0.【答案】1.【例7】 当______k =时,关于x 的方程1322k x x x--=---有增根. 【答案】1.【例8】 如果32y x =,则2x yx+=______________.【答案】4.【例9】已知:如图,在正方形ABCD中,点E在边BC上,将DCE∆绕点D按顺时针方向旋转,与DAF∆重合,那么旋转角等于_________度.【答案】ο90.【例10】如图,一块含有60︒角(60BCA∠=︒)的直角三角板ABC,在水平的桌面上绕C点按顺时针方向旋转到''A B C的位置,那么旋转角是________度.【答案】ο120.【例11】若2210a a+-=,则22_______a a-+=.【答案】6【例12】已知21525x-=,则15_______x=.【答案】51±.【例13】下面是用棋子摆成的“上”字:第一个“上”字需用6枚棋子,第二个“上”字需用10枚棋子,第三个“上”字需用14枚棋子,如果按照这样的规律继续摆下去,那么第n个“上”字需用枚棋子.【答案】24+n.【例14】如图,已知正方形ABCD的边长为8,M在DC上,且2DM=,N是AC上的一个动点,则DN MN+的最小值是____________.【答案】10【例15】因式分解:()()222812x x x x+-++.CBB'AA'BAMDCNABCDA′B′C′D′【例25】 如图,在长方形ABCD 中,8AB cm =,10BC cm =,现将长方形向右平 移xcm ,再向下平移()1x cm +后到长方形''''A B C D 的位置,(1)用x 的代数式表示长方形ABCD 与长方形A B C D ''''的重叠部分的面积,这时应满 足怎样的条件?(2)用的代数式表示六边形'''ABB C D D (阴影部分)的面积.【答案】(1)70<≤x ;(2)()29018cm x +=.【例26】 设为正整数,求证:11111335(21)(21)2n n +++<⨯⨯-+L . 【答案】()()2112121 (5)31311-+-++⨯+⨯n n21121121...7151513131121-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=n n 11112212n ⎛⎫=-- ⎪+⎝⎭=142n -+, ∵为正整数,∴1042n -<+;故原不等式得证. 【例27】 如图,已知等腰直角三角形ACB 的边AC =BC =a ,等腰直角三角形BED 的 边 BE = DE =b ,且a b <,点C 、B 、E 放置在一条直线上,联结AD . (1)求三角形ABD 的面积;(2)如果点P 是线段CE 的中点,联结AP 、DP 得到三角形APD ,求三角形APD 的面积; (3)(2)中的三角形APD 与三角形ABD 面积那个较大?大多少? (结果都可用、代数式表示,并化简) 【答案】.(1)BED ACB ACED ABD S S S S ∆∆∆--=梯形 ()DE BE BC AC CE DE AC ⋅-⋅-⋅+=212121ABCD x x n n a b ADBCa abb()222111222a b a b =+--ab =;(2)PED ACP ACED APD S S S S ∆∆∆--=梯形()DE PE CP AC CE DE AC ⋅-⋅-⋅+=212121()()()21111122222a b a a b b a b =+-⋅+-⋅+()214a b =+;(3)ABD APD S S ∆∆>, ∵()()()222211120444APD ABD S S a b ab a ab b a b -=+-=-+=->V V , ∴ABD APD S S ∆∆>.【习题1】小马虎在下面的计算中只做对了一道题,他做对的题目是 ( )A .222()a b a b +=+B .432101102-⨯⨯⨯=C .3252a a a +=D .326(2)4a a -=【答案】D 【习题2】分式2y x ,23x y,14xy 的最简公分母是( )A .26xyB .224xyC .212xyD .12xy【答案】C【习题3】在下图右侧的四个三角形中,由ABC △既不能经过旋转也不能经过平 移得到的三角形是( )BC【答案】B【习题4】下列图形中,是中心对称图形的是( )【答案】D【习题5】从甲到乙的图形变换,判断全正确的是 ( )A .(1)翻折,(2)旋转,(3)平移 B .(1)翻折,(2)平移,(3)旋转 C .(1)平移,(2)翻折,(3)旋转 D .(1)平移,(2)旋转,(3)翻折 【答案】A【习题6】已知253x y -=,那么432x y -÷的值为()A .8B .9C .8-D .9-【答案】C 【习题7】0x y >>,则下列不等式错误的是()A .11x y> B .11x y --< C .22x y > D .22x y --<【答案】A【习题8】 因式分解:221________4a ab b ++=.【答案】221⎪⎭⎫ ⎝⎛+b a .【习题9】 用科学记数表示0.000025_________=. 【答案】5-105.2⨯.正三角形等腰梯形正五边形正六边形A CDB(1)甲 乙 甲 乙乙甲(2)(3)。
七年级下册数学期末复习专题1省公开课获奖课件市赛课比赛一等奖课件

技能训练
一. a 2的平方根是 3, 3 b 2,则a b
。
3. 81的平方根是 a, 3 b 2,则a b
。
. 4.已知:a 1 a b 2 0,则a2012 b2013的值是
.
5. 15的整数部分是
; 15的小数部分是
25a 5b c 60.
三.不等式(组)旳解法
解一元一次不等式 4 x 3 x 2 ,并把 它旳解集在数轴上表达5 出来. 2
解:去分母:8x 30 (5 x 2) 去括号:8x 30 5x 10 移项:8x 5x 30 10 合并同类项:3x 20 系数化为1:x 20 3
例题:用代入法解下列二元一次方程组:
3s t 5 ,① s 2t 15 ;②
解:由①得 t 5 3s ③
代入②得 s 2(5 3s) 15
s 1
把 s 1 代入③,得 t 8
ts
1, 8.
例题 用代入法解下列二元一次方程组:
(2)
3x 4 y 16, ① 5x 6 y 33. ②
9.解下列不等式,并在数轴上表达解集:
(1) 2 x > 2x 1 (2)x x 2≥1 4x
2
3
2
3
(3)1 3x 1 1 2x (4)x 3 x 1 < 0
2
3
25
领略
利用口诀拟定下列不等式组旳解集:
(1)
x x
3, 7;
(2)
x x
3, 1;
(3) xx
1, 5;
(4) xx
解:由①得 x 1 (16 4 y) ③ 3
解得 y 1 2
代入③,得 x 6
金钥匙学校2011年秋季初一数学期末大串讲张

初 一 期 末 复 习一. 有理数 (一)选择题1.中国月球探测工程“嫦娥一号”卫星发射成功.已知地球距离月球表面384000千米,那么这个距离用科学记数法(保留三个有效数字)表示应为 ( ) .A .3.84×104千米B .3.84×105千米C .3.84×106千米D .38.4×104千米 2.对于以下几种说法,其中正确的说法个数是( ).①平方等于本身的数是1 ; ②任何一个有理数加上它的相反数都等于0; ③如果|a|=|b|,那么a=b ; ④两个负数相加一定等于负数;⑤立方等于本身的数是0和1 ; ⑥有理数的平方是非负数; ⑦绝对值等于本身的数是正数; ⑧任何有理数的平方是正数; ⑨两个数比较,绝对值大的反而小; ⑩任何一个整数的绝对值都是自然数 A .3个B .2个C .1个D .0个3.若a 、b 为有理数,a>0,b<0,且│a │<│b │,那么a ,b ,—a ,—b 的大小关系是( ) A.b< —a< —b<a B.b< —b< —a<a C.b< —a< a<—b D.—a< —b < b <a 4.下列各数互为相反数的是( )A.—32与23B.32与(—2)3C.(—3)2与—32D.—32与—(—3)25.当0<x<1时,x 2,x ,1x的大小关系是( ) A 、x 2<x <1x B 、1x <x 2<x C 、x <1x < x 2 D 、x <x 2<1x6. 一个数在数轴上的对应点与它的相反数在数轴上的对应点的距离是5个单位长度,那么这个数是( ) A .5或-5 B .5522-或 C .552-或 D .552-或 7. 若x+|x|=0,则x 一定是 ( )A 、正数B 、负数C 、正数或零D 、负数或零 8. 一根1m 长的小棒,第一次截去它的13,第二次截去剩下的13,如此截下去,第五次后剩下的小棒的长度是 ( )A.51()3m B.51[1()]3m - C .52()3m D 52[1()]3m - (二)填空题1.已知∣a-1∣与(b+2)2互为相反数,则(a+b)2007+a2008的值 .2.有理数a 、b 、c 在数轴上对应的点分别是A 、B 、C ,其位置如图所示,试化简a b c a b c c ++-++-= .3. 若2x =,29y =,且x y >,则x y +=___________.12<<-x 时,=--+12x x __________.4.若a 、b 是互为相反数,c 的绝对值为2,m 与n 互为倒数,则mn c cb a 422001-++ 的值是 。
著名机构七年级数学秋季班讲义整式的乘法拓展(教师)

第3课时 整式的乘法(拓展)1. 现将一多项式[(17x 2-3x +4)-(ax 2+bx +c )],除以(5x +6)后,得商式为(2x +1),余式为0。
求a -b -c =( D )A .3B .23C .25D .29 解析:(5x +6) (2x +1)=10 x 2+17x +6;[(17x 2-3x +4)-(ax 2+bx +c )]= (17-a )x 2-(3+b )x +4-c则a =7 b =-20 c =-2,a -b -c =292. 观察下列算式:12=2,22=4,32=8,42=16,52=32,62=64,72=128,82=256,……根据其规律可知108的末位数是 ( B )A .2B .4C .6D .8 解析:因为108=(23)10=302,观察上述算式,其末尾数字是2、4、8、6、2、4、8、6……渐次循环下去,所以302的指数30=28+2,其末位数为4.3.(22+1)(24+1)(28+1)(216+1)(232+1)+1的个位数是( C )A .4B .5C .6D . 8 解析:已知 24+1=16+1 ; 28+1=256+1216+1=2562+1 ; 232+1=2564+1……末位都是7,则(24+1)(28+1)(216+1)(232+1)的末位必为1,且(22+1)=5 所以原式的末位数定为6.4. 已知552=a ,443=b ,334=c , 则a 、b 、c 、的大小关系为:( D )A .c b a >>B .b c a >>C .c a b >>D .a c b >> 解析:552=a ,334=c =266 则 a c >。
排除法,只能选D5. 已知221a b +=,1c 22=+d ,0ac bd +=,求证:0ab cd +=解析:∵221a b += ∴221a b =-又0ac bd += 即ac bd =- ∴2222a c b d =∴2222(1)b c b d -= 整理得:2222()0c b c d -+= ∴22c b = ∴22222()2ab cd a b c d abcd +=++=22222a c b d abcd ++=2()ac bd +=0∴0ab cd +=6. 把一根长64cm 的铁丝截成两段,再把每一段折成正方形,这两个正方形面积的差为322cm ,求这两段铁丝的长。
金钥匙学校(东区)初三年级数学入学测试1月2

金钥匙学校2009—2010学年度入学测试初三数学班级_________姓名_________学号__________一、选择题:(本题共32分,每题4分)在下列各题的四个备选答案中,有且只有一个是正确的. 请将正确选项前的字母填在表格中相应的位置.题号 1 2 3 4 5 6 7 8 答案1.4的平方根等于A .±2B . -2C . 2D . 162.据报道,在“十一五”期间,我国民用航天工作排在首位的大事是做好月球探测工程的研制工作,确保2007年飞行成功.已知月球与地球的距离约为384000km ,这个距离用科学记数法表示为 A .310384⨯km B .4104.38⨯km C .41084.3⨯km D .51084.3⨯km 3.在函数21-=x y 中,自变量x 的取值范围是A. 0≠xB. 2≠xC. x >2D. 2-≠x4.在△ABC 中,∠C=90°,BC=3,AB=5,则下列结论正确的是A .4sin 5A =B .3cos 4A =C .3sin 5A =D .4tan 3A =5.估算243+的值( )A .在5和6之间B .在6和7之间C .在7和8之间D .在8和9之间 6、已知在ABC∆中,A ∠、B ∠都是锐角,231sin cos 022A B ⎛⎫-+-= ⎪ ⎪⎝⎭,则C ∠的度数是A.30° B.45° C.60° D.90°7.从1,2,3,4,5五个数中任意取出2个数做加法,其和为偶数的概率是( ) A .49B .35C .25D .128.如图,四边形ABCD 、A 1B 1BA 、…、A 5B 5B 4A 4都是边长为1的小正方形. 已知∠ACB=α,∠A 1CB 1=1α,…,∠A 5CB 5=5α. 则54211tan tan tan tan tan tan αααααα⋅++⋅+⋅ 的值为A. 1B.5C.45 D. 56二、填空题:(本题共16分,每题4分)9. 把3222a ab a b +-分解因式的结果是 .10.已知圆心在y 轴上的两圆相交于A (y x +2,-2)和B (4,y x 2+)两点,那么y x +=________.11.用“¤”定义一种运算:对于任意实数m 、n 和抛物线2ax y =,当2ax y =¤(m ,n )后都可得到n m x a y +-=2)(.例如:当23x y =¤(2,4)后得到4)2(32+-=x y .当函数2x y =¤(1,n )后得到了新A 2B 2B 5A 5B 4B 3A 4A 3A 1B 1DC BA 11题函数的图象(如图),则n= .12.小明把8个棱长为1分米的正方体摆在课桌上成如图形式,然后把露出 的表面都涂上颜色,则被他图上颜色部分的面积为_________分米2. 三、解答题:(本题共18分,每题6分) 13.化简:()()234226123x x xx-+-÷ 14.解分式方程:23222x x x -=+-.15.已知2a+b -1=0,求代数式22()(1)()aa b a b a b-+÷-+的值.四、解答题(本题共18分)16.(6分)小刚想给小东打电话,但忘了电话号码中的一位数字,只记得号码是185□9456(□表示忘记的数字). (1)若小刚从0至9的自然数中随机选取一个数放在□位置,求他拨对小东电话号码的概率; (2)若□位置的数字是不等式组2110142x x x ->⎧⎪⎨+⎪⎩,≤的整数解,求□可能表示的数字. (3) 在(2)的条件下,若规定小东八位电话号码的奇数位是奇数,偶数位是偶数,则小刚拨对小东电话号码的概率是多少? (注:小刚知道(2)中不等式组的整数解.)17.(6分)已知:如图,在Rt ABC △中,90ACB ∠=,4AC =,BC =,以AC 为直径的O 交AB 于点D ,点E 是BC 的中点,连结OD ,OB 、DE 交于点F . (1)求证:DE 是O 的切线; (2)求EF :FD 的值.E ABPCD18.(6分)如图,梯形ABCD 中,AD ∥BC ,∠ABC=90°,AD=9,BC=12,AB=a ,在线段BC 上取一点P ,连结DP ,作射线PE ⊥DP ,PE 与直线..AB 交于点E. (1)试确定CP=3时,点E 的位置;(2)若设CP=x ,BE=y ,试写出y 关于自变量x 的函数关系式;(3)若在线段BC 上只找到唯一一点P ,使上述作法得到的点E 与点A 重合,试求出此时a 的值.五、解答题(本题共16分)19.(8分)在平面直角坐标系xOy 中,抛物线2y mx n =++经过(02)P A ,两点.(1)求此抛物线的解析式;(2)设抛物线的顶点为B ,将直线AB 沿y 轴向下平移两个单位得到直线l ,直线l 与抛物线的对称轴交于C 点,求直线l 的解析式;(3)在(2)的条件下,求到直线OB OC BC ,,距离相等的点的坐标.20、(8分)在平面直角坐标系xOy 中,已知直线y=-33x+332交x 轴于点C,交y 轴于点A.等腰直角三角板OBD 的顶点D 与点C 重合,如图16-①所示.把三角板绕着点O顺时针旋转,旋转角度为)1800(︒<<︒αα,使B点恰好落在AC上的B'处,如图16-②所示.(1) 求图16-①中的点B 的坐标;(2) 求α的值;(3) 若二次函数y=mx2+3x的图象经过(1)中的点B ,判断点B'是否在这条抛物线上,并说明理由.图16-① 图16-②答案:一、选择题:(本题共32分,每题4分) 题号 1 2 3 4 5 6 7 8 答案ADBCCCCD二、填空题:(本题共16分,每题4分) 9.()2a ab -; 10.-2; 11.2; 12. 25.三、解答题:(本题共18分,每题6分)13. 解:原式=22424x x x +-……………………3分 =2x ……………………6分14.解:22(2)3(2)2(4)x x x x --+=-. ……………………2分22243628x x x x ---=-,72x -=-,27x =. ……………………4分 经检验:27x =是原方程的解. ……………………5分 ∴原方程的解为27x =. …………………6分15.解: 22()(1)()aa b a b a b-+÷-+= 21()()a b a b a b a b a b+-++- ……………………2分= 2a+b , ……………………4分 因为 2a+b -1=0,所以 2a+b =1. ……………………5分 ∴ 原式=1 . ……………………6分 四、(本题共18分)16.(6分)解:(1)画出树状图或列表正确给2分,(图略)所以,他拨对小东电话号码的概率是110……………………2分 (2)解不等式(1)得x >112解不等式(2)得x ≤8 ∴ 解不等式组的解集是:112<x ≤8 ……………………3分 ∴ 整数解是6,7,8∴□表示的数字可能是 6,7,8……………………4分 (3)他拨对小东电话号码的概率是21……………………6分 17.(6分)(1)证明:连结CD (如图),……………………1分则90ADC BDC ∠=∠=. E 是BC 的中点, DE BE EC ∴==.OA OD DE BE ==,, ADO A ∴∠=∠,DBE BDE ∠=∠.90DBE A ∠+∠=, 90BDE ADO ∴∠+∠=. 90EDO ∴∠=. ∴OD DE ⊥.即 DE 是O 的切线 . ……………………3分 (也可以连结OE ,由证明△ODE ≌△OCE 证明OD DE ⊥) (2)解:连结OE .则OE ∥AB ,△OEF ∽△BDF . 在Rt ABC △中,AC = 4,BC =∴ AB = 8,OE = 4,∠A =60°.∴ AOD △是边长为2的等边三角形, ∴ 2AD =,BD = AB -AD =6.∴ EF :FD = OE :BD = 4:6 = 2:3 .……………………6分18.(6分)解:(1)当CP=3时∵BC=12,AD=9 ∴BP=9 ∴AD=BP∵AD ∥BC ,∠ABC=90°∴四边形ABPD 是矩形 ∴∠DPB=90° 又 ∵PE ⊥DP∴∠DPE=∠DPB =90°且点E 在AB 上 ∴点E 与点B 重合……………………2分 (2)如图过点D 作DM ⊥BC 于M当点P 在BM 上时∴∠DMB=∠DMC=∠ABC =90°∴∠1+∠3=90° ∵PE ⊥DP∴∠DPE=90°∴∠1+∠2=90° ∴∠3=∠2∴PBE ∽DMP ∴BE BPMP MD=……………………3分 同(1)可证四边形ABMD 是矩形 ∴AB=DM=a ∵CP=x ,BE=y 又∵MC=3∴MP=x -3,BP=12-x ∴123y xx a-=- ∴()211536y x x a=--+ 当点P 在MC 上时,如图,同理可得()211536y x x a=-+……………………4分 (3)方法一:若以AD 为直径作⊙O ,与BC 切于点P ,连接AP 、DP 、OP ,则∠APD=90o,OP ⊥BC 于点P ,∵∠ABC=90o,AD ∥BC∴∠BAD=∠BPO=90o∴四边形ABPO 是矩形321MEP DCBAAB CDPEM (E)O D A∴2992121=⨯===AD OP AB ∴当a 的值为29时,在BC 上存在一点P ,使PE ⊥DP ,且E 与A 重合.方法二:若在线段BC 上找到一点P ,使上述作法得到的点E 与点A 重合,则BE=AB=a ,且点P 在BM 上 ∴()211536a x x a=--+ ∴2215360xx a -++=由题意:22254(36)0a ∆=-+=即92a =±∵AB=a>0 ∴29=a ……………………6分 五、解答题(本题共16分)19.(8分) .解:(1)根据题意得3652.m m n n ++=⎧⎨=⎩,解得132.m n ⎧=⎪⎨⎪=⎩,所以抛物线的解析式为2123y x x =++.----------------------------------2分 (2)由2123y x x =+得抛物线的顶点坐标为(B .依题意,可得(1)C -,且直线l 过原点. 设直线l 的解析式为y kx =.则1=-,解得k =所以直线l的解析式为y x =.(3)到直线OB OC BC ,,距离相等的点有四个.如图,由勾股定理得2OB OC BC ===,所以OBC △为等边三角形. 易证x 轴所在直线平分BOC ∠,y 轴是OBC △的一个外角的平分线.作BCO ∠的平分线,交x 轴于1M 点,交y 轴于2M 点,作OBC △的BCO ∠相邻外角的平分线,交y 轴于3M 点,反向延长交x 轴于4M 点.321ME P DCBA可得点1234M M M M ,,,就是到直线OB ,OC ,BC 距离相等的点. 可证2OBM △,4BCM △,3OCM △均为等边三角形. 可求得: ① 132333OM OB ==,所以点1M 的坐标为2303⎛⎫- ⎪ ⎪⎝⎭,.----------------------5分 ② 点2M 与点A 重合,所以点2M 的坐标为(02),.-------------------------------------6分 ③ 点3M 与点A 关于x 轴对称,所以点3M 的坐标为(02)-,.-----------------------7分 ④ 设抛物线的对称轴与x 轴的交点为N .4332M N BC ==,且4ON M N =,所以点4M 的坐标为(230)-,.--------8分 综上所述,到直线OB OC BC ,,距离相等的点的坐标分别为12303M ⎛⎫-⎪ ⎪⎝⎭,,2(02)M ,,3(02)M -,,4(230)M -,.20.(8分).解:(1)∵直线y=-33x+332交x 轴于点C,交y 轴于点A , ∴点A的坐标为(0,332),点C的坐标为(2,0). ---------------1分 ∵等腰直角三角板OBD 的顶点D 与点C 重合, ∴OD=2,︒=∠45BOD . 过点B 作BM ⊥OC 于M. ∴OM=121=OD . ∴BM=1,OB=2.∴点B的坐标为(1,1).------------------2分 (2)∵OA=332,OC=2,90AOC ∠=︒, ∴∠ACO=30∘. 过点O 作OE ⊥ ∴OE=1.∵在Rt ΔB 'EO 中,OB '=2,OE=1, ∴∠B ‘OE=45∘.∴∠EOD=90∘. 又∵∠EOC=60∘, ∴∠COD=30∘.∴α=30∘.--------4分 分理由:∵点B'在直线AC 上, ∴点B'的坐标为(a ,-33a+332). ∵a2+(-33a+332)2=OB '2, ∴a2+(-33a+332)2=(2)2. 解方程,得a1=231+,a2=231-(不合题意,舍去). ∴点B '的坐标为(231+,213-).--------6分又∵二次函数y=mx2+3x过B(1,1),∴m=-2.∴二次函数的解析式为y=-2x2+3x.--------7分 把x=231+代入y=-2x2+3x,得y=213-∴。
2011学年度秋期初一数学科教学工作计划

2011学年度秋期初一数学科教学工作计划泸州泸县四中刘建春一、班级情况分析:全年级共8个班,每班平均54人,根据升学考试的成绩差生达到90人以上。
二、教材分析:本套教材切合《标准》的课程目标,有以下特点:1.为学生的数学学习构筑起点,提供大量数学活动的线索,成为供所有学生从事数学学习的出发点。
2.向学生提供现实、有趣、富有挑战性的学习素材。
所有数学知识的学习,都力求从学生实际出发,以他们熟悉或感兴趣的问题情境引入学习主题,并展开数学探究。
3.为学生提供探索、交流的时间和空间。
设立了“做一做”、“想一想”、“议一议”等栏目,以使学生通过自主探索与合作交流,形成新的知识。
4.展现数学知识的形成与应用过程,让学生经历真正的“做数学”、“用数学”的过程。
5.满足不同学生发展的需求。
三、教学目标及要求:第一章:1.经历展开与折叠、切截以及不同同方向看等数学活动,积累数学活动经验。
2.通过丰富的实例,进一步认识点、线、面,了解有关点、线及某些平面图形的一些简单性质。
3、能识别简单物体的三视图,会画立方体及其简单组合体的三视图。
4、了解直棱柱、圆柱、圆锥的侧面展开图,能根据展开图想像和制作立体模型,激发对空间与图形学习的好奇心,初步形成积极参与数学活动、主动与他人合作交流的意识。
第二章:1.理解有理数及其运算的意义。
2.用数轴上的点表示有理数,会比较有理数大小。
3、理解相反数和绝对值的意义,并会求。
4、经历探索有理数运算法则和运算律的过程,掌握有理数的加、减、乘、除、乘方及简单的混合运算,并进行灵活运算和解决简单的实际问题。
第三章:1.理解代数式的含义,能解释一些简单代数式的实际背景或几何意义。
2.理解合并同类项和去括号的法则,并会进行运算。
3、理解和会求代数式的值,能根据代数式的值推断代数式反映的规律。
4、理解合并同类项和去括号的法则,并会进行运算。
第四章:1.能用符号表示角、线段、互相平行或垂直两直线。
2.认识平面图形,了解平面上两条直线的平行和垂直关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初 一 期 末 复 习一. 有理数 (一)选择题1.中国月球探测工程“嫦娥一号”卫星发射成功.已知地球距离月球表面384000千米,那么这个距离用科学记数法(保留三个有效数字)表示应为 ( ) .A .3.84×104千米B .3.84×105千米C .3.84×106千米D .38.4×104千米 2.对于以下几种说法,其中正确的说法个数是( ).①平方等于本身的数是1 ; ②任何一个有理数加上它的相反数都等于0; ③如果|a|=|b|,那么a=b ; ④两个负数相加一定等于负数;⑤立方等于本身的数是0和1 ; ⑥有理数的平方是非负数; ⑦绝对值等于本身的数是正数; ⑧任何有理数的平方是正数; ⑨两个数比较,绝对值大的反而小; ⑩任何一个整数的绝对值都是自然数 A .3个B .2个C .1个D .0个3.若a 、b 为有理数,a>0,b<0,且│a │<│b │,那么a ,b ,—a ,—b 的大小关系是( ) A.b< —a< —b<a B.b< —b< —a<a C.b< —a< a<—b D.—a< —b < b <a 4.下列各数互为相反数的是( )A.—32与23B.32与(—2)3C.(—3)2与—32D.—32与—(—3)25.当0<x<1时,x 2,x ,1x的大小关系是( ) A 、x 2<x <1x B 、1x <x 2<x C 、x <1x < x 2 D 、x <x 2<1x6. 一个数在数轴上的对应点与它的相反数在数轴上的对应点的距离是5个单位长度,那么这个数是( ) A .5或-5 B .5522-或 C .552-或 D .552-或 7. 若x+|x|=0,则x 一定是 ( )A 、正数B 、负数C 、正数或零D 、负数或零 8. 一根1m 长的小棒,第一次截去它的13,第二次截去剩下的13,如此截下去,第五次后剩下的小棒的长度是 ( )A.51()3m B.51[1()]3m - C .52()3m D 52[1()]3m - (二)填空题1.已知∣a-1∣与(b+2)2互为相反数,则(a+b)2007+a2008的值 .2.有理数a 、b 、c 在数轴上对应的点分别是A 、B 、C ,其位置如图所示,试化简a b c a b c c ++-++-= .3. 若2x =,29y =,且x y >,则x y +=___________.12<<-x 时,=--+12x x __________.4.若a 、b 是互为相反数,c 的绝对值为2,m 与n 互为倒数,则mn c cb a 422001-++ 的值是 。
5. 观察下面一列数: -12 -3 4-5 6 -7 8 -910 -11 12 -13 14 -15 16……按照上述规律排下去,那么第10行从左边数第9 个数是 . (三)计算题 1、)21(32231213-++⎪⎭⎫ ⎝⎛-- 2.1)51(542-⨯÷-;3. )43125.0()41(5412-⨯-⨯ 4. [])4()81()2(1183-⨯----÷5. 2211210.53(2)3⎡⎤⎛⎫⎡⎤----⨯⨯-- ⎪⎢⎥⎣⎦⎝⎭⎣⎦ 6. 41-12524()236-⨯+-+3)2(25.1-⨯(四)解答题魔术师为大家表演魔术. 他请观众想一个数,然后将这个数按以下步骤操作:魔术师立刻说出观众想的那个数.(1)如果小明想的数是1- ,那么他告诉魔术师的结果应该是 ;(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是 ;(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,请你说出其中的奥妙. 二.整式的加减1. 在代数式222515,1,32,,,1x x x x x x π+--+++,322yx π-中,整式有 ( )A.3个B.4个C.5个D.6个2. 代数式22225233,22,4,,,35b a b x abc xy z c π----中单项式有 ( ) A. 2个 B. 3个 C. 4个 D. 5个3. 下列几组式子中,互为同类项的有 ( ) (1)-3和23(2) 22x y - 和23yx (3) 3ab 和32a b - (4) 3x 和3 A. 1组 B. 2组 C. 3组 D. 4组4. 已知2y 32x 和32m x y -是同类项,则式子4m-24的值是 ( ) A.20 B.-20 C.28 D.-285. 32281x x x -+-若多项式与多项式323253x mx x +-+的和不含二次项,则m 是( ) A .2 B.-2 C.4 D.-46. 下列运算正确的是 ( )A.325a b ab +=B. 22a a a -=C.22232x y yx x y -=D. 33220a b ab -= 7. 已知,012=--x x 则9442++-x x = .8. 单项式322yx π-的系数是 次数是 .多项式2-152xy -4y x 3-2x y-它的项数为 ,次数是 ; 9. 已知n 为非负整数,多项式()4132n x y n x ++--是四次三项式,则n = .10. 先化简,再求值(1)),23(231423223x x x x x x -+--+其中x =-3(2)若2(23)|1|0a b b +++-=,求代数式5{23[28(321)]1}a a b a b a +---+---+ 的值.三.一元一次方程1、运用等式性质进行的变形,正确的是( ) )(A 如果a b c c =,那么b a = )(B 如果b a =,那么a b c c= )(C 如果b a =,那么c b c a -=+ )(D 如果a a 32=,那么3=a2、已知x=3是方程2x 2+(m-1)x=6的解,则m=3、已知1=y 是关于y 的方程y y m 2)(312=--的解,那么关于x 的方程 )42(4+=+x m m mx 的解是 4、已知 ()0332=-+--m x m m 是关于x 的一元一次方程, 则m = .5、果方程412312+=-x x 与关于x 的方程()n x x +=-2214的解相同, 求()23-n 的值. 6、在公式d n a a n )1(1-+=中,n a a ,1分别代表两个数,0≠d ,若已知n a a d ,,1, 则=n ________.7.解方程(1))1(16)12(32+-=-+x x x (2).151423=+--x x (3) 323221+-=--x x x (4)2532386123=-⎪⎭⎫ ⎝⎛+x x四.二元一次方程组1.下列各式,属于二元一次方程的个数有( )①xy+2x -y=7;②4x+1=x -y ; ③1x+y=5; ④x=y ; ⑤x 2-y 2=2 ⑥6x -2y ⑦x+y+z=1 ⑧y (y -1)=2y 2-y 2+xA .1B .2C .3D .42. 已知10x y =-⎧⎨=⎩和23x y =⎧⎨=⎩都是方程y ax b =+的解,则a 和b 的值是( )A .11a b =-⎧⎨=-⎩ B .11a b =-⎧⎨=⎩ C .11a b =⎧⎨=⎩ D . 11a b =⎧⎨=-⎩ 3.关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解,那么m 的值是( )A .2;B. -1;C. 1;D. -2;4.若⎩⎨⎧-==21y x 是关于x 、y 的方程1=-by ax 的一个解,且3-=+b a ,则b a -2=__ .5.从方程组4330(0)30x y z xyz x y z ⎧--=≠⎨-+=⎩中可以知道,x:y:z=6.解方程组⎩⎨⎧-=+-=7212y x x y()()344126x y x y x y x y⎧+--=⎪⎨+-+=⎪⎩7. 应用题(1)汽车从甲地到乙地,若每小时行驶45千米,就要延误30分钟到达;若每小时行驶50千米,那就可以提前30分钟到达,求甲、乙两地之间的距离及原计划行驶的时间?(2)甲、乙两人练习赛跑,如果甲让乙先跑10米,那么甲跑5秒钟就可以追上乙;如果甲让乙先跑2秒钟,那么甲跑4秒钟就能追上乙,求两人每秒钟各跑多少米?(3)甲桶装水49升,乙桶装水56升,如果把乙桶的水倒入甲桶,甲桶装满后,乙桶剩下的水,恰好是乙桶容量的一半;若把甲桶的水倒入乙桶,待乙桶装满后则甲桶剩下的水恰好是甲桶容量的31,求这两个水桶的容量各是多少.(4)刘亮从家步行去学校,计划每小时走5千米,恰好能按时到校.当他走到与学校还有0.5千米的路程的时候,发现有件东西忘带了,立即沿原路原速返回家,到家拿东西耽误了5分钟,之后立即骑车以15千米/时的速度出发去学校,结果还是迟到了15分钟.问刘亮家与学校相距多少千米?(5)运动会前甲乙两班学生去超市买某品牌矿泉水,超市对该品牌矿泉水的销售方法如下:购买不超过30瓶时,按零售价销售,每瓶3元;购买30瓶但不超过50 瓶时,按批发价销售,是零售价的八折;购买超过50瓶时,按批发价销售,是零售价的六折。
甲班分两天两次共购70瓶,(第二天买的比第一天多),共付183元,而乙班一次购买70瓶, (1) 乙班比甲班少付多少瓶?(2) 甲班第一天第二天分别购买多少瓶?五.几何题1. 下列语句正确的是 ( )A .过一点有且只有一条直线与已知直线平行B .不相交的两条直线是平行线C .线段AB 是点A 与点B 的距离D .连结两点的线段的长度叫做两点间的距离. 2. 下列说法中正确的是( )A.若AP=21AB ,则P 是AB 的中点 B.若AB =2PB ,则P 是AB 的中点 C .若AP =PB ,则P 为AB 的中点 D.若AP =PB=21AB ,则P 是AB 的中点3. 下列说法中,正确的有( )。
(1)过两点有且只有一条线段(2)连结两点的线段叫做两点的距离 (3)两点之间,线段最短 (4)AB =BC ,则点B 是线段AC 的中点 (5) 射线比直线短A .1个B .2个C .3个D .4个 4. 如图,OC 是平角∠AOB 的平分线,90EOD ∠=,图中和∠COD 互余的角有( )个。
EDCOBAO A BCE F A.1 B.2 C.3 D.05.如图是某一立方体的侧面展开图,则该立方体是( )6.若线段AB=10cm,在直线AB 上有一点C,且BC=4cm,M 是线段AC 的中点,则AM 的长为________cm. 7.27.24°= 度 分秒,108o 21'36''= 度。
