2015秋八年级数学上册 12.3 角的平分线的性质(第1课时)导学案2

合集下载

八年级数学上册 12.3 角的平分线的性质第1课时角的平分线的性质教案 (新版)新人教版

八年级数学上册12.3 角的平分线的性质第1课时角的平分线的性质教案（新版）新人教版一. 教材分析《角的平分线的性质》是八年级数学上册12.3节的内容，本节课的主要内容是让学生掌握角的平分线的性质，并能够运用角的平分线解决一些简单的几何问题。

在教材中，已经给出了角的平分线的性质的定义和证明，学生在学习本节课之前，已经掌握了角的概念、角的大小比较、角的平分线定义等知识。

二. 学情分析八年级的学生已经具备了一定的几何知识，对于角的概念、角的大小比较等知识有一定的了解。

但是，对于角的平分线的性质，学生可能还没有听说过，因此，教师需要通过导入环节，激发学生的学习兴趣，引导学生主动探索角的平分线的性质。

三. 教学目标1.了解角的平分线的性质，并能够运用角的平分线解决一些简单的几何问题。

2.培养学生的观察能力、推理能力、动手能力。

3.激发学生的学习兴趣，培养学生的合作意识。

四. 教学重难点1.角的平分线的性质的证明。

2.运用角的平分线解决几何问题。

五. 教学方法1.引导探究法：教师引导学生通过观察、推理、动手操作等方法，探索角的平分线的性质。

2.案例分析法：教师通过给出一些具体的几何问题，让学生运用角的平分线进行解决。

3.小组合作法：教师学生进行小组合作，共同探讨角的平分线的性质，并解决一些几何问题。

六. 教学准备1.教学PPT：教师需要准备角的平分线的性质的教学PPT，包括角的平分线的性质的定义、证明、应用等内容。

2.几何图形：教师需要准备一些几何图形，用于引导学生观察、推理。

3.练习题：教师需要准备一些练习题，用于巩固学生的学习效果。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾角的概念、角的大小比较等知识，然后引入角的平分线的概念，并提问：角的平分线有什么性质呢？2.呈现（15分钟）教师通过PPT呈现角的平分线的性质的定义和证明，让学生观察并理解角的平分线的性质。

3.操练（10分钟）教师给出一些几何图形，让学生运用角的平分线的性质进行判断和解决。

角平分线的性质导学案

12.3 角的平分线的性质导学案学习目标：1、会用尺规作已知角的平分线，知道作法的合理性；2、探索并证明角的平分线的性质定理；3、能用角的平分线的性质解决简单问题。

学习重点：探索并证明角的平分线的性质定理。

学习难点：角平分线性质定理的应用。

学习过程：一、情境导入问题：在S区有一个集贸市场P，它建在公路与铁路所成角的平分线上，要从P点建两条路，一条到公路，一条到铁路。

问题1：怎样修建道路最短？问题2：往哪条路走更近呢？P二、自学指导让学生先阅读课本48-49页内容，思考下面的问题：1、平分角的仪器怎么使用？2、用尺规如何平分已知角？3、角平分线的性质是4、角平分线的性质怎么证明？5、证明几何命题的一般步骤是：（1）；（2）；（3）。

三、自主探究合作展示探究（一）：角平分仪平分角的道理：1、为什么角平分仪能平分一个角？（小组讨论回答）。

探究（二）如何作尺规作出一个角的平分线呢？1、分析角平分仪原理，你能利用圆规和直尺作角的平分线吗？（小组讨论）2、师生共同用尺规作角的平分线。

已知：∠AOB．求作：∠AOB的平分线．作法：（1）以O为圆心，适当长为半径作弧，分别交OA、OB于M、N．（2）分别以M、N为圆心，大于1MN的长为半径作弧．两弧在2∠AOB内部交于点C．（3）作射线OC。

射线OC 即为所求．3、让学生回答为什么射线OC 是∠AOB 的平分线。

4、在上面作法的第二步中，去掉“大于12MN 的长”这个条件行吗？探究（三）、探究角平分线的性质：如图4，OA 是∠BAC 的平分线，点O 是射线AM 上的任意一点. 操作测量：取点O 的三个不同的位置，分别过点O 作OE ⊥AB ，OD ⊥AC,点D 、E 为垂足，测量OD 、OE 的长.将三次数据填入下表：根据测量结果，猜想线段OD 与OE 的大小关系，猜想角平分线的性质结论是：。

让学生用学过的知识证明此结论：教师引导学生分析这个文字命题的条件和结论，并找出结论中的隐含条件，最后让学生画出图形，用符号语言写出已知和求证，图4ODOE 第一次第二次第三次BOAM并独立完成证明过程。

八年级数学上册第十二章全等三角形 12.3 角的平分线的性质第1课时角的平分线的作法及性质教案

12.3 角的平分线的性质第1课时角的平分线的作法及性质【知识与技能】1.掌握角的平分线的作法.2.会利用角平分线的性质.【过程与方法】经历折纸、画图、文字与符号的翻译活动,培养学生的联想、探索、概括归纳的能力.【情感态度】通过实际操作与探究交流,激发学生学习数学的兴趣.【教学重点】角平分线的性质及其应用.【教学难点】灵活应用两个性质解决问题.一、情境导入，初步认识活动 1 学生预习教材,掌握角平分线的作法,小组间交流并动手实际画一画,总结出画角平分线的步骤.活动 2 让学生用准备好的白纸与剪刀,自己动手,剪一个角,把剪好的角对折,使角的两边叠合在一起,再把纸片展开,看到了什么?【教学说明】发现第一次对折后的折痕是这个角的平分线;再折一次,又会出现两条折痕,而且这两条折痕是等长的.这种方法可以做无数次,所以这种等长的折痕可以折出无数对.请同学们折出如图所示的折痕PD、PE,并研究这个图形中隐含了哪些等量关系,互相交流,形成结论.教师讲课前，先让学生完成“自主预习”.二、思考探究，获取新知由上述活动及交流情况,教师总结以下新知识:1.角平分线上的点到角两边的距离相等.2.到角两边距离相等的点在角的平分线上.【教学说明】1.这两个性质的条件和结论正好相反,分别可以作为证线段相等和证角相等的依据.2.在用几何语言表述性质时,注意强调“点到直线的距离”中的垂直条件.例1 如图所示，要在S 区建一个集贸市场，使它到公路、铁路距离相等，离公路与铁路交叉处500m ，这个市场应建于何处（在图上标出它的位置，比例尺为1∶20000）?【教学说明】教师提出下列问题，引导学生理清思路：(1)集贸市场建于何处，和本节学的角平分线性质有关吗？用哪一个性质可以解决这个问题？(2)比例尺为1∶20000是什么意思？(3)图形上，表示500m 的是个什么距离？例2 如图所示，BD 为∠ABC 的平分线，AB=BC,点P 、D 分别在BF 上，PM ⊥AD 于M,PN ⊥CD 于N ，求证：PM=PN.△ABD ≌△CBD 即可得证.【证明】∵BD 为∠ABC 的平分线，∴∠ABD=∠CBD.在△ABD 和△CBD 中，,,,AB CB ABD CBD BD BD =⎧∠=∠=⎪⎨⎪⎩∴△ABD ≌△CBD(SAS).∴∠ADB=∠CDB.即射线DP 为∠ADC 的平分线.又∵PM ⊥AD,PN ⊥CD,∴PM=PN.例3如图，点P 是∠AOB 的平分线OM 上一点，作PD ⊥OB,PC ⊥OA,垂足分别是点D 、C ，点E 、F 分别在线段OD,OC 上，且∠PED=∠PFC,求证：OP平分∠EPF.【分析】欲证OP平分∠EPF，可设法证∠OPE=∠OPF,而要证∠OPE=∠OPF,需证∠OPD=∠OPC和∠DPE=∠CPF.【证明】∵OP平分∠AOB,PD⊥OB,PC⊥OA,垂足分别是点D，C，∴PD=PC，∠ODP=∠OCP=90°.在Rt△ODP与Rt△OCP中，,, PD PC OP OP==⎧⎨⎩∴Rt△ODP≌Rt△OCP（HL）.∴OD=OC,∠OPD=∠OPC.在Rt△EDP与Rt△FCP中，∠PED=∠PFC,∠ODP=∠OCP=90°,∴90°-∠PED=90°-∠PFC,即∠DPE=∠CPF.∴∠OPD-∠DPE=∠OPC-∠CPF,∴∠OPE=∠OPF,即OP平分∠EPF.三、运用新知，深化理解______相等.2.如图，在△ABC中,∠A=80°,∠B与∠C的平分线相交于点I,则∠BIC=___.第2题图第3题图△ABC中,∠B=30°,∠C=90°,AD平分∠CAB,交CB于D,且DE⊥AB于E,则∠BDE=_______=_______=_______.【教学说明】指导学生解答上述习题时，应适当启发学生对角平分线性质的灵活运用.°3.∠EDA∠CDA∠CAB四、师生互动，课堂小结1.角平分线的两个性质应牢记并应用于解题中.2.与角平分线有关的求证线段相等,角相等问题,我们可以直接用角平分线性质,不必再利用证三角形全等得到线段相等或角相等.1.布置作业：从教材“”中选取部分题.2.完成练习册中本课时的练习.本课时教学思路按操作、猜想、验证的学习过程，遵循学生的认知规律，充分体现了数学学习的必然性，教学时要始终围绕问题展开，先从出示问题开始，鼓励学生思考、探索问题中所包含的数学知识，再要求学生开展活动——折纸，体验三角形角平分线交于一点的事实，并得出进一步的猜想和开展新活动——尺规作图，从中猜想结论并思考证明的方法，整堂课以学生操作、探究、合作贯穿始终，并充分给学生思考留下足够的空间与时间，形成动手、合作、概括与解决问题的意识与能力.。

人教版数学八年级上册12.3角的平分线的性质(第一课时)教学设计

三、教学重难点和教学设想
（一）教学重难点
1.重点：角的平分线的定义、性质及其应用。
2.难点：
（1）角的平分线性质的推理与证明。
（2）运用角的平分线性质解决实际问题，如构造等腰三角形、解决角度分配问题等。
（二）教学设想
1.教学方法：
（1）采用直观演示法，通过动态图示、实际操作等方式，让学生直观感受角的平分线的形成过程，为理解性质打下基础。
2.教师总结：
（1）强调角的平分线的定义及性质。
（2）指出角的平分线在实际问题中的应用价值。
（3）鼓励学生继续探索几何知识，提高自己的空间观念和逻辑思维能力。
五、作业布置
为了巩固本节课所学的角的平分线的性质，提高学生的应用能力，特布置以下作业：
1.基础练习题：
（1）完成课本习题12.3第1题，判断下列各图中，哪些是角的平分线，并说明理由。
（1）联系生活实际，设计一道角的平分线性质的应用题，要求解题步骤详细，答案正确。
（2）运用角的平分线性质，解决一道实际生活中的问题，如角度分配、构造图形等。
4.思考题：
（1）思考：如何运用角的平分线性质求解等腰三角形的顶角？
（2）思考：在平面几何中，角的平分线有哪些重要性质？它们在解决实际问题中有什么作用？
3.生活实例导入：通过生活中的实例，如红绿灯的指示牌、墙壁上的挂钟等，让学生感受到角在生活中的应用，激发学生的学习兴趣。
4.提出问题：引导学生思考如何将一个角平均分成两个相等的角。从而引出本节课的主题——角的平分线。
（二）讲授新知
1.角的平分线的定义：介绍角的平分线的概念，强调角的平分线将一个角分成两个相等的角。
（2）新课：以直观演示、问题驱动方式引入角的平分线的定义和性质，让学生通过自主探究、小组合作等方式掌握性质。

八年级数学上册 12.3 角的平分线的性质第1课时角的平分线的性质教学设计 (新版)新人教版

八年级数学上册 12.3 角的平分线的性质第1课时角的平分线的性质教学设计（新版）新人教版一. 教材分析《新人教版八年级数学上册》第12.3节讲述了角的平分线的性质。

这部分内容是在学生已经掌握了角的概念、角的计算、线段的性质等基础知识的基础上进行讲解的。

角的平分线的性质是数学中的重要概念，对于学生理解和应用角的概念有重要意义。

本节课的内容包括角的平分线的定义、角的平分线的性质及其应用。

二. 学情分析八年级的学生已经具备了一定的数学基础，对于角的概念和线段的性质有一定的了解。

但是，对于角的平分线的性质及其应用可能还存在一定的困难。

因此，在教学过程中，需要注重引导学生通过观察、思考、探究来理解角的平分线的性质，并能够运用角的平分线解决实际问题。

三. 教学目标1.知识与技能：使学生理解角的平分线的性质，能够运用角的平分线解决实际问题。

2.过程与方法：通过观察、思考、探究，培养学生的逻辑思维能力和解决问题的能力。

3.情感态度与价值观：激发学生对数学的兴趣，培养学生的团队合作意识和勇于探究的精神。

四. 教学重难点1.重点：角的平分线的性质。

2.难点：角的平分线的性质的应用。

五. 教学方法采用问题驱动法、合作探究法、讲解法等教学方法。

通过问题引导学生思考，合作探究来理解角的平分线的性质，讲解法来讲解角的平分线的性质及其应用。

六. 教学准备1.准备相关的教学材料，如PPT、黑板、粉笔等。

2.准备一些实际问题，用于引导学生运用角的平分线解决实际问题。

七. 教学过程1.导入（5分钟）通过复习角的概念、角的计算、线段的性质等基础知识，引导学生进入新的学习内容。

2.呈现（10分钟）讲解角的平分线的定义，角的平分线的性质。

通过PPT展示角的平分线的性质的图示和解释，让学生直观地理解角的平分线的性质。

3.操练（10分钟）讲解角的平分线的性质的应用。

通过一些实际问题，引导学生运用角的平分线解决实际问题。

让学生在解决问题的过程中，加深对角的平分线的性质的理解。

12.3 角的平分线的性质(1) 人教版八年级数学上学期教案

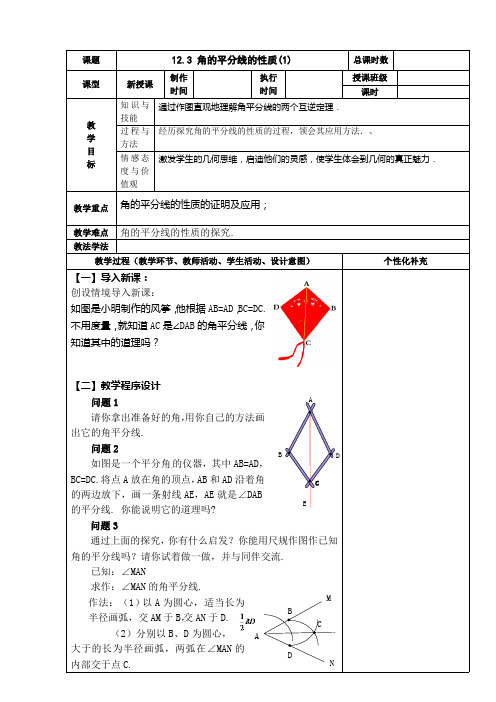
放在角的顶点，ADBA（3）画射线AC.∴射线AC 即为所求.【三】巩固练习已知：OC 是∠AOB 的平分线，点P 在OC 上，PD ⊥OA ，PE ⊥OB ，垂足分别是D 、E （课本图11．3─4）求证：PD=PE ．证明：∵PD ⊥OA ，PE ⊥OB ，∴∠PDO=∠PEO=90°在△PDO 和△PEO 中，∴△PDO ≌△PEO （AAS ） ∴PD=PE如图，AB ∥CD ，以点A 为圆心，小于AC 长为半径作圆弧，分别交AB ，AC 于E ，F 两点，再分别以E 、F 为圆心，大于12EF 的长为半径画弧，两弧交于点P ，作射线AP ，交CD 于点M .若∠ACD ＝120°，求∠MAB 的度数．解析：根据AB ∥CD ，∠ACD ＝120°，得出∠CAB ＝60°，再根据AM 是∠CAB 的平分线，即可得出∠MAB 的度数．解：∵AB ∥CD ，∴∠ACD ＋∠CAB ＝180°，又∵∠ACD ＝120°，∴∠CAB ＝60°，由作法知，AM 是∠CAB 的平分线，∴∠MAB ＝12∠CAB ＝30°.方法总结：通过本题要掌握角平分线的作图步骤，根据作图明确AM 是∠BAC 的角平分线是解题的关键．如图，AD 是△ABC 的角平分线，DE ⊥AB ，垂足为E ，S △ABC ＝7，DE ＝2，AB ＝4，则AC 的长是( )A ．6B ．5C ．4D ．3解析：过点D 作DF ⊥AC 于F ，∵AD 是△ABC 的角平分线，DE ⊥AB ，∴DF ＝DE ＝2，∴S △ABC ＝12×4×2＋12AC ×2＝7，解得AC ＝3.故选D.方法总结：利用角平分线的性质作辅助线构造三角形的高，再利用三角形面积公式求出线段的长度是常用的方法．拓展延伸，巩固强化知识。

【五】布置作业1.课本练习2.同步练习对应习题OCN别为点D、E.∴ PD=PE二次备课。

人教版-数学-八年级上册-12.3 角的平分线的性质(1) 教案

12.3 角的平分线的性质一、教学目标（一）核心素养（二）学习目标会用尺规作一个角的平分线，知道作法的合理性；探索并证明角平分线的性质；能用角的平分线的性质解决简单问题.（三）学习重点角的平分线的性质的证明及应用.（四）学习难点角的平分线的性质的探究.二、教学设计(一)课前设计预习任务用尺规作图作一个角的平分线的方法，其依据是SSS .角的平分线上的点到角的两边的距离相等.预习检测一、填空题1.如图，在△ABC中，∠C＝90°，AD是∠BAC的角平分线，若BC＝8cm，BD＝5cm，则点D到AB的距离为.答案：3cm解析：根据题意画出图形，过点D作DE⊥AB，交AB于点E，D点到AB的距离即为DE 的长.∵∠BCA=90°∴AC⊥BC∵AC⊥BC，DE⊥AB，AD平分∠CAB∴CD=DE∵BC=8cm，BD=5cm，CD=DE，BC=CD+BD∴DE=3cm即D点到直线AB的距离是3cm.点拨：根据角平分线的性质添加辅助线作答2.∠AOB的平分线上一点P，P到OA的距离为2.5cm，则P到OB的距离为cm.答案：2.5解析：∵P是∠AOB平分线上一点，点P到OA的距离是2.5cm，∴P到OB的距离等于点P到OA的距离，为2.5cm.因此，本题正确答案是:2.5.点拨：根据角平分线上的点到角的两边的距离相等解答.二、选择题3.如图，∠1＝∠2，PD⊥OA，PE⊥OB，垂足分别为D，E，下列结论错误的是（）A.PD＝PEB.OD＝OEC.∠DPO＝∠EPOD.PD＝OD答案：D解析：A项；由角分线性质，正确B项；由角分线性质知PD＝PE，由HL知Rt△OEP≌△ODP，则两三角形全等知OD＝OE，正确.C项；同B项，由两三角形全等知∠DPO＝∠EPOD项；错误点拨：由题设可知OP为∠AOB的角平分线，PE为P到OB的距离，PD为P到OA的距离，再由角的平分线性质判断即可.可由角分线的性质找出相应的结论.(二)课堂设计1.知识回顾（1）三角形的判断方法有哪些？SSS，SAS，AAS，ASA，HL（2）三角形中有哪些重要线段？三角形中有三条重要线段，它们分别是：三角形的高，三角形的中线，三角形的角的平分线．（3）从直线外一点到这条直线的垂线段的长叫做点到直线的距离.2.问题探究探究一角的平分线的作法●活动①请同学们拿出准备好的角，用你自己的方法画出它的角平分线，然后与大家交流分享.【设计意图】通过学生动手实践，寻找作已知角的平分线的方法，目的是为了引入尺规作图作已知角的平分线.12BD●活动②如图是一个平分角的仪器，其中AB=AD ，BC=DC.将点A 放在角的顶点，AB 和AD 沿着角的两边放下，画一条射线AE ，AE 就是∠DAB 的平分线. 你能说明它的道理吗？让同学们把推理过程写在课堂作业本上，老师巡查学生完成情况，对个别学生进行引导，最后教师把有典型错误的解答过程展示出来，让同学们去纠正错误.【设计意图】为如何用尺规作图作已知角的平分线作铺垫.●活动③老师提出问题：通过上述探究，能否总结出尺规作已知角的平分线的一般方法．自己动手做做看．然后与同伴交流操作心得．（分小组完成这项活动，教师可参与到学生活动中，及时发现问题，给予启发和指导，使讲评更具有针对性）讨论结果展示：已知：∠MAN求作：∠MAN 的角平分线.作法：（1）以A 为圆心，适当长为半径画弧，交AM 于B ，交AN 于D.（2）分别以 B.D 为圆心，大于的长为半径画弧，两弧在∠MAN 的内部交于点C.（3）画射线AC.∴射线AC 即为所求.分组讨论： 1．在上面作法的第二步中，去掉“大于12BD的长”B这个条件行吗？2．第二步中所作的两弧交点一定在∠MAN的内部吗？学生讨论结果总结：1．去掉“大于12BD的长”这个条件，所作的两弧可能没有交点，所以就找不到角的平分线．2．若分别以B.D为圆心，大于12BD的长为半径画两弧，两弧的交点可能在∠MAN的内部，也可能在∠MAN的外部，而我们要找的是∠MAN内部的交点，否则两弧交点与顶点连线得到的射线就不是∠MAN的平分线了．3．角的平分线是一条射线．它不是线段，也不是直线，所以第二步中的两个限制缺一不可．4．这种作法的可行性可以通过全等三角形来证明．练一练：任意画一角∠AOB，作它的平分线．【设计意图】设计这两个问题的目的在于加深对角的平分线的作法的理解，培养数学严密性的良好学习习惯探究二角的平分线的性质●活动①如图，将∠AOB对折，再折出一个直角三角形（使第一条折痕为斜边），然后展开.观察两次折叠形成的三条折痕，三条折痕分别表示什么？你能得出什么结论？学生回答后师生归纳：OC表示∠AOB的角平分线，PD和PE分别表示P到OA和OB的距离，P到角两边的距离相等（PD=PE）【设计意图】让学生感知角平分线的性质.●活动②学生活动：作已知∠AOB的平分线，过平分线上一点P，作两边的垂线段.投影出下面两个图形，让学生评一评.结论：同学乙的画法是正确的．同学甲画的是过角平分线上一点画角平分线的垂线，而不是过角平分线上一点作两边的垂线段，所以他的画法不符合要求．问题1：如何用文字语言叙述所画图形的性质？师生共同归纳：角平分线上的点到角的两边的距离相等．问题2：能否用符号语言来翻译“角平分线上的点到角的两边的距离相等”这句话？已知事项：OC平分∠AOB，PD⊥OA，PE⊥OB，D.E为垂足．由已知事项推出的事项：PD=PE．【设计意图】进一步理解角平分线的题设和结论.●活动③以上结论成立吗？让同学们独立进行证明，然后展示学生的证明过程：证明：∵PD⊥OA，PE⊥OB (已知)∴∠PDO = ∠PEO=90°(垂直的定义)在△PDO和△PEO中∠PDO = ∠PEO（已证）∠AOC = ∠BOC （已知）OP=OP （公共边）∴△PDO ≌△PEO（AAS）∴PD=PE（全等三角形的对应边相等）于是我们得角的平分线的性质：角的平分线上的点到角的两边的距离相等．符号语言：∵∠AOC=∠BOC，PD⊥OA，PE⊥OB，垂足分别为点D.E.（已知）∴PD=PE（角的平分线上的点到角的两边的距离相等）【设计意图】展示符号语言的目的在于规范学生的书写过程，培养学生严谨的推理能力.探究三用角的平分线的性质解决简单问题●活动①应用角平分线的性质，就可以省去证明三角形全等的步骤，使问题简单化．所以若遇到有关角平分线，又要证线段相等的问题，我们可以直接利用性质解决问题．例1(1) 下面四个图中，点P都在∠AOB的平分线上，则图形( )中PD＝PE.A B C D【知识点】角平分线的性质.【思路点拨】利用角平分线的性质时，非常重要的条件是PD和PE是到角两边的距离.【解答过程】选项A中如果增加一个条件OD＝OE，就能得出PD＝PE；选项B和C中PD不是到OA的距离；选项D中P到OA和OB的距离为PD和PE.【答案】D(2)下图中，PD⊥OA，PE⊥OB，垂足分别为点D.E，则图中PD＝PE吗？【知识点】角平分线的性质.【思路点拨】已知没有告诉OC为∠AOB的平分线，由此PD与PE不相等.【解答过程】PD与PE不相等，因为OC不是∠AOB的平分线.（3）如图，△ABC中，∠C＝90°，BD平分∠ABC，CD＝2cm，则点D到AB的距离为cm．【知识点】角平分线的性质.【思路点拨】过D作AB的垂线段DE，垂足为E，由BD平分∠ABC，可得DC=DE=2.【解答过程】解：过D作AB的垂线段DE，垂足为E，∵BD平分∠ABC，CD⊥BC，DE⊥AB，∴DC=DE∵CD＝2cm，∴DE=2cm，即点D到AB的距离为2cm【答案】2练习：如图，△ABC中，∠C＝90°，BD平分∠ABC，DE⊥AB，垂足为点E，AC=7cm，则AD+DE= cm.EDCBA【知识点】角平分线的性质.【思路点拨】由BD平分∠ABC，可得DC=DE，AD+DE=AD+DC=AC.【解答过程】解：∵BD平分∠ABC，CD⊥BC，DE⊥AB，∴DC=DE∴AD+DE=AD+DC=AC.∵AC=7cm，∴AD+DE=7cm.【答案】7【设计意图】通过练习，理解角平分线的性质.●活动②例2如图所示，要在S区建一个集贸市场，使它到公路、铁路距离相等，离公路与铁路交叉处500m，这个集贸市场应建于何处（在图上标出它的位置，比例尺为1:20 000）？【知识点】角平分线的性质【思路点拨】1．这个集贸市场应该建在公路与铁路形成的角的平分线上，并且要求离角的顶点500米处．2．在纸上画图时，我们经常以厘米为单位，而题中距离又是以米为单位，这就涉及一个单位换算问题了．1 m=100 cm，所以比例尺为1:20 000，其实就是图中1 cm表示实际距离200 m的意思．作图如下：【答案】第一步：尺规作图法作出∠AOB的平分线OP．第二步：在射线OP上截取OC=2.5 cm，确定C点，C点就是集贸市场所建地了．练习：在S区有一个贸易市场P，它建在公路与铁路所成角的平分线上，要从P点建两条路，一条到公路，一条到铁路，怎样修才能使路最短？它们有怎样的数量关系呢？【知识点】角平分线的性质【思路点拨】过P分别作公路和铁路的垂线段，这两条垂线段就是P点到公路和铁路的最短距离.【答案】过P点分别作铁路和公路的垂线段，它们的数量关系为相等.●活动3例3如图，△ABC中，∠C＝90°，BD平分∠ABC，DE⊥AB于E，F在BC上，AD=DF 求证：CF=EA【知识点】角平分线的性质和三角形的判定和性质S公路铁路P初中-数学-打印版【思路点拨】证CF和EA所在的两个三角形全等【解答过程】证明：∵∠C＝90°，BD平分∠ABC，DE⊥AB于E，∴DC=DE又∵AD=DF∴△DCF≌△DEA（HL）∴CF=EA练习：如图，CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且AO平分∠BAC，求证：OB=OC．【知识点】角平分线的性质和全等三角形的判定【思路点拨】利用角平分线的性质可得OD=OE，证明△BOD ≌△COE可得OB=OC 【答案】证明：∵CD⊥AB，BE⊥AC，AO平分∠BAC，∴OD=OE，∠BDO=∠CEO=90°．∵∠BOD=∠COE，∴△BOD ≌△COE．∴OB=OC．3. 课堂总结知识梳理（以课堂内容为根据，结合教学目标的几点要求，对涉及到的知识细致梳理）（1）会用尺规作一个角的平分线，知道作法的理论依据；（2）探索并证明角平分线的性质；（3）能用角的平分线的性质解决简单问题.重难点归纳（本节课的中心知识点在此进行回顾，对课堂上的典型方法、特殊例题进行归纳点拨）（1）角的平分线的性质的探究.（2）角的平分线的性质的证明及应用.（3）证明线段相等通常证明线段所在的两个三角形全等.初中-数学-打印版。

数学人教版八年级上册数学 12.3角的平分线的性质(1) 导学案

优质资料---欢迎下载12．3 角的平分线的性质（第1课时）助学稿班级姓名学号___________一、学习目标1．会用尺规作一个角的平分线，知道作法的合理性．2．探索并证明角的平分线的性质．3．能用角的平分线的性质解决简单问题．二、自学指导一认真阅读课本P48内容，要求：掌握角平分线的画法.三、自学检测一问题1 在练习本上画一个角，怎样得到这个角的平分线？追问1 你能评价这些方法吗？在生产生活中，这些方法是否可行呢？追问2 下图是一个平分角的仪器，其中AB =AD，BC =DC，将点A 放在角的顶点，AB 和AD 沿着角的两边放下，沿AC 画一条射线AE，AE 就是∠DAB 的平分线．你能说明它的道理吗？追问3 从利用平分角的仪器画角的平分线中，你受到哪些启发？如何利用直尺和圆规作一个角的平分线？追问4 你能说明为什么射线OC 是∠AOB 的平分线吗？四、自学指导二认真阅读课本P49，要求：经历实验过程，发现并证明角的平分线的性质五、自学检测二问题2利用尺规我们可以作一个角的平分线，那么角的平分线有什么性质呢？追问1 通过动手实验、观察比较，我们发现“角的平分线上的点到角的两边的距离相等”，你能通过严格的逻辑推理证明这个结论吗？追问2 由角的平分线的性质的证明过程，你能概括出证明几何命题的一般步骤吗？追问3 角的平分线的性质的作用是什么？六、当堂检测1.在△ABC 中，∠C ＝90°，AD 是∠BAC 的角平分线，若BC ＝5㎝，BD ＝3㎝，则点D 到AB 的距离为。

2.∠AOB 的平分线上一点M ，M 到OA 的距离为1.5㎝，则M 到OB 的距离为㎝。

3.如图,∠A ＝90°,BD 是△ABC 的角平分线,AC ＝8㎝,DC ＝3DA,则点D 到BC 的距离为。

ABO PCDE 第3题图DA BC4.如图，∠1＝∠2，PD⊥OA，PE⊥OB，垂足分别为D，E，下列结论错误的是（）A、PD＝PEB、OD＝OEC、∠DPO＝∠EPOD、PD＝OD5、如图，△ABC中，∠B =∠C，AD 是∠BAC 的平分线，DE⊥AB，DF⊥AC，垂足分别为E，F．求证：EB =FC．七、作业布置课本51页习题12.3第2题AB CDE F。

八年级数学上册 12.3 角的平分线的性质第1课时角的平分线的性质导学案 (新版)新人教版

第1课时角的平分线的性质1.掌握角平分线的性质，理解三角形的三条角平分线的性质.2.掌握角平分线的画法.阅读教材P48-49“两个探究”，掌握并理解三角形的三条角平分线的性质，掌握角平分线的画法，学生独立完成下列问题：(1)把一个角分成两个相等的角的射线叫做角的平分线.(2)角的平分线的性质是角的平分线上的点到角的两边的距离相等.它的题设是角的平分线上的点，结论是到角的两边的距离相等.自学反馈(1)如图，已知∠C＝90°，AD平分∠BAC，BD＝2CD，若点D到AB的距离等于5cm，则BC的长多少？解：15cm.(2)已知：如图，∠AOB.求作：∠AOB的平分线OC.作法：略.角平分线的性质是证明线段相等的另一途径，通常能使证明过程简略.其前提条件有两条，角平分线和垂直.活动1 小组讨论例1 已知：如图，直线AB及其上一点P.求作：直线MN，使得MN⊥AB于P.作法：略.例2 已知：如图，△ABC中，AB＝AC，D是BC的中点，DE⊥AB于E，DF⊥AC于F.求证：DE＝DF.证明：在△ABD与△ACD中，∵AB=AC，AD=AD，BD=CD，∴△ABD≌△ACD.∴∠BAD＝∠CAD.∵DE⊥AB，DF⊥AC，∴DE＝DF.先利用等腰三角形顶角平分线、底边上的中线互相重合证得AD为顶角平分线，然后运用角平分线的性质证DE=DF.活动2 跟踪训练1.已知：如图，△ABC中，∠C＝90°，试在AC上找一点P，使P到斜边的距离等于PC.(画出图形，并写出画法)解：作∠B的平分线交AC于点P.2.如图，已知△ABC内，∠ABC，∠ACB的角平分线交于点P，且PD、PE、PF分别垂直于BC、AC、AB于D、E、F三点.求证：PD＝PE＝PF.证明：∵BP是∠ABC的平分线，PF⊥AB，PD⊥BC，∴PF=PD.同理证得PE=PD.∴PD=PE=PF.角平线的性质是证线段相等的另一途径.3.已知,如图，在△ABC中，AD是△ABC的角平分线，E、F分别是AB、AC上一点，并且有∠EDF＋∠EAF＝180°.试判断DE和DF的大小关系并说明理由.解：结论：DE=DF.(提示：过点D作DM⊥AB于点M，作DN⊥AC于点N，则DM⊥DN，再证△DME≌△DNF，∴DE=DF.)在已知角的平分线的前提下，做两边的垂线段是常用辅助线之一.活动3 课堂小结在本节中，在已知角平分线的条件下，常想到过角平分线上的点向角两边做垂线段的方法.在已知角平分线的条件下，也可想到翻折造全等的方法.教学至此，敬请使用学案当堂训练部分.。

新人教版八年级数学上册导学案《12.3角的平分线的性质》

《12.3角的平分线的性质》（1）导学案【学习目标】1、经历角的平分线性质的发现过程，初步掌握角的平分线的性质定理．2、能运用角的平分线性质定理解决简单的几何问题.3、极度热情、高度责任、自动自发、享受成功。

教学重点：掌握角的平分线的性质定理教学难点: 角平分线定理的应用。

一、预习案1、复习思考什么是角的平分线？怎样画一个角的平分线？2．如右图，AB＝AD，BC＝DC，沿着A、C画一条射线AE，AE就是∠BAD的角平分线，你知道为什么吗探究案3．OC是∠AOB的平分线，点P是射线OC上的任意一点，操作测量：取点P的三个不同的位置，分别过点P作PD⊥OA，PE ⊥OB,点D、E 为垂足，测量PD、PE的长.将三次数据填入下表：观察测量结果,猜想线段PD与PE的大小关系，写出结论4、命题：角平分线上的点到这个角的两边距离相等.题设：一个点在一个角的平分线上结论：这个点到这个角的两边的距离相等结合第4题图形请你写出已知和求证，并证明命题的正确性O A BE D CP D C A 思考：证明一个几何命题的步骤有那些？6、用数学语言来表述角的平分线的性质定理：如右上图，∵OC 是∠AOB 的平分线，点P 是∴三、训练案1、如图所示OC 是∠AOB 的平分线,P 是OC 上任意一点,问PE=PD?为什么?2、如图：在△ABC 中，∠C=90°，AD 是∠BAC 的平分线，DE ⊥AB 于E ，F 在AC上，BD=DF ；求证：CF=EB如图,在△ABC 中，AC ⊥BC ，AD 为∠BAC 的平分线，DE ⊥AB ，AB ＝7㎝，AC ＝3㎝，求BE 的长我的收获：1、知识方面：2、我的困惑：3、思想感悟：P N MC BA《12.3角的平分线的性质》（2）导学案【学习目标】1、会叙述角的平分线的性质及“到角两边距离相等的点在角的平分线上”．2、能应用这两个性质解决一些简单的实际问题．3、极度热情、高度责任、自动自发、享受成功。

新人教版八年级数学上册12.3角的平分线的性质(第1课时)导学案2

新人教版八年级数学上册12.3角的平分线的性质（第1课时）导学案流程具体内容学法指导知识链接学习目标1.经历探究角的平分线性质的过程，发展几何直觉.2.会证明角的平分线的性质，会简单运用角的平分线的性质.幻灯片检测1.全等三角形的概念及表示方法2.判定全等的方法有哪些？自学1.角平分仪为什么能平分一个角？P192.如何画一个角的平分线？P193.如何通过作一个平角的平分线得到直线的垂线？P19练习4.角的平分线的性质是什么？如何证明？用几何符号如何表示？P205.证明一个几何命题的步骤是什么？P216.课本中利用角平分线的性质解决了一个什么实际问题？P211.细心研读P19页“探究”结合图形，先画成数学图形，然后写成命题证明形式来说明理由。

已知：求证：证明：展示2.画出∠AOB的角平分线，并复述画法。

3.完成P19中“练习”4.按P20页“探究”完成操作进行观察分析，写出你得出的结论：______________________________________________________________5.角平分线的性质6.角平分线的性质命题的证明,结合证明过程说明:文字命题证明的几个步骤.OABDABC127题图反馈7.填空：如图，∠C＝90°，∠1＝∠2，BC＝7，BD＝4，则(1)D点到AC的距离＝ .(2)D点到AB的距离＝ .8.填空：如图，CD⊥AB，BE⊥AC，∠1＝∠2，根据角平分线的性质可得＝ .9.如图所示, 在△ABC中， AD平分∠BAC, DE⊥AB于E,且DE=5.8cm,BC=11.2cm,则BD=_______10.已知：如图，CD⊥AB，BE⊥AC，∠1＝∠2.求证：OB＝OC.DABC12E9题图OAB CD E1210题图OAB CD E128题11.画出△ABC中∠BAC的平分线AD, 并画出点D到两边的距离.学后反思（教学反思）：B AC。

新人教版八年级数学上册导学案：12-3角的平分线的性质(第1课时,无答案)

新人教版八年级数学上册导学案12.3角的平分线的性质（第1课时）【课前准备】什么是角的平分线？怎样画一个角的平分线？【学习流程】一、问题提出，获取概念1、如右图，AB ＝AD ，B C ＝DC ，沿着A 、C 画一条射线AE ，AE 就是∠BAD 的角平分线，你知道为什么吗2.根据角平分仪的制作原理，如何用尺规作角的平分线？自学课本48页后，思考为什么要用大于21MN 的长为半径画弧？3．OC 是∠AOB 的平分线，点P 是射线OC 上的任意一点，操作测量：取点P 的三个不同的位置，分别过点P 作PD ⊥O A ，PE ⊥OB,点D 、E 为垂足，测量PD 、PE 的长.将三次数据填入下表：观察测量结果,猜想线段PD 与PE 的大小关系，写出结论PD PE 第一次第二次第三次4、命题：角平分线上的点到这个角的两边距离相等.题设：，结论：。

结合第4题图形请你写出已知和求证，并证明命题的正确性解后思考：证明一个几何命题的步骤有那些？5、用数学语言来表述角的平分线的性质定理：如右上图，∵OC 是∠AOB 的平分线，点P 是 ∴二、知识深化，问题解决如图：在△ABC 中，∠C=90°，AD 是∠BAC 的平分线，DE ⊥AB 于E ，F 在AC 上，BD=DF ；求证：CF=EBE D C【学以致用】在Rt △A BC 中，BD 平分∠ABC ， DE ⊥AB 于E ，则⑴图中相等的线段有哪些？相等的角呢？ ⑵哪条线段与DE 相等？为什么？⑶若AB ＝10，BC ＝8，AC ＝6，求BE ，AE 的长和△AED 的周长。

【总结与反思】1、你学到了什么？2、你能提出的问题是？。

人教版数学八年级上册 12.3角的平分线的性质(2) 导学案

12.3角的平分线的性质（2）
班级：姓名：学习日期：评价等级：学习目标：
1、掌握三角形全等的“S ＡS ”条件，能运用“S ＡS ”证明简单的三角形全等问题 2．经历探索三角形全等条件的过程，体会利用操作、•归纳获得数学结论的过程．学习重点：三角形全等的条件．学习难点：寻求三角形全等的条件．
学法指导：数形结合，根据图形培养学生分析问题和解决问题的能力
认真阅读课本50页，完成以下问题 1、复习引入思考（学生合作、教师引导）（1）、画出三角形三个内角的平分线
你发现了什么特点吗？（2）、如图，△ABC 的角平分线BM ，CN 相交于点P ，求证：点P 到三边AB ，BC ，CA 的距离相
等。

2、求证：到角的两边的距离相等的点在角的平分线上。

（提示：先画图，并写出已知、求证，再加以证明）（学生合作、教师引导）
例1、如图，CD ⊥AB ，BE ⊥AC ，垂足分别为D 、E ，BE 、 CD 相交于点O ，OB ＝OC ，求证∠1＝∠ 2
例2：如图3，△ABC 的角平分线BM 、CN 相交于点P ．求证：点P 到三边AB 、BC 、CA 的距离相等．
1.如图，在ABC △中，90C ∠=， AD 平分CAB ∠，8cm 5cm BC BD ==，，那么D 点到直
线AB 的距离是 cm ．
2.如图，AD 平分∠BAC ，DE ⊥AB 于E ，DF ⊥AC 于F ，且DB=DC ，
求证：EB=FC
课前热身、自主预习课堂展示、合作学习
课堂反馈、巩固提升
P
N
M
C
B
A
A
B D
C。

八年级数学上册 12.3 角平分线的性质导学案2(新版)新人教版

八年级数学上册 12.3 角平分线的性质导学案2(新版)新人教版1、会叙述角平分线的性质及“到角的两边距离相等的点在角的平分线上”2、能利用两个性质解决一些实际问题学习重点：角平分线的性质及应用学习难点：利用两个性质解决一些实际问题学习方法：探索归纳法一、课前预习:阅读课本，完成下列的问题：角平分线的判定及几何语言表述【自能学习】复习旧知角平分线的性质定理1、性质定理：角平分线上的点到角的的距离、2、几何语言：（注意：三个已知条件缺一不可）∵，，∴二、探究新知：1、求证：到角的两边的距离相等的点在角的平分线上。

（提示：先画图，并写出已知、求证，再加以证明）小帅已经做出了一些步骤，请你帮他补充完整：解：如右图，过______做射线，已知：，；并且_______=_______求证：_____是的平分线证明：结论：角平分线的判定定理:角的内部到角的两边的点在角的＿＿＿上。

注意：（1）该定理也是证明两角相等的一种方法；（2）三角形的三条角平分线交于一点，这点是三角形的内心，到三边的距离相等、(3）符号语言：∵ PD⊥OA，PE⊥OB，PD= PE ∴ ＿＿＿＿＿＿（）（4）作用：常证明两个角相等2、比较角平分线的性质与判定三、例题学习例1、如图，CD⊥AB，BE⊥AC，垂足分别为D，E，BE，CD相交于点O，OB＝OC，求证：∠1＝∠2例2、如图，△ABC的角平分线BM，CN相交于点P。

求证：点P 到三边AB、BC、CA的距离相等PMNABC四、当堂检测1如图，在四边形中，，平分交于，且，求证：平分2、如图，在△ABC中，BD为∠ABC的平分线，DE⊥AB于点E，且DE＝2cm，AB＝9cm，BC＝6cm，求△ABC的面积、【自能训练】1、已知△ABC中，∠A=60，∠ABC,∠ACB的平分线交于点O，则∠BOC的度数为2、到三角形三条边的距离相等的点是（）A、三条中线的交点B、三条高线的交点C、三条边的垂直平分线的交点D、三条角平分线的交点3、下面哪个点到三角形三边的距离相等（）A、三条角平分线的交点B、三条中线的交点C、三条高的交点D、三角形内任意一点4、如图，的两个外角平分线相交于点，则下面结论正确的是（）A、不平分B、平分C、平分D、5、在中，，是的角平分线，若，，则点到的距离为、6、如图，的三边、、的长分别为20、30、40，其三条角平分线的交点为，则、7、的平分线上一点，到的距离为，则到的距离为、8、如图，在直线上求一点，使得点到射线和的距离相等、9、如图，在中，，点为三条角平分线的交点，于，于，于，且，，，求的长、10、如图，是内一点，在上，在上，且，与的面积相等、求证：平分。

数学人教版八年级上册数学导学案：12.3角的平分线的性质(二)

PNMC B A优质资料---欢迎下载12.3角的平分线的性质(二)学习目标1．会叙述角的平分线的性质及“到角两边距离相等的点在角的平分线上”． 2．能应用这两个性质解决一些简单的实际问题．掌握尺规作图作角平分线 3. 全力以赴，激情投入，享受成功学习的快乐，感受数学严谨推理美. 重点: 角的平分线的判定方法的证明及应用. 难点: 角的平分线的判定方法的探究.预习案使用说明学法指导诵读教材P49-P50的内容，进行知识梳理；熟记基础知识. 教材助读1.画出三角形三个内角的平分线你发现了什么特点吗？2.如图，△ABC 的角平分线BM ，CN 相交于点P ，求证：点P 到三边AB ，BC ，CA 的距离相等。

探究案探究点一1.求证：角的内部到角的两边的距离相等的点在角的平分线上。

（提示：先画图，并写出已知、求证，再加以证明）探究点二2.比较角平分线的性质与判定3.完成书上49页思考探究点三 4.如图，CD ⊥AB ，BE ⊥AC ，垂足分别为D ，E ，BE ，CD 相交于点O ，OB ＝OC ，求证∠1＝∠2当堂检测1. 如图点M ，N 分别是OA ，OB 上的点，点P 在射线OC 上，下列条件不能推出OC 平分∠AOB 的是( ) A. PM=PN ，OM=ON B.OM=ON ，∠OPM=∠OPN C. PM ⊥OA ，PN ⊥OB ，PM=PN D. PM ⊥OA ，PN ⊥OB ，OM=ON2. 如图，DE ⊥AB 于D ，CE ⊥BC 于C ，且DE=CE ，则下列结论不一定正确的是( ) A. BE 平分∠ABC B. EB 平分∠CED C . AE 十DE=AC D. ∠A=∠ABE3. 如图在△ABC 中，AD 平分∠BAC ， DE ⊥AB 于E ，DF ⊥AC 于F ，M 为AD上任意一点，则下列结论错误的是 ( )A. DE=DFB. ME=MFC. AE=AFD. BD=DC 4. 如图直线I 1，l 2，l 3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有( ) A.1处 B .2处 C. 3处 D. 4处5.已知:如图，BE=CF ，BF ⊥AC 于点F ，CE ⊥AB 于点E ，BF 和CE 交于点D. 求证:AD 平分∠BAC.。

新人教版八年级数学上册12.3角平分线性质(第1课时)导学案

新人教版八年级数学上册 12.3 角均分线的性质（第 1 课时）导教案【学习目标】：1、经历角的均分线性质的发现过程，初步掌握角的均分线的性质定理．2、能运用角的均分线性质定理解决简单的几何问题 .3、极度热忱、高度责任、自动自觉、享受成功。

【学习要点】：掌握角的均分线的性质定理【课前预习】： 1、复习思虑什么是角的均分线？如何画一个角的均分线？2．如右图， AB ＝ AD ， BC ＝ DC ，沿着 A 、 C 画一条射线 AE ， AE 就是∠ BAD 的角均分线，你知道为何吗3. 依据角均分仪的制作原理，如何用尺规作角的均分线？自学课本 48 页后，思虑为何要用大于1MN 的长为半径画弧？24． OC 是∠ AOB 的均分线，点 P 是射线 OC 上的随意一点，操作丈量：取点 P 的三个不一样的地点，分别过点 P 作 PD ⊥ OA ，PE ⊥ OB,点 D 、 E 为垂足，丈量 P D 、 PE 的长 . 将三次数据填入下表：察看丈量结果, 猜想线段 PD 与 PE 的大小关系，写出结论PDPE第一次第二次第三次5、命题：角均分线上的点到这个角的两边距离相等 .题设：结论：联合第 4 题图形请你写出已知和求证，并证明命题的正确性解后思虑：证明一个几何命题的步骤有哪些？（ 1）明确命题中的和；（ 2）依据题意 , 画出,并用表示已知和求证：（3）经过剖析 , 找出由已知推出求证的门路 , 写出证明过程 .6、用数学语言来表述角的均分线的性质定理：如右上图，∵∴【讲堂学习】：【合作研究·释疑】：1、如下图OC是∠ AOB 的均分线 ,P 是 OC上随意一点 , 问 PE=PD?为何 ?EAO CPD B2、如图：在△ABC 中，∠ C=90°， AD 是∠ BAC 的均分线， DE⊥ AB 于 E， F 在 AC 上， BD=DF；求证： CF=EB【知识拓展】：在 Rt△ ABC中， BD均分∠ ABC， DE⊥ AB于 E，则⑴图中相等的线段有哪些？相等的角呢？⑵哪条线段与 DE相等？为何？⑶若 AB＝ 10， BC＝ 8， AC＝ 6，求 BE， AE 的长和△ AED的周长。