离散10_answer
离散数学试题及答案

Mock ExamNotes___________________________________________________________________________________ 1. There are 38 questions in this mock exam. The real exam will consist of about 25 questions that will be relatively similar to those here... that does not mean “identical” to those...2. If you do these well, you should have no big difficulties in the final exam.3. I encourage you to work these questions first on your own, without help, to see what you do or do not understand. You may seek help after that. Remember that no one will help you or give you hints during the exam. We will clarify the questions if something is not clear but not more than that.#01 - Page 13 #8Let p and q be the propositionsp : I bought a lottery ticket this week.q : I won the million dollar jackpot.Express each of these propositions as an English sentence.a) ¬p I did not buy a lottery ticket this week.b) p ∨q I bought a lottery ticket this week or I won the million dollar jackpot.c) p → q If I bought a lottery ticket this week then I won the million dollar jackpot.d) p ∧q I bought a lottery ticket this week and I won the million dollar jackpot.e) p ↔ q I bought a lottery ticket this week if, and only if, I won the million dollar jackpot.#02 - Page 15 #36Construct a truth table for each of these compound propositions.a) (p ∨q) ∨rp q r p ∨q(p ∨q) ∨rT T T T TT T F T TT F T T TT F F T TF T T T TF T F T TF F T F TF F F F Fc) (p ∧q) ∨r∧(p q)∧∨rp q r p qT T T T TT T F T TT F T F TT F F F FF T T F TF T F F FF F T F TF F F F Fe) (p ∨q)∧¬r∨∧¬rp q r p ∨q¬r(p q)T T T T F FT T F T T TT F T T F FT F F T T TF T T T F FF T F T T TF F T F F FF F F F T F#03 - Page 35 #9Show that each of these conditional statements is a tautology by using truth tables.c) ¬p → (p → q)p q¬p p → q¬p → (p → q)T T F T TT F F F TF T T T TF F T T Td) (p ∧q) → (p → q)∧p → q(p q) → (p → q)∧p q p qT T T T TT F F F TF T T T TF F T T Te) ¬(p → q) → pp q p → q¬(p → q)¬(p → q) → p T T T F TT F F T TF T T F TF F T F T#04 - DNFWrite the following proposition in disjunctive normal form:s = (r → p) → (p∧q)p q r r → p p∧q sT T T T T TT T F T T TT F T T F FT F F T F FF T T F F TF T F T F FF F T F F TF F F T F Fs=(p∧q∧r)∨(p∧q∧¬r)∨(¬p∧q∧r)∨(¬p∧¬q∧r)=(p∧q)∨(¬p∧r)#05 - Page 53 #8Let I (x) be the statement “x has an Internet connection” and C(x, y) be the statement “x and y have chatted over the Internet,” where the domain for the variables x and y consists of all students in your class. Use quantifiers to express each of these statements.b) Rachel has not chatted over the Internet with Chelsea.C(Rachel, Charles)e) Sanjay has chatted with everyone except Joseph.∀x(x ≠ Joseph → C(Sanjay, x))f ) Someone in your class does not have an Internet connection.∃x(¬I(x))i) Everyone except one student in your class has an Internet connection.!∃y[¬I(y) ∧∀x(x ≠ y → I(x))]j) Everyone in your class with an Internet connection has chatted over the Internet with at least one other student in your class.∃∀x yC(x, y)m) There is a student in your class who has chatted with everyone in your class over the Internet.∃x∀yC(x, y)#07 – Page 67 #27Determine the truth value of each of these statements if the domain for all variables consists of all real numbers.a) ∀x∃y(x2 = y) Truec) ∃x∀y(xy = 0)Truee) ∀x(x = 0 → ∃y(xy = 1))False∧x − y = 1)Falsei) ∀x∃y(x + y = 2 2j) ∀x∀y∃z(z = (x + y)/2)TrueUse rules of inference to show that the hypotheses “If it does not rain or if it is not foggy, then the sailing race will be held and the lifesaving demonstration will go on,” “If the sailing race is held, then the trophy will be awarded,” and “The trophy was not awarded” imply the conclusion “It rained.”Define the following literals:r It rainsf It is foggys The sailing race will be heldd The lifesaving demonstration will go ont The trophy will be awardedThe premises are then∧P1(¬r ∨ ¬f) → (s d)P2s → tP3¬tand the conclusion isrThe proof proceeds as follows:1¬t P32s → t P23¬s Modus tollens with 1 and 2'∨Addition to 34¬s ¬d∧De Morgan's law5¬(s d)∨) → (s d)∧P16(¬r ¬f∨)Modus tollens with 5 and 67¬(¬r ¬f∧De Morgan's law8r f9r Simplification of 8#09 – Page 80 #27Use rules of inference to show that if ∀x(P(x) → (Q(x) ∧S(x))) and ∀x(P(x) ∧R(x)) are true, then∀x(R(x) ∧S(x)) is true.∀∧Premise1x(P(x) R(x))∧Universal instantiation2P(c) R(c)3P(c)Simplification from 24x(P(x) →∧Premise∀(Q(x) S(x)))∧Universal instantiation5P(c) → (Q(c) S(c))∧Modus ponens with 3 and 56Q(c) S(c)7S(c)Simplification from 68R(c)Simplification from 2∧Conjunction of 7 and 89R(c) S(c)∀∧Universal generalization10x(R(x) S(x))Prove that if n is a positive integer, then n is odd if and only if 5n + 6 is odd.First, assume that n is odd, so that n = 2k+1 for some integer k. Then 5n+6 = 5(2k+1)+6 = 10k + 11 = 2(5k + 5) + 1. Hence, 5n + 6 is odd. To prove the converse, suppose that n is even, so that n = 2k for some integer k. Then 5n + 6 = 10k + 6 = 2(5k + 3), so 5n + 6 is even. Hence, n is odd if and only if 5n + 6 is odd.#11 – Page 126 #19What is the cardinality of each of these sets?a) {a}1b) {{a}}1c) {a, {a}}2d) {a, {a}, {a, {a}}}3#12 – Page 126 #40Explain why (A × B) × (C × D) and A × (B × C) × D are not the same.The tuples in those sets do not have the same composition. The tuplets in (A × B) × (C × D) are pairs of pairs: ((x,y),(u,v)). However, the tuplets in A × (B × C) × D are ordered triplets with two singletons and a pair: (u, (x,y), v).#13 – Page 136 #27Draw the Venn diagrams for each of these combinations of the sets A, B, and C.b) (A ∩ B) ∪(A ∩ C)c) (A ∩ B) ∪(A ∩ C)#14 – Page 153 #22Determine whether each of these functions is a bijection from R to R.a) f (x) = −3x + 4Yesb) f (x) = −3x2 + 7No: elements greater than 7 have no preimages.c) f (x) = (x + 1)/(x + 2)No: -2 has no imaged) f (x) = x5 + 1YesFor each of these sequences find a recurrence relation satisfied by this sequence. (The answers are not unique because there are infinitely many different recurrence relations satisfied by any sequence.)a) a n= 3a n= a n-1c) a n= 2n + 3a n-1= 2(n - 1)+ 3 = 2n + 3 – 2 = a n – 2. This implies that a n= a n-1+ 2.f ) a n= n2 + n(e1)Here we have two independent terms with n. We will need two additional formulas:a n-1= (n-1)2 + n – 1 = n2 – 2n + 1 + n – 1 = n2 – n(e2)a n-2= (n-2)2 + n – 2 = n2 – 4n + 4 + n – 2 = n2 – 3n + 2(e3)From (e1) and (e2), we have a n – a n-1 = 2n(e4)From (e2) and (e3), we have a n-1 – a n-2 = 2n – 2(e5)From (e4) and (e5), we have a n – a n-1 – (a n-1 – a n-2) = a n – 2a n-1+ a n-2 = 2, or a n = 2a n-1– a n-2+ 2 g) a n= n + (−1)n(e1)a n-1 = n – 1 + (−1)n-1 = n – 1 – (−1)n(e2)From (e1) and (e2), we have a n – a n-1 = 1 + 2(−1)nor a n = a n-1 + 1 + 2(−1)nWe can split this into the odd an even n's:a2k = a2k-1 + 1a2k+1 = a2k− 1h) a n= n!a n = n a n-1#16 – Page 583 #30 (+ additional questions)Let R1 = {(1, 2), (2, 3), (3, 4)} and R2 = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (3, 4)} be relations from {1, 2, 3, 4} to {1, 2, 3, 4}. Finda) R1∪R2 = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (3, 4)} = R2b) R1 ∩ R2 = {(1, 2), (2, 3), (3, 4)} = R1c) R1 − R2 = ∅d) R2 − R1 = {(1, 1), (2, 1), (2, 2), (3, 1), (3, 2), (3, 3)}e) R1 ◦ R2 = {(1, 2), (1, 3), (2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4)}f ) R2 ◦ R1 =g) Draw the graph of R1 ◦ R2.h) Find the reflexive, symmetric and transitive closures ofReflexive closure = {(1, 1), (1, 2), (2, 2), (2, 3), (3, 4), (3, 4), (4, 4)}Symmetric closure = {(1, 2), (2, 1), (2, 3), (3, 2), (3, 3), (4, 3)}Transitive closure = {(1, 2), (1, 3), (2, 3), (2, 4), (3, 1), (3, 4), (4, 1), (4, 2)}Let R be the relation consisting of all pairs (x, y) such that x and y are strings of uppercase and lowercase English letters with the property that for every positive integer n, the n th characters in x and y are the same letter, either uppercase or lowercase. Show that R is an equivalence relation.That definition basically means that two strings are equivalent if, and only if, they have the same length and every corresponding characters x i and y i are the same letter, either lower or upper case.Let c and C stand for the lower and upper cases of a same letter in the English alphabet.Clearly k, x∀k = x k. So (x, x) ∈ R.So R is reflexive.If (x,y)∈ R, then k, x∀k∈ {c, C} and y k∈ {c, C}. So (y, x) ∈ R also. So R is symmetric.If (x,y)∈ R and (y,z)∈ R, then [x k∈ {c, C}, y k∈ {c, C}] and [y k∈ {c, C}, z k∈ {c, C}], which implies that [x k∈ {c, C},z k∈ {c, C}]. So (x, z) ∈ R. So R is transitive.Therefore R is an equivalence relation.#18 – Page 631 #34Answer these questions for the poset ({2, 4, 6, 9, 12, 18, 27, 36, 48, 60, 72}, |).a) Find the maximal elements.27, 48, 60, 72b) Find the minimal elements.2, 9c) Is there a greatest element?Nod) Is there a least element?Noe) Find all upper bounds of {2, 9}.18,36 72f ) Find the least upper bound of {2, 9}, if it exists.18g) Find all lower bounds of {60, 72}.2, 4, 6, 12h) Find the greatest lower bound of {60, 72},if it exists.12#19 – Group TheoryConsider the set G={a1+a2√3 | a1,a2∈ℚ∧a1a2≠0}with the usual multiplication operation.a) Show that G is a group by verifying the axioms of closure, associativity, existence of an identity element, and existence of an inverse element for every element. Specify what the identity element is and the form an an inverse element.1. Closure: Let a,b∈G. Then ab=(a1+a2√3)(b1+b2√3)=(a1b1+3a2b2)+(a1b2+a2b1)√(3)∈G2 Associativity: Let a ,b ,c ∈G . Then (ab )c =[(a 1+a 2√3)(b 1+b 2√3)]c=[(a 1b 1+3a 2b 2)+(a 1b 2+a 2b 1)√(3)](c 1+c 2√3)=[(a 1b 1+3a 2b 2)c 1+3(a 1b 2+a 2b 1)c 2]+[(a 1b 1+3a 2b 2)c 2+(a 1b 2+a 2b 1)c 1]√(3)=a 1b 1c 1+3a 2b 2c 1+3a 1b 2c 2+3a 2b 1c 2+[a 1b 1c 2+3a 2b 2c 2+a 1b 2c 1+a 2b 1c 1]√(3)=[a 1(b 1c 1+3b 2c 2)+3a 2(b 1c 2+b 2c 1)]+[a 2(b 1c 1+3b 2c 2)+a 1(b 1c 2+b 2c 1)]√(3)=(a 1+a 2√3)[(b 1c 1+3b 2c 2)+(b 1c 2+b 2c 1)√(3)]=a [(b 1+b 2√3)(c 1+c 2√3)]=a (bc )3. Identity element. Let this element be e =e 1+e 2√. Thenea =(e 1+e 2√3)(a 1+a 2√3)=(e 1a 1+3e 2a 2)+(e 1a 2+e 2a 1)√(3)=(a 1+a 2√3).This implies that for every a 1 and a 2:e 1a 1+3e 2a 2=a 1e 1a 2+e 2a 1=a 2That implies e 1=1and e 2=0. Thus e =1.4. Inverse element. Consider a =a 1+a 2√3∈G and let its inverse be a −1=x 1+x 2√3if it exists. Then we must havea −1a =(x 1+x 2√3)(a 1+a 2√3)=(x 1a 1+3x 2a 2)+(x 1a 2+x 2a 1)√(3)=1=e This impliesx 1a 1+3x 2a 2=1x 1a 2+x 2a 1=0The solution isa −1=a 1−a 2√3a 12−3a 22.Thus G forms a group.b) Is G Abelian?Yes: ab =(a 1+a 2√3)(b 1+b 2√3)=(a 1b 1+3a 2b 2)+(a 1b 2+a 2b 1)√(3)=ba because this expression is symmetric.#20 – Page 665 #9Determine the number of vertices and edges and find the in-degree and out-degree of each vertex for the shown directed multigraph:5 vertices 13 edgesdeg+(a) = 1, deg+(b) = 1, deg+(c) = 5, deg+(d) = 4, deg+(e) = 0deg−(a) = 6, deg−(b) = 5, deg−(c) = 2, deg−(d) = 2, deg−(2) = 0#21 – Page 666 #28Suppose that a newcompany has five employees: Zamora, Agraharam, Smith, Chou, and Macintyre. Each employee will assume one of six responsiblities: planning, publicity, sales, marketing,development, and industry relations. Each employee is capable of doing one or more of these jobs: Zamora could do planning, sales, marketing, or industry relations; Agraharam could do planning or development; Smith could do publicity, sales, or industry relations; Chou could do planning, sales, or industry relations; and Macintyre could do planning, publicity, sales, or industry relations.a) Model the capabilities of these employees using a bipartite graph.b) Find an assignment of responsibilites such that each employee is assigned one responsibility.Note: the assignment is not unique. The only forced choices are (Z, ma) and (A, de). There is a variety of possibilities for the other 3.c) Is the matching of responsibilities you found in part (b) a complete matching? Is it a maximum matching?The matching (from {Z, A, S, C, M} to {ma, de, sa, pl, pu, ir}) is complete because every employee is matched with a job. It is a maximum because |M| = 5 = |{Z, A, S, C, M}|#22 – Page 676 #21 (+ additional questions)Consider the following grapha) Find the adjacency matrix A of the graph A =(1110100220111210)b) Find how many paths of length 3 there are from c to b A 3=A (1110100220111210)(1110100220111210)=(1110100220111210)(4123353054415125)=(12109414361318710121512124)So there are 6 paths from c to b.#23 – Page 676 #38Determine whether the following two graphs are isomorphic. If so, construct an isomorphism.Notice the second graph can be deformed like this (by moving v 2 all the way down and rotating the other vertices by about a quarter of a turn):It has 2 circuits of length 4 whereas the graph on the left has only 1. That immediately implies that these graphs are not isomorphic.#24 – Page 692 #31-32Consider the following graphs#31#31a) List the cut vertices c c, db) List the cut edges none(c,d)c) What is the vertex connectivity κ(G)?11d) What is the edge connectivity λ(G)?21#25 – Page 704 #22Determine whether the directed graph shown has an Euler circuit. Construct an Euler circuit if one exists. If no Euler circuit exists, determine whether the directed graph has an Euler path. Construct an Euler path if one exists.The vertices' total degrees are all even except for vertices b and c. So it has no Euler circuit but there might be an Euler path, although this is not guaranteed because the graph is directed. However every vertex with an even total degree has equal in and out degrees. Beccause the out-degree of c is larger than its in-degree, then the starting point has to be c. In fact, we o find an Euler path:c → e → b → c → b → f → a → f → e → f →d →e → a → b → d → c → b#26 – Page 716 #8Find a shortest path (in mileage) between each of the following pairs of cities in the airline system shown in Figure 1.Note: You must show every steps of the algorithmB N M ACD S L-0------N 191/N-1090/N760/N722/N-2534/N2451/N B --1090/N760/N722/N-2534/N2451/N C --1090/N760/N-1630/C2534/N2451/N A --1090/N--1630/C2534/N2451/N D --1090/N---2534/N2451/N M ------2534/N2451/N LPath = N → L Distance = 2451b) Boston and San FranciscoB N M ACD S L0-------B -191/B--860/B---N --1281/N951N860/B-2725/N2642/N C --1281/N951N-1768/C2715/C2642/N A --1281/N--1768/C2715/C2642/N M -----1768/C2715/C2642/N D ------2715/C2602/D L ------2715/C-SPath = B → C → S Distance = 2715c) Miami and DenverB N M ACD S L--0-----M -1090/M-595/M----A -1090/M--1201/A---N 1281/N---1201/A-3624/N3541/N C 1281/N----2109/C3056/C3541/N B -----2109/C3056/C3541/N DPath = M → A → C → D Distance = 2109B N M ACD S L--0-----M-1090/M-595/M----A-1090/M--1201/A---N1281/N---1201/A-3624/N3541/N C1281/N----2109/C3056/C3541/N B-----2109/C3056/C3541/N D------3056/C2943/D LPath = M → A → C → D → L Distance = 2943#27 – Page 726 #12Suppose that a connected planar graph has eight vertices, each of degree three. Into how many regions is the plane divided by a planar representation of this graph?We have V = 8. Each node has a degree equal to 3. The sum of all the degrees is therefore 24 and we know it is equal to twice the number of edges; thus E = 12. Recall Euler's formula: V – E + F = 2. So we have 8 – 12 + F = 2, which implies that F = 6.#28 – Page 732 #4Construct the dual graph for the map shown. Then find the number of colors needed to color the map so that no two adjacent regions have the same color.#29 – Page 733 #17Schedule the final exams for Math 115, Math 116, Math 185, Math 195, CS 101, CS 102, CS 273, and CS 473, using the fewest number of different time slots, if there are no students taking both Math 115and CS 473, both Math 116 and CS 473, both Math 195 and CS 101, both Math 195 and CS 102, both Math 115 and Math 116, both Math 115 and Math 185, and both Math 185 and Math 195, but there are students in every other pair of courses.The best way to obtain a graph for this is to draw a complete graph and then remove edges according to the description in the above paragraph.{MAT115, MAT116, CS473}{MAT185, MAT195}{CS101}{CS102}{CS273}The scheduling is not unique.#30 – Page 755 #4Consider the following rooted tree:a) Which vertex is the root?ab) Which vertices are internal?b, d, e, g, h, i, oc) Which vertices are leaves?c, f, j, k, l, m, n, p, q, r, sd) Which vertices are children of n?nonee) Which vertex is the parent of g?bf ) Which vertices are siblings of k?jg) Which vertices are ancestors of o?a, d, ih) Which vertices are descendants of d?h, i, n, o, p, q, r, s#31 – Page 756 #20How many leaves does a full 3-ary tree with 100 vertices have?L=(m−1)n+1n =(3−1)×100+13=2013=67MATMATMAT185MAT195CS473CS273CS101CS102#32 – Page 769 #2Build a binary search tree for the words oenology, phrenology, campanology, ornithology, ichthyology , limnology, alchemy , and astrology using alphabetical order.#33 – Page 770 #24Use Huffman coding to encode these symbols with given frequencies: A: 0.10, B: 0.25, C: 0.05, D: 0.15, E: 0.30, F: 0.07, G: 0.08. What is the average number of bits required to encode a symbol?0.050.070.080.100.150.250.30 C F G A D B E0.080.100.120.150.250.30 GADBE0.120.150.180.250.30 DB E0.180.250.270.30 BE0.270.300.43Eoenologyphrenologycampanology ichthyology alchemy astrologylimnologyornithology0.430.571.00Codes:A = 110B = 10C = 0111D = 010E = 00F = 0110G = 111Average nuber of bits = (3 + 2 + 4 + 3 + 2 + 4 + 3) / 7 = 21/7 = 3#34 – Page 783 #10-11Consider the following rooted tree:In which order are the vertices visited using a preorder traversal?a, b, d, e, i, j, m, n, o, c, f, g, h, k, p, l#35 – Page 784 #23What is the value of the following prefix expression?a) − 2 / 8 4 3∗− 2 ∗/ 8 4 3=− 2 2∗ 3=− 4 3=1GACFCFb) ↑ − 3 3 4 2 5∗∗∗ 5=↑ − 3 3∗ 8 5∗ 4 2↑ − 3 3=↑ − 9 8 5=↑ 1 5=1c) + − ↑ 3 2 ↑ 2 3 / 6 − 4 2+ − ↑ 3 2 ↑ 2 3 / 6 − 4 2=+ − ↑ 3 2 ↑ 2 3 / 6 2=+ − ↑ 3 2 ↑ 2 3 3=+ − ↑ 3 2 8 3=+ − 9 8 3=+ 1 3=4∗d) + 3 + 3 ↑ 3 + 3 3 3+ 3 + 3 ↑ 3∗↑ 3 6 3∗+ 3 3 3= + 3 + 3∗+ 3 729 3= + 3=∗+ 3 732 3∗= 735 3=2205#36 – Page 795 #13Use depth-first search to produce a spanning tree for the following simple graph. Choose vertex 'a' as the root of this spanning tree and assume that the vertices are ordered alphabetically.a →b →c →d →e →f →g →h → Ig → j#37 – Page 802 #3Use Prim's algorithm to find a minimum spanning tree (and its total weight) for the following weighted graph:(ef)1(cf)3(eh)3(hi)2(gh)4(bc)4(bd)3(ad)2Total weight = 22#38 – Page 802 #8Use Kruskal’s algorithm to find a minimum spanning tree for the weighted graph in Exercise 4 (#37). (ef)1(ad)2(hi)2(bd)3(cf)3(eh)3(bc)4(gh)4Total weight = 22The spanning tree is identical to that in Exercise 4 (#37).。
离散数学习题及答案01

CIS 607: Mathematical Basis for ComputingSOLUTIONS OF HOMEWORK 1Homework 1 -- Propositional Logic, Predicate Logic and ProofsDue Date: February 14, 2017In this homework, you will answer the following questions. Prepare a pdf file for your solutions and upload that pdf file into the blackboard system.Q1)Let p and q be the propositionsp : I bought a lottery ticket this week.q : I won the million dollar jackpot.Express each of these propositions as an English sentence.∙p →qo If I bought a lottery ticket this week, then I won the million dollar jackpot on Friday.∙¬p ∨(p ∧q)o Either I did not buy a lottery ticket this week, or else I did buy one and won the million dollar jackpot on Friday.∙¬p →¬qo If I did not buy a lottery ticket this week, then I did not win the million dollar jackpot on Friday.Q2)Let p and q be the propositionsp : It is below freezing.q : It is snowing.Write these propositions using p and q and logical connectives (including negations).∙It is not below freezing and it is not snowing.o(¬p ∧¬q)∙If it is below freezing, it is also snowing.o p →q∙Either it is below freezing or it is snowing, but it is not snowing if it is below freezing.o(p ∨ q) ∧ ( p →¬q)Q3)Construct a truth table for each of these compound propositions.∙p →(¬q ∨r)∙(p →q) ∧(¬p →r)∙(¬p ↔¬q) ↔(q ↔r)∙Show that ¬(p ↔q) and p ↔¬q are logically equivalent.o p q ¬(p ↔q) p ↔¬qo T T F Fo T F T To F T T To F F F F∙Show that (p →q) →r and p →(q →r) are not logically equivalent.o p q r (p →q) →r p →(q →r)o F F F F TQ5)Determine the truth value of each of these statements if the domain consists of all integers.∙∀n(n + 1 > n)o T∙∃n(2n = 3n)o T (when n=0)∙∃n(n = −n)o T (when n=0)∙∀n(3n ≤4n)o F (when n is a negative integer)Q6)Suppose that the domain of the propositional function P(x) consists of the integers 1, 2, and 3. Write out each of these propositions using disjunctions, conjunctions, and negations.∙∃xP(x)o P(1) ∨P(2) ∨P(3)∙∀xP(x)o P(1) ∧P(2) ∧P(3)∙¬∃xP(x)o¬ (P(1) ∨P(2) ∨P(3))∙¬∀xP(x)o¬ (P(1) ∧P(2) ∧P(3))Express the negations of each of these statements so that all negation symbols immediately precede predicates.∙∀x∃y∀zT (x, y, z)o∃x∀y∃z¬T (x, y, z)∙∀x∃yP(x, y) ∨∀x∃yQ(x, y)o∃x∀y¬P(x, y) ∧∃x∀y¬Q(x, y)∙∀x∃y(P(x, y) ∧∃zR(x, y, z))o∃x∀y(¬P(x, y) ∨∀z¬R(x, y, z))∙∀x∃y(P(x, y) →Q(x, y))o∃x∀y(P(x, y) ∧¬Q(x, y))Q8)∙Determine whether ∀x(P(x) →Q(x)) and ∀xP(x) →∀xQ(x) are logically equivalent. Justify your answer.o NOTo P: is even number, Q: is odd numbero∀x P(x) →∀xQ(x) is true since ∀xP(x) is false and ∀xQ(x) is falseo But ∀x(P(x) →Q(x)) is false∙Determine whether ∀x(P(x) ↔Q(x)) and ∀x P(x) ↔∀xQ(x) are logically equivalent. Justify your answer.o NOTo P: is even number, Q: is odd numbero∀x P(x) ↔∀xQ(x) is true since ∀xP(x) is false and ∀xQ(x) is falseo But ∀x(P(x) ↔Q(x)) is false∙Show that ∃x(P(x) ∨Q(x)) and ∃xP(x) ∨∃xQ(x) are logically equivalent.o if ∃x(P(x) ∨Q(x)) is trueo P(a) ∨Q(a) is true for a constant ‘a’ (∃-inst)o If P(a) is true →∃xP(x)is true →∃xP(x) ∨∃xQ(x) is trueo If Q(a) is true →∃xQ(x)is true →∃xP(x) ∨∃xQ(x) is trueoo if ∃x(P(x) ∨Q(x)) is falseo→ there is no constant such that P(a) ∨Q(a) is trueo→ there is no constant such that P(a) is true or there is no constant such that Q(a) is trueo→∃xP(x) is false and ∃xQ(x) is falseo→∃xP(x) ∨∃xQ(x) is falseQ9)∙Use rules of inference to show that if ∀x(P(x) →(Q(x) ∧S(x))) and ∀x(P(x) ∧R(x)) are true, then ∀x(R(x) ∧S(x)) is true.Step Reason1.∀x(P(x) → (Q(x) ∧ S(x))) Premise2.∀x(P(x) ∧ R(x)) Premise3.P(a) ∧ R(a) for arbitrary a UI from 24.P(a) for arbitrary a Simplification from 35.R(a) for arbitrary a Simplification from 36.P(a) → (Q(a) ∧ S(a))) for arbitrary a UI from 17.(Q(a) ∧ S(a)) for arbitrary a MP from 4 and 68.S(a) for arbitrary a Simplification from 79.R(a) ∧ S(a) for arbitrary a Conjunction from 5 and 810.∀x(R(x) ∧ S(x)) UG from 9∙Use rules of inference to show that if ∀x(P(x) ∨Q(x)), ∀x(¬Q(x) ∨S(x)), ∀x(R(x)→¬S(x)), and ∃x¬P(x) are true, then ∃x¬R(x) is true.Step Reason1.∀x(P(x) ∨ Q(x)) Premise2.∀x(¬Q(x) ∨ S(x)) Premise3.∀x(R(x) →¬S(x)) Premise4.∃x¬P(x) Premise5.¬P(a) for some a EI from 46.P(a) ∨ Q(a) UI from 17.Q(a) for some a Disjunctive Syllogism from 5 and 68.¬Q(a) ∨ S(a) UI from 29.S(a) for some a Disjunctive Syllogism from 7 and 810.R(a) →¬S(a) UI from 311.¬R(a) for some a Modes Tollens from 9 and 1012.∃x¬R(x) Existential Generalization (EG) from 11Q10)∙Use a direct proof to show that every odd integer is the difference of two squares.Direct Proofo Let n be an odd integer such that n=2k+1 where k is an integer (definition of odd integers) o Let squares of two integers k and (k+1) such as k2 and (k+1)2= k2+2k+1o(k+1)2 - k2 = 2k+1o So, n is the difference of two squares.o QED∙Show that if n is an integer and n3+ 5 is odd, then n is even using a proof by contraposition.Proof by Contrapositiono Assume n is an odd integer (negation of even is odd)o So, n=2k+1 where k is an integer (definition of odd integers)o n3 + 5 = (2k+1)3 + 5 = 8k3+12k2 +6k+1+5 = 2(4k3+6k2 +3k+3)o So, n3 + 5 = 2m where m is an integer such that m = (4k3+6k2 +3k+3)o Thus, n3 + 5 is an even integer (negation of “n3 + 5 is odd”)o Then, n is even (not odd)o QED.∙Prove that if n is an integer and 3n + 2 is even, then n is even using a proof by contradiction.Proof by Contradictiono Assume that n is an odd integer (negation of even is odd)o So, n=2k+1 where k is an integer (definition of odd integers)o3n+2 = 3(2k+1)+2 = 6k+5 = 2(3k+2)+1o So, 3n+2 = 2m+1 where m is an integer such that m=3k+2o Thus, 3n+2 is odd (contradiction with our assumption “3n + 2 is even”)o So, n is eveno QED.。
离散数学自考试题

离散数学自考试题离散数学是计算机科学、信息科学等领域中的一门基础课程,它涉及到离散结构、逻辑、证明、图论、集合论等内容。
为了帮助大家更好地应对离散数学自考,以下是一些典型的离散数学试题。
第一部分:命题逻辑与谓词逻辑1. 简单命题与复合命题假设p表示"今天下雨",q表示"我会带伞",请写出以下复合命题的真值表:(1)p∨q(2)¬p∧q2. 谓词逻辑与谓词符号转换将以下自然语言句子转换为谓词逻辑符号表示:(1)"每个人都喜欢巧克力"(2)"存在一个学生没有按时交作业"第二部分:集合与关系1. 集合运算与分拣问题设A={1,2,3,4,5},B={3,4,5,6,7},C={4,5,6,7,8},求出以下集合的并、交、差:(1)A∪B(2)B∩C(3)A-B2. 关系的性质与运算定义集合A={1,2,3},B={3,4,5},请回答以下问题:(1)关系R={(x,y)|x∈A, y∈B, x+y>5}是自反的吗?(2)关系S={(x,y)|x∈A, y∈B, x<y}是对称的吗?第三部分:图论1. 图的遍历与连通性给定以下无向图的邻接矩阵,请使用深度优先搜索算法遍历整个图,并判断该图是否连通。
```[0 1 1 1 0][1 0 0 1 0][1 0 0 1 1][1 1 1 0 1][0 0 1 1 0]```2. 最短路径问题给定以下有向带权图的邻接矩阵,请使用Dijkstra算法求解从顶点A到其他各顶点的最短路径及其长度。
```[0 1 3 ∞ ∞][∞ 0 1 2 ∞][∞ ∞ 0 ∞ 4][∞ ∞ ∞ 0 2][∞ ∞ ∞ ∞ 0]```第四部分:计数与概率1. 排列组合问题从1、2、3、4、5这五个数字中任选3个数字组成不重复的数,有多少种可能的情况?2. 概率计算一个有10个红球和5个蓝球的盒子,从中依次取球,不放回。
离散期末考试题及答案

离散期末考试题及答案离散数学期末考试题及答案一、选择题(每题2分,共20分)1. 在集合论中,以下哪个符号表示属于关系?A. ∈B. ∉C. ⊆D. ⊂答案:A2. 有限集合A和B的并集,其元素个数最多是A和B元素个数之和,这个性质称为:A. 德摩根定律B. 幂集C. 并集原理D. 子集原理答案:C3. 命题逻辑中,以下哪个命题是真命题?A. (p ∧ ¬p) ∨ qB. (p ∨ ¬p) ∧ qC. (p ∨ q) ∧ ¬pD. (p ∧ q) ∨ ¬p答案:B4. 在图论中,一个无向图的边数至少是顶点数的多少倍才能保证图中至少存在一个环?A. 1B. 2C. 3D. 4答案:B5. 以下哪个算法用于生成一个集合的所有子集?A. 欧拉回路B. 哈密顿回路C. 深度优先搜索D. 子集生成算法答案:D6. 在关系数据库中,以下哪个操作用于删除表中的行?A. SELECTB. INSERTC. UPDATED. DELETE答案:D7. 以下哪个是有限自动机的状态?A. 初始状态B. 终止状态C. 转移状态D. 所有选项答案:D8. 以下哪个是图论中的一个基本定理?A. 欧拉定理B. 哈密顿定理C. 狄拉克定理D. 所有选项答案:D9. 在命题逻辑中,以下哪个是德摩根定律的逆命题?A. ¬(p ∨ q) ≡ ¬p ∧ ¬qB. ¬(p ∧ q) ≡ ¬p ∨ ¬qC. ¬(p ∨ q) ≡ ¬p ∨ ¬qD. ¬(p ∧ q) ≡ ¬p ∧ ¬q答案:B10. 在集合论中,以下哪个操作表示集合的差集?A. ∩B. ∪C. -D. ×答案:C二、填空题(每空3分,共30分)11. 集合{1, 2, 3}的幂集包含________个元素。
离散数学第二版罗熊课后答案

离散数学第二版罗熊课后答案第1章绪论 1 .试述数据、数据库、数据库系统、数据库管理系统的概念。
答:( l )数据( Data ) :叙述事物的符号记录称作数据。
数据的种类存有数字、文字、图形、图像、声音、正文等。
数据与其语义就是不可分的。
解析在现代计算机系统中数据的概念就是广义的。
早期的计算机系统主要用作科学计算,处置的数据就是整数、实数、浮点数等传统数学中的数据。
现代计算机能够存储和处置的对象十分广为,则表示这些对象的数据也越来越繁杂。
数据与其语义就是不可分的。
500 这个数字可以表示一件物品的价格是 500 元,也可以表示一个学术会议参加的人数有 500 人,还可以表示一袋奶粉重 500 克。
( 2 )数据库( DataBase ,缩写 DB ) :数据库就是长期储存在计算机内的、存有非政府的、可以共享资源的数据子集。
数据库中的数据按一定的数据模型非政府、叙述和储存,具备较小的冗余度、较低的数据独立性和易扩展性,并可向各种用户共享资源。
( 3 )数据库系统( DataBas 。
Sytem ,缩写 DBS ) :数据库系统就是所指在计算机系统中导入数据库后的系统形成,通常由数据库、数据库管理系统(及其开发工具)、应用领域系统、数据库管理员形成。
解析数据库系统和数据库就是两个概念。
数据库系统就是一个人一机系统,数据库就是数据库系统的一个组成部分。
但是在日常工作中人们常常把数据库系统缩写为数据库。
期望读者能从人们讲话或文章的上下文中区分“数据库系统”和“数据库”,不要引发混为一谈。
( 4 )数据库管理系统( DataBase Management sytem ,简称 DBMs ) :数据库管理系统是位于用户与操作系统之间的一层数据管理软件,用于科学地组织和存储数据、高效地获取和维护数据。
DBMS 的主要功能包含数据定义功能、数据压低功能、数据库的运转管理功能、数据库的创建和保护功能。
解析 DBMS 就是一个大型的繁杂的软件系统,就是计算机中的基础软件。
离散期中考试题及答案

离散期中考试题及答案《离散数学⼀》期中考试题学院:软件学院级:07级专业:通软/计应⼀.填空(共20分):1. 设集合A={a,b,c,d,e,f,g},A上的⼀个划分π={{a,b},{c,d,e},{f,g}},则π所对应的等价关系有_____个⼆元组。
(2分)Let A be {a,b,c,d,e,f,g} and a partition πof A be {{a,b},{c,d,e},{f,g}}.There are____ ordered pairs in the equivalent relation corresponding to π.答:172.某⼀计算机系统的标号标识符是由⼀个英⽂字母后跟3个数字组成,如果允许重复,那么不同的标号标识符可能有多少种?________ (2分)A label identifier, for a computer system, consists of one letter followed by three digits. If repetitions are allowed, how many distinct label identifiers are possible?________答:26×10×10×10即26 000种。
3.从20个⼥⼠和30个男⼠中选出3个⼥⼠和4个男⼠构成7⼈委员会,那么能形成多少种不同的7⼈委员会?________ (2分)How many different seven-person committees can be formed each containing three women from an available set of 20 women and four men from an available set of 30 men?_______答:20C3×30C4或者1140×27405或者31 241 700.4.从10个志愿者中产⽣三⼈委员会。
离散26-answer

江苏技术师范学院20 —20 学年第 学期 《离散数学》试卷(26)参考答案与评分标准 一、选择题(本大题共5道小题,每小题2分,共10分) 1.下列语句中是命题的是( C )。
A .1+1=10 B .x+y=10 C .sinx+siny<0 D .x mod 3=2 2.在自然数集N 上,下列定义的运算*中不可结合的是( D )。
A .a*b=min(a,b) B .a*b=a+b C .a*b=GCD(a,b)(a,b 的最大公约数) D .a*b=a+3b 3.设集合A={a,b,c},A 上的关系R={(a,a),(b,b)}具备下列性质( D )。
A .等价性 B .自反性 C .反自反性 D .反对称性 4. 设A={Φ},B=P(P(A)),以下正确的式子是( A ) A .{Φ,{Φ}}∈B B .{{Φ,Φ}}∈B C .{{Φ},{{Φ}}}∈B D .{Φ,{{Φ}}}∈B 5.设F(x):x 在北京工作,G(x):x 是北京人;则“在北京工作的人未必都是北京人”可符号化为( B )。
A. )()(x G x xF →⌝∀ B. ))()((x G x F x →⌝∀ C. )()(x G x xF ⌝∧∀ D. ))()((x G x F x ⌝∧∀ 二、填空题(本大题共10道小题,每小题2分,共20分) 1.命题公式q q p ∧→⌝)(的类型是___矛盾式_______。
2.设p :选小王当班长,q :选小李当班长。
命题“选小王或小李中的一人当班长”符号化为 (p ∧q)∨(p ∧q) 。
3.设集合A={a,b,c}及其上的二元关系R={<b,c>,<c,b>}A I ⋃,则R 是A 上的______等价________(等价、偏序)关系。
4.在整数集合Z 上定义二元运算:2a b a b **=++,则Z 上关于*的单位元是___-2_______。
(完整word版)离散数学习题集(十五套)
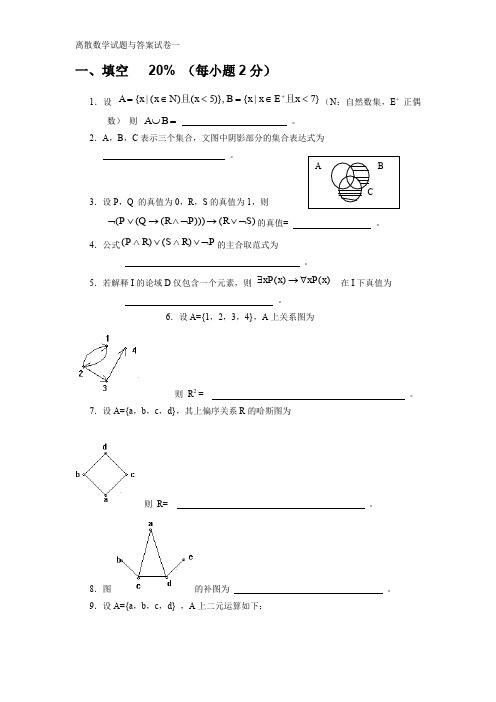
离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:那么代数系统<A ,*>的幺元是 ,有逆元的元素为 ,它们的逆元分别为 。
10.下图所示的偏序集中,是格的为 。
二、选择 20% (每小题 2分)1、下列是真命题的有( ) A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有( )个。
A . 23 ; B . 32 ; C . 332⨯; D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是() A .若R ,S 是自反的, 则S R 是自反的; B .若R ,S 是反自反的, 则S R 是反自反的; C .若R ,S 是对称的, 则S R 是对称的; D .若R ,S 是传递的, 则S R 是传递的。
5、设A={1,2,3,4},P (A )(A 的幂集)上规定二元系如下|}||(|)(,|,{t s A p t s t s R =∧∈><=则P (A )/ R=( )A.A ;B.P(A) ;C.{{{1}},{{1,2}},{{1,2,3}},{{1,2,3,4}}};D.{{Φ},{2},{2,3},{{2,3,4}},{A}}6、设A={Φ,{1},{1,3},{1,2,3}}则A上包含关系“⊆”的哈斯图为()7、下列函数是双射的为()A.f : I→E , f (x) = 2x ;B.f : N→N⨯N, f (n) = <n , n+1> ;C.f : R→I , f (x) = [x] ;D.f :I→N, f (x) = | x | 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《离散数学》试卷(10)参考答案与评分标准
一、单项选择题(本大题共10道小题,每小题2分,共20分)
1.设A 、B 均为非空集合,则下列命题正确的是( C )
A B A B B A C A B A ⊆ D A B A ⊆
2.设R 是Z 上的关系,r (R )是R 的自反闭包,则r(R)=( B )。
A .R B.{}Z x x x R ∈, C.{}Z x x x ∈, D.{}Z x x x R ∈,
3.下面命题中为假的命题是(B ) A.若2+2=4 则3+3=6 B. 若2+2=4 则3+3≠6 C 若2+2≠4 则3+3=6 D. 若2+42
≠则3+3≠6 4.设 <S, > 是一代数系统,则下列说法正确的是( B )。
A .一定有单位元 B.若单位元存在,则必唯一C .零元素一定存在 D.若单位元存在,单位元可能不唯一
5.群中每一元素的逆元(A )
A 存在且唯一
B 存在但不唯一
C 可能不存在
D 若存在,一定与零元相同
6.图G (n ,m ),其中{}n v v v V
,,,21 =则∑==n i i v 1)deg(( C ) A 22-m B 12-m C m 2 D 12+m
7.下列是命题的为 (C )
A 坐下!
B 你住在那里?
C 实践是检验真理的唯一标准。
D 今天天气真好啊!
8.设命题公式G=(P ∧Q )→P 则G 是( B )
A 恒假的
B 恒真的
C 可满足的
D 析取范式
9.在自然数集N 上定义二元运算,满足交换律的是( C )。
A .a*b=a-b
B .a*b=a+2b
C .a*b=a
D .a*b=b a -
10.当且仅当为下面条件中的哪一个时,无向图G 是欧拉图?( C )。
A .G 的所有结点的度数为偶数;
B .G 的所有结点的度数为奇数;
C .G 连通且所有结点的度数为偶数;
D .G 连通且所有结点的度数为奇数。
二、填空题(本大题共10空,每空2分,共20分)
1.设{}f e d c b a E ,,,,,=,{}b a A ,=,{}d c a B ,,=,则~A ∪~B={b,c,d,e,f}
2.设P :a 是偶数,Q :b 是偶数,R :a+b 是偶数;则命题“若a 是偶数,b 是偶数,则a+b 也是偶数”符号化为_____R Q P →∧_____________________________。
3.设T 是树,T 有15个结点,则T 的总度数为 28 。
4. 命题公式q q p ∧→⌝)(的类型是_____矛盾式_______________________。
5. 在布尔代数中,有()b a b a a ∙=+∙,则该式的对偶式为 b a b a a +=∙+)( 。
6.无向完全图G 有n 个结点,则G 的边数=m n(n-1)/2
7.设A={a,b,c},A 上关系R 的关系图为,则具有性质 传递性 。
8.谓词公式∃x(P(x)∨∀yQ(y))→R(x)中∃x 的辖域是 P(x)∨∀yQ(y) 。
9.集合A={1,2,…,10}上的关系R 为整除关系,则R 为 等价 关系。
10.设B(x):x 是鸟;F (x ):x 会飞,“鸟都会飞”可符号化为:∀x(B(x)→F(x)).
三、判断题(本大题共10小题,每小题1分,共10分)
1. (√ )若A={Ф},B=P (A ),则有{Ф}∈B 及{Ф}⊆B 。
2. (× )设A,B 为无限集,则A-B 还是无限集。
3. (× )欧拉通路一定是初级通路。
4. (√ )简单连通图 G(n,m),若m=n-1,则它一定是树。
5. (× )集合R 上的关系满足对称性与传递性,则一定满足自反性。
6. (× )群中既有零元又有单位元。
7. (× )q →命题公式p 的所有成真赋值是00、01和10。
8. (× )设图>=<E V G ,,G '=<V ',E '>,若V V ⊆'且E E ⊆',则G '是G 的生成子图。
9. (√ )命题公式
)(P Q P →→是重言式。
10. (× )如果太阳从西边升起,则雪是黑的。
这句话不是命题。
四、证明题(本大题共3小题,每小题各6分,共18分)
1.设集合A={0,1,2,3,4,5},R={<0,0>,<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<2,3>,<3,1>,<3,2>,<3,3>,<4,4>,<4,5>,<5,4>,<5,5>},试用关系图验证R是A是上的等价关系。
证明:只需证R 满足自反性、对称性、传递性。
(6分)
2.在一阶逻辑中符号化下述命题,并推证之。
凡人必有一死,苏格拉底是人,所以苏格拉底会死的。
证明:令F(x):x 是人,G(x):x 是要死的,a :苏格拉底
前提:∀x(F(x)→G(x)),F(a)
结论:G(a) (2分)
证明:① F(a) 前提引入
② ∀x(F(x)→G(x)) 前提引入
③ F(a)→G(a) ②UI
④ G(a) ①③假言推理 (4分)
3.证明不存在具有奇数个面且每个面都具有奇数条棱的多面体。
证 用反证法. 假设存在这样的多面体, 作无向图G =<V,E >,
其中 V ={v | v 为多面体的面},
E ={(u,v ) | u,v ∈V ∧u 与v 有公共的棱∧u ≠v }.(3分)根据假设,|V |为奇数且∀v ∈V , d (v )为奇数。
这与握手定理的推论矛盾。
(3分)
五、计算、应用题(本大题共5小题,1-4小题各6分,第5小题8分,共32分)
1. 设有一棵树,它有两个结点度数为3,三个结点度数为2,一个结点度数为4,问它有几个结点度数为1? 解:设有x 片树叶,12+16+x=2*(2+3+4+x-1),28+x=16+x
解得x=12,故T 有12片树叶。
2. 求Q ∨(Q →R)的主析取范式及主合取范式。
(6分)
解:Q ∨(Q →R)⇔Q ∨(⌝Q ∨R)⇔(Q ∨⌝Q)∨R
⇔T(主合取范式) (3分)
⇔(⌝Q ∧⌝R)∨(⌝Q ∧R)∨(Q ∧⌝R)∨(Q ∧R)(主析取范式) (3分)
3. 有10个人参加聚会,每个人都认识其中的7个,问能否安排坐在一个圆桌上,使每个人认识与坐在他两边的
人是认识的?为什么?(6分)
解:可以。
(2分)
将每个人对应成相应的顶点,若两人认识,则对应的两个顶点间连上一条无向边,作出一个简单无向图。
由已知,图中每个顶点的度数都等于7,故图中任两个不相邻的顶点的度数和14大于等于10,即顶点数。
故这个图是一个哈密尔顿图,从而存在哈密尔顿回路。
任取一条哈密尔顿回路,按回路经过的顶点的次序安排对应的人的座位,就可以了。
(4分)
4. 设G 是具有四个节点的有向图,它的邻接矩阵表示如下
⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛0010101011001010 (1) 画出图G 。
(3分)
(2) G 是单向连通还是强连通?(3分)
解:(1)图略(3分)
(2)G 单向连通的(3分)
5.A={1,2,3},R 为A 上关系,关系矩阵为⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡101011001, (1) 画出关系图。
(2) 求R R ,R -1。
(3) 指出R 具有的性质。
(4) R 是偏序关系吗?若是画出哈斯图。
解:
(1)
(2分)
(2) R R ={<1,1>,<2,1>,<2,2>,<3,1>,<3,3>}
R -1
={<1,1>,<1,2>,<1,3>,<2,2>,<3,3>} (2分)
(3) R 的性质:自反性、反对称性、传递性。
(2分)
(4) R 是偏序。
(2分)。
