单筋矩形截面计算
单筋矩形截面计算公式

单筋矩形截面计算公式单筋矩形截面是一种常见的结构截面形式,广泛应用于建筑、桥梁、机械和航空航天等领域。
在工程设计中,需要根据单筋矩形截面的几何参数和材料性质来计算其相关的力学性能,以确保结构的安全可靠。
单筋矩形截面的计算公式主要涉及截面的面积、惯性矩和抵抗力等参数。
下面将分别介绍这些参数的计算方法。
1. 面积计算公式:单筋矩形截面的面积可以通过矩形的宽度和高度来计算。
假设矩形的宽度为b,高度为h,则截面的面积A为A=b*h。
2. 惯性矩计算公式:惯性矩是描述截面抵抗弯曲变形的重要参数,常用的有一阶惯性矩和二阶惯性矩。
对于单筋矩形截面,一阶惯性矩I和二阶惯性矩Iy 可以通过以下公式计算:I = b*h^3/12Iy = h*b^3/123. 抵抗力计算公式:单筋矩形截面对外力的抵抗性能可以通过计算抵抗弯曲力矩和抵抗轴向力来评估。
对于受弯构件,其抵抗弯曲力矩M可以通过以下公式计算:M = f*y*Z其中,f为截面上的应力,y为截面离中性轴的距离,Z为截面的抵抗力矩。
对于受轴向压力的构件,其抵抗轴向力N可以通过以下公式计算:N = f*A其中,f为截面上的应力,A为截面的面积。
值得注意的是,单筋矩形截面的计算公式是基于一系列假设和简化条件得出的,因此在具体工程设计中需要根据实际情况进行修正和调整。
此外,对于大跨度和高强度的结构,还需要考虑截面的非线性效应和失稳问题。
单筋矩形截面的计算公式是工程设计中重要的基础知识,它可以帮助工程师评估截面的力学性能并进行结构设计。
通过合理应用这些公式,可以确保结构的安全可靠,满足工程项目的要求。
因此,工程师在实际工作中应该熟练掌握这些公式的使用方法,并结合具体情况进行合理的设计和计算。
单筋矩形截面受弯构件正截面承载力计算
60
第三章 受弯构件正截面承载力计算
翼缘计算宽度bf′取下表所列各项中的最小值。
翼缘计算宽度bf′
项 次
考虑情况
1
按计算跨度l0考虑
2
按梁(纵肋)净距sn考虑
3
按翼缘高度
hf'考虑
hf'/h0≥0.1
0.1>
hf'/h0≥0.05
x xb bh0
防止超筋脆性破坏:
b
As bh0
max
b
1 fc
fy
防止少筋脆性破坏: min AS AS,min minbh
单筋矩形截面所能承受的最大弯矩(极限弯矩):
Mu,max 1 fcbh02b (1 0.5b )
3.3 受弯构件正截面承载力计算
第三章 受弯构件正截面承载力计算
一、基本公式及适用条件 1.基本公式
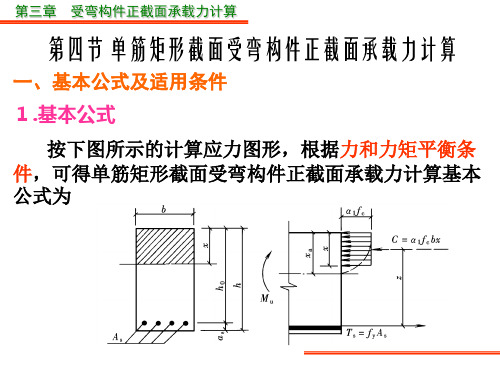
按下图所示的计算应力图形,根据力和力矩平衡条 件,可得单筋矩形截面受弯构件正截面承载力计算基本 公式为
第三章 受弯构件正截面承载力计算
1 fcbx fy As
M Mu 1 fcbxh0 x 2
M M u f y As h0 x 2
1 fcb
②若x≤ξbho,且x≥2as′,则将x值代入第二个基本 公式 求Mu;
56
第三章 受弯构件正截面承载力计算
③若x>ξ bho,说明属超筋梁,此时应取x=ξ bho代 入第二个基本公式求Mu;
④若x<2as′,则
Mu AS f y h0 as'
⑤若Mu≥M则截面安全,否则截面不安全。
04 单筋矩形截面正截面承载能力计算

在梁的正截面强度计算中 用等效矩形应力图代替受压 区抛物线应力图,x为等效矩 形应力图的高度,h0为截面 有效高度,它们的比 值:ξ=x/h0, ξ称为相对受压区 高度。
相对受压区高度ξ不仅反映了钢筋与混凝土的面积比(配筋率ρ), 也反映了钢筋与混凝土的材料强度比,是反映构件中两种材料配比 本质的参数。
钢筋混凝土构件在按承载能力极限状态计算时,引入下列假定: ①构件弯曲后,其截面仍保持平面,受压区混凝土平均应变和 钢筋的应变沿截面高度符合线性分布。平截面假定 ②正截面破坏时,构件受压区混凝士应力取抗压强度设计值fcd fcd,应力计算图形为矩形。等效矩形应力图 ③正截面破坏时,受弯、大偏心受压、大偏心受拉构件的受拉 主筋达到抗拉强度设计值fsd ,受拉区混凝土不参与工作(抗剪计算除外)。
2 正截面承载力计算的基本假定
以IIIa阶段作为承载力极限状态的计算依据
(l)上图为钢筋混凝土梁对应三个工作阶段的应变图。由图可见, 梁在第I阶段受压与受拉应变图呈直线分布,说明混凝土与钢筋应 变的变化规律符合平截面假定。随着弯矩的增加,当梁进入第II 阶段时,受压区混凝土压应变与受拉区钢筋拉应变的实测值均不 断增长,但应变图基本上仍是上、下两个三角形,平均应变仍符 合平截面假定。这种状况一直延续至第Ⅲ阶段,即梁破坏前。最 后,当梁破坏时,受压区混凝土边缘纤维压应变达到(或接近)混 凝上受弯时极限压应变,这标志着梁已开始破坏。
(4)由公式fsdAs=fcdbx或fsdAs(h0-x/2)=γ0Md 计算钢筋截面面积As;
(5)根据计算所得和构造要求选择钢筋直径、根数并布置,确定实际的As 实 ;实际采用的钢筋宜为计算所需钢筋截面面积的0.95~1.05倍。
(6)检查假定as是否接近实际,如误差大,重新计算(因为若as假<as实,则
单筋矩形截面计算例题

单筋矩形截面计算例题例题1:某矩形截面梁,截面b×h =300×500,混凝土为C30,该截面承担弯矩为200kNm,配置HRB335级钢筋,请计算该截面所需配置的最小钢筋面积。
ΣM=0 M=а1f c bx(h0-x/2)由于混凝土强度等级为C30,不超过C50,所以а1取为1.0,可以查相应的材料表格,f c=14.3 N/mm2;对于HRB335级钢筋,f y=300 N/mm2。
设受拉区钢筋配置为梁底单排,因此有:h0=h-35=500-35=465mm因此有:200×106 = 14.3×300 × x(465-x/2)解得x=112mm对于计算结果x,进行校核x,防止出现大于x b的情况而超筋。
x b=ξb h0对于C30混凝土与HRB335级钢筋,ξb=0.55。
x b=ξb h0=0.55×465=255.75mm > x,结果满足适筋梁要求。
因此A s =а1f c bx/f y= 14.3×300×112/300=1601.6mm2截面配筋率:ρ=A s/bh0=1601.6/300×465=1.15%>ρmin查钢筋表,对于HRB 335(20MnSi)钢筋,选择4Φ20+2Φ16,A S= 1256+402=1658 mm2>1601.6 mm2,可以满足要求。
通过本例题可以看出,求解方程组必须校核其结果x,只有x< x b才可以作进一步的设计,截面配筋率也必须大于最小配筋率。
同时在解方程时也要注意,由于ΣM=0:M=а1f c bx(h0-x/2)为一个一元二次方程,可能出现两个方程根,根据截面的尺度状况,可以自然约减下去一个根。
例题2:某矩形截面梁,截面b×h =400×600,混凝土为C30,该截面梁底配有双排HRB335级钢筋4Φ25+4Φ20,求该截面能够承担的最大弯矩。
单筋矩形截面受弯构件正截面承载能力计算
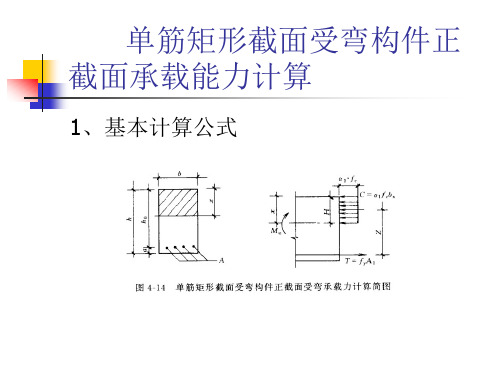
两种T型截面梁
受压区在翼缘内 受压区在翼缘外 受压区在翼缘内同矩形梁(已经解决, b 'f ) 受压区在翼缘外,把它分解成T型梁计算 关键问题: 如何判别 如何分解
截面校核 给定条件:截面配筋、截面尺寸、材料强 度 求:截面能抵抗的最大弯矩(与已知的截 面最大弯矩比较) 过程: 1)根据给定条件,分析截面适用条件。 2)如果截面适用条件满足,直接用弯矩 平衡方程求最大弯矩。 3)如果截面平衡方程不满足要求,重新 按截面设计问题进行计算。
正截面承载能力计算系数与 计算方法
x
如 满足适用条件,根据弯矩 平衡方程求弯矩
x
如不满足适用条件
向受压区钢筋取矩求弯矩 或 按最大受压区高度求弯矩
主要公式
M u1 f y' As' h0 a '
x M u 2 M M u1 1 f c bx h0 2 1 f c bx M u2 As 2 x fy f y h0 2 f y' ' As1 As fy As As1 As 2 f y' fy A
M u M ui M u 2
几个注意的问题
求出相对受压区高度大于界限受压区高 度如何处理; 求出受压区高度小于2a,如何求As 是否存在按单筋计算比按向受压区受压 钢筋合力点计算,求出的受拉钢筋还小 的情况
As , A
' s
单筋矩形梁正截面受弯承载力计算实例
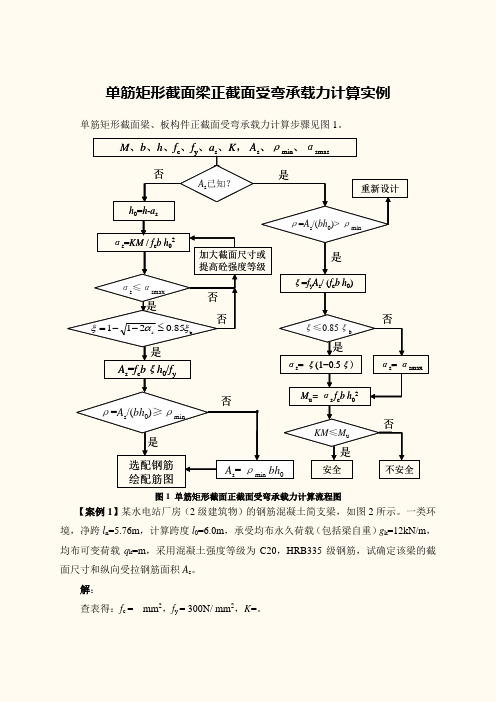
单筋矩形截面梁正截面受弯承载力计算实例单筋矩形截面梁、板构件正截面受弯承载力计算步骤见图1。
选配钢筋加大截面尺寸或是M 、b 、h 、f c 、f y 、a s 、K ,A s 、ρmin 、αsmasαs =KM / f c b h 02A s =f c b ξh 0/f ybs 85.0211ξαξ≤--=h 0=h -a s否A s = ρmin bh 0绘配筋图是是A s 已知?αs ≤αsmax提高砼强度等级ρ=A s /(bh 0)≥ρmin是ξ=f y A s / (f c b h 0)ξ≤0.85ξbαs = ξ(1−0.5ξ)M u = αs f c b h 02KM ≤M u是是安全αs = αsmax否否不安全否否否ρ=A s /(bh 0)> ρmin是重新设计图1 单筋矩形截面正截面受弯承载力计算流程图【案例1】某水电站厂房(2级建筑物)的钢筋混凝土简支梁,如图2所示。
一类环境,净跨l n =5.76m ,计算跨度l 0=6.0m ,承受均布永久荷载(包括梁自重)g k =12kN/m ,均布可变荷载q k =m ,采用混凝土强度等级为C20,HRB335级钢筋,试确定该梁的截面尺寸和纵向受拉钢筋面积A s 。
解:查表得:f c = mm 2,f y = 300N/ mm 2,K =。
(1)确定截面尺寸 由构造要求取:h =(1/8~1/12)l 0 =(1/8~1/12)×6000=750~500,取h =500mm b =(1/2~1/3)h =(1/2~1/3)×500=250~167,取b =250mm (2)内力计算M =(+ )l 02/8=(×12+×)×62 /8 = ·m (3)配筋计算取a s =40mm ,则h 0=h –a s =500–40=460mm==2c s bh f KMα248.04602506.91076.10420.126=⨯⨯⨯⨯ 290.0248.0211211s =⨯--=--=αξ<ξb =×=A s =f c bξh 0/f y =×250××460/300=1067mm 2 ρ= 1067/(250×460)=﹪>ρmin =﹪(4)选配钢筋,绘制配筋图选受拉纵筋为322(A s =1140 mm 2),需要最小梁宽b min =2c +3d +2e =2×30+ 3×22+2×25=176(mm )<250mm ,符合构造要求。
钢筋混凝土受弯构件正截面承载力计算—单筋矩形截面梁计算

受压混凝土的应力-应变关系
计算原则
2)等效矩形应力图
简化原则:受压区混凝土的合力大小不变;受压区混凝土的合力作用点不变。
等效矩形应力图形的混凝土受压区高度 x 1xn ,等效矩形应力图形的应力值 为 1 fc, 1、1 的值见下表。
表 1、1 值
混凝土强 度等级
≤C50
C55
C60
C65
C70
C75
(2)求跨中截面的最大弯矩设计值。
因仅有一个可变荷载,故弯矩设计值应有取下列两者中的较大值:
M 1 1.2g 1.4q l 2
8
1 1.2 5 1.4 10 5.02 62.5
8
M 1 1.35g 1.4 0.7q l 2
8
1 1.35 5 1.4 0.7 10 5.02 51.7
需要加固、补强
计算原则
1)基本假定
01 平截面假定。
02
钢筋的应力 s 等于钢筋应变 s 与其弹性模量 Es 的乘积,但不得大
于其强度设计值 fy,即
s sEs fv
03 不考虑截面受拉区混凝土的抗拉强度。
计算原则
04
受压混凝土采用理想化的应力-应变关系,当混凝土强度等级为
C50及以下时,混凝土极限压应变 cu=0.0033。
(1)受拉钢筋为4 25,As=1964 mm2; (2)受拉钢筋为3 18,As=763 mm²。
单筋矩形截面梁计算
解 查表得:
fc 9.6N/mm2
ft 1.10N/mm2
f y 300N/mm2 c 1.0
b 0.550
c 30mm
单筋矩形截面梁计算
(1)
d
25
h0 h c 2 450 30 2 408
单筋矩形截面梁、板正截面受弯承载力计算教学课件.

0.96
0.76
0.95
0.73
0.94
0.74
水工混凝土结构
1.3 相对受压区计算高度
相对受压区计算高度是等效矩形混凝土受压区计算高度x
与截面有效高度h0的比值,用ξ= x/h0表示。 当梁发生界限破坏时,即受拉钢筋屈服的同时,受压区
混凝土也达到极限压应变εcu。这时混凝土受压区计算高度xb
与截面有效高度h0的比值,称为相对界限受压区计算高度ξb, ξb= xb/h0。这一临界破坏状态,就是适筋梁与超筋梁的界限。
HPB235
≤C50 HRB335 HRB400 RRB400
0.614
0.550 0.518
0.425
0.399 0.384
0.522
0.468 0.440
0.386
0.358 0.343
水工混凝土结构
1.4 受拉钢筋配筋率 受拉钢筋的配筋率ρ是指受拉钢筋截面面积As与截面有效 截面面积bh0比值的百分率,即ρ =As /(bh0 )×100﹪。 通常用ρmax表示受拉钢筋的最大配筋率; 用ρmin表示受拉钢筋的最小配筋率。 当ρ>ρmax时,将发生超筋破坏; 当ρ<ρmin时,将发生少筋破坏; 当ρmin≤ρ≤ρmax时,将发生适筋破坏。 为避免发生超筋破坏与少筋破坏,截面设计时,应控制 受拉纵筋的配筋率ρ在ρmin~ρmax范围内。
水工混凝土结构
2015.03
钢筋混凝土梁板设计
单筋矩形截面梁、板正截面承载力计算
1 正截面承载力计算的一般规定
1.1 计算方法的基本假定
(1) 截面应变保持为平面:
c
x
c
y
c
混凝土单筋矩形截面计算课件

挠度验算
挠度验算的目的
保证混凝土结构在使用期间不会 因挠度过大而影响结构的正常使
用和安全性能。
计算方法
根据结构力学原理,采用有限元 分析或近似计算方法,考虑结构 自重、活载、风载等作用下的挠
度。
影响因素
混凝土的弹性模量、截面尺寸、 跨度、荷载等都会影响挠度的计
算结果。
耐久性评估
耐久性评估的目的
01
钢筋的配置原则
根据结构受力要求,合理选择钢 筋的种类、规格和数量。
确保钢筋在截面中的位置和间距 满足规范要求,以保证结构的承
载力和稳定性。
考虑施工的可操作性,合理安排 钢筋的布置,以方便施工。
截面设计的基本原则
01
根据结构的功能和要求 ,确定合理的截面尺寸 和形状。
02
根据承载力要求,合理 配置钢筋,并满足构造 要求。
混凝土单筋矩形截面计 算课件
目录
Contents
• 引言 • 混凝土材料特性 • 单筋矩形截面设计原理 • 单筋矩形截面承载力计算 • 裂缝宽度和挠度验算 • 案例分析
01 引言
课程背景
混凝土结构在现代建筑中广泛应用, 单筋矩形截面作为最基本的混凝土结 构形式之一,其计算是工程设计和施 工中的重要基础。
某高层建筑,采用混凝土单筋矩形截面梁作为主 要受力构件。
结构形式
梁的截面尺寸为200mm×400mm,采用C30混 凝土,承受弯矩设计值M=150kN·m。
3
施工条件
施工现场具备标准的混凝土搅拌和浇筑设备,材 料质量符合规范要求。
案例分析方法
计算简图
根据实际工程情况,建立混凝土单筋矩形截面梁 的计算简图。
配筋率计算
根据截面尺寸和所需承载力计算 配筋率
4.4单筋矩形截面受弯构件正截面承载力计算-PPT课件
43
第三章 受弯构件正截面承载力计算
αs、γs均为ξ 的函数,可编制成计算表格供查用。 但通常采用如下方法计算:
①计算αs ②计算ξ 或γs
M s 2 1 f cbho
1 1 2 s
γs=1-0.5ξ
44
第三章 受弯构件正截面承载力计算
③ 求纵向钢筋面积As 若 ξ ≤ξ 或
40
第三章 受弯构件正截面承载力计算
2)求纵向受拉钢筋面积As
1 f c bx As 若 x≤ξ bho,则 fy 若 x>ξ bho,则属于超筋梁,应加大截面尺寸或提 高混凝土强度等级,并重新设计计算。
fyA 1 fcbx s
3)验算最小配筋率ρmin As≥ρminbh 若 或按 As<ρminbh,应适当减少截面尺寸, As=ρminbh 配筋。
能力的不足。 ② 在不同荷载组合情况下,其中在某一组合情况下截面承受 正弯矩,另一种组合情况下可能承受负弯矩,即梁截面承 受异号弯矩。
③ 在抗震结构中要求框架梁必须配置一定比例的受压钢筋, 受压钢筋可以提高截面的延性。
48
二、纵向受压钢筋的抗压强度设计取值 混凝土受压高度x满足下述条件,且配置必要的封 闭箍筋,则纵向受压钢筋的应力可取《规范》规定的 设计强度值ƒy' ' x 2a
b
则
As bh o
1 fc
fy
M As f y rs h o
若ξ >ξ b,则为超筋梁,应重新计算。
④ 验算最小配筋率
As≥ρminbh
45
2. 截面复核
己知:截面尺寸b×h,截面配筋As,材料强度fc、fy ,弯矩设计值M 求:复核截面是否安全 、弯矩承载力Mu= ?
矩形截面设计

=
f y As α1 fcbh0
(
x
=
ξ h0 )
2. 判别:判别ξ 与ξb
a) 如果ξ ≥ ξb , Mu = α1 fcbh02ξb (1− 0.5ξb ) ;
b) 如果ξ < ξb , Mu = α1 fcbh02ξ (1− 0.5ξ ) ;。
1. 比较: M > Mu ,不安全; M ≤ Mu ,安全。
⎛
⎜
( ) ( ) ⎜
另法:
x
=
h0
⎜1 ⎜
−
⎡ 2 ⎢M 1− ⎢⎣
− α1 fc
b'f − b h'f α1 fcbh02
⎛ ⎜⎜⎝
h0
−
h'f 2
⎞⎤ ⎟⎟⎠⎥⎥⎦
⎞ ⎟ ⎟ ⎟ ⎟
,
x
≤
xb
时,
As
= α1 fcbx + α1 fc fy
b'f − b h'f
⎜⎜⎝
⎟⎟⎠
x > xb 时,截面超筋,应加大截面或提高混凝土强度等级。
2.
比较
M1
与
M
:
M1
=
α1
fcbxb
⎛ ⎜⎝
h0
−
xb 2
⎞ ⎟⎠
a) 如果 M1 ≥ M ,只需配单筋;
b) 如果 M1 < M ,应配双筋。
3.
求
As1
=
α1
fcbxb fy
ቤተ መጻሕፍቲ ባይዱ
4. 求 M 2 、 As' 、 As2
M2 = M − M1
( ) As'
=
f
计算公式
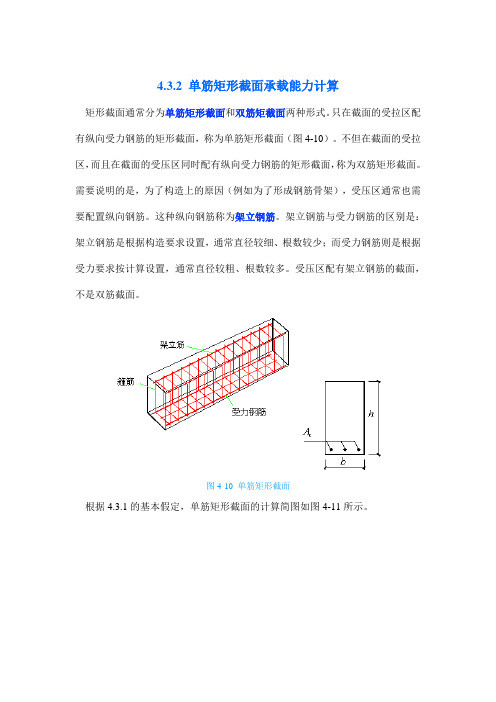
4.3.2 单筋矩形截面承载能力计算矩形截面通常分为单筋矩形截面和双筋矩截面两种形式。
只在截面的受拉区配有纵向受力钢筋的矩形截面,称为单筋矩形截面(图4-10)。
不但在截面的受拉区,而且在截面的受压区同时配有纵向受力钢筋的矩形截面,称为双筋矩形截面。
需要说明的是,为了构造上的原因(例如为了形成钢筋骨架),受压区通常也需要配置纵向钢筋。
这种纵向钢筋称为架立钢筋。
架立钢筋与受力钢筋的区别是:架立钢筋是根据构造要求设置,通常直径较细、根数较少;而受力钢筋则是根据受力要求按计算设置,通常直径较粗、根数较多。
受压区配有架立钢筋的截面,不是双筋截面。
图4-10 单筋矩形截面根据4.3.1的基本假定,单筋矩形截面的计算简图如图4-11所示。
图4-11 单筋矩形截面计算简图为了简化计算,受压区混凝土的应力图形可进一步用一个等效的矩形应力图代替。
矩形应力图的应力取为α1f c(图4-12),f c为混凝土轴心抗压强度设计值。
所谓“等效”,是指这两个图不但压应力合力的大小相等,而且合力的作用位置完全相同。
图4-12 受压区混凝土等效矩形应力图按等效矩形应力计算的受压区高度x与按平截面假定确定的受压区高度x o之间的关系为:(4-7)系数α1和β1的取值见表4-2。
系数α1和β1的取值表表4-2◆基本计算公式由于截面在破坏前的一瞬间处于静力平衡状态,所以,对于图4-12 的受力状态可建立两个平衡方程:一个是所有各力的水平轴方向上的合力为零,即(4-8)式中b——矩形截面宽度;A s——受拉区纵向受力钢筋的截面面积。
另一个是所有各力对截面上任何一点的合力矩为零,当对受拉区纵向受力钢筋的合力作用点取矩时,有:(4-9a)当对受压区混凝土压应力合力的作用点取矩时,有:(4-9b)式中M——荷载在该截面上产生的弯矩设计值;h o——截面的有效高度,按下计算h o=h-a s。
h为截面高度,a s为受拉区边缘到受拉钢筋合力作用点的距离。
第三章 第四节 单筋矩形截面受弯构件正截面承载力计算
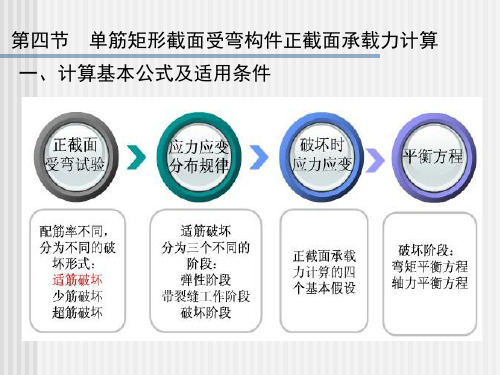
Mu
xc
C
Z
x 0 T C
xt
h0
Tc T s
M 0
M u TZ CZ
设AS—钢筋的面积;fy—钢筋的屈服强度,T= ASfy 。 Z和C与压区高度及压区应力分布有关。
第四节
单筋矩形截面受弯构件正截面承载力计算
b x h
一、计算基本公式及适用条件
基本公式 h0 受弯构件正截面承载能力计算,应满足作用 在结构上的荷载在结构截面中产生的弯矩设计 值M不超过按材料的强度设计值计算得到的受 as 弯构件承载能力设计值Mu, 即:M ≤ Mu
h0——截面有效高度, h0=h-as h——截面高度 as ——受拉钢筋合力点至混凝土受拉边缘的距离,初步计算时,对 于C25~C45等级的混凝土,可按35mm(单排受拉筋)、60mm(双排受拉 筋)、20mm(平板)取值。
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
◆ 例题3-1
解:查表得: fc=9.6N/mm2 ,; fy=300N/mm2 ; ξb=0.55;截面有效 高度 h。=500-40=460mm ;纵向受拉钢筋按一排放置,则梁的有效 高度h0=500—40=460mm。 1.计算受压区高度x
f y As 300 804 x 125.6mm b h0 0.55 460 253mm 1 f cb 1.0 9.6 200
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
单筋矩形截面 仅在受拉区布置纵向受力钢筋的矩形截面 双筋矩形截面 同时在受拉区和受压区布置纵向受力钢筋的矩形截面
最新版建筑工程承载力计算表(抗弯-矩形截面-单筋)
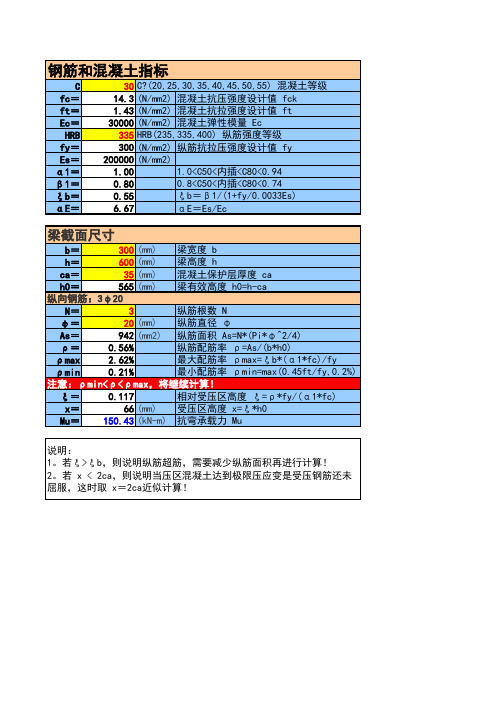
335 HRB(235,335,400) 纵筋强度等级
300 (N/mm2) 纵筋抗拉压强度设计值 fy
200000 (N/mm2)
1.00
1.0<C50<内插<C80<0.94
0.80
0.8<C50<内插<C80<0.74
0.55
ξb=β1/(1+fy/0.0033Es)
6.67
αE=Es/Ec
梁截面尺寸
C35 16.7 1.57 500
C45 21.1 1.8 33500
C50 23.1 1.89 34500
C55 25.3 1.96 35500
钢筋和混凝土指标
C fc= ft= Ec= HRB fy= Es= α1= β1= ξb= αE=
30 C?(20,25,30,35,40,45,50,55) 混凝土等级
14.3 (N/mm2) 混凝土抗压强度设计值 fck
1.43 (N/mm2) 混凝土抗拉强度设计值 ft
30000 (N/mm2) 混凝土弹性模量 Ec
混凝土强度及弹性模量
强度 fc ft Ec 强度 fy Es
类型 C20 C25 C30 N/mm2 9.6 11.9 14.3 N/mm2 1.1 1.27 1.43 N/mm2 25500 28000 30000 类型 HPB235 HRB335 HRB400 N/mm2 210 300 360 N/mm2 210000 200000 200000
b=
300 (mm) 梁宽度 b
h=
600 (mm) 梁高度 h
ca=
35 (mm)
h0=
565 (mm)
纵向钢筋:3φ20
单筋截面计算

③求As
As = M /fy h0 γs
或 As = ξb h0 α1 f c/fy
⑤验算配筋率(和公式法相同)
④选配钢筋(和公式法相同) 一般情况下接近计算值,范围为5%。
3.3单筋矩形截面受弯承载能力计算
◆截面复核步骤
已知弯矩设计值M ,混凝土等级和钢筋级别,截面尺寸b、h0 ,钢筋 截面积As 。求截面的受弯承载能力Mu(极限弯矩),并根据已知设计值M , 复核截面是否安全。 (1)公式求解步骤
(3-16)
则有:M= fyAs h0 γs
As = M /fy h0 γs
(3-17)
由αs=ξ(1-0.5 ξ )可得: ξ=1-(1-2 αs )0.5
3.3单筋矩形截面受弯承载能力计算
通过αs = M/ α1 f cb h0 2 、 ξ=1-(1-2 αs )0.5
γs=1-0.5 ξ、 As = M /fy h0 γs 的关系可以看出,αs 一但确定下 来 ,ξ、 γs也就确定下来,这样可以编制出αs 与 ξ、 γs的关系表。 见教材表3-7。
min bh 0 . 002 250 500 250 mm
2
AS =704mm2
由以上验算,截面符合适要求。
4.选配钢筋 选用2 Φ18+1 Φ 16(As=710mm2)
一排钢筋所需要的最小宽度为:
bmin=4×25+2×18+1×16=152mm <250mm
◆例题3-2
3.3单筋矩形截面受弯承载能力计算
◆公式适用条件 ①防止超筋破坏 ξ=x/h0 ≤ ξb x ≤xb= ξb h0 ρ ≤ ρ max 以上三条只需满足一条,其余必定满足。 将xb= ξb h0 代入(3-11)可得到单筋矩形截面所能承受的最大弯矩 (极限弯矩)Mu,max Mu,max= α1 f cb h02 ξb(1-0.5 ξb ) ② 防至少筋破坏 ρ ≥ ρ min 或 AS ≥ ρ min bh (3-15) (3-14) (3-13)
单筋矩形截面受弯构件抗裂度计算原理

单筋矩形截面受弯构件抗裂度计算原理1. 引言嘿,朋友们,今天咱们聊聊一个跟建筑、工程有关的话题,虽然听起来有点“高大上”,但其实也是个实用的知识,咱们就用轻松的语气来聊聊。
你知道吗,单筋矩形截面受弯构件这玩意儿,其实就是一种常见的混凝土构件。
没错,咱们日常生活中看到的很多楼房、桥梁,都用得上它。
今天,我们重点说说抗裂度计算,这可是确保这些构件能安全使用、避免裂缝的重要环节。
好啦,开始之前,先给自己泡杯茶,咱们慢慢聊。
2. 单筋矩形截面简介2.1 什么是单筋矩形截面?简单来说,单筋矩形截面就是一种横截面呈矩形的构件,里面只放了一根钢筋,想象一下,一个乖乖的矩形小盒子,里面塞着一根坚强的钢筋,这样的搭配既省钱又好用。
它的结构特性让它在受弯时表现得相当稳健,像个不怕风雨的汉子,挺拔而坚强。
2.2 为啥要计算抗裂度?说到抗裂度,咱们可以想象成一场“抗压大赛”。
这个“大赛”里,构件要承受各种力的挑战,尤其是弯曲力。
如果抗裂度不够,构件就可能会像被压扁的罐头一样,冒出裂缝,虽然小裂缝听起来没什么大不了,但可别小瞧了它,长时间下去可就“麻烦”了。
因此,计算抗裂度就成了一个非常重要的环节,确保我们的建筑物像钢铁侠一样,强壮无比。
3. 抗裂度计算的基本原理3.1 力的作用与分布在这个计算过程中,首先要了解构件受力的情况。
想象一下,构件就像个小小的桥梁,站在上面的人越多,桥梁的负担就越重。
而这负担可不是均匀的,可能在某些点上会更重。
咱们得考虑这些力是怎么分布的,有些地方压力大得像个胖子坐上去,有些地方则轻飘飘的。
为了确保抗裂度,我们得确保在最重的地方,构件依然能抵挡住压力。
3.2 材料的性质接下来,就是材料的性质了。
混凝土和钢筋各有千秋,混凝土是强压弱拉,钢筋则相反。
我们要算得准这二者的配合度,确保它们在一起时,能发挥出最佳的效果。
就像咱们做菜一样,调料加多了会失去原味,比例不对可就大事不妙。
因此,在计算中,要充分考虑材料的强度和延展性,才能让这个构件稳稳当当。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.4 单筋矩形截面受弯承载力计算
第4章 受弯构件正截面承载力
4 截面设计
已知:M 、b 、h 、f y 、f c 、 s 求: A s 未知数:x 、A s 。 基本公式:
(1) s
M = 1 fcbh02
, 1 12s
(2)当 b 时,说明是超筋梁,改用双筋梁或增大截面尺寸重新计算;
第4章 受弯构件正截面承载力
1 基本计算公式
4.4 单筋矩形截面受弯承载力计算
第4章 受弯构件正截面承载力
2 适用条件
防止发生超筋破坏
xbh0 或 b
As
MMu smax 1fcbh02
或 s smax
防止发生少筋破坏
As mibn h
4.4 单筋矩形截面受弯承载力计算
单筋矩形截面计算框图
第4章 受弯构件正截面承载力
3 截面复核
已知:b 、h 、A s 、f y 、f c 、M u 、 s 求: M u 未知数: x 、M u
基本公式: 1fcbxfyA s MM u1fcbx(h02 x)fyA s(h02 x)
(1)当 x bh0且 As mibn h时,用基本公式直接计算 M u ;
(2)当 x bh0时,说明是超筋梁,取 x bh0,M u sm ax 1fcbh02;
(3)当 As minbh时,说明是少筋梁,分别按素混凝土构件和钢筋
混凝土构件计算 M
,取小值。
(3)当 b时,用基本公式直接计算 A s;
(4)如果 As minbh ,说明是少筋梁, 取 As minbh 。
4.4 单筋矩形截面受弯承载力计算
第4章 受弯构件正截面承载力(选讲)
应用(选讲)
4.4 单筋矩形截面受弯承载力计算
