23.2.1中心对称(课件)
合集下载
《23.2.1中心对称》课件

2、学习反思: _____________________________ ___________________________.
作业设计
• 作业: • P69习题23.2复习巩固第1题
心对称的条件吗? B
O
C
C A B O
阅读教材P65,按步骤作图:作 △ABC关于点O的中心对称图形。
B′
A′
C' 画好图形后思考: (1)点 O 在线段 AA'上吗?如果在,在什么位置? (2)△ABC 和△A' B' C' 有什么关系? (3)你能从这个探究中归纳出中心对称的性质吗?
书P66练习第2题 要求:先独立思考,再小组交流,交流完毕 坐下。时间控制在5分钟内。
阅读教材P64思考:
问题1 如图23.2-1,把其中一个图案绕点 O 旋转 180°,你有什么发现?
问题2 观察下列图形的旋转,填空: (1)图形中旋转中心是点 ,该点被叫做 。 (2)旋转的角度是 度。 (3)△ABO ≌△CDO, 点A的对称点是 。 你还能找出其他的对称点吗? A D 问题3 你能归纳一下两个图形成中
1、中心对称与轴对称的区别.
1 ①中心对称,有_______ 个对称中心,图形绕 着某个点 旋转_______ _________ 度,旋转后与另一图形 180° 重合 __________. 一条直线 折叠后 1 条对称轴,图形沿_________, ②轴对称有____ 重合 与另一图形_________.
第二十三章 旋转
23.2.1 中心对称Fra bibliotek和硕县第一中学 魏美玉
• 每课5分钟:我骄傲,我是中国人 • 视频播放 • 我要融入的是:社会主义核心价值观的深 刻涵义 • 体现的是:《战狼2》中所展现的我骄傲, 我是中国人,我们都是和平的捍卫者
23.2.1中心对称图形课件

∴四边形ABCD是平行四边形
如图:过□ABCD的对角线交点O作两条互相垂
直的直线分别交□ABCD各边于点E、F、G、H,
求证:四边形EFGH是菱形 A
GD
证明:∵O是□ABCD的对称中心
EF、GH经过点O
E
F
O
∴E、F和G、H分别关于点O对称 B H
C
∴ OE=OF,OG=OH
∵EF⊥GH
∴四边形EGFH是菱形
y 5
4
②3 ① 2
1
-5 -4 -3 -2 -1 O -1
③ -2 -3 -4 -5
1 2 3 4 5x
④
练习(见学案例2):在如图的方格纸中,每个小正方形 的边长都是为1. (1)画出点C关于点O的对称点C1 (2)画出线段BC关于点O的对称线段B1C1 (3)画出将A △ABC关于点O对称△A1B1C1;
判断下列说法是否正确 (1)轴对称图形也是中心对称图形。(×)
(2)旋转对称图形也是中心对称图形。( ×)
(3)平行四边形、长方形和正方形都是中心对称图 形,对角线的交点是它们的对称中心。( √ )
(4)角是轴对称图形也是中心对称图形。( × )
(5)在成中心对称的两个图形中,对应线段平行
(或在同一直线上)且相等。
如果将中心对称图形,对称的部分看成 两个图形,则它们是关于中心对称。
轴对称图形与中心对称图形:
轴对称图形
中心对称图形
有一条对称轴—直线 有一个对称中心—点 图形沿轴对折 图形绕这个点旋转180O
对折部分与另一部分 旋转后与原图形重合 重合
想一想
下面哪些图形是中心对称图形? o
在下列图形中,是中心对称图形的是
( C)
如图:过□ABCD的对角线交点O作两条互相垂
直的直线分别交□ABCD各边于点E、F、G、H,
求证:四边形EFGH是菱形 A
GD
证明:∵O是□ABCD的对称中心
EF、GH经过点O
E
F
O
∴E、F和G、H分别关于点O对称 B H
C
∴ OE=OF,OG=OH
∵EF⊥GH
∴四边形EGFH是菱形
y 5
4
②3 ① 2
1
-5 -4 -3 -2 -1 O -1
③ -2 -3 -4 -5
1 2 3 4 5x
④
练习(见学案例2):在如图的方格纸中,每个小正方形 的边长都是为1. (1)画出点C关于点O的对称点C1 (2)画出线段BC关于点O的对称线段B1C1 (3)画出将A △ABC关于点O对称△A1B1C1;
判断下列说法是否正确 (1)轴对称图形也是中心对称图形。(×)
(2)旋转对称图形也是中心对称图形。( ×)
(3)平行四边形、长方形和正方形都是中心对称图 形,对角线的交点是它们的对称中心。( √ )
(4)角是轴对称图形也是中心对称图形。( × )
(5)在成中心对称的两个图形中,对应线段平行
(或在同一直线上)且相等。
如果将中心对称图形,对称的部分看成 两个图形,则它们是关于中心对称。
轴对称图形与中心对称图形:
轴对称图形
中心对称图形
有一条对称轴—直线 有一个对称中心—点 图形沿轴对折 图形绕这个点旋转180O
对折部分与另一部分 旋转后与原图形重合 重合
想一想
下面哪些图形是中心对称图形? o
在下列图形中,是中心对称图形的是
( C)
人教版数学九年级上册..中心对称课件PPT优秀课件

练习:
• 1.下列说法中正确的有( c )
A.全等的两个图形的两个图形全等 D.旋转后能够重合的两个图形成中心对称
人教版数学九年级上册2.3.中.2心.1中 对心 称对课 称 件课PP件T优 秀课件
人教版数学九年级上册2.3.中.2心.1中 对心 称对课 称 件课PP件T优 秀课件
人教版数学九年级上册23.2.1中心对 称课件
(1)如图1,把其中一个图案绕点O旋转180°,你 有什么发现?
(2)如图2,线段AC, BD相交于点O,OA=OC, OB=OD.把 △OCD绕点O旋转180°,你有 什么发现?
重合
重合
O
B
(2) C
人教版数学九年级上册23.2.1中心对 称课件
人教版数学九年级上册2.3.中.2心.1中 对心 称对课 称 件课PP件T优 秀课件
人教版数学九年级上册23.2.1中心对 称课件
练习
• 3.已知如图所示,△AOB与△COD关于点O 成中心对称,连接BC,AD.
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15 cm2,求四边形 ABCD的面积.
人教版数学九年级上册23.2.1中心对 称课件
中心对称的作法: 人教版数学九年级上册23.2.1中心对称课件
C’ A
B’
O
B
A’ C
人教版数学九年级上册2.3.中.2心.1中 对心 称对课 称 件课PP件T优 秀课件
人教版数学九年级上册2.3.中.2心.1中 对心 称对课 称 件课PP件T优 秀课件
练习
• 1.如图所示,在下列四组图形中,右边图形 与左边图形成中心对称的有_(_1_)(_2.)(3)
人教版数学九年级上册2.3.中.2心.1中 对心 称对课 称 件课PP件T优 秀课件
23.中心对称课件

23.2.1 中心对称
23.2.1 中心对称
23.2.1 中心对称
学习目标
1. 理解中心对称的定义; 2. 探究中心对称的性质;(难点) 3. 掌握中心对称的性质及其应用.(重点)
23.2.1 中心对称
新课导入
情境引入
D
C O
B A
从A旋转到B,旋转中心 是什么?旋转角是多少?
从A旋转到C呢?
从A旋转到D呢?
FO EO, FOD EOB, DO BO.
∴△FOD≌△EOB(SAS). ∴ DF = BE.
23.2.1 中心对称
课堂小结
概念
旋转角是 180°
中 心 性质 对 称
作图
对称点的连线经过对称中心,且被 对称中心平分
应用1:作图形关于某点对称的图形; 应用2:找出对称中心.
形绕某一点旋转 180° 后能否与另一个图形重合.
23.2.1 中心对称
要点归纳
1. 中心对称是一种特殊的旋转,其旋转角是180°; 2. 中心对称是两个图形之间一种特殊的位置关系;
3. 成中心对称的两个图形只有一个对称中心,对 称中心可能在图形的外部、内部或图形上,对称 点一定在对称中心两侧或与对称中心重合.
解法2:根据视察,B、B′ 及 C、C′ 应是两组对称点,连接 BB′、
CC′ 相交于点 O,则点 O 即为所求(如图).
C A′
O B′
B A
C′
注意:如果限定只用无刻度直尺作图,我们用解法2.
23.2.1 中心对称
归纳总结: 确定成中心对称的两个图形的对称中心的方法: ①连接任意一组对称点,取这条线段的中点,这个 中点就是对称中心; ②连接任意两组对称点,两条线段的交点就是对称 中心.
23.2.1 中心对称
23.2.1 中心对称
学习目标
1. 理解中心对称的定义; 2. 探究中心对称的性质;(难点) 3. 掌握中心对称的性质及其应用.(重点)
23.2.1 中心对称
新课导入
情境引入
D
C O
B A
从A旋转到B,旋转中心 是什么?旋转角是多少?
从A旋转到C呢?
从A旋转到D呢?
FO EO, FOD EOB, DO BO.
∴△FOD≌△EOB(SAS). ∴ DF = BE.
23.2.1 中心对称
课堂小结
概念
旋转角是 180°
中 心 性质 对 称
作图
对称点的连线经过对称中心,且被 对称中心平分
应用1:作图形关于某点对称的图形; 应用2:找出对称中心.
形绕某一点旋转 180° 后能否与另一个图形重合.
23.2.1 中心对称
要点归纳
1. 中心对称是一种特殊的旋转,其旋转角是180°; 2. 中心对称是两个图形之间一种特殊的位置关系;
3. 成中心对称的两个图形只有一个对称中心,对 称中心可能在图形的外部、内部或图形上,对称 点一定在对称中心两侧或与对称中心重合.
解法2:根据视察,B、B′ 及 C、C′ 应是两组对称点,连接 BB′、
CC′ 相交于点 O,则点 O 即为所求(如图).
C A′
O B′
B A
C′
注意:如果限定只用无刻度直尺作图,我们用解法2.
23.2.1 中心对称
归纳总结: 确定成中心对称的两个图形的对称中心的方法: ①连接任意一组对称点,取这条线段的中点,这个 中点就是对称中心; ②连接任意两组对称点,两条线段的交点就是对称 中心.
2021年人教版数学九年级上册23 中心对称(第一课时)课件

A.点 E C.点 G
B.点 F D.点 H
8
3.如图,△ABC 与△A′B′C′关于点 O 成中心对称,则下列结论不成立的是 ( D)
A.点 A 与点 A′是对称点 C.AB∥A′B′
B.BO=B′O D.∠ACB=∠C′A′B′
9
4.如图,在△ABC 中,AB=AC,△ABC 与△FEC 关于点 C 成中心对称,连 接 AE、BF.若四边形 ABFE 为矩形,则∠ACB 为( C )
另外两个矩形,得到连接各自中心
的第二条线段,两条线段交于点G,
点G即为重心.
22
图2
►在有欢声笑语的校园里,满地都是雪,像一块大地毯。房檐上挂满了冰凌 ,一根儿一根儿像水晶一样,真美啊!我们一个一个小脚印踩在大地毯上 ,像画上了美丽的图画,踩一步,吱吱声就出来了,原来是雪在告我们: 和你们一起玩儿我感到真开心,是你们把我们这一片寂静变得热闹起来。 对了,还有树。树上挂满了树挂,有的树枝被压弯了腰,真是忽如一夜春 风来,千树万树梨花开。真好看呀! ►冬天,一层薄薄的白雪,像巨大的轻软的羊毛毯子,覆盖摘在这广漠的荒 原上,闪着寒冷的银光。
B.(- 3,2),( 3,-2)
C.(- 3,2),(2,- 3)
D.- 27,
221, 27,-
21 2
14
8.如图,四边形 ABCD 是中心对称图形,对称中心为点 O,过点 O 的直线与 AD、BC 分别交于点 E、F,则图中相等的线段有( C )
A.3 对 C.5 对
B.4 对 D.6 对
►走进颐和园,眼前是繁华的苏州街,现在依稀可以想象到当年的热闹场面, 苏州街围着一片湖,沿着河岸有许多小绿盘子里装着美丽的荷花。这里是 仿照江南水乡--苏州而建的买卖街。当年有古玩店、绸缎店、点心铺等, 店铺中的店员都是太监、宫女妆扮的,皇帝游览的时候才营业。我正享受 着皇帝的待遇,店里的小贩都在卖力的吆喝着。 ►走近一看,我立刻被这美丽的荷花吸引住了,一片片绿油油的荷叶层层叠 叠地挤在水面上,是我不由得想起杨万里接天莲叶无穷碧这一句诗。荷叶 上滚动着几颗水珠,真像一粒粒珍珠,亮晶希望对您有帮助,谢谢 晶的。 它们有时聚成一颗大水珠,骨碌一下滑进水里,真像一个顽皮的孩子!
23.2.1 中心对称(共43张PPT)
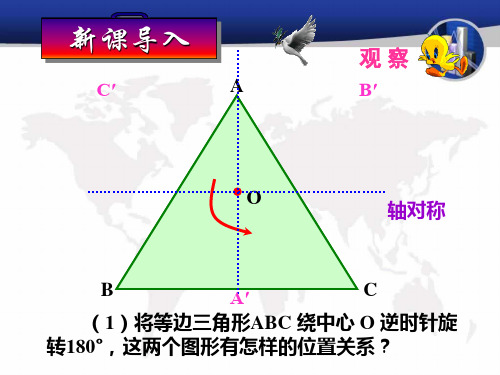
15 8
2
OF
15 8
同理OE 15 ,即 OF OE OF 15
8
4
A
D
C′
D′
O 重合
B′
A′
B
C
(4)将平行四边形ABCD绕中心O逆时针旋 转180°,这两个图形有怎样的位置关系?
有的轴对称, 有的重合。
绕中心旋转180°,旋转后的图 形与原图的位置关系有什么不同?
教学目标
【知识与能力】
了解中心对称、对称中心、关于中心的对称 点等概念。 通过具体实例认识两个图形关于某一点成中 心对称的本质:就是一个图形绕一点旋转180° 而成。 作出中心对称的图形。
它是轴对称图形吗? 不是轴对称图形。
这个图形是否能够通过某种图形运动与自 身重合?
探究
下列图形是否能够通过某种图形运动与自
身重合?图旋Biblioteka 形转绕后中与
线段绕中点旋转180°
心原 旋图
旋转后与原图重合
转重
180 合
°
知识要点
把一个图形绕着某一个点旋转180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对称 (central symmetry),这个点叫做对称中 心。这两个图形中的对应点叫做关于中心 的对称点。
经历对日常生活中与中心对称有关的图形进行 观察、分析、欣赏、动手操作、画图等过程,发 展审美能力,增强对图形的欣赏意识。
从图形变化过程中,树立正确的辩证唯物主义 观点。
认识几何图形的对称美,培养学生热爱数学, 热爱生活。
教学重难点
利用中心对称、对称中心、关于中心的 对称点的概念解决一些问题。 从一般旋转中导入中心对称。 中心对称的性质及初步应用。 中心对称与旋转之间的关系。
中心对称--PPT课件

如图,已知△ABC与△A’B’C’中心对称,求出它们 的对称中心O。
C
B A
A’ B’
C’
王母娘娘被考神说服,她表示作出下面这道题就解除对
懒星和美星的惩罚,就让她们见面,大家一起来帮帮她们 吧!
小结:
• 这节课你有那些收获?
• 请你说给大家听听
最后通过大家的帮助懒星和美星两姐妹终于又到了 一起!
结论:
1.关于中心对称的两个图形,对称点所连线段都经过对称 中心,而且被对称中心所平分.
2.关于中心对称的两个图形是全等图形.
△ABC与△ADE就是成中心对称的两个三角形,点 A是对称中心,点B关于对称中心A的对称点为点 ___D______,点C关于对称中心A的对称点为点 ___E_______。
23.2.1中心对称
你能给出中心对称的定义吗?
定义: 把一个图形绕着某一个点旋转180度,如果它能够与
另一个图形重合,那么就说这两个图形关于这个点对称或 中心对称,这个点叫做对称中心.
思考:如何作出已知图形关于某点的对称图形?
作该图形绕该点旋转180度后的图形即为 所求!
善良的你能帮助懒星根据自己和天宫找到她妹妹美星的 位置吗?
.
懒星
天宫
作出ΔABC关于点O的对称图形ΔDEF并说明作图
步骤
A
. 0
B
C
F E
D
辩一辩哪组同学的作图方法更好一点:
自己动手量一量,比一比,看一看你能得出哪些结论?
Ao=__O_D_____ BO=_O_E ______ co=__O_F______
ΔABC__≌___ΔDEF
新人教版初中数学九年级上册《中心对称》优质教学课件

O
图1
引入新知
问题1 (2)如图2,线段AC,BD相交于点O,OA=OC, OB=OD.把△OCD绕点O逆时针(或顺时针)方向旋 转180°,你有什么发现?
A
D
B
O
C 图2
引入新知
问题2 你能说说上述两个旋转的 共同点吗?
180°
O
图1
A
180°
D
B
O
C
图2
引入新知
180°
问题2
你能说说上述两个旋转的
复习回顾
• 旋转的性质: 旋转前、后的图形全等.
A
B C
A'
O
C'
B'
复习回顾
• 旋转的作图: 明确旋转中心; 明确旋转方向; 明确旋转角度.
A
B C
A'
O
C'
B'
引入新知
问题1 (1)如图1,把其中一个图案绕点O逆时针方向 旋转180°,你有什么发现?
O
图1
引入新知
问题1 (1)如图1,把其中一个图案绕点O逆时针方向 旋转180°,你有什么发现?若是顺时针方向旋转 180°呢?
巩固落实
法1:如图15,连接AD,取AD的中点O, 则点O即为所求.
F
E
A
O
D
B
C
图图1511
巩固落实
法2:如图16,连接AD、CF相交于点O, 则点O即为所求.
F
A O
B
C
图图1126
E D
巩固落实
练习
如图17,△ABC与△A'B'C'关于某一个点成
中心对称,点 A,B的对称点分别为点A'和B'.
图1
引入新知
问题1 (2)如图2,线段AC,BD相交于点O,OA=OC, OB=OD.把△OCD绕点O逆时针(或顺时针)方向旋 转180°,你有什么发现?
A
D
B
O
C 图2
引入新知
问题2 你能说说上述两个旋转的 共同点吗?
180°
O
图1
A
180°
D
B
O
C
图2
引入新知
180°
问题2
你能说说上述两个旋转的
复习回顾
• 旋转的性质: 旋转前、后的图形全等.
A
B C
A'
O
C'
B'
复习回顾
• 旋转的作图: 明确旋转中心; 明确旋转方向; 明确旋转角度.
A
B C
A'
O
C'
B'
引入新知
问题1 (1)如图1,把其中一个图案绕点O逆时针方向 旋转180°,你有什么发现?
O
图1
引入新知
问题1 (1)如图1,把其中一个图案绕点O逆时针方向 旋转180°,你有什么发现?若是顺时针方向旋转 180°呢?
巩固落实
法1:如图15,连接AD,取AD的中点O, 则点O即为所求.
F
E
A
O
D
B
C
图图1511
巩固落实
法2:如图16,连接AD、CF相交于点O, 则点O即为所求.
F
A O
B
C
图图1126
E D
巩固落实
练习
如图17,△ABC与△A'B'C'关于某一个点成
中心对称,点 A,B的对称点分别为点A'和B'.
人教版九年级上册23.2.1中心对称课件 (共38张PPT)

O
重合
ቤተ መጻሕፍቲ ባይዱ
B
(2) C
重合
概念
把一个图形绕 着某一个点旋 B’
A’
转180°,如果
O
它能够与另一 C’
C
个图形重合,那
么就说这两个 图形关于这个
B A
点对称,也称这
这个点叫作对称中心
两个图形成中
心对称
2个图形中的对应点叫做对称点
位够定置 重理两关合个系,1 图。所形从以图关关定这形于于义两是中中可个心全心知图对,形对等称关一称形,于定的。是中全两指心等个两对。个称所图的以形两有之个:间图的形形必状须、能
观察下面的图形,你有什么发现?
观察下面的两个图形你有什么发现?
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
灵活运用,体会内涵
1、点的中心对称点的作法
以点O为对称中心,作出点A的对称点A′;
AO
A′
点A′即为所求的点
2、线段的中心对称线段的作法
以点O为对称中心,作出线段AB的对称线段点A′B′
23.2.1 中心对称 课件 2022-2023学年人教版九年级数学上册

A.0个 B.1个 C.2个
D.3个
课堂小结
5.如图,△ABC与△A′B′C′关于某个点 成中心对称,则这个点是( )
A.D
B.E
C.F D.G
6.如图,两个半圆分别以P、Q为圆心,它们成中心对称,点A1, P,B1,B2,Q,A2在同一条直线上,则对称中心为( )
A.A2P的中点 C.A1Q的中点
跟踪练习
1.画一个与已知四边形ABCD中心对称图形. (1)以顶点A为对称中心; (2)以BC边的中点为对称中心.
N
F
B
B.
M
A
O
G
CA
C
E
D
D
中考链接
如图,在平面直角坐标系中, 若△ABC与△A1B1C1关于点E成中
心对称, 则对称中心E点的坐标是
.
课堂小结
1.了解中心对称及对称中心的概念; 2.会画成中心对称的图形 3.知道中心对称的图形性质: ①成中心对称的两个图形全等 ②对称点与对称中心三点共线 ③对称点所连线段经过对称中心,而且被对称中心所平分. ④中心对称图形对应点的连线交于一点,这个点为对称中心
B.A1B2的中点 D.PQ的中点
课堂小结
7.如图,已知AD是△ABC的中线,画出以点D为对 称中心与△ABD成中心对称的三角形
8.如图,在边长为1的正方形网格中,△ABC 与△A′B′C′是中心对称图形.
(1)在图中标出△ABC与△A′B′C′的对称 中心点O.
(2)求出△A′B′C′的面积.
旋转角是1800 对称点有:点C与点A;点B与点D.
A
D
O
B
C
画中心对称图形
①点的中心对称图形的画法 已知点A与点O,画点A关于的点O的对称点
23.2.1 中心对称与中心对称图形 课件(人教版九年级上)

∠A′C′B′,∠AOB=∠A′OB′.
【跟踪训练】 1.下列说法:①成中心对称的两个图形形状、大小一样; ②成中心对称的两个图形必须重合;③形状、大小一样的两个 图形成中心对称;④旋转后能够重合的两个图形成中心对称. 其中说法正确的个数是( B ) A.0 个 B.1 个 C.2 个 D.3 个 解析:成中心对称的两个图形经过旋转后能够重合,②不 正确;绕点旋转180°后能够重合的两个图形才成中心对称,当
(1)对称中心是______,点 A 的对称点是______; (2)指出图中相等的线段与相等的角(各写 4 组).
思路点拨:中心对称是旋转的特例,如果两个图形的对称 点连成的线段都经过某一点且被该点平分,那么这两个图形关 于这一点成中心对称. 解:(1)O A′ (2)AB=A′B′,BC=B′C′,AC=A′C′,OA=OA′, ∠BAC=∠B′A′C′,∠ABC=∠A′B′C′,∠ACB=
图形. 3.中心对称图形的概念 把一个图形绕着某一个点旋转 180°,如果旋转后的图形能 中心对称图形. 够与原来的图形重合,那么这个图形叫做____________
4.中心对称与中心对称图形 探究:如图 23-2-1 在
ABCD 中,
图 23-2-1
△COD 关于点 O 成中心对称,△AOD 与 (1) △AOB 与________ △COB 关于点 O 成中心对称; ________ (2)△ABD 与________ △CDB 关于点 O 成中心对称,由这两个成中 中心对称图形 . 心对称的三角形组成的 ABCD 是_____________ 归纳:中心对称是指两个图形间的位置关系,中心对称图 形是指一个图形所具有的性质.
图 D12
CA′C′A.
【跟踪训练】 3.如图 23-2-5,△ABC 与△PMN 是关于某点成中心对称
23.2.1中心对称_PPT
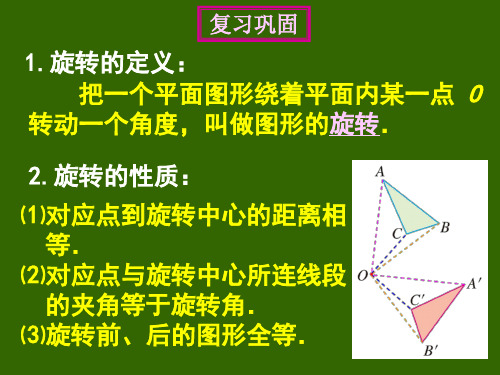
2 图形绕中心旋转180° 图形沿轴折叠
3
旋转后和另一个 图形重合
折叠后和另一个 图形重合
?
对称点的连线被对称 轴垂直平分
2.探究中心对称的性质
问题5中心对称是特殊的旋转,它有哪些性质?
C
A
B
O B′
A′
C'
思考: 1. 点 O 在线段 AA′上吗?在什么位置? 2. △ABC 和△A′ B′ C′有什么关系? 3. 你能从这个探究中得到什么结论?
复习巩固
1.旋转的定义:
把一个平面图形绕着平面内某一点 O
转动一个角度,叫做图形的旋转.
2.旋转的性质:
⑴对应点到旋转中心的距离相 等.
⑵对应点与旋转中心所连线段 的夹角等于旋转角.
⑶旋转前、后的图形全等.
第二十三章 旋转
23.2 中心对称
23.2.1中心对称
1.了解中心对称的概念
问题1(1)如图,把其中一个图案绕 点 O 旋转180°,你有什么发现?
叫做关于对称中心的对称点.A
D
O
B
C
1.了解中心对称的概念
问题3 中心对称与一般旋转的联系和区别?
联系:中心对称和一般的旋转都是绕 着某一点进行旋转;
区别:中心对称的旋转角度都是180°, 一般的旋转的旋转角度不固定,中心对称 是特殊的旋转.
对 比 理 解
中心对称
轴对称
1 有一个对称中心(点) 有一条对称轴(直线)
(3)两个图形的关系?
(重合)
这个我点们对称称具或有中这心样对特称点.A的两个图形关D于 你能试着O给中心对称B下个定O义吗C?
中心对称的概念:
把一个图形绕着某一点旋转 180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对 称.这个点叫做对称中心.
23.2.1中心对称 课件2024-2025学年人教版数学九上

证明:∵△ABO与△CDO关于O点中心对称,
∴BO=DO,AO=CO,
∵AF=CE,∴AO-AF=CO-CE,∴FO=EO,
FO EO ,
在△FOD和△EOB中,∠FOD ∠EOB,
DO BO ,
∴△FOD≌△EOB(SAS), ∴DF=BE.
随堂练习
3. 如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABD
称中心平分.(即对称点与对称中心三点共线)
2.中心对称的两个图形是全等形.
知识讲解
知识点1 中心对称的定义及性质
【例 1】如下图所示的四组图形中,左边图形与右边图形成中心对称的
有(
A.1组
)
B.2组
C.3组
D.4组
知识讲解
知识点1 中心对称的定义及性质
解析:将选项中左边图形沿着某一点旋转180°能与右边图形重合的
②同样可得:BD=B′D,CD=C′D;
③连接A′B′、B′C′、C′D,则四边形A′B′C′D为所
求的四边形,如图所示.
知识讲解
知识点2 中心对称作图
(1)这两个图形是否成中心对称?如果是,对称中心是哪一点?如果不
是,请说明理由.
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点?
数量关系,并说明理由.
∴∠F=∠CPM﹣∠PMF=α﹣β,
∠MCD=∠CDE﹣∠DMC=α﹣β,
∴∠F=∠MCD.
课后小结
中心对称的定义
及性质
定义
定义相关
性质
中心对称
中心对称作图
作图形关于某点对
称的图形
找出对称中心
数量关系,并说明理由.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质 2 对称轴是对称点连线 的垂直平分线。
对称点连线都过对称中心,
且被对称中心平分。
A
C1
B1
B
轴对称
O
C
A1
中心对称
1 有一条对称轴——直线 有一个对称中心——点
2 图形沿轴对折(翻转180°) 图形绕中心旋转180°
3 翻转后和另一个图形重合 旋转后和另一个图形重合
AC=AE
证明:
(1). 点A′是绕点A旋转180°后得到的,即线段OA绕点O旋转
180°得到线段OA′,所以点O在线段AA′上,且OA= OA′,即点 O是线段AA′的中点.
同样地,点O是线段BB′ CC′的中点. A’
(2).在△AOB与△ A′ O B′中 C’
B’
OA=OA ′,OB=OB ′ ∠AOB= ∠AOB ′
OB
C
∴ △AOB≌△ A′ O B′(SAS)
∴AB=A ′ B ′
A
同理 : BC=B ′ C ′,AC=A ′ C ′
∴ △ABC≌△ A′ B′C ′(SSS)
找一找:
下图中△A′B′C′与△ABC 关于点O是成中心对称的, 你能从图中找到哪些等量 关系?
(1)OA=OA′、OB=OB′、 OC=OC′ (2)△ABC≌△A′B′C′
A
B′
O
B
A′
例1 (3).如图.选择点O为对称中心,画出与△ABC
关于点O对称的△A′B′C′.
怎么办?可以帮 帮我吗? B′
A′
C′
△A′B′C′即为所求的三角形。
例1(4) 已知四边形ABCD和点O,画四边 形A′B′C′D′,使它与已知四边形关于这一点 对称。
B′ A′
C′
O
D′
D
C
A B
23.2.1 中心对称
一、复习提问:
1.什么是轴对称呢?
把一个图形沿着某一条直线折叠能与另一个图形完 全重合,那么就说这两个图形关于这条直线对称或轴对 称.
2.关于轴对称的两个图形有哪些性质?
1.两个图形是全等形. 2.对称轴是对称点连线的垂直平分线.
图形的旋转
旋转的定义
在平面内,把一个图形绕一个 定点,沿某个方向转动一个角度, 像这样的图形变换称作旋转 这个定点称为旋转中心
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
CB Aຫໍສະໝຸດ B’A’O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
有什么发现?
二.新课探究
三、中心对称性质
B' A
C O
C'
A' B
(1)关于中心对称的两个图形是全等形;
(2)关于中心对称的两个图形,对称点 所连线段都经过对称中心,而且被对称中 心平分.
四、灵活运用
1、点的中心对称点的作法
以点O为对称中心,作出点A的对称点A′;
AO
A′
点A′即为所求的点
2、线段的中心对称线段的作法
以点O为对称中心,作出线段AB的对称线段点A′B′
C B
如果将一个图形绕一点旋转180度得到
一个新的图形,这样的两个图形是什么 A 关系呢? D
A
你知道吗?可以
E
告诉我吗?
研究观察
(1)把其中一个图案绕点O旋转180°.你有什么发现? (2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕 点O旋转180°.你有什么发现?
C
O
D
O
所转动的角称为旋转角
旋转三要素
旋转中心、旋转方向、
旋转角度
旋转的基本性质
1、旋转前后的图形全等 2、对应点到旋转中心的距离相等 3、对应点与旋转中心连线的夹角
等于旋转角
一、看看下面的图形旋转
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
C’
C
B A
B’
A’
O
四边形A1B1C1D1即为所求的图形。
五、轴对称 与中心对称定义、性质对比对:
轴对称
中心对称
定 1 有一条对称轴—直线 有一个对称中心—点。
2 图形沿轴对折,(翻 图形绕中心旋转180度。 转达180度。)
义 3 翻转后与另一个图形 旋转后与另一个图形重合。 重合。
性 1 两个图形是全等形。 两个图形是全等形。
B
重合
重合
A
1.中心对称的定义: 像这样把一个图形绕着
C
某一点旋转180度,如果它
能够和另一个图形重合,那
么,我们就说这两个图形
A
B
A
D 关于这个点对称或中心 对称,这个点就叫对称中
心,这两个图形中的对应点,
叫做关于中心的对称点.
E
观察:C、A、E三点的位置关系怎样?线段AC、
AE的大小关系呢?
C、A、E三点在一条直线上或∠CAE= 180°.
