平均碰撞频率和自由程
6-4 分子的平均碰撞频率和平均自由程

气体分子速率分布律和能量分布律
平均自由程
热运动分子之间 频繁碰撞 分子的运动路径 曲折复杂
碰撞时两 分子质心距 离的平均值 称为分子的 有效直径
研究碰撞的意义:
分子间通过碰撞,实现能量的交换; 分子间通过碰撞交换能量达到能量按自由度均分; 分子间通过碰撞,由非平衡状态向平衡状态过渡; 分子间通过碰撞交换速度,使速度分布达到稳定。
二、平均自由程和平均碰撞频率的计算
1、分子碰撞模型 (1)分子视为直径为分子有效作用距离d 的刚球; (2)分子间的碰撞是弹性碰撞;
2、平均碰撞次数
“跟踪”一个分子 A,认为其它分子不 动,A以平均相对速 率 u 相对其它分子 运动。
圆柱体的截面积为 = d
2
,叫做分子的碰撞截面。
u t 2 •以折线为轴的曲折圆柱体积 u t d 2 •圆柱内分子数 n u t d 2 •单位时间内平均碰撞次数 n u d
一、平ห้องสมุดไป่ตู้自由程 和平均碰撞频率的定义
1、平均自由程 分子两次相邻碰撞之间自由通过的路程, 叫做自由程;分子在连续两次碰撞之间所经过 的路程的平均值叫做平均自由程。
2、平均碰撞频率 Z 在单位时间内一个分子与其它分子碰撞 的平均次数,叫做分子的平均碰撞次数或平 均碰撞频率。 3、二者的关系
v v T Z
•时间 t 内,A通过的折线长 平均相对速率
v
u 2v
u
B
u
v
A
A
d
2v
平均碰撞次数
Z 2 π d vn
2
3、平均自由程
v 1 2 z 2π d n
1 T 一定时 p
气体分子的平均自由程和碰撞频率

B A
平均碰撞频率:每个分子平均在单位时间与其他
分子相碰的次数平均值,用 z 表示。
平均自由程与平均碰撞频率之间的关系为:
vt v
zt z
首页
Байду номын сангаас
上页
下页
末页
退出
二、平均自由程与平均碰撞频率之间的关系
简化模型 (1)分子为刚性小球;
(2)分子有效直径为 d (分子间距平均值);
(3)其他分子皆静止,某一分子以平均速率 u 相
首页
上页
下页
末页
退出
【例题7–4】计算空气分子在标准状态下的平均自 由程和平均碰撞频率。取分子的有效直径d=3.5×10-10m 。 已知空气的平均分子量为29。
解: T 273K P 1.0atm 1.013105 Pa
d 3.51010 m
kT
2πd 2P
1.38 10 23 273 1.41 3.14 (3.510 10 ) 1.01105
6.9 10 8 m
首页
上页
下页
末页
退出
v 8RT 448m / s πM mol
z
v
448 6.9 108
6.5109 / s
首页
上页
下页
末页
退出
首页
上页
下页
末页
退出
问:在常温下,气体的方均根速率(或平均速率) 达几百米每秒。为什么在几米远的地方,打开酒精瓶塞, 需几秒甚至更长的时间才能嗅到酒精味 ?
首页
上页
下页
末页
退出
一、分子的平均自由程和平均碰撞频率
气体分子的平均自由程与碰撞频率

气体分子的平均自由程与碰撞频率气体分子在运动中会发生相互碰撞,这些碰撞对于气体的性质和行为有着重要的影响。
本文将探讨气体分子的平均自由程和碰撞频率以及它们在气体动力学中的意义。
1. 气体分子的平均自由程气体分子的平均自由程是指在单位时间内,分子在不受碰撞影响时所能走过的平均距离。
它与气体分子的碰撞次数、碰撞概率等因素密切相关。
计算平均自由程的方法是通过统计分子在一段时间内的位移,并将其平均值作为结果。
平均自由程与气体分子的直径和气体的密度有关。
当气体分子的直径较小时,分子之间的相互作用较小,平均自由程较大;而当气体分子的直径较大时,分子之间的相互作用较强,平均自由程较小。
此外,当气体的密度较小时,气体分子之间的碰撞次数较少,平均自由程较大;而当气体的密度较大时,气体分子之间的碰撞次数较多,平均自由程较小。
2. 气体分子的碰撞频率碰撞频率是指单位时间内气体分子发生碰撞的次数。
它与气体的温度、密度等因素息息相关。
碰撞频率的计算可以通过统计单位时间内发生的碰撞次数来实现。
碰撞频率与气体分子的速度和相对速度有关。
当气体的温度增加时,气体分子的速度增大,碰撞频率也增加;反之,当气体的温度降低时,气体分子的速度减小,碰撞频率也减小。
此外,当气体的密度增加时,气体分子之间的距离减小,碰撞频率也增加。
3. 平均自由程与碰撞频率的关系平均自由程和碰撞频率是气体分子运动的两个重要参数,它们之间存在着相互关系。
根据气体动力学理论,平均自由程与碰撞频率成反比关系。
当气体分子的平均自由程较大时,分子之间的相互作用较小,碰撞次数相对较少,碰撞频率较低;而当平均自由程较小时,分子之间的相互作用较强,碰撞次数相对较多,碰撞频率较高。
4. 平均自由程与碰撞频率的实际应用平均自由程和碰撞频率在气体动力学中有着广泛的应用。
例如,在研究气体扩散过程中,通过计算气体分子的平均自由程可以估算扩散的速率和距离;在研究气体传热过程中,通过计算气体分子的碰撞频率可以评估热传导的效率和速率。
分子碰撞频率和平均自由度

(二) λ Z 间的关系
v ----气体分子运动的平均速度,即每秒走过的平均距离.
Z -故(-1-)-,气气λ体体或分分Z子子平平与气均均体自每所由秒出程碰的:撞状态次有数λ关.=,如Zv气体单位体积内分子
数n大,分子碰撞的机会多.
(2) λ 或 Z 与气体种类(或性质)有关,分子直径大,碰撞机会多.
过程看作弹性碰撞过程,两这直径只是分 子有效直径,并非分子真正大小.
r0
r
f斥
d
Z = πd 2un
u = 2v 平均相对速率 , v 平均速率.
所以: Z = 2πd 2nv
看出λ 与宏观平均速率 v 无关.
与宏观λ 量(p,V,T)的关系:
λ= v =
Q p=nkT
n = p /kT
Z
∴ λ = kT 2π d 2 p
1
2π d 2 n
a
• 讨论:(1)气体温度一定p增大, λ 减小数量级概念,
v (3) 大,其它条件一定,碰撞机会多.
简略推导: 1) 气体分子为弹性小球,直径d.
2) 假设一定量气体中只有一个分子在运动,其它分子不动,平
均速率为 v ,而此分子运动相对其它分子的相对速率为u ,分
子a运动,轨迹为直线,和分子球心距离等于或小于分子直径 的那些分子与a碰撞.
则a分子在单位时间内和其它分子碰撞的次数为:
地球海平面 p=1大气压=
帕,
T=237K
此时 1.01=31×0-710米5
{ 地面上空(100公里处) p=0.133帕,
=1米λ
地面上空(300公里处) p=
帕
=10米λ
§12.5-气体分子的平均碰撞频率和平均自由程

·3 ·
Chapter 12. 气体动理论 §12. 5 气体分子的平均碰撞频率和平均自由程
一、定义
▲平均自由程:分子在连续两次碰撞间所经过的平均
路程。常用 表示。
▲平均碰撞频率:分子在单位时间内的平均碰撞次数。
归纳
1. 平均碰撞频率: z 2 n d 2v 2. 平均自由程: kT
2 d2 p
( The end·)9 ·
感谢您的阅读收藏,谢谢!
2021/4/9
10
撞的分子个数为:
N n d 2ut
z
N t
n d2u
理论修正: u 2 v
分子数密度 :n
·5 ·
Chapter 12. 气体动理论 §12. 5 气体分子的平均碰撞频率和平均自由程
z 2 n d 2v ~ 109 (s-1 ) 可知:z n , d 2 , v
则,平均自由程为:
v z
1
解:空气分子的有效直径 d = 3.5×10-10m,T = 373K 考虑到保温性能,应取:
1.5cm 1.5 102 m kT
2 d2 p p kT 0.63 (Pa) 6.22 106 atm
2 d2 瓶胆承受的压力~1.01×104kg/m2!
1.5cm
·8 ·
Chapter 12. 气体动理论 §12. 5 气体分子的平均碰撞频率和平均自由程
p (Pa)
(m)
1.01 105 1.33 102 1.33 1.33 102 1.33 104
6.9 108 5.2 105 5.2 103 5.2 101 52
平均自由程和平均碰撞频率

平均自由程和平均碰撞频率在物理的世界里,平均自由程和平均碰撞频率就像是空气中的那股清新气息,听起来很专业,但其实挺有意思的。
想象一下,咱们在一个人多热闹的派对上,大家都在忙着交谈、跳舞。
这个时候,你得在众人中间穿梭,偶尔被人撞一下,或者和朋友聊聊。
这就像是气体分子在空间里移动,发生碰撞,听起来是不是挺有画面感的?平均自由程,就像你在派对上能顺利移动的距离。
分子在这个空间里就像是你,四处游荡,能走多远,就取决于周围有多少“障碍物”。
如果人多得像热锅上的蚂蚁,那你可得小心翼翼,才能不被撞到。
相反,如果人少,那就简单多了,能畅通无阻。
简单来说,平均自由程就是气体分子在碰撞之前能走多远的一个数值。
你可能会问,这个数值是怎么计算的呢?它和气体的性质、温度、压力都有关系。
像夏天的空气,热得让人受不了,分子动得飞快,碰撞频率自然就高,这样一来,平均自由程就会变得小一些。
说到平均碰撞频率,那就是在单位时间内,分子之间碰撞的次数。
再把它换个角度看,就像是你在派对上,跟朋友聊得开心,突然有人从旁边冲过来把你撞了一下,感觉一下子被打断了。
这个频率高了,你的谈话就得时不时被打断,显得有点混乱。
反过来,如果碰撞频率低了,那大家的聊天就显得井然有序,就像是一场优雅的舞会,大家都在轻声细语,享受这份宁静。
这里面还有个有趣的地方。
气体分子如果是小颗粒,平均自由程就会长一些;如果是大颗粒,碰撞的机会就多了,平均自由程就短了。
这就好比你在派对上,身材高大的人总是更容易被注意到,走动起来也能避开一些障碍。
但如果是小个子,就得更加灵活,才能在人群中穿梭自如。
这不禁让人想起“人外有人,天外有天”这句话,确实每种情况都有它的道理。
碰撞频率还和温度、压力有关系。
高温下,分子运动得飞快,撞得也多,频率自然就高。
就像夏天的海滩,大家都兴奋得不行,玩得不可开交,彼此碰撞得频繁。
相反,气温低了,分子们就懒洋洋的,像冬天的围炉夜话,大家都安静下来,不再热闹,这时候碰撞频率自然就降了下来。
20平均自由程与碰撞频率10
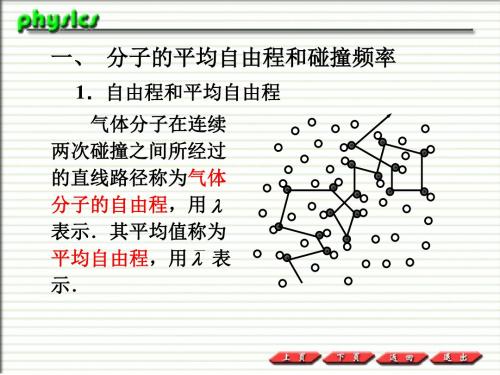
d 2vn
dd
平均碰撞频率为
A
Z d 2vn
d
(2) 考虑到所有分子的运动,应以平均相 对速度来代替上式中的平均速度
理论上可以证明,平均相对速度等于平均
速度的 2 倍
所以
Z 2 d 2vn
上式表明
平均碰撞次数与分子数密度,分子平均速 率成正比,也是与分子的直径的平方成正比.
把 Z 2 d 2vn代入
2 (3.11010 )2 1.33 103
6.62(m)
从上面计算可知,在通常的容器中,在高
度真空的情况下,分子间发生碰撞的概率是很 小的.
例题分析
例1 求在标准状态下,空气分子的平均自由 程、平均速率及平均碰撞次数. (已知空气的 平均摩尔质量为 2910-3kg·mol-1, 空气分子 的有效直径为3. 5 10-10m).
解 T 273K, p 1.013 105 Pa ,
d 3.5 1010m, 29 103kg mol1
小于或等于有效直径
dd
d 的分子,都要与A A
分子相碰.
d
以A 的中心运动轨迹为轴线,以分子的有 效直径为半径做一个曲折的圆柱体,那么,凡
中心在此圆柱体内的分子都要与A 相碰.
设:A 的平均速率为 v ,单位体积内的分子数 n A在单位时间内走过的长度为 v
圆柱体的体积为 d 2v
圆柱体内分子数为
vt v Zt Z
得 上式表明
1
2 d 2n
平均自由程与分子碰撞截面、分子数密度 成反比,而与分子平均速率无关.
因为 所以
p nkT
kT
2 d 2 p
分子的平均碰撞次数及平均自由程
较大的分子数较少,能量较小的分子数较多。 (3)在大小相等的各区间(坐标区间和速度区间)中比较,
分子总是处于低能态的概率大些。 (4)分布在某一坐标区间具有各种速度的分子总数只与坐标
区间的间隔成正比,与粒子的能量无关。 (A)只有(1),(2)是正确的; (B)只有(2),(3)是正确的; (C)只有(1),(2),(3)是正确的;(D)全部是正确的;
(`1) 10-10m (2) 102~103m/s (3) 108~109s-1
v 1.6 RT M mol
T=300K
v kT z 2d 2 P
把 P 1.01105 Pa
z 2d 2vP
kT T 273K 代入即可得到。
8
例6-12 气缸内有一定量的氢气(可视作理想气体),当
温度不变而压强增大一倍时,氢气分子的平均碰撞次数 z
分子的平均碰撞次数及平均自由程
问题的提出 前面已经说过:分子速率在几百米/秒的数量级,但为什
么食堂炸油饼时并不能马上闻到油香味呢? 原来分子速率虽高,但分子在运动中还要和大量的分子碰撞。
1
一、分子的有效直径d
分子的一种最简单的模型:将分子看成是具有一定体积 的弹性小球。
则分子的有效直径d定义为:两个分子质心之间所能允许的 最小距离。
距离小于或等于分子有效直径d的分子都会与A分子发生碰撞。
为此我们以A分子中心的运动轨迹为曲线,以分子直径d
为半径,做一曲折圆柱体,那么,凡分子中心在圆柱体内的
分子,都会与A分子发生碰撞,
z n d 2 u
4
理论证明:气体分子的平均相对速率 u与平均速率 v间有
分子的平均碰撞频率和平均自由程

第21讲 分子的平均碰撞频率和平均自由程 习题课教学要求理解气体分子的平均碰撞次数及平均自由程。
重点与难点重点:分子的平均碰撞次数及平均自由程。
难点:分子的平均碰撞次数及平均自由程。
7.7 分子的平均碰撞频率和平均自由程气体分子无规则热运动,频繁碰撞。
每个分子在两次碰撞之间自由行进多长的路径和用多长时间完全是偶然的、不确定的(如图7-10)。
但对大量分子,从统计的角度看,每个分子在单位时间内与其它分子平均碰撞多少次和平均自由行进多少路径却是有规律的。
7.7.1 平均碰撞频率z平均碰撞频率z 就是对于处于平衡状态下的大量气体分子组成的系统,一个分子单位时间内与其它分子的平均碰撞次数。
根据简化的气体分子模型,同种气体分子中每个分子都是直径为d 的刚性球,设想跟踪一个气体分子A ,为简化计算起见,首先假定其它分子不动,A 分子以平均相对速率u 接近其它分子,那么1秒内有哪些分子能与A 分子相碰呢?在A 分子运动过程中,它的质心轨迹是一条折线abce , 凡是其它分子的质心离开此折线的距离小于或等于分子有效直径d 的,都将与A 分子相碰(图7-11)。
如果以1秒内A 分子质心运动轨迹为轴,以分子有效直径d 为半径作一圆柱体(该圆柱体体积为2πd u )。
质心在该圆柱体内的分子都将与A 分子相碰。
设n 为分子数密度,则该圆柱体内的分子数为2πn d u ,亦即1秒内A 分子与其它分图7-10气体分子的碰撞e子发生碰撞的平均次数。
所以平均碰撞频率2πZ n d u =式中,,2πd σ=称为分子的碰撞截面。
考虑所有分子同时以平均速率υ运动,分子间平均相对运动速率为υ2=u , 故2Z d n υ=(7-23)上式表明,分子热运动平均碰撞频率与分子数密度n 、分子平均速率υ成正比,也与分子碰撞截面σ或分子有效直径d 的平方成正比。
7.7.2 平均自由程 λ平均自由程 λ 就是在平衡状态下,一个分子在连续两次碰撞之间所经过的路程的平均值。
6气体分子的平均碰撞频率及平均自由程

解答:根据公式
1
2n d 2
dengyonghe1@
质量一定,体积保持不变,则气体的分子数 密度 n 也不变,
1
2n d 2
平均自由程也不变。
讲解例题:P343,Example10.7
dengyonghe1@
第六节
气体分子的平 均碰撞频率及
平均自由程
dengyonghe1@
一、平均碰撞频率
发难:分子运动论佯谬 在常温下,空气分子速率 400~500米/秒,如果在讲台上打开一瓶香水,后排的 同学立刻就可闻到香水味。但实际需要 1~2 分钟才能 闻到,扩散与分子速率102m/s矛盾.
解释: 实际上由于 分子激烈的热运动,不 断地和其它分子碰撞, 分子不是走直线,而是 折线。
Z 2n d 2 v
例:求空气在27ºC、1atm下平均碰撞频率是多少? (空气分子直径为310-10m )
解:由 P nkT 有
n
1
.
1.013 38 10
10 -23
5
300
n P kT
2.45 10 25 m -3
dengyonghe1@
由
v 8RT
气分子直径为310-10m )
解:标准状态
T0 273 K , P0 1.013 105 Pa
dengyonghe1@
kT
2d 2P
1.38 10 -23 273
2 (3 10 -10 )2 1.013 10 5
9.3 10 -8 m
问题:一定质量的气体,保持体积不变,当温度增加 时,分子运动变得剧烈,平均碰撞频率增加了,平均 自由程如何变化?
分子平均碰撞次数和平均自由程

12-6 麦克斯韦气体分子速率分布律
第十二章 气体动理论
12-6 麦克斯韦气体分子速率分布律
热运动分子之间 频繁碰撞 分子的运动路径 曲折复杂 自由程 : 分 子两次相邻碰 撞之间自由通 过的路程 .
第十二章 气体动理论
12-6 麦克斯韦气体分子速率分布律
简化模型
(1) 分子为刚性小球 .d (2) 分子有效直径为 (分子间距平均值). (3) 其它分子皆静止,某分子以平均速率 u 相对其它分子运动 .
第十二章 气体动理论
12-8 分子平均碰撞次数和平均自由程
碰撞时两分子质心距离的平均值称为
分子的有效直径
平均碰撞频率:分子在单位时间内与其它分子碰撞的平均次数称 碰撞频率的倒数为 相邻两次碰撞时间
分子在与其它分子的相邻两次碰撞之间所经历路程的平均值为
平均自由程
为分子的平均速率
可联系
进行估算
第十二章 气体动理论
3、理想气体的内能
1 mol 理想气体的内能 1 i E N A N Ai kT RT 2 2
( R N Ak )
理想气体的内能
m' i i E RT RT M 2 2
m' ( 为气体的摩尔数 ) M
试指出下列各式所表示的物理意义
1 3 i i m i (1) kT , (2) kT , (3) kT , (4) RT , (5) RT 2 2 2 2 M2
12-8 分子平均碰撞次数和平均自由程
平均自由程
若能找出
与
的关系,则
可求
设分子 的碰撞路径ABCD长度
设气体分子数密度
则柱内分子数为
平均碰撞频率
质心在半径为 、长度为 的圆柱 体内的分子都会与 相碰。
理想气体的平均自由程和碰撞频率

思考题
1、容器内储有一定量的气体,保持容积不变, 使气体温度升高,则分子的平均碰撞频率和平均自 由程各怎样变化?
2、理想气体定压膨胀时,分子的平均自由程和 平均碰撞频率与温度的关系如何?
分子的碰撞截面 =3.85 ×10-15 cm2 ,求在标准状态下,
空气分子的平均自由程和平均碰撞频率。
解: 标准状态下 T 273K p 1.013105 Pa kT kT 6.83108 m 2 d 2 p 2 p
v 8RT 446m s1
M
Zv
446 6.83108
6.53109 s1
t
考虑其它分子的运动,由统计理论可知: u 2 v
Z 2 d 2nv
vZ
一秒钟内分子走过的平均路程为 v
一秒钟内与其它分子发生碰撞的平均次数为 Z
平均自由程 v
Z
1 2 d 2n
p nkT
kT
2 d 2 p
——平均自由程与压强的关系
例题:已知空气的摩尔质量为 M= 29 ×10-3 kg·mol-1
2、只有一个分子A 在运动,其它分子都认为是静
止不动的,且A 运动的相对速率为 u 。
t 时间内A分子走过的路程为: s ut
V d2 u t
在体积V 内的所有 其它分子在t 时间 内都与A 碰撞 设分子数密度为n
A 分子在t 时间内与其它分子碰撞的次数: n d 2u t
分子平均碰撞频率
Z n d 2ut n d 2u
❖平均自由程 mean free path :
分子在连续两次碰撞之间所经过的自由程的平均值。
❖平均碰撞频率 mean collision frequency Z : 单位时间内一个分子和其它分子碰撞的平均次数。
第9章热学(93)平均自由程与碰撞频率_能均分定理
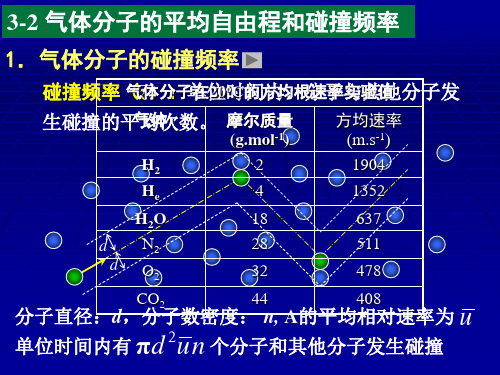
1mol 理想气体内能:
ii Emol NA 2 kT 2 RT
质量为m,摩尔质量为M的理想气体内能:
结论:
E
m M
Emol
m M
i RT 2
理想气体的内能只是温度的单值函数。
内能的改变量: E m i RT M2
例4 容器内有某种理想气体,气体温度为273K,压 强为1.013×103 Pa ,密度为1.24×10-2 kg·m-3。试求: (1) 气体分子的方均根速率; (2) 气体的摩尔质量,并确定它是什么气体; (3) 气体分子的平均平动动能和平均转动动能各是
RT p
12.824110032kg18..m0311o3l)或一氧化碳(CO)气体
(3)分子的平均平动动能:
3 kT 3 1.381023 273J 5.61021J 22
分子的平均转动动能:
2 kT 1.381023 273J 3.7 1021J
k
i 2
kT
“i”为分子自由度数
i3
k
3 2
kT
刚性双原子分子: i 5
k
5 2
kT
刚性多原子分子: i 6
k
6 2
kT
说明:能量均分定理是一个统计规律,是在平衡态下
对大量分子统计平均的结果。
3-4 理想气体的内能
内能: 气体中所有分子的动能和分子间相互作用势能
的总和。
理想气体内能:气体中所有分子的动能。
多少?
(4) 单位体积内分子的平动动能是多少? (5) 若气体的物质的量为0.3 mol,其内能是多少?
解:(1)气体分子的方均根速率为
v2 3RT
由物态方程 pV m RT
高二物理竞赛课件平均碰撞频率平均自由程

平均碰撞频率 平均自由程
【问题】摔碎一个汽油瓶,为什么先听到声音,后 闻到气味?
平均碰撞频率 平均自由程
一.碰撞简化模型
1. 气体分子是直径为d的刚球
(有效直径)
2.假设某分子a以平均相对
d
速率u运动 u 2v
二.平均碰撞频率mean collision frequency
20 oC 时,水为 1.01 10-3 Pa·s 空气为 1.82 10-5 Pa·s
微观上,这种粘滞力是动量传递的结果
z
z0
1 6
v
n
1 6
v
n
u(z0+ )
x
u(z0 - )
下层 平均自由程 l 的区域, 单位时间通过 dS 面积,向 上层输运动量的平均 x 分量
1 6
vnmu
(z0 - )dS
BE 过饱和蒸汽 遇凝结核心 - 液化 云室 人工降雨
CF 过热液体 遇汽化核心 - 汽化
气泡室
1.定义:单位时间内分子的平均碰撞次数 Z 。
平均碰撞频率 平均自由程
2.Z的计算 ①柱体中的分子数
N n d 2ut
② 平均碰撞频率
Z n d 2 u
Z 2nd 2 v
平均碰撞频率 平均自由程
三.平均自由程 mean free path 1.定义: 分子在连续两次碰撞之间所通过的 自由路程的平均值2.计算vZ来自Z2nd 2 v
1
2 d 2n
3.与P、T的关系
P nkT kT
2 d 2P
平均碰撞频率 平均自由程
Z 2nd 2 v
kT
2 d 2 p
1
2 d 2n
气体分子的平均碰撞频率和平均自由程

气体动理论
第9讲 气体分子的平均碰撞频率 和平均自由程
一、分子的平均碰撞频率
平均碰撞频率和平均自由程
平衡态宏观性质的维持 非平衡态向平衡态过渡
依靠分子间的频繁碰撞实现
刚性球 模型
不可以像讨论压强那样 将分子看成质点
不需像讨论内能那样考 虑分子内部结构
分子的有效直径 d 约为10-10 m
无引力刚 性球模型
=
1.013×105 1.38×10−23 × 273
=
2.69 ×1025 m−3
λ = 1 = 2.14 ×10−7 m 2π d 2n
z = v = 7.95×109 s−1
λ
(约80亿次)
平均碰撞频率和平均自由程
d d
假定: 分子是直径为d 的弹性小球
分子A以平均相对速率 u 运动, 其他分子静止 由麦克斯韦速率分布可证 u = 2 v
球心轨迹为轴, d 为半径作折圆柱体
平均碰撞频率和平均自由程
d d
球心在圆柱体内的分子将与A碰撞
单位时间内有 πd 2u n 个分子与A发生碰撞
平均碰撞频率: z = 2π d 2nv
• 当温度一定时,平均自由程与压强成反比,压强越小,平 均自由程越长.
平均碰撞频率和平均自由程
例. 求氢在标准状态下一秒内分子的平均碰撞次数. (已知 分子直径d = 2×10-10m )
解:
v=
8RT =
Mπ
8×8.31× 273
2 ×10−3π
= 1.70 ×103 m ⋅ s−1
n
=
P kT
二、平均自由程平均碰撞频率平均自由程平均自由程( λ ): 分子在连续两次和其它分子发生碰撞
平均碰撞频率和自由程

dN (r ,v ) Ce /kT dvxdvydvz dxdydz
2
§12.10 平均碰撞频率和平均自由程
一. 分子的平均碰撞频率 Z
一个分子单位时间内 和其它分子碰撞的平 均次数,称为分子的 平均碰撞频率。
·假设
每个分子都可以看成直径为 d 的弹性小球,分子间的碰 撞为完全弹性碰撞。大量分子中,只有被考察的特定分
可以推知:有 N 个分子时,分子的总微观态数 2N ,总宏
观态数( N+1 ) ,每一种微观态概率 (1/2N )
10
20个分子的位置分布
宏观状态
一种宏观状态对应的微观状态数
左20
右0
1
左18
右2
190
左15
右5
15504
左11 左10
右9 右10
167960 184756
左9
右11
167960
左5
25
二. 熵 熵增原理
1. 熵
孤立系统 状态(1)
能否自动进行? 判据是什么?
状态(2)
微观态数少的宏观态
微观态数多的宏观态
为了定量的表示系统状态的这种性质,从而定量说明自发 过程进行的方向,而引入熵的概念。
14
玻尔兹曼(Ludwig Edward Boltzmann, 1844-1906)
奥地利物理学家和哲学家,热力学和统计物理学的奠基人之一
一. 热力学第二定律的统计意义
1. 气体分子位置的分布规律
3个分子的分配方式
a b c
气体的自由膨胀
左半边 abc ab bc ac a b c 0
右半边 0 c a b bc ac ab abc
第三讲 平均碰撞频率与平均自由程

5.试以气体为例,用分子热运动观点对内摩擦、 热传导、扩散现象做出微观定性解释。
答案
—— 热学 ——
真实气体 范德瓦斯方程
作业
P149:1.26
预习 第二章 1、2、3、4节
—— 热学 ——
气体分子的平均自由程
1、粘滞现象
河流中水流的流速分布:
河岸
河流 u
河岸
f
u2
下层对上层的阻力
u1
f
上层对下层的作用力
—— 热学 ——
真实气体 范德瓦斯方程
各层气流的流速不同 相邻两层气流之间产生阻碍气体流动的阻力 ——称为粘性力。(这种现象称为内摩擦现象)
du -----速度梯度 dy
平均碰撞频率
z
平均自由程
平均速率
—— 热学 ——
λυ z
气体分子的平均自由程
(实际上其它分子也在运动)
平均相对速率 u 2υ 分子有效直径:d
—— 热学 ——
气体分子的平均自由程
d
u u
d
A
d
引入: 碰撞截面
d 2
结论: z 2σnυ
1
kT
λ
2σn 2πd 2 p
注:实际平均自由程可能与容器线度有关。
迁移现象产生的原因: 流速、温度、密度不均匀
无外界干预时,系统要从非平衡态自发地向平衡态 过渡。亦称输运过程。 讨论气体在非平衡态下的三种特殊过程。 即:三种迁移现象:
粘 滞 现 象 ——分子动量迁移; 热 传 导 现 象——分子能量迁移; 扩 散 现 象 ——分子密度迁移;
—— 热学 ——
混合气体分子的平均碰撞频率和平均自由程的初等推导

混合气体分子的平均碰撞频率和平均自由程的初等推导
混合气体是指由多种不同种类分子组成的气体,其中包括氢和氦,氧和氮,氯和氩等。
对
于混合气体,人们想知道分子碰撞频率和自由程。
平均碰撞频率是指单个分子碰撞其他分子的平均频率。
计算混合气体的平均碰撞频率需要
用到平均碰撞频率常数。
它可以用以下公式表示:
k=∑_i(f_i*k_i)
其中k代表混合气体的平均碰撞频率常数。
f_i 的值等于混合气体内每种分子的浓度或含量,K_i代表单种分子的碰撞频率常数。
自由程是指分子能够直接穿过物体而不受物体的阻碍而飞行的距离。
在一般情况下,计算
混合气体的平均自由程也可以用到平均碰撞频率常数:
f=K/f
其中l为混合气体的平均自由程,K代表混合气体的平均碰撞频率常数,f代表流体的密度。
上述就是混合气体的平均碰撞频率和平均自由程的初等推导。
平均碰撞频率常数可以用于计算不同种类分子平均碰撞频率,而平均自由程可以用流体密度计算。
在研究气体性质时,这也是有益的推导。
大学物理 7.5 气体分子的平均碰撞频率和平均自由程
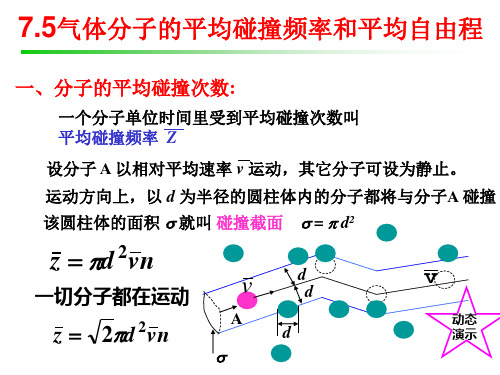
7
氮
氧
7
空气
7
(m ) 1.123 10
0.599 10
0.647 10
7.00 10
8
d ( m ) 2.30 10 10 3.10 10 10 2.98 1010 3.10 1010
例1
计算空气分子在标准状态下的平均自由程和 平均碰撞频率。取分子的有效直径 d = 3.10
空气摩尔质量为2910-3kg/mol 空气分子在标准状态下 8 RT v 448m / s 的平均速率 M
448 9 1 Z 5.1 10 s 8 8.71 10
v
=
v
Z
=
1
2 d2 n
=
kT
2 d2 P
10-10m。已知空气的平均分子量为29。
解: 已知 T 273 K , P 1.0atm 1.013 105 Pa ,
d 3.10 10 10 m
kT 2d 2 P
23
1.38 10 273 8 8.71 10 m 10 5 1.41 3.14 ( 3.5 10 ) 1.01 10
7.5气体分子的平均碰撞频率和平均自由程
一、分子的平均碰撞次数:
一个分子单位时间里受到平均碰撞次数叫 平均碰撞频率 Z 设分子 A 以相对平均速率 v 运动,其它分子可设为静止。 运动方向上,以 d 为半径的圆柱体内的分子都将与分子A 碰撞 该圆柱体的面积 就叫 碰撞截面
= d2
d d
z d v n
2
一切分子都在运动
v
A d
v
动态 演示
z 2d v n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
能量按自由度均分原理
在温度为 T 的平衡状态下,分子每个自由度的平均动能均 为 kT 2 。
玻耳兹曼分布律
在外势场中的分子总是优先占据势能较低的状态
n n0 e
p k BT
平衡态下温度为 T 的气体中,位于空间某一小区间 x~x+dx, y~y+dy, z~z+dz 中的分子数为
性质,但其仍不完善。
25
r
靠近器壁而位于厚度 · 为 r 的表面层内的任 一分子,将受到一个 指向气体内部的分子 引力的合力。
F
r
23
F'
p i )(v b ) RT
其中内压强 pi 为
a pi 2 v
(a 为常数)
考虑两种修正后,1mol 气体的范德瓦尔斯方程为
Ω2
S1 k ln 1
S 2 k ln 2
17
从状态(1)变化到状态(2) 的过程中,熵的增量为
2 S 2 S1 k ln 0 (等号仅适用于可逆过程) 1
孤立系统的熵永不会减少。这一结论称为熵增原理
说明
熵增原理只能应用于孤立系统,对于开放系统,熵是可以 减少的。
例如某溶液在冷却过程中的结晶的现象。其内的分子从溶 液中无序的运动转变为晶体的有规则排列,熵是减少的。
微观态: 在微观上能够加以区别的每一种分配方式
宏观态: 宏观上能够加以区分的每一种分布方式
对于孤立系统,各个微观态出现的概率是相同的
9
4个分子时的分配方式
左半边 右半边
abcd abc bcd cda dab 0 d a b c
ab cd
bc ad
cd ab 0
da
bc
ac
db
bd
ac
a
b
c
d
bcd cda dab abc abcd
2
4
二. 分子的平均自由程
分子在连续两次碰撞之间自由运动的平均路程,称为分子 的平均自由程。
v 1 λ 2 Z 2πd n
用宏观量 p、T 表示的分子平均自由程为
k T T λ 2 2π d p p
说明 在标准状态下,各种气体分子的平均碰撞频率的数量级 约为 109 s-1,平均自由程的数量级约为10-7 ~ 10-8 m 。
3. 熵的宏观表示(1865年) 在无限小的可逆过程中,系统熵的元增量等于其热温比, 即
18
dQ dS T
对于系统从状态(1) 变化到状态(2) 的有限可逆过程来说,则 熵的增量为
S
说明
(2)
(1)
dS
(2)
(1)
dQ T
对于可逆过程可以直接使用上式计算熵变 · 对于不可逆过程,欲计算熵变必须设计一条连接状态(1) · 与状态(2) 的可逆过程。
13
(3) 功热转换 功转化为热就是有规律的宏观运动转变为分子的无序热 运动,这种转变的概率极大,可以自动发生。相反, 热转化为功的概率极小,因而实际上不可能自动发生。
二. 熵 熵增原理
1. 熵
孤立系统
状态(1) 能否自动进行? 判据是什么? 状态(2)
微观态数少的宏观态
微观态数多的宏观态
为了定量的表示系统状态的这种性质,从而定量说明自发 过程进行的方向,而引入熵的概念。
1 1 2 2π d n 2π (3 1010 ) 2 3.21 1017 7.79 m
7
在这种情况下气体分子相互之间很少发生碰撞,只是不断 地来回碰撞真空管的壁,因此气体分子的平均自由程就应 该是容器的线度。 即
10 2 m
8kT v 468.7 m/s π
15
16
玻耳兹曼熵公式(1877年) · k 为玻耳兹曼常数 说明
S k ln
(1) 一个系统的熵是该系统的可能微观态的量度,是系统内 分子热运动的无序性的一种量度。 (2) 熵是系统状态的函数。
(3) 熵是一个宏观量,对大量的分子才有意义。
2. 熵增原理
孤立系统
Ω1
Ω2 > Ω1 (自动进行)
a ( p 2 )(v b ) RT v
任意质量气体的范德瓦尔斯方程为
m2 a m m ( p 2 2 )(V b ) RT M V M M
24
三 范德瓦尔斯等温线
从图中看出范德瓦尔斯 ·
等温线与实际气体等温 线颇为相似。
在临界等温线以上,二 · 者很接近,并且温度愈 高二者愈趋于一致。但 在临界等温线以下,二 者却有明显的区别。 尽管范德瓦尔斯方程能 · 较好地反映实际气体的
14
玻尔兹曼(Ludwig Edward Boltzmann, 1844-1906)
奥地利物理学家和哲学家,热力学和统计物理学的奠基人之一 • 1869年,将麦克斯韦速度分布律推广到保守 力场作用下的情况,得到了玻尔兹曼分布律 • 1872年,建立了玻尔兹曼输运方程,用来描 述气体从非平衡态到平衡态过渡的过程 • 1877年,提出了著名的玻尔兹曼熵公式 • 最先把热力学原理应用于辐射现象,导出热 辐射定律,称斯忒藩-玻尔兹曼定律 • 著有《物质的动理论》等,反对实证论和现 象论,坚决捍卫原子论。 “如果对于气体理论的一时不喜欢而把它埋没,对科学将 是一个悲剧;例如:由于牛顿的权威而使波动理论受到的 待遇就是一个教训。我意识到我只是一个软弱无力的与时 代潮流抗争的个人,但仍在力所能及的范围内做出贡献, 使得一旦气体理论复苏,不需要重新发现许多东西。”
19
例 用熵增原理证明理想气体的自由膨胀是不可逆过程。
证 设膨胀前系统的状态参数为 ( V1 ,p1 ,T ,S1 ) 膨胀后系统的状态参数为 ( V2 ,p2 ,T ,S2 ) 设想一可逆等温膨胀过程, 在此过程中系统吸热
dQ 0
dQ dS 0 T
V2
1
熵增加的过程是一个不可逆过程 另解: S
(2)
(1)
dS V
V2 d V pdV V2 R R ln 0 V 1 T V V1
20
实际气体的性质
一. 实际气体的等温线
实际气体的等温线 可以分成四个区域
汽态区(能液化) 汽液共存区 液态区 气态区(不能液化)
CO 2 等温线
从图中的曲线可知
只有在较高温度或低的 压强时,CO2气体的性 质才和理想气体相近。
21
二. 范德瓦尔斯方程
由于实际气体分子有大小,并且分子之间存在有相互作用, 使得理想气体状态方程不完全符合实际气体的状态变化规律。 通过对理想气体状态方程的修正,可以得出更接近实际气体 性质的状态方程。 1. 分子体积所引起的修正
1mol 理想气体的状态方程为
p v RT
考虑气体分子本身有大小,将上式修改为
6
-2 -3 例 真空管的线度为 10 m ,其中真空度为 1.33× 10 Pa。 设空气分子的有效直径为 3×10-10 m。
求 27℃ 时单位体积内的空气分子数、平均自由程、平均碰撞 次数 。 解 由气体的状态方程, 有
p 1.33 10 3 17 3 n 3 . 21 10 m kT 1.38 10 23 300
d N n d V n0 e
p / kT
d xd yd z
麦克斯韦–玻耳兹曼分布律
dN (r ,v ) Ce / kT dv x dv y dv z dxdydz
2
§12.10 平均碰撞频率和平均自由程
一. 分子的平均碰撞频率 Z
一个分子单位时间内 和其它分子碰撞的平 均次数,称为分子的 平均碰撞频率。 假设 · 每个分子都可以看成直径为 d 的弹性小球,分子间的碰 撞为完全弹性碰撞。大量分子中,只有被考察的特定分 子 A 以平均速率
v Z 4.68 10 4 s 1
8
§12.12 热力学第二定律的统计意义和熵的概念
一. 热力学第二定律的统计意义
1. 气体分子位置的分布规律
a b c
气体的自由膨胀
3个分子的分配方式
左半边
abc 0
ab c
bc a
ac b
a bc
b ac
c ab
0 abc
右半边
(微观态数23, 宏观态数4,每一种微观态概率(1/23) )
左11 左10
左9
右9 右10
右11
167960 184756
167960
左5
左2 左0
右15
右18 右20
15504
190 1
包含微观状态数最多的宏观状态是出现的概率最大的状态
11
结论 (1) 系统某宏观态出现的概率 与该宏观态对应的微观态 数成正比。 (2) N 个分子全部聚于一侧 的概率为1/(2N) (3) 平衡态是概率最大的宏观 态,其对应的微观态数目 最大。 ( n )
N/2
左侧分子数n
2. 热力学第二定律的统计意义
孤立系统中发生的一切实际过程都是从微观态数少的宏观态 向微观态数多的宏观态进行.
12
3. 分析几个不可逆过程 (1) 气体的自由膨胀 气体可以向真空自由膨胀但却不能自动收缩。因为气体 自由膨胀的初始状态所对应的微观态数最少,最后的均 匀分布状态对应的微观态数最多。如果没有外界影响, 相反的过程,实际上是不可能发生的。 (2) 热传导 两物体接触时,能量从高温物体传向低温物体的概率, 要比反向传递的概率大得多!因此,热量会自动地从 高温物体传向低温物体,相反的过程实际上不可能自 动发生。
p (v b ) RT
b 为常数,可由实验测定或理论估计。
22
2. 分子间引力引起的修正
