磁场的高斯定理
合集下载
磁场-4 磁场中的高斯定理

大学物理
恒定磁场
第4讲 磁场中的高斯定理
一、磁感应线
磁场中的高斯定理
磁感应线(B线):为形象描绘磁场的空间分布而人为 绘制出的一系列曲线
1.磁感应线上任一点的切线方向都与该点的磁感应强
度的方向一致。
v
2.垂直通过单位面积的磁
B
感应线条数等于该处磁感
应强度的大小。
条形磁铁周围的磁感应线
直线电流的磁感应线
解: 建立如图所示的坐标系
x处磁场: B = μ0I
2πx
rr
元通量: dΦm = B ⋅ dS = Bldx
= μ0I ldx
O x +dx
x
2πx
∫ ∫ Φm =
SdΦm
=
μ0 Il
2π
a+b 1 dx = μ0 Il ln a + b
ax
2π b
三、磁场中的高斯定理
磁场中的高斯定理
对封闭曲面,规定外法向为正
进入封闭曲面的磁通量 Φ < 0 m
穿出封闭曲面的磁通量 Φ > 0 m
磁场中高斯定理:
磁场中通过任意闭合曲面的磁感应强度通量等于
∫ ∫ 零。
v B
⋅
v dS
=
B cosθ dS = 0
S
S
磁场是“无源场”
磁场中的高斯定理
例题1. 如图所示,在磁感应强度为B的均匀磁场中,有一 半径为R的半球面S,S的边线所在平面法线方向n与B的 夹角为α ,求通过半球面S 的磁通量。
磁场中的高斯定理
磁感应线为一组环绕电流的闭合曲线。
圆电流的磁感应线
磁场中的高斯定理
I
磁感应线为一组环绕电流Leabharlann 闭合曲线。磁场中的高斯定理
恒定磁场
第4讲 磁场中的高斯定理
一、磁感应线
磁场中的高斯定理
磁感应线(B线):为形象描绘磁场的空间分布而人为 绘制出的一系列曲线
1.磁感应线上任一点的切线方向都与该点的磁感应强
度的方向一致。
v
2.垂直通过单位面积的磁
B
感应线条数等于该处磁感
应强度的大小。
条形磁铁周围的磁感应线
直线电流的磁感应线
解: 建立如图所示的坐标系
x处磁场: B = μ0I
2πx
rr
元通量: dΦm = B ⋅ dS = Bldx
= μ0I ldx
O x +dx
x
2πx
∫ ∫ Φm =
SdΦm
=
μ0 Il
2π
a+b 1 dx = μ0 Il ln a + b
ax
2π b
三、磁场中的高斯定理
磁场中的高斯定理
对封闭曲面,规定外法向为正
进入封闭曲面的磁通量 Φ < 0 m
穿出封闭曲面的磁通量 Φ > 0 m
磁场中高斯定理:
磁场中通过任意闭合曲面的磁感应强度通量等于
∫ ∫ 零。
v B
⋅
v dS
=
B cosθ dS = 0
S
S
磁场是“无源场”
磁场中的高斯定理
例题1. 如图所示,在磁感应强度为B的均匀磁场中,有一 半径为R的半球面S,S的边线所在平面法线方向n与B的 夹角为α ,求通过半球面S 的磁通量。
磁场中的高斯定理
磁感应线为一组环绕电流的闭合曲线。
圆电流的磁感应线
磁场中的高斯定理
I
磁感应线为一组环绕电流Leabharlann 闭合曲线。磁场中的高斯定理
大学物理-7-3 磁通量 磁场的高斯定理

B
磁通量:通过某一曲面 的磁感线数为通过此曲面 的磁通量.
Φ BS cosBS
Φ B S B enS dΦ B dS
B dΦ BdS cos
s
Φ s BdS
单位 1Wb 1T 1m2
B dS1
1 B1
S
B2
2
dS2
dΦ1 B1 dS1 0 dΦ2 B2 dS2 0
SB cosdS 0
S B d S 0
3a
2a 5a
l
Φ s BdS = 0
I
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的磁通量必等于零。
(故磁场是无源的.)
求磁通量(1)用磁通量的定义求(2)用高斯定理求
例1 如图载流长直导线的电流为
积的磁通量.
解 先求
,试I 求 通过矩形面 ,B对变磁场给出
B
后积B 分dΦ求0I
2π x
Φ
B // S
I
l
d1 d2
dΦ BdS 0I ldx
Φ
S
B
dS
2π x
0Il
2π
d2
d1
dx x
o
x Φ 0Il ln d2
2π d1
例2 一半径为a的无限长直载流导线,沿轴向均
匀地流有电流I,若作一个半径为 R= 5a,高为l
的柱形曲面,已知此柱形曲面的轴与载流导线的 轴平行且相距3a(如图),则在圆柱侧面S上的 磁通量=?
第三节 磁场的高斯定理
一 磁感线
规定:曲线上每一点的切线方向就是该点的磁感
强度 B 的方向,曲线的疏密程度表示该点的磁感强 度 B 的大小.
I
2、磁场的高斯定理和安培环路定理

L
B dl o I i
L
S
B dS 0 j dS
S
B 0 j
安培环路定理的物理意义 磁场是有旋场(或磁场是非保守场,磁感应线 是闭合曲线)。
三、安培环路定理的应用
O
R
r
例3、求长直螺线管内的磁场。设螺线管的长度为 L,共有N匝线圈,单位长度上有 n = N/L匝线圈, 通过每匝线圈电流为I。管内中间部分的磁场是均 匀的,方向与管的轴线平行,在管的外侧磁场很 弱,可以忽略不计。
B
a
b
c d [解]: 若螺线管很长,则边缘效应可以忽略,螺 线管可看成是无限长,由对称性可知管内磁场是 均匀的,方向与管的轴线平行,并由右手螺旋定 则确定。在管的外侧磁场很弱,可以忽略不计。
B dl B 2πr μ0 I ,
j I / R2
且 I j s jπr 2 (r <R)
B
1 B μ0 jr 2
μ0 Ir B 2π R 2
0 I B 2R
μ0 I r = R处 B 2π R
B
0 Ir 1 0 jr, ( r R) 2 2 R 2 0 I 1 R2 0 j , r R ) ( 2 r 2 r
例2、求均匀载流无限长圆柱导体内外的磁场分布。
[解]:当r R时 B dl B 2r 0 I
L
I
R
μ0 I B 2π r
I 由 j πR 2
1 R2 B μ0 j 2 r
(r >R)
I jπR2
r
L
L
12磁场的高斯定理和安培环路定理解读

穿过一面元的磁通量:
d m BdS BdS cos B dS 式中:dS dSn ˆ 称为面元矢量。 ˆ 为法线方向单位矢量。 n
4
2.穿过某一曲面的磁通量
m d m B dS
d m
B
BdS cos
dS
ˆ n
S
3.穿过闭合曲面的磁通量
m d m B dS
规定:取闭合面外法线方向为正向。 磁力线穿出闭合面为正通量, 磁力线穿入闭合面为负通量。
2
B
磁通量单位:韦伯,Wb
2
ˆ n
Байду номын сангаас
B
5
3.磁场中的高斯定理 定理表述:穿过任意闭合面的磁通量等于 0。
dB
dB ' dB' '
dl '
p
d
dl ' '
l
c
B
结果
o j
2
o
方向如图所示。
a
b
在无限大均匀平面电流的两侧的磁场都为 均匀磁场,并且大小相等,但方向相反。
15
例5 一矩形截面的空心环形螺线管,尺寸如图所示, 其上均匀绕有N匝线圈,线圈中通有电流I。试求: (1)环内距轴线为r 远处的磁感应强度;(2)通过 螺线管截面的磁通量。 I
解:在管内作环路半径为 r的圆环 ,
环路内电流代数和为: I NI
rR
o R1
2
当 r >> ( R2 – R1) 时N n 为沿轴向线圈密度;
0 NI B 2r 0 NI B 2r
磁场的高斯定理课件

磁力线
磁场中磁力方向相同的闭 合曲线,表示磁力作用的 路径。
磁感应强度
描述磁场强弱的物理量, 与磁力线密度和方向有关 。
高斯定理的背景与重要性
高斯定理的起源
高斯定理是电磁学中的基本定理之一 ,由德国物理学家卡尔·高斯提出。
定理的重要性
高斯定理在电磁学中具有重要地位, 它揭示了磁场分布与电荷之间的内在 关系,是解决磁场问题的重要工具。
05
磁场的高斯定理的实验验证
实验设计思路与原理
设计思路
01
利用磁场的高斯定理,推导实验中需要测 量的物理量,并设计合适的实验装置。
03
02
通过磁场的高斯定理实验,验证磁场在封闭 曲面上的通量守恒性质。
04
实验原理
磁场的高斯定理指出,穿过任意封闭曲面 的磁场通量等于零,即磁场是无源场。
05
06
通过测量封闭曲面内的磁场强度,可以验 证高斯定理的正确性。
实验操作过程与注意事项
01
操作过程
02
搭建实验装置,包括磁场发生器、测量线圈和数据采集系统。
将测量线圈放置在封闭曲面上,并确保测量过程中线圈与曲面
03
保持相对静止。
实验操作过程与注意事项
01
启动磁场发生器,记录测量线圈 中的感应电动势。
02
重复实验,改变封闭曲面的形状 和大小,以验证高斯定理的普遍 性。
高斯定理的证明过程
总结词
高斯定理的证明过程涉及矢量场的基本性质和微积分的知识,通过一系列严密的数学推导,最终得出高斯定理的 结论。
详细描述
证明高斯定理通常从矢量场的闭合曲面积分等于其内部区域散度的积分这一基本性质出发。通过选取适当的坐标 系和参考系,利用矢量运算和微积分的基本定理,逐步推导出穿过封闭曲面的磁通量等于该曲面所包围区域内磁 场强度的积分,从而证明了高斯定理。
11-4磁场的高斯定理和安培环路定理

S
闭合路径包围的电流为电流密度 沿所包围的曲面的积分
ห้องสมุดไป่ตู้
∑I =∫∫
i i
v v r r ∫∫S (∇×B)⋅ d S = µ0 ∫∫S j ⋅ dS v v 安培环路定理微分形式 ∇× B = µ j 0
S
v v j ⋅ dS
安培环路定理的存在说明磁场不是保守场 磁场不是保守场, 安培环路定理的存在说明磁场不是保守场,不 存在标量势函数。这是恒磁场不同于静电场的一 存在标量势函数。 个十分重要的性质。 个十分重要的性质。 安培环路定理可以用来处理电流分布具有一定 安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。 对称性的恒磁场问题。
dl ' o dl ' ' 垂线, 做 PO 垂线,取对称的长直 电流元,其合磁场方向平行于电流平面。 电流元,其合磁场方向平行于电流平面。无数对 点的总磁场方向平行于电流平面。 称元在 P点的总磁场方向平行于电流平面。 点的总磁场方向平行于电流平面
电流平面无限大, 电流平面无限大,故与电流平面等距离的各点 B 的大小相等。在该平面两侧的磁场方向相反。 14 的大小相等。在该平面两侧的磁场方向相反。
其磁场方向与电流满足右手螺旋。 其磁场方向与电流满足右手螺旋。
R2
R
L
R 1
L
同理可求得在螺绕管外部的磁场为零: 同理可求得在螺绕管外部的磁场为零:
∴B = 0
r ≤R 1
12
磁场的高斯定理
∫∫
∫L
S
v v B⋅ dS = 0
v ∇⋅ B = 0
安培环路定理
v v B⋅ dl = µ0 ∑Ii
i
v v ∇× B = µ0 j
闭合路径包围的电流为电流密度 沿所包围的曲面的积分
ห้องสมุดไป่ตู้
∑I =∫∫
i i
v v r r ∫∫S (∇×B)⋅ d S = µ0 ∫∫S j ⋅ dS v v 安培环路定理微分形式 ∇× B = µ j 0
S
v v j ⋅ dS
安培环路定理的存在说明磁场不是保守场 磁场不是保守场, 安培环路定理的存在说明磁场不是保守场,不 存在标量势函数。这是恒磁场不同于静电场的一 存在标量势函数。 个十分重要的性质。 个十分重要的性质。 安培环路定理可以用来处理电流分布具有一定 安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。 对称性的恒磁场问题。
dl ' o dl ' ' 垂线, 做 PO 垂线,取对称的长直 电流元,其合磁场方向平行于电流平面。 电流元,其合磁场方向平行于电流平面。无数对 点的总磁场方向平行于电流平面。 称元在 P点的总磁场方向平行于电流平面。 点的总磁场方向平行于电流平面
电流平面无限大, 电流平面无限大,故与电流平面等距离的各点 B 的大小相等。在该平面两侧的磁场方向相反。 14 的大小相等。在该平面两侧的磁场方向相反。
其磁场方向与电流满足右手螺旋。 其磁场方向与电流满足右手螺旋。
R2
R
L
R 1
L
同理可求得在螺绕管外部的磁场为零: 同理可求得在螺绕管外部的磁场为零:
∴B = 0
r ≤R 1
12
磁场的高斯定理
∫∫
∫L
S
v v B⋅ dS = 0
v ∇⋅ B = 0
安培环路定理
v v B⋅ dl = µ0 ∑Ii
i
v v ∇× B = µ0 j
133磁场的基本特征 高斯定理和安培环路定理
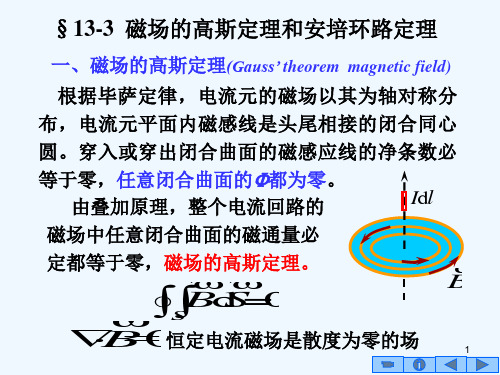
S 恒定电流磁场是散度为零的场 B = 0
B d S = 0
1
1.磁感线
切线方向—— B 的方向; 疏密程度—— B 的大小.
I I I
2
I S N S I N
3
直线电流的磁感应线
I I B
4
圆电流的磁感应线
I
5
通电螺线管的磁感应线
I
I
6
各种典型的磁感应线的分布:
围绕单根载流导线的任一回路 L
L2
对L每个线元 d l 以过垂直导线平面作参考分解 为分量 dl// 和垂直于该平面的分量 d l d l B 0 B d l B d l B d l //
L
B d l B d l I 证明步骤同上 // 0 L L //
直线电流的磁感线
圆形电流的磁感线
7
直螺线管电流的磁感线
环形螺线管电流的磁感线
8
1.磁力线的特征 无头无尾 与电流套连 与电流成右手螺旋关系 闭合曲线
I
2. 磁通量
B d s 单位:韦伯(Wb) m S
9
2. 磁通量 磁场的高斯定理
S B
ΔN B ΔS
磁场中某点处垂直 B 矢量的单位面积上 通过的磁感线数目等于该点 B 的数值.
讨论
S 0 1)Bd
S
磁场的基本性质方程
2)关于磁单极:
将电场和磁场对比: 由电场的高斯定理
d Sq 0 D
S
可把磁场的高斯定理写成 与电场类似的形式
BdS qm
S
q0 -自由电荷
qm - 磁荷
磁场中的高斯定理

高斯定理表明,在通电导线周 围的磁场中,穿过任意一个闭 合曲面的磁通量等于电流的代 数和。
通过高斯定理,可以计算出通 电导线周围的磁场分布和特点, 例如磁场的方向和强度。
磁通量的计算实例
磁通量是指穿过某个面的磁场的强弱和方向的量。通过计算磁通量,可 以了解磁场的分布和特点。
计算磁通量需要使用高斯定理,通过积分来计算穿过某个面的磁通量。
磁场矢量场
高斯定理的应用使得我们可以方便地处理磁场矢量场问题。通过计算矢量场的散度,我们可以得到特定区域内磁 场的变化情况,从而更好地理解磁场的行为和性质。
磁场中的高斯定理的推导
高斯定理推导
高斯定理在磁场中的推导基于磁场的高斯定理和安培环路定律。通过引入磁通量密度和磁通量等概念 ,我们可以利用微积分的方法推导出高斯定理在磁场中的形式。
磁场与电场的关系
磁场和电场是相互联系的,变化的电 场会产生磁场,变化的磁场也会产生 电场。因此,磁场和电场可以相互转 化,形成电磁波。
磁场的方向
磁场的方向
在磁场中任意一点,磁场都有一个特定的方向,称为该点的磁场方向。磁场方 向可以通过放入该点的磁针的指向来确定,磁针的北极指向磁场方向。
磁场方向的确定
高斯定理表明,在磁场中,穿过任意一个闭合曲面的磁通量等于零,即磁场是无源 场。
在地球磁场中,由于地球内部的物理过程,产生了磁场分布。高斯定理可以用来分 析地球磁场的分布和特点,例如地磁场的极性和强度分布。
通电导线周围的磁场高斯定理分析
当导线中电流发生变化时,会 在导线周围产生磁场。高斯定 理可以用来分析这个磁场的分 布和特点。
磁场大小的测量
测量磁场大小的方法有多种,如高斯计、特斯拉计等。这些 仪器通过测量磁感应线的密度或磁通量来计算磁场的大小。 在地球表面,地磁场的大小约为0.5-0.6特斯拉。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
惟一的一次 从宇宙射线中捕捉到磁单极子的实验记录:
斯坦福大学Cabrera等人的研究组利用超导 线圈中磁通的变化测量来自宇宙的磁单极子。
基本装置:
有磁单极子穿过时,感应电流
qm
超导线圈 Φ2Φ0
I
电感 L
I 2Φ0 / L
I
8Φ 0 L
t
1982.2.14,13:53
qm
超导线圈 Φ2Φ0
I
电感 L
y
Idl rˆ
R I
o
Idl r组成的平面
r
dB
x
.d
d BPx
B
yz
x
z
BxIdBsinI 40 πIrd2lR r 4π 0Ir3R Idl
0 IR 2 2r3
由对称性可知 每一对对称的电流元在P点的 磁场垂直分量相互抵消 所以
y
Idl rˆ
R I
o
Idl r组成的平面
r
dB
x
.d
一、磁场 电流 或运动电荷周围既有电场 又有磁场 磁场的宏观性质: 1)对运动电荷(或电流)有力的作用 2)磁场有能量 二、磁感强度 运动电荷在电磁场中受力:
fqE q B
洛仑兹力公式
§3 磁场的高斯定理 一、磁力线 磁通量 二、 磁通连续原理
§3 磁场的高斯定理 一、磁力线 磁通量
I
1.磁力线的特征 无头无尾 闭合曲线
若考虑方向,则可写成
B
0 pm
2πr3
结论:磁偶极子的场沿磁矩方向
4)电磁学中物质分子的模型
3) 平面载流线圈的磁矩 磁偶极子
定义平面载流线圈的磁矩 Pm IS
如果 场点距平面线圈的距 离很远,这样的平面载流
线圈称为磁偶极子 磁偶极矩 pm
Pm
SI
平面载流线圈
p m I
磁偶极子的场用磁偶极矩表示
I
. pm r
P
B20IxR32 20Ir3R2
0IπR 2
2πr 3
0 pm
2πr 3
S
qm - 磁荷
见过单 独的磁 荷吗?
1931年 Dirac预言了磁单极子的存在 量子理论给出电荷q和磁荷qm存在关系:
qqmn( hn1 , 2, 3 )
只要存在磁单极子就能证明电荷的量子化。 预言:磁单极子质量:
m21 0 11 g110m 6p 这么大质量的粒子尚无法在加速器中产生 人们寄希望于在宇宙射线中寻找
rˆ
相互垂直
所以
dB
在
Idlr2Fra bibliotek组成的平面内
且垂直 r
由此可知
dB 0Idl
4πr2
第三步:根据坐标
y
Idl rˆ
R I
o
z
写分量式
Idl
r组成的平面
r
dB
x
.d
d BPx
B
yz
x
dB
0Idl
4πr2
dBxdBsin40 πIrd2lR r
dByzdBcos
第四步:考虑所有电流元在P点的贡献
B ds
S
单位:韦伯(Wb)
二、 磁通连续原理(磁场的高斯定理)
BdS 0
S
S
dS
B
微分形式
dS
B0
磁场是不发散的(磁场是无源场)
讨论
1)BdS 0 磁场的基本性质方程
S
2)关于磁单极:
将电场和磁场对比:
由电场的高斯定理
DdSq0
S
q0 -自由电荷
可把磁场的高斯定理写成
与电场类似的形式
BdS qm
d BPx
B
yz
x
z
Byz dBcos0
I
结论:在P点的磁感强度
BBx20Ir3R 22x20IR R 22 32
方向:沿轴向 与电流成右手螺旋关系
讨论
BBx20Ir3R 22x20IR R 22 32
1)圆电流中心的场
x0
B0I
2R
2)若x >> R
即场点离圆电流很远
B20IxR32 20Ir3R2
与电流套连
与电流成右手螺旋关系
直线电流的磁感应线 I I B
圆电流的磁感应线 I
通电螺线管的磁感应线
I I
各种典型的磁感应线的分布:
直线电流的磁感线
圆形电流的磁感线
直螺线管电流的磁感线
环形螺线管电流的磁感线
1.磁力线的特征
无头无尾 闭合曲线
I
与电流套连
与电流成右手螺旋关系
2. 磁通量
m
R I
x.
o
P
x
z
y
Idl rˆ
R I
o
Idl
r组成的平面
r
dB
x .P
x
z
解:第一步:在圆电流上任取一电流元 Idl
由毕-萨定律 知其在场点P产生的磁感
强度
dB04Idπlr2rˆ
第二步:分析各量关系 明确 dB的方向和大小
y
Idl rˆ
R I
o
Idl r组成的平面
r
dB
x .P
x
z
Idl
第8章 稳恒磁场 §1 基本磁现象 §2 磁场 磁感强度 §3 磁场的高斯定理 §4 毕-萨-拉定律 §5 安培环路定理及应用
§1 基本磁现象
小故事:1820年 奥斯特 磁针的一跳 说明电流具有磁效应
法国物理学家迅速行动 代表人物: 阿拉果 安培 毕奥 萨伐尔 拉普拉斯 从奥斯特磁针的一跳到对磁现象的系统认识 只用半年时间 说明科学家的锲而不舍的精神
绚丽多彩的极光
在地磁两极附近,由于磁感线与地面垂直,外层 空间入射的带电粒子可直接射入高空大气层内, 它们和空气分子的碰撞产生的辐射就形成了极光。
进水
出水
发动机
B
电流
F B
•
电极
海水
•I
接发电机
F
磁流体船
电磁轨道炮
~ 10 6 A
a ~ 10 6 g ,在1ms内,弹块速度可达10km/s
§2 磁场 磁感强度 一、磁场 二、磁感强度
I
8Φ 0 L
t
1982.2.14,13:53
实验中: 4匝直径5cm的铌线圈 连续等待151天 1982.2.14自动记录仪 记录到了预期电流的跃变
以后再未观察到此现象。
结论: 目前不能在实验中确认磁单极子存在
§4 毕奥-萨伐尔-拉普拉斯定律 要解决的问题是: 已知任一电流分布 其磁感强度的计算 方法:将电流分割成许多电流元 Idl
磁感应线绕向与电流流向成右手螺旋关系
叠加原理:
BBi , BdB i
例1 求圆电流中心的磁感强度
dB 0Idl 4R2
I
Idl
dBoR
B 0Idl
(I) 4R2
0I 4R2
dl
(I )
0 I
B
2R
B N 0I
2R
N---分数和整数
原因:各电流元在中心产生的磁场方向相同
例2 圆电流轴线上任一点的磁场 圆电流的电流强度为I 半径为R 建如图所示的坐标系 设圆电流在yz平面内 场点P坐标为x y
毕-萨-拉定律:每个电流元在场
点的磁感强度为:
dB
0Idl rˆ
4πr2
Idl r P
I
dB
0Idl
rˆ
4πr2
大小: dB0I4dπlrs2in
方向: Idlr如图所示
Idl
r
P
I
dB
既垂直电流元 又垂直矢径
04π107 H/m
真空中的磁导率
O
dB
P
Idl
dB
I dl rP
电流元的磁感应线在垂直于电流元的平面内 是圆心在电流元轴线上的一系列同心圆
