整式的除法(一)优秀教案
《整式的除法》word教案 (公开课获奖)2022北师版 (10)
《1.7 整式的除法（一）》三维目标：1. 知识与技能目标：掌握单项式除以单项式运算法则，通过法则的应用，训练学生的综合解题能力和计算能力．2. 数学思考目标：理解单项式除以单项式是在同底数幂的除法基础上进行的.3. 问题解决目标：能熟练进行单项式与单项式的除法运算.4. 情感态度目标：培养学生抽象概括能力、运算能力，发展有条理的思考及表达能力.批 注重点难点：教学重点：单项式除以单项式的运算法则及其应用.教学难点：法则的探索过程以及能够灵活地运用法则进行计算和化简. 教具准备： 教学方法：教 学 过 程教学环节设计： 一、复习1、同底数幂的除法法则是什么？2、计算：（1）a 7÷a 4； （2）( - x ) 6÷ ( - x ) 3；（3）( xy ) 4÷( xy )； （4）b 2 m + 2÷b 2． 二、探索单项式的除法法则1、计算下列各题，并说说你的理由．（1）x 5y ÷x 2； （2）8 m 2n 2÷2 m 2n 1；（3）a 4b 2c ÷3 a 2b ．鼓励学生利用已经学过的知识独立解决这几个题目.然后再集体交流不同的算法，并让学生理解其中的算理.2、如何进行单项式除以单项式的运算？引导学生根据上面的算式，概括出单项式除以单项式运算法则，并用自己的语言进行描述.3、教师明晰单项式的除法法则，指出运用法则时应注意的问题. 三、例题教学 例1、计算：（1）-31x 2y 3÷3 x 2y ； （2）10 a 4b 3c 2÷5 a 3bc ； （3）( 2 x 2y )3· ( - 7 xy 2)÷14 x 4y 3；（4）( 2 a + b )4÷( 2 a + b )2． 四、做一做如图所示，三个大小相同的球恰好放在一个圆柱形盒子里，三个球的体积占整个盒子容积的几分之几？ 学生独立解决问题，再集体交流算法.五、练一练教材：随堂练习六、小结1、单项式的除法法则是什么？2、应用单项式除法法则应注意：①系数先相除,把所得的结果作为商的系数,运算过程中注意单项式的系数包含它前面的符号.②把同底数幂相除,所得结果作为商的因式,由于目前只研究整除的情况,所以被除式中某一字母的指数不小于除式中同一字母的指数.③被除式单独有的字母及其指数,作为商的一个因式,不要遗漏.④要注意运算顺序,有乘方要先做乘方,有括号先算括号里的,同级运算从左到右的顺序进行.七、作业布置教材：习题1.13教学反思：第五章反比例函数一、学生知识状况分析通过本章的学习，学生已经经历抽象反比例函数概念的过程，理解了反比例函数的概念，会作出反比例函数的图象，并探索和掌握其性质，能从函数图象中获取信息来解决实际问题。
整式的除法教案
整式的除法(1)教学目标：1.会进行单项式除以单项式的整式除法运算。
2.理解单项式除以单项式的运算算理。
教学重点：单项式除以单项式的整式除法运算教学难点：单项式除以单项式运算法则的探究过程教学准备：自学1、自读文本：根据学习目标，认真阅读课本第28-29页，做到整体理解，在你预习的过程中，你有哪些疑问请纪录下来。
2、思路整理：从同底数幂的乘除法入手，通过计算，总结出单项式除以单项式的法则，并运用法则进行计算。
(5x)·(2xy2 )(-3mn)·（4n2 )3、基础自清：（1）两数相除，号得正，号得负，并把相除。
（2）同底数幂的除法法则是。
（3）零指数幂的意义。
4、计算：（2m2n)·( )=8m2n2 →（8m2n2) ÷（2m2n)＝(-x)·( )=-2x3 →（-2x3) ÷（-x)＝教学过程：一：自学检测（检测昨天预习效果）1、计算：(8m 2n 2) ÷（2m 2n) (-2x 3) ÷ (－x) （－53x 2y 3) ÷（3x 2 y) (10a 4b 3c 2)÷(5a 3bc) 学生口答，并回答怎么做的。
单项式相除，把系数、同底数幂分别相除，作为商的因式.2、计算：(8m 2n 2x ) ÷（2m 2n) (-2x 3y 2) ÷ (－x)对于只在被除式里含有的 x 、y 2，应该怎样处理 ？（对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式.）二：研学（要求：先独立完成，再同桌之间互对答案，并把不一致的题目交至组长处，组长带领全组解决疑问较多的题目，最后确定展示人选。
）1、 计算：（－5m 2n 2) ÷ (3m)(2x 2y)3 · (－7xy 2) ÷ (14x 4y 3)[9(2a+b)4] ÷ [ 3(2a+b)2]注意：1、运算顺序：先算乘方，在算乘除，最后算加减；如果有括号，先算括号里面的。
初中数学_整式的除法（1）教学设计学情分析教材分析课后反思
初中数学_整式的除法（1）教学设计学情分析教材分析课后反思《整式的除法》（第1课时）教学设计教学目标：知识与技能：1、经历探索单项式的除法法则的过程，会进行简单的单项式除法运算（只要求单项式除以单项式，并且结果都是整式）。
2、体会在单项式除法运算中转化思想的应用。
过程与方法：通过学生观察、独立思考等过程，培养学生归纳、概括的能力和猜测、验证能力。
情感、态度与价值观：通过观察、归纳、概括等一系列的数学活动，感受数学思考过程的条理性和数学结论的严密性。
教学重点：理解单项式的除法法则，并正确应用。
教学难点：整式除法算理的理解。
教学方法：目标教学法，自主、合作、探究。
教学资源：教材、多媒体课件。
教学过程：一、知识回顾1. 同底数幂除法的运算法则？2.单项式与单项式相乘的运算法则？3.计算：二、教学目标1.在实践中归纳总结单项式除以单项式的运算法则。
2.熟练运用单项式除以单项式的法则进行计算。
三、新知探究（一）情境引入：下雨时，常常是“先见闪电，后闻雷鸣”，这是因为光速比声速)91()5)(4(2224y x yz x ?-23))(1(x y x ?)4()2)(2(2n n m ?)3()31)(3(22b a bc a ?-)91()35)(4()31())(3()4()8)(2())(1(22252242225y x yz x bc a c ba n n m x y x ÷-÷-÷÷24342323234232)2()2)(4(14)7()2)(3(510)2(353)1(b a b a y x xy y x bc a c b a y x y x -÷-÷-?÷÷-快的缘故.已知光在空气中的传播速度为3.0×108米/秒，而声音在空气中的传播速度约为300米/秒，你知道光速是声速的多少倍吗？（二）自主学习目标一：归纳总结单项式除以单项式的运算法则问题1：运用乘除法互逆的原则，你一定能完成下列运算。
2024北师大版数学七年级下册1.7.1《整式的除法》教案1
2024北师大版数学七年级下册1.7.1《整式的除法》教案1一. 教材分析《整式的除法》是北师大版数学七年级下册第1章第7节的内容，本节课主要介绍整式除法的基本概念和运算方法。
通过本节课的学习，学生能够理解整式除法的意义，掌握整式除法的运算方法，并能够应用整式除法解决实际问题。
二. 学情分析学生在学习本节课之前，已经学习了整式的加减法和乘法，对整式的基本概念和运算方法有一定的了解。
但是，对于整式除法这一概念，学生可能较为陌生，需要通过实例和练习来理解和掌握。
三. 教学目标1.理解整式除法的概念和意义。
2.掌握整式除法的运算方法。
3.能够应用整式除法解决实际问题。
四. 教学重难点1.整式除法的概念和意义。
2.整式除法的运算方法。
五. 教学方法采用问题驱动法、实例教学法和练习法，通过引导学生思考和解决问题，让学生理解和掌握整式除法。
六. 教学准备1.PPT课件。
2.练习题。
七. 教学过程1.导入（5分钟）通过一个实际问题引导学生思考：已知两个整式的商和余数，如何求被除式？让学生回顾整数除法的概念，为新课的学习做好铺垫。
2.呈现（10分钟）讲解整式除法的定义和运算方法，通过PPT课件展示实例，让学生跟随老师一起完成整式除法的运算。
在此过程中，强调整式除法的基本步骤：确定除数、试除、商式、余式。
3.操练（10分钟）让学生独立完成PPT课件上的练习题，老师巡回指导，解答学生遇到的问题。
在此过程中，注意引导学生运用整式除法的基本步骤，培养学生的运算能力。
4.巩固（10分钟）通过PPT课件上的练习题，让学生巩固整式除法的运算方法。
老师选取部分学生的作业进行点评，指出优点和不足，并进行针对性的讲解。
5.拓展（10分钟）让学生思考：整式除法在实际问题中的应用。
老师出示几个实际问题，让学生运用整式除法进行解决。
通过这个过程，培养学生运用数学知识解决实际问题的能力。
6.小结（5分钟）对本节课的内容进行总结，强调整式除法的概念和运算方法。
《整式的除法》第一课时参考教案
1.9 整式的除法(一)●教学目标(一)教学知识点1.单项式除以单项式的运算法则及其应用.2.单项式除以单项式的除法运算算理.(二)能力训练要求1.经历探索单项式除以单项式的运算法则的过程，会进行单项式与单项式的除法运算.2.理解单项式与单项式相除的算理，发展有条理的思考及表达能力.(三)情感与价值观要求1.经历探索单项式除以单项式的运算法则的过程，获得成功的体验，积累丰富的数学经验.2.鼓励多样化的算法，培养学生的创新能力.●教学重点单项式除以单项式的运算法则及其应用.●教学难点单项式除以单项式的运算法则的探索过程.●教学方法自主探索法学生凭借已有的数学经验，自主探索单项式与单项式相除的法则，并能用自己的语言有条理的思考及表达.●教具准备投影片四张第一张：提出问题，记作(§1.9.1 A)第二张：议一议，记作(§1.9.1 B)第三张：例1，记作(§1.9.1 C)●教学过程Ⅰ.创设问题情景，引入新课［师］(出示投影片§1.9.1 A)我们看下面几个算式.计算下列各题，并说说你的理由.(1)(x5y)÷x2;(2)(8m2n2)÷(2m2n);(3)(a4b2c)÷(3a2b).同学们观察上式，可知它们属于哪一种运算？［生］这三个算式都是单项式与单项式相除.［师］我们前面学习了整式的加法、减法、乘法，从今天开始我们来学习整式的除法，先来学习单项式与单项式的除法.Ⅱ.讲授新课1.探索单项式除以单项式的运算法则［师］在除法运算中，我们都有一个限制条件，是什么呢？［生］除数不能为零.制：除式恒不为零.下面就请同学们凭借自己的数学经验计算上面的三个算式，可以用多种算法.但要说明每一步的理由，同学之间可互相交流算法.(教师可深入到学生探索交流过程中，对较困难的学生以启示)［生］我们已学习了整式的乘法运算，而乘法的运算法则大多是联系整数的运算法则和运算律得出的.于是我想到了整数除法运算.根据乘法和除法互为逆运算，来解答上面三个算式如下：(1)我们可想象x2·( )=x5y与单项式相乘，是把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变作为积的因式.可继续联想：所求单项式系数肯定为1；x2·( )=x5.所以所求单项式字母部分应包含x 5÷x 2即x 3,还应包含y.由此可知x 2·(x 3y)=x 5y.所以(x 5y)÷x 2=x 3y(2)可想象(2m 2n)·( )=8m 2n 2,根据单项式与单项式相乘的法则，可知：8÷2=4,n 2÷n=n.即(2m 2n)·(4n)=8m 2n 2所以(8m 2n 2)÷(2m 2n)=4n. (3)可想象(3a 2b)·( )=a 4b 2c.根据单项式与单项式相乘的法则，可得系数部分应为1÷3=31,a 4÷a 2=a 2,b 2÷b=b,即(3a 2b)·)31(2bc a =a 4b 2c.所以(a 4b 2c)÷(3a 2b)= 31a 2bc.［生］我是用类似于分数的约分的方法计算的. (1)(x 5y)÷x 2=25x y x =232)(x y x x ⋅=x 3y;(2)(8m 2n 2)÷(2m 2n)=nm n m 22228=nm n n m222)4()2(⋅=4n;(3)(a 4b 2c)÷(3a 2b) =b ac b a 2243=ba b a bc a 2223)(⋅=32bc a=31a 2bc.［师生共析］上面两位同学的想法都是有理有据的.我们一块再来看一下前后式子的联系出示投影片(§1.9.1 B)议一议：如何进行单项式除以单项式的运算？你能用自己的语言有条理的描述出来吗？［生］从上述分析的过程，可得出：单项式相除，把系数、同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式.实际上单项式相除是在同底数幂的基础上进行的.［生］其实单项式相除可以分为系数、同底数幂，只在被除式里含有的字母三部分运算.［师］同学们用很条理的语言描述出了单项式相除的运算法则，下面我们就来具体做几个单项式的除法.(出示投影片§1.9.1 C)［例1］计算：3x2y3)÷(3x2y);(1)(－5(2)(10a4b3c2)÷(5a3bc);(3)(2x2y)3·(－7xy2)÷(14x4y3);(4)(2a+b)4÷(2a+b)2.分析：(1)、(2)直接运用单项式除法的运算法则；(3)注意运算顺序(先乘方再乘除，再加减)；(4)鼓励学生悟出，将(2a+b)视为一个整体来进行单项式除以单项式的运算.3x2y3)÷(3x2y)解：(1)(－5=(－53÷3)·(x 2÷x 2)·(y 3÷y)=－51·x 2－2y 3－1=－51y 2;(2)(10a 4b 3c 2)÷(5a 3bc)=(10÷5)·(a 4÷a 3)·(b 3÷b)·(c 2÷c) =2·a 4－3b 3－1c 2－1=2ab 2c; (3)(2x 2y)3·(－7xy 2)÷(14x 4y 3) =(8x 6y 3)·(－7xy 2)÷(14x 4y 3) =－56x 7y 5÷(14x 4y 3) =－4x 3y 2;(4)(2a+b)4÷(2a+b)2 =(2a+b)4－2 =(2a+b)2 =4a 2+4ab+b 2. Ⅲ.随堂练习 1.(课本P 40)计算： (1)(2a 6b 3)÷(a 3b 2); (2)(481x 3y 2)÷(161x 2y);(3)(3m 2n 3)÷(mn)2; (4)(2x 2y)3÷(6x 3y 2). 解：(1)(2a 6b 3)÷(a 3b 2)=(2÷1)·(a 6÷a 3)·(b 3÷b 2)=2a 3b; (2)(481x 3y 2)÷(161x 2y)=(481÷161)·(x 3÷x 2)·(y 2÷y)=31xy;(3)(3m2n3)÷(mn)2=(3m2n3)÷(m2n2)=3·(m2÷m2)·(n3÷n2)=3n;(4)(2x2y)3÷(6x3y2)4x3y=(8x6y3)÷(6x3y2)=3(注意(3)(4)题中的运算顺序)2.我们都知道“先看见闪电，后听见雷声”，那是因为在空气中光的传播速度比声音快.科学家们发现，光在空气里的传播速度约为3×108米/秒，而声音在空气里的传播速度大约只有300米/秒.你能进一步算出光的传播速度是声音的多少倍吗？解：(3×108)÷300=(3×108)÷(3×102)=106(倍)光的传播速度是声音的106倍.Ⅳ.课时小结这节课同学们结合我们学过的分数约分、乘法和除法互为逆运算，从不同的方面出发探索出单项式除法的法则，并运用到整式除法的运算，积累了一定的数学经验.Ⅴ.课后作业，习题1.15，第1、2、3题.1.课本P412.如果你刷牙时一直开着水龙头，估计会白白地流走多少水？说说你是如何获得这个数据的.(提示：本题的解决需将测量、幂的运算等内容综合起来).Ⅵ.活动与探究已知a=2002x+2001,b=2002x+2002,c=2002x+2003,求a2+b2+c2－ab－bc－ca 的值.［过程］由题设条件是求不出a,b,c的值的.观察代数式，联想到公式2(a2+b2+c2－ab－bc－ca)=(a－b)2+(b－c)2+(c－a)2,所以a2+b2+c2－ab－bc－1［(a－b)2+(b－c)2+(c－a)2］,因此只需求出a－b、b－c、c－a即可.ca=2［结果］a=2002x+2001 ①b=2002x+2002 ②c=2002x+2003③由①－②得a －b=－1; 由②－③得b －c=－1; 由③－①得c －a=2.则a 2+b 2+c 2－ab －bc －ca=21［(a －b)2+(b －c)2+(c －a)2］=21［(－1)2+(－1)2+22］=21×6=3.●板书设计1.9 整式的除法(一)一、(x 5y)÷x 2=x 3y=(x 5÷x 2)·y(8m 2n 2)÷(2m 2n)=4n=(8÷2)·(m 2÷m 2)·(n 2÷n) (a 4b 2c)÷(3a 2b)= 31a 2bc=(1÷3)·(a 4÷a 2)·(b 2÷b)·c单项式相除，把系数、同底数幂分别相除后，作为商的因式；对于只含在被除式里的字母，则连同它的指数一起作为商的一个因式.二、应用例1(略) 例2(略) ●备课资料 一、参考例题 ［例1］计算(1)(－5x 5y 4)÷(－3x 3y 3) (2)15a 2m+1b 2n c ÷(－5a 2m b n ) (3)(1.2×107)÷(5×104)(4)［5(x+y)2(x －y)］3÷［3(x+y)2(x －y)］2 解：(1)(－5x 5y 4)÷(－3x 3y 3)=［－5÷(－3)］(x 5÷x 3)(y 4÷y 3) =35x 2y(2)15a 2m+1b 2n c ÷(－5a 2m b n )=［15÷(－5)］(a 2m+1÷a 2m )(b 2n ÷b n )c =－3ab n c(3)(1.2×107)÷(5×104) =(1.2÷5)(107÷104) =0.24×103=240(4)［5(x+y)2(x －y)］3÷［3(x+y)2(x －y)］2 =［125(x+y)6(x －y)3］÷［27(x+y)4·(x －y)2］ =(125÷27)［(x+y)6÷(x+y)4］［(x －y)3÷(x －y)2］ =27125(x+y)2(x －y)=27125x 3+27125x 2y －27125xy 2－27125y 3［例2］计算(1)(－32a 2b 4c 6)(－9a 2c)÷34ab 4c 3(2)(3xy)2(x 2－y 2)－(4x 2y 2)2÷8y 2+18x 6y 8÷2x 2y 6+9x 2y 4 解：(1)(－32a 2b 4c 6)(－9a 2c)÷34ab 4c 3=6a 4b 4c 7÷34ab 4c=(6×43)a 3c 6=29a 3c 6(2)(3xy)2(x 2－y 2)－(4x 2y 2)2÷8y 2+18x 6y 8÷2x 2y 6+9x 2y 4 =9x 2y 2(x 2－y 2)－(16x 4y 4)÷8y 2+18x 6y 8÷2x 2y 6+9x 2y 4 =9x 4y 2－9x 2y 4－2x 4y 2+9x 4y 2+9x 2y 4 =16x 4y 2 二、参考练习 1.填空(1)12x8y3z÷(－4x2yz)= .(2)－9a2m b2m+3c÷3a m b2m= .(3)8a3b2c÷ =2a2bc.1a3bc.(4) ÷2ab2=2(5)3.2×105÷ =－1.6×106.(6) ÷(2×107)=－5×103.2.计算(1)－12a6b3c2÷(－3a4b2)(2)18a m+2x n+3y5÷(－6a m x n+1y)(3)12(a+b)7(a+2b)5÷［－3(a+b)6(a+2b)］(4)(－1.1×104)(2.3×105)÷(－5.06×1013)答案：1.(1)－3x6y2 (2)－3a m b3c (3)4ab (4)a4b3c (5)－0.2 (6)－10112.(1)4a2bc2 (2)－3a2x2y4 (3)－4(a+b)(a+2b)4 (4)5×10－5。
人教版八年级数学上册14.1.5整式的除法优秀教学案例
（一）知识与技能
1.让学生掌握整式除法的基本概念，理解整式除法的运算方法。
2.培养学生能够运用整式除法解决实际问题的能力，提高他们的数学应用意识。
3.通过对整式除法的学习，使学生能够进一步理解数学知识之间的联系，提高他们的数学素养。
（二）过程与方法
1.利用生动、直观的教学方法，引导学生通过自主学习、合作交流的方式，探索整式除法的运算规律。
2.鼓励学生自主完成作业，培养他们的自主学习能力。
3.教师及时批改作业，给予学生反馈，提高他们的学习效果。
五、案例亮点
1.生活情境导入：通过生动有趣的生活情境导入新课，让学生感受到整式除法的实际意义，激发学生的学习兴趣，提高他们的学习主动性。
2.问题导向：本节课以问题为导向，引导学生提出问题、思考问题、解决问题。这种教学方式有助于培养学生的独立思考能力和解决问题的能力。
5.作业小结：布置具有针对性的作业，让学生在课后巩固所学知识。同时，鼓励学生自主完成作业，培养他们的自主学习能力。教师及时批改作业，给予学生反馈，提高他们的学习效果。
本节课通过以上五个亮点，充分体现了以学生为主体的教学理念，注重培养学生的独立思考能力、解决问题的能力和团队合作意识。同时，教师以人性化的语言进行教学，关注学生的情感态度与价值观的培养，使学生在轻松愉快的氛围中学习，提高他们的数学素养。
1.讲解整式除法的定义和运算规则，让学生理解整式除法的基本概念。
2.通过示例，演示整式除法的运算过程，让学生直观地感受和理解。
3.引导学生总结整式除法的运算规律，培养他们的归纳能力。
（三）学生小组讨论
1.设计具有探究性的问题，让学生在小组内进行讨论。例如：“整式除法在实际生活中有哪些应用？”
整式的除法第1课时教案说课稿教学反思
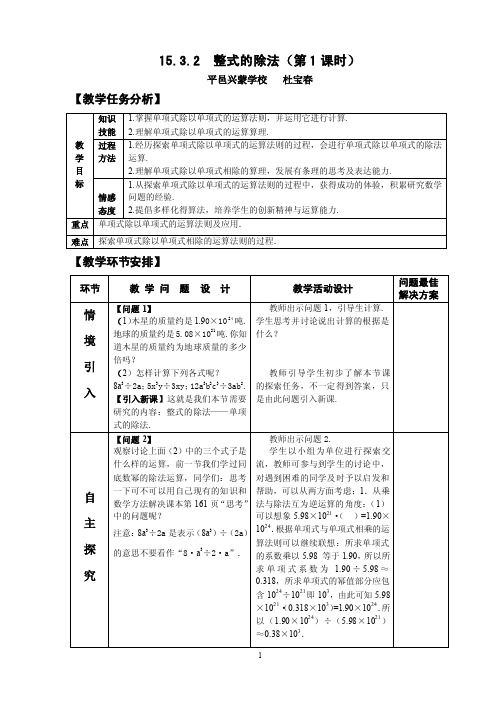
结 论 ：单项 式除以单 项式的法 则：
交
单 项式相除 ，把系数 与同底数 幂分 别 相除作为 商的因式 ，对于只 在被
1.901024 5.981021
1.90 5.98
1024 1021
0.318103.
流
除 式里含有 的字母， 则连同它 的指
数作为商的一个因 式.
（2）8a3÷2a= 8a3 8 a3 4a.
算乘方，有 括号先算 括号里的 ，同
一级运算从左到右的顺序进行.
教
后
反
思
3
【当堂达标自测题】
一、 填空题：
1.直接写出结果： (1) m4÷m4=______ ； (3) (-xy)3÷(-xy)= _____ ； 2.直接写出结果： (1)(4×105) ÷(5×104)=________；
(2) (b4)2÷(b2)3=_________ ； (4) (ab2)4÷(ab2)2=_______.
2a 2 a
尝 试 应 用
成果 展示
其余的同理可得.上述两种算法有理 有据，所以结果正确．
教师引导学生从三方面总结：1.
系数；2.同底数幂的指数；3.只在被
除式里含有的字母.
教师肯定学生的总结，规范单项
式除法法则 ，板演单 项式除以 单项
式的法则.
【例 1】计算 （1）28x4y2÷7x3y；
(2) -5a5b3c÷15a4b.
） 学生思考并解答.
）
2
A. xy B. y C. x D. xy2
(3)已知 28a3bx÷7ayb2=4b2,则 x,y 的
值是（ ）
Ａ.ｘ＝４，ｙ＝３；
Ｂ.ｘ＝２，ｙ＝３；
七年级数学第一章整式运算整式除法(一)教案北师大版 教案
讲学合一 学习模式 课型：新授课课题：1.9整式的除法（1）学习目标：1、经历探索整式除法运算法则的过程，会进行简单的整式除法运算； 2、理解整式除法运算的算理，发展有条理的思考及表达能力。
学习重点：可以通过单项式与单项式的乘法来理解单项式的除法，要确实弄清单项式除法的含义，会进行单项式除法运算。
学习难点：确实弄清单项式除法的含义，会进行单项式除法运算。
学习方法：探索讨论、归纳总结。
复习回顾：1、=÷x x 42、=÷-1n n aa3、36x x =÷自主学习 整体感知（1）()25x y x ÷ （2）()()n m n m 22228÷ （3）()()b a c b a 2243÷合作交流 文本探究：通过上面的计算，该如何进行单项式除以单项式的运算？★ 结论：课内检测 巩固提高：1、计算（1）()2232353y x y x ÷⎪⎭⎫⎝⎛- （2）()()bc a c b a 2234510÷（3）()()b a b a +÷+2232、月球距离地球大约3.84×105千米，一架飞机的速度约为8×102千米／时，如果乘坐此飞机飞行这么远的距离，大约需要多少时间？3、计算：（1）()z y x z y x 22243412-÷- （2）c a c b a 346241÷-（3） ()b a b a 32383÷⋅ （4）()()35316b a b a -÷-拓展延伸 迁移升华：（1）()123182++÷n n mm（2）()()⎪⎭⎫⎝⎛-⋅÷2332343228bc a b a c b a作 业： 课本P 48习题1.15：1、2、 教学反思：。
初中数学_1.7整式的除法(1)教学设计学情分析教材分析课后反思
【教学设计】1.7整式的除法（1）一、教材分析本节内容是在学生学习了整式的加减、幂的运算性质、整式的乘法基础上，对整式的除法运算进行探索和研究的一个重要课题。
单项式除以单项式用到了有理数的除法、幂的运算性质，而后续的多项式除以单项式要转化为单项式除以单项式。
因此，单项式除以单项式将起到承前启后的作用，在整式的除法中占有独特地位,是学生完整、全面掌握整式运算的必备环节。
本节教学内容属于新授课，授课时数为一课时。
让学生通过对已学知识的回顾，从实际问题导入，引导学生主动探索，类比整式乘法的学习总结得出单项式除以单项式的运算法则，并能够综合运用所学知识解决问题。
为此，本节课的教学目标是：1．知识与技能：理解单项式除以单项式运算的算理，会进行简单的整式除法运算。
2．过程与方法：经历探索单项式除以单项式运算法则的过程，发展有条理的思考能力及语言表达能力。
3．情感与态度：主动参与到探索过程中，进一步丰富数学学习的成功体验，激发对数学学习的好奇心，形成独立思考、主动探索的习惯和主动与他人合作交流的意识。
教学重点：单项式除以单项式的运算法则及其应用。
教学难点：探索单项式除以单项式运算法则的过程。
二、学情分析学生的知识技能基础：在七年级上册的学习中，学生已经学习了有理数的运算、整式的加减法等内容。
学生通过对本章前几节课的学习，已经学习了整式的乘法，同底数幂的乘，除法，积的乘方，幂的乘方，平方差公式及完全平方公式，并利用其解决了一些问题，这些知识储备为学生本节课的学习奠定了良好的知识技能基础。
学生的活动经验基础：七年级学生的好奇心和求知欲强，敢于质疑，通过类比，学生会产生“整式的除法是否也有相应的运算？如果有的话，该怎样进行”等问题。
在本章前面知识的学习过程中，学生已经经历了一些探索、发现的数学活动，积累了初步的数学活动经验，具备了一定的探究能力。
同时在本章前面的数学学习中学生已经经历了探究幂的乘法除法以及乘法运算的过程，为探究除法运算打下了基础，并且经历了很多合作学习的过程，具有了一定的合作学习的经验，具备了一定的合作与交流的能力。
北师大版数学七年级下册1.7《整式的除法》教案1
北师大版数学七年级下册1.7《整式的除法》教案1一. 教材分析《整式的除法》是北师大版数学七年级下册第1章第7节的内容。
本节课主要介绍整式除法的基本概念和运算方法，包括单项式除以单项式、多项式除以单项式和多项式除以多项式的运算规则。
通过学习本节课，学生能够掌握整式除法的基本运算方法，并能够运用整式除法解决实际问题。
二. 学情分析学生在学习本节课之前，已经掌握了整式的加减法和乘法运算，具备一定的代数基础。
但是，对于整式除法这一概念，学生可能较为陌生，需要通过实例和练习来逐步理解和掌握。
此外，学生可能对于除法运算在代数中的应用有一定的疑惑，需要教师进行引导和解释。
三. 教学目标1.知识与技能：学生能够理解整式除法的基本概念，掌握整式除法的运算方法，能够熟练地进行整式除法的计算。
2.过程与方法：通过实例分析和练习，学生能够运用整式除法解决实际问题，提高解决问题的能力。
3.情感态度与价值观：学生能够积极参与课堂讨论和练习，培养合作意识和解决问题的能力。
四. 教学重难点1.重点：整式除法的基本概念和运算方法。
2.难点：整式除法在实际问题中的应用。
五. 教学方法1.情境教学法：通过实例和实际问题，激发学生的学习兴趣，引导学生主动参与课堂讨论和练习。
2.引导发现法：教师引导学生发现整式除法的运算规则，培养学生的观察和思考能力。
3.练习法：通过大量的练习，巩固学生的知识和技能。
六. 教学准备1.教学PPT：制作相关的教学PPT，展示整式除法的运算规则和实例。
2.练习题：准备一些练习题，用于学生在课堂上进行操练和巩固。
七. 教学过程1.导入（5分钟）教师通过一个实际问题引入整式除法的概念，例如：“已知两个多项式的乘积是2x^3 - 3x^2 + 2x - 1，其中一个多项式是x - 1，求另一个多项式。
”2.呈现（15分钟）教师引导学生观察和分析问题，引导学生发现整式除法的运算规则。
通过PPT展示整式除法的运算步骤和实例。
初中整式教案
初中整式教案初中整式教案初中整式教案篇一整式的除法（1）教学目标①经历探索整式除法运算法则的过程，会进行简单的整式除法运算(只要求单项式除以单项式，并且结果都是整式)，培养学生独立思考、集体协作的能力．②理解整式除法的算理，发展有条理的思考及表达能力．教学重点与难点重点：整式除法的运算法则及其运用．难点：整式除法的运算法则的推导和理解，尤其是单项式除以单项式的运算法则．教学准备卡片及多媒体课件．教学设计情境引入教科书第161页问题：木星的质量约为1.90×1024吨，地球的质量约为5.98×1021吨，你知道木星的质量约为地球质量的多少倍吗?重点研究算式(1.90×1024)÷(5.98×1021)怎样进行计算，目的是给出下面两个单项式相除的模型．注：教科书从实际问题引入单项式的除法运算，学生在探索这个问题的过程中，将自然地体会到学习单项式的除法运算的必要性，了解数学与现实世界的联系，同时再次经历感受较大数据的过程．探究新知(1)计算(1.90×1024)÷(5.98×1021)，说说你计算的根据是什么?(2)你能利用(1)中的方法计算下列各式吗?8a3÷2a；6x3y÷3xy；12a3b2x3÷3ab2．(3)你能根据(2)说说单项式除以单项式的运算法则吗?注：教师可以鼓励学生自己发现系数、同底数幂的底数和指数发生的变化，并运用自己的语言进行描述．单项式的除法法则的推导，应按从具体到一般的步骤进行．探究活动的安排，是使学生通过对具体的特例的计算，归纳出单项式的除法运算性质，并能运用乘除互逆的关系加以说明，也可类比分数的约分进行．在这些活动过程中，学生的化归、符号演算等代数推理能力和有条理的表达能力得到进一步发展．重视算理算法的渗透是新课标所强调的．归纳法则单项式相除，把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式．注：通过总结法则，培养学生的概括能力，养成用数学语言表达自己想法的数学学习习惯．应用新知例2计算：(1)28x4y2÷7x3y；(2)-5a5b3c÷15a4b．首先指明28x4y2与7x3y分别是被除式与除式，在这儿省去了括号．对本例可以采用学生口述，教师板书的形式完成。
七年级数学下册《整式的除法》教案、教学设计
2.汇报交流：每个小组选出代表，向全班汇报他们的讨论成果，分享解题思路和经验。
3.教师点评：教师对每个小组的讨论情况进行点评，指出优点和不足，给予鼓励和建议。
（四）课堂练习，500字
在课堂练习阶段，学生将独立完成一系列整式除法的练习题，巩固所学知识。
1.知识梳理：教师带领学生回顾整式除法的运算规则和步骤，总结解题技巧。
2.学生反思：学生反思自己在学习过程中的收获和不足，分享学习体会。
3.教师总结：教师对整节课的教学内容进行总结，强调重点和难点，并对学生的学习表现给予肯定和鼓励。
五、作业布置
为了巩固学生对整式除法的掌握，培养他们独立解决问题的能力，特布置以下作业：
4.个性化作业：针对学生的个体差异，教师可根据学生在课堂上的表现，布置难易适度的个性化作业。这有助于学生在巩固基础知识的同时，提高自己的思维能力。
5.预习作业：布置下一节课的预习内容，让学生提前了解下节课将要学习的内容，为课堂学习做好充分准备。
作业要求：
1.学生需独立完成作业，确保作业质量。
2.作业完成后，学生之间可以互相交流、讨论，取长补短。
1.完成课后练习题，巩固所学知识。
2.收集生活中运用整式除法的例子，下节课分享。
七、课后反思
教师根据学生的课堂表现和作业完成情况，反思教学效果，调整教学方法，以提高教学效果。
二、学情分析
七年级的学生在数学学习上已经具备了一定的基础，掌握了整式的乘法法则，对于整式的运算有了一定的了解。在此基础上，他们对于整式的除法运算会有一定的认知基础，但可能还不够系统和熟练。学生在思维方式上，已经逐渐从具体形象思维向抽象逻辑思维转变，但仍有部分学生依赖直观感受，缺乏对抽象概念的理解和运用能力。此外，学生在合作交流、解决问题的过程中，可能存在依赖心理，需要教师在教学过程中给予适当的引导和鼓励。因此，在本章节的教学中，应注重以下几点：
初中数学《整式的除法》教案
初中数学《整式的除法》教案 整式的除法〔1〕教学目标①经历探索整式除法运算法那么的过程，会进行简单的整式除法运算(只要求单项式除以单项式，并且结果都是整式)，培养学生独立思考、集体协作的能力．②理解整式除法的算理，发展有条理的思考及表达能力．教学重点与难点重点：整式除法的运算法那么及其运用．难点：整式除法的运算法那么的推导和理解，尤其是单项式除以单项式的运算法那么．教学准备卡片及多媒体课件．教学设计情境引入教科书第161页问题：木星的质量约为1.901024吨，地球的质量约为5.981021吨，你知道木星的质量约为地球质量的多少倍吗?重点研究算式(1.901024)(5.981021)怎样进行计算，目的是给出下面两个单项式相除的模型．注：教科书从实际问题引入单项式的除法运算，学生在探索这个问题的过程中，将自然地体会到学习单项式的除法运算的必要性，了解数学与现实世界的联系，同时再次经历感受较大数据的过程．探究新知(1)计算(1.901024)(5.981021)，说说你计算的根据是什么?(2)你能利用(1)中的方法计算以下各式吗?8a32a； 6x3y3xy； 12a3b2x33ab2．(3)你能根据(2)说说单项式除以单项式的运算法那么吗?注：教师可以鼓励学生自己发现系数、同底数幂的底数和指数发生的变化，并运用自己的语言进行描述．单项式的除法法那么的推导，应按从具体到一般的步骤进行．探究活动的安排，是使学生通过对具体的特例的计算，归纳出单项式的除法运算性质，并能运用乘除互逆的关系加以说明，也可类比分数的约分进行．在这些活动过程中，学生的化归、符号演算等代数推理能力和有条理的表达能力得到进一步发展．重视算理算法的渗透是新课标所强调的．归纳法那么单项式相除，把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，那么连同它的指数作为商的一个因式．注：通过总结法那么，培养学生的概括能力，养成用数学语言表达自己想法的数学学习习惯．应用新知例2 计算：(1)28x4y27x3y；(2)-5a5b3c15a4B、首先指明28x4y2与7x3y分别是被除式与除式，在这儿省去了括号．对本例可以采用学生口述，教师板书的形式完成。
整式的除法教案
课题：15.4.2 整式的除法(1)教学设计教学目标：1、经历探索单项式除以单项式运算法则的过程，会进行单项式除以单项式的除法运算，培养学生独立思考、集体协作的能力；2、理解单项式与单项式相除的算理，发展有条理的思考及表达能力。
教学重点：可以通过单项式与单项式的乘法来理解单项式的除法，要确实弄清单项式除法的含义，会进行单项式除法运算。
教学难点：确实弄清单项式除法的含义，会进行单项式除法运算。
教学方法：探索讨论、归纳总结。
教学工具：投影仪。
教学过程：（一）创设情境，复习导入1.请同学们回答如下问题，看哪位同学回答得又快又准确计算：（1）a9÷a5；（2）y4÷y；（3）105÷105；（4）y3÷y3.以上计算是什么运算？能否叙述这种运算的法则？法则的使用条件与结论各是什么？学生活动：学生回答上述问题。
a m÷a n＝a m－n（（a≠0，m，n为正整数，且m＞n）【教法说明】利用练习复习巩固同底数幂除法法则．着重强调使用同底数幂除法法则的条件是被除式与除式一定要符合是同底幂的形式，且底数不能为0，结论(法则的内容)是“商的底数不变(与被除式与除式的底相同)，商的指数是被除式的指数减去除式的指数的差”．同时为本节的学习基础，注意要指出零指数幂的意义。
2.计算并回答问题：3a2b·2ab2c2以上计算是什么运算？能否叙述这种运算的法则？【教法说明】通过实例引起学生回忆，复习单项式乘法法则．着重说明单项式与单项式的乘法是利用乘法交换律与结合律，转化为同底数幂的乘法来计算的．看来化“新”为“旧”是解决某些数学问题的重要思想方法．3.填空：（）·3ab2＝12a3b2x3 （学生回答结果）（二）指出问题，探究新知这个问题就是让我们去求一个单项式，使它与3ab2相乘，积为12a3b2x3，这个过程能列出一个算式吗？由一个学生回答，教师板书。
9_整式的除法_教案1
整式的除法（一）
教学目标：
1、经历探索整式除法运算法则的过程，会进行简单的整式除法运算（只要求单项式除以单项式，多项式除以单项式，并且结果都是整式）。
2、理解整式除法运算的算理，发展有条理的思考及表达能力。
教学媒体：
无
教学过程：
计算下列各题，并说说你的理由
（1）（x2y）÷x2
（2）（8m2n2）÷（2m2n）
（3）（a4b2c）÷（3a2b）
分组讨论：如何进行单项式除以单项式的运算？
单项式相除，把系数、同底数幂分别相除后，作为商的因式，对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。
例1计算：
（1）（－x2y2）÷（3x2y）
（2）（10a4b3c2）÷（5a3bc）
（3）（2x2y）2·（－7xy2）÷（14x4y3）
（4）（2a＋b）4÷（2a＋b）2
解：略
例2月球距离地球大约3.84×105千米，一架飞机的速度约为8×102千米/时，如果乘坐此飞机飞行这么远的距离大约需要多少时间？
解：略
随堂练习
P40 1
作业
P41 1、2、3、4。
(完整word版)整式的除法(一)教学设计(word文档良心出品)
第一章 整式的运算９．整式的除法（一）山东省济南实验初级中学 郑悦一、课时安排说明:《整式的除法》是第一章《整式的运算》的最后一节。
本节内容共分两课时，第一课时，主要内容是单项式除以单项式；第二课时，主要内容是多项式除以单项式。
二、学生起点分析：学生的知识技能基础：学生在小学已经学习过整数除法，对整数除法的运算掌握较为熟练。
在本章前面几节课中，又学习了同底数幂的除法，单项式乘以单项式的法则，并利用其解决了一些问题，这些知识储备为学生本节课的学习奠定了良好的知识技能基础。
学生活动经验基础：在本章前面知识的学习过程中，学生已经经历了一些探索、发现的数学活动，积累了初步的数学活动经验，具备了一定的探究能力。
同时在本章前面的数学学习中学生已经经历了探究整式加减以及乘法运算的过程，为探究除法运算打下了基础，并且经历了很多合作学习的过程，具有了一定的合作学习的经验，具备了一定的合作与交流的能力。
三、教学任务分析：教科书基于学生对整式运算（加减以及乘法）以及整数除法的认识，提出了本课的具体学习任务：掌握单项式除以单项式的运算法则，并能够综合运用所学知识解决实际问题。
本课内容从属于“数与代数”这一数学学习领域，因而必须服务于代数教学的远期目标：“让学生经历观察、操作、推理、想象等探索过程，能够在实际情境中，抽象概括出所要研究的数学问题，增强学生的数感符号感。
发展学生的合作交流能力、推理能力和有条理的表达能力”，同时也应力图在学习中逐步达成学生的有关情感态度目标。
为此，本节课的教学目标是：1．经历探索整式除法运算法则的过程，会进行简单的整式除法运算；2．理解整式除法运算的算理，发展有条理的思考及表达能力。
四、教学设计分析：本节课设计了九个教学环节：：复习回顾、情境引入、探究新知、对比学习、例题讲解、课堂练习、思维拓广、知识小结、布置作业。
第一环节：复习回顾活动内容：复习准备1．同底数幂的除法 ),,,0(n m n m a a a a n m n m >≠=÷-且都是正整数同底数幂相除，底数不变，指数相减。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
15.3.1整式地除法（一 ）
----同底数幂地除法
一、教学分析
（一）教学目标：1. 熟练掌握同底数幂地除法运算法则 .
2 会用同底数幂地除法性质进行计算.
3知道任何不等于0地数地0次方都等于1.
二、指导自学
（一）基本训练，巩固旧知
1.填空：
(1)同底数幂相乘，不变，相加，即n m a a ⋅=；
(2)幂地乘方，不变，相乘，即()n
m a =； (3)积地乘方，等于把积地每一个因式分别地积，即()n ab =；
2.直接写出结果：
(1)-b ·b 2= (2)a ·a 3·a 5= (3)(x 4)2=
(4)(y 2)3·y =(5)(-2b)3= (6)(-3xy 3)2=
3.填空：（1）（）·28=216（2）（）·53=55
(3)（）·m 3=m 8(4)（）·a ５=a ７
（5）·(-6)3=(-6)5（6）x ５·x 8=x 12；
（二）创设情境，探究法则
前面我们学习了整式地乘法，从今天开始，我们学习整式地除法.
在学习整式乘法之前，我们学习了同底数幂地乘法、幂地乘方、积地乘方这些准备知识，同样，学习整式除法之前也需要先学习准备知识.本节课我们就来学习整式除法地准备知识——同底数幂地除法问题1：一种数码照片地文件大小是28K ，一个存储量为26M （1M=210K ）地移动存储器能存储多少张这样地数码照片？分析问题：移动器地存储量单位与文件大小地单位不一致，所以要先统一单位．移动存储器地容量为K ．
所以它能存储这种数码照片地数量为．（列出式子）
问题２：怎样计算问题1中你所列出地式子？
分析：你能由同底数幂相乘可得：16
88222=⨯，再根据除法地意义计算出216÷28 =？
答：
问题３：根据问题２地方法，计算下列各题.
（1）216÷28=（2）55÷53=
（3）107÷105=（4）a 6÷a 3=
（5）()()3
566-÷-＝（6）812x x ÷＝ 问题４：仔细体会问题3地运算过程，看看计算结果有什么规律？
（提示：仔细观察商与除数、被除数有什么关系？从底数和指数两方面来总结）
根据总结地规律计算，得到公式：
a m ÷a n =
在这个公式中，m ，n 都是，对a 什么要求？
问题５：用文字叙述同底数幂地除法法则：
问题6：问题４得到地公式中指数n m ,之间是否有大小关系？
答：
问题７：在公式中地m ，n 还有什么大小关系呢？
答：
问题8：通过实例先研究m=n 时，会有什么样地结论？请计算32÷32 103÷103 a m ÷a m （a ≠0）
（提示：由除法意义和利用a m ÷a n =a m-n 两种方法来研究当m=n 时会有什么样地结论，另一种情况我们以后再研究.）答：
当m=n 时得到结论是：
三、应用提高
（一）巩固应用
例1：（1）x 8÷x 2（2）a 4÷a （3）（a b ）5÷（a b ）2
（4）（-a ）7÷（-a ）5（5）(-b ) 5÷(-b )2
例２：若1)32(0
=-b a 成立，则b a ,满足什么条件？
例３：下面地计算对不对？如果不对，应当怎样改正？
（1）326x x x =÷ （2）66644=÷ （3）3
3a a a =÷
（4）()()224c c c -=-÷-
四、落实训练
（一）当堂训练
计算：
75(1)x x ÷88(2)m m ÷
()()107(3)a a -÷-()()53
(4)xy xy ÷
()()53(5)ax ax ÷()()5322(6)x x ÷
（二）.应用提高、拓展创新 若4910,4
710==y x ，则y x -210等于？
（三）回顾提升
思考：通过这节课地学习你有哪些收获？
班级组别姓名学号
五、检测反馈
()()2332(1)a
a ÷()()3
(2)xy xy ÷ 53(3)()()c c -÷-32(4)()()m x y x y ++÷+
()()33
(5)xy xy ÷1023(6)()x x x ÷-÷
()()3222(7)ab ab ÷-()()32
(8)m n n m -÷-
２若0
)52(-+y x 无意义，且1023=+y x ，求y x ,地值。