7.5三角形的内角和(1)
北师大版八年级数学上册7.5三角形内角和定理(第1课时)教学设计

1.教师引导学生回顾已学的三角形知识,如三角形的定义、分类等。
2.教师以直观的方式,通过动态课件或实物演示,让学生观察并发现三角形内角和等于180°的现象。
3.教师给出三角形内角和定理的表述,并对定理进行讲解,强调“任意三角形内角和都等于180°”。
4.教师通过具体的例子,如等边三角形、等腰三角形等,说明三角形内角和定理的适用范围。
3.教学评价:
(1)关注学生在课堂上的表现,评价他们的参与度、合作能力和解决问题的能力;
(2)通过课后作业和小测验,了解学生对三角形内角和定理的掌握情况;
(3)开展小组评价,让学生相互评价,提高他们的自我认知和团队协作能力。
4.教学反思:
教师在教学过程中要关注学生的反馈,及时调整教学策略,以提高教学效果。同时,教师要注重自身教学能力的提升,不断学习新的教学理念和方法,为学生提供更优质的教育。
1.培养学生的探究精神,鼓励学生主动发现问题、解决问题;
2.增强学生对数学美的感受,体会数学在生活中的应用价值;
3.培养学生严谨的学习态度,养成良好的学习习惯;
4.激发学生的爱国情怀,通过学习我国数学家的贡献,增强民族自豪感。
在教学过程中,教师要关注学生的个体差异,因材施教,使每个学生都能在原有基础上得到提高,实现全面发展。同时,注重启发式教学,引导学生主动思考、探索,使学生在轻松愉快的氛围中学习数学。
四、教学内容与过程
(一)导入新课
1.教师出示一块三角形的纸板,引导学生观察三角形,并提出问题:“同学们,你们知道三角形的内角和是多少度吗?如何证明三角形的内角和是180°呢?”
2.学生自由发表观点,教师收集不同的解题思路,为后续教学做好铺垫。
3.教师通过多媒体展示生活中含有三角形的实物图片,如房屋屋顶、三角形标志等,让学生感受三角形在生活中的广泛应用,从而引出本节课的学习内容:三角形内角和定理。
八年级数学上册 7.5.1 三角形内角和定理教案 (新版)北师大版-(新版)北师大版初中八年级上册数

课题:三角形内角和定理教学目标:1.掌握“三角形内角和定理”,理解三角形内角和定理的证明方法及证明过程.2.灵活运用三角形内角和定理解决相关问题.3.通过猜想、推理等数学活动,探究三角形内角和定理的证明思路和过程,初步体会辅助线在证明中的作用.教学重点与难点:重点:三角形内角和定理及其证明.难点:三角形内角和定理的证明及灵活应用解决相关问题.课前准备:多媒体课件、三角形纸板等 .一、创设情境,复习引入问题1:平行线的性质?问题2:证明一个命题有哪些步骤?问题3: 关于三角形的知识,你都知道哪些呢?问题4:如图,按规定,一块模板中AB、CD的延长线应相交成85°角.因交点不在板上,不便测量,工人师傅连接AC,测得∠BAC=32°,∠DCA=65°,此时AB、C D的延长线相交所成的角是不是符合规定?为什么?处理方式:教师出示题目,学生回答问题,问题的设置不仅起到复习的目的,也为新课的引入做了铺垫.预设学生回答.1.两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角相等.2.证明一个命题的一般步骤:(1)分清命题的条件和结论,根据题意,画出图形.(2)根据条件、结论,结合图形,写出已知、求证.(3)经过分析,找出由已知推出求证的途径,写出证明过程.3.三角形两边之和大于第三边;三角形具有稳定性;三角形按角分为直角三角形,锐角三角形和钝角三角形;三角形按边分为不等边三角形、等边三角形和等腰三角形;三角形三个内角和为180°......4.不符合规定.延长AB、CD交于点O,∵△AOC中,∠BAC=32°,∠DCA=65°,∴∠AOC=180°-∠BAC-∠DCA=180°-32°-65°=83°<80°,∴模板不符合规定.师导语:三角形的内角和从小学就开始学习,七年级又有了新的认识,这一节课我们将进一步通过动手操作、观察、合作、交流探究等方法来验证这一定理,并通过这一定理来解决有关问题.设计意图:设置问题情景,与学生前面所学知识紧密相连,在教学过程设计上从学生熟悉的知识创设情境,让学生简单地对三角形内角和的知识加以回忆,激发学生探究三角形内角和的兴趣.二、情境再现,探究新知(一)探索三角形内角和等于180°我们知道,三角形内角和等于180°.1.你还记得这个结论的探索过程吗?2.如图,如果我们只把∠A移到∠1的位置,你能说明这个结论吗?如果不移动∠A,那么你还有什么方法可以达到同样的效果?处理方式:对于第一个问题教师引导学生可以用量角器测量,用准备好的三角形纸片或三角形纸板进行折叠或剪拼,完成后小组讨论并展示结果.对于第二个问题,教师结合学生的完成情况,让学生代表说出结论和思路,针对学生的回答教师给予肯定和补充.预设学生回答:1.(1)用测量的方法:由于误差原因,有时可能不是180°.(2)用折纸的方法:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行,然后把另外两角相向对折,使其顶点与已折角的顶点相嵌合,最后得图示的结果.(3)用剪拼(撕纸)的方法:剪三个角,拼成一个平角;剪两个角,也是拼成一个平角;剪一个角,构造平行线,利用平行线判定和性质说明.2.构造平行线,可得同样效果.设计意图:在回忆中学习,在学习中探索,在探索中验证,通过学生亲身经历的探索活动,让学生进一步理解验证三角形内角和等于180°,不仅调动小组愉快的合作学习,也激发学生的学习兴趣.(二)证明三角形内角和等于180°根据前面给出的基本事实和定理,你能用自己的语言说说“三角形内角和等于180°”这一结论的证明思路吗?处理方式:结合探索三角形内角和,引导学生小组完成问题,学生发言后教师总结并板书证明过程及三角形内角和定理.已知:如图,△ABC.求证:∠A+∠B+∠C=180°。
7.5 三角形内角和定理 知识考点梳理(课件)北师大版数学八年级上册

巧 点
又 ∵∠C=90°,
拨 ∴∠D=180°-90°-55°=35°.
[答案] A
返回目录
混
分 析
领悟提能 三角形的外角是由三角形的一边与另一边的
反向延长线组成的,由外角的性质可以把不在同一个三角
形中的几个内角联系起来.
7.5 三角形内角和定理
返回目录
方 ■方法:转化法求角度
法 技
用已知角的度数求未知角的度数时,若几个角的位置分
巧 点
布比较分散,那么我们利用平行线的性质、对顶角的性质
拨 等将所求角与已知角“转移”到一个图形中求解.
7.5 三角形内角和定理
● 考点清单解读 ● 重难题型突破 ● 易错易混分析 ● 方法技巧点拨
7.5 三角形内角和定理
返回目录
考 ■考点一 三角形内角和定理
点
清 三角形内角和
单 解
定理
三角形的内角和等于 180°
读 如图,在△ABC 中,∠A+∠B+∠C=180°
数学语言描述
7.5 三角形内角和定理
7.5 三角形内角和定理
返回目录
方 例 如图,已知∠A=35°,∠B=∠C=90°,则∠D 的度
法
技 数是 (
)
巧 点
A. 35° B. 45°
C. 55°
D. 65°
拨
7.5 三角形内角和定理
方 [解析] ∵∠A=35 ° ,∠B=90°,
法 技 ∴∠COD=∠AOB=180°-90°-35°=55°.
________(选填“增加”或“减少”)_______°.
7.5 三角形内角和定理
返回目录
重 [解析]如解析图,延长 EF,交 CD 于点 G.
数学 7.5 三角形内角和定理-课件

C.180° D.140°
9.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2等于( B )
A.90° B.100°
C.130° D.180°
第七章
7.5 三角形内角和定理
知识要点基础练
综合能力提升练
拓展探究突破练
-6-
10.如图是由线段AB,CD,DF,BF,CA组成的平面图形.若∠D=28°,则∠A+∠B+∠C+∠F的度数
C,∠1=30°,∠B=60°,∠C=20°,则∠2= 50° ,∠A= 70° .
-3-
第七章
7.5 三角形内角和定理
知识要点基础练
综合能力提升练
拓展探究突破练
6.( 改编 )如图,∠1,∠2,∠3之间的大小关系为 ∠2<∠3<∠1 ( 用“<”连接 ).
-4-
第七章
7.5 三角形内角和定理
知识要点基础练
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°.
( 2 )FE=FD.
在 AC 上截取 AG=AE,连接 FG.
∵AD 是∠BAC 的平分线,∴∠BAD=∠DAC,
又∵AF=AF,∴△AEF≌△AGF( SAS ),
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°.
于点F.
( 1 )求∠EFD的度数;
( 2 )判断FE与FD之间的数量关系,并证明你的结论.
第七章
7.5 三角形内角和定理
知识要点基础练
综合能力提升练
解:( 1 )∵△ABC 中,∠ACB=90°,∠B=60°,
三角形的内角和 (1)

《三角形的内角和》教学案例一、教材分析:“三角形的内角和”是三角形的一个重要性质,是在学生学习了三角形的相关概念,边、角之间关系的基础上,引导学生通过探索实践、讨论发现、合作交流的基础上,得出无论是什么样的三角形的内角和都是180度。
为今后掌握多边型的内角和及相关知识打下坚实的基础。
所以掌握三角形的内角和是180度这个规律具有重要的意义。
教材创设了一个有趣的问题情境,以此激发学生的兴趣,引出探索活动。
首先,教师应使学生明确“内角”的意义,然后引导学生探索三角形内角和等于多少。
绝大局部学生会想到用测量角的方法,此时就能够安排小组活动。
每组同学能够画出大小、形状不同的若干个三角形,分别量出三个内角的度数,并求出它们的和,填写在教材提供的表中。
最后发现,大小、形状不同的三角形,每一个三角形内角和都在180°左右。
三角形的内角和是否正好等于180°呢?教材中安排了两个活动:一是把三角形三个内角撕下来,再拼在一起,组成一个平角,所以三角形内角和是180度。
二是把三个内角折叠在一起,发现也能组成一个平角。
每个活动都要使学生动手试一试,加深对三角形内角和的理解,体验三角形内角和性质的探索过程。
另外,教材还从两个方面引导学生应用三角形的内角和:一是根据三角形中已知的两个角的度数,求另一个角的度数;二是直角三角形里的两个锐角和等于90度,钝角三角形里的两个锐角和小于90度。
二、学生状况分析:学生在本课学习前已经理解了三角形的基本特征及分类,并且在四年级(上册)教材里已经知道了两块三角尺上的每一个角的度数,学生课上对数学知识、水平和思考问题的角度有一定的差异,所以比较容易出现解决问题的策略多样化。
三、学习目标:1.通过测量、撕拼、折叠等方法,探索和发现三角形三个内角的和等于180°。
2.知道三角形两个角的度数,能求出第三个角的度数。
3.发展学生动手操作、观察比较和抽象概括的水平。
体验数学活动的探索乐趣,体会研究数学问题的思想方法。
7.5三角形内角和定理的证明

D
E C
(第3题)
∴ ∠ AED= ∠ C = 700 (两直线平行,同位角相等)
∵ ∠ A+ ∠ AED+ ∠ ADE=1800(三角形的内角和定理) ∠ A=600(已知) ∴ ∠ ADE=1800—600—700=500(等量代换) 即∠ ADE= 500
证明: 因为 ∠A+∠B+∠ACB=180°(三角形内角和定理)
所以 ∠A+∠B=180°-∠ACB(等式性质) 又因为 ∠ACF+∠ACB=180°(三角形外角定义) 所以 ∠ACF=180°-∠ACB(等式性质)
所以 ∠ACF=∠A+∠B(等量代换)
• 在任意一个三角形中,无论这个三角形的形状如 何,三角形的内角和总等于180度。
1、△ABC中,∠C=90°,∠A=30°,∠B=? 2、 △ABC中∠A=50°,∠B=∠C,则∠B=?
练一练
3、三角形的三个内角中,只能有__个直角或__个钝角 4、任意一个三角形,至少有__个锐角,至多有__个锐角 5、任意一个三角形,最大的角一定不小于 度; 6、三角形中三角之比为1∶2∶3,则三个角各为多少度?
证明: 因为 ∠A+∠B+∠ACB=180°(三角形内角和定理)
所以 ∠A+∠B=180°-∠ACB(等式性质) 又因为 ∠ACF+∠ACB=180°(三角形外角定义) 所以 ∠ACF=180°-∠ACB(等式性质)
所以 ∠ACF=∠A+∠B(等量代换)
实际问题
如图,一艘轮船按箭头所示方向行驶, C处有一灯塔,轮船行驶到哪一点时距离 灯塔最近?当轮船从A点行驶到B点时, ∠ACB的度数是多少?当轮船行驶到距离 灯塔最近点时呢? C
7.5三角形的内角和(1)
第七章平面图形的认识(二)(教案)
课时分配
本课(章节)需3课时
本节课为第1课时
为本学期总第课时
7.5三角形的内角和(1)
教学目标
1.会利用三角形的内角和解决问题(较高要求)
2.知道三角形的两个锐角的关系
3.掌握三角形的外角的概念及三角形的外角与不相邻两个内角的关系(以上两条为较低要求)
重点
三角形的内角和
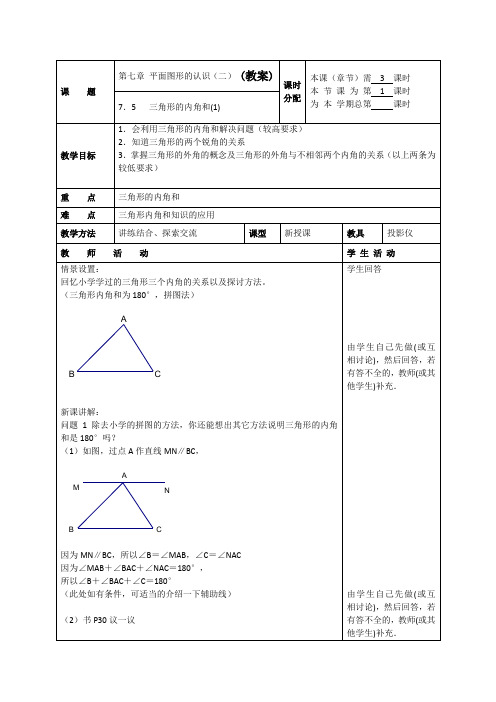
因为MN∥BC,所以∠B=∠MAB,∠C=∠NAC
因为∠MAB+∠BAC+∠NAC=180°,
所以∠B+∠BAC+∠C=180°
(此处如有条件,可适当的介绍一下辅助线)
(2)书P30议一议
由图(1)a∥b,可得∠1+∠2=180°,若将木条a绕点A
转动,使它与b相交于点C,得图(2),因为a’和b平行,
分析:第(1)题较简单,由三角形内角和为180º,可列式∠B=180-∠A-∠B=18本版0-37-89=54º;
第(2)题可采用方程的思想,设∠C=xº,则∠A=3 xº,由三角形内角和为180º,可列方程x+3x+30=180,解得x=37.5,则3 x=112.5
练习:填空
在ABC中,
(1)∠C = 90º,∠B = 30º,则∠A =_______;
由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充.
学生板演
由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充.
作业
P371.2.3.4.
板书设计
8.5三角形的内角和
问题一问题三
问题二问题四
(2)∠A = 100º,∠B =∠C ,则∠B =_______;
(3)∠B = 30º,∠C = 2∠A ,则∠C =_______;
八年级数学上册教学课件《三角形的内角和定理(第1课时)》

②在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是 ____直__角___三角形 ;
③在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则∠A= 60°, ∠ B= 50°,∠ C= 70°.
探究新知
7.5 三角形的内角和定理
素养考点 3 利用三角形的内角和定理解决实际问题
∵∠B=38°(已知),∠BAD=40°(已证),
∴∠ADB=180°-38°-40°=102°(等式的性质).
巩固练习
7.5 三角形的内角和定理
如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是
△ABC的角平分线,求∠ADB的度数.
解:由∠BAC=40 °, AD是△ABC的角平分线,得
数学 八年级 上册
7.5 三角形的内角和定理
7.5 三角形的内角和定理 (第1课时)
导入新知
7.5 三角形的内角和定理
情
一天,三类三角形通过对自身的特点,讲出了
境 自己对三角形内角和的理解,请同学们作为小判官
引 给它们评判一下吧. 入
不对,我有一
个钝角,所以
我的形状最 大,那我的 内角和最大.
我的内角和才
是最大的.
我的形状最 小,那我的 内角和最小.
素养目标
7.5 三角形的内角和定理
2. 会运用三角形内角和定理进行计算.
1.会用平行线的性质与平角的定义证明三角 形内角和等于180°.
探究新知
7.5 三角形的内角和定理
知识点 1 三角形的内角和定理 我们在小学已经知道,任意一个三角形的内角和等于180°. 与三角形的形状、大小无关,所以它们的说法都是错误的.
三角形的内角和(1)

A
在△AOB中,
∠A+∠B+∠AOB=180°,即 ∠A+∠B=180°-∠AOB.
B
O
在△COD中,
∠C+∠D+∠COD=180° ,即
C D
∠C+∠D=180°-∠COD. 因为∠AOB与∠COD是对顶角, 所以∠AOB= ∠COD,
所以∠A+∠B= ∠C+∠D
A
B
D
Байду номын сангаас
三角形的一边与另一边的延长线 所组成的角,叫做三角形的外角 .
“外角”是三角形的外角,不是它相邻内 角的外角.对三角形的外角,称某个角是某 个三角形的外角,而不称三角形某个角的 外角.
结论: 三角形的一个外角等于与它不相邻 的两个内角的和.
C
看一看
如图,画△ABC的边AB的
延长线,得到∠1.
A B D
(1)度量∠A、∠C和∠CBD的度数. 你有什么发现? (2) 你能用所学的知识加以说明吗?
180° 因为∠A+∠C+∠CBA=________, 180° ∠CBD+ ∠CBA=_________, = 所以∠A+∠C_____ ∠CBD.
你知道吗?
三角形的外角
C
图中的∠CBD称为△ABC 的一个外角.
方法一:度量法. 方法二:剪拼法.
与
与
你还有其他方法说明‘‘三角形3 个内角的和等于1800”吗?
如图,3根木条相交得∠1、∠2.若a∥b,则 ∠1+∠2= 180° .理由:两直线平行,同旁内角互补 .
A 3 2 2 B 1
2011-无锡-初一(下)数学实验手册参考标准答案

回顾与反思本题运用了同底数幂的乘法公式,即将22005作为一整体,把22006转化为2×22005,然后利用合并同类项的法则进行计算.
【训练与提高】
1.(1)×(2)×(3)×(4)×(5)×(6)×
(2)原式=107+1=108;
(3)原式=-x3·x5=-x3+5=-x8;
(4)、(5)、(6)略.
回顾与反思(1)同底数幂是指底数相同的幂,底数可以是具体的数,也可以是单项式或多项式,如(y-x)2与(y-x)2的底数相同且是多项式;
(2)当3个或3个以上同底数幂相乘时,法则仍然适用,即am·an·ap=am+n+p(m、n、p都是正整数),如-b3·(-b)2·bn=-b3+2+n=-b5+n;
2.0
8.2幂的乘方与积的乘方(1)
【实践与探索】
例1解(1)(107)2=107×2=1014;(2)(z4)4=z4×4=z16;
(3)-(y4)3=-y4×3=-y12;(4)(am)4=a4×m=a4m.
回顾与反思 不要把幂的乘方法则与同底数幂的乘法法则混淆.幂的“乘方运算”的底是“一个幂”,同底数幂的乘法是指“两个幂”之间的乘法运算.
7.同位角相等,两直线平行
拓展与延伸
1.略2.正确,小强构造了90度的同位角
7.1探索直线平行的条件(2)
例1:内错角,同旁内角,同位角; 例2:平行
训练与提高
1.C2.A3.同位角,内错角,邻补角,对顶角,同旁内角
4.AB,ED,EF,EF,BC,AB,AB,ED,BC5.∠1=∠C或∠2=∠DEB 6.平行7.平行;82
7.5三角形的内角和(1)

例题
B O
A
又 由 “ 对 顶 角 相 等 ” 知 D
C
D
做一做
1、n=____
81 72 n
x
x=_______ y=_______
y
122 x
31
2、在直角三角形中, ∠C是直角,则∠A 与∠B的和是多少?
结论 总结:
直角三角形的两个锐角互余。
A
D
C
E
延伸练习:
给你一个五角星,求 ∠A+∠B+∠C+∠D+∠E
A B C D
E
综合提高
如图,AB//CD,∠ABD与∠BDC的平分线 相交于点E,求∠BED的度数.
解:因为AB//CD,
A E
所以∠ABD+∠BDC=180°, B
1 所以∠EBD=2 1 ∠BDE= 2
因为BE平分∠ABD,DE平分∠BDC,
试一试
把△ABC的边AB延长,得到∠CBD,度 量∠A、∠C和∠CBD的度数,你能得到 什么关系?
C
1
A
B
D
外角
1、三角形的一边与另一边的延长线 的夹角,叫做外角 。 2、想一想,三角形的外角共有几个? 共有六个。 注意:每个顶点处有两个外角,它们 是对顶角。研究与三角形外角有关的 问题时,通常每个顶点处取一个外角.
∠ABD ,
∠BDC,
C
D
所以∠EBD+ ∠BDE=90°,
在△BED中, ∠EBD+ ∠BDE+∠E=180°, 所以∠BED= 180°- 90°=90°.
课堂小结
(1)重点探究了三角形3个内角之间的 关系以及三角形外角的性质. 三角形3个内角的和等于180°. 三角形的一个外角等于与它不相邻的两 个内角的和.
7.5.1三角形内角和定理(教案)

(五)总结回顾(用时5分钟)
今天的学习,我们了解了三角形内角和定理的基本概念、重要性和应用。通过实践活动和小组讨论,我们加深了对三角形内角和定理的理解。我希望大家能够掌握这些知识点,并在解决实际问题时灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
举例:通过实际操作,让学生观察不同类型的三角形,引导他们发现并理解内角和恒等于180°。
(2)三角形内角和定理的证明:掌握几何证明方法,理解证明过程中的逻辑关系。
举例:运用几何画板或实际操作,引导学生通过拼接、旋转等手段,感受并理解证明过程。
(3)应用三角形内角和定理解决实际问题:学会将定理应用于求解与三角形内角相关的问题。
5.培养学生的数学建模能力:通过设计相关练习题,让学生运用三角形内角和定理解决实际问题,培养数学建模能力。
本节课旨在让学生在掌握知识的同时,提高数学核心素养,为学生的终身发展奠定基础。
三、教学难点与重点
1.教学重点
(1)三角形内角和定理的引入与理解:强调三角形内角和等于180°的概念,使学生能够准确把握定理内容。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“三角形内角和定理在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.例题讲解:结合三角形内角和定理,讲解如何求解与三角形内角相关的问题。
7.5三角形内角和(教案)

在今天的教学过程中,我发现学生们对三角形内角和的概念接受程度较高,但在实际应用和证明过程的理解上还存在一些困难。这让我意识到,在今后的教学中,我需要更加注重以下几个方面:
首先,对于基本概念的讲解,我应尽量使用生动的例子和直观的教具,让学生能够更好地理解和接受。在今天的教学中,我通过剪裁和拼接三角形纸片的实验操作,让学生们直观地看到了三角形内角和为180°,这种教学方式取得了较好的效果。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过剪裁和拼接三角形纸片,学生可以直观地看到三角形内角和为180°。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“三角形内角和在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解三角形内角和的基本概念。三角形内角和是指一个三角形三个内角的度数总和,它是一个固定的数值——180°。这个概念在几何学中非常重要,因为它帮助我们理解和解决许多与三角形有关的实际问题。
2.案例分析:接下来,我们来看一个具体的案例。通过测量一个已知三角形的两个内角,我们可以利用三角形内角和定理轻松求出第三个内角。
(3)掌握三角形内角和定理的证明过程,培养逻辑推理能力。
举例:讲解三角形内角和定理时,教师应着重强调三角形的三个内角相加等于180°,并通过实际操作让学生直观感受这一性质。在解决实际问题时,如已知三角形的两个内角,引导学生运用内角和定理求出第三个内角,巩固重点知识。
2.教学难点
(1)理解三角形内角和定理的证明过程,尤其是通过平行线的性质和同位角、内错角等概念进行推理;
完整版三角形的内角和与外角和关系基础知识讲解

三角形的内角和与外角和关系(基础)知识讲解【学习目标】1理解三角形内角和定理的证明方法;2•掌握三角形内角和定理及三角形的外角性质;3•能够运用三角形内角和定理及三角形的外角性质进行相关的计算,证明问题【要点梳理】要点一、三角形的内角和1. 三角形内角和定理:三角形的内角和为180° •2. 结论:直角三角形的两个锐角互余.要点诠释:应用三角形内角和定理可以解决以下三类问题:①在三角形中已知任意两个角的度数可以求出第三个角的度数;②已知三角形三个内角的关系,可以求出其内角的度数;③求一个三角形中各角之间的关系.要点二、三角形的外角1 •定义:三角形的一边与另一边的延长线组成的角叫做三角形的外角•如图,/ ACD是△ ABC的一个外角.L L)要点诠释:(1)外角的特征:①顶点在三角形的一个顶点上;②一条边是三角形的一边;③另一条边是三角形某条边的延长线.(2 )三角形每个顶点处有两个外角,它们是对顶角.所以三角形共有六个外角,通常每个顶点处取一个外角,因此,我们常说三角形有三个外角.2. 性质:(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任意一个与它不相邻的内角.要点诠释:三角形内角和定理和三角形外角的性质是求角度及与角有关的推理、证明经常使用的理论依据•另外,在证明角的不等关系时也常想到外角的性质.3. 三角形的外角和:三角形的外角和等于360° .要点诠释:因为三角形的每个外角与它相邻的内角是邻补角,由三角形的内角和是180° ,可推出三角形的三个外角和是360°.【典型例题】类型一、三角形的内角和1 .证明:三角形的内角和为180° .【答案与解析】解:已知:如图,已知△ ABC求证:/ A+Z B+Z C= 180° .••• AB // CD (已作),••• /仁/A (两直线平行,内错角相等)/ B=/ 2 (两直线平行,同位角相等) 又•••/ ACB+/ 1 + / 2=180°(平角定义), •••/ ACB+/ A+/ B=180。
7.5三角形的内角和1

7.5三角形的内角和(1)目的要求:探索并感知“三角形内角和是180°”、直角三角形两个内角的性质及三角形的外角的性质 教学过程:1、做一做:每人准备一个三角形,撕下三角形的三个角,拼在一起,你有什么发现? 问题:还有其它的方法说明“三角形的内角和是180°”吗?3、做一做;(1)根据图形填空n ︒81︒72︒122︒x ︒x ︒y ︒31︒n = , x = , y = (2)在直角三角形ABC 中,90C ∠=︒,A ∠与B ∠的和为多少度? 由此,我们得到: 。
4、试一试:如图把ABC ∆的边AB 延长,得到CBD ∠,度量,A C ∠∠和CBD ∠的度数1A C ∠+∠+∠= 1CBD ∠+∠=则A C ∠+∠与CBD ∠的关系是定义:三角形的外角:三角形外角的性质: 。
练习:课本P32 1、2、35、例1 如图,AC 、BD 相交于点O , A ∠与B ∠的和等于C ∠与D ∠的和吗?为什么?1DCBAODCBAEDCBAE D CBA例2 如图,AB ∥CD ,ABD ∠与BDC ∠的平分线相交于点E 。
求BED ∠的度数三、练习1、在ABC ∆中,70,50A B ∠=︒∠=︒,求C ∠的度数2、根据下列条件,求ABC ∆中A ∠的度数(1)20,;C A B ∠=︒∠=∠(2),A B C ∠∠∠的度数之比为1:2:3。
3、如图,在ABC ∆中,70ACB ∠=︒,12∠=∠,求BPC ∠的度数。
4、如图,在ABC ∆中,AD 是高,AE 是角平分线,20B ∠=︒,60C ∠=︒,求,CAD AEC ∠∠的度数。
5、如图,在ABC ∆中,BE 、CD 相交与点E ,1∠和2∠分别是哪一个三角形的外角?如果276,2143A ACD ∠=∠=︒∠=︒,试求1∠和DBE ∠的度数。
21PC BA21E DCBA。
三角形的内角和与外角和

练一练:
• 4.如下图(1)∠A=310,∠D=410, 0,则∠B= 460 ∠CFD=62 . • 5.如图(2)P是△ABC内的一点,延长BP 交AC于点D,用“<”表示∠1、∠2、 ∠A ∠1<∠2<∠A A 的大小关系: B
E F
P 1 2 D
A (1)
C
D
B (2)
C
练一练:
• 6.如图,求∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1=∠A+∠C ∠2=∠B+∠E 又∵∠1+∠2+∠D=1800 ∴∠A+∠B+∠C+∠D+∠E=1800 C B A E 21 D
综合提高
如图,AB//CD,∠ABD与∠BDC的平分线 相交于点E,求∠BED的度数.
解:因为AB//CD,
Aபைடு நூலகம்
E B
所以∠ABD+∠BDC=180°,
1 所以∠EBD=2 1 ∠BDE= 2
【解析】∠A+∠B=∠C+∠D 在△AOB中,∠A+∠B+∠AOB=1800, ∠A+∠B= 1800 -∠AOB △COD中,∠C+∠D+∠COD= 1800 , ∠C+∠D= 1800 -∠COD
B O
A
又 由 “ 对 顶 角 相 等 ” 知 ∠AOB=∠COD 所以∠A+∠B=∠C+∠D
C
D
做一做
从折角和拼角的过程你能想出证明的办法吗?
三角形的内角和等于1800.
证法2:延长BC到D,过C作
CE∥BA, ∴ ∠A=∠1 (两直线平行,内错角相等) A ∠B=∠2 (两直线平行,同位角相等) 又∵∠1+∠2+∠ACB=180° ∴∠A+∠B+∠ACB=180°
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第(2)题可采用方程的思想,设∠C=xº,则∠A=3 xº,由三角形内角和为180º,可列方程x+3x+30=180,解得x=37.5,则3 x=112.5
练习:填空
在△ABC中,
(1)∠C = 90º,∠B = 30º,则∠A =_______;
4.在△ABC中,∠A=70°,∠B=58°,CD是
△ABC的角平分线,则∠BDC的度数为度。
B组题:
1.在△ABC中,三个内角的度数比为2∶3∶4;则相应的外角度数的比是。
2.已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高(如图),求∠DBC的度数。
学生回答
由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充.
(2)∠A = 100º,∠B =∠C ,则∠B =_______;
(3)∠B = 30º,∠C = 2∠A ,则∠C =_______;
(4)∠A :∠B :∠C = 2 : 3 : 4,则∠A =_______;
∠B =_______;∠C =_______。
问题2上面练一练(1)中的△ABC的∠C = 90º,这是一个直角三角形,那么∠A与∠B有什么关系?其他的直角三角形也是如此吗?
因为MN∥BC,所以∠B=∠MAB,∠C=∠NAC
因为∠MAB+∠BAC+∠NAC=180°,
所以∠B+∠BAC+∠C=180°
(此处如有条件,可适当的介绍一下辅助线)
(2)书P30议一议
由图(1)a∥b,可得∠1+∠2=180°,若将木条a绕点A
转动,使它与b相交于点C,得图(2),因为a’和b平行,
结论:直角三角形的两个锐角互余。
问题3书P32试一试按照书上编排讲解
外角:一条边是公共边,另外一条边是延长线。
结论:三角形的一个外角等于和它不相邻的两个内角的和。
练习:书P32练一练1. 2.
问题4书P31例题
练习:
书P32练一练3
小结:
1.三角形内角和
2.直角三角形的两个锐角互余
3.三角形的外角
4.综合应用
由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充.
学生板演
由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充.
作业
P37 1.2.3.4.
板书设计
8.5三角形的内角和
问题一问题三
问题二问题四
难点
三角形内角和知识的应用
教学方法
讲练结合、探索交流
课型
新授课
教具
投影仪
教师活动
学生活动
情景设置:
回忆小学学过的三角形三个内角的关系以及探讨方法。
(三角形内角和为180°,拼图法)
新课讲解:
问题1除去小学的拼图的方法,你还能想出其它方法说明三角形的内角和是180°吗?
(1)如图,过点A作直线MN∥BC,
教学素材:
A组题:
1.△ABC中,若∠A=30°,∠B= ∠C,则∠B=____________∠C=____________。
2.△ABC中,∠B=42°,∠C=52°,AD平分∠BAC,则∠DAC=__________,CD⊥AB,∠B=56°,则∠DCA=______________。
则∠1+(∠2+∠3)=180°,∠ACB=∠3,所以
∠1+(∠2+∠ACB)=180°,即△ABC的内角和为
180°。
例题1:
填空
在△ABC中,
(1)∠A = 37º,∠C= 89º,则∠B=_______;
(2)∠B = 30º,∠A = 3∠C,则∠C =_______,∠A =_______。
课题
第七章平面图形的认识(二)教案
课时分配
本课(章节)需3课时
本节课为第1课时
为本学期总第课时
7.5三角形的内角和(1)
教学目标
1.会利用三角形的内角和解决问题(较高要求)
2.知道三角形的两个锐角的关系
3.掌握三角形的外角的概念及三角形的外角与不相邻两个内角的关系(以上两条为较低要求)
重点
三角形的内角和
