高考数学一轮复习 第五章 数列 5.4 数列求和课件.pptx
合集下载
高三数学一轮总复习 第五章 数列 5.4 数列求和课件.ppt

12
n
4.一个数列{an},当 n 是奇数时,an=5n+1;当 n 为偶数时,an=22 ,则这 个数列的前 2m 项的和是__________。
解析:当 n 为奇数时,{an}是以 6 为首项,以 10 为公差的等差数列;当 n 为偶 数时,{an}是以 2 为首项,以 2 为公比的等比数列。所以,S2m=S 奇+S 偶=ma1+mm2-1 ×10+a211--22m
7
2 种思路——解决非等差、等比数列求和问题的两种思路 (1)转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往 通过通项分解或错位相减来完成。 (2)不能转化为等差或等比数列的,往往通过裂项相消法、倒序相加法等来求和。
8
3 个注意点——应用“裂项相消法”和“错位相减法”应注意的问题 (1)裂项相消法,分裂通项是否恰好等于相应的两项之差。 (2)在正负项抵消后,是否只剩下第一项和最后一项,或有时前面剩下两项,后 面也剩下两项,未消去的项有前后对称的特点。 (3)在应用错位相减法求和时,若等比数列的公比含有参数,应分 q=1 和 q≠1 两种情况求解。
=6m+5m(m-1)+2(2m-1) =6m+5m2-5m+2m+1-2 =2m+1+5m2+m-2。 答案:2m+1+5m2+m-2
13
5.已知数列{an}的前 n 项和为 Sn 且 an=n·2n,则 Sn=__________。
解析:∵an=n·2n, ∴Sn=1·21+2·22+3·23+…+n·2n。① ∴2Sn=1·22+2·23+…+(n-1)·2n+n·2n+1。② ①-②,得-Sn=2+22+23+…+2n-n·2n+1 =211--22n-n·2n+1=2n+1-2-n·2n+1 =(1-n)2n+1-2。 ∴Sn=(n-1)2n+1+2。 答案:(n-1)2n+1+2
2025年高考数学一轮复习-5.4-数列求和【课件】

√
2.数列 的前 项和为( )
A. B. C. D.
解析:选C.由题意得 ,所以 .
√
3.(人A选择性必修第二册 练习 变条件)一个球从 高处自由落下,每次着地后又弹回到原高度的一半再落下,当它第10次着地时,经过的路程是( )
A. B. C. D.
【练一练】
1.判断正误(正确的打“√”,错误的打“×”)
(1)若数列 为等比数列,且公比不等于1,则其前 项和 .( )
√
(2)当 时, .( )
√
(3)求 时只要把等号两边同时乘以 即可根据错位相减法求得.( )
×
(4)若数列 , , , 是首项为1,公比为3的等比数列,则数列 的通项公式是 .( )
(1)求数列 的通项公式;
【解】设等差数列 的公差为 .由题意得 解得 所以 .所以数列 的通项公式是 .
(2)设 ,数列 的前 项和为 ,若 ,求 的值.
已知数列 为公差大于0的等差数列, ,且 , , 成等比数列.
【解】 由(1)知, ,所以 .因为 ,所以 ,解得 .所以 的值为20.
必备知识 自主排查
核心考点 师生共研
必备知识 自主排查
01
数列求和的常用方法
(1)公式法①等差数列 的前 项和 .②等比数列 的前 项和
(2)分组转化法:一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成的,则求和时可用分组求和法,分别求和后再相加减.
(3)裂项相消法:把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得前 项和.
【对点训练】
(2023·山西太原第一学期统考)已知在数列 中, , .
(1)证明:数列 为等比数列,并求 的通项公式;
2.数列 的前 项和为( )
A. B. C. D.
解析:选C.由题意得 ,所以 .
√
3.(人A选择性必修第二册 练习 变条件)一个球从 高处自由落下,每次着地后又弹回到原高度的一半再落下,当它第10次着地时,经过的路程是( )
A. B. C. D.
【练一练】
1.判断正误(正确的打“√”,错误的打“×”)
(1)若数列 为等比数列,且公比不等于1,则其前 项和 .( )
√
(2)当 时, .( )
√
(3)求 时只要把等号两边同时乘以 即可根据错位相减法求得.( )
×
(4)若数列 , , , 是首项为1,公比为3的等比数列,则数列 的通项公式是 .( )
(1)求数列 的通项公式;
【解】设等差数列 的公差为 .由题意得 解得 所以 .所以数列 的通项公式是 .
(2)设 ,数列 的前 项和为 ,若 ,求 的值.
已知数列 为公差大于0的等差数列, ,且 , , 成等比数列.
【解】 由(1)知, ,所以 .因为 ,所以 ,解得 .所以 的值为20.
必备知识 自主排查
核心考点 师生共研
必备知识 自主排查
01
数列求和的常用方法
(1)公式法①等差数列 的前 项和 .②等比数列 的前 项和
(2)分组转化法:一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成的,则求和时可用分组求和法,分别求和后再相加减.
(3)裂项相消法:把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得前 项和.
【对点训练】
(2023·山西太原第一学期统考)已知在数列 中, , .
(1)证明:数列 为等比数列,并求 的通项公式;
高考数学一轮总复习 第5章 数列 第4节 数列求和课件 理 新人教版
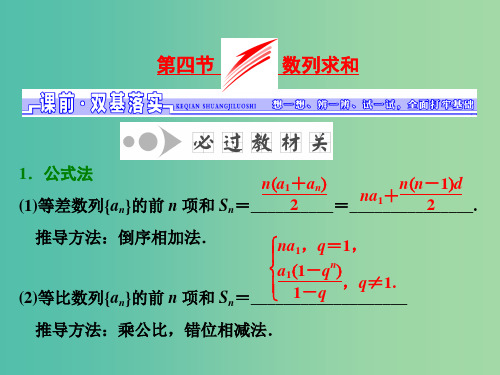
2.若等比数列{an}满足 a1+a4=10,a2+a5=20,则{an}的前 n 项和 Sn=________.
解析:由题意 a2+a5=q(a1+a4),得 20=q×10,故 q=2, 代入 a1+a4=a1+a1q3=10,得 9a1=10,即 a1=190. 故 Sn=19011--22n=190(2n-1). 答案:190(2n-1)
(2015·湖北高考)设等差数列{an}的公差为 d,前 n 项和为 Sn,等 比数列{bn}的公比为 q.已知 b1=a1,b2=2,q=d,S10=100. (1)求数列{an},{bn}的通项公式; (2)当 d>1 时,记 cn=abnn,求数列{cn}的前 n 项和 Tn.
解析
[由题悟法]
bn=3
an+1 2
,求数列an+2 1·bn的前
n
项和
Sn.
an+1
解:由(1)可得 bn=3 2 =3n,
所以an+2 1·bn=n·3n,
[即时应用]
已知等比数列{an}中,首项 a1=3,公比 q>1,且 3(an+2 +an)-10an+1=0(n∈N*). (1)求数列{an}的通项公式; (2)设bn+13an是首项为 1,公差为 2 的等差数列,求数列 {bn}的通项公式和前 n 项和 Sn.
解析
考点三 错位相减法求和 重点保分型考点——师生共研 [典例引领]
(3)错位相减法:如果一个数列的各项是由一个等差数列和 一个等比数列的对应项之积构成的,那么求这个数列 的前 n 项和即可用错位相减法求解.
(4)倒序相加法:如果一个数列{an}与首末两端等“距离” 的两项的和相等或等于同一个常数,那么求这个数列 的前 n 项和即可用倒序相加法求解.
高考数学一轮复习 第五章 数列 5.4 数列求和与数列的综合应用课件 理 高三全册数学课件

2021/12/8
第二十三页,共五十七页。
解析:(1)令数列{an}的前 n 项和为 Sn,则 S20=a1+a2+a3 +…+a20=2(1+2+3+…+20)-12+212+213+…+2120=420- 1-2120=419+2120.
(2)an=2+22+23+…+2n=2-1-2n2+1=2n+1-2, 所以 Sn=(22+23+24+…+2n+1)-(2+2+2+…+2)= 221--22n+2-2n=2n+2-4-2n.
2021/12/8
第十八页,共五十七页。
课堂探究·深度剖析
课堂升华 强技提能
2021/12/8
第十九页,共五十七页。
考向一 分组求和法
【例 1】 (1)若数列{an}的通项公式为 an=2n+2n-1,则数列{an}
的前 n 项和为( C )
A.2n+n2-1
B.2n+1+n2-1
C.2n+1+n2-2 D.2n+n-2
2021/12/8
第十三页,共五十七页。
4.(2019·武汉市调研考试)对任一实数序列 A=(a1,a2,a3,…), 定义新序列 ΔA=(a2-a1,a3-a2,a4-a3,…),它的第 n 项为 an+1-an.
假定序列 Δ(ΔA)的所有项都是 1,且 a12=a22=0,则 a2= 100 .
第五章
数列(shùliè)
2021/12/8
第一页,共五十七页。
第四节 数列求和(qiúhé)与数列的综合应用
2021/12/8
第二页,共五十七页。
2021/12/8
第三页,共五十七页。
知识(zhī shi)梳理·自主学
习
课堂(kètáng)探究·深度剖 析
高三数学一轮复习数列求和(必修5)精品PPT课件
考点一 分组转化求和
分组转化求和就是从通项入手, 若无通项,则先求通项,然后通过对 通项变形,转化为等差或等比或可求 数列前n项和的数列来求之.
课堂互动讲练
例1 已知数列{an}的前几项是3+2- 1,6+22-1,9+23-1,12+24-1,写出 数列{an}的通项并求其前n项和Sn.
课堂互动讲练
1.利用裂项相消法求和时,应 注意抵消后并不一定只剩下第一项和 最后一项,也有可能前面剩两项,后 面也剩两项,再就是将通项公式裂项 后,有时候需要调整前面的系数,使 裂开的两项之差和系数之积与原通项 公式相等.
课堂互动讲练
课堂互动讲练
例2 已知等差数列{an}的首项a1≠0,前n项 和为Sn,且S4+a2=2S3;等比数列{bn}满足 b1=a2,b2=a4.
第4课时 数列求和
基础知识梳理
求数列的前n项和的方法 1.公式法 (1)等差数列的前n项和公式
Sn=
=
.
基础知识梳理
(2)等比数列前n项和公式 ①当q=1时,Sn=na1;
基础知识梳理
2.分组转化法 把数列的每一项分成两项,使其 转化为几个等差、等比数列,再求 解. 3.裂项相消法 把数列的通项拆成两项之差求 和,正负相消剩下首尾若干项.
课堂互动讲练
课堂互动讲练
课堂互动讲练
【误区警示】 利用错位相减法 求和时,转化为等比数列求和.若公 比是个参数(字母),则应先对参数加 以讨论,一般情况下分等于1和不等于 1两种情况分别求和.
课堂互动讲练
考点四 数列求和的综合应用
对于由递推关系给出的数列,常 借助于Sn+1-Sn=an+1转换为an与an+1 的关系式或Sn与Sn+1的关系式,进而 求出an或Sn使问题得以解决.
分组转化求和就是从通项入手, 若无通项,则先求通项,然后通过对 通项变形,转化为等差或等比或可求 数列前n项和的数列来求之.
课堂互动讲练
例1 已知数列{an}的前几项是3+2- 1,6+22-1,9+23-1,12+24-1,写出 数列{an}的通项并求其前n项和Sn.
课堂互动讲练
1.利用裂项相消法求和时,应 注意抵消后并不一定只剩下第一项和 最后一项,也有可能前面剩两项,后 面也剩两项,再就是将通项公式裂项 后,有时候需要调整前面的系数,使 裂开的两项之差和系数之积与原通项 公式相等.
课堂互动讲练
课堂互动讲练
例2 已知等差数列{an}的首项a1≠0,前n项 和为Sn,且S4+a2=2S3;等比数列{bn}满足 b1=a2,b2=a4.
第4课时 数列求和
基础知识梳理
求数列的前n项和的方法 1.公式法 (1)等差数列的前n项和公式
Sn=
=
.
基础知识梳理
(2)等比数列前n项和公式 ①当q=1时,Sn=na1;
基础知识梳理
2.分组转化法 把数列的每一项分成两项,使其 转化为几个等差、等比数列,再求 解. 3.裂项相消法 把数列的通项拆成两项之差求 和,正负相消剩下首尾若干项.
课堂互动讲练
课堂互动讲练
课堂互动讲练
【误区警示】 利用错位相减法 求和时,转化为等比数列求和.若公 比是个参数(字母),则应先对参数加 以讨论,一般情况下分等于1和不等于 1两种情况分别求和.
课堂互动讲练
考点四 数列求和的综合应用
对于由递推关系给出的数列,常 借助于Sn+1-Sn=an+1转换为an与an+1 的关系式或Sn与Sn+1的关系式,进而 求出an或Sn使问题得以解决.
高考数学一轮复习第五章数列第4讲数列求和课件文

已知数列{an}的通项公式是 an=2·3n-1+ (-1)n(ln 2-ln 3)+(-1)nnln 3,求其前 n 项和 Sn. [解] Sn=2(1+3+…+3n-1)+[-1+1-1+…+(-1)n](ln 2 -ln 3)+[-1+2-3+…+(-1)nn]ln 3, 所以当 n 为偶数时, Sn=2×11--33n+n2ln 3=3n+n2ln 3-1; 当 n 为奇数时,
分组转化法求和的常见类型 (1)若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采用分 组转化法求{an}的前 n 项和. (2)通项公式为 an=bcnn,,nn为为偶奇数数的数列,其中数列{bn},{cn} 是等比数列或等差数列,可采用分组转化法求{an}的前 n 项 和.
3.等比数列{an}的首项为 a,公比为 q,Sn 为其前 n 项的和, 求 S1+S2+…+Sn. [解] 当 q=1 时,an=a,Sn=na, 所以 S1+S2+…+Sn=(1+2+…+n)a=n(n2+1)a. 当 q≠1 时, 因为 Sn=a(11--qqn),所以 S1+S2+…+Sn
Tn=11-12+12-13+13-14+…+n1-n+1 1=1-n+1 1=
n n+1.
利用裂项相消法求和时,应注意抵消后并不一定只剩下第一 项和最后一项,也有可能前面剩两项,后面也剩两项,再就 是将通项公式裂项后,有时候需要调整前面的系数,使裂开 的两项之差和系数之积与原通项公式相等.
2Tn=3×[2×23+3×24+…+(n+1)×2n+2], 两 式 作 差 , 得 - Tn = 3×[2×22 + 23 + 24 + … + 2n + 1 - (n +
1)×2n+2]=3×4+4(11--22n)-(n+1)×2n+2
高考数学一轮复习第五章数列5.4数列求和理

答 2 案(1 : 1 2 1 2 1 3 1 3 1 4 1 1 0 1 1 1 ) 1 2 1 0 .
20
11
考向一 裂项相消法求和
【典例1】(2015·全国卷Ⅰ)Sn为数列{an}的前n项和. 已知an>0,an2+2an=4Sn+3. (1)求{an}的通项公式. (2)设bn= ,求数列{bn}的前n项和.
Sn,若an=
,则S5等于 ( )
1
n n 1
A .1 B .5 C .1 D .1 6 6 3 0
【解析】选B. annn11n nn1 1nn 1n1 1,
所以S5=a1+a2+a3+a4+a5
1 1 1 1 1 1 223 56
5. 6
2.(必修5P61习题2.5A组T4(3)改编)1+2x+3x2+…+nxn-1
A.n(n1) C. n(n1)
2
B.n(n1) D.n(n1)
2
【解析】选A.因为d=2,a2,a4,a8成等比数列,所以 a42=a2a8,即(a2+2d)2=a2(a2+6d),解得a2=4,所以 a1=2. 所以利用等差数列的求和公式可求得Sn=n(n+1).
4.(2016·唐山模拟)(2-3×5-1)+(4-3×5-2)+…+(2n-
2 (2)1+3+5+7+…+2n-1=__.
n2 (3)2+4+6+8+…+2n=____.
(4)12+22+…+n2= n2+n
.
第5章 第4讲数列求和-2022版高三数学(新高考)一轮复习课件_ppt(56张)

天气骤冷2,0红2旗0 冻结。这句诗形象的写出了色彩鲜明、红白映衬的景象,“掣”字用了拟人的修辞手法,生动形象的写出了塞外天气的恶劣,寒风的呼啸。但在这样的环境下,红
旗却被冻的不会翻动了,更加突出了雪之大、天气之寒冷。从“红”字能反衬出白雪皑皑的景象,而“不翻”则衬托出了天气的寒冷。 二是语言清新淡雅而又晶莹明丽,明白晓畅而又情韵悠长。
返回导航
第五章 数列
高考一轮总复习 • 数学 • 新高考
返回导航
3.(必修 5P47T4 改编)数列{an}的通项公式是 an=
1 n+
n+1,前
n
项和为
9,则
n=( B ) A.9
B.99
C.10
D.100
[解析]
因为 an=
1 n+
n+1=
n+1-
n.所以 Sn=a1+a2+a3+…+an=(
返回导航
知识梳理 • 双基自测
第五章 数列
高考一轮总复习 • 数学 • 新高考
返回导航
知识点一 公式法求和
(1)如果一个数列是等差数列或等比数列,则求和时直接利用等差、等比数列的 前 n 项和公式.
(2)等差数列的前 n 项和公式: Sn=na1+ 2 an=___n_a_1+__n__n_2-__1__d__=___d2_n_2+__(_a_1_-__d2_)n________.
第五章 数列
高考一轮总复习 • 数学 • 新高考
(3)等比数列的前 n 项和公式: na1,q=1,
Sn=a11--aqnq=_______________,q≠1. 注意等比数列公比 q 的取值情况,要分 q=1,q≠1.
返回导航
第五章 数列
高考一轮总复习 • 数学 • 新高考
旗却被冻的不会翻动了,更加突出了雪之大、天气之寒冷。从“红”字能反衬出白雪皑皑的景象,而“不翻”则衬托出了天气的寒冷。 二是语言清新淡雅而又晶莹明丽,明白晓畅而又情韵悠长。
返回导航
第五章 数列
高考一轮总复习 • 数学 • 新高考
返回导航
3.(必修 5P47T4 改编)数列{an}的通项公式是 an=
1 n+
n+1,前
n
项和为
9,则
n=( B ) A.9
B.99
C.10
D.100
[解析]
因为 an=
1 n+
n+1=
n+1-
n.所以 Sn=a1+a2+a3+…+an=(
返回导航
知识梳理 • 双基自测
第五章 数列
高考一轮总复习 • 数学 • 新高考
返回导航
知识点一 公式法求和
(1)如果一个数列是等差数列或等比数列,则求和时直接利用等差、等比数列的 前 n 项和公式.
(2)等差数列的前 n 项和公式: Sn=na1+ 2 an=___n_a_1+__n__n_2-__1__d__=___d2_n_2+__(_a_1_-__d2_)n________.
第五章 数列
高考一轮总复习 • 数学 • 新高考
(3)等比数列的前 n 项和公式: na1,q=1,
Sn=a11--aqnq=_______________,q≠1. 注意等比数列公比 q 的取值情况,要分 q=1,q≠1.
返回导航
第五章 数列
高考一轮总复习 • 数学 • 新高考
高三数学(理)一轮复习课件:5.4 数列求和

(1)解 : 设 首 项 为 a1 19, d 2 a1, 公 差 为 d
an a1 (n 1)d 19 (n 1) (2)
21 2n
n(a1 an ) n(19 21 2n) n 2 20 n Sn 2 2
的等差数列,S n为数列an 的前n项和 ( 1 )求 : an 及S n
1 1 1 1 1 2 2 n 1 n 2
3 2n 3 4 2n 1n 2
拓展训练: 已知等差数列an 的前项n和Sn满足S3 0, S5 5 (1)求an 的通项公式; 1 (2)求数列 的前项和. a2 n1a2 n1
(2010 重庆, 17)已知数列an 是首项为1 9,公差为- 2
(2)设数列bn an 是首项为1,公比为3 的等比数列, 求 : b n 及前n项和T n
( 2) 解 : 由 题 意 知
: bn an 1 3n1, 即 bn 3n1 21 2n
Tn b1 b2 b3 bn
P90 变式训练2
例 4:
an 中前n项和为Sn,前6项和为36, 已知: 等差数列
最后6项的和为 180 (n 6),求Sn 解:由题意知 :
a1 a2 a3 a4 a5 a6 36
n
①
an an1 an2 an3 an4 an5 180
2 1 2 2 n 3 n 5n 2 8
的等差数列,S n为数列an 的前n项和 ( 1 )求 : an 及S n
(2010 重庆, 17)已知数列an 是首项为1 9,公差为- 2
拓展训练:
(2)设数列bn an 是首项为1,公比为3 的等比数列, 求 : b n 及前n项和T n
an a1 (n 1)d 19 (n 1) (2)
21 2n
n(a1 an ) n(19 21 2n) n 2 20 n Sn 2 2
的等差数列,S n为数列an 的前n项和 ( 1 )求 : an 及S n
1 1 1 1 1 2 2 n 1 n 2
3 2n 3 4 2n 1n 2
拓展训练: 已知等差数列an 的前项n和Sn满足S3 0, S5 5 (1)求an 的通项公式; 1 (2)求数列 的前项和. a2 n1a2 n1
(2010 重庆, 17)已知数列an 是首项为1 9,公差为- 2
(2)设数列bn an 是首项为1,公比为3 的等比数列, 求 : b n 及前n项和T n
( 2) 解 : 由 题 意 知
: bn an 1 3n1, 即 bn 3n1 21 2n
Tn b1 b2 b3 bn
P90 变式训练2
例 4:
an 中前n项和为Sn,前6项和为36, 已知: 等差数列
最后6项的和为 180 (n 6),求Sn 解:由题意知 :
a1 a2 a3 a4 a5 a6 36
n
①
an an1 an2 an3 an4 an5 180
2 1 2 2 n 3 n 5n 2 8
的等差数列,S n为数列an 的前n项和 ( 1 )求 : an 及S n
(2010 重庆, 17)已知数列an 是首项为1 9,公差为- 2
拓展训练:
(2)设数列bn an 是首项为1,公比为3 的等比数列, 求 : b n 及前n项和T n
高考数学一轮复习第5章数列4数列求和课件新人教版

(2)1+3+5+7+…+(2n-1)=n2;
(+1)(2+1)
(3)1 +2 +3 +…+n =
;
6
2
(+1)
(4)13+23+33+…+n3=
.
2
2
2
2
2
【知识巩固】
1.下列说法正确的画“ ”,错误的画“×”.
(1)利用倒序相加法可求得
sin21°+sin22°+sin23°+…+sin288°+sin289°=44.5.(
2
②求 ∑ aici(n∈N*).
=1
解 (1)设等差数列{an}的公差为 d,等比数列{bn}的公比为 q.依题意得
6 = 6 + 2,
= 3,
n-1
n
解得
故
a
=4+(n-1)×3=3n+1,b
=6×2
=3×2
.
n
n
2
= 2,
6 = 12 + 4,
所以,数列{an}的通项公式为 an=3n+1,数列{bn}的通项公式为 bn=3×2n.
当
当
故
3(1-3 )
为偶数时,Sn=n+
1-3
3+1
3
n
= 2 +n-2;
3(1-3 )
3+1
7
n 为奇数时,Sn=(n-1)-(2n+1)+
= 2 -n-2.
1-3
3+1
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分组转化法求和的常见类型 1.若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采用分组求和法求
{an}的前 n 项和. 2.通项公式为 an=cbnn,,nn为为偶奇数数, 的数列,其中数列{bn},{cn}是等比 数列或等差数列,可采用分组求和法求和. 提醒:某些数列的求和是将数列转化为若干个可求和的新数列的和或差,
Sn=na12+an=_n_a_1_+__n_n_-2__1__d___.
(2)等比数列的前 n 项和公式: Sn=naa11-1-,aqqnq==1_a,_11_1-_-_q_q_n_,__q_≠__1_._ 2.倒序相加法 如果一个数列{an}的前 n 项中首末两端等“距离”的两项的和相等或等于同 一个常数,那么求这个数列的前 n 项和即可用倒序相加法,如等差数列的前 n 项 和公式即是用此法推导的.
1.必会结论 常用求和公式
前 n 个正整数之和 前 n 个正奇数之和
前 n 个正整数的平方和
前 n 个正整数的立方和
1+2+…+n=nn2+1 1+3+5+…+(2n-1)=n2
nn+12n+1 12+22+…+n2=________6_______
13+23+…+n3=nn+2 12
2.必知联系 (1)直接应用公式求和时,要注意公式的应用范围,如当等比数列公比为参数 (字母)时,应对其公比是否为 1 进行讨论. (2)在应用错位相减法时,注意观察未合并项的正负号;结论中形如 an,an+1 的式子应进行合并. (3)在应用裂项相消法时,要注意消项的规律具有对称性,即前剩多少项则后 剩多少项.
(2)由(1)可得 bn=2n+n, 所以 b1+b2+b3+…+b10 =(2+1)+(22+2)+(23+3)+…+(210+10) =(2+22+23+…+210)+(1+2+3+…+10) =211--2210+1+102×10 =(211-2)+55=211+53=2 101.
归纳升华
【答案】
20 11
(2)①由 a2n+2an=4Sn+3,(*)
可知 a2n+1+2an+1=4Sn+1+3.(**)
(**)-(*),得 a2n+1-a2n+2(an+1-an)=4an+1,
即 2(an+1+an)=a2n+1-a2n=(an+1+an)(an+1-an).
由 an>0,得 an+1-an=2.
3.错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成 的,这个数列的前 n 项和可用错位相减法. 4.裂项相消法 (1)把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而 求得其和.
(2)裂项时常用的三种变形:
①nn1+1=1n-n+1 1;
②2n-112n+1=122n1-1-2n1+1;
考点分类突破
考向 1 分组转化法求和 1.已知数列{an}的前 n 项是 3+2-1,6+4-1,9+8-1,12+16-1,…,
3n+2n-1,则其前 n 项和 Sn=________.
【解析】 由题意知 an=3n+2n-1, ∴Sn=a1+a2+…+an =3×1+21-1+3×2+22-1+…+3n+2n-1 =3×(1+2+3+…+n)+21+22+…+2n-n =3×1+n2×n+211--22n-n =3n22+n+2n+1-2. 【答案】12(3n2+n)+2n+1-2
【解析】 (1)由题意有 a2-a1=2,a3-a2=3,…,an-an-1=n(n≥2).以上 各式相加,得 an-a1=2+3+…+n=n-122+n=n2+2n-2.
又∵a1=1,∴an=n2+2 n(n≥2). ∵当 n=1 时也满足此式,∴an=n2+2 n(n∈N*).
∴a1n=n2+2 n=21n-n+1 1. ∴S10=2×11-12+12-13+…+110-111 =2×1-111=2110.
又 a21+2a1=4a1+3,解得 a1=-1(舍去)或 a1=3.
所以{an}是首项为 3,公差为 2 的等差数列,通项公式为 an=2n+1.
②由 an=2n+1 可知 bn=ana1n+1=2n+112n+3=122n1+1-2n1+3. 设数列{bn}的前 n 项和为 Tn,则 Tn=b1+b2+…+bn =1213-15+15-17+…+2n1+1-2n1+3 =32nn+3.
2.(2015·福建高考)等差数列{an}中,a2=4,a4+a7=15. (1)求数列{an}的通项公式; (2)设 bn=2an-2+n,求 b1+b2+b3+…+b10 的值.
【解】 (1)设等差数列{an}的公差为 d, 由已知得aa1+1+d3=d4+,a1+6d=15, 解得da=1=13., 所以 an=a1+(n-1)d=n+2.
从而求得原数列的和,注意在含有字母的数列中对字母的讨论.
考点分类突破
考向 2 裂项相消法求和 (1)(2015·江苏高考)设数列an满足 a1=1,且 an+1-an=n+1(n∈N*), 则数列a1n前 10 项的和为______. (2)(2015·全国卷Ⅰ)Sn 为数列{an}的前 n 项和.已知 an>0,a2n+2an=4Sn+3. ①求{an}的通项公式; ②设 bn=ana1n+1,求数列{bn}的前 n 项和.
第五章 数列 5.4 数列求和
考纲解读
1.熟练掌握等差、等比数列的前 n 项和公式. 2.掌握非等差、等比数列求和的几种常见方法. 3.能在具体的问题情境中识别数列的等差关系或等比关系,并能用相关知识 解决相应的问题.
知识梳理
知识点 数列求和的常见方法 1.公式法 直接利用等差数列、等比数列的前 n 项和公式求和 (1)等差数列的前 n 项和公式:
③
1 n+
n+1=
n+1-
n.
5.分组求和法 一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成, 则求和时可用分组求和法,分别求和后相加减. 6.并项求和法 一个数列的前 n 项和中,可两两结合求解,则称之为并项求和.形如 an=(- 1)nf(n)类型,可采用两项合并求解. 例如,Sn=1002-992+982-972+…+22-12 =(100+99)+(98+97)+…+(2+1)=5 050.
{an}的前 n 项和. 2.通项公式为 an=cbnn,,nn为为偶奇数数, 的数列,其中数列{bn},{cn}是等比 数列或等差数列,可采用分组求和法求和. 提醒:某些数列的求和是将数列转化为若干个可求和的新数列的和或差,
Sn=na12+an=_n_a_1_+__n_n_-2__1__d___.
(2)等比数列的前 n 项和公式: Sn=naa11-1-,aqqnq==1_a,_11_1-_-_q_q_n_,__q_≠__1_._ 2.倒序相加法 如果一个数列{an}的前 n 项中首末两端等“距离”的两项的和相等或等于同 一个常数,那么求这个数列的前 n 项和即可用倒序相加法,如等差数列的前 n 项 和公式即是用此法推导的.
1.必会结论 常用求和公式
前 n 个正整数之和 前 n 个正奇数之和
前 n 个正整数的平方和
前 n 个正整数的立方和
1+2+…+n=nn2+1 1+3+5+…+(2n-1)=n2
nn+12n+1 12+22+…+n2=________6_______
13+23+…+n3=nn+2 12
2.必知联系 (1)直接应用公式求和时,要注意公式的应用范围,如当等比数列公比为参数 (字母)时,应对其公比是否为 1 进行讨论. (2)在应用错位相减法时,注意观察未合并项的正负号;结论中形如 an,an+1 的式子应进行合并. (3)在应用裂项相消法时,要注意消项的规律具有对称性,即前剩多少项则后 剩多少项.
(2)由(1)可得 bn=2n+n, 所以 b1+b2+b3+…+b10 =(2+1)+(22+2)+(23+3)+…+(210+10) =(2+22+23+…+210)+(1+2+3+…+10) =211--2210+1+102×10 =(211-2)+55=211+53=2 101.
归纳升华
【答案】
20 11
(2)①由 a2n+2an=4Sn+3,(*)
可知 a2n+1+2an+1=4Sn+1+3.(**)
(**)-(*),得 a2n+1-a2n+2(an+1-an)=4an+1,
即 2(an+1+an)=a2n+1-a2n=(an+1+an)(an+1-an).
由 an>0,得 an+1-an=2.
3.错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成 的,这个数列的前 n 项和可用错位相减法. 4.裂项相消法 (1)把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而 求得其和.
(2)裂项时常用的三种变形:
①nn1+1=1n-n+1 1;
②2n-112n+1=122n1-1-2n1+1;
考点分类突破
考向 1 分组转化法求和 1.已知数列{an}的前 n 项是 3+2-1,6+4-1,9+8-1,12+16-1,…,
3n+2n-1,则其前 n 项和 Sn=________.
【解析】 由题意知 an=3n+2n-1, ∴Sn=a1+a2+…+an =3×1+21-1+3×2+22-1+…+3n+2n-1 =3×(1+2+3+…+n)+21+22+…+2n-n =3×1+n2×n+211--22n-n =3n22+n+2n+1-2. 【答案】12(3n2+n)+2n+1-2
【解析】 (1)由题意有 a2-a1=2,a3-a2=3,…,an-an-1=n(n≥2).以上 各式相加,得 an-a1=2+3+…+n=n-122+n=n2+2n-2.
又∵a1=1,∴an=n2+2 n(n≥2). ∵当 n=1 时也满足此式,∴an=n2+2 n(n∈N*).
∴a1n=n2+2 n=21n-n+1 1. ∴S10=2×11-12+12-13+…+110-111 =2×1-111=2110.
又 a21+2a1=4a1+3,解得 a1=-1(舍去)或 a1=3.
所以{an}是首项为 3,公差为 2 的等差数列,通项公式为 an=2n+1.
②由 an=2n+1 可知 bn=ana1n+1=2n+112n+3=122n1+1-2n1+3. 设数列{bn}的前 n 项和为 Tn,则 Tn=b1+b2+…+bn =1213-15+15-17+…+2n1+1-2n1+3 =32nn+3.
2.(2015·福建高考)等差数列{an}中,a2=4,a4+a7=15. (1)求数列{an}的通项公式; (2)设 bn=2an-2+n,求 b1+b2+b3+…+b10 的值.
【解】 (1)设等差数列{an}的公差为 d, 由已知得aa1+1+d3=d4+,a1+6d=15, 解得da=1=13., 所以 an=a1+(n-1)d=n+2.
从而求得原数列的和,注意在含有字母的数列中对字母的讨论.
考点分类突破
考向 2 裂项相消法求和 (1)(2015·江苏高考)设数列an满足 a1=1,且 an+1-an=n+1(n∈N*), 则数列a1n前 10 项的和为______. (2)(2015·全国卷Ⅰ)Sn 为数列{an}的前 n 项和.已知 an>0,a2n+2an=4Sn+3. ①求{an}的通项公式; ②设 bn=ana1n+1,求数列{bn}的前 n 项和.
第五章 数列 5.4 数列求和
考纲解读
1.熟练掌握等差、等比数列的前 n 项和公式. 2.掌握非等差、等比数列求和的几种常见方法. 3.能在具体的问题情境中识别数列的等差关系或等比关系,并能用相关知识 解决相应的问题.
知识梳理
知识点 数列求和的常见方法 1.公式法 直接利用等差数列、等比数列的前 n 项和公式求和 (1)等差数列的前 n 项和公式:
③
1 n+
n+1=
n+1-
n.
5.分组求和法 一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成, 则求和时可用分组求和法,分别求和后相加减. 6.并项求和法 一个数列的前 n 项和中,可两两结合求解,则称之为并项求和.形如 an=(- 1)nf(n)类型,可采用两项合并求解. 例如,Sn=1002-992+982-972+…+22-12 =(100+99)+(98+97)+…+(2+1)=5 050.
