第16章 位移法及力矩分配法
建筑力学(力矩分配法)

第十八章力矩分配法力矩分配法理论基础:位移法;计算对象:杆端弯矩;适用范围:连续梁和无侧移刚架。
一、转动刚度转动刚度表示杆端对转动的抵抗能力。
它在数值上等于使杆端产生单位转角时需要施加的力矩,以SAB表示。
A是施力端(近端),B为远端。
1S AB=4i1S AB=3iS AB= i1S AB=0远端固定远端铰支远端滑动远端自由第一节力矩分配法的基本原理1S AB =4i1S AB =3iS AB = i 1S AB =0远端固定远端铰支远端滑动远端自由转动刚度远端固定,S =4i 远端简支,S =3i 远端定向,S =i 远端自由,S =0S AB 与杆的线刚度i 和远端支承情况有关。
i —杆件的线刚度,lEI i二、传递系数M AB = 4i AB ϕAM BA = 2i AB ϕA21==AB BA ABM M C M AB = 3i AB ϕA 0==ABBA ABM M C M AB = i AB ϕAM BA = -i AB ϕA1-==ABBA ABM M C ϕAlAB远端固定ABϕAϕAAB远端铰支远端滑动M BA = 0远端支承转动刚度传递系数固定S=4i C =1/2简支S=3i C =0定向S=i C = -1自由S=0三、力矩分配法的基本原理杆端弯距:取结点A 作隔离体,由∑M =0,得分配系数CA BDi ABi AC i ADAAB A AB AB S i M ϕϕ==4A AC A AC AC S i M ϕϕ==AAD A AD AD S i M ϕϕ==3}M M ABM ACM ADAAD AC AB S S S M ϕ)(++=∑=++=AAD AC AB A SMS S S M ϕMSSM AADAD ∑=M SS M A ABAB ∑=M S S M AACAC ∑=注:1)分配弯矩是杆端转动时产生的近端弯矩。
2)结点集中力偶顺时针为正。
∑=AAkAkSS μMM Ak Ak μ=分配弯矩A ϕM1321=++=∑A A A Ak μμμμ各杆的远端弯矩M kA 可以利用传递系数求出。
结构力学教案位移法和力矩分配法
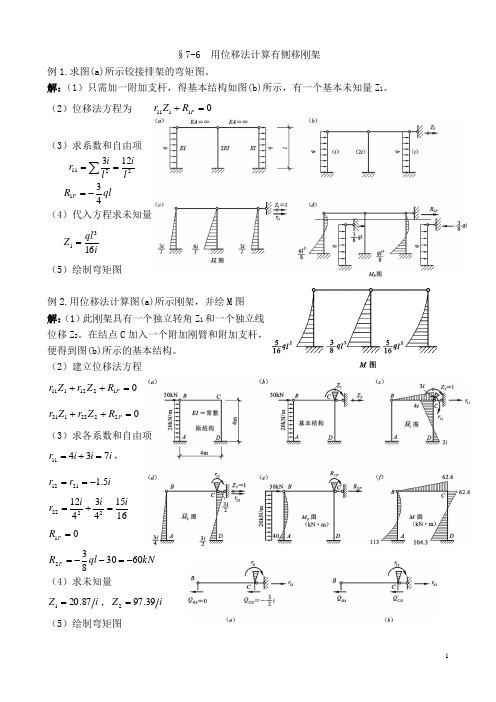
§7-6 用位移法计算有侧移刚架例1.求图(a)所示铰接排架的弯矩图。
解:(1)只需加一附加支杆,得基本结构如图(b)所示,有一个基本未知量Z 1。
(2)位移法方程为 01111=+P R Z r(3)求系数和自由项2211123l il i r ==∑ql R P 431-=(4)代入方程求未知量iql Z 1631=(5)绘制弯矩图例2.用位移法计算图(a)所示刚架,并绘M 图 解:(1)此刚架具有一个独立转角Z 1和一个独立线位移Z 2。
在结点C 加入一个附加刚臂和附加支杆,便得到图(b)所示的基本结构。
(2)建立位移法方程01212111=++P R Z r Z r 02222121=++P R Z r Z r (3)求各系数和自由项i i i r 73411=+=, i r r 5.12112-==1615434122222ii i r =+=01=P RkN ql RP 6030832-=--=(4)求未知量i Z 87.201=,i Z 39.972= (5)绘制弯矩图例3.用直接平衡法求刚架的弯矩图。
解:(1)图示刚架有刚结点C 的转角Z 1和结点C 、D 的水平线位移Z 2两个基本未知量。
设Z 1顺时针方向转动,Z 2向右移动。
(2)求各杆杆端弯矩的表达式3421+-=Z Z M CA 3221--=Z Z M AC 13Z M CD = 25.0Z M BD -= (3)建立位移法方程有侧移刚架的位移法方程,有下述两种:Ⅰ.与结点转角Z 1对应的基本方程为结点C 的力矩平衡方程。
∑=0CM , 037021=+-⇒=+Z Z M M CD CAⅡ.与结点线位移Z 2对应的基本方程为横梁CD 的截面平衡方程。
∑=0xF, 0=+D C CA Q Q取立柱CA 为隔离体(图(d)),∑=0A M , 331216262121-+-=---=Z Z ql Z Z Q CA 同样,取立柱DB 为隔离体((e)),∑=0B M , 2212165.0Z Z Q DB =--= 代入截面平衡方程得 03125012133121221=-+-⇒=+-+-Z Z Z Z Z(4)联立方程求未知量 Z 1=0.91 Z 2=9.37(5)求杆端弯矩绘制弯矩图将Z 1、Z 2的值回代杆端弯矩表达式求杆端弯矩作弯矩图。
结构力学——6位移法和力矩分配法

△ △
4、5、6 三个固定端都是不动的点,结点1 、2、3均无竖向位移。又因两根横梁其长 度不变,故三个结点均有相同的水平位移 FP △ 。
1
2
3
4
5
6
(a)
事实上,图(a)所示结构的独立线位移数 将结构的刚结点(包括固定支座)都变成 目,与图(b)所示铰结体系的线位移数目 铰结点(成为铰结体系),则使其成为几何 是相同的。因此,实用上为了能简捷地确 不变添加的最少链杆数,即为原结构的独 定出结构的独立线位移数目,可以 立线位移数目(见图b)。
4
5
6
(a)
共有四个刚结点,结点线位移数目为二 ,基本未知量为六个。基本结构如图所 示。
7
10 返回
5
6
(b)
例:确定图a所示连续梁的基本结构。 D B A C D B A C
(图a)
A A
B B
基本结构 基本结构
C C
D (图b) D
在确定基本结构的同时,也就确定了基本未知量及其数目。
EI
第六章
位移法和力矩分配法
§6—1 位移法的基本概念 §6—2 位移法基本未知量的确定 §6—3 位移法典型方程计算步骤和示例 §6—4 力矩分配法的基本概念 §6—5 用力矩分配法计算连续梁 §6—6 用力矩分配法计算无接点线位移刚架
1
§6—1
位移法的基本概念
一、位移法的提出(Displacement Method)
M
A
B
0
2i
r11 4i 4i 0
8EI r11 8i l
2i
M1
得
15
求自由项R1P,作出基本结构在荷载作用时的弯矩 图(MP图)。 取结点B为隔离体
结构力学——力矩分配法分解

3 . 一般最终的杆端力矩与固端力矩是同量级的,要求精确 到三位有效数字,计算中取4位计算,以保证前三位的 精确度
第三节 多结点力矩分配法
计算的指导思想由两个步骤说明:
固定状态的计算(与单点固定一样)。
即刚臂→荷载→固端力矩→约束力矩;
100k0N
EI
1 EI
2 EI
0.43 0.57 0.57 0.43
-500 -1000
M3B=1000
例题:有支座移动(已知结点线位移)E=200GPa,I = 2500cm4
绘制弯矩图。
A
B
C
D
EI
EI
=1cm
10m
10m
10m
0.429 0.571
0.571 0.429
MF
3000
3000 -1500
2 . 不相邻 点可同时 释放.
例题:用力矩分配法求图示结构弯矩图(利用传递系数的概念) 。
A
EI
10m
1 EI
10m
100k0N 2 EI 3 B 3B是悬臂梁,
转动结点3 时,
10m 1m 悬臂可自由转
0.43 0.57 0.5 0.5 1 0
动,固其转动
MF
1000 刚度为零
或A
MF
100k0N
放松状态的计算(与单点放松不同)。
力矩的分配和传递是在远端约束已知的情况下进行的, 因此,分配单元的相邻结点不应同时放松。每次只能 放松一个结点,同时相邻结点保持固定,所以,整个 放松过程是轮流放松每一个结点来逐步完成的。
第三节 多结点力矩分配法
力矩分配法

1渐近法2用力法、位移法分析超静定结构,都需要求解多元联立方程组,求出基本未知量。
当未知量较多时,计算颇为繁重。
渐近法—采用逐步地逼近真实解的方法。
渐近法主要有:一、渐近法概述(1)力矩分配法:适于连续梁与无侧移刚架。
(2)无剪力分配法:适于规则的有侧移刚架。
(3)迭代法:适于梁的刚度大于柱刚度的各种刚架。
3力矩分配法理论基础:位移法;计算对象:杆端弯矩;计算方法:逐渐逼近的方法;适用范围:连续梁和无侧移刚架。
4只有结点角位移而无结点线位移的梁和刚架。
?力矩分配法的适用范围:力矩分配法的适用范围:5只有结点角位移而无结点线位移的梁和刚架。
√6力矩分配法以杆端弯矩为计算对象,采用:固定放松分配、传递逐次逼近杆端弯矩的精确解。
计算原理及符号规则均与位移法相同,只是计算过程不相同。
7计算过程:1.固定结点求出固定状态的杆端弯矩FijM 附加刚臂处的不平衡弯矩iM依次将结点上的不平衡弯矩反号分配于各杆近端,并传向远端。
2.逐次放松各结点8若干次循环计算= 也即逐次恢复转角的过程直接表达为各杆端弯矩逐次修正的过程放松结束,也即变形(转角)、内力趋于实际状态。
9——基本运算A BCM ABM BAM BC A BCM FAB M FBAM FBCM BM BM F BAM F BCM B =M F BA +M F BCABC-M BBAM ′BCM ′AB M ′0-M BBAM ′BCM ′)(B BA BAM M −⋅=′μ)(B BC BCM M −⋅=′μ+=最后杆端弯矩:M BA =M F BA +BAM ′M BC =M F BC +BCM ′M AB =M F AB +AB M ′然后各跨分别叠加简支梁的弯矩图,即得最后弯矩图。
固端弯矩带本身符号单结点的力矩分配分配系数分配弯矩10例1. 用力矩分配法作图示连续梁的弯矩图。
3m 3m 6m EI EI 200kN 20kN/m (1)固定B 结点A BC 200kN 20kN/m M F AB =M F BA =M F BC=mkN ⋅−=×−15086200m kN ⋅150m kN ⋅−=×−9086202M B =M F BA + M F BC =m kN ⋅60-150150-90(2)放松结点B,即加-60进行分配60A B C-60设i =EI/l 计算转动刚度:S BA =4iS BC =3i分配系数:571.0344=+=i i iBAμ429.073==iiBCμ0.5710.429分配力矩:3.34)60(571.0−=−×=′BAM 7.25)60(429.0−=−×=′BCM -34.3-25.7-17.2+(3) 最后结果。
力矩分配法ppt课件

Z1 MA'
D
A
Z1
Z1
C Aj
M jA M Aj
B
M BA 2iAB Z1 MCA 0 M DA iADZ1
M BA M AB
CAB
1 2
M CA M AC
C AC
0
M DA M AC
C
AC
1
MAC
MA' A
MAD
在等截面杆件中,弯矩传递系数 C 随远端的MAB支承情况而 不同。三种基本等截面直杆的传递系数如下:
一、单结点连续梁的力矩分配法
⑶放松刚臂,计算刚臂转动
A
Z1时结点的反力矩R11。
3m
M B A 4iZ1 SBAZ1
M B C 3iZ1 SBCZ1 R11 M B A M B C 0
A
基本体系
R11 (M B A M B C ) (SBA SBC )Z1
17
第7章 力 矩 分 配 法
§7.2 力 矩 分 配 法 的 基 本 原 理
⑵计算固端弯矩
20kN/m
100kN
M
F AB
ql 2
12
30 42
12
60.0kN m
A EI=1 B EI=2
92.6
C EI=1 D
M
F BA
60.0kN
m
M
F BC
Fl 8
1008 8
远端固定
C Aj
1 2
远端滑动 C Aj 1
远端铰支 CAj 0
7
第7章
力矩分配法
16力矩分配法讲解

第十六章 力矩分配法\力矩分配法的基本原理
为了区别由其他运算得到的杆端弯矩值,把由式(d)算 得的杆端弯矩以M表示,称为分配弯矩。即
M ij ij M i
利用上式计算各杆近端分配弯矩的过程,又称为力矩分配。
目录
第十六章 力矩分配法\力矩分配法的基本原理 3.传递系数和传递弯矩
等直杆ij,当i端转动时,杆ij变形,从而使远端j也产生一定
S
(1)
M1
ij
S ij ——汇交于结点1的各杆1端转动刚度之和。 式中: (1)
目录
第十六章 力矩分配法\力矩分配法的基本原理
将Z1代入式(a),得
S12 S12 M 12 M1 ( R1F ) Sij Sij (1) (1) S13 S13 M 13 M1 ( R1F ) Sij Sij (1) (1) S14 S14 M 14 M1 ( R1F ) Sij Sij (1) (1)
约束时的转动刚度。
SAB=4i A
SAB=3i A B
B
1
SAB=i A B SAB=0 A
1
B
1
(f) 目录
第十六章 力矩分配法\力矩分配法的基本原理
由结点1的平衡条件(图e),有
M + M +M = M
12 13 14
1
或 S Z +S Z +S Z = M
12 1 13 1 14 1 1
故
Z1
16.1 力矩分配法的基本原理
16.2 多结点的力矩分配法 16.3 多层多跨刚架的近似计算
返回
第十六章 力矩分配法
第十六章 力矩分配法
【学习要求】
力法位移法。力矩分配法常见问题

力法位移法。
力矩分配法常见问题建筑力学常见问题解答6 超静定结构內力计算1.什么是超静定结构?它和静定结构有何区别?答:单靠静力平衡条件不能确定全部反力和內力的结构为超静定结构。
从几何组成的角度看,静定结构是没有多余约束的几何不变体系。
若去掉其中任何一个约束,静定结构即成为几何可变体系。
也就是说,静定结构的任何一个约束,对维持其几何不变性都是必要的,称为必要约束。
对于超静定结构,若去掉其中一个甚至多个约束后,结构仍可能是几何不变的。
2.什么是超静定结构的超静定次数?答:超静定结构多余约束的数目,或者多余约束力的数目,称为结构的超静定次数。
73.超静定结构的基本结构是否必须是静定结构?答:超静定结构的基本结构必须是静定结构。
4.如何确定超静定结构的超静定次数?答:确定结构超静定次数的方法是:去掉超静定结构的多余约束,使之变为静定结构,则去掉多余约束的个数,即为结构的超静定次数。
5.撤除多余约束的方法有哪几种?答:撤除多余约束常用方法如下:(1)去掉一根支座链杆或切断一根链杆,等于去掉一个约束。
(2)去掉一个固定铰支座或拆去一个单铰,等于去掉两个约束。
(3)去掉一个固定端支座或把刚性连接切开,等于去掉三个约束。
76.用力法计算超静定结构的基本思路是什么?答:用力法计算超静定结构的基本思路是:去掉超静定结构的多于约束,代之以多余未知力,形成静定的基本结构;取多余未知力作为基本未知量,通过基本结构的位移谐调条件建立力法方程,利用这一变形条件求解多余约束力;将已知外荷载和多余约束力所引起的基本结构的内力叠加,即为原超静定结构在荷载作用下产生的内力。
7.什么是力法的基本结构和基本未知量?答:力法的基本结构是:超静定结构去掉多余约束后得到的静定结构。
力法的基本未知量是对应于多余约束的约束反力。
8.简述n次超静定结构的力法方程,及求原结构的全部反力和內力的方法。
答:(1)n次超静定结构的力法方程对于n次超静定结构,撤去n个多余约束后77可得到静定的基本结构,在去掉的n 个多余约束处代以相应的多余未知力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
16.3位移法的应用
利用位移法求解超静定结构的一般步骤如下: (1)确定基本未知量。 (2)将结构拆成超静定或个别静定的单杆。 (3)查表16-1,列出各杆端转角位移方程。 (4)根据平衡条件建立平衡方程(一般对有转 角位移的刚结点取力矩平衡方程,有结点线位移 时,则考虑线位移方向的静力平衡方程)。 (5)解出未知量,求出杆端内力。 (6)作出内力图。
1 4i B 3i B ql 2 0 16
1 i B ql 2 112
(负号说明
B 逆时针转)
(5) 代回转角位移方程,求出各杆的杆端弯矩: 3 2 23 2 M AB 2i B ql ql 16 112 3 2 17 2 M BA 4i B ql ql 16 112 1 2 17 2 M BC 3i B ql ql 8 112 M CB 0 (6)根据杆端弯矩求出杆端剪力, (7)并作出弯矩图、剪力图。
(1). 转动刚度 杆件固定端转动单位角位移所引起的力矩称 为该杆的转动刚度(转动刚度也可定义为使杆件 固定端转动单位角位移所需施加的力矩),记作S。 等截面直杆的转动刚度与远端约束及线刚度 有关: 远端固定: S=4i 远端铰支: S=3i 远端双滑动支座: S=i 远端自由: S=0(i为线刚度)
(5)依次对各结点循环进行分配、传递计算, 当误差在允许范围内时,终止计算,然后将各杆 端的固端弯矩、分配弯矩与传递弯矩进行代数相 加,得出最后的杆端弯矩;
(6)根据最终杆端弯矩值及位移法下的弯矩正 负号规定,用叠加法绘制弯矩图。
【例16-2 】用力矩分配法求图(a)所示两跨连续梁 的弯矩图。 【解】: 该梁只有一个刚节点B。 1. 查表求出各杆端的固端弯矩 Fl 120 4 F M AB 60 kN m 8 8
刚节点B将产生一个转角位移 固端弯矩( MF ):是被约束隔离各杆件在荷载单独 作用下引起的杆端弯矩。
M M
F B
F B
F BA
M
F BC
M
F BD
一般地 M 不等于零,称为节点不平衡力矩。
现放松转动约束,即去掉刚臂, 这个状态称为放松状态 节点B将产生角位移,并在各杆端(包括近端 和远端)引起杆端弯矩,记作 M 则固端弯矩与位移弯矩的代数和就是最终杆端弯矩。
解得的未知量代回杆近端位移弯矩的表达式, 得到:
将未知量代回杆近端分配弯矩的表达式,得到:
S BA F S BA M BA ( M B ) SB
上式中括号前的系数称为分配系数,记作μ ,即: S BA S BC S BD BA BC BD SB SB SB 一个杆件的杆端分配系数等于自身杆端转动刚度 除以杆端节点所连各杆的杆端转动刚度之和。 各结点分配系数之和等于1
16.2位移法的原理
将刚架拆为两个单杆。AB杆B端为固定支座, A端为刚节点,视为固定支座。 AC杆C端为固定铰支座, A端为刚节点,视为固定支座。
写出各杆的杆端弯矩表达式(注意到AC杆既有荷 载,又有节点角位移,故应叠加)
。
M BA 2i A M AB 4i A M AC M CA 3 3i A Fl 16 0
16.1位移法的基本概念
16.1.1 位移法基本变形假设
位移法的计算对象是由等截面直杆组成的杆系 结构,例如刚架、连续梁。在计算中认为结构仍然 符合小变形假定。同时位移法假设: (1)各杆端之间的轴向长度在变形后保持不变; (2)刚性结点所连各杆端的截面转角是相同的。
16.1.2 位移法基本未知量
再把iθA代回各杆端弯矩式得到:
位移法的基本思路就:选取结点位移为基本 未知量,把每段杆件视为独立的单跨超静定梁, 然后根据其位移以及荷载写出各杆端弯矩的表达 式,再利用静力平衡条件求解出位移未知量,进 而求解出各杆端弯矩。该方法称为位移法。 力法则以多余未知力为基本未知量,故名为力法。 在建立方程的时候,位移法是根据静力平衡条件 来建立,而力法则是根据位移几何条件来建立, 这是两个方法的相互对应之处。
第16章 位移法及力矩分配法
第16章 位移法及力矩分配法
16.1 位移法的基本概念 16.2 位移法的原理 16.3 位移法的应用 16.4 力矩分配法的基本概念 16.5 用力矩分配法计算连续梁 和无侧移刚 架
学习目标
• 通过本章的学习,熟悉位移 法的基本概念、力矩分配法 的概念;掌握位移法的原理, 能进行位移法的应用; 能够用力矩分配法计算连续梁 和无侧移刚架。
弯矩图
剪力图
16.4力矩分配法的基本概念
力矩分配法是在位移法基础上发展起来的一 种数值解法,它不必计算结点位移,也无须求解 联立方程,可以直接通过代数运算得到杆端弯矩。 计算时,逐个结点依次进行,和力法、位移法相 比。力矩分配法的适用对象是连续梁和无结点线 位移刚架。在力矩分配法中,内力正负号的规定 同位移法的规定一致。 杆端弯矩使杆端顺时针转向为正, 固端剪力使杆端顺时针转向为正。
近端杆端分配弯矩可通过固端弯矩按比例分配得到, 而远端传递弯矩则可通过近端位移弯矩得到。 设: M BA CM C M BA AB
M AB
式中C称为传递系数, 它只与远端约束有关。 远端为固定支座:
远端为铰支座:
1 C= 2 C =0
远端为双滑动支座: C = -1 远端为自由: C =0
S BC F S BC M BC ( M B ) SB S BD F S BD M BD ( M B ) SB
BA BC BD 1
由此可知,一个节点所连各杆的近端杆端分配 弯矩总和在数值上等于节点不平衡力矩,但符 号相反,即:
S BA M BA
S BC M BC
S BD M BD
由B节点的力矩平衡条件 ΣM = 0得:
M BA M BC M BD 0
S BA M S BC M
F BA
F BC
S BD M
F BD
0
解得未知量θ为:
F F F F (M BC M BC M BC ) ( M B ) S BA S BC S BD SB
M M BC M BC
F BC
3i M
F BC
S BC M
F BC
M BD
F F F M BD M BD i M BD S BD M BD
式中:
F M BA
ql 2 12
M
F BC
3Fl 16
M
F BD
0
显然,杆的近端位移弯矩为:
•(3)位移法的杆端内力主要是剪力和弯矩, 位移法下的单杆都是超静定梁,所以不仅荷载 会引起杆端内力,杆端支座位移也会引起内力, 这些杆端内力可通过查表16-1获得。 • 荷载引起的弯矩称为固端弯矩,由荷载引 起的剪力称为固端剪力。固端剪力使杆端顺时 针转向为正,逆时针转向为负(对于结点也是 如此),表中的i称为线刚度,即i=EI/L,式 中EI——杆件的抗弯刚度 L——杆长。
独立节点线 位移数为1
独立节点线 位移数为2
16.1.3 位移法的杆端内力
•(1)运用位移法计算超静定结构时,需要将结 构拆成单杆,单杆的杆端约束视结点而定,刚结点 视为固定支座,铰结点视为固定铰支座。当讨论杆 件的弯矩与剪力时可不予考虑,从而铰支座可进一 步简化为垂直于杆轴线的可动铰支座。结合边界支 座的形式,位移法的单杆超静定梁有三种形式,如 图16-4所示。
。
•= (2)位移法规定杆端弯矩使杆端顺时针转向 为正,逆时针转向为负(对于结点就变成逆时 针转向为正),如图16-5所示。这和前面梁的 内力计算中规定梁弯矩下侧受拉为正是不一样 的,因为对于整体结构来说,杆件不仅仅有水 平杆件,还有竖向、斜向杆件。对于剪力、轴 力的正负规定,则和前面的规定保持一致。
M BC M BD M BA S BC S BA S BD F F F ( M B ) ( M B ) ( M B ) SB SB SB
F ( M B )
而各杆的近端分配弯矩是将不平衡力矩变号后 按比例分配得到的。
(3)远端传递弯矩的计算及传递系数
1 3 M AB 2i B Fl 2i B ql 2 8 16 1 3 2 M BA 4i B Fl 4i B ql 8 16 1 M BC 3i B ql 2 8 M CB 0
(4) 考虑刚节点B的力矩平衡,
M
B
0
M BA M BC 0
以上各杆端弯矩表达式中均含有未知量θA, 所以又称为转角位 M AC 0
3 i A Fl 112
把上面的表达式代入:
3 4i A 3i A Fl 0 16
M BA M AB M AC M AC 3 Fl 56 6 Fl 56 6 Fl 56 0
力法的基本未知量是未知力,位移法的基 本未知量是结点位移。 结点是指计算结点,即结构各杆件的联结 点。结点位移分为结点角位移和结点线位移两 种。 结点分为刚结点和铰结点,特点:铰结点 对各杆端截面的相对角位移无约束作用,只有 刚结点处才有作为未知量的角位移。每一个独 立刚结点就有一个转角位移,则整个结构的独 立刚结点数就是角位移数。
•【例16-1】 用位移法画图(a)所示连续梁的 弯矩图。已知F=3ql/2,各杆刚度EI为常数。
【解】:(1)确定基本未知量。此连续梁只有一 个刚结点θ ,转角位移个数为1,记作θ ,整个 梁无线位移,因此,基本未知量只有B结点角位移 θ 。 (2)将连续梁拆成两个单杆梁。
(3) 写出转角位移方程(两杆的线刚度相等):
(2)近端位移弯矩的计算及分配系数 AB杆:远端为固定支座,转动刚度SBA = 4i BC杆:远端为铰支座,转动刚度SBC = 3i BD杆:远端为双滑动支座,转动刚度SBD = i
