信号与系统徐天成第四版第1章
信号与系统第一章信号与系统讲课文档

第18页,共94页。
f (t)
2
1 4
-4-3 -2-10 1 2 3
t
Байду номын сангаас
-1
-2
f (t) 2 1 -4-3 -2-10 1 2 3 4 t
(a)
确定信号
(b)
随机信号
School of Physics Science and Technology
f(t)
离散点的间隔Tk=tk+1-tk可以相等也可不等。
2
通常取等间隔T,离散信号可表示为f(kT),简 1
2 1
写为f(k),这种等间隔的离散信号也常称为序
列。其中k称为序号。
t-1 o t1 t2 t3 t4
t
-1 .5
School of Physics Science and Technology
信号与系统第一章信号与系统
第1页,共94页。
参考书目:
1.《信号与系统》(上、下),郑君里等编著,高等 教育出版社;
2.《信号与线性系统》(上、下),管致中等编著,高等教育出版
社;
3.《信号与系统》(英文第二版),A. V.Oppenheim等著,刘树
堂译,西安交大出版社;
4.《信号与系统-理论、方法与应用》,徐守时编著,中国科技大学
School of Physics Science and Technology
第24页,共94页。
❖ 如果若干周期信号的周期具有公倍数, 则它们叠加后仍为周期信号, 叠加信号的周 期是所有周期的最小公倍数; 其频率为周期的倒数。 只有两项叠加时, T1、 T2与ω1、ω2分别是两个周期信号的周期与角频率, 叠加后信号的角频率、 周期的
信号与线性系统(第四版)

信号与线性系统(第四版)第一章:信号与系统概述1.1 信号的分类与特性1. 按照幅度是否连续:连续信号和离散信号2. 按照时间是否连续:连续时间信号和离散时间信号3. 按照周期性:周期信号和非周期信号4. 按照能量与功率:能量信号和功率信号连续信号:在任意时间点上都有确定值的信号,如正弦波、矩形波等。
离散信号:在离散时间点上才有确定值的信号,如采样信号、数字信号等。
连续时间信号:时间轴上连续变化的信号,如语音信号、图像信号等。
离散时间信号:时间轴上离散变化的信号,如数字音频、数字图像等。
周期信号:在一定时间间隔内重复出现的信号,如正弦波、方波等。
非周期信号:不具有周期性的信号,如爆炸声、随机信号等。
能量信号:信号的能量有限,如脉冲信号。
功率信号:信号的功率有限,如正弦波、方波等。
1.2 系统的定义与分类1. 按照输入输出关系:线性系统和非线性系统2. 按照时间特性:时变系统和时不变系统3. 按照因果特性:因果系统和非因果系统4. 按照稳定性:稳定系统和不稳定系统线性系统:满足叠加原理和齐次性原理的系统。
即输入信号的线性组合,输出信号也是相应输出的线性组合。
非线性系统:不满足线性系统条件的系统,如饱和非线性、幂次非线性等。
时变系统:系统的特性随时间变化而变化,如放大器的增益随时间衰减。
时不变系统:系统的特性不随时间变化,如理想滤波器、积分器等。
因果系统:当前输出仅取决于当前及过去的输入,与未来的输入无关。
非因果系统:当前输出与未来输入有关,如预测滤波器等。
稳定系统:对于有界输入,输出也有界;或者输入趋于零时,输出也趋于零。
不稳定系统:对于有界输入,输出无界;或者输入趋于零时,输出不趋于零。
第二章:线性时不变系统2.1 线性时不变系统的基本性质2.1.1 叠加性LTI系统对多个输入信号的叠加响应,等于这些输入信号单独作用于系统时的响应之和。
这意味着系统可以处理多个信号而不会相互干扰。
2.1.2 齐次性如果输入信号放大或缩小一个常数倍,那么系统的输出也会相应地放大或缩小同样的倍数。
信号与系统徐天成

5
第1章 引言
例如:由一个电阻器和一个电容器可以组成微分电路(高 通滤波器)或积分电路(低通滤波器)。 微分器: 微分器: C
vi(t)
积分器: 积分器:
R C vo(t)
R
vo(t)
vi(t)
一般通信系统的组成可用如下框图来表示: 一般通信系统的组成可用如下框图来表示:
6
第1章 引言
对于一般系统可用下图所示的方框图表示。
3
第1章 引言
信号:一种物理量(电、光、声)的变化。 消息:待传送的一种以收发双方事先约定的方式组成消息(语言、文字、图像、数据)相对应
的变化的电流或电压,或电容上的电荷、电感中 的磁通等。
信息:所接收到的未知内容的消息,即传输的信号是带有
信息的。
2
参考教材
1、信号与系统(第二版)上、下册 、信号与系统(第二版) 郑君里 应启珩 杨为理 高等教育出版社 2、Signals & Systems (Second edition) 、 Alanv.Oppenheim Alans.Willsky 清华大学出版社 3、信号与系统重点、难点解析及习题、模拟题精解 、信号与系统重点、难点解析及习题、 徐天成编 哈尔滨工程大学出版社
教材:徐天成,谷亚林, 教材:徐天成,谷亚林,钱玲 信号与系统 电子工业出版社
1
《信号与系统》课程简介 信号与系统》
1、课程地位 、 《信号与系统》课程是各高等院校电子信息工程及通 信号与系统》 信工程等专业的一门重要的基础课程和主干课程。 信工程等专业的一门重要的基础课程和主干课程。该课程 也是通信与信息系统以及信号与信息处理等专业研究生入 学考试的必考课程。 学考试的必考课程。 2、主要研究的内容及课时安排 、 该课程主要讨论确定性信号和线性时不变系统的基本 概念与基本理论、信号的频谱分析, 概念与基本理论、信号的频谱分析,以及研究确定性信号 经线性时不变系统传输与处理的基本分析方法。 经线性时不变系统传输与处理的基本分析方法。从连续到 离散、从时域到变换域、从输入输出分析到状态变量分析, 离散、从时域到变换域、从输入输出分析到状态变量分析, 共八章。 共八章。 课时分配: 学时 学时( 学时理论课 学时实验) 学时理论课+8学时实验 课时分配:72学时(64学时理论课 学时实验)
《信号与系统(第四版)》习题详解图文

故f(t)与{c0, c1, …, cN}一一对应。
7
3.3 设
第3章 连续信号与系统的频域分析
试问函数组{ξ1(t),ξ2(t),ξ3(t),ξ4(t)}在(0,4)区间上是否 为正交函数组,是否为归一化正交函数组,是否为完备正交函 数组,并用它们的线性组合精确地表示题图 3.2 所示函数f(t)。
题图 3.10
51
第3章 连续信号与系统的频域分析 52
第3章 连续信号与系统的频域分析 53
第3章 连续信号与系统的频域分析 54
第3章 连续信号与系统的频域分析 55
第3章 连续信号与系统的频域分析 56
第3章 连续信号与系统的频域分析 57
第3章 连续信号与系统的频域分析
题解图 3.19-1
8
第3章 连续信号与系统的频域分析
题图 3.2
9
第3章 连续信号与系统的频域分析
解 据ξi(t)的定义式可知ξ1(t)、ξ2(t)、ξ3(t)、ξ4(t)的波形如题 解图3.3-1所示。
题解图 3.3-1
10
不难得到:
第3章 连续信号与系统的频域分析
可知在(0,4)区间ξi(t)为归一化正交函数集,从而有
激励信号为f(t)。试证明系统的响应y(t)=-f(t)。
69
证 因为
第3章 连续信号与系统的频域分析
所以
即
70
系统函数
第3章 连续信号与系统的频域分析
故
因此
71
第3章 连续信号与系统的频域分析
3.23 设f(t)的傅里叶变换为F(jω),且 试在K≥ωm条件下化简下式:
72
第3章 连续信号与系统的频域分析 73
107
第1章信号与系统

➢ 信号在系统中按一定规律运动、变化,系统在输入 信号的驱动下对它进行“加工”、“处理”并发送 输出信号。
小结1
第一章 信号与系统基本概念
1.2 信号的描述与分类
信号的描述
信号是信息的一种物理体现。它一般是随时间或位置变化 的物理量。 信号按物理属性分:电信号和非电信号。电信号易产生, 易处理,便于控制。本课程讨论电信号-简称“信号”。
数字信号:时间和幅值均为离散的信号。
第一章 信号与系统基本概念
1.2 信号的描述与分类
一 连续时间信号和离散时间信号
上述离散信号可简画为 用表达式可写为 1 ,
f(k)
2,
2
2
1
1
1 .5,
f
(k )
2,
-1 o 1 2 3 4 k
0,
1,
-1 .5
或写为
0,
k 1 k0 k 1 k2 k3 k4 其他 k
描述信号的常用方法(1)表示为时间的函数 (2)信号的图形表示--波形
“信号”与“函数”两词常相互通用。
以 单边指数信号 为例
f
t
0 e-t
t 0 t 0
函数表达 式f(t)
f(t)
1
0
波形
t
第一章 信号与系统基本概念
1.2 信号的描述与分类
信号的分类
信号
根据定义域的特点
连续时间信号(时间变量t连续,又称模拟信号)
这里的“连续”指函数的定义域—时间是连续 的,但可含间断点,至于值域可连续也可不连续。
值域连 续
f1(t) =sin(πt)
1
o1 -1
2t
f2(t) 1
o1 2 t -1
信号与线性系统(第四版)

信息源
发送 设备
信道
接收 设备
信宿
发送端 消息 信号
噪声源 信号
接收端 消息
3. 尺度变换(横坐标展缩)
• 将f (t) → f (a t) , 称为对信号f (t)的尺度变换。 • 若a >1 ,则波形沿横坐标压缩;若0< a < 1 ,则展 开。如
也可以先压缩、再平移、最后反转。
1.4 阶跃函数和冲激函数
• 阶跃函数和冲激函数不同于普通函数,称为奇异函 数。研究奇异函数的性质要用到广义函数ห้องสมุดไป่ตู้或分配 函数)的理论。 • 这节课首先直观地引出阶跃函数和冲激函数。 • 一、阶跃函数 • 下面采用求函数序列极限 的方法定义阶跃函数。 • 选定一个函数序列γ n(t)如图所示。
对于离散信号,由于f (a k) 仅在为a k 为整数时才有意 义, 进行尺度变换时可能会使部分信号丢失。因此一 般不作波形的尺度变换。
• 信号的尺度变换在实际生活中的例子 见p10
平移、反转、尺度变换相结合
• 三种运算的次序可任意。但一定要注意始终对 时间t 进行。 • 例:已知f (t),画出f (– 4 – 2t)。
•例1 判断下列信号是否为周期信号,若是,确定其周 期。 •(1)f1(t) = sin2t + cos3t (2)f2(t) = cos2t + sinπ t • 解:两个周期信号x(t),y(t)的周期分别为T1和T2, 若其周期之比T1/T2为有理数,则其和信号x(t)+y(t)仍 然是周期信号,其周期为T1和T2的最小公倍数。 • (1)sin2t是周期信号,其角频率和周期分别为 • ω 1= 2 rad/s , T1= 2π / ω 1= π s • cos3t是周期信号,其角频率和周期分别为 • ω 2= 3 rad/s , T2= 2π / ω 2= (2π /3) s • 由于T1/T2= 3/2为有理数,故f1(t)为周期信号,其周 期为T1和T2的最小公倍数2π 。 • (2) cos2t 和sinπ t的周期分别为T1=π s, T2= 2 s,由于T1/T2为无理数,故f2(t)为非周期信号。
信号与系统课后习题参考答案

1.20
解:(a)
x1 (t)
=
cos( 2t )
=
1 2
(e j2t
+
e− j2t
)
则:
y1 (t)
= T{1 (e j2t 2
+ e − j2t )} =
1 (e j3t 2
+ e − j3t ) ;
(b)
x2 (t)
=
cos(2(t
−
1 )) 2
=
1 (e j(2t−1) 2
+ e − j(2t−1) )
-1/2
-1
1 1/2 -2 -1 0 1
1 1 1 x[-n+3]
1/2 n
678 2 34 5
-1/2 -1
(c) x[3n]
1 x[3n]
1/2 n
-4 -3 -2 -1 0 1 2 3 -1/2
7
(d) x[3n+1]
x[n+1]
11 1 1
1/2 1/2
1/2 n
-5 -4 -3 -2 -1 0 1 2 3
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 (-1/2)
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
-5
-4 -3 -2
精品课件-信号与系统-第1章

第 章 信号与系统的基本概念
信号与系统之间有着十分密切的联系。 离开了信号, 系统 将失去意义。 信号作为待传输消息的表现形式, 可以看做运载 消息的工具, 而系统则是为传送信号或对信号进行加工处理而 构成的某种组合。 研究系统所关心的问题是, 对于给定信号形 式与传输、 处理的要求, 系统能否与其相匹配, 它应具有怎 样的功能和特性。
第 章 信号与系统的基本概念
图1.1 电路中电容两端的电压变化
第 章 信号与系统的基本概念
如果我们只能得到某些采样点的值, 则信号便不是连续曲 线了, 自变量也不是在时间上连续的, 而是一个个离散的点, 通常用x[n]表示, n=…-3, -2, -1, 0, 1, 2, 3, …。 x[n]可以表示自变量本来就是离散的现象, 例如有关人口统 计学中的一些数据、 股票市场的指数等。 图1.2给出了近94年 的道琼斯工业平均(Doe Jones Industrial Average)指数值。 也有一些离散信号是由本来连续的时间信号经过采样而得到的, 这时离散信号x[n]则代表了一个自变量是连续变化的连续时间 信号在一系列离散时刻点上的样本值。
第 章 信号与系统的基本概念
随着信号传输、 信号交换理论与应用的发展, 出现了所 谓“信号处理”的新课题。 信号处理可以理解为对信号进行 某种加工或变换。 信号处理的应用已遍及许多科学技术领域, 例如, 从月球探测器发来的信号可能被淹没在噪声之中, 但 是, 利用信号处理技术进行增强, 就可以在地球上得到清晰 的月球图像。 石油勘探、 地震测量以及核试验监测仪所得数 据的分析都依赖于信号处理技术的应用。 此外, 在心电图、 脑电图分析, 语音识别与合成, 图像数据压缩以及经济形势 预测(如股票市场分析)等各种领域中都广泛采用了信号处理技 术。
信号与系统第四版第1章

时不变系统与时变系统
时不变系统:系统的元件参数不随时间变化; 时不变性:
或系统的方程为常系数。 否则为时变系统。
若f(t)y(t)
则 f ( t t0 ) y ( t t0 ) 见下图。
图1 时不变特性示意图
线性时不变系统(LTI): 系统既是线性的,又是时不变的; 或系统的方程为线性常系数微分方程。
•
时域分析:波形参数、波形变化、重复周期、
时域分解与合成等。 频域分析:频率结构、频带宽度、能量分布、 信息的变化等。 信号测量:模拟式仪器、数字式仪器。
•
•
end
1.4 基本信号和信号处理
基本信号:
图1
信号处理:
信号的相加与相乘
图2
信号的压缩与扩展
图3
信号的反折与平移
图4Байду номын сангаас
信号的综合处理
图3
光纤
图4
人体断层扫描图像
图5
空间技术
图6
end
我国载人航天工程
1.3 信号的概念
信号(signal): 物质的运动形式或状态的变化。 (声、光、电、力、振动、流量、温度… … )
• •
消息(message):声音、文字、图像、符号… … 信息(information):消息中的新内容、新知识。
图1 一些实际信号
图2 气象信号与天体星云
图3 银河外星系M81(2003年12月)
信号分类: • 确定性信号与随机信号
• 周期信号与非周期信号 • 连续信号与离散信号 • 因果信号与非因果信号
图4 确定性信号与随机信号
信号与系统基础知识完整版

信号与系统基础知识 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第1章 信号与系统的基本概念引言系统是一个广泛使用的概念,指由多个元件组成的相互作用、相互依存的整体。
我们学习过“电路分析原理”的课程,电路是典型的系统,由电阻、电容、电感和电源等元件组成。
我们还熟悉汽车在路面运动的过程,汽车、路面、空气组成一个力学系统。
更为复杂一些的系统如电力系统,它包括若干发电厂、变电站、输电网和电力用户等,大的电网可以跨越数千公里。
我们在观察、分析和描述一个系统时,总要借助于对系统中一些元件状态的观测和分析。
例如,在分析一个电路时,会计算或测量电路中一些位置的电压和电流随时间的变化;在分析一个汽车的运动时,会计算或观测驱动力、阻力、位置、速度和加速度等状态变量随时间的变化。
系统状态变量随时间变化的关系称为信号,包含了系统变化的信息。
很多实际系统的状态变量是非电的,我们经常使用各种各样的传感器,把非电的状态变量转换为电的变量,得到便于测量的电信号。
隐去不同信号所代表的具体物理意义,信号就可以抽象为函数,即变量随时间变化的关系。
信号用函数表示,可以是数学表达式,或是波形,或是数据列表。
在本课程中,信号和函数的表述经常不加区分。
信号和系统分析的最基本的任务是获得信号的特点和系统的特性。
系统的分析和描述借助于建立系统输入信号和输出信号之间关系,因此信号分析和系统分析是密切相关的。
系统的特性千变万化,其中最重要的区别是线性和非线性、时不变和时变。
这些区别导致分析方法的重要差别。
本课程的内容限于线性时不变系统。
我们最熟悉的信号和系统分析方法是时域分析,即分析信号随时间变化的波形。
例如,对于一个电压测量系统,要判断测量的准确度,可以直接分析比较被测的电压波形)(in t v (测量系统输入信号)和测量得到的波形)(out t v (测量系统输出信号),观察它们之间的相似程度。
信号与线性系统分析第四版(吴大正)习题答案
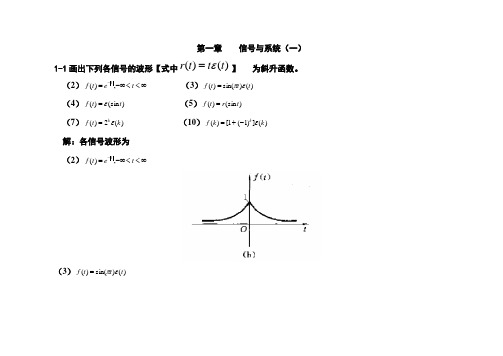
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】 为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))tf=r(sin)(t(7))tf kε(k=(2)(10))f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与系统第一至三章讲义

By yljy52725一、绪论1、明确信号、系统1)信号:信息的载体,实际通过信号进行信息的传递,常见于电类和非电类2)系统:信号的产生及传输、处理需要一定的物理装置,该装置即为系统(若干个相互关联的整体)2、信号处理:对信号进行某种变换或加工,其目的是消除信号中多余内容、滤除噪声干扰、使得信号便于研究其特性及还原。
3、信号传输:1)通信的目的为了信号的传输;2)信号的传输方式:声、光、电(弱电、电磁波);4、信号的表示:时间函数、信号波形;*区别连续信号(函数的自变量取值连续,信号的值域可以不连续)和离散信号(信号的自变量取值离散)的概念(通常自变量只为时间t),并且对于连续信号和离散信号会用数学方式表示(连续函数、不同取值点的函数)5、区别模拟信号(时间、幅值均连续)、抽样信号(时间离散、幅值连续)、数字信号(时间、幅值均离散)(理解模拟信号数字化的过程 抽样、量化、编码)6、区别周期信号和非周期信号(会求周期余弦信号的周期T=2pi/w)*周期信号的表示:1)连续型:f(t)=f(t+mT), m=0,+-1,+-2,…2)离散型:f(k)=f(k+mN),m=0,+-1,+-2…7、能量信号、功率信号(连续<t>、离散<k>)1)能量信号的能量有限,功率为0;2)功率信号的功率有限,能量无穷。
*并非所有信号都是功率信号或能量信号8、了解信号有左边信号、右边信号;因果信号、非因果信号*9、典型的确知信号指数信号、余弦信号、复指数信号(理论模型)、抽样信号(钟形信号)Sa(t) 1)指数信号:f(t)=Ke ata = 0; 直流信号;a>0;指数增长;a<0;指数衰减通常将1/|a|作为指数信号的时间常数,记作τ2)余弦信号:f(t)=Ksin(wt+θ)振幅、周期、频率、角频率、相位(初相位θ)3)抽样信号:Sa(t)=sint/t*10、信号的基本运算1)信号之间的和、差、积(对应位置的取值进行相应的运算)2)平移、反转(针对于信号的时域变换)3)尺度变换(展缩)(针对于信号的时域变换,对于信号的幅度不作任何变化)f(t) f(at):当a>1时,信号时域压缩;当a<1时,信号扩展*一般对于离散信号而言尺度变换并不常用,由于离散信号只在时间的具体位置有意义,若对其进行尺度变换可能会会使得原始信号丢失。
信号与系统第1章

速率越慢。 指数信号的一个重要特性是其对时间的微 分和积分仍然是指数信号。 实际上, 用得较多的是单边指数信号, 其表达式为
0, f (t ) e 1 t, K t0 t0
(1.5)
第一章 信号与系统的基本概念
当a为复数时, f(t)为复指数信号, 其数学表达式为
第一章 信号与系统的基本概念
除此以外, 抽样信号还具有以下性质:
Sa (t )dt 2
0
(1.9)
Sa(t )dt
(1.10)
第一章 信号与系统的基本概念
图 1.7 抽样信号
第一章 信号与系统的基本概念
1.2.3 阶跃信号与冲激信号
1. 单位阶跃信号 单位阶跃信号ε(t)的数学表达式为
第一章 信号与系统的基本概念
第一章
信号与系统的基本概念
1.1 信号的概念与分类 1.2 基本的连续时间信号 1.3 信号的运算与变换
1.4 系统的描述与分类
1.5 线性时不变系统的基本性质 1.6 连续时不变系统分析方法综述 1.7 信号变换与运算及系统判断的 MATLAB实现
第一章 信号与系统的基本概念
描述信号的基本方法是写出它的数学表达式, 此表达式
是时间的函数, 依据函数绘出的图像称为信号的波形。 为方便讨论, 本书中将信号与函数两名词通用。 除了用 数学表达式和波形进行描述外, 随着问题的深入, 还引用 了频谱分析、 各种变换等方式来描述和研究信号。
第一章 信号与系统的基本概念
1.1.2 信号的分类
g 2 (t ) (t ) e(t ) 2 2
(1.13b)
第一章 信号与系统的基本概念
信号与系统第一章
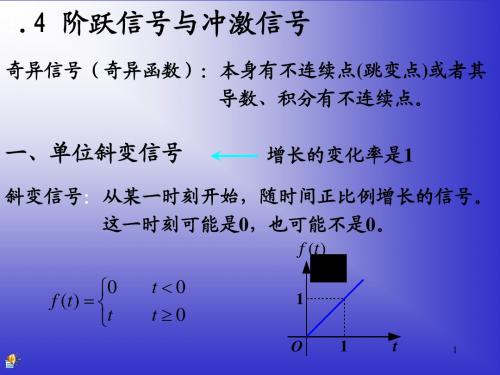
t
1
f (t )
R( t )
延迟的单位斜变信 号 f (t t 0 )
R( t t 0 )
1
1 t
0 f (t ) t
t 0 t 0
1
O
O
t t0 0 f (t t0 ) t t0 t t0 三角形脉冲可用单位斜变信号表示:
f1 (t ) f (t )
冲激强度为1
(1) t
6
o
(t )
(1) t
o
(t t0 )
延时的单位冲激信号
(1)
o
t0
t
只在 t 0 有一个“单位冲激”,在 处,信号值 t0 都为 0,单位冲激的强度为 1。若矩形脉冲面积为 A,则冲 激强度为A。 三角形脉冲、双边指数脉冲、钟形信号、抽样信号等 取极限,都可以得到冲激信号。
f 2 (t ) e t u(t ) u(t t 0 )
0
t0
t
1
sgnt
• 可用阶跃信号表示符号函数。
1 sgn(t ) 1 t 0 t 0
O
-1
t
sgn(t ) u(t ) u(t ) 2u(t ) 1
1 u (t ) [sgn( t ) 1] 2 5
0
t
同样,对于电感电路,由于
当i L (t )为阶跃信号时,v L (t )为冲激信号,说明由于冲激 电压的出现,允许电感电流在无限短时间内产生跳变。
12
四、冲激偶信号
冲激信号求导,称为冲激偶信号。是正、负极性的一 对冲激,强度均为无限大。
s( t )
1
信号与系统 第一章精品PPT课件

主要参考书
[5] 吴湘淇等. 信号、系统与信号处理(上). 第2版. 电子工业出版社,2001
[6] 吴湘淇等. 信号、系统与信号处理——软硬件实现. 电子工业出版社,2002
[7] 陈后金等. 信号与系统. 清华大学出版社, 2003 [8] 陈后金等. 信号与系统学习指导与习题精解.
Examples: Biomedical Signal Processing (生物信号处理)
The traces shown in (a), (b), and (c) are three examples of EEG signals recorded from the hippocampus of a rat. Neurobiological studies suggest that the hippocampus plays a key role in certain aspects of learning and memory.
2. 作业: 书面作业(理论)+ MATLAB上机作业(实践)。
3. 期中和期末考试:闭卷形式。主要考察学生对本门课的基本 理论基本原理及重点内容的掌握程度。
4.课程成绩的组成: 由书面作业、MATLAB作业、期中考试和期末考试4部分组成。
主要参考书
[1] Simon H.,Barry V.V. Signals and Systems. John Wiley & Sons,Inc.1999
Contents
第一章 信号与系统简介 (Introduction)
介绍信号与系统的基本概念; 信号分类及基本信号;系统分类和特性。
信号与系统入门学习教程(完整版)

狄拉克定义
狄拉克函数
(t )
(t )dt 1
0
(1) 冲激强度
(t ) 0 (t 0)
t
E (t )
33
矩形脉冲演变成冲激函数
1
2
0
2
t
1 (t ) lim u(t ) u(t ) 0 2 2
f (t0 ) (t t0 )dt f (t0 )
筛选特性
37
( 2)
(1)
f (t0 t ) (t )dt f (t0 )
(3) (t sin t ) (t )dt 0 1 6 sin(2t ) sin( 2t ) ( 4) (t )dt 2 (t )dt 2 2t t 3 5 2 3 (5) (t 1) (t ) (t ) 2 4 2
0
df (t ) u (t ) dt
29
u(t t0 )
1
0 u (t t0 ) 1
t
t t0 t t0
t0
RT(t) 1
GT(t)
-T/2 0 T/2 0 T
t
t
RT (t ) u(t ) u(t T )
T T GT (t ) u (t ) u (t ) 2 2
sin(8t )
sin(8t )
sin(t ) sin(8t )
sin(t ) sin(8t )
25
1.4 阶跃信号与冲激信号
奇异信号(也称奇异函数): 允许函数本身有不连续点(跳变点) 或其导数与积分有不连续点。 斜变信号、阶跃信号 冲激信号、冲激偶信号
信号与系统(第四版)

0
10
2负逻辑
数字信号是一种二值信号,用两个电平(高电平和低电 平)分别来表示两个逻辑值(逻辑1和逻辑0)。 有两种逻辑体制: 正逻辑体制规定:高电平为逻辑1,低电平为逻辑0。 负逻辑体制规定:低电平为逻辑1,高电平为逻辑0。
下图为采用正逻辑体制所表的示逻辑信号:
(二)、逻辑函数的表示方法
1.真值表——将输入逻辑变量的各种可能取值和相应的函数值排列 在一起而组成的表格。 2.函数表达式——由逻辑变量和“与”、“或”、“非”三种运算 符所构成的表达式。 由真值表可以转换为函数表达式。例如,由“三人表决”函数的真 值表可写出逻辑表达式:
L ABC ABC ABC ABC
1.3 逻辑函数的代数化简法
一、逻辑函数式的常见形式
一个逻辑函数的表达式不是唯一的,可以有多种形 式,并且能互相转换。例如:
其中,与—或表达式是逻辑函数的最基本表达形式。
二、逻辑函数的最简“与—或表 达式” 的标准
(1)与项最少,即表达式中“+”号最少。 (2)每个与项中的变量数最少,即表达式中 “· ”号最少。
3.用卡诺图化简逻辑函数的步骤:
(1)画出逻辑函数的卡诺图。 (2)合并相邻的最小项,即根据前述原则画圈。 (3)写出化简后的表达式。每一个圈写一个最简与项,规 则是,取值为l的变量用原变量表示,取值为0的变量用反变 量表示,将这些变量相与。然后将所有与项进行逻辑加,即 得最简与—或表达式
例
用卡诺图化简逻辑函数:
L( A, B, C) AB AC
解:
L( A, B, C) AB AC AB(C C) AC( B B)
ABC ABC ABC ABC
信号与系统 第四版 第一章 信号与系统

一阶微分方程组 -------状态方程
15
系统的分类(描述):
连续时间系统:微分方程 混合系统 离散时间系统:差分方程
即时系统(非记忆系统):代数方程 动态系统(记忆系统):微分方程或差分方程
微分方程 (t ) 集总参数系统 : 分布参数系统 : 偏微分方程 (t , x, y, z )
系统基本概念:系统模型;系统描述(分类)
系统线性(零输入、零状态响应)
系统时不变性、稳定性、因果性
系统(连续)的框图模型与微分方程模型
9
p23:
第一章作业
1.9 ; 1.10 (1) (3) (5)
1.2 (1) (5) (7) ; 1.29
?
1.32
-
4 sin d ( - 6 )d = 4sin d ( - 6 )d =
(1-2)
(1-1)与(1-2)是形式上完型可有多种不同的数学表现形式
高阶微分方程 --------------称为输入/输出方程 状态方程 ---------------适合于多输入多输出系统分析(一阶微分方程组)
例:
1.4 系统分析方法
+
u s (t )
Zk (S=s+ jw) (Z = rejq)
est
数学方法
系统模型
LT
H (S) 4
ZT
H (Z) 3
8
h (t)
h (k) H (jw) H (ejq ) <3 > (6+3)
3+2
第一章小结
信号分类:连续&离散(模拟、数字);能量、功率信号
典型连续信号(抽样信号)
信号与系统第1至8章习题参考解答

《信号与系统》第1~8章习题参考解答第一章 (2)第二章 (13)第三章 (22)第四章 (35)第五章 (48)第六章(无) (56)第七章 (57)第八章 (65)第一章1-4 对于例1-1所示信号,由f (t )求f (−3t − 2),但改变运算顺序,先求f (3t )或先求f (−t ),讨论所得结果是否与原例之结果一致。
解:(1). 例1-1的方法: f (t )→ f (t − 2)→ f (3t − 2)→ f (−3t − 2) (2). 方法二:f (t )→ f (3t )→ 2[3()]3f t − →f (−3t − 2) (3). 方法三:f (t )→f (−t ) →[(2)]f t −+ →f (−3t − 2)方法三:1-5 已知()f t ,为求0()f t at −应按下列哪种运算求得正确结果(式中0t ,a 都为正值)?(1)()f at −左移0t (2)()f at 右移0t (3)()f at 左移0t a (4)()f at −右移0ta解:(4)()f at −右移t a:故(4)运算可以得到正确结果。
注:1-4、1-5 题考察信号时域运算:1-4 题说明采用不同的运算次序可以得到一致的结果; 1-5 题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换,再进行移位变换,一定要注意移位量和移位的方向。
1-9 粗略绘出下列各函数式的波形图: (1)()(2)()t f t e u t −=− (2)2()(36)()t t f t e e u t −−=+ (3)3()(55)()t t f t e e u t −−=−(4)()cos(10)[(1)(2)]t f t e t u t u t π−=−−− 解:(1)()(2)()tf t e u t −=−(2)2()(36)()ttf t e eu t −−=+(3)3()(55)()ttf t e eu t −−=−(4)()cos(10)[(1)(2)]tf t e t u t u t π−=−−−1-12 绘出下列各时间函数的波形图,注意它们的区别:(1)[()(1)]−−;t u t u t(2)(1)�;t u t−(3)[()(1)](1)−−+−;t u t u t u t(4)(1)(1)−−;t u t(5)(1)[()(1)]−−−−;t u t u t(6)[(2)(3)]−−−;t u t u t(7)(2)[(2)(3)]t u t u t−−−−。
信号与系统第1章5

12
也就是说,去除具体系统的物理含义外,它们 都具有相同的数学模型,从而揭示了系统分析 的意义所在。 3.二阶LTI连续系统的数学模型一般表示式
5
时不变系统与时变系统 • 时不变系统:系统内元器件的参数不随时间
变化又称非时变系统或定常系统。比如由 RLC元件组成的各种电路。 • 时变系统:系统内元器件的参数随时间而变 化。又称参变系统。比如含有热敏或压敏电 阻电容元件组成的各种电路。
6
因果系统与非因果系统 • 因果系统:系统在激励信号作用之后才会产
1.5.1 系统的描述与分类
1.系统的描述
• 系统定义:是一个由若干相互关联的一类事 物组成的具有某种特定功能的有机整体。
• 电系统:是指对电信号进行产生、传输、加 工处理和储存的电路(网络)或设备(包 括软硬件设备),简称系统。
• 连续时间系统表示为:
f (•)
系统
y(•)
y(•) T f (•) 或 f (•) y(•)
a1
y (t )
a0
d2 dt 2
y(t) a1
d dt
y(t) a0 y(t) b0 f (t)
uR (t)
uL (t)
R
L
f (t)
i(t)
C
y(t)
17
2)离散系统的模拟框图表示
一阶系统的差分方程
y(k) a1 y(k 1) b0 f (k)
则有 y(k) b0 f (k) a1y(k 1)
7
1.5.2 系统的数学模型 本课主要研究给定系统在输入信号作用下,其 输出信号的变化,不涉及系统本身的设计,因 此要着重研究系统本身的特性。这种分析是建 立在系统数学模型的基础上进行的。通常是用 数学的方法或计算机仿真的方法进行求解,并 对其结果赋予实际的物理意义。 下面将介绍几种不同系统的数学模型,并说明 它对研究系统特性实际的意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
参考教材
1、信号与系统(第二版)上、下册 郑君里 应启珩 杨为理 高等教育出版社 2、Signals & Systems (Second edition) Alanv.Oppenheim Alans.Willsky 清华大学出版社
3、信号与系统重点、难点解析及习题、模拟题精解
徐天成编 哈尔滨工程大学出版社
5
第1章 引言
例如:由一个电阻器和一个电容器可以组成微分电路(高 通滤波器)或积分电路(低通滤波器)。 微分器: C
vi(t)
积分器:
R C vo ( t )
R
vo ( t )
vi(t)
一般通信系统的组成可用如下框图来表示:
6
第1章 引言
对于一般系统可用下图所示的方框图表示。
输出y(t)与输入x(t)可表示成:
y(t) = T[x(t)]
7
教材:徐天成,谷亚林,钱玲 电子工业出版社 第四版
ISBN:978-7-121-17341-7
主讲:郗 涛
Email:xitao@
1
《信号与系统》课程简介
1、课程地位 《信号与系统》课程是各高等院校测控专业、电子信 息工程及通信工程等专业的一门重要的基础课程和主干课 程。该课程也是通信与信息系统以及信号与信息处理等专 业研究生入学考试的必考课程。 2、主要研究的内容及课时安排 该课程主要讨论确定性信号和线性时不变系统的基本 概念与基本理论、信号的频谱分析,以及研究确定性信号 经线性时不变系统传输与处理的基本分析方法。从连续到 离散、从时域到变换域、从输入输出分析到状态变量分析, 共八章。 课时分配:45学时(39学时理论课+6学时实验)
3
第1章 引言
消息:待传送的一种可以收发的符号,表达知识状态的改变。 信息:所接收到的有意义内容的消息。 信号:信息的载体,表现为一种物理量的变化。
(电、光、声)信号
电信号:与上述消息(语言、文字、图像、数据)相对应
的变化的电流或电压,或电容上的电荷、电感中 的磁通等。
4
第1章 引言
系统:一组相互有联系的事物并具有特定功能的整体。
