中考数学复习轨迹和作图2[人教版]
2020届中考数学总复习(23)尺规作图-精练精析(2)及答案解析

图形的性质——尺规作图2一.选择题(共9小题)1.用直尺和圆规作一个角等于已知角,如图,能得出的依据是()A.边边边B.边角边C.角边角D.角角边2.下列作图语句正确的是()A.延长线段AB到C,使AB=BC B.延长射线ABC.过点A作AB∥CD∥EF D.作∠AOB的平分线OC3.下列语句()正确.A.射线比直线短一半B.延长AB到CC.两点间的线叫做线段D.经过三点A,B,C不一定能画出直线来4.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP 并延长交BC于点D,则下列说法中正确的个数是()①AD是∠BAC的平分线②∠ADC=60°③点D在AB的垂直平分线上④AB=2AC.A.1 B.2 C.3 D.45.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据图形全等的知识,说明画出∠A′O′B′=∠AOB的依据是()A.SSS B.SAS C.ASA D.AAS6.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y+1),则y关于x的函数关系为()A.y=x B.y=﹣2x﹣1 C.y=2x﹣1 D.y=1﹣2x7.如图,已知线段AB,分别以点A、点B为圆心,以大于AB的长为半径画弧,两弧交于点C和点D,作直线CD,在CD上取两点P、M,连接PA、PB、MA、MB,则下列结论一定正确的是()A.PA=MA B.MA=PE C.PE=BE D.PA=PB8.如图,已知∠AOB,按照以下步骤画图:(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.(2)分别以点M、N为圆心,大于MN的长半径画弧,两弧在∠AOB内部相交于点C.(3)作射线OC.则判断△OMC≌△ONC的依据是()A.SAS B.SSS C.ASA D.AAS9.如图,七年级(下)教材第4页给出了利用三角尺和直尺画平行线的一种方法,能说明AB∥DE的条件是()A.∠CAB=∠FDE B.∠ACB=∠DFE C.∠ABC=∠DEF D.∠BCD=∠EFG二.填空题(共6小题)10.∠AOB如图所示,请用直尺和圆规作出∠AOB的平分线(要求保留作图痕迹,不写作法)._________11.如图,点A是直线l外一点,在l上取点B、C.按下列步骤作图:分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D.则四点A、B、C、D可组成的图形是_________ .12.如图,是格点(横、纵坐标都为整数的点)三角形,请在图中画出与全等的一个格点三角形.13.在如图所示的方格纸上过点P画直线AB的平行线.14.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_________ 个.15.如图,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.三.解答题(共6小题)16.如图,△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC)(1)在图1中画1条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角度数分别是_________ 度和_________ 度;(2)在图2中画2条线段,使图中有4个等腰三角形;(3)继续按以上操作发现:在△ABC中画n条线段,则图中有_________ 个等腰三角形,其中有_________ 个黄金等腰三角形.17.如图,Rt△ABC的直角边BC=8,AC=6(1)用尺规作图作AB的垂直平分线l,垂足为D,(保留作图痕迹,不要求写作法、证明);(2)连结D、C两点,求CD的长度.18.如图①,将一张直角三角形纸片△ABC折叠,使点A与点C重合,这时DE为折痕,△CBE 为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A 在格点上,且△ABC折成的“叠加矩形”为正方形;(3)若一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是什么?19.如图,在△ABC中,AB=AC,AD⊥BC,AE∥BC.(1)作∠ADC的平分线DF,与AE交于点F;(用尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若AD=2,求DF的长.20.如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=10.(1)在BC边上求作一点E,使OE=OA;(保留作图痕迹,不写画法)(2)求出点E的坐标.21.如图,在△ABC中,BC=AC,且CD∥AB,设△ABC的外心为O.(1)用尺规作出△ABC的外接圆O.(不写作法,保留痕迹)(2)在(1)中,连接OC,并证明OC是AB的中垂线;(3)直线CD与⊙O有何位置关系,试证明你的结论.图形的性质——尺规作图2参考答案与试题解析一.选择题(共9小题)1.用直尺和圆规作一个角等于已知角,如图,能得出的依据是()A.边边边B边角边C角边角D.角角边考点:作图—基本作图;全等三角形的判定.专题:压轴题.分析:通过分析作图的步骤,发现△OCD与△O′C′D′的三条边分别对应相等,于是利用边边边,判定△OCD≌△O′C′D′,根据全等三角形对应角相等得出∠A′O′B′=∠AOB.解答:解:作图的步骤:①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;②作射线O′B′,以O′为圆心,OC长为半径画弧,交O′B′于点C′;③以C′为圆心,CD长为半径画弧,交前弧于点D′;④过点D′作射线O′A′.所以∠A′O′B′就是与∠AOB相等的角.在△O′C′D′与△OCD中,,∴△O′C′D′≌△OCD(SSS),∴∠A′O′B′=∠AOB,显然运用的判定方法是边边边.故选A.点评:此题是一道综合题,不但考查了学生对作图方法的掌握,也是对全等三角形的判定的方法的考查.2.下列作图语句正确的是()A.延长线段AB到C,使AB=BC B.延长射线ABC.过点A作AB∥CD∥EF D.作∠AOB的平分线OC考点:作图—尺规作图的定义.分析:根据基本作图的方法,逐项分析,从而得出正确的结论.解答:解:A、应为:延长线段AB到C,BC=AB,故本选项错误;B、射线本身是无限延伸的,不能延长,故本选项错误;C、过点A作只能作CD或EF的平行线,CD不一定平行于EF,故本选项错误;D、作∠AOB的平分线OC,正确.故选D.点评:此题主要考查图形中延长线、平行线、角平分线的画法,是基本题型,特别是A选项,应该是作出的等于原来的,顺序不能颠倒.3.下列语句()正确.A.射线比直线短一半B.延长AB到CC.两点间的线叫做线段D.经过三点A,B,C不一定能画出直线来考点:作图—尺规作图的定义.专题:推理填空题.分析:根据直线、射线、线段有关知识,对每个选项注意判断得出正确选项.解答:解:A、直线和射线都没有长短,所以射线比直线短一半错误,故本选项错误;B、延长AB到C,正确的说法是延长线段AB到C,故本选项错误;C、两点间的线叫做线段,不符合线段的定义,故本选项错误;D、若三点A,B,C在一条直线上,则经过三点A,B,C能画出直线来;若三点A,B,C不在一条直线上,则经过三点A,B,C不能画出直线来.所以说经过三点A,B,C不一定能画出直线来,故本选项正确.故选:D.点评:此题考查的知识点是作图﹣﹣尺规作图的定义,熟练掌握概念是解题的关键.4.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP 并延长交BC于点D,则下列说法中正确的个数是()①AD是∠BAC的平分线②∠ADC=60°③点D在AB的垂直平分线上④AB=2AC.A. 1 B.2 C.3 D.4考点:作图—基本作图.分析:根据角平分线的做法可得①正确,再根据三角形内角和定理和外角与内角的关系可得∠ADC=60°,再根据线段垂直平分线的性质逆定理可得③正确.根据直角三角形中30°角所对的直角边等于斜边的一半可得④正确.解答:解:①AD是∠BAC的平分线,说法正确;②∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD平分∠CAB,∴∠DAB=30°,∴∠ADC=30°+30°=60°,因此∠ADC=60°正确;③∵∠DAB=30°,∠B=30°,∴AD=BD,∴点D在AB的中垂线上,故③说法正确,④∵∠C=90°,∠B=30°,∴AB=2AC,故选:D.点评:此题主要考查了角平分线的做法以及垂直平分线的性质,熟练根据角平分线的性质得出∠ADC度数是解题关键.5.请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据图形全等的知识,说明画出∠A′O′B′=∠AOB的依据是()A.SSS B.SAS C.ASA D.A AS考点:作图—基本作图;全等三角形的判定.分析:根据作图过程可知O′C′=OC,O′D′=OD,C′D′=CD,所以运用的是三边对应相等,两三角形全等作为依据.解答:解:根据作图过程可知O′C′=OC,O′D′=OD,C′D′=CD,在△OCD与△O′C′D′中,∴△OCD≌△O′C′D′(SSS),∴∠A′O′B′=∠AOB.故选:A.点评:本题考查基本作图“作一个角等于已知角”的相关知识,其理论依据是三角形全等的判定“边边边”定理和全等三角形对应角相等.从作法中找已知,根据已知条件选择判定方法.6.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y+1),则y关于x的函数关系为()A.y=x B.y=﹣2x﹣1 C.y=2x﹣1 D.y=1﹣2x考点:作图—基本作图;坐标与图形性质.分析:根据角平分线的性质以及第二象限点的坐标特点,进而得出答案.解答:解:由题意可得出:P点在第二象限的角平分线上,∵点P的坐标为(2x,y+1),∴2x=﹣(y+1),∴y=﹣2x﹣1.故选:B.点评:此题主要考查了角平分线的性质以及坐标与图形的性质,得出P点位置是解题关键.7.如图,已知线段AB,分别以点A、点B为圆心,以大于AB的长为半径画弧,两弧交于点C和点D,作直线CD,在CD上取两点P、M,连接PA、PB、MA、MB,则下列结论一定正确的是()A.PA=MA B.MA=PE C.PE=BE D.P A=PB考点:作图—基本作图;线段垂直平分线的性质.分析:根据作图的过程可知PD是线段AB的垂直平分线,利用垂直平分线的性质即可得到问题的选项.解答:解:由题意可知:PD是线段AB的垂直平分线,所以PA=PB,故选D.点评:本题考查了基本作图﹣作已知线段的垂直平分线以及考查了线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离线段.8.如图,已知∠AOB,按照以下步骤画图:(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.(2)分别以点M、N为圆心,大于MN的长半径画弧,两弧在∠AOB内部相交于点C.(3)作射线OC.则判断△OMC≌△ONC的依据是()A.SAS B.SSS C.ASA D.A AS考点:作图—基本作图;全等三角形的判定.分析:根据角平分线的作图方法解答.解答:解:根据角平分线的作法可知,OM=ON,CM=CN,又∵OC是公共边,∴△OMC≌△ONC的根据是“SSS”.故选:B.点评:本题考查了全等三角形的判定,熟悉角平分线的作法,找出相等的条件是解题的关键.9.如图,七年级(下)教材第4页给出了利用三角尺和直尺画平行线的一种方法,能说明AB∥DE的条件是()A.∠CAB=∠FDE B.∠ACB=∠DFE C.∠ABC=∠DEF D.∠BCD=∠EFG考点:作图—基本作图;平行线的判定.分析:根据同位角相等,两直线平行可得,∠CAB=∠FDE可以说明AB∥DE.解答:解:利用三角尺和直尺画平行线,实际就是画∠CAB=∠FDE,故答案为:A.点评:此题主要考查了画平行线的方法,关键是掌握平行线的判定定理:同位角相等,两直线平行.二.填空题(共6小题)10.∠AOB如图所示,请用直尺和圆规作出∠AOB的平分线(要求保留作图痕迹,不写作法).参见解答考点:作图—基本作图.分析:∵只要在OB上取C,以O为圆心,OC为半径画圆,交OA于点D,连接CD,再分别以大于CD为半径,C,D,为圆心画圆,两圆相交于P,D,连接OP,则OP即为∠AOB 的平分线.解答:解:作法如下:(1)在OB上取C,以O为圆心,OC为半径画圆,交OA于点D,连接CD;(2)再分别以大于CD为半径,C,D,为圆心画圆,两圆相交于P,D,连接OP,则OP即为∠AOB的平分线.点评:本题考查了运用三角形全等的判定与性质,结合圆的性质作等角的方法,需同学们熟练掌握.11.如图,点A是直线l外一点,在l上取点B、C.按下列步骤作图:分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D.则四点A、B、C、D可组成的图形是平行四边形或梯形.考点:作图—复杂作图.分析:根据题意画出图形,可得两弧有两个交点,连接可得答案.解答:解:如图所示:,四点A、B、C、D可组成的图形是平行四边形或梯形.故答案为:平行四边形或梯形.点评:此题主要考查了复杂作图,关键是根据题意画出图形,找到D点位置.12.如图,是格点(横、纵坐标都为整数的点)三角形,请在图中画出与全等的一个格点三角形.考点:作图—复杂作图.专题:作图题.分析:本题答案不唯一,最简单的方法就是从点B所以在的纵坐标找一点,作BC 的平行线,且长度相等,然后再作AB的平行线且长度相等,最后连接,构成三角形.解答:解:点评:本题主要考查了利用网格画图的能力.13.在如图所示的方格纸上过点P画直线AB的平行线.考点:作图—基本作图.专题:网格型.分析:由题意可知应根据小正方形的格数及勾股定理作图,只要在直线找点A,B,D,P使其连接起来构成平行四边形即可.解答:解:作图如下:(1)连接PA,假设图中每个小方格的边长为1,则AP==,AB==;(2)找点D,使得AP=BD,AP∥BD,连接DP,即可.点评:本题考查的是平行四边形的性质,勾股定理的运用,利用图中每个小格的边长相等作图.14.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 4 个.考点:作图—复杂作图.分析:能画4个,分别是:以D为圆心,AB为半径画圆;以E为圆心,AC为半径画圆.两圆相交于两点(DE上下各一个),分别于D,E连接后,可得到两个三角形.以D为圆心,AC为半径画圆;以E为圆心,AB为半径画圆.两圆相交于两点(DE上下各一个),分别于D,E连接后,可得到两个三角形.因此最多能画出4个解答:解:如图,可以作出这样的三角形4个.点评:本题考查了学生利用基本作图来做三角形的能力.15.如图,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.考点:作图—复杂作图;全等三角形的性质;勾股定理.分析:若是三边对应相等的两个三角形互为全等三角形,根据此可画出图.解答:解:从图上可看出两个三角形的三条边对应相等.所以△DEF即为所求.点评:本题考查全等三角形的性质,三边对应相等,以及在表格中如何画出全等的三角形.三.解答题(共6小题)16.如图,△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC)(1)在图1中画1条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角度数分别是108 度和36 度;(2)在图2中画2条线段,使图中有4个等腰三角形;(3)继续按以上操作发现:在△ABC中画n条线段,则图中有2n 个等腰三角形,其中有n 个黄金等腰三角形.考点:作图—应用与设计作图;黄金分割.专题:作图题;探究型.分析:(1)利用等腰三角形的性质以及∠A的度数,进而得出这2个等腰三角形的顶角度数;(2)利用(1)种思路进而得出符合题意的图形;(3)利用当1条直线可得到2个等腰三角形;当2条直线可得到4个等腰三角形;当3条直线可得到6个等腰三角形,进而得出规律求出答案.解答:解:(1)如图1所示:∵AB=AC,∠A=36°,∴当AE=BE,则∠A=∠ABE=36°,则∠AEB=108°,则∠EBC=36°,∴这2个等腰三角形的顶角度数分别是108度和36度;故答案为:108,36;(2)如图2所示:(3)如图3所示:当1条直线可得到2个等腰三角形;当2条直线可得到4个等腰三角形;当3条直线可得到6个等腰三角形;…∴在△ABC中画n条线段,则图中有2n个等腰三角形,其中有n个黄金等腰三角形.故答案为:2n,n.点评:此题主要考查了应用作图与设计以及等腰三角形的性质,得出分割图形的规律是解题关键.17.如图,Rt△ABC的直角边BC=8,AC=6(1)用尺规作图作AB的垂直平分线l,垂足为D,(保留作图痕迹,不要求写作法、证明);(2)连结D、C两点,求CD的长度.考点:作图—基本作图;线段垂直平分线的性质;直角三角形斜边上的中线.分析:(1)根据垂直平分线的作法得出答案即可;(2)根据垂直平分线的性质以及直角三角形的性质得出AB进而得出CD即可.解答:解;(1)如图.直线DE即为所求作的图形.(2)连接CD,∵DE是AB的垂直平分线,∠C=90°,∴AD=B D=CD,∵AC=6,BC=8,∴AB=10,∴CD是Rt△ABC斜边上的中线等于斜边的一半,∴CD=5.点评:此题主要考查了垂直平分线的作法以及直角三角形的性质,根据Rt△ABC斜边上的中线等于斜边的一半得出是解题关键.18.如图①,将一张直角三角形纸片△ABC折叠,使点A与点C重合,这时DE为折痕,△CBE 为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A 在格点上,且△ABC折成的“叠加矩形”为正方形;(3)若一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是什么?考点:作图—应用与设计作图.专题:新定义;开放型.分析:(1)应先在三角形的格点中找一个矩形,折叠即可;(2)根据正方形的边长应等于底边及底边上高的一半可得所求三角形的底边与高相等;(3)由(2)可得相应结论.解答:解:(1);(2);(3)由(2)可得,若一个三角形所折成的“叠加矩形”为正方形,那么三角形的一边长与该边上的高相等的直角三角形或锐角三角形.点评:解决本题的关键是得到相应矩形的边长等于所给三角形的底边与底边上的高的一半的关系.19.如图,在△ABC中,AB=AC,AD⊥BC,AE∥BC.(1)作∠ADC的平分线DF,与AE交于点F;(用尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若AD=2,求DF的长.考点:作图—基本作图;等腰三角形的性质;勾股定理.分析:(1)利用角平分线的作法得出DF即可;(2)首先得出∠DAF=90°,即可得出∠ADF=45°,进而利用勾股定理求出即可.解答:解:(1)如图所示,DF就是所求作;(2)∵AD⊥BC,AE∥BC,∴∠DAF=90°,又∵DF平分∠ADC,∴∠ADF=45°,∴AD=AF,.点评:此题主要考查了基本作图以及等腰三角形的性质和勾股定理等知识,熟练掌握角平分线的做法是解题关键.20.如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=10.(1)在BC边上求作一点E,使OE=OA;(保留作图痕迹,不写画法)(2)求出点E的坐标.考点:作图—复杂作图;坐标与图形性质;勾股定理;矩形的性质.分析:(1)利用EO=AO,以O为圆心AO为半径画弧得出E即可;(2)首先过点E作EF⊥OA,垂足为F,得出B点坐标,进而求出FO的长,即可得出E点坐标.解答:解:(1)如图所示:E点即为所求;(2)过点E作EF⊥OA,垂足为F.∵矩形OABC中OC=6,OA=10,∴B点坐标为(10,6).∴E F=6.又∵OE=OA,∴OF==8.∴点E的坐标为(8,6).点评:此题主要考查了基本作图以及勾股定理和矩形的性质,得出B点坐标是解题关键.21.(如图,在△ABC中,BC=AC,且CD∥AB,设△ABC的外心为O.(1)用尺规作出△ABC的外接圆O.(不写作法,保留痕迹)(2)在(1)中,连接OC,并证明OC是AB的中垂线;(3)直线CD与⊙O有何位置关系,试证明你的结论.考点:作图—复杂作图;线段垂直平分线的性质;直线与圆的位置关系.分析:(1)首先作出三角形两边的中垂线进而得出圆心求出△ABC的外接圆O;(2)利用等腰三角形的性质得出答案即可;(3)利用切线的判定方法求出∠OCG=90°,进而得出答案.解答:解:(1)如图所示:(2)方法一:连接BO、CO、OA,∵OB=OA,AC=BC,∴OC是AB的中垂线;方法二:在⊙O中,∵AC=BC,∴=,∴∠BOC=∠AOC,∵OB=OA,1 ∴OC是AB的中垂线;(3)直线CD与⊙O相切,证明:∵CD∥AB,CO是AB的垂线,∴∠OCG=90°,∴直线CD与⊙O相切.点评:此题主要考查了切线的判定与性质以及三角形外接圆的作法等知识,熟练掌握等腰三角形的性质是解题关键.2。
2022年人教版中考数学考点复习第七章第24节-尺规作图(数学)

解:方法一,作图依据是勾股定理的逆定理.
如答图1,在OA上截取线段OP,并依次在OA,OB上
分别截取 OC = 4OP,OD = 3OP,连接 CD,若
CD的长为5OP,则∠AOB = 90°.
方法二,作图依据是直径所对的圆周角为 90°.
如答图2,在OA,OB上分别取点C,D,以CD
为直径画圆,若点O在圆上,则∠AOB = 90°.
BD上用尺规作一点E,使∠BEC = ∠A(不写作法,保留作图痕迹).
点拨:(1)画出草图:
解:方法一,过点C作∠ACE = ∠ABD,则CE与
射线BD的交点 E满足条件 .如答图1所示,点 E即
为所求.
(2)用草图分析:①可以转化为作一个角等于已知角,
方法二,如答图2所示,点E即为所求.
即∠BEC = ∠A.但是点E的位置不确定,不能直接作∠BEC.
半径作弧且两弧相交于点C
(3)连接 AC,BC,则
△ABC即为所求作的三角形
返回目录
续表
基本尺规作图
已知两边及其
夹角作三角形
已知两角及其
夹边作三角形
步骤
图示
应用
(1)作∠A = ∠α
(2)在角的一边截取 AB
= n,在角的另一边截取
AC = m
(3)连接BC,则△ABC
即为所求作的三角形
(1)作线段AB = m
给出了她证明∠AOB 是直角的方法,请仿照小丽的方式,再用两种
不同的方法判断∠AOB 是不是直角(仅限使用直尺和圆规).
小丽的方法:
如图2,在 OA,OB上分别
取点C,点 D,以点 D为圆心,
CD长为半径画弧,交OA的反向
延 长 线 于 点 E,若 OE = OC,
中考数学复习轨迹和作图2[人教版]
![中考数学复习轨迹和作图2[人教版]](https://img.taocdn.com/s3/m/9d52826d80eb6294dd886cfa.png)
中考数学-尺规作图专题复习

中考总复习一尺规作图一、理解“尺规作图”的含义在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的.2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角・利用这两个基本作图,可以作两条线段或两个角的和或差・二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言:①过点X、点X作直线XX;或作直线XX;或作射线XX;②连结两点XX;或连结XX;③延长XX到点X;或延长(反向延长)XX到点X,使xx = xx;或延长XX 交XX于点X;2.用圆规作图的几何语言:①在XX上截取xx = xx;②以点X为圆心,XX的长为半径作圆(或弧);③以点X为圆心,XX的长为半径作弧,交XX于点X;④分别以点X、点X为圆心,以XX、XX的长为半径作弧,两弧相交于点X、X .三、了解尺规作图题的一般步骤尺规作图题的步骤:1 •已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写岀题目中的条件;2•求作:能根据题目写出要求作出的图形及此图形应满足的条件;3•作法:能根据作图的过程写出每一步的操作过程■当不要求写作法时,一般要保留作图痕迹•对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写岀作法,可见在解作图题时,保留作图痕迹很重要.四、最基本,最常用的尺规作图,通常称基本作图。
一些复杂的尺规作图都是由基本作图组成的。
五种基本作图:①、作一条线段等于已知线段;(D、作已知线段的垂直平分线(中点);③、作已知直线的垂线(分过直线外一点作直线的垂线和过直线上一点作直线的垂线两种情况);④、作一个角等于已知角;⑤、作已知角的角平分线;补充:⑥、作已知线段的黄金分割点;4.1 >但矢钳段减己無戋(2)段是翊乍 的图腹B,使AB 二a ・作射线AP ;在射线AP 上用圆规截取4.2、作已知线段的垂直平分线(中点) 已知:女郵:线觸埶N.(1)点0,使M0二N (0即0是MN 的分别以M 、N 为圆心,大 于的相同线段为半径画 弧,两弧相交于P, Q ; (2 )连接PQ 交MN 于0. 则点0就是所求作的MN 的中 点。
2021年中考数学复习专题二 无刻度直尺作图(精讲课件)

典重例点题精型讲
解:(1)如图①,点P′即为所求. (2)如图②,点P′即为所求.
题组训练
【思路分析】(1)根据等腰三角形的性质即可在AC上找出一 点P′,使AP=AP′;
(2)根据等腰三角形的性质即可在CD上找出一点P′,使BP= CP′.
典重例点题精型讲
题组训练
例2.(2020·江西模拟)如图,已知点C为AB的中点,分别以AC ,BC为边,在AB的同侧作等边△ACD和等边△BCE,连接AE 交CD于点O,请仅用无刻度的直尺按下列要求作图(保留作图痕 迹,不写作法).
题组训练
【思路分析】(1)连接AC交BD于O,作直线EO交BC于F,连 接DF,线段DF即为所求.
(2)连接CA,延长BE交CA的延长线于J,连接DG,延长BA交 DJ于G,线段DG即为所求.
典重例点题精型讲
题组训练
类型3 以正多边形为背景 例5.如图,已知正六边形ABCDEF,请仅用无刻度的直尺, 分别按下列要求画图. (1)在图1中,画出一个以BC为边的矩形; (2)在图2中,画出一个以AB为边的菱形.
典重例点题精型讲
解:(1)平行四边形ABCD如图所示. (2)菱形AEBF如图所示.
题组训练
【思路分析】(1)利用数形结合的思想解决问题即可; (2)构造边长为5的菱形即可.
典重例点题精型讲
题组训练
例10.(2020·江西南昌一模)如图,在6×7的正方形的网格图中 ,点A,B,C均为格点,仅用无刻度直尺按要求作图.
典重例点题精型讲
解:(1)如图1,四边形BCEF为所作; (2)如图2,四边形OABC为所作.
题组训练
【思路分析】(1)连接BF,CE,利用正六边形的性质得到四 边形BCEF为矩形;
2020年中考数学人教版专题复习:尺规作图

2020年中考数学人教版专题复习:尺规作图基本作图1.最基本、最常用的尺规作图,通常称为基本作图.2.基本作图有五种:(1)作一条线段等于已知线段;(2)作一个角等于已知角;(3)作一个角的平分线;(4)作一条线段的垂直平分线;(5)过一点作已知直线的垂线.典例精析典例1如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是A.AD=BD B.BD=CDC.∠A=∠BED D.∠ECD=∠EDC【答案】D【解析】∵MN为AB的垂直平分线,∴AD=BD,∠BDE=90°,∵∠ACB=90°,∴CD=BD,∵∠A+∠B=∠B+∠BED=90°,∴∠A=∠BED,∵∠A≠60°,AC≠AD,∴EC≠ED,∴∠ECD≠∠EDC.故选D.典例2如图,已知∠MAN,点B在射线AM上.(1)尺规作图:①在AN上取一点C,使BC=BA;②作∠MBC的平分线BD,(保留作图痕迹,不写作法)(2)在(1)的条件下,求证:BD∥AN.1 2【解析】(1)①以B点为圆心,BA长为半径画弧交AN于C点;如图,点C即为所求作;②利用基本作图作BD平分∠MBC;如图,BD即为所求作;(2)先利用等腰三角形的性质得∠A=∠BCA,再利用角平分线的定义得到∠MBD=∠CBD,然后根据三角形外角性质可得∠MBD=∠A,最后利用平行线的判定得到结论.∵AB=AC,∴∠A=∠BCA,∵BD平分∠MBC,∴∠MBD=∠CBD,∵∠MBC=∠A+∠BCA,即∠MBD+∠CBD=∠A+∠BCA,∴∠MBD=∠A,∴BD∥AN.拓展1.根据下图中尺规作图的痕迹,可判断AD一定为三角形的A.角平分线B.中线C.高线D.都有可能2.(1)请你用尺规作图,作AD平分∠BAC,交BC于点D(要求:保留作图痕迹);(2)∠ADC的度数.复杂作图利用五种基本作图作较复杂图形.典例精析典例2如图,在同一平面内四个点A,B,C,D.(1)利用尺规,按下面的要求作图.要求:不写画法,保留作图痕迹,不必写结论.①作射线AC;②连接AB,BC,BD,线段BD与射线AC相交于点O;③在线段AC上作一条线段CF,使CF=AC–BD.(2)观察(1)题得到的图形,我们发现线段AB+BC>AC,得出这个结论的依据是__________.【答案】见解析.【解析】(1)①如图所示,射线AC即为所求;②如图所示,线段AB,BC,BD即为所求;③如图所示,线段CF即为所求;(2)根据两点之间,线段最短,可得AB+BC>AC.故答案为:两点之间,线段最短.拓展3.作图题:学过用尺规作线段与角后,就可以用尺规画出一个与已知三角形一模一样的三角形来.比如给定一个△ABC,可以这样来画:先作一条与AB相等的线段A′B′,然后作∠B′A′C′=∠BAC,再作线段A′C′=AC,最后连接B′C′,这样△A′B′C′就和已知的△ABC一模一样了.请你根据上面的作法画一个与给定的三角形一模一样的三角形来.(请保留作图痕迹)同步测试1.根据已知条件作符合条件的三角形,在作图过程中主要依据是A.用尺规作一条线段等于已知线段B.用尺规作一个角等于已知角C.用尺规作一条线段等于已知线段和作一个角等于已知角D.不能确定2.下列作图属于尺规作图的是A.画线段MN=3 cmB.用量角器画出∠AOB的平分线C.用三角尺作过点A垂直于直线l的直线D.已知∠α,用没有刻度的直尺和圆规作∠AOB,使∠AOB=2∠α3.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;步骤3:连接AD,交BC延长线于点H.下列叙述正确的是A .BH 垂直平分线段ADB .AC 平分∠BAD C .S △ABC =BC ·AHD .AB =AD4.如图,点C 在∠AOB 的OB 边上,用尺规作出了∠AOB =∠NCB ,作图痕迹中,弧FG 是A .以点C为圆心,OD 为半径的弧 B .以点C 为圆心,DM 为半径的弧 C .以点E 为圆心,OD 为半径的弧 D .以点E 为圆心,DM 为半径的弧5.如图,△ABC 中,∠C =90°,∠CAB =50°.按以下步骤作图:①以点A 为圆心,小于AC 长为半径画弧,分别交AB 、AC 于点E 、F ; ②分别以点E 、F 为圆心,大于EF 长为半径画弧,两弧相交于点G ; ③作射线AG 交BC 边于点D . 则∠ADC 的度数为A .65°B .60°C .55°D .45°6.如图,△ABC 为等边三角形,要在△ABC 外部取一点D ,使得△ABC 和△DBC 全等,下面是两名同学做法: 甲:①作∠A 的角平分线l ;②以B 为圆心,BC 长为半径画弧,交l 于点D ,点D 即为所求;12乙:①过点B作平行于AC的直线l;②过点C作平行于AB的直线m,交l于点D,点D即为所求.A.两人都正确B.两人都错误C.甲正确,乙错误D.甲错误,乙正确交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=__________.8.如图,在△ABC中,AB=A C.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连接BD.若∠A=32°,则∠CDB的大小为__________度.9.按要求用尺规作图(要求:不写作法,但要保留作图痕迹,并写出结论)已知:线段AB;求作:线段AB的垂直平分线MN.10.如图,已知△ABC,∠BAC=90°,(1)尺规作图:作∠ABC的平分线交AC于D点(保留作图痕迹,不写作法)(2)若∠C=30°,求证:DC=DB.。
2024年中考数学微专题复习+尺规作图+课件

+ +
= , = +
10.[原创新题]如图,一次函数 y = 3x 与反比例函数
y=
k
x
x > 0 的图象交于点 A 1, a ,点 B 在 x 轴正半轴
上.
(1)求反比例函数的表达式.
[答案] 将 , 代入 = ,得 = , ∴ , . 将 , 代入 =
[答案] ∵ 四边形 是菱形, ∴ = , // ,
∴△ ∼△ , ∴
=
.
设 = ,则 = − ,
∴
−
=
,解得
= ,
∴ 中所作菱形 的边长为6.
5.[2023洛阳二模] 如图,在 △ ABC 中,
∴ = , ∴ ∠ = ∠ , ∴ ∠ = ∠ , ∴ // , ∴ △ =
△ = .
8.[原创新题]如图,点 A , B 在反比例函数
y=
k
x
x > 0 的图象上, AC ⊥ x 轴于点 C , BD ⊥ x
轴于点 D .已知 OC =
=
.
4.如图,已知 △ ABC .
(1)请用无刻度的直尺和圆规在边 BC , CA , AB 上
分别确定点 D , E , F ,使四边形 BDEF 是菱形,并画
出菱形 BDEF (要求:不写作法,保留作图痕迹).
[答案] 如图所示,菱形 即为所求.
(2)若 AB = 10 , BC = 15 ,求(1)中所作菱形 BDEF 的边长.
中考数学考点32尺规作图总复习(解析版)
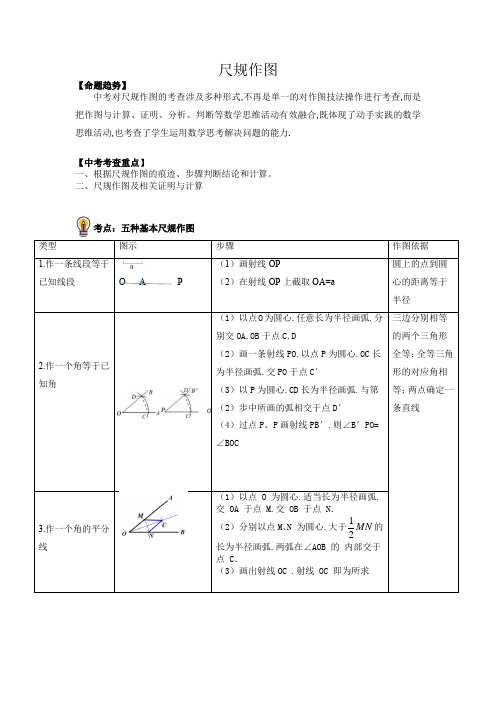
尺规作图【命题趋势】中考对尺规作图的考查涉及多种形式,不再是单一的对作图技法操作进行考查,而是把作图与计算、证明、分析、判断等数学思维活动有效融合,既体现了动手实践的数学思维活动,也考查了学生运用数学思考解决问题的能力.【中考考查重点】一、根据尺规作图的痕迹、步骤判断结论和计算。
二、尺规作图及相关证明与计算考点:五种基本尺规作图类型图示步骤作图依据1.作一条线段等于已知线段O A P (1)画射线OP(2)在射线OP上截取OA=a圆上的点到圆心的距离等于半径2.作一个角等于已知角(1)以点O为圆心.任意长为半径画弧.分别交OA.OB于点C,D(2)画一条射线PO.以点P为圆心.OC长为半径画弧.交PO于点C′(3)以P为圆心.CD长为半径画弧.与第(2)步中所画的弧相交于点D′(4)过点P、P画射线PB′.则∠B′PO=∠BOC三边分别相等的两个三角形全等;全等三角形的对应角相等;两点确定一条直线3.作一个角的平分线(1)以点 O 为圆心.适当长为半径画弧.交 OA 于点 M.交 OB 于点 N.(2)分别以点M、N 为圆心.大于MN21的长为半径画弧.两弧在∠AOB 的内部交于点 C.(3)画出射线OC .射线 OC 即为所求点在直•广元)观察下列作图痕迹A.B.C.D.【答案】C【解答】解:根据基本作图.A、D选项中为过C点作AB的垂线.B选项作AB的垂直平分线得到AB边上的中线CD.C选项作CD平分∠ACB.故选:C.2.(2021秋•广州期中)如图.在△ABC中.以A为圆心.任意长为半径画弧.分别交AB、AC于点M、N;再分别以M、N为圆心.大于MN的长为半径画弧.两弧交于点P;连结AP并延长交BC于点D.则下列说法正确的是()A.AD+BD<AB B.AD一定经过△ABC的重心C.∠BAD=∠CAD D.AD是三角形的高【答案】C【解答】解:由题可知AD是∠BAC的角平分线.∴∠BAD=∠CAD.故选:C.3.(2021•济宁)如图.已知△ABC.(1)以点A为圆心.以适当长为半径画弧.交AC于点M.交AB于点N.(2)分别以M.N为圆心.以大于MN的长为半径画弧.两弧在∠BAC的内部相交于点P.(3)作射线AP交BC于点D.(4)分别以A.D为圆心.以大于AD的长为半径画弧.两弧相交于G.H两点.(5)作直线GH.交AC.AB分别于点E.F.依据以上作图.若AF=2.CE=3.BD=.则CD的长是()A.B.1C.D.4【答案】C【解答】解:由作法得AD平分∠BAC.EF垂直平分AD.∴∠EAD=∠F AD.EA=ED.F A=FD.∵EA=ED.∴∠EAD=∠EDA.∴∠F AD=∠EDA.∴DE∥AF.同理可得AE∥DF.∴四边形AEDF为平行四边形.而EA=ED.∴四边形AEDF为菱形.∴AE=AF=2.∵DE∥AB.∴=.即=.∴CD=.故选:C.4.(2021秋•开封期末)已知线段AB如图所示.延长AB至C.使BC=AB.反向延长AB 至D.使AD=BC.点M是CD的中点.点N是AD的中点.(1)依题意补全图形;(2)若AB长为10.求线段MN的长度.【答案】略【解答】解:(1)如图.(2)∵BC=AD=AB=10.∴DC=30.∵点M是CD的中点.∴DM=CD=15.∵点N是AD的中点.∴DN=AD=5.∴MN=DM﹣DN=15﹣5=10.答:线段MN的长度为10.5.(2022•雨花区校级开学)下面是小华设计的“作三角形一边上的高”的尺规作图过程.已知:△ABC.求作:△ABC的边BC上的高AD.作法:①以点A为圆心.适当长为半径画弧.交直线BC于点M.N;②分别以点M.N为圆心.以大于MN的长为半径画弧.两弧相交于点P;③作直线AP交BC于点D.则线段AD即为所求△ABC的边BC上的高.根据小华设计的尺规作图过程:(1)AP是线段MN的;(2)证明AD是△ABC的高.【答案】(1)垂直平分线(2)略【解答】(1)解:由作法得AP为线段MN的垂直平分线;故答案为:垂直平分线;(2)证明:∵AM=AN.PM=PN.∴A点和P点在MN的垂直平分线上.∴即AP垂直平分MN.即AD是△ABC的高.6.(2021•烟台)如图.已知Rt△ABC中.∠C=90°.(1)请按如下要求完成尺规作图(不写作法.保留作图痕迹).①作∠BAC的角平分线AD.交BC于点D;②作线段AD的垂直平分线EF与AB相交于点O;③以点O为圆心.以OD长为半径画圆.交边AB于点M.(2)在(1)的条件下.求证:BC是⊙O的切线;(3)若AM=4BM.AC=10.求⊙O的半径.【答案】略【解答】解:(1)如图所示.①以A为圆心.以任意长度为半径画弧.与AC、AB相交.再以两个交点为圆心.以大于两点之间距离的一半为半径画弧相交于∠BAC内部一点.将点A与它连接并延长.与BC交于点D.则AD为∠BAC的平分线;②分别以点A、点D为圆心.以大于AD长度为半径画圆.将两圆交点连接.则EF为AD的垂直平分线.EF与AB交于点O;③如图.⊙O与AB交于点M;(2)证明:∵EF是AD的垂直平分线.且点O在EF上.∴∠OAD=∠ODA.∵AD是∠BAC的平分线.∴∠OAD=∠CAD.∴∠ODA=∠CAD.∴OD∥AC.∵AC⊥BC.∴OD⊥BC.故BC是⊙O的切线.(3)根据题意可知OM=OA=OD=AM.AM=4BM.∴OM=2BM.BO=3BM.AB=5BM.∴==.由(2)可知Rt△BOD与Rt△BAC有公共角∠B.∴Rt△BOD∽Rt△BAC.∴=.即=.解得DO=6.故⊙O的半径为6.1.(2021秋•盱眙县期末)如图.在Rt△ABC中.∠C=90°.以顶点A为圆心.适当长为半径画圆弧.分别交AB、AC于点D、E.再分别以点D、E为圆心.大于DE长为半径画圆弧.两弧交于点F.作射线AF交边BC于点G.若CG=4.AB=10.则△ABG的面积是()A.10B.20C.30D.40【答案】B【解答】解:如图.过点G作GH⊥AB于点H.由作图过程可知:AG平分∠BAC.∵∠C=90°.∴GC⊥AC.∴GH=GC=4.∴△ABG的面积=AB•GH=10×4=20.故选:B.2.(2021秋•宁波期末)如图.在Rt△ABC中.∠B=90°.分别以A.C为圆心.大于AC长为半径作弧.两弧相交于点M.N.作直线MN.与AC.BC分别交于D.E.连结AE.若AB=6.AC=10.则△ABE的周长为()A.13B.14C.15D.16【答案】B【解答】解:由作法得ED垂直平分AC.∴EA=EC.在Rt△ABC中.BC===8.∴△ABE的周长=AB+BE+AE=AB+BE+CE=AB+BC=6+8=14.故选:B.3.(2021秋•定西期末)下列选项中的尺规作图.能推出P A=PC的是()A.B.C.D.【答案】B【解答】解:∵P A=PC.∴P点为AC的垂直平分线的上的点.故选:B.4.(2021秋•郧阳区期末)如图为用直尺和圆规作一个角等于已知角.那么能得出∠A′O′B′=∠AOB的依据是运用了我们学习的全等三角形判定()A.角角边B.边角边C.角边角D.边边边【答案】D【解答】解:由作法得OD=OC=OC′=OD′.CD=C′D′.则可根据“SSS”可判定△OCD≌△OC′D′.所以∠A′O′B′=∠AOB.故选:D.5.(2021秋•朝阳区校级期末)如图.在Rt△ABC中.∠ACB=90°.分别以点B和点C 为圆心.大于BC的长为半径作弧.两弧相交于D、E两点.作直线DE交AB于点F.交BC与点G.连接CF.若AC=3.CG=2.则CF的长为.【答案】【解答】解:由作图可知.DE垂直平分线段BC.∴CG=GB=2.FG⊥CB.∴∠FGB=∠ACB=90°.∴FG∥AC.∵CG=GB.∴AF=FB.∴FG=AC=.∵∠FGC=90°.∴CF===.故答案为.1.(2021•阿坝州)如图.在△ABC中.∠BAC=70°.∠C=40°.分别以点A和点C为圆心.大于AC的长为半径画弧.两弧相交于点M.N.作直线MN交BC于点D.连接AD.则∠BAD的大小为()A.30°B.40°C.50°D.60°【答案】A【解答】解:由作图可知.直线MN是线段AC的垂直平分线.∴DA=DC.∴∠DAC=∠C=40°.∵∠BAC=70°.∴∠BAD=∠BAC﹣∠DAC=70°﹣40°=30°.故选:A.2.(2021•百色)如图.在⊙O中.尺规作图的部分作法如下:(1)分别以弦AB的端点A、B为圆心.适当等长为半径画弧.使两弧相交于点M;(2)作直线OM交AB于点N.若OB=10.AB=16.则tan B等于()A.B.C.D.【答案】B【解答】解:如图.连接OA.∴OA=OB.根据作图过程可知:OM是AB的垂直平分线.∴AN=BN=AB=8.在Rt△OBN中.OB=10.BN=8.根据勾股定理.得ON==6.∴tan B===.故选:B.3.(2021•黄石)如图.在Rt△ABC中.∠ACB=90°.按以下步骤作图:①以B为圆心.任意长为半径作弧.分别交BA、BC于M、N两点;②分别以M、N为圆心.以大于MN 的长为半径作弧.两弧相交于点P;③作射线BP.交边AC于D点.若AB=10.BC=6.则线段CD的长为()A.3B.C.D.【答案】A【解答】解:由作法得BD平分∠ABC.过D点作DE⊥AB于E.如图.则DE=DC.在Rt△ABC中.AC===8.∵S△ABD+S△BCD=S△ABC.∴•DE×10+•CD×6=×6×8.即5CD+3CD=24.∴CD=3.故选:A.4.(2021•铜仁市)如图.在Rt△ABC中.∠C=90°.AB=10.BC=8.按下列步骤作图:步骤1:以点A为圆心.小于AC的长为半径作弧分别交AC、AB于点D、E.步骤2:分别以点D、E为圆心.大于DE的长为半径作弧.两弧交于点M.步骤3:作射线AM交BC于点F.则AF的长为()A.6B.3C.4D.6【答案】B【解答】解:由作法得AF平分∠BAC.过F点作FH⊥AB于H.如图.∵AF平分∠BAC.FH⊥AB.FC⊥AC.∴FH=FC.在△ABC中.∵∠C=90°.AB=10.BC=8.∴AC==6.设CF=x.则FH=x.∵S△ABF+S△ACF=S△ABC.∴×10•x+×6•x=×6×8.解得x=3.在Rt△ACF中.AF===3.故选:B.5.(2021•永州)如图.在△ABC中.AB=AC.分别以点A.B为圆心.大于AB的长为半径画弧.两弧相交于点M和点N.作直线MN分别交BC、AB于点D和点E.若∠B=50°.则∠CAD的度数是()A.30°B.40°C.50°D.60°【答案】A【解答】解:由作法得MN垂直平分AB.∴DA=DB.∴∠DAB=∠B=50°.∵AB=AC.∴∠C=∠B=50°.∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣50°=80°.∴∠CAD=∠BAC﹣∠DAB=80°﹣50°=30°.故选:A.6.(2021•长春)在△ABC中.∠BAC=90°.AB≠AC.用无刻度的直尺和圆规在BC边上找一点D.使△ACD为等腰三角形.下列作法不正确的是()A.B.C.D.【答案】A【解答】解:A、由作图可知AD是△ABC的角平分线.推不出△ADC是等腰三角形.本选项符合题意.B、由作图可知CA=CD.△ADC是等腰三角形.本选项不符合题意.C、由作图可知DA=CD.△ADC是等腰三角形.本选项不符合题意.D、由作图可知DA=CD.△ADC是等腰三角形.本选项不符合题意.故选:A.7.(2021•贵阳)如图.已知线段AB=6.利用尺规作AB的垂直平分线.步骤如下:①分别以点A.B为圆心.以b的长为半径作弧.两弧相交于点C和D.②作直线CD.直线CD就是线段AB的垂直平分线.则b的长可能是()A.1B.2C.3D.4【答案】D【解答】解:根据题意得b>AB.即b>3.故选:D.8.(2021•荆州)如图.在△ABC中.AB=AC.∠A=40°.点D.P分别是图中所作直线和射线与AB.CD的交点.根据图中尺规作图痕迹推断.以下结论错误的是()A.AD=CD B.∠ABP=∠CBP C.∠BPC=115°D.∠PBC=∠A 【答案】D【解答】解:由作图可知.点D在AC的垂直平分线上.∴DA=DC.故选项A正确.∴∠A=∠ACD=40°.由作图可知.BP平分∠ABC.∴∠ABP=∠CBP.故选项B正确.∵AB=AC.∠A=40°.∴∠ABC=∠ACB=(180°﹣40°)=70°.∵∠PBC=∠ABC=35°.∠PCB=∠ACB﹣∠ACD=30°.∴∠BPC=180°﹣35°﹣30°=115°.故选项C正确.若∠PBC=∠A.则∠A=36°.显然不符合题意.故选:D.1.(2021•广陵区二模)用直尺和圆规作已知角∠AOB的平分线的作法如图.能得出∠AOC=∠BOC的依据是()A.(SAS)B.(SSS)C.(AAS)D.(ASA)【答案】B【解答】解:由作图可知.OD=OE.PD=PE.在△OPD和△OPE中..∴△OPD≌△OPE(SSS).∴∠AOC=∠BOC.故选:B.2.(2021•河南模拟)如图.在Rt△ABC中.∠ACB=90°.AC=BC=2.按以下步骤作图:①以点A为圆心.适当长度为半径作弧.分别交AC.AB于M.N两点;②分别以点M.N为圆心.大于MN的长为半径作弧.两弧相交于点P;③作射线AP.交BC于点E.则EC的长为()A.B.1C.D.【答案】C【解答】解:由作法得AP平分∠BAC.作EH⊥AB于H.如图.∵AE为角平分线.EC⊥AC.EH⊥AB.∴EC=EH.∵∠ACB=90°.AC=BC=2.∴∠B=45°.AB=BC.∴△BEH为等腰直角三角形.∴BH=EH=BE.设EH=x.则BH=EC=x.BE=x.∴x+x=2.∴x=2﹣2.∴EC=2﹣2.故选:C.3.(2021•高阳县模拟)如图.已知∠MAN=60°.AB=6.依据尺规作图的痕迹可求出BD的长为()A.2B.3C.3D.6【答案】B【解答】解:由题意.AB=AC.∠BAC=60°.∴△ABC是等边三角形.∴AB=BC=AC=6.∵AD平分∠BAC.∴AD⊥BC.BD=CD=3.故选:B.4.(2021•范县模拟)如图.在Rt△ABC中.∠ACB=90°.AC=2BC.分别以点A和B为圆心.以大于AB的长为半径作弧.两弧相交于点M和N.作直线MN.交AC于点E.连接BE.若CE=3.则BE的长为()A.5B.4C.3D.6【答案】A【解答】解:解:由作图可知.MN垂直平分线段AB.∴AE=EB.设AE=EB=x.∵EC=3.AC=2BC.∴BC=(x+3).在Rt△BCE中.∵BE2=BC2+EC2.∴x2=32+[(x+3)]2.解得.x=5或﹣3(舍弃).∴BE=5.故选:A.5.(2021•开平区一模)用尺规作图作直线l的一条垂线.下面是甲.乙两个同学作图描述:甲:如图1.在直线l上任取一点C.以C为圆心任意长为半径画弧.与直线l相交于点A、B两点.再分别以A、B为圆心以大于长为半径画弧.两弧相交于点D.作直线CD 即为所求.乙:如图2在直线l上任取两点M.N作线段MN的垂直平分线.下面说法正确的是()A.甲对.乙不对B.乙对甲不对C.甲乙都对D.甲乙都不对【答案】C【解答】解:根据过一点作已知直线的垂线的方法可知:甲正确;根据作已知线段的垂直平分线的方法可知:乙正确.所以甲乙都对.故选:C.6.(2021•莲都区校级模拟)下列三幅图都是“作已知三角形的高”的尺规作图过程.其中作图正确的是()A.(1)(2)(3)B.(1)(2)C.(1)(3)D.(2)(3)【答案】A【解答】解:图(1)和图(2)中.由“到线段两端距离相等的点在线段的垂直平分线上”可知.AJ垂直平分GH.BC垂直平分AK.故作图正确;图(3)中.依据“直径所对的圆周角等于90°”可知.BC所对的圆周角为直角.故作图正确;故选:A.7.(2021•马山县模拟)如图.已知AB=AC.AB=5.BC=3.以A.B两点为圆心.大于AB 的长为半径画弧.两弧相交于点M.N.连接MN与AC相交于点D.则△BDC的周长为()A.10B.8C.11D.13【答案】B【解答】解:由作法得MN垂直平分AB.∴DA=DB.∴△BDC的周长=DB+DC+BC=DA+DC+BC=AC+BC=AB+BC=5+3=8.故选:B.8.(2021•平泉市一模)如图.已知直线AB和AB外一点C.用尺规过点C作AB的垂线.步骤如下:第一步:任意取一点K.使点K和点C在AB的两旁;第二步:以C为圆心.以a为半径画弧.交直线AB于点D.E;第三步:分别以D.E为圆心.以b为半径画弧.两弧交于点F;第四步:画直线CF.直线CF即为所求.下列正确的是()A.a.b均无限制B.a=CK.b>DE的长C.a有最小限制.b无限制D.a≥CK.b<DE的长【答案】B【解答】解:由作图可知.a=CK.b>DE的长.故选:B.9.(2021•河北一模)嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:已知:∠AOB求作:∠A'O'B'.使∠A'O'B'=∠AOB.作法:(1)如图.以点O为圆心.m为半径画弧.分别交OA.OB于点C.D;(2)画一条射线O'A'.以点O'为圆心.n为半径画弧.交O'A'于点C';(3)以点C'为圆心.p为半径画弧.与第(2)步中所画的弧相交于点D';(4)过点D'画射线O'B'.则∠A'O'B'=∠AOB.下列说法正确的是()A.m=p>0B.n=p>0C.D.m=n>0【答案】D【解答】解:由作图得OD=OC=OD′=OC′.CD=C′D′.则m=n>0.故选:D.10.(2021•定兴县一模)如图.在Rt△ABC中.∠C=90°.以顶点A为圆心.适当长为半径画弧.分别交AC.AB于点M.N.再分别以点M.N为圆心.大于MN长为半径画弧.两弧交于点P.作射线AP交边BC于点D.若CD=2.AB=7.则△ABD的面积是()A.7B.30C.14D.60【答案】A【解答】解:如图.过点D作DH⊥AB于H.∵AP平分∠CAB.DC⊥AC.DH⊥AB.∴DC=DH=2.∴S△ABD=×7×2=7.故选:A.。
(完整版)中考数学尺规作图专题复习(含答案)

中考尺规作图专题复习(含答案)尺规作图定义:用无刻度的直尺和圆规画图,中考中常见画的图是线段的垂线,垂直平分线,角平分线、画等长的线段,画等角。
1.直线垂线的画法:【分析】:以点C为圆心,任意长为半径画弧交直线与A,B两点,再分别以点A,B为圆心,大于12AB的长为半径画圆弧,分别交直线l两侧于点M,N,连接MN,则MN即为所求的垂线2.线段垂直平分线的画法【分析】:作法如下:分别以点A,B为圆心,大于12AB的长为半径画圆弧,分别交直线AB两侧于点C,D,连接CD,则CD即为所求的线段AB的垂直平分线.3.角平分线的画法【分析】1.选角顶点O为圆心,任意长为半径画圆,分别交角两边A,B点,再分别以A,B为圆心,大于12AB的长为半径画圆弧,交H点,连接OH,并延长,则射线OH即为所求的角平分线.4.等长的线段的画法直接用圆规量取即可。
5.等角的画法【分析】以O为圆心,任意长为半径画圆,交原角的两边为A,B两点,连接AB;画一条射线l,以上面的那个半径为半径,l的顶点K为圆心画圆,交l与L,以L为圆心,AB 为半径画圆,交以K为圆心,KL为半径的圆与M点,连接KM,则角LKM即为所求.备注:1.尺规作图时,直尺主要用作画直线,射线,圆规主要用作截取相等线段和画弧;2.求作一个三角形,其实质是依据三角形全等的基本事实或判定定理来进行的;3.当作图要满足多个要求时,应逐个满足,取公共部分.例题讲解例题1.已知线段a,求作△ABC,使AB=BC=AC=a.解:作法如下:①作线段BC=a;(先作射线BD,BD截取BC=a).②分别以B、C为圆心,以a半径画弧,两弧交于点A;③连接AB、AC.则△ABC 要求作三角形.例2.已知线段a 和∠α,求作△ABC ,使AB=AC=a ,∠A=∠α.解:作法如下:①作∠MAN=∠α;②以点A 为圆心,a 为半径画弧,分别交射线AM ,AN 于点B ,C. ③连接B ,C.△ABC 即为所求作三角形.例3.(深圳中考)如图,已知△ABC ,AB <BC ,用尺规作图的方法在BC 上取一点P ,使得PA +PC =BC ,则下列选项中,正确的是(D )【解析】由题意知,做出AB 的垂直平分线和BC 的交点即可。
人教版2023中考数学专题复习:尺规作图

尺规作图命题点1 五种基本尺规作图类型一判定作图结果1.(2022•德州)在△ABC中,根据下列尺规作图的痕迹,不能判断AB与AC 大小关系的是()A.B.C.D.2.(2022•益阳)如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是()A.I到AB,AC边的距离相等B.CI平分∠ACBC.I是△ABC的内心D.I到A,B,C三点的距离相等3.(2022•盘锦)如图,线段AB是半圆O的直径.分别以点A和点O为圆心,大于的长为半径作弧,两弧交于M,N两点,作直线MN,交半圆O于点C,交AB于点E,连接AC,BC,若AE=1,则BC的长是()A.B.4C.6D.4.(2022•长春)如图,在△ABC中,根据尺规作图痕迹,下列说法不一定正确的是()A.AF=BF B.AE=ACC.∠DBF+∠DFB=90°D.∠BAF=∠EBC 5.(2022•威海)过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是()A.B.C.D.6.(2022•舟山)用尺规作一个角的角平分线,下列作法中错误的是()A.B.C.D.类型二根据作图步骤进行计算、证明或结论判断7.(2022•淄博)如图,在△ABC中,AB=AC,∠A=120°.分别以点A和C 为圆心,以大于AC的长度为半径作弧,两弧相交于点P和点Q,作直线PQ 分别交BC,AC于点D和点E.若CD=3,则BD的长为()A.4B.5C.6D.7 8.(2022•黄石)如图,在△ABC中,分别以A,C为圆心,大于AC长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若AE=2cm,△ABD的周长为11cm,则△ABC的周长为()A.13cm B.14cm C.15cm D.16cm 9.(2022•资阳)如图所示,在△ABC中,按下列步骤作图:第一步:在AB、AC上分别截取AD、AE,使AD=AE;第二步:分别以点D和点E为圆心、适当长(大于DE的一半)为半径作圆弧,两弧交于点F;第三步:作射线AF交BC于点M;第四步:过点M作MN⊥AB于点N.下列结论一定成立的是()A.CM=MN B.AC=AN C.∠CAM=∠BAM D.∠CMA=∠NMA 10.(2022•锦州)如图,在矩形ABCD中,AB=6,BC=8,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线MN分别交AD,BC于点E,F,则AE的长为()A.B.C.D.11.(2022•聊城)如图,△ABC中,若∠BAC=80°,∠ACB=70°,根据图中尺规作图的痕迹推断,以下结论错误的是()A.∠BAQ=40°B.DE=BD C.AF=AC D.∠EQF=25°12.(2022•百色)如图,是求作线段AB中点的作图痕迹,则下列结论不一定成立的是()A.∠B=45°B.AE=EB C.AC=BC D.AB⊥CD 13.(2022•营口)如图,在△ABC中,AB=AC,∠A=36°,由图中的尺规作图得到的射线与AC交于点D,则以下推断错误的是()A.BD=BC B.AD=BD C.∠ADB=108°D.CD=AD 14.(2022•鄂州)如图,直线l1∥l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为()A.10°B.15°C.20°D.30°15.(2022•枣庄)如图,在矩形ABCD中,按以下步骤作图:①分别以点B和D 为圆心,以大于BD的长为半径作弧,两弧相交于点E和F;②作直线EF 分别与DC,DB,AB交于点M,O,N.若DM=5,CM=3,则MN=.16.(2022•辽宁)如图,在△ABC中,AB=AC,∠B=54°,以点C为圆心,CA长为半径作弧交AB于点D,分别以点A和点D为圆心,大于AD长为半径作弧,两弧相交于点E,作直线CE,交AB于点F,则∠ACF的度数是.类型三依据要求直接作图17.(2022•淮安)如图,已知线段AC和线段a.(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)①作线段AC的垂直平分线l,交线段AC于点O;②以线段AC为对角线,作矩形ABCD,使得AB=a,并且点B在线段AC的上方.(2)当AC=4,a=2时,求(1)中所作矩形ABCD的面积.18.(2022•襄阳)如图,在△ABC中,AB=AC,BD是△ABC的角平分线.(1)作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);(2)求证:AD=AE.19.(2022•宁夏)如图,四边形ABCD中,AB∥DC,AB=BC,AD⊥DC于点D.(1)用尺规作∠ABC的角平分线,交CD于点E;(不写作法,保留作图痕迹)(2)连接AE.求证:四边形ABCE是菱形.20.(2022•赤峰)如图,已知Rt△ABC中,∠ACB=90°,AB=8,BC=5.(1)作BC的垂直平分线,分别交AB、BC于点D、H;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的条件下,连接CD,求△BCD的周长.类型四转化类作图21.(2022•陕西)如图,已知△ABC,CA=CB,∠ACD是△ABC的一个外角.请用尺规作图法,求作射线CP,使CP∥AB.(保留作图痕迹,不写作法)命题点2无刻度直尺作图类型一网格中作图22.(2022•长春)图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.(1)网格中△ABC的形状是;(2)在图①中确定一点D,连结DB、DC,使△DBC与△ABC全等;(3)在图②中△ABC的边BC上确定一点E,连结AE,使△ABE∽△CBA;(4)在图③中△ABC的边AB上确定一点P,在边BC上确定一点Q,连结PQ,使△PBQ∽△ABC,且相似比为1:2.23.(2022•江西)如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).(1)在图1中作∠ABC的角平分线;(2)在图2中过点C作一条直线l,使点A,B到直线l的距离相等.类型二根据图形性质作图24.(2022•湖北)已知四边形ABCD为矩形,点E是边AD的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.(1)在图1中作出矩形ABCD的对称轴m,使m∥AB;(2)在图2中作出矩形ABCD的对称轴n,使n∥AD.25.(2022•无锡)如图,△ABC为锐角三角形.(1)请在图1中用无刻度的直尺和圆规作图:在AC右上方确定点D,使∠DAC=∠ACB,且CD⊥AD;(不写作法,保留作图痕迹)(2)在(1)的条件下,若∠B=60°,AB=2,BC=3,则四边形ABCD的面积为.26.(2022•绥化)已知:△ABC.(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.27.(2022•扬州)【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O 作一条直线,使扇形的面积被这条直线平分;【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.(友情提醒:以上作图均不写作法,但需保留作图痕迹)11。
课件 基本尺规作图-【慕联】中考数学复习基本图形(二)

照设计要求,发射塔到两个城镇A,B的距
C1
离必须相等,到两条公路l1,l2的距离也必
须相等,发射塔C应修建在什么位置?请
用尺规作图找出所有符合条件的点,注明
C2
点C的位置(保留作图痕迹,不要求写出画 法).
P F
考点 基本尺规作图
如图,已知在△ABC中,∠A=90°. (1)请用圆规和直尺作出⊙P,使圆心P在 AC边上,且与AB,BC两边都相切(保留作图
A
37°
16°
D C
37°
B
考点 基本尺规作图
尺规作图的关键: (1)先分析题目,读懂题意,判断题目要求作什么. (2)读懂题意后,再运用几种基本作图方法解决问题. (3)作图时,要保留作图痕迹,作完后不要忘记写结论.
考点 基本尺规作图
E
在公路l1同侧、l2异侧有两个城镇A,B,如
D
图,电信部门要修建一座信号发射塔,按
AP=3 • tan30°
A 3 P
3
痕迹,不写作法和证明).
30°
(2)若∠B=60°,AB=3,求⊙P的面积.
B
C
=
π • AP2 =3π
慕联提示
亲爱的同学,课后请做一下相关的题 目进行巩固。这节课就到这里了,我们下 节课再见!
则直线CD即为所求.连结AC,BC,AD,BD,
根据她的作图方法可知,四边形ADBC一定是
( )B
形
考点 基本尺规作图
2.如图,在平面直角坐标系中,以点O为圆心,适
当长为半径画弧,交x轴于点M,交y轴于点N,再 分别以点M,N为圆心,大于 MN的长为1半径画弧,
中考复习 基本尺规作图
[慕联教育专题课程] 课程编号:ZS10202Z060401LL
2024年中考数学复习 瓜豆原理中动点轨迹直线型最值问题以及逆向构造(原卷版+答案解析)

瓜豆原理中动点轨迹直线型最值问题以及逆向构造【专题说明】近些年的中考中,经常出现动点的运动轨迹类问题,通常出题以求出轨迹的长度或最值最为常见。
很多考生碰到此类试题常常无所适从,不知该从何下手。
动点轨迹问题是中考的重要压轴点.受学生解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的一个黑洞.掌握该压轴点的基本图形,构建问题解决的一般思路,是中考专题复习的一个重要途径.本文就动点轨迹问题的基本图形作一详述.动点轨迹基本类型为直线型和圆弧型.其实初中阶段如遇求轨迹长度仅有2种类型:“直线型”和“圆弧型”(两种类型中还会涉及点往返探究“往返型”),对于两大类型该如何断定,通常老师会让学生画图寻找3处以上的点来确定轨迹类型进而求出答案,对于填空选择题而言不外乎是个好方法,但如果要进行说理很多考生难以解释清楚。
瓜豆原理:一个主动点,一个从动点(根据某种约束条件,跟着主动点动),当主动点运动时,从动点的轨迹相同.只要满足:1.两“动”,一“定”;2.两动点与定点的连线夹角是定角3.两动点到定点的距离比值是定值。
【引例】(选讲)如图,△APQ是等腰直角三角形,∠P AQ=90°且AP=AQ,当点P在直线BC上运动时,求Q点轨迹?【分析】当AP与AQ夹角固定且AP:AQ为定值的话,P、Q轨迹是同一种图形.当确定轨迹是线段的时候,可以任取两个时刻的Q点的位置,连线即可,比如Q点的起始位置和终点位置,连接即得Q点轨迹线段.【模型总结】必要条件:主动点、从动点与定点连线的夹角是定量(∠P AQ是定值);主动点、从动点到定点的距离之比是定量(AP:AQ是定值).结论:P、Q两点轨迹所在直线的夹角等于∠P AQ(当∠P AQ≤90°时,∠P AQ等于MN与BC夹角)P、Q两点轨迹长度之比等于AP:AQ(由△ABC∽△AMN,可得AP:AQ=BC:MN)如图,D 、E 是边长为4的等边三角形ABC 上的中点,P 为中线AD 上的动点,把线段PC 绕C 点逆时针旋转60°,得到P ’,EP ’的最小值【分析】结合这个例题我们再来熟悉一下瓜豆模型第一层:点P ’运动的轨迹是直线吗?第二层:点P ’的运动长度和点P 的运动长度相同吗?第三层:手拉手模型怎么构造?第四层:分析∠CAP 和∠CBP ’第五层:点P 和点P ’轨迹的夹角和旋转角的关系P'P'P'总共提到了3种处理方式: 1.找始末,定轨迹2.在轨迹上找一点旋转,构造手拉手模型,再通过角度相等得到从动点轨迹.3.反向旋转相关定点,构造手拉手模型,代换所求线段,即逆向构造. 那么什么具体选择什么方法更合适呢?我们再看一道例题 【例题2 宿迁中考】如图,正方形ABCD 的边长为4,E 为BC 上一点,且BE =1,F 为AB 边上的一个动点,连接EF ,以EF 为边向右侧作等边△EFG ,连接CG ,则CG 的最小值为 .现在,我们分别用上面提到的3种策略来处理这个题目策略一:找始末,定轨迹我们分别以BE ,AE 为边,按题目要求构造等边三角形得到G 1与G 2,连接G 1与G 2得到点G 的轨迹,再作垂线CH 得到最小值.前面提到过从动点轨迹和主动点轨迹的夹角与旋转角有关,我们可以调用这个结论,得到∠AMG 1=60°,BABABABA22进一步得到△MBG 1为等腰三角形后,求CH 就不难了.策略二:在点F 轨迹上找一点进行旋转.我们分别对A ,B 顺时针旋转60°,构造手拉手模型,再通过角度相等得到从动点轨迹,对A 点旋转会得到一个正切值为14的角,即1tan tan 4∠G M E =∠A FE=,然后进一步算出最值【简证】311202EM AE EN NEC IC ⇒°⇒∠,则5=2CH对B 点旋转得到∠EMG =∠FBE =90°,相对来说要容易一些.策略三:反向旋转相关定点,构造手拉手模型,代换所求线段.将点C 逆时针旋转60°,得到点H ,易证△CGE ≌△HFE ,则有CG =HF ,作MH ⊥AB 于M ,HM 即为所求.相比之下,先求轨迹后再求垂线段时,比较麻烦,而反向旋转代换所求线段感觉清爽很多.BABA如图,正方形ABCD 的边长为4,E 为BC 上一点,且BE =1,F 为AB 边上的一个动点,连接EF ,以EF 为底向右侧作等腰直角△EFG ,连接CG ,则CG 的最小值为 .如图,正方形ABCD 的边长为4,E 为BC 上一点,F 为AB 边上一点,连接EF ,以EF 为底向右侧作等腰直角△EFG ,连接CG ,则AG 的最小值为 .1.如图,在△ABC中,∠ACB=90°,AC=BC=4,点D是BC边的中点,点P是AC边上一个动点,连接PD,以PD为边在PD的下方作等边△PDQ,连接CQ.则CQ的最小值是2.如图,在矩形ABCD中,AB=5,BC=5 3,点P在线段BC上运动(含B、C两点),连接AP,以点A 为中心,将线段AP逆时针旋转60°到AQ,连接DQ,则线段DQ的最小值为3、如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转,使∠1=∠2,且过点D作DG⊥PG,连接CG.则CG最小值为瓜豆原理中动点轨迹直线型最值问题以及逆向构造【专题说明】近些年的中考中,经常出现动点的运动轨迹类问题,通常出题以求出轨迹的长度或最值最为常见。
中考数学复习轨迹和作图2[人教版]
![中考数学复习轨迹和作图2[人教版]](https://img.taocdn.com/s3/m/ba1bd4aa0b4e767f5bcfce16.png)
优游游戏 www.fqvukБайду номын сангаас.cn
提高功率因数的方法,是在负载上并联适当的电容。A、电阻性B、感性C、容性D、磁性 腹部触诊 转子推力盘的瓢偏度允许值为mm。A.0.01B.0.02C.0.03D.0.04 女性,68岁。慢性咳喘、咳痰近20年,近3年来症状加重,登二楼困难。有高血压病,服药控制较稳定。心电图示左心室肥大。昨傍晚无明确诱因突感胸闷、气急渐渐加重,不能平卧,彻夜未眠,今晨前来急诊。体检:端坐呼吸,紫绀。血压18/12kPa。气管位置无明显偏移。两肺叩诊过清音,呼 “依法治国,建设社会主义法治国家”被写入现行宪法是。A、1988年宪法修正案B、1993年宪法修正案C、1999年宪法修正案D、2004年宪法修正案 炎症早期用热可()A.促进炎症局限B.促进炎性渗出物的吸收和消散C.使白细胞吞噬功能下降D.使新陈代谢降低E.使组胺类物质堆积 电子商务的形式有A、EDI商务B、Internet商务C、Intranet商务D、电子合同 类风湿关节炎治疗的目的不包括A.控制关节疼痛B.防止关节破坏C.保护关节功能D.提高患者的生活质量E.彻底治愈疾病 如何理解危险具有普遍性? 促进乳房发育成熟的主要激素是A.雌激素B.孕酮C.肾上腺皮质激素D.催乳素E.生长素 实施CRM的具体目标可归结为提高、减低。 对于链球菌感染后急性肾炎,下列说法不正确的是A.电镜可见肾小球上皮细胞下有驼峰状大块电子致密物沉积B.免疫病理可见IgG、C3呈线条样沿毛细血管壁和系膜区沉积C.多在感染后1~3周起病,起病急、预后良好D.有持续性高血压、大量蛋白尿和肾功能损害者预后差E.有的患者可表现为肾病 尸检时肉眼见脾被膜明显皱缩、体积变小,重量减轻;脑组织色苍白。显微镜下脾窦内含血量明显减少,部分肺泡腔内有少量水肿液,肝小叶中央静脉周围肝细胞凝固性坏死,部分近端肾小管上皮细胞也呈现凝固性坏死改变,上述病变提示A.脾功能亢进B.肝硬化C.脑膜炎D.溶血性疾病E.失血性休 热水是指温度在以上的水,温水是温度在的水,冷水指以下的水。 公共关系的基本含义是什么? 虹膜炎继发性青光眼是由于()A.玻璃体大量炎症细胞B.房水分泌过多C.血-房水屏障功能破坏D.虹膜周边前粘连、瞳孔闭锁E.炎症反复发作使房角后退 男,50岁,咳嗽伴声音嘶哑3个月,右锁骨上窝触及一个肿大的淋巴结,质硬无压痛。提示该患者的诊断是A.喉炎B.肺癌C.胃癌D.鼻咽癌E.肺结核 HTK-196型车号自动识别设备系统工作频点是多少? 检测钩体病病原体应采取发病1周内的标本是A.局部分泌液B.小便C.脑脊液D.血液E.粪便 甲公司拟与乙公司合并(经营者集中),丙公司为甲公司直接控制的公司,丁公司为间接控制甲公司的公司。在确定甲公司的营业额时,根据反垄断法律制度的规定,下列表述中,不正确的是。A.丙公司的营业额应计入甲公司的营业额B.丁公司的营业额应计入甲公司的营业额C.丙公司和丁公司共 关于功能独立性评定(FIM)的作用不正确的描述是()A.用于确定患者功能丧失的严重程度、康复医学的成果B.评定康复部门或机构的效率与成果C.可以作为多学科、多机构之间研讨残疾问题的共同语言,促进小组成员间的交流D.用于残疾预后的估计E.医疗保险机构可依此确定支付或拒付 体温昼夜变化的特点是A.昼夜间呈现周期性波动B.清晨及午后体温均较高C.傍晚体温最低D.波动幅度在2℃以上E.体温波动与生物钟无关 下列各项,属对症治疗功效的是。A.止痛B.安神C.理气D.息风E.泻下 情感高涨与欣快症的区别点,下列哪项是错误的A.前者对任何事都感兴趣,表现出轻松愉快,洋洋自得;后者给人以呆傻、愚蠢的印象B.前者有较大的感染力;后者缺乏感染力,不能与正常人产生共鸣C.前者对知识和智力的利用增加;后者则下降D.前者与环境的协调性保持完整;后者与环境保持 在基于信息技术的自动的信息系统中,系统进行自动操作来实现对交易信息的创建、记录、处理和报告,并将相关信息保存为电子形式,相关控制活动也可能同时包括手工的分。A.订单的审批和事后审阅以及会计记录调整之类的手工控制B.电子的采购订单C.电子的采购D.电子的发运凭证和相关会 属于口腔癌瘤一级预防的是A.早发现B.早诊断C.早治疗D.病因预防E.防止复发 在改扩建管道施工图中,粗实线代表管子。A.新设B.原有C.预设D.遮蔽 红细胞破坏后,受何者吞噬A.单核-巨噬细胞系统B.单核细胞C.中性粒细胞D.脾E.肝 面神经迷路段由内耳道底前上方进入面神经管,于前庭与耳蜗之间到达膝神经节,此段最窄,其长度为()A.2~3mmB.3~5mmC.5~10mmD.10~12mmE.12~15mm 铸件上常出现金属小结的原因是A.包埋材料透气性差B.包埋材料调得过稠C.包埋时未完全包埋措型D.包埋材料调得过稀E.包埋材料中气泡末排尽 心肌灌注常用显像剂为A.['['C-PAB.F-FDGC.D.E. 以下哪个不是中秋节相关的传说A.鹊桥相会B.玉兔捣药C.嫦娥奔月D.吴刚伐桂 按血肿出现于头皮内的具体层次,头皮血肿可分为、和3种。 正常的肺间质主要包括的成分有A.血管B.细胞外基质C.肺泡结构D.支气管E.细胞 有经验的眼科医师可以从眼底检查中发现的血液疾病可能是()A.粒细胞缺乏症B.巨幼细胞贫血C.巨球蛋白血症D.轻型血友病E.皮肤性淋巴瘤 工业污水、船舶废弃物排放入海,会产生影响。A、损害海洋生物资源B、危害人体健康C、损坏海水使用素质D、A+B+C 某船Lbp=78m,吃水dm=4.80m,船宽B=12.2m,排水体积为2924m3,则其方形系数Cb为。(小吨位船试题)A.0.53B.0.64C.0.73D.0.68 民用爆炸物品使用单位申请购买民用爆炸物品的,应当向所在地人民政府公安机关提出购买申请。A.乡(镇)B.县级C.县级以上D.市级 数据通信网是一个有分布在各地的数据终端设备、数据交换设备和所构成的网络,在网络协议的支持下实现数据终端间的数据传输和交换。 CPD-A抗凝血的保存期为A.15天B.25天C.21天D.35天
人教版备考2023中考数学二轮复习 专题23 尺规作图(教师版)

人教版备考2023中考数学二轮复习专题23 尺规作图一、作图题1.(2022九上·深圳期中)定义:在边长为1的小正方形方格纸中,把顶点落在方格交点上的线段、三角形、四边形分别称为格点线段、格点三角形、格点四边形,在5×5的正方形网格中,若每一个小正方形的边长均为1,请仅用无刻度直尺按要求画图.(1)在图①中画一个以AB为边画一个格点正方形ABCD.(2)在图②中画一个格点平行四边形AEBF,使平行四边形面积为6.(3)在图③中画一个格点菱形AMBN,AMBN不是正方形(温馨提示:请画在答题卷相对应的图上)【答案】(1)解:画一个以AB为边画一个格点正方形ABCD,如图所示,(2)解:画一个格点平行四边形AEBF.如图所示,S▱AEBF=2×3=6;(3)解:画一个格点菱形AMBN,AMBN不是正方形,如图所示,【知识点】平行四边形的判定;正方形的判定;作图-直线、射线、线段【解析】【分析】(1)根据题意作图即可;(2)根据题意作图,再利用平行四边形的面积公式计算求解即可;(3)根据题意作图即可。
2.(2022七下·浑南期末)如图,在正方形网格中,△ABC的三个顶点均在格点上.(1)画出△A1B1C1,使得△A1B1C1和△ABC关于直线l对称;(2)过点C作线段CD,使得CD∥AB,且CD=AB.【答案】(1)解:△A1B1C1如图所示:(2)解:如图,CD1、CD2即为所求.【知识点】作图﹣轴对称;作图-直线、射线、线段【解析】【分析】(1)利用轴对称的性质找出点A、B、C的对应点,再连接即可;(2)根据要求作出图形即可。
3.(2022八上·瑞安月考)在5×5的正方形网格中,点A,点B均在格点上,连结AB,请根据要求完成下列作图:(1)在图1中找一个格点C,使得△ABC是直角三角形.(2)在图2中找一个格点D,使得△ABD是三个内角都是锐角的等腰三角形.【答案】(1)解:当∠A=90°或∠B=90°时;当∠C=90°时(2)当AB=BD时【知识点】等腰三角形的性质;勾股定理;作图-三角形【解析】【分析】(1)要使△ABC是直角三角形,分情况讨论,画出图形,当∠A=90°,当∠B=90°,当∠C=90°,分别画出符合题意的三角形.(2)利用勾股定理,根据两边相等的三角形是等腰三角形:当AB=BD时;当AB=AD时,画出三个角都是锐角的等腰三角形即可.4.(2022八上·北仑期中)如图,已知在△ABC中,∠A=120°,∠B=20°,∠C=40°,请在三角形的边上找一点P,并过点P和三角形的一个顶点画一条线段,将这个三角形分成两个等腰三角形.(要求两种不同的分法并写出每个等腰三角形的内角度数)【答案】解:如图,【知识点】等腰三角形的性质;作图-三角形【解析】【分析】由∠A=120°,可过点A作∠BAP=20°,则∠PAC=100°,∠APC=40°,则△APB、△APC 均为等腰三角形;可过点A作∠BAP=80°,则∠PAC=40°,∠APC=100°,则△APB、△APC均为等腰三角形;5.(2022八上·青田期中)如图,在△ABC中,点E在AB边上,请用直尺和圆规求作一点F,使得FE=FA,且F点到AB和BC的距离相等.(保留作图痕迹,不写作法)【答案】解:如图,点F为所作.【知识点】作图-角的平分线;作图-线段垂直平分线【解析】【分析】分别作∠ABC的平分线,线段AE的垂直平分线,两直线的交点即为点F. 6.(2022九上·博白月考)已知四边形ABCD为矩形,点E是边AD的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.(1)在图1中作出矩形ABCD的对称轴m,使m//AB;(2)在图2中作出矩形ABCD的对称轴n,使n//AD.【答案】(1)解:如图1中,直线m即为所求;(2)解:如图2中,直线n即为所求;【知识点】矩形的性质;作图-平行线【解析】【分析】(1)由矩形的性质作矩形的对角线,两条对角线的交点为O,过点O作AD的垂线交AD于点E,直线OE即为所求;(2)结合(1)的作法,过点O作OE的垂线交AB于点R,直线OR即为所求.7.(2022八上·嘉兴期中)如图,在△ABC中,AC=BC.尺规作图(保留作图痕迹,不写作法)⑴作边AC的垂直平分线;⑵在△ABC内确定一点O,使得点O到三个顶点的距离相等.【答案】解:解:⑴如图,直线l为所作;⑵如图,点O为所作.【知识点】作图-线段垂直平分线【解析】【分析】(1)根据垂直平分线的作法作图即可;(2)作出线段AB的垂直平分线,与AC的垂直平分线的交点即为点O.8.如图方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,ΔABC的顶点都在格点上,且三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).⑴画出△ABC关于原点O的中心对称图形△A′B′C′,并写出点B的对应点B′的坐标.⑵画出将△ABC绕原点O逆时针方向旋转90度后的图形△A′′B′′C′′.【答案】解:⑴如图,ΔA′B′C′即为所求,则点B′(−3,−4)⑵如图,ΔA′′B′′C′′即为所求.【知识点】作图﹣旋转【解析】【分析】(1)利用中心对称的性质,作出点A,B,C分别关于原点的对称点A′,B′,C′,再画出△A′B′C′,写出点B′的坐标.(2)利用旋转的性质,将△ABC绕着点O逆时针旋转90°,可得到对称点A",B",C",再画出△A"B"C".9.(2022八上·宝安期末)如图,在边长为1的小正方形所组成的网格上,每个小正方形的顶点都称为“格点”,△ABC的顶点都在格点上,用直尺完成下列作图.(1)作出△ABC关于直线MN的对称图形;(2)在网格中建立直角坐标系,使点A坐标为(−1,3);(3)在直线MN上取一点P,使得AP+CP最小.【答案】(1)解:作出点A、B、C关于MN的对称点A′、B′、C′,顺次连接,则ΔA′B′C′即为所求作的三角形,如图所示:(2)解:由点A坐标为(−1,3)可知,坐标原点在点A右侧一个单位,下方3个单位处,然后建立平面直角坐标系,如图所示:(3)解:连接A′C,交MN于点P,则点P即为所求,如图所示:【知识点】作图﹣轴对称;轴对称的应用-最短距离问题;平面直角坐标系的构成【解析】【分析】(1)利用轴对称的性质找出点A、B、C的对应点,再连接即可;(2)根据点A的坐标建立平面直角坐标系即可;(3)连接A′C,交MN于点P,则点P即为所求。
中考数学复习轨迹问题的解题策略

轨迹问题的解题策略对于初中数学中动点轨迹的问题,一般有两种情况:线段或圆弧.在研究动点问题时,可以在运动中寻找不变的量,即不变的数量关系或位置关系.如果动点的轨迹是一条线段,那么其中不变的量便是该动点到某条直线的距离始终保持不变;如果动点的轨迹是一段圆弧,那么其中不变的量便是该动点到某个定点的距离始终保持不变.因此,解决此类动点轨迹问题便可转化为寻找定直线或定点,下面就以原文中两个例题来阐明这类动点轨迹问题的解题策略.一、运动路径是线段例1(2012年张家界中考题)如图1,已知线段AB=6,C、D是AB上两点,且AC =DB=1,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为_______.解析此题中主动点是P,动点G是因点P的变化而变化,动点P在运动过程中始终保持不变的量是AP+BP=6.另外,题中还有不变的量是△APE和△PBF始终为等边三角形.解答此问题需牢牢把握住这两个不变的量,而既然是求动点G的运动轨迹,则需考虑点G是到某条直线的距离保持不变,还是到某个定点的距离保持不变,显然此题首先考虑的是点G是否到直线AB的距离保持不变,因此尝试作GQ⊥AB,垂足为Q.又根据△APE 和△PBF均是等边三角形这一性质,不难想到分别作EM⊥AB和FN⊥AB,垂足分别为M,N(如图2).此时容易得到EM =2AP ,FN =2BP ,所以EM +FN (AP +BP )=.再根据梯形中位线的性质,可得到CQ =12(EM +FN . 因此得到点G 到直线AB 的距离始终保持不变,从而得证点G 的运动轨迹是一条线段.而此时就点G 的运动路径长,便可转化为求点Q 的运动路径长,这时只要分别求出点P 在C 点和D 点时AQ 的长度即可.当点P 在点C 时(如图3),MQ 1=12MN =32, 所以AQ 1=AM +MQ 1=12+32=2.当点P 在点D 时(如图4),MQ 2=12MN =32, 所以AQ 2=AM +MQ 2=5322 =4. 所以点G 运动的路径长为4-2=2.事实上,点G 在运动过程中,MQ 的长度也是始终保持不变,因此G 的运动路径长度就是M 点的运动路径长度,而整个运动过程中M 点是从AC 的中点运动到AD 的中点,即M 1M 2(如图5).笔者认为,如果用这样的方式去分析问题,那么最终学生头脑中对整个变化过程会有一个全面而清晰的了解.此题的解题思路中还体现了转化思想,对培养学生的数学思维是有积极作用的.二、运动路径是圆弧例2(2011年湖州中考题)如图6,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.(1)求点D的坐标(用含m的代数式表示);(2)当△APD是等腰三角形时,求m的值;(3)设过P、M、B三点的抛物线与x轴正半轴交予点E,过点O作直线ME的垂线,垂足为H(如图7).当点P从点O向点C运动时,点H也随之运动,请直接写出点H所经过的路径长.(不必写解答过程)解析(1)、(2)略.(3)此题中主动点是P,动点H是因点P的变化而变化.动点P在运动过程中始终保持不变的量是OH始终垂直ME,即日始终为垂足.而求动点H的运动轨迹,则需考虑点H 是到某条直线的距离始终不变,还是到某个定点的距离始终保持不变.由于OH⊥ME,连结OM后,△AMH始终为直角三角形,而斜边OM不变,因此根据直角三角形的性质容易得到动点日到DM的中点的距离始终不变,从而可得到点H的运动轨迹是一段圆弧.下面只需确定圆弧的度数即可,即要找到动点H的始点和终点,根据图形的变化容易分析得动点H无限接近点C,因此可将点C定为动点H的终点.当点P在O点时,点H 在始点,记为H1,由对称性可知,此时点E的坐标为(3,0),作MN⊥OE,垂足为N,取DM的中点F,再连结FC、F H1(如图8).因为M点的坐标为(1,2),所以可得MN=NE=2,所以得到∠MEN=45°,所以∠H1OE =45°,所以∠H1OC=45°.因为C,D,H1,M四点共圆,所以∠CFH1=90°.又因为FC=OM,所以弧CH1的长为:902180π∙,所以点H所经过.以上两个例题刚好反映了初中数学轨迹问题中的两种典型情况.此类问题的解题策略便是确定动点到定直线的距离保持不变,还是到定点的距离保持不变.沿着这个思路走下去,便能找到变化过程中不变的量,从而找到解题的突破口.。
中考数学总复习 第27讲 尺规作图二次函数(基础讲练+锁定考试目标+导学必备知识+探究重难方法)(含

第27讲尺规作图考标要求命题趋势1.能用尺规完成五种基本作图.2.会写已知、求作,了解作图的道理,保留作图的痕迹,不要求写出作法.3.能运用尺规的基本作图方法解决作图的简单应用问题.中考对本部分内容的考查主要是利用尺规作图解决实际问题的能力,题型主要以设计、探究形式的解答题为主.知识梳理一、尺规作图1.定义只用没有刻度的__________和__________作图叫做尺规作图.2.步骤①根据给出的条件和求作的图形,写出已知和求作部分;②分析作图的方法和过程;③用直尺和圆规进行作图;④写出作法步骤,即作法.二、五种基本作图1.作一条线段等于已知线段;2.作一个角等于已知角;3.作已知角的平分线;4.过一点作已知直线的垂线;5.作已知线段的垂直平分线.三、基本作图的应用1.利用基本作图作三角形(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆).(2)作三角形的内切圆.自主测试1.如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于12AB的长为半径画弧,两弧相交于C,D两点,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )A.矩形B.菱形C.正方形D.等腰梯形2.用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是( )A.一组邻边相等的四边形是菱形B.四边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.每条对角线平分一组对角的平行四边形是菱形3.如图,△ABC是直角三角形,∠ACB=90°.(1)实验与操作利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).①作△ABC的外接圆,圆心为O;②以线段AC为一边,在AC的右侧作等边△ACD;③连接BD,交⊙O于点E,连接AE.(2)综合运用在你所作的图中,若AB=4,BC=2,则①AD与⊙O的位置关系是__________.②线段AE的长为__________.4.A,B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A,B两校的距离相等?如果有,请用尺规作图找出该点,保留作图痕迹,不求该点坐标.(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,并求出它的坐标.考点一、基本作图【例1】按要求用尺规作图(只保留作图痕迹,不必写出作法).(1)在图(1)中作出∠ABC的平分线;(2)在图(2)中作出△DEF的外接圆O.解:如图.方法总结依据基本作图的方法步骤,规范作图,注意一定保留好作图痕迹.触类旁通1画△ABC,使其两边为已知线段a,b,夹角为β.(要求:用尺规作图,写出已知、求作;保留作图痕迹;不在已知的线、角上作图;不写作法)已知:求作:考点二、基本作图的实际应用【例2】如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB,BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法).分析:∵圆与AB,BC都相切,∴圆心到AB,BC的距离相等.∴圆心应是∠ABC的角平分线与AC的交点.解:下图即为所求图形.方法总结要作一个圆与角的两边都相切,根据角平分线的性质,角平分线上的点到角两边的距离相等,即可解决问题.触类旁通2为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P 到该镇所属A村、B村、C村的村委会所在地的距离都相等(A,B,C不在同一直线上,地理位置如下图),请你用尺规作图的方法确定点P的位置.要求:写出已知、求作;不写作法,保留作图痕迹.1. (2012湖南益阳)如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB,AD,CD,则四边形ABCD一定是( )A.平行四边形B.矩形C.菱形D.梯形»FG2. (2012河北)如图,点C在∠AOB的OB边上,用尺规作出了CN∥OA,作图痕迹中,是( )A.以点C为圆心,OD为半径的弧B.以点C为圆心,DM为半径的弧C.以点E为圆心,OD为半径的弧D.以点E为圆心,DM为半径的弧3.(2012浙江绍兴)如图,AD为⊙O的直径,作⊙O的内切正三角形ABC,甲、乙两人的作法分别如下:甲:1.作OD的中垂线,交⊙O于B,C两点.2.连接AB,AC.△ABC即为所求作的三角形.乙:1.以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点.2.连接AB,BC,AC.△ABC即为所求作的三角形.A.甲、乙均正确B.甲、乙均错误C.甲正确,乙错误D.甲错误,乙正确4.(2012贵州铜仁)某市计划在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图所示,请在原图上利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)5. (2012山东德州)有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)1. 如图,锐角△ABC中,BC>AB>AC,小靖依下列方法作图:(1)作∠A的角平分线交BC于D点.(2)作AD的中垂线交AC于E点.(3)连接DE.根据他画的图形,判断下列关系何者正确?( )A.DE⊥AC B.DE∥AB C.CD=DE D.CD=BD2.如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO 长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于__________.3.数学活动课上,老师在黑板上画直线平行于射线AN(如图),让同学们在直线l和射线AN上各找一点B和C,使得以A,B,C为顶点的三角形是等腰直角三角形.这样的三角形最多能画__________个.4.如图,已知∠AOB,点M,N,求作点P,使点P在∠AOB的角平分线上,且PM=PN.(保留作图痕迹,不写作法)5.某汽车探险队要从A城穿越沙漠去B城,途中需要到河流l边为汽车加水,汽车在河边哪一点加水,才能使行驶的总路程最短?请你在图上画出这一点.6.如图,在△ABC 中,∠A =90°.(1)用尺规作图的方法,作出△ABC 绕点A 逆时针旋转45°后的图形△AB 1C 1(保留作图痕迹);(2)若AB =3,BC =5,求tan∠AB 1C 1.参考答案【知识梳理】 一、1.直尺 圆规 导学必备知识 自主测试1.B ∵分别以A 和B 为圆心,大于12AB 的长为半径画弧,两弧相交于C ,D ,∴AC =AD =BD =BC ,∴四边形ADBC 一定是菱形.故选B.2.B 由图形作法可知,AD =AB =DC =BC , ∴四边形ABCD 是菱形,故选B. 3.解:(1)如图,(2)①相切 ②47214.解:(1)存在满足条件的点C . 作出图形,如图所示.(2)作点A 关于x 轴对称的点A ′(2,-2),连接A ′B ,与x 轴的交点即为所求的点P.设A ′B 所在直线的解析式为y =kx +b ,把(2,-2)和(7,3)代入得⎩⎪⎨⎪⎧7k +b =3,2k +b =-2,解得⎩⎪⎨⎪⎧k =1,b =-4.∴y =x -4,当y =0时,x =4, ∴交点P 为(4,0). 探究考点方法触类旁通1.解:已知:线段a ,b ,角β. 求作:△ABC ,使边BC =a ,AC =b ,∠C =β. 画图(保留作图痕迹)触类旁通2.解:已知A 村、B 村、C 村,求作新建一个医疗点P ,使P 到该镇所属A 村、B 村、C 村的村委会所在地的距离都相等.品鉴经典考题1.A 由作图知,AD =BC ,AB =CD ,∴四边形ABCD 一定是平行四边形.2.D 根据尺规作一个角等于已知角的方法,即可知»FG是以点E 为圆心,DM 为半径的弧.3.A 根据甲的思路,作出图形如下:连接OB .∵BC 垂直平分OD , ∴E 为OD 的中点,且OD ⊥BC ,∴OE =DE =12OD .在Rt△OBE 中,∵OB =OD ,∴OE =12OB ,∴∠OBE =30°.又∠OEB =90°,∴∠BOE =60°. ∵OA =OB ,∴∠OAB =∠OBA . 又∠BOE 为△AOB 的外角, ∴∠OAB =∠OBA =30°,∴∠ABC =∠ABO +∠OBE =60°. 同理∠C =60°,∴∠BAC =60°, ∴∠ABC =∠BAC =∠C ,∴△ABC 为等边三角形,故甲的作法正确. 根据乙的思路,作图如下:连接OB ,BD .∵OD =BD ,OD =OB ,∴OD =BD =OB ,∴△BOD 为等边三角形, ∴∠OBD =∠BOD =60°.同理可知△COD 也为等边三角形,∠OCD =∠COD =60°, ∴∠BOC +∠OCD =∠BOD +∠COD +∠OCD =180°, ∴BO ∥CD .又∵△BOD 和△COD 是等边三角形, ∴四边形BDCO 是菱形, ∴∠OBM =∠DBM =30°.又OA =OB ,且∠BOD 为△AOB 的外角, ∴∠BAO =∠ABO =30°,∴∠ABC =∠ABO +∠OBM =60°, 同理∠ACB =60°,∴∠BAC =60°, ∴∠ABC =∠ACB =∠BAC ,∴△ABC 为等边三角形,故乙的作法正确.故选A. 4.解:作图如图所示.5.解:作图如图所示:研习预测试题1.B 依据题意画出图形.可得知∠1=∠2,AE =DE ,∴∠2=∠3, ∴∠1=∠3,即DE ∥AB .故选B. 2.12 3.34.解:如图,连接MN ,作线段MN 的垂直平分线EF ,∠AOB 的角平分线OC ,EF 与OC 相交于点P .则点P 即为所求.5.解:如图所示,点C 即为所求.6.解:(1)作∠CAB 的平分线,在平分线上截取AB 1=AB , 作C 1A ⊥AB 1,在AC 1上截取AC 1=AC , 如图所示即是所求.(2)∵AB =3,BC =5,∴AC =4, ∴AB 1=3,AC 1=4,tan∠AB 1C 1=AC 1AB 1=43.。
中考数学专题复习格点作图题(二)

中考数学专题复习格点作图题(二)学校:___________姓名:___________班级:___________考生__________评卷人得分一、解答题1.如图,在6×8的方格纸中有直线l,点A、B、C都在格点上.按要求画四边形,使它的顶点都在格点上,点A、B、C在它的边上(包括顶点).(1)在图①中画一个轴对称图形,使直线l是对称轴;(2)在图①中画一个中心对称图形,使直线l平分它的面积.2.图①、图①均为44⨯的正方形网格,线段AB、BC的端点均在格点上,按要求在图①、图①中作图并计算其面积.(1)在图①中画一个四边形ABCD,使四边形ABCD有一组对角相等,S四边形ABCD=;(2)在图①中画一个四边形ABCE,使四边形ABCE有一组对角互补,S四边形ABCE=.3.如图均是66⨯的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,ABC∆的顶点均在格点上.只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹.(1)在图中的线段AB上找一点D,连结CD,使BCD BDC∠=∠.(2)在图中的线段AC上找一点E,连结BE,使ABE BAE∠=∠.(3)在图中的线段AC上找一点F,连结BF,使CBF CFB∠=∠.4.图①、图①、图①都是44⨯的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB的端点都在格点上,在给定的网格中,只用无刻度的直尺,在图①、图①、图①中,按下列要求画图,只保留作图痕迹,不要求写出画法,所画的图形的顶点均在格点上.(1)在图①中画一个ABC,使其面积为2.(2)在图①中画一个ABD△,使其面积为4.(3)在图①中画一个四边形ABEF,使其面积为5.5.如图,网格中有一条线段AB,点A、B都在格点上,网格中的每个小正方形的边长为1.请在图①和图①中各画出一个格点ABC,使ABC是直角三角形,且90ACB∠=︒,并满足以下要求:(1)在图①中画出的三角形的两条直角边的长度均为有理数(画出一个即可).(2)在图①中画出的三角形的两条直角边的长度均为无理数(画出一个即可).(3)满足(1)、(2)的ABC共有个.6.如图,在66⨯的方格纸中,每个小正方形的边长为1,每个小正方形的顶点称为格点,请按要求画出格点三角形与格点四边形.(1)在图1中以线段AB为边画一个格点ABC∆,使2AB BC=;(2)在图2中以线段AB为边画一个格点四边形ABCD,使其面积为7,且90BAD∠=︒.7.在6×6的正方形网格中,①ABC的顶点均在格点上,请用无刻度直尺画图.(保留必要的画图痕迹)(1)在图1中,画一个与①BAC相等的①BDC,且点D在格点上.(2)在图2中,画一个与①ABC面积相等,且以BC为边的平行四边形BCDE,D、E均在格点上.(3)在图3中,在AC上找一点D,连接BD,使①ABD的面积是①BCD面积的4倍.参考答案:1.(1)作图见解析;(2)作图见解析.【解析】(1)根据轴对称图形的定义画出图形即可.(2)根据中心对称图形作出图形即可.【详解】解:(1)轴对称图形如图所示(答案不唯一).(2)中心对称图形如图所示(答案不唯一).【点睛】本题考查作图-旋转变换,轴对称图形,中心对称图形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.2.(1)6;(2)92.【解析】【分析】(1)过C画AB的平行线,过A画BC的平行线,两线交于一点D,根据平行四边形的判定定理可得四边形ABCD是平行四边形,由平行四边形的性质可知①CBA=①CDA,然后用用割补法求出面积即可;(2)根据图中正方形网格和①B的特点,作出①E与①B互补,然后用割补法求面积即可.【详解】解:(1)如图,S四边形12223422622ABCD ⨯⨯=⨯-⨯-⨯=, (2)如图,S 四边形12221193322222ABCE ⨯⨯⨯=⨯-⨯--=. 【点睛】此题主要考查了应用设计作图.首先要理解题意,弄清问题中对所作图形的要求,然后利用割补法求面积.3.(1)见解析;(2)见解析;(3)见解析【解析】【分析】(1)根据等腰三角形的性质,在AB 上取一点D 使得3BD BC ==即可;(2)根据矩形的性质,可以得到点E 的位置;(3)由题意可知,利用三角形相似的性质,对AC 进行分段,使得3CF =.【详解】解:(1)取格点D ,连接CD 即可,如下图:(2)取格点P ,连接BP ,交AC 于点E ,如下图:则ABE BAE ∠=∠;(3)如图,取格点H 、N ,连接HN ,交AC 于点F ,连接BF ,①CH ①AB ,①ANF CHF △∽△,3CH =、2AN =,①23AN AF CH CF ==,则CF =35AC , ①AB =4,BC =3,①AC =22435+=,①CF =35AC =3, ①CF =BC =3,①CBF CFB ∠=∠.①点F 即为所求作.【点睛】此题主要考查了等腰三角形、矩形、相似三角形等有关性质,熟练掌握和应用有关知识的性质是解题的关键.4.(1)见解析;(2)见解析;(3)见解析【解析】【分析】(1)取格点C ,连接AC 、BC ,利用三角形的面积的计算方法得出符合题意的图形;(2)在(1)的基础上作点A关于BC的对称点D即可;(3)在(2)的基础上增加一个面积为1的三角形即可.【详解】(1)取格点C,连接AC、BC,如图所示,①ABC即为所求:①AC=2,BC=22,AB=221310+=,由于()()()22222210+=,①222AC BC AB+=,①△ABC是直角三角形,且①ACB=90°,①11222222ABCS AC BC=⨯=⨯⨯=;(2)如图所示,①ABD即为所求;(3)如图所示,四边形ABEF即为所求;.【点睛】本题考查了作图-应用与设计,勾股定理,勾股定理的逆定理,三角形面积等知识,解题的关键是理解题意,灵活运用所学知识解决问题.5.(1)见解析;(2)见解析;(3)6.【解析】【分析】(1)根据要求作出图形即可,有两种情形,任意一种即可;(2)根据要求作出图形即可,有四种情形,任意一种即可;(3)根据(1)(2)的图形即可解答.【详解】解:(1)点C的位置如图①所示,①ABC、①ABC1中任意一个即为所求;(2)点C的位置如图①所示,①ABC、①ABC1、①ABC2、①ABC中任意一个即为所求;(3)如图可得:满足(1)的ABC共有2个,满足(2)的ABC有4个,则满足(1)、(2)的ABC共有共有6个.【点睛】本题主要考查了基本作图、无理数、直角三角形等知识,掌握数形结合的思想成为解答本题的关键.6.(1)图见详解;(2)图见详解【解析】【分析】(1)由图及题意易得10AB,进而可得5BC=,然后问题可求解;(2)根据题意及旋转的性质可先作出90BAD∠=︒,然后再利用割补法进行作图即可.【详解】解:(1)由题意得:10AB,①2AB BC=,①5BC=,则以线段AB 为边画一个格点ABC ,如图所示:(2)由题意可得如图所示:【点睛】本题主要考查勾股定理及旋转的性质,熟练掌握勾股定理及旋转的性质是解题的关键. 7.(1)见解析(2)见解析(3)见解析【解析】【分析】(1)如图,根据网格的特点以及对称性找到点D ,连接,BD DC ,则BDC BAC ∠=∠; (2)根据题意,与①ABC 面积相等,且以BC 为边的平行四边形BCDE ,则平行四边形BC 边上的高等于ABC 中,BC 边上高的一半,根据网格的特点,在格点上找到点D ,E ,连接,,CD DE EB 即可;(3)根据勾股定理求得5AC =,找到5FC =,根据网格的特点作GH AF ∥,根据平行线分线段成比例可得14CD DA =,即找到符合题意的点D . (1)如图所示,BDC BAC ∠=∠且D 在格点上,(2)如图,(3)如图,22345AC =+=作AF GH ∥14CD CH DA FH ∴== ∴①ABD 的面积是①BCD 面积的4倍.则点D 即为所求.【点睛】本题考查了作轴对称图形,作平行四边形,平行线分线段成比例,掌握以上知识是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下列哪一项不是家庭资产负债表中实物资产项目应该包括的内容。A.现金B.汽车C.房屋D.首饰 在长途三级信令网中,第一级采用A、B平面连接,A和B平面间为格子状连接。 正常运行时下降管及水冷壁下联箱是否可以作为放水阀来使用? 产生闭锁综合征脑梗死部位位于A.双侧脑桥基底部B.双侧中脑腹侧C.双侧脑桥背部D.双侧丘脑E.双侧内囊 植物的最大需水期 原砂的性能指标主要指那些? ___是对各种信息技术的理解和运用的能力。A.信息能力 B.判断分析能力 C.推理能力 D.表达能力 已知风险组合M的预期报酬率和标准差分别为15%和20%,无风险报酬率为8%,假设某投资者除自有资金外还可以按无风险利率取得20%的资金,并将其投资于风险组合M.则投资组合的总预期报酬率和总标准差分别为()。A、16.4%和24%B、13.6%和16%C、16.75%和12.5%D、13.65%和25% 患者Berg平衡量表得30分提示A.需乘坐轮椅B.无法步行C.步行需辅助D.可独立步行E.无跌倒危险 某县侦查机关接到特情人员王某密报:某农村多人贩卖鸦片,农民某甲和某乙有贩卖毒品鸦片的嫌疑最大。公安机关立案后,经过公安机关负责人批准,对乙实施技术侦查,采取全天跟踪监控措施。侦查人员嘱王某加强对甲的观察,必要时可以靠上去,确证后再报。王某遂接近某甲,问其是否有 美国管理学家莱金(Lakein)提出了A.目标管理法B.ABC时间管理法C.成果管理法D.计划管理法E.效益管理法 矿井竣工工期(或建井工期)是指从项目正式开工之El起到按照设计规定,并经过试生产,试运转后正式交付生产所经历的时间。A.施工人员进场B.竣工完成建设工程C.开始场内施工准备工作D.施工许可证办理完毕 乌龙茶的产地主要有哪几个省? 手术护理记录由巡回护士在手术结束后及时完成。A.正确B.错误 监理招标有哪些特点? CDMA采用独特的,降低了掉话率。 关于情绪、情感的作用表述不正确的是A.积极的情绪、情感有助于工作效率的提高B.消极的情绪、情感会影响工作效率C.只有在身心放松的状态下才能发挥最佳工作效率D.情绪是心身联系的纽带,临床上许多常见病都与不良情绪有关E.人际情感一旦形成就不易改变 是银行盈利能力分析中既考虑预期损失,有考虑非预期损失,同时也是银行进行价值管理的核心指标。A.风险调整后资本回报率B.净利息收益率C.平均净资产回报率D.拨备前利润 商业空间设计环境特征较为活跃,讲求极佳的展示效果并具有较强的,其目的是为了吸引购物者。A.顾客吸引力B.设计特征C.视觉冲击力D.第一印象 将一切造价纠纷通过业主、监理工程师和承包商的共同努力得到解决,既由合同双方根据工程项目的合同文件规定及有关的法律条例,通过有好商量和妥协达成一致的解决工程造价争议纠纷的途径是。A.友好协商解决B.调解解决C.仲裁D.诉讼解决 异相睡眠期电活动相当于.A.慢波四期B.慢波三期C.慢波二期D.慢波一期 改建工程竣工后,应按规定进行验收。在确认工程符合技术标准、设计文件的要求,并检查竣工文件和技术设备使用说明书等资料齐全后,方可交接。A.正确B.错误 舌弓指A.第一鳃弓B.第一鳃沟C.第二鳃弓D.第二鳃沟E.第三鳃弓 安定面配平可以通过来完成A.主电配平B.自动驾驶配平C.人工用钢索配平D.以上都对 “甘温除热”的代表方是A.四君子汤B.参苓白术散C.归脾汤D.补中益气汤E.生脉散 良好的职业道德有利于人们养成的道德习惯。A.优良B.良好C.善良D.良性 用SPECT进行局部脑血流断层显像(rCBF)诊断脑梗死时,下面哪一项不是其特征表现()A.rCBF显像表现为病灶局部放射性缺损B.rCBF显像所显示的放射性缺损面积往往大于CT和MRIC.病灶四周放射性异常增高D.病灶对侧小脑的放射性减低,又称交叉性小脑失联络E.出现多个类圆形放射性增高区 平均型吃水是指在船舶中线面上,从正浮水线沿垂直于基平面的方向量到龙骨板的垂直距离。A.上边缘B.中心C.下边缘D.视具体情况而定 行单纯乳突切开术时在乳突尖与耳垂连线中点皮下注射麻醉药2ml是为了阻滞哪根神经A.耳颞神经外耳道支B.耳大神经C.迷走神经耳支D.枕小神经E.面神经 颞叶性癫痫是指A.发作形式多为复杂部分性发作B.病因多为海马硬化C.EEG检查有时需加蝶骨电极D.表现为各种类型遗忘症E.有时为不典型失神发作 在WPS处于改写状态时,若光标已位于文本的最后一行,这时按回车键,结果是。A.仅简单地将光标移到本行行尾B.仅简单地将光标移到本行行首C.插入一行D.没有任何变化 一护士遵照医嘱给某病人服药,待病人服药后该护士才想起给患者服错了药,就漫不经心地站在走廊一头对另一头的护士大喊:"老张头儿吃错药了!"此话被患者听到后,急忙自己寻来肥皂水喝下打算把"错药"呕吐出来,结果引发了严重呕吐加上心力衰竭当场死亡。事后经查吃错的药是维生素B 患者,68岁,急性心肌梗死,一旦出现房颤。患者此时最可能出现的脉搏异常()A.间歇脉B.二联律C.缓脉D.短绌脉E.洪脉 当单元机组的汽轮机发电机跳闸时,要求锅炉维持运行,必须投入。A、灭火保护系统;B、协调控制系统;C、燃烧控制系统;D、旁路系统。 车辆行驶中,放开调速踏板,行驶电机不断电,车辆失控,驾驶员应。A、拔下总电源开关B、立即踏下制动踏板C、拔下总电源开关并踏下制动踏板D、拔下电源线 泰勒的科学管理理论和制度主要是从劳动者的方面研究劳动效率问题。A.行为和思想B.生理和物理C.科学和哲学D.动作和时间 我国女性生殖器官恶性肿瘤发生率最高的是。A.子宫颈癌B.子宫内膜癌C.子宫肉瘤D.卵巢癌E.绒毛膜上皮癌 稳性力矩是指。A.船舶倾斜前后两浮力作用点距离与排水量之积B.船舶倾斜前后两重力作用点距离与排水量之积C.船舶自身具备的惯性力矩D.船舶重力与浮力作用线之间垂直距离与排水量之积 人乳哺育者,每日需要的蛋白质量是。A.1g/kgB.2g/kgC.3g/kgD.4g/kgE.5g/kg 内容产业包括。A.计算机业B.电信业C.旅游业D.制造业E.媒体业
