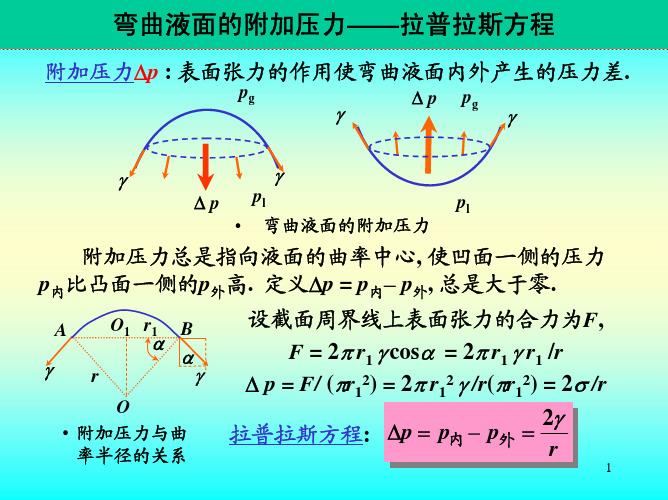
2 弯曲液面的附加压力
弯曲液面的附加压力拉普拉斯方程
(1) 过饱和蒸气: 按相平衡条件应当凝 p 结而未凝结的蒸气. 原因是蒸气不能 变成化学势更高的微小液滴.
过饱和蒸气的压力超过了相应温 度下通常体积液体的饱和蒸气压, 但 仍小于该液体微小液滴的饱和蒸气压 (见图示). 引入凝结中心可使液滴核心易于生 成, 减轻过饱和程度(如人工降雨).
过饱和蒸气的产生 4 g
在过冷液体中投入小 晶体作为新相的种子, 能使 液体迅速凝固.
气相区
T′ f Tf
T
6
过冷液体的产生
亚稳状态及新相的生成
(4) 过饱和溶液: 在一定温度下, 浓度超过饱和浓度, 而仍未析 出晶体的溶液. 原因是微小晶粒具有高表面吉布斯函数(高的 饱和蒸气压)而不能在正常饱和浓度下析出.
与微小液滴一样, 微小晶体的 饱和蒸气压大于普通晶体. 蒸气压 与溶解度有密切的关系, 微小晶粒 具有比普通晶体更大的溶解度. 晶 体的颗粒愈小, 溶解度愈大. (见图) 可知, 当溶液浓度达到普通晶 体的饱和浓度时, 相对于微小晶粒 还未饱和, 微小晶粒就不能从中析 出.
p2 (g ) Vm (l ){ p2 (l ) p1 (l )} ln = p1 (g ) RT (Vm = M / ρ )
用 p 和 pr 分别表示平面液体和微小液滴的蒸气压, 结合 拉普拉斯方程, 得 小液滴 3
Pr / p
pr 2γ M 开尔文公式: RT ln = p ρr
2 1 平面液体
式中液面曲率半径 r1 与毛细管半径 r 及接 触角 θ 间的关系为:
r1 r
θ
θ
h
cosθ = r / r1
2 γ cos θ h= rρ g
γ : 液体表面张力; ρ: 液体密度;
g : 重力加速度.
界面现象

第九章 界面现象讲解:日常生活和生产中,有很多现象和界面有关。
如:水在玻璃细管中会上升,这叫毛细现象;水可以在桌面上铺开,水银却成球状等。
通常把气液和气固界面成为表面。
第一节 表面张力和表面吉布斯函数一、表面现象及其本质 1.界面层的定义界面的5种类型:g-l,g-s,l-l,l-s,s-s. 其中g-l 和g-s 界面也叫表面。
界面分子和内部分子的区别:内部分子受力对称,界面分子受力不对称,不均匀。
液体自发使表面积缩小。
讲解:测定液体蒸气压,不能有空气存在,液体表面指纯液体与其纯蒸气之间的过渡层,只有几个分子厚。
日常生活中讲的液体表面,是指液体与空气之间的界面,其中空气被液体蒸气饱和。
2.系统的比表面(分散度)单位质量具有的表面积,或单位体积具有的表面积。
def defS S m V A AA A m V==质量表面积体积表面积例:一个边长为0.01米的立方体表面积是多少?把这个立方体分成10-9m 的小立方体,求其总面积。
解:边长为0.01米的立方体表面积 2-421=60.01=610m A ⨯⨯()321390.011010-=小立方体的个数为-92213226(10)10610m A =⨯⨯=⨯小立方体总面积物体被分散后的体积变化,请看358页表9.1。
二、表面张力、表面功、表面吉布斯函数 在等温等压条件下者3个概念是一回事。
讲解:吉布斯函数变就是等温等压条件下可逆过程得体积功。
:γ等温等压下可逆地增加单位表面积所需的功。
B,,S T p n G A γ⎛⎫∂=⎪∂⎝⎭ 表面张力就是表面功表面张力F:表面上,每米长度所受的收缩力,垂直于表面切线方向。
-2-2-1J m N m m N m⋅=⋅⋅=⋅单位: 表面功 表面张力2F l γ= 2Flγ= 影响表面张力的因素 (1)物质的本性()()s l γγ>一般相同聚集态时(γγγγ>>>金属键)(离子键)(极性共价键)(非极性共价键)讲解:可以看出键的极性越强,σ越大,因为非极性共价键组成的非极性分子之间只有色散力,极性分子间有色散力、取向力、诱导力。
09章 表面现象
所有点产生的合力之和为 ps
这合力称为附加压力,指向圆心 气泡内壁受的总压力为
p0 ps
ps p0
A
溶液
ps
二、Laplace 公式
Laplace公式给出了附加压力、表面张力与曲率
h高度的水柱压力就等于 附加压力
p 0
h
B
管内液面上升后又达成
了新的平衡
H2O
纯水与管壁的接触角小 于90º
ps
2
R'
(l g )gh
(l g ) 代表管内液
体和管外气体的密度差
忽略管外气体的密度,
得
2
R'
l gh
若管外是另一种液体,
则2
R'
(l,内 l,外 )gh
界面(interface)
不同相态之间,两相紧密接触、约有几个分子 厚度的过渡区,称为该两相的界面。
常见的界面有: 气-液界面 气-固界面
液-液界面
液-固界面 固-固界面 但没有气-气界面,不同气体接触总是很快就
混合均匀。
气-液界面
空气
CuSO4 溶液
气-液 界面
气-固界面
气-固界面
液-液界面
p 0
A
Hg
h
ps
2
R'
(g l )gh
lgh
( g
l
)代表管内气体
和管外液体的密度差
忽略管内气体的密度,
第二章 液体表面

表面能是指表面所具有的内能。 表面能是指表面所具有的内能。实际表面的内能的绝对值是无法测量 的,可以测量到的仅是当物质状态发生改变时,其内能的改变量∆U 可以测量到的仅是当物质状态发生改变时,其内能的改变量∆ ∆U = Q + W Q为体系自环境吸收的热量;W为环境对体系做的功 为体系自环境吸收的热量; 为环境对体系做的功 为体系自环境吸收的热量
从液相内部将一个分子移到表面层要克服这种分子间引力而做功, 从液相内部将一个分子移到表面层要克服这种分子间引力而做功, 从而使系统的自由能增加;反之,表面层分子移人液体内部, 从而使系统的自由能增加;反之,表面层分子移人液体内部,系统 自由能下降。 自由能下降。
因为系统的能量越低越稳定,故液体表面具有自动收缩的能力。 因为系统的能量越低越稳定,故液体表面具有自动收缩的能力。
附加压力与曲率半径的关系Laplace方程 附加压力与曲率半径的关系Laplace方程 设在大气压为P 的液面下,有一半径为r的气泡, 设在大气压为P外的液面下,有一半径为r的气泡,若 维持这一气泡平衡,则气泡内的压力须等于P 维持这一气泡平衡,则气泡内的压力须等于P外+P附。 下可逆地推动活塞,使气泡半径由r 在压力P 在压力P外+P附下可逆地推动活塞,使气泡半径由r增加 一微量dr 这时气泡的体积和面积也相应地增加dV dA。 dr。 dV和 一微量dr。这时气泡的体积和面积也相应地增加dV和dA。 整个过程中,因活塞上的大气压力和泡外的大气压力互 整个过程中, 相抵消,所以实际上就是克服了附加压力作了体积功。 相抵消,所以实际上就是克服了附加压力作了体积功。 此功等于增大表面积的功, 此功等于增大表面积的功,即 P附dV = σdA P附 = σ (dA/dV) 因 得 4π 8π A = 4πr2 dA = 8πrdr 2σ P附 = 2σ/r (4/3)π V = (4/3)πr3 (2 - 5 ) dV=4π dV=4πr2dr
弯曲液面的一些现象.

液体(T,pl)/ 饱和蒸汽(T,pg),相平衡时化学势相等
Gm (g) Gm (l) dpg dpl pl T pg T
Vm (l)dpl Vm (g)dpg
Vm (l) dpl RT d ln pg
pl,0 pg,0 pl pg
' ,则: 8. 如果是球面, R1' R2
2 Ps R'
2.对活塞稍加压力,将毛细管内液 体压出少许,使液滴体积增加dV, 相应地其表面积增加dA。克服附加 压力ps环境所作的功与可逆增加表 面积的吉布斯自由能增加应该相等。
4 V R '3 3
dV 4 R '2 dR '
弯曲液体表面的蒸气压—Kelvin公式
液体(T,pl)/ 饱和蒸汽(T,pg),相平衡时化学势相等
对小液滴与蒸汽的平衡,应有相同形式, 设气体为理想气体。 化学势的定义 对于单组分体系
B ( )
G nB T , P , nC ,( C B )
Gm (l) Gm (g)
Gm (g) Gm (l) dpg dpl pl T pg T
§7.2 弯曲液面的一些现象
1.在平面上
弯曲表面下的附加压力
2.在凸面上
3.在凹面上
1.在平面上
设向下的大气压 力为Po,向上的反作 用力也为Po ,附加压 力Ps(ΔP,以后用Ps表 示)等于零。
Ps = Po - Po =0
剖面图
平面分子受力俯视图
(2)在凸面上: 表面张力都与液 面相切,大小相 等,但不在同一 平面上,所以会 产生一个向下的 合力。 所有的点产生的总压力为Ps ,称为 附加压力。凸面上受的总压力为:
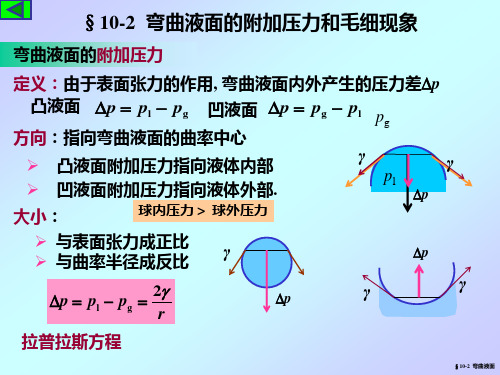
弯曲液面的附加压力

2
R'
gh
1g
当 1 g
2
h
R '1g
1.曲率半径 R'与毛细管半径R的关系:
R´ R
cos
如果曲面为球面
R'=R, cos 1
2. ps 2R´ (l g)gh
2
R´
gh
ps
2cosgh
R
1.曲率半径 R'与毛细管半径R的关系:
RTln
pr p0
2M R'
p p0
2 M RTR '
Kelvin公式也可以表示为两种不同曲率半径的
液滴或蒸汽泡的蒸汽压之比
RTlnp2 p1
2MR12'
R11'
对凸面,R' 取正值,R' 越小,液滴的蒸汽压越高;
对凹面, R' 取负值, R' 越小,小蒸汽泡中的 蒸汽压越低。
z
使曲面扩大到A'B'C'D'(蓝色面),
则x与y各增加dx和dy 。
Young-Laplace 公式
移动后曲面面积增量为: d A s (x d x )(y d y ) x y
D'
x dx C'
o'
x d y y d x(d y d x 0 )
增加这额外表面所需功为
A'
pg
2
r
ppg
pl
2
r
③肥皂泡
p p i p o ( p g ,i p l) ( p l p g ,o )
④毛细管连通的大小不等的
弯曲表面的性质
二、曲面的蒸气压
液滴(气泡) 液滴(气泡)半径与蒸气压关系
r /m 小液滴 pr* / p* 小气泡 105 1.0001 0.9999 106 1.001 0.9989 107 1.011 0.9897 108 1.114 0.8977 109 2.937 0.3405
从表中的数据可以看出: 从表中的数据可以看出: 当液体的曲率半径较大时,蒸气压的改变并不明显, 当液体的曲率半径较大时,蒸气压的改变并不明显, 当曲率半径小于10 当曲率半径小于 8 m时,蒸气压的变化超过 时 蒸气压的变化超过10%; ; 当曲率半径减小至10 当曲率半径减小至 9m时,蒸气压的变化已有三倍之多。 时 蒸气压的变化已有三倍之多。
式中a 和分别为与微小晶体及普通晶体成平衡时溶液(饱和 式中 r和分别为与微小晶体及普通晶体成平衡时溶液 饱和 溶液)的活度 的活度, 为固液界面张力。 溶液 的活度,σsl为固液界面张力。 根据上式可以得知: 根据上式可以得知: 晶体溶解度和其粒子半径成反比, 晶体溶解度和其粒子半径成反比,越小的晶体颗粒溶解度 越大。 越大。 实验室中常采用陈化的方法来得到较大的晶体。 实验室中常采用陈化的方法来得到较大的晶体。
二、曲面的蒸气压
(一)弯曲液面的蒸气压——开尔文公式 弯曲液面的蒸气压 开尔文公式 用热力学的基本原理可以导出在指定温度下液体的蒸气 压和曲率半径之间的关系。 压和曲率半径之间的关系。 的球形液滴或气泡,在温度T 曲率半径为 r 的球形液滴或气泡,在温度 下的蒸气压 为 pr* ,液体在此温度下的正常蒸气压为 p*
任意区域 表面张力合力= 表面张力合力 0
p内 凸面 p外 p p内 凹面 p外 p p内 p 附加压力 p p内 = p外 + p
弯曲表面的附加压力和蒸气压

Kelvin公式的应用:可以解释过饱和蒸气,过热液
体,过冷液体,过饱和液体等亚稳态的存在
例如:过饱和蒸气
在无杂质的情况下,水蒸汽可达很大的过饱和度 (常常几倍)而无水滴凝结。因为此时对于将要形 成的微小液滴来说,其蒸气压很大,尚未达饱和。 但若有杂质(灰尘微粒)存在,则初始的凝聚可在 微粒表面上进行(微粒半径较大,饱和蒸气压小),
2.859
18
过热液体:
沸腾时, 液体生成的微小气泡为凹面, 蒸汽压低
(Kelvin公式),另外由laplace 公式,
⊿P=2γ/R’,
2 所以沸腾条件: P' (气泡内部)( P大气+ ) r
P 2Vl RT ln 0 P R
R' 0 正常沸点下, P' P0
所以出现过热或暴沸现象, 可加入多孔沸石
28
1. 液-固粘附功:将单位
面积的液-固粘附在一起
体系所作的(可逆)功
体系作功:-Wa = G = G S = ( SL L S )
Wa>0,
液体沾湿固体的条件。
|Wa|越大,体系越稳定,液固的沾湿性越好 如,农药在植物叶面上的沾附
SL, S 难以测量!!
29
2. 液-固浸湿功 将单位表面积的固体浸 入液体时体系作的可逆 功叫液-固浸湿功 。 体系作功: -Wi = G = G S = ( SL S )
Wi>0, 液体自动浸湿固体的条件
30
3. 液-固铺展系数 铺展过程是固液界面取代气固界 面的过程,同时扩大了气液界面 γl γs S
γsl
G gl sl gs
或者S =- △G= γgs –γgl – γls;
物理化学表面现象练习题(含答案及详细讲解)

物理化学表面现象练习题一、判断题:1.只有在比表面很大时才能明显地看到表面现象,所以系统表面增大是表面张力产生的原因。
2.对大多数系统来讲,当温度升高时,表面张力下降。
3.比表面吉布斯函数是指恒温、恒压下,当组成不变时可逆地增大单位表面积时,系统所增加的吉布斯函数,表面张力则是指表面单位长度上存在的使表面张紧的力。
所以比表面吉布斯函数与表面张力是两个毫无联系的概念。
4.恒温、恒压下,凡能使系统表面吉布斯函数降低的过程都是自发过程。
5.过饱和蒸气之所以可能存在,是因新生成的微小液滴具有很低的表面吉布斯自由能。
6.液体在毛细管内上升或下降决定于该液体的表面张力的大小。
7.单分子层吸附只能是化学吸附,多分子层吸附只能是物理吸附。
8.产生物理吸附的力是范德华力,作用较弱,因而吸附速度慢,不易达到平衡。
9.在吉布斯吸附等温式中,Γ为溶质的吸附量,它随溶质(表面活性物质)的加入量的增加而增加,并且当溶质达饱和时,Γ达到极大值。
10.由于溶质在溶液的表面产生吸附,所以溶质在溶液表面的浓度大于它在溶液内部的浓度。
11.表面活性物质是指那些加入到溶液中,可以降低溶液表面张力的物质。
二、单选题:1.下列叙述不正确的是:(A) 比表面自由能的物理意义是,在定温定压下,可逆地增加单位表面积引起系统吉布斯自由能的增量;(B) 表面张力的物理意义是,在相表面的切面上,垂直作用于表面上任意单位长度切线的表面紧缩力;(C) 比表面自由能与表面张力量纲相同,单位不同;(D) 比表面自由能单位为J·m-2,表面张力单位为N·m-1时,两者数值不同。
2.在液面上,某一小面积S周围表面对S有表面张力,下列叙述不正确的是:(A) 表面张力与液面垂直;(B) 表面张力与S的周边垂直;(C) 表面张力沿周边与表面相切;(D) 表面张力的合力在凸液面指向液体内部(曲面球心),在凹液面指向液体外部。
3.同一体系,比表面自由能和表面张力都用σ表示,它们:(A) 物理意义相同,数值相同;(B) 量纲和单位完全相同;(C) 物理意义相同,单位不同;(D) 物理意义不同,单位不同。
物理化学知识点chap 10

Pa
2.356
103
kPa
【10.5】水蒸气迅速冷却至298.15K时可达到过饱和状态。已
知该温度下水的表面张力为71.97×10-3 N·m -1 ,密度为997
kg·m-3。 当过饱和水蒸气压力为平液面水的饱和蒸气压的4
倍时,计算: (1)开始形成水滴的半径;(2)每个水滴中
所含水分子的个数。
m
= 7.569 ? 10- 10m
(2)每个水滴的体积
( ) V 水滴=
4 3
pr
3
=
4 创3.14 3
7.569 ? 10- 10 3 m 3
1.815 ? 10- 27m 3
每个水分子的体积
V 水分子=
M rL
=
骣 琪 琪 琪 桫997
创
0.018 6.022
m 3 = 3.00 ? 10- 29m 3 1023
分析: 利用拉普拉斯方程
p 2
r
解: (1)和(2)两种情况下均只存在一个气-液界面, 其附加压力相同。根据拉普拉斯方程
p
2
r
2 58.91103 0.1106
Pa
1.178
103
kPa
(3)空气中存在的气泡,有两个气-液界面,其附加压力 为
p
4
r
4
58.91103 0.1106
•
pg
••
•
气
•
p
• •
pl
(a)
pg
• 气 p • •
液•
pl (b)
附加压力方向示意图
•
•
气•
•
•
• •
p=• 0
弯曲液面的附加压力拉普拉斯方程

以图示凹液面为例, 液面上升至平衡时, 有
p = 2γ / r1 = ρ gh
式中液面曲率半径 r1 与毛细管半径 r 及接 触角 θ 间的关系为:
r1 r
θ
θ
h
cosθ = r / r1
2 γ cos θ h= rρ g
γ : 液体表面张力; ρ: 液体密度;
g : 重力加速度.
毛细管上升
2
微小液滴的饱和蒸气压—开尔文公式
纯液体的饱和蒸气压与温度和液体压力有关. 微小液滴的 蒸气压因附加压力的作用而比普通体积时高. 已从相平衡条件推出纯液体蒸气压受外压影响的关系式:
p2 (g ) Vm (l ){ p2 (l ) p1 (l )} ln = p1 (g ) RT (Vm = M / ρ )
用 p 和 pr 分别表示平面液体和微小液滴的蒸气压, 结合 拉普拉斯方程, 得 小液滴 3
而水气泡内水蒸气的压力仅能达到 pr = 94.34 kPa(凹液 面). 可见小气泡在正常沸点下不能生成, 而凹液面上的附加 压力是造成液体过热的主要原因. 在液体中加入少量素烧瓷片或毛细管等物质可大大降低 过热的程度. 5
亚稳状态及新相的生成
(3) 过冷液体: 按相平衡条件应当凝固而未凝固的液体. 原因 是微小晶粒具有高表面吉布斯函数(高的饱和蒸气压)而不能 在正常凝固温度下生成. p
p
c3 c2 c1
T0
T
7
分散度对溶解度的影响
亚稳状态及新相的生成
亚稳状态: 热力学不完全稳定的状态. 按照相平衡条件应当相 变的物质, 由于初始新相体积极小, 具有很大的比表面积和表 面吉布斯函数而难以形成, 系统仍以原相存在, 处于亚稳状态.
(1) 过饱和蒸气: 按相平衡条件应当凝 p 结而未凝结的蒸气. 原因是蒸气不能 变成化学势更高的微小液滴.
二、弯曲液面下的附加压强 气体栓塞

二、弯曲液面下的附加压强气体栓塞PPPS∆fd 二、弯曲液面下的附加压强 气体栓塞自然界中的静止的液面,有平面、凹面和凸面。
有许多情况下液面是弯曲的,如前面说的水滴、肥皂泡,还有固体与液体的接触面等,弯曲液面内外存在一压强差,称为附加压强。
1、附加压强(1)定义:弯曲液面内外存在一压强差, 用Ps 表示(2)附加压强的产生——分别从平面、凸面和凹面三个方面来说明附加压强的产生。
1)平液面 在液体表面上取一小面积△S ,由于液面水平,表面张力沿水平方向, △S 平衡时,其边界表面张力相互抵消,不产生垂直与液面的压力,△S 上下压强相等:P=P 0, P s=02)液面弯曲①凸液面时,如图仍在液体表面上取一小面积△S ,△S 周界上表面张力沿切线方向,合力指向液面内,△S 好象紧压在液体上,使液体受一附加压强Ps ,由力平衡条件,液面下液体的压强:P=P0+Ps,如果我们规定附加压强与外部压强相同为正,相反为负。
则此时,Ps 为正②凹液面时,如图△S 周界上表面张力的合力指向外部,△S 如好象被拉出,液面内部压强小于外部压强,液面下压强:P=P0-Ps ,Ps 为负总之:附加压强的产生原因是由于表面张力存在。
附加压强使弯曲液面内外压强不等,与液面曲率中心同侧的压强恒大于另一侧,附加压强方向恒指向曲率中心 (3)附加压强的计算如图,取球形液面的一部分,曲率半径为R ,面积为dS ,其周界是半径为r 的圆周。
在周界上取一线元dl ,作用在dl 上的表面张力d f =αdl .(1)由图可见,将df 分解为半径r 垂直和平行的两个分力由圆对称性,在圆周界上的其他线元上,作用着同样大小的表面张力,这些力的水平分力相互抵消,垂直分力方向相同,合力为:2r02f df sin dl sin 2rr 2r sin ,f R Rπ⊥⊥⊥=⎰=⎰αϕ=αϕ⋅ππϕ==α由图可见则. (2)由式(2)可求得液面下液体所受的附加压强Rr R r r f p sαπαππ22222===⊥(3-5)可见,球形液面下液体的附加压强与液体的表面张力系数α成正比,与液面的曲率半径P 成反比。
物化第十章习题

板上,滴上一小滴水,再在水上覆盖上油,这时
水对毛细管的润湿角为,如习题 10.7 图图(b)所
示。油和水的密度分别用O 和W 表示,AA/为油水界面,油层的深度为 h/。请导出水在毛细管中 上升的高度 h 与油-水界面张力WO 之间的定量关
系。
解:因为在油中水可以润湿玻璃管,在玻璃毛细管中油-水界面为凹面,毛细管半径
பைடு நூலகம்
题 10.8 图示
10.9 已知在 273.15K 时,用活性炭吸附 CHCl3,其饱和吸附量为 93.8dm3kg-1, 若 CHCl3 的分压力为 13.375kPa,其平衡吸附量为 82.5dm3kg-1,试求:
(1) 朗谬尔吸附等温式中的 b 值;
(2) CHCl3 的分压力为 6.6672kPa 时,平衡吸附量为若干?
解:(1)因为
Va
Vma
bp 1 bp
依题意 V a=93.8dm3kg-1, Vma=82.5dm3kg-1 p=13.375kPa 代入上式得 b=[82.5/13.375×(93.8-82.5)] kPa-1= 0.5459 kPa-1
(2)当 p=6.6672kPa 时
V
a
Vma
bp 1 bp
答:亚稳态是热力学不完全稳定的状态,常见的亚稳态有过饱和蒸气、过热液体、 过冷液体、过饱和溶液。产生的原因是在新的相生成时,颗粒极其微小,其比表面积和表 面吉布斯函数都很大,因此在系统中产生新相极为困难而造成亚稳态的产生。防止亚稳 态产生的方法一般是引入“种子”,使之形成结晶或凝聚或气化核心。
(2)在一个封闭的钟罩内,有大小不等的两个球形液滴,问长时间恒温放置后,会 出现什么现象?
解:对方程 V a=kpn 取对数可得:
物理化学 弯曲液面附加压力

1 1 •一般式: p ( ' ' ) R1 R2
•特殊式(对球面):
2 p r
总结
1
附加压力与曲面半径成 反比,与液面张力成正 比
2
定义的Δp为凹面一侧的 压力减去图面一侧的压 力,故曲率半径r总是 正值,Δp亦总为正值。
№
毛细现象
液面被压入管内,直至上升的液 柱所产生的静压力gh 与附加压力p 在量值上相等,方可达到力的平衡, 即:
弯曲液面附加压力
小组成员:xxxxx
№
1、弯曲液面的附加压力
•一般情况下液体表面是水平的,而液滴、水中的
气泡表面则是弯曲的。
•液面可以是凸的,也可以是凹的。
弯曲表面上的附加压力
1.在平面上
p0
f
A B
对一小面积AB,沿AB的
四周每点的两边都存在表面 张力,大小相等,方向相反, 所以没有附加压力 设向下的大气压力为po, 向上的反作用力也为po ,附 加压力ps等于零。
2 p gh R
R cos ' R
由左图的几何关系可知:
由此可知: 2 cos h R g
自由液滴或气泡通常为何都呈球形 ?
1、假若液滴具有不规则的形状,则在表面上的不
同部位曲面弯曲方向及其曲率不同,所具的附加压力
的方向和大小也不同,这种不平衡的力,必将迫使液
滴呈现球形。 2、相同体积的物质,球形的表面积最小,则表 面总的Gibbs自由能最低,所以变成球状就最稳定。
1
2
凸面上受的总液体与平面不同,它受到一种
附加的压力,附加压力的方向都指 向曲面的圆心(曲率半径的方向)。
大于平面上的压力
3
物理化学(第五版) 演示文稿8-2 弯曲液面的表面现象

3
298.15 K
小液滴 2
平面液体
1 小气泡
10-1 100 101 102 103 r / nm
11
图8-7 表面曲率半径对水的蒸汽压的影响
关于Kelvin方程 将Kelvin方程用于难溶物质的溶解平衡
ln Cr 2 M 1 C0 RT r
已知:c1 > c2 > c3 > c4 r1 < r2 < r3 < r4
• ••p•
• •
• •• 液
(a)液滴(凸液面) (b)气泡(凹液面)
图8-4 弯曲液面的附加压力
1. 附加压力:由于表面张力的作用,弯曲液面的气液 两侧存在一压力差p。
def
p pl pg
2
两种弯曲液面的附加压力
pg
气
A
B
液 p
pl
凸液面:附加压力指向 液体内部,平衡时,液 体内部的压力大于外侧 压力,即为 p0+p。
pl<pg,附加压力指向气相 对于平液面:r=,p=0。
若为液泡(肥皂泡):则泡内气体的压力比泡外 气体的压力大,其差值为 p =4 / r
因为液膜内外两个面,其半径几乎相等。
5
3、实例:冶金熔池中的气泡
如图,气泡内的总压力p为:
p = pex+gh+p = pex+gh + 2 /r
钢 液
图 8-6 熔池中的气泡
§8-2 弯曲液面的表面现象
引言
纯液体液面形状
平面 面 曲面 面
凹液面 (气泡) 凸液面 (液滴)
平液面: 表面张力σ是水平的,相互抵消,液体表面
的内外两侧压力相等,都等于外压 p0。
10-2弯曲液面讲解
3. 亚稳状态和新相的生成
1). 微小液滴的化学势
r p
2). 微小液滴的饱和蒸气压—开尔文公式 3). 亚稳定状态和新相的生成 过饱和蒸气 过饱和溶液 4). 微小颗粒的化学势高、化学性质活泼
pr 2 M ln p RT r 过热液体 过冷液体
BC P
r
ln (pr / p) > 0,
对凹液面,凹面液体, 液滴的转入导致曲率半径减小,dr<0 p 2 M ln (p / pr) > 0, pr < p ln pr RT r p (凸面) > p (平面) > p (凹面) 且曲率半径越小, 偏离程度越大.
3. 亚稳状态和新相的生成 p 2 / r1 gh
F = 2 r1 γ cos p = F/ (r12) = 2 r12γ /r(r12) = 2γ/r 水平液面: r = , p=0. 空气中的气泡: p = 4γ /r.
γ
= 2 r12 γ /r
cos r1 r
γ
•圆球形液滴的附加压力
A r1 O 1 r O B
§10-2 弯曲液面的附加压力和毛细现象
毛细现象 将毛细管插入液体后 液面将沿毛细管上升(润湿,水,凹)或下降 (不润湿,汞,凸)的现象
产生的原因是毛细管内的弯曲液面上存在附加压力 p . 以凹液面为例, 液面上升至平衡时, 有
r1 θ r θ
p 2 / r1 gh
液面曲率半径 r1 与毛细管半径 r 及接触角 间的关系为:
2 2 72.0 103 N m 1 5 p 144 10 Pa 142atm 8 r 10 m
§22弯曲液面附加压力

所受表面张力也有拉平液面的趋势,其
方向不与液面平行,作用在dS周线上的
B
表面张力的合力不为0,产生附加压强PS 向上。
PB
=
Po
−
Ps
pB (c)
因为受力平衡,所以液面两侧的压强也平衡, 即:
PB + PS = P0
第二章 液体的表面现象
§2-2 弯曲液面的附加压力
二、拉普拉斯公式
p0
利用拉普拉斯公式可以定量
第二章 液体的表面现象 2、液面是凸形(2)
§2-2 弯曲液面的附加压力
p0
f
A ps f '
B pB
(c)
因液面受力平衡,所以,液面两侧的压强也 平衡,即:
Po + PS = PB
第二章 液体的表面现象
§2-2 弯曲液面的附加压力
3、液面是凹形
p0
(如水中气泡、细玻璃管中的水面等) f
A ps f '
§2-2 弯曲液面的附加压力
Po = PB = PA
f A p0 f ' B pB
第二章 液体的表面现象
§2-2 弯曲液面的附加压力
2、液面是凸形(1)
f A p0 f '
B pB
ps
(如液滴表面、细玻璃管中的水银面)所受表面
张力有拉平液面的趋势,其方向不与液面平行, 作用在 dS周线上的表面张力的合力不为0,产生 附加压强PS方向向下。
算出附加压强p0 的大小。
设想液面下有一气泡,气泡靠
近液面,不考虑静压(即水
压),气泡外压强等于大气压强
P0。设想气泡在外力作用下膨
胀:
p1
p1 R p1
界面现象--第2节:弯曲液面的附加压力及其后果

拉普拉斯方程的简单应用
思考题:已知水在两块玻璃间形成凹液面,而在两块石蜡 板间形成凸液面。试解释:为什么两块玻璃间放一点水后 很难拉开,而两块石蜡板间放一点水后很容易拉开。
答:水在两玻璃和两石蜡板间的状态如下图。对玻璃板, 附加压力Δp指向液体外部,说明液体压力P小于外压力, 且两板越靠近,此压力差越大,使两板难以拉开。石蜡板 的情况相反,液体压力 p 大于外压力,易于拉开。
在过冷液体中投入小 晶体作为新相的种子, 能 使液体迅速凝固.
气相区
Tf Tf
• 过冷液体的产生
T
18
亚稳状态及新相的生成
(4) 过饱和溶液: 在一定温度下, 浓度超过饱和浓度, 而仍 未析出晶体的溶液. 原因是微小晶粒具有高表面吉布斯函数 (高的饱和蒸气压)而不能在正常饱和浓度下析出. 与微小液滴一样, 微小晶体 p 的饱和蒸气压大于普通晶体. 蒸 气压与溶解度有密切的关系, 微 小晶粒具有比普通晶体更大的溶解 度. 晶体的颗粒愈小, 溶解度愈大. 可知, 当溶液浓度达到普通晶 体的饱和浓度时, 相对于微小晶粒 还未饱和, 微小晶粒就不能从中析 出.
pr 2gM 开尔文公式: RTl n p r
3
Pr / p
小液滴
2 1
小气泡
0.1 1 10 100 1000
平面液体
公式中:表面张力γ大于0,摩尔质量M 大于0,密度ρ大于0,微小液滴半径r大 于0,所以Pr(液滴) > P(平面)
r / nm
• 曲率半径对水的蒸气 压的影响(25℃) 12
而水气泡内水蒸气的压力仅能达到 pr = 94.34 kPa(凹液 面). 可见小气泡在正常沸点下不能生成, 而凹液面上的附加 压力是造成液体过热的主要原因. 在液体中加入少量素烧瓷片或毛细管等物质可大大降低 过热的程度,防止液体暴沸而发生危险. 17
10-2弯曲液面讲解
炸毁三个车间 1300m2,伤亡三百余人
ln pr 2 M p RT r
ln pr 1 • 2 • M p RT r
r 1mm 103 m p 144Pa r 10nm 108 m p 144105 Pa
pr 1.000 p pr 1.111 p
pr 3168Pa pr 3519Pa
对凸液面(如小液滴), 凸面液体曲率半径增大,dr>0
r p
2). 微小液滴的饱和蒸气压—开尔文公式 3). 亚稳定状态和新相的生成 过饱和蒸气
过饱和溶液
ln pr 2 M p RT r
过热液体 过冷液体
4). 微小颗粒的化学势高、化学性质活泼
BC P
r p
rGm P B C 0
rGm P Br C 0
Br B
• 水磨米粉较细
(1) 过饱和蒸气 (2) 过热液体 (3) 过冷液体 (4) 过饱和溶液
压力超过常规饱和蒸气压的蒸气 温度高于沸点的液体 温度在凝固点以下的液体 浓度超过饱和浓度的溶液
3. 亚稳定状态
3. 亚稳定状态和新相的生成 (1) 过饱和蒸气 压力超过常规饱和蒸气压的蒸气
人工降雨 干冰
过饱和蒸气的压力尚未达到该液体微小液滴的饱和蒸气压
➢ 与表面张力成正比 ➢ 与曲率半径成反比
γ
γ
p
p
pl
pg
2
r
p
γ
γ
拉普拉斯方程
§10-2 弯曲液面
§10-2 弯曲液面的附加压力和毛细现象
弯曲液面的附加压力
1. 拉普拉斯方程 证明: F = 2rγ
2
p pl pg r γ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于液滴(凸面,r>0),其半径越小,蒸汽压越大; 对于蒸汽泡(凹面,r<0),半径越小,气泡内的蒸 气泡内的蒸 汽压也越低;对于平面, r=∞ , pr*=p* 汽压也越低 即,pr*(凸液面)>pr*(平液面)>pr*(毛细管中凹液面),
• • • • • • • • P(凸) • • • • • • • • • • • p(平) • • • • 气 • p(凹) • •
z
' 1 ' 2
D'
x + dx o'
C'
A'
y
D
dz
B'
o
R1
C
A
x'
B
' R2
令曲面沿法线方向移动dz , 使曲面扩大到A'B'C'D'(蓝色面), 则x与y各增加dx和dy 。
Young-Laplace 公式
移动后曲面面积增量为: dAs = ( x + dx )( y + dy ) − xy
微小物质化学势 微物熔融应满足:µ r,B = µ B(l) 微物熔融应满足: 只有降低熔点, 减小,故有: 只有降低熔点,才能使 µ r,B减小,故有: Tf(微小)< Tf(大块) (微小) (大块)
µ r,B = µ + RT ln
Θ
pr,B
▲ 微小固体物质的溶解度大 溶解度: 溶解度:恒T﹑p下,溶质在溶剂中达到溶解 ﹑ 下 平衡时的(饱和)浓度。 平衡时的(饱和)浓度。 将开尔文公式与亨利定律结合,推导得: 将开尔文公式与亨利定律结合,推导得: cr 2γ M 1 c2 2γ M 1 1 ln = ( − ) 和 ln = c1 ρ RT r2 r1 c0 ρ RT r 若r2<r1,则c2 > c1, 即:物质颗粒越小,其溶解度越大; 物质颗粒越小,其溶解度越大; 因为固体颗粒的r> , 因为固体颗粒的 >0,所以微小物质的溶解度 (c r)大于正常条件下物质的溶解度 0) 大于正常条件下物质的溶解度(c 大于正常条件下物质的溶解度
o
R1
C
ydz dy = ' A R2 若 R '1 = R '2 = R '
x'
B
z
' R2
2γ ps = ' R
这两个都称为 Young-Laplace 公式
注意: 注意: 1) r 的符号: 的符号: 凸液面, > , 固相)内部 凸液面,r>0,ps>0, r 指向液相 固相 内部 , 指向液相(固相 凹液面, 凹液面,r <0,ps<0, r 指向气相 , , 平液面, 平液面,r→∞,ps→0, , 2)气泡的附加压强: )气泡的附加压强: 气 肥皂泡两个l-g界面 界面, 肥皂泡两个 界面,r1≈r2 气 ps=ps,1+ ps,2= 4γ/r ps,1 r1 r2 p
表面物理化学
§13.2 弯曲表面上的附加压力和蒸气压
弯曲表面上的附加压力 Young-Laplace 公式 弯曲表面上的蒸气压——Kelvin 公式
弯曲表面上的附加压力
1.在平面上
p0
对一小面积AB,沿AB的 四周每点的两边都存在表面
f
A
B
f
张力,大小相等,方向相反, 所以没有附加压力 设向下的大气压力为po, 向上的反作用力也为po ,附 加压力ps等于零。
3. 在凹面上 由于液面是凹面,沿AB 的周界上的表面张力不能抵 消,作用于边界的力有一指
向凹面中心的合力
所有的点产生的合力 为 ps ,称为附加压力 凹面上受的总压力为:
p总 = p0 − ps
弯曲液面下的附加压强
p0 p0 A B A A B p = p0 ps p = p0 + ps B A p = p0 - ps B p0 ps
∆p
加热 ∆p
加热
微小液滴的饱和蒸汽压
足够长的时间
半径不同的小水滴
结论:根据液体蒸汽的大小决定于液体分子向空间逃逸的倾向,可知 结论:根据液体蒸汽的大小决定于液体分子向空间逃逸的倾向,可知:
∗ ∗ p小水滴 > p大水滴
p*反比于曲率半径 反比于曲率半径
弯曲表面上的蒸汽压——Kelvin公式
2γ M ∆G2 = ∫ Vm dp = Vm ∆p = ' Rρ ∆G2 + ∆G4 = 0 p0 pr ∆G4 = RT ln = − RT ln pr p0 pr 2γ M 这就是Kelvin公式 RT ln = ' p0 Rρ
'2
'
As = 4π R
代入
'2
dAs = 8π R dR
'
'
ps dV = γ dAs
2γ ps = ' R
R'
p0
ps
得
2γ ps = ' R
曲率半径越小,附加压力越大 凸面上因外压与附加压力的方向一致,液体 所受的总压等于外压和附加压力之和,总压比平 面上大。相当于曲率半径取了正值。
p总 = p0 + ps
2。相同体积的物质,球形的表面积最小, 则表面总的Gibbs自由能最低,所以变成球状就 最稳定
毛细管现象
由于附加压力而引起的液面与管外液面有高 度差的现象称为毛细管现象。 把毛细管插入水中,管中的水柱表面会呈凹 形曲面,致使水柱上升到一定高度。当插入汞中 时,管内汞面呈凸形,管内汞面下降。
p' p0
公式应用: 公式应用:测表面张力 —— 最大泡压法 ps+p控=p大气 减小p 气泡长大, 减小 控 :气泡长大,最终逸出 气泡半径r 变化: 气泡半径 变化: 大→小→大 小 大 ps变化:小→大→小 变化: 大 小 ps,max= 2γ/r (r曲率=r毛细管) ps,max = p大气 - p控
气
•
气 •
液 液
•
液 附图 pr*(凸液面)>pr*(平液面)>pr*(毛细管中凹液面)
微小物质的熔点低(凸面) ▲ 微小物质的熔点低(凸面) 微小物质的饱和蒸气压> 微小物质的饱和蒸气压>大块物质饱和蒸气压
pΘ pB Θ µ B = µ + RT ln Θ 大块物质化学势 p µ r,B> µ B ,熔融时, µ B = µ B(l) 则: r,B>µ B(l) µ 熔融时,
∆ vapG1 = ∆ vapG3 = 0
弯曲表面上的蒸汽压——Kelvin公式
pr 2γ M RT ln = ' p0 Rρ pr ∆p = 1+ p0 p0
设 ∆p = pr − p0 ∆p ∆p ln = ln 1 + ≈ p0 p0 p0
凹液面, < , ★ 凹液面,r<0,则:pr= p凹< p0, 越小, 越小; 且|r|越小,p凹越小; 越小 凸液面, > , ★ 凸液面,r>0,则:pr= p凸> p0, r/m pr / p0 10-6 10-7 10-8 10-9 1.001 1.011 1.114 2.95
物质要小到一定程度, ★ 物质要小到一定程度,表面效应才显著 增大, ★ 微小物质的饱和蒸气压 pr 增大, 其化学势增高
p0 + ps
p总 = p0 + ps
对活塞稍加压力,将 毛细管内液体压出少许 使液滴体积增加dV 相应地其表面积增加dA 克服附加压力ps所作的 功等于可逆增加表面积的 Gibbs自由能
R'
p0
p0
ps
ps dV = γ dAs
ps dV = γ dAs
V = 4 3
πR
'3
dV = 4π R dR
p大气 p控 pS
最大泡压法测定表面张力装置
1-滴液漏斗 2-支管试管 3-毛细管 4-恒温槽 5-压差计
最大泡压法测定溶液的表面张力 最大泡压法测定溶液的表面张力
Young-Laplace 公式
在任意弯曲液面上取小矩形 ABCD(红色面),其面积为xy。 曲面边缘AB和BC弧的曲 率半径分别为 R 和 R 作曲面的两个相互垂直的正 截面,交线Oz为O点的法线。
对凸面,R' 取正值,R' 越小,液滴的蒸汽压越高; 对凹面, R' 取负值, R' 越小,小蒸汽泡中的 蒸汽压越低。
pr 2γ M RT ln = ' p0 Rρ
∆p 2γ M = ' p0 RTR ρ
p2 2γ M 1 1 RT ln = ' − ' ρ R2 R1 p1
Kelvin公式也可以表示两种不同大小颗粒的饱 和溶液浓度之比。
c2 2γ l − s M RT ln = c1 ρ
1 1 ' − ' R2 R1
颗粒总是凸面, R' 取正值, R' 越小,小颗 粒的饱和溶液的浓度越大,溶解度越大。
二、微小物质的特性 微小物质:比表面积大, 微小物质:比表面积大,Gs=γAs大 1.弯曲液面的饱和蒸气压与表面曲率半径的关系 弯曲液面的饱和蒸气压与表面曲率半径的关系
p0
ps = p0 − p0 = 0
弯曲表面上的附加压力
2. 在凸面上 由于液面是弯曲的,则 沿AB的周界上的表面张力不 是水平的,作用于边界的力
f
A
p0
B
f
ps
将有一指向液体内部的合力
所有的点产生的合力 为 ps ,称为附加压力 凸面上受的总压力为:
p0 + ps
p总 = p0 + ps
弯曲表面上的附加压力
s,2
分析: 分析:
