2018年高三数学(理)一轮复习课件 解三角形
高考数学一轮复习第四章三角函数解三角形5两角和与差的正弦余弦与正切公式课件新人教A版(理)

A. 3
π
1
+ = 3,cos
4
π
- =
4 2
√3
,则
3
等于( C )
√3
5√3
B.- 3
C.
1
(2)已知 cos - 2 =-9,sin
2
√6
D.- 9
9
2
π
π
- = 3,且2 <α<π,0<β<2 ,则
239
cos(α+β)=
-729
.
思考已知一个角或两个角的三角函数值,求另一角的三角函数值
-sin αcos -
cos α-cos +
π
1
6
2
π
6
π
3
+
π
π
3
2
sin α
- =sin = ,
故选 A.
(2)(方法一)因为角 α 与角 β 的终边关于 y 轴对称,根据三角函数
1
定义可得 sin β=sin α= ,cos β=-cos α,因此,cos(α-β)=cos αcos β+sin
π
4
+tan
7
= .
5
(方法二)∵tan 7
π
4
7
∴tan α= 5,答案为5.
=
tan -tan
π
4
1+tan ·tan
π
4
=
tan -1
1+tan
1
= ,
6
-14考点1
考点2
考点3
考点 2
三角函数公式的逆用及变用
2018年高考数学(理)一轮复习文档第三章三角函数、解三角形第2讲同角三角函数的基本关系与诱导公式Word版
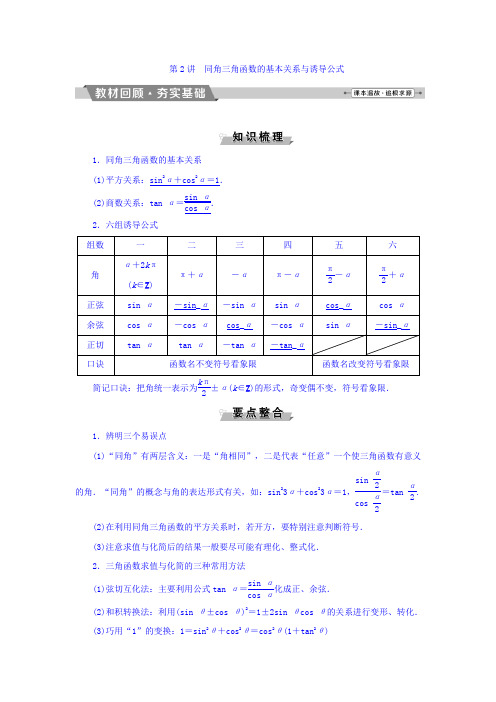
第2讲 同角三角函数的基本关系与诱导公式1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1. (2)商数关系:tan α=sin αcos α.2.六组诱导公式简记口诀:把角统一表示为k π2±α(k ∈Z )的形式,奇变偶不变,符号看象限.1.辨明三个易误点(1)“同角”有两层含义:一是“角相同”,二是代表“任意”一个使三角函数有意义的角.“同角”的概念与角的表达形式有关,如:sin 23α+cos 23α=1,sinα2cosα2=tan α2.(2)在利用同角三角函数的平方关系时,若开方,要特别注意判断符号. (3)注意求值与化简后的结果一般要尽可能有理化、整式化. 2.三角函数求值与化简的三种常用方法(1)弦切互化法:主要利用公式tan α=sin αcos α化成正、余弦.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化. (3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=tan π4=….1.cos ⎝ ⎛⎭⎪⎫-20π3=( ) A.12 B.32 C .-12D .-32C2.已知sin ⎝ ⎛⎭⎪⎫π2+α=35,α∈⎝⎛⎭⎪⎫0,π2,则sin(π+α)等于( )A.35 B .-35C.45D .-45D 因为sin ⎝⎛⎭⎪⎫π2+α=35,α∈⎝ ⎛⎭⎪⎫0,π2, 所以cos α=35,所以sin α=45,所以sin(π+α)=-sin α=-45.3.若sin θcos θ=12,则tan θ+cos θsin θ的值是( )A .-2B .2C .±2D.12B tan θ+cos θsin θ=sin θcos θ+cos θsin θ=1cos θsin θ=2.4.若sin θ=-45,tan θ>0,则cos θ=________.由已知,θ在第三象限, 所以cos θ=-1-sin 2θ=-1-(-45)2=-35.-355.教材习题改编 已知tan θ=2,则sin θ·cos θ=________. sin θcos θ=sin θ·cos θsin 2θ+cos 2θ=tan θtan 2θ+1=222+1=25. 25同角三角函数的基本关系式(高频考点)同角三角函数的基本关系式的应用很广泛,也比较灵活.高考中常以选择题、填空题的形式出现.高考对同角三角函数基本关系式的考查主要有以下三个命题角度: (1)知弦求弦; (2)知弦求切; (3)知切求弦.(1)(2016·高考全国卷丙)若tan α=34,则cos 2α+2sin 2α=( )A.6425 B.4825C .1D.1625(2)已知sin α+2cos α=3,则tan α=( ) A.22 B. 2 C .-22D .- 2【解析】 (1)法一:由tan α=sin αcos α=34,cos 2α+sin 2α=1,得⎩⎪⎨⎪⎧sin α=35,cos α=45或⎩⎪⎨⎪⎧sin α=-35,cos α=-45,则sin 2α=2sin αcos α=2425,则cos 2α+2sin 2α=1625+4825=6425. 法二:cos 2α+2sin 2α=cos 2α+4sin αcos αcos 2α+sin 2α=1+4tan α1+tan 2α=1+31+916=6425. (2)因为sin α+2cos α=3, 所以(sin α+2cos α)2=3,所以sin 2α+22sin αcos α+2cos 2α=3, 所以sin 2α+22sin αcos α+2cos 2αsin 2α+cos 2α=3,所以tan 2α+22tan α+2tan 2α+1=3, 所以2tan 2α-22tan α+1=0,所以tan α=22. 【答案】 (1)A (2)A同角三角函数关系式及变形公式的应用(1)利用sin 2α+cos 2α=1可以实现角α的正弦、余弦的互化,利用sin αcos α=tan α可以实现角α的弦切互化.(2)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.角度一 知弦求弦1.(2017·雅安模拟)已知sin θ+cos θ=43,θ∈(0,π4),则sin θ-cos θ的值为( )A.23 B.13 C .-23D .-13C (sin θ+cos θ)2=169,所以1+2sin θcos θ=169,所以2sin θcos θ=79,由(sin θ-cos θ)2=1-2sin θ·cos θ=1-79=29,可得sin θ-cos θ=±23.又因为θ∈(0,π4),sin θ<cos θ,所以sin θ-cos θ=-23.角度二 知弦求切2.已知cos ⎝ ⎛⎭⎪⎫π2+α=35,且α∈⎝ ⎛⎭⎪⎫π2,3π2,则tan α=( )A.43 B.34 C .-34D .±34B 因为cos ⎝⎛⎭⎪⎫π2+α=35,所以sin α=-35,显然α在第三象限,所以cos α=-45,故tan α=34.角度三 知切求弦3.若sin α=2sin β,tan α=3tan β,则cos α=________. 因为sin α=2sin β,① tan α=3tan β, tan 2α=9tan 2β.②由①2÷②得:9cos 2α=4cos 2β.③ 由①2+③得sin 2α+9cos 2α=4. 又sin 2α+cos 2α=1, 所以cos 2α=38,所以cos α=±64. ±64诱导公式的应用(1)sin(-1 200°)cos 1 290°+cos(-1 020°)·sin(-1 050°)=________.(2)已知cos α是方程3x 2-x -2=0的根,且α是第三象限角,则sin (-α+3π2)cos (3π2+α)tan 2(π-α)cos (π2+α)sin (π2-α)等于________.(3)已知cos(π6-α)=23,则sin(α-2π3)=________.【解析】 (1)原式=-sin 1 200°cos 1 290°-cos 1 020°·sin 1 050°=-sin(3×360°+120°)cos(3×360°+210°)-cos(2×360°+300°)sin(2×360°+330°)=-sin 120°cos 210°-cos 300°sin 330°=-sin(180°-60°)cos(180°+30°)-cos(360°-60°)·sin(360°-30°) =sin 60°cos 30°+cos 60°sin 30° =32×32+12×12=1. (2)因为方程3x 2-x -2=0的根为x 1=1,x 2=-23,由题知cos α=-23,所以sin α=-53,tan α=52. 所以原式=-cos αsin αtan 2α-sin αcos α=tan 2α=54.(3)因为⎝ ⎛⎭⎪⎫π6-α+⎝ ⎛⎭⎪⎫α-2π3=-π2,所以α-2π3=-π2-⎝ ⎛⎭⎪⎫π6-α,所以sin ⎝ ⎛⎭⎪⎫α-2π3=sin ⎣⎢⎡⎦⎥⎤-π2-⎝ ⎛⎭⎪⎫π6-α=-cos ⎝ ⎛⎭⎪⎫π6-α=-23.【答案】 (1)1 (2)54 (3)-23(1)诱导公式用法的一般思路 ①化大角为小角.②角中含有加减π2的整数倍时,用公式去掉π2的整数倍.(2)常见的互余和互补的角①常见的互余的角:π3-α与π6+α;π3+α与π6-α;π4+α与π4-α等.②常见的互补的角:π3+θ与2π3-θ;π4+θ与3π4-θ等.(3)三角函数式化简的方向 ①切化弦,统一名. ②用诱导公式,统一角.③用因式分解将式子变形,化为最简.1.(2017·福建省毕业班质量检测)若sin(π2+α)=-35,且α∈(π2,π),则sin(π-2α)=( )A.2425 B.1225C .-1225D .-2425D 由sin(π2+α)=cos α=-35,且α∈(π2,π),得sin α=45,所以sin(π-2α)=sin 2α=2sin αcos α=-2425,选项D 正确.2.sin(-1 071°)si n 99°+sin(-171°)sin(-261°)=________. 原式=(-sin 1 071°)·sin 99°+sin 171°·sin 261°=-sin (3×360°-9°)sin(90°+9°)+sin(180°-9°)·sin(270°-9°)=sin 9°cos 9°-sin 9°cos 9°=0.故填0.3.已知cos(π+α)=-12,求sin[α+(2n +1)π]+sin (π+α)sin (π-α)·cos (α+2n π)(n ∈Z ).因为cos(π+α)=-12,所以-cos α=-12,cos α=12.sin[α+(2n +1)π]+sin (π+α)sin (π-α)cos (α+2n π)=sin (α+2n π+π)-sin αsin αcos α=sin (π+α)-sin αsin αcos α=-2sin αsin αcos α=-2cos α=-4.——方程思想求解三角函数值已知sin θ+cos θ=713,θ∈(0,π),则tan θ=________.【解析】 法一:因为sin θ+cos θ=713,θ∈(0,π),所以(sin θ+cos θ)2=1+2sin θcos θ=49169,所以sin θcos θ=-60169.由根与系数的关系,知sin θ,cos θ是方程x 2-713x -60169=0的两根,所以x 1=1213,x 2=-513.又sin θcos θ=-60169<0,所以sin θ>0,cos θ<0.所以sin θ=1213,cos θ=-513.所以tan θ=sin θcos θ=-125.法二:同法一,得sin θcos θ=-60169,所以sin θcos θsin 2θ+cos 2θ=-60169. 齐次化切,得tan θtan 2 θ+1=-60169,即60tan 2θ+169tan θ+60=0, 解得tan θ=-125或tan θ=-512.又θ∈(0,π),sin θ+cos θ=713>0,sin θcos θ=-60169<0.所以θ∈(π2,3π4),所以tan θ=-125.【答案】 -125(1)本题利用方程思想法一:由sin θ+cos θ、sin θcos θ的值构造一元二次方程,把sin θ与cos θ看作此方程的两根,即可求出sin θ与cos θ的值,便可求解.法二:利用三角函数的基本关系转化为关于tan θ的一元二次方程求解.(2)所谓方程思想就是在解决问题时,用事先设定的未知数沟通问题中所涉及的各量间的等量关系,建立方程或方程组,求出未知数及各量的值,或者用方程的性质去分析、转化问题,使问题获得解决.已知sin(3π-α)=-2sin(π2+α),则sin αcos α等于( )A .-25 B.25C.25或-25D .-15A 因为sin(3π-α)=sin(π-α)=-2sin(π2+α),所以sin α=-2cos α,所以tan α=-2,当α在第二象限时,⎩⎪⎨⎪⎧sin α=255cos α=-55,所以sin αcos α=-25;当α在第四象限时,⎩⎪⎨⎪⎧sin α=-255cos α=55,所以sin αcos α=-25,综上,sin αcosα=-25,故选A.1.tan(-233π)的值为( )A. 3 B .- 3 C.33D .-33A A tan(-233π)=tan(-8π+π3)=tan π3= 3.2.已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于( )A .-π6B .-π3C.π6D.π3D 因为sin(π+θ)=-3cos(2π-θ), 所以-sin θ=-3cos θ,所以tan θ= 3. 因为|θ|<π2,所以θ=π3.3.(2017·福建省毕业班质量检测)已知cos(α+π2)=13,则cos 2α的值等于( )A.79 B .-79C.89D .-89A 法一:因为cos(α+π2)=13,所以sin α=-13,所以cos α=±223,所以cos 2α=cos 2α-sin 2α=(±223)2-(-13)2=79,故选A.法二:因为cos(α+π2)=13,所以sin α=-13,所以cos 2α=1-2sin 2α=1-2×19=79,故选A.4.已知sin α+3cos α3cos α-sin α=5,则sin 2α-sin αcos α的值为( )A .-15B .-25C.15D.25D 依题意得tan α+33-tan α=5,所以tan α=2.所以sin 2α-sin αcos α=sin 2α-sin αcos αsin 2α+cos 2α=tan 2α-tan αtan 2α+1=22-222+1=25. 5.已知f (x )=a sin(πx +α)+b cos(πx +β)+4,若f (2 016)=5,则f (2 017)的值是( )A .2B .3C .4D .5B 因为f (2 016)=5.所以a sin(2 016π+α)+b cos(2 016π+β)+4=5, 即a sin α+b cos β=1.所以f (2 017)=a sin(2 017π+α)+b cos(2 017π+β)+4=-a sin α-b cos β+4=-1+4=3.6.已知sin α+3cos α+1=0,则tan α的值为( ) A.43或34 B .-34或-43C.34或-43D .-43或不存在D 由sin α=-3cos α-1,可得(-3cos α-1)2+cos 2α=1,即5cos 2α+3cos α=0,解得cos α=-35或cos α=0,当cos α=0时,tan α的值不存在,当cos α=-35时,sin α=-3cos α-1=45,tan α=sin αcos α=-43,故选D.7.化简sin (π2+α)cos (π2-α)cos (π+α)+sin (π-α)cos (π2+α)sin (π+α)=________. 原式=cos αsin α-cos α+sin α(-sin α)-sin α=-sin α+sin α=0. 08.在△ABC 中,若tan A =23,则sin A =________. 因为tan A =23>0,所以A 为锐角,于是1+tan 2A =1+29=119=1cos 2A ,cos 2A =911,cos A =31111,sin A =tan A cos A =2211. 2211 9.sin 43π·cos 56π·tan(-43π)的值是________. 原式=sin(π+π3)·cos(π-π6)·tan(-π-π3) =(-sin π3)·(-cos π6)·(-tan π3) =(-32)×(-32)×(-3)=-334. -33410.已知sin ⎝ ⎛⎭⎪⎫7π12+α=23,则cos ⎝⎛⎭⎪⎫α-11π12=________. cos ⎝ ⎛⎭⎪⎫α-11π12=cos ⎝ ⎛⎭⎪⎫11π12-α =cos ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π12+α=-cos ⎝ ⎛⎭⎪⎫π12+α, 而sin ⎝ ⎛⎭⎪⎫7π12+α=sin ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫π12+α =cos ⎝ ⎛⎭⎪⎫π12+α=23, 所以cos ⎝⎛⎭⎪⎫α-11π12=-23. -2311.已知sin θ=45,π2<θ<π. (1)求tan θ的值;(2)求sin 2θ+2sin θcos θ3sin 2θ+cos 2θ的值.(1)因为sin 2θ+cos 2θ=1,所以cos 2θ=925.又π2<θ<π,所以cos θ=-35.所以tan θ=sin θcos θ=-43.(2)由(1)知,sin 2θ+2sin θcos θ3sin 2θ+cos 2 θ=tan 2θ+2tan θ3tan 2θ+1=-857.12.已知α为第三象限角,f (α)=sin (α-π2)·cos (3π2+α)·tan (π-α)tan (-α-π)·sin (-α-π).(1)化简f (α);(2)若cos(α-3π2)=15,求f (α)的值.(1)f (α)=sin (α-π2)·cos (3π2+α)·tan (π-α)tan (-α-π)·sin (-α-π)=(-cos α)·sin α·(-tan α)(-tan α)· sin α=-cos α.(2)因为cos(α-3π2)=15,所以-sin α=15,从而sin α=-15.又α为第三象限角,所以cos α=-1-sin 2α=-265,所以f (α)=-cos α=265.13.已知sin αcos α=18,且5π4<α<3π2,则cos α-sin α的值为() A .-32 B.32C .-34 D.34B 因为5π4<α<3π2,所以cos α<0,sin α<0且|cos α|<|sin α|,所以cos α-sin α>0.又(cos α-sin α)2=1-2sin αcos α=1-2×18=34, 所以cos α-sin α=32. 14.化简1-2sin 40°cos 40°cos 40°-1-sin 250°=________. 原式=sin 240°+cos 240°-2sin 40°cos 40°cos 40°-cos 50°=|sin 40°-cos 40°|sin 50°-sin 40° =|sin 40°-sin 50°|sin 50°-sin 40° =sin 50°-sin 40°si n 50°-sin 40° =1.115.已知在△ABC 中,sin A +cos A =15. (1)求sin A cos A 的值;(2)判断△ABC 是锐角三角形还是钝角三角形;(3)求tan A 的值.(1)因为sin A +cos A =15,① 所以两边平方得1+2sin A cos A =125, 所以sin A cos A =-1225. (2)由sin A cos A =-1225<0,且0<A <π, 可知cos A <0,所以A 为钝角,所以△ABC 是钝角三角形.(3)因为(sin A -cos A )2=1-2sin A cos A =1+2425=4925, 又sin A >0,cos A <0,所以sin A -cos A >0,所以sin A -cos A =75,② 所以由①,②可得sin A =45,cos A =-35,所以tan A =sin A cos A =45-35=-43. 16.已知f (x )=cos 2(n π+x )·sin 2(n π-x )cos 2[(2n +1)π-x ](n ∈Z ). (1)化简f (x )的表达式; (2)求f ⎝ ⎛⎭⎪⎫π2 016+f ⎝ ⎛⎭⎪⎫1 007π2 016的值. (1)当n 为偶数,即n =2k (k ∈Z )时,f (x )=cos 2(2k π+x )·sin 2(2k π-x )cos 2[(2×2k +1)π-x ]=cos 2x ·sin 2(-x )cos 2(π-x )=cos 2x ·(-sin x )2(-cos x )2 =sin 2x (n =2k ,k ∈Z );当n 为奇数,即n =2k +1(k ∈Z )时,f (x )=cos 2[(2k +1)π+x ]·sin 2[(2k +1)π-x ]cos 2{[2×(2k +1)+1]π-x }=cos 2[2k π+(π+x )]·sin 2[2k π+(π-x )]cos 2[2×(2k +1)π+(π-x )]=cos 2(π+x )·sin 2(π-x )cos 2(π-x )=(-cos x )2sin 2x (-cos x )2 =sin 2x (n =2k +1,k ∈Z ).综上得f (x )=sin 2x . (2)由(1)得f ⎝ ⎛⎭⎪⎫π2 016+f ⎝ ⎛⎭⎪⎫1 007π2 016 =sin2π2 016+sin 21 007π2 016 =sin2π2 016+sin 2⎝ ⎛⎭⎪⎫π2-π2 016 =sin2π2 016+cos 2π2 016=1.。
高考数学一轮复习第四章三角函数解三角形4.1任意角蝗制及任意角的三角函数课件理

(2)已知角α的终边在如图所示阴影表示的范围内(不包括边界),则角α 用集合可表示为_(2_k_π_+__π4_,__2_k_π_+__56_π_)_(k_∈__Z__) . 答案 解析
在[0,2π)内,终边落在阴影部分角的集合为π4,56π, ∴所求角的集合为2kπ+4π,2kπ+56π(k∈Z).
弧度数是 答案 解析
π
π
A.3
B.6
C.-π3
D.-π6
将表的分针拨快应按顺时针方向旋转,为负角,故A、B不正确;
又因为拨快10分钟,故应转过的角为圆周的 1 . 6
即为-16×2π=-π3.
(2)若圆弧长度等于圆内接正三角形的边长,则其圆心角的弧度数为
π
π
A.6
B.3
C.3
D. 3
答案
解析
如图,等边三角形ABC是半径为r的圆O的内接三角形,
2.弧度制
(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号
rad表示,读作弧度.正角的弧度数是一个 正数 ,负角的弧度数是一个
负数 ,零角的弧度数是 0 .
π
180
(2)角度制和弧度制的互化:180°= π
rad,1°=180 rad,1 rad=
π
.
1 (3)扇形的弧长公式:l= |α|·r ,扇形的面积公式:S= 2lr =
②若扇形的周长为20,求扇形面积的最大值,并求此时扇形圆心角的 弧度数. 解答
由题意知l+2r=20,即l=20-2r, S=12l·r=12(20-2r)·r=-(r-5)2+25, 当r=5时,S的最大值为25. 当 r=5 时,l=20-2×5=10,α=rl=2(rad). 即扇形面积的最大值为25,此时扇形圆心角的弧度数为2 rad.
高考数学一轮复习正弦定理余弦定理及解三角形课件理

基础诊断 考点突破
课堂总结
解 (1)由题意可知 c=8-(a+b)=72.
由余弦定理得 cos C=a2+2ba2b-c2=22+2×5222×-52722
=-15.
(2)由 sin Acos2B2+sin Bcos2A2=2sin C 可得:
sin
1+cos A· 2
B+sin
1+cos B· 2
a2+b2-c2 2ab
基础诊断 考点突破
课堂总结
2.S△ABC=12absin C=12bcsin A=12acsin B=a4bRc=12(a+b+c)·r(r 是 三角形内切圆的半径),并可由此计算 R,r.
基础诊断 考点突破
课堂总结
• 3.实际问题中的常用角
• (1)仰角和俯角
• 在同一铅垂平面内的水平视线和目标视线
1-2419=2
7 7.
而∠AEB=23π-α,所以
cos∠AEB=cos23π-α=cos23πcos α+sin23πsin α
=-12cos
α+
3 2 sin
α
=-12·2 7 7+
3 21 2 ·7
=
7 14 .
基础诊断 考点突破
课堂总结
在
Rt△EAB
中,cos∠AEB=EBAE=B2E,故
课堂总结
5.(人教 A 必修 5P10B2 改编)在△ABC 中,acos A=bcos B, 则这个三角形的形状为________. 解析 由正弦定理,得 sin Acos A=sin Bcos B, 即 sin 2A=sin 2B,所以 2A=2B 或 2A=π-2B, 即 A=B 或 A+B=2π, 所以这个三角形为等腰三角形或直角三角形. 答案 等腰三角形或直角三角形
高三数学一轮课件 第四章 三角函数与解三角形 4.2 同角三角函数的基本关系及诱导公式

=
25.
5
关闭 关闭
解析 答案
知识梳理 双基自测
12345
-11-
自测点评
1.平方关系和商数关系式中的角都是同一个角,且商数关系式中
α≠
π 2
+kπ,k∈Z.
2.利用平方关系式解决问题时,要注意开方运算结果的符号,需要
根据角α的范围确定.
3.公式化简求值时,要利用公式化任意角的三角函数为锐角三角
函数,其步骤:去负—脱周—化锐,特别注意函数名称和符号的确定.
(2)若 α∈R,则 tan α=csoins������������恒成立. (
)
(3)sin(π+α)=-sin α成立的条件是α为锐角. ( )
(4)若 cos(nπ-θ)=13(n∈Z),则 cos θ=13. ( )
(1)× (2)× (3)× (4)×
关闭
答案
-7-
知识梳理 双基自测
12345
什(1)么1 ? (2) 3
答案
考点1
考点2
考点3
-25-
解析: (1)原式=-sin 1 200°·cos 1 290°-cos 1 020°sin 1 050°
=-sin(3×360°+120°)cos(3×360°+210°)-
cos(2×360°+300°)sin(2×360°+330°)
=
-
4 5
,
cos������
=
3 5
,
于是 1
cos ������-sin ������
=
1 35- -45
= 57.
考点1
考点2
考点3
高三数学一轮复习课件:第四章 三角函数 解三角形 4-1

解法二:扇形周长 C=2R+L,面积 S=12LR=12R(C-2R)= -R2+12CR=-R-C4 2+1C620<R<C2 ,
仅当 R=C4,即 C=4R 时,扇形的面积 S 最大, 此时 C=4R=2R+L,L=2R,由 L=2R 得 α=2, 即 α=2 时,扇形面积有最大值1C62.
涉及弧长和扇形面积的计算时,可用的公式有角度表示和弧 度表示两种,其中弧度表示的公式结构简单,易记好用,在使用 前,应将圆心角用弧度表示.弧长和扇形面积公式:l=|α|R,S =12|α|R2=12LR.在公式的选择上以简单、计算量小为原则,如本例 中解法二比解法一计算量小.
[跟踪演练]
已知扇形的面积为 2,扇形圆心角的弧度数是 4,则扇形的周
扇形有最大面积? [思路引导] (1)利用弧长公式求. (2)寻求周长、半径 R 及圆心角 α 的关系,用其中两个量表示
扇形面积.
[解] (1)设弧长为 l,则 α=60°=3π,R=10,l=π3×10=130π(cm). (2)解法一:扇形周长 C=2R+l=2R+αR,∴R=2+C α,
∴S 扇=12α·R2=12α·2+C α2 =C22α·4+41α+α2=C22·4+α1+α4≤C162.当且仅当 α2=4,即 α=2 时,扇形面积有最大值C162.
第
四
三角函数 解三角形
章
第一节
任意角和弧度制及任意角的三角函数
高考概览 1.了解任意角的概念;2.了解弧度制的概念,能进行弧度与角 度的互化;3.理解任意角的三角函数(正弦、余弦、正切)的定义.
吃透教材 夯双基
填一填 记一记 厚积薄发
[知识梳理] 1.角的概念 (1)角的形成 角可以看成平面内一条射线绕着端点从一个位置 旋转 到另 一个位置所成的图形.
高考数学一轮复习第3章三角函数解三角形3.5两角和与差的正弦余弦与正切公式课件理

(2)将三角变换与代数变换密切结合:三角变换主要是 灵活应用相应的三角公式,对于代数变换主要有因式分解、 通分、提取公因式、利用相应的代数公式等,例如,sin4x +cos4x=(sin2x+cos2x)2-2sin2xcos2x=1-12sin22x.
第八页,共45页。
[诊断自测] 1.概念思辨 (1)两角和与差的正弦、余弦公式中的角 α,β 是任意 的.( √ ) (2)存在实数 α,β,使等式 sin(α+β)=sinα+sinβ 成 立.( √ ) (3)在锐角△ABC 中,sinAsinB 和 cosAcosB 大小关系不 确定.( × ) (4)公式 tan(α+β)=1t-anαta+nαttaannββ可以变形为 tanα+tanβ =tan(α+β)(1-tanαtanβ),且对任意角 α,β 都成立.( × )
第二十页,共45页。
冲关针对训练
已知锐角 α,β 满足 sinα= 55,cosβ=31010,则 α+β
等于( )
3π A. 4
B.π4或34π
π C.4
D.2kπ+π4(k∈Z)
第二十一页,共45页。
解析 由 sinα= 55,cosβ=31010,且 α,β 为锐角,可
知 cosα=255,sinβ= 1100,
(1)求函数 f(x)的最小正周期和单调递增区间;
(2)若函数 g(x)=f(x)-m 在0,π2上有两个不同的零点 x1,x2,求实数 m 的取值范围,并计算 tan(x1+x2)的值.
本题采用转化法、数形结合思想.
第二十三页,cosx+ 3, 化简可得 f(x)=2sinxcosx-2 3cos2x+ 3 =sin2x-2 312+21cos2x+ 3 =sin2x- 3cos2x =2sin2x-π3.
高考数学一轮复习第三章三角函数解三角形考前增分微课2解三角形的综合应用课件理新人教A版

“=”,故cosC的最小值是
6- 4
2。
答案
6- 2 4
2.求边的最值 【例4】 (2019·石家庄市一模)如图,四边形ABCD的对角线交点位于 四边形的内部,AB=BC=1,AC=CD,AC⊥CD,当∠ABC变化时,BD的 最大值为________。
解析 设∠ACB=θ0<θ<2π,则∠ABC=π-2θ,∠DCB=θ+π2,由余 弦定理可知,AC2=AB2+BC2-2AB·BCcos∠ABC,即AC=DC=
考前增分微课(二) 三角函数与三角形中的最值问题
纵观近几年的高考试题和高考模拟试题,不难发现在三角函数和三角 形中求最值问题成为其中一个亮点,本文从求三角函数的最值、三角形中 的最值两个方面举例说明,希望对高考备考有所帮助。
类型一 三角函数的最值 1.可化为“y=Asin(ωx+φ)+B”型的最值问题 【例1】 (2018·北京高考)已知函数f(x)=sin2x+ 3sinxcosx。 (1)求f(x)的最小正周期; (2)若f(x)在区间-π3,m上的最大值为32,求m的最小值。
化为y=Asin(ωx+φ)+B的形式求最值时,特别注意自变量的取值范围 对最大值、最小值的影响,可通过比较闭区间端点的取值与最高点、最低 点的取值来确定函数的最值。
【变式训练】 函数f(x)=3sinx+4cosx,x∈[0,π]的值域为 ________。
解析 f(x)=3sinx+4cosx=5 35sinx+45cosx =5sin(x+φ),其中cosφ= 35,sinφ=45 ,0<φ<π2 。因为0≤x≤π,所以φ≤x+φ≤π+φ。所以当x+φ= π2 时,f(x)max=5;当x+φ=π+φ时,f(x)min=5sin(π+φ)=-5sinφ=-4。所 以f(x)的值域为[-4,5]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
余弦定理 a2=b2+c2-2bccos A; b2=a2+c2-2accos B; c2=a2+b2-2abcos C cos A= cos B=
b 2 +c 2 -a 2 2bc a 2 +c 2 -b 2
; ;
cos C=
2ac a 2 +b 2 -c 2 2ab
第四章
知识梳理 双基自测
解析
63
关闭
4
5
3
12
答案
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-12-
1
2
3
4
5
5.(教材习题改编P10T2)在△ABC中,acos A=bcos B,则这个三角形 的形状为 .
关闭
由正弦定理,得 sin Acos A=sin Bcos B, 即 sin 2A=sin 2B, 所以 2A=2B 或 2A=π-2B, 即 A=B 或 A+B=2. 故△ABC 为等腰三角形或直角三角形. 等腰三角形或直角三角形
4.7
解三角形
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-2-
1
2
3
4
1.正弦定理和余弦定理 在△ABC中,若角A,B,C所对的边分别是a,b,c,则
正弦定理 内 = ������������������ B = ������������������ C =2R(R 为 ������������������ A 容 △ABC 外接圆的半径) (1)a=2Rsin A,b= 常 2Rsin B,c=2Rsin C; a b c 见 (2)sin A= ,sin B= ,sin C= ; 2R 2R 2R 变 (3)a∶b∶c=sin A∶ 形 sin B∶sin C
4.7
解三角形
知识梳理 核心考点
-3-
1
2
3
4
正弦定理 解 决 的 问 题 (1)已知两角和任一边,求其他 两边和一角; (2)已知两边和其中一边的对 角,求另一边和其他两角
余弦定理 (1)已知三边,求三个角; (2)已知两边和它们的夹 角,求第三边和其他两角
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-4-
1
2
3
4
2.三角形中的常见结论 (1)在△ABC中,A+B+C=π. (2)在△ABC中,A>B⇔a>b⇔sin A>sin B. (3)任意两边之和大于第三边,任意两边之差小于第三边.
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-5-
1
2
3
4
3.△ABC 的面积公式 (1)S△ABC=2a· h(h 表示 a 边上的高).
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-7-
1
2
3
4
(2)方向角:相对于某正方向的水平角,如南偏东30°、北偏西45°、 西偏北60°等. 顺时针 转到目标方向线的水平角, (3)方位角:指从正北方向 如B点的方位角为α(如图②). (4)坡度:坡面与水平面所成的二面角的度数.
第四章
解析
关闭
答案
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-10-
1
2
3
4
5
3.△ABC 的内角 A,B,C 的对边分别为 a,b,c.已知 a=√5,c=2,cos
2 A=3,则
b=(
) B.√3 C.2 D.3
A.√2
关闭
由余弦定理,得 a =b +c -2bccos A,即 5=b 又 b>0,解得 b=3,故选 D.
解析
π
关闭
答案
第四章
考点1 考点2 考点3 考点4
4.7
解三角形
知识梳理 核心考点
-13-
考点 1
利用正弦定理、余弦定理解三角形
例1(2016山东师大附中模拟)在△ABC中,角A,B,C的对边分别是
a,b,c,已知 cos 2A=- ,c=√3,sin A=√6sin C.
(1)求a的值; (2)若角A为锐角,求b的值及△ABC的面积. 思考已知怎样的条件能用正弦定理解三角形?已知怎样的条件能 用余弦定理解三角形?
1 1 1 1 1 ������������������
(2)S△ABC=2absin C=2acsin B=2bcsin A= 4������ . (3)S△ABC=2r(a+b+c)(r 为内切圆半径).
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-6-
1
2
3
4
4.实际问题中的常用角 (1)仰角和俯角:与目标视线在同一铅垂平面内的水平视线和目标 视线的夹角,目标视线在水平视线 上方 的角叫做仰角,目标视 线在水平视线 下方 的角叫做俯角(如图①).
关闭
(1)√ (2)√ (3)× (4)√ (5)×
答案
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-9-
1
2
3
4
5
2.在△ABC中,化简bcos C+ccos B的结果为(
)Байду номын сангаас
1
A.a
B.b
C.c
D.2b
关闭
由正弦定理,得bcos C+ccos B =2R(sin Bcos C+cos Bsin C)=2Rsin(B+C)=2Rsin A=a. A
D
2
2
2
2
2 +4-4b× ,即 3b2-8b-3=0, 3
关闭
解析
答案
第四章
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-11-
1
2
3
4
5
4 cos A=5,cos
4.△ABC 的内角 A,B,C 的对边分别为 a,b,c,若
5 C= ,a=1,则 13
b=
.
关闭
因为 cos A=5,cos C=13,且 A,C 为△ABC 的内角, 所以 sin A=5,sin C=13,sin B=sin[π-(A+C)] =sin (A+C)=sin Acos C+cos Asin C= . 65 ������ ������ ������sin������ 21 21 又因为sin������ = sin������,所以 b= sin������ = 13. 13
知识梳理 双基自测
4.7
解三角形
知识梳理 核心考点
-8-
1
2
3
4
5
1.下列结论正确的打“√”,错误的打“×”. (1)在△ABC中,已知a,b和角B,能用正弦定理求角A;已知a,b和角C, 能用余弦定理求边c. ( ) (2)在三角形中,已知两角和一边或已知两边和一角都能解三角形. ( ) (3)在△ABC中,sin A>sin B的充分不必要条件是A>B. ( ) (4)在△ABC中,a2+b2<c2是△ABC为钝角三角形的充分不必要条 件. ( ) (5)在△ABC的角A,B,C,边长a,b,c中,已知任意三个可求其他三个. ( )
