斜截面上的应力正负号规定

工程力学(高教版)教案：8.2 平面应力状态

第二节平面应力状态如图8-3(a)所示的单元体，因外法线与z 轴重合的平面上其剪应力、正应力均为零，说明该单元体至少有一个主应力的为零，因此该单元体处于平面应力状态。

为便于研究，取其中平面abcd 来代表单元体的受力情况（图8-3b ）。

任意斜截面的表示方法及有关规定如下：（1）用x 轴与截面外法线n 间的夹角α表示该截面。

（2）α得正负号：由x 轴向n 旋转，逆时针转向为正，顺时针转向为负（图8-3b 的α角为正）。

（3）ασ得正负号：拉应力为正，压应力为负（图8-3的x σ、y σ、ασ均为正值）。

（4）ατ得正负号：ατ对截面内此任一点的力矩转向，顺时针转向为正，逆时针转向为负（图8-3的x τ、ατ均为正值，y τ为负值）。

图8-3一、任意斜截面上的应力计算任意斜截面上应力有两种方法：解析法和图解法。

（一）解析法因研究的构件是平衡的，因此从构件内一点取单元体，并从单元体上取一部分（图8-3c ），则该部分也处于平衡。

由平衡条件可以求得平面应力状态下单元体任一斜截面上的应力计算公式ατασσσσσα2sin 2cos 22x yx yx --++= （8-1）ατασστα2cos 2sin 2x yx +-=（8-2）应用上式计算ασ、ατ时，各已知应力x σ、y σ、x τ和α均用其代数值。

例8-1 求图8-4所示各点应力状态下斜截面上的应力（各应力单位是Mpa ），并用图表示出来。

解（1）已知：x σ=30Mpa ，y σ=-40 Mpa ，x τ=60 Mpa ，α=30º，将各数值代入式（8-1）、（8-2）得斜截面上的应力46.3960sin 6060cos 240302403030-=-++-=σ Mpa 31.6060cos 6060sin 2403030=++= τ Mpa将 30σ、 30τ方向画在斜截面上，如图8-4(1-b)所示。

（2）已知：x σ=-80Mpa ，y σ=0 Mpa ，x τ=-40 Mpa ，α=120º，将各数值代入式（8-1）、（8-2）得斜截面上的应力64.54240sin 40240cos 280280120-=+-+-=σ Mpa 64.54240cos 40240sin 280120=--=τ Mpa将 120σ、 120τ方向画在斜截面上，如图8-4(2-b)所示。

3-2平面应力在任意斜截面上的应力分量pdf

3-2 平面应力在任意斜截面上的应力分量
说明：弹性力学符号体系与传统的材料力学符号体系中，切应力τ 的符号规定方向相反，孙国钧，赵社戌编教材采用弹性力学符号体系，金忠谋等编教材采用材料力学符号体系，下面分述之。
弹性力学符号体系
y y’
σy τy
σy’
τx’y’ σx
τx σx
x’
τ
α
x
σx'
= σα
在应力状态中主应力是正应力中的最大值或最小值。在平面应力状态下主应力的方向，即σ1 和与 x 轴的夹角αo 满足：
主应力σ1 和σ2
为
⎜⎜⎝⎛
σ σ
1 2
⎟⎟⎠⎞＝⎜⎜⎝⎛σσ
max min
⎟⎟⎠⎞
=
σx
+σ 2
y
±
⎜⎜⎝⎛
σ
x
−σ 2
y
⎟⎟⎠⎞
+τ
2 xy
最大剪应力所在的截面，满足：
如令角满足上式，则
=
σx
+ σy 2
+
σx
− σy 2
cos 2α + τxy
sin 2α
τx' y' = τα =
−
σx
− 2
σy
sin
2α
+
τxy
cos 2α
σy'
= σα+90o
=
σx
+ σy 2
−
σx
− σy 2
cos 2α − τxy sin 2α
上式建立了任意斜截面以及与其垂直的截面上的应力分量σ x' ，σ y' ，τ x' y' 与坐标面上应力分量σx, σy, τxy 之间的关系。

材料力学习题解答[第五章]

5-1构件受力如图5-26所示。

试：(1)确定危险点的位置；(2)用单元体表示危险点的应力状态（即用纵横截面截取危险点的单元体，并画出应力）。

题5-1图解：a) 1) 危险点的位置：每点受力情况相同，均为危险点；2）用单元体表示的危险点的应力状态见下图。

b) 1) 危险点的位置：外力扭矩3T与2T作用面之间的轴段上表面各点；2）应力状态见下图。

c) 1) 危险点：A点，即杆件最左端截面上最上面或最下面的点；2）应力状态见下图。

d) 1）危险点：杆件表面上各点；2）应力状态见下图。

5-2试写出图5-27所示单元体主应力σ1、σ2和σ3的值，并指出属于哪一种应力状态（应力单位为MPa）。

10题5-2图解：a)1σ=50 MPa,2σ=3σ=0,属于单向应力状态AAT （a）（c）（d）364dFlπτ=a) b) c) d)a) b) c)b) 1σ=40 MPa, 2σ=0, 3σ=－30 MPa ，属于二向应力状态 c) 1σ=20 MPa, 2σ=10 MPa, 3σ=－30 MPa ，属于三向应力状态5-3已知一点的应力状态如图5-28所示（应力单位为MPa ）。

试用解析法求指定斜截面上的正应力和切应力。

题5-3图解：a) 取水平轴为x 轴，则根据正负号规定可知： x σ=50MPa , y σ=30MPa , x τ=0, α=－30 带入式（5-3），（5-4）得 ατασσσσσα2sin 2cos 22x yx yx --++==45MPaατασστα2cos 2sin 2x yx +-== -8.66MPab) 取水平轴为x 轴，根据正负号规定：x σ= -40MPa , y σ=0 , x τ=20 MPa , α=120带入公式，得：240sin 20240cos 20402040---++-=ασ=7.32MPa x τ= 240cos 20240sin 2040+--=7.32MPac) 取水平轴为x 轴，则x σ= -10MPa , y σ=40MPa , x τ= -30MPa,α=30代入公式得：60sin )30(60cos 2401024010----++-=ασ=28.48MPa x τ= 60cos 3060sin 24010---=-36.65MPa5-4已知一点的应力状态如图5-29所示（应力状态为MPa ）。

工程力学第二单元斜截面应力

元体内任一点的矩为顺时针转向者为正，反之为负。
2
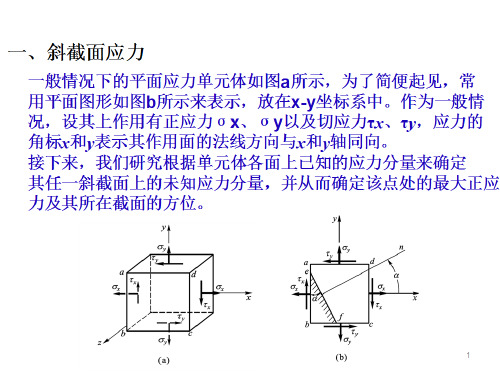
如果斜截面ef的面积为dA，则体元左侧面eb的面积为 dA·cosa，而底面bf的面积为 dA·sina。
脱离体efb处于平衡状态，可利用平衡条件来求各截面上应力之间的关系，取斜截面的法线n和切线t为投影轴，体元的平衡方程为：
Fn 0，sa d A t x d Acosa sina s x d Acosa cosa
的计算公式为：
σα

σx
σy 2

σx
σy 2
cos 2α

τx
sin 2α
(13-3)
τα

σx
σy 2
sin 2α

τx
cos 2α
(13-4)
4
t y d Asina cosa s y d Asina sina 0
Ft 0，ta d A t x d Acosa cosa s x d Acosa sina
t y d Asin a sin a s y d Asin a cosa 0
3
一、斜截面应力
一般情况下的平面应力单元体如图a所示，为了简便起见，常用平面图形如图b所示来表示，放在x-y坐标系中。作为一般情况，设其上作用有正应力σx、σy以及切应力τx、τy，应力的角标x和y表示其作用面的法线方向与x和y轴同向。接下来，我们研究根据单元体各面上已知的应力分量来确定其任一斜截面上的未知应力分量，并从而确定该点处的最大正应力及其所在截面的方位。
根据切应力互等定理有： τ y τ x
将其代入平衡方程可得：
σα σx cos2 α σ y sin2 α 2τx sin αcosα (13-1)

材料力学公式大全

材料⼒学公式⼤全材料⼒学常⽤公式1.外⼒偶矩计算公式（P功率，n转速）2.弯矩、剪⼒和荷载集度之间的关系式3.轴向拉压杆横截⾯上正应⼒的计算公式（杆件横截⾯轴⼒F N，横截⾯⾯积A，拉应⼒为正）4.轴向拉压杆斜截⾯上的正应⼒与切应⼒计算公式（夹⾓a 从x 轴正⽅向逆时针转⾄外法线的⽅位⾓为正）5.纵向变形和横向变形（拉伸前试样标距l，拉伸后试样标距l1；拉伸前试样直径d，拉伸后试样直径d1）6.纵向线应变和横向线应变7.泊松⽐8.胡克定律9.受多个⼒作⽤的杆件纵向变形计算公式?10.承受轴向分布⼒或变截⾯的杆件，纵向变形计算公式11.轴向拉压杆的强度计算公式12.许⽤应⼒，脆性材料，塑性材料13.延伸率14.截⾯收缩率15.剪切胡克定律（切变模量G，切应变g ）16.拉压弹性模量E、泊松⽐和切变模量G之间关系式17.圆截⾯对圆⼼的极惯性矩（a）实⼼圆（b）空⼼圆18.圆轴扭转时横截⾯上任⼀点切应⼒计算公式（扭矩T，所求点到圆⼼距离r）19.圆截⾯周边各点处最⼤切应⼒计算公式20.扭转截⾯系数，（a）实⼼圆（b）空⼼圆21.薄壁圆管（壁厚δ≤ R0 /10 ，R0为圆管的平均半径）扭转切应⼒计算公式22.圆轴扭转⾓与扭矩T、杆长l、扭转刚度GH p的关系式23.同⼀材料制成的圆轴各段内的扭矩不同或各段的直径不同（如阶梯轴）时或24.等直圆轴强度条件25.塑性材料；脆性材料26.扭转圆轴的刚度条件? 或27.受内压圆筒形薄壁容器横截⾯和纵截⾯上的应⼒计算公式,28.平⾯应⼒状态下斜截⾯应⼒的⼀般公式,29.平⾯应⼒状态的三个主应⼒,,30.主平⾯⽅位的计算公式31.⾯内最⼤切应⼒32.受扭圆轴表⾯某点的三个主应⼒，，33.三向应⼒状态最⼤与最⼩正应⼒ ,34.三向应⼒状态最⼤切应⼒35.⼴义胡克定律36.四种强度理论的相当应⼒37.⼀种常见的应⼒状态的强度条件，38.组合图形的形⼼坐标计算公式，39.任意截⾯图形对⼀点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式40.截⾯图形对轴z和轴y的惯性半径? ,41.平⾏移轴公式（形⼼轴z c与平⾏轴z1的距离为a，图形⾯积为A）42.纯弯曲梁的正应⼒计算公式43.横⼒弯曲最⼤正应⼒计算公式44.矩形、圆形、空⼼圆形的弯曲截⾯系数? ，，45.⼏种常见截⾯的最⼤弯曲切应⼒计算公式（为中性轴⼀侧的横截⾯对中性轴z的静矩，b为横截⾯在中性轴处的宽度）46.矩形截⾯梁最⼤弯曲切应⼒发⽣在中性轴处47.⼯字形截⾯梁腹板上的弯曲切应⼒近似公式48.轧制⼯字钢梁最⼤弯曲切应⼒计算公式49.圆形截⾯梁最⼤弯曲切应⼒发⽣在中性轴处50.圆环形薄壁截⾯梁最⼤弯曲切应⼒发⽣在中性轴处51.弯曲正应⼒强度条件52.⼏种常见截⾯梁的弯曲切应⼒强度条件53.弯曲梁危险点上既有正应⼒σ⼜有切应⼒τ作⽤时的强度条件或，54.梁的挠曲线近似微分⽅程55.梁的转⾓⽅程56.梁的挠曲线⽅程?57.轴向荷载与横向均布荷载联合作⽤时杆件截⾯底部边缘和顶部边缘处的正应⼒计算公式58.偏⼼拉伸（压缩）59.弯扭组合变形时圆截⾯杆按第三和第四强度理论建⽴的强度条件表达式，60.圆截⾯杆横截⾯上有两个弯矩和同时作⽤时，合成弯矩为61.圆截⾯杆横截⾯上有两个弯矩和同时作⽤时强度计算公式62.63.弯拉扭或弯压扭组合作⽤时强度计算公式64.剪切实⽤计算的强度条件65.挤压实⽤计算的强度条件66.等截⾯细长压杆在四种杆端约束情况下的临界⼒计算公式67.压杆的约束条件：（a）两端铰⽀µ=l（b）⼀端固定、⼀端⾃由µ=2（c）⼀端固定、⼀端铰⽀µ=（d）两端固定µ=68. 压杆的长细⽐或柔度计算公式，69. 细长压杆临界应⼒的欧拉公式70. 欧拉公式的适⽤范围传动轴所受的外⼒偶矩通常不是直接给出，⽽是根据轴的转速n 与传递的功率P 来计算。

一点应力状态概念及其表示方法

一点应力状态概念及其表示方法凡提到“应力”，必须指明作用在哪一点，哪个（方向）截面上。

因为受力构件同一截面上不同点的应力一般是不同的，通过同一点不同（方向）截面上应力也是不同的。

例如，图8-1弯曲梁横截面上各点具有不同的正应力与剪应力；图8-2通过轴向拉伸杆件同一点的不同（方向）截面上具有不同的应力。

２．一点处的应力状态是指通过一点不同截面上的应力情况，或指所有方位截面上应力的集合。

应力分析就是研究这些不同方位截面上应力随截面方向的变化规律。

如图8-3是通过轴向拉伸杆件点不同（方向）截面上的应力情况（集合）３．一点处的应力状态可用围绕该点截取的微单元体（微正六面体）上三对互相垂直微面上的应力情况来表示。

如图8-4（a,b）为轴向拉伸杆件围绕点截取的两种微元体。

特点：根据材料的均匀连续假设，微元体（代表一个材料点）各微面上的应力均匀分布，相互平行的两个侧面上应力大小相等、方向相反；互相垂直的两个侧面上剪应力服从剪切互等关系。

§8-２平面应力状态的工程实例１．薄壁圆筒压力容器为平均直径，为壁厚由平衡条件得轴向应力：（8-1a）图8-5c（Ⅰ-Ⅰ，Ⅱ-Ⅱ为相距为的横截面，H-H为水平径向面）由平衡条件或, 得环向应力：（8-1b）2．球形贮气罐（图8-6）由球对称知径向应力与纬向应力相同，设为对半球写平衡条件：得（8-2）3．弯曲与扭转组合作用下的圆轴4．受横向载荷作用的深梁§8-3平面一般应力状态分析——解析法空间一般应力状态如图8-9a所示，共有9个应力分量：面上的，，；面上的，，；面上的，，。

1）应力分量的下标记法：第一个下标指作用面（以其外法线方向表示），第二个下标指作用方向。

由剪应力互等定理，有：，，。

2）平面一般应力状态如图8-9b所示，即空间应力状态中，方向的应力分量全部为零（）；或只存在作用于x-y平面的应力分量，，，，其中，分别为，的简写，而= 。

3）正负号规定：正应力以拉应力为正，压为负；剪应力以对微元体任意一点取矩为顺时针者为正，反之为负。

等直圆杆扭转时斜截面上的应力

[] = ( 0.8 ~ 1.0 ) [ ] ( 铸铁 )
强度计算三方面：
① 校核强度：
max
Tm a x Wt
[ ]
② 设计截面尺寸：
Wt
Tm a x
[ ]
Wt
实：D3 16 空：1D6（3 1 4）
③ 计算许可载荷： Tmax Wt[ ]
[例2] 功率为150kW，转速为15.4转/秒的电动机转子轴如图，
(a)
´ (b)
M
1. 点M的应力单元体如图(b)：
2. 斜截面上的应力；
取分离体如图(d)：
´ (c)
x
´ (d)
(d)
n
x
´ t
转角规定：
轴正向转至截面外法线由平衡方程：
逆时针：为“+” 顺时针：为“–”
Fn 0 ; dA (dAcos)sin ( dAsin)cos 0
Ft 0 ; dA (dAcos)cos ( dAsin)sin 0
非圆截面等直杆：平面假设不成立。即各截面发生翘曲成空间曲面。因此，由等直圆杆扭转时推出的应力、变形公式不适用，须由弹性力学方法求解。
一、自由扭转：杆件扭转时，横截面的翘曲不受限制，任意两相邻截面的翘曲程度完全相同。
(纵向纤维长度不变, 无 , 只有 ) 二、约束扭转：杆件扭转时，横截面的翘曲受到限制，相邻截面
此杆的强度和刚度。
h 100 2 ; 0.246; 0.229
b 50
②校核强度
Wt hb2 0.246 0.1 0.052 61.6106 m3
max
T max Wt
4000 61.6 106
65MPa
③校核刚度
It h b3 0.229 0.1 0.053 284 10 8 m4

材料力学典型例题及解析7.应力应变状态典型习题解析

应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。

绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。

b = 60 mm ，h = 100 mm 。

解题分析：从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。

则各点处的应力状态如图示。

2、梁截面惯性矩为点微体上既有正应力又有切应力。

解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z 1点处弯曲正应力（压应力）MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态，所以021==σσ，MPa 1003−=σ2点为纯剪切应力状态，MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。

应力和应变状态

由应力圆可计算出： 1 5P， 2 P
例3 已知受力构件的A点处于平面应力状态，过A点两斜截面上的应力圆如图，试用应力圆求该点的主应力、主平面和最大剪应力。
解：
1 OA1 232.5MPa
3 OB1 107.5MPa
100
max 170MPa R
四、三向应力状态和最大剪应力
若单元体是主单元体，即各面上的应力为主应力；各方向的主应变为：
1 2
3
1
E 1
E 1
E
1 2 3
2 1 2
3 3 1
各平面的剪应变为零
12 23 31 0.
例1、测得A点处的x=400×10-6，y=-120×10-6 （）。已知： E=200GPa，=0.3，求A点在x和y方向上的正应力。
3）夹角关系：圆上某两条半径夹角等于单元体上对应截面外法线夹角的两倍，且转向相同。
3.应力圆的应用:
1）确定单元体上任一斜截面上的正应力σα、剪应力τα；
2）确定两个主应力的大小和方位；
3）确定两个最大最小剪应力的大小和方位；
例1 σx=60MPa,τxy=20.6MPa ,σy= 0 , 用图解法求： 1）该点的主应力和主平面的方位； 2）求与轴线方向成-450的应力σ-450、τ -450 ？
100 (80) sin 600 40cos600 2
97.64(MPa)
4）计算σmax、σmin及主平面方位角
max
min
x
y
2
x
2
y
2
2 xy
10888.5.（5 MPa）
1 108 .5, 2 0, 3 88.5
t g20
2xy x y

大连理工大学工程力学 19应力状态8-1

不相同----------应力的面的概念。
应力
指明
哪一个面上？哪一点？
哪一点？哪个方位面？
过一点不同方向面上应力的集合，
称为这一点的应力状态 State of the
Stresses of a Given Point
三、一点应力状态的描述
1. 微元体
Element
dz
（又称应力单元体）
特点：（1）正六面体；
yx dAsin sin
y dAsin cos
yx t
y
0
整理后得到
x
y
2
x
y
2
cos 2
xy
sin
2
x
y
2
sin
2
xy
cos 2
y
有界、周期函数
x
xy
一定存在极值
求主应力的极值
d—— = 0 d
x
2
y
sin
2
xy
cos
2
0
即在=0的平面，记为0平面
x
2
y
sin
20
xy
x
n
x
yx t
y
Fn 0
dA
dA x d Acos cos xy
n
xy d Acos sin
x
α
α
x
yx dAsin cos
y dAsin sin
yx t
y
0
Ft 0
dA
n
dA x d Acos sin xy d Acos cos
xy
x
α
α
x
Principal planes

材料力学-应力状态分析

+
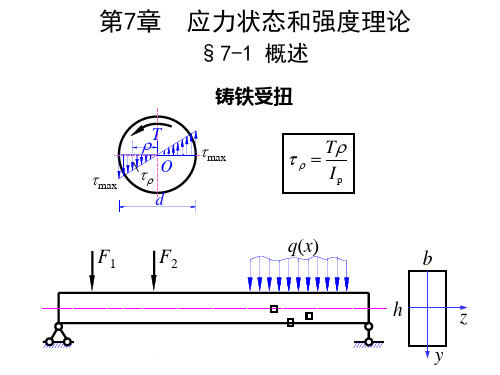
σ x σ y
2
cos 2α τ x sin 2α
sin 2α + τ x cos 2α
注意：的正负号，注意：1）σx 、σy 、τx 和 α的正负号， 2）公式中的切应力是τx ，而非τy，而非的正负号。 3）计算出的σα和τα 的正负号。
τα τ α>0
τα τ α<0
图示圆轴中，已知圆轴直径d=100mm，轴向拉例：图示圆轴中，已知圆轴直径，力 F=500kN，外力矩Me=7kNm。求 C点α = 30°截，外力矩。点 ° 面上的应力。面上的应力。 y
σy
τ
D
x
τx τy
σx
o A2
C
A1
σ
D
y
σ1 =
σ x +σ y
2
σ x +σ y + 2
2 +τ x
2
2
σ2 =
σ x +σ y
2
σ x +σ y 2 +τ x 2
σy
τ
D
x
τx τy
σx
o A2
2α0
C
A1
σ
D
y
2τ x 2α 0 = arctan σ x σ y
σ x σ y R= 2
+τ x2
2
σ x +σ y σ α 2
σy
σ x σ y 2 2 + τα = +τ x 2 τ
2 2
D
x
τx τy
σx
o
C D
y
σ
50MPa

材料力学第六章应力状态理论和强度理论

单元体的各个面均为主平面，其上的主应力为：单元体的各个面均为主平面，其上的主t
9
工程力学
Engineering mechanics
§6-1 应力状态理论的概念和实例
3、三向应力状态（空间应力状态）、三向应力状态（空间应力状态）定义：三个主应力均不为零。定义：三个主应力均不为零。例如：导轨与滚轮接触点处，取导轨表面任一点的单元体的单元体，例如：导轨与滚轮接触点处，取导轨表面任一点A的单元体，它各侧面均受到压力作用，属于三向应力状态。它各侧面均受到压力作用，属于三向应力状态。
工程力学
Engineering mechanics
第六章应力状态理论和强度理论
1
工程力学
Engineering mechanics
引
言
前面的分析结果表明，前面的分析结果表明，在一般情况下杆件横截面上不同点的应力是不相同的，过一点不同方向面上的应力也是不相同的。的应力是不相同的，过一点不同方向面上的应力也是不相同的。因此，当提及应力时，必须明确“哪一个面上哪一点” 因此，当提及应力时，必须明确“哪一个面上哪一点”的应力或哪一点哪一个方向面上”的应力。者“哪一点哪一个方向面上”的应力。如果危险点既有正应力，又有切应力，应如何建立其强度如果危险点既有正应力，又有切应力，条件？条件？如何解释受力构件的破坏现象？如何解释受力构件的破坏现象？对组合变形杆应该如何进行强度计算？对组合变形杆应该如何进行强度计算？要全面了解危险点处各截面的应力情况。要全面了解危险点处各截面的应力情况。
2
工程力学
Engineering mechanics
§6-1 应力状态理论的概念和实例
一、一点的应力状态定义：过受力体内一点所有方向面上应力的集合。定义：过受力体内一点所有方向面上应力的集合。一点的应力状态的四要素四要素：一点的应力状态的四要素：）、应力作用点的坐标（1）、应力作用点的坐标；）、应力作用点的坐标；）、过该点所截截面的方位（2）、过该点所截截面的方位；）、过该点所截截面的方位；）、应力的大小（3）、应力的大小；）、应力的大小；）、应力的类型（4）、应力的类型。）、应力的类型。二、研究应力状态的目的对受到轴向拉伸（压缩）、扭转、弯曲等基本变形的杆件，对受到轴向拉伸（压缩）、扭转、弯曲等基本变形的杆件，）、扭转其危险点处于单向应力状态或纯剪切应力状态，受力简单，其危险点处于单向应力状态或纯剪切应力状态，受力简单，可直接由相应的试验确定材料的极限应力，建立相应的强度条件。接由相应的试验确定材料的极限应力，建立相应的强度条件。

工程力学第2节二向应力状态分析

例12-1 已知构件内某点处的应力单元体如图所示，
试求斜截面上的正应力和切应力。
解：按正负号规定则有：
x 60 MPa x 120 MPa y 80 MPa 300
代入公式得：

x
y
2
x
y
2
cos2
x
sin 2
78.9MPa
低碳钢试件扭转破坏是被剪断的，且其抗剪能力
低于其抗拉能力。
铸铁试件扭转破坏是被拉断的，且其抗拉能力低于其抗剪能力。
例12-3 图示单元体，x=100MPa，x= –20MPa，
y=30MPa。试求：1） = 40º的斜截面上的和； 2）确定A点处的max、max和它们所在的位置。

x
y
2
sin 2
x
cos2

121MPa
二、主应力和极限切应力
1、主应力和主平面

x
y
2
x
y
2
cos2
x
sin 2

x
y
2
sin 2
x
cos2
将公式对求一阶导数、并令其为0：
d d

x

2
y
(2 sin
由切应力互等定理有x=y，并利用三角关系：
sin2 1 cos2 、 cos2 1 cos2 及
2
2
ቤተ መጻሕፍቲ ባይዱ
2sin cos sin 2 对以上二式进行整理得到：

x
y
2

x
y
2

材料力学

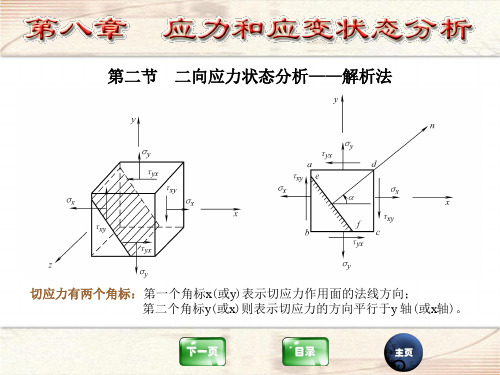
50 100 50 100 cos60 70sin 60
2
2
73.1MPa
30
x
y 2
sin 2
xy cos2
50 100 sin 60 70cos60 2
30MPa
（2）主应力及主平面的方位

max m in

0
tan 21

x 2 xy
y
上式可求出相差900的两个角a 1，对应两个互相垂直的极值切应力截面。

m
ax

min

x

2
y
2

2 xy
比较公式可见所以有
tan 20

2 xy x
y
tan
21

x xy
y

max min

x
y
2

x

2
y
2

2 xy
三、最大切应力及其作用平面的位置

x
y
2
sin 2
xy cos 2
令 1 时
即
d 0 d
d d
( x
y ) cos21 2 xy sin 21
tan 2 0

1
tan 21
2a1

2a0

π 2
,
a1

a0

π 4
例图a所示为受力构件内单元体各面上的应力，试用

材料力学第七章应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明）有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2