静电场的环路定理电势及其与场强关系副本
合集下载
§8-4静电场的环路定律电势(精)
dq C V p dV V E d l p Q 4 r p 0 关于电势零点的选择: •原则上可以任意选取; VC (rC ) 0. •源电荷分布在有限区域,自然有: •源电荷分布为无限大时,可指定电势零点, 可令 V p (r p ) 0 V p V p V p0 0 0
0
(Wb Wa ) W 电场力对qo作功=静电势能减少 •电势能属于qo与电场系统所有. •场点a 的电势能是相对电势能零点的. 取C为电势能零点,WC= 0.选择原则:任意
a点的电势能为: W A q C E dl a a0 0
a
Wa Wb Aab q 0 E dl
[例1] 已知: q1=-q2=410-8C, r =0.1m, q0=110-8C,将电荷q0从a点移到b点时, 静电场力所作的功为多少? q1 q0 q2
r a r r
b
V a =V q 1 + V q 2 = 0 q1 q2 q1 q 1 ( + 2) Vb= + = 4 4 πε o3r πε o r 4 πε o r 3 8 9 1 4.0 4.0)×10 = 9 ×10 ×0.1 ( 3 = 2.40×10 (V)
点电荷的等势面
+
带电平行板电容器 电场的等势面
++ ++ + + + + +
电偶极子的等势面
+
二. 电势梯度与电场强度的关系
dV E en gradV dn V V V Ex Ey Ez x y z [ 例1 ] 已知均匀带电圆环轴线上任一点 q 的电势为: V q 2 2 1/ 2 40r 40 (x R ) 求:轴线上任一点的场强 V q x E Ex [ 2 ] 2 3 /2 x 40 (x R )
静电场的环路定理静电场力的功电势能
静电场力的功
02
电场力的定义
电场力是电荷在电场中受到的 力，其大小和方向由电场强度
和电荷的乘积决定。
电场力的大小为 F=qE，其 中 F 是电场力，q 是电荷量，
E 是电场强度。
电场力的方向与电场强度的方 向相同，即由正电荷指向负电
荷。
电场力做功的计算
电场力做功可以通过积分计算，即 W=∫F·dr，其中 W 是电场力做的功， F 是电场力，dr 是位移矢量。
在匀强电场中，电场力做功可以通过 W=qEd计算，其中 W 是电场力做 的功，q 是电荷量，E 是电场强度，d 是位移。
在非匀强电场中，需要计算电场力在路径上的积分来计算电场力做的功。
电场力做功的特点
01
电场力做功与路径无关，只与初末位置的电势差有关。
02
电场力做功是标量，没有方向。
03
电场力做功的过程是能量转化的过程，可以转化为其他形式 的能量。
电势能
03
电势能的定义
电势能是指电荷在电场中由于位置差 异而具有的能量。
电势能是电荷与电场共同具有的能量， 其大小由电场强度和电荷量共同决定。
电势能是相对的，与零电势点的选择 有关。
电势能的变化规律
1
电场力做功与路径无关，只与初末位置有关。
2
电场力做正功，电势能减少；电场力做负功，电 势能增加。
3
静电力做功与电荷的运动路径无关，只与初末位 置有关。
电势能与电场力的关系
01
电场力做功等于电势能的减少量。
02
电势能的变化量等于电场力做的功。
03 电势能与电场力做功的关系是能量守恒定律在静 电场中的具体表现。
THANKS.
静电场的环路定理、静 电场力的功、电势能
7.4+5 静电场的环路定理、电势及其与场强关系 - 副本
电荷 q 在静电场中 r 点处的电势能:
r
W(r) q
E(r ) dr
势能零点
(积分路径任选)
数值上等于把电荷从该点移到势能零点过程中静电力 对该电荷所做的功。
例：电荷q0 在点电荷Q产生的静电场中的电势能 (无穷远处为0)：
W
(r
)
q0
Q
40 r
rQ
电势（Electric Potential） [§7.4]
前知，静电力所做的功可写成
b
Aab a q0E dl [W (rb ) W (ra )]
其中函数W (r ) 称为电荷 q0 在电场 E 中的电势能。
关于静电场力的功能原理： A W
注意： ➢ 电势能反映电荷在静电场中特定位置处的势能， 它与电荷所处在静电场中的位置有关； ➢ 电势能是系统的能量，属于电荷与静电场共有； ➢ 电势能也存在零点选择问题。 ［视方便而选；常选无穷远处为0］
λ
UP
E dl
P
r
E(r)dr
无意义
λ dr λ (ln ln r) o
r 2πε0r
2πε0
选取某一距带电直导线为rB 的B点为电势零点，
E λ 2πε0r
rB
rP B r
UP
B
E dl
P
rB
dr
r 20r
ln rB 2 0 r
当电荷分布扩展到无穷远时，电势零点不能再选在
静电场的环路定理 电势能 (§7.4)
Circulation Theorem of Electrostatic Field and Electric Potential Energy
静电场的性质： 1）电荷在电场中受到电场力
静电场的环路定理
q
j
V V V 1 2 k q q q 1 2 n 4 r r 4 r 0 1 4 0 2 0 n
q i
电势叠加原理
V V P i r 0 i i i 4
任意带电体场中的电势
VP q
4 0r
dq
a b
即：a、b两点的电势差 = A/q0
将单位正电荷 从ab电场力作的功 与路径无关
6
例: 已知真空中两金属圆筒电极间电压为U ，半径分别为 R1、 R2 。 求：负极上静止电子到正极时的速度？ 解：由电势差的定义可得
A q ( V V )
( e)( U )
R
R
2
1
F
c
dl
q0
dr
b
r +dr
r
a
rb
+
积分
1 1 q q q q 0 0 A d r 2 a4 r 4 r 0 0 a r b
b
ra
q
——点电荷的电场力作功 只与被移动电荷距离场源电荷的距离相关 与路径无关
2
2.在点电荷系的电场中(或连续带电体的电场)
结论
b b b A q E d l q E d l q E d l 0 1 0 2 0 n a a a
电场强度的线积分与路径无关
电场力是保守力，静电场是保守力场。
3
二、环路定理
在任意电场中, 将q0从a
b L2 经L1
经L2
b电场力作功：
A q E d l 0 L
9-1 静电场的环路定理-电势及其计算-电场强度与电势梯度(2016)
WAB Ep
WAB
B A
EpB q0 E dl EpA
说明：静电场力对电荷所做的功等于系统 系统 （电荷＋电场） 电势能的减少.
设 B 点为电势能零点，即 EpB 0
静电场中，电场强度 E 沿任意闭合路径 的线积分（环流 的线积分（ 环流）为零。 ）为零。
？
五 . 电场强度与电势梯度
1.等势面 （ Equipotential Surfaces ）
电场中电势相等的点连接起来所形成的曲面。
dl + + + + + +R o +
y
r
V
q 4π 0 ( x R )
2 2 1 2
（ 1 ）规定
任意两相邻等势面间的电势差相等； 等势面法线方向 en 的正方向垂直于等势面 且从低电势指向高电势。
五 . 电场强度与电势梯度
et
El A E
en
dl B
V dV
2. 电场强度与电势梯度
（ 3 ） 在直角坐标系中
V E ( x i
V V j k ) gradV y z V
dV en dln
V
电场中某点的电场强度大小等于电势沿过该点的 等势面法线方向上的空间变化率,方向由高电势处指 向低电势处。
z
+ +
+ +
+ + +
x
P
x
（ 2 ）等势面的性质
等势面的疏密程度同样表示场强的强弱； 电荷沿等势面移动时，电场力不做功； 在静电场中，电场线和等势面处处正交。
思考：若为均匀带电圆盘呢？
WAB
B A
EpB q0 E dl EpA
说明：静电场力对电荷所做的功等于系统 系统 （电荷＋电场） 电势能的减少.
设 B 点为电势能零点，即 EpB 0
静电场中，电场强度 E 沿任意闭合路径 的线积分（环流 的线积分（ 环流）为零。 ）为零。
？
五 . 电场强度与电势梯度
1.等势面 （ Equipotential Surfaces ）
电场中电势相等的点连接起来所形成的曲面。
dl + + + + + +R o +
y
r
V
q 4π 0 ( x R )
2 2 1 2
（ 1 ）规定
任意两相邻等势面间的电势差相等； 等势面法线方向 en 的正方向垂直于等势面 且从低电势指向高电势。
五 . 电场强度与电势梯度
et
El A E
en
dl B
V dV
2. 电场强度与电势梯度
（ 3 ） 在直角坐标系中
V E ( x i
V V j k ) gradV y z V
dV en dln
V
电场中某点的电场强度大小等于电势沿过该点的 等势面法线方向上的空间变化率,方向由高电势处指 向低电势处。
z
+ +
+ +
+ + +
x
P
x
（ 2 ）等势面的性质
等势面的疏密程度同样表示场强的强弱； 电荷沿等势面移动时，电场力不做功； 在静电场中，电场线和等势面处处正交。
思考：若为均匀带电圆盘呢？
4.4静电场的环路定理和电势
q0 q 1 1 − = 4πε 0 ra rb
静电力对单位正电荷做功与路径无关 场 静电力对单位正电荷做功与路径无关 场 强线积分与路径无关 点电荷的静电场是保 点电荷的静电场是保 守力场
个静止点电荷组成的电荷系统： 对由 n 个静止点电荷组成的电荷系统：
dq ϕ = ∫ dϕ = ∫ 4 πε 0 r q = 4 πε 0 r q = 2 2 4 πε 0 R + x
【例4.12】求均匀带电无限长圆柱面外部的电 】 势。带电圆柱面的电荷线密度为λ。 圆柱面内部场强为零，外部场强： 解 圆柱面内部场强为零，外部场强： 不能取无穷远为 λ E= 电势零点， 电势零点，否则计算 2πε 0 r 电势的积分不收敛。 电势的积分不收敛。 电势的积分不收敛。 电势零点：距轴线 远的P 电势零点：距轴线r0远的 0点 圆柱面外部任意一点的电势： 圆柱面外部任意一点的电势：
∫
b
a ( L)
E ⋅ dl = ∫
b
a ( L)
n b n ∑ Ei ⋅ dl = ∑ ∫ Ei ⋅ dl a i =1 i =1
与路径无关
E 的线积分与路径无关 任何带电系统都可看成由点电荷组成 结论： 结论：任何电荷系统的静电场都是保守力场
4.4.2 静电场的环路定理 静电场的保守性， 静电场的保守性 ，即场强的线积分与路径无 关的性质可表示为静电场的环路定理 静电场的环路定理： 关的性质可表示为静电场的环路定理： 静电场场强沿任一闭合回路的线积分（环流） 静电场场强沿任一闭合回路的线积分（环流） 都等于零
ϕ a − ϕ b = ∫ E ⋅ dl
a
点为电势零点或电势参考点， 选 P0 点为电势零点或电势参考点， 则 P点的 点的 电势： 电势：
第10讲 静电场的环路定理 静电场力的功 电势能
W W o W 28.8 10 7 J 0
电场力作功等于电势能增量的负值！
电势能
例题2 如图已知+q 、-q、R。求： ①单位正电荷沿odc 移至c ，电场力所作的功。 ②将单位负电荷由∞移到 o 点电场力所作的功。
d
解：① 由对称性知
Uo 0
a
q
o
b q
c
0
rR
U r E dl E dl
R r R
q
rR
P1
q r 0
2
0
4
R
q
0
r
2
dr
Ur
4
r
dr
P2
q 4 0 R
q 4 0 r
例题5 L长一节同轴圆柱面，内外半径RA 、RB，均匀 带电等量异号。①求电场分布； ②若UAB = 450V，求电荷线密度λ＝？ 解： 由高斯定理
xp
y
qxdx
2 3 2
xp
4 0 ( x R )
2
z
q 4 0 R x
2 2
R
x
□
O
例题4 求均匀带电球面电场中电势的分布，已知R,q.
q
解：由高斯定理求出场强分布 E
由定义 U p E dl
P
4 0 r
2
rR rR
U 最小
r U r
U 最大
以q为球心的同一球面上各点的电势相等。
② 电势叠加原理 若场源为q1 、q2 qn构成的点电荷系，则场中任一点 的电势等于各点电荷单独存在时在该点电势的代数和。
电场力作功等于电势能增量的负值！
电势能
例题2 如图已知+q 、-q、R。求： ①单位正电荷沿odc 移至c ，电场力所作的功。 ②将单位负电荷由∞移到 o 点电场力所作的功。
d
解：① 由对称性知
Uo 0
a
q
o
b q
c
0
rR
U r E dl E dl
R r R
q
rR
P1
q r 0
2
0
4
R
q
0
r
2
dr
Ur
4
r
dr
P2
q 4 0 R
q 4 0 r
例题5 L长一节同轴圆柱面，内外半径RA 、RB，均匀 带电等量异号。①求电场分布； ②若UAB = 450V，求电荷线密度λ＝？ 解： 由高斯定理
xp
y
qxdx
2 3 2
xp
4 0 ( x R )
2
z
q 4 0 R x
2 2
R
x
□
O
例题4 求均匀带电球面电场中电势的分布，已知R,q.
q
解：由高斯定理求出场强分布 E
由定义 U p E dl
P
4 0 r
2
rR rR
U 最小
r U r
U 最大
以q为球心的同一球面上各点的电势相等。
② 电势叠加原理 若场源为q1 、q2 qn构成的点电荷系，则场中任一点 的电势等于各点电荷单独存在时在该点电势的代数和。
静电场的环路定理
已知q的电场分布 E
根据定义, P点的电势为
4
q
0r
2
er
VP
P
E dl
r
q
40r
2Pdr4q04r2qe0rrP dl
q > 0时, VP为正, r V, r处V= 0 min q < 0时, VP为负, r V, r处V = 0 max
2.电场强度与电势梯度的关系
根据电势差的定义, 把单位正电荷从P1移到P2 电场力所作的功为：
dA E dn V (V dV )
r E
dn
n
P1
P2
V V dV
E dn dV
E
dV dn
grad V
E
ቤተ መጻሕፍቲ ባይዱ
dV dn
n
r E grad V
r 即:电场中某点的场强 E 等于该点电势梯度的负值
无意义
VP
P
E
dr
rP
2 0r
dr
2 0
ln
rP
r
P
P'
令某处 r = r0（有限值） V=0，则
VP
P0
P
E
dl
P
P
E dl
P0
P
E dl
r0 P0
P
P
2
0r
dr
2 0
ln
r0 r
可见：当电荷分布到无穷远时，
22
归纳 电场强度与电势的关系
积分关系：
6-3 静电场的环路定理 电势
1）方法一（电势叠加原理）
x
dV
dQ 4 0 r
r R2 x 2
V
1 dQ dQ V 4Q r 0r 4 0 Q 4 0 r
Q 4 0 R 2 x 2
2）方法二（定义）
o
x
E
X
R
E
4 0 x R
2
xQ
i
2
3
2
E d l 0
L
静电场的环路定理： 静电场中场强沿任意闭合环路的 线积分（环流）恒等于零。
二、电势能 电势
1、电势能
设EpA 和 EpB 分别表示试探电荷 q0 在起点A和终点B处的电势能
若取∞点: E p 0
q0
在 A、B 点处的电势能：
E pA WA q0
V Q 4 o R x
2 2
dQ
R
r
P x
x
0
V xQ Ex 3 2 2 2 x 4 0x R V V Ey 0 Ez 0 y z
E Ex i Ey j Ez k
4 0 x R
2
xQ
2
3
i
E pB WB q0
A
B
E dl E dl
B EpB
WAB
B
A
B F dl q0 E dl E pA E pB
A
A EpA
1）电势能零点的选取是任意的, 一般视问题方便而定, 通常 参考点不同,电势能不同。对于有限带电体，一般选无限远为势 能零点, 实际应用中或研究电路问题时常取大地、仪器外壳等 为势能零点；对于无限大带电体，常取有限远为势能零点； 2）电势能是属于系统的 (电场 + 试验电荷)
高二物理竞赛课件：静电场的环路定理和电势
dr
b
rb
dl
dr
E
r
q ra a q0
Aab
dA
rb ra
q0
E
dl
q0q
4 π0
rb dr r ra 2
q0q ( 1 1 )
4 π 0 ra rb
b
rb
dl
dr
E
结论: 当检验电荷 q0 在电场中从 a 移到 b 点时, 电场力做的功 A 只与
r
q0 的始末位置有关, 与路径无关.
原子物理中能量单位 1eV 1.602 1019 J
2、点电荷系的电势
E Ei
i
VP E dl Ei dl
P
iP
q1 q2
r1 r2
q3
r3
E3
E2
P
E1
VP
VPi
i
i
qi （代数和）
4 π 0ri
点电荷系电场中某点的电势，等于各个点电荷单独存 在时在该点电势的代数和，此即电势叠加原理。
电势定义：
Va
Wa q0
零点 E dl
a
③电势是相对于电势零点而言的，电势零点选择方法：
有限大小带电体通常以无穷远处为电势零点，实际问 题中也常选取大地、电器外壳或某公共点为电势零点.
地球是一个带负电的大导体, 取地球为电势零点与取无穷远处
为电势零点是一致的.
④电势高低的判断:沿着电场线方向,电势降低 (dV E d l )
L
q0
E
dl
0
q0 0,
E dl 0
L
静电场的环路定理：静电场的电场强度沿任意闭合回路
的积分(称为静电场的环流)等于零。
静电场的环路定理 电势
7-4 静电场的环路定理电势一、静电场力做功由电场强度的定义可知，在静电场E中,电荷q0受到电场力F=q0·E的作用。
当q0在电场中的位移为d时,电场力F做功：dA=q0E／d在力 F 作用下，q0从a点经某路径L到达b点，电场力做的总功为A=q0∫E／d电场强度E沿路径L的线积分∫F·d=A／q0取决于电场强度E的分布1.在点电荷q的电场中电场力做功dA=q0E／d——点电荷的电场力做功点电荷的电场力作功只与被移动电荷距离场源电荷的距离相关与路径无关2.在点电荷系的电场中(或连续带电体的电场)将电荷q0从a点移动到b点，在任意点c受电场力F=q0·E电场强度的线积分与路径无关结论：电场力是保守力，静电场是保守力场。
二、静电场的环路定理任何力场，只要具备场强的环流为零的特性，就叫做保守力场或叫做势场。
综合静电场的高斯定理和环路定理，可知静电场是有源的保守力场，又由于电场线是不闭合的，即不形成漩涡的，所以静电场属于无旋场。
三、电势3.1 电势能由环路定理知，静电场是保守场。
保守场必有相应的势能，对静电场则为电势能。
静电力的功，等于静电势能的减少。
3.2 电势某点电势能Wa与q0之比只取决于电场，定义为该点的电势电势零点的选取是任意的。
V=Wa／q03.3 电势差电场中两点电势之差V=Va-Vb,沿着电场线方向，电势降低。
把单位正电荷从P点沿任意路径移动到零势点,电场力力做的功单位：伏特或焦耳/库仑, 记为V或J/C, 1V＝1J/C注意：1电场中某点的“V”由场源电荷及场点位置决定，与q0无关。
它描述的是电场“能的性质”。
2电势是标量,有正、负。
3电势是相对量,相对于V=0处而言。
原则上可选电场中任意一点的电势为零.4电势零点的选取理论上电荷分布在有限空间时，取无穷远为V=0点。
电荷分布在无限空间，取有限远点为V=0点。
一般工程上选大地或设备外壳为V=0点四、电势的计算如果q是正的，各点的电势是正的，离点电荷愈远处电势愈低，在无限远处电势为零；如果q是负的，各点的电势也是负的，离点电荷愈远处电势愈高，在无限远处电势最大为零值。
静电场的环路定律与电势
E dl
Q 4π 0 r
dl dr
1）公式
r
r
ˆ dr r 2
r
Q 4 0 r
2
dr
Q 4π 0 r
2）说明：
①Q含符号，
■ ②∞为电势零点。 14
（2）点电荷系的场
1）公式
P 0 P 0 E dl Ei dl Ei dl
a b
1）定义：静电场中a、b两点的电势差等于电场 力把单位正电荷从a点移到b所做的功。■ 11
2）说明： ①若求任意点的电势，则需选一电势零点 ， 如选b点为电势零点，则 a点的电势：
a E dl
a
b
②积分路径为连接a、b两点的任意路径。
③电势零点的选择(参考点)任意，视分析问题 方便而定，参考点不同电势不同。■
dq
ra
结论： 电场力的功与路径无关，只与始末位置及试 验电荷的电量有关。 对闭合路径，A=?
F dl q 0 E dl 0
■
5
2、静电场力的功的特点： 只与始末位置及试验电荷的电量有关，而与具 体的路径无关。
｛静电场是保守力场。
F d l 0
§4.4 静电场的环路定理 和电势(electric potential) 4.4.1静电场的保守性 4.4.2静电场的环路定理
4.4.3电势(electric potential)
4.4.4由电势求电场强度
1
4.4.1静电场的保守性
1、静电场力的功 （电荷q0在电场中移动时静电场力所做的功） 1）点电荷激发的场：
静电场的环路定理和电势综述
dl
P
Edr
P
E0
(r R)
V (r)
r
Q
4π 0
r
2
dr
Q 4πε0r
(r R)
R
Q
V (r) 0 dr
dr
Q
r
R 4π 0r 4π 0 R
(r R)
在球面处场强不连续，但电势却是连续的。
9.4 静电场的环路定理和电势
试验电荷在电场中某点的电势能We ，在数值上等于把 它从该点移到零电势能处(参考点)电场力所做的功。
9.4 静电场的环路定理和电势
电势能属于静电场和试验点电荷
电势能的大小是相对的
电势能是状态（位置）的单值函数
2、电势与电势差
电势
VP
WeP q0
VQ
WeQ q0
参考点
E dl
P 参考点
静电力是保守力， 静电场是无旋场
环流
电势能
9.4 静电场的环路定理和电势
9.4.2 电势能和电势
一、电势能、电势、电势差
WeQQ
1、电势能We
Q
WeP WeQ q0 P E dl
若设零电势能 WeQ 0
q
rQ
rP
WeP
P
q0
参考点 静电力做正功时，电势能减少
WeP q0 P E dl 电场力做负功时，电势能增加
W qU
1.601019C1V 1.601019 J
一个电子伏特的能量
电子伏特是近代物理学中能量单位
9.4 静电场的环路定理和电势
9.4.3 电势的计算
一、点电荷q的电场中任一场点的电势
无穷远处为电势零点
V (P)
08.3静电场的环路定理、电势
E a E b
b
a
u 3
u 2 u 1
2.电势梯度 电势梯度 单位正电荷从 a到 b电场力的功 到 电场力的功
u+d +u
E•d = Ec sθ l =u−(u+d ) l o d u Ec sθ l =− u o d d
在 l E d 方向上的分量 电场强度沿某 一方向的分量 一般
u
E l
n
a
b
l 由电势定义得 u =∫ E•d =∫ P
r
∞
4 ε0r π
d = r
q 4 ε0r π
讨论 大小
q>0 u>0 r ↑ u↓ r → u 小 ∞ 最 q<0 u<0 r ↑ u↑ r → u 大 ∞ 最
为球心的同一球面上的点电势相等 对称性 以q为球心的同一球面上的点电势相等
点电荷系的电势 由电势叠加原理， 的电势为 由电势叠加原理，P的电势为
单位正电荷在该点 所具有的电势能
∞
W = ∫q E•d l a 0
a
∞
单位正电荷从该点到无穷远 电势零)电场力所作的功 点(电势零 电场力所作的功 电势零
定义电势差 a b 定义电势差 u −u 电场中任意两点 的 电势之差（电压） 电势之差（电压）
u =u −u =∫ E•d −∫ E•d =∫ E•d l l l ab a b
d q −q A =u −u =0−( ) + oc o c 4 03R 4 0R a πε πε b c q +q 0 −q = 6 0R πε R R R
② 将单位负电荷由 ∞ O电场力所作的功
A O =u −u =0 o ∞ ∞
功、电势差、电势能之间的关系 电势差、
b
a
u 3
u 2 u 1
2.电势梯度 电势梯度 单位正电荷从 a到 b电场力的功 到 电场力的功
u+d +u
E•d = Ec sθ l =u−(u+d ) l o d u Ec sθ l =− u o d d
在 l E d 方向上的分量 电场强度沿某 一方向的分量 一般
u
E l
n
a
b
l 由电势定义得 u =∫ E•d =∫ P
r
∞
4 ε0r π
d = r
q 4 ε0r π
讨论 大小
q>0 u>0 r ↑ u↓ r → u 小 ∞ 最 q<0 u<0 r ↑ u↑ r → u 大 ∞ 最
为球心的同一球面上的点电势相等 对称性 以q为球心的同一球面上的点电势相等
点电荷系的电势 由电势叠加原理， 的电势为 由电势叠加原理，P的电势为
单位正电荷在该点 所具有的电势能
∞
W = ∫q E•d l a 0
a
∞
单位正电荷从该点到无穷远 电势零)电场力所作的功 点(电势零 电场力所作的功 电势零
定义电势差 a b 定义电势差 u −u 电场中任意两点 的 电势之差（电压） 电势之差（电压）
u =u −u =∫ E•d −∫ E•d =∫ E•d l l l ab a b
d q −q A =u −u =0−( ) + oc o c 4 03R 4 0R a πε πε b c q +q 0 −q = 6 0R πε R R R
② 将单位负电荷由 ∞ O电场力所作的功
A O =u −u =0 o ∞ ∞
功、电势差、电势能之间的关系 电势差、
静电场的环路定理电势能等势面场强与电势的关系PPT课件
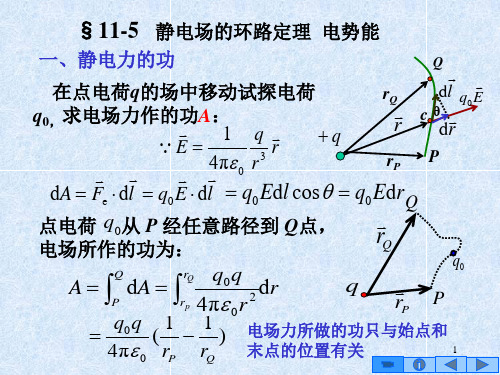
LF
dl
0
A
D
可以证明在静电场中有
E dl 0 L
C
B
E dl E dl E dl E dl E dl 0
L
ACB
BDA
ACB
ADB
在静电场中，场强沿任意闭合路径的环路积分
等于零。称为静电场的环路定理。
二、电势能 电势
静电场是保守场，可引入仅与位置有关 Q
的电势能概念。用WP和WQ分别表示试探
三、电势的计算 (electric potential ) 1. 点电荷产生的电场中的电势分布
可用场强分布和电势的定义直接积分。
p
E r
E
q
4π 0r 2
er
Vp
E dl
p
p
q
4π 0
r
2
dr
q
Vp
q
4π 0rp
正点电荷周围的场电势为正 离电荷越远，电势越低。
负点电荷周围的场电势为负
V内
Vq内
Vq内
q
4 0
(1 R1
1 R2
)
V外 Vq外 Vq外 0
这样二球面电势差为：
V内
V外
q
4 0
1 (
R1
1 R2
rQ
q0
电荷q0在电场中P点和Q点的电势能。电场 q 力对试探电荷q0所作的功可以表示为
rP
P
APQ q0 E dl WQ WP q0UQP
3
PQ
实际中为了确定q0在电场中一点的电势能，必须 选择一个电势能为零的参考点。
由于电势能的减小与试探电荷之比，完全由电
场在P、Q两点的状况所决定。可把(WP/q0)-(WQ/q0)
4 静电场的环路定理
2.当r> R 时
q 4 0 R
R
1
3.电势分布
V
q 40 R
q 4o r 1
1
rR
rR
P.
r r
P .
电势的计算例题
结论：均匀带电球面，球内的电势等于球表面的电势， 球外的电势等效于将电荷集中于球心的点电荷的电势。 E 2 q
40 R
2
r
场强分布曲线
O
R
V
r
电势分布曲线
E1 dl E2 dl ....... En dl
P P
u1 u2 ...... un ui
i 1
P
P
n
P
4 0 ri
qi
各点电荷单独存在时在该点电势的代数和, 注意(电势是一个标量)
1.3 连续带电体的电势 由电势叠加原理
W F dl
(L1)
p2
L2
P2
q0 (
(L1) 1
p
p2 E dl p1 E dl )
(L2)
(L2)
电场力做功与路径无关，故
W q0 E dl 0
L
P1
即
L E dl 0
L1
静电场的环路定理
L E dl 0
q q dl 2R u du 4 0 r L 4 0 r 4 0 r 4 0 R 2 x 2 L
则
电势的计算例题
例5.半径为R的均匀带电薄圆盘轴线上的电势分布。
解：以O为圆心，取半径为LL+dL的薄圆环， 带电dq=ds= •2L •dL 到P点距离
大学物理：第7章-静电场3-环路定理和电势
如何形象表示电势？
找到相等的电势： ( x, y, z) C(常量）
三维空间 + 限定条件 = 二维曲面 1. 定义等势面：电场中电势相等的各个点所构成的曲面。
作图规则：相邻等势面之间电势差相等
2. 等势面的性质 1) 沿等势面，电场力不做功（定义） 2) 闭合，不相交（数学上，单值，连续） 3) 等势面与电场线处处正交（直观表达）
解：(1) 选无限远处为电势零点，根据 q1
q2
电势叠加原理，O点电势为
O 1 2 3 4
O
41
4q1
4π 0
r
4.1103 V
q4
q3
(2) A q0( O ) 4.1 106 J
(3) o点电势能高，增加了4.1106 J
例4：均匀带电直线，长L，线电荷密度为 ，求直线延
长线上到其一端距离为d的一点P的电势。
解：在直线上取电荷元dl，它到P点 距离为l，在P点产生的电势为
电势叠加法
L
d
d
dq
dx
O
4π0 (d L x) 4π0 (d L x) dx
d+L-x
P
d L dx dL dy ln d L
4π0 0 (d L x) 4π0 d y 4π0 d
例5：均匀带电球层，内半径为R1，外半径为R2，体电
带电量为q。 解：场强已由高 E
斯定理求得
0
q
4π 0r
2
er
(r R) (r R)
以无限远为电势零点。
球面外：从场点积分到电势零点，各场点电场=点电荷
电场，积分结果等同点电荷。即： q
(r R)
球面外，电势和场点半径成反比
电场力的功场强与电势的关系电势环路定理
B
rB
dl
dr
r
E
q rA q0
A
电场力的功、电势、环路定理、等势面、场强与电势梯度的关系
任意电荷的电场（视为点电荷的组合）
E Ei
i
A q0
E dl
l
i
q0 l Ei dl
结论：静电场力做功只与路径的起点和终点位
置有关，与路时，
q0 E dl q0 E dl
a
① Aab 0
Wa Wb
② Aab 0
Wa Wb
q 0 则 ua ub
q 0 则 ua ub
q 0 则 ua ub
q 0 则 ua ub
静电力做功的正、负可以确定电势能是增加了， 还是减少了。但是不能确定电势是增加了，还是 减小了。
电场力的功、电势、环路定理、等势面、场强与电势梯度的关系
A1B
B2A
q0 0
E dl 0
l
1
B
E
A
2
在静电场中，电场强度的环流
恒为零。这说明静电场是保守场(conservative field)
注意
如果描述场强度的物理量环流（安培定理）恒为零， 就称该场为“无旋场”；否则称为“有旋场”。
如果描述场强度的物理量闭合曲面积分（高斯定理） 恒为零，就称该场为“无源场”；否则称为“有源 场”。
A1B A2B q0 ( E dl E dl ) 0
A
A1B
B2A
势能函数
1B
2E
电场力的功、电势、环路定理、等势面、场强与电势梯度的关系
静电场的环路定理 （circuital theorem of electrostatic field）
静电场的环路定理
a ( L2 )
b
a ( L1 )
v v b q0 E ⋅ dl − ∫
v v q0 E ⋅ dl
环路定理
=0
∫
L
v v E ⋅ dl = 0
该定理还可表达为：电场强度的环流等于零。 该定理还可表达为：电场强度的环流等于零。 根据保守力的定义，任何力场， 根据保守力的定义，任何力场，只要其场强的环流 为零，该力场就叫保守力场 势场。 保守力场或 为零，该力场就叫保守力场或势场。可以引入相应 的势能，即电势能。 的势能，即电势能。
q 4πε 0 x
•从电荷分布求场强，再由场强分布求电势 从电荷分布求场强， 从电荷分布求场强
U P = ∫ E • d r （场强积分法） 场强积分法）
P ∞
例4 求均匀带电球面的电场中电势的分布 解 由高斯定理可以求的球面内外的场强分布为
+ P1 + + + + +
2
r <R r ≥R
对球外一点P 对球外一点
二 电势
某点电势电W 之比只取决于电场， 某点电势电 a与q0之比只取决于电场，定义电该 点的电势 单位：伏特（ ） 电势. 点的电势. 单位：伏特（V） 电势电
W a = q0 ∫
"0"
a
v E ⋅ dl
电势
WA VA = q0
=∫
"0"
A
v E⋅ E⋅ dl
由上式可以看出, 由上式可以看出,静电场中某点的电势在数值上 等于单位正电荷放在该点处时的电势能, 等于单位正电荷放在该点处时的电势能,也等于单位 正电荷从该点经任意路径到电势零点处(无穷远处) 正电荷从该点经任意路径到电势零点处(无穷远处) 时电场力所做的功。 时电场力所做的功。
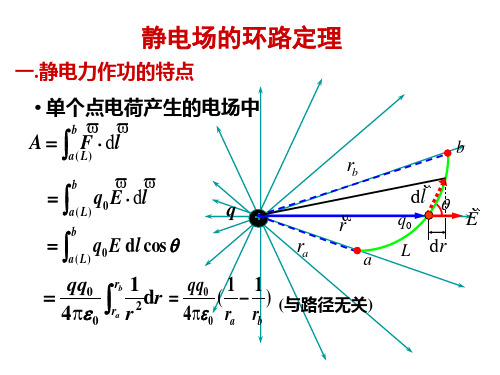
b
a ( L1 )
v v b q0 E ⋅ dl − ∫
v v q0 E ⋅ dl
环路定理
=0
∫
L
v v E ⋅ dl = 0
该定理还可表达为：电场强度的环流等于零。 该定理还可表达为：电场强度的环流等于零。 根据保守力的定义，任何力场， 根据保守力的定义，任何力场，只要其场强的环流 为零，该力场就叫保守力场 势场。 保守力场或 为零，该力场就叫保守力场或势场。可以引入相应 的势能，即电势能。 的势能，即电势能。
q 4πε 0 x
•从电荷分布求场强，再由场强分布求电势 从电荷分布求场强， 从电荷分布求场强
U P = ∫ E • d r （场强积分法） 场强积分法）
P ∞
例4 求均匀带电球面的电场中电势的分布 解 由高斯定理可以求的球面内外的场强分布为
+ P1 + + + + +
2
r <R r ≥R
对球外一点P 对球外一点
二 电势
某点电势电W 之比只取决于电场， 某点电势电 a与q0之比只取决于电场，定义电该 点的电势 单位：伏特（ ） 电势. 点的电势. 单位：伏特（V） 电势电
W a = q0 ∫
"0"
a
v E ⋅ dl
电势
WA VA = q0
=∫
"0"
A
v E⋅ E⋅ dl
由上式可以看出, 由上式可以看出,静电场中某点的电势在数值上 等于单位正电荷放在该点处时的电势能, 等于单位正电荷放在该点处时的电势能,也等于单位 正电荷从该点经任意路径到电势零点处(无穷远处) 正电荷从该点经任意路径到电势零点处(无穷远处) 时电场力所做的功。 时电场力所做的功。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
➢ 电势能是系统的能量，属于电荷与静电场共有；
➢ 电势能也存在零点选择问题。 ［视方便而选；常选无穷远处为0］
电荷 q 在静电场中 rr 点处的电势能:
W (rr ) q rr
Er (rr ) drr
势能零点
(积分路径任选)
数值上等于把电荷从该点移到势能零点过程中静电力 对该电荷所做的功。
例：电荷q0 在点电荷Q产生的静电场中的电势能 (无穷远处为0)：
电势零点
注：
➢ 电势是静电场的属性，与产生该电场的电荷源 有关，但与场中的试验电荷无关；
➢ 电势有相对性，需要选择零点(常取地球、仪器 外壳、无穷远处等为电势零点)；
➢ 电势的单位：V. [能量单位eV的由来]
电势差（电压）:
Uba
Ub Ua
rrb rra
Er (rr
)
drr
（电势差与电势零点的选择无关。）
3、电势计算的方法：
1）场强积分法
已知场强分布时,
场点 r r
U场点
E dl
零点
步骤： (1)先求场强分布; (2)选择合适的路径; (3)计算积分.
[当带电体为无限大时，只能用该方法计算]
2）电势叠加法:
已知源电荷分布(有限尺寸)时,各源的电势标量叠加
U (rr ) 1
4 0
i
rr
Qi
定理 积分形式 微分形式 物理含义
高斯定理
(关于场强的通量)
Ò r r
E dS
1
dV
S
0 VS内
r
E
0
静电场是有源场
环路定理 (关于场强的环流)
vv
Ñl E静 dl 0
r E静 0
静电场是保守场 （静电场是无旋场）
注意：一般地，如果电场包含有非静电场，则不是保守场。
三、电势能 (Electric Potential Energy) :
q0Q
4 0
rrb rr rra rr
rr rr d ( rr rr ) rr rr 3
q0Q
4 0
1
r rb
rr
1
r ra
rr
在点电荷的静电场中移动电荷q0 时，电场力做的功只 与q0的始末位置有关，而与路径无关。
2A、aF点rb 电q荷r0rrarbEr系Fr的 d电irr 4场q0Q中i0i :(rrrrrrrarbAarrrbirirr都rri4iq3)可0Q写0i 成(rrrr[Wrrrrii(3)rrb)d
静电场的环路定理 电势能 (§7.4)
Circulation Theorem of Electrostatic Field and Electric Potential Energy
静电场的性质： 1）电荷在电场中受到电场力
电场强度 E
2）当电荷在电场中移动时， 电场力要对电荷作功。
电势能 W
从库仑定律和场强叠加原理出发，可以证明，静电场 力对电荷所做的功与路径无关，说明静电场是保守场， 可以引入电势能的概念。在此基础上，还可以引入描 述静电场的另一个状态量——电势。
二、电势的计算:
1、点U电(rr荷) 的电势rr 4:Q(0以rr无rr 穷rrrrQQ远3处 d为rr 0)
40
Q rr
r rQ
讨论 Q 0: U 0; r ,U ，r 处U 最小
Q 0: U 0; r ,U ，r 处U最大
对称性：以Q为球心的同一球面上各点的电势相等
2、电势叠加原理: rr
二、静电场的环路定理:
静电力做功只与移动的起止位置有关，而与路径无关。
vv
vv
vv
q0E dl q0E dl q0E dl
ABC
ADvC v
v CvDA
A环路 q0( E dl E dl ) 0
C B
ABC
CDA
在静电场中沿[任意]闭合环路移动 [任意]电荷时，静电场对电荷所做
E Ei
i
（矢量叠加）
场点 r r
U E dl 零点
Ui
i
（标量叠加）ຫໍສະໝຸດ 点电荷系的电场中某点的电势，等于各点电荷单独 存在时在该点的电势的代数和。
点电荷系的电势:
U (rr ) 1
4 0
i
rr
Qi
rri
连续分布电荷的电势:
r 1 (rr)dV
U (r )
40 V
rr rr
r ri
1
4 0
V
( rr)dV
rr rr
例 求均匀带电圆环轴线上的电势分布。 (已知：R、q )
解： 方法一 点电荷电势 + 电势叠加原理
dU dq 4πε0r
U dU
q dq
r
R
x
1
q
dq
4πε0r 0
o x dU
q
4πε0 ( x 2 R2 )1/ 2
静电场是保守场，静电力是保守力；故可引入势能。
前知，静电力所做的功可写成
Aab
br a q0E
r dl
[W (rrb )
W (rra )]
其中函数
W
(rr
)
称为电荷
q0
在电场
r E
中的电势能。
关于静电场力的功能原理： A W
注意： ➢ 电势能反映电荷在静电场中特定位置处的势能， 它与电荷所处在静电场中的位置有关；
r W (ra )]
(rr rri
形式
)
q0
i
Qi
4 0
rrb
1 rri
1 rra rri
2、连续分布电荷的电场中:
Aab
q0
V
(rr) 4 0
rrb
1 rr
rra
1 rr
dV
静电场力可对处于其中的电荷做功→静电场具有能量； 静电力做功只与场点的起止位置有关，而与路径无关。
一、静电场力所做的功:
1、点电荷的电场中:
dA
r F
r dl
v q0 E
drr
q0Q
40
(rr rr) rr rr 3
drr
b
Q
rr
rr drr rr
drr
r E
q0
a
Aab
b
dA
a
q Q rrb rr 0
4 rra rr
0
(rr rr) rr rr 3
O
d (rr
rr)
A
D
的功的代v 数和总是为0。v v
静电场的
Ñ E静的环流
lrE静v dl 0
r
环路定理
r
利用数学中Green定理 ÑLV dl ( V ) dS ，则
S ( L围成)
静电场的环路定理 的微分形式
v E静 0
静电场无涡旋；即 电场线不形成回路
静电场的两条基本定理 （反映真空中静电场的两条特性）
W
(rr
)
q0
Q
40 rr
rrQ
电势（Electric Potential） [§7.4]
一、电势的定义: U (rr ) W (rr ) q0
比值与q0的大小无关，仅取决于 电场的性质及场点的位置。
电势：单位正电荷在场点处所具有的电势能。
U (rr ) rr
r E
(rr
)
drr
(积分路径任选)