第4章 三铰拱和悬索结构的受力分析33页PPT
合集下载
3_4三铰拱

d2y 1 qc y q x qc y 则 2 dx H q y y c 即 H H
特征方程为: 2
方程的通解为:
y x A ch
H
x B sh
H
x
qc
其中待定常数A、B可由边界条件确定。
x 0 时, y 0
RB
如果拱受分布荷载,压力线呈 曲线,称为压力曲线;如果是集中 荷载,压力线呈多边形,称压力多 边形。
各截面合力R若都沿拱轴切线方向作用是最理想的情况,此时各截面内只有 均匀分布的正应力,拱处于轴向受压状态,拱的经济效果将最好。
三、三铰拱的合理轴线
在固定荷载作用下,使拱各截面处于无弯矩状态的轴线称
Fr 0 :
q ds 2 N sin
d 0 2
q Rd N d 0
N qR
R
N q
因N为常数,q也为常数,所以任一点的曲率半径R也是常数,即拱轴为圆弧。
例3、设三铰拱上承受填土荷载,填土表面为一水平面,试求拱的合理轴线。设填土 的容重为,拱所受的分布荷载为 q qC y。 [解] 拱截面弯矩计算式 M M Hy 在本例坐标系中须改为:
2、内力计算 以截面D为例 Q 取截面D左侧内为隔离体,并设截面弯矩以 P
o
1
x-a1
M
使拱内侧纤维受拉为正。
H
y
D H
MD 0 :
A
x
M VA x P 1 x a1 H y
M M Hy Q Q cos H sin
Qo
VA
P1
Q
特征方程为: 2
方程的通解为:
y x A ch
H
x B sh
H
x
qc
其中待定常数A、B可由边界条件确定。
x 0 时, y 0
RB
如果拱受分布荷载,压力线呈 曲线,称为压力曲线;如果是集中 荷载,压力线呈多边形,称压力多 边形。
各截面合力R若都沿拱轴切线方向作用是最理想的情况,此时各截面内只有 均匀分布的正应力,拱处于轴向受压状态,拱的经济效果将最好。
三、三铰拱的合理轴线
在固定荷载作用下,使拱各截面处于无弯矩状态的轴线称
Fr 0 :
q ds 2 N sin
d 0 2
q Rd N d 0
N qR
R
N q
因N为常数,q也为常数,所以任一点的曲率半径R也是常数,即拱轴为圆弧。
例3、设三铰拱上承受填土荷载,填土表面为一水平面,试求拱的合理轴线。设填土 的容重为,拱所受的分布荷载为 q qC y。 [解] 拱截面弯矩计算式 M M Hy 在本例坐标系中须改为:
2、内力计算 以截面D为例 Q 取截面D左侧内为隔离体,并设截面弯矩以 P
o
1
x-a1
M
使拱内侧纤维受拉为正。
H
y
D H
MD 0 :
A
x
M VA x P 1 x a1 H y
M M Hy Q Q cos H sin
Qo
VA
P1
Q
结构力学 05三铰拱和悬索.

(2)H MC0
f
推力只与三铰位置及荷载有关,与拱轴线无关。 f 大,H 小。
(3)在竖向荷载作用下,拱截面上有轴力,轴力较大,是拱的 主要内力。 N Q0 sin H cos
(4) M M 0 Hy
由于水平推力H 的存在,三铰拱横截
面上的弯矩要比相应简支梁的弯矩小。
二、三铰拱优缺点:
P2
VA0
V
B
C
b2 VB0 三代H铰梁拱的1的反f [竖 力VA向 相 反 等l1 力 ;P与 水1(l其 平1 等 反a1 )]
力与M拱C0轴线[V形A0 状l1无 关P1(。l1 荷a1)]
载与跨度H一= M定C时0 /,f 水平推
力与矢高成反比。
结构力学电子教程
拉杆拱
5 三铰拱和悬索
三铰拱 拉杆拱
5 三铰拱和悬索
三铰拱{
平拱 斜拱
超静定拱
两铰拱
超静定拱
拉杆
静定拱
拉杆拱
无铰拱 斜拱
高差h
结构力学电子教程
4.拱的有关名称
5 三铰拱和悬索
顶铰
拱肋 拱趾铰
拱肋 矢高 拱趾铰
跨度
高跨比=f / l
结构力学电子教程
5 三铰拱和悬索
5.2 在竖向荷载作用下三铰拱的支座反力
结构力学电子教程
QD左 QD0左 cosD H sinD (-2) 0.832-10.5 (0.555) 4.16kN
ND左 QD0左 sinD H cosD =-(-2) (0.555)-10.5 0.832 9.85kN
QD右 QD0右 cosD H sinD =(-12) 0.832-10.5 (0.555) 4.16kN
结构力学 第四章 三铰拱

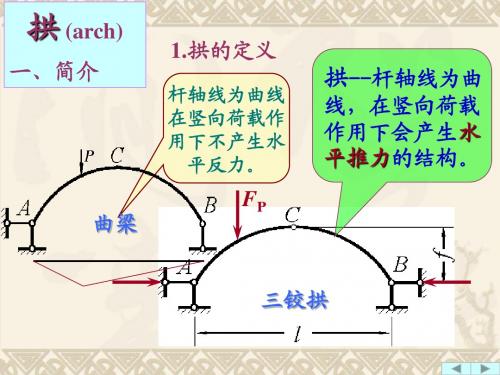
杆轴线为曲线 在竖向荷载作 用下不产生水 平反力。 平反力。
FP
曲梁
三铰拱
第四章 三铰拱
三、拱常用的形式
静定拱
三铰拱
两铰拱
超静定拱
无铰拱
第四章 三铰拱
四、拱的有关概念
顶铰 拱轴线 平拱 拱趾铰 跨度 拱趾铰 拱轴线 拱(矢)高
斜拱
拉杆拱
第四章 三铰拱 §4-2 三铰拱的支座反力和内力 一、支反力 1、竖向反力 A ∑ M A = 0, VB l − M ABP = 0 H A
第四章 三铰拱
第四章 三铰拱
§4-1 概述 §4-2 三铰拱的支座反力和内力 §4-3 压力线与合理拱轴
第四章 三铰拱
§4-1 概述 实例——拱桥 一、实例 拱桥 拱桥是承受轴向压力为主的拱圈或拱肋作为主要 承受轴向压力为主 拱桥是承受轴向压力为主的拱圈或拱肋作为主要 承重构件的桥梁,拱结构由拱圈(拱肋)及其支座组成。 承重构件的桥梁,拱结构由拱圈(拱肋)及其支座组成。
第四章 三铰拱 [例4-1]三铰拱及其所受荷载如图所示,拱的轴线为抛物线: 1]三铰拱及其所受荷载如图所示,拱的轴线为抛物线: 三铰拱及其所受荷载如图所示 y=4fx(l-x)/l2,求支座反力,并绘制内力图。 求支座反力,并绘制内力图。 解: (1) 反力计算
4 × 4 + 1× 8 ×12 0 VA = VA = 16 = 7kN ( ↑ ) 7kN
M ABP VB = l l 同跨度同荷载简支梁(代 同跨度同荷载简支梁( 的支座反力: 梁)的支座反力:
i i
P
q
C
f
B
l1
l − l1
HB VB
∑ Pa =
VA
结构力学三铰拱ppt课件

精选课件
第一节 三铰拱的组成和类型
2. 三铰拱的构成
拱顶
矢高:起拱线至拱顶的
竖直距离。
矢高f
拱趾
起拱线
精选课件 跨度L
拱轴 拱趾
第一节 三铰拱的组成和类型
2. 三铰拱的构成
精选课件
带拉杆的拱:在 屋架中,为消除 水平推力对墙或 柱的影响,在两 支座间增加一拉 杆,由拉杆来承 担水平推力,桥 梁中应用也非常 广泛。
精选课件
第三节 竖向荷载作用下三铰拱的内力特点
三铰拱在竖向荷载作用下的弯矩由两部分组成,水平反力 产生负弯矩,可以抵消一部分正弯矩,与简支梁相比拱的弯 矩、剪力较小,轴力较大(压力),应力沿截面高度分布较均 匀。
拱结构的优点:选用耐压性能好而抗拉性能差的砖石、混凝 土材料,节省用料,重量轻,可用于大跨、大空间结构。
• 集中力偶作用处,弯矩图将发生突变;
• 上述公式仅适合于平拱,且承受竖向荷载情况;
• 拱的内力仍然有FQ=dM/ds
精选课件
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算 2 竖向荷载作用下指定截面内力计算 3 拱的内力图
由于拱轴线是弯曲的,所以内力图都是曲 线形的,内力图要通过逐点描图的方法绘制, 总的规律仍符合荷载和内力的微分关系。
第一节 三铰拱的组成和类型
2. 三铰拱的构成
铁路拱桥:在桥梁中为了降低桥面高 度,可将桥面吊在拱上。
精选课件
第一节 三铰拱的组成和类型
3. 三铰拱的分类
三铰拱 拉杆拱1
两铰拱 无铰拱
拉杆拱2 精选课件
斜拱
第一节 三铰拱的组成和类型
4. 三铰拱的受力特点
FP
曲梁
第一节 三铰拱的组成和类型
2. 三铰拱的构成
拱顶
矢高:起拱线至拱顶的
竖直距离。
矢高f
拱趾
起拱线
精选课件 跨度L
拱轴 拱趾
第一节 三铰拱的组成和类型
2. 三铰拱的构成
精选课件
带拉杆的拱:在 屋架中,为消除 水平推力对墙或 柱的影响,在两 支座间增加一拉 杆,由拉杆来承 担水平推力,桥 梁中应用也非常 广泛。
精选课件
第三节 竖向荷载作用下三铰拱的内力特点
三铰拱在竖向荷载作用下的弯矩由两部分组成,水平反力 产生负弯矩,可以抵消一部分正弯矩,与简支梁相比拱的弯 矩、剪力较小,轴力较大(压力),应力沿截面高度分布较均 匀。
拱结构的优点:选用耐压性能好而抗拉性能差的砖石、混凝 土材料,节省用料,重量轻,可用于大跨、大空间结构。
• 集中力偶作用处,弯矩图将发生突变;
• 上述公式仅适合于平拱,且承受竖向荷载情况;
• 拱的内力仍然有FQ=dM/ds
精选课件
第二节 竖向荷载作用下三铰拱的受力分析
1 竖向荷载作用下拱反力计算 2 竖向荷载作用下指定截面内力计算 3 拱的内力图
由于拱轴线是弯曲的,所以内力图都是曲 线形的,内力图要通过逐点描图的方法绘制, 总的规律仍符合荷载和内力的微分关系。
第一节 三铰拱的组成和类型
2. 三铰拱的构成
铁路拱桥:在桥梁中为了降低桥面高 度,可将桥面吊在拱上。
精选课件
第一节 三铰拱的组成和类型
3. 三铰拱的分类
三铰拱 拉杆拱1
两铰拱 无铰拱
拉杆拱2 精选课件
斜拱
第一节 三铰拱的组成和类型
4. 三铰拱的受力特点
FP
曲梁
美院4.6三铰拱的受力分析

拱顶
拱高
拱肋 拱趾 跨度
拱肋 拱趾
f/l——高跨比 f/ ——高跨比 ——
5、拱的共性
1.曲杆 1.曲杆 2.竖向荷载作用下有水平推力 2.竖向荷载作用下有水平推力 在竖向荷载作用下产生水平推力的曲杆结构称为拱。 在竖向荷载作用下产生水平推力的曲杆结构称为拱。 3.由于水平推力的存在,拱比同跨度、 3.由于水平推力的存在,拱比同跨度、同荷载的简支梁的 由于水平推力的存在 弯矩小; 弯矩小; 4.内力一般有M 许多情况下F 是主要内力。 4.内力一般有M、FQ、FN,许多情况下FN是主要内力。 内力一般有
15kN 16.图示三铰拱的水平推力为________。
12.5kN
17.5kN
12.图示三铰拱,水平推力H__________。
Pl 8f
P/4
3 P/4
F2
FBH
FAH
A
FAV
x
l1
1 ( Fa1 + F2a2 ) 1 l 1 FAV = ( Fb1 + F2b2 ) 1 l
0 FBV = FBV
0 FAV = FAV
∑ Fx = 0
FAH = FBH = FH
以AC为研究对象 AC为研究对象
∑ MC = 0
A F1
0 FAV
B
FH
0 FBV
x
A l1
4.6.3 三铰拱合理拱轴线的概念
在固定荷载作用下,使拱处于无弯矩状态的轴线称为合理轴 在固定荷载作用下,使拱处于无弯矩状态的轴线称为合理轴 无弯矩状态 线。由上述可知,按照压力曲线设计的拱轴线就是合理轴线。 由上述可知,按照压力曲线设计的拱轴线就是合理轴线。 从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型。 从结构优化设计观点出发,寻找合理轴线即拱结构的优化选型。 对拱结构而言,任意截面上弯矩计算式子为: 对拱结构而言,任意截面上弯矩计算式子为:
05三铰拱和悬索

结构力学电子教程
5 三铰拱和悬索
【例5.2】 求三铰拱在沿水平方向均匀分布竖向荷载作 用下的合理拱轴线。
【解】
M y H
0
MC0 H f
M0=qlx/2-qx2 /2 =qx(l-x)/2 MC0=ql2/8 H=ql2/8f
y=4fx(l-x)/l2
抛物线
结构力学电子教程
5 三铰拱和悬索
(1)在沿水平线均匀 分布的竖向荷载作用下 ,三铰拱的合理轴线为 二次抛物线。
结构力学电子教程
5 三铰拱和悬索
b. 截面D的内力
0 MD MD HyD =12 3-10.5 3 4.5kN m
0
1
2
3
4
5
6
7
8
0 QD左 QD 0.832-10.5 (0.555) 4.16kN 左 cos D H sin D (-2) 0 ND左 QD (0.555)-10.5 0.832 9.85kN 左 sin D H cos D =-(-2) 0 QD右 QD 0.832-10.5 (0.555) 4.16kN 右 cos D H sin D =(-12) 0 ND右 QD (0.555)-10.5 0.832 15.4kN 右 sin D H cos D -(-12)
结构力学电子教程
5 三铰拱和悬索
结构力学电子教程
5 三铰拱和悬索
结构力学电子教程
5 三铰拱和悬索
5.4 三铰拱的受力特性
一、三铰拱的受力特征:
0 0 VA VA VB VB ,与拱轴线形状及拱高无关。 (1)竖向反力, (2)H M C 0 推力只与三铰位置及荷载有关,与拱轴线无关。 f f 大,H 小。 (3)在竖向荷载作用下,拱截面上有轴力,轴力较大,是拱的 0 主要内力。 N Q sin H cos
张系斌《结构力学简明教程》讲义教案三铰拱精品PPT课件

一、概述
3.拱的分类
静定拱Biblioteka 三铰拱拉杆超静定拱
拉杆拱
超静定拱
两铰拱
无铰拱 斜拱
高差h
拱 (arch)
一、概述
4.拱的有关名称 顶铰
拱肋 拱趾铰
拱肋 矢高 拱趾铰
跨度
二、三铰拱的数解法 ----支反力计算
P1
C
P2
三铰拱的竖向反 力与其等代梁的
A
f
B XB 反H力相等;水平反
XA
YA
l/2 l/2
l
在竖向荷载作用下,三
铰拱的合理拱轴线的纵
只限于三铰平拱受 坐标与相应简支梁弯矩 竖向荷载作用 图的竖标成正比。
试求图示对称三铰拱在均布荷载作用下 的合理拱轴线
MC0=ql2/8 H=ql2/8f M0=qlx/2-qx2 /2 =qx(l-x)/2 y=4fx(l-x)/l2
抛物线
写在最后
成功的基础在于好的学习习惯
H= MC0 / f
二、y三铰P1拱的K 数C解法
----内力计算 P2
载及A 三三个x铰铰拱y的的位内f 置力有不关但,与B而荷 XB X A
XA且与拱轴l/线2 的形状l/有2x 关。
YA
QK MK P1
NK
P1
M
0 K
YA 由于推力的l 存在,拱Y的B
Y
0 A
Q
0 K
弯矩比相应简支梁的弯矩要
第二章 静定结构受力分析
§2-3 三铰拱受力分析
拱 (arch)
一、概述
杆轴线为曲线 在竖向荷载作 用下不产生水
平反力。
1.拱的定义 这是拱结构吗?
曲梁
拱--杆轴线为曲
结构力学三铰拱图文共31页

39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
第4章三铰拱
M = M − FH y = 0 0 M y= FH 在竖向荷载作用下, 在竖向荷载作用下,三
0
铰拱的合理拱轴线的纵 只限于三铰平拱受 坐标与相应简支梁弯矩 竖向荷载作用 图的竖标成正比。 图的竖标成正比。
试求图示对称三铰拱在均布荷载作用下 的合理拱轴线 MC0=ql2/8 FH=ql2/8f /8f
K
y P 1
QK M K
C
A
C
B
FQK=F cosϕ−FHsinϕ QK
0
三铰拱在竖向荷载作用 F =−F0 sin ϕ−F cosϕ a1 b1 NK H QK 下轴向受压。 下轴向受压。 FVA0 a2 b2 FVB0
q=2kN .m y
2 1 0 A 3 4 5 6
P=8kN
例 1、三铰拱及其所受荷载如 图所示拱的轴线为抛物线方程
4f ⋅ x(l − x) 2 l 制内力图。 y=
ϕ2 y2 x
7 8 B
f=4m FH = 7.5kN FVB= 9kN
计算反力并绘
7.5kN x2=3m FVA =11kN 3m 6m 6m
(1)计算支座反力
(2)内力计算
y2 =
以截面2为例
4f 4×4 x( l − x ) = × 3(12 − 3) = 3m 2 2 M 2 = M 2 − FHy 2 = (11× 3 − 2 × 3 × 1.5) − 7.5 × 3 l 12
拱 (arch)
一、简介
1.拱的定义 拱的定义
杆轴线为曲线 在竖向荷载作 用下不产生水 平反力。 平反力。
--杆轴线为曲 拱--杆轴线为曲 线,在竖向荷载 作用下会产生水 作用下会产生水 平推力的结构 的结构。 平推力的结构。
4 第四章 三铰拱

无铰拱
凡在竖向荷载作用下会产生水平反力的 结构都可称为拱式结构或 推力结构。
P
FAH
FBH
推力结构
VA VB
3)拱结构的应用:主要用于拱坝、屋架结构、桥梁结构。 拱结构的优缺点:
a、在拱结构中,由于水平推力的存在,其各截面的弯 矩要比相应简支梁或曲梁小得多,因此它的截面就 可做得小一些,能节省材料、减小自重、加大跨度 b、在拱结构中,主要内力是轴压力,因此可以用抗拉 性能比较差而抗压性能比较好的材料来做。
相应简支 梁的弯矩
(2)弯矩计算 求拱轴线上任意点k的弯矩, 为此取Ak为隔离体:
Mk FAV xk FP1 xk a1 FH yk (3)剪力计算 求拱轴线上任意点k的剪力, 同样以Ak为隔离体: 0 FSk FYACos k HSin k FP1Cosk FYA FP1 Cos k HSin k
三铰刚架 例:
c、由于拱结构会对下部支撑结构产生水平的推力,因 此它需要更坚固的基础或下部结构。同时它的外形 比较复杂,导致施工比较困难,模板费用也比较大
拱各部分的名称:
拱顶
拱顶
拱轴线 拱高 f 起拱线 拱趾 跨度 l
f
L
L—跨度(拱趾之间的水平距离) f—矢高或拱高(两拱趾间的连线到拱顶的竖向距离)
f/L——高跨比(拱的主要性能与它有关,工程中这 个值控制在1—1/10 )
位于河北赵县,又名安济桥,由石工李春主持设计建造,完成 于公元605年左右。 该桥为空腹敞肩式坦拱桥,桥长64.4m,净跨37.02m,桥宽 9m,净矢高7.23m,桥面纵坡6.5%。 拱由28圈拱石平行砌筑,每圈有拱石43块;为加强拱石间的结 合,拱石各面均凿有相当细密的斜纹。另外,还在拱石之间设置X 形锚铁和铁锚杆。 在拱圈两肩各设两个跨度不等的腹拱,既减轻了桥身自重,又 节省了材料,还便于排洪。 该桥构思巧妙,造型美观,施工精度高,工艺精致,历1300多 年而无恙,举世闻名,不愧为桥梁文物宝库中的精品。 赵州桥被列为“全国重点文物保护单位”。在90年代初,赵州 桥被美国土木工程师学会选为“国际历史土木工程里程碑”。
结构力学——组合结构-三铰拱ppt课件

(A,B,C三铰在一直线上,成为几何瞬变体。)
.
②拱内力计算:
QM
P1
N
D
HA
VA
弯矩:受拉侧做弯矩图; 剪力:垂直于拱轴线的切线(顺时针为正); 轴力:平行于拱轴线的切线(拉为正)。
.
a1
M
P1 D
y HA x
VA
•弯矩:
由 MD0
M V A x P 1 ( x a 1 ) H y 0 M M oH y
C
Mc0q2l /8
l
Mc0 / 6
Mc0 / 6
B
A
C
B
Mc0 / 6
0.207 l 0.586 l 0.207 l
优点:方便,简单; 缺点:截面仍有弯矩。
.
②三铰曲拱:
f MM0Hy (HM c0/ f)
优点:截面弯矩很小或无弯矩; 缺点:曲线杆件施工复杂。
.
③桁架: 上弦、下弦承受弯矩;腹杆承受剪力。
其中:M o V A x P 1 (x a 1 )— 对应点的简支梁弯矩
.
Qo
Q
M
P1
φ
DH
HA
VA
•剪力:
其中:
QQ oco sH sin
Q VAP 1–– 对应点的简支梁剪力
— 切线与水平线所成锐角
(由水平向逆时针为正)
+φ -φ
左右
.
Qo M N
P1
φ
DH
y
HA x
•轴力:
VA
N Q s i n H c os
q M
qr
C
d θ
A
r
任意截面内力:
M q2r(1co )so qrdrsin () q2r(1co )sq2r(1co )s0
.
②拱内力计算:
QM
P1
N
D
HA
VA
弯矩:受拉侧做弯矩图; 剪力:垂直于拱轴线的切线(顺时针为正); 轴力:平行于拱轴线的切线(拉为正)。
.
a1
M
P1 D
y HA x
VA
•弯矩:
由 MD0
M V A x P 1 ( x a 1 ) H y 0 M M oH y
C
Mc0q2l /8
l
Mc0 / 6
Mc0 / 6
B
A
C
B
Mc0 / 6
0.207 l 0.586 l 0.207 l
优点:方便,简单; 缺点:截面仍有弯矩。
.
②三铰曲拱:
f MM0Hy (HM c0/ f)
优点:截面弯矩很小或无弯矩; 缺点:曲线杆件施工复杂。
.
③桁架: 上弦、下弦承受弯矩;腹杆承受剪力。
其中:M o V A x P 1 (x a 1 )— 对应点的简支梁弯矩
.
Qo
Q
M
P1
φ
DH
HA
VA
•剪力:
其中:
QQ oco sH sin
Q VAP 1–– 对应点的简支梁剪力
— 切线与水平线所成锐角
(由水平向逆时针为正)
+φ -φ
左右
.
Qo M N
P1
φ
DH
y
HA x
•轴力:
VA
N Q s i n H c os
q M
qr
C
d θ
A
r
任意截面内力:
M q2r(1co )so qrdrsin () q2r(1co )sq2r(1co )s0
第5章三铰拱和悬索.ppt

上一张 下一张 主 页 退 出
2019/10/25 14:39
主 讲:朱占元、李静
上一张 下一张 主 页 退 出
§5-4 三铰拱的合理轴线
当各截面弯矩为零,只受轴力作用,正应力沿 截面均匀分布,拱处于无弯矩状态。这时材料的使 用最经济。在固定荷载作用下使拱处于无弯矩状态
的轴线称为合理拱轴线。
M M 0 Hy 0 y M0
0 A
6 8 3 1 6 3 4kN() 12
VB
VB0
1 69 89 6 12
10kN()
H
M
0 C
466
4.5kN
f
4
(2)内力计算(以x=3m的截面E为例说明)
A、截面E的几何参数
y3
4f l2
x(l x)
44 (12)2
E 的 内 力
M
Z 3
M
0 3
Z
Hy
4 3 4.5 3
1.5kN m
M
y 3
M
0 3
y
Hy
436
4.5 3
7.5kN m
Q3 Q30 cos H sin 40.832 4.50.555 0.83kN
N3 Q30 sin H cos 40.555 4.50.832 5.96kN
第5章 三铰拱和悬索
§5-1 三铰拱的组成和类型
…
§5-2 竖向荷载作用下三铰拱的支座反力
及截面内力计算公式
…
§5-3 三铰拱的受力特性
…
§5-4 三铰拱的合理轴线
铰拱和悬索结构的受力分析

稳定性分析
悬索结构在长期荷载作用 下可能发生屈曲失稳,需 要进行稳定性分析。
悬索结构的优缺点
优点
自重轻、跨越能力强、施工方便、经济性好等。
缺点
对锚固和固定端的构造要求高,易受环境因素影响,如风雨、温度变化等。
03
铰拱与悬索结构的比较
结构形式的比较
铰拱
由拱圈和铰支座组成,通过铰支座将拱圈与基础连接。铰拱 的拱圈在竖向荷载作用下产生弯曲变形,并通过铰支座传递 到基础。
悬索结构
悬索结构适用于大跨度、轻质结构的桥梁和大型工业厂房等建筑结构。由于悬索结构的受力性能较为简单,因此 在设计、施工和维护方面相对较为方便。
04
铰拱和悬索结构的设计与优 化
结构设计的基本原则
稳定性
确保结构在各种工况下 都能保持稳定,不发生
失稳或过大变形。
承载能力
满足结构的承载要求, 保证结构在承受设计载
荷时不会发生破坏。
经济性
在满足功能和安全的前 提下,尽量降低结构的
成本。
耐久性
考虑结构的寿命和耐久 性,确保结构在使用期
限内保持良好性能。
结构优化的方法与技巧
尺寸优化
通过调整结构尺寸,如梁的截 面尺寸、杆的直径等,以实现
最优的结构性能。
形状优化
改变结构的形状,如拱的曲线 形状、梁的弯曲程度等,以改 善结构的受力性能。
优点
铰拱结构具有较好的适应性和灵活性,能够适应地基的不均匀沉降和温度变化 的影响。同时,铰拱结构的构造简单,施工方便,造价相对较低。
缺点
铰拱结构的承载能力相对较低,且在水平推力作用下可能产生较大的位移和剪 切变形,需要采取相应措施进行加固。此外,铰拱结构的抗震性能也较差,需 要进行抗震设计。
第4章-三铰拱和悬索结构的受力分析PPT课件

(10)(0.894)(60)(0.447) 17.88kN
FQE右FQ0E右cosE FHsinE
(50)(0.894)(60)(0.447) 17.88kN
3)轴力计算
FNE左 FN0E左sinE FHcos E
(10)(0.447)(60)(0.894) 58.11kN
FNE右 FN0E右sinE FH cosE
.
26
二、三铰拱的合理拱轴线
1 、合理拱轴线
在固定荷载作用下,使拱处于无弯矩状态的轴线,称为 合理拱轴线。
2 、合理拱轴的数解法
由 MM 0FHy0 得
y M0 FH
上式表明,在固定荷载作用下,三铰拱的合理拱轴
线y与相当简支梁弯矩图的竖标M 0成正比。
.
27
(1)满跨竖向均布荷载
【例4-4】设三铰拱承受沿水平方向均匀分布的竖向荷载, 试求其合理拱轴线。
(1)计算支座反力
由整体平衡条件∑Fy = 0、 ∑MB = 0和∑MA = 0,可分 别求得
F H 0 , F V A F V 0 A , F V B F V 0 B
FH=0是其计算特点之一
(2)计算拉杆内力
取截面I-I之右为隔离体。
由∑MC = 0,得
FS(FVB2 lFP3lCF )/f
FS
M
0 C
f
.
FP FP2 I lC FP3
FH
1
F
EC
AD
f
F
B
拉杆
I
FVA l/2
l/2
FVB
l
FP1 FP2
A
C
DE
F
0 VA
l/2
l
FQE右FQ0E右cosE FHsinE
(50)(0.894)(60)(0.447) 17.88kN
3)轴力计算
FNE左 FN0E左sinE FHcos E
(10)(0.447)(60)(0.894) 58.11kN
FNE右 FN0E右sinE FH cosE
.
26
二、三铰拱的合理拱轴线
1 、合理拱轴线
在固定荷载作用下,使拱处于无弯矩状态的轴线,称为 合理拱轴线。
2 、合理拱轴的数解法
由 MM 0FHy0 得
y M0 FH
上式表明,在固定荷载作用下,三铰拱的合理拱轴
线y与相当简支梁弯矩图的竖标M 0成正比。
.
27
(1)满跨竖向均布荷载
【例4-4】设三铰拱承受沿水平方向均匀分布的竖向荷载, 试求其合理拱轴线。
(1)计算支座反力
由整体平衡条件∑Fy = 0、 ∑MB = 0和∑MA = 0,可分 别求得
F H 0 , F V A F V 0 A , F V B F V 0 B
FH=0是其计算特点之一
(2)计算拉杆内力
取截面I-I之右为隔离体。
由∑MC = 0,得
FS(FVB2 lFP3lCF )/f
FS
M
0 C
f
.
FP FP2 I lC FP3
FH
1
F
EC
AD
f
F
B
拉杆
I
FVA l/2
l/2
FVB
l
FP1 FP2
A
C
DE
F
0 VA
l/2
l
3_4三铰拱

Q2 Q2 cos 2 H sin 2 11 2 3 0.832
0.667
7.5 0.555 0.0025kN 0.003kN
N 2 Q2 sin 2 H cos 2 11 2 3 0.555
2 33 41,sin 2 0555 . ,cos 2 0832 .
例2、设三铰拱承受均匀分布的水压力,试证明其合理轴线是圆弧曲线。
[证明] 设拱在静水压力作用下处于无弯矩状态,然后由平衡条件推导轴线方程。
q
s
D
E
ds R d
M0 0: ND R NE R dR 0
ND NE N
这表明拱在法向均布荷载作用下处于无弯矩状态时,截面的轴力为常数。
MC 11 6 2 6 3 H 7.5kN f 4
M2 M2 Hy2 11 3 2 3 15 . 7.5 3
15 . kN m
tg 2 4 f 2x 1 l l
x 3
4 4 2 3 1 12 12
q=2kN∙m y
1 0 3 4 5
P=8kN
例 1、三铰拱及所受荷载如图
2
所示,拱的轴线为抛物线方程
6 7 8 B
2
y2 x
f=4m H 7.5kN VB 9kN
7.5kN
A
4f y 2 xl x ,计算反力并 l 绘制内力图。
x2=3m VA 11kN
3m 6m 6m
d2y 1 qc y q x qc y 则 2 dx H q y y c 即 H H
结构力学-曲杆和三铰拱-PPT

(5)构造复杂,施工费用高。
三、拱的种类:
三铰拱
两铰拱
无铰拱
吊杆 拉杆
花篮螺丝
带拉杆的三铰拱
带吊杆的三铰拱
四、拱各部分的名称:
§4-1概述
一.三铰拱的基本形式
(一)无拉杆的三铰拱
1.平拱- 两个拱脚铰在同一水平线 2.斜拱-两个拱脚铰不在同一水平线上
(二)有拉杆的三铰拱(弓弦拱)
二. 三铰拱的组成
(4-17)
D
3、剪力计算 VD VAcosφ D P1cosφ D Hsin φD
(VA P1 )cosφ D Hsin φD
0 0 VD VA P1 VA P1
0 VA VD cosφD Hsin φD
HA A VA P1 A VA0 xD D C P2 B
三铰拱计算简图
P1 A VA0
X 0 :
H A HB H
M
B VB0
C
VAl1 P1 (l1 a1 ) Hf 0
1 [VA l1 P1 (l1 a 1 )] f
0 MC H f
HA0 = 0
D
C
P2
H
xK
0 MC VAl1 P1 (l1 a1 )
P C HA
P HB B VB HA=0
A
VA
A VA
B VA
拱结构
曲梁结构
例题4-1 求图4-5a所示圆弧形曲杆任意截面的内力M、V、N。 解:以极坐标φ表示B截面的位置,取图4-5c所示BC部分隔离体, 设B截面的内力分别为Mφ、Vφ、Nφ, 参照图4-5b并考虑到ds=Rdα, 由平衡条件得 ∑MB=0 Mφ=∫S qdsRsin(φ-α) =qR2∫0φsin(φ-α)dα=qR2(1-cosφ) 式 (4-1)
